(完整版)利用轴对称求最短距离问题
13.4轴对称之最短路径问题人教版2024—2025学年八年级上册

13.4轴对称之最短路径问题人教版2024—2025学年八年级上册二、例题讲解例1.如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC,已知线段AB=4,DE=2,BD=8,设CD=x.(1)用含x的代数式表示AC+CE的长;(2)请问点C满足什么条件时,AC+CE最小?最小为多少?(3)根据(2)中的规律和结论,请构图求代数式的最小值.变式1.如图,C为线段BD上一动点,分别过点B,D作AB⊥BD,ED⊥BD,连结AC,EC,已知AB=5,DE=1,BD=8.(1)请问点C什么位置时AC+CE的值最小?最小值为多少?(2)设BC=x,则AC+CE可表示为,请直接写出的最小值为.例2.如图,直线l是一条河,P,Q是两个村庄,欲在l上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是()A.B.C.D.变式1.如图,在⊥ABC中,BA=BC,BD平分⊥ABC,交AC于点D,点M、N 分别为BD、BC上的动点,若BC=10,⊥ABC的面积为40,则CM+MN的最小值为.变式2.如图,等腰三角形ABC的底边BC长为8,面积是24,腰AC的垂直平分线EF分别交AC,AB于E,F点,若点D为BC边的中点,点M为线段EF 上一动点,则⊥CDM的周长的最小值为()A.7B.8C.9D.10变式3.如图,在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.(1)点D的坐标为;(2)若E为边OA上的一个动点,当⊥CDE的周长最小时,求点E的坐标.例3.如图,⊥AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若⊥PMN的周长是6cm,则P1P2的长为()A.6cm B.5cm C.4cm D.3cm变式1.已知点P在⊥MON内.如图1,点P关于射线OM的对称点是G,点P 关于射线ON的对称点是H,连接OG、OH、OP.(1)若⊥MON=50°,求⊥GOH的度数;(2)如图2,若OP=6,当⊥P AB的周长最小值为6时,求⊥MON的度数.变式2.如图,⊥MON=45°,P为⊥MON内一点,A为OM上一点,B为ON上一点,当⊥P AB的周长取最小值时,⊥APB的度数为()A.45°B.90°C.100°D.135°变式3.如图,⊥AOB=30°,P是⊥AOB内的一个定点,OP=12cm,C,D分别是OA,OB上的动点,连接CP,DP,CD,则⊥CPD周长的最小值为.变式4.如图,在五边形中,⊥BAE=140°,⊥B=⊥E=90°,在边BC,DE上分别找一点M,N,连接AM,AN,MN,则当⊥AMN的周长最小时,求⊥AMN+⊥ANM 的值是()A.100°B.140°C.120°D.80°例4.如图,在⊥ABC中,AB=AC,⊥A=90°,点D,E是边AB上的两个定点,点M,N分别是边AC,BC上的两个动点.当四边形DEMN的周长最小时,⊥DNM+⊥EMN的大小是()A.45°B.90°C.75°D.135°变式1.如图,在平面直角坐标系中,已知点A(0,1),B(4,0),C(m+2,2),D(m,2),当四边形ABCD的周长最小时,m的值是()A.B.C.1D.变式2.如图,在四边形ABCD中,⊥B=90°,AB⊥CD,BC=3,DC=4,点E 在BC上,且BE=1,F,G为边AB上的两个动点,且FG=1,则四边形DGFE 的周长的最小值为.例5.如图,⊥AOB=20°,点M、N分别是边OA、OB上的定点,点P、Q分别是边OB、OA上的动点,记⊥MPQ=α,⊥PQN=β,当MP+PQ+QN最小时,则β﹣α的值为()A.10°B.20°C.40°D.60°变式1.如图,∠AOB=20°,M,N分别为OA,OB上的点,OM=ON=3,P,Q分别为OA,OB上的动点,求MQ+PQ+PN的最小值。
利用轴对称求两点一线型最短距离

利用轴对称求“两点一线”型最短距离几何模型:模型:“两点一线”模型条件:如图,A、B是直线l同旁的两个定点.+的值最小.问题:在直线l上确定一点P,使PA PB方法:作点A关于直线l的对称点A',连结A B'交l于点P,+=的值最小.则PA PB A B'模型应用:一. 两点一线间的对称二.三角形中的对称1.如图,在△ABC中,AC=BC=2,∠ACB=90°,D是BC边上的中点,E是AB边上的一动点,则EC+ED的最小值是__2.如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、AC、BC的中点,点P为线段EF上一个动点,连接BP、GP,则△BPG的周长的最小值是.三.四边形中的对称1.如图,正方形ABCD的边长为8, M在DC上,且DM=2,N是AC上的动点,则DN+MN的最小值为多少?2.如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连结BD,由正方形对称性可知,B与D关于直线AC对称.连结ED交AC于P,则+的最小值是___________;PB PE△是等边三角形,点E在正方形3.如图所示,正方形ABCD的面积为12,ABE+的和最小,则这个最小值为()ABCD内,在对角线AC上有一点P,使PD PEA.B.C.3 D四.圆中的对称1.如图,已知点A 是⊙O 上的一个六等分点,点B 是弧AN 的中点,点P 是半径ON 上的动点,若⊙O 的半径长为1,求AP+BP 的最小值。
2.如图,O ⊙的半径为2,点A B C 、、在O ⊙上,OA OB ⊥,60AOC ∠=°,P 是OB 上一动点,求PA PC +的最小值;五.立体图形中的对称如图是一个没有上盖的圆柱形食品盒,一只蚂蚁在盒外表面的A 处,它想吃到盒内表面对侧中点B 处的食物,已知盒高h =10cm ,底面圆的周长为32cm ,A 距离下底面3cm .请你帮小蚂蚁算一算,为了吃到食物,它爬行的最短路程为 cm .课堂练习: 1.如图,在菱形ABCD 中,对角线AC=6,BD=8,点E 、F 分别是边AB 、BC 的中点,点P 在AC 上运动,在运动过程中,存在PE+PF 的最小值,则这个最小值是 .2.如图,在梯形ABCD 中,AB ∥CD ,∠BAD=90°,AB=6,对角线AC 平分∠BAD ,点E 在AB 上,且AE=2 (AE <AD ),点P 是AC 上的动点,则PE+PB 的最小值是 .3.如图,等边△ABC 的边长为6,AD 是BC 边上的中线,M 是AD 上的动点,E 是AC 边上一点,5.动手操作:在矩形纸片ABCD中,AB=3,AD=5.如图所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点A′在BC边上可移动的最大距离为.6.如图,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为 cm.7.在三角形纸片ABC中,已知∠ABC=90°,AB=6,BC=8.过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的T处,折痕为MN.当点T在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,则线段AT长度的最大值与最小值之和为(计算结果不取近似值).8.如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N 分别是边AB、BC的中点,则PM+PN的最小值是.9.如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若PM+PB 的最小值是3,则AB长为.解答题:1.如图,45AOB∠=°,P是AOB∠内一点,10PO=,Q R、分别是OA OB、上的动点,求PQR△周长的最小值.2.一次函数y kx b=+的图象与x、y轴分别交于点A(2,0),B(0,4).(1)求该函数的解析式;(2)O为坐标原点,设OA、AB的中点分别为C、D,P为OB上一动点,求PC+PD的最小值,并求取得最小值时P点坐标.ABPRQ图3中考题综合演练:1.(1)观察发现:如(a)图,若点A,B在直线l同侧,在直线l上找一点P,使AP+BP 的值最小.做法如下:作点B关于直线l的对称点B',连接AB',与直线l的交点就是所求的点P.再如(b)图,在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小.做法如下:作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这点就是所求的点P,故BP+PE的最小值为.(2)实践运用:如(c)图,已知⊙O的直径CD为4,∠AOD的度数为60°,点B是AD^的中点,在直径CD上找一点P,使BP+AP的值最小,并求BP+AP的最小值.(3)拓展延伸:如(d)图,在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD.保留作图痕迹,不必写出作法.2.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.⑴求证:△AMB≌△ENB;⑵①当M点在何处时,AM+CM的值最小;②当M点在何处时,AM+BM+CM的值最小,并说明理由;3 时,求正方形的边长.⑶当AM+BM+CM的最小值为1。
初二数学上册:利用轴对称求解最短路径问题

初二数学上册:利用轴对称求解最短路径问题一、知识重点1、最短路径问题(1)求直线异侧的两点与直线上一点所连线段的和最小的问题,只要连接这两点,与直线的交点即为所求.(2)求直线同侧的两点与直线上一点所连线段的和最小的问题,只要找到其中一个点关于这条直线的对称点,连接对称点与另一个点,则与该直线的交点即为所求.2、运用轴对称解决距离最短问题运用轴对称及两点之间线段最短的性质,将所求线段之和转化为一条线段的长,是解决距离之和最小问题的基本思路,不论题目如何变化,运用时要抓住直线同旁有两点,这两点到直线上某点的距离和最小这个核心,所有作法都相同.3、利用平移确定最短路径选址解决连接河两岸的两个点的最短路径问题时,可以通过平移河岸的方法使河的宽度变为零,转化为求直线异侧的两点到直线上一点所连线段的和最小的问题.二、经典例子解析【例一】有两棵树位置如图,树脚分别为A,B.地上有一只昆虫沿A—B的路径在地面上爬行.小树顶D处一只小鸟想飞下来抓住小虫后,再飞到大树的树顶C处,问小鸟飞至AB之间何处时,飞行距离最短,在图中画出该点的位置.解:如图,作D关于AB的对称点D′,连接CD′交AB于点E,则点E就是所求的点.【例二】如图所示,点A,B分别是直线l异侧的两个点,在l上找一个点C,使CA+CB最短,这时点C是直线l与AB的交点解:如图,【例三】如图所示,点A,B分别是直线l同侧的两个点,在l上找一个点C,使CA+CB最短。
解:先作点B关于直线l的对称点B′,则点C是直线l与AB′的交点.为了证明点C的位置即为所求,我们不妨在直线上另外任取一点C′,连接AC′,BC′,B′C′,证明AC+CB<AC′+C′B.如下:证明:由作图可知,点B和B′关于直线l对称,所以直线l是线段BB′的垂直平分线.因为点C与C′在直线l上,所以BC=B′C,BC′=B′C′.在△AB′C′中,AB′<AC′+B′C′,所以AC+B′C<AC′+B′C′,所以AC+BC<AC′+C′B【例四】在图中直线l上找到一点M,使它到A,B两点的距离和最小解:如图,作点B关于直线l的对称点B′;连接AB′交直线l于点M.则点M即为所求的点.【例五】如图,小河边有两个村庄A,B,要在河边建一自来水厂向A 村与B村供水。
轴对称最短路线问题原理

轴对称最短路线问题原理
一、问题描述
轴对称最短路线问题,即求平面上两点间沿轴对称线走的最短距离。
二、问题解法
1. 构造对称轴
首先需要找到两点的对称轴,对称轴的构造方法有多种,常用的有以
下两种:
(1)连接两点,垂直平分线即为对称轴。
(2)以两点为圆心,以它们之间的距离为半径,画两个圆;两圆的交
点就是对称轴。
2. 沿对称轴转换
对称轴将平面分为两个对称部分,假设起点在对称轴左侧(或右侧),求出终点在对称轴右侧(或左侧)的最短距离,即为要求的轴对称最
短路线。
3. 求最短距离
最短距离可以使用最短路算法(如 Dijkstra 算法、Bellman-Ford 算法等)来计算。
三、应用领域
轴对称最短路线问题常见于自动化生产线、机器人运动等领域,在这
些领域中,机器人需要在不碰撞的情况下从一个点到达另一个点,同
时保证走的路径最短。
该问题的解决方法可以为机器人运动路径规划
提供参考。
利用轴对称求最短距离精修订

分析:由题意知:首先找点D或者点E关于AC所在直线的对称点。由正方形的轴对称性不难发现:点B即是点D关于直线AC的对称点,则连接BE与线段AC的交点即为P点。那么PD+PE的最小值实际上就是线段BE的长度,BE=2。
(2)、以正方形为媒介的最短距离问题:
如下图,正方形ABCD边长为2,△ABE为等边三角形,且点E在正方形ABCD内部,在对角线AC上找一点P,使PD+PE最小,则这个最小值为多少?
(3)、以圆为媒介的最短距离问题:
如下图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,
∠AOB=60°,P是OB上一动点,求PA+PC的最小值
(4)、以二次函数为媒介的最短距离:
如下图,抛物线y=x^2+2x-3与x轴交与A、B两点,与y轴交与点C,对称轴上存在一点P,使△PBC周长最小,求P点坐标。
三、巩固加深:
(5)、以三角形为媒介的最短距离问题:
如下图,在锐角△ABC 中,AB=4,∠BAC=45°,∠BAC的角平分线交BC于D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少
分析:由AD是∠BAC的角平分线得,点N关于直线AD对称的点N′一定在线段AC上,则直线AD是线段NN′的垂直平分线,则MN=MN′,则求BM+MN的最小值就是求BM+MN′的最小值。易知点B、M、N′三点共线时BM+MN′最小,根据“点到直线上点的距离中垂线段最短”得:过点B作AC的垂线,垂足为N′′,则BN′′的长度就是BM+MN′的最小值,也就是BM+MN的最小值。由△ABN′′为等腰直角三角形,AB=4立得。
(完整版)利用轴对称求最短距离问题

利用轴对称求最短距离问题基本题引入:如图(1),要在公路道a上修建一个加油站,有A,B两人要去加油站加油。
加油站修在公路道的什么地方,可使两人到加油站的总路程最短?你可以在a上找几个点试一试,能发现什么规律?·B ·A·B·Aa·B·Aa·A′图1M·A′MNa 图2图3思路分析:如图2,我们可以把公路a近似看成一条直线,问题就是要在a上找一点M,使AM与BM的和最小。
设A′是A的对称点,本问题也就是要使A′M与BM的和最小。
在连接A′B的线中,线段A′B最短。
因此,线段A′B与直线a的交点C的位置即为所求。
如图3,为了证明点C的位置即为所求,我们不妨在直线a上另外任取一点N,连接AN、BN、A′N。
因为直线a是A,A′的对称轴,点M,N在a上,所以AM= A′M,AN= A′N。
∴AM+BM= A′M+BM= A′B在△A′BN中,∵A′B<A′N+BN∴AM+BM<AN+BN即AM+BM最小。
点评:经过复习学生恍然大悟、面露微笑,不一会不少学生就利用轴对称知识将上一道中考题解决了。
思路如下:②∵BC=9(定值),∴△PBC的周长最小,就是PB+PC最小.由题意可知,点C关于直线DE的对称点是点A,显然当P、A、B三点共线时PB+PA最小.此时DP=DE,PB+PA=AB.由∠ADF=∠FAE,∠DFA=∠ACB=90°,得△DAF∽△ABC.EF∥BC,1159AB=,EF=.∴AF∶BC=AD∶AB,即6∶9=AD∶15.∴AD=10.Rt△ADF22292525中,AD=10,AF=6,∴DF=8.∴DE=DF+FE=8+=.∴当x=时,△PBC的周长222得AE=BE=最小, y值略。
数学新课程标准告诉我们:教师要充分关注学生的学习过程,遵循学生认知规律,合理组织教学内容,建立科学的训练系统。
使学生不仅获得数学基础知识、基本技能,更要获得数学思想和观念,形成良好的数学思维品质。
初中数学轴对称最短路径问题

在直线 l1 、 l2 上分别求 点 M 、N ,使四边形 PQMN 的周⻓长最小小。
分别作点 Q 、P 关于直线 l1 、l2 的 对称点 Q'和 P' 连 Q'P',与两直 线交点即为 M,N.
两点之间线段最短 四边形 PQMN 周⻓长的 最小小值为线段 Q'P'的 ⻓长。
【问题 5】“造桥选址” 作法
使 AM+MN+NB 的值最
小小.
【问题 9】
作法
作图
连 AB,作 AB 的 中垂线与直线 l 在直线 l 上求一一点 P,使 的交点即为 P.
的值最小小 .
【问题 10】
作法
作图
2
两点之间线段最短. AM+MN+BN 的最小小值 为 A'B+MN.
原理理
两点之间线段最短. AM+MN+BN 的最小小值 为 A''B+MN.
4.如图,在锐⻆角△ABC 中,AB=4 ,∠ BAC=45°,∠ BAC=45°,∠ BAC 的平分线交 BC 于 点 D,M、N 分别是 AD 和 AB 上的动点,则 BM+MN 的最小小值是__________。
5.如图,Rt△ABC 中,∠ C=90°,∠ B=30°,AB=6,点 E 在 AB 边上,点 D 在 BC 边 上(不不与点 B、C 重合),且 ED=AE,则线段 AE 的取值范围是__________。 6.如图,∠ AOB=30°,点 M、N 分别在边 OA、OB 上,且 OM=1,ON=3,点 P、Q 分 别在边 OB、OA 上,则 MP+PQ+QN 的最小小值是_________.(注“勾股定理理”:直⻆角三⻆角 形中两直⻆角边的平方方和等于斜边的平方方,即 Rt△ABC 中,∠ C=90°,则有 AC 2 + BC 2 = AB 2) 7.如图,三⻆角形△ABC 中,∠ OAB=∠ AOB=15°,点 B 在 x 轴的正半轴,坐标为 B( 6 , 0).OC 平分∠ AOB,点 M 在 OC 的延⻓长线上,点 N 为边 OA 上的点,则 MA+MN 的最 小小值__________。 8.已知 A(2,4)、B(4,2).C 在 y 轴上,D 在 x 轴上,则四边形 ABCD 的周⻓长最小小值 为__________。
轴对称中的最短路径问题

分析:此题的出题背景就是角。
此题主要利用了两点之间线段最短的性质通过轴对称图形的性质确定三角形的另两点.
分别以直线OX、OY为对称轴,作点P的对应点P1与P2,连接P1P2交OX于M,交OY于N,那么PM+MN+NP最短.
例4.如图,荆州古城河在CC′处直角转弯,河宽均为5米,从A处到达B处,须经两座桥:DD′,EE′〔桥宽不计〕,设护城河以及两座桥都是东西、南北方向的,A、B在东西方向上相距65米,南北方向上相距85米,恰当地架桥可使ADD′E′EB的路程最短,这个最短路程是多少米?
分析:
这就是“造桥选址问题〞
解:作AF⊥CD,且AF=河宽,
作BG⊥CE,且BG=河宽,
连接GF,与河岸相交于E′、D′.
作DD′、EE′即为桥.
证明:由作图法可知,AF∥DD′,AF=DD′,
那么四边形AFD′D为平行四边形,
于是AD=FD′,
同理,BE=GE′,
由两点之间线段最短可知,GF最小;
即当桥建于如下图位置时,ADD′E′EB最短.
例5.如图,当四边形PABN的周长最小时,a= 。
分析:
此题中的PN就相当于“造桥选址问题〞中的桥,其思路与上题是一样的。
通过构造平行四边形和轴对称将折线转之和最短转化为两点之间线段最短.
至于“抛物线〞“折〞转“直〞,再利用“两点之间线段最短〞这一性质来解决。
利用图形的对称性(轴对称)求最短路径问题
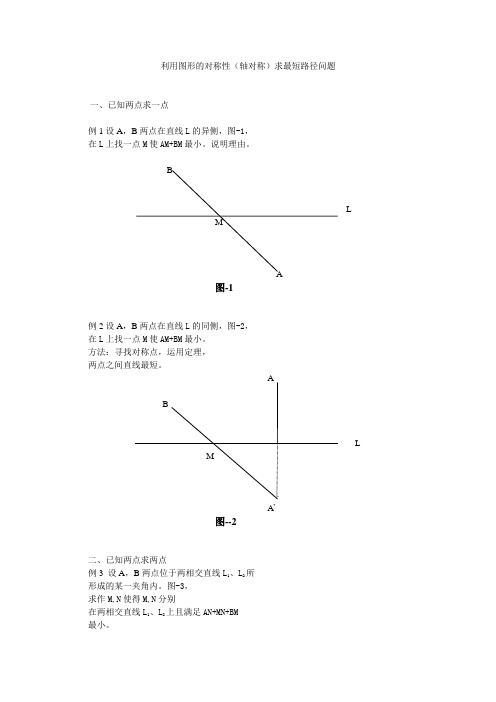
利用图形的对称性(轴对称)求最短路径问题一、已知两点求一点例1设A,B两点在直线L的异侧,图-1,在L上找一点M使AM+BM最小。
说明理由。
BLMA图-1例2设A,B两点在直线L的同侧,图-2,在L上找一点M使AM+BM最小。
方法:寻找对称点,运用定理,两点之间直线最短。
ABLMA’图--2二、已知两点求两点例3 设A,B两点位于两相交直线L1、L2所形成的某一夹角内。
图-3,求作M,N使得M,N分别在两相交直线L1、L2上且满足AN+MN+BM最小。
L1B’. AM . BL2NA’图--3例4 设P,Q两点位于锐角 ABC的BC边上,有两动点M,N分别位于另外两边上,图-4,求作M,N使四边形PQNM的周长最短。
P’ BM PQCA N图--4Q’三、已知一点求两点例5 点P位于三角形的某一边上,动点M,N分别位于另外两边上。
图-5,试作M,N使得❒PMN周长最短。
P’ BPMA N CP’’图—5例6 点P位于两相交直线L1,L2所形成的夹角内,动点M,N分别位于两直线上。
图-6,试作M,N使得❒PMN周长最短。
L2PML1N图-6我们将这些情况放在直角坐标系下考虑。
第一种情况:设A,B两点都在第一象限,直线L与X轴重合,M点在X轴上,且使AM+BM最小。
求(1)M点的坐标。
(2)AM+BM的长度。
第二种情况设A,B两点,B点在第Ⅰ象限,M,N分别在Y轴,X轴上,A点分别在第Ⅰ象限,第Ⅱ象限,第Ⅲ象限,第Ⅳ象限时,试求(1)M,N的坐标,使得AM+MN+BN最小,并求出最小值。
(2)两动点M,N到达何处时,四边形AMNB周长最短。
Y训练题1.已知,AB是圆O的直径,P、Q是圆O上的两点,且直线PQ//AB,M是直径AB是上动点,试问:∆PQM周长最短时,M点处于何处?并证明。
A B【思路】由于三角形∆PQM的一边PQ是定长,因此要使它的周长最短就是要求动点M到点P、Q的距离之和最短。
利用图形的对称性,作Q关于直线AB的对称点Q’,连接PQ’,它与AB相交于M即为所求。
最短路径问题最短路径(完整版)4

3.如图,已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上 有一点B,当△PAB的周长取最小值时,求∠APB的度数. 解:如图,依题意,分别作点P关于ON、OM的 对称点P1、P2,连接P1P2交ON于点B,交OM于
点A,依次连接A、B、P,此时△PAB的周长为
最小值.
祝你学业有成
角形,就是最短路径。
求解原理 两点之间,线段最短
A1
m
B A
C
n
A2
探索新知
知识点1 将军饮马问题
例1 如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点
,AD=5,F是AD边上的动点,则BF+EF的最小值为( )
A.7.5
B.5
C.4
D.不能确定
E BF
EF B
E BF
探索新知
知识点1 将军饮马问题
l
A
问
题
将两地抽象为A、B两个 点,将河抽象为直线l .
B 数 学 问 题
引例
将两地抽象为A、B两个点,将河抽象为直线l .
A
问题一 你能用自己的语言把问题抽象为
l
数学问题吗?
C B
连接AB,与l 交于C点
在直线l 上找一点C,使AC+BC最短
问题二 点C应该在哪里? 为什么呢?
两点之间线段最短
知识点1 将军饮马问题
例1 如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点
,AD=5,F是AD边上的动点,则BF+EF的最小值为(B )
A.7.5
B.5
C.4
D.不能确定
【解析】∵△ABC为等边三角形,D是BC边的中点,∴
利用轴对称求最短距离

利用轴对称求最短距离轴对称知识在近来的中考题中,经常出现,笔者浏览最近几年各地的中考试题,发现各地中考试题除考察轴对称图形的基本知识和性质,还考察了利用轴对称知识解决最短距离问题,这类问题在各地中考试题中,屡见不鲜,如何利用轴对称的性质解决最短距离问题呢?根据本人多年从事初三数学教学工作的一些体会。
概括一些一些常见的题型。
一、基础知识如图直线l 同侧有两点A 、B ,在直线l 上找点P ,使得PA+PB 最短,并简要说明理由。
解:作点关于直线l 的对称点A ′,连A ′B 交直线l 于点P,则点P 即为所求,此时PA+PB=PA ′+PB= A ′B 。
A 1二、典型例题:A 组(1)以菱形为载体的最短距离问题:如图所示,菱形ABCD 中, ∠ BAD=60°,AB=4,M 是AB 的中点,P 是对角线AC 上的一个动点,则PM+PB 的最小值是_________。
解:∵菱形ABCD 是以AC 为对称轴的轴对称图形。
∴点B 关于直线AC 的对称点为点D,ABLP连接DM 交AC 于点P,则PM+PB 的最小值即为线段DM,此时DM=32 ∴PM+PM 的最小值为32.(2)以矩形为载体求最短距离问题在矩形ABCD 中,AB=2,AD=4,E 为为边CD 中点。
P 为边BC 上的任一点,求PA+EP 的最小值。
解:作点A 关于BC 的对称点A ′,连A ′E 交BC 于点P,则点P 为所求,此时PA+PE 的最小值即为A ′E,过点E ,作EF ⊥AB , A ′E=2243 =5 ∴PA+PE 的最小值为5。
MA A 1ED如图所示,正方形ABCD 的边长为2,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上找一点P,使PD+PE 最小,则这个最小值为_________.解:∵正方形ABCD 是以AC 为对称轴的轴对称图形。
∴点B 关于点D 关于AC 对称 ∵BE 即为PD+PE 的最小值 ∴PD+PE 的最小值为2(4) 以圆形为载体的最短距离问题:如图,⊙O 的半径为2,点A 、B 、C 在⊙O 上,OA ⊥OB, ∠ABC=60°,P 是OB 上一动点,求PA+PC 的最小值。
(完整版)利用轴对称求最短距离

利用轴对称求最短距离一、问题引入:1、如下图,在直线异侧各有点A、B,在直线上找一点p,使PA+PB最小。
分析:根据“两点之间线段最短”,可知:连接AB,与直线的交点即为P点.此基本类型为:一线(直线)两定点(点A、B)。
分析:作点A关于直线的对称点A′,连接AA′,则直线就是线段AA′的垂直平分线,根据“垂直2、如下图,在直线同侧各有点A、B,在直线上找一点p,使平分线上一点到线段两PA+PB最小。
端点的距离相等”可得,直线上任一点到点A的距离都等于到点A′的距离。
事实上,这个问题就可以转化成:在直线异侧各有点A′、B,在直线上找一点p,使PA′+PB最小。
即:一线两定点的问题。
由(1)得,连接BA′,与直线的交点即为点P。
分析:由题意知:首先找二、典型例题:点B或者点M关于AC所(1)、以菱形为媒介的最短距离问题:在直线的对称点。
由菱形如下图,菱形ABCD中,∠BAD=60°,AB=4,点M是AB中点,的轴对称性不难发现:点P是对角线AC上的一个动点,则PM+PB的最小值是多少?D即是点B关于直线AC的对称点,则连接DM与线段AC的交点即为P点。
那么PM+PB的最小值实际上就是线段DM的长度分析:由题意知:首先找(2)、以正方形为媒介的最短距离问题:点D或者点E关于AC所如下图,正方形ABCD边长为2,△ABE为等边三角形,且点E在直线的对称点。
由正方在正方形ABCD内部,在对角线AC上找一点P,使PD+PE最小,形的轴对称性不难发现:则这个最小值为多少?点B即是点D关于直线AC的对称点,则连接BE与线段AC的交点即为P点。
那么PD+PE的最小值实际上就是线段BE的长度,BE=2。
分析:由题意知:首先找(3)、以圆为媒介的最短距离问题:点A或者点C关于OB所如下图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,在直线的对称点。
由圆的∠AOB=60°,P是OB上一动点,求PA+PC的最小值轴对称性不难发现:延长AO交圆于点A′,则点A′即是点A关于直线OB的对称点,则连接CA′与线段OB的交点即为P点。
(完整版)利用轴对称求最短距离[1]
![(完整版)利用轴对称求最短距离[1]](https://img.taocdn.com/s3/m/62c2a46e240c844768eaee60.png)
④ 如图所示,在/ AOB 的边AO , BO 上分别找一点 E , F 使得DE + EF + CF 最小.分别 过点C , D 作关于AO , BO 的对称点 DC ',连接D C ',并与AO , BO 分别交于点 E , F , 此时DE + EF + CF 最小,则点E , F 即为所求.最短路径问题 和最小【方法说明】 “和最小”问题常见的问法是,在一条直线上面找一点,使得这个点与两个定点距离 的和最小(将军饮马问题)•如图所示,在直线 直线AB 与直线I 的交点时,PA + PB 最小. l 上找一点 P 使得PA + PB 最小.当点P 为 B 4P , B' 【方法归纳】 ①如图所示,在直线I 上找一点B 使得线段AB AB 即为所求.最小•过点A 作AB 丄I ,垂足为B ,则线段 ②如图所示,在直线 BB 与直线I 交于点 I 上找一点P 使得PA + PB 最小.过点B 作关于直线I 的对称点B P ,此时PA + PB 最小,则点P 即为所求. B a p. B'③如图所示,在/ AOB 的边AO , BO 上分别找一点 C , D 使得PC + CD + PD 最小.过点P 分别作关于 AO , BO 的对称点E , F ,连接EF ,并与AO , BO 分别交于点 C , D ,此时PC + CD + PD 最小,则点C , D 即为所求.BA D' A⑤如图所示,长度不变的线段CD在直线I上运动,在直线I上找到使得AC + BD最小的CD的位置.分别过点A, D作AA 7/ CD , DA '// AC, AA '与DA '交于点A',再作点B关于直线I的对称点B ',连接A'B与直线I交于点D 7,此时点D'即为所求.0 Ir f f-A'D D'B'1⑥如图所示,在平面直角坐标系中,点P为抛物线(y= -x2) 上的一点,点 A (0, 1 )在y 轴正半轴.点P在什么位置时PA+ PB最小?过点B作直线I: y=- 1的垂线段BH BH ' 与抛物线交于点P',此时PA+ PB最小,则点P即为所求.1.(13广东)已知二次函数y= x2—2mx + m2- 1.(1)当二次函数的图象经过坐标原点0( 0, 0)时,求二次函数的解析式;(2)如图,当m = 2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;(3)在(2)的条件下,x轴上是否存在一点P,使得PC + PD最短?若P点存在,求出P 点的坐标;若P点不存在,请说明理由.A D' A【思路点拨】(1)由二次函数的图象经过坐标原点0(0, 0),直接代入求出m的值即可;(2)把m= 2代入求出二次函数解析式,令x= 0,求出y的值,得出点C的坐标;利用配方法或顶点坐标公式求出顶点坐标即可;(3)根据当P、C、D共线时根据“两点之间,线段最短”得出PC + PD最短,求出CD 的直线解析式,令y= 0,求出x的值,即可得出P点的坐标.【解题过程】解:(1)•••二次函数的图象经过坐标原点O (0,0),•••代入二次函数y= x2—2mx + m2—1,得出:m2— 1 = 0,解得:m=± 1,•••二次函数的解析式为:y= x2—2x或y= x2+ 2x;(2)• m= 2,•••二次函数y= x2—2mx + m2—1 得:y = x2—4x + 3 =(x—2)2—1,•抛物线的顶点为:D (2,—1),当x= 0 时,y= 3,「. C 点坐标为:(0,3),• C (0,3)、D (2,—1);(3)当P、C、D共线时PC+ PD最短,【方法一】• C (0,3)、D (2,—1),设直线CD的解析式为y= kx + 3,代入得:2k+ 3 =—1,• k=—2,「.y=—2x + 3,当y= 0时,一2x+ 3= 0,解得x= 3,• PC + PD最短时,P点的坐标为:P (|,0).【方法二】过点D作DE丄y轴于点E,•PO〃DE,• DO=CO,• P0=4 解得:PO=2,•PC + PD最短时,P点的坐标为:P (2,0).12. (11荷泽)如图,抛物线 y = ?x 2+ bx -2与x 轴交于A , B 两点,与y 轴交于C 点,且A (-1, 0).(1)求抛物线的解析式及顶点 D 的坐标;(2) 判断△ ABC 的形状,证明你的结论;(3) 点M ( m , 0)是x 轴上的一个动点,当 MC + MD 的值最小时,求 m 的值.【思路点拨】(1) 把点A 的坐标代入求出b 的值,即可得出抛物线的解析式,通过配方法即可求出顶点 D 的坐标;(2)观察发现厶ABC 是直角三角形,可以通过勾股定理的逆定理证明.由抛物线的解析式,分别求出点B , C 的坐标,再得出AB , AC , BC 的长度,易得AC 2+ BC 2= AB 2,得出△ ABC 是直角三角形;(3) 作出点C 关于x 轴的对称点C',连接C'D 交x 轴于点M ,根据“两点之间,线段最 短”可知MC + MD 的值最小.求出直线 C'D 的解析式,即可得出点 M 的坐标,进而求出 m 的值. 【解题过程】解:(1 )• ••点A (- 1, 0)在抛物线 y =护+ bx —2 上,1X 2(—1 ) 2+ b X(— 1)— 2=0,解得 . 3b 一 3,-25) 抛物线的解析式为1 2 y=2x2-3 1/3、-?x—2=(x—p2 25—8 ,•顶点D的坐标为 (j,(2) 当x= 0 时y=—2,. • C (0,—2), OC = 2 .当y= 0 时,|x2—|x—2= 0,• •• X1=—1 , X2=4, • B(4, 0), • OA = 1 , OB = 4,AB = 5.•/ AB 2= 25, AC 2 = 0A 2+ 0C 2= 5, BC 2= 0C 2+ OB 2= 20,「. AC 2 + BC 2 = AB 2. •••△ ABC 是直角三角形.(3)作出点C 关于x 轴的对称点C',贝U C ' ( 0, 2), 0C = 2,连接C 'D 交x 轴于点M ,根据轴对称性及两点之间线段最短可知, MC + MD 的值最小.【方法一】x + 2.24• m =41.41 24.•.当 y = 0 时,—祛 + 2= 0, x = 41 【方法二】 设抛物线的对称轴交 x 轴于点E .•/ ED // y 轴,•/ OC 'M = / EDM ,/ C'OM =Z .OM = OCJ • EM = ED , 2 24 = ,…m =25 41 .DEM C 'OMDEM .设直线C D 的解析式为y = kx + n ,则 n = 2 |k + n 一 25 解得: n = 2k =-芸.y = 4112。
用轴对称求最短距离

用轴对称求最短距离最值问题,也就是最大值和最小值问题,这类问题出现的试题,内容丰富,知识点多,涉及面广,解法灵活多样,本文举例介绍一些常见的求解方法,供读者参考。
例1. (湖北潜江)如图1,小河边有两个村庄A、B.要在河边建一自来水厂向A村与B村供水.(1)若要使厂部到A、B村的距离相等,则应选择在哪建厂?(2)若要使厂部到A、B村的水管最省料,应建在什么地方?分析(1)到A、B两点距离相等,可联想到“线段垂直平分线上的点到线段两端点的距离相等”.(2)要使厂部到A村、B村的距离和最短,可联想到“两点之间线段最短”.解:(1)如图2,取线段AB的中点G,过中点G画AB的垂线,交EF与P,则P到A、B的距离相等.(2)如图3,画出点A关于河岸EF的对称点A′,连结A′B交EF于P,则P到AB的距离和最短.点评:如果我们注意一下,在我们的生活中有很多都利用了轴对称,如果平时多观察、多思考,就会发现轴对称还可以帮助我们解决问题.例2. 如图3,两条公路OA、OB相交,在两条公路的中间有一个油库,设为点P,如在两条公路上各设置一个加油站,,请你设计一个方案,把两个加油站设在何处,可使运油车从油库出发,经过一个加油站,再到另一个加油站,最后回到油库所走的路程最短.分析这是一个实际问题,我们需要把它转化为数学问题,经过分析,我们知道此题是求运油车所走路程最短,OA与OB相交,点P在∠AOB内部,通常我们会想到轴对称,分别做点P关于直线OA和OB的对称点P1、P2,连结P1P2分别交OA、OB于C、D,C、D两点就是使运油车所走路程最短,而建加油站的地点,那么是不是最短的呢?我们可以用三角形的三边关系进行说明.解:分别做点P关于直线OA和OB的对称点P1、P2,连结P1P2分别交OA、OB于C、D,则C、D就是建加油站的位置.若取异于C、D两点的点,则由三角形的三边关系,可知在C、D两点建加油站运油车所走的路程最短.点评:在这里没有详细说明为什么在C、D两点建加油站运油车所走的路程最短,请同学们思考弄明白。
8.3 轴对称之最短路径问题

8.3 轴对称之最短路径问题破解策略最短路径问题通常会转化为“两点之间,线段最短”来解决,而轴对称是实现这一转化的有效方法之一.常见的题型如下.1.两点在一条直线异侧如图,点A ,B 在直线l 的两侧.(1)在直线l 上找一点P ,使得P A +PB 最小.作法:如图,连接AB ,与直线l 的交点即为所求点P .(2)在直线l 上找一点P ,使得PA PB -最小.作法:如图,连接AB ,作AB 的垂直平分线,与直线l 的交点即为所求点P .2.两点在一条直线同侧如图,点A ,B 在直线l 的同侧.(1)在直线l 上找一点P ,使P A +PB 最小.作法:如图,作点B 关于直线l 的对称点B ,连接AB 1,与直线l 的交点即为所求点P .(2)在直线l 上找一点P ,使得PA PB -最小.作法:如图,连接AB ,作AB 的垂直平分线,与直线l 的交点即为所求点P .llll(3)在直线l 上找一点P ,使得PA PB 最大.作法:如图,作:直线AB ,与直线l 的交点即为所求点P .(4)在直线l 上找两点P 、Q (PQ 的长度等于已知线段a 的长度),使得AP +PQ +QB 是最小.作法:如图,先将点B 向若平移a 个单位长度到点B 1,再作B 1关于直线l 的对称点B 2,连接AB 2,与直线l 的交点即为所求点P ,然后将点P 向右平移a 个单位长度,所得点即为点Q .3.一点在角的内部如图,点P 在∠AOB 的内部.(1)分别在边OA ,OB 上确定点M ,N 使得PM +MN +NP 最小.作法,如图,分别作点P 关于OA ,OB 的对称点P 1,P 2,连接P 1P 2,与OA ,OB 的交点即为所求的点M 、N .(2)分别在边OA ,OB 上确定点M ,N ,使得PM +MN 最小.作法:如图,作点P 关于OA 的对称点P 1,过点P 1作OB 的垂线,与OA ,OB 的交点即为所求的点M ,N .ll P al例题讲解例1 如图,A ,B 两点在直线MN 的同侧,AC ∠MN 于点C ,BD ∠MN 于点D ,点P 在直线MN 上运动,若AC =16,BD =10,CD =8,则PA PB -的最大值等于____.分析 显然PA PB -的最大值即为线段AB 的长,只需过点B 作AC 的垂线,构成直角三角形求AB 的长即可.解答例2 如图,等边∠ABC 的面积为P 、Q 、R 分别为边AB ,BC ,AC 上的动点,则PR +QR 的最小值是____.分析 点R 在AC 上,而点P 、Q 在AC 的同侧,故作点P 关于AC 的对称点P ',当点P ',R ,Q 三点共线且P Q '⊥BC 时,PR +QR 取最小值.解答例3 如图,AB ∠BD 于点B ,DE ⊥BD 于点D ,C 为线段BD 上一动点,连接AC ,CE ,已知AB =5,DE =2,BD =12,设CD =x .(1)用含x 的代数式表示AC +CE 的长;(2)求AC +CE 的最小值;ABP C D M NAB CPRQ(3)解答例4 如图,在四边形ABCD 中,∠BAD =120°,∠B =∠D =90°,在BC ,CD 上各找一点,分别为点M ,N ,使得∠AMN 的周长最小,则此时∠AMN +∠ANM 的度数为____.分析 点A 在∠BCD 内部,作点A 关于∠BCD 两边的对称点A 1,A 2,连接A 1A 2,则A 1A 2即为∠AMN 周长的最小值.解答例5 如图,长为1的线段AB 在x 轴上移动,点C (0,1),D (0,2)在y 轴上,则AC +BD 的最小值是____.分析 AB 为x 轴上的定线段,点C ,D 在x 轴同侧,故作点C 关于x 轴的对称点C ',将点D 沿x 轴负方向平移AB 长至点D ',则C D ''的长即为AC +BD 的最小值.解答:例6 如图,∠MON =30°,点A ,D 分别在OM ,ON 上,且OA =2,OD =4,C ,B 分别为OM ,ON 上任意一点,则折线AB -BC -CD 的最短长度为____.分析 线段和差的最值问题通常都转化为“两点之间线段最短”的问题,可利用轴对称将分散的线段变成两定点间的折线,然后再化“折”为“直”即可.解答例7 如图,在△ABC 中,AC ⊥BC ,∠B =30°,E ,F 是线段AB 的三等分点,P ,Q 分别是线段BC ,AC 上的动点,若AC =3,则四边形EPQF 周长的最小值是解答例8 如图,在边长为1的正方形ABCD 中,点E ,F ,G ,H 分别是边AB ,BC ,CD ,DA 上的点,且3AE = EB ,有一只蚂蚁从点E 出发,经过点F ,G ,H ,最后回到点E ,则蚂蚁所走的最短路程是解答进阶训练1.如图1,在Rt △ABC 中,∠ACB =90°,AC =BC =4,D ,E 分别是AB ,AC 的中点,在CD 上找一点P ,使P A +PE 最小,则这个最小值是2.如图2,P 为∠AOB 内部的一点,且OP =2,E ,F 分别是OA ,OB 上的动点,若△PEF 周长的最小值等于2,则∠AOB =3.已知y =y 的最小值是4.如图3,在平面直角坐标系中有四个点A (-6,3),B (-2,5),C (0,m ),D (n ,0),当四边形ABCD 的周长最短时,m +n =5.如图4,在Rt△ABC中,∠ACB=90°,AC=BC=4,∠BAC的平分线交BC于点D,若P,Q分别是AC,AD 上的动点,求CQ+PQ的最小值.6.已知三点A(a,1),B(3,1),C(6,0),且点A在正比例函数12y x的图象上,P为x轴上的动点,当△OAP与△CBP周长之和取最小值时,求点P的坐标.7.如图5,等边△ABC的边长为2,D是边AB的中点,P,Q分别是边BC,AC上的动点,当P,Q的位置在何处时,才能使△DPQ的周长最小?并求出这个最值.8.如图6,正方形ABCD的边长为4,E为边CD的中点,点F在边BC上,且满足BF=3CF,M,N均为对角线BD上的动点,且MN求四边形EMNF周长的最小值.9.如图7,在矩形ABCD中,点E在对角线AC上,满足CE=3AE,P,Q分别为AB,AC上任意的点,若AC=2,BC=1,求折线EP+PQ+QB长的最小值.10.如图8,在平面直角坐标系xOy中,分别以点A(2,3),B(3,4)为圆心,以1,3为半径作⊙A,⊙B ,M,N分别是⊙A,⊙B上的动点,P为x轴上的动点,求PM+PN的最小值.。
轴对称最短路线问题

最短路线问题在直线L上的同侧有两个点A、B,在直线L上有到A、B的距离之和最短的点存在,可以通过轴对称来确定,即作出其中一点关于直线L的对称点,对称点与另一点的连线与直线L 的交点就是所要找的点.1.已知:如图,四边形ABCD中,∠ABC=60°,AB=BC=2,对角线BD平分∠ABC,E是BC的中点,P是对角线BD上的一个动点,则PE+PC的最小值为()A 3B 32C2 D 22.如图,已知A、B两村分别距公路l的距离AA’=10km,BB’=40km,且A’B’=50km.在公路l上建一中转站P使AP+BP的最小,则AP+BP的最小值为()A 100kmB 80kmC 60km D502km 3.如图,矩形ABCD中,AD=5,AB=12,点M在AC上,点N在AB上,则BM+MN的最小值为()A 9 B12 C 12013D14401694.如图,点P为∠AOB内一点,分别作点P关于OA,OB的对称点P1,P2,连接P1,P2交OA于M,交OB于N,若P1P2=6,则△PMN周长为()A 4B 5C 6D 75.如图,∠AOB=30°,∠AOB内有一定点P,且OP=10.在OA上有一点Q,OB上有一点R.若△PQR 周长最小,则最小周长是()A 10B 15C 20D 306.如图,E是正方形ABCD边BC上一点,CE=2,BE=6,P是对角线BD上的一动点,则AP+PE的最小值是()A 82 B.8 C .10 D 以上答案都不对7.如图,一牧童在A处牧马,牧童家在B处,A、B处距河岸的距离AC、BD的长分别为500m和700m,且C、D两地的距离为500m,天黑前牧童从A点将马牵引到河边去饮水后,再赶回家,那么牧童至少要走()A 10029 B.1200 C .1300 D 17008.如图,矩形ABCD中,AB=20,BC=10,若在AB、AC上各取一点N、M,使得BM+MN的值最小,这个最小值为()A 12 2 C 16 D 209.已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一B,当△PAB的周长取最小值时,∠APB的度数是()A.40° B .100°C140° D 50°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
利用轴对称求最短距离问题
基本题引入:如图(1),要在公路道a上修建一个加油站,有A,B两人要去加油站加
油。
加油站修在公路道的什么地方,可使两人到加油站的总路程最短?
使AM与BM的和最小。
设A'是A的对称点,本问题也就是要使A M与BM的和最小。
在连
接A B的线中,线段A B最短。
因此,线段 A B与直线a的交点C的位置即为所求。
如图3,为了证明点C的位置即为所求,我们不妨在直线a上另外任取一点N,连接AN
BN A No
因为直线a是A A'的对称轴,点M,N在a上,所以AM= A M,AN= A N。
••• AM+BM= A M+BM= A B
在厶A BN中,
•/ A B< A N+BN
• AM+B< AN+BN
即AM+BMt小。
点评:经过复习学生恍然大悟、面露微笑,不一会不少学生就利用轴对称知识将上一道
中考题解决了。
思路如下:②••• BC= 9 (定值),•△ PBC的周长最小,就是PB+ PC最小.由题意可知,点C关于直线DE的对称点是点A,显然当P、A B三点共线时PB+ PA最小•此时DP= DE PB+ PA= AB.由/ ADM/ FAE / DFA=Z ACB= 90°,得厶DAF^A ABC. EF// BC,
1 15 9
得AE= BE= AB= , EF= . • AF: BC= AD:AB, 即卩 6 : 9 = AD:15. • AD= 10. Rt△ ADF
2 2 2
9 25 25
中,AD= 10, AF= 6,「. DF= 8. • DE= DF+ FE= 8+ =一. •••当x = 时,△ PBC的周长
2 2 2
最小,y值略。
数学新课程标准告诉我们:教师要充分关注学生的学习过程,遵循学生认知规律,合理
组织教学内容,建立科学的训练系统。
使学生不仅获得数学基础知识、基本技能,更要获得
数学思想和观念,形成良好的数学思维品质。
同时每年的中考题也千变万化,为了提高学生的应对能力,除了进行专题训练外,还要多归纳多总结,将一类问题集中呈现给学生。
一、两条直线间的对称
题目1如图,在旷野上,一个人骑马从A出发,他欲将马引到河al饮水后再到a2饮
水,然后返回A地,问他应该怎样走才能使总路程最短。
点评:这道题学生拿到时往往无从下手。
但只要把握轴对称的性质就能迎刃而解了。
作法:过点A作al的对称点A',作a2的对称点A ,连接A A"交al、a2于B、C,连接BC. 所经过路线如图5: A-B-C-A,所走的总路程为A A"。
第2题图
二、三角形中的对称
题目2 如图,在厶ABC中,AC=BC=2, / ACB=90 ,D是BC边上的中点,E是AB边上的一动点,则EC+ED勺最小值是_______
点评:本题只要把点C、D看成基本题中的A、E两镇,把线段AB看成燃气管道a,问
题就可以迎刃而解了,本题只是改变了题目背景,所考察的知识点并没有改变。
三、四边形中的对称
题目3 如图,正方形ABCD的边长为8, M在DC上,且DM=2,N是AC上的动点,则
DN+MN勺最小值为多少?
点评:此题也是运用到正方形是轴对称图形这一特殊性质,点D关于直线AC的对称点
正好是点B,最小值为MB= 10。
四、圆中的对称
题目4已知:如图,已知点 A 是O O 上的一个六等分点,点 B 是弧AN 的中点,点P 是 半径ON 上的动点,若O O 的半径长为1,求AP+BP 的最小值。
点评:这道题也运用了圆的对称性这一特殊性质。
点
B 的对称点B'在圆上,AB 交ON
于点 p ',由/ AON= 60° , / B ' ON= 30°,/ AOB = 90°,半径长为 1 可得 AB'=2。
当点P 运动到点p '时,此时AP+BP 有最小值为 2
B '
五、立体图形中的对称
题目5如图1是一个没有上盖的圆柱形食品盒,一只蚂蚁在盒外表面的
A 处,它想吃
到盒内表面对侧中点 B 处的食物,已知盒高h = 10cm,底面圆的周长为 32cm, A 距离下底面 3cm.请你帮小蚂蚁算一算,为了吃到食物,它爬行的最短路程为
_cm •
点评:如图2,此题是一道立体图形问题需要转化成平面问题来解决,将圆柱的侧面展 开得矩形EFGH 作出点B 关于EH 的对称点B',作AC 丄GH 于点C,连接A B '。
在Rt △ A B ' C 中,AC= 16, B ' C= 12,求得A B ' = 20,则蚂蚁爬行的最短路程为
20cm 。
通过变式训练既解决了一类问题, 又归纳出了最本质的东西, 以后学生再碰到类似问题 时学生就不会不知所措。
同时变式训练培养了学生思维的积极性和深刻性,
E
* *
/
f
H
*
事 /
/ f
i
*
F J
B
A
/ L
--
C
发展了学生的应
A
第3题图
M
第4题图
第5题图1
B
F
G
第5题图2
变能力。
综上所述,引导学生在熟练掌握书本例题、习题的基础上,进行科学的变式训练,对巩固基础、提高能力有着至关重要的作用。
更重要的是,变式训练能培养和发展学生的求异思
维、发散思维、逆向思维,进而培养学生全方位、多角度思考问题的能力,有助于提高学生分析问题、解决问题的能力。
题目6长方体问题如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C i 处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?
析:展开图如图所示,.25 .. 29 . 37
路线1即为所求。
长、宽、高中,较短的两条边的和作为一条直角边,最
长的边作为另一条直角边,斜边长即为最短路线长。
B i G
i
A 4
B 2 C
AC J二AC=V6"+1乜7;
点E 、F 是否关于AD 对称?若对称,请说明理由。
由学生引申总结以下1―― 4:
1、已知:如图,A B 两点在直线I 的同侧,点 A 与A 关于直线I 对称,连结 AB 交I 于P 点,若
AB =a ,( 1 )求AP+PB (2)若点 M 是直线I 上异于P 点的任意一点,求证:
AM MB AP PB .
2、已知:A B 两点在直线|的同侧,试分别画出符合条件的点
M
(1) 在I 上求作一点M,使得AM BM 最小;
■ B
A ,
I
(2) 在|上求作一点
M,使得 AM BM 最大;
(3) 在I 上求作一点 M,使得AM+BM ft 小。
3、如图,AD 为/ BAC 的平分线,DE 丄AB 于E , DF 丄AC 于F ,那么
4、已知:如图,点P I,P2分别是P点关于/ ABC的两边BA BC的对称点,连接P1P2,分
别交BA BC边于E、D点,若p1 p2=m
(1)求厶PDE的周长;
(2)若M是BA边上异于E的一点,N是BC边上异于D的一点,求证:△ PMN的周长>△ PDE的周长。
轴对称在本题中的主要作用是将线段在保证长度不变的情况下改变位置,要注
意体会轴对称在这方面的应用。
以此作为模型我们可以解决
下列求最小值的问题。
5. _______________________ 如图,菱形ABCD中, AB=2, / BAD=60 , E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是。
分析:首先分解此图形,构建如图5模型,因为E、B在直线AC的同侧,要在AC上找
一点P,使PE+PB最小,关键是找出点B或E关于AC的对称点。
如图6,由菱形的对称性可知点B和D关于AC对称,连结DE此时DE即为PE+PB勺最小值,
E
A
8
C
由/ BAD=60 , AB=AD AE=BE知,
DE
故PE+PB的最小值为3。
P l
C
A。
