北大数学系本科教材
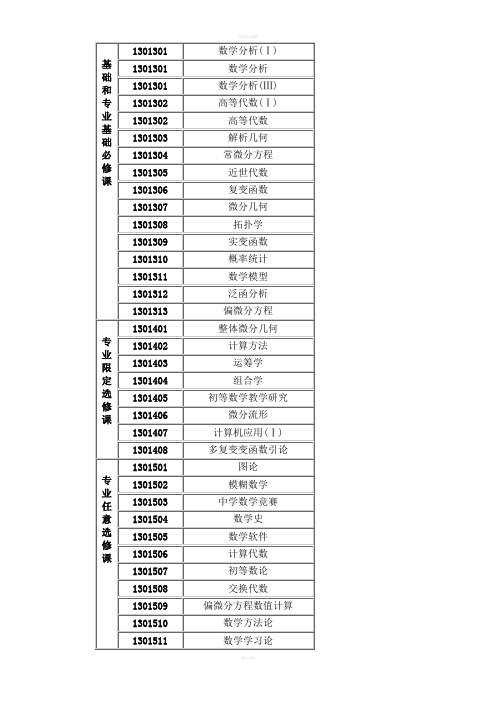
北大数学系本科课程
另外一个版本:北大数学科学学院本科生课程课程号00130011 课程名数学分析(一)课程号00130012 课程名数学分析(二)课程号00130013 课程名数学分析(三)课程号00130031 课程名高等代数(上)课程号00130032 课程名高等代数(下)课程号00130051 课程名解析几何课程号00130061 课程名解析几何习题课课程号00130072 课程名初等数论课程号00130081 课程名常微分方程课程号00130091 课程名计算机原理与算法语言课程号0013010. 课程名计算机实习课程号00130110 课程名复变函数课程号00130120 课程名微分几何学课程号00130130 课程名抽象代数(A)课程号00130140 课程名实变函数论课程号00130150 课程名偏微分方程课程号00130161 课程名拓朴学(一)课程号00130162 课程名拓朴学(二)课程号00130170 课程名泛函分析课程号00130190 课程名微分流形课程号00130201 课程名高等数学(B)(一)课程号00130202 课程名高等数学(B)(二)课程号00130203 课程名高等数学(B)(三)课程号00130221 课程名高等数学(C)(一)课程号00130222 课程名高等数学(C)(二)课程号00130241 课程名高等数学(D)(一)课程号00130242 课程名高等数学(D)(二)课程号00130250 课程名高等数学(E)课程号00130260 课程名线性代数(B)课程号00130270 课程名线性代数(C)课程号00130280 课程名计算方法课程号00130290 课程名汇编语言课程号00130300 课程名数理逻辑及其在人工智能中的应用课程号00130310 课程名数据结构课程号00130320 课程名计算机图形学课程号00130330 课程名数字信号处理课程号00130340 课程名编译原理课程号00130350 课程名抽象代数(B)课程号00130360 课程名代数数论基础课程号00130370 课程名有限群课程号00130380 课程名代数选讲课程号00130390 课程名图论课程号00230020 课程名概率统计(B)课程号00230030 课程名概率统计(C)课程号00230040 课程名普通统计学课程号00230050 课程名概率论课程号00230060 课程名数理统计课程号00230070 课程名测度论和概率论基础课程号00230080 课程名应用多元统计分析课程号00230090 课程名应用随机过程课程号00230100 课程名应用时间序列分析课程号00230110 课程名保险统计学课程号00230120 课程名决策分析课程号00230130 课程名抽样调查课程号00230140 课程名试验设计课程号00230150 课程名统计计算课程号00230160 课程名算法分析与数据结构课程号00230170 课程名图论( 离散数学) 课程号00230180 课程名保险风险模型课程号00230190 课程名运筹学课程号00230200 课程名复变函数课程号00230210 课程名FORTRAN课程号00230220 课程名热力学与统计物理 . ..。
北大高等数学教材哪本难

北大高等数学教材哪本难北大高等数学教材是中国知名大学北京大学(Peking University)出版的一套教材系列,此系列教材内容深入、全面,被广大学生和数学爱好者所关注和研究。
其中有很多本书都以其难度较高而著名,那么在北大高等数学教材中,究竟哪本教材是最难的呢?接下来,本文将探讨北大高等数学教材中的难点所在,以及评述认为最难的一本教材。
首先,要谈到北大高等数学教材中的难点,不能不提到题目的设计和解题思路。
在这套教材中,不仅出现了大量复杂的计算题,更有许多具有创新性的问题需要学生运用数学知识解决。
这些问题往往需要学生在理解数学概念的基础上,灵活运用数学方法,形成自己的解决思路。
这种思维上的转变和拓展,对于许多学生来说都是一项巨大的挑战。
其次,北大高等数学教材中的难点还体现在知识的广度和深度上。
在这套教材中,不仅包含了微积分、线性代数、概率论等基础数学知识,更涉及到了高等数学的各个分支领域。
例如,微分方程、多元函数、级数等内容都被充分覆盖。
学生需要全面理解并掌握这些知识,才能在解题过程中游刃有余。
而对于没有接触过这些领域的学生来说,这些新知识的学习和理解可能会带来较大的困难。
最后,北大高等数学教材中难点的另一个重要因素是题目的抽象性和复杂性。
有些题目的表述较为抽象,需要学生结合自己的数学直觉去理解题意。
同时,这套教材中也包含了很多具有挑战性的证明题,学生需要通过严谨的数学推理来论证问题的正确性。
这些题目既考察了学生对数学概念的理解,又要求学生具备较强的逻辑思维和推导能力。
综上所述,北大高等数学教材中的难点主要体现在题目设计、知识广度和深度,以及题目的抽象性和复杂性上。
在这套教材中,有很多本书都非常具有挑战性,难以评断哪本最难。
不同的学生在面对不同的难题时,可能会有不同的感受和困惑。
因此,挑选适合自己的教材,根据自身的学习能力和兴趣爱好来学习数学,才是最重要的。
总结来说,北大高等数学教材中的难点主要来自于题目设计和解题思路上的挑战、知识广度和深度上的涉及,以及题目的抽象性和复杂性。
北大高等数学b教材

北大高等数学b教材北大高等数学B教材是北京大学数学与应用数学系编写的一本教材,专为高等数学B课程而设计。
本教材涵盖了高等数学B课程的各个主题,旨在帮助学生全面理解和掌握数学的基本概念、原理和方法。
本文将对北大高等数学B教材的内容进行详细介绍。
1. 微积分部分在微积分部分中,教材首先介绍了极限和连续这两个基本概念。
它详细解释了极限的定义、性质和计算方法,并给出了一系列精确的例子和习题。
然后,教材讲述了导数和微分的概念,包括导数的定义和运算法则,以及一些常见函数的导数。
最后,教材引入了不定积分和定积分的概念,讲解了它们的基本性质和计算方法。
2. 线性代数部分线性代数部分主要介绍了向量和矩阵的基本知识。
教材首先讲解了向量的定义、线性运算和内积,以及向量的线性相关和线性无关的概念。
然后,它介绍了矩阵的定义、运算法则和特殊矩阵的性质。
接着,教材引入了矩阵的行列式和逆矩阵,并讲解了它们的计算方法。
最后,教材阐述了线性方程组和矩阵的秩的概念,包括求解线性方程组和判断矩阵秩的方法。
3. 多元函数微分学部分多元函数微分学部分主要涉及多元函数的导数、偏导数和极值。
教材详细讲解了多元函数的偏导数的计算法则和性质,以及二阶偏导数和高阶偏导数的概念。
接着,教材介绍了多元函数的极值和条件极值的求解方法。
最后,教材讲述了多元函数的隐函数和参数方程的求导法则。
4. 多元函数积分学部分多元函数积分学部分主要包括二重积分和三重积分的概念和计算方法。
教材介绍了二重积分的定义、性质和计算法则,包括直角坐标系和极坐标系下的二重积分计算方法。
然后,教材引入了三重积分的概念和计算方法,包括直角坐标系、柱坐标系和球坐标系下的三重积分计算方法。
最后,教材讲解了曲线积分和曲面积分的基本概念和运算法则。
综上所述,北大高等数学B教材是一本涵盖了微积分、线性代数、多元函数微分学和多元函数积分学的综合性教材。
它深入浅出地讲解了各个数学概念和原理,提供了丰富的例题和习题,以帮助学生掌握和运用数学知识。
高等代数北京大学第三版

高等代数北京大学第三版简介高等代数是数学中的一门重要课程,是数学的基础和核心课程之一。
北京大学的高等代数课程被广泛认为是高等代数学习中的经典教材之一。
本文将介绍北京大学第三版《高等代数》教材的主要内容和特点。
内容概述《高等代数北京大学第三版》是一本教材,由北京大学吴传荣、李建平合著。
全书共分为十五章,每章围绕一个主题展开讲解。
主要内容包括线性方程和矩阵、行列式、矩阵的相抵标准形及其应用、线性空间与线性变换、特征值与特征向量、正交线性变换与二次型、群、环和域等。
特点1. 详细而全面的内容本教材详细介绍了高等代数的各个重要概念和定理,并给出了充分的例题和习题来帮助学生掌握和巩固所学的知识。
每章的开头都给出了该章的学习目标,使学生能够清晰地了解该章的所学内容,并有针对性地学习。
2. 理论与实践相结合教材既注重理论的讲解,又注重实践的应用。
通过大量的实例和应用,教材将抽象的数学概念与实际问题相结合。
这有助于学生更好地理解数学原理,并在实践中灵活运用。
3. 重点突出,条理清晰教材对于重要的概念和定理都做了重点强调,并给出了详细的证明过程和推导。
条理清晰的内容安排使学生能够逐步建立起完整的知识体系。
4. 多样化的习题除了充分的例题之外,本书还提供了丰富的习题,涵盖了各个难度级别。
习题中融入了不同类型的问题,既能巩固基础知识,又能培养学生的综合运用能力。
习题的解答也提供了详细的步骤和解析,方便学生检查自己的答案和思考方式。
5. 适用范围广泛这本教材不仅适合北京大学的高等代数课程,也适合其他高校的相应课程。
无论是学生还是教师,都能从本书中获得很多学习和教学的帮助。
总结《高等代数北京大学第三版》是一本经典的高等代数教材,内容详细而全面,既注重理论讲解,又注重实际应用。
教材的特点包括多样化的习题和解答、重点突出、条理清晰以及适用范围广泛。
这本教材不仅帮助学生掌握高等代数的基本概念和定理,也培养了学生的分析问题和解决问题的能力。
高等数学北大版教材下册

高等数学北大版教材下册高等数学是一门重要的数学学科,对于理工科学生而言尤为重要。
北大版教材下册是高等数学的一本经典教材,深受广大学生的喜爱和认可。
下面,将对该教材下册进行详细地介绍和评价。
一、教材概述高等数学北大版教材下册是由北京大学数学科学学院编写出版的。
该教材下册主要涵盖了微分方程、无穷级数、矢量分析等内容。
教材内容科学全面,结构严谨,且注重理论与实践相结合,旨在培养学生的数学思维和问题解决能力。
二、教材特点1. 知识系统全面:教材内容涵盖了高等数学的各个重要方向,如微分方程、无穷级数、矢量分析等。
不仅能够满足学生基本学习需求,还能为进一步的学术研究打下坚实基础。
2. 理论与应用相结合:教材在理论阐述的同时,注重将理论知识与实际问题相结合,引导学生将数学知识应用于实际场景,拓宽解决问题的思路。
3. 网络辅助教学:教材配套的网络资源丰富而实用,包括习题解答、教学视频等,能够帮助学生更好地理解和应用所学知识。
4. 突出数学思维:教材注重培养学生的数学思维能力,引导学生从多个角度思考问题,进而锻炼逻辑推理和问题解决能力。
三、教材内容1. 微分方程:教材对微分方程进行了全面细致的讲解,包括常微分方程和偏微分方程。
通过例题和习题的训练,能够帮助学生理解和掌握微分方程的基本理论和解题方法。
2. 无穷级数:教材准确介绍了无穷级数的概念、性质和收敛条件。
通过大量的实例讲解和习题练习,能够培养学生处理无穷级数相关问题的能力。
3. 矢量分析:教材系统讲解了矢量、曲线与曲面的基本概念和性质,以及重要的定理和应用。
通过矢量分析的学习,学生能够深入理解三维空间的几何特性,并能够应用矢量分析方法解决实际问题。
四、教材评价高等数学北大版教材下册是一本内容充实、结构严谨的教材,具有以下几个方面的优点:1. 知识系统全面,能够满足学生的学习需求。
2. 理论与应用相结合,能够培养学生的问题解决能力。
3. 突出数学思维,培养学生的逻辑推理和创新能力。
高等数学 北大版

高等数学北大版引言高等数学是大学理工科专业中的一门重要课程,帮助学生奠定数学基础和培养解决问题的能力。
北大版高等数学教材是我国高校中广泛采用的教材之一。
本文将介绍高等数学北大版教材的主要特点和内容概述。
特点1.知识结构完整:高等数学北大版教材以培养学生的数学思维和分析问题的能力为主要目的,内容全面且体系完整。
包含了微积分、数列、级数、多元函数等重要内容,将数学的基本概念、定理和方法有机地结合起来。
2.理论与实践结合:该教材以理论为主线,同时注重理论的应用和实际问题的解决。
通过大量的例题和习题,使学生能够将所学知识运用到实际生活和学科应用中。
3.推理和证明能力培养:高等数学北大版教材注重培养学生的逻辑思维和推理能力。
在教材中,作者给出了一系列证明和推导的例子,引导学生学会分析问题和解决问题的方法。
内容概述第一册第一册主要介绍微积分的相关内容。
包括函数与极限、连续与导数、微分学的基本定理、微分中值定理、不定积分与定积分等。
第二册第二册重点讲解了数列与级数的概念和性质。
通过介绍极限与数列、数列极限的性质、无穷级数与级数收敛性等内容,帮助学生理解和掌握数列与级数的基本概念和方法。
第三册第三册的重点是多元函数与偏导数。
通过多元函数的极限与连续、偏导数与全微分、多元函数微分中值定理等内容,帮助学生了解多元函数的性质和计算方法。
第四册第四册主要介绍了多元函数的导数和积分。
包括多元函数的导数与微分法、定积分、重积分、曲线积分和曲面积分等内容。
通过这些知识,学生能够更深入地理解多元函数的性质和应用。
总结高等数学北大版教材是一套完整而系统的教材,适用于大学理工科专业的学生。
该教材的特点是知识结构完整、理论与实践结合以及推理和证明能力培养。
通过学习这套教材,学生能够建立起扎实的数学基础,培养问题解决能力和分析能力。
希望本文对您了解高等数学北大版教材有所帮助。
北京大学数学教学系列丛书(本科生)

北京大学数学教学系列丛书
本科生数学基础课教材
《抽象代数Ⅰ》赵春来徐明曜编著
《高等代数简明教程》(上册)(第二版)蓝以中编著
《数学分析》(第一册)伍胜健编著
《数学分析》(第二册)伍胜健编著
《数学分析》(第三册)伍胜健编著
《高等代数简明教程》(上册)(第二版)蓝以中编著
《高等代数简明教程》(下册)(第二版)蓝以中编著
《金融数学引论》吴岚黄海编著
《概率论》何书元编著
《随机过程》何书元编著
《抽样调查》孙山泽编著
《应用多元统计分析》高惠璇编著
《应用时间序列分析》何书元编著
《测度论与概率论基础》程士宏编著
《偏微分方程》周蜀林编著
《偏微分方程数值解讲义》李治平编著
《寿险精算基础》杨静平编著
《非寿险精算学》杨静平编著
《复变函数简明教程》谭小江伍胜健编著
《实变函数与泛函分析》郭懋正编著
《概率与统计》陈家鼎郑忠国编著。
北大版高等数学教材如何

北大版高等数学教材如何高等数学作为大学本科数学教材中的重要组成部分,对学生们的数学基础和思维能力有着重要的培养作用。
北大版高等数学教材在教学实践中逐渐积累了丰富的经验,通过多年的改革和创新,得到了广大师生的认可与好评。
下面将从教材内容安排、教学方法和知识体系等几个方面来介绍北大版高等数学教材。
一、教材内容安排北大版高等数学教材的内容安排合理,注重培养学生的数学思维能力和解决实际问题的能力。
教材以函数、极限、微分、积分、微分方程等为核心内容,系统地介绍了数学分析的基本概念和方法。
同时,教材还融入了一些具体的应用背景,通过例题和习题的训练,培养学生的应用能力和创新思维。
二、教学方法北大版高等数学教材注重启发式教学,强调培养学生的独立思考和解决问题的能力。
教材中的例题和习题设置合理,既有基础题目帮助学生巩固知识,又有拓展题目激发学生的兴趣,提高解决问题的能力。
同时,教材还提供了详细的解题方法和答案解析,方便学生进行自我评估和巩固。
三、知识体系北大版高等数学教材的知识体系完整,层次清晰。
教材将数学的基本概念和方法有机地串联起来,通过逐层深入的讲解,帮助学生建立完整的数学知识结构。
同时,教材还强调数学与其他学科的联系,拓宽了学生的学科视野,培养了学生的科学素养。
四、配套资源北大版高等数学教材还提供了一系列的配套资源,如习题集、教学辅导书等。
这些资源涵盖了教材中的重点难点内容,有助于学生对知识的掌握和理解。
同时,配套资源中还提供了一些拓展性问题和实际应用题,激发学生的求知欲望和创新思维。
总之,北大版高等数学教材在教学实践中积累了丰富的经验,通过合理的内容安排、启发式的教学方法和完整的知识体系,有效地提高了学生的数学素养和解决问题的能力。
同时,配套资源的提供也方便了师生对教学内容的深入学习和探索。
可以说,北大版高等数学教材在数学教育中起到了重要的作用,对于培养高素质的数学人才,具有不可替代的作用。
高等数学教材北大第四版

高等数学教材北大第四版高等数学是许多大学理工科专业的必修课程,对于培养学生的数学思维能力和解决实际问题的能力具有重要意义。
在高等数学的教学中,教材的选择是十分重要的。
本文将重点介绍一本备受推崇的高等数学教材——北大第四版。
北大第四版的高等数学教材是由北京大学教授们耗时多年编写的权威教材。
它包含了高等数学的核心内容,涵盖微积分、数列、级数、多元函数等各个方面的知识。
该教材的编写经验丰富,详实的例题和练习题能够帮助学生掌握重要概念和方法,培养他们的解决问题的能力。
北大第四版高等数学教材具有以下几个显著特点:首先,该教材注重理论和实践的结合。
在每章的开头,教材会引入一些实际问题,并通过数学的方法加以解决,使学生能够直观地理解数学在实际问题中的应用。
这样的设计能够增强学生的学习兴趣,使他们从抽象的概念中得到实际启发。
其次,教材的难度分布适中。
教材的内容从基础到深入,由浅入深,层层递进。
每一章的内容都有明确的学习目标,教材通过大量清晰的图表和案例,帮助学生理解和掌握重要概念和方法。
同时,教材也提供了一些挑战性问题,供学生进一步拓展思维,提高解决问题的能力。
此外,北大第四版高等数学教材还注重培养学生的数学思想和证明能力。
教材中有一些重要理论的证明过程,通过引导学生自己去思考和构建证明,培养他们的逻辑思维和推理能力。
这样的训练对于学生以后的学习和研究具有重要意义。
最后,该教材还配套有丰富的练习题和习题解析。
练习题的难度与教材的内容相匹配,涵盖了各种类型的问题。
习题解析详细地介绍了解题思路和方法,帮助学生巩固知识点,提高解题能力。
此外,教材的附录还提供了一些常用的数学公式和表格,方便学生复习和查阅。
总结起来,北大第四版高等数学教材凭借其权威性和教学实用性,成为了许多高校的首选教材。
它的内容全面,难度适中,注重理论与实践的结合,培养学生的思维能力和解决问题的能力。
如果你是一位学习高等数学的学生,那么北大第四版绝对是你不可错过的教材选择。
高等数学教材北大版本目录

高等数学教材北大版本目录目录第一章极限与连续函数第一节极限的概念与性质1.1 实数集的性质1.2 数列极限的定义与性质1.3 无穷小量与无穷大量的比较1.4 函数极限的定义与性质1.5 极限存在准则1.6 极限运算法则1.7 极限存在的计算方法第二节一元函数的连续性2.1 连续函数的概念与性质2.2 连续函数的运算法则2.3 连续函数的分段定义与分段连续性2.4 介值定理及其推论2.5 零点存在性的判定第三节导数与微分3.1 导数的概念与几何意义3.2 导数的计算3.3 切线与法线方程3.4 高阶导数与莱布尼茨公式3.5 微分的概念与性质3.6 高阶导数的计算方法第二章微分学第一节函数的单调性与极值1.1 单调数列的判定1.2 函数单调性的判定1.3 极值的概念1.4 极值的判定条件1.5 函数的最值与最值存在性的判定第二节函数的凹凸性与拐点2.1 函数的凹凸性的概念与性质2.2 函数的拐点概念2.3 拐点的判定与求法2.4 函数的凹凸区间与拐点的图像第三节函数的图形与曲率3.1 函数的图形与切线方程3.2 曲率的概念与曲率圆方程3.3 渐近线与极限曲线第三章积分学第一节不定积分1.1 不定积分的概念与基本性质1.2 不定积分的计算方法1.3 牛顿-莱布尼茨公式与定积分第二节定积分2.1 定积分的概念与性质2.2 定积分的计算2.3 定积分与不定积分的关系2.4 定积分的应用第三节微积分基本定理与换元积分法3.1 微积分基本定理3.2 定积分的换元积分法3.3 径向对称函数的定积分第四章无穷级数第一节数项级数的概念与性质1.1 数项级数的概念1.2 数项级数收敛性的判定1.3 常见数项级数的性质与收敛域第二节幂级数2.1 幂级数的概念与收敛域2.2 幂级数的运算法则2.3 幂级数的收敛半径与收敛区间 2.4 幂级数的和函数及其性质第五章二元函数与多元函数的微分学第一节二元函数的极限与连续性1.1 二元函数的极限概念1.2 二元函数的连续性1.3 多元函数的限制与间断点第二节多元函数的偏导数与全微分 2.1 多元函数的偏导数2.2 隐函数的求导2.3 多元函数的全微分第三节多元函数的泰勒公式与极值 3.1 多元函数的泰勒公式3.2 多元函数的极值与条件极值 3.3 多元函数的拉格朗日乘数法第六章多元函数的积分学第一节二重积分1.1 二重积分的概念与性质1.2 二重积分的计算1.3 二重积分的应用第二节三重积分2.1 三重积分的概念与性质2.2 三重积分的计算2.3 三重积分的应用第七章常微分方程第一节常微分方程的基本概念1.1 常微分方程的基本概念1.2 一阶常微分方程的解1.3 可分离变量的方程第二节一阶常微分方程的应用2.1 可解的方程2.2 高效变量的方程2.3 齐次方程第三节高阶常微分方程3.1 二阶线性常微分方程3.2 常系数齐次线性方程3.3 变动参数法与电路问题总结以上为高等数学北大版本教材目录,涵盖了极限与连续函数、微分学、积分学、无穷级数、二元函数与多元函数的微分学、多元函数的积分学、常微分方程等多个主要章节。
北大数学专业课程及教材

北大数学专业课程及教材
北大数学专业的课程和教材可能会根据不同的专业方向和学年的安排有所不同。
以下是北大数学专业的一些常见课程及其常用的教材参考:
1. 高等数学:《高等数学》(同济大学版)、《高等数学》(朱承本、冯跃龙等合编)
2. 线性代数:《线性代数及其应用》(北京大学出版社出版)
3. 概率论与数理统计:《概率论与数理统计》(清华大学出版社出版)
4. 数学分析:《数学分析》(北京大学数学学院编写)
5. 数学建模与计算实践:根据具体的课程内容可能有不同教材
6. 微分方程:《常微分方程教程》(北京大学出版社出版)
7. 数值分析:《数值分析》(北京大学数学学院编写)
8. 抽象代数:《抽象代数》(高等教育出版社出版)
9. 实变函数:《实变函数与泛函分析》(清华大学出版社出版)
10. 积分方程:《积分方程教程》(北京大学出版社出版)
以上仅为一些常见的课程及教材参考,具体的课程安排和教材
使用可以根据北大数学专业的教学计划和师资组织安排而有所不同。
北大本科生高等数学教材

北大本科生高等数学教材高等数学作为一门基础学科,对于理工类本科生而言,具有极其重要的地位。
北大本科生高等数学教材,作为北大为学生量身定制的教材,旨在全面系统地讲解高等数学的各个知识点,培养学生的数学思维和解决问题的能力。
第一章: 极限与连续1.1 极限的概念与性质1.1.1 极限的定义1.1.2 极限的性质1.1.3 两个重要极限1.2 函数的连续性与间断点1.2.1 点的分类1.2.2 连续函数的性质与判定1.2.3 间断点与连续性1.3 无穷小量与无穷大量1.3.1 无穷小量的概念与性质1.3.2 无穷大量的概念与性质1.3.3 无穷小量的比较第二章: 导数与微分2.1 导数的定义与几何意义2.1.1 导数的定义2.1.2 导数的几何意义2.1.3 导数的计算方法2.2 微分与微分中值定理2.2.1 微分的概念与性质2.2.2 微分中值定理的原理与应用 2.2.3 函数的单调性与判定2.3 高级导数与泰勒公式2.3.1 高级导数的定义与计算2.3.2 泰勒公式的原理与应用2.3.3 高级函数的性质与判定第三章: 定积分与不定积分3.1 定积分的概念与性质3.1.1 定积分的定义3.1.2 定积分的计算方法3.1.3 定积分的应用3.2 不定积分与牛顿-莱布尼茨公式3.2.1 不定积分的定义与计算3.2.2 牛顿-莱布尼茨公式的原理与应用 3.2.3 不定积分的常见形式与求解技巧3.3 定积分与不定积分的关系3.3.1 定积分与不定积分的联系3.3.2 定积分与不定积分的互相转化3.3.3 定积分与不定积分的应用领域第四章: 多元函数及其微分学4.1 二元函数的极限与连续性4.1.1 二元函数的极限的定义与性质4.1.2 二元函数的连续性与判定4.1.3 二元函数的多个变量极限4.2 多元函数的偏导数与全微分4.2.1 多元函数的偏导数的定义与计算 4.2.2 全微分的概念与性质4.2.3 多元函数的可微性与判定4.3 隐函数与参数方程4.3.1 隐函数的存在定理与求导法则 4.3.2 参数方程的性质与应用4.3.3 隐函数与参数方程的相互转化第五章: 重积分与曲线积分5.1 二重积分的概念与性质5.1.1 二重积分的定义5.1.2 二重积分的计算方法5.1.3 二重积分的应用5.2 三重积分的概念与性质5.2.1 三重积分的定义5.2.2 三重积分的计算方法5.2.3 三重积分的应用5.3 曲线积分与曲面积分5.3.1 曲线积分的定义与计算5.3.2 曲面积分的定义与计算5.3.3 曲线积分与曲面积分的应用第六章: 无穷级数与傅里叶级数6.1 数项级数的概念与性质6.1.1 数项级数的定义与收敛性6.1.2 数项级数的判定方法6.1.3 数项级数的应用6.2 幂级数的概念与性质6.2.1 幂级数的收敛区间与收敛域6.2.2 幂级数的求和计算6.2.3 幂级数的应用6.3 傅里叶级数与傅里叶变换6.3.1 傅里叶级数的概念与性质6.3.2 傅里叶级数的计算方法6.3.3 傅里叶级数的应用通过北大本科生高等数学教材的学习,学生将全面了解高等数学的各个知识点,并能运用数学思维和解决问题的能力进行的深入研究。
北京大学数学系高等数学教材

北京大学数学系高等数学教材北京大学数学系高等数学教材是一本经典的教材,深受广大学子和数学爱好者的喜爱。
它不仅在数学教育领域具有重要影响力,而且为数学研究与应用提供了坚实的基础。
本文将从不同角度介绍北京大学数学系高等数学教材的特点和价值。
一、严谨的数学内容体系北京大学数学系高等数学教材以严谨的数学内容体系为基础,涵盖了微积分、数理方程、数值计算等多个数学分支。
教材总结了数学的基本理论和方法,让学生逐步掌握数学分析的核心概念和技巧。
内容既有丰富的数学理论推导,又有实际问题的应用实例,使学生能够在学习中综合运用数学知识解决实际问题。
二、系统化的知识结构北京大学数学系高等数学教材采用系统化的知识结构,每一章节都有明确的学习目标和重点。
教材逐步引导学生学习数学的发展过程,从基础概念到高级应用,系统化地组织了数学知识的内容和思维方式。
这种系统化的结构使学生能够逐步建立起数学知识的框架,形成完整的思维体系。
三、注重数学应用与拓展教材不仅注重理论知识的学习,还重视数学应用和知识的拓展。
通过丰富的例题和习题,学生可以巩固基础知识,培养解决实际问题的能力。
此外,教材还提供了一些数学应用的拓展内容,引导学生深入了解数学在现实生活和科学研究中的应用价值,激发学生的兴趣和创造力。
四、注重数学思维培养北京大学数学系高等数学教材注重培养学生的数学思维能力。
在教学过程中,通过引导学生思考数学问题、分析解题思路,培养学生的抽象思维和逻辑推理能力。
教材也强调数学思维与跨学科思维的结合,培养学生解决实际问题的能力和数学建模的思维方式,为学生今后的学习和科研打下坚实基础。
五、独具特色的数学活动教材还设计了一系列独具特色的数学活动,如探究性学习、讨论分析、数学建模等。
这些数学活动既可以促进学生的自主学习和独立思考,又可以增强学生对数学的兴趣和解决问题的能力。
通过数学活动,学生能够更加深入地理解和应用所学数学知识,提升数学学习的主动性和创造性。
北大版高等数学上册教材

北大版高等数学上册教材高等数学是大学理工科学生必修的一门基础课程,对于培养学生的数学思维和解决实际问题的能力具有重要作用。
北大版高等数学上册教材是一本经典教材,被广大师生普遍认可。
本篇文章将从教材的详细内容、教学方法和学生学习经验三个方面探讨北大版高等数学上册教材的优势。
一、教材的详细内容北大版高等数学上册教材共分为十三章,内容涵盖了微积分、数列、函数、极限等重要概念和方法。
教材以系统性和逻辑性为特点,每个章节都依次引入新的概念和方法,并通过例题和习题进行巩固和训练。
教材中的解题思路清晰明了,让学生能够较为轻松地掌握和应用相关的数学知识。
二、教学方法北大版高等数学上册教材在教学方法上注重培养学生的独立思考和问题解决能力。
教材中每章都设置了练习题和习题,既有理论性的综合题,也有实际问题的应用题,让学生在解题过程中更好地理解和掌握知识点。
同时,教材还鼓励学生进行数学建模和研究性学习,培养学生的创新思维和实际运用能力。
三、学生学习经验北大版高等数学上册教材已经经过多年的使用和改进,得到了广大学生的一致好评。
学生们认为教材中的例题和习题设置得很到位,能够帮助他们逐步掌握和巩固知识点。
同时,教材的语言通俗易懂,没有过多的数学专业术语,使得学生更容易理解和接受。
此外,教材中还穿插了一些拓展和应用实例,使得学生能够将所学的数学知识与实际问题相结合,提升了学习的兴趣和动力。
综上所述,北大版高等数学上册教材以其详细的内容、科学的教学方法和学生的良好学习经验而备受欢迎。
它不仅为学生打下了坚实的数学基础,也培养了学生的数学思维能力和实际应用能力。
因此,我们大力推荐北大版高等数学上册教材,相信它能够帮助广大学生更好地学习和掌握高等数学知识。
北京大学数学科学学院本科生教学手册.doc

北京大学数学科学学院本科生教学手册(2016年版)Catalog of Undergraduate Education School of Mathematical SciencesPeking University北京大学数学科学学院修订 2016年5月北京大学教务部审定 2016年7月本册编辑柳彬冯荣权目录北京大学数学科学学院 (1)一、学院简介 (1)二.专业及专业方向: (2)三、教学行政管理人员 (2)四、师资力量(姓名前打*者为博士生导师) (3)数学系 (3)概率统计系 (5)科学与工程计算系 (6)信息科学系 (7)金融数学系 (7)五、教学设备与设施 (7)1.教学与研究实验室 (7)2.图书资料 (8)数学与应用数学专业 (9)一、专业简介 (9)二、专业培养要求、目标 (9)三、授予学位 (9)四、学分要求与课程设置 (9)1.公共与基础课程40-46学分 (9)2.核心课程29学分 (10)3.限选课程32学分 (10)4.通识与自主选修课程31学分 (10)五、其他要求 (11)1.保研要求: (11)1)基础数学方向: (11)2)金融数学方向: (11)统计学专业 (11)一、专业简介 (11)二、专业培养要求、目标 (11)三、授予学位 (11)四、学分要求与课程设置 (12)1.公共与基础课程40-46学分 (12)2.核心课程29学分 (12)3.限选课程32学分 (12)4.通识与自主选修课程31学分 (12)五、其他要求 (13)1.保研要求与保研排名: (13)2.保研准备: (13)1)概率论方向: (13)2)统计学方向和应用统计方向: (13)信息与计算科学专业 (14)一、专业简介 (14)二、专业培养要求、目标 (14)三、授予学位 (14)四、学分要求与课程设置 (15)1.公共与基础课程40-46学分 (15)2.核心课程29学分 (15)3.限选课程32学分 (15)4.通识与自主选修课程31学分 (15)五、其他要求 (16)1.保研要求: (16)1)计算数学方向: (16)2)信息科学方向: (16)数据科学与大数据技术专业 (17)一、专业简介 (17)二、专业培养要求、目标 (17)三、授予学位 (17)四、学分要求与课程设置 (17)1.公共与基础课程40-46学分 (17)2.核心课程29学分 (17)3.限选课程32学分 (17)4.通识与自主选修课程31学分 (17)五、其他要求 (18)1.保研要求: (18)2. 读研准备: (18)课程列表 (19)1.公共与基础课程40-46学分 (19)2.核心课程29学分 (18)3.限选课程32学分 (18)通选课选课的相关规定 (22)港澳台选课规定 (23)相关课程介绍 (25)一、课程目录 (25)二、课程简介 (28)北京大学数学科学学院一、学院简介数学科学学院起源于1904年京师大学堂的算学门。
北大版高等数学下册教材

北大版高等数学下册教材北京大学版高等数学下册教材简介北京大学版高等数学下册教材是一本专门为高等数学学习者准备的教材。
本教材通过分章节的方式,系统介绍了高等数学下册的各个知识点和概念,力求深入浅出地让读者理解和掌握这门学科的核心内容。
下面将对本教材的主要特点和章节内容进行介绍。
第一章微分方程本章主要介绍了微分方程的基本概念和解法。
首先对微分方程的定义进行了详细解释,然后介绍了一阶微分方程和高阶微分方程的求解方法。
此外,还对常微分方程和偏微分方程进行了区分和讲解,通过一系列例题和习题,帮助读者巩固所学知识。
第二章微分方程的应用本章主要介绍了微分方程在物理和工程等领域的应用。
通过讲解物理问题和工程实际案例,引导读者将微分方程的概念和解法应用到实际问题中。
同时,介绍了一些经典的物理方程和工程方程,如振动方程和热传导方程等。
第三章多元函数微分学本章主要介绍了多元函数的导数和微分学的基本概念。
首先介绍了多元函数的概念和性质,然后对偏导数和全微分进行了详细解释。
同时,还介绍了多元函数的极值和条件极值的判定方法,以及拉格朗日乘子法等高级计算技巧。
第四章多元函数积分学本章主要介绍了多元函数的积分和积分学的基本概念。
首先介绍了多元函数积分的定义和性质,然后讲解了重积分和曲线、曲面积分的计算方法。
同时,还介绍了格林公式和高斯公式等重要的积分计算定理。
第五章级数本章主要介绍了级数的概念和性质。
首先讲解了数项级数和函数项级数的定义,然后介绍了级数收敛和发散的判定方法。
同时,通过一些经典的级数例题,帮助读者加深对级数的理解和掌握。
第六章傅里叶级数本章主要介绍了傅里叶级数的概念和性质。
首先介绍了周期函数和傅里叶级数的定义,然后讲解了傅里叶级数的计算方法和傅里叶级数的收敛性。
同时,还介绍了傅里叶级数的应用领域,如信号处理和波动现象等。
第七章偏微分方程本章主要介绍了偏微分方程的基本概念和解法。
首先介绍了一阶偏微分方程和二阶偏微分方程的定义,然后讲解了常见的偏微分方程解法,如分离变量法和特征线法等。
北京大学数学教学系列丛书(本科生)

北京大学数学教学系列丛书(本科生)第一篇:北京大学数学教学系列丛书(本科生)北京大学数学教学系列丛书本科生数学基础课教材《抽象代数Ⅰ》赵春来徐明曜编著《高等代数简明教程》(上册)(第二版)蓝以中编著《数学分析》(第一册)伍胜健编著《数学分析》(第二册)伍胜健编著《数学分析》(第三册)伍胜健编著《高等代数简明教程》(上册)(第二版)蓝以中编著《高等代数简明教程》(下册)(第二版)蓝以中编著《金融数学引论》吴岚黄海编著《概率论》何书元编著《随机过程》何书元编著《抽样调查》孙山泽编著《应用多元统计分析》高惠璇编著《应用时间序列分析》何书元编著《测度论与概率论基础》程士宏编著《偏微分方程》周蜀林编著《偏微分方程数值解讲义》李治平编著《寿险精算基础》杨静平编著《非寿险精算学》杨静平编著《复变函数简明教程》谭小江伍胜健编著《实变函数与泛函分析》郭懋正编著《概率与统计》陈家鼎郑忠国编著第二篇:北京大学法学院2013级本科生北京大学法学院2013级本科生《刑法分论》期末考试题本文系北京大学法学院2013级本科生《刑法分论》期末案例分析试题。
四个小时的考试,说长很长,说短却也很短。
也许多年之后,天南海北的我们还能够想起在大二的某一个下午,我们曾经一起考过一场四个多小时的考试,还能想起那春夏秋冬东南西北的无比鲜活而又无比悲喜的人物。
感谢车浩老师一个学期的教诲,感谢这一场史诗级考试的饕餮盛宴。
考试时间:四小时考试方式:开卷考查范围:刑法分则出题老师:车浩答题要点:简要说明案中人的犯罪及理由,并进一步分析其中可能存有的争议之处,题中时间系联系需要,答题时以现行刑法为依据,无需考虑效力问题。
1977年冬天,中国恢复高考,周小东、吴小南、郑小西和王小北经过激烈竞争,考入西京大学法律系。
1978年春天入校,被分至同一件宿舍。
四人志向各异,但都珍惜机遇,发奋读书,同窗四载,互相砥砺,结下了深厚友谊。
1982年大学毕业,周小东被分配至西京省政府办公厅调研室工作,郑小西留校任教,王小北被分配至市检察院,吴小南则阴差阳错进入国有钢厂。
北大数学系所用教材

北大数学系所用教材
北大数学系所用教材有很多,以下是一些常见的教材:
1.《高等数学》(上、下册):经典的大学数学教材,包括微
积分、线性代数、概率与统计等内容。
2.《数学分析》(上、下册):重点介绍实数、数列、函数、
极限、连续等数学分析中的基本概念和定理。
3.《代数学》(上、下册):介绍抽象代数的基础理论,包括
群论、环论、域论等内容。
4.《解析几何与线性代数》(上、下册):重点介绍向量空间、矩阵理论、线性变换等内容。
5.《常微分方程》:介绍常微分方程的基本理论和常见的解法。
6.《数理方程》:介绍偏微分方程的基本理论和求解方法。
7.《概率论与数理统计》:介绍概率论和数理统计的基本概念、定理和应用。
除了以上主要教材外,北大数学系还会根据具体课程的需求选用一些辅助教材或参考书。
具体使用的教材可能会因教师、课程、年级和学期的不同而有所差异。
对于具体的教材使用情况,可以参考北大数学系的教学计划和教师布置的课程大纲。
北大高等数学教材abc

北大高等数学教材abc高等数学是大学理工科专业中的一门重要课程,对于掌握数学基础和培养科学思维具有重要意义。
而北大高等数学教材ABC,作为国内一流的数学教材之一,旨在帮助学生全面理解和掌握高等数学的知识和方法。
本文将从教材内容、教学特点以及使用体验三个方面对北大高等数学教材ABC进行综合介绍。
一、教材内容北大高等数学教材ABC包含了数学分析、数学方法、高等代数、解析几何等多个领域的内容,旨在覆盖大学高等数学各个重要知识点。
该教材内容设计合理、条理清晰,每个章节都以引入、定义、定理证明、例题讲解以及习题训练等环节构成,能够有效帮助学生逐步理解和掌握数学的基本概念和方法。
二、教学特点1.系统性强:北大高等数学教材ABC在内容编排上坚持逻辑严谨、系统完整的原则,将各个概念、定理有机地联系起来,形成了一个完整而严谨的数学体系,有助于学生形成全面的数学思维框架。
2.注重应用:教材ABC在知识体系的讲解中注重应用和实例,通过大量的例题讲解,引导学生将抽象的理论应用到实际问题中,并培养学生分析和解决实际问题的能力。
3.强调思辨:北大高等数学教材ABC鼓励学生主动思考和思辨,通过引导学生提出问题、分析问题并合理解决问题,培养了学生的逻辑思维、创造性思维和问题解决能力。
4.扩展拓展:教材ABC不仅包含了基础的数学知识,还注重对一些扩展和拓展内容的讲解,帮助学生拓宽数学学习的视野,丰富数学学科的内容。
三、使用体验北大高等数学教材ABC得到了广大学生的一致好评。
学生们普遍认为教材内容全面、详细,具有很强的学习性和适用性。
教材中的例题讲解详尽,习题难度适中,有效地辅助了学生的自学。
同时,该教材还提供了配套的习题答案和教辅材料,方便学生查阅和巩固练习。
综上所述,北大高等数学教材ABC作为一本优秀的高等数学教材,以其严谨的内容、注重应用的特点以及出色的使用体验,深受学生和教师的喜爱。
它不仅能够帮助学生全面掌握数学知识,还能够培养学生的数学思维和问题解决能力,为学生未来的学习和科研提供坚实的基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北大数学系本科教材
北大数学系本科教材包括以下几门课程的教材:
1. 微积分:北大的微积分教材包括《微积分(修订版)》和《微积分习题讲义(修订版)》。
2. 线性代数:北大的线性代数教材包括《线性代数与解析几何(修订版)》和《线性代数习题指导与解答》。
3. 概率论与数理统计:北大的概率论与数理统计教材包括《概率论与数理统计教程(修订版)》和《概率论与数理统计习题讲义》。
4. 离散数学:北大的离散数学教材包括《离散数学》。
5. 数学分析:北大的数学分析教材包括《数学分析习题解答》和《数学分析辅导教程》。
这些教材都是经过北大数学系教授和专家精心编写的,旨在提供给本科学生综合学习和参考。
另外,北大数学系还有其他教材,涵盖更多的专业课程和研究领域,如代数学、几何学等。
