2020高考数学原创 公开课一等奖课件
合集下载
2020高考数学原创.2函数的表示法(二) 公开课一等奖课件

ae bf cg
de bf cg
例3.下列对应关系(A 到 B)中,其中 x∈A, y∈B. (1)A B N , f : x y x 3 ;
(2)A N , B Z , f : x y 2x 3; (3)A { x | 0 x 1}, B { y | y 1},
45
2
60
3
90
2
1
观察下列对应,并思考:
①开平方
3
9
-3
4
2 -2
1
1
-1
1 ②求平方
-1
2
1
-2
4
3 -3
9
③求正弦 1
2
30
2
45
2
60
3
90
2
1
④乘以2 1
1
2 3
2
4
3
5
6
映射的定义:
一般地,设A、B是两个集合,如果 按照某种对应法则f,对于集合A中的 任一个元素,在集合B中都有唯一的元素 和它对应,那么这样的对应(包括A、B 以及A到B的对应法则f )叫做集合A到集 合B的一个映射.
班主任: 我觉得何旋今天取得这样的成绩, 我觉得,很重要的是,何旋是土生土长的北京 二中的学生,二中的教育理念是综合培养学生 的素质和能力。我觉得何旋,她取得今天这么 好的成绩,一个来源于她的扎实的学习上的基 础,还有一个非常重要的,我觉得特别想提的, 何旋是一个特别充满自信,充满阳光的这样一 个女孩子。在我印象当中,何旋是一个最爱笑 的,而且她的笑特别感染人的。所以我觉得她 很阳光,而且充满自信,这是她突出的这样一 个特点。所以我觉得,这是她今天取得好成绩 当中,心理素质非常好,是非常重要的。
2020高考数学原创.3椭圆的几何性质 公开课一等奖课件

1
一. 教材分析
(1) 教材的地位和作用 (2) 课时安排
2
一. 教材分析
(一)教材的地位和作用
“椭圆的几何性质”是解析几何研究的 一个重要问题之一。它是学生学习圆锥曲 线所研究的第一个有关性质的内容,其方 法可贯穿于解析几何学习的始终。所以, 通过这部分内容的学习,可以帮助学生更 好的理解解析几何的核心问题------圆锥 曲线的概念,也能为学好后续几种圆锥曲 线作好理论和方法上的准备,是解析几何 中承上启下的关键内容。
6
二. 教法分析
(二)教学方法
建构主义认为,知识是在原有知识的基础上, 在人与环境的相互作用过程中,通过同化和顺应, 使自身的认知结构得以转换和发展。元认知理论指 出,学习过程既是认识过程又是情感过程,是“知、 情、意、行”的和谐统一。结合本节课的具体内容, 参考学习和信息加工模型、广义知识学习阶段和分 类模型,确立教学法。
3
一. 教材分析 (二)课时安排
椭圆几何性质问题研究可安排三课时。本 节作为第一课时,重在研究椭圆的性质。教学 中注重概念的引入,定义的理解。在这个过程 中培养学生分析解决问题的能力,培养学生讨 论交流的合作意识。
4
二. 教法分析
(一)学情分析 (二)教学方法 (三)具体措施
5
二. 教法分析
(一)学情分析
[5]2a 和 2b是什么量? a和 b是什么量? [6]关于离心率讲了几点?
17
标准方程
图象
范围 对称性 顶点坐标 焦点坐标 半轴长 焦距 a,b,c关系 离心率
x2 a2
y2 b2
1(a
b
0)
x2 b2
y2 a2
1(a
一. 教材分析
(1) 教材的地位和作用 (2) 课时安排
2
一. 教材分析
(一)教材的地位和作用
“椭圆的几何性质”是解析几何研究的 一个重要问题之一。它是学生学习圆锥曲 线所研究的第一个有关性质的内容,其方 法可贯穿于解析几何学习的始终。所以, 通过这部分内容的学习,可以帮助学生更 好的理解解析几何的核心问题------圆锥 曲线的概念,也能为学好后续几种圆锥曲 线作好理论和方法上的准备,是解析几何 中承上启下的关键内容。
6
二. 教法分析
(二)教学方法
建构主义认为,知识是在原有知识的基础上, 在人与环境的相互作用过程中,通过同化和顺应, 使自身的认知结构得以转换和发展。元认知理论指 出,学习过程既是认识过程又是情感过程,是“知、 情、意、行”的和谐统一。结合本节课的具体内容, 参考学习和信息加工模型、广义知识学习阶段和分 类模型,确立教学法。
3
一. 教材分析 (二)课时安排
椭圆几何性质问题研究可安排三课时。本 节作为第一课时,重在研究椭圆的性质。教学 中注重概念的引入,定义的理解。在这个过程 中培养学生分析解决问题的能力,培养学生讨 论交流的合作意识。
4
二. 教法分析
(一)学情分析 (二)教学方法 (三)具体措施
5
二. 教法分析
(一)学情分析
[5]2a 和 2b是什么量? a和 b是什么量? [6]关于离心率讲了几点?
17
标准方程
图象
范围 对称性 顶点坐标 焦点坐标 半轴长 焦距 a,b,c关系 离心率
x2 a2
y2 b2
1(a
b
0)
x2 b2
y2 a2
1(a
2020高考数学 公开课一等奖课件

3.常见的升幂变换是:cos 2α=2cos2 α-1=1-2sin2 α;常见 1-cos 2α 1+cos 2α 2 2 的降幂变换是:sin α= ,cos α= . 2 2 4.利用辅助角公式将含两项的三角函数式化成一个三角函数 的形式:asin α+bcos α= a2+b2sin(α+φ)= a2+b2cos(α-φ),这 是研究三角函数性质的非常重要的思想方法, 也是历年高考的热点 内容. 5.不仅能正用三角公式,而且能逆用和变用公式,也是三角 变换的重要手段.
y=sin
预习测评 1.(2014 年长春一模) 函数 f (x)=(sin x+cos x)2 的一条对称轴的方 程是( )
A.x= 4
B.x= 3
C.x= 2
D.x=π
【答案】A
2.设 a=2sin 24° ,b=2(sin 47° sin 66° -sin 24° sin 43° ),c=sin 85° + 3 cos 95° ,则 a,b,c 的大小关系是( ) A.a>c>b B.b>c>a C.c>b>a D.c>a>b
5 3 10 正解:∵α、β 均为锐角,∴由 sin α= ,cos β= 得 cos α 5 10 2 5 10 = ,sin β= .且 0<α+β<π. 5 10 2 5 3 10 5 10 于是 cos(α+β)=cos αcos β-sin αsin β= · - · = 5 10 5 10 2 .故选 C. 2 答案:C 纠错心得:在经过讨论得到 0<α+β<π 后,仅仅求出 sin(α+β) 的值是不够的,应求 cos(α+β)的值,才能得出正确答案.
2020年高考数学复习精选课件 第3节 三角函数的图象与性质 公开课一等奖课件
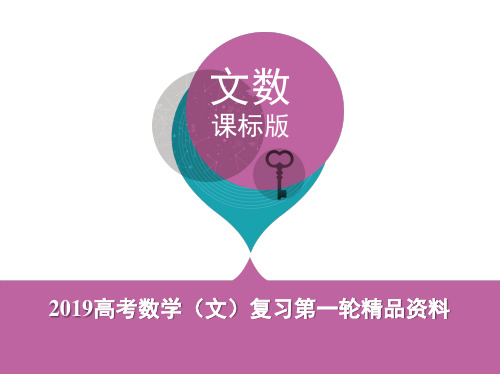
x= 2
sin x
4
≥0,将x- 4 视为一个整体,由正弦函数y=
栏目索引
文数
课标版
2019高考数学(文)复习第一轮精品资料
sin x的图象和性质可知2kπ≤x- ≤π+2kπ,k∈Z.
4
解得2kπ+ 4 ≤x≤2kπ+ 54 ,k∈Z.
所以定义域为x
|
2k
π 4
x
2k
5π 4
,k
Z .
栏目索引
栏目索引
1-2 函数y=sin x-cos x+sin xcos x的值域为
.
答案
1 2
2,1
解析 设t=sin x-cos x,则- 2 ≤t≤ 2 ,t2=sin2x+cos2x-2sin xcos x,则
sin xcos x= 1 t2 , 2
ω3 3 2
∴0<ω<6,且ω= 3 +6k(k∈Z),∴ω=3 ,经检验,满足题意.
2
2
栏目索引
2-2
若函数f(x)=sin ωx
4
(0<ω<1)在 2 ,
上单调递减,求ω的取值范
围.
解析 当 <x<π时,由0<ω<1得 < ω π+ <ωx+ <ωπ+ <5 π,又y=sin x
B.最小正周期为π的偶函数
C.最小正周期为 的奇函数
2
D.最小正周期为 的偶函数
2
(2)函数f(x)=sin x
2020年高考数学复习精选课件 第3节 等比数列及其前n项和 公开课一等奖课件
栏目索引
解析 (1)设等比数列{an}的公比为q,由题易知q>0.由等比数列的性质
及题意知 a32=a2a4=1,又a2+a4= 52 ,且{an}单调递减,所以a2=2,a4= 12 ,则q2= 14 ,q
= 12 (舍负),所以a1= aq2 =4,故选B.
(2)根据已知条件得
a1q2 a1
栏目索引
2-1 已知x,y,z∈R,若-1,x,y,z,-3成等比数列,则xyz的值为 ( ) A.-3 B.±3 C.-3 3 D.±3 3 答案 C 由题意知y2=3,∴y=± 3 , 又∵y与-1,-3符号相同, ∴y=- 3 ,又y2=xz, 所以xyz=y3=-3 3 .
栏目索引
2-2 记等比数列{an}的前n项积为Tn(n∈N*),已知am-1·am+1-2am=0,且T2m-1=1 28,则m的值为 ( ) A.4 B.7 C.10 D.12 答案 A 因为{an}是等比数列, 所以am-1am+1= am2 , 故由am-1am+1-2am=0, 可知am=2(am=0舍去). 由等比数列的性质可知前(2m-1)项积T2m-1=a m2m1 , ∴22m-1=128,故m=4.
栏目索引
1.已知{an}是等比数列,a2=2,a5= 14 ,则公比q=(
)
A.- 1 B.-2 C.2 D. 1
2
2
答案 D 由通项公式及已知得a1q=2①,a1q4= 14 ②,由②÷①得q3= 18 ,解得
q= 1 .故选D.
2
栏目索引
2.已知等比数列{an}的前三项依次为a-1,a+1,a+4,则an= ( )
7,① a1q a1q
2020高考数学原创.2 弧度制 课件(共29张PPT) 公开课一等奖课件

题型二 用弧度制表示角的集合 例2 (1)把-1 480°写成α+2kπ(k∈Z)的形式,
其中0≤α≤2π. (2)若β∈[-4π,0],且β与(1)中α终边相同,求β.
【解】 (1)∵-1 480°=-1 148800π=-749π=-10π+169π, 又 0≤196π≤2π, ∴-1 480°=169π-2×5π=169π+2×(-5)π.
答案:103π
10π 3
典题例证技法归纳
题型探究
题型一 角度制与弧度制的转化
例1 将下列角度与弧度进行互化:
(1)20°;(2)-15°;(3)71π2;(4)-115π. 【解】 (1)20°=2108π0=π9; (2)-15°=-1158π0=-1π2;
(3)71π2=1π80×71π2°=172×180°=7×15°=105°;
(2)如图所示,设扇形的半径为 r cm,弧长为 l cm,圆心角为 θ(0<θ<2π), 由 l+2r=20,得 l=20-2r, 由12lr=9,得12(20-2r)r=9, ∴r2-10r+9=0,解得 r1=1,r2=9. 当 r1=1 cm 时,l=18 cm,θ=rl=118=18>2π(舍去). 当 r2=9 cm 时,l=2 cm,θ=rl=29. ∴扇形的圆心角的弧度数为29.
栏目 导引
第一章 三角函数
栏目 导引
第一章 三角函数
栏目 导引
第一章 三角函数
附赠 中高考状元学习方法
栏目 导引
第一章 三角函数
栏目 导引
第一章 三角函数
前言
高考状元是一个特殊的群体,在许多 人的眼中,他们就如浩瀚宇宙里璀璨夺目 的星星那样遥不可及。但实际上他们和我 们每一个同学都一样平凡而普通,但他们 有是不平凡不普通的,他们的不平凡之处 就是在学习方面有一些独到的个性,又有 着一些共性,而这些对在校的同学尤其是 将参加高考的同学都有一定的借鉴意义。
(2020获奖版)数学说课课件模板 绝对精品

一、教学内容及其解析
阅读材料
疑问1:赵爽是用什么方法
根据两数和与积求得两数的?
x1
x2 x1x2
2c b
2c 2c2 4b
疑问2:这个类似求根公式 x1,2
2
的结果是怎么得来的?
引发探究
疑问3:为什么要引进代数 符号?
……
二
教学目标及其解析
二、教学目二标、目及标其与解目析标解析
教学目标
“一元二次方程求根公式” 背景下的探究活动
某某学校 马某
目录
CATALOG
01 教学内容及其解析 02 教学目标及其解析 03 学生学情分析 04 教学策略分析 05 教学过程设计 06 教学目标检测
一
教学内容及其解析
一、教学内容及其解析
阅读材料《关于一元二次方程的求根公式》
·《勾股圆方图注》中 “已知两数和、两数积,求两数”问题的解决方法 · 一元二次方程根与系数关系
1
阅读思考 提出问题
2
自发合作 探索方法
3
推广归纳 发现规律
4
猜想论证 总结规律
5
概括小结 延伸问题
五、教学过程设计
1.阅读思考,提出问题
问题1:人们在研究一元二次方程的过程中,经历了怎样的历程? 你有什么感受?还有什么疑问?
教学策略1 问题驱动,阅读引发思考
引出赵爽“已知两数和,两数积,求这两数”问题的方法.
问题4:已知长方形面积为q,且相邻两边的和为p,长方形相邻两 边的长是多少?
问题5:如果一元二次方程 ax2 + bx + c = 0(a ? 0) 的两个实数根
是x1、x2,那么两根与系数之间具有怎样的关系?
2020高考数学原创.2组合 公开课一等奖课件

排列与组合的 概念有什么共 同点与不同点?
★组合与排列的区别:
排列定义: 一般地,从n个不同元素中取出m (m≤n) 个元素,按照一定的顺序排成一列,叫做从 n 个不 同元素中取出 m 个元素的一个排列.
组合定义: 一般地,从n个不同元素中取出m(m≤n) 个元素并成一组,叫做从n个不同元素中取出m个元 素的一个组合.
a
b
c
b cd
cd
ab , ac , ad , bc , bd , cd
d
(6个)
2、组合数的定义
从n个不同元素中取出m(m≤n)个元素的
所有组合的个数,叫做从n个不同元素中取出m个
元素的组合数,用符号
C
m n
表示.
C
m n
?
3、组合数公式
组合数公式:
Cnm
Anm Amm
Cnm
n! m!(n
班主任: 我觉得何旋今天取得这样的成绩, 我觉得,很重要的是,何旋是土生土长的北京 二中的学生,二中的教育理念是综合培养学生 的素质和能力。我觉得何旋,她取得今天这么 好的成绩,一个来源于她的扎实的学习上的基 础,还有一个非常重要的,我觉得特别想提的, 何旋是一个特别充满自信,充满阳光的这样一 个女孩子。在我印象当中,何旋是一个最爱笑 的,而且她的笑特别感染人的。所以我觉得她 很阳光,而且充满自信,这是她突出的这样一 个特点。所以我觉得,这是她今天取得好成绩 当中,心理素质非常好,是非常重要的。
高考总分:711分 毕业学校:北京八中 语文139分 数学140分 英语141分 理综291分 报考高校: 北京大学光华管理学院
北京市理科状元杨蕙心
例2、 1平面内有10个点,以其中每2个点为
★组合与排列的区别:
排列定义: 一般地,从n个不同元素中取出m (m≤n) 个元素,按照一定的顺序排成一列,叫做从 n 个不 同元素中取出 m 个元素的一个排列.
组合定义: 一般地,从n个不同元素中取出m(m≤n) 个元素并成一组,叫做从n个不同元素中取出m个元 素的一个组合.
a
b
c
b cd
cd
ab , ac , ad , bc , bd , cd
d
(6个)
2、组合数的定义
从n个不同元素中取出m(m≤n)个元素的
所有组合的个数,叫做从n个不同元素中取出m个
元素的组合数,用符号
C
m n
表示.
C
m n
?
3、组合数公式
组合数公式:
Cnm
Anm Amm
Cnm
n! m!(n
班主任: 我觉得何旋今天取得这样的成绩, 我觉得,很重要的是,何旋是土生土长的北京 二中的学生,二中的教育理念是综合培养学生 的素质和能力。我觉得何旋,她取得今天这么 好的成绩,一个来源于她的扎实的学习上的基 础,还有一个非常重要的,我觉得特别想提的, 何旋是一个特别充满自信,充满阳光的这样一 个女孩子。在我印象当中,何旋是一个最爱笑 的,而且她的笑特别感染人的。所以我觉得她 很阳光,而且充满自信,这是她突出的这样一 个特点。所以我觉得,这是她今天取得好成绩 当中,心理素质非常好,是非常重要的。
高考总分:711分 毕业学校:北京八中 语文139分 数学140分 英语141分 理综291分 报考高校: 北京大学光华管理学院
北京市理科状元杨蕙心
例2、 1平面内有10个点,以其中每2个点为
2020年高考数学复习精选课件 第5节 指数与指数函数 公开课一等奖课件

5
a 16
2
1
b-3÷(4 a 3 ·b-3) 2
2
栏目索引
=-
5
1
a 6
b-3÷( a 13 b32
)
4
=-
5
1
a 2
3
·b 2
4
=- 5 · 1 4 ab3
=- 54aabb2
.
1 1 1 1
(3)原式= a
3b2 a
15
2b3
a6b6
111 115
= a 3 2 6 ·b 2 3 6
=1
a
.
栏目索引
栏目索引
易错警示 (1)指数幂的运算首先将根式、小数指数幂统一化为分数指数幂,以便 利用法则计算,但应注意:①必须同底数幂相乘,指数才能相加;②运算的 先后顺序.(2)当底数是负数时,先确定符号,再把底数化为正数.(3)运算 结果不能同时含有根号和分数指数,也不能既有分母又含有负指数.
栏目索引
1-1
27 8
2 3
1
+(0.002 ) 2
-10×( 5
-2)-1+( 2
- 3
)0=
.
答案 - 167
9
解析
原式=
27 8
2 3
+
1 500
1 2
- 10
5
2
+1
2
=
8 27
3ห้องสมุดไป่ตู้
1
+50 02 -10( 5
应使y=ax2-4x+3的值域为R,
2020年高考数学复习精选课件 第2节 平面向量基本定理及坐标表示 公开课一等奖课件
解得
x y
5, 14.
故点B的坐标为(5,14).
栏目索引
2-2
在△ABC中,点P在BC上,且 BP
=2P C
,点Q是AC的中点,若P A
=(4,3),
PQ
=(1,5),则 BC
=
(
)
A.(-2,7) B.(-6,21) C.(2,-7)
答案
B
∵ BP
=2 PC
,
0, 5,
解得
x
y
3, 或
1
x
y
5, 3,
∴d=(3,-1)或d=(5,3).
变式3-2 在本例条件下,若ma+nb与a-2b共线,求 m 的值.
n
解析 易得ma+nb=(3m-n,2m+2n),a-2b=(5,-2). 由题意得-2(3m-n)-5(2m+2n)=0.
5.在平面直角坐标系中,已知A B
=(-1,3),A C
=(2,-1),则| BC
|=
答案 5
解析
BC
= AC
- AB
=(2,-1)-(-1,3)=(3,-4),∴| BC
|=5.
栏目索引
.
栏目索引
6.已知向量 OA
=(k,12),O B
=(4,5),O C
=(-k,10),且A、B、C三点共线,则k=
2x
x
2
y y
0, 5, 2
解得
2020年高考数学复习精选课件 第1节 任意角和弧度制及任意角的三角函数 公开课一等奖课件
cm.
答案 (1) 1 (2) 8 3 π
2
3
解析 (1)设圆心角是θ,半径是r,
则
2r
1 2
θ
rθ r2
10, 4
⇒
r θ
4,
1或
2
r θ
1,(舍),
8
故扇形的圆心角的大小为 1 .
2
(2)设扇形的半径为r cm,如图.
由sin 60°= 6 ,得r=4 3 ,
•习惯是养成的,除了必要的约束,还需要较长的时 间。行为养成习惯,习惯形成品质,品质决定人生。 自觉保持公共场所的安静,就是良好的行为,就能形 成良好的品质,就会对你的人生起到良好影响。
• 日本火车与瑞士和欧洲各国的火车类似,就是乘客自觉 恬静,读书看报,或者上网工作。这方面,难怪日本早身在 西方文明国家之列,公共交通,首重一个“公”字,国民无 公德,国家再强,GDP再高,没有人心中真正看得起你。
静之内涵
栏目索引
• 文静有礼之仪态 • 安静宜人之环境 • 平静淡然之心境 • 冷静处事之素养
我们可以安静一点吗?(节选)
• 德国摄影记者在东京旅行,拍下一辑东京地铁挤拥的照 片。许多日本人默默承受挤拥,不论西装笔挺,脸孔压在车 厢门的玻璃上,鼻扁嘴凸,面容扭曲,就是一副死忍,绝不 吭声半句。这个照片系列,成为日本国民性格的代表作。
• 日本人乘搭公共交通工具,不论地铁还是飞机,其恬静 是一大景观。手机不会响,为他人着想,固不必说,车厢里 鲜有交谈,即使有,声音也自觉低下来,令西方记者称奇。
4
不能混用,故A、B不对.
栏目索引
2.给出下列命题: ①第二象限角大于第一象限角; ②三角形的内角是第一象限角或第二象限角; ③无论是用角度制还是用弧度制度量一个角,它们与扇形半径的大小无 关; ④若sin α=sin β,则α与β的终边相同; ⑤若cos θ<0,则θ是第二或第三象限的角. 其中正确命题的个数是 ( ) A.1 B.2 C.3 D.4
答案 (1) 1 (2) 8 3 π
2
3
解析 (1)设圆心角是θ,半径是r,
则
2r
1 2
θ
rθ r2
10, 4
⇒
r θ
4,
1或
2
r θ
1,(舍),
8
故扇形的圆心角的大小为 1 .
2
(2)设扇形的半径为r cm,如图.
由sin 60°= 6 ,得r=4 3 ,
•习惯是养成的,除了必要的约束,还需要较长的时 间。行为养成习惯,习惯形成品质,品质决定人生。 自觉保持公共场所的安静,就是良好的行为,就能形 成良好的品质,就会对你的人生起到良好影响。
• 日本火车与瑞士和欧洲各国的火车类似,就是乘客自觉 恬静,读书看报,或者上网工作。这方面,难怪日本早身在 西方文明国家之列,公共交通,首重一个“公”字,国民无 公德,国家再强,GDP再高,没有人心中真正看得起你。
静之内涵
栏目索引
• 文静有礼之仪态 • 安静宜人之环境 • 平静淡然之心境 • 冷静处事之素养
我们可以安静一点吗?(节选)
• 德国摄影记者在东京旅行,拍下一辑东京地铁挤拥的照 片。许多日本人默默承受挤拥,不论西装笔挺,脸孔压在车 厢门的玻璃上,鼻扁嘴凸,面容扭曲,就是一副死忍,绝不 吭声半句。这个照片系列,成为日本国民性格的代表作。
• 日本人乘搭公共交通工具,不论地铁还是飞机,其恬静 是一大景观。手机不会响,为他人着想,固不必说,车厢里 鲜有交谈,即使有,声音也自觉低下来,令西方记者称奇。
4
不能混用,故A、B不对.
栏目索引
2.给出下列命题: ①第二象限角大于第一象限角; ②三角形的内角是第一象限角或第二象限角; ③无论是用角度制还是用弧度制度量一个角,它们与扇形半径的大小无 关; ④若sin α=sin β,则α与β的终边相同; ⑤若cos θ<0,则θ是第二或第三象限的角. 其中正确命题的个数是 ( ) A.1 B.2 C.3 D.4
2020年高考数学复习精选课件 第1节 数列的概念及简单表示法 公开课一等奖课件
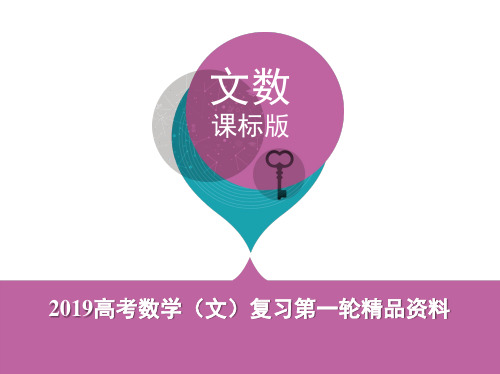
解析 设递推公式an+1=2an+3可以转化为an+1-t=2(an-t),即an+1=2an-t,解得t=
-3.
故an+1+3=2(an+3).
令bn=an+3,则b1=a1+3=5,且
bn1 bn
=
an1 3 an 3
=2.
所以{bn}是以5为首项,2为公比的等比数列.
所以bn=5×2n-1,故an=5×2n-1-3.
栏目索引
文数
课标版
2019高考数学(文)复习第一轮精品资料
栏目索引
文数
课标版
第一节 数列的概念及简单表示法
教材研读
栏目索引
1.数列的定义
按照① 一定顺序 排列的一列数叫做数列,数列中的每一个数叫做这
个数列的② 项 . 2.数列的分类
分类原则
类型
满足条件
按项数分类 有穷数列
项数③ 有限
无穷数列
项数④ 无限
当b≠-1时,an=
3 2
b, n 3n1,
1, n 2.
栏目索引
方法指导 已知Sn求an的三个步骤: (1)先利用a1=S1求出a1; (2)用n-1替换Sn中的n得出Sn-1,利用an=Sn-Sn-1(n≥2)便可求出当n≥2时an的 表达式; (3)看a1是否符合n≥2时an的表达式,若符合,则可以把数列的通项公式合 写;若不符合,则应该分n=1与n≥2两段来写.
4.数列的通项公式
如果数列{an}的第n项与⑩ 序号n 之间的关系可以用一个式子来表
示,那么这个公式叫做这个数列的通项公式.
5.已知数列{an}的前n项和Sn,
2020年高考数学复习精选课件 第5节 椭圆 公开课一等奖课件

A. x2 - y2 =1 64 48
B. x2 + y2 =1 48 64
C. x2 - y2 =1 48 64
D. x2 + y2 =1 64 48
(2)已知椭圆C: ax22 + by22 =1(a>b>0)的左、右焦点为F1、F2,离心率为 33 ,过
F2的直线l交C于A、B两点.若△AF1B的周长为4 3 ,则C的方程为
b2
轴.过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE
的中点,则C的离心率为 ( )
A. 1 B. 1 C. 2 D. 3
3
2
3
4
(2)已知动点P(x,y)在椭圆 x2 + y2 =1上,若A点的坐标为(3,0),| AM |=1,且
25 16
PM
· AM
=0,则| PM
所以 2 = 1 ,
ac ac
即2a-2c=a+c,
所以e= c = 1 .故选A.
a3
解法二:如图,设OE的中点为N,
由题意知|AF|=a-c,|BF|=a+c,|OF|=c,|OA|=|OB|=a,
∵PF∥y轴,∴ | MF | = | AF | = a c , | MF | = | BF | = a c , | OE | | AO | a | ON | | OB | a
2.椭圆的标准方程和几何性质
标准方程 图形
xa 22 + by22 =1(a>b>0)
栏目索引
ay22 + xb22 =1(a>b>0)
性质
范围 对称性
顶点 轴 焦距 离心率
2020高考数学原创.2指数函数及其性质(三) 公开课一等奖课件

作出图象,显示出函数数据表
x
-3 -2 -1 0 1 2 3
y 2 x 0.125 0.25 0.5 1 2 4 8
y 2 x1 0.25 0.5 1 2 4 8 16
y 2 x2 0.5 1 2 4 8 16 32
比较函数
y 2x
y 2x1 y 2x2 的图象关系.
9
比较函数
8
y 2x
7
6
y 2x 1
5
y 2x 1
4
3
的图象关系.
2
1
-4 -2 O
2
4x
(3) y 2 x 1, y 2 x 1. y
9
比较函数
8
y 2x
7
6
y 2x 1
5
y 2x 1
4
3
的图象关系.
2
1
-4 -2 O
2
4x
小 结:
f(x)的图象 向左平移a个单位得到f(x+a)的图象; 向右平移a个单位得到f(x-a)的图象; 向上平移a个单位得到f(x)+a的图象; 向下平移a个单位得到f(x)-a的图象.
性 过点(0,1),即x=0时,y=1
质 在 R 上是增函数
x>0时,ax>1;
在 R 上是减函数
x<0时,0<ax<1
复习引入
指数函数的图象和性质:
a>1
0<a<1
图
y
y=ax y=ax
y
(a>1) (0<a<1)
象
O
x
O
x
定义域 R;值域(0,+∞)
性 过点(0,1),即x=0时,y=1
质 在 R 上是增函数
2020年高考数学复习精选课件 第1节 平面向量的概念及其线性运算 公开课一等奖课件
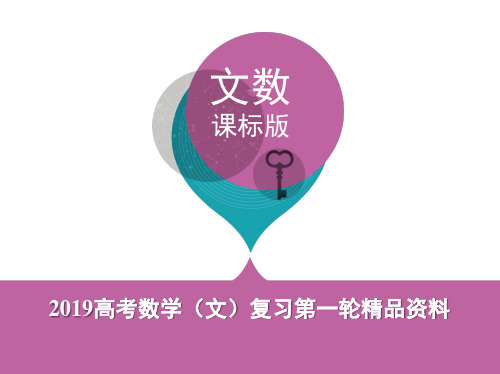
当a=2b时,| aa | = | 22bb | = | bb | ,故a=2b是 | aa | = | bb | 成立的充分条件.
栏目索引
1-2 给出下列命题: ①两个具有公共终点的向量一定是共线向量. ②两个向量不能比较大小,但它们的模能比较大小. ③若λa=0(λ为实数),则λ必为零. ④若λa=μb(λ,μ为实数),则a与b共线. 其中错误命题的个数为 ( ) A.1 B.2 C.3 D.4 答案 C ①错误,两向量是否共线要看其方向,而不是起点或终点.② 正确,因为向量既有大小,又有方向,故两个向量不能比较大小,但两个向 量的模均为实数,故可以比较大小.③错误,当a=0时,无论λ为何值,均有λa =0.④错误,当λ=μ=0时,λa=μb=0,此时,a与b可以是任意向量.故选C.
栏目索引
1-1 设a,b都是非零向量,下列四个条件中,使| aa | = | bb | 成立的充分条件
是 ( )
A.a=-b B.a∥b
C.a=2b D.a∥b且|a|=|b|
答案 C 因为向量 a 的方向与向量a相同,向量 b 的方向与向量b相
|a|
|b|
同,且 | aa | = | bb |,所以向量a与向量b方向相同,故可排除选项A,B,D.
= AC
- AB
=b-c,∵ BD
=2D C
,∴B D
=23 B C
=23 (b
-c),则 AD
= AB
+ BD
= AB
+ 2 BC
=c+ 2 (b-c)= 2 b+1 c.故选D.
3
3
33
栏目索引
2020高考数学原创.2指数函数及其性质 第一课时 公开课一等奖课件

1
,1
在实数范
围内的函数值不存在.
24
(3)若a=1时,函数值y=1,没有研究的必要.
检测.下列函数是指数函数的是:(1)
(1) y 4x (2) y x4 (3) y 4x (4) y (4)x
二、指数函数的图像和性质
x
用描点法作函数
y 2x
和
1 y 2
课题导入
某种细胞分裂时,由1个分裂成2个,2个分 裂成4个…一个这样的细胞分裂x次后,得 到的细分裂的个数y与x的函数关系是什么?
2.1.2指数函数及其性质
第一课时
目标引领
1.理解指数函数的定义 2.能画出指数函数的草图,并能通过观察
函数图象,得出指数函数的定义域、值 域和单调性。
独立自学
1.指数函数的定义是什么? 2.指数函数的图像如何? 3.通过观察指数函数的图象,写出函数的
青 春 风 采
高考总分:
692分(含20分加分) 语文131分 数学145 分英语141分 文综 255分
毕业学校:北京二中 报考高校:
北京大学光华管理学 院
北京市文科状元 阳光女孩--何旋
来自北京二中,高考成绩672分,还有20 分加分。“何旋给人最深的印象就是她 的笑声,远远的就能听见她的笑声。” 班主任吴京梅说,何旋是个阳光女孩。 “她是学校的摄影记者,非常外向,如 果加上20分的加分,她的成绩应该是 692。”吴老师说,何旋考出好成绩的秘 诀是心态好。“她很自信,也很有爱心。 考试结束后,她还问我怎么给边远地区 的学校捐书”。
其中x是自变量,函数的定义域是R.
注意 (1)ax为一个整体,前面系数为1
(2) a>0,且 a≠1 ;
2020年高考数学复习精选课件 第2节 函数的单调性与最值 公开课一等奖课件
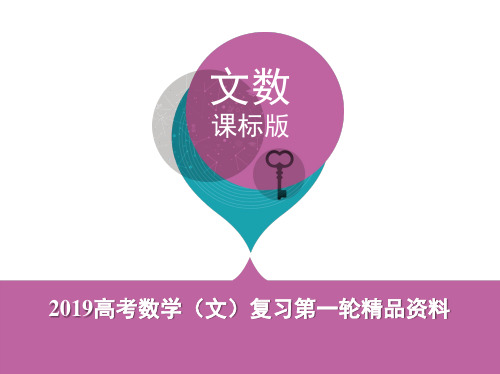
(2)y=
2x2 x2
2x 3 x 1
=
2(
x2 x 1) x2 x 1
1
=∵2+x x2 121x2+1 34=≥2+ 34,x
1 1 2 2
3 4
.
∴2<2+
x
1
1
2
2
3 4
≤2+ 4 = 10 ,
2x 5
2 2x 5
7
因为 2 ≠0,所以y≠- 1 ,
2x 5
2
所以函数y= 1 x
2x 5
的值域为 y |
y
1 2
.
(2)y= 3k 2 k2
1
= 3(k 2 k
1) 2 1
3
=3- 3
k2
1
,因为- 3
<k< 3
,所以1≤k2+1<4,所以-3
则t≥0,且x=t2+1,
∴原函数变为y=t2+1+t,t≥0.
配方得y=
t
1 2
2
+ 3 ,
4
栏目索引
栏目索引
又∵t≥0,∴y≥ 1 + 3 =1.
44
故函数y=x+ x 1的最小值为1.
解法二:因为函数y=x和y= x 1在定义域内均为增函数,故函数y=x+
x 1在[1,+∞)内为增函数,所以ymin=1.
∵1<2< 52 <e,∴f(2)>f 52 >f(e),
2020年高考数学复习精选课件 第节 圆锥曲线的综合问题 公开课一等奖课件
栏目索引
栏目索引
考点二 圆锥曲线中的定点、定值问题
典例2 (2016北京,19,14分)已知椭圆C: ax22 + by22 =1过A(2,0),B(0,1)两点.
(1)求椭圆C的方程及离心率; (2)设P为第三象限内一点且在椭圆C上,直线PA与y轴交于点M,直线PB 与x轴交于点N.求证:四边形ABNM的面积为定值. 解析 (1)由题意得,a=2,b=1.
0,
将(*)代入,得t=- 1 .
2
∴直线l过定点 0,
1 2
.
栏目索引
考点三 圆锥曲线中的探索性问题
典例3 (2015四川,20,13分)如图,椭圆E: ax22 + by22 =1(a>b>0)的离心率是
2 ,点P(0,1)在短轴CD上,且 PC
· PD
=-1.
2
(1)求椭圆E的方程;
由.
解析 (1)由已知条件知,直线l的方程为y=kx+ 2 ,代入椭圆方程得 x2 + 2
(kx+ 2 )2=1,
整理得
1 2
k
2
x2+2 2
kx+1=0.
①
栏目索引
直线l与椭圆有两个不同的交点P和Q等价于Δ=8k2-4 12
k
2
=4k2-2>0,解
得k<- 2 或k> 2 .
栏目索引
2-1 已知椭圆C: ax22 +y2=1(a>1)的上顶点为A,右焦点为F,直线AF与圆M:
(x-3)2+(y-1)2=3相切.
(1)求椭圆C的标准方程;
2020年高考数学复习精选课件 第1节 绝对值不等式 公开课一等奖课件
栏目索引
3-1 (2016河北保定模拟)设函数f(x)=|x-1|+|x-a|(a∈R). (1)当a=4时,求不等式f(x)≥5的解集; (2)若f(x)≥4对x∈R恒成立,求a的取值范围.
解析 (1)当a=4时,不等式即为|x-1|+|x-4|≥5,等价于x2x1, 5 5 或
栏目索引
栏目索引
当x∈[1,2]时,|x-4|-|x-2|≥|x+a|⇔4-x-(2-x)≥|x+a|⇔-2-a≤x≤2-a. 由条件得-2-a≤1且2-a≥2,即-3≤a≤0. 故满足条件的a的取值范围为[-3,0]. 方法技巧 解绝对值不等式的基本方法: (1)利用绝对值的定义,通过分类讨论转化为解不含绝对值符号的普通 不等式; (2)当不等式两端均非负时,可通过两边平方的方法,转化为解不含绝对 值符号的普通不等式; (3)利用绝对值的几何意义,数形结合求解.
栏目索引
即(|x+1|+|x-a|)min>2. 而|x+1|+|x-a|≥|(x+1)-(x-a)|=|1+a|, 所以|1+a|>2,解得a>1或a<-3. 故a的取值范围为(-∞,-3)∪(1,+∞). 方法技巧 绝对值不等式的恒成立问题 (1)研究含有绝对值的函数问题时,根据绝对值的定义,分类讨论去掉绝 对值符号,将原函数转化为分段函数,然后利用数形结合解决问题,这是 常用的思想方法. (2)f(x)<a恒成立⇔f(x)max<a. f(x)>a恒成立⇔f(x)min>a.
2, 3
或 32 5
x
1,
或
x x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
以高考为主线,以教材为根本,锁定高考热点,研析命题角 度,点拨方法技巧,融会贯通知识. ○真题感悟·考点整合——明确备考方向,整合知识要点 ○热点聚焦·题型突破——锁定高考热点,研析命题角度 ○归纳总结·思维升华——总结规律方法,防范易错易混 ○专题训练·对接高考——对接高考热点,限时规范训练
第1讲 函数图象与性质及函数与方程
2.函数的性质 (1)单调性:单调性是函数在其定义域上的局部性质.证明函 数的单调性时,规范步骤为取值、作差、变形、判断符号和 下结论.复合函数的单调性遵循“同增异减”的原则; (2)奇偶性:奇偶性是函数在定义域上的整体性质.偶函数的 图象关于y轴对称,在关于坐标原点对称的定义域区间上具 有相反的单调性;奇函数的图象关于坐标原点对称,在关于 坐标原点对称的定义域区间上具有相同的单调性; (3)周期性:周期性也是函数在定义域上的整体性质.若函数 满足f(a+x)=f(x)(a不等于0),则其周期T=ka(k∈Z).
fx-f-x x <0
的解集为
( ).
A.(-2,0)∪(0,2)
B.(-∞,-2)∪(0,2)
C.(-∞,-2)∪(2,+∞) D.(-2,0)∪(2,+∞) 解析 (1)法一 函数 y=xl|nx||x|的图象过点(e,1),排除 C,D;函
数 y=xl|nx||x|的图象过点(-e,-1),排除 A,选 B.
3.(2014·福建卷)若函数y=logax( a>0,且a≠1)的图象如下图
所示,则下列函数图象正确的是
( ).
解析 因为函数y=logax过点(3,1),所以1=loga 3,解得a=3.y = 3 - x 不 可 能 过 点 (1,3) , 排 除 A ; y = ( - x)3 = - x3 不 可 能 过 点 (1,1),排除C; y=log3(-x)不可能过点(-3,-1), 排除D,故选 B. 答案 B
答案 B
1.解决函数问题忽视函数的定义域或求错函数的定义域,如求 函数 f(x)=xl1n x的定义域时,只考虑 x>0,忽视 ln x≠0 的限 制.
2.函数定义域不同,两个函数也不同;对应关系不同,两个函 数也不同;定义域和值域相同,也不一定是相同的函数.
3.如果一个奇函数 f(x)在原点处有意义,即 f(0)有意义,那么一 定有 f(0)=0.
[微题型 2] 函数性质的应用
【例 1-2】 (1)(2014·安徽卷)若函数 f(x)(x∈R)是周期为 4 的奇
函数,且在[0,2]上的解析式为 f(x)=xsin1-πxx,,1<0≤x≤x≤2,1, 则
f(249)+f(461)=________.
(2)函数 f(x)的定义域为 R,f(-1)=2,对任意 x∈R,f′(x)>2,
3.函数的零点与方程的根 (1)函数的零点与方程根的关系 函数F(x)=f(x)-g(x)的零点就是方程f(x)=g(x)的根,即函数y =f(x)的图象与函数y=g(x)的图象交点的横坐标. (2)零点存在性定理 如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲 线,且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零 点,即存在c∈(a,b)使得f(c)=0, 这个c也就是方程f(x)=0的 根.
答案 C
2.(2014·新课标全国卷Ⅰ)设函数f(x),g(x)的定义域都为R,且 f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是 ( ). A.f(x)g(x)是偶函数 B.|f(x)|g(x)是奇函数 C.f(x)|g(x)|是奇函数 D.|f(x)g(x)|是奇函数 解析 f(x)为奇函数,g(x)为偶函数,故f(x)g(x)为奇函数, f(x)|g(x)|为奇函数,|f(x)|g(x)为偶函数,|f(x)g(x)|为偶函数,故 选C. 答案 C
的零点个数为
( ).
A.1
B.2
C.3
D.4
解析 (1)当x≤0时,由f(x)=0,即x2+2 014x-2 015=0,得(x -1)(x+2 015)=0,解得x=1(舍去)或x=-2 015; (2)当x>0时,设g(x)=x-2,h(x)=ln x,如图,分别作出两个函 数的图象,由图可知,两函数图象有两个交点,所以函数f(x)在 x>0时有两个零点. 综上,函数f(x)有3个零点,故选C.
法二 由已知,设 f(x)=xl|nx||x|,则 f(-x)=-f(x),故函数 f(x)为
奇函数,当 x>0 时,f(x)=ln x 在(0,+∞)上为增函数,故选 B.
(2)由奇函数的定义和 f(2)=0 得出函数在(-∞,0)上也为增函 数.画出函数草图(如图),可得在(-2,0)和(2,+∞)上 f(x)>0, 在(-∞,-2)和(0,2)上 f(x)<0.当 x>0 时,由fx-xf-x<0,可得 f(x)-f(-x)=2f(x)<0,结合图象可知(0,2)符合;当 x<0 时,由 fx-xf-x<0,可得 f(x)-f(-x)=2f(x)>0,结合图象可知(-2,0) 符合.
答案 C
探究提高 (1)本题利用分段函数考查了解决零点问题的两种方 法——解方程与函数图象,当x>0时,不能直接解方程,所以要 利用数形结合的方法将其转化为两函数图象的交点问题来求 解.(2)解决函数零点问题要把握零点的实质——方程的根、函数 图象与x轴的交点的横坐标.判断函数零点个数问题一般都要转 化为两个函数图象的交点个数来求解.
(2)若 g(x)-f(x)=0 有两个相异的实根,即 g(x)=f(x)中函数 g(x) 与 f(x)的图象有两个不同的交点, 作出 g(x)=x+ex2(x>0)的大致图象. ∵f(x)=-x2+2ex+m-1 =-(x-e)2+m-1+e2. 其对称轴为 x=e,开口向下,最大值为 m-1+e2.
[微题型 2] 由函数零点的存在情况求参数 【例 2-2】 已知函数 f(x)=-x2+2ex+m-1,g(x)=x+ex2(x>
0). (1)若 g(x)=m 有实根,求 m 的取值范围; (2)确定 m 的取值范围,使得 g(x)-f(x)=0 有两个相异实根.
解 (1)∵g(x)=x+ex2≥2 e2=2e, 等号成立的条件是 x=e. 故 g(x)的值域是[2e,+∞),因而只需 m≥2e, 则 g(x)=m 就有实根. 故 m∈[2e,+∞).
(2)由题可知,当-2<x<2 时,f(x)>0.由 f(x-1)>0,得-2<x-1<2, 即-1<x<3.
答案 (1)C (2)(-1,3)
热点二 以函数零点为背景的函数问题
[微题型 1] 函数零点个数的求解
【例 2-1】 已知 f(x)=x22-+x2+0l1n4xx,-x2>0105,,x≤0, 则函数 f(x)
故当m-1+e2>2e,即m>-e2+2e+1时, g(x)与f(x)有两个交点, 即g(x)-f(x)=0有两个相异实根. ∴m的取值范围是(-e2+2e+1,+∞). 探究提高 解决由函数零点的存在情况求参数的值或取值范围 问题,关键是利用函数方程思想或数形结合思想,构建关于参 数的方程或不等式求解.
4.奇函数在两个对称的区间上有相同的单调性,偶函数在两个 对称的区间上有相反的单调性.
注意以下两点: ①满足条件的零点可能不唯一; ②不满足条件时,也可能有零点.
热点一 函数图象与性质的融合问题 [微题型 1] 函数图象的识别与应用 【例 1-1】 (1)函数 y=xl|nx||x|的图象可能是
( ).
(2)设奇函数 f(x)在(0,+∞)上为增函数,且 f(2)=0,则不等式
【训练 2】 (2014·山东卷)已知函数 f(x)=|x-2|+1,g(x)=kx.若
方程 f(x)=g(x)有两个不相等的实根,则实数 k 的取值范围是
( ).
A.0,12 C.(1,2)
B.12,1 D.(2,+∞)
解析 由 f(x)=g(x),∴|x-2|+1=kx,即|x-2|=kx-1, 所以原题等价于函数 y=|x-2|与 y=kx-1 的图象有 2 个不同交 点. 如图: ∴y=kx-1 在直线 y=x-1 与 y=12x-1 之间, ∴12<k<1,故选 B.
A.a>b>c
B.b>a>c
C.a>c>b
D.c>b>a
(2)(2014·新课标全国卷Ⅱ)已知偶函数 f(x)在[0,+∞)单调递
减,f(2)=0.若 f(x-1)>0,则 x 的取值范围是________.
解析 (1)∵log2π>1,log1π<0,0<π-2<1,∴a>c>b,故选 C. 2
若使得 f(x)-a=0 在 x∈[-3,4]上有 10 个零点,由于 f(x)的周期 为 3,则只需直线 y=a 与函数 f(x)=|x2-2x+12|,x∈[0,3)的应有 4 个交点,则有 a∈0,12. 答案 0,12
[考点整合] 1.函数及其图象
(1)定义域、值域和对应关系是确定函数的三要素,是一个整 体,研究函数问题时务必遵循“定义域优先”的原则. (2)对于函数的图象要会作图、识图和用图,作函数图象有两 种基本方法:一是描点法;二是图象变换法,其中图象变换 有平移变换、伸缩变换和对称变换.
探究提高 (1)根据函数的奇偶性、单调性和周期性,把所求函数 值转化为给定范围内的函数值,再利用所给范围内的函数解析 式求出函数值.(2)第(2)题求解的关键是对条件“f′(x)>2”的 巧妙转化,利用函数的单调性求解不等式.
【训练 1】 (1)(2014·天津卷)设 a=log2π,b=log1π,c=π-2,则 2 ( ).
高考定位 1.高考对函数图象与性质的考查主要体现在函数的定 义域、值域、解析式、单调性、奇偶性、周期性等方面.函数 图象的考查角度有两个方面,一是函数解析式与函数图象的对 应关系;二是利用图象研究函数性质、方程及不等式的解等, 综合性较强.2.考查函数零点所在区间、零点个数的判断以及由 函数零点的个数或取值范围求解参数的取值范围问题.
第1讲 函数图象与性质及函数与方程
2.函数的性质 (1)单调性:单调性是函数在其定义域上的局部性质.证明函 数的单调性时,规范步骤为取值、作差、变形、判断符号和 下结论.复合函数的单调性遵循“同增异减”的原则; (2)奇偶性:奇偶性是函数在定义域上的整体性质.偶函数的 图象关于y轴对称,在关于坐标原点对称的定义域区间上具 有相反的单调性;奇函数的图象关于坐标原点对称,在关于 坐标原点对称的定义域区间上具有相同的单调性; (3)周期性:周期性也是函数在定义域上的整体性质.若函数 满足f(a+x)=f(x)(a不等于0),则其周期T=ka(k∈Z).
fx-f-x x <0
的解集为
( ).
A.(-2,0)∪(0,2)
B.(-∞,-2)∪(0,2)
C.(-∞,-2)∪(2,+∞) D.(-2,0)∪(2,+∞) 解析 (1)法一 函数 y=xl|nx||x|的图象过点(e,1),排除 C,D;函
数 y=xl|nx||x|的图象过点(-e,-1),排除 A,选 B.
3.(2014·福建卷)若函数y=logax( a>0,且a≠1)的图象如下图
所示,则下列函数图象正确的是
( ).
解析 因为函数y=logax过点(3,1),所以1=loga 3,解得a=3.y = 3 - x 不 可 能 过 点 (1,3) , 排 除 A ; y = ( - x)3 = - x3 不 可 能 过 点 (1,1),排除C; y=log3(-x)不可能过点(-3,-1), 排除D,故选 B. 答案 B
答案 B
1.解决函数问题忽视函数的定义域或求错函数的定义域,如求 函数 f(x)=xl1n x的定义域时,只考虑 x>0,忽视 ln x≠0 的限 制.
2.函数定义域不同,两个函数也不同;对应关系不同,两个函 数也不同;定义域和值域相同,也不一定是相同的函数.
3.如果一个奇函数 f(x)在原点处有意义,即 f(0)有意义,那么一 定有 f(0)=0.
[微题型 2] 函数性质的应用
【例 1-2】 (1)(2014·安徽卷)若函数 f(x)(x∈R)是周期为 4 的奇
函数,且在[0,2]上的解析式为 f(x)=xsin1-πxx,,1<0≤x≤x≤2,1, 则
f(249)+f(461)=________.
(2)函数 f(x)的定义域为 R,f(-1)=2,对任意 x∈R,f′(x)>2,
3.函数的零点与方程的根 (1)函数的零点与方程根的关系 函数F(x)=f(x)-g(x)的零点就是方程f(x)=g(x)的根,即函数y =f(x)的图象与函数y=g(x)的图象交点的横坐标. (2)零点存在性定理 如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲 线,且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零 点,即存在c∈(a,b)使得f(c)=0, 这个c也就是方程f(x)=0的 根.
答案 C
2.(2014·新课标全国卷Ⅰ)设函数f(x),g(x)的定义域都为R,且 f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是 ( ). A.f(x)g(x)是偶函数 B.|f(x)|g(x)是奇函数 C.f(x)|g(x)|是奇函数 D.|f(x)g(x)|是奇函数 解析 f(x)为奇函数,g(x)为偶函数,故f(x)g(x)为奇函数, f(x)|g(x)|为奇函数,|f(x)|g(x)为偶函数,|f(x)g(x)|为偶函数,故 选C. 答案 C
的零点个数为
( ).
A.1
B.2
C.3
D.4
解析 (1)当x≤0时,由f(x)=0,即x2+2 014x-2 015=0,得(x -1)(x+2 015)=0,解得x=1(舍去)或x=-2 015; (2)当x>0时,设g(x)=x-2,h(x)=ln x,如图,分别作出两个函 数的图象,由图可知,两函数图象有两个交点,所以函数f(x)在 x>0时有两个零点. 综上,函数f(x)有3个零点,故选C.
法二 由已知,设 f(x)=xl|nx||x|,则 f(-x)=-f(x),故函数 f(x)为
奇函数,当 x>0 时,f(x)=ln x 在(0,+∞)上为增函数,故选 B.
(2)由奇函数的定义和 f(2)=0 得出函数在(-∞,0)上也为增函 数.画出函数草图(如图),可得在(-2,0)和(2,+∞)上 f(x)>0, 在(-∞,-2)和(0,2)上 f(x)<0.当 x>0 时,由fx-xf-x<0,可得 f(x)-f(-x)=2f(x)<0,结合图象可知(0,2)符合;当 x<0 时,由 fx-xf-x<0,可得 f(x)-f(-x)=2f(x)>0,结合图象可知(-2,0) 符合.
答案 C
探究提高 (1)本题利用分段函数考查了解决零点问题的两种方 法——解方程与函数图象,当x>0时,不能直接解方程,所以要 利用数形结合的方法将其转化为两函数图象的交点问题来求 解.(2)解决函数零点问题要把握零点的实质——方程的根、函数 图象与x轴的交点的横坐标.判断函数零点个数问题一般都要转 化为两个函数图象的交点个数来求解.
(2)若 g(x)-f(x)=0 有两个相异的实根,即 g(x)=f(x)中函数 g(x) 与 f(x)的图象有两个不同的交点, 作出 g(x)=x+ex2(x>0)的大致图象. ∵f(x)=-x2+2ex+m-1 =-(x-e)2+m-1+e2. 其对称轴为 x=e,开口向下,最大值为 m-1+e2.
[微题型 2] 由函数零点的存在情况求参数 【例 2-2】 已知函数 f(x)=-x2+2ex+m-1,g(x)=x+ex2(x>
0). (1)若 g(x)=m 有实根,求 m 的取值范围; (2)确定 m 的取值范围,使得 g(x)-f(x)=0 有两个相异实根.
解 (1)∵g(x)=x+ex2≥2 e2=2e, 等号成立的条件是 x=e. 故 g(x)的值域是[2e,+∞),因而只需 m≥2e, 则 g(x)=m 就有实根. 故 m∈[2e,+∞).
(2)由题可知,当-2<x<2 时,f(x)>0.由 f(x-1)>0,得-2<x-1<2, 即-1<x<3.
答案 (1)C (2)(-1,3)
热点二 以函数零点为背景的函数问题
[微题型 1] 函数零点个数的求解
【例 2-1】 已知 f(x)=x22-+x2+0l1n4xx,-x2>0105,,x≤0, 则函数 f(x)
故当m-1+e2>2e,即m>-e2+2e+1时, g(x)与f(x)有两个交点, 即g(x)-f(x)=0有两个相异实根. ∴m的取值范围是(-e2+2e+1,+∞). 探究提高 解决由函数零点的存在情况求参数的值或取值范围 问题,关键是利用函数方程思想或数形结合思想,构建关于参 数的方程或不等式求解.
4.奇函数在两个对称的区间上有相同的单调性,偶函数在两个 对称的区间上有相反的单调性.
注意以下两点: ①满足条件的零点可能不唯一; ②不满足条件时,也可能有零点.
热点一 函数图象与性质的融合问题 [微题型 1] 函数图象的识别与应用 【例 1-1】 (1)函数 y=xl|nx||x|的图象可能是
( ).
(2)设奇函数 f(x)在(0,+∞)上为增函数,且 f(2)=0,则不等式
【训练 2】 (2014·山东卷)已知函数 f(x)=|x-2|+1,g(x)=kx.若
方程 f(x)=g(x)有两个不相等的实根,则实数 k 的取值范围是
( ).
A.0,12 C.(1,2)
B.12,1 D.(2,+∞)
解析 由 f(x)=g(x),∴|x-2|+1=kx,即|x-2|=kx-1, 所以原题等价于函数 y=|x-2|与 y=kx-1 的图象有 2 个不同交 点. 如图: ∴y=kx-1 在直线 y=x-1 与 y=12x-1 之间, ∴12<k<1,故选 B.
A.a>b>c
B.b>a>c
C.a>c>b
D.c>b>a
(2)(2014·新课标全国卷Ⅱ)已知偶函数 f(x)在[0,+∞)单调递
减,f(2)=0.若 f(x-1)>0,则 x 的取值范围是________.
解析 (1)∵log2π>1,log1π<0,0<π-2<1,∴a>c>b,故选 C. 2
若使得 f(x)-a=0 在 x∈[-3,4]上有 10 个零点,由于 f(x)的周期 为 3,则只需直线 y=a 与函数 f(x)=|x2-2x+12|,x∈[0,3)的应有 4 个交点,则有 a∈0,12. 答案 0,12
[考点整合] 1.函数及其图象
(1)定义域、值域和对应关系是确定函数的三要素,是一个整 体,研究函数问题时务必遵循“定义域优先”的原则. (2)对于函数的图象要会作图、识图和用图,作函数图象有两 种基本方法:一是描点法;二是图象变换法,其中图象变换 有平移变换、伸缩变换和对称变换.
探究提高 (1)根据函数的奇偶性、单调性和周期性,把所求函数 值转化为给定范围内的函数值,再利用所给范围内的函数解析 式求出函数值.(2)第(2)题求解的关键是对条件“f′(x)>2”的 巧妙转化,利用函数的单调性求解不等式.
【训练 1】 (1)(2014·天津卷)设 a=log2π,b=log1π,c=π-2,则 2 ( ).
高考定位 1.高考对函数图象与性质的考查主要体现在函数的定 义域、值域、解析式、单调性、奇偶性、周期性等方面.函数 图象的考查角度有两个方面,一是函数解析式与函数图象的对 应关系;二是利用图象研究函数性质、方程及不等式的解等, 综合性较强.2.考查函数零点所在区间、零点个数的判断以及由 函数零点的个数或取值范围求解参数的取值范围问题.
