小学奥数和倍、差倍、和差问题经典例题及练习题
小学生奥数差倍问题、和差问题练习题

【导语】解奥数题时,如果能合理的、科学的、巧妙的借助点、线、⾯、图、表将奥数问题直观形象的展⽰出来,将抽象的数量关系形象化,可使同学们容易搞清数量关系,沟通“已知”与“未知”的联系,抓住问题的本质,迅速解题。
以下是整理的《⼩学⽣奥数差倍问题、和差问题练习题》相关资料,希望帮助到您。
1.⼩学⽣奥数差倍问题练习题 1、⼀个车间,⼥⼯⽐男⼯少35⼈,男⼥⼯各调出17⼈后,男⼯⼈数是⼥⼯⼈数的2倍。
原有男⼯、⼥⼯各多少⼈? 2、甲、⼄两数的差及商都等于6,那么甲、⼄两数的和等于多少? 3、某车间男⼯⼈数是⼥⼯⼈数的2倍,若调⾛18个男⼯,那么⼥⼯⼈数是男⼯⼈数的两倍,这个车间有⼥⼯多少⼈? 4、有两缸⾦鱼,如果从甲缸中取出5条放⼊⼄缸,两缸内的⾦鱼数相等。
已知原来甲缸的⾦鱼数是⼄缸的1⼜2/3倍,甲缸原有⾦鱼多少条? 4、两筐重量相等的苹果,甲筐卖出7千克,⼄筐卖出19千克以后,甲筐余下的千克数是⼄筐的3倍,两筐苹果各有多少千克? 2.⼩学⽣奥数差倍问题练习题 1、四年级有4个班,不算甲班其余三个班的总⼈数是131⼈;不算丁班其余三个班的总⼈数是134⼈;⼄、丙两班的总⼈数⽐甲、丁两班的总⼈数少1⼈,问这四个班共有多少⼈? 解答:⽤131+134=265,这是1个甲、丁和2个⼄、丙的总和,因为⼄、丙两班的总⼈数⽐甲、丁两班的总⼈数少1⼈,所以⽤265-1=264就刚好是3个⼄、丙的和,264÷3=88,就是说⼄丙的和是88,那么甲丁和是88+1=89,所以四个班的和是88+89=177⼈。
2、有四个数,其中每三个数的和分别是45,46,49,52,那么这四个数中最⼩的⼀个数是多少? 解答:⼤家想想,我如果把4个数全加起来是什么?实际上是每个数都加了3遍!⼤家⼀定要记住这种思想!(45+46+49+52)÷3=64就是这四个数的和,题⽬要求最⼩的数,我就⽤64减去52(某三个数和的`)就是最⼩的数,等于12。
和倍,差倍,和差问题

和倍,差倍,和差问题(基础例题详解)和倍、差倍、和差问题是小学阶段很典型的一类问题,这类问题的数量关系简单,有固定的解题思路,可以依据线段图分析题中的数量关系。
和倍问题就是已知大数与小数的和,还知道大数是小数的几倍,求这两个数。
差倍问题就是已知大数与小数的差,还知道大数是小数的几倍,求这两个数。
和差问题就是已知大数和小数的和,还知道它们的差,求这两个数。
例题1.(和倍问题)甲乙共有人民币285元,已知甲的钱数是乙的2倍,甲乙各有人民币多少元?解析:已知甲的钱数是乙的2倍,可知乙的钱数是一倍量,而甲的钱数是2个一倍量,画线段图表示它们的关系:乙的钱数:甲的钱数从图中可知,甲的钱数和乙的钱数一共是(1+2)个一倍量,先求出1个一倍量就是乙的钱数,再求出2个一倍量就是甲的钱数。
列式解答:285÷(1+2)=95(元)95×2=190(元)答:甲有人民币190元,乙有人民币95元。
从例题可以看到,解决和倍问题的关键是先找一倍量,再找两个数的和以及它们的倍数和(就是一共几个一倍量),就可以先求出一倍量,再另一个数。
公式:两数和÷(倍数+1)=一倍量的数一倍量的数×倍数=几倍量的数(还可以:两数和-一倍量的数=几倍量的数)例题2.(差倍问题)参加读书活动的女生比男生多18人,女生人数是男生人数的3倍,参加读书活动的男生和女生各多少人?解析:已知女生人数是男生人数的3倍,可知男生人数是一倍量,而女生人数是3个一倍量,画线段图表示它们的关系:男生人数:女生人数女生比男生多18人从图中可知,女生人数比男生人数多(3-1)个一倍量,先求出1个一倍量就是男生人数,再求出3个一倍量就是女生人数。
列式解答:18÷(3-1)=9(人)9×3=27(人)答:参加读书活动的女生有27人,男生有9人。
从例题可以看到,解决差倍问题的关键也是先找一倍量,再找两个数的差以及它们的倍数差,就可以先求出一倍量,再求另一个数。
三年级奥数和倍、差倍、和差问题

三年级奥数和倍、差倍、和差问题和倍问题【例题1】学校有科技书和故事书共480本,科技书的本数是故事书的3倍。
两种书各有多少本?【思路导航】为了便于理解题意,我们画图来分析:由图可知,如果把故事书的本数看作一份,那么科技书的本数就是这样的3份,两种书的总本数就是这样的1+3=4份。
把480本书平均分成4份,1份是故事书的本数,3份是科技书的本数。
480÷(1+3)=120(本)120×3=360(本).练习1:1.用锡和铝制成的合金是720千克,其中铝的重量是锡的5倍。
铝和锡各用了多少千克?2.甲、乙两数的和是112.甲数除以乙数的商是6,甲、乙两数各是多少?3.一块长方形黑板的周长是96分米,长是宽的3倍。
这块长方形黑板的长和宽各是多少分米?【例题2】果园里有梨树、桃树和苹果树共1200棵,其中梨树的棵数是苹果树的3倍,桃树的棵数是苹果树的4倍。
求梨树、桃树和苹果树各有多少棵?【思路导航】如果把苹果树的棵数看作1份,三种树的总棵数是这样的1+3+4=8份。
所以,苹果树有1200÷8=150(棵),梨树有150×3=450(棵),桃树有150×4=600(棵).练习2:3,果园里种了一批苹果树和桃树,已知苹果树比桃树多1600棵,苹果树的棵数比桃树的3倍多100棵。
苹果树和桃树各种了多少棵?例3:育红小学买了一些足球、排球和篮球,已知足球比排球多7只,排球比篮球多11只,足球的只数是篮球的3倍。
足球、排球和篮球各买了多少只?分析与解答:由题意可知,足球比篮球多买了7+11=18只,它是篮球的3-1=2倍。
所以,买篮球18÷2=9只,买排球9+11=20只,买足球20+7=27只。
练习三1,玩具厂二月份比一月份多生产玩具2000个,三月份比二月份多生产3000个,三月份生产的玩具个数是一月份的2倍。
每个月各生产多少个?2,某农具厂第三季度比第二季度多生产2800套轴承,第一季度比第二季度少生产1200套。
小学奥数和差问题、和倍问题、差倍问题专项练习附答案

小学奥数和差问题、和倍问题、差倍问题专项练习附答案(1)学校去年有12人参加体育兴趣小组,今年是去年的2倍少3人,今年体育兴趣小组有多少人?(2)小红和小明共有零花钱9元,小红的钱数是小明的2倍,小红和小明分别有零花钱多少元?(3)小英和小林共有15个果冻布丁,其中小林的个数比小英少3个。
小英和小林各有多少个果冻布丁?(4)一根电线长22米,剪掉一半后,是另一根电线的5倍少4米,那么另一根电线长多少米?(5)期中考试王平和李杨语文成绩的总和是188分,李杨比王平少4分,两人各考了多少分?(6)两筐水果共重124千克,第一筐比第二筐多8千克,两筐水果各重多少千克?(7)明明家有课外书20本,亮亮家的课外书是明明家的3倍,两人共有课外书多少本?(8)明明和亮亮共有课外书33本,亮亮的课外书是明明的2倍,两人各有课外书多少本?(9)学校苗圃中有月季花和菊花共30棵,其中月季花的棵数比菊花多6棵。
学校的月季花和菊花各有多少棵?(10)甲有19元钱,是乙的3倍少5元,乙有多少钱?(11)幼儿园大班共有14个小朋友,男孩比女孩多2个。
则男孩女孩各有多少人?(12)甲、乙两人年龄的和是35岁,甲比乙小5岁。
问甲、乙各多少岁?(13)甲班和乙班共有图书160本。
甲班的图书本数是乙班的3倍,甲班和乙班各有图书多少本?(14)一次画展中,人物画和风景画共20幅,其中人物画比风景画少2幅。
风景画有多少幅?(15)小红和妈妈的年龄加在一起是40岁,妈妈年龄是小红年龄的4倍,小红和妈妈各几岁?(16)小红有15颗星,亮亮的颗数是小红的3倍还少4颗,亮亮有多少颗星?(17)小茜和小敏两人今年的年龄和是23岁,4年后,小茜将比小敏大3岁,问小茜和小敏今年各多少岁?(18)小明的邮票比小红多15张,小明的张数是小红的4倍,两人各几张?(19)甲乙两数之和是341,甲数的最后一位数字是0,如果把0去掉,就与乙数相同,问甲乙两数各是多少?(20)两笼鸡蛋共19只,若甲笼再放入4只,乙笼中取出两只,这时乙笼比甲笼鸡蛋还多1只。
六年级奥数及倍、差倍、及差问题

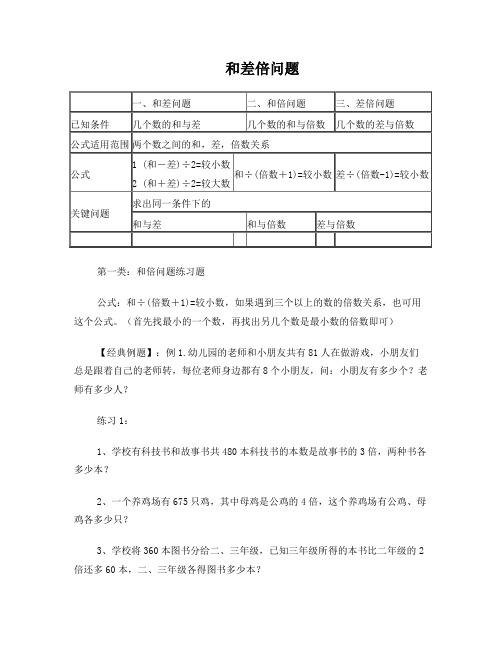
优选文档和差倍问题一、和差问题二、和倍问题三、差倍问题已知条件几个数的和与差几个数的和与倍数几个数的差与倍数公式适用范两个数之间的和,差,倍数关系围① ( 和-差 ) ÷ 2=较小数和÷ ( 倍数+ 1)= 较小数差÷ (倍数-1)=较小数公式② ( 和+差 ) ÷ 2=较大数求出同一条件下的要点问题和与差和与倍数差与倍数第一类:和倍问题练习题公式:和÷ ( 倍数+ 1)= 较小数,若是遇到三个以上的数的倍数关系,也可用这个公式。
(第一找最小的一个数,再找出另几个数是最小数的倍数即可)【经典例题】:例 1. 少儿园的老师和小朋友共有 81 人在做游戏,小朋友们总是跟着自己的老师转,每位老师身边都有 8 个小朋友,问:小朋友有多少个?老师有多少人?练习 1:1、学校有科技书和故事书共480 本科技书的本3、学校将 360 本图书分给二、三年级,已知三数是故事书的 3 倍,两种书各多少本?年级所得的本书比二年级的 2 倍还多 60 本,二、三年级各得图书多少本?2、一个养鸡场有675 只鸡,其中母鸡是公鸡的4 倍,这个养鸡场有公鸡、母鸡各多少只?4、爸爸要把 140 张邮票分给弟弟和妹妹,已知弟弟分得的邮票张数比妹妹的 4 倍少 10 张,弟弟和妹妹各分得邮票多少张?例2、甲、乙、丙 3 数和是 183, 乙比丙的 2 倍少 4,甲比丙的 3 倍多 7,求甲、乙、丙三数各是多少?练习 2、1 、三堆糖果共有 105 颗,其中第一堆糖果的 5. 果园里有桃树、梨树、苹果树共552 棵.桃数量是第二堆的3 倍,而第三堆糖果的数量又树比梨树的2倍多12棵,苹果树比梨树少20比第二堆的 2 倍少 3 颗.第三堆糖果有多少颗?棵,求桃树、梨树和苹果树各有多少棵?(☆☆☆)2.甲、乙、丙三个粮仓一共存有 109 吨粮食.其中甲粮仓的粮食总量比乙粮仓的 3 倍多 1 吨, 6. 某驻军有三个坦克连,共有 115 辆坦克,一而乙粮仓的粮食总量则是丙粮仓的 2 倍.问:连坦克数量比二连的 2 倍多 2,而二连的坦克数甲粮仓比丙粮仓多存粮多少吨?量比三连的 3 倍多 1.请问:一连比三连多几辆坦克?(★★★)【重难点例题】:甲组的图书是乙组的 3 倍,若乙组给甲组 6 本,则甲组的图书是乙组的 5 倍,甲组原来有图书多少本?练习 1. 小明原来的画片是小红的 3 倍,今后二 2. 少儿园买来的苹果个数是梨的 3 倍,吃掉 10 人各买了5 张,这样,小明的画片就是小红的 2 个梨和 6 个苹果后,剩下苹果正好是梨的 5 倍。
三年级奥数:和倍问题,和差问题,差倍问题,周期问题,时间问题

三年级奥数:和倍问题,和差问题,差倍问题,周期问题,时间问题和倍问题,就是已知几个数的和与这几个数之间的倍数关系,求这几个数各是多少的应用题。
解和倍问题的关键是要找准“和”与“倍”,并能借助线段图来解决问题。
解和倍问题的一般思路是:(1)读题,找出最小的一个数,把它看成1倍量;(2)画图,用线段图表示出数与数之间的倍数关系;(3)比较,观察图形准确判断“和”里面一共是几倍或几倍多几(几倍少几),即判断“和”相当于几个1倍量,并求出1倍量;(4)代入,根据1倍量与几个数之间的倍数关系求出其他的数。
已知两个数的倍数关系,把较小的数看成1份,较大的数就是较小数的几倍,较大的数就是几份。
下面我们来看例题1。
例题1解决这类和倍问题时,首先根据倍数关系画出线段图,以较小量为一段,先画出较小的的量,然后找到和相当于多少份,求出一份数。
一份的数知道了,其他的问题也就好解决了。
例题2我们知道,平均数(每份数)=总数÷总份数。
师傅和徒弟的总份数根据题意可以看成是和徒弟加工个数一样的4份。
当两个量的和与倍数关系不对应时,先求出与倍数关系对应的和,再画线段图求出两个量。
例题3求三个量的和倍问题时,先比较三个数的大小,再找出1倍量,画出线段图,然后通过“剪尾巴”或“填坑”找到三个数的和相当于多少份,求出1份数。
通过以上的例子,详细大家已经对和倍问题有了一定的了解,下面我就给大家出一些相关的练习1、甲乙两人共有150张画片,甲的张数比乙的2倍多30张。
两人各有多少张画片?2、四、五年级共有165人,四年级学生比五年级学生人数的2倍少6人。
四五年级各有学生多少人?3、小丽有红、黄、白三种颜色的珠子54粒,红珠子是黄珠子的2倍,白珠子是黄珠子的3倍。
三种颜色的珠子各有多少粒?和差问题与和倍问题、差倍问题一起统称“和差倍问题”,是小学阶段尤其是中年级常见的典型应用题。
和差问题的特点是已知几个数的和与这几个数的差,求这几个数各是多少的应用题。
四年级下册奥数试题-和差问题、和倍问题、差倍问题

和差问题、和倍问题、差倍问题一、和差问题:已知两个数的和与差,求出这两个数各是多少的应用题,叫做和差应用题。
基本数量关系是:(和+差)÷2=大数(和-差)÷2=小数解答和差应用题的关键是选择合适的数作为标准,设法把若干个不相等的数变为相等的数,某些复杂的应用题没有直接告诉我们两个数的和与差,可以通过转化求它们的和与差,再按照和差问题的解法来解答。
例1:有甲乙两堆煤,共重52吨,已知甲比乙多4吨,两堆煤各重多少吨?分析:根据公式,我们要找出两个数的和与差,就能解决问题。
由题意:堆煤共重52吨知:两数和是52;甲比乙多4吨知:两数差是4。
甲的煤多,甲是大数,乙是小数。
故解法如下:甲:(52+4)÷2=28(吨)乙:28-4=24(吨)例2:两只笼子里共有15只鸡,从甲笼提出3只后,甲笼比乙笼还多2只,两只笼子原来各有多少只鸡?分析:从题意知:甲比乙多5只,所以,两数和是15,两数差是5.甲是大数。
甲:(15+5)÷2=10(只)乙: 15-10=5(只)练习:1、两堆石子共有800吨,第一堆比第二堆多200吨,两堆石子各有多少吨?2、黄茜和胡敏两人今年的年龄是23岁,4年后,黄茜比胡敏大3岁,问黄茜和胡敏今年各是多少岁?3、把长84厘米的铁丝围成一个使长比宽多6厘米的长方形。
长和宽各是多少厘米?二、和倍问题已知两个数的和,又知两个数的倍数关系,求这两个数分别是多少,这类问题称为和倍问题。
解决和倍问题的基本方法:将小数看成1份,大数是小数的n倍,大数就是n份,两个数一共是n+1份。
基本数量关系:小数=和÷(n+1)大数=小数×倍数或和-小数=大数例1 :甲班和乙班共有图书160本,甲班的图书是乙班的3倍,甲乙两班各有图书多少本?分析:从题目中知,乙班的图书数较少,故乙是小数,占1份,甲占(3+1)份。
乙:160÷(3+1)=40(本)甲:160-40=120(本)例2:果园里有梨树和桃树共165棵,桃树棵数比梨树棵数的2倍少6棵,梨树和桃树各多少棵?分析:由题意,桃树增加6棵,桃树正好是梨树的2倍,这时总数就是:165+6=171,这样就转化成标准和倍问题,将梨树看成1份,一共是3份。
小学四年级奥数:较复杂的和差倍问题

【导语】解答较复杂的和差倍问题,需要我们从整体上把握住问题的本质,将题⽬进⾏合理的转化,从⽽将较复杂的问题转化为⼀般和倍、差倍、和差应⽤题来解决。
以下是⽆忧考整理的《⼩学四年级奥数:较复杂的和差倍问题》,希望帮助到您。
【篇⼀】 例题:甲的存款是⼄的4倍,如果甲取出110元,⼄存⼊110元,那么⼄的存款是甲的3倍。
甲、⼄原来各有存款多少元? 分析与解答:由“⼄存⼊110元,甲取出110元”,可知⼄存⼊110元后相当于甲存款数的3倍,取出110×3=330元;⽽由甲的存款是⼄的4倍,可知甲原有存款的3倍相当于⼄原有存款的4×3=12倍,⼄现在存⼊110元后相当于甲原有的12倍,取110×3=330元,所以,330+110=440元,相当于⼄原有的12-1=11倍。
所以,⼄原有存款440÷11=40元,甲原有存款40×4=160元。
练习题: 1、甲的存款是⼄的5倍,如果甲取出60元,⼄存⼊60元,那么⼄的存款是甲的2倍。
甲、⼄原来各有存款多少元? 2、刘叔叔的存款是李叔叔的6倍,如果刘叔叔取出1100元,李叔叔存⼊1100元,那么刘叔叔的存款是李叔叔的2倍。
刘叔叔和李叔叔原来各有存款多少元? 3、有⼤、中、⼩三筐菠萝,⼩筐装的是中筐的⼀半,中筐⽐⼤筐少装16千克,⼤筐装的是⼩筐的4倍。
⼤、中、⼩三筐各装菠萝多少千克?【篇⼆】 例题:某⼯⼚⼀、⼆、三车间共有⼯⼈280⼈,第⼀车间⽐第⼆车间多10⼈,第⼆车间⽐第三车间多15⼈。
三个车间各有⼯⼈多少⼈? 分析与解答:这是多量的和差问题,解题的时候确定的标准不同,解法也就不同。
如果以第⼆车间的⼈数为标准,第⼀车间减少10⼈,第三车间增加15⼈,那么280-10+15=285⼈是第⼆车间⼈数的3倍,由此可以求出第⼆车间有285÷3=95⼈,第⼀车间有95+10=105⼈,第三车间有95-15=80⼈。
奥数问题(和倍、差倍、和差问题)

除法应用姓名:一、和倍问题。
小的数量=和÷(倍数+1)大的数量=小的数量×倍数或大的数量=和—小的数量1、小明家养鸡和兔共有36只,鸡的只数是兔的3倍,小明家的鸡和兔各有多少只?2、学校购进篮球和足球共有56个,其中篮球的个数是足球的3倍,学校购进的篮球和足球各有多少个?3、一支钢笔和一支铅笔共21元,已知钢笔的单价是铅笔的6倍,钢笔和铅笔每支各需要多少元?4、甲、乙两个仓库共有粮食60吨,甲仓库的粮食是乙仓库的4倍。
甲、乙两个仓库各存粮多少吨?5、在一个除法算式中,被除数、除数和商的和是185,若商是5,求被除数和除数各是多少?6、有大、小两个数,它们的和是56,它们的商是7。
则它们的积是多少?7、弟弟有课外书20本,哥哥有25本。
哥哥送给弟弟多少本后,弟弟的书正好是哥哥的2倍?8、有两筐苹果,第一筐有16千克,第二筐有24千克,从第一筐中拿多少千克到第二筐中,第二筐的苹果就会是第一筐的3倍?8、小明有36元钱,小亮有24元钱,小明给小亮多少元后,小亮的钱就是小明的3倍?9、一车间有45名工人,二车间有75名工人,一车间调入二车间多少人后,二车间的人数才是一车间的3倍?10、棋盘上有白棋与黑棋两种棋子,白棋67枚,黑棋有53枚。
从白棋中拿多少枚到黑棋,就能使黑棋是白棋的2倍?例:春风小学共有学生760人,男生比女生的3倍多40人,春风小学的男、女生各有多少人?由上面线段图可知:女生:(760—40)÷(3+1)=720÷4男生:180×3+40=580(人)=180(人)或:760-180=580(人)答:春风小学有男生580人,女生180人。
1、两筐梨共重76千克,其中第一筐比第二筐的2倍少14千克,那么这两筐梨各有多少千克?2、小明的叔叔和小明的年龄之和是38岁,叔叔的年龄是小明的3倍多2岁,叔叔和小明各多少岁?3、果园里有苹果树与桃树一共340棵,桃树的棵数是苹果树的3倍多20棵,果园里这两种树各有多少棵?4、商店里有红花和黄花共123朵,当红花卖出7朵后,红花的朵数就正好是黄花的3倍,那么商店里原有红花与黄花各多少朵?5、学校原有足球和排球共58个,王老师又买来5个足球,这时的足球正好是排球的6倍,求学校现有足球和排球各多少个。
六年级奥数-和倍、差倍、和差问题
5、某专业户养鸡、鸭、鹅共有960只,养鸡的只数是鹅的3倍,养鸭的只数是鹅的4倍。这个专业户养鸡、鸭、鹅各多少只?
6、甲、乙、丙三个数之和是400,又知甲是乙的3倍,丙是甲的4倍。求这三个数。
例2、甲、乙、丙3数和是183,乙比丙的2倍少4,甲比丙的3倍多7,求甲、乙、丙三数各是多少?
练习2、
1、三堆糖果共有105颗,其中第一堆糖果的数量是第二堆的3倍,而第三堆糖果的数量又比第二堆的2倍少3颗.第三堆糖果有多少颗?
2.甲、乙、丙三个粮仓一共存有109吨粮食.其中甲粮仓的粮食总量比乙粮仓的3倍多1吨,而乙粮仓的粮食总量则是丙粮仓的2倍.问:甲粮仓比丙粮仓多存粮多少吨?
2、菜场运来的西红柿是黄瓜的3倍,卖出西红柿950千克,黄瓜120千克后,剩下的两种蔬菜重量相等,菜场运来西红柿和黄瓜各多少千克?
3、两袋盐的重量相等,甲袋取出24千克,乙袋装入28千克,这时乙袋的重量是甲袋的3倍,甲乙两袋原来各有盐多少千克?
4、甲、乙两数的和是112.甲数除以乙数的商是6,甲、乙两数各是多少?
11、被除数、除数与商的和是79,已知商是4。被除数和除数各是多少?
12、两数相除商是5,没有余数,已知被除数、除数与商的和是59。被除数和除数各是多少?
第二类:和差问题练习题
公式:(和-差)÷2=较小数(和+差)÷2=较大数
例1、王师傅一天生产的零件比他的徒弟一天生产的零件多128个,且是徒弟的3倍。师徒二人一天各生产多少个零件?
7、三块钢板共重621千克,第一块的重量是第二块的3倍,第二块的重量是第三块的2倍。三块钢板各是多少千克?
三年级数学:和差、和倍与差倍问题详解(附例题)

和差问题已知两个数量的和与差,求这两个数量各是多少,这类应用题叫和差问题。
其实,解和差问题,还有一段顺口溜:和加上差,越加越大;除以2,便是大的;和减去差,越减越小;除以2,便是小的。
和差问题的解题公式:大数=(和+差)÷2小数=(和-差)÷2例1、甲乙两班共有学生98人,甲班比乙班多6人,求两班各有多少人?解甲班人数=(98+6)÷2=52(人)乙班人数=(98-6)÷2=46(人)答:甲班有52人,乙班有46人。
例2、长方形的长和宽之和为18厘米,长比宽多2厘米,求长方形的面积。
解长=(18+2)÷2=10(厘米)宽=(18-2)÷2=8(厘米)长方形的面积=10×8=80(平方厘米)答:长方形的面积为80平方厘米。
和倍问题已知两个数的和及大数是小数的几倍(或小数是大数的几分之几),要求这两个数各是多少,这类应用题叫做和倍问题。
总和÷(几倍+1)=较小的数总和-较小的数=较大的数较小的数×几倍=较大的数为了帮助我们理解题意,弄清两种量彼此间的关系,常采用画线段图的方法来表示两种量间的这种关系,以便于找到解题的途径。
例1、果园里有杏树和桃树共248棵,桃树的棵数是杏树的3倍,求杏树、桃树各多少棵?解(1)杏树有多少棵?248÷(3+1)=62(棵)(2)桃树有多少棵?62×3=186(棵)答:杏树有62棵,桃树有186棵。
例2、东西两个仓库共存粮480吨,东库存粮数是西库存粮数的1.4倍,求两库各存粮多少吨?解(1)西库存粮数=480÷(1.4+1)=200(吨)(2)东库存粮数=480-200=280(吨)答:东库存粮280吨,西库存粮200吨。
例3、甲班和乙班共有图书160本.甲班的图书本数是乙班的3倍,甲班和乙班各有图书多少本?解:160÷(3+1)=40本乙40×3=120本甲答:甲班120本,已班40本。
四年级和差倍思维训练奥数题

四年级和差倍思维训练奥数题一、和差问题1. 题目四年级甲、乙两班共有学生98人,甲班比乙班多6人,求两班各有多少人?解析已知两班人数的和是98人,差是6人。
我们可以先求出较大数(甲班人数),根据公式:大数=(和 + 差)÷2。
所以甲班人数=(98 + 6)÷2 = 104÷2 = 52(人)乙班人数 = 甲班人数 6 = 52 6 = 46(人)2. 题目两个数的和为36,差为22,求这两个数。
解析同样根据和差问题的公式,大数=(和+差)÷2,小数=(和差)÷2。
大数=(36+22)÷2 = 58÷2 = 29小数=(36 22)÷2 =14÷2 = 7二、和倍问题1. 题目学校将360本图书分给二、三两个年级,已知三年级所分得的本数是二年级的2倍,问二、三年级各分得多少本图书?解析已知两个年级图书总数是360本,三年级本数是二年级的2倍。
我们把二年级分得的图书本数看作1份,三年级就是2份,总共就是1+2 = 3份。
那么二年级分得的图书数量为:360÷(1 + 2)=360÷3 = 120(本)三年级分得的图书数量为:120×2 = 240(本)2. 题目被除数与除数的和是320,商是7,被除数和除数各是多少?解析因为商是7,说明被除数是除数的7倍。
把除数看作1份,被除数就是7份,总共8份。
除数为:320÷(1 + 7)=320÷8 = 40被除数为:40×7 = 280三、差倍问题1. 题目四年级学生参加课外活动,做游戏的人数比打球人数的3倍多2人,已知做游戏的比打球的多38人,打球和做游戏的各有多少人?解析设打球的人数为x人,那么做游戏的人数就是3x+2人。
又因为做游戏的比打球的多38人,所以可列方程:(3x + 2)-x=382x+2 = 382x=36x = 18(人),即打球的人数是18人。
(完整版)三年级下和倍、差倍问题

三年级奥数班讲义姓名和倍、差倍问题家长当已知两个数的和以及倍数关系或者已知两个数的差以及倍数关系,求各个数是多少。
解决此类问题的的方法是根据条件画出线段图,从而理清思路。
在解决具体问题时,也可以应用以下关系式:和÷(倍数+1)=小数小数×倍数=大数或和一小数=大数和÷(倍数-1)=大数小数×倍数=大数或小数 + 差= 大数二、例题精选1、某专业户养有鸡鸭共480只,其中鸭的只数是鸡的3倍,这个专业户养鸡、鸭各几只?2、甲乙两桶油,甲桶有油25千克,乙桶有油17千克,乙桶给甲桶几千克后,甲桶油是乙桶的5倍?3、水果店有梨和苹果共240箱,梨卖出40箱,又运进苹果70箱,这时苹果的箱数正好是梨的2倍,水果店原来有梨和苹果各多少箱?4、爷爷的年龄是孙子的7倍,爷爷比孙子大60岁,他俩分别是多少岁?5、某厂五月份比四月份多生产零件400个,六月份比五月份多生产500个,六月份的个数正好是四月份的2倍,三个月各生产零件多少个?6、甲筐苹果的重量是乙筐的3倍,如果从甲筐取出24千克,从乙筐取出6千克,两筐剩余的重量相等。
甲、乙两筐原来各有苹果多少千克?三、课堂练习1、学校图书室共分给二、三年级360本书,已知三年级所得的书比二年级的2倍还多60本,两个年级各有多少本书?2、小明有书18本,小芳有书8本,现在又买来16本书,怎样分配才能使小明的书是小芳的2倍?3、学校三年级原有学生280人,本学期又转进12名男生和4名女生,这时男生人数比女生人数的2倍少61人,原来有男生和女生各多少人?4、甲、乙两数,如果甲数加上280,就等于乙数,如果乙数加上320,就等于甲数的3倍,两数分别是多少?5、白粉笔的盒数是彩色粉笔的4倍,若彩色粉笔再买来20盒,而白粉笔用去一半,两种粉笔就同样多了,原来两种粉笔各有多少?四、能力提升有一道除法算式,被除数、除数、商和余数的和为222,商为2,余数为5,被除数和除数分别是几?。
小学三年级数学:和差、和倍与差倍问题详解(附例题)

和差问题已知两个数量的和与差,求这两个数量各是多少,这类应用题叫和差问题。
其实,解和差问题,还有一段顺口溜:和加上差,越加越大;除以2,便是大的;和减去差,越减越小;除以2,便是小的。
和差问题的解题公式:大数=(和+差)÷2小数=(和-差)÷2例1、甲乙两班共有学生98人,甲班比乙班多6人,求两班各有多少人?解甲班人数=(98+6)÷2=52(人)乙班人数=(98-6)÷2=46(人)答:甲班有52人,乙班有46人。
例2、长方形的长和宽之和为18厘米,长比宽多2厘米,求长方形的面积。
解长=(18+2)÷2=10(厘米)宽=(18-2)÷2=8(厘米)长方形的面积=10×8=80(平方厘米)答:长方形的面积为80平方厘米。
和倍问题已知两个数的和及大数是小数的几倍(或小数是大数的几分之几),要求这两个数各是多少,这类应用题叫做和倍问题。
总和÷(几倍+1)=较小的数总和-较小的数=较大的数较小的数×几倍=较大的数为了帮助我们理解题意,弄清两种量彼此间的关系,常采用画线段图的方法来表示两种量间的这种关系,以便于找到解题的途径。
例1、果园里有杏树和桃树共248棵,桃树的棵数是杏树的3倍,求杏树、桃树各多少棵?解(1)杏树有多少棵?248÷(3+1)=62(棵)(2)桃树有多少棵?62×3=186(棵)答:杏树有62棵,桃树有186棵。
例2、东西两个仓库共存粮480吨,东库存粮数是西库存粮数的1.4倍,求两库各存粮多少吨?解(1)西库存粮数=480÷(1.4+1)=200(吨)(2)东库存粮数=480-200=280(吨)答:东库存粮280吨,西库存粮200吨。
例3、甲班和乙班共有图书160本.甲班的图书本数是乙班的3倍,甲班和乙班各有图书多少本?解:160÷(3+1)=40本乙40×3=120本甲答:甲班120本,已班40本。
小学奥数(典型例题口诀及解析)

小学数学中的典型例题口诀及解析一、倍数问题(和差倍问题)(一)和差问题已知两数的和与差,求这两个数各是多少的应用题。
1、线段图:2、数量关系式:①先求大数大数=(和+差)÷2小数=和-大数②先求小数小数=(和-差)÷2大数=和-大数【口诀】:和加上差,越加越大;除以2,便是大的;和减去差,越减越小;除以2,便是小的。
典型例题:1.已知两数和是10,差是2,求这两个数。
按口诀,则大数=(10+2)÷2=6,小数=(10-2)÷2=4。
2.两筐梨子共有120个,如果从第一筐中拿出10个放入第二筐中,那么两筐的梨子的个数相等,问两筐原来各有多少梨?【解析】从第一个筐拿10个放第二个筐,个数相等,说明第一个筐比第二个筐多20个梨,故第一个筐梨数为(120+20)÷2=70(个),第二个筐梨数为(120-20)÷2=50(个).(二)和倍问题已知两个数的和与这两个数的倍数关系,求这两个数各是多少的应用题。
1、线段图2、数量关系式:两数和÷(倍数+1)=小数(1倍数)小数×倍数=大数(几倍数)两数和—小数=大数(几倍数)典型例题:1.学校将360本图书分给二、三两个年级,已知三年级所分得的本数是二年级的2倍,问二、三两个年级各分得多少本图书?【解析】:二、三年级所得图书本数的和360本相当于二年级的(1+2)倍,则二年级所得图书本数的360÷(1+2)=120本,三年级为120×2=240本。
2.书架上有文艺书和科技书共15本,文艺书的本数比科技书的2倍多3本,文艺书和科技书各有多少本?【解析】科技书为(15-3)÷(2+1)=4(本)文艺书为15—4=11(本)(三)差倍问题典型例题:1.某养鸡场的母鸡只数是公鸡只数的6倍,后来公鸡、母鸡各增加60只,母鸡的只数变为公鸡只数的4倍,则养鸡场原来一共养了___________只鸡。
(完整版)奥数题(和倍、差倍、和差问题)

三年级奥数测试题
1.小红和妈妈的年龄加在一起是40岁,妈妈年龄是小红年龄的4倍,小红和妈妈各有几岁?
2、.小明、小红两人集邮,小明的邮票比小红多36张,小明的张数是小红的3倍,小明和小红各有邮票多少张?
3、.两筐水果共重124 千克,第一筐比第二筐多8 千克,两筐水果各重多少千克?
4、小丽的科技书的本数是小红的4倍,如果小丽借给小红15本科技书,则两人的科技书本数就相等。
原来小丽、小红各有多少本科技书?
5、师傅和徒弟共生产零件190个,师傅生产的个数比徒弟的3倍少10个;师、徒各生产零件多少个?
6、一车间原有男工人数比女工多55人,如果调走女工5人,那么男工人数正好是女工的3倍,原有男工多少人?
7、期末考试小兰语文、数学的平均成绩是97分,语文比数学少4分,小兰的语文、数学各得了多少分?
8、被除数比除数大124,商是5,.被除数,、除数各是多少?
9、明明和红红共有邮票50张,如果明明给红红8 张,则两人的张数相等。
问明明和红红原来各有多少张?
10、甲筐苹果是乙筐苹果的4倍,如果再放入乙筐70千克,从甲筐取出50千克,那么两筐苹果重量就相等,两筐原来各有多少千克?
11、水果店有两筐橘子,第一筐橘子的个数是第二筐的3倍,第一筐取出380个橘子,第二筐取出110个橘子,那么两筐橘子个数相等。
现在两筐橘子各有多少个?
12、甲、乙两个冷库原来共存肉92吨,从甲库运出17吨后,甲库存肉是乙库的2倍,甲、乙两个冷库原来各存肉多少吨?
13、两筐重量相等的苹果,如果乙筐加上16千克,这时乙筐的重量是甲筐重量的3倍,原来两筐各有苹果多少千克?
14、被除数与除数的和为120,商是7,被除数和除数各是几?。
小学数学:和差、和倍与差倍问题详解(附例题)

小学数学:和差、和倍与差倍问题详解(附例题)已知两个数量的和与差,求这两个数量各是多少,这类应用题叫和差问题。
其实,解和差问题,还有一段顺口溜:和加上差,越加越大;除以2,便是大的;和减去差,越减越小;除以2,便是小的。
和差问题的解题公式:大数=(和+差)÷2小数=(和-差)÷2例1、甲乙两班共有学生98人,甲班比乙班多6人,求两班各有多少人?解甲班人数=(98+6)÷2=52(人)乙班人数=(98-6)÷2=46(人)答:甲班有52人,乙班有46人。
例2、长方形的长和宽之和为18厘米,长比宽多2厘米,求长方形的面积。
解长=(18+2)÷2=10(厘米)宽=(18-2)÷2=8(厘米)长方形的面积=10×8=80(平方厘米)答:长方形的面积为80平方厘米。
已知两个数的和及大数是小数的几倍(或小数是大数的几分之几),要求这两个数各是多少,这类应用题叫做和倍问题。
总和÷(几倍+1)=较小的数总和-较小的数=较大的数较小的数×几倍=较大的数为了帮助我们理解题意,弄清两种量彼此间的关系,常采用画线段图的方法来表示两种量间的这种关系,以便于找到解题的途径。
例1、果园里有杏树和桃树共248棵,桃树的棵数是杏树的3倍,求杏树、桃树各多少棵?解(1)杏树有多少棵?248÷(3+1)=62(棵)(2)桃树有多少棵?62×3=186(棵)答:杏树有62棵,桃树有186棵。
例2、东西两个仓库共存粮480吨,东库存粮数是西库存粮数的1.4倍,求两库各存粮多少吨?解(1)西库存粮数=480÷(1.4+1)=200(吨)(2)东库存粮数=480-200=280(吨)答:东库存粮280吨,西库存粮200吨。
例3、甲班和乙班共有图书160本.甲班的图书本数是乙班的3倍,甲班和乙班各有图书多少本?解:160÷(3+1)=40本乙40×3=120本甲答:甲班120本,已班40本。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
For personal use only in study and research; not for commercial use和倍问题专题简析:已知两个数的和与两个数间的倍数关系,求这两个数分别是多少,像这样的应用题,通常叫做和倍问题。
要想顺利地解答和倍应用题,最好的方法就是根据题意,画出线段图,使数量关系一目了然,从而正确列式解答。
解答和倍应用题,关键是要找出两数的和以及与其对应的倍数和,从而先求出1倍数,再求出几倍数。
数量关系可以这样表示:两数和÷(倍数+1)=小数(1倍数)小数×倍数=大数(几倍数)两数和-小数=大数例题1 学校将360本图书分给二、三两个年级,已知三年级所分得的本数是二年级的2倍,问二、三两个年级各分得多少本图书思路导航:将二年级所得图书的本数看作1倍数,则三年级所得本数是这样的2倍。
如图所示:由图可知,二、三年级所得图书本数的和360本相当于二年级的(1+2)倍,则二年级所得图书本数的360÷(1+2)=120本,三年级为120×2=240本。
练习一1,小红和小明共有压岁钱800元,小红的钱数是小明的3倍。
小红和小明各有压岁钱多少元2,学校将360本图书分给二、三年级,已知三年级所得本数比二年级的2倍还多60本。
二、三年级各得图书多少本3,甲桶有油25千克,乙桶有油17千克,乙桶倒入多少千克油给甲桶后,甲桶油是乙桶的5倍例题2 小宁有圆珠笔芯30枝,小青有圆珠笔芯15枝,问小青给小宁多少枝后,小宁的圆珠笔芯枝数是小青的8倍思路导航:我们把变化后小青的圆珠笔芯枝数看作1倍数,那么小宁与小青圆珠笔芯的枝数和相当于变化后小青枝数的9倍,所以变化后小青的枝数为(30+15)÷(1+8)=5枝,再用15-5=10枝,则表示小青给小宁的枝数。
练习二1,红红有邮票80张,佳佳有邮票60张,要使红红的邮票张数是佳佳的4倍,那么佳佳必须给红红多少张邮票2,甲水池有水69吨,乙水池有水36吨,如果甲水池中的水以每分钟2吨的速度流入乙水池,那么多少分钟后,乙水池的水是甲水池的2倍3,甲书架有图书18本,乙书架有图书8本,班图书管理员又买来图书16本,怎样分配才能使甲书架图书的本数是乙书架的2倍例题3 被除数与除数的和为320,商是7,被除数和除数各是多少思路导航:由商是7可知,被除数是除数的7倍,把除数看作1份数,被除数就有这样的7份,一共7+1=8份。
除数:320÷8=40被除数:40×7=280练习三1,被除数和除数和为120,商是7,被除数和除数各是多少2,被除数、除数、商的和为79,商是4,被除数、除数各是多少3,两个整数相除商是21,余数为1,已知被除数、除数、商、余数的和一共是441。
被除数、除数各是多少例题4 两数相除商为17余6,被除数、除数、商和余数的和是479。
被除数和除数分别为多少思路导航:被除数、除数、商和余数的和是479,减去商17和余数6,得到被除数与除数的和为479-17-6=456;又因为被除数比除数的17倍多6,所以456-6=450就相当于除数的(17+1)倍,因此除数为450÷(17+1)=25,被除数为25×17+6=431。
练习四1,两个整数相除商14余2,被除数、除数、商和余数的和是243,被除数比除数大多少2,在一个减法算式里,被减数、减数与差的和等于240,而减数是差的5倍。
差是多少3,学校买来83本书,其中科技书是故事书的2倍,故事书比文艺书多5本,这三种书各多少本例题5 两个数之和是792,其中一个数的最后一位数数字是0,如果把0去掉,就与另一个数相同。
这两个数分别是多少思路导航:把一个数的最后一位数字0去掉,就与另一个数相同,说明这两个数中大数是小数的10倍。
又已知两个数之和是792,那我们就可以求出这两个数分别是多少了。
小数:792÷(10+1)=72大数:72×10=720练习五1,两个数之和是253,其中一个数的最后一位数字是0,如果把0去掉,就与另一个数相同。
这两个数分别是多少2,师徒两人加工一批零件共693个,师傅加工零件个数的末位数字是0,如果去掉这个0,加工的个数就与徒弟一样多。
师徒二人分别加工零件多少个3,甲、乙两数的和是209,甲数缩小10倍就和乙数同样大,甲、乙两数分别是多少第二十六周差倍问题(一)专题简析:前面我们已经初步掌握了“和倍问题”的特征和解题方法。
如果知道了两个数的差与两个数间的倍数关系,要求两个数各是多少,这一类题,我们则把它称为“差倍问题”。
小朋友,你们有没有想到用解答和倍问题的类似方法解答差倍问题呢解答差倍问题与解答和倍问题相类似,要先找出差所对应的倍数,先求1倍数,再求出几倍数。
此外,还要充分利用线段图帮助分析数量关系。
用关系式可以这样表示:两数差÷(倍数-1)=较小的数(1倍数)较小的数×倍数=较大的数(几倍数)例题1 小明到市场去买水果,他买的苹果个数是梨的3倍,苹果比梨多18个。
小明买苹果和梨各多少个思路导航:将梨的个数看作1倍数,则苹果的个数是这样的3倍。
如下图:从线段图上可以看出,苹果的个数比梨多了3-1=2倍,梨的2倍是18个,所以梨有18÷2=9个,苹果有:9×3=27个。
练习一1,学校合唱组,女同学人数是男同学的4倍,女同学比男同学多42人。
合唱组有男、女同学各多少人2,一件皮衣价钱是一件羽绒服价钱的5倍,又已知一件皮衣比一件羽绒服贵960元。
皮衣与羽绒服各多少元3,甲筐苹果是乙筐苹果的3倍,如果从甲筐取出60千克放入乙筐,那么两筐苹果重量就相等。
两筐原来各有苹果多少千克例题2 被除数比除数大252,商是7,被除数、除数各是多少思路导航:根据“商是7”可知,被除数是除数的7倍,把除数看作1倍数,被除数就是这样的7份,比除数多6份。
所以除数是:252÷(7-1)=42被除数是:42+252=294练习二1,被除数比除数大168,商是22,被除数、除数各是多少2,除数比被除数小212,商是5,被除数、除数各是多少3,被除数比商大144,除数是7,被除数、商各是多少例题3 水果店有两筐橘子,第一筐橘子的重量是第二筐的5倍,如果从第一筐中取出300个放入第二筐,那么第一筐橘子还比第二筐多60个。
原来两筐橘子各有多少个思路导航:根据“如果从第一筐中取出300个放入第二筐,那么第一筐橘子还比第二筐多60个”,说明原来第一筐比第二筐橘子多300×2+60=660个。
把第二筐的橘子重量看作1倍数,第一筐橘子是这样的5倍,比第二筐多4倍,第二筐橘子的4倍正好是660个,所以第二筐原有橘子:660÷4=165个,第一筐橘子原来有:165×5=825个。
练习三1,同学们捐助残,六年级捐款钱数是三年级的3倍。
如果从六年级捐款钱数中取出160元放入三年级,那么六年级捐款的钱数还比三年级多40元。
两个年级分别捐款多少元2,人民公园的杜鹃花盆数是长春园的4倍,如果从人民公园搬出188盆杜鹃花放入长春园,则人民公园的杜鹃花盆数就比长春园的少25盆。
原来两个公园各有杜鹃花多少盆3,两堆煤重量相等,现从甲堆中运走24吨到乙堆,而乙堆煤中又运入8吨,这时乙堆煤的重量正好是甲堆煤重量的3倍。
问两堆煤原来各有多少吨例题4 甲、乙两个数,如果甲数加上280就等于乙数,如果乙数加上320就等于甲数的3倍。
两个数各是多少思路导航:根据题意,画出线段图:“甲数加上280就等于乙数”,说明乙数比甲数大280;如果乙数再加上320,甲、乙就相差320+280=600,把甲数看作1倍数,从图上可以看出,600就相当于甲数的3-1=2倍。
所以,甲数为600÷2=300,乙数为300+280=580。
练习四1,甲、乙两人的存款相等,甲取出60元,乙存入20元后,乙的存款是甲的3倍。
甲、乙两人原有存款各多少元2,小明和小华的连环画本数相等,若小明借给小华6本,小华的本数是小明的4倍。
原来两人各有连环画多少本3,两筐千克数相同的苹果,甲筐卖出7千克,乙筐卖出19千克后,甲筐余下的苹果是乙筐的3倍。
两筐苹果原来各有多少千克例题5 两个书架所存书的本数相等,如果从第一个书架里取出200本书,而第二个书架再放入40本书,那么第二个书架的本数是第一个书架的3倍。
问两个书架原来各存书多少本思路导航:根据题意,画出线段图。
从线段图上可以看出,第一个书架取出200本,第二个书架放进40本书后,两个书架就相差200+40=240本,把变化后的第一个书架看作1倍数,两个书架相差的240本就相当于变化后第一个书架的(3-1)倍。
所以,变化后第一个书架有书:(200+40)÷(3-1)=120本两个书架原来各有:120+200=320本。
练习五1,两个仓库所存粮食重量相等,如果从第一个仓库里取出2000千克,而第二个仓库再存入400千克,那么第二个仓库的粮食重量就是第一个仓库的7倍。
两个仓库原来各存粮食多少千克2,小红和小明的铅笔枝数相等,如果奶奶再给小红16枝铅笔,给小明2枝铅笔,那么小红的铅笔枝数就是小明的3倍。
原来小红和小明各有铅笔多少枝3,商店有数量相等的英语本和算术本,英语本卖出160本,算术本卖出420本后,余下的英语本数是算术本的3倍。
两种本子原来各有多少本第二十七周差倍问题(二)专题简析:有些差倍问题比较复杂,不能直接利用公式进行解答,这时需要我们小朋友仔细审题,尤其注意一些隐含条件,同时借助线段图帮助理解题意,从而找到解题方法。
较复杂的差倍应用题,数量关系比较隐蔽。
先依题意画出线段图,数量关系就会比较清晰地展现出来,然后借助线段图找出两个数的差以及所对应的倍数,再利用公式进行解答。
例题1 有两袋玉米,大袋比小袋多56千克,如果将小袋的玉米吃掉4千克,这时大袋的玉米重量是小袋的4倍。
两袋玉米原来各重量多少千克思路导航:根据题意,画出线段图。
从图上可以看出,小袋玉为吃掉4千克后,大袋里的玉米就比小袋现有玉米重4+56=60千克;又根据“这时大袋的玉米重量是小袋的4倍”,可知把小袋现有的玉米重量看作1倍数,大袋比小袋多的60千克正好相当于现有小袋的4-1=3倍,所以小袋现有玉米60÷3=20千克,原有重量20+4=24千克,大袋原有20×4=80千克。
练习一1,有两箱玩具,第一盒比第二盒多60只。
如果从第二盒中取出3只,这时第一盒的只数是第二盒的8倍。
求两箱玩具原来各有多少只2,一个书架上放着一些书,第二层比第一层多12本。
如果从第一层中拿走6本,这时第二层的本数是第一层的4倍。
