中考复习多结论几何综合题专题试卷
初中数学中考复习 第3关 多结论的几何及二次函数问题为背景的选择填空题(原卷版)

第3关 多结论的几何及二次函数问题为背景的选择填空题【考查知识点】以多结论的几何图形为背景的选择填空题题,主要考察了学生对三角形、四边形、圆知识的综合运用能力;以二次函数为背景的选择填空题,主要考察了二次函数的性质及二次函数系数与图象的关系。
【解题思路】1.以多结论的几何图形为背景的选择填空题题中,用“全等法”和“相似法”证题应该是两个基本方法,为了更好掌握这两种方法,应该熟悉一对全等或一对相似三角形的基本图形,下图中是全等三角形的基本图形。
大量积累基本图形,并在此基础上“截长补短”,“能割善补”,是学习几何图形的一个诀窍,每一个重要概念,重要定理都有一个基本图形,三线八角可以算做一个基本图形.2. 以二次函数为背景的选择填空题中,根据图象的位置确定a 、b 、c 的符号,a >0开口向上,a <0开口向下.抛物线的对称轴为x=2ba-,由图像确定对称轴的位置,由a 的符号确定出b 的符号.由x=0时,y=c ,知c 的符号取决于图像与y 轴的交点纵坐标,与y 轴交点在y 轴的正半轴时,c >0,与y 轴交点在y 轴的负半轴时,c <0.确定了a 、b 、c 的符号,易确定abc 的符号;根据对称轴确定a 与b 的关系;根据图象还可以确定△的符号,及a+b+c 和a -b+c 的符号。
【典型例题】【例1】(2019·新疆中考真题)如图,正方形ABCD 的边长为2,点E 是BC 的中点,AE 与BD 交于点P ,F 是CD 上的一点,连接AF 分别交BD ,DE 于点M ,N ,且AF ⊥DE ,连接PN ,则下列结论中:①4ABMFDM SS=;②PN =;③tan ∠EAF=34;④.PMN DPE ∽正确的是()A .①②③B .①②④C .①③④D .②③④【名师点睛】此题考查三角函数,相似三角形的判定与性质,全等三角形的判定与性质,正方形的性质难度较大,解题关键在于综合掌握各性质【例2】(2019·湖北中考真题)抛物线2y ax bx c =++的对称轴是直线1x =-,且过点(1,0).顶点位于第二象限,其部分图像如图所示,给出以下判断: ①0ab >且0c <; ②420a b c -+>; ③8>0+a c ; ④33c a b =-;⑤直线22y x =+与抛物线2y ax bx c =++两个交点的横坐标分别为12x x 、,则12125x x x x ++⋅=-.其中正确的个数有( )A .5个B .4个C .3个D .2个【名师点睛】本题考查了二次函数图象与系数的关系:对于二次函数y=ax 2+bx+c (a≠0),当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b 和二次项系数a 共同决定对称轴的位置:当a 与b 同号时(即ab>0),对称轴在y 轴左侧;当a 与b 异号时(即ab<0),对称轴在y 轴右侧;常数项c 决定抛物线与y 轴交点,抛物线与y 轴交于(0,c );抛物线与x 轴交点个数由△决定:△=b 2-4ac>0时,抛物线与x 轴有2个交点;△=b 2-4ac=0时,抛物线与x 轴有1个交点;△=b 2-4ac<0时,抛物线与x 轴没有交点.【例3】(2019·辽宁中考真题)如图,正方形ABCD 和正方形CGFE 的顶点C ,D ,E 在同一条直线上,顶点B ,C ,G 在同一条直线上.O 是EG 的中点,∠EGC 的平分线GH 过点D ,交BE 于点H ,连接FH 交EG 于点M ,连接OH .以下四个结论:①GH ⊥BE ;②△EHM ∽△GHF;③BCCG =﹣1;④HOM HOGS S =2)A.①②③B.①②④C.①③④D.②③④【名师点睛】本题考查了正方形的性质,以及全等三角形的判定与性质,相似三角形的判定与性质,正确求得两个三角形的边长的比是解决本题的关键.【例4】(2018·广西中考真题)如图,抛物线y=14(x+2)(x﹣8)与x轴交于A,B两点,与y轴交于点C,顶点为M,以AB为直径作⊙D.下列结论:①抛物线的对称轴是直线x=3;②⊙D的面积为16π;③抛物线上存在点E,使四边形ACED为平行四边形;④直线CM与⊙D相切.其中正确结论的个数是()A.1B.2C.3D.4【名师点睛】本题考查了二次函数与圆的综合题,涉及到抛物线的对称轴、圆的面积、平行四边形的判定、待定系数法、两直线垂直、切线的判定等,综合性较强,有一定的难度,运用数形结合的思想灵活应用相关知识是解题的关键.【方法归纳】1.多结论的几何选择填空题考查的知识点较多,如相似三角形的判定与性质、等腰直角三角形的性质、平行线的性质、直角三角形的性质、四边形的知识、圆的知识、等腰三角形的判定与性质以及特殊角三角函数等知识.这类题目的综合性很强,难度较大,解题的关键是注意数形结合思想的应用.2. 多结论的二次函数选择题主要考查了二次函数图象与系数的关系.二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.数形结合思想贯穿这类题目的始终,解题时应时时注意.【针对练习】1.(2018·四川中考真题)如图,在矩形ABCD 中,E 是AB 边的中点,沿EC 对折矩形ABCD ,使B 点落在点P 处,折痕为EC ,连结AP 并延长AP 交CD 于F 点,连结CP 并延长CP 交AD 于Q 点.给出以下结论:①四边形AECF 为平行四边形; ②∠PBA=∠APQ ; ③△FPC 为等腰三角形; ④△APB ≌△EPC ;其中正确结论的个数为( )A .1B .2C .3D .42.(2018·辽宁中考真题)已知抛物线y=ax 2+bx+c (0<2a≤b )与x 轴最多有一个交点.以下四个结论: ①abc >0;②该抛物线的对称轴在x=﹣1的右侧; ③关于x 的方程ax 2+bx+c+1=0无实数根; ④a b cb++≥2. 其中,正确结论的个数为( ) A .1个B .2个C .3个D .4个3.(2019·四川中考真题)如图,在正方形ABCD 的对角线AC 上取一点E .使得15CDE ︒∠=,连接BE 并延长BE 到F ,使CF CB =,BF 与CD 相交于点H ,若1AB =,有下列结论:①BE DE =;②CE DE EF +=;③14DEC S ∆=-;④1DH HC =-.则其中正确的结论有( )A .①②③B .①②③④C .①②④D .①③④4.(2019·广西中考真题)如图,E 是正方形ABCD 的边AB 的中点,点H 与B 关于CE 对称,EH 的延长线与AD 交于点F ,与CD 的延长线交于点N ,点P 在AD 的延长线上,作正方形DPMN ,连接CP ,记正方形ABCD ,DPMN 的面积分别为1S ,2S ,则下列结论错误的是( )A .212S S CP +=B .2AF FD =C .4CD PD = D .3cos 5HCD ∠=5.(2019·山东中考真题)如图,在正方形ABCD 中,E 、F 分别是BC 、CD 上的点,且∠EAF =45°,AE 、AF 分别交BD 于M 、N ,连按EN 、EF 、有以下结论:①AN =EN ,②当AE =AF 时,BEEC=2,③BE+DF =EF ,④存在点E 、F ,使得NF >DF ,其中正确的个数是( )A .1B .2C .3D .46.(2019·黑龙江中考真题)如图,在正方形ABCD 中,E F 、是对角线AC 上的两个动点,P 是正方形四边上的任意一点,且42AB EF =,=,设AE x =.当PEF 是等腰三角形时,下列关于P 点个数的说法中,一定正确的是( )①当0x =(即E A 、两点重合)时,P 点有6个②当02x <<时,P 点最多有9个③当P 点有8个时,x =﹣2④当PEF 是等边三角形时,P 点有4个 A .①③B .①④C .②④D .②③7.(2019·广东中考真题)如图,正方形ABCD 的边长为4,延长CB 至E 使2EB =,以EB 为边在上方作正方形EFGB ,延长FG 交DC 于M ,连接AM 、AF ,H 为AD 的中点,连接FH 分别与AB 、AM 交于点N 、K .则下列结论:①ANH GNF ∆≅∆;②AFN HFG ∠=∠;③2FN NK =;④:1:4AFN ADM S S ∆∆=.其中正确的结论有( )A .1个B .2个C .3个D .4个8.(2019·湖北中考真题)如图所示,已知二次函数2y ax bx c =++的图象与x 轴交于,A B 两点,与y 轴交于点C ,OA OC =,对称轴为直线1x =,则下列结论:①0abc <;②11024a b c ++=;③10ac b -+=;④2c +是关于x 的一元二次方程20ax bx c ++=的一个根.其中正确的有( )A .1个B .2个C .3个D .4个9.(2018·黑龙江中考真题)抛物线()2y ax bx c a 0=++≠的部分图象如图所示,与x 轴的一个交点坐标为()4,0,抛物线的对称轴是x 1.=下列结论中:abc 0>①;2a b 0+=②;③方程2ax bx c 3++=有两个不相等的实数根;④抛物线与x 轴的另一个交点坐标为()2,0-;⑤若点()A m,n 在该抛物线上,则2am bm c a b c ++≤++. 其中正确的有( )A .5个B .4个C .3个D .2个10.(2018·黑龙江中考真题)如图,平行四边形ABCD 的对角线AC 、BD 相交于点O ,AE 平分∠BAD ,分别交BC 、BD 于点E 、P ,连接OE ,∠ADC=60°,AB=12BC=1,则下列结论:①∠CAD=30°②③S 平行四边形ABCD =AB•AC ④OE=14AD ⑤S △APO =12,正确的个数是( )A .2B .3C .4D .511.(2018·山东中考真题)如图,在矩形ABCD 中,∠ADC 的平分线与AB 交于E ,点F 在DE 的延长线上,∠BFE=90°,连接AF 、CF ,CF 与AB 交于G ,有以下结论: ①AE=BC ②AF=CF ③BF 2=FG•FC ④EG•AE=BG•AB其中正确的个数是( )A .1B .2C .3D .412.(2019·四川中考真题)二次函数2(0)y ax bx c a =++≠的部分图象如图所示,图象过点(1,0)-,对称轴为直线x =1,下列结论:①0abc <;②b c <;③30a c +=;④当0y >时,13x -<<其中正确的结论有( )A .1个B .2个C .3个D .4个13.(2019·山东中考真题)如图,正方形ABCD ,点F 在边AB 上,且:1:2AF FB =,CE DF ⊥,垂足为M ,且交AD 于点E ,AC 与DF 交于点N ,延长CB 至G ,使12BG BC =,连接CM .有如下结论:①DE AF =;②4AN AB =;③ADF GMF ∠=∠;④:1:8ANF CNFB S S ∆=四边形.上述结论中,所有正确结论的序号是( )A .①②B .①③C .①②③D .②③④14.(2018·湖北中考真题)如图,在四边形ABCD 中,AB=AD=5,BC=CD 且BC >AB ,BD=8.给出以下判断:①AC 垂直平分BD ;②四边形ABCD 的面积S=AC•BD ;③顺次连接四边形ABCD 的四边中点得到的四边形可能是正方形; ④当A ,B ,C ,D 四点在同一个圆上时,该圆的半径为256; ⑤将△ABD 沿直线BD 对折,点A 落在点E 处,连接BE 并延长交CD 于点F ,当BF ⊥CD 时,点F 到直线AB 的距离为678125. 其中正确的是_____.(写出所有正确判断的序号)15.(2019·广西中考真题)我们定义一种新函数:形如2y ax bx c =++(0a ≠,且240b a ->)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x 2-2x -3|223y x x =--的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为()1,0-,()3,0和()0,3;②图象具有对称性,对称轴是直线1x =;③当11x -≤≤或3x ≥时,函数值y 随x 值的增大而增大;④当1x =-或3x =时,函数的最小值是0;⑤当1x =时,函数的最大值是4.其中正确结论的个数是______.16.(2018·新疆中考真题)如图,已知抛物线y 1=﹣x 2+4x 和直线y 2=2x .我们规定:当x 取任意一个值时,x 对应的函数值分别为y 1和y 2,若y 1≠y 2,取y 1和y 2中较小值为M ;若y 1=y 2,记M=y 1=y 2.①当x >2时,M=y 2;②当x <0时,M 随x 的增大而增大;③使得M 大于4的x 的值不存在;④若M=2,则x=1.上述结论正确的是_____(填写所有正确结论的序号).17.(2018·黑龙江中考真题)如图,抛物线y=ax 2+bx+c (a≠0)的对称轴为直线x=﹣1,下列结论中: ①abc <0;②9a ﹣3b+c <0;③b 2﹣4ac >0;④a >b , 正确的结论是_____(只填序号)18.(2019·湖南中考真题)如图,函数ky x=(k 为常数,k >0)的图象与过原点的O 的直线相交于A ,B 两点,点M 是第一象限内双曲线上的动点(点M 在点A 的左侧),直线AM 分别交x 轴,y 轴于C ,D 两点,连接BM 分别交x 轴,y 轴于点E ,F .现有以下四个结论:①△ODM 与△OCA 的面积相等;②若BM ⊥AM于点M ,则∠MBA =30°;③若M 点的横坐标为1,△OAM 为等边三角形,则2k =④若25MF MB =,则MD =2MA .其中正确的结论的序号是_______.19.(2019·辽宁中考真题)如图,点P 是正方形ABCD 的对角线BD 延长线上的一点,连接PA ,过点P 作PE ⊥PA 交BC 的延长线于点E ,过点E 作EF ⊥BP 于点F ,则下列结论中:①PA =PE ;②CE PD ;③BF ﹣PD =12BD ;④S △PEF =S △ADP ,正确的是___(填写所有正确结论的序号)20.(2019·内蒙古中考真题)如图,在Rt ABC ∆中,90,3,ABC BC D ︒∠==为斜边AC 的中点,连接BD ,点F 是BC 边上的动点(不与点B C 、重合),过点B 作BE BD ⊥交DF 延长线交于点E ,连接CE ,下列结论:①若BF CF =,则222CE AD DE +=;②若,4BDE BAC AB ∠=∠=,则158CE =; ③ABD ∆和CBE ∆一定相似;④若30,90A BCE ︒︒∠=∠=,则DE =其中正确的是_____.(填写所有正确结论的序号)21.(2018·湖北中考真题)如图,已知∠MON=120°,点A ,B 分别在OM ,ON 上,且OA=OB=a ,将射线OM 绕点O 逆时针旋转得到OM′,旋转角为α(0°<α<120°且α≠60°),作点A 关于直线OM′的对称点C ,画直线BC 交OM′于点D ,连接AC ,AD ,有下列结论:①AD=CD ;②∠ACD 的大小随着α的变化而变化;③当α=30°时,四边形OADC 为菱形;④△ACD a 2;其中正确的是_____.(把你认为正确结论的序号都填上).。
2016中考复习四边形综合题
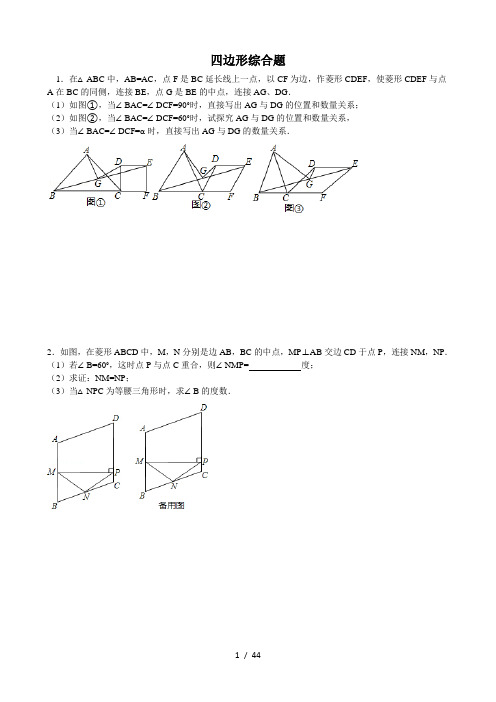
四边形综合题1.在△ABC中,AB=AC,点F是BC延长线上一点,以CF为边,作菱形CDEF,使菱形CDEF与点A在BC的同侧,连接BE,点G是BE的中点,连接AG、DG.(1)如图①,当∠BAC=∠DCF=90°时,直接写出AG与DG的位置和数量关系;(2)如图②,当∠BAC=∠DCF=60°时,试探究AG与DG的位置和数量关系,(3)当∠BAC=∠DCF=α时,直接写出AG与DG的数量关系.2.如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.(1)若∠B=60°,这时点P与点C重合,则∠NMP=度;(2)求证:NM=NP;(3)当△NPC为等腰三角形时,求∠B的度数.3.菱形ABCD中,两条对角线AC,BD相交于点O,∠MON+∠BCD=180°,∠MON绕点O旋转,射线OM交边BC于点E,射线ON交边DC于点F,连接EF.(1)如图1,当∠ABC=90°时,△OEF的形状是;(2)如图2,当∠ABC=60°时,请判断△OEF的形状,并说明理由;(3)在(1)的条件下,将∠MON的顶点移到AO的中点O′处,∠MO′N绕点O′旋转,仍满足∠MO′N+∠BCD=180°,射线O′M交直线BC于点E,射线O′N交直线CD于点F,当BC=4,且=时,直接写出线段CE的长.4.如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,(1)求证:四边形AECF为平行四边形;(2)若△AEP是等边三角形,连结BP,求证:△APB≌△EPC;(3)若矩形ABCD的边AB=6,BC=4,求△CPF的面积.5.如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD 于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.(1)试探究AP与BQ的数量关系,并证明你的结论;(2)当AB=3,BP=2PC,求QM的长;(3)当BP=m,PC=n时,求AM的长.6.如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点.(1)求证:△ADP≌△ECP;(2)若BP=n•PK,试求出n的值;(3)作BM丄AE于点M,作KN丄AE于点N,连结MO、NO,如图2所示,请证明△MON是等腰三角形,并直接写出∠MON的度数.7.在正方形ABCD中,对角线AC与BD交于点O;在Rt△PMN中,∠MPN=90°.(1)如图1,若点P与点O重合且PM⊥AD、PN⊥AB,分别交AD、AB于点E、F,请直接写出PE与PF的数量关系;(2)将图1中的Rt△PMN绕点O顺时针旋转角度α(0°<α<45°).①如图2,在旋转过程中(1)中的结论依然成立吗?若成立,请证明;若不成立,请说明理由;②如图2,在旋转过程中,当∠DOM=15°时,连接EF,若正方形的边长为2,请直接写出线段EF的长;③如图3,旋转后,若Rt△PMN的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP时,猜想此时PE与PF的数量关系,并给出证明;当BD=m•BP时,请直接写出PE与PF的数量关系.8.在正方形ABCD中,BD是一条对角线,点P在射线CD上(与点C、D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于H,连接AH,PH.(1)若点P在线段CD上,如图1.①依题意补全图1;②判断AH与PH的数量关系与位置关系并加以证明;(2)若点P在线段CD的延长线上,且∠AHQ=152°,正方形ABCD的边长为1,请写出求DP长的思路.(可以不写出计算结果)9.如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是;(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF=AD,请给出证明;(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.10.如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.(1)如图a,求证:△BCP≌△DCQ;(2)如图,延长BP交直线DQ于点E.①如图b,求证:BE⊥DQ;②如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由.11.已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:(1)当t为何值时,四边形APFD是平行四边形?(2)设四边形APFE的面积为y(cm2),求y与t之间的函数关系式;(3)是否存在某一时刻t,使S四边形APFE:S菱形ABCD=17:40?若存在,求出t的值,并求出此时P,E两点间的距离;若不存在,请说明理由.12.已知菱形ABCD的边长为1,∠ADC=60°,等边△AEF两边分别交DC、CB于点E、F.(1)特殊发现:如图1,若点E、F分别是边DC、CB的中点,求证:菱形ABCD对角线AC、BD的交点O即为等边△AEF的外心;(2)若点E、F始终分别在边DC、CB上移动,记等边△AEF的外心为P.①猜想验证:如图2,猜想△AEF的外心P落在哪一直线上,并加以证明;②拓展运用:如图3,当E、F分别是边DC、CB的中点时,过点P任作一直线,分别交DA边于点M,BC边于点G,DC边的延长线于点N,请你直接写出的值.13.已知:在四边形ABCD中,AD∥BC,∠BAC=∠D,点E、F分别在BC、CD上,且∠AEF=∠ACD.(1)如图1,若AB=BC=AC,求证:AE=EF;(2)如图2,若AB=BC,(1)中的结论是否仍然成立?证明你的结论;(3)如图3,若AB=kBC,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出AE与EF 之间的数量关系,并证明.14.正方形ABCD的边长为4cm,点E在边AB上,将线段AE绕点E顺时针旋转α°(0<α<90)得线段EF,以EF为边在EF右侧作正方形EFGH;(1)如图①,分别连接线段AF、FH、AH,AH交EF于点I;①求证∠FAH的度数是一个常数;②求证:2AE2=AH•IH.(2)如图②,若α=60,点E为AB的中点,在直线AG上是否存在一点J,使△EBJ的周长最小?若存在,求出△EBJ的最小周长;若不存在,说明理由.(3)如图③,若α=45,点E从A出发,按1cm/s的速度沿AB方向运动,直至点C落在GH上停止运动,设点E的运动时间为t(t>0),正方形EFGH与正方形ABCD重叠部分的面积为S,请用含t的代数式表示S.15.请你认真阅读下面的小探究系列,完成所提出的问题.(1)初步探究:如图(1),点E、F分别在正方形ABCD边AB、AD上,DE⊥CF于点P,小芳看到该图后,发现DE=CF,这是因为∠EDA和∠FCD都是∠EDC的余角,就会由ASA判定得出△ADE≌△DCF.(2)类比发现:小芳进一步思考,如果四边形ABCD是矩形,如图(2),且DE⊥CF于点P,她发现,请你替她完成证明;(3)拓展延伸:如图(3),若四边形ABCD是平行四边形,试探究:当∠B与∠EPC满足什么关系时,使得成立?并证明你的结论.16.如图1,在矩形ABCD中,点E为矩形的边CD上任意一点,点P为线段AE的中点,连接BP并延长交边AD于点F,点M为边CD上一点,连接FM,且∠DMF=∠ABF.(1)若AD=2,DE=1,求AP的长;(2)求证:PB=PF+FM;(3)若矩形ABCD改为□ABCD,如图2,(2)中的结论成立吗?若成立,请证明;不成立,说明理由.17.在菱形ABCD和正三角形BGF中,∠ABC=60°,P是DF的中点,连接PG、PC.(1)如图1,当点G在BC边上时,猜想PG与PC的关系,并证明.(提示:延长GP交CD于点E)(2)如图2,当点F在AB的延长线上时,线段PC、PG还满足(1)中的结论吗?写出你的猜想,并给与证明;(3)如图3,当点F在CB的延长线上时,线段PC、PG又有怎样的关系,直接写出你猜想.18.问题情境:小彬、小颖和小明对一道教学问题进行研究.已知,如图1,正方形ABCD中,对角线AC,BD相交于点O,点E是线段OC上一点,过点A作BE的垂线,交线段OB于点G,垂足为点F,易知:OG=OE.变式探究:分析完图1之后,小彬和小颖分别对此进行了研究,并提出了下面两个问题,请回答:(1)小彬:如图2,将图1中的点E改为线段OC延长线上的一点,过点A作BE 垂线,交OB的延长线于点G,垂足为点F.求证:OG=OE.(2)小颖:如图3,将图中的“正方形ABCD”改为“菱形ABCD”,且∠ABC=60°,其余条件不变,试求的值.拓展延伸:(3)小明解决完上述问题后,又提出了如下问题:如图4,将图3中的“∠ABC=60°”改为“∠ABC=α”,并且点E,G分别在OC,OB的延长线上,其余条件不变,直接用含“α”的式子表示的值.19.已知矩形ABCD,AB=4,BD=2.现有另一个与矩形ABCD相似矩形EFGH,相似比为2:1.最初矩形EFGH的GH边放置在∠BCD的平分线处(如图1),现将矩形EFGH 沿着FG作一条直线l,再连接AH、BH、DH、BE,设BC与EH的交点为M,CD与GH的交点为N(若没有交点则不计),回答下列问题.(1)如图1,当矩形ABCD矩形EFGH都不动时,求出矩形ABCD与矩形EFGH重合部分三角形的面积.(2)如图2,现矩形ABCD不动,矩形EFGH沿直线l开始出发,以1m/s的速度移动.设移动时间为t,矩形ABCD与矩形EFGH重合部分的面积为S,求出S关于t的函数关系式,并写出相应的取值范围,并且求出当t为多少时,S为最大值?(3)如图3,矩形ABCD仍然不动,矩形EFGH运动一段时间后停止在某一个点,并且此时△CEH为等腰三角形,这时,在△AHC中,AH=HC成立吗?请说明理由,并求出此时S和t的值.20.在菱形ABCD中,∠A=60°,以D为顶点作等边三角形DEF,连接EC,点N、P分别为EC、BC的中点,连接NP(1)如图1,若点E在DP上,EF与CD交于点M,连接MN,CE=3,求MN的长;(2)如图2,若M为EF中点,求证:MN=PN;(3)如图3,若四边形ABCD为平行四边形,且∠A=∠DBC≠60°,以D为顶点作三角形DEF,满足DE=DF 且∠EDF=∠ABD,M、N、P仍分别为EF、EC、BC的中点,请探究∠ABD与∠MNP的和是否为一个定值,并证明你的结论.21.已知矩形ABCD的一条边AD=8,E是BC边上的一点,将矩形ABCD沿折痕AE折叠,使得顶点B 落在CD边上的点P处,PC=4(如图1).(1)求AB的长;(2)擦去折痕AE,连结PB,设M是线段PA的一个动点(点M与点P、A不重合).N是AB沿长线上的一个动点,并且满足PM=BN.过点M作MH⊥PB,垂足为H,连结MN交PB于点F(如图2).①若M是PA的中点,求MH的长;②试问当点M、N在移动过程中,线段FH的长度是否发生变化?若变化,说明理由;若不变,求出线段FH的长度.22.如图1,▱ABCD中,AE⊥BC于E,AE=AD,EG⊥AB于G,延长GE、DC交于点F,连接AF.(1)若BE=2EC,AB=,求AD的长;(2)求证:EG=BG+FC;(3)如图2,若AF=5,EF=2,点M是线段AG上的一个动点,连接ME,将△GME沿ME翻折得△G′ME,连接DG′,试求当DG′取得最小值时GM的长.23.如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD,BC于点E,F,作BH⊥AF 于点H,分别交AC,CD于点G,P,连接GE,GF.(1)求证:△OAE≌△OBG;(2)试问:四边形BFGE是否为菱形?若是,请证明;若不是,请说明理由;(3)试求:的值(结果保留根号).24.在四边形ABCD中,对角线AC、BD相交于点O,将△COD绕点O按逆时针方向旋转得到△C1OD1,旋转角为θ(0°<θ<90°),连接AC1、BD1,AC1与BD1交于点P.(1)如图1,若四边形ABCD是正方形.①求证:△AOC1≌△BOD1.②请直接写出AC1与BD1的位置关系.(2)如图2,若四边形ABCD是菱形,AC=5,BD=7,设AC1=kBD1.判断AC1与BD1的位置关系,说明理由,并求出k的值.(3)如图3,若四边形ABCD是平行四边形,AC=5,BD=10,连接DD1,设AC1=kBD1.请直接写出k 的值和AC12+(kDD1)2的值.25.已知,如图1,矩形ABCD中,AD=6,DC=8,矩形EFGH的三个顶点E,G,H分别在矩形ABCD 的边AB,CD,DA上,AH=2,连接CF.(1)如图2,当四边形EFGH为正方形时,求CF的长和△FCG的面积;(2)如图1,设AE=x,三角形FCG的面积=y,求与x之间的函数关系式与y的最大值;(3)当△CGF是直角三角形时,求x和y值.26.如图,点E是矩形ABCD的边BC的中点,连接DE交AC于点F.(1)如图①,求证:AF=2CF;(2)如图②,作DG⊥AC于G,试探究:当AB与AD满足什么关系时,使得AG=CF成立?并证明你的结论;(3)如图③,以DE为斜边在矩形ABCD内部作等腰Rt△DEM,交对角线BD于N,连接AM,若AB=AD,请直接写出的值.27.数学课上,张老师出示了问题1:如图1,四边形ABCD是正方形,BC=2,对角线交点记作O,点E 是边BC延长线上一点.联结OE交CD边于F,设CE=x,CF=y,求y关于x的函数解析式及其定义域.(1)经过思考,小明认为可以通过添加辅助线﹣﹣过点O作OM⊥BC,垂足为M求解.你认为这个想法可行吗?请写出问题1的答案及相应的推导过程;(2)如果将问题1中的条件“四边形ABCD是正方形,BC=2”改为“四边形ABCD是平行四边形,BC=3,CD=2,”其余条件不变(如图2),请直接写出条件改变后的函数解析式;(3)如果将问题1中的条件“四边形ABCD是正方形,BC=2”进一步改为:“四边形ABCD是梯形,AD∥BC,BC=4,CD=3,AD=2”其余条件不变(如图3),请你写出条件再次改变后y关于x的函数解析式以及相应的推导过程.28.如图,在正方形ABCD中,E、F分别是BC、DC上的两点,若EF=BE+DF.(1)求证:∠EAF=45°;(2)作∠EFC的平分线FG交AE的延长线于G,连接CG,如图2.求证:BC﹣CF=CG;(3)若F是DC的中点,AB=4,如图3,求EG的长.29.已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.(1)如图1,若四边形ABCD是矩形,且DE⊥CF.则DE•CD CF•AD(填“<”或“=”或“>”);(2)如图2,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,使得DE•CD=CF•AD 成立?并证明你的结论;(3)如图3,若BA=BC=3,DA=DC=4,∠BAD=90°,DE⊥CF.则的值为.30.如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形ABE.点F是对角线BD上一动点(点F不与点B、D重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.(1)求AO的长;(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:∠ACM=30°;(3)连接EM,若△AEM的面积为40,请画出图形,并直接写出△AFM的周长答案1.在△ABC中,AB=AC,点F是BC延长线上一点,以CF为边,作菱形CDEF,使菱形CDEF与点A 在BC的同侧,连接BE,点G是BE的中点,连接AG、DG.(1)如图①,当∠BAC=∠DCF=90°时,直接写出AG与DG的位置和数量关系;(2)如图②,当∠BAC=∠DCF=60°时,试探究AG与DG的位置和数量关系,(3)当∠BAC=∠DCF=α时,直接写出AG与DG的数量关系.【分析】(1)延长DG与BC交于H,连接AH、AD,通过证得△BGH≌△EGD求得BH=ED,HG=DG,得出BH=DC,然后证得△ABH≌△ACD,得出∠BAH=∠CAD,AH=AD,进而求得∠HAD=90°,即可求得AG⊥GD,AG=GD;(2)延长DG与BC交于H,连接AH、AD,通过证得△BGH≌△EGD求得BH=ED,HG=DG,得出BH=DC,然后证得△ABH≌△ACD,得出∠BAH=∠CAD,AH=AD,进而求得△HAD是等边三角形,即可证得AG⊥GD,AG=DG;(3)延长DG与BC交于H,连接AH、AD,通过证得△BGH≌△EGD求得BH=ED,HG=DG,得出BH=DC,然后证得△ABH≌△ACD,得出∠BAH=∠CAD,AH=AD,进而求得△HAD是等腰三角形,即可证得DG=AGtan.2.如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.(1)若∠B=60°,这时点P与点C重合,则∠NMP=30度;(2)求证:NM=NP;(3)当△NPC为等腰三角形时,求∠B的度数.【分析】(1)根据直角三角形的中线等于斜边上的一半,即可得解;(2)延长MN交DC的延长线于点E,证明△MNB≌△ENC,进而得解;(3)NC和PN不可能相等,所以只需分PN=PC和PC=NC两种情况进行讨论即可.①若PN=PC,则∠PNC=∠NCP=2x°,在△PNC中,2x+2x+x=180,解得:x=36,∴∠B=∠PNC+∠NPC=2x°+x°=36°×3=108°,②若PC=NC,则∠PNC=∠NPC=x°,在△PNC中,2x+x+x=180,解得:x=45,∴∠B=∠PNC+∠NPC=x°+x°=45°+45°=90°.3.菱形ABCD中,两条对角线AC,BD相交于点O,∠MON+∠BCD=180°,∠MON绕点O旋转,射线OM交边BC于点E,射线ON交边DC于点F,连接EF.(1)如图1,当∠ABC=90°时,△OEF的形状是等腰直角三角形;(2)如图2,当∠ABC=60°时,请判断△OEF的形状,并说明理由;(3)在(1)的条件下,将∠MON的顶点移到AO的中点O′处,∠MO′N绕点O′旋转,仍满足∠MO′N+∠BCD=180°,射线O′M交直线BC于点E,射线O′N交直线CD于点F,当BC=4,且=时,直接写出线段CE的长.【分析】(1)先求得四边形ABCD是正方形,然后根据正方形的性质可得∠EBO=∠FCO=45°,OB=OC,再根据同角的余角相等可得∠BOE=∠COF,然后利用“角边角”证明△BOE和△COF全等,根据全等三角形对应边相等即可得证;(2)过O点作OG⊥BC于G,作OH⊥CD于H,根据菱形的性质可得CA平分∠BCD,∠ABC+BCD=180°,求得OG=OH,∠BCD=180°﹣60°=120°,从而求得∠GOH=∠EOF=60°,再根据等量减等量可得∠EOG=∠FOH,然后利用“角边角”证明△EOG和△FOH全等,根据全等三角形对应边相等即可得证;(3)过O点作OG⊥BC于G,作OH⊥CD于H,先求得四边形O′GCH是正方形,从而求得GC=O′G=3,∠GO′H=90°,然后利用“角边角”证明△EO′G和△FO′H全等,根据全等三角形对应边相等即可证得△O′EF 是等腰直角三角形,根据已知求得等腰直角三角形的直角边O′E的长,然后根据勾股定理求得EG,即可求得CE的长.4.如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,(1)求证:四边形AECF为平行四边形;(2)若△AEP是等边三角形,连结BP,求证:△APB≌△EPC;(3)若矩形ABCD的边AB=6,BC=4,求△CPF的面积.【分析】(1)由折叠的性质得到BE=PE,EC与PB垂直,根据E为AB中点,得到AE=EB=PE,利用三角形内一边上的中线等于这条边的一半的三角形为直角三角形,得到∠APB为90°,进而得到AF与EC平行,再由AE与FC平行,利用两对边平行的四边形为平行四边形即可得证;(2)根据三角形AEP为等边三角形,得到三条边相等,三内角相等,再由折叠的性质及邻补角定义得到一对角相等,根据同角的余角相等得到一对角相等,再由AP=EB,利用AAS即可得证;(3)过P作PM⊥CD,在直角三角形EBC中,利用勾股定理求出EC的长,利用面积法求出BQ的长,根据BP=2BQ求出BP的长,在直角三角形ABP中,利用勾股定理求出AP的长,根据AF﹣AP求出PF 的长,由PM与AD平行,得到三角形PMF与三角形ADF相似,由相似得比例求出PM的长,再由FC=AE=3,求出三角形CPF面积即可.5.如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD 于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.(1)试探究AP与BQ的数量关系,并证明你的结论;(2)当AB=3,BP=2PC,求QM的长;(3)当BP=m,PC=n时,求AM的长.【分析】(1)要证AP=BQ,只需证△PBA≌△QCB即可;(2)过点Q作QH⊥AB于H,如图.易得QH=BC=AB=3,BP=2,PC=1,然后运用勾股定理可求得AP (即BQ)=,BH=2.易得DC∥AB,从而有∠CQB=∠QBA.由折叠可得∠C′QB=∠CQB,即可得到∠QBA=∠C′QB,即可得到MQ=MB.设QM=x,则有MB=x,MH=x﹣2.在Rt△MHQ中运用勾股定理就可解决问题;(3)过点Q作QH⊥AB于H,如图,同(2)的方法求出QM的长,就可得到AM的长.6.如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点.(1)求证:△ADP≌△ECP;(2)若BP=n•PK,试求出n的值;(3)作BM丄AE于点M,作KN丄AE于点N,连结MO、NO,如图2所示,请证明△MON是等腰三角形,并直接写出∠MON的度数.【分析】(1)根据菱形的性质得到AD∥BC,根据平行线的性质得到对应角相等,根据全等三角形的判定定理证明结论;(2)作PI∥CE交DE于I,根据点P是CD的中点证明CE=2PI,BE=4PI,根据相似三角形的性质证明结论;(3)作OG⊥AE于G,根据平行线等分线段定理得到MG=NG,又OG⊥MN,证明△MON是等腰三角形,根据直角三角形的性质和锐角三角函数求出∠MON的度数.7.在正方形ABCD中,对角线AC与BD交于点O;在Rt△PMN中,∠MPN=90°.(1)如图1,若点P与点O重合且PM⊥AD、PN⊥AB,分别交AD、AB于点E、F,请直接写出PE与PF的数量关系;(2)将图1中的Rt△PMN绕点O顺时针旋转角度α(0°<α<45°).①如图2,在旋转过程中(1)中的结论依然成立吗?若成立,请证明;若不成立,请说明理由;②如图2,在旋转过程中,当∠DOM=15°时,连接EF,若正方形的边长为2,请直接写出线段EF的长;③如图3,旋转后,若Rt△PMN的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP时,猜想此时PE与PF的数量关系,并给出证明;当BD=m•BP时,请直接写出PE与PF的数量关系.【分析】(1)根据正方形的性质和角平分线的性质解答即可;(2)①根据正方形的性质和旋转的性质证明△FOA≌△EOD,得到答案;②作OG⊥AB于G,根据余弦的概念求出OF的长,根据勾股定理求值即可;③过点P作HP⊥BD交AB于点H,根据相似三角形的判定和性质求出PE与PF的数量关系,根据解答结果总结规律得到当BD=m•BP时,PE与PF的数量关系.8.在正方形ABCD中,BD是一条对角线,点P在射线CD上(与点C、D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于H,连接AH,PH.(1)若点P在线段CD上,如图1.①依题意补全图1;②判断AH与PH的数量关系与位置关系并加以证明;(2)若点P在线段CD的延长线上,且∠AHQ=152°,正方形ABCD的边长为1,请写出求DP长的思路.(可以不写出计算结果)【分析】(1)①根据题意画出图形即可;②连接CH,先根据正方形的性质得出△DHQ是等腰直角三角形,再由SAS定理得出△HDP≌△HQC,故PH=CH,∠HPC=∠HCP,由正方形的性质即可得出结论;(2)根据四边形ABCD是正方形,QH⊥BD可知△DHQ是等腰直角三角形,再由平移的性质得出PD=CQ.作HR⊥PC于点R,由∠AHQ=152°,可得出∠AHB及∠DAH的度数,设DP=x,则DR=HR=RQ,由锐角三角函数的定义即可得出结论.9.如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是DE+DF=AD;(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF=AD,请给出证明;(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.【分析】(1)利用正方形的性质得出角与线段的关系,易证得△APE≌△DPF,可得出AE=DF,即可得出结论DE+DF=AD,(2)取AD的中点M,连接PM,利用菱形的性质,可得出△MDP是等边三角形,易证△MPE≌△FPD,得出ME=DF,由DE+ME=AD,即可得出DE+DF=AD,(3)①当点E落在AD上时,DE+DF=AD,②当点E落在AD的延长线上时,DF﹣DE=AD.10.如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.(1)如图a,求证:△BCP≌△DCQ;(2)如图,延长BP交直线DQ于点E.①如图b,求证:BE⊥DQ;②如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由.【分析】(1)根据旋转的性质证明∠BCP=∠DCQ,得到△BCP≌△DCQ;(2)①根据全等的性质和对顶角相等即可得到答案;②根据等边三角形的性质和旋转的性质求出∠EPD=45°,∠EDP=45°,判断△DEP的形状.11.已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:(1)当t为何值时,四边形APFD是平行四边形?(2)设四边形APFE的面积为y(cm2),求y与t之间的函数关系式;(3)是否存在某一时刻t,使S四边形APFE:S菱形ABCD=17:40?若存在,求出t的值,并求出此时P,E两点间的距离;若不存在,请说明理由.【分析】(1)由四边形ABCD是菱形,OA=AC,OB=BD.在Rt△AOB中,运用勾股定理求出AB=10.再由△DFQ∽△DCO.得出=.求出DF.由AP=DF.求出t.(2)过点C作CG⊥AB于点G,由S菱形ABCD=AB•CG=AC•BD,求出CG.据S梯形APFD=(AP+DF)•CG.S△EFD=EF•QD.得出y与t之间的函数关系式;(3)过点C作CG⊥AB于点G,由S菱形ABCD=AB•CG,求出CG,由S四边形APFE:S菱形ABCD=17:40,求出t,再由△PBN∽△ABO,求得PN,BN,据线段关系求出EM,PM再由勾股定理求出PE.12.已知菱形ABCD的边长为1,∠ADC=60°,等边△AEF两边分别交DC、CB于点E、F.(1)特殊发现:如图1,若点E、F分别是边DC、CB的中点,求证:菱形ABCD对角线AC、BD的交点O即为等边△AEF的外心;(2)若点E、F始终分别在边DC、CB上移动,记等边△AEF的外心为P.①猜想验证:如图2,猜想△AEF的外心P落在哪一直线上,并加以证明;②拓展运用:如图3,当E、F分别是边DC、CB的中点时,过点P任作一直线,分别交DA边于点M,BC边于点G,DC边的延长线于点N,请你直接写出的值.【分析】(1)连接OE、0F,由四边形ABCD是菱形,得出AC⊥BD,BD平分∠ADC,AD=DC=BC,又由E、F分别为DC、CB中点,证得0E=OF=OA,则可得点O即为△AEF的外心;(2)①连接PE、PA,过点P分别作PI⊥CD于I,PJ⊥AD于J,求出∠IPJ的度数,又由点P是等边△AEF 的外心,易证得△PIE≌△PJA,可得PI=PJ,即点P在∠ADC的平分线上,即点P落在直线DB上;②连接BD、AC交于点P,由(1)可得点P即为△AEF的外心.设DM=x,DN=y(x≠0,y≠O),则CN=y ﹣1,先利用AAS证明△GBP≌△MDP,得出BG=DM=x,CG=1﹣x,再由BC∥DA,得出△NCG∽△NDM,根据相似三角形对应边成比例得出=,进而求出为定值2.13.已知:在四边形ABCD中,AD∥BC,∠BAC=∠D,点E、F分别在BC、CD上,且∠AEF=∠ACD.(1)如图1,若AB=BC=AC,求证:AE=EF;(2)如图2,若AB=BC,(1)中的结论是否仍然成立?证明你的结论;(3)如图3,若AB=kBC,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出AE与EF 之间的数量关系,并证明.【分析】(1)中所给的是最特殊的一种情况,但对整个题来说,要从(1)中找到基本的解题思路,此题难的是构造全等三角形,从而证明线段相等.虽然(1)中没有要求步骤,但能正确的解出(1)可以给(2)和(3)定一个基调;(2)是将(1)中的等边三角形变为等腰三角形,但起关键作用的条件没变,任然可以仿照(1)中的方法去做;(3)中将三角形变为更一般的三角形,但和(1)比较起来还是有两个条件没变,而利用这两个条件能证明两个三角形相似,从而利用相似的对应边成比例得出结论.14.正方形ABCD的边长为4cm,点E在边AB上,将线段AE绕点E顺时针旋转α°(0<α<90)得线段EF,以EF为边在EF右侧作正方形EFGH;(1)如图①,分别连接线段AF、FH、AH,AH交EF于点I;①求证∠FAH的度数是一个常数;②求证:2AE2=AH•IH.(2)如图②,若α=60,点E为AB的中点,在直线AG上是否存在一点J,使△EBJ的周长最小?若存在,求出△EBJ的最小周长;若不存在,说明理由.(3)如图③,若α=45,点E从A出发,按1cm/s的速度沿AB方向运动,直至点C落在GH上停止运动,设点E的运动时间为t(t>0),正方形EFGH与正方形ABCD重叠部分的面积为S,请用含t的代数式表示S.【分析】(1)①易证A、F、H在以点E为圆心,AE为半径的圆上,根据圆周角定理可得∠FAH=∠FEH=45°;②由于FH=EF=AE,要证2AE2=AH•IH,只需证到FH2=AH•IH,只需证到△FHI∽△AHF即可;(2)连接DE与直线AG交于点N,连接NB,如图②,易证△AFG≌△AEH,则有∠FAG=∠EAH,从而可得∠DAG=∠GAE.由AD=AB可得点D与点B关于直线AG对称,从有而ND=NB,从而可求得EN+BN+EB=2+2.根据两点之间线段最短可得:当点J运动到点N处,△EBJ的周长最短,问题得以解决;(3)点E运动的过程中,依次出现图③a、图③b、图③c、图③d、图③e、图③f的情况,只需运用割补法分别求出图③a、图③c、图③e中S与t的关系式,运用方程思想求出图③b、图③d、图③f中对应t的值,就可解决问题.15.请你认真阅读下面的小探究系列,完成所提出的问题.(1)初步探究:如图(1),点E、F分别在正方形ABCD边AB、AD上,DE⊥CF于点P,小芳看到该图后,发现DE=CF,这是因为∠EDA和∠FCD都是∠EDC的余角,就会由ASA判定得出△ADE≌△DCF.(2)类比发现:小芳进一步思考,如果四边形ABCD是矩形,如图(2),且DE⊥CF于点P,她发现,请你替她完成证明;(3)拓展延伸:如图(3),若四边形ABCD是平行四边形,试探究:当∠B与∠EPC满足什么关系时,使得成立?并证明你的结论.【分析】(2)根据∠A=∠ADC=90°,DE⊥CF,证明∠ADE=∠DCF,得到△ADE∽△DCF,得到答案;(3)在AD的延长线上取点M,使CM=CF,证明△ADE∽△DCM,得到答案.16.如图1,在矩形ABCD中,点E为矩形的边CD上任意一点,点P为线段AE的中点,连接BP并延长交边AD于点F,点M为边CD上一点,连接FM,且∠DMF=∠ABF.(1)若AD=2,DE=1,求AP的长;(2)求证:PB=PF+FM;(3)若矩形ABCD改为▱ABCD,如图2,(2)中的结论成立吗?若成立,请证明;不成立,说明理由.【分析】(1)由矩形的性质和勾股定理求出AE,即可得出AP的长;(2)延长BF、CD交于点N,由矩形的性质得出CN∥AB,得出∠N=∠PBA,∠NEP=∠BAP,由ASA 证明△NEP≌△BAP,得出PB=PN,再证出FN=FM,即可得出结论;(3)延长BF、CD交于点N,由矩形的性质得出CN∥AB,得出∠N=∠PBA,∠NEP=∠BAP,由ASA 证明△NEP≌△BAP,得出PB=PN,再证出FN=FM,即可得出结论.【点评】本题是四边形综合题目,考查了矩形的性质、平行四边形的性质、全等三角形的判定与性质、等腰三角形的判定等知识;本题综合性强,难度较大,需要通过作辅助线证明三角形全等才能得出结论.17.在菱形ABCD和正三角形BGF中,∠ABC=60°,P是DF的中点,连接PG、PC.(1)如图1,当点G在BC边上时,猜想PG与PC的关系,并证明.(提示:延长GP交CD于点E)。
中考复习三角形综合题

中考复习三角形综合题1.已知,如图,Rt△ABC中,∠ACB=90°,BC=8,cot∠BAC=,点D在边BC上(不与点B、C重合),点E在边BC的延长线上,∠DAE=∠BAC,点F在线段AE上,∠ACF=∠B.设BD=x.(1)若点F恰好是AE的中点,求线段BD的长;(2)若y=,求y关于x的函数关系式,并写出它的定义域;(3)当△ADE是以AD为腰的等腰三角形时,求线段BD的长.2.如图,△ABC边AB上点D、E(不与点A、B重合),满足∠DCE=∠ABC,∠ACB=90°,AC=3,BC=4;(1)当CD⊥AB时,求线段BE的长;(2)当△CDE是等腰三角形时,求线段AD的长;(3)设AD=x,BE=y,求y关于x的函数解析式,并写出定义域.3.如图,已知△ABC中,AB=AC=3,BC=2,点D是边AB上的动点,过点D作DE∥BC,交边AC于点E,点Q是线段DE上的点,且QE=2DQ,连接BQ并延长,交边AC于点P.设BD=x,AP=y.(1)求y关于x的函数解析式及定义域;(2)当△PQE是等腰三角形时,求BD的长;(3)连接CQ,当∠CQB和∠CBD互补时,求x的值.4.如图,在Rt△ABC中,∠ACB=90°,=,CD⊥AB于点D,点E是直线AC上一动点,连接DE,过点D作FD⊥ED,交直线BC于点F.(1)探究发现:如图1,若m=n,点E在线段AC上,则= ;(2)数学思考:①如图2,若点E在线段AC上,则= (用含m,n的代数式表示);②当点E在直线AC上运动时,①中的结论是否任然成立?请仅就图3的情形给出证明;(3)拓展应用:若AC=,BC=2,DF=4,请直接写出CE的长.5.如图1,在△ABC中,AB=AC,射线BP从BA所在位置开始绕点B顺时针旋转,旋转角为α(0°<α<180°)(1)当∠BAC=60°时,将BP旋转到图2位置,点D在射线BP上.若∠CDP=120°,则∠ACD ∠ABD (填“>”、“=”、“<”),线段BD、CD与AD之间的数量关系是;(2)当∠BAC=120°时,将BP旋转到图3位置,点D在射线BP上,若∠CDP=60°,求证:BD﹣CD=AD;(3)将图3中的BP继续旋转,当30°<α<180°时,点D是直线BP上一点(点P不在线段BD上),若∠CDP=120°,请直接写出线段BD、CD与AD之间的数量关系(不必证明)6.已知,在△ABC中,∠ACB=90°,CA=CD,CG⊥AD于点H,交AB于点G,E为AB上一点,连接CE交AD 于点F.(1)如图1,若CE⊥AB于点E,HG=1,CH=5,求CF的长;(2)如图2,若AC=AE,∠GEH=∠ECH,求证:CE=HE;(3)如图3,若E为AB的中点,作A关于CE的对称点A′,连接CA′,EA′,DA′,请直接写出∠CEH,∠A′CD,∠EA′D之间的等量关系.7.(1)问题发现如图1,在Rt△ABC中,∠A=90°,=1,点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接CD.填空:①= ;②∠ACD的度数为.(2)拓展探究如图2,在Rt△ABC中,∠A=90°,=k.点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接CD,请判断∠ACD与∠B的数量关系以及PB与CD之间的数量关系,并说明理由.(3)解决问题如图3,在△ABC中,∠B=45°,AB=4,BC=12,P是边BC上一动点(不与点B重合),∠PAD=∠BAC,∠APD=∠B,连接CD.若PA=5,请直接写出CD的长.8.Rt△ABC与Rt△DEF的位置如图所示,其中AC=2,BC=6,DE=3,∠D=30°,其中,Rt△DEF沿射线CB以每秒1个单位长度的速度向右运动,射线DE、DF与射线AB分别交于N、M两点,运动时间为t,当点E运动到与点B重合时停止运动.(1)当Rt△DEF在起始时,求∠AMF的度数;(2)设BC的中点的为P,当△PBM为等腰三角形时,求t的值;(3)若两个三角形重叠部分的面积为S,写出S与t的函数关系式和相应的自变量的取值范围.9.如图,已知等腰△ABC中,AC=BC,点D、E、F分别是线段AC、BC、AD的中点,连接FE、ED,BF的延长线交ED的延长线于点G,连接GC.(1)求证:EF∥CG;(2)若AC=AB,求证:AC=CG;(3)如图2,若CG=EG,则= .10.在Rt△ABC中,∠CAB=90°,AC=AB=6,D,E分别是AB,AC的中点,若等腰Rt△ADE绕点A逆时针旋转,得到Rt△AD1E1,设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.(1)如图1,当α=90°时,线段BD1的长等于,线段CE1的长等于;(2)如图2,当α=135°时,设直线BD1与CA的交点为F,求证:BD1=CE1,且BD1⊥CE1;(3)点P到AB所在直线的距离的最大值是.11.如图,在Rt△ABC中,∠ACB=90°,点D为边BC上任意一点,以直线AD为对称轴,作Rt△ABC的轴对称图形Rt△AEF,点M、点N、点P、点Q分别为AB、BC、EF、EA的中点.(1)求证:MN=PQ;(2)如图2,当BD=时,判断点M、点N、点P、点Q围成的四边形的形状,并说明理由;(3)若BC=6,请你直接写出当①BD=3;②BD=6时,点M、点N、点P、点Q围成图形的形状.12.在Rt△ABC中,∠ACB=90°,点D在AB边上,AD=BD,过点D作射线DH,交BC边于点M.(1)如图1,若∠B=30°,求证:△ACD是等边三角形;(2)如图2,若AC=10,AD=13,∠CDH=∠A.①求线段DM的长;②点P是射线DH上一点,连接AP交CD于点N,当△DMN是等腰三角形时,求线段MP的长.13.等腰三角形ABC中,AB=CB,BO⊥AC,点P为射线BC上的动点(不与点B重合),在射线CA上截取CD=CB,作PF⊥BD,分别交射线BO,BD于点E,F.设∠ABC=α.(1)令∠ABC=90°.①如图1,当点P与点C重合时,求证:△BOD≌△POE;②如图2,当点P在点C的左边时,求的值;③猜想:当点P在点C的右边时,的值又是多少?请直接写出.(2)设点P在点C的右边,请在图3(∠ABC>90°)或图4(∠ABC<90°)中继续探究的值(用含α的式子表示),并说明理由.14.如图1,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D,点E在AC边上,连接BE.(1)若AF是△ABE的中线,且AF=5,AE=6,连接DF,求DF的长;(2)若AF是△ABE的高,延长AF交BC于点G.①如图2,若点E是AC的中点,连接EG,求证:AG+EG=BE;②如图3,若点E是AC边上的动点,连接DF.当点E在AC边上(不含端点)运动时,∠DFG的大小是否改变,如果不变,请求出∠DFG的度数;如果要变,请说明理由.15.在△ABC中,AD、AE分别是△ABC的内、外角平分线.(1)如图①,CG⊥AD于G,BG的延长线交AE于H,求证:AH=EH;(2)如图①,在(1)的条件下,若AE=2AD,BE=5BC,则tan∠AHB= ;(3)如图②,点M是DE的中点,BE=5BC=10,求MD的长.16.如图,△ABC是等边三角形,AB=2,D是边BC的中点,点P从点A出发,沿AB﹣BD以每秒1个单位长度的速度向终点D运动.同时点Q从点C出发,沿CA﹣AC以每秒1个单位长度的速度运动.当点P停止运动时,点Q也随之停止运动,设点P的运动时间为t(秒),△PQD的面积为S.(1)求线段PB的长(用含t的代数式).(2)当△PQD是等边三角形时,求t的值.(3)当S>0时,求S与t的函数关系式.(4)若点D关于直线PQ的对称点为点D′,且S>0,直接写出点D′落在△ABC的边上时t的值.17.在Rt△AOB中,OA=3,sinB=,P、M、分别是BA、BO边上的两个动点.点M从点B出发,沿BO以1单位/秒的速度向点O运动;点P从点B出发,沿BA以a单位/秒的速度向点A运动;P、M两点同时出发,任意一点先到达终点时,两点停止运动.设运动的时间为t.(1)线段AP的长度为(用含a、t的代数式表示);(2)如图①,连结PO、PM,若a=1,△PMO的面积为S,试求S的最大值;(3)如图②,连结PM、AM,试探究:在点P、M运动的过程中,是否存在某个时刻,使得△PMB为直角三角形且△PMA是等腰三角形?若存在,求出此时a和t的取值,若不存在,请说明理由.18.在直角△ABC中,∠ACB=90°,点E在AC边上,连结BE,作∠ACF=∠CBE交AB于点F,同时点D在BE上,且CD⊥AB.(1)已知:如图,,.①求证:△ACF≌△BCD.②求的值.(2)若,,则的值是多少(直接写出结果)19.已知,AB=5,tan∠ABM=,点C、D、E为动点,其中点C、D在射线BM上(点C在点D的左侧),点E和点D分别在射线BA的两侧,且AC=AD,AB=AE,∠CAD=∠BAE.(1)当点C与点B重合时(如图1),联结ED,求ED的长;(2)当EA∥BM时(如图2),求四边形AEBD的面积;(3)联结CE,当△ACE是等腰三角形时,求点B、C间的距离.20.在△ABC中,D、E、F分别为BC、AB、AC上的点.(1)如图1,若EF∥BC、DF∥AB,连CE、AD分别交DF、EF于N、M,且E为AB的中点,求证:EM=MF;(2)如图2,在(1)中,若E不是AB的中点,请写出与MN平行的直线,并证明;(3)若BD=DC,∠B=90°,且AE:AB:BC=1:3:2,AD与CE相交于点Q,直接写出tan∠CQD的值.21.我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC 的中线,AF⊥BE,垂足为P.像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.特例探索(1)①如图1,当∠ABE=45°,时,a= ,b= ;②如图2,当∠ABE=30°,c=4时,求a和b的值归纳证明(2)请你观察(1)中的计算结果,猜想三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.22.如图,一个直角三角形纸片的锐角顶点A在∠MCN的边OM上移动,移动过程中始终有AB⊥ON于点B,AC⊥OM于点A,∠MON的平分线OP分别交AB,AC于点D、E.(1)点A在移动的过程中,线段AD和AE有怎样的数量关系?(不必证明)(2)点A在移动的过程中,若射线ON上始终存在一点F与点A关于OP所在的直线对称,判断并证明以A、D、F、E为顶点的四边形是什么特殊四边形?(3)若∠MON=45°,猜想线段AC、AD、OC之间有怎样的数量关系?请证明你的猜想.23.如图①,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与点A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM,射线AE 于点F、D.(1)问题发现:直接写出∠NDE= 度;(2)拓展探究:试判断,如图②当∠EAC为钝角时,其他条件不变,∠NDE的大小有无变化?请给出证明.(3)如图③,若∠EAC=15°,BD=,直线CM与AB交于点G,其他条件不变,请直接写出AC的长.24.在△ABC中,∠ABC=2∠ACB,延长AB至点D,使BD=BC,点E是直线BC上一点,点F是直线AC上一点,连接DE.连接EF,且∠DEF=∠DBC.(1)如图1,若∠D=∠EFC=15°,AB=,求AC的长.(2)如图2,当∠BAC=45°,点E为线段BC的延长线上,点F在线段AC的延长线上时,求证:CF=BE.(3)如图3,当∠BAC=90°,点E为线段CB的延长线上,点F在线段CA的延长线上时,猜想线段CF与线段BE的数量关系,并证明猜想的结论.25.中点、平行线、等腰直角三角形、等边三角形都是常见的几何图形!(1)如图1,若点D为等腰直角三角形ABC斜边BC的中点,点E、F分别在AB、AC边上,且∠EDF=90°,连接AD、EF,当BC=5,FC=2时,求EF的长度;(2)如图2,若点D为等边三角形ABC边BC的中点,点E、F分别在AB、AC边上,且∠EDF=90°;M为EF的中点,连接CM,当DF∥AB时,证明:3ED=2MC;(3)如图3,若点D为等边三角形ABC边BC的中点,点E、F分别在AB、AC边上,且∠EDF=90°;当BE=6,CF=0.8时,直接写出EF的长度.26.已知,△ABC为直角三角形,∠ACB=90°,点P是射线CB上一点(点P不与点B、C重合),线段AP 绕点A顺时针旋转90°得到线段AQ,连接QB交射线AC于点M.(1)如图①,当AC=BC,点P在线段CB上时,线段PB、CM的数量关系是;(2)如图②,当AC=BC,点P在线段CB的延长线时,(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由.(3)如图③,若,点P在线段CB的延长线上,CM=2,AP=13,求△ABP的面积.27.在Rt△ABC中,∠C=90°,Rt△ABC绕点A顺时针旋转到Rt△ADE的位置,点E在斜边AB上,连结BD,过点D作DF⊥AC于点F.(1)如图1,若点F与点A重合,求证:AC=BC;(2)若∠DAF=∠DBA,。
人教版中考数学中考压轴题突破 一、选填题压轴题突破 重难点突破六 多结论选填题

B.②④
C.③④
D.②③
3.★(2022·广元)二次函数y=ax2+bx+c(a≠0)的部分图象如图所
示,图象过点(-1, 0),对称轴为直线x=2,下列结论:①abc<0;② 1
4a+c>2b;③ 3b- 2c>0;④若点A(-2,y1),点B -2,y2 ,点 7
C 2,y3 在该函数图象上,则y1<y3<y2;⑤ 4a+2b≥m (am+b) (m为常 数).
2.(2022·临沂)二次函数y=ax2+bx+c (a≠0)的部分图象如图所示,
1 其对称轴为直线x=- 2 ,且与x轴的一个交点坐标为(-2,0).下列结
论:①abc>0;②a=b;③2a+c=0;④关于x的一元二次方程ax2+bx+
c-1=0有两个相等的实数根.其中正确结论的序号是
( D)
A.①③
其中正确的结论有 A.5个 B.4个 C.3个 D.2个
(C)
4.★(2021·荆门)抛物线y=ax2+bx+c(a,b,c为常数)开口向下且过
点A(1,0),B(m,0)(-2<m<-1),下列结论:① 2b+c>0;② 2a+
c<0;③ a(m+1)-b+c>0;④若方程a(x-m)(x-1)-1=0有两个不等
对称轴x=-
b 2a
=1,得b=-2a,∴y=ax2-
2ax-1,
确 当x=-1时,
y>0,∴aa++2a2-a-1>0, 1
11 ∴a>33
,故②正正确;当m=1时,m(am+b)= 确
aa++b,故③错错误 ;∵点(-2, y1)到对称轴的距离大大于点(2, y3)到
新课标九年级数学中考复习强效提升分数精华版综合题

综合题综合题一直是中考复习最后阶段的重点和难点.综合题所考查的内容涉及初中代数或几何中若干不同的知识点,这就需要我们既要扎实地掌握好数学基础知识,又具备灵活综合运用数学知识解决问题的能力.在近年的中考命题中,综合题的难度有所下降,形式与内容也有一定程度的创新. (Ⅰ)方程型综合题 【简要分析】方程是贯穿初中代数的一条知识主线.方程型综合题也是中考命题的热点,中考中的方程型综合题主要有两类题:一类是与地、一元二次方程根的判别式、根与系数有关的问题,另一类是与几何相结合的问题. 【典型考题例析】例1:已知关x 的一元二次方程 230x x m +-=有实数根. (1)求m 的取值范围(2)若两实数根分别为1x 和2x ,且1x x +221211x x +=求m 的值.例2:已知关于x 的方程2(2)20a x ax a +-+=有两个不相等的实数根1x 和2x ,并且抛物线2(21)25y x a x a =-++-与x 轴的两个交点分别位于点(2,0)的两旁.(1) 求实数a 的取值范围. 当1222x x +=时,求a 的值.说明 运用一元二次方程根的差别式时,要注意二次项系数不为零,运用一元二次方程根与系数的关系时,要注意根存在的前提,即要保证△≥0.例3: 如图2-4-18,090B ∠=,O 是AB 上的一点,以O 为圆心,OB 为半径的圆与AB 交于点E ,与AC 切于点D .若AD=23,且AB 的长是关于x 的方程280x x k -+=的两个实数根.(1)求⊙O 的半径.(2)求CD 的长. 【提高训练1】1.已知关于x 的方程221(1)104x k x k -+++=的两根是一矩形两邻边的长.(1)k 取何值时,方程有两个实数根?(2)当矩形的对角线长为5时,求k 的值. 2.已知关于x 的方程222(1)230x m x m m -++--=的两个不相等的实数根中有一个根为0,是否存在实数k ,使关于x 的方程22()520x k m x k m m ----+-=的两个实数根1x 、2x 之差的绝对值为1?若存在,求出k 的值;若不存在,请说明图2-4-18EDCBAO理由.3.已知方程组221y xy kx ⎧=⎨=+⎩有两个不相等的实数解.(1)求k 有取值范围.(2)若方程组的两个实数解为11x x y y =⎧⎨=⎩和22x x y y =⎧⎨=⎩是否存在实数k ,使11221x x x x ++=?若存在,求出k 的值;若不存在,请说明理由.4.如图2-4-19,以△ABC 的直角边AB 为直径的半圆O 与斜边AC 交于点D ,E 是BC 边的中点,连结DE .(1)DE 与半圆O 相切吗?若不相切,请说明理由.(2)若AD 、AB 的长是方程210240x x -+=的个根,求直角边BC 的长. 【提高训练1答案】1.(1)32k ≥ (2)2k = 2.存在,24k =-或 3.(1)12k < (2)满足条件的k 存在,3k =- 4.(1)相切,证明略 (2)35(Ⅱ)函数型综合题 【简要分析】中考中的函数综合题,聊了灵活考查相关的基础知识外,还特别注重考查分析转化能力、数形结合思想的运用能力以及探究能力.此类综合题,不仅综合了《函数及其图象》一章的基本知识,还涉及方程(组)、不等式(组)及几何的许多知识点,是中考命题的热点.善于根据数形结合的特点,将函数问题、几何问题转化为方程(或不等式)问题,往往是解题的关键. 【典型考题例析】例1:如图2-4-20,二次函数的图象与x 轴交于A 、B 两点,与y 轴交于点C ,点C 、D 是二次函数图象上的一对对称点,一次函数的图象过点B 、D .(1)求D 点的坐标.(2)求一次函数的解析式.(3)根据图象写出使一次函数值大于二次函数的值的x 的取值范围.说明:本例是一道纯函数知识的综合题,主要考查了二次函的对称性、对称点坐标的求法、一次函数解析式的求法以及数形结合思想的运用等.例2 如图2-4-21,二次函数2(0)y ax bx c a =++≠的图象与x 轴交于A 、B 两点,其中A 点坐标为(-1,0),点C (0,5)、D (1,8)在抛物线上,M 为抛物线的顶点.(1)求抛物线的解析式. (2)求△MCB 的面积.说明:以面积为纽带,以函数图象为背景,结合图2-4-19E O D CBA图2-4-203yx321-3-2-1OCBANM D C BA O图2-4-21y x常见的平面几何图形而产生的函数图象与图形面积相结合型综合题是中考命题的热点.解决这类问题的关键是把相关线段的长与恰当的点的坐标联系起来,必要时要会灵活将待求图形的面积进行分割,转化为特殊几何图形的面积求解.例3 :已知抛物线2(4)24y x m x m =-+-++与x 轴交于1(,0)A x 、2(,0)B x ,与y 轴交于点C ,且1x 、2x 满足条件1212,20x x x x <+=(1)求抛物线的角析式;(2)能否找到直线y kx b =+与抛物线交于P 、Q 两点,使y 轴恰好平分△CPQ 的面积?求出k 、b 所满足的条件.说明 本题是一道方程与函数、几何相结合的综合题,这类题主要是以函数为主线.解题时要注意运用数形结合思想,将图象信息与方程的代信息相互转化.例如:二次函数与x 轴有交点.可转化为一元二次旗号有实数根,并且其交点的横坐标就是相应一元二次方程的解.点在函数图象上,点的坐标就满足该函数解析式等.例4 已知:如图2-4-23,抛物线2y ax bx c =++经过原点(0,0)和A (-1,5).(1)求抛物线的解析式.(2)设抛物线与x 轴的另一个交点为C .以OC 为直径作⊙M ,如果过抛物线上一点P 作⊙M 的切线PD ,切点为D ,且与y 轴的正半轴交于点为E ,连结MD .已知点E 的坐标为(0,m ),求四边形EOMD 的面积.(用含m 的代数式表示)(3)延长DM 交⊙M 于点N ,连结ON 、OD ,当点P 在(2)的条件下运动到什么位置时,能使得DON EOMD S S ∆=四边形?请求出此时点P 的坐标. 【提高训练2】1.已知抛物线的解析式为2(21)y x m x m m =--+-,(1)求证:此抛物线与x 轴必有两个不同的交点.(2)若此抛物线与直线34y x m =-+的一个交点在y 轴上,求m 的值.2.如图2-4-24,已知反比例函数12y x=的图象与一次函数4y kx =+的图象相交于P 、Q 两点,并且P 点的纵坐标是6.(1)求这个一次函数的解析式.(2)求△POQ 的面积.3.在以O 这原点的平面直角坐标系中,抛物线2(0)y ax bx c a =++≠与y 轴交于点C (0,3).与xA D EP N My O 图2-4-21xCy xB 'M GBAO f x () = 2⋅x2轴正半轴交于A 、B 两点(B 点在A 点的右侧),抛物线的对称轴是2x =,且32A O C S ∆=.(1)求此抛物线的解析式.(2)设抛物线的顶点为D ,求四边形ADBC 的面积.4.OABC 是一张平放在直角坐标系中的矩形纸片,O 为原点,点A 在x 轴上,点C 在y 轴上,OA=10,OC=6.(1)如图2-4-25,在AB 上取一点M ,使得△CBM 沿CM 翻折后,点B 落在x 轴上,记作B ′点,求所B ′点的坐标.(2)求折痕CM 所在直线的解析式.(3)作B ′G ∥AB 交CM 于点G ,若抛物线216y x m =+过点G ,求抛物线的解析式,交判断以原点O 为圆心,OG 为半径的圆与抛物线除交点G 外,是否还有交点?若有,请直接写出交点的坐标. 5.如图2-4-26,在Rt △ABC 中,∠ACB=900,BC AC >,以斜边AB 所在直线为x 轴,以斜边AB 上的高所在的直线为y 轴,建立直角坐标系,若2217OA OB +=,且线段OA 、OB 的长是关于x 的一元二次方程22(3)0x mx m -+-=的两根.(1)求点C 的坐标.(2)以斜边AB 为直径作圆与y 轴交于另一点E ,求过A 、B 、E 三点的抛物线的解析式,并画出此抛物线的草图.(3)在抛物线的解析式上是否存在点P ,使△ABP 和△ABC 全等?若相聚在,求出符合条件的P 点的坐标;若不存在,请说明理由. 【提高训练2答案】1.(1)22[(21)]4()10m m m ∆=----=>,∴抛物线与x 轴必有两个不同的交点.(2)15m =-+或15m =--.2.(1)4y x =+.(2)16POQ S ∆=.3.(1)243y x x =-+.(2)4ADBC S =四边形.4.(1)B ′(8,0);(2)163y x =-+ (3)抛物线方程为212263y x =-.除了交点G 外,另有交点为点G 关于y 轴的对称点,其坐标为(-8,103).5.(1)C (0,2).(2)213222y x x =--.(3)存在,其坐标为(0,-2)和(3,-2).(Ⅲ)几何型综合题 【简要分析】几何型综合题包括几何论证型综合题和几何计算型综合题两大类,一般以相似为中心,以圆为重点,还常与代数综合.它以知识上的综合性与中考中的重要E图2-4-25Cy BAO f x () = 2⋅x 2性而引人注目.值得一提的是,在近两年各地的中考试题,几何综合题的难度普遍下降,出现了一大批探索性试题,根据新课标的要求,减少几何中推理论证的难度,加强探索性训练,将成为几何型综合题命题的新趋势. 【典型考题例析】例1:如图2-4-27,四边形ABCD 是正方形,△ECF 是等腰直角三角形,其中CE=CF ,G 是CD 与EF 的交点.(1)求证:△BCF ≌△DCE . (2)若BC=5,CF=3,∠BFC=900,求DG :GC 的值.例2:已知如图2-4-28,BE 是⊙O 的走私过圆上一点作⊙O 的切线交EB 的延长线于P .过E 点作ED ∥AP交⊙O 于D ,连结DB 并延长交PA 于C ,连结AB 、AD . (1)求证:2AB PB BD = .(2)若PA=10,PB=5,求AB 和CD 的长. 例2:如图2-4-29,⊙1O 和⊙2O 相交于A 、B 两点,圆心1O 在⊙2O 上,连心线1O 2O 与⊙1O 交于点C 、D ,与⊙2O 交于点E ,与AB 交于点H ,连结AE .(1)求证:AE 为⊙1O 的切线. (2)若⊙1O 的半径r=1,⊙2O 的半径32R =,求公共弦AB 的长. (3)取HB 的中点F ,连结1O F ,并延长与⊙2O 相交于点G ,连结EG ,求EG 的长例4 如图2-4-30,A 为⊙O 的弦EF 上的一点,OB 是和这条弦垂直的半径,垂足为H,BA 的延长线交⊙O 于点C ,过点C 作⊙O 的切线与EF 的延长线交于点D . (1)求证:DA=DC(2)当DF :EF=1:8且DF=2时,求AB AC 的值.(3)将图2-4-30中的EF 所在的直线往上平移到⊙O 外,如图2-4-31,使EF 与OB 的延长线交⊙O 于点C ,过点C 作⊙O 的切线交EF 于点D .试猜想DA=DC是否仍然成立,并证明你的结论. 【提高训练3】1.如图2-4-32,已知在△ABC 中,AB=AC ,D 、E 分别是AB 和BC 上的点,连结DE 并延长与AC 的延长线相交于点F .若DE=EF ,求证:BD=CF . 2.点O 是△ABC 所在平面内一动点,连结OB 、OC ,并将AB 、OB 、OC 、AC 的中点D 、E 、F 、G 依次连结,如果DEFG 能构成图2-4-28C321OEPB A O 2O 1H GF EDBCA图2-4-28图2-4-27G F ED C B AK 图2-4-30H FE DOC BA O GFE D CBA四边形.(1)如图2-4-33,当O 点在△ABC 内时,求证四边形DEFG 是平行四边形.(2)当点O 移动到△ABC 外时,(1)中的结论是否成立?画出图形,并说明理由.(3)若四边形DEFG 为矩形,O 点所在位置应满足什么条件?试说明理由.3.如图2-4-35,等腰梯形ABCD 中,AD ∥BC ,∠DBC=450.翻折梯形ABCD ,使点B 重合于点D ,折痕分别交边AB 、BC 于点F 、E .若AD=2,BC=8,求:(1)BE 的长.(2)∠CDE的正切值.4.如图2-4-35,四边形ABCD 内接于⊙O ,已知直径AD=2,∠ABC=1200,∠ACB=450,连结OB 交AC 于点E .(1)求AC 的长.(2)求CE :AE 的值.(3)在CB 的延长上取一点P ,使PB=2BC ,试判断直线PA 和⊙O 的位置关系,并加以证明你的结论.5.如图2-4-36,已知AB 是⊙O 的直径,BC 、CD 分别是⊙O 的切线,切点分别为B 、D ,E 是BA 和CD 的延长线的交点.(1)猜想AD 与OC 的位置关系,并另以证明.(2)设AD OC 的值为S ,⊙O 的半径为r ,试探究S 与r 的关系.(3)当r=2,1sin 3E ∠=时,求AD 和OC 的长.【提高训练3答案】1.过D 作DG ∥AC 交BC 于G ,证明△DGE ≌△FCE 2.(1)证明DG ∥EF 即可 (2)结论仍然成立,证明略 (3)O 点应在过A 点且垂直于BC 的直线上(A 点除外),说理略. 3.(1)BE=5 (2)3tan 5CDE ∠= 4.(1)3AC = (2)1:2CE AE =(3)∵1:2CE AE =,PB=2BC ,∴CE :AE=CB :PB .∴BE ∥AP .∴AO ⊥AP .∴PA 为⊙O 的切线 5.(1)AD ∥OC ,证明略 (2)连结BD ,在△ABD 和△OCB 中,∵AB 是直径,∴∠ADB=∠OBC=900.又∵∠OCB=∠BAD ,∴Rt △ABD ∽Rt △OCB .∴AD ABOB OC=.222S AD OC AB OB r r r ==== ,∴22S r = (3)433AD =,23OC =(Ⅳ)动态几何综合题【简要分析】函数是中学数学的一个重要概念.加强对函数概念、图象和性质,以及函数思想方法的考查是近年中考试题的一个显著特点.大量涌现的动态几何问题,即建立几何中元素的函数关系式问题是这一特点的体现.这类题目的三乱扣帽子解法是抓住变化中的“不变”.以“不变”应“万变”.同时,要善于利用相似三角形的性质定理、勾股定理、圆幂定理、面积关系,借助议程为个桥梁,从而得到函数关系式,问题且有一定的实际意义,因此,对函数解析式中自变量的取值范围必须认真考虑,一般需要有约束条件.图2-4-34F ED C B A O 图2-4-35PE DCBA图2-4-36OE DCBA【典型考题例析】例1:如图2-4-37,在直角坐标系中,O 是原点,A 、B 、C 三点的坐标分别为A (18,0)、B (18,6)、C (8,6),四边形OABC 是梯形.点P 、Q 同时从原点出发,分别作匀速运动,其中点P 沿OA 向终点A 运动,速度为每秒1个单位,点Q 沿OC 、CB 向终点B 运动,当这两点有一点到达自己的终点时,另一点也停止运动.(1)求出直线OC 的解析式.(2)设从出发起运动了t 秒,如果点Q 的速度为每秒2个单位,试写出点Q 的坐标,并写出此时t 的取值范围.(3)设从出发起运动了t 秒,当P 、Q 两点运动的路程之和恰好等于梯形OABC 的周长的一半时,直线PQ 能否把梯形的面积也分成相等的两部分?如有可能,请求出t 的值;如不可能,请说明理由.例2: 如图2-5-40,在Rt △PMN 中,∠P=900,PM=PN ,MN=8㎝,矩形ABCD 的长和宽分别为8㎝和2㎝,C 点和M 点重合,BC 和MN 在一条直线上.令Rt △PMN 不动,矩形ABCD 沿MN 所在直线向右以每秒1㎝的速度移动(图2-4-41),直到C 点与N 点重合为止.设移动x 秒后,矩形ABCD 与△PMN 重叠部分的面积为y ㎝2.求y 与x 之间的函数关系式.NP(M)D C BA 图2-4-40NPM D C BA图2-4-41Q NNAB C DGFH T M22x图2-4-44PP图2-4-43x 22MTH FG D CBA.说明:此题是一个图形运动问题,解答方法是将各个时刻的图形分别画出,将图形 则“动”这“静”,再设法分别求解.这种分类画图的方法在解动态几何题中非常有效,它可帮我们理清思路,各个击破. 【提高训练4】 1.如图2-4-45,在ABCD 中,∠DAB=600,AB=5,BC=3,鼎足之势P 从起点D 出发,沿DC 、CB 向终点B 匀速运动.设点P 所走过的路程为x ,点P 所以过的线段与绝无仅有AD 、AP 所围成图形的面积为y ,y 随x 的函数关系的变化而变化.在图2-4-46中,能正确反映y 与x 的函数关系的是( )图2-4-37O C BA x y Q POOOOXXXXYYYY8888ABCD2.如图2-4-47,四边形AOBC 为直角梯形,OC=5,OB=%AC ,OC 所在直线方程为2y x =,平行于OC 的直线l 为:2y x t =+,l 是由A 点平移到B 点时,l 与直角梯形AOBC两边所转成的三角形的面积记为S .(1)求点C 的坐标.(2)求t 的取值范围.(3)求出S 与t 之间的函数关系式.3.如图2-4-48,在△ABC 中,∠B=900,点P 从点A 开始沿AB 边向点B 以1㎝/秒的速度移动,点Q 从点B 开始沿BC 边向点C 以2㎝/秒的速度移动.(1)如果P 、Q 分别从A 、B 同时出发,几秒后△PBQ 的面积等于8㎝2?(2)如果P 、Q 分别从A 、B 同时出发,点P 到达点B 后又继续沿BC 边向点C 移动,点Q 到达点C 后又继续沿CA 边向点A 移动,在这一整个移动过程中,是否存在点P 、Q ,使△PBQ 的面积等于9㎝2?若存在,试确定P 、Q 的位置;若不存在,请说明理由. 4.如图2-4-49,在梯形ABCD 中,AB=BC=10㎝,CD=6㎝,∠C=∠D=900.(1)如图2-4-50,动点P 、Q 同时以每秒1㎝的速度从点B 出发,点P 沿BA 、AD 、DC 运动到点C 停止.设P 、Q 同时从点B 出发t 秒时,△PBQ 的面积为1y (㎝2),求1y (㎝2)关于t (秒)的函数关系式.(2)如图2-4-51,动点P 以每秒1㎝的速度从点B 出发沿BA 运动,点E 在线段CD 上随之运动,且PC=PE .设点P 从点B 出发t 秒时,四边形PADE 的面积为2y (㎝2).求2y (㎝2)关于t (秒)的函数关系式,并写出自变量t 的取值范围.图2-4-51图2-4-50QPDC BAA BCDP Q【提高训练4答案】图2-4-47xy lCBAO图2-4-48Q P CBA8cm6cm D CBA图2-4-4910cm8cm6cm1.A 2.(1)C (1,2) (2)-10≤t ≤2 (3)S 与t 的函数关系式为215(100)20S t t t =++-≤≤或211(02)4S t t t =-+≤≤3.(1)2秒或4秒 (2)存在点P 、Q ,使得△PBQ 的面积等于9㎝2,有两种情况:①点P 在AB 边上距离A 为3㎝,点Q 在BC 边上距离点B 为6㎝时②点P 在BC 边上,距B 点3㎝时,此时Q 点就是A 点 4.(1)当点P 在BA 上运动时,21310y t =;当点P 在AD 上运动时,130y =;当点P 在DC 上运动时,190y t =-+ (2)221299025BPC PEC ABCD y S S S t t ∆∆=--=-+梯形,自变量t 的取值范围是0≤t ≤5.。
2019届深圳中考复习《多结论几何综合题》专题试卷含解析

2017届中考复习多结论几何综合题专题试卷一、单选题1、如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①tan∠AEC=;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的个数是()A、1个B、2个C、3个D、4个2、如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△AED≌△AEF;②=;③△ABC的面积等于四边形AFBD的面积;④BE2+DC2=DE2⑤BE+DC=DE;其中正确的是( )A、①②④B、③④⑤C、①③④D、①③⑤3、如图,将等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD ,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形;④BD⊥DE;其中正确的个数是().A、1B、2C、3D、44、如图,把一张长方形纸片ABCD沿对角线BD折叠,使C点落在E处,BE与AD相交于点F,下列结论:①BD=AD2+AB2;②△ABF≌△EDF;③=④AD=BD•cos45°.其中正确的一组是()A、①②B、②③C、①④D、③④5、如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°,②OC=OE,③tan∠OCD= ,④S△ODC=S四边形BEOF中,正确的有()A、1个B、2个C、3个D、4个6、如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③△GDE∽△BEF;④S△BEF=.在以上4个结论中,正确的有()A、1B、2C、3D、47、如图,▱ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S▱ABCD=AB•AC;③OB=AB;④OE=BC,成立的个数有()A、1个B、2个C、3个D、4个8、如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下列四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④AE+DF=AF+DE.其中正确的是()A、②③B、②④C、①③④D、②③④9、如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH,其中,正确的结论有()A、1个B、2个C、3个D、4个10、如图,PA=PB,OE⊥PA,OF⊥PB,则以下结论:①OP是∠APB的平分线;②PE=PF③CA=BD;④CD∥AB;其中正确的有()个.A、4B、3C、2D、111、如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF.下列结论:①tan∠ADB=2;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点D不一定落在AC上;④BD=BF;⑤S四边形DFOE=S△AOF,上述结论中正确的个数是()A、1个B、2个C、3个D、4个12、如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:①AC=AD;②BD⊥AC;③四边形ACED是菱形.其中正确的个数是()A、0B、1C、2D、313、如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ•AC,其中正确的结论的个数是( )A 、1B 、2C 、3D 、414、如图,矩形ABCD 中,O 为AC 中点,过点O 的直线分别与AB 、CD 交于点E 、F ,连结BF 交AC 于点M ,连结DE 、BO .若∠COB=60°,FO=FC ,则下列结论:①FB 垂直平分OC ;②△EOB ≌△CMB ;③DE=EF ;④S △AOE :S △BCM =2:3.其中正确结论的个数是( )A 、4个B 、3个C 、2个D 、1个15、(2016•攀枝花)如图,正方形纸片ABCD 中,对角线AC 、BD 交于点O ,折叠正方形纸片ABCD ,使AD 落在BD 上,点A 恰好与BD 上的点F 重合,展开后折痕DE 分别交AB 、AC 于点E 、G ,连结GF ,给出下列结论:①∠ADG=22.5°;②tan ∠AED=2;③S △AGD =S △OGD ;④四边形AEFG 是菱形;⑤BE=2OG ;⑥若S △OGF =1,则正方形ABCD 的面积是6+4 ,其中正确的结论个数为( )A 、2B 、3C 、4D 、516、如图,在正方形ABCD 中,E 、F 分别为BC 、CD 的中点,连接AE ,BF 交于点G ,将△BCF 沿BF 对折,得到△BPF ,延长FP 交BA 延长线于点Q ,下列结论正确的个数是( )①AE=BF ;②AE ⊥BF ;③sin ∠BQP= ;④S四边形ECFG=2S △BGE .A 、4B 、3C 、2D 、117、如图所示,抛物线y=ax 2+bx+c (a≠0)与x 轴交于点A (﹣2,0)、B (1,0),直线x=﹣0.5与此抛物线交于点C ,与x 轴交于点M ,在直线上取点D ,使MD=MC ,连接AC 、BC 、AD 、BD ,某同学根据图象写出下列结论: ①a ﹣b=0;②当﹣2<x <1时,y >0; ③四边形ACBD 是菱形; ④9a ﹣3b+c >你认为其中正确的是()A、②③④B、①②④C、①③④D、①②③18、如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是()A、2B、3C、4D、519、如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足= ,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE= ;④S△DEF=4 ,其中正确的是()A、①②③B、②③④C、①②④D、①③④20、如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB 于点P、Q,连接AC,给出下列结论:①∠DAC=∠ABC;②AD=CB;③点P是△ACQ的外心;④AC2=AE•AB;⑤CB∥GD,其中正确的结论是()A、①③⑤B、②④⑤C、①②⑤D、①③④答案解析部分一、单选题1、【答案】D【考点】等腰三角形的性质,梯形中位线定理,锐角三角函数的定义【解析】【分析】①根据等腰直角三角形的性质及△ABC∽△CDE的对应边成比例知,;然后由直角三角形中的正切函数,得tan∠AEC=,再由等量代换求得tan∠AEC=;②由三角形的面积公式、梯形的面积公式及不等式的基本性质a2+b2≥2ab(a=b时取等号)解答;③、④通过作辅助线MN,构建直角梯形的中位线,根据梯形的中位线定理及等腰直角三角形的判定定理解答.【解答】解:∵△ABC和△CDE均为等腰直角三角形,∴AB=BC,CD=DE,∴∠BAC=∠BCA=∠DCE=∠DEC=45°,∴∠ACE=90°;∵△ABC∽△CDE∴①∴tan∠AEC=,∴tan∠AEC=;故本选项正确;②∵S△ABC=a2,S△CDE=b2,S梯形ABDE=(a+b)2,∴S△ACE=S梯形ABDE-S△ABC-S△CDE=ab,S△ABC+S△CDE=(a2+b2)≥ab(a=b时取等号),∴S△ABC+S△CDE≥S△ACE;故本选项正确;④过点M作MN垂直于BD,垂足为N.∵点M是AE的中点,则MN为梯形中位线,∴N为中点,∴△BMD为等腰三角形,∴BM=DM;故本选项正确;③又MN=(AB+ED)=(BC+CD),∴∠BMD=90°,即BM⊥DM;故本选项正确.故选D.【点评】本题综合考查了等腰直角三角形的判定与性质、梯形的中位线定理、锐角三角函数的定义等知识点.在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.2、【答案】C【考点】全等三角形的判定,勾股定理,相似三角形的判定,旋转的性质【解析】【分析】①根据旋转的性质知∠CAD=∠BAF,AD=AF,因为∠BAC=90°,∠DAE=45°,所以∠CAD+∠BAE=45°,可得∠EAF=45°=∠DAE,由此即可证明△AEF≌△AED;②当△ABE∽△ACD时,该比例式成立;③根据旋转的性质,△ADC≌△ABF,进而得出△ABC的面积等于四边形AFBD 的面积;④据①知BF=CD,EF=DE,∠FBE=90°,根据勾股定理判断.⑤根据①知道△AEF≌△AED,得CD=BF,DE=EF;由此即可确定该说法是否正确;【解答】①根据旋转的性质知∠CAD=∠BAF,AD=AF,∵∠BAC=90°,∠DAE=45°,∴∠CAD+∠BAE=45°.∴∠EAF=45°,∴△AED≌△AEF;故本选项正确;②∵AB=AC,∴∠ABE=∠ACD;∴当∠BAE=∠CAD时,△ABE∽△ACD,∴=;当∠BAE≠∠CAD时,△ABE与△ACD不相似,即≠;∴此比例式不一定成立;故本选项错误;③根据旋转的性质知△ADC≌△AFB,∴S△ABC=S△ABD+S△ABF=S四边形AFBD,即三角形ABC的面积等于四边形AFBD的面积;故本选项正确;④∵∠FBE=45°+45°=90°,∴BE2+BF2=EF2,∵△ADC绕点A顺时针旋转90°后,得到△AFB,∴△AFB≌△ADC,∴BF=CD,又∵EF=DE,∴BE2+DC2=DE2,故本选项正确;⑤根据①知道△AEF≌△AED,得CD=BF,DE=EF,∴BE+DC=BE+BF>DE=EF,即BE+DC>DE,故本选项错误;综上所述,正确的说法是①③④;故选C.【点评】此题主要考查了图形的旋转变换以及全等三角形的判定等知识,解题时注意旋转前后对应的相等关系.3、【答案】D【考点】等边三角形的性质,菱形的判定与性质,平移的性质【解析】【解答】∵△ABC、△DCE是等边三角形,∴∠ACB=∠DCE=60°,AC =CD ,∴∠ACD=180°-∠ACB-∠DCE=60°,∴△ACD是等边三角形,∴AD=AC=BC ,故①正确;由①可得AD=BC ,∵AB=CD ,∴四边形ABCD是平行四边形,∴BD、AC互相平分,故②正确;由①可得AD=AC=CE=DE ,故四边形ACED是菱形,即③正确;∵四边形ACED是菱形,∴AC⊥BD ,∵AC∥DE ,∴∠BDE=∠COD=90°,∴BD⊥DE ,故④正确;综上可得①②③④正确,共4个,故选D.【分析】先求出∠ACD=60°,继而可判断△ACD是等边三角形,从而可判断①是正确的;根据①的结论,可判断四边形ABCD是平行四边形,从而可判断②是正确的;根据①的结论,可判断③正确;根据菱形的对角线互相垂直可得AC⊥BD ,再根据平移后对应线段互相平行可得∠BDE=∠COD=90°,进而判断④正确.4、【答案】B【考点】勾股定理,翻折变换(折叠问题),相似三角形的判定与性质,特殊角的三角函数值【解析】【解答】①∵△ABD为直角三角形,∴BD2=AD2+AB2,不是BD=AD2+AB2,故说法错误;②根据折叠可知:DE=CD=AB,∠A=∠E,∠AFB=∠EFD,∴△ABF≌△EDF,故说法正确;③根据②可以得到△ABF∽△EDF,∴=,故说法正确;④在Rt△ABD中,∠ADB≠45°,∴AD≠BD•cos45°,故说法错误.所以正确的是②③.故选B.【分析】①直接根据勾股定理即可判定是否正确;②利用折叠可以得到全等条件证明△ABF≌△EDF;③利用全等三角形的性质即可解决问题;④在Rt△ABD中利用三角函数的定义即可判定是否正确.此题主要考查了折叠问题,也考查了勾股定理、相似三角形的性质、全等三角形的性质及三角函数的定义,它们的综合性比较强,对于学生的综合能力要求比较高,平时加强训练.5、【答案】C【考点】全等三角形的判定与性质,勾股定理,正方形的性质,锐角三角函数的定义【解析】【解答】解:∵正方形ABCD的边长为4,∴BC=CD=4,∠B=∠DCF=90°,∵AE=BF=1,∴BE=CF=4﹣1=3,在△EBC和△FCD中,∴△EBC≌△FCD(SAS),∴∠CFD=∠BEC,∴∠BCE+∠BEC=∠BCE+∠CFD=90°,∴∠DOC=90°;故①正确;若OC=OE,∵DF⊥EC,∴CD=DE,∵CD=AD<DE(矛盾),故②错误;∵∠OCD+∠CDF=90°,∠CDF+∠DFC=90°,∴∠OCD=∠DFC,∴tan∠OCD=tan∠DFC= = ,故③正确;∵△EBC≌△FCD,∴S△EBC=S△FCD,∴S△EBC﹣S△FOC=S△FCD﹣S△FOC,即S△ODC=S四边形BEOF.故④正确.故选C.【分析】由正方形ABCD的边长为4,AE=BF=1,利用SAS易证得△EBC≌△FCD,然后全等三角形的对应角相等,易证得①∠DOC=90°正确;②由线段垂直平分线的性质与正方形的性质,可得②错误;易证得∠OCD=∠DFC,即可求得③正确;由①易证得④正确.6、【答案】C【考点】全等三角形的判定与性质,正方形的性质,翻折变换(折叠问题),相似三角形的判定与性质【解析】【解答】由折叠可知,DF=DC=DA,∠DFE=∠C=90°,∴∠DFG=∠A=90°,∴△ADG≌△FDG,①正确;∵正方形边长是12,∴BE=EC=EF=6,设AG=FG=x,则EG=x+6,BG=12﹣x,由勾股定理得:EG2=BE2+BG2,即:(x+6)2=62+(12﹣x)2,解得:x=4∴AG=GF=4,BG=8,BG=2AG,②正确;BE=EF=6,△BEF是等腰三角形,易知△GED不是等腰三角形,③错误;S△GBE=×6×8=24,S△BEF=•S△GBE==,④正确.故选:C.【分析】根据正方形的性质和折叠的性质可得AD=DF,∠A=∠GFD=90°,于是根据“HL”判定△ADG≌△FDG,再由GF+GB=GA+GB=12,EB=EF,△BGE为直角三角形,可通过勾股定理列方程求出AG=4,BG=8,进而求出△BEF的面积,再抓住△BEF是等腰三角形,而△GED显然不是等腰三角形,判断③是错误的.7、【答案】C【考点】等边三角形的判定与性质,含30度角的直角三角形,平行四边形的性质【解析】【解答】∵四边形ABCD是平行四边形,∴∠ABC=∠ADC=60°,∠BAD=120°,∵AE平分∠BAD,∴∠BAE=∠EAD=60°∴△ABE是等边三角形,∴AE=AB=BE,∵AB=BC,∴AE=BC,∴∠BAC=90°,∴∠CAD=30°,故①正确;∵AC⊥AB,∴S▱ABCD=AB•AC,故②正确,∵AB=BC,OB=BD,∵BD>BC,∴AB≠OB,故③错误;∵CE=BE,CO=OA,∴OE=AB,∴OE=BC,故④正确.故选:C.【分析】由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据AE平分∠BAD,得到∠BAE=∠EAD=60°推出△ABE是等边三角形,由于AB=BC,得到AE=BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正确;由于AC⊥AB,得到S▱ABCD=AB•AC,故②正确,根据AB=BC,OB=BD,且BD>BC,得到AB≠OB,故③错误;根据三角形的中位线定理得到OE=AB,于是得到OE=BC,故④正确.8、【答案】D【考点】全等三角形的判定与性质,角平分线的性质,正方形的判定【解析】【解答】如果OA=OD,则四边形AEDF是矩形,∠A=90°,不符合题意,∴①不正确;∵AD是△ABC的角平分线,∴∠EAD∠FAD,在△AED和△AFD 中,∴△AED≌△AFD(AAS),∴AE=AF,DE=DF,∴AE+DF=AF+DE,∴④正确;在△AEO和△AFO中,,∴△AE0≌△AF0(SAS),∴EO=FO,又∵AE=AF,∴AO是EF的中垂线,∴AD⊥EF,∴②正确;∵当∠A=90°时,四边形AEDF的四个角都是直角,∴四边形AEDF是矩形,又∵DE=DF,∴四边形AEDF是正方形,∴③正确.综上,可得正确的是:②③④.故选:D.【分析】①如果OA=OD,则四边形AEDF是矩形,∠A=90°,不符合题意,所以①不正确.②首先根据全等三角形的判定方法,判断出△AED≌△AFD,AE=AF,DE=DF;然后根据全等三角形的判定方法,判断出△AE0≌△AFO,即可判断出AD⊥EF.③首先判断出当∠A=90°时,四边形AEDF的四个角都是直角,四边形AEDF是矩形,然后根据DE=DF,判断出四边形AEDF是正方形即可.④根据△AED≌△AFD,判断出AE=AF,DE=DF,即可判断出AE+DF=AF+DE成立,据此解答即可.9、【答案】B【考点】全等三角形的判定与性质,正方形的性质,相似三角形的判定与性质【解析】【解答】∵四边形ABCD是正方形,∴∠B=∠DCB=90°,AB=BC,∵AG=CE,∴BG=BE,由勾股定理得:BE=GE,∴①错误;∵BG=BE,∠B=90°,∴∠BGE=∠BEG=45°,∴∠AGE=135°,∴∠GAE+∠AEG=45°,∵AE⊥EF,∴∠AEF=90°,∵∠BEG=45°,∴∠AEG+∠FEC=45°,∴∠GAE=∠FEC,在△GAE和△CEF中∴△GAE≌△CEF,∴②正确;∴∠AGE=∠ECF=135°,∴∠FCD=135°﹣90°=45°,∴③正确;∵∠BGE=∠BEG=45°,∠AEG+∠FEC=45°,∴∠FEC<45°,∴△GBE和△ECH不相似,∴④错误;即正确的有2个.故选B.【分析】根据正方形的性质得出∠B=∠DCB=90°,AB=BC,求出BG=BE ,根据勾股定理得出BE=GE,即可判断①;求出∠GAE+∠AEG=45°,推出∠GAE=∠FEC,根据SAS推出△GAE≌△CEF,即可判断②;求出∠AGE=∠ECF=135°,即可判断③;求出∠FEC<45°,根据相似三角形的判定得出△GBE和△ECH不相似,即可判断④.10、【答案】A【考点】全等三角形的判定与性质,圆心角、弧、弦的关系,相似三角形的判定与性质【解析】【解答】连接OP、OC、OA、OD、OB、CD、AB.∵PC•PA=PD•PB(相交弦定理),PA=PB(已知),∴PC=PD,∴AC=BD;在△AOC和△BOD中,∵∠AOC=∠BOD(等弦对等角),OA=OB(半径),OD=OC(半径),∴△AOC≌△BOD,∴③CA=BD;OE=OF;又∵OE⊥PA,OF⊥PB,∴①OP是∠APB的平分线;∴②PE=PF;在△PCD和△PAB中,PC:PA=PD:PB,∠DPC=∠BPA,∴△PCD∽△PAB,∴∠PDC=PBA,∴④CD∥AB;综上所述,①②③④均正确,故答案选A.【分析】①通过证明△AOC≌△BOD,再根据全等三角形的对应高相等求得OE=OF;再根据角平分线的性质证明OP是∠APB的平分线;②由角平分线的性质证明PE=PF;③通过证明△AOC≌△BOD,再根据全等三角形的对应边相等求得CA=BD;④通过证明△PCD∽△PAB,再根据相似三角形的性质对应角相等证得∠PDC=PBA;然后由平行线的判定得出结论CD∥AB.11、【答案】C【考点】全等三角形的判定与性质,翻折变换(折叠问题),锐角三角函数的定义【解析】【解答】①由折叠可得BD=DE,而DC>DE,∴DC>BD,∴tan∠ADB≠2,故①错误;②图中的全等三角形有△ABF≌△AEF,△ABD≌△AED,△FBD≌△FED,(由折叠可知) ∵OB⊥AC,∴∠AOB=∠COB=90°,在Rt△AOB和Rt△COB中,AB="CB" ,BO=BO ,∴Rt△AOB≌Rt△COB(HL),则全等三角形共有4对,故②正确;③∵AB=CB,BO⊥AC,把△ABC折叠,∴∠ABO=∠CBO=45°,∠FBD=∠DEF,∴∠AEF=∠DEF=45°,∴将△DEF沿EF折叠,可得点D一定在AC上,故③错误;④∵OB⊥AC,且AB=CB,∴BO为∠ABC的平分线,即∠ABO=∠OBC=45°,由折叠可知,AD是∠BAC的平分线,即∠BAF=22.5°,又∵∠BFD为三角形ABF的外角,∴∠BFD=∠ABO+∠BAF=67.5°,易得∠BDF=180°-45°-67.5°=67.5°,∴∠BFD=∠BDF,∴BD=BF,故④正确;⑤连接CF,∵△AOF和△COF等底同高,∴S△AOF=S△COF,∵∠AEF=∠ACD=45°,∴EF∥CD,∴S△EFD=S△EFC,∴S四边形DFOE=S△COF,∴S四边形DFOE=S△AOF,故⑤正确;故正确的有3个.故选C.12、【答案】D【考点】等边三角形的性质,菱形的判定,旋转的性质【解析】【解答】解:∵将等边△ABC绕点C顺时针旋转120°得到△EDC,∴∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE,∴∠ACD=120°﹣60°=60°,∴△ACD是等边三角形,∴AC=AD,AC=AD=DE=CE,∴四边形ACED是菱形,∵将等边△ABC绕点C顺时针旋转120°得到△EDC,AC=AD,∴AB=BC=CD=AD,∴四边形ABCD是菱形,∴BD⊥AC,∴①②③都正确,故选D.【分析】根据旋转和等边三角形的性质得出∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE,求出△ACD是等边三角形,求出AD=AC,根据菱形的判定得出四边形ABCD和ACED都是菱形,根据菱形的判定推出AC⊥BD.本题考查了旋转的性质,菱形的性质和判定,等边三角形的性质和判定的应用,能灵活运用知识点进行推理是解此题的关键.13、【答案】D【考点】全等三角形的判定与性质,矩形的判定与性质,正方形的性质,相似三角形的判定与性质,等腰直角三角形【解析】【解答】解:∵四边形ADEF为正方形,∴∠FAD=90°,AD=AF=EF,∴∠CAD+∠FAG=90°,∵FG⊥CA,∴∠C=90°=∠ACB,∴∠CAD=∠AFG,在△FGA和△ACD中,,∴△FGA≌△ACD(AAS),∴AC=FG,①正确;∵BC=AC,∴FG=BC,∵∠ACB=90°,FG⊥CA,∴FG∥BC,∴四边形CBFG是矩形,∴∠CBF=90°,S△FAB= FB•FG= S四边形CBFG,②正确;∵CA=CB,∠C=∠CBF=90°,∴∠ABC=∠ABF=45°,③正确;∵∠FQE=∠DQB=∠ADC,∠E=∠C=90°,∴△ACD∽△FEQ,∴AC:AD=FE:FQ,∴AD•FE=AD2=FQ•AC,④正确;故选:D.【分析】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质、矩形的判定与性质、等腰直角三角形的性质;熟练掌握正方形的性质,证明三角形全等和三角形相似是解决问题的关键.由正方形的性质得出∠FAD=90°,AD=AF=EF,证出∠CAD=∠AFG,由AAS证明△FGA≌△ACD,得出AC=FG,①正确;证明四边形CBFG是矩形,得出S△FAB= FB•FG= S四边形CEFG,②正确;由等腰直角三角形的性质和矩形的性质得出∠ABC=∠ABF=45°,③正确;证出△ACD∽△FEQ,得出对应边成比例,得出D•FE=AD2=FQ•AC,④正确.14、【答案】B【考点】全等三角形的判定与性质,线段垂直平分线的性质,等腰三角形的性质,矩形的性质【解析】【解答】解:①∵矩形ABCD中,O为AC中点,∴OB=OC,∵∠COB=60°,∴△OBC是等边三角形,∴OB=BC,∵FO=FC,∴FB垂直平分OC,故①正确;②∵FB垂直平分OC,∴△CMB≌△OMB,∵OA=OC,∠FOC=∠EOA,∠DCO=∠BAO,∴△FOC≌△EOA,∴FO=EO,易得OB⊥EF,∴△OMB≌△OEB,∴△EOB≌△CMB,故②正确;③由△OMB≌△OEB≌△CMB得∠1=∠2=∠3=30°,BF=BE,∴△BEF是等边三角形,∴BF=EF,∵DF∥BE且DF=BE,∴四边形DEBF是平行四边形,∴DE=BF,∴DE=EF,故③正确;④在直角△BOE中∵∠3=30°,∴BE=2OE,∵∠OAE=∠AOE=30°,∴AE=OE,∴BE=2AE,∴S△AOE:S△BCM=S△AOE:S△BOE=1:2,故④错误;所以其中正确结论的个数为3个;故选B【分析】①利用线段垂直平分线的性质的逆定理可得结论;②证△OMB≌△OEB得△EOB≌△CMB;③先证△BEF是等边三角形得出BF=EF,再证▱DEBF得出DE=BF,所以得DE=EF;④由②可知△BCM≌△BEO,则面积相等,△AOE和△BEO属于等高的两个三角形,其面积比就等于两底的比,即S△AOE:S△BOE=AE:BE,由直角三角形30°角所对的直角边是斜边的一半得出BE=2OE=2AE,得出结论S△AOE:S△BOE=AE:BE=1:2.本题综合性比较强,既考查了矩形的性质、等腰三角形的性质,又考查了全等三角形的性质和判定,及线段垂直平分线的性质,内容虽多,但不复杂;看似一个选择题,其实相当于四个证明题,属于常考题型.15、【答案】B【考点】菱形的判定与性质,翻折变换(折叠问题),等腰直角三角形【解析】【解答】解:∵四边形ABCD是正方形,∴∠GAD=∠ADO=45°,由折叠的性质可得:∠ADG= ∠ADO=22.5°,故①正确.∵由折叠的性质可得:AE=EF,∠EFD=∠EAD=90°,∴AE=EF<BE,∴AE<AB,∴>2,故②错误.∵∠AOB=90°,∴AG=FG>OG,△AGD与△OGD同高,∴S△AGD>S△OGD,故③错误.∵∠EFD=∠AOF=90°,∴EF∥AC,∴∠FEG=∠AGE,∵∠AGE=∠FGE,∴∠FEG=∠FGE,∴EF=GF,∵AE=EF,∴AE=GF,故④正确.∵AE=EF=GF,AG=GF,∴AE=EF=GF=AG,∴四边形AEFG是菱形,∴∠OGF=∠OAB=45°,∴EF=GF= OG,∴BE= EF= ×OG=2OG.故⑤正确.∵四边形AEFG是菱形,∴AB∥GF,AB=GF.∵∠BAO=45°,∠GOF=90°,∴△OGF时等腰直角三角形.∵S△OGF=1,∴OG2=1,解得OG= ,∴BE=2OG=2 ,GF= ==2,∴AE=GF=2,∴AB=BE+AE=2 +2,∴S正方形ABCD=AB2=(2 +2)2=12+8 ,故⑥错误.∴其中正确结论的序号是:①④⑤.故选B.【分析】①由四边形ABCD是正方形,可得∠GAD=∠ADO=45°,又由折叠的性质,可求得∠ADG的度数;②由AE=EF<BE,可得AD>2AE;③由AG=GF>OG,可得△AGD的面积>△OGD的面积;④由折叠的性质与平行线的性质,易得△EFG是等腰三角形,即可证得AE=GF;⑤易证得四边形AEFG是菱形,由等腰直角三角形的性质,即可得BE=2OG;⑥根据四边形AEFG是菱形可知AB∥GF,AB=GF,再由∠BAO=45°,∠GOF=90°可得出△OGF时等腰直角三角形,由S△OGF=1求出GF的长,进而可得出BE及AE的长,利用正方形的面积公式可得出结论.此题考查的是四边形综合题,涉及到正方形的性质、折叠的性质、等腰直角三角形的性质以及菱形的判定与性质等知识.此题综合性较强,难度较大,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.16、【答案】B【考点】全等三角形的判定与性质,正方形的性质,翻折变换(折叠问题),相似三角形的判定与性质【解析】【解答】解:∵E,F分别是正方形ABCD边BC,CD的中点,∴CF=BE,在△ABE和△BCF中,,∴Rt△ABE≌Rt△BCF(SAS),∴∠BAE=∠CBF,AE=BF,故①正确;又∵∠BAE+∠BEA=90°,∴∠CBF+∠BEA=90°,∴∠BGE=90°,∴AE⊥BF,故②正确;根据题意得,FP=FC,∠PFB=∠BFC,∠FPB=90°∵CD∥AB,∴∠CFB=∠ABF,∴∠ABF=∠PFB,∴QF=QB,令PF=k(k>0),则PB=2k在Rt△BPQ中,设QB=x,∴x2=(x﹣k)2+4k2,∴x= ,∴sin=∠BQP= = ,故③正确;∵∠BGE=∠BCF,∠GBE=∠CBF,∴△BGE∽△BCF,∵BE= BC,BF= BC,∴BE:BF=1:,∴△BGE的面积:△BCF的面积=1:5,∴S四边形ECFG=4S△BGE,故④错误.故选:B.【分析】首先证明△ABE≌△BCF,再利用角的关系求得∠BGE=90°,即可得到①AE=BF;②AE⊥BF;△BCF沿BF对折,得到△BPF,利用角的关系求出QF=QB,解出BP,QB,根据正弦的定义即可求解;根据AA可证△BGE与△BCF相似,进一步得到相似比,再根据相似三角形的性质即可求解.本题主要考查了四边形的综合题,涉及正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质以及折叠的性质的知识点,解决的关键是明确三角形翻转后边的大小不变,找准对应边,角的关系求解.17、【答案】D【考点】二次函数的图象,二次函数的性质,菱形的判定【解析】【解答】解:①∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣2,0)、B(1,0),∴该抛物线的对称轴为x=﹣=﹣0.5,∴a=b,a﹣b=0,①正确;②∵抛物线开口向下,且抛物线与x轴交于点A(﹣2,0)、B(1,0),∴当﹣2<x<1时,y>0,②正确;③∵点A、B关于x=0.5对称,∴AM=BM,又∵MC=MD,且CD⊥AB,∴四边形ACBD是菱形,③正确;④当x=﹣3时,y<0,即y=9a﹣3b+c<0,④错误.综上可知:正确的结论为①②③.故选D.【分析】①由抛物线与x轴的两交点坐标即可得出抛物线的对称轴为x=﹣=﹣0.5,由此即可得出a=b,①正确;②根据抛物线的开口向下以及抛物线与x轴的两交点坐标,即可得出当﹣2<x<1时,y>0,②正确;③由AB关于x=0.5对称,即可得出AM=BM,再结合MC=MD以及CD⊥AB,即可得出四边形ACBD是菱形,③正确;④根据当x=﹣3时,y<0,即可得出9a﹣3b+c<0,④错误.综上即可得出结论.本题考查了二次函数的图象、二次函数的性质以及菱形的判定,解题的关键是逐条分析四条结论是否正确.本题属于中档题,难度不大,解决该题型题目时,根据给定的函数图象结合二次函数的性质逐条分析给定的结论是关键.18、【答案】D【考点】全等三角形的判定与性质,正方形的性质,翻折变换(折叠问题)【解析】【解答】解:∵正方形ABCD的边长为6,CE=2DE,∴DE=2,EC=4,∵把△ADE沿AE折叠使△ADE落在△AFE的位置,∴AF=AD=6,EF=ED=2,∠AFE=∠D=90°,∠FAE=∠DAE,在Rt△ABG和Rt△AFG中,∴Rt△ABG≌Rt△AFG(HL),∴GB=GF,∠BAG=∠FAG,∴∠GAE=∠FAE+∠FAG= ∠BAD=45°,所以①正确;设BG=x,则GF=x,C=BC﹣BG=6﹣x,在Rt△CGE中,GE=x+2,EC=4,CG=6﹣x,∵CG2+CE2=GE2,∴(6﹣x)2+42=(x+2)2,解得x=3,∴BG=3,CG=6﹣3=3∴BG=CG,所以②正确;∵EF=ED,GB=GF,∴GE=GF+EF=BG+DE,所以③正确;∵GF=GC,∴∠GFC=∠GCF,又∵Rt△ABG≌Rt△AFG,∴∠AGB=∠AGF,而∠BGF=∠GFC+∠GCF,∴∠AGB+∠AGF=∠GFC+∠GCF,∴∠AGB=∠GCF,∴CF∥AG,所以④正确;过F作FH⊥DC∵BC⊥DH,∴FH∥GC,∴△EFH∽△EGC,∴,EF=DE=2,GF=3,∴EG=5,∴△EFH∽△EGC,∴相似比为:= ,∴S△FGC=S△GCE﹣S△FEC= ×3×4﹣×4×(×3)= =3.6,所以⑤正确.故正确的有①②③④⑤,故选:D.【分析】先计算出DE=2,EC=4,再根据折叠的性质AF=AD=6,EF=ED=2,∠AFE=∠D=90°,∠FAE=∠DAE,然后根据“HL”可证明Rt△ABG≌Rt△AFG,则GB=GF,∠BAG=∠FAG,所以∠GAE= ∠BAD=45°;GE=GF+EF=BG+DE;设BG=x,则GF=x,CG=BC﹣BG=6﹣x,在Rt△CGE中,根据勾股定理得(6﹣x)2+42=(x+2)2,解得x=3,则BG=CG=3,则点G为BC的中点;同时得到GF=GC,根据等腰三角形的性质得∠GFC=∠GCF,再由Rt△ABG≌Rt△AFG得到∠AGB=∠AGF,然后根据三角形外角性质得∠BGF=∠GFC+∠GCF,易得∠AGB=∠GCF,根据平行线的判定方法得到CF∥AG;过F作FH⊥DC,则△EFH∽△EGC,△EFH∽△EGC,由相似比为,可计算S△FGC.本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了三角形全等的判定与性质、勾股定理和正方形的性质.19、【答案】C【考点】垂径定理,圆周角定理,相似三角形的判定与性质,解直角三角形【解析】【解答】解:①∵AB是⊙O的直径,弦CD⊥AB,∴,DG=CG,∴∠ADF=∠AED,∵∠FAD=∠DAE(公共角),∴△ADF∽△AED;故①正确;②∵= ,CF=2,∴FD=6,∴CD=DF+CF=8,∴CG=DG=4,∴FG=CG﹣CF=2;故②正确;③∵AF=3,FG=2,∴AG= = ,∴在Rt△AGD中,tan∠ADG= = ,∴tan∠E= ;故③错误;④∵DF=DG+FG=6,AD= = ,∴S△ADF= DF•AG= ×6×=3 ,∵△ADF∽△AED,∴=()2,∴= ,∴S△AED=7 ,∴S△DEF=S△AED﹣S△ADF=4 ;故④正确.故选C.【分析】①正确.由AB是⊙O的直径,弦CD⊥AB,根据垂径定理可得:,DG=CG,继而证得△ADF∽△AED;②正确.由= ,CF=2,可求得DF的长,继而求得CG=DG=4,则可求得FG=2;③错误.由勾股定理可求得AG的长,即可求得tan∠ADF的值,继而求得tan∠E=.④首先求得△ADF的面积,由相似三角形面积的比等于相似比的平方,即可求得△ADE的面积,继而求得S△DEF=4 .20、【答案】D【考点】垂径定理,圆周角定理,相似三角形的判定与性质【解析】【解答】解:∵在⊙O中,点C是的中点,∴= ,∴∠CAD=∠ABC,故①正确;∵≠ ,∴≠ ,∴AD≠BC,故②错误;∵AB是⊙O的直径,∴∠ACB=90°,又∵CE⊥AB,∴∠ACE+∠CAE=∠ABC+∠CAE=90°,∴∠ACE=∠ABC,又∵C为的中点,∴= ,∴∠CAP=∠ABC,∴∠ACE=∠CAP,∴AP=CP,∵∠ACQ=90°,∴∠ACP+∠PCQ=∠CAP+∠PQC=90°,∴∠PCQ=∠PQC,∴PC=PQ,∴AP=PQ,即P为Rt△ACQ斜边AQ的中点,∴P为Rt△ACQ的外心,故③正确;∵AB是⊙O的直径,∴∠ACB=90°,又∵CE⊥AB∴根据射影定理,可得AC2=AE•AB,故④正确;如图,连接BD,则∠ADG=∠ABD,∵≠ ,∴≠ ,∴∠ABD≠∠BAC,∴∠ADG≠∠BAC,又∵∠BAC=∠BCE=∠PQC,∴∠ADG≠∠PQC,∴CB与GD不平行,故⑤错误.故答案为:D.【分析】在同圆或等圆中,同弧或等弧所对的圆周角相等,据此推理可得①正确,②错误;通过推理可得∠ACE=∠CAP,得出AP=CP,再根据∠PCQ=∠PQC,可得出PC=PQ,进而得到AP=PQ,即P为Rt△ACQ斜边AQ的中点,故P为Rt△ACQ 的外心,即可得出③正确;连接BD,则∠ADG=∠ABD,根据∠ADG≠∠BAC,∠BAC=∠BCE=∠PQC,可得出∠ADG≠∠PQC,进而得到CB与GD不平行,可得⑤错误.。
专题02 几何图形的多结论问题(解析版)

专题二几何图形的多结论问题【专题解读】几何类多结论判断题考查的知识点较多,主要以圆和四边形为核心开放研究型问题,所谓“开放”简单来说就是答案不唯一的,解题的方向不确定,条件或者结论不止一种情况的试题,解答此类试题时,需要对问题全方位、多层次、多角度思考审视,尽量找到解决问题的方法,根据开放性的试题的特点,主要有如下几种类型:条件开放性、结论开放性、选择开放型、综合开放型,属于中考必考题型.(2020•广东二模)如图,已知▱ABCD的对角线AC、BD交于点O,DE平分∠ADC 交BC于点E,交AC于点F,且∠BCD=60°,BC=2CD,连结OE.下列结论:①OE∥AB;②S平行四边形ABCD=BD•CD;③AO=2BO;④S△DOF=2S△EOF.其中成立的个数有(C)A.1个B.2个C.3个D.4个【思路点拨】①证明BE=CE,OA=OC,根据三角形中位线定理可得结论正确;②证明BD⊥CD,可得结论正确;③设AB=x,分别表示OA和OB的长,可以作判断;④先根据平行线分线段成比例定理可得:DF=2EF,由同高三角形面积的比等于对应底边的比可作判断.【自主解答】①∵四边形ABCD是平行四边形,∴AD∥BC,OA=OC,∴∠ADC+∠BCD=180°,∵∠BCD=60°,∴∠ADC=120°,∵DE平分∠ADC,∴∠CDE=60°=∠BCD,∴△CDE是等边三角形,∴CE=CD,∵BC=2CD,∴BE=CE,∵OA=OC,∴OE∥AB;故①正确;②∵△DEC是等边三角形,∴∠DEC=60°=∠DBC+∠BDE,∵BE=EC=DE,∴∠DBC=∠BDE=30°,∴∠BDC=30°+60°=90°,∴BD⊥CD,∴S平行四边形ABCD=BD•CD;故②正确;③设AB=x,则AD=2x,则BD=√3x,∴OB=√32x,由勾股定理得:AO=(√3x2)=√72x,故③不正确;④∵AD ∥EC ,∴AD EC =DF EF =21,∴DF =2EF ,∴S △DOF =2S △EOF . 故④正确;故选:C .1.(2020•深圳模拟)在边长为2的正方形ABC D 中,P 为AB 上的一动点,E 为A D 中点,PE 交CD 延长线于Q ,过E 作EF ⊥PQ 交BC 的延长线于F ,则下列结论:①△APE ≌△DQE ;②PQ =EF ;③当P 为A B 中点时,CF =√2;④若H 为QC 的中点,当P 从A 移动到B 时,线段EH 扫过的面积为1,其中正确的有( )A .1个B .2个C .3个D .4个【答案】B【接卸】①∵四边形ABCD 是正方形,∴AB =BC =CD =AD ,∠A =∠B =∠ADC =90°,∴∠A =∠EDQ =90°,∵E 为A D 中点,∴AE =ED ,在△APE 和△DQE 中,{∠A =∠EDQAE =ED ∠AEP =∠DEQ,∴△APE ≌△DQE (ASA ),故①正确;②作PG ⊥CD 于G ,EM ⊥BC 于M ,如图1所示:∴∠PGQ =∠EMF =90°,∵EF ⊥PQ ,∴∠PEF =90°,∴∠PEM +∠MEF =90°,∵∠GPE +∠MEP =90°,∴∠GPE =∠MEF ,在△EFM 和△PQG 中,{∠EMF =∠PGQEM =PG ∠MEF =∠GPQ,∴△EFM ≌△PQG (ASA ),∴EF =PQ ,故②正确;③连接QF ,如图2所示:则QF =PF ,PB 2+BF 2=QC 2+CF 2,设CF =x ,则(2+x )2+12=32+x 2,∴x =1,故③错误;④如图3所示:当P 在A 点时,Q 与D 重合,QC 的中点H 在DC 的中点S 处, 当P 运动到B 时,QC 的中点H 与D 重合,故EH 扫过的面积为△ESD 的面积为12,故④错误;故选:B .2.(2020•灌南县一模)如图,正方形ABC D 中,E 、F 分别为BC 、CD 的中点,AF 与DE 交于点G .则下列结论中:①AF ⊥DE ;②AD =BG ;③GE +GF =√2GC ;④S △AGB =2S 四边形ECFG .其中正确的是( )A .1个B .2个C .3个D .4个【答案】D【解析】∵正方形ABCD ,E ,F 均为中点,∴AD =BC =DC ,EC =DF =12BC,∵在△ADF 和△DCE 中,{AD =DC∠ADF =∠DCE DF =CE,∴△ADF ≌△DCE (SAS ),∴∠AFD =∠DEC ,∵∠DEC +∠CDE =90°,∴∠AFD +∠CDE =90°=∠DGF ,∴AF ⊥DE ,故①正确;如图1,过点B 作BH ∥DE 交AD 于H ,交AF 于K ,∵AF ⊥DE ,BH ∥DE ,E 是BC 的中点,∴BH ⊥AG ,H 为AD 的中点,∴BH 是AG 的垂直平分线,∴BG =AB =AD ,故②正确,如图2,延长DE 至M ,使得EM =GF ,连接CM ,∵∠AFD =∠DEC ,∴∠CEM =∠CFG ,又∵E ,F 分别为BC ,DC 的中点,∴CF =CE ,∵在△CEM 和△CFG 中,{CE =CF∠CEM =∠CFG EM =FG,∴△CEM ≌△CFG (SAS ),∴CM =CG ,∠ECM =∠GCF ,∵∠GCF +∠BCG =90°,∴∠ECM +∠BCG =∠MCG =90°,∴△MCG 为等腰直角三角形,∴GM =GE +EM =GE +GF =√2GC ,故③正确;如图3,过G 点作TL ∥AD ,交AB 于T ,交DC 于L ,则GL ⊥AB ,GL ⊥DC ,设EC =x ,则DC =2x ,DF =x ,由勾股定理得DE =√5x ,由DE ⊥GF ,易证得△DGF ∽△DCE , ∴DE DF =GF EC =√5x x ,∴S △DEC S △DGF =(√51)2=51, ∴S △DGF =15S △DEC ,∴S 四边形ECFG =S △DEC ﹣S △DGF =45S △DEC ,∵S △DEC =12⋅2x ⋅x =x 2,∴S 四边形ECFG =45x 2,S △DGF =15x 2∵DF =x , ∴GL =15x 212x =25x ,∴TG =2x −25x =85x ,∴S △AGB =12•AB •TG =12•2x •85x =85x 2,∴S △AGB =2S 四边形ECFG 故④正确,故选:D .3.(2020•东莞市一模)如图,在菱形ABC D 中,∠BAD =60°,AC 与BD 交于点O ,E 为CD 延长线上的一点,且CD =DE ,连接BE 分别交AC 、AD 于点F 、G ,连接OG ,则下列结论中一定成立的是 ①④ .(把所有正确结论的序号都填在横线上)①OG =12AB ;②与△EGD 全等的三角形共有5个;③S 四边形ODGF >S △ABF ; ④由点A 、B 、D 、E 构成的四边形是菱形.【答案】①④【解析】∵四边形ABCD 是菱形,∴AB =BC =CD =DA ,AB ∥CD ,OA =OC ,OB =OD ,AC ⊥BD ,∴∠BAG =∠EDG ,△ABO ≌△BCO ≌△CDO ≌△AOD ,∵CD =DE ,∴AB =DE ,在△ABG 和△DEG 中,{∠BAG =∠EDG ∠AGB =∠DGE AB =DE,∴△ABG ≌△DEG (AAS ),∴AG =DG ,∴OG 是△ACD 的中位线,∴OG =12CD =12AB ,①正确;∵AB ∥CE ,AB =DE ,∴四边形ABDE是平行四边形,∵∠BCD=∠BAD=60°,∴△ABD、△BCD是等边三角形,∴AB=BD=AD,∠ODC=60°,∴OD=AG,四边形ABDE是菱形,④正确;∴AD⊥BE,由菱形的性质得:△ABG≌△BDG≌△DEG,在△ABG和△DCO中,{OD=AG∠ODC=∠BAG=60°AB=DC,∴△ABG≌△DCO(SAS),∴△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,②不正确;∵OB=OD,AG=DG,∴OG是△ABD的中位线,∴OG∥AB,OG=12AB,∴△GOD∽△ABD,△ABF∽△OGF,∴△GOD的面积=14△ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,∴△AFG的面积=△OGF的面积的2倍,又∵△GOD的面积=△AOG的面积=△BOG的面积,∴S四边形ODGF=S△ABF;不正确;正确的是①④.故答案为:①④.4.(2020•天河区一模)如图,在正方形ABC D中,对角线AC,BD交于点O,点E,F分别在AB,BD上,且△ADE≌△FDE,DE交AC于点G,连接GF.得到下列四个结论:①∠ADG=22.5°;②S△AGD=S△OGD;③BE=2OG;④四边形AEFG是菱形,其中正确的结论是①③④.(填写所有正确结论的序号)【答案】①③④.【解析】∵四边形ABCD是正方形,∴∠GAD=∠ADO=45°,∴由△ADE≌△FDE,可得:∠ADG=12∠ADO=22.5°,故①正确;∵△ADE≌△FDE,∴AD=FD,∠ADG=∠FDG,又∵GD=GD,∴△ADG≌△FDG(SAS),∴S△AGD>S△OGD,故②错误;∵△ADE≌△FDE,∴EA=EF,∵△ADG≌△FDG,∴GA=GF,∠AGD=∠FGD,∴∠AGE=∠FGE.∵∠EFD=∠AOF=90°,∴EF∥AC,∴∠FEG=∠AGE,∴∠FGE=∠FEG,∴EF=GF,∴EF=GF=EA=GA,∴四边形AEFG是菱形,故④正确;∵四边形AEFG是菱形,∴AE∥FG,∴∠OGF=∠OAB=45°,∴△OGF为等腰直角三角形,∴FG=√2OG,∴EF=√2OG,∵△BFE为等腰直角三角形,∴BE=√2EF=√2×√2OG=2OG,∴③正确.综上,正确的有①③④.故答案为:①③④.5.(2020•福田区一模)如图,正方形ABC D中,E是BC延长线上一点,在AB上取一点F,使点B关于直线EF的对称点G落在AD上,连接EG交CD于点H,连接BH交EF于点M,连接CM.则下列结论,①∠1=∠2;②∠3=∠4;③GD=√2CM;④若AG=1,GD =2,则BM=√5,其中正确的是..【答案】①②③④【解析】如图1中,过点B作BK⊥GH于K.∵B,G关于EF对称,∴EB=EG,∴∠EBG=∠EGB,∵四边形ABCD是正方形,∴AB=BC,∠A=∠ABC=∠BCD=90°,AD∥BC,∴∠AGB=∠EBG,∴∠AGB=∠BGK,∵∠A=∠BKG=90°,BG=BG,∴△BAG≌△BKG(AAS),∴BK=BA=BC,∠ABG=∠KBG,∵∠BKH=∠BCH=90°,BH=BH,∴Rt△BHK≌Rt△BHC(HL),∴∠1=∠2,∠HBK=∠HBC,故①正确,∴∠GBH=∠GBK+∠HBK=1∠ABC=45°,2过点M作MQ⊥GH于Q,MP⊥CD于P,MR⊥BC于R.∵∠1=∠2,∴MQ=MP,∵∠MEQ=∠MER,∠BCD=45°,∴MQ=MR,∴MP=MR,∴∠4=∠MCP=12∴∠GBH=∠4,故②正确,如图2中,过点M作MW⊥AD于W,交BC于T.∵B,G关于EF对称,∴BM=MG,∵CB=CD,∠4=∠MCD,CM=CM,∴△MCB≌△MCD(SAS),∴BM=DM,∴MG=MD,∵MW⊥DG,∴WG=WD,∵∠BTM=∠MWG=∠BMG=90°,∴∠BMT+∠GMW=90°,∵∠GMW+∠MGW=90°,∴∠BMT=∠MGW,∵MB=MG,∴△BTM≌△MWG(AAS),∴MT=WG,∵MC=√2TM,DG=2WG,∴DG=√2CM,故③正确,∵AG=1,DG=2,∴AD=AB=TM=3,EM=WD=TM=1,BT=AW=2,∴BM=√BT2+MT2=√22+12=√5,故④正确,故答案为:①②③④.。
第7关 以几何图形中的图形操作与变换问题为背景的解答题(原卷版)-中考数学专题复习

第七关以几何图形中的图形操作与变换问题为背景的解答题【考查知识点】图形的变换有轴对称、平移和旋转,在此类问题中轴对称问题多以折叠的形式出现。
折叠问题也是最近中考的热点,这类问题不但考察学生对基本几何图形性质的掌握情况,而且可以培养学生的空间思维能力和运动变化观念,提高学生的实践操作水平。
图形的旋转是中考题的新题型,热点题型,考察内容:①中心对称和中心对称图形的性质和别。
②旋转,平移的性质.【解题思路】折叠类题目的主要出题结合点有:与三角形结合,与平行四边形结合,与圆结合,与函数图像结合,题型多以选择题和填空题的形式出现,少数题目也会在大题中作为辅助背景。
在解决这类问题时,要注意折叠出等角,折叠出等长,折叠出等腰三角形,折叠出全等与相似等。
图形的旋转是中考题的新题型,热点题型,解题方法①熟练掌握图形的对称,图形的平移,图形的旋转的基本性质和基本作图法。
②结合具体的问题大胆尝试,动手操作平移,旋转,探究发现其内在的规律。
③注重对网格内和坐标内的图形的变换试题的研究,熟练掌握其常用的解题方法。
④关注图形与变换创新题,弄清其本质,掌握基本解题方法,如动手操作法,折叠法,旋转法,旋转可以移动图形的位置而不改变图形的大小,是全等变换.变换的目的是为了实现已知与结论中的相关元素的相对集中或分散重组,使表面上不能发生联系的元素联系起来.在转化的基础上为问题的解决铺设桥梁,沟通到路.一些难度较大的问题借助平移、对称、旋转的合成及相互关系可能会更容易一些.【典型例题】【例1】(2019·河北中考模拟)如图1,在▱ABCD中,DH⊥AB于点H,CD的垂直平分线交CD于点E,交AB于点F,AB=6,DH=4,BF:FA=1:5.(1)如图2,作FG⊥AD于点G,交DH于点M,将△DGM沿DC方向平移,得到△CG′M′,连接M′B.①求四边形BHMM′的面积;②直线EF上有一动点N,求△DNM周长的最小值.(2)如图3,延长CB交EF于点Q,过点Q作QK∥AB,过CD边上的动点P作PK∥EF,并与QK交于点K,将△PKQ沿直线PQ翻折,使点K的对应点K′恰好落在直线AB上,求线段CP的长.【例2】(2019·湖南中考模拟)在矩形ABCD中,AB=12,P是边AB上一点,把△PBC沿直线PC折叠,顶点B的对应点是点G,过点B作BE⊥CG,垂足为E且在AD上,BE交PC于点F.(1)如图1,若点E是AD的中点,求证:△AEB≌△DEC;(2)如图2,①求证:BP=BF;②当AD=25,且AE<DE时,求cos∠PCB的值;③当BP=9时,求BE•EF的值.【例3】(2019·辽宁中考真题)思维启迪:(1)如图1,A,B两点分别位于一个池塘的两端,小亮想用绳子测量A,B间的距离,但绳子不够长,聪明的小亮想出一个办法:先在地上取一个可以直接到达B点的点C,连接BC,取BC的中点P(点P可以直接到达A点),利用工具过点C作CD∥AB交AP的延长线于点D,此时测得CD=200米,那么A,B间的距离是米.思维探索:(2)在△ABC和△ADE中,AC=BC,AE=DE,且AE<AC,∠ACB=∠AED=90°,将△ADE 绕点A顺时针方向旋转,把点E在AC边上时△ADE的位置作为起始位置(此时点B和点D位于AC的两侧),设旋转角为α,连接BD,点P是线段BD的中点,连接PC,PE.①如图2,当△ADE在起始位置时,猜想:PC与PE的数量关系和位置关系分别是;②如图3,当α=90°时,点D落在AB边上,请判断PC与PE的数量关系和位置关系,并证明你的结论;③当α=150°时,若BC=3,DE=l,请直接写出PC2的值.【方法归纳】实践操作性试题以成为中考命题的热点,很多省市的压轴的都是这类题型,解决这种类型的题目可从以下方面切入:1.构造定理所需的图形或基本图形.在解决问题的过程中,有时添辅助线是必不可少的。
2024年中考复习-11 几何图形中求线段,线段和,面积等最值问题(4题型)(解析版)
抢分秘籍11几何图形中求线段,线段和,面积等最值问题(压轴通关)目录【中考预测】预测考向,总结常考点及应对的策略【误区点拨】点拨常见的易错点【抢分通关】精选名校模拟题,讲解通关策略(含新考法、新情境等)几何图形中求线段、线段和、面积最值题是全国中考的热点内容,更是全国中考的必考内容。
每年都有一些考生因为知识残缺、基础不牢、技能不熟、答欠规范等原因导致失分。
1.从考点频率看,几何图形中的性质综合问题,是高频考点、也是必考点。
2.从题型角度看,以解答题的最后一题或最后二题为主,分值12分左右,着实不少!题型一线段最值问题【例1】(2024·四川成都·一模)如图1,在四边形ABFE 中,90F ∠=︒,点C 为线段EF 上一点,使得AC BC ⊥,24AC BC ==,此时BF CF =,连接BE ,BE AE ⊥,且AE BE =.(1)求CE 的长度;(2)如图2,点D 为线段AC 上一动点(点D 不与A ,C 重合),连接BD ,以BD 为斜边向右侧作等腰直角三角形BGD .①当DG AB ∥时,试求AD 的长度;②如图3,点H 为AB 的中点,连接HG ,试问HG 是否存在最小值,如果存在,请求出最小值;如果不存在,请说明理由.DC =,即可得出DM GF =,证明DMG GFB ≌,进而证明G 在EF 上,根据已知条件证明D 在EB 上,然后解直角三角形,即可求解;②如图所示,过点H 作HP EF ⊥于点P ,连接EH ,由①可得G 在EF 上运动,当HG EF ⊥时,HG 取得最小值,即,G P 重合时,HP 的长即为HG 的最小值,由①可得103AT =,求得sin 10ETA ∠=,根据45HEF ETA α∠=+︒=∠,即可求解.【详解】(1)解:如图所示,取AB 的中点H ,连接,EH HC ,∵BF CF =,90F ∠=︒,∴45BCF ∠=︒,BC =,又∵AC BC⊥∴45ECA ∠=︒∵AE BE =,BE AE⊥∴45EBA ∠=︒∴45ECA ABE ∠=∠=︒∴FEB CAB∠=∠∵24AC BC ==,∴2BC =∴BF CF ==∴1tan 2CB CAB AC ∠==∴1tan tan 2FB FEB CAB EF ∠==∠=∴12BF EF =∴EF =∴CE EF CF =-=(2)①如图所示,过点D 作DM EF ⊥于点M ,过点D 作DN AB ⊥于点N,由(1)可得45ACE ABE ∠=∠=︒∴CDM V 是等腰直角三角形,∴CD =,∵,CBF DBG 都是等腰直角三角形,∴CB DB BF BG =∴BD BG BC BF=又∵DBG CBF∠=∠∴DBC GBF∠=∠∴DBC GBF∽∴DC DB GF GB==∴DC =∴DM GF=在,DMG GFB 中,DM GF DMG F DG BG =⎧⎪∠=∠⎨⎪=⎩∴DMG GFB≌∴MGD FBG∠=∠∵90FBG FGB ∠+∠=︒∴90MGD FGB ∠+∠=︒又∵90DGB ∠=︒∴180MGF ∠=︒∴G 在EF 上,∵DG AB ∥,90DGB ∠=︒∴90GBA ∠=︒∵45,45ABE DBG ABD∠=︒∠=︒=∠∴D 在EB 上,∵1tan 2CAB ∠=,∴12DN AN =,则AD ==∵,45DN AB ABE ⊥∠=︒∴DN DB=∴3AB DN =,∵4AC =,2CB =∴AB =∴133DN AB ==,∴103AD ==,②如图所示,过点H 作HP EF ⊥于点P ,连接EH ,由①可得G 在EF 上运动,∴当HG EF ⊥时,HG 取得最小值,即,G P 重合时,HP 的长即为HG 的最小值,设,AC EB 交于点T ,即与①中点D 重合,由①可得103AT =∵AB =∴AE =,12EH AB ==∴sin 10103AE ETA AT ∠==设FEB CAB α∠=∠=则45HEF ETA α∠=+︒=∠,在Rt PEH △中,sin sin 102PH HEF EH ETA EH =∠⨯=∠⨯=⨯.【点睛】证明G 点在EF 上是解题的关键.本题考查了相似三角形的性质与判定,等腰三角形的性质,全等三角形的性质与判定,解直角三角形.【例2】(2024·天津红桥·一模)在平面直角坐标系中,点()0,0O ,()2,0A,(2,B ),C ,D 分别为OA ,OB 的中点.以点O 为中心,逆时针旋转OCD ,得OC D '' ,点C ,D 的对应点分别为点C ',D ¢.(1)填空∶如图①,当点D ¢落在y 轴上时,点D ¢的坐标为_____,点C '的坐标为______;(2)如图②,当点C '落在OB 上时,求点D ¢的坐标和BD '的长;(3)若M 为C D ''的中点,求BM 的最大值和最小值(直接写出结果即可).(),D为OB中点,B2,23()∴,D1,3()22132OD∴=+=,∵以点O为中心,逆时针旋转由(1)知60AOB ∠=︒,30GD O '∴∠=︒,112OG OD '∴==,D G '()1,3D ∴'-,()2,23B ,∵C ,D 分别为OA ,OB 的中点,此时M 在BO 的延长线上,()2,23B ,()222234OB ∴=+=,742BM OB OM ∴=+=+;即BM 最大值为742+;此时M 在线段OB 上,BM BM ∴最小值为427-;综上所述,BM 最大值为1.(2024·山东济宁·模拟预测)已知,四边形ABCD 是正方形,DEF 绕点D 旋转(DE AB <),90EDF ∠=︒,DE DF =,连接AE CF ,.(1)如图1,求证:ADE CDF ≅ ;(2)直线AE 与CF 相交于点G .①如图2,BM AG ⊥于点M ,⊥BN CF 于点N ,求证:四边形BMGN 是正方形;②如图3,连接BG ,若6AB =,3DE =,直接写出在DEF 旋转的过程中,线段BG 长度的最小值为.【详解】(1)证明: 四边形ABCD 是正方形,AD DC ∴=,90ADC ∠=︒,DE DF = ,90EDF ∠=︒,ADC EDF ∴∠=∠,ADE CDF \Ð=Ð,在ADE V 和CDF 中,DA DC ADE CDF DE DF =⎧⎪∠=∠⎨⎪=⎩,SAS ADE CDF ∴() ≌.(2)解:①证明:如图2中,设AG 与CD 相交于点P ,90ADP ∠=︒ ,90DAP DPA ∴∠+∠=︒,ADE CDF ≅ ,DAE DCF ∴∠=∠,DPA GPC ∠∠= ,90DAE DPA GPC GCP ∠∠∠∠∴+=+=︒,90PGN ∠∴=︒,BM AG ⊥ ,BN GN ⊥,∴四边形BMGN 是矩形,90MBN ∴∠=︒,四边形ABCD 是正方形,AB BC ∴=,90ABC MBN ∠∠==︒,ABM CBN ∴∠=∠,又90AMB BNC ∠∠==︒ ,AMB CNB ∴≅ ,MB NB ∴=,∴矩形BMGN 是正方形;∵DAH BAM ∠+∠=∠∴DAH ABM ∠=∠,又∵AD BA =,DHA ∠∴AMB DHA ≌△△,BM AH ∴=,222AH AD DH =- ,DH ∴最大时,AH 最小,即点(1)若AC AB AD BC >⊥,,当点E 在线段AC 上时,AD BE ,交于点F ,点F 为BE 中点.①如图1,若37BF BD AD ===,,求AE 的长度;②如图2,点G 为线段AF 上一点,连接GE 并延长交BC 的延长线于点H .若点E 为GH 中点,602BAC DAC EBC ∠=︒∠=∠,,求证:12AG DF AB +=.(2)如图3,若360AC AB BAC ︒==∠=,.当点E 在线段AC 的延长线上时,连接DE ,将DCE △沿DC 所在直线翻折至ABC 所在平面内得到DCM △,连接AM ,当AM 取得最小值时,ABC 内存在点K ,使得ABK CAK ∠=∠,当KE 取得最小值时,请直接写出2AK 的值.AD BC EG AD ⊥⊥ ,,90BDF ∴∠=︒,EGF ∠=BDF EGF ∴∠=∠,在Rt BDF △中,90BDF ∠=(22DF BF BD ∴=-=AD BC ⊥ ,90ADC ∴∠=︒,点E 为GH 的中点,GE HE ∴=,在AGE 和KHE △中,12AE KE =⎧⎪∠=∠⎨,由题意可知:160∠=︒,AC 30CAM ∴∠=︒,1322CM AC ∴==,32CE CM ∴==,(1)如图①,在ABC 中,点M ,N 分别是AB ,AC 的中点,若BC =MN 的长为__________.问题探究:(2)如图②,在正方形ABCD 中,6AD =,点E 为AD 上的靠近点A 的三等分点,点F 为AB 上的动点,将AEF △折叠,点A 的对应点为点G ,求CG 的最小值.问题解决:(3)如图③,某地要规划一个五边形艺术中心ABCDE ,已知120ABC ∠=︒,60BCD ∠=︒,40m AB AE ==,80m BC CD ==,点C 处为参观入口,DE 的中点P 处规划为“优秀”作品展台,求点C 与点P 之间的最小距离.∵点E为AD上的靠近点∴11633 AE AD==⨯在Rt EDC中,EC 根据折叠的性质,EG(1)如图1,点D 为ABC 的边BC 上一点,连接2,,3BD AD BDA BAC AB ∠=∠=,若ABD △的面积为4,则ACD 的面积为______;【问题探究】(2)如图2,在矩形ABCD 中,6,5AB BC ==,在射线BC 和射线CD 上分别取点E F 、,使得65BE CF =,连接AE BF 、相交于点P ,连接CP ,求CP 的最小值;【问题解决】(3)如图3,菱形ABCD 是某社区的一块空地,经测量,120AB =米,60ABC ∠=︒.社区管委会计划对该空地进行重新规划利用,在射线AD 上取一点E ,沿BE CE 、修两条小路,并在小路BE 上取点H ,将CH 段铺设成某种具有较高观赏价值的休闲通道(通道宽度忽略不计),根据设计要求,BHC BCE ∠=∠,为了节省铺设成本,要求休闲通道CH 的长度尽可能小,问CH 的长度是否存在最小值?若存在,求出CH 长度的最小值;若不存在,请说明理由.【答案】(1)5;(2)343-;(3)存在,最小值为403米【分析】(1)证明C ABD BA ∽△△,利用相似三角形的性质得到994CBA ABD S S == ,即可得到ACD 的面积;(2)证明ABE BCF ∽△△,进一步得到90APB ∠=︒,则证明点P 在矩形ABCD 内部以AB 为直径的O 上运动,连接,OP OC ,OC 交O 于点P ',进一求出3,34OP OP OB OC '====,则343CP OC OP ''=-=-,由CP OC OP ≥-,即可得到CP 的最小值;(3)证明,CBH EBC ∽得到2BC BE BH =⋅,则2AB BE BH =⋅,再证明,ABH EBA ∽得到120AHB EAB ∠=∠=︒,证明点H 在O 的劣弧 AB 上运动,求得90OBC ∠=︒,进一步求得403OH AO BO ===米,勾股定理可得803OC =米,记OC 与O 相交于点H ',则403OH OH '==米,求出403CH OC OH ''=-=米,由403CH OC OH '≥-=米,即可得到答案.【详解】(1)解:∵,BDA BAC ∠=∠B B ∠=∠,∴C ABD BA ∽△△,∴2439ABDCBA S BD S AB ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭ ,∴994CBA ABD S S == ,∴ACD 的面积为945CBA ABD S S -=-= ,故答案为:5(2)∵四边形ABCD 是矩形,∴90ABE BCF ∠=∠=︒,∵65BE CF =,6,5AB BC ==,∴65BE AB CF BC ==,∴ABE BCF ∽△△,∴BAE CBF ∠=∠,∵90CBF ABP ∠+∠=︒∴90BAE ABP ∠+∠=︒∴()18090APB BAE ABP ∠=︒-∠+∠=︒∴点P 在矩形ABCD 内部以AB 为直径的O 上运动,则1602BM AM AB ===米,题型二线段和的最小值问题【例1】(2024·四川达州·模拟预测)【问题发现】(1)如图1,在OAB 中,3OB =,若将OAB 绕点O 逆时针旋转120︒得OA B '',连接BB ',则BB '=________.【问题探究】(2)如图2,已知ABC 是边长为BC 为边向外作等边BCD △,P 为ABC 内一点,连接AP BP CP ,,,将BPC △绕点C 逆时针旋转60︒,得DQC △,求PA PB PC ++的最小值;【实际应用】(3)如图3,在长方形ABCD 中,边1020AB AD ==,,P 是BC 边上一动点,Q 为ADP △内的任意一点,是否存在一点P 和一点Q ,使得AQ DQ PQ ++有最小值?若存在,请求出此时PQ 的长,若不存在,请说明理由.在OAB 中,3OB =,将 120BOB '∴∠=︒,OB OB '==OBB OB B ''∴∠=∠,OBB OB B B OB '''∠+∠+∠=PA PB PC PA ∴++=+∴当点D、Q、P、A⊥连接AD,作DE AC∠=∠=︒DCB BCA60本题主要考查了等边三角形的性质与判定,矩形的性质与判定,旋转的性质,勾股定理,含30度角的直角三角形的性质,解题的关键在于利用旋转构造等边三角形,从而把三条不在一条直线的线段之和的问题,转换成几点共线求线段的最值问题是解题的关键.【例2】(2024·贵州毕节·一模)在学习了《图形的平移与旋转》后,数学兴趣小组用一个等边三角形继续进 是边长为2的等边三角形.行探究.已知ABC(1)【动手操作】如图1,若D为线段BC上靠近点B的三等分点,将线段AD绕点A逆时针旋转60︒得到线段AE,连接CE,则CE的长为________;(2)【探究应用】如图2,D 为ABC 内一点,将线段AD 绕点A 逆时针旋转60︒得到线段AE ,连接CE ,若,,B D E 三点共线,求证:EB 平分AEC ∠;(3)【拓展提升】如图3,若D 是线段BC 上的动点,将线段AD 绕点D 顺时针旋转60︒得到线段DE ,连接CE .请求出点D 在运动过程中,DEC 的周长的最小值.(3)由ABD ACE ≌△△,得CE BD =,可得DEC 的周长BC DE =+,而DE AD =,知AD 的最小时,DEC 的周长最小,此时AD BC ⊥,即可求得答案.∵ABD ACE ≌△△,∴CE BD =,∴DEC 的周长DE CE =+∴当点D 在线段BC 上时,∵DEC 为等边三角形,1.(2024·陕西·二模)在平面直角坐标系中,A 为y 轴正半轴上一点,B 为x 轴正半轴上一点,且4OA OB ==,连接AB .(1)如图1,C 为线段AB 上一点,连接OC ,将OC 绕点O 逆时针旋转90︒得到OD ,连接AD ,求AC AD +的值.(2)如图2,当点C 在x 轴上,点D 位于第二象限时,90ADC ∠=︒,且AD CD =,E 为AB 的中点,连接DE ,试探究线段AD DE +是否存在最小值?若存在,求出AD DE +的最小值;若不存在,请说明理由.又90AOB ∠=︒,∴四边形DMON 是矩形,∴90MDN ∠=︒,大值和最小值分别是______和______;(2)如图2,在矩形ABCD 中,4AB =,6AD =,点P 在AD 上,点Q 在BC 上,且AP CQ =,连接CP 、QD ,求PC QD +最小时AP 的长;(3)如图3,在ABCD Y 中,10AB =,20AD =,点D 到AB 的距离为,动点E 、F 在AD 边上运动,始终保持3EF =,在BC 边上有一个直径为BM 的半圆O ,连接AM 与半圆O 交于点N ,连接CE 、FN ,求CE EF FN ++的最小值.如图,当点P 在AO 的延长线上时,此时PA 的最大值为:PO OA +故答案为:11;3;(2)延长BA 至点B ',使AB ∵在矩形ABCD 中,4AB =,∴DAB BAP CBA '∠=∠=∠=∠∴DA 垂直平分BB ',∴PB PB '=,(3)如图,过点F 作FG EC ∥,交BC OG ',NO ,∵在ABCD Y 中,10AB =,20AD =,点∴AD BC ∥,即EF CG ∥,BC AD =∴四边形EFGC 是平行四边形,∴3GC EF ==,FG EC =,【点睛】本题考查圆的基本性质,全等三角形的判定和性质,相似三角形的判定和性质,矩形的性质,平行四边形的判定和性质,对称的性质,勾股定理,三角形三边关系定理,两点之间线段最短等知识点.灵活运用所学知识、弄清题意并作出适当辅助线是解题的关键.3.(2024·陕西西安·三模)【问题提出】(1)如图①,AB 为半圆O 的直径,点P 为半圆O 的 AB 上一点,BC 切半圆O 于点B ,若10AB =,12BC =,则CP 的最小值为;【问题探究】(2)如图②,在矩形ABCD 中,3AB =,5BC =,点P 为矩形ABCD 内一点,连接PB 、PC ,若矩形ABCD 的面积是PBC 面积的3倍,求PB PC +的最小值;【问题解决】(3)如图③,平面图形ABCDEF 为某校园内的一片空地,经测量,AB BC ===60B ∠︒,150BAF BCD ∠=∠=︒,DE DC ⊥,20CD =米,劣弧 EF所对的圆心角为90︒, EF 所在圆的圆心在AF 的延长线上,10AF =米.某天活动课上,九(1)班的同学准备在这块空地上玩游戏,每位同学在游戏开始前,在BC 上选取一点P ,在弧 EF上选取一点Q ,并在点P 和点Q 处各插上一面小旗,从点A 出发,先到点P 处拔下小旗,再到点Q 处拔下小旗,用时最短者获胜.已知晓雯和晓静的跑步速度相同,要使用时最短,则所跑的总路程()AP PQ +应最短,问AP PQ +是否存在最小值?若存在,请你求出AP PQ +的最小值;若不存在,请说明理由.【答案】(1)8;(2)41;(3)AP PQ +存在最小值,最小值为()20310m -.【分析】(1)连接OC 交O 于点1P ,则1CP是CP 的最小值,求出1CP 的长即可,(2)过点P 作PH BC ⊥于点H ,作EF BC ∥,连接BC ',BP C P '+的最小值,即为BC '的长度,求出BC '即可,(3)连接AC ,作点A 关于BC 的对称点A ',连接PA ',A Q ',AA ',过A '作A N ED '⊥,分别交ED 、AC 的延长线于点N 、M ,分别延长AF ,DE 交于点O ,连接OQ ,OA ',当A Q '取得最小值时,AP PQ +的值最小,即A Q ''的长,求出A Q ''即可.解:(1)如图,连接OC 交O 于点1P ,连接OP ,点P 为半圆O 的AB上一点,∴当点P 与点1P 不重合时,CP OC OP >-,当点P 与点1P 重合时,1CP CP OC OP ==-,CP OC OP ∴≥-,CP ∴的最小值OC OP =-,BC 切半圆O 于点B ,90ABC ∴∠=︒,152OB OP AB === ,12BC =,2212513OC ∴=+=,CP ∴的最小值1358OC OP =-=-=,故答案为:8.(2)过P 作PH BC ⊥,如图,矩形ABCD 的面积是13553PBC S ∴=⨯⨯= 2PH ∴=,60ABC ∠=︒ ,AB BC ==ABC ∴ 是等边三角形,60BAC BCA ∴∠=∠=︒,150BAF BCD ∠=∠=︒ ,DE ACD MCD CAO ∴∠=∠=∠=AA M '∴ 和OA N '△都是直角三角形,四边形,E G分别作,,⊥⊥与EF交于点F,连接CF.EF AD FG AB FG特例感知(1)以下结论中正确的序号有______;ED CF BG为边围成的三角形不是直①四边形AGFE是矩形;②矩形ABCD与四边形AGFE位似;③以,,角三角形;类比发现(2)如图2,将图1中的四边形AGFE绕着点A旋转,连接BG,观察CF与BG之间的数量关系和位置关系,并证明你的发现;拓展应用(3)连接CE ,当CE 的长度最大时,①求BG 的长度;②连接,,AC AF CF ,若在ACF △内存在一点P ,使CP AP ++的值最小,求CP AP ++的最小值.∴HF DE =,CH BG =∴CHF 是直角三角形,∵四边形ABCD 是矩形,∴43AB CD ==,AD =∴228AC AB BC =+=,则由(2)知,90CEF ∠=︒,∵2247CF CE EF =+=∴3221BG CF ==;根据旋转,可得30PAF KAL ∠=∠=∴3KL PF =,过P 作PS AK ⊥于S ,则12PS AP =∴32KS AK AS AP =-=,则tan ∠题型三面积的最小值问题【例1】(新考法,拓视野)(2024·陕西西安·一模)【问题提出】(1)如图1,已知在边长为5的等边ABC 中,点D 在边BC 上,3BD =,连接AD ,则ACD 的面积为;【问题探究】(2)如图2,已知在边长为6的正方形ABCD 中,点E 在边BC 上,点F 在边CD 上,且45EAF ∠=︒,若5EF =,求AEF △的面积;【问题解决】(3)如图3是某座城市廷康大道的一部分,因自来水抢修在4AB =米,AD =ABCD 区域内开挖一个AEF △的工作面,其中B 、F 分别在BC CD 、边上(不与B 、C 、D 重合),且60EAF ∠=︒,为了减少对该路段的拥堵影响,要求AEF △面积最小,那么是否存在一个面积最小的AEF △?若存在,请求出AEF △面积的最小值;若不存在,请说明理由.(2)如图所示,延长∵四边形ABCD 是正方形,∴AB AD D =,∠∴ABG ADF ≌∴AG AF DAF =,∠(3)把ADF △绕点A ∴33AG AF FAG =,∠∵60EAF ∠=︒,∴30EAG ∠=︒,本题主要考查了圆周角定理,勾股定理,旋转的性质,解直角三角形,正方形的性质,等边三角形的性质与判定,矩形的性质与判定,全等三角形的性质与判定等等,通过作出辅助线构造直角三角形,全等三角形是解题的关键.【例2】(2024·陕西西安·二模)图形旋转是解决几何问题的一种重要方法.如图1,正方形ABCD 中,E F 、分别在边AB BC 、上,且45EDF ∠=︒,连接EF ,试探究AE CF EF 、、之间的数量关系.解决这个问题可将ADE V 绕点D 逆时针旋转90︒到CDH △的位置(易得出点H 在BC 的延长线上),进一步证明DEF 与DHF △全等,即可解决问题.(1)如图1,正方形ABCD 中,45,3,2EDF AE CF ∠=︒==,则EF =______;(2)如图2,正方形ABCD 中,若30EDF ∠=︒,过点E 作EM BC ∥交DF 于M 点,请计算AE CF +与EM 的比值,写出解答过程;(3)如图3,若60EDF ∠=︒,正方形ABCD 的边长8AB =,试探究DEF 面积的最小值.,,,D F H G 四点共圆;进而可得30FHG ∠=,根据13tan 30AE CF CH CF FH EM GH GH ++====︒,即可求解;(3)过点E 作EK CD ⊥于K ,交DF 于M ,作FT EK ⊥于T ,得出4DEF S EM = ,进而根据(2)的方法得出3EM GH FH ==,根据FC AE CH ==时,面积最小,得出32163OF =-,即可求解.【详解】(1)解:∵将ADE V 绕点D 逆时针旋转90︒,∴90DCH A DCB ∠=∠=︒=∠,DH DE HDC EDA=∠=∠,∴点H 在BC 的延长线上,∵四边形ABCD 是正方形∴90ADC ∠=︒,∵45EDF ∠=︒,∴45HDF CDH FDC ADE FDC EDF∠=∠+∠=∠+∠=︒=∠又∵DF DF =,∴DEF ()SAS DHF ≌,∴235EF FH FC CH FC AE ==+=+=+=,故答案为:5.(2)解:将ADE V ,DEM △绕点D 逆时针旋转90︒,得,DCH DHG∴,AED CHD DEM DHG ∠=∠∠=∠,∵EM BC ∥,则EM AB ⊥,∴90AEM ∠=︒,∴90CHG CHD DHG AED DEM AEM ∠=∠+∠=∠+∠=∠=︒,∵30EDF ∠=︒,EM BC ∥则EM AD ∥,∴ADE CDH ∠=∠,30GDH MDE ∠=∠=︒,∵EM BC ∥,∴EMF DFC ∠=∠,∴180EMD EMF EMD DFC ∠+∠=∠+∠=︒,即180DFC DGH ∠+∠=︒,∴,,,D F H G 四点共圆;∴30GFH GDH ∠=∠=︒,又30FHG ∠=︒∴1tan 30AE CF CH CF FH EM GH GH ++====︒(3)如图,过点E 作EK CD ⊥于K ,交DF 于M ,作FT EK ⊥于T ,90FTK TKC BCD ∠=∠=∠=︒∴四边形CFTK 是矩形,FT CK∴=8DK CK DK FT ∴+=+=111()4222DEF EMD EMF S S S DK EM FT EM DK FH EM ∴=+=⋅+⋅=+= 同(2)将ADE V ,DEM △绕点D 逆时针旋转90︒,得,DCH DHG ,可得60GFH EDM ∠=∠=︒,EM GH=∵2220-+=≥,∴FH x y =+≥当且仅当x y =时取得等于号,此时FC AE CH ==,设,,,D F H G 的圆心为O ,∵DC FH ⊥,FC CH =,∴DC 经过点O ,∴OF OD =,sin 602OC OF OF =︒=∵8OD OC +=即82OF +=解得:32OF =-∴232FH FC OF ===-∴48GH ==-,∴()44448192DEF S EM GH ===-=- ,即DEF 面积的最小为192-.【点睛】本题考查了旋转的性质,正方形的性质、全等三角形的判定与性质、四点共圆等知识,解直角三角形,熟练掌握旋转的性质是解题的关键.1.(2023·陕西西安·一模)问题发现(1)在ABC 中,2AB =,60C ∠=︒,则ABC 面积的最大值为;(2)如图1,在四边形ABCD 中,6AB AD ==,90BCD BAD ∠=∠=︒,8AC =,求BC CD +的值.问题解决(3)有一个直径为60cm 的圆形配件O ,如图2所示.现需在该配件上切割出一个四边形孔洞OABC ,要求60O B ∠=∠=︒,OA OC =,并使切割出的四边形孔洞OABC 的面积尽可能小.试问,是否存在符合要求的面积最小的四边形OABC ?若存在,请求出四边形OABC 面积的最小值及此时OA 的长;若不存在,请说明理由.∴当点C 在C '的位置,即∴C A C B ''=,BD =∴ABC '△是等边三角形,∴2C B AB '==,∴B ADE ∠=∠,BAC ∠∵6AB AD ==,BCD ∠∴180B ADC ∠+∠=︒,∵180ADE ADC ∠+∠=∵60AOC ∠=︒,OA OC =∴将AOB 绕O 点顺时针旋转∴60BOE ∠=︒,OE OB =∴BOE △是等边三角形,∴160302BE OB ==⨯=,(1)如图①,已知ABC 是面积为AD 是BAC ∠的平分线,则AB 的长为______.问题探究:(2)如图②,在ABC 中,90C ∠=︒,AC BC =,4AB =,点D 为AB 的中点,点E ,F 分别在边AC ,BC 上,且90EDF ∠=︒.证明:DE DF =.问题解决:(3)如图③,李叔叔准备在一块空地上修建一个矩形花园ABCD ,然后将其分割种植三种不同的花卉.按照他的分割方案,点P ,Q 分别在AD ,BC 上,连接PQ 、PB 、PC ,60BPC ∠=︒,E 、F 分别在PB 、PC 上,连接QE 、QF ,QE QF =,120EQF ∠=︒,其中四边形PEQF 种植玫瑰,ABP 和PCD 种植郁金香,剩下的区域种植康乃馨,根据实际需要,要求种植玫瑰的四边形PEQF 的面积为2,为了节约成本,矩形花园ABCD 的面积是否存在最小值?若存在,请求出矩形ABCD 的最小面积,若不存在,请说明理由.当PQ BC ⊥时,矩形ABCD 的面积最小,根据2ABCD PEQF S S =四边形四边形,即可求解.【详解】解:(1)∵ABC 是面积为AD 是BAC ∠的平分线,∴12BD CD AB ==设ABC 的边长为a∴2AD a =∴2112224ABC S BC AD a a a =�创=∴24a =解得:4a =,故答案为:4.(2)如图所示,连接CD,∵在ABC 中,90C ∠=︒,AC BC =,4AB =,点D 为AB 的中点,∴CD AD =,90ADC ∠=︒,45A DCF ∠=∠=︒又∵90EDF ∠=︒∴ADE ADC CDE EDF EDC CDF∠=∠-∠=∠-∠=∠在,ADE CDF △△中,45A DCF ADE CDF AD CD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴ADE CDFV V ≌∴DE DF =;(3)如图所示,∵60BPC ∠=︒,120EQF ∠=︒,∴36060120180PFQ PEQ ∠+∠=︒-︒-︒=︒将QFP △绕点Q 逆时针旋转120︒,得到EQG ,∴,,P E G 三点共线,∴四边形PEQF 的面积等于PQG ,又∵120,PQG PQ GQ ∠=︒=,∴30QPG QGP ∠=∠=︒过点Q 作QN PG ⊥于点N ,则12QN PQ =设PQ b =,则1,22NQ b PN b ==∴2PG PN ==∴21112224PQG S PG NQ b b =⨯=⨯⨯=∵四边形PEQF 的面积为∴16b =,即16PQ =,如图所示,作QM PM ⊥于点M ,∵30EPQ FPQ ∠=∠=︒,QM PM ⊥,QN PG ⊥,则QN QM =,在,ENQ FMQ 中,QN QM EQ FQ=⎧⎨=⎩∴()HL ENQ FMQ ≌,同理可得PNQ PMQ≌则2PNQPEQF S S = 四边形∴PEQF PNQM S S =四边形四边形,作点Q 关于PE 的对称点T ,连接PT ,则PTQ 是等边三角形,则PTQ S = ,如图所示,依题意,当PQ BC ⊥时,矩形ABCD 的面积最小,此时,E F 与,N M 重合,,∴22128ABCD PEQF S S ==⨯四边形四边形∴矩形ABCD 的最小面积为2【点睛】本题考查了全等三角形的性质与判定,等边三角形的性质与判定,等腰三角形的性质与判定,勾股定理,旋转的性质,综合运用以上知识是解题的关键.3.(2024·陕西榆林·二模)(1)如图1,AB CD ∥,1,2AB CD ==,AD ,BC 交于点E ,若4=AD ,则AE =;(2)如图2,矩形ABCD 内接于O ,2,AB BC ==,点P 在 AD 上运动,求PBC 的面积的最大值;(3)为了提高居民的生活品质,市政部门计划把一块边长为120米的正方形荒地ABCD (如图3)改造成一个户外休闲区,计划在边AD ,BC 上分别取点P ,Q ,修建一条笔直的通道PQ ,要求2CQ AP =,过点B 作BE PQ ⊥于点E ,在点E 处修建一个应急处理中心,再修建三条笔直的道路BE CE DE ,,,并计划在CDE 内种植花卉,DEP 内修建老年活动区,BCE 内修建休息区,在四边形ABEP 内修建儿童游乐园.问种植花卉的CDE 的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由.∵四边形ABCD 是矩形,90ABC ∴∠=︒,AC ∴是O 的直径.在Rt ABC △中,tan BC BAC AB∠=60BPC BAC ∴∠=∠=︒过点O 作OE BC ⊥,垂足为E ,延长连接P B P C ₂,₂,此时P BC ₂的面积最大.理由:在 AD 上任意另取一点P。
中考数学题型三 填空压轴题

.
思路分析 根据△EFC 为直角三角形时,哪个角为直角的情况,再分别计算即可.
考法 类型 1 多解题
例4
高分技法
图形 变换时 的分类 情况. 1.图形 平移方 向不确 定时 ,可分 四种情 况: ①图形 向左平 移; ②图形 向右平 移;③图形 向上平 移;④ 图形 向下平 移. 2.图形 旋转方 向不确 定时 ,可分 两种情 况: ①图形 绕旋转 中心顺 时针旋 转;②图形 绕旋转 中心逆 时 针旋转. 3.图形 沿某条 直线折 叠,当这 条直线 的位置 不确定 时, 需结 合折叠 后的图 形的特 点分情 况讨论.
.
思路分析 先确定出能得到平行四边形的裁剪方法,再根据平行四边形的面积计算即可.
考法 类型1 多解题
例4
高分技法
[2018 合肥瑶海区一模]如图,矩形纸片 ABCD 中,已知 AD=8,AB=6,点 E 是边 BC 上的点,以 AE
为折痕折叠纸片,使点 B 落在点 F 处,连接 FC,当△EFC 为直角三角形时,BE 的长为
考法 类型 2 多结论问题
例6
高分技法
2.几何 类多结 论问题
[2018 广东广州]如图,CE 是▱ ABCD 的边 AB 的垂直平分线,垂足为点 O,CE 与 DA 的延长线交
于点 E.连接 AC,BE,DO,DO 与 AC 交于点 F,则下列结论:①四边形 ACBE 是菱形;②∠ACD=∠BAE;③
第二部分 中考题型过关
题型三 填空压轴题
考法
类型1 多解题 类型2 多结论问题
考法 类型1 多解题
例1
高分技法
1.点、线的位置不确定
[2018 江西]在正方形 ABCD 中,AB=6,连接 AC,BD,P 是正方形边上或对角线上一点,若 PD=2AP,
2023年中考数学综合模拟试题四(含答案)

2023年中考数学综合模拟试题四一、选择题(每题3分,共30分) 1、-2 023的相反数等于( ) A .2 023 B .-2 023C. 12023D .-120232、下列图形中,既可以看作是轴对称图形,又可以看作是中心对称图形的为( )3、下列运算正确的是( )A .(-m 2n)3=-m 6n 3B .m 5-m 3=m 2C .(m +2)2=m 2+4D .(12m 4-3m)÷3m=4m 34、由一些大小相同的小正方体搭成的几何体的主视图和俯视图,如图所示,则搭成该几何体的小正方体最多是( )个. A.4 B.5 C.6 D.75、关于x 的一元二次方程(a +2)x 2-3x +1=0有实数根,则a 的取值范围是( )A .a <14且a≠-2B .a≤14C .a≤14且a≠-2D .a <146、我国古代某数学著作中有“多人共车”问题:“今有三人共车,二车空;二人共车,九人步.问:人与车各几何?”其大意如下:有若干人要坐车,如果每3人坐一辆车,那么有2辆空车;如果每2人坐一辆车,那么有9人需要步行,问人与车各多少?设共有x 人,y 辆车,则可列方程组为( )A.{3(y −2)=x 2y −9=x B.{3(y +2)=x 2y +9=x C.{3(y −2)=x 2y +9=x D.{3(y +2)=x2y −9=x7、如图,D ,E ,F 分别是△ABC 各边中点,则以下说法错误的是( ) A .△BDE 和△DCF 的面积相等 B .四边形AEDF 是平行四边形 C .若AB =BC ,则四边形AEDF 是菱形D .若∠A=90°,则四边形AEDF 是矩形 ( 第7题图)8、关于x 的不等式组{x −m <0,3x −1>2(x −1)无解,那么m 的取值范围为( )A. m ≤-1B.m<-1C.-1<m ≤0D.-1≤m<09、如图所示,已知点A,B 分别在反比例函数y= 1x (x>0), y=- 4x (x>0))的图象上,且OA ⊥OB,则OBOA 的值为( ) A.√2 B.4 C.√3 D.2( 第9题图)10、如图所示,△ABC 是等腰直角三角形,∠A=90°,BC=4,点P 是 △ABC 边上一动点,沿B →A →C 的路径移动,过点P 作PD ⊥BC 于点D,设 BD=x,△BDP 的面积为y,则下列能大致反映y 与x 函数关系图象的是( )二、填空题(每题3分,共24分)11、我国某探测器距离地球约3.2亿千米.数据3.2亿千米用科学记数法可以表示为 km.12、一组数据5,2,x,6,4的平均数是4,这组数据的方差_____.13、动物学家通过大量的调查,估计某种动物活到20岁的概率为0.8,活到25岁的概率为0.5,据此若设刚出生的这种动物共有a 只,则现年20岁的这种动物活到25岁的概率是 ________.14、如图所示,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于12MN的长为半径作弧,两弧相交于点P;③作射线AP,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD的周长为. (第14题图)15、某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到敬老院慰问老人.如果分给每位老人 4盒牛奶,那么剩下28盒牛奶;如果分给每位老人 5盒牛奶,那么最后一位老人分得的牛奶不足4盒,但至少1盒.则这个敬老院的老人最少有__________人.16、如图,在矩形ABCD中,AB=3,AD=4,E,F分别是边BC,CD上一点,EF⊥AE,将△ECF沿EF翻折得△EC′F,连接AC′,当BE=________时,△AEC′是以AE 为腰的等腰三角形.(第16题图)(第17题图)(第18题图)17、如图,已知正方形ABCD的边长为6,点F是正方形内一点,连接CF,DF,且∠ADF=∠DCF,点E是AD边上一动点,连接EB,EF,则EB+EF长度的最小值为 ________________.18、如图,△ABC是边长为2的等边三角形,AD是BC边上的高,CE是AB边上的高.将△ADC绕点D顺时针旋转得到,其中点A的对应点为点,点C的对应点为点.在旋转过程中,当点落在直线EC上时,的长为______.三、解答题(共9小题,计66分)19、(5分)(12)-1-√−83+|√3-2|+2sin 60°.A DC''A'C'A'A C'20、(5分)先化简,再求值:(3a+1-a+1)÷a 2−4a 2+2a+1,其中a 从-1,2,3中取一个你认为合适的数代入求值.21、(6分)将正面分别写着数字1,2,3的三张卡片(注:这三张卡片的形状、大小、质地、颜色等其他方面完全相同,若背面朝上放在桌面上,这三张卡片看上去无任何差别)洗匀后,背面朝上放在桌面上,甲从中随机抽取一张卡片,记该卡片上的数字为m ,然后放回洗匀,背面朝上放在桌面上,再由乙从中随机抽取一张卡片,记该卡片上的数字为n ,组成一数对(m ,n). (1)请写出(m ,n)所有可能出现的结果;(2)甲、乙两人玩游戏,规则如下:按上述要求,两人各抽一次卡片,卡片上数字之和为奇数则甲赢,数字之和为偶数则乙赢.你认为这个游戏公平吗?请说明理由.22、(6分)如图所示,某测量小组为了测量山BC 的高度,在地面A 处测得山顶B 的仰角为45°,然后沿着坡度为1∶3的坡面AD 走了200 m 达到D 处,此时在D 处测得山顶B 的仰角为60°,求山BC 的高度.(结果保留根号)23、(6分))某校从全体学生中随机抽取部分学生,调查他们平均每周的劳动时间t(单位:h),按劳动时间分为四组:A 组“t<5”,B 组“5≤t<7”,C 组“7≤t<9”,D 组“t ≥9”.将收集的数据整理后,绘制成如图所示的两幅尚不完整的统计图.根据以上信息,解答下列问题:(1)这次抽样调查的样本容量是,C组所在扇形的圆心角的大小是;(2)将条形统计图补充完整;(3)该校共有1 500名学生,请估计该校平均每周劳动时间不少于7 h的学生人数.24、(8分)某乡镇对河道进行整治,由甲乙两工程队合做 20天可完成.已知甲工程队单独整治需60天完成.(1)乙工程队单独完成河道整治需多少天?(2)若甲乙两工程队合做a天后,再由甲工程队单独做天(用含a 的代数式表示)可完成河道整治任务;(3)如果甲工程队每天施工费为5 000元,乙工程队每天施工费为1.5万元,先由甲乙两工程队合做,剩余工程由甲工程队单独完成,要使支付两工程队费用最少,并且确保河道在40天内(含 40天)整治完毕,问需支付两工程队费用最少多少万元?25、(8分)如图所示,在Rt△ABC中,∠ABC=90°,以AB 为直径作⊙O,点D 为⊙O上一点,且CD=CB,连接DO并延长交CB的延长线于点E.(1)判断直线CD与⊙O的位置关系,并说明理由;(2)若BE=2,DE=4,求圆的半径及AC的长.26.(10分)已知在△ABC中,O为BC边的中点,连接AO,将△AOC绕点O顺时针方向旋转(旋转角为钝角),得到△EOF,连接AE,CF.(1)如图1,当∠BAC=90°且AB=AC时,则AE与CF满足的数量关系是;(2)如图2,当∠BAC=90°且AB≠AC时,(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.(3)如图3,延长AO到点D,使OD=OA,连接DE,当AO=CF=5,BC =6时,求DE的长.27.(12分)已知,抛物线y=x2+bx+c与x轴交点为A(﹣1,0)和点B,与y轴交点为C(0,﹣3),直线L:y=kx﹣1与抛物线的交点为点A和点D.(1)求抛物线和直线L的解析式;(2)如图,点M为抛物线上一动点(不与A、D重合),当点M在直线L下方时,过点M作MN∥x轴交L于点N,求MN的最大值;(3)点M为抛物线上一动点(不与A、D重合),M'为直线AD上一动点,是否存在点M,使得以C、D、M、M′为顶点的四边形是平行四边形?如果存在,请直接写出点M的坐标,如果不存在,请说明理由.参考答案二.填空题第11题:3.2×108 第12题:2 第13题: 58第14题:15 第15题:30 第16题:78 或 43第17题:3√13−3 第18题:√11−√32或√11+√32三.解答题第19题:原式=8第20题:化简,可得,原式=−a −1,因为a ≠−1且a ≠2,所以,当a =3时,原式=−4第21题:(1) 所有可能出现的结果为:(1,1) 、(1,2) 、(1,3) 、(2,1) 、(2,2) 、(2,3) 、(3,1) 、(3,2) 、(3,3) 。
中考复习特殊四边形综合题

特殊四边形综合题1.如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;(3)在平移变换过程中,设y=S,BP=x(0≤x≤2),求y与x之间的函数关系式,并求出△OPBy的最大值.2.已知在矩形ABCD中,∠ADC的平分线DE与BC边所在的直线交于点E,点P是线段DE 上一定点(其中EP<PD)(1)如图1,若点F在CD边上(不与D重合),将∠DPF绕点P逆时针旋转90°后,角的两边PD、PF分别交射线DA于点H、G.①求证:PG=PF;②探究:DF、DG、DP之间有怎样的数量关系,并证明你的结论.(2)拓展:如图2,若点F在CD的延长线上(不与D重合),过点P作PG⊥PF,交射线DA 于点G,你认为(1)中DF、DG、DP之间的数量关系是否仍然成立?若成立,给出证明;若不成立,请写出它们所满足的数量关系式,并说明理由.3.已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与边BC、DC的延长线交于点E、F,连接EF.设CE=a,CF=b.(1)如图1,当∠EAF被对角线AC平分时,求a、b的值;(2)当△AEF是直角三角形时,求a、b的值;(3)如图3,探索∠EAF绕点A旋转的过程中a、b满足的关系式,并说明理由.4.如图,正方形ABCD的对角线相交于点O,点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于点E,F,且∠MAN始终保持45°不变.(1)求证:=;(2)求证:AF⊥FM;(3)请探索:在∠MAN的旋转过程中,当∠BAM等于多少度时,∠FMN=∠BAM?写出你的探索结论,并加以证明.5.如图,矩形ABCD中,点E为BC上一点,F为DE的中点,且∠BFC=90°.(1)当E为BC中点时,求证:△BCF≌△DEC;(2)当BE=2EC时,求的值;(3)设CE=1,BE=n,作点C关于DE的对称点C′,连结FC′,AF,若点C′到AF的距离是,求n的值.6.如图1,在菱形ABCD中,AB=6,tan∠ABC=2,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CF.(1)求证:BE=DF;(2)当t=秒时,DF的长度有最小值,最小值等于;(3)如图2,连接BD、EF、BD交EC、EF于点P、Q,当t为何值时,△EPQ是直角三角形?(4)如图3,将线段CD绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CG.在点E 的运动过程中,当它的对应点F位于直线AD上方时,直接写出点F到直线AD的距离y关于时间t的函数表达式.7.已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.8.如图①,AD为等腰直角△ABC的高,点A和点C分别在正方形DEFG的边DG和DE上,连接BG,AE.(1)求证:BG=AE;(2)将正方形DEFG绕点D旋转,当线段EG经过点A时,(如图②所示)①求证:BG⊥GE;②设DG与AB交于点M,若AG:AE=3:4,求的值.9.如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC 的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.(1)请直接写出线段AF,AE的数量关系;(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.10.如图(1)矩形ABCD中,AB=2,BC=5,BP=1,∠MPN=90°将∠MPN绕点P从PB处开始按顺时针方向旋转,PM交AB(或AD)于点E,PN交边AD(或CD)于点F,当PN旋转至PC处时,∠MPN的旋转随即停止(1)特殊情形:如图(2),发现当PM过点A时,PN也恰好过点D,此时,△ABP∽△PCD(填:“≌”或“~”(2)类比探究:如图(3)在旋转过程中,的值是否为定值?若是,请求出该定值;若不是,请说明理由;(3)拓展延伸:设AE=t,△EPF面积为S,试确定S关于t的函数关系式;当S=4.2时,求所对应的t的值.11.已知:点P是平行四边形ABCD对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BP作垂线,垂足分别为点E、F,点O为AC的中点.(1)当点P与点O重合时如图1,易证OE=OF(不需证明)(2)直线BP绕点B逆时针方向旋转,当∠OFE=30°时,如图2、图3的位置,猜想线段CF、AE、OE之间有怎样的数量关系?请写出你对图2、图3的猜想,并选择一种情况给予证明.12.如图,在正方形ABCD中,点E为对角线AC上的一点,连接BE,DE.(1)如图1,求证:△BCE≌△DCE;(2)如图2,延长BE交直线CD于点F,G在直线AB上,且FG=FB.①求证:DE⊥FG;②已知正方形ABCD的边长为2,若点E在对角线AC上移动,当△BFG为等边三角形时,求线段DE的长(直接写出结果,不必写出解答过程).13.如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.①求证:△AGE≌△AFE;②若BE=2,DF=3,求AH的长.(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.14.如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.(1)求证:四边形EFDG是菱形;(2)探究线段EG、GF、AF之间的数量关系,并说明理由;(3)若AG=6,EG=2,求BE的长.15.如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;(2)当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.①求证:BD⊥CF;②当AB=2,AD=3时,求线段DH的长.16.如图1,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD、BC分别交于点E、F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G.(1)求证:①△DOK≌△BOG;②AB+AK=BG;(2)若KD=KG,BC=4﹣.①求KD的长度;②如图2,点P是线段KD上的动点(不与点D、K重合),PM∥DG交KG于点M,PN∥KG=时,求m的值.交DG于点N,设PD=m,当S△PMN17.已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB 的延长线上,连接EA、EC.(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;(2)若点P在线段AB上.①如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由;②如图3,设AB=a,BP=b,当EP平分∠AEC时,求a:b及∠AEC的度数.18.在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.(1)当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′.(2)当四边形ABCD为平行四边形时,设AC=kBD,如图2.①猜想此时△AOC′与△BOD′有何关系,证明你的猜想;②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.19.已知菱形ABCD的边长为1,∠ADC=60°,等边△AEF两边分别交DC、CB于点E、F.(1)特殊发现:如图1,若点E、F分别是边DC、CB的中点,求证:菱形ABCD对角线AC、BD的交点O即为等边△AEF的外心;(2)若点E、F始终分别在边DC、CB上移动,记等边△AEF的外心为P.①猜想验证:如图2,猜想△AEF的外心P落在哪一直线上,并加以证明;②拓展运用:如图3,当E、F分别是边DC、CB的中点时,过点P任作一直线,分别交DA边于点M,BC边于点G,DC边的延长线于点N,请你直接写出的值.20.在正方形ABCD中,BD是一条对角线,点E在直线CD上(与点C,D不重合),连接AE,平移△ADE,使点D移动到点C,得到△BCF,过点F作FG⊥BD于点G,连接AG,EG.(1)问题猜想:如图1,若点E在线段CD上,试猜想AG与EG的数量关系是,位置关系是;(2)类比探究:如图2,若点E在线段CD的延长线上,其余条件不变,小明猜想(1)中的结论仍然成立,请你给出证明;(3)解决问题:若点E在线段DC的延长线上,且∠AGF=120°,正方形ABCD的边长为2,请在备用图中画出图形,并直接写出DE的长度.21.如图,正方形ABCD边长为6,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.(1)求证:∠HEA=∠CGF;(2)当AH=DG=2时,求证:菱形EFGH为正方形;(3)设AH=x,DG=2x,△FCG的面积为y,试求y的最大值.22.如图1,四边形ABCD中,AD∥BC,AB⊥BC,点E在边AB上,∠DEC=90°,且DE=EC.(1)求证:△ADE≌△BEC;(2)若AD=a,AE=b,DE=c,请用图1证明勾股定理:a2+b2=c2;(3)线段AB上另有一点F(不与点E重合),且DF⊥CF(如图2),若AD=2,BC=4,求EF 的长.23.如图1,正方形ABCD中,AC是对角线,等腰Rt△CMN中,∠CMN=90°,CM=MN,点M 在CD边上,连接AN,点E是AN的中点,连接BE.(1)若CM=2,AB=6,求AE的值;(2)求证:2BE=AC+CN;(3)当等腰Rt△CMN的点M落在正方形ABCD的BC边上,如图2,连接AN,点E是AN的中点,连接BE,延长NM交AC于点F.请探究线段BE、AC、CN的数量关系,并证明你的结论.24.正方形ABCD的边长为3,点E,F分别在射线DC,DA上运动,且DE=DF.连接BF,作EH⊥BF所在直线于点H,连接CH.(1)如图1,若点E是DC的中点,CH与AB之间的数量关系是;(2)如图2,当点E在DC边上且不是DC的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由;(3)如图3,当点E,F分别在射线DC,DA上运动时,连接DH,过点D作直线DH的垂线,交直线BF于点K,连接CK,请直接写出线段CK长的最大值.25.问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足关系时,仍有EF=BE+FD.【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:=1.41,=1.73)26.如图1,正方形OABC与正方形ODEF放置在直线l上,连结AD、CF,此时AD=CF.AD ⊥CF成立.(1)正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?若成立,请证明;若不成立,请说明理由.(2)正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,求证:AD⊥CF.(3)在(2)小题的条件下,AD与OC的交点为G,当AO=3,OD=时,求线段CG的长.27.如图,在正方形ABCD与等腰直角三角形BEF中,∠BEF=90°,BE=EF,连接PF,点P是FD的中点,连接PE、PC.(1)如图1,当点E在CB边上时,求证:PE=CE;(2)如图2,当点E在CB的延长线上时,线段PC、CE有怎样的数量关系,写出你的猜想,并给与证明.28.已知:l1∥l2∥l3∥l4,平行线l1与l2、l2与l3、l3与l4之间的距离分别为d1、d2、d3,且d1=d3=1,d2=2.我们把四个顶点分别在l1、l2、l3、l4这四条平行线上的四边形称为“格线四边形”.(1)如图1,正方形ABCD为“格线四边形”,则正方形ABCD的边长为.(2)矩形ABCD为“格线四边形”,其长:宽=2:1,求矩形ABCD的宽.(3)如图1,EG过正方形ABCD的顶点D且垂直l1于点E,分别交l2,l4于点F,G.将∠AEG 绕点A顺时针旋转30°得到∠AE′D′(如图2),点D′在直线l3上,以AD′为边在E′D′左侧作菱形AB′C′D′,使B′,C′分别在直线l2,l4上,求菱形AB′C′D′的边长.29.正方形ABCD边长为4cm,点E,M分别是线段AC,CD上的动点,连接DE并延长,交正方形ABCD的边于点F,过点M作MN⊥DF于H,交AD于N.(1)如图1,若点M与点C重合,求证:DF=MN;(2)如图2,若点M从点C出发,以1cm/s的速度沿CD向点D运动,点E同时从点A出发,以cm/s速度沿AC向点C运动,运动时间为t(t>0);①当点F是边AB的中点时,求t的值;②连结FM,FN,当t为何值时△MNF是等腰三角形(直接写出t值).30.已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边长分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.(1)如图①,当∠MAN点A旋转到BM=DN时,请你直接写出AH与AB的数量关系:;(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.特殊四边形综合题答案1.如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;(3)在平移变换过程中,设y=S,BP=x(0≤x≤2),求y与x之间的函数关系式,并求出△OPBy的最大值.解:(1)四边形APQD为平行四边形;(2)OA=OP,OA⊥OP,理由如下:∵四边形ABCD是正方形,∴AB=BC=PQ,∠ABO=∠OBQ=45°,∵OQ⊥BD,∴∠PQO=45°,∴∠ABO=∠OBQ=∠PQO=45°,∴OB=OQ,在△AOB和△OPQ中,∴△AOB≌△POQ(SAS),∴OA=OP,∠AOB=∠POQ,∴∠AOP=∠BOQ=90°,∴OA⊥OP;(3)如图,过O作OE⊥BC于E.①如图1,当P点在B点右侧时,则BQ=x+2,OE=,∴y=וx,即y=(x+1)2﹣,又∵0≤x≤2,∴当x=2时,y有最大值为2;②如图2,当P点在B点左侧时,则BQ=2﹣x,OE=,∴y=וx,即y=﹣(x﹣1)2+,又∵0≤x≤2,∴当x=1时,y有最大值为;综上所述,∴当x=2时,y有最大值为2;2.已知在矩形ABCD中,∠ADC的平分线DE与BC边所在的直线交于点E,点P是线段DE 上一定点(其中EP<PD)(1)如图1,若点F在CD边上(不与D重合),将∠DPF绕点P逆时针旋转90°后,角的两边PD、PF分别交射线DA于点H、G.①求证:PG=PF;②探究:DF、DG、DP之间有怎样的数量关系,并证明你的结论.(2)拓展:如图2,若点F在CD的延长线上(不与D重合),过点P作PG⊥PF,交射线DA 于点G,你认为(1)中DF、DG、DP之间的数量关系是否仍然成立?若成立,给出证明;若不成立,请写出它们所满足的数量关系式,并说明理由.【分析】(1)①若证PG=PF,可证△HPG≌△DPF,已知∠DPH=∠HPG,由旋转可知∠GPF=∠HPD=90°及DE平分∠ADC得△HPD为等腰直角三角形,即∠DHP=∠PDF=45°、PD=PH,即可得证;②由△HPD为等腰直角三角形,△HPG≌△DPF知HD=DP,HG=DF,根据DG+DF=DG+GH=DH 即可得;(2)过点P作PH⊥PD交射线DA于点H,先证△HPD为等腰直角三角形可得PH=PD,HD=DP,再证△HPG≌△DPF可得HG=DF,根据DH=DG﹣HG=DG﹣DF可得DG﹣DF=DP.解:(1)①∵∠GPF=∠HPD=90°,∠ADC=90°,∵DE平分∠ADC,∴∠PDF=∠ADP=45°,∴△HPD为等腰直角三角形,∴∠DHP=∠PDF=45°,在△HPG和△DPF中,∵,∴△HPG≌△DPF(ASA),∴PG=PF;②结论:DG+DF=DP,由①知,△HPD为等腰直角三角形,△HPG≌△DPF,∴HD=DP,HG=DF,∴HD=HG+DG=DF+DG,∴DG+DF=DP;(2)不成立,数量关系式应为:DG﹣DF=DP,如图,过点P作PH⊥PD交射线DA于点H,∵PF⊥PG,∴∠GPF=∠HPD=90°,∴∠GPH=∠FPD,∵DE平分∠ADC,且在矩形ABCD中,∠ADC=90°,∴∠HDP=∠EDC=45°,得到△HPD为等腰直角三角形,∴∠DHP=∠EDC=45°,且PH=PD,HD=DP,∴∠GHP=∠FDP=180°﹣45°=135°,在△HPG和△DPF中,∵∴HG=DF,∴DH=DG﹣HG=DG﹣DF,∴DG﹣DF=DP.3.已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与边BC、DC的延长线交于点E、F,连接EF.设CE=a,CF=b.(1)如图1,当∠EAF被对角线AC平分时,求a、b的值;(2)当△AEF是直角三角形时,求a、b的值;(3)如图3,探索∠EAF绕点A旋转的过程中a、b满足的关系式,并说明理由.【分析】(1)当∠EAF被对角线AC平分时,易证△ACF≌△ACE,因此CF=CE,即a=b.(2)分两种情况进行计算,①先用勾股定理得出CF2=8(CE+4)①,再用相似三角形得出4CF=CE (CE+4)②,两式联立解方程组即可;(3)先判断出∠AFD=∠CEF,再判断出AF=EF,从而得到△ADF≌△FCE即可.解:(1)∵四边形ABCD是正方形,∴∠BCF=∠DCE=90°∵AC是正方形ABCD的对角线,∴∠ACB=∠ACD=45°,∴∠ACF=∠ACE,∵∠EAF被对角线AC平分,∴∠CAF=∠CAE,在△ACF和△ACE中,,∴△ACF≌△ACE,∴CE=CE,∵CE=a,CF=b,∴a=b,∵△ACF≌△ACE,∴∠AEF=∠AFE,∵∠EAF=45°,∴∠AEF=∠AFE=67.5°,∵CE=CF,∠ECF=90°,∠AEC=∠AFC=22.5°,∵∠CAF=∠CAE=22.5°,∴∠CAE=∠CEA,∴CE=AC=4,即:a=b=4;(2)当△AEF是直角三角形时,①当∠AFE=90°时,∴∠AFD+∠CFE=90°,∵∠CEF+∠CFE=90°,∴∠AFD=∠CEF∵∠AFE=90°,∠EAF=45°,∴∠AEF=45°=∠EAF∴AF=EF,在△ADF和△FCE中∴△ADF≌△FCE,∴FC=AD=4,CE=DF=CD+FC=8,∴a=8,b=4②当∠AEF=90°时,同①的方法得,CF=4,CE=8,∴a=4,b=8.(3)ab=32,理由:如图,∵AB∥CD∴∠BAG=∠AFC,∵∠BAC=45°,∴∠BAG+∠CAF=45°,∴∠AFC+∠CAF=45°,∵∠AFC+∠AEC=180°﹣(∠CFE+∠CEF)﹣∠EAF=180°﹣90°﹣45°=45°,∴∠CAF=∠AEC,∵∠ACF=∠ACE=135°,∴△ACF∽△ECA,∴,∴EC×CF=AC2=2AB2=32∴ab=32.4.(2016•淄博)如图,正方形ABCD的对角线相交于点O,点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于点E,F,且∠MAN始终保持45°不变.(1)求证:=;(2)求证:AF⊥FM;(3)请探索:在∠MAN的旋转过程中,当∠BAM等于多少度时,∠FMN=∠BAM?写出你的探索结论,并加以证明.【分析】(1)先证明A、B、M、F四点共圆,根据圆内接四边形对角互补即可证明∠AFM=90°,根据等腰直角三角形性质即可解决问题.(2)由(1)的结论即可证明.(3)由:A、B、M、F四点共圆,推出∠BAM=∠EFM,因为∠BAM=∠FMN,所以∠EFM=∠FMN,推出MN∥BD,得到=,推出BM=DN,再证明△ABM≌△ADN即可解决问题.(1)证明:∵四边形ABCD是正方形,∴∠ABD=∠CBD=45°,∠ABC=90°,∵∠MAN=45°,∴∠MAF=∠MBE,∴A、B、M、F四点共圆,∴∠ABM+∠AFM=180°,∴∠AFM=90°,∴∠FAM=∠FMA=45°,∴AM=AF,∴=.(2)由(1)可知∠AFM=90°,∴AF⊥FM.(3)结论:∠BAM=22.5时,∠FMN=∠BAM理由:∵A、B、M、F四点共圆,∴∠BAM=∠EFM,∵∠BAM=∠FMN,∴∠EFM=∠FMN,∴MN∥BD,∴=,∵CB=DC,∴CM=CN,∴MB=DN,在△ABM和△ADN中,,∴△ABM≌△ADN,∴∠BAM=∠DAN,∵∠MAN=45°,∴∠BAM+∠DAN=45°,∴∠BAM=22.5°.5.(2016•丽水)如图,矩形ABCD中,点E为BC上一点,F为DE的中点,且∠BFC=90°.(1)当E为BC中点时,求证:△BCF≌△DEC;(2)当BE=2EC时,求的值;(3)设CE=1,BE=n,作点C关于DE的对称点C′,连结FC′,AF,若点C′到AF的距离是,求n的值.【分析】(1)由矩形和直角三角形斜边上的中线性质得出CF=DE=EF,由等腰三角形的性质得出∠FEC=∠FCE,证出CF=CE,由ASA证明△BCF≌△DEC即可;(2)设CE=a,则BE=2a,BC=3a,证明△BCF∽△DEC,得出对应边成比例=,得出ED2=6a2,由勾股定理得出DC=a,即可得出结果;(3)过C′作C′H⊥AF于点H,连接CC′交EF于M,由直角三角形斜边上的中线性质得出∠FEC=∠FCE,证出∠ADF=∠BCF,由SAS证明△ADF≌△BCF,得出∠AFD=∠BFC=90°,证出四边形C′MFH是矩形,得出FM=C′H=,设EM=x,则FC=FE=x+,由勾股定理得出方程,解方程求出EM=,FC=FE=+;由(2)得:,把CE=1,BE=n代入计算即可得出n的值.(1)证明;∵在矩形ABCD中,∠DCE=90°,F是斜边DE的中点,∴CF=DE=EF,∴∠FEC=∠FCE,∵∠BFC=90°,E为BC中点,∴EF=EC,∴CF=CE,在△BCF和△DEC中,,∴△BCF≌△DEC(ASA);(2)解:设CE=a,由BE=2CE,得:BE=2a,BC=3a,∵CF是Rt△DCE斜边上的中线,∴CF=DE,∵∠FEC=∠FCE,∠BFC=∠DCE=90°,∴△BCF∽△DEC,∴=,即:=,解得:ED2=6a2由勾股定理得:2222=-=-=,65DC DE EC a a a∴==;(3)解:过C′作C′H⊥AF于点H,连接CC′交EF于M,如图所示:∵CF是Rt△DCE斜边上的中线,∴FC=FE=FD,∴∠FEC=∠FCE,∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∴∠ADF=∠CEF,∴∠ADF=∠BCF,在△ADF和△BCF中,,∴△ADF≌△BCF(SAS),∴∠AFD=∠BFC=90°,∵CH⊥AF,C′C⊥EF,∠HFE=∠C′HF=∠C′MF=90°,∴四边形C′MFH是矩形,∴FM=C′H=,设EM=x,则FC=FE=x+,在Rt△EMC和Rt△FMC中,由勾股定理得:CE2﹣EM2=CF2﹣FM2,∴12﹣x2=(x+)2﹣()2,解得:x=,或x=﹣(舍去),∴EM=,FC=FE=+;由(2)得:,把CE=1,BE=n代入上式计算得:CF=,∴,解得:n=4.6.如图1,在菱形ABCD中,AB=6,tan∠ABC=2,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CF.(1)求证:BE=DF;(2)当t=6+6秒时,DF的长度有最小值,最小值等于12;(3)如图2,连接BD、EF、BD交EC、EF于点P、Q,当t为何值时,△EPQ是直角三角形?(4)如图3,将线段CD绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CG.在点E 的运动过程中,当它的对应点F位于直线AD上方时,直接写出点F到直线AD的距离y关于时间t的函数表达式.【分析】(1)由∠ECF=∠BCD得∠DCF=∠BCE,结合DC=BC、CE=CF证△DCF≌△BCE即可得;(2)当点E运动至点E′时,由DF=BE′知此时DF最小,求得BE′、AE′即可得答案;(3)①∠EQP=90°时,由∠ECF=∠BCD、BC=DC、EC=FC得∠BCP=∠EQP=90°,根据AB=CD=6,tan∠ABC=tan∠ADC=2即可求得DE;②∠EPQ=90°时,由菱形ABCD的对角线AC⊥BD知EC与AC重合,可得DE=6;(4)连接GF分别角直线AD、BC于点M、N,过点F作FH⊥AD于点H,证△DCE≌△GCF 可得∠3=∠4=∠1=∠2,即GF∥CD,从而知四边形CDMN是平行四边形,由平行四边形得MN=CD=6;再由∠CGN=∠DCN=∠CNG知CN=CG=CD=6,根据tan∠ABC=tan∠CGN=2可得GM=6+12,由GF=DE=t得FM=t﹣6﹣12,利用tan∠FMH=tan∠ABC=2即可得FH.解:(1)∵∠ECF=∠BCD,即∠BCE+∠DCE=∠DCF+∠DCE,∴∠DCF=∠BCE,∵四边形ABCD是菱形,∴DC=BC,在△DCF和△BCE中,∵,∴△DCF≌△BCE(SAS),∴DF=BE;(2)如图1,当点E运动至点E′时,DF=BE′,此时DF最小,在Rt△ABE′中,AB=6,tan∠ABC=tan∠BAE′=2,∴设AE′=x,则BE′=2x,∴AB=x=6,则AE′=6∴DE′=6+6,DF=BE′=12,故答案为:6+6,12;(3)∵CE=CF,∴∠CEQ<90°,①当∠EQP=90°时,如图2①,∵∠ECF=∠BCD,BC=DC,EC=FC,∴∠CBD=∠CEF,∵∠BPC=∠EPQ,∴∠BCP=∠EQP=90°,∵AB=CD=6,tan∠ABC=tan∠ADC=2,∴DE=6,∴t=6秒;②当∠EPQ=90°时,如图2②,∵菱形ABCD的对角线AC⊥BD,∴EC与AC重合,∴DE=6,∴t=6秒;(4)y=t﹣12﹣,如图3,连接GF分别角直线AD、BC于点M、N,过点F作FH⊥AD于点H,由(1)知∠1=∠2,又∵∠1+∠DCE=∠2+∠GCF,∴∠DCE=∠GCF,在△DCE和△GCF中,∵,∴△DCE≌△GCF(SAS),∴∠3=∠4,∵∠1=∠3,∠1=∠2,∴∠2=∠4,∴GF∥CD,又∵AH∥BN,∴四边形CDMN是平行四边形,∴MN=CD=6,∵∠BCD=∠DCG,∴∠CGN=∠DCN=∠CNG,∴CN=CG=CD=6,∵tan∠ABC=tan∠CGN=2,∴GN=12,∴GM=6+12,∵GF=DE=t,∴FM=t﹣6﹣12,∵tan∠FMH=tan∠ABC=2,∴FH=(t﹣6﹣12),即y=t﹣12﹣.7.已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.【分析】(1)结论AE=EF=AF.只要证明AE=AF即可证明△AEF是等边三角形.(2)欲证明BE=CF,只要证明△BAE≌△CAF即可.(3)过点A作AG⊥BC于点G,过点F作FH⊥EC于点H,根据FH=CF•cos30°,因为CF=BE,只要求出BE即可解决问题.(1)解:结论AE=EF=AF.理由:如图1中,连接AC,∵四边形ABCD是菱形,∠B=60°,∴AB=BC=CD=AD,∠B=∠D=60°,∴△ABC,△ADC是等边三角形,∴∠BAC=∠DAC=60°∵BE=EC,∴∠BAE=∠CAE=30°,AE⊥BC,∵∠EAF=60°,∴∠CAF=∠DAF=30°,∴AF⊥CD,∴AE=AF(菱形的高相等),∴△AEF是等边三角形,∴AE=EF=AF.(2)证明:如图2中,∵∠BAC=∠EAF=60°,∴∠BAE=∠CAE,在△BAE和△CAF中,,∴△BAE≌△CAF,∴BE=CF.(3)解:过点A作AG⊥BC于点G,过点F作FH⊥EC于点H,∵∠EAB=15°,∠ABC=60°,∴∠AEB=45°,在RT△AGB中,∵∠ABC=60°AB=4,∴BG=2,AG=2,在RT△AEG中,∵∠AEG=∠EAG=45°,∴AG=GE=2,∴EB=EG﹣BG=2﹣2,∵△AEB≌△AFC,∴AE=AF,EB=CF=2﹣2,在RT△CHF中,∵∠HCF=180°﹣∠BCD=60°,CF=2﹣2,∴FH=CF•sin60°=(2﹣2)•=3﹣.∴点F到BC的距离为3﹣.8.如图①,AD为等腰直角△ABC的高,点A和点C分别在正方形DEFG的边DG和DE上,连接BG,AE.(1)求证:BG=AE;(2)将正方形DEFG绕点D旋转,当线段EG经过点A时,(如图②所示)①求证:BG⊥GE;②设DG与AB交于点M,若AG:AE=3:4,求的值.【分析】(1)如图①,根据等腰直角三角形的性质得AD=BD,再根据正方形的性质得∠GDE=90°,DG=DE,则可根据“SAS“判断△BDG≌△ADE,于是得到BG=AE;(2)①如图②,先判断△DEG为等腰直角三角形得到∠1=∠2=45°,再由△BDG≌△ADE得到∠3=∠2=45°,则可得∠BGE=90°,所以BG⊥GE;②设AG=3x,则AE=4x,即GE=7x,利用等腰直角三角形的性质得DG=GE=x,由(1)的结论得BG=AE=4x,则根据勾股定理得AB=5x,接着由△ABD为等腰直角三角形得到∠4=45°,BD=AB=x,然后证明△DBM∽△DGB,则利用相似比可计算出DM=x,所以GM=x,于是可计算出的值.(1)证明:如图①,∵AD为等腰直角△ABC的高,∴AD=BD,∵四边形DEFG为正方形,∴∠GDE=90°,DG=DE,在△BDG和△ADE中,∴△BDG≌△ADE,∴BG=AE;(2)①证明:如图②,∵四边形DEFG为正方形,∴△DEG为等腰直角三角形,∴∠1=∠2=45°,由(1)得△BDG≌△ADE,∴∠3=∠2=45°,∴∠1+∠3=45°+45°=90°,即∠BGE=90°,∴BG⊥GE;②解:设AG=3x ,则AE=4x ,即GE=7x ,∴DG=GE=x ,∵△BDG ≌△ADE ,∴BG=AE=4x ,在Rt △BGA 中, 2222(4)(3)5AB BG AG x x x =+=+=,∵△ABD 为等腰直角三角形,∴∠4=45°,BD=AB=x ,∴∠3=∠4,而∠BDM=∠GDB ,∴△DBM ∽△DGB ,∴BD :DG=DM :BD ,即x :x=DM :x ,解得DM=x , ∴GM=DG ﹣DM=x ﹣x =x , ∴==.9.如图①,在△ABC 中,∠BAC=90°,AB=AC ,点E 在AC 上(且不与点A ,C 重合),在△ABC 的外部作△CED ,使∠CED=90°,DE=CE ,连接AD ,分别以AB ,AD 为邻边作平行四边形ABFD ,连接AF .(1)请直接写出线段AF ,AE 的数量关系 AF=AE ;(2)将△CED 绕点C 逆时针旋转,当点E 在线段BC 上时,如图②,连接AE ,请判断线段AF ,AE 的数量关系,并证明你的结论;(3)在图②的基础上,将△CED 绕点C 继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.【分析】(1)如图①中,结论:AF=AE,只要证明△AEF是等腰直角三角形即可.(2)如图②中,结论:AF=AE,连接EF,DF交BC于K,先证明△EKF≌△EDA再证明△AEF是等腰直角三角形即可.(3)如图③中,结论不变,AF=AE,连接EF,延长FD交AC于K,先证明△EDF≌△ECA,再证明△AEF是等腰直角三角形即可.解:(1)如图①中,结论:AF=AE.理由:∵四边形ABFD是平行四边形,∴AB=DF,∵AB=AC,∴AC=DF,∵DE=EC,∴AE=EF,∵∠DEC=∠AEF=90°,∴△AEF是等腰直角三角形,∴AF=AE.故答案为AF=AE.(2)如图②中,结论:AF=AE.理由:连接EF,DF交BC于K.∵四边形ABFD是平行四边形,∴AB∥DF,∴∠DKE=∠ABC=45°,∴EKF=180°﹣∠DKE=135°,EK=ED,∵∠ADE=180°﹣∠EDC=180°﹣45°=135°,∴∠EKF=∠ADE,∵∠DKC=∠C,∴DK=DC,∵DF=AB=AC,∴KF=AD,在△EKF和△EDA中,,∴△EKF≌△EDA,∴EF=EA,∠KEF=∠AED,∴∠FEA=∠BED=90°,∴△AEF是等腰直角三角形,∴AF=AE.(3)如图③中,结论不变,AF=AE.理由:连接EF,延长FD交AC于K.∵∠EDF=180°﹣∠KDC﹣∠EDC=135°﹣∠KDC,∠ACE=(90°﹣∠KDC)+∠DCE=135°﹣∠KDC,∴∠EDF=∠ACE,∵DF=AB,AB=AC,∴DF=AC在△EDF和△ECA中,,∴△EDF≌△ECA,∴EF=EA,∠FED=∠AEC,∴∠FEA=∠DEC=90°,∴△AEF是等腰直角三角形,∴AF=AE.10.如图(1)矩形ABCD中,AB=2,BC=5,BP=1,∠MPN=90°将∠MPN绕点P从PB处开始按顺时针方向旋转,PM交AB(或AD)于点E,PN交边AD(或CD)于点F,当PN旋转至PC处时,∠MPN的旋转随即停止(1)特殊情形:如图(2),发现当PM过点A时,PN也恰好过点D,此时,△ABP∽△PCD(填:“≌”或“~”(2)类比探究:如图(3)在旋转过程中,的值是否为定值?若是,请求出该定值;若不是,请说明理由;(3)拓展延伸:设AE=t,△EPF面积为S,试确定S关于t的函数关系式;当S=4.2时,求所对应的t的值.【分析】(1)根据矩形的性质找出∠B=∠C=90°,再通过角的计算得出∠BAP=∠CPD,由此即可得出△ABP∽△PCD;(2)过点F作FH⊥PC于点H,根据矩形的性质以及角的计算找出∠B=∠FHP=90°、∠BEP=∠HPE,由此即可得出△BEP∽△HPE,根据相似三角形的性质,找出边与边之间的关系即可得出结论;(3)分点E在AB和AD上两种情况考虑,根据相似三角形的性质找出各边的长度,再利用分割图形求面积法找出S与t之间的函数关系式,令S=4.2求出t值,此题得解.解:(1)∵四边形ABCD为矩形,∴∠B=∠C=90°,∴∠BAP+∠BPA=90°.∵∠MPN=90°,∴∠BPA+∠CPD=90°,∴∠BAP=∠CPD,∴△ABP∽△PCD.故答案为:∽.(2)是定值.如图3,过点F作FH⊥PC于点H,∵矩形ABCD中,AB=2,∴∠B=∠FHP=90°,HF=AB=2,∴∠BPE+∠BEP=90°.∵∠MPN=90°,∴∠BPE+∠HPE=90°,∴∠BEP=∠HPE,∴△BEP∽△HPE,∴,∵BP=1,∴.(3)分两种情况:①如图3,当点E在AB上时,0≤t≤2.∵AE=t,AB=2,∴BE=2﹣t.由(2)可知:△BEP∽△HPE,∴,即,∴HP=4﹣2t .∵AF=BH=PB +BH=5﹣2t ,∴S=S 矩形ABHF ﹣S △AEF ﹣S △BEP ﹣S △PHF=AB•AF ﹣AE•AF ﹣BE•PB ﹣PH•FH=t 2﹣4t +5(0≤t ≤2).当S=4.2时,t 2﹣4t +5=4.2,解得:t=2±.∵0≤t ≤2,∴t=2﹣; ②如图4,当点E 在AD 上时,0≤t ≤1,过点E 作EK ⊥BP 于点K ,∵AE=t ,BP=1,∴PK=1﹣t .同理可证:△PKE ∽△FCP , ∴,即,∴FC=2﹣2t .∴DF=CD ﹣FC=2t ,DE=AD ﹣AE=5﹣t ,∴S=S 矩形EKCD ﹣S △EKP ﹣S △EDF ﹣S △PCF =CD•DE ﹣EK•KP ﹣DE•DF ﹣PC•FC=t 2﹣2t +5(0≤t ≤1). 当S=4.2时,t 2﹣2t +5=4.2,解得:t=1±. ∵0≤t ≤1,∴t=1﹣.综上所述:当点E 在AB 上时,S=t 2﹣4t +5(0≤t ≤2),当S=4.2时,t=2﹣;当点E 在AD 上时,S=t 2﹣2t +5(0≤t ≤1),当S=4.2时,t=1﹣.11.(2016•龙东地区)已知:点P 是平行四边形ABCD 对角线AC 所在直线上的一个动点(点P 不与点A 、C 重合),分别过点A 、C 向直线BP 作垂线,垂足分别为点E 、F ,点O 为AC 的中点.(1)当点P与点O重合时如图1,易证OE=OF(不需证明)(2)直线BP绕点B逆时针方向旋转,当∠OFE=30°时,如图2、图3的位置,猜想线段CF、AE、OE之间有怎样的数量关系?请写出你对图2、图3的猜想,并选择一种情况给予证明.【分析】(1)由△AOE≌△COF即可得出结论.(2)图2中的结论为:CF=OE+AE,延长EO交CF于点G,只要证明△EOA≌△GOC,△OFG 是等边三角形,即可解决问题.图3中的结论为:CF=OE﹣AE,延长EO交FC的延长线于点G,证明方法类似.解:(1)∵AE⊥PB,CF⊥BP,∴∠AEO=∠CFO=90°,在△AEO和△CFO中,,∴△AOE≌△COF,∴OE=OF.(2)图2中的结论为:CF=OE+AE.图3中的结论为:CF=OE﹣AE.如图2中的结论证明如下:延长EO交CF于点G,∵AE⊥BP,CF⊥BP,∴AE∥CF,∴∠EAO=∠GCO,在△EOA和△GOC中,,∴△EOA≌△GOC,∴EO=GO,AE=CG,在Rt△EFG中,∵EO=OG,∴OE=OF=GO,∵∠OFE=30°,∴∠OFG=90°﹣30°=60°,∴△OFG是等边三角形,∴OF=GF,∵OE=OF,∴OE=FG,∵CF=FG+CG,∴CF=OE+AE.选图3的结论证明如下:延长EO交FC的延长线于点G,∵AE⊥BP,CF⊥BP,∴AE∥CF,∴∠AEO=∠G,在△AOE和△COG中,,∴△AOE≌△COG,∴OE=OG,AE=CG,在Rt△EFG中,∵OE=OG,∴OE=OF=OG,∵∠OFE=30°,∴∠OFG=90°﹣30°=60°,∴△OFG是等边三角形,∴OF=FG,∵OE=OF,∴OE=FG,∵CF=FG﹣CG,∴CF=OE﹣AE.12.如图,在正方形ABCD中,点E为对角线AC上的一点,连接BE,DE.(1)如图1,求证:△BCE≌△DCE;(2)如图2,延长BE交直线CD于点F,G在直线AB上,且FG=FB.①求证:DE⊥FG;②已知正方形ABCD的边长为2,若点E在对角线AC上移动,当△BFG为等边三角形时,求线段DE的长(直接写出结果,不必写出解答过程).【分析】(1)利用判定定理(SAS)可证;(2)①利用(1)的结论与正方形的性质,只需证明∠FDE+∠DFG=90°即可;②由DE⊥FG可构造直角三角形,利用等边三角形的性质及三角函数可求DE的长.解:(1)∵四边形ABCD是正方形,AC是其对角线,∴∠DCE=∠BCE,CD=CB在△BCE与△DCE中,∴△BCE≌△DCE(SAS).(2)①证明:∵由(1)可知△BCE≌△DCE,∴∠FDE=∠FBC又∵四边形ABCD是正方形,∴CD∥AB,∴∠DFG=∠BGF,∠CFB=∠GBF,又∵FG=FB,∴∠FGB=∠FBG,∴∠DFG=∠CFB,。
部编数学七年级上册专题15选择压轴题多结论问题专题复习课堂学案及配套作业(解析版)含答案

专题15 选择压轴题多结论问题专题复习(解析版)第一部分教学案1.(2022秋•西山区期中)下列说法正确的有( )个.①如果地面向上15米记作+15米,那么地面向下6米记作﹣6米;②一个有理数不是正数就是负数;③任何一个有理数的绝对值都不可能小于零;④﹣a一定在原点左边;⑤在数轴上,一个数对应的点离原点越远,这个数越小.A.1B.2C.3D.4思路引领:根据正数和负数的定义,有理数的分类,绝对值的性质,有理数的大小比较和数轴的性质对各选项分析判断利用排除法求解.解:①如果地面向上15米记作15米,那么地面向下6米记作﹣6米,故本选项正确;②一个有理数不是正数就是零和负数,故本选项错误;③任何一个有理数的绝对值都是非负数,故本选项正确;④﹣a可以表示任意数,不一定在原点左边,故本选项错误;⑤在数轴上,原点右边的一个数对应的点离原点越远,这个数越大,故本选项错误;故选:B.总结提升:本题考查有理数,正数和负数,绝对值和数轴,解题的关键是掌握有理数的分类标准和数轴的性质.2.(2021秋•沿河县期末)现有以下四个结论:①绝对值等于其本身的有理数只有零;②相反数等于其本身的有理数只有零;③倒数等于其本身的有理数只有1;④平方等于其本身的有理数只有1.其中正确的有( )A.3个B.2个C.1个D.0个思路引领:根据绝对值的性质,相反数的定义,倒数的定义,有理数乘方的定义对各小题分析判断即可得解.解:①绝对值等于其本身的有理数是零和正数,故本小题错误;②相反数等于其本身的有理数只有零,正确;③倒数等于其本身的有理数是1和﹣1,故本小题错误;④平方等于其本身的有理数是0和1,故本小题错误;综上所述,正确的说法有②共1个.故选:C.总结提升:本题考查了有理数的乘方,相反数的定义,绝对值的性质,倒数的定义,是基础概念题,熟记概念是解题的关键.3.(2021秋•抚州)如图,数轴上点A,B,C对应的有理数分别为a,b,c,则下列结论中:①a+b+c>0;②a•b•c>0;③a+b﹣c>0;④0<ba<1;⑤|a|>|b|>|c|,正确的有( )A.4个B.3个C.2个D.1个思路引领:先由数轴得出a<﹣2<b<﹣1<0<c<1,再根据有理数的加法法则、有理数的乘除法法则等分别分析,可得答案.解:由数轴可得:a<﹣2<b<﹣1<0<c<1,∴a+b+c<0,故①错误;∵a,b,c中两负一正,∴a•b•c>0,故②正确;∵a<0,b<0,c>0,∴a+b﹣c<0,故③错误;∵a<﹣2<b<﹣1,∴0<ba<1,故④正确;a|>|b|>|c|,故⑤正确;综上可知,正确的有3个.故选:B.总结提升:本题考查了数轴在有理数加减乘除法运算中的应用,数形结合,是解题的关键.4.(2022秋•惠济区期中)有理数a,b在数轴上的对应点如图所示,则下面式子中正确的是( )①b<0<a;②|b|<|a|;③b﹣a>0;④a﹣b>a+b.A.①②B.①④C.②③D.③④思路引领:由数轴直观得出b<0<a,且|b|>|a|,然后关键有理数的有关知识解答.解:①由数轴直观得出b<0<a,故①正确;②由数轴直观得出|b|>|a|,故②错;③b﹣a=b+(﹣a)<0;故③错;④a﹣b=a+(﹣b)>0,a+b<0,故④正确.故答案为:B.总结提升:本题考查的是有理数的有关运算,解题的关键是关键数轴判断正负和绝对值的大小.5.(2022秋•金水区校级期中)已知数a,b,c在数轴上的位置如图,下列说法:①b+c>0;②a+b−c>0;③a|a|+b|b|+c|c|=1;④|a−b|−2|c+b|+|a−c|=−3b+c.其中正确结论的个数是( )个.A.1B.2C.3D.4思路引领:根据数轴上的位置关系.判断出a,b,c的大小关系以及各自绝对值得大小关系,在进行判断即可.解:∵|c|>|b|,b<0<c,∴b+c>0,正确,故①正确;∵b<0<a,|b|>|a|,c>0,∴a+b−c<0,故②错误;a|a|+b|b|+c|c|=aa+bb+cc=1﹣1+1=1,正确,故③正确;∵a﹣b>0,c+b>0,a﹣c<0∴|a−b|−2|c+b|+|a−c|,=a﹣b﹣2(b+c)+c﹣a,=a﹣b﹣2b﹣2c+c﹣a,=﹣3b﹣c,故④错误,∴正确的有两个.故选:B.总结提升:本题主要考查数轴与绝对值的综合运用,解题的关键在于掌握绝对值化简的技巧.6.(2022秋•海城市校级期中)已知a、b、c在数轴上的位置如图,下列说法:①abc<0;②c+a>0;③c﹣b<0;④cb>0.正确的有( )A.1个B.2个C.3个D.4个思路引领:根据数轴上点的位置,利用有理数的加减乘除法则判断即可.解:根据数轴上点的位置得:c<b<0<a,且|b|<|a|<|c|,∴abc>0,c+a<0,c﹣b<0,cb>0,则正确的有2个.故选:B.总结提升:此题考查了有理数的除法,数轴,有理数的加减法,以及有理数的乘法,熟练掌握运算法则是解本题的关键.7.(2022秋•行唐县校级期中)一个两位数,它的十位数字为a,个位数字为b,若把它的十位数字和个位数字对调,得到一个新的两位数,则下列判断正确的是( )甲同学:新的两位数可表示为b+a;乙同学:新的两位数与原两位数的和是11的倍数;丙同学:若b﹣a能被2整除,则新的两位数与原两位数的差能被18整除A.只有乙同学的正确B.只有乙、丙同学的正确C.只有甲、丙同学的正确D.三名同学的都不正确思路引领:根据题意表示出原数与新数即可;求出两数的差,化简后判断即可.解:由题意得:这个两位数是10a+b,新的两位数是:10b+a,故甲判断错误;新的两位数与原两位数的和是:10b+a+10a+b=11a+11b=11(a+b),则其和是11的倍数,故乙判断正确;新的两位数与原两位数的差是:10b+a﹣(10a+b)=9b﹣9a=9(b﹣a),∵b﹣a能被2整除,∴新的两位数与原两位数的差能被18整除,故丙判断正确;故判断正确的有乙、丙.故选:B.总结提升:本题主要考查整式的加减,列代数式,解答的关键是对整式的加减运算的法则的掌握.8.(2022秋•金水区校级期中)下列说法正确的有( )个.①单项式x的系数和次数都是0;②3x4﹣5x2y2﹣6y3+2的次数是11;③多项式1﹣2x+12x2是由1,﹣2x,12x2三项组成;④在13a2,x yπ,5y4x,0中整式有2个.A.1B.2C.3D.4思路引领:根据多项式、单项式、整式的相关概念解答即可.解:①单项式x的系数和次数都是1,原说法错误;②3x4﹣5x2y2﹣6y3+2的次数是4,原说法错误;③多项式1﹣2x+12x2是由1,﹣2x,12x2三项组成,原说法正确;④在13a2,x yπ,5y4x,0中整式有3个,原说法错误.说法正确的有1个.故选:A.总结提升:本题主要考查了整式的有关概念.要能准确的分清什么是整式.整式是有理式的一部分,在有理式中可以包含加,减,乘,除四种运算,但在整式中除式不能含有字母.单项式和多项式统称为整式.单项式是字母和数的乘积,只有乘法,没有加减法.多项式是若干个单项式的和,有加减法.9.(2022秋•九龙坡区校级期中)对于4个整式:A:a2,B:a+2,C:b2,D:2a,有以下几个结论:①对于a、b取任意数,都有B•D﹣2A﹣4B=﹣8;②若b为正数,则B•C+D+A的值一定是正数;③若多项式M=A﹣D+m•B•D(m为常数)不含a2,则m的值为―12,上述结论中,正确的有( )A.①B.①②C.②③D.①③思路引领:根据整式混合运算的顺序与运算法则分别计算即可求解.解:①:B•D﹣2A﹣4B=(a+2)•2a﹣2a2﹣4(a+2)=2a2+4a﹣2a2﹣4a﹣8=﹣8,故结论①正确;②:若b为正数,则B•C+D+A=(a+2)•b2+2a+a2=ab2+2b2+2a+a2,∵a可取任意数,∴ab2+2a可以是负数,∴ab2+2b2+2a+a2不一定是正数,故结论②错误;③:M=A﹣D+m•B•D=a2﹣2a+m(a+2)•2a=a2﹣2a+2ma2+4ma=(1+2m)a2+(4m﹣2)a,∵多项式M=A﹣D+m•B•D(m为常数)不含a2,∴1+2m=0,∴m=―1 2,∴M=9x2﹣3≥﹣3,故结论③正确.故选:D.总结提升:本题考查整式的混合运算,掌握运算法则是解题的关键.10.(2022秋•涟源市期中)规定:f(x)=|x﹣2|,g(y)=|y+3|.例如f(﹣4)=|﹣4﹣2|,g(﹣4)=|﹣4+3|.下列结论中:①若f(x)+g(y)=0,则2x﹣3y=13;②若x<﹣3,则f(x)+g(x)=﹣1﹣2x:③若x>﹣3,则f(x)+g(x)=2x+1;④式子f(x﹣1)+g(x+1)的最小值是7.其中正确的所有结论是( )A.①②B.①②④C.①③④D.①②③④思路引领:①根据新定义运算和非负数的性质求得x、y,再代值计算便可判断①的正误;②根据新定义运算和绝对值的性质进行计算便可;③根据新定义运算和绝对值的性质,分两种情况:﹣3<x<2;x≥2;分别计算便可;④根据新定义运算和绝对值的性质,进行解答便可.解:①∵f(x)+g(y)=0,∴|x﹣2|+|y+3|=0,∴x﹣2=0,y+3=0,∴x=2,y=﹣3,∴2x﹣3y=13=4+9=13,故①正确;②∵x<﹣3,∴f(x)+g(x)=|x﹣2|+|x+3|=﹣x+2﹣x﹣3=﹣2x﹣1,故②正确:③∵x>﹣3,f(x)+g(x)=|x﹣2|+|x+3|∴当﹣3<x<2时,f(x)+g(x)=﹣x+2+x+3=5,当x≥2时,f(x)+g(x)=x﹣2+x+3=2x+1,故③错误;④f(x﹣1)+g(x+1)=|x﹣1﹣2|+|x+1+3|=|x﹣3|+|x+4|,当﹣4≤x≤3时,④式子f(x﹣1)+g(x+1)有最小值为:3﹣x+x+4=7,故④正确;故选:B .总结提升:本题考查了求代数式的值,非负数的性质,绝对值的定义,关键是应用新定义和绝对值的性质解题.11.(2022秋•庐阳区校级期中)下列各变形中:①由x =y ,得到x a =y a ;②由x +2=y +2,可得到x =y ;③由x a =y a 可得到x =y ;④由x 0.3―2x 10.7=7,可得到10x 3―20x 107=70.其中一定正确的有( )A .1个B .2个C .3个D .4个思路引领:根据等式的性质对各小题进行逐一分析即可.解:①当a =0时,x a 与y a 无意义,故不符合题意;②由x +2=y +2,可得到x =y ,符合等式的性质1,故符合题意;③由x a =y a 可得到x =y ,符合等式的性质2,故符合题意;④由x 0.3―2x 10.7=7,可得到10x 3―20x 107=7,故不符合题意.故选:B .总结提升:本题考查的是等式的性质,熟知等式的两个基本性质是解题的关键.12.(2022秋•丹江口市期中)已知m =n ,则下列变形中正确的个数为( )①m +2=n +2;②am =an ;③m n =1;④m a 21=n a 21A .1个B .2个C .3个D .4个思路引领:根据等式的性质对各小题进行解答即可.解:①∵m =n ,∴m +2=n +2,故本小题符合题意;②∵m =n ,∴am =an ,故本小题符合题意;③当n =0时,m m 无意义,故本小题不符合题意;④∵m =n ,a 2+1>0,∴m a 21=n a 21,故本小题符合题意.故选:C .总结提升:本题考查的是等式的性质,熟知等式的性质是解题的关键.13.(2022秋•怀柔区校级月考)有m 辆客车及n 个人,若每辆客车乘40人,则还有10人不能上车,若每辆客车乘43人,则只有1人不能上车,有下列四个等式:①40m +10=43m﹣1;②n1040=n143;③n1040=n143;④40m+10=43m+1.其中正确的是( )A.①②B.②④C.①③D.③④思路引领:由乘车的人数不变,可得出关于m的一元一次方程;由客车辆数不变,可得出关于n的一元一次方程,再对照给定的4个等式即可得出结论.解:由人数不变,可列出方程:40m+10=43m+1,∴等式④正确;由客车的辆数不变,可列出方程:n1040=n143,∴等式③正确.∴正确的结论是③④.故选:D.总结提升:本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键.14.(2021秋•高新区校级期末)鸡兔同笼问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”图是嘉淇解题过程,需要补足横线上符号所代表的内容,则下列判断不正确的是( )解:设鸡有x只,那么兔子有□只.因为☆+兔的足数=94,所以列方程为〇x+△(35﹣x)=94,解这个方程,得x=23,从而35﹣23=12.答:鸡有23只,兔子有12只.A.□代表(35﹣x)B.☆代表鸡的足数C.〇代表2D.△代表2思路引领:设鸡有x只,则兔子有(35−x)只,根据鸡的脚的数量+兔子的脚的数量=94可列方程,解方程即可.解:设鸡有x只,则兔子有(35−x)只,∵鸡的足数+兔的足数=94,∴列方程为2x+4(35−x)=94,解这个方程,得:x=23,从而35−23=12,∴鸡有23只,兔子有12只,∴□代表(35−x),☆代表鸡的足数,〇代表2,△代表4,故选:D.总结提升:本题主要考查一元一次方程的应用,解题的关键是理解题意,找到题目蕴含的相等关系.15.(2021秋•阳东区期末)将方程3x+6=2x﹣8移项后,四位同学的结果分别是(1)3x+2x =6﹣8;(2)3x﹣2x=﹣8+6;(3)3x﹣2x=8﹣6;(4)3x﹣2x=﹣6﹣8,其中正确的有( )A.0个B.1个C.2个D.3个思路引领:移项时注意改变该项的符号,据此判断即可.解:将方程3x+6=2x﹣8移项后,可得到3x﹣2x=﹣8﹣6,∴只有(4)是正确的,故选:B.总结提升:本题主要考查一元一次方程的知识,熟练掌握移项时改变该项的符号是解题的关键.16.(2021秋•普陀区期末)下列说法正确的是( )①若x=1是关于x的方程a+bx+c=0的一个解,则a+b+c=0;②在等式3x=3a﹣b两边都除以3,可得x=a﹣b;③若b=2a,则关于x的方程ax+b=0(a≠0)的解为x=―1 2;④在等式a=b两边都除以x2+1,可得ax21=bx21.A.①③B.②④C.①④D.②③思路引领:把x=1代入方程a+bx+c=0,即可判断①;根据等式的性质即可判断②④,把b=2a代入方程ax+b=0得出ax+2a=0,求出x,即可判断③.解:把x=1代入方程a+bx+c=0得:a+b+c=0,故①正确;等式3x=3a﹣b两边都除以3得:x=a―13b,故②错误;把b=2a代入方程ax+b=0得:ax+2a=0,解得:x=﹣2,故③错误;等式a=b两边都除以x2+1得:ax21=bx21,故④正确;即正确的为①④,故选:C.总结提升:本题考查了一元一次方程的解,等式的性质和解一元一次方程,能熟记一元一次方程的解的定义和等式的性质是解此题的关键.17.(2021秋•南谯区期末)有下列说法:①若∠A+∠B+∠C=180°,则∠A,∠B,∠C互补;②若∠1是∠2的余角,则∠2是∠1的余角;③一个锐角的补角一定比它的余角大90°;④互补的两个角中,一定是一个钝角与一个锐角.其中正确的有( )A.1个B.2个C.3个D.4个思路引领:余角和补角一定指的是两个角之间的关系,同角的补角比余角大90°.解:①补角一定指的是两个角之间的关系,错误.②若∠1是∠2的补角,则∠2是∠1的补角,正确.③同一个锐角的补角一定比它的余角大90°,正确,180﹣α﹣(90﹣α)=90.④互补的两个角中,一定是一个钝角与一个锐角,错误,90°+90°=180°.故选:B.总结提升:本题主要考查了余角和补角的知识,掌握余角的和等于90°,互补的两角之和为180°是关键.18.(2021秋•浦北县期末)已知∠1与∠2互为余角,∠1与∠3互为补角,下列结论:①∠3<∠1+∠2;②∠3﹣∠2=90°;③∠3+∠2=270°﹣2∠1;④∠3﹣∠1=2∠2.其中正确的有( )A.1个B.2个C.3个D.4个思路引领:根据互余的两角之和为90°,互补的两角之和为180°,即可求出有关的结论.解:由:∠1+∠2=90°(1),∠1+∠3=180°(2),得,∠3=180°﹣∠1=2∠1+2∠2﹣∠1=∠1+2∠2,∴∠3>∠1+∠2,∴①错误.∵∠1+∠2=90°(1),∠1+∠3=180°(2),∴(2)﹣(1)得,∠3﹣∠2=90°,∴②正确.(1)+(2)得,∠3+∠2=270°﹣2∠1,∴③正确.(2)﹣(1)×2得,∠3﹣∠1=2∠2,∴④正确.故选:C.总结提升:本题主要考查了余角和补角的知识,掌握余角的和等于90°,互补的两角之和为180°是关键.19.(2022秋•大东区期中)下列说法正确的有( )①n棱柱有2n个顶点,2n条棱,(n+2)个面(n为不小于3的正整数);②圆锥的侧面展开图是一个圆;③用平面去截一个正方体,截面形状可以是三角形、四边形、五边形、六边形.A.0个B.1个C.2个D.3个思路引领:根据立体图形的特征,截几何体的方法进行判定是几边形.解:①n梭柱有2n个顶点,3n条棱,(n+2)个面(n为不小于3的正整数),故说法错误;②圆锥的侧面展开图是一个扇形,故说法错误;③用平面去截一个正方体,截面的形状可以是三角形、四边形、五边形、六边形是正确的.故选:B.总结提升:本题考查了立体图形的性质,几何体的特征,截面图形的边数,解题的关键是熟练掌握几何体的定义.20.(2022秋•灞桥区校级期中)下列说法正确的个数是( )①连接两点之间的线段叫两点间的距离;②线段AB和线段BA表示同一条线段;③木匠师傅锯木料时,一般先在模板上画出两个点,然后过这两点弹出一条墨线,这样做的原理是:两点之间,线段最短;④若AB=2CB,则点C是AB的中点.A.1个B.2个C.3个D.4个思路引领:由直线的性质,两点的距离的概念,线段中点的概念即可判断.解:连接两点之间的线段的长叫两点间的距离,故①不符合题意;线段AB和线段BA表示同一条线段,正确,故②符合题意;木匠师傅锯木料时,一般先在模板上画出两个点,然后过这两点弹出一条墨线,这样做的原理是:两点确定一条直线,故③不符合题意;若AB=2CB,点C可能在AB外,则点C不一定是AB的中点,故④不符合题意.故选:A.总结提升:本题考查直线的性质,两点的距离的概念,线段中点的概念,关键是掌握:连接两点间的线段的长度叫两点间的距离;经过两点有且只有一条直线.21.(2022秋•城关区校级期中)下列说法不正确的是( )①长方体一定是柱体;②八棱柱有10个面;③六棱柱有12个顶点;④用一个平面去截几何体,若得到的图形是三角形,则这个几何体一定有一个面的形状是三角形.A.①B.④C.①④D.②③思路引领:根据棱柱的特征以及截一个几何体的方法解答即可.解:①因为长方体是棱柱,所以长方体一定是柱体,原说法正确,不符合题意;②八棱柱的侧面有8个面,有两个底面,共有10个面,原说法正确,不符合题意;③六棱柱上底面有6个顶点,下底面有6个顶点,共有12个顶点,原说法正确,不符合题意;④用一个平面去截几何体,若得到的图形是三角形,则这个几何体不一定有一个面的形状是三角形,如圆锥,原说法不正确,符合题意.说法不正确的是④.故选:B.总结提升:本题考查几何体,掌握常见几何体的概念和性质是解题的关键.22.(2022秋•山亭区校级月考)下列判断正确的有( )(1)正方体是棱柱,长方体不是棱柱;(2)正方体是棱柱,长方体也是棱柱;(3)正方体是柱体,圆柱也是柱体;(4)正方体不是柱体,圆柱是柱体.A.1个B.2个C.3个D.4个思路引领:根据棱柱和柱体的概念判断即可.解:(1)正方体是棱柱,长方体不是棱柱,故原题说法错误;(2)正方体是棱柱,长方体也是棱柱,故原题说法正确;(3)正方体是柱体,圆柱也是柱体,故原题说法正确;(4)正方体不是柱体,圆柱是柱体,故原题说法错误.故选:B.总结提升:此题主要考查了认识立体图形,关键是掌握各种立体图形的特点.23.(2022春•新泰市期中)下列语句中:①两点确定一条直线;②圆上任意两点A、B间的部分叫做圆弧;③两点之间直线最短;④三角形、四边形、五边形、六边形等都是多边形.其中正确的个数有( )A.1个B.2个C.3个D.4个思路引领:利用线段的性质、直线的性质、多边形以及圆弧的概念进行判断,即可得出结论.解:①两点确定一条直线,说法正确;②圆上任意两点A、B间的部分叫做圆弧,说法正确;③两点之间,线段最短,故原说法错误;④三角形、四边形、五边形、六边形等都是多边形,说法正确.故选:C.总结提升:本题主要考查了线段的性质、直线的性质、多边形以及圆弧的概念.两点的所有连线中,可以有无数种连法,如折线、曲线、线段等,这些所有的线中,线段最短.24.(2022•南昌模拟)如图,AB与CD相交于点O,OE是∠AOC的平分线,且OC恰好平分∠EOB,则下列结论中正确的个数有( )①∠AOE=∠EOC②∠EOC=∠COB③∠AOD=∠AOE④∠DOB=2∠AODA.1个B.2个C.3个D.4个思路引领:根据角平分线的定义得出∠AOE=∠COE,∠COE=∠BOC,求出∠AOE=∠COE=∠BOC,根据∠AOE+∠COE+∠BOC=180°求出∠AOE=∠COE=∠BOC=60°,再根据对顶角相等求出答案即可.解:∵OE是∠AOC的平分线,OC恰好平分∠EOB,∴∠AOE=∠COE,∠COE=∠BOC,∴∠AOE=∠COE=∠BOC,∵∠AOE+∠COE+∠BOC=180°,∴∠AOE=∠COE=∠BOC=60°,∴∠AOD=∠BOC=60°,∴∠BOD=120°,∴①②③④都正确.故选:D.总结提升:本题考查了邻补角、对顶角,角平分线的定义等知识点,注意:①邻补角互补,②从角的顶点出发的一条射线,如果把这个角分成相等的两个角,那么这条射线叫这个角的平分线,③对顶角相等.25.(2022•定远县模拟)下列说法:①把弯曲的河道改直,能够缩短航程,这是因为两点之间,线段最短;②若线段AC=BC,则C是线段AB的中点;③﹣a一定是负数;④非负数的任何次幂都是非负数;⑤一个角的补角大于这个角本身.其中正确的个数为( )A.1B.2C.3D.4思路引领:根据两点之间,线段最短,线段中点的定义,负数,乘方,补角的性质,逐项判断即可求解.解:①把弯曲的河道改直,能够缩短航程,这是因为两点之间,线段最短,故①正确;②当点C在线段AB上时,若线段AC=BC,则C是线段AB的中点,故②错误;③当a>0时,﹣a一定是负数,故③错误;④非负数的任何次幂都是非负数,故④正确;⑤一个锐角的补角大于这个角本身,故⑤错误;∴正确的有①④,共2个.故选:B.总结提升:本题主要考查两点之间,线段最短,线段中点的定义,负数,乘方,补角的性质,熟练掌握相关知识点是解题的关键.26.(2022春•香坊区期末)下列说法:①正数和负数统称为有理数;②若m+n=0,则m、n互为相反数;③如果a>b,则有|a|>|b|;④几个角的和等于180°,我们就说这几个角互补;⑤23x4是7次单项式,其中正确的有( )A.1个B.2个C.3个D.4个思路引领:根据有理数的定义,相反数的定义,补角的定义,单项式的次数,非负数的性质对各项进行分析即可.解:①有理数是整数(正整数、0、负整数)和分数的统称;故①说法错误;②若m+n=0,则m、n互为相反数;故②说法正确;③如果0>a>b,则有|a|<|b|;故③说法错误;④两个角的和等于180°,我们就说这两个角互补;故④说法错误;⑤23x4是4次单项式,故⑤说法错误,正确的有②,共1个.故选:A.总结提升:本题主要考查补角,有理数,非负数性质,单项式,解答的关键是对相应的知识的掌握.27.(2022春•南岗区期末)下列四个说法:①射线AB和射线BA是同一条射线;②若点B 为线段AC的中点,则AB=BC;③锐角和钝角互补;④一个角的补角一定大于这个角.其中正确说法的个数是( )A.0个B.1个C.2个D.3个思路引领:①根据射线的定义判断;②根据线段中点的定义判断;③根据钝角与锐角的定义判断;④根据补角的定义判断.解:①射线AB和射线BA表示的方向不同,不是同一条射线,故原说法错误;②若点B为线段AC的中点,则AB=BC,故原说法正确;③锐角和钝角是相对于直角的大小而言,没有一定的数量关系,不一定构成互补关系,故原说法错误;④一个角的补角不一定大于这个角,如一个角是130°,它的补角是50°,即一个角的补角小于这个角,故原说法错误.故正确的说法有②,共1个.故选:B.总结提升:本题考查了射线的定义,线段中点的定义,钝角与锐角的定义,补角的定义,对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义,要善于区分不同概念之间的联系和区别.28.(2022•驿城区校级开学)下列几种说法:①两点之间线段最短;②任何数的平方都是正数;③2(2x+1)是一元一次方程;④34x3是7次单项式;⑤任何有理数的绝对值都是非负数.其中正确的语句有( )个.A.1B.2C.3D.4思路引领:根据两点之间线段最短;任何数的平方都是非负数;一元一次方程的定义;单项式中所有字母的指数的和叫做单项式的次数;绝对值的定义进行分析即可.解:①两点之间线段最短;故符合题意;②任何数的平方都是非负数;故不符合题意;③2(2x+1)不是一元一次方程;故不符合题意;④34x3是3次单项式;故不符合题意;⑤任何有理数的绝对值都是非负数,故符合题意;故选:B.总结提升:此题主要考查了线段的性质、一元一次方程定义、单项式的次数、绝对值的定义,关键是掌握课本基础知识,不能混淆.29.(2018秋•洪山区期末)如图,O为直线AB上一点,∠DOC为直角,OE平分∠BOC,OF平分∠AOD,OG平分∠AOC,下列结论:①∠BOE与∠DOF互为余角;②2∠AOE ﹣∠BOD=90°;③∠EOD与∠COG互为补角;④∠BOE﹣∠DOF=45°;其中正确的是( )A.①②③④B.③④C.②③D.②③④思路引领:根据余角和补角的定义以及角平分线的定义计算出各选项的结果判断即可.解:∵OE平分∠BOC,OG平分∠AOC,∴∠BOE+∠AOG=90°,∵∠AOG≠∠DOF,∴①错误;∵∠DOC=∠GOE=90°,∴∠AOE=135°―12∠AOD,∴2∠AOE=270°﹣∠AOD,∴2∠AOE﹣∠BOD=90°,∴②正确;∵∠DOC=∠GOE=90°,∴∠EOD+∠COG=180°,∴③正确;∵OE平分∠BOC,OF平分∠AOD,∴∠DOF+∠COG=45°,∵OE平分∠BOC,OG平分∠AOC,∴∠BOE+∠COG=90°,∴∠BOE﹣∠DOF=45°;∴④正确.综上所述,正确的有②③④.故选:D.总结提升:本题考查了余角和补角的定义及性质,角平分线定义,角的和差计算,准确识图是解题的关键.30.(2018秋•青山区期末)如图,货轮A在航行过程中,发现灯塔B在它北偏东60°的方向上,货轮C在它南偏东30°方向上.则下列结论:①∠NAB=60°;②∠WAC=120°;③图中∠NAC的补角有两个,分别是∠SAC和∠EAB;④图中有4对互余的角,其中正确的个数有( )A.1个B.2个C.3个D.4个思路引领:根据方向角以及余角与补角的定义解答即可.解:灯塔B在它北偏东60°的方向上,即∠NAB=60°,故①正确;∠SAC=30°,∠WAC=90°+30°=120°,故②正确;∠NAC=150°,∠SAC=∠EAB=30°,故③正确;图中两个60°角两个30°角,一共四对互余的角,故④正确.故正确的有①②③④共4个.故选:D.总结提升:本题考查了余角与补角以及方向角的定义,正确理解方向角的定义,是解答本题的关键.第二部分配套作业1.(2022秋•巴东县期中)下列对“0”的描述:①0℃表示没有温度②0是正数③0比任何负数都大④0是自然数其中,正确的个数有( )A.1B.2C.3D.4思路引领:根据有理数的定义对各小题进行逐一分析即可.解:①0℃表示温度是0摄氏度,故本小题不符合题意;②0既不是正数,也不是负数,故本小题不符合题意;③0比任何负数都大,故本小题符合题意;④0是自然数,故本小题符合题意.故选:B.总结提升:本题考查的是有理数,熟知0既不是正数,也不是负数是解题的关键.2.(2022秋•永安市期中)下列说法正确的是( )①正有理数和负有理数统称为有理数;②一个数的相反数等于它本身,那么这个数为零;③如果一个数的绝对值等于它本身,那么这个数是正数;④﹣3.14既是负数、分数,也是有理数.A.①②③④B.①②③C.①②D.②④思路引领:分别根据有理数的分类,相反数的定义,绝对值的定义逐一判断即可.解:正有理数,0和负有理数统称为有理数,故说法①错误;一个数的相反数等于它本身,那么这个数为零,故说法②正确;如果一个数的绝对值等于它本身,那么这个数是正数或0,故说法③错误;﹣3.14既是负数,分数,也是有理数,故说法④正确.所以正确的有②④.故选:D.总结提升:本题考查了有理数的分类依据、相反数与绝对值的定义,熟记定义是解题的关键.3.(2022秋•芜湖期中)如图,A,B两点在数轴上的位置表示的数分别为a,b.有下列四个结论:①(b﹣1)(a+1)>0;②b1|a3|>0;③(a+b)(a﹣b)>0;④b>﹣a>﹣b>a.其中正确的结论是( )A.①④B.①②C.②③D.②④思路引领:根据数轴判断A和B所表示的数的符号,然后逐一分析即可.解:由图可知,﹣1<a<0,b>1,∴b﹣1>0,a+1>0,∴①正确;∵|a﹣3|>0,b﹣1>0,∴②正确;(a+b)(a﹣b)=a2﹣b2<0,∴③错误;∵0<﹣a<1,﹣b<﹣1,∴b>﹣a>a>﹣b,∴④错误.综上①②正确,故选:B.总结提升:本题考查数轴和绝对值,能够通过数轴判断一个数的符号是解答本题的关键.4.(2022秋•桐乡市期中)数轴上点A,B,C分别表示数﹣1,m,﹣1+m,下列说法正确的是( )A.点C一定在点A的右边B.点C一定在点A的左边C.点C一定在点B的右边D.点C一定在点B的左边思路引领:由于不知道数m的数值,所以不清楚点A与点C,点A与点B的位置关系,再根据点B,C分别表示数m,﹣1+m即可判断.。
押中考数学第9-10题(多结论问题)(学生版)

押中考数学第9-10题(多结论问题)专题诠释:一直以来,函数都是中考数学的重点考察题型。
在选择题中,主要考察函数的性质、函数的图像和函数的应用,难度的跨度较大,从基础到压轴都有可能出现,满分难度较大。
多做、多想、多总结,掌握做题规律,力争不丢分!目录知识点一:函数的性质及探究1模块一〖真题回顾〗 1模块二〖押题冲关〗 5模块三〖考前预测〗 9知识点一:函数的性质及探究模块一〖真题回顾〗1.(2022·辽宁丹东·统考中考真题)如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(5,0),与y轴交于点C,其对称轴为直线x=2,结合图象分析如下结论:①abc>0;②b+3a<0;③当x>0时,y随x的增大而增大;④若一次函数y=kx+b(k≠0)的图象经过点A,则点E(k,b)在第四象限;⑤点M是抛物线的顶点,若CM⊥AM,则a=66.其中正确的有()A.1个B.2个C.3个D.4个2.(2022·贵州黔西·统考中考真题)如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,AF⊥x轴,垂足为F.若OE=3,EF=1.以下结论正确的个数是()①OA=3AF;②AE平分∠OAF;③点C的坐标为(-4,-2);④BD=63;⑤矩形ABCD的面积为242.A.2个B.3个C.4个D.5个3.(2022·四川宜宾·统考中考真题)如图,△ABC 和△ADE 都是等腰直角三角形,∠BAC =∠DAE =90°,点D 是BC 边上的动点(不与点B 、C 重合),DE 与AC 交于点F ,连结CE .下列结论:①BD =CE ;②∠DAC =∠CED ;③若BD =2CD ,则CF AF=45;④在△ABC 内存在唯一一点P ,使得PA +PB +PC 的值最小,若点D 在AP 的延长线上,且AP 的长为2,则CE =2+3.其中含所有正确结论的选项是()A.①②④B.①②③C.①③④D.①②③④4.(2022·四川眉山·中考真题)如图,四边形ABCD 为正方形,将△EDC 绕点C 逆时针旋转90°至△HBC ,点D ,B ,H 在同一直线上,HE 与AB 交于点G ,延长HE 与CD 的延长线交于点F ,HB =2,HG =3.以下结论:①∠EDC =135°;②EC 2=CD ⋅CF ;③HG =EF ;④sin ∠CED =23.其中正确结论的个数为()A.1个B.2个C.3个D.4个5.(2022·山东东营·统考中考真题)如图,已知菱形ABCD的边长为2,对角线AC、BD相交于点O,点M,N分别是边BC、CD上的动点,∠BAC=∠MAN=60°,连接MN、OM.以下四个结论正确的是()①△AMN是等边三角形;②MN的最小值是3;③当MN最小时S△CMN=18S菱形ABCD;④当OM⊥BC时,OA2=DN⋅AB.A.①②③B.①②④C.①③④D.①②③④6.(2022·黑龙江·统考中考真题)如图,正方形ABCD的对角线AC,BD相交于点O,点F是CD上一点,OE⊥OF交BC于点E,连接AE,BF交于点P,连接OP.则下列结论:①AE⊥BF;②∠OPA=45°;③AP-BP=2OP;④若BE:CE=2:3,则tan∠CAE=47;⑤四边形OECF的面积是正方形ABCD面积的14.其中正确的结论是()A.①②④⑤B.①②③⑤C.①②③④D.①③④⑤7.(2022·湖南益阳·统考中考真题)如图,已知△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕A点逆时针旋转50°得到△AB′C′,以下结论:①BC=B′C′,②AC∥C′B′,③C′B′⊥BB′,④∠ABB′=∠ACC′,正确的有()A.①②③B.①②④C.①③④D.②③④8.(2022·黑龙江牡丹江·统考中考真题)下列图形是黄金矩形的折叠过程:第一步,如图(1),在一张矩形纸片一端折出一个正方形,然后把纸片展平;第二步,如图(2),把正方形折成两个相等的矩形再把纸片展平;第三步,折出内侧矩形的对角线AB ,并把AB 折到图(3)中所示的AD 处;第四步,如图(4),展平纸片,折出矩形BCDE 就是黄金矩形.则下列线段的比中:①CD DE ,②DE AD ,③DE ND ,④AC AD,比值为5-12的是()A.①②B.①③C.②④D.②③9.(2022·黑龙江绥化·统考中考真题)如图,在矩形ABCD 中,P 是边AD 上的一个动点,连接BP ,CP ,过点B 作射线,交线段CP 的延长线于点E ,交边AD 于点M ,且使得∠ABE =∠CBP ,如果AB =2,BC =5,AP =x ,PM =y ,其中2<x ≤5.则下列结论中,正确的个数为()(1)y 与x 的关系式为y =x -4x ;(2)当AP =4时,△ABP ∽△DPC ;(3)当AP =4时,tan ∠EBP =35.A.0个B.1个C.2个D.3个10.(2022·江苏连云港·统考中考真题)如图,将矩形ABCD 沿着GE 、EC 、GF 翻折,使得点A 、B 、D 恰好都落在点O 处,且点G 、O 、C 在同一条直线上,同时点E 、O 、F 在另一条直线上.小炜同学得出以下结论:①GF ∥EC ;②AB =435AD ;③GE =6DF ;④OC =22OF ;⑤△COF ∽△CEG .其中正确的是()A.①②③B.①③④C.①④⑤D.②③④模块二〖押题冲关〗1.(2023·江苏连云港·统考一模)如图,在边长为4的正方形ABCD中,点E是边BC的中点,连接AE、DE,分别交BD、AC于点P、Q,过点P作PF⊥AE交CB的延长线于F,下列结论:①∠AED+∠EAC+∠EDB=90°;②AP=FP;③AE=102AO;④四边形OPEQ的面积为43;⑤BF=43.其中正确的结论有()A.2个B.3个C.4个D.5个2.(2023·广东深圳·深圳市南山外国语学校校联考二模)如图,在正方形ABCD中,AD=4,E为CD中点,F为BC上的一点,且∠EAF=45°,∠ABG=∠DAE,连接EF,延长BG交AE于点M,交AD于点N,则以下结论;①DE+BF=EF②BN⊥AE③BF=83④S△BGF=1615中正确的是()A.1个B.2个C.3个D.4个3.(2023·辽宁铁岭·校联考一模)如图,正方形ABCD的对角线AC,BD相交于点O,点E是AB上一点,OF⊥OE交AD于点F,连接CF,DE交于点P,连接OP.则下列结论:①∠OPC=45°;②DE⊥CF;③CP -DP =2OP ;④若AF :FD =3:2,则tan ∠ACF =47;⑤四边形OEAF 的面积是正方形ABCD 面积的14.其中正确的结论是()A.①②④⑤B.①②③⑤C.①②③④D.①③④⑤4.(2023·江苏无锡·校考二模)如图,在正方形ABCD 中,F 是BC 边上一点,连接AF ,以AF 为斜边作等腰直角△AEF .有下列四个结论:①∠CAF =∠DAE ;②点E 在线段BD 上;③当∠AEC =135°时,CE 平分∠ACD ;④若点F 在BC 上以一定的速度由B 向C 运动,则点F 的运动速度是点E 运动速度的2倍.其中正确的结论的个数为()A.1B.2C.3D.45.(2023·黑龙江绥化·统考一模)如图,正方形ABCD 中,BE =EF =FC ,CG =2GD ,BG 分别交AE ,AF于点M ,N .下列结论:①AF ⊥BG ;②BN =23NF ;③BM MG=38;④S 四边形CGNF :S 四边形ANGD =18:31.其中结论正确的个数有()A.1个B.2个C.3个D.4个6.(2023·安徽滁州·校考模拟预测)如图,在边长为1的正方形ABCD 中,E 、F 是AD 边上的两个动点,且AE =FD ,连接BE 、CF 、BD ,CF 与BD 交于点G ,连接AG 交BE 于点H ,连接DH ,下列结论正确的个数是()①AG ⊥BE ;②HD 平分∠EHG ;③△ABG ∽△FDG ;④S △HDG:S △HBG =tan ∠DAG ;⑤线段DH 的最小值是5-12;⑥当E 、F 重合时,延长AG 交CD 于M ,则tan ∠EBM =34.A.5个B.4个C.3个D.2个7.(2023·黑龙江绥化·校联考一模)如图,在正方形ABCD 中,E 是线段CD 上一动点,连接AE 交BD 于点F ,过点F 作FG ⊥AE 交BC 于点G ,连接AG ,EG ,现有以下结论:①△AFG 是等腰直角三角形;②DE+BG =EG ;③点A 到EG 的距离等于正方形的边长;④当点E 运动到CD 的三等分点时,BG BC =12或BG BC=13.以上结论正确的个数有()A.1个B.2个C.3个D.4个8.(2023·山东泰安·宁阳二中校考一模)如图,在矩形ABCD 中,AC ,BD 相交于点O ,过点B 作BF ⊥AC 于点M ,交CD 于点F ,过点D 作DE ∥BF 交AC 于点N .交AB 于点E ,连接FN ,EM .有下列结论:①图中共有三个平行四边形;②当BD =2BC 时,四边形DEBF 是菱形;③BD ⊥ME ;④AD 2=BD ⋅CM .其中,正确结论的序号是()A.①②③B.①②④C.①③④D.②③④9.(2023·广东深圳·模拟预测)如图,正方形ABCD 中,E 、F 分别为边AD 、DC 上的点,且AE =FC ,过F 作FH ⊥BE ,交AB 于G ,过H 作HM ⊥AB 于M ,若AB =9,AE =3,则下列结论中:①△ABE ≅△CBF ;②BE =FG ;③2DH =EH +FH ;④HM AE=35,其中结论正确有()A.1个B.2个C.3个D.4个10.(2023·浙江杭州·校联考一模)如图,在△ABC中,∠BAC=90°,AB=AC=12,点P在边AB上,D,E分别为BC,PC的中点,连接DE.过点E作BC的垂线,与BC,AC分别交于F,G两点.连接DG,交PC于点H.有以下判断:①∠EDC=45°;②DG⊥PE,且DG=PE;③当AP=6时,△APG的面积为9;④CHCE的最大值为2+12.其中正确的是()A.①③B.①③④C.①②④D.①②③④模块三〖考前预测〗11.(2023·山东东营·东营市东营区实验中学校考一模)如图,PA、PB是⊙O的切线,切点分别为A、B,BC是⊙O的直径,PO交⊙O于E点,连接AB交PO于F,连接CE交AB于D点.下列结论:①PA= PB;②OP⊥AB;③CE平分∠ACB;④OF=12AC;⑤E是△PAB的内心;⑥△CDA≌△EDF.其中一定成立的有( )个.A.5B.4C.3D.212.(2023·山东枣庄·校考模拟预测)如图,△ABC内接于⊙O,∠A所对弧的度数为120°.∠ABC、∠ACB的角平分线分别交于AC、AB于点D、E,CE、BD相交于点F.以下四个结论:①cos∠BFE=12;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号数是()A.①和②B.①和③C.②和③D.③和④13.(2023·天津·模拟预测)如图,△ABC 中,AC =BC ,点M ,N 分别在AC ,AB 上,将△AMN 沿直线MN 翻折,点A 的对应点D 恰好落在BC 边上(不含端点B ,C ),下列结论:①直线MN 垂直平分AD ;②∠CDM =∠BND ;③AD =CD ;④若M 是AC 中点,则AD ⊥BC .其中一定正确的是()A.①②B.②③C.①②④D.①③④14.(2023·安徽芜湖·统考一模)如图,在Rt △ABC 中,∠BAC =90°,AB =AC ,D 为线段BC 上一点,以AD 为一边构造Rt △ADE ,∠DAE =90°,AD =AE ,下列说法正确的是()①∠BAD =∠EDC ;②△ADO ∼△ACD ;③BD OE =AD AO ;④2AD 2=BD 2+CD 2.A.仅有①② B.仅有①②③ C.仅有②③④ D.①②③④15.(2023·广东惠州·模拟预测)如图,已知正方形ABCD 的边长为a ,E 为CD 边上一点(不与端点重合),将ΔADE 沿AE 翻折至△AFE ,延长EF 交边BC 于点G ,连接AG ,CF .则下列给出的判断:①∠EAG =45°;②若DE =13a ,则tan ∠GFC =2;③若E 为CD 的中点,则△GFC 的面积为110a 2;④若CF =FG ,则DE =(2-1)a ,其中正确的是()A.①②③B.①②④C.②③④D.①②③④16.(2023·广东深圳·一模)如图,将正方形ABCD 翻折,使点C 、D 分别与点C '、D '重合,折痕为MN ,C 'D '交AD 于点E ,CC 交MN 于点F ,连接CE 、C 'M .给出以下结论:①MN 垂直平分CC ;②DN +BC =CM ;③∠C CE =45°;④△AC 'E 的周长等于AB 的2倍.其中正确的个数有()A.1个B.2个C.3个D.4个17.(2023·山东青岛·模拟预测)如图,菱形ABCD 中,∠BAD =60°,AC 与BD 交于点O ,E 为CD 延长线上一点,且CD =DE ,连结BE ,分别交AC ,AD 于点F ,G ,连结OG ,①OG =12AB ②S 四边形ODGF =S △ABF ③由点A 、B 、D 、E 构成的四边形是菱形;④S △ACD =2S △ABG 中正确的结论是()A.①③B.②④C.①②③D.①②③④18.(2023·江苏无锡·模拟预测)如图,在平面直角坐标系中,点O 为坐标原点,矩形OABC 按如图所示摆放在第一象限,点B 的坐标为3m ,m ,将矩形OABC 绕着点O 逆时针旋转α(0<α<90°),得到矩形OA BC .直线OA 、B C 与直线BC 相交,交点分别为点D 、E ,有下列说法:①当m =1,α=30°时,矩形OA B C 与矩形OABC 重叠部分的面积为32;②当m =1,且B 落到y 轴的正半轴上时,DE 的长为103;③当点D 为线段BE 的中点时,点D 的横坐标为43m ;④当点D 是线段BE 的三等分点时,sin α的值为25或45.其中,说法正确的是()A.①②B.③④C.①②③D.①②④19.(2023·山东德州·统考一模)如图,在矩形ABCD中,AC,BD相交于点O,过点B作BF⊥AC于点M,交CD于点F,过点D作DE∥BF交AC于点N.交AB于点E,连接FN,EM.有下列结论:①四边形NEMF为平行四边形;②DN2=MC•NC;③△DNF为等边三角形;④当AO=AD时,四边形DEBF是菱形.其中,正确结论的序号是()A.①②④B.①②③C.①③D.②③④20.(2023·天津·一模)如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE,EF.下列结论:①AB=2BD;②图中有DFOE= 4对全等三角形;③BD=BF;④若将△DEF沿EF折叠,则点D不一定落在AC上;⑤S四边形S△AOF,上述结论中正确的个数是()A.1B.2C.3D.4。
中考数学几何多结论问题

∴正确的有4个. 故选D.
3. 如图,P为正方形ABCD的对角线BD上任一
点,过点P作PE⊥BC于点E,PF⊥CD于点F,
连接EF.给出以下4个结论:
①△FPD是等腰直角三角形;②AP=EF;③
AD=PD;④∠PFE=∠BAP.
其中,所有正确的结论是( )
A. ①②
B. ①④
C. ①②④
D. ①③④
∴FH≠FD, ∴S△EFH≠S△EFD, ∴S四边形EFHG=S△HEG+S△EFH=S△AHG+ S△EFH≠S△DEF+S△AGH,故③错误,
18. 如图,点E,F分别为正方形ABCD的边BC,
CD上一点,AC,BD交于点O,且∠EAF=
45°,AE,AF分别交对角线BD于点M,N,
则有以下结论:①△AOM∽△ADF;②EF=
∵CG=GF,∴∠CFG=∠FCG, ∵∠BGF=∠CFG+∠FCG, 又∵∠BGF=∠AGB+∠AGF, ∴∠CFG+∠FCG=∠AGB+∠AGF, ∵∠AGB=∠AGF,∠CFG=∠FCG, ∴∠AGB=∠FCG, ∴AG∥CF, ∴④正确;
8. 如图,在菱形ABCD中,AB=6,∠DAB=
60°,AE分别交BC,BD于点E,F,CE=2,
连接CF,以下结论:①△ABF≌△CBF;②
点E到AB的距离是 ;③AF=CF;④△ABF
的面积为 .其中一定成立的有( )个
A. 1
B. 2
C. 3 D. 4
10. 如图,在正方形ABCD中,E,F分别为BC,
CD的中点,连接AE,BF交于点G,将△BCF
11. 如图,正方形ABCD边长为6,E是BC的中
点,连接AE,以AE为边在正方形内部作
∠EAF=45°,边AF交CD于F,连接EF.则下
2022年九年级数学中考专题十一几何多结论题

专题11 几何多结论选择题一.试题(共14小题)1.如图,矩形ABCD中,AC,BD相交于点O,过点B作BF⊥AC交CD于点F,交AC于点M,过点D作DE ∥BF交AB于点E,交AC于点N,连接FN,EM.则下列结论:①DN=BM;②EM∥FN;③AE=FC;④当AO=AD时,四边形DEBF是菱形.其中,正确的结论是()A.①③B.①②③C.①③④D.①②③④2.如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确结论的个数为()A.1B.2C.3D.43.如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°.连接AC,BD交于点M,连接OM.下列结论:①∠AMB=36°,②AC=BD,③OM平分∠AOD,④MO平分∠AMD.其中正确的结论个数有()个.A.4B.3C.2D.14.如图,在△ABC中,AB=AC,AD和CE是高,∠ACE=45°,点F是AC的中点,AD与FE,CE分别交于点G、H,∠BCE=∠CAD,有下列结论:①图中存在两个等腰直角三角形;②△AHE≌△CBE;③BC•AD=√2AE2;④S△ABC=4S△ADF.其中正确的个数有()A .1B .2C .3D .45.已知如图等腰△ABC ,AB =AC ,∠BAC =120°,AD ⊥BC 于点D .点P 是BA 延长线上一点,O 点是线段AD 上一点,OP =OC ,下面的结论:①AC 平分∠P AD ;②∠APO =∠DCO ;③△OPC 是等边三角形;④AC =AO +AP ;⑤S △ABC =S 四边形AOCP .其中正确的序号是 .6.如图,分别以Rt △ABC 的斜边AB ,直角边AC 为边向外作等边△ABD 和等边△ACE ,F 为AB 的中点,DE ,AB 相交于点G ,若∠BAC =30°,下列结论:①EF ⊥AC ;②四边形ADFE 为菱形;③AD =4AG ;④△DBF ≌△EF A .其中正确结论的个数有( )A .1B .2C .3D .47.如图,在矩形ABCD 中,AD =√2AB ,AE 平分∠BAD ,DF ⊥AE 于F ,BF 交DE 、CD 于O 、H ,下列结论:①∠DEA =∠DEC ;②BF =FH ;③OE =OD ;④BC ﹣CH =2EF ;⑤AB =HF ,其中正确结论的个数是( )A .2个B .3个C .4个D .5个 8.如图,平行四边形ABCD 的对角线AC ,BD 相交于点O ,AE 平分∠BAD ,分别交BC ,BD 于点E ,P ,连接OE ,∠ADC =60°,AB =12BC =2,下列结论:①∠CAD =30°;②BD =2√7;③S 四边形ABCD =AB •AC ;④OE =14AD ;⑤S △BOE =√32.其中正确的个数有( )个A.2B.3C.4D.59.如图,在等腰Rt△ABC中,AB=AC,过A作直线交BC于G,BG<GC,BD⊥AG于D,CE⊥AD于E,F 为BC边中点,则下列结论中:①∠BAD=∠ACE;②BD=CE﹣ED;③FE=FD;④EF⊥DF,其中正确结论的个数为()A.1个B.2个C.3个D.4个10.如图,已知△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=90°,BD,CE交于点F,连接AF.下列结论:①BD=CE;②BF⊥CF;③AF平分∠CAD;④∠AFE=45°.其中正确结论的个数有()A.1个B.2个C.3个D.4个11.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=3:2.其中正确结论的个数是()A.4个B.3个C.2个D.1个12.如图,在平行四边形ABCD中,AD=2AB,CE⊥AB于点E,点F、G分别是AD、BC的中点,连接CF、EF、FG,下列结论:①CE⊥FG;②四边形ABGF是菱形;③EF=CF;④∠EFC=2∠CFD.其中正确的个数是()A.1个B.2个C.3个D.4个13.如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③BC平分∠ABD;④AF=DF;⑤BD=2OF.其中正确结论的个数是()A.2B.3C.4D.514.如图,△ABC中,AB=AC,以AB为直径的⊙O交AC于E,交BC于D,DF⊥AC于F.给出以下五个结论:①BD=DC;②CF=EF;③弧AE=弧DE;④∠A=2∠FDC;⑤DF是⊙O的切线.其中正确的有()A.5个B.4个C.3个D.2个专题11 几何多结论选择题参考答案与试题解析一.试题(共14小题)1.【解答】解:∵四边形ABCD 是矩形,∴AB =CD ,AB ∥CD ,∠DAE =∠BCF =90°,OD =OB =OA =OC ,AD =BC ,AD ∥BC , ∴∠DAN =∠BCM ,∵BF ⊥AC ,DE ∥BF ,∴DE ⊥AC ,∴∠DNA =∠BMC =90°,在△DNA 和△BMC 中,{∠DAN =∠BCM ∠DNA =∠BMC AD =BC,∴△DNA ≌△BMC (AAS ),∴DN =BM ,∠ADE =∠CBF ,故①正确;在△ADE 和△CBF 中,{∠ADE =∠CBF AD =BC ∠DAE =∠BCF,∴△ADE ≌△CBF (ASA ),∴AE =FC ,DE =BF ,故③正确;∴DE ﹣DN =BF ﹣BM ,即NE =MF ,∵DE ∥BF ,∴四边形NEMF 是平行四边形,∴EM ∥FN ,故②正确;∵AB =CD ,AE =CF ,∴BE =DF ,∵BE ∥DF ,∴四边形DEBF 是平行四边形,∵AO =AD ,∴AO =AD =OD ,∴△AOD 是等边三角形,∴∠ADO =∠DAN =60°,∴∠ABD =90°﹣∠ADO =30°,∵DE ⊥AC ,∴∠ADN =∠ODN =30°,∴∠ODN =∠ABD ,∴DE =BE ,∴四边形DEBF 是菱形;故④正确;故选:D .2.【解答】证明:∵BC =EC ,∴∠CEB =∠CBE ,∵四边形ABCD 是平行四边形,∴DC ∥AB ,∴∠CEB=∠EBF,∴∠CBE=∠EBF,∴①BE平分∠CBF,正确;∵BC=EC,CF⊥BE,∴∠ECF=∠BCF,∴②CF平分∠DCB,正确;∵DC∥AB,∴∠DCF=∠CFB,∵∠ECF=∠BCF,∴∠CFB=∠BCF,∴BF=BC,∴③正确;∵FB=BC,CF⊥BE,∴B点一定在FC的垂直平分线上,即PB垂直平分FC,∴PF=PC,故④正确.故选:D.3.【解答】解:∵∠AOB=∠COD=36°,∴∠AOB+∠BOC=∠COD+∠BOC,即∠AOC=∠BOD,在△AOC和△BOD中,{OA=OB∠AOC=∠BOD OC=OD∴△AOC≌△BOD(SAS),∴∠OCA=∠ODB,AC=BD,故②正确;∵∠OAC=∠OBD,由三角形的外角性质得:∠AMB+∠OBD=∠OAC+∠AOB,∴∠AMB=∠AOB=36°,故①正确;法一:作OG⊥AM于G,OH⊥DM于H,如图所示,则∠OGA=∠OHB=90°,∵△AOC≌△BOD,∴OG =OH ,∴MO 平分∠AMD ,故④正确;法二:∵△AOC ≌△BOD ,∴∠OAC =∠OBD ,∴A 、B 、M 、O 四点共圆,∴∠AMO =∠ABO =72°,同理可得:D 、C 、M 、O 四点共圆,∴∠DMO =∠DCO =72°=∠AMO ,∴MO 平分∠AMD ,故④正确;假设MO 平分∠AOD ,则∠DOM =∠AOM ,在△AMO 与△DMO 中,{∠AOM =∠DOMOM =OM ∠AMO =∠DMO,∴△AMO ≌△DMO (ASA ),∴AO =OD ,∵OC =OD ,∴OA =OC ,而OA <OC ,故③错误;正确的个数有3个;故选:B .4.【解答】解:∵CE ⊥AB ,∠ACE =45°,∴△ACE 是等腰直角三角形,∵AF =CF ,∴EF =AF =CF ,∴△AEF ,△EFC 都是等腰直角三角形,∴图中共有3个等腰直角三角形,故①错误,∵∠AHE +∠EAH =90°,∠DHC +∠BCE =90°,∠AHE =∠DHC ,∴∠EAH =∠BCE ,∵AE =EC ,∠AEH =∠CEB =90°,∴△AHE ≌△CBE ,故②正确,∵S △ABC =12BC •AD =12AB •CE ,AB =AC =√2AE ,AE =CE ,∴BC •AD =√2CE 2,故③正确,∵AB =AC ,AD ⊥BC ,∴BD =DC ,∴S △ABC =2S △ADC ,∵AF =FC ,∴S △ADC =2S △ADF ,∴S △ABC =4S △ADF .故选:C .5.【解答】解:①∵AB=AC,∠BAC=120°,AD⊥BC;∴∠CAD=12∠BAC=60°,∠P AC=180°﹣∠CAB=60°,∴∠P AC=∠DAC,∴AC平分∠P AD故①正确;②由①知:∠APO=∠ABO,∠DCO=∠DBO,∵点O是线段AD上一点,∴∠ABO与∠DBO不一定相等,则∠APO与∠DCO不一定相等,故②不正确;③∵∠APC+∠DCP+∠PBC=180°,∴∠APC+∠DCP=150°,∵∠APO+∠DCO=30°,∴∠OPC+∠OCP=120°,∴∠POC=180°﹣(∠OPC+∠OCP)=60°,∵OP=OC,∴△OPC是等边三角形;故③正确;④如图2,在AC上截取AE=P A,连接PB,∵∠P AE=180°﹣∠BAC=60°,∴△APE是等边三角形,∴∠PEA=∠APE=60°,PE=P A,∴∠APO+∠OPE=60°,∵∠OPE+∠CPE=∠CPO=60°,∴∠APO=∠CPE,∵OP=CP,在△OP A和△CPE中,{PA=PE∠APO=∠CPE OP=CP,∴△OP A≌△CPE(SAS),∴AO=CE,∴AC=AE+CE=AO+AP;故④正确;如图3,过点C作CH⊥AB于H,∵∠P AC=∠DAC=60°,AD⊥BC,∴CH=CD,∴S△ABC=12AB•CH,S 四边形AOCP =S △ACP +S △AOC =12AP •CH +12OA •CD =12AP •CH +12OA •CH =12H •(AP +OA )=12CH •AC , ∴S △ABC =S 四边形AOCP ;故⑤正确.本题正确的结论有:①③④⑤故答案为:①③④⑤.6.【解答】解:连接FC ,如图所示:∵∠ACB =90°,F 为AB 的中点,∴F A =FB =FC ,∵△ACE 是等边三角形,∴EA =EC ,∵F A =FC ,EA =EC ,∴点F 、点E 都在线段AC 的垂直平分线上,∴EF 垂直平分AC ,即EF ⊥AC ;∵△ABD 和△ACE 都是等边三角形,F 为AB 的中点,∴DF ⊥AB 即∠DF A =90°,BD =DA =AB =2AF ,∠DBA =∠DAB =∠EAC =∠ACE =60°. ∵∠BAC =30°,∴∠DAC =∠EAF =90°,∴∠DF A =∠EAF =90°,DA ⊥AC ,∴DF ∥AE ,DA ∥EF ,∴四边形ADFE 为平行四边形而不是菱形;∵四边形ADFE 为平行四边形,∴DA =EF ,AF =2AG ,∴BD =DA =EF ,DA =AB =2AF =4AG ;在△DBF 和△EF A 中,{BD =FE ∠DBF =∠EFA BF =FA,∴△DBF ≌△EF A ;综上所述:①③④正确,故选:C .7.【解答】解:∵四边形ABCD为矩形,AE平分∠BAD,∴∠BAE=∠DAE=∠AEB=45°,∵∠AFD=∠ABE=90°,∴△AFD与△ABE都为等腰直角三角形,即AF=DF,AB=BE,∴AE=√2AB,又∵AD=√2AB,∴AD=AE,∴∠AED=∠ADE=67.5°,∴∠DEC=180°﹣45°﹣67.5°=67.5°,∴∠DEA=∠DEC,选项①正确;过F作GM⊥AD,与AD交于G点,与BC交于M点,利用三线合一得到G为AD中点,∴F为BH中点,M为BC中点,∴BF=FH,选项②正确;∵AD=√2AF,AD=√2AB,∴AF=AB,∴∠AFB=67.5°,∴∠OFE=∠OEF=67.5°,∴OE=OF,∴∠ODF=∠OFD=22.5°,∴OF=OD,∴OD=OE,选项③正确;∴∠DEF=67.5°﹣45°=22.5°,∠EDC=90°﹣67.5°=22.5°,∴∠EDF=∠DEC,∵EF⊥DF,EC⊥CD,∴EF=EC,∵△EFM为等腰直角三角形,∴FM=ME,∴BC﹣CH=2CM﹣2FM=2CM﹣2ME=2EF,选项④正确;∵AB=AF,∠BAE=45°,∴△ABF不是等边三角形,∴AB≠BF,∴即AB≠HF,故⑤错误;综上所述,结论正确的是①②③④.则正确的序号有4个.故选:C.8.【解答】解:①∵AE平分∠BAD,∴∠BAE=∠DAE,∵四边形ABCD是平行四边形,∴AD∥BC,∠ABC=∠ADC=60°,∴∠DAE=∠BEA,∴∠BAE=∠BEA,∴AB=BE=2,∴△ABE是等边三角形,∴AE=BE=2,∵BC=4,∴EC=2,∴AE=EC,∴∠EAC=∠ACE,∵∠AEB=∠EAC+∠ACE=60°,∴∠ACE=30°,∵AD∥BC,∴∠CAD=∠ACE=30°,故①正确;②∵BE=EC,OA=OC,∴OE=12AB=1,OE∥AB,∴∠EOC=∠BAC=60°+30°=90°,Rt△EOC中,OC=√EC2−OE2=√3,∵四边形ABCD是平行四边形,∴∠BCD=∠BAD=120°,∴∠ACB=30°,∴∠ACD=90°,Rt△OCD中,OD=√OC2+CD2=√7 BD=2OD=2√7故②正确③由②知:∠BAC=90°,∴S▱ABCD=AB•AC,故③正确;④由②知:OE是△ABC的中位线,∴OE=12AB,∵AB=12BC,∴OE=14BC=14AD,故④正确;⑤∵BE=EC=2∴S△BOE=S△EOC=12OE•OC=√32故⑤正确故选:D.9.【解答】解:如图连接AF.∵AB=AC,BF=FC,∴AF⊥BC,∵BD⊥AD,CE⊥AD,∴∠ADB=∠AEC=∠BAC=90°,∵∠CAE+∠BAD=90°,∠BAD+∠ABD=90°,∴∠CAE=∠ABD,故①正确,∴△ABD≌△CAE(AAS),∴BD=AE,AD=CE,∴CE﹣ED=AD﹣DE=AE=BD,故②正确,∵∠BAC=90°,BF=FC,∴AF=BF=FC,∵∠AGF=∠BGF,∠BDG=∠AFG=90°,∴∠DBG=∠GAF,∵AE=BD,∴△FBD≌△FEA(SAS),∴EF=DF,∠AFE=∠BFD,∴∠AFB=∠EFD=90°,∴EF⊥DF,故③④正确.故选:D.10.【解答】解:如图,作AM⊥BD于M,AN⊥EC于N,设AD交EF于O.∵∠BAC=∠DAE=90°,∴∠BAD=∠CAE,∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS),∴EC=BD,∠BDA=∠AEC,故①正确∵∠DOF=∠AOE,∴∠DFO=∠EAO=90°,∴BD⊥EC,故②正确,∵△BAD≌△CAE,AM⊥BD,AN⊥EC,∴AM=AN,∴F A平分∠EFB,∴∠AFE=45°,故④正确,若③成立,则∠EAF=∠BAF,∵∠AFE=∠AFB,∴∠AEF=∠ABD=∠ADB,推出AB=AD,由题意知,AB不一定等于AD,所以AF不一定平分∠CAD,故③错误,故选:C.11.【解答】解:①∵矩形ABCD中,O为AC中点,∴OB=OC,∵∠COB=60°,∴△OBC是等边三角形,∴OB=BC,∵FO=FC,∴FB垂直平分OC,故①正确;②∵△BOC为等边三角形,FO=FC,∴BO⊥EF,BF⊥OC,∴∠CMB=∠EOB=90°,∴BO≠BM,∴△EOB与△CMB不全等;故②错误;③易知△ADE≌△CBF,∠1=∠2=∠3=30°,∴∠ADE=∠CBF=30°,∠BEO=60°,∴∠CDE=60°,∠DFE=∠BEO=60°,∴∠CDE=∠DFE,∴DE=EF,故③正确;④易知△AOE≌△COF,∴S△AOE=S△COF,∵S△COF=2S△CMF,∴S△AOE:S△BCM=2S△CMF:S△BCM=2FMBM,∵∠FCO=30°,∴FM=CM√3,BM=√3CM,∴FMBM=13,∴S△AOE:S△BCM=2:3,故④错误;所以其中正确结论的个数为2个;故选:C.12.【解答】解:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∵点F、G分别是AD、BC的中点,∴AF=12AD,BG=12BC,∴AF=BG,∵AF∥BG,∴四边形ABGF是平行四边形,∴AB∥FG,∵CE⊥AB,∴CE⊥FG;故①正确;∵AD=2AB,AD=2AF,∴AB=AF,∴四边形ABGF是菱形,故②正确;延长EF,交CD延长线于M,∵四边形ABCD是平行四边形,∴AB∥CD,∴∠A=∠MDF,∵F为AD中点,∴AF=FD,在△AEF和△DFM中,{∠A=∠FDM AF=DF∠AFE=∠DFM,∴△AEF≌△DMF(ASA),∴FE=MF,∠AEF=∠M,∵CE⊥AB,∴∠AEC=90°,∴∠AEC=∠ECD=90°,∵FM=EF,∴FC=EF=FM,故③正确;∴∠FCD=∠M,∵四边形ABCD是平行四边形,∴AB=CD,AD∥BC,∵AF=DF,AD=2AB,∴DF=DC,∴∠DCF=∠DFC,∴∠M=∠FCD=∠CFD,∵∠EFC=∠M+∠FCD=2∠CFD;故④正确,故选:D.13.【解答】解:∵AB是⊙O的直径,∴∠ADB=90°,即AD⊥BD,故①正确;∵∠AEC=∠DAB+∠EBA,∠AOC=2∠EBA,∴∠AOC≠∠AEC,故②不正确;∵OC∥BD,∴∠OCB=∠CBD,∵OC=OB,∴∠OCB=∠OBC,∴∠OBC=∠CBD,即BC平分∠ABD,故③正确;∴OC⊥AD,∴AF=FD,故④正确;∴OF为△ABD的中位线,∴BD=2OF,故⑤正确,综上可知正确的有4个,故选:C.14.【解答】解:连接OD,AD.∵AB是⊙O的直径,∴∠ADB=90°(直径所对的圆周角是直角),∴AD⊥BC;而在△ABC中,AB=AC,∴AD是边BC上的中线,∴BD=DC(正确);∵AB是⊙O的直径,∴AD⊥BC,∵AB=AC,∴DB=DC,∵OA=OB,∴OD是△ABC的中位线,即:OD∥AC,∵DF⊥AC,∴DF⊥OD.∴DF是⊙O的切线(正确);∵DF⊥AC,AD⊥BC,∴∠FDC+∠C=∠CAD+∠C=90°,∴∠FDC=∠CAD,又AB=AC,∴∠BAD=∠CAD,∴∠A=2∠CAD=2∠FDC(正确);∵DF是⊙O的切线,∴∠FDE=∠CAD=∠FDC,∴∠C=∠DEC,∴DC=DE,又DF⊥AC,∴CF=EF(正确);̂=DÊ,此时△ABC为等边三角形,当∠EAD=∠EDA时,AE当△ABC不是等边三角形时,∠EAD≠∠EDA,̂≠DÊ,则AÊ=DÊ(不正确);∴AE综上,正确结论的序号是①②④⑤,故选:B.。
2023年中考地理复习:七年级下册综合题提分练习

七年级下册地理中考复习综合题提分练习1. 阅读图文材料,完成问题。
材料一番茄喜温、光。
工业番茄果皮厚,利于机械化作业。
欧洲番茄酱消费量巨大。
农产品加工业是意大利的第三大工业部门,完善的旅游设施及服务使意大利的入境旅游收入居世界前列。
随“一带一路”的发展,意大利与哈萨克斯坦开展了番茄种植业、旅游业的国际合作。
材料二中亚区域图(图1),阿斯塔纳气候资料图(图2)材料三意大利主要风景名胜分布图(图3)(1)描述中亚地区的地势特点。
(2)分析哈萨克斯坦番茄种植的有利气候条件,简述两国番茄合作如何实现互利共赢。
(3)分析意大利吸引中亚居民出境游的优势条件。
2. 随着“一带一路”倡议逐步落实,沿线众多国家的命运更紧密地交织在了一起,每天有大量人员和物资往返于中国和“一带一路”沿线,其中往来最频繁的区域,就是东南亚地区。
读东南亚简图,曼谷气温曲线和降水量柱状图,完成下列问题。
东南亚简图曼谷气温曲线和降水量柱状图(1)东南亚地处亚洲和、太平洋和印度洋之间的“十字路口”,图中①海峡是其“咽喉要道”。
图中河流②是,依据该河的流向判断,中南半岛的部地势较高。
(2)曼谷是的首都,据“曼谷气温曲线和降水量柱状图”,曼谷属于气候。
(3)来自中国电商网站的采购员来到曼谷郊区的一家工厂,确认一批发往中国的货物包裹,请你猜测包裹里装的可能是。
3. 读下图,完成下列各题。
(1)印度冬季吹 (风向)季风,为 (雨/旱)季;夏季吹 (风向)季风,为(雨/旱)季。
(2)印度大部分地区位于带和亚热带,以气候为主。
该气候对印度发展农业的有利条件是光热,雨季降水不利条件是雨季降水,易形成灾;旱季降水易形成灾。
4. 图左为世界局部区域图,图右为伊朗等高线地形图。
读图,完成下列各题。
(1)2021年3月23日,一艘重型货船在A运河搁浅,该运河是洲与洲两大洲的分界线。
(2)2021年3月,中国与伊朗签署一项长达25年的全面合作协议。
中国将从伊朗进口(矿产),该矿产从波斯湾运出的唯一出口是B海峡。
广东省深圳市中考数学复习 多结论几何综合题专题-人教版初中九年级全册数学试题

多结论几何综合题专题试卷一、单选题1、如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①tan∠AEC=;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的个数是()A、1个B、2个C、3个D、4个2、如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC 绕点A 顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△AED≌△AEF;②=;③△ABC的面积等于四边形AFBD的面积;④BE2+DC2=DE2⑤BE+DC=DE;其中正确的是( )A、①②④B、③④⑤C、①③④D、①③⑤3、如图,将等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD ,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形;④BD⊥DE;其中正确的个数是().A、1B、2C、3D、4 4、如图,把一X长方形纸片ABCD沿对角线BD折叠,使C点落在E处,BE与AD相交于点F,下列结论:①BD=AD 2+AB2;②△ABF≌△EDF;③=④AD=BD•cos45°.其中正确的一组是()A、①②B、②③C、①④D、③④5、如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE 、DF交于点O.下列结论:①∠DOC=90°,②OC=OE,③tan∠OCD= ,④S△ODC=S 四边形BEOF中,正确的有()A、1个B、2个C、3个D、4个6、如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③△GDE∽△BEF;④S△BEF=.在以上4个结论中,正确的有()A、1B、2C、3D、47、如图,▱ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC 于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S ▱ABCD=AB•AC;③OB=AB;④OE=BC,成立的个数有()A、1个B、2个C、3个D、4个8、如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下列四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④AE+DF=AF+DE.其中正确的是()A、②③B、②④C、①③④D、②③④9、如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE ,AE⊥EF,AE=EF,现有如下结论:①BE=GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH,其中,正确的结论有()A、1个B、2个C、3个D、4个10、如图,PA=PB,OE⊥PA,OF⊥PB,则以下结论:①OP是∠APB的平分线;②PE=PF③CA=BD;④CD∥AB;其中正确的有()个.A、4B、3C、2D、1 11、如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B 与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF.下列结论:①tan∠ADB=2;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点D不一定落在AC上;④BD=BF;⑤S四边形DFOE=S△AOF,上述结论中正确的个数是()A、1个B、2个C、3个D、4个12、如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:①AC=AD;②BD⊥AC;③四边形ACED是菱形.其中正确的个数是()A、0B、1C、2D、313、如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF 为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ•AC,其中正确的结论的个数是()A、1B、2C、3D、414、如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是()A、4个B、3个C、2个D、1个15、(2016•某某)如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:①∠ADG=22.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG;⑥若S△OGF=1,则正方形ABCD的面积是6+4 ,其中正确的结论个数为()A、2B、3C、4D、516、如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是()①AE=BF;②AE⊥BF;③sin∠B QP= ;④S四边形ECFG=2S△BGE.A、4B、3C、2D、1 17、如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣2,0)、B(1,0),直线x=﹣0.5与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC、BC、AD、BD,某同学根据图象写出下列结论:①a﹣b=0;②当﹣2<x<1时,y>0;③四边形ACBD是菱形;④9a﹣3b+c>0你认为其中正确的是()A、②③④B、①②④C、①③④D、①②③18、如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是()A、2B、3C、4D、519、如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足=,连接AF并延长交⊙O于点E,连接AD ,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE= ;④S△DEF=4 ,其中正确的是()A、①②③B、②③④C、①②④D、①③④20、如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB 于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB 于点P、Q,连接AC,给出下列结论:①∠DAC=∠ABC;②AD=CB;③点P是△ACQ的外心;④AC2=AE•AB;⑤CB∥GD,其中正确的结论是()A、①③⑤B、②④⑤C、①②⑤D、①③④答案解析部分一、单选题1、【答案】D 【考点】等腰三角形的性质,梯形中位线定理,锐角三角函数的定义【解析】【分析】①根据等腰直角三角形的性质及△ABC∽△CDE的对应边成比例知,;然后由直角三角形中的正切函数,得tan∠AEC=,再由等量代换求得tan∠AEC=;②由三角形的面积公式、梯形的面积公式及不等式的基本性质a2+b2≥2ab(a=b 时取等号)解答;③、④通过作辅助线MN,构建直角梯形的中位线,根据梯形的中位线定理及等腰直角三角形的判定定理解答.【解答】解:∵△ABC和△CDE均为等腰直角三角形,∴AB=BC,CD=DE,∴∠BAC=∠BCA=∠DCE=∠DEC=45°,∴∠ACE=90°;∵△ABC∽△CDE∴①∴tan∠AEC=,∴tan∠AEC=;故本选项正确;②∵S△ABC =a2, S△CDE=b2, S梯形ABDE=(a+b)2,∴S△ACE=S 梯形ABDE-S△ABC-S△CDE=ab ,S△ABC+S△CDE=(a2+b2)≥ab(a=b时取等号),∴S△ABC+S△CDE≥S△ACE;故本选项正确;④过点M作MN垂直于BD,垂足为N.∵点M是AE的中点,则MN为梯形中位线,∴N 为中点,∴△BMD 为等腰三角形,∴BM=DM;故本选项正确;③又MN=(AB+ED)=(BC+CD),∴∠BMD=90°,即BM⊥DM;故本选项正确.故选D.【点评】本题综合考查了等腰直角三角形的判定与性质、梯形的中位线定理、锐角三角函数的定义等知识点.在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.2、【答案】C 【考点】全等三角形的判定,勾股定理,相似三角形的判定,旋转的性质【解析】【分析】①根据旋转的性质知∠CAD=∠BAF,AD=AF,因为∠BAC=90°,∠DAE=45°,所以∠CAD+∠BAE=45°,可得∠EAF=45°=∠DAE,由此即可证明△AEF≌△AED;②当△ABE∽△ACD时,该比例式成立;③根据旋转的性质,△ADC≌△ABF,进而得出△ABC的面积等于四边形AFBD的面积;④据①知BF=CD,EF=DE,∠FBE=90°,根据勾股定理判断.⑤根据①知道△AEF≌△AED,得CD=BF,DE=EF;由此即可确定该说法是否正确;【解答】①根据旋转的性质知∠CAD=∠BAF,AD=AF,∵∠BAC=90°,∠DAE=45°,∴∠CAD+∠BAE=45°.∴∠EAF=45°,∴△AED≌△AEF;故本选项正确;②∵AB=AC,∴∠ABE=∠ACD;∴当∠BAE=∠CAD时,△ABE∽△ACD,∴=;当∠BAE≠∠CAD 时,△ABE与△ACD不相似,即≠;∴此比例式不一定成立;故本选项错误;③根据旋转的性质知△ADC≌△AFB,∴S△ABC=S△ABD+S△ABF=S四边形AFBD,即三角形ABC的面积等于四边形AFBD的面积;故本选项正确;④∵∠FBE=45°+45°=90°,∴BE2+BF2=EF2,∵△ADC绕点A顺时针旋转90°后,得到△AFB,∴△AFB≌△ADC,∴BF=CD,又∵EF=DE,∴BE2+DC2=DE2,故本选项正确;⑤根据①知道△AEF≌△AED,得CD=BF,DE=EF,∴BE+DC=BE+BF>DE=EF,即BE+DC>DE,故本选项错误;综上所述,正确的说法是①③④;故选C.【点评】此题主要考查了图形的旋转变换以及全等三角形的判定等知识,解题时注意旋转前后对应的相等关系.3、【答案】D 【考点】等边三角形的性质,菱形的判定与性质,平移的性质【解析】【解答】∵△ABC、△DCE是等边三角形,∴∠ACB=∠DCE=60°,AC=CD ,∴∠ACD=180°-∠ACB-∠DCE=60°,∴△ACD是等边三角形,∴AD=AC=BC ,故①正确;由①可得AD=BC ,∵AB =CD ,∴四边形ABCD是平行四边形,∴BD、AC互相平分,故②正确;由①可得AD=AC=CE=DE ,故四边形ACED是菱形,即③正确;∵四边形ACED是菱形,∴AC⊥BD ,∵AC∥DE ,∴∠BDE=∠COD=90°,∴BD⊥DE ,故④正确;综上可得①②③④正确,共4个,故选D.【分析】先求出∠ACD=60°,继而可判断△ACD是等边三角形,从而可判断①是正确的;根据①的结论,可判断四边形ABCD是平行四边形,从而可判断②是正确的;根据①的结论,可判断③正确;根据菱形的对角线互相垂直可得AC⊥BD ,再根据平移后对应线段互相平行可得∠BDE=∠COD=90°,进而判断④正确.4、【答案】B 【考点】勾股定理,翻折变换(折叠问题),相似三角形的判定与性质,特殊角的三角函数值【解析】【解答】①∵△ABD为直角三角形,∴BD2=AD2+AB2,不是BD=AD2+AB2,故说法错误;②根据折叠可知:DE=CD=AB,∠A=∠E,∠AFB=∠EFD,∴△ABF≌△EDF,故说法正确;③根据②可以得到△ABF∽△EDF,∴=,故说法正确;④在Rt△ABD 中,∠ADB≠45°,∴AD≠BD•cos45°,故说法错误.所以正确的是②③.故选B.【分析】①直接根据勾股定理即可判定是否正确;②利用折叠可以得到全等条件证明△ABF≌△EDF;③利用全等三角形的性质即可解决问题;④在Rt△ABD中利用三角函数的定义即可判定是否正确.此题主要考查了折叠问题,也考查了勾股定理、相似三角形的性质、全等三角形的性质及三角函数的定义,它们的综合性比较强,对于学生的综合能力要求比较高,平时加强训练.5、【答案】C 【考点】全等三角形的判定与性质,勾股定理,正方形的性质,锐角三角函数的定义【解析】【解答】解:∵正方形ABCD的边长为4,∴BC=CD=4,∠B=∠DCF=90°,∵AE=BF=1,∴BE=CF=4﹣1=3,在△EBC和△FCD中,∴△EBC≌△FCD(SAS),∴∠CFD=∠BEC,∴∠BCE+∠BEC=∠BCE+∠CFD=90°,∴∠DOC=90°;故①正确;若OC=OE,∵DF⊥EC,∴CD=DE,∵CD=AD<DE(矛盾),故②错误;∵∠OCD+∠CDF=90°,∠CDF+∠DFC=90°,∴∠OCD=∠DFC,∴tan∠OCD=tan∠D FC= = ,故③正确;∵△EBC≌△FCD,∴S△EBC=S△FCD,∴S△EBC﹣S△FOC=S△FCD﹣S△FOC,即S△ODC=S四边形BEOF.故④正确.故选C.【分析】由正方形ABCD的边长为4,AE=BF=1,利用SAS易证得△EBC≌△FCD,然后全等三角形的对应角相等,易证得①∠DOC=90°正确;②由线段垂直平分线的性质与正方形的性质,可得②错误;易证得∠OCD=∠DFC,即可求得③正确;由①易证得④正确.6、【答案】C 【考点】全等三角形的判定与性质,正方形的性质,翻折变换(折叠问题),相似三角形的判定与性质【解析】【解答】由折叠可知,DF=DC=DA,∠DFE=∠C=90°,∴∠DFG=∠A=90°,∴△ADG≌△FDG,①正确;∵正方形边长是12,∴BE=EC=EF=6,设AG=FG=x,则EG=x+6,BG=12﹣x,由勾股定理得:EG2=BE2+BG2,即:(x+6)2=62+(12﹣x)2,解得:x=4∴AG=GF=4,BG=8,BG=2AG,②正确;BE=EF=6,△BEF是等腰三角形,易知△GED不是等腰三角形,③错误;S△GBE=×6×8=24,S△BEF=•S△GBE==,④正确.故选:C.【分析】根据正方形的性质和折叠的性质可得AD=DF,∠A=∠GFD=90°,于是根据“HL”判定△ADG≌△FDG,再由GF+GB=GA+GB=12,EB=EF,△BGE为直角三角形,可通过勾股定理列方程求出AG=4,BG=8,进而求出△BEF的面积,再抓住△BEF是等腰三角形,而△GED显然不是等腰三角形,判断③是错误的.7、【答案】C 【考点】等边三角形的判定与性质,含30度角的直角三角形,平行四边形的性质【解析】【解答】∵四边形ABCD 是平行四边形,∴∠ABC=∠ADC=60°,∠BAD=120°,∵AE平分∠BAD,∴∠BAE=∠EAD=60°∴△ABE是等边三角形,∴AE=AB=BE,∵AB=BC,∴AE=BC,∴∠BAC=90°,∴∠CAD=30°,故①正确;∵AC⊥AB,∴S ▱ABCD=AB•AC,故②正确,∵AB=BC,OB=BD,∵BD>BC,∴AB≠OB,故③错误;∵CE=BE,CO=OA ,∴OE=AB ,∴OE=BC,故④正确.故选:C.【分析】由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据AE 平分∠BAD,得到∠BAE=∠EAD=60°推出△ABE是等边三角形,由于AB=BC,得到AE=BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正确;由于AC⊥AB,得到S▱ABCD=AB•AC,故②正确,根据AB=BC,OB=BD,且BD>BC,得到AB≠OB,故③错误;根据三角形的中位线定理得到OE=AB,于是得到OE=BC,故④正确.8、【答案】D 【考点】全等三角形的判定与性质,角平分线的性质,正方形的判定【解析】【解答】如果OA=OD,则四边形AEDF是矩形,∠A=90°,不符合题意,∴①不正确;∵AD是△ABC的角平分线,∴∠EAD∠FAD,在△AED和△AFD中,∴△AED≌△AFD (AAS),∴AE=AF,DE=DF,∴AE+DF=AF+DE,∴④正确;在△AEO和△AFO中,,∴△AE0≌△AF0(SAS),∴EO=FO,又∵AE=AF,∴AO是EF的中垂线,∴AD⊥EF,∴②正确;∵当∠A=90°时,四边形AEDF的四个角都是直角,∴四边形AEDF是矩形,又∵DE=DF,∴四边形AEDF是正方形,∴③正确.综上,可得正确的是:②③④.故选:D.【分析】①如果OA=OD,则四边形AEDF是矩形,∠A=90°,不符合题意,所以①不正确.②首先根据全等三角形的判定方法,判断出△AED≌△AFD,AE=AF,DE=DF;然后根据全等三角形的判定方法,判断出△AE0≌△AFO,即可判断出AD⊥EF.③首先判断出当∠A=90°时,四边形AEDF的四个角都是直角,四边形AEDF是矩形,然后根据DE=DF,判断出四边形AEDF是正方形即可.④根据△AED≌△AFD,判断出AE=AF,DE=DF,即可判断出AE+DF=AF+DE 成立,据此解答即可.9、【答案】B 【考点】全等三角形的判定与性质,正方形的性质,相似三角形的判定与性质【解析】【解答】∵四边形ABCD 是正方形,∴∠B=∠DCB=90°,AB=BC,∵AG=CE,∴BG=BE,由勾股定理得:BE=GE,∴①错误;∵BG=BE,∠B=90°,∴∠BGE=∠BEG=45°,∴∠AGE=135°,∴∠GAE+∠AEG=45°,∵AE⊥EF,∴∠AEF=90°,∵∠BEG=45°,∴∠AEG+∠FEC=45°,∴∠GAE=∠FEC,在△GAE和△CEF中∴△GAE≌△CEF,∴②正确;∴∠AGE=∠ECF=135°,∴∠FCD=135°﹣90°=45°,∴③正确;∵∠BGE=∠BEG=45°,∠AEG+∠FEC=45°,∴∠FEC<45°,∴△GBE和△ECH不相似,∴④错误;即正确的有2个.故选B.【分析】根据正方形的性质得出∠B=∠DCB=90°,AB=BC,求出BG=BE,根据勾股定理得出BE=GE,即可判断①;求出∠GAE+∠AEG=45°,推出∠GAE=∠FEC,根据SAS推出△GAE≌△CEF,即可判断②;求出∠AGE=∠ECF=135°,即可判断③;求出∠FEC<45°,根据相似三角形的判定得出△GBE和△ECH不相似,即可判断④.10、【答案】A 【考点】全等三角形的判定与性质,圆心角、弧、弦的关系,相似三角形的判定与性质【解析】【解答】连接OP、OC、OA、OD、OB、CD、AB.∵PC•PA=PD•PB(相交弦定理),PA=PB(已知),∴PC=PD,∴AC=BD;在△AOC和△BOD中,∵∠AOC=∠BOD(等弦对等角),OA=OB (半径),OD=OC (半径),∴△AOC≌△BOD,∴③CA=BD;OE=OF;又∵OE⊥PA,OF⊥PB,∴①OP是∠APB的平分线;∴②PE=PF;在△PCD和△PAB中,PC:PA=PD:PB,∠DPC=∠BPA,∴△PCD∽△PAB,∴∠PDC=PBA,∴④CD∥AB;综上所述,①②③④均正确,故答案选A.【分析】①通过证明△AOC≌△BOD,再根据全等三角形的对应高相等求得OE=OF;再根据角平分线的性质证明OP是∠APB的平分线;②由角平分线的性质证明PE=PF;③通过证明△AOC≌△BOD,再根据全等三角形的对应边相等求得CA=BD;④通过证明△PCD∽△PAB,再根据相似三角形的性质对应角相等证得∠PDC=PBA;然后由平行线的判定得出结论CD∥AB.11、【答案】C 【考点】全等三角形的判定与性质,翻折变换(折叠问题),锐角三角函数的定义【解析】【解答】①由折叠可得BD=DE,而DC>DE,∴DC>BD,∴tan∠ADB≠2,故①错误;②图中的全等三角形有△ABF≌△AEF,△ABD≌△AED,△FBD≌△FED,(由折叠可知)∵OB⊥AC,∴∠AOB=∠COB=90°,在Rt△AOB和Rt△COB中,AB="CB" ,BO=BO ,∴Rt△AOB≌Rt△COB(HL),则全等三角形共有4对,故②正确;③∵AB=CB,BO⊥AC,把△ABC折叠,∴∠ABO=∠CBO=45°,∠FBD=∠DEF,∴∠AEF=∠DEF=45°,∴将△DEF沿EF折叠,可得点D一定在AC上,故③错误;④∵OB⊥AC,且AB=CB,∴BO 为∠ABC的平分线,即∠ABO=∠OBC=45°,由折叠可知,AD是∠BAC的平分线,即∠BAF=22.5°,又∵∠BFD为三角形ABF的外角,∴∠BFD=∠ABO+∠BAF=67.5°,易得∠BDF=180°-45°-67.5°=67.5°,∴∠BFD=∠BDF,∴BD=BF,故④正确;⑤连接CF,∵△AOF和△COF等底同高,∴S△AOF=S△COF,∵∠AEF=∠ACD=45°,∴EF∥CD,∴S△EFD=S△EFC,∴S四边形DFOE=S△COF,∴S四边形DFOE=S△AOF,故⑤正确;故正确的有3个.故选C.12、【答案】D 【考点】等边三角形的性质,菱形的判定,旋转的性质【解析】【解答】解:∵将等边△ABC绕点C顺时针旋转120°得到△EDC,∴∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE,∴∠ACD=120°﹣60°=60°,∴△ACD是等边三角形,∴AC=AD,AC=AD=DE=CE,∴四边形ACED是菱形,∵将等边△ABC绕点C顺时针旋转120°得到△EDC,AC=AD,∴AB=BC=CD=AD,∴四边形ABCD是菱形,∴BD⊥AC,∴①②③都正确,故选D.【分析】根据旋转和等边三角形的性质得出∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE,求出△ACD是等边三角形,求出AD=AC,根据菱形的判定得出四边形ABCD和ACED都是菱形,根据菱形的判定推出AC⊥BD.本题考查了旋转的性质,菱形的性质和判定,等边三角形的性质和判定的应用,能灵活运用知识点进行推理是解此题的关键.13、【答案】D 【考点】全等三角形的判定与性质,矩形的判定与性质,正方形的性质,相似三角形的判定与性质,等腰直角三角形【解析】【解答】解:∵四边形ADEF为正方形,∴∠FAD=90°,AD=AF=EF,∴∠CAD+∠FAG=90°,∵FG⊥CA,∴∠C=90°=∠ACB,∴∠CAD=∠AFG,在△FGA 和△ACD中,,∴△FGA≌△ACD(AAS),∴AC=FG,①正确;∵BC=AC,∴FG=BC,∵∠ACB=90°,FG⊥CA,∴FG∥BC,∴四边形CBFG 是矩形,∴∠CBF=90°,S△FAB= FB•FG= S四边形CBFG,②正确;∵CA=CB,∠C=∠CBF=90°,∴∠ABC=∠ABF=45°,③正确;∵∠FQE=∠DQB=∠ADC,∠E=∠C=90°,∴△ACD∽△FEQ,∴AC:AD=FE:FQ,∴AD•FE=AD2=FQ•AC,④正确;故选:D.【分析】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质、矩形的判定与性质、等腰直角三角形的性质;熟练掌握正方形的性质,证明三角形全等和三角形相似是解决问题的关键.由正方形的性质得出∠FAD=90°,AD=AF=EF,证出∠CAD=∠AFG,由AAS证明△FGA≌△ACD,得出AC=FG,①正确;证明四边形CBFG是矩形,得出S△FAB= FB•FG= S四边形CEFG,②正确;由等腰直角三角形的性质和矩形的性质得出∠ABC=∠ABF=45°,③正确;证出△ACD∽△FEQ,得出对应边成比例,得出D•FE=AD2=FQ•AC,④正确.14、【答案】B 【考点】全等三角形的判定与性质,线段垂直平分线的性质,等腰三角形的性质,矩形的性质【解析】【解答】解:①∵矩形ABCD中,O为AC中点,∴OB=OC,∵∠COB=60°,∴△OBC是等边三角形,∴OB=BC,∵FO=FC,∴FB垂直平分OC,故①正确;②∵FB垂直平分OC,∴△CMB≌△OMB,∵OA=OC,∠FOC=∠EOA,∠DCO=∠BAO,∴△FOC≌△EOA,∴FO=EO,易得OB⊥EF,∴△OMB≌△OEB,∴△EOB≌△CMB,故②正确;③由△OMB≌△OEB≌△CMB得∠1=∠2=∠3=30°,BF=BE,∴△BEF是等边三角形,∴BF=EF,∵DF∥BE且DF=BE,∴四边形DEBF是平行四边形,∴DE=BF,∴DE=EF,故③正确;④在直角△BOE中∵∠3=30°,∴BE=2OE,∵∠OAE=∠AOE=30°,∴AE=OE,∴BE=2AE,∴S△AOE:S△BCM=S△AOE:S△BOE=1:2,故④错误;所以其中正确结论的个数为3个;故选B【分析】①利用线段垂直平分线的性质的逆定理可得结论;②证△OMB≌△OE B得△EOB≌△CMB;③先证△BEF是等边三角形得出BF=EF,再证▱DEBF得出DE=BF,所以得DE=EF;④由②可知△BCM≌△BEO,则面积相等,△AOE和△BEO属于等高的两个三角形,其面积比就等于两底的比,即S△AOE:S△BOE=AE:BE,由直角三角形30°角所对的直角边是斜边的一半得出BE=2OE=2AE,得出结论S:S=AE:BE=1:2.本题综合性比较强,既考查了矩形的性质、等腰三角形的性质,又考查了全等三角形的性质和判定,及线段垂直平分线的性质,内容虽多,但不复杂;看似一个选择题,其实相当于四个证明题,属于常考题型.15、【答案】B 【考点】菱形的判定与性质,翻折变换(折叠问题),等腰直角三角形【解析】【解答】解:∵四边形ABCD 是正方形,∴∠GAD=∠ADO=45°,由折叠的性质可得:∠ADG= ∠ADO=22.5°,故①正确.∵由折叠的性质可得:AE=EF,∠EFD=∠EAD=90°,∴AE=EF<BE,∴AE <AB,∴ >2,故②错误.∵∠AOB=90°,∴AG=FG>OG ,△AGD与△OGD 同高,∴S △AGD>S△OGD,故③错误.∵∠EFD=∠AOF=90°,∴EF∥AC,∴∠FEG=∠AGE,∵∠AGE=∠FGE,∴∠FEG=∠FGE,∴EF=GF,∵AE=EF,∴AE=GF,故④正确.∵AE=EF=GF,AG=GF,∴AE=EF=GF=AG,∴四边形AEFG是菱形,∴∠OGF=∠OAB=45°,∴EF=GF= OG ,∴BE= EF= × OG=2OG .故⑤正确.∵四边形AEFG是菱形,∴AB∥GF,AB=GF.∵∠BAO=45°,∠GOF=90°,∴△OG F 时等腰直角三角形.∵S△OGF=1,∴ OG2=1,解得OG= ,∴BE=2OG=2 ,GF= = =2,∴AE=GF=2,∴AB=BE+AE=2 +2,∴S正方形ABCD=AB2=(2 +2)2=12+8 ,故⑥错误.∴其中正确结论的序号是:①④⑤.故选B.【分析】①由四边形ABCD是正方形,可得∠GAD=∠ADO=45°,又由折叠的性质,可求得∠ADG的度数;②由AE=EF<BE,可得AD>2AE;③由AG=GF>OG,可得△AGD的面积>△OGD的是等腰三角形,即可证得AE=GF;⑤易证得四边形AEFG 是菱形,由等腰直角三角形的性质,即可得BE=2OG;⑥根据四边形AEFG是菱形可知AB∥GF,AB=GF,再由∠BAO=45°,∠GOF=90°可得出△OGF时等腰直角三角形,由S△OGF=1求出GF的长,进而可得出BE及AE的长,利用正方形的面积公式可得出结论.此题考查的是四边形综合题,涉及到正方形的性质、折叠的性质、等腰直角三角形的性质以及菱形的判定与性质等知识.此题综合性较强,难度较大,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.16、【答案】B 【考点】全等三角形的判定与性质,正方形的性质,翻折变换(折叠问题),相似三角形的判定与性质【解析】【解答】解:∵E,F分别是正方形ABCD边BC,CD的中点,∴CF=BE,在△ABE和△BCF中,,∴Rt△ABE≌Rt△BCF(SAS),∴∠BAE=∠CBF,AE=BF,故①正确;又∵∠BAE+∠BEA=90°,∴∠CBF+∠BEA=90°,∴∠BGE=90°,∴AE⊥BF,故②正确;根据题意得,FP=FC,∠PFB=∠BFC,∠FPB=90°∵CD∥AB,∴∠CFB=∠ABF,∴∠ABF=∠PFB,∴QF=QB,令PF=k(k>0),则PB=2k在Rt△BPQ 中,设QB=x ,∴x2=(x ﹣k)2+4k2,∴x= ,∴sin=∠BQP= = ,故③正确;∵∠BGE=∠BCF,∠GBE=∠CBF,∴△BGE∽△BCF,∵BE= BC,BF= BC,∴BE:BF=1:,∴△BGE的面积:△BCF的面积=1:5,∴S四边形ECFG=4S△BGE,故④错误.故选:B.【分析】首先证明△ABE≌△BCF,再利用角的关系求得∠BGE=90°,QF=QB,解出BP,QB,根据正弦的定义即可求解;根据AA可证△BGE与△BCF相似,进一步得到相似比,再根据相似三角形的性质即可求解.本题主要考查了四边形的综合题,涉及正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质以及折叠的性质的知识点,解决的关键是明确三角形翻转后边的大小不变,找准对应边,角的关系求解.17、【答案】D 【考点】二次函数的图象,二次函数的性质,菱形的判定【解析】【解答】解:①∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣2,0)、B(1,0),∴该抛物线的对称轴为x=﹣=﹣0.5,∴a=b,a ﹣b=0,①正确;②∵抛物线开口向下,且抛物线与x轴交于点A(﹣2,0)、B(1,0),∴当﹣2<x<1时,y>0,②正确;③∵点A、B关于x=0.5对称,∴AM=BM,又∵MC=MD,且CD⊥AB,∴四边形ACBD是菱形,③正确;④当x=﹣3时,y<0,即y=9a﹣3b+c<0,④错误.综上可知:正确的结论为①②③.故选D.【分析】①由抛物线与x轴的两交点坐标即可得出抛物线的对称轴为x=﹣=﹣0.5,由此即可得出a=b,①正确;②根据抛物线的开口向下以及抛物线与x轴的两交点坐标,即可得出当﹣2<x<1时,y>0,②正确;③由AB关于x=0.5对称,即可得出AM=BM,再结合MC=MD以及CD⊥AB,即可得出四边形ACBD 是菱形,③正确;④根据当x=﹣3时,y<0,即可得出9a﹣3b+c<0,④错误.综上即可得出结论.本题考查了二次函数的图象、二次函数的性质以及菱形的判定,解题的关键是逐条分析四条结论是否正确.本题属于中档题,难度不大,解决该题型题目时,根据给定的函数图象结合二次函数的性质逐条分析给定的结论是关键.18、【答案】D 【考点】全等三角形的判定与性质,正方形的性质,翻折变换(折叠问题)【解析】【解答】解:∵正方形ABCD的边长为6,CE=2DE,∴DE=2,EC=4,∵把△ADE沿AE折叠使△ADE落在△AFE的位置,∴AF=AD=6,EF=ED=2,∠AFE=∠D=90°,∠FAE=∠DAE,在Rt△ABG和Rt△AFG中,∴Rt△ABG≌Rt△AFG(HL ),∴GB=GF,∠BAG=∠FAG,∴∠GAE=∠FAE+∠FAG= ∠BAD=45°,所以①正确;设BG=x,则GF=x ,C=BC﹣BG=6﹣x,在Rt△CGE中,GE=x+2,EC=4,CG=6﹣x,∵CG2+CE2=GE2,∴(6﹣x)2+42=(x+2)2,解得x=3,∴BG=3,CG=6﹣3=3∴BG=CG,所以②正确;∵EF=ED,GB=GF,∴GE=GF+EF=BG+DE,所以③正确;∵GF=GC,∴∠GFC=∠GCF,又∵Rt△ABG≌Rt△AFG,∴∠AGB=∠AGF,而∠BGF=∠GFC+∠GCF,∴∠AGB+∠AGF=∠GFC+∠GCF,∴∠AGB=∠GCF,∴CF∥AG,所以④正确;过F作FH⊥DC∵BC⊥DH,∴FH∥GC,∴△EFH∽△EGC,∴,EF=DE=2,GF=3,∴EG=5,∴△EFH∽△EGC,∴相似比为:= ,∴S△FGC=S△GCE﹣S△FEC= ×3×4﹣×4×(×3)= =3.6,所以⑤正确.故正确的有①②③④⑤,故选:D.【分析】先计算出DE=2,EC=4,再根据折叠的性质AF=AD=6,EF=ED=2,∠AFE=∠D=90°,∠FAE=∠DAE,然后根据“HL”可证明Rt△ABG≌Rt△AFG,则GB=GF,∠BAG=∠FAG,所以∠GAE= ∠BAD=45°;GE=GF+EF=BG+DE;设BG=x,则GF=x,CG=BC﹣BG=6﹣x,在Rt△CGE中,根据勾股定理得(6﹣x)2+42=(x+2)2,解得x=3,则BG=CG=3,则点G为BC的中点;同时得到GF=GC,根据等腰三角形的性质得∠GFC=∠GCF,再由Rt△ABG≌Rt△AFG得到∠AGB=∠AGF,然后根据三角形外角性质得∠BGF=∠GFC+∠GCF,易得∠AGB=∠GCF,根据平行线的判定方法得到CF∥AG;过F 作FH⊥DC,则△EFH∽△EGC,△EFH∽△EGC,由相似比为,可计算S△FGC.本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了三角形全等的判定与性质、勾股定理和正方形的性质.19、【答案】C 【考点】垂径定理,圆周角定理,相似三角形的判定与性质,解直角三角形【解析】【解答】解:①∵AB是⊙O的直径,弦CD⊥AB,∴ ,DG=CG ,∴∠ADF=∠AED,∵∠FAD=∠DAE(公共角),∴△ADF∽△AED;故①正确;②∵ = ,CF=2,∴FD=6,∴CD=DF+CF=8,∴CG=DG=4,∴FG=CG﹣CF=2;故②正确;③∵AF=3,FG=2,∴AG= = ,∴在Rt△AGD 中,tan∠ADG= = ,∴tan∠E= ;故③错误;④∵DF=DG+FG=6,AD= = ,∴S △ADF= DF•AG= ×6× =3 ,∵△ADF∽△AED,∴ =()2,∴ = ,∴S△AED=7 ,∴S △DEF=S△AED ﹣S△ADF=4 ;故④正确.故选C.【分析】①正确.由AB是⊙O的直径,弦CD⊥AB,根据垂径定理可得:,DG=CG,继而证得△ADF∽△AED;②正确.由= ,CF=2,可求得DF的长,继而求得CG=DG=4,则可求得FG=2;③错误.由勾股定理可求得AG的长,即可求得tan∠ADF的值,继而求得tan∠E= .④首先求得△ADF的面积,由相似三角形面积的比等于相似比的平方,即可求得△ADE 的面积,继而求得S△DEF =4 .20、【答案】D 【考点】垂径定理,圆周角定理,相似三角形的判定与性质【解析】【解答】解:∵在⊙O中,点C是的中点,∴ = ,∴∠CAD=∠ABC,故①正确;∵ ≠ ,∴ ≠ ,∴AD≠BC,故②错误;∵AB是⊙O的直径,∴∠ACB=90°,又∵CE⊥AB,∴∠ACE+∠CAE=∠ABC+∠CAE=90°,∴∠ACE=∠ABC,又∵C为的中点,∴ = ,∴∠CAP=∠ABC,∴∠ACE=∠CAP,∴AP=CP,∵∠ACQ=90°,∴∠ACP+∠PCQ=∠CAP+∠PQC=90°,∴∠PCQ=∠PQC,∴PC=PQ,∴AP=PQ,即P 为Rt△ACQ斜边AQ的中点,∴P为Rt△ACQ的外心,故③正确;∵AB是⊙O的直径,∴∠ACB=90°,又∵CE⊥AB∴根据射影定理,可得AC2=AE•AB,故④正确;如图,连接BD,则∠ADG=∠ABD,∵ ≠ ,∴ ≠ ,∴∠ABD≠∠BAC,∴∠ADG≠∠BAC,又∵∠BAC=∠BCE=∠PQC,∴∠ADG≠∠PQC,∴CB与GD不平行,故⑤错误.故答案为:D.【分析】在同圆或等圆中,同弧或等弧所对的圆周角相等,据此推理可得①正确,②错误;通过推理可得∠ACE=∠CAP,得出AP=CP,再根据∠PCQ=∠PQC,可得出PC=PQ,进而得到AP=PQ,即P为Rt△ACQ斜边AQ的中点,故P为Rt△A CQ的外心,即可得出③正确;连接BD,则∠ADG=∠ABD,根据∠ADG≠∠BAC,∠BAC=∠BCE=∠PQC,可得出∠ADG≠∠PQC,进而得到CB与GD不平行,可得⑤错误.。
初中几何多结论问题

专题—几何多结论问题【考题研究】以函数/几何为背景多结论问题自13年以来深圳广州等地每年必考,出现的位置是选择题或者填空题的压轴题.其难度不言自于,对学生综合分析问题的能力要求比较高.【解题策略】常见类型有:(1)代数中的多结论题;特别是有关二次函数中的多结论选填题是综合性比较强的题目,解决此类题目不仅要掌握二次函数的图象与性质、抛物线位置与字母系数的关系、二次函数与方程、不等式的关系等知识,还要学会代入特殊值的方法并结合二次函数的图象去验证一些不等式的正误;(2)几何中的多结论题;几何中的多结论选填题则结合了三角形、四边形、圆的有关性质和判定,是几何中综合性很强的题目,掌握三角形、四边形、圆的有关性质并能熟练的运用才能解决此类问题.具体求解时,一是从题干出发考虑,探求结果;二是题干和选择支联合考虑或从选择支出发探求是否满足题干条件. 事实上,后者在解答选择题时更常用、更有效.常用方法有以下几种:1.直接法从题设条件出发,通过正确的运算、推理或判断,直接得出结论再与选择支对照,从而作出选择的一种方法。
运用此种方法解题需要扎实的数学基础.2.特例法运用满足题设条件的某些特殊数值、特殊位置、特殊关系、特殊图形、特殊数列、特殊函数等对各选择支进行检验或推理,利用问题在某一特殊情况下不真,则它在一般情况下也不真的原理,由此判明选项真伪的方法。
用特例法解选择题时,特例取得愈简单、愈特殊愈好.3.筛选法(也叫排除法、淘汰法)运用选择题中单选题的特征,即有且只有一个正确选择支这一信息,从选择支入手,根据题设条件和各选项之间的关系,通过分析、推理、计算、判断,对选择项进行筛选,将其中与题设相矛盾的干扰逐一排除从而获得正确结论的方法。
使用筛选法的前提是“答案唯一”,即四个选项中有且只有一个答案正确.4.逆推代入法将选择项中给出的答案或其特殊值,代入题干逐一去验证是否满足题设条件,然后选择符合题设条件的择题项的一种方法. 在运用验证法解题时,若能据题意确定代入顺序,则能较大提高解题速度. 5.直观选择法利用函数图像或数学结果的几何意义,将数的问题(如解方程、解不等式、求最值,求取值范围等)与某些图形结合起来,利用直观几性,再辅以简单计算,确定正确答案的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考复习多结论几何综合题专题试卷一、单选题1、如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE 的中点,下列结论:①tan∠AEC=;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的个数是()A、1个B、2个C、3个D、4个2、如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC 绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△AED≌△AEF;②=;③△ABC的面积等于四边形AFBD的面积;④BE2+DC2=DE2⑤BE+DC=DE;其中正确的是( )A、①②④B、③④⑤C、①③④D、①③⑤3、如图,将等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD ,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形;④BD⊥DE;其中正确的个数是().A、1B、2C、3D、44、如图,把一张长方形纸片ABCD沿对角线BD折叠,使C点落在E处,BE与AD相交于点F,下列结论:①BD=AD2+AB2;②△ABF≌△EDF;③=④AD=BD•cos45°.其中正确的一组是()A、①②B、②③C、①④D、③④5、如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°,②OC=OE,③tan∠OCD= ,④S△ODC=S四边形BEOF 中,正确的有()A、1个B、2个C、3个D、4个6、如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③△GDE∽△BEF;④S△BEF=.在以上4个结论中,正确的有()A 、1 B、2 C、3 D、47、如图,▱ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S▱ABCD=AB•AC;③OB=AB;④OE=BC,成立的个数有()A、1个B、2个C、3个D、4个8、如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下列四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④AE+DF=AF+DE.其中正确的是()A、②③B、②④C、①③④D、②③④9、如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH,其中,正确的结论有()A、1个B、2个C、3个D、4个10、如图,PA=PB,OE⊥PA,OF⊥PB,则以下结论:①OP是∠APB的平分线;②PE=PF③CA=BD;④CD∥AB;其中正确的有()个.A、4B、3C、2D、111、如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B 与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF.下列结论:①tan ∠ADB=2;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点D不一定落在AC 上;④BD=BF;⑤S四边形DFOE=S△AOF,上述结论中正确的个数是()A、1个B、2个C、3个D、4个12、如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:①AC=AD;②BD⊥AC;③四边形ACED是菱形.其中正确的个数是()A、0B、1C、2D、313、如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ•AC,其中正确的结论的个数是()A、1B、2C、3D、414、如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是()A、4个B、3个C、2个D、1个15、如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:①∠ADG=22.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG;⑥若S△OGF=1,则正方形ABCD的面积是6+4 ,其中正确的结论个数为()A、2B、3C、4D、516、如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是()①AE=BF;②AE⊥BF;③sin∠BQP= ;④S四边形ECFG=2S△BGE.A、4B、3C、2D、117、如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣2,0)、B(1,0),直线x=﹣0.5与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC、BC、AD、BD,某同学根据图象写出下列结论:①a﹣b=0;②当﹣2<x<1时,y>0;③四边形ACBD是菱形;④9a﹣3b+c>0你认为其中正确的是()A、②③④B、①②④C、①③④D、①②③18、如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是()A、2B、3C、4D、519、如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足= ,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF ∽△AED;②FG=2;③tanE= ;④S△DEF=4 ,其中正确的是()A、①②③B、②③④C、①②④D、①③④20、如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB 于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,给出下列结论:①∠DAC=∠ABC;②AD=CB;③点P是△ACQ的外心;④AC2=AE•AB;⑤CB∥GD,其中正确的结论是()A、①③⑤B、②④⑤C、①②⑤D、①③④答案解析部分一、单选题1、【答案】D【考点】等腰三角形的性质,梯形中位线定理,锐角三角函数的定义【解析】【分析】①根据等腰直角三角形的性质及△ABC∽△CDE的对应边成比例知,;然后由直角三角形中的正切函数,得tan∠AEC=,再由等量代换求得tan∠AEC=;②由三角形的面积公式、梯形的面积公式及不等式的基本性质a2+b2≥2ab(a=b时取等号)解答;③、④通过作辅助线MN,构建直角梯形的中位线,根据梯形的中位线定理及等腰直角三角形的判定定理解答.【解答】解:∵△ABC和△CDE均为等腰直角三角形,∴AB=BC,CD=DE,∴∠BAC=∠BCA=∠DCE=∠DEC=45°,∴∠ACE=90°;∵△ABC∽△CDE∴①∴tan∠AEC=,∴tan∠AEC=;故本选项正确;②∵S△ABC=a2,S△CDE=b2,S梯形ABDE=(a+b)2,∴S△ACE=S梯形ABDE-S△ABC-S△CDE=ab,S△ABC+S△CDE=(a2+b2)≥ab(a=b时取等号),∴S△ABC+S△CDE≥S△ACE;故本选项正确;④过点M作MN垂直于BD,垂足为N.∵点M是AE的中点,则MN为梯形中位线,∴N为中点,∴△BMD为等腰三角形,∴BM=DM;故本选项正确;③又MN=(AB+ED)=(BC+CD),∴∠BMD=90°,即BM⊥DM;故本选项正确.故选D.【点评】本题综合考查了等腰直角三角形的判定与性质、梯形的中位线定理、锐角三角函数的定义等知识点.在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.2、【答案】C【考点】全等三角形的判定,勾股定理,相似三角形的判定,旋转的性质【解析】【分析】①根据旋转的性质知∠CAD=∠BAF,AD=AF,因为∠BAC=90°,∠DAE=45°,所以∠CAD+∠BAE=45°,可得∠EAF=45°=∠DAE,由此即可证明△AEF≌△AED;②当△ABE∽△ACD时,该比例式成立;③根据旋转的性质,△ADC≌△ABF,进而得出△ABC的面积等于四边形AFBD的面积;④据①知BF=CD,EF=DE,∠FBE=90°,根据勾股定理判断.⑤根据①知道△AEF≌△AED,得CD=BF,DE=EF;由此即可确定该说法是否正确;【解答】①根据旋转的性质知∠CAD=∠BAF,AD=AF,∵∠BAC=90°,∠DAE=45°,∴∠CAD+∠BAE=45°.∴∠EAF=45°,∴△AED≌△AEF;故本选项正确;②∵AB=AC,∴∠ABE=∠ACD;∴当∠BAE=∠CAD时,△ABE∽△ACD,∴=;当∠BAE≠∠CAD时,△ABE与△ACD不相似,即≠;∴此比例式不一定成立;故本选项错误;③根据旋转的性质知△ADC≌△AFB,∴S△ABC=S△ABD+S△ABF=S四边形AFBD,即三角形ABC的面积等于四边形AFBD的面积;故本选项正确;④∵∠FBE=45°+45°=90°,∴BE2+BF2=EF2,∵△ADC绕点A顺时针旋转90°后,得到△AFB,∴△AFB≌△ADC,∴BF=CD,又∵EF=DE,∴BE2+DC2=DE2,故本选项正确;⑤根据①知道△AEF≌△AED,得CD=BF,DE=EF,∴BE+DC=BE+BF>DE=EF,即BE+DC>DE,故本选项错误;综上所述,正确的说法是①③④;故选C.【点评】此题主要考查了图形的旋转变换以及全等三角形的判定等知识,解题时注意旋转前后对应的相等关系.3、【答案】D【考点】等边三角形的性质,菱形的判定与性质,平移的性质【解析】【解答】∵△ABC、△DCE是等边三角形,∴∠ACB=∠DCE=60°,AC=CD ,∴∠ACD=180°-∠ACB-∠DCE=60°,∴△ACD是等边三角形,∴AD=AC=BC ,故①正确;由①可得AD=BC ,∵AB=CD ,∴四边形ABCD是平行四边形,∴BD、AC互相平分,故②正确;由①可得AD=AC=CE=DE ,故四边形ACED是菱形,即③正确;∵四边形ACED是菱形,∴AC⊥BD ,∵AC∥DE ,∴∠BDE=∠COD=90°,∴BD⊥DE ,故④正确;综上可得①②③④正确,共4个,故选D.【分析】先求出∠ACD=60°,继而可判断△ACD是等边三角形,从而可判断①是正确的;根据①的结论,可判断四边形ABCD是平行四边形,从而可判断②是正确的;根据①的结论,可判断③正确;根据菱形的对角线互相垂直可得AC⊥BD ,再根据平移后对应线段互相平行可得∠BDE=∠COD=90°,进而判断④正确.4、【答案】B【考点】勾股定理,翻折变换(折叠问题),相似三角形的判定与性质,特殊角的三角函数值【解析】【解答】①∵△ABD为直角三角形,∴BD2=AD2+AB2,不是BD=AD2+AB2,故说法错误;②根据折叠可知:DE=CD=AB,∠A=∠E,∠AFB=∠EFD,∴△ABF≌△EDF,故说法正确;③根据②可以得到△ABF∽△EDF,∴=,故说法正确;④在Rt△ABD中,∠ADB≠45°,∴AD≠BD•cos45°,故说法错误.所以正确的是②③.故选B.【分析】①直接根据勾股定理即可判定是否正确;②利用折叠可以得到全等条件证明△ABF≌△EDF;③利用全等三角形的性质即可解决问题;④在Rt△ABD中利用三角函数的定义即可判定是否正确.此题主要考查了折叠问题,也考查了勾股定理、相似三角形的性质、全等三角形的性质及三角函数的定义,它们的综合性比较强,对于学生的综合能力要求比较高,平时加强训练.5、【答案】C【考点】全等三角形的判定与性质,勾股定理,正方形的性质,锐角三角函数的定义【解析】【解答】解:∵正方形ABCD的边长为4,∴BC=CD=4,∠B=∠DCF=90°,∵AE=BF=1,∴BE=CF=4﹣1=3,在△EBC和△FCD中,∴△EBC≌△FCD(SAS),∴∠CFD=∠BEC,∴∠BCE+∠BEC=∠BCE+∠CFD=90°,∴∠DOC=90°;故①正确;若OC=OE,∵DF⊥EC,∴CD=DE,∵CD=AD<DE(矛盾),故②错误;∵∠OCD+∠CDF=90°,∠CDF+∠DFC=90°,∴∠OCD=∠DFC,∴tan∠OCD=tan∠DFC= = ,故③正确;∵△EBC≌△FCD,∴S△EBC=S△FCD,∴S△EBC﹣S△FOC=S△FCD﹣S△FOC,即S△ODC=S四边形BEOF.故④正确.故选C.【分析】由正方形ABCD的边长为4,AE=BF=1,利用SAS易证得△EBC≌△FCD,然后全等三角形的对应角相等,易证得①∠DOC=90°正确;②由线段垂直平分线的性质与正方形的性质,可得②错误;易证得∠OCD=∠DFC,即可求得③正确;由①易证得④正确.6、【答案】C【考点】全等三角形的判定与性质,正方形的性质,翻折变换(折叠问题),相似三角形的判定与性质【解析】【解答】由折叠可知,DF=DC=DA,∠DFE=∠C=90°,∴∠DFG=∠A=90°,∴△ADG≌△FDG,①正确;∵正方形边长是12,∴BE=EC=EF=6,设AG=FG=x,则EG=x+6,BG=12﹣x,由勾股定理得:EG2=BE2+BG2,即:(x+6)2=62+(12﹣x)2,解得:x=4∴AG=GF=4,BG=8,BG=2AG,②正确;BE=EF=6,△BEF是等腰三角形,易知△GED不是等腰三角形,③错误;S△GBE=×6×8=24,S△BEF=•S△GBE==,④正确.故选:C.【分析】根据正方形的性质和折叠的性质可得AD=DF,∠A=∠GFD=90°,于是根据“HL”判定△ADG≌△FDG,再由GF+GB=GA+GB=12,EB=EF,△BGE为直角三角形,可通过勾股定理列方程求出AG=4,BG=8,进而求出△BEF的面积,再抓住△BEF是等腰三角形,而△GED显然不是等腰三角形,判断③是错误的.7、【答案】C【考点】等边三角形的判定与性质,含30度角的直角三角形,平行四边形的性质【解析】【解答】∵四边形ABCD是平行四边形,∴∠ABC=∠ADC=60°,∠BAD=120°,∵AE平分∠BAD,∴∠BAE=∠EAD=60°∴△ABE是等边三角形,∴AE=AB=BE,∵AB=BC,∴AE=BC,∴∠BAC=90°,∴∠CAD=30°,故①正确;∵AC⊥AB,∴S▱ABCD=AB•AC,故②正确,∵AB=BC,OB=BD,∵BD>BC,∴AB≠OB,故③错误;∵CE=BE,CO=OA,∴OE=AB,∴OE=BC,故④正确.故选:C.【分析】由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据AE 平分∠BAD,得到∠BAE=∠EAD=60°推出△ABE是等边三角形,由于AB=BC,得到AE=BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正确;由于AC⊥AB,得到S▱ABCD=AB•AC,故②正确,根据AB=BC,OB=BD,且BD>BC,得到AB≠OB,故③错误;根据三角形的中位线定理得到OE=AB,于是得到OE=BC,故④正确.8、【答案】D【考点】全等三角形的判定与性质,角平分线的性质,正方形的判定【解析】【解答】如果OA=OD,则四边形AEDF是矩形,∠A=90°,不符合题意,∴①不正确;∵AD是△ABC的角平分线,∴∠EAD∠FAD,在△AED和△AFD中,∴△AED≌△AFD(AAS),∴AE=AF,DE=DF,∴AE+DF=AF+DE,∴④正确;在△AEO和△AFO中,,∴△AE0≌△AF0(SAS),∴EO=FO,又∵AE=AF,∴AO是EF的中垂线,∴AD⊥EF,∴②正确;∵当∠A=90°时,四边形AEDF的四个角都是直角,∴四边形AEDF是矩形,又∵DE=DF,∴四边形AEDF是正方形,∴③正确.综上,可得正确的是:②③④.故选:D.【分析】①如果OA=OD,则四边形AEDF是矩形,∠A=90°,不符合题意,所以①不正确.②首先根据全等三角形的判定方法,判断出△AED≌△AFD,AE=AF,DE=DF;然后根据全等三角形的判定方法,判断出△AE0≌△AFO,即可判断出AD⊥EF.③首先判断出当∠A=90°时,四边形AEDF的四个角都是直角,四边形AEDF是矩形,然后根据DE=DF,判断出四边形AEDF是正方形即可.④根据△AED≌△AFD,判断出AE=AF,DE=DF,即可判断出AE+DF=AF+DE成立,据此解答即可.9、【答案】B【考点】全等三角形的判定与性质,正方形的性质,相似三角形的判定与性质【解析】【解答】∵四边形ABCD是正方形,∴∠B=∠DCB=90°,AB=BC,∵AG=CE,∴BG=BE,由勾股定理得:BE=GE,∴①错误;∵BG=BE,∠B=90°,∴∠BGE=∠BEG=45°,∴∠AGE=135°,∴∠GAE+∠AEG=45°,∵AE⊥EF,∴∠AEF=90°,∵∠BEG=45°,∴∠AEG+∠FEC=45°,∴∠GAE=∠FEC,在△GAE和△CEF中∴△GAE≌△CEF,∴②正确;∴∠AGE=∠ECF=135°,∴∠FCD=135°﹣90°=45°,∴③正确;∵∠BGE=∠BEG=45°,∠AEG+∠FEC=45°,∴∠FEC<45°,∴△GBE和△ECH不相似,∴④错误;即正确的有2个.故选B.【分析】根据正方形的性质得出∠B=∠DCB=90°,AB=BC,求出BG=BE,根据勾股定理得出BE=GE,即可判断①;求出∠GAE+∠AEG=45°,推出∠GAE=∠FEC,根据SAS推出△GAE≌△CEF,即可判断②;求出∠AGE=∠ECF=135°,即可判断③;求出∠FEC<45°,根据相似三角形的判定得出△GBE和△ECH不相似,即可判断④.10、【答案】A【考点】全等三角形的判定与性质,圆心角、弧、弦的关系,相似三角形的判定与性质【解析】【解答】连接OP、OC、OA、OD、OB、CD、AB.∵PC•PA=PD•PB(相交弦定理),PA=PB(已知),∴PC=PD,∴AC=BD;在△AOC和△BOD中,∵∠AOC=∠BOD(等弦对等角),OA=OB(半径),OD=OC(半径),∴△AOC≌△BOD,∴③CA=BD;OE=OF;又∵OE⊥PA,OF⊥PB,∴①OP是∠APB的平分线;∴②PE=PF;在△PCD和△PAB中,PC:PA=PD:PB,∠DPC=∠BPA,∴△PCD∽△PAB,∴∠PDC=PBA,∴④CD∥AB;综上所述,①②③④均正确,故答案选A.【分析】①通过证明△AOC≌△BOD,再根据全等三角形的对应高相等求得OE=OF;再根据角平分线的性质证明OP是∠APB的平分线;②由角平分线的性质证明PE=PF;③通过证明△AOC≌△BOD,再根据全等三角形的对应边相等求得CA=BD;④通过证明△PCD∽△PAB,再根据相似三角形的性质对应角相等证得∠PDC=PBA;然后由平行线的判定得出结论CD∥AB.11、【答案】C【考点】全等三角形的判定与性质,翻折变换(折叠问题),锐角三角函数的定义【解析】【解答】①由折叠可得BD=DE,而DC>DE,∴DC>BD,∴tan∠ADB≠2,故①错误;②图中的全等三角形有△ABF≌△AEF,△ABD≌△AED,△FBD≌△FED,(由折叠可知) ∵OB⊥AC,∴∠AOB=∠COB=90°,在Rt△AOB和Rt△COB中,AB="CB" ,BO=BO ,∴Rt△AOB≌Rt△COB(HL),则全等三角形共有4对,故②正确;③∵AB=CB,BO⊥AC,把△ABC折叠,∴∠ABO=∠CBO=45°,∠FBD=∠DEF,∴∠AEF=∠DEF=45°,∴将△DEF沿EF折叠,可得点D一定在AC上,故③错误;④∵OB⊥AC,且AB=CB,∴BO为∠ABC的平分线,即∠ABO=∠OBC=45°,由折叠可知,AD是∠BAC的平分线,即∠BAF=22.5°,又∵∠BFD为三角形ABF的外角,∴∠BFD=∠ABO+∠BAF=67.5°,易得∠BDF=180°-45°-67.5°=67.5°,∴∠BFD=∠BDF,∴BD=BF,故④正确;⑤连接CF,∵△AOF和△COF等底同高,∴S△AOF=S△COF,∵∠AEF=∠ACD=45°,∴EF∥CD,∴S△EFD=S△EFC,∴S四边形DFOE=S△COF,∴S四边形DFOE=S△AOF,故⑤正确;故正确的有3个.故选C.12、【答案】D【考点】等边三角形的性质,菱形的判定,旋转的性质【解析】【解答】解:∵将等边△ABC绕点C顺时针旋转120°得到△EDC,∴∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE,∴∠ACD=120°﹣60°=60°,∴△ACD是等边三角形,∴AC=AD,AC=AD=DE=CE,∴四边形ACED是菱形,∵将等边△ABC绕点C顺时针旋转120°得到△EDC,AC=AD,∴AB=BC=CD=AD,∴四边形ABCD是菱形,∴BD⊥AC,∴①②③都正确,故选D.【分析】根据旋转和等边三角形的性质得出∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE,求出△ACD是等边三角形,求出AD=AC,根据菱形的判定得出四边形ABCD和ACED都是菱形,根据菱形的判定推出AC⊥BD.本题考查了旋转的性质,菱形的性质和判定,等边三角形的性质和判定的应用,能灵活运用知识点进行推理是解此题的关键.13、【答案】D【考点】全等三角形的判定与性质,矩形的判定与性质,正方形的性质,相似三角形的判定与性质,等腰直角三角形【解析】【解答】解:∵四边形ADEF为正方形,∴∠FAD=90°,AD=AF=EF,∴∠CAD+∠FAG=90°,∵FG⊥CA,∴∠C=90°=∠ACB,∴∠CAD=∠AFG,在△FGA和△ACD中,,∴△FGA≌△ACD(AAS),∴AC=FG,①正确;∵BC=AC,∴FG=BC,∵∠ACB=90°,FG⊥CA,∴FG∥BC,∴四边形CBFG是矩形,∴∠CBF=90°,S△FAB= FB•FG= S四边形CBFG,②正确;∵CA=CB,∠C=∠CBF=90°,∴∠ABC=∠ABF=45°,③正确;∵∠FQE=∠DQB=∠ADC,∠E=∠C=90°,∴△ACD∽△FEQ,∴AC:AD=FE:FQ,∴AD•FE=AD2=FQ•AC,④正确;故选:D.【分析】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质、矩形的判定与性质、等腰直角三角形的性质;熟练掌握正方形的性质,证明三角形全等和三角形相似是解决问题的关键.由正方形的性质得出∠FAD=90°,AD=AF=EF,证出∠CAD=∠AFG,由AAS证明△FGA≌△ACD,得出AC=FG,①正确;证明四边形CBFG是矩形,得出S△FAB= FB•FG= S四边形CEFG,②正确;由等腰直角三角形的性质和矩形的性质得出∠ABC=∠ABF=45°,③正确;证出△ACD∽△FEQ,得出对应边成比例,得出D•FE=AD2=FQ•AC,④正确.14、【答案】B【考点】全等三角形的判定与性质,线段垂直平分线的性质,等腰三角形的性质,矩形的性质【解析】【解答】解:①∵矩形ABCD中,O为AC中点,∴OB=OC,∵∠COB=60°,∴△OBC是等边三角形,∴OB=BC,∵FO=FC,∴FB垂直平分OC,故①正确;②∵FB垂直平分OC,∴△CMB≌△OMB,∵OA=OC,∠FOC=∠EOA,∠DCO=∠BAO,∴△FOC≌△EOA,∴FO=EO,易得OB⊥EF,∴△OMB≌△OEB,∴△EOB≌△CMB,故②正确;③由△OMB≌△OEB≌△CMB得∠1=∠2=∠3=30°,BF=BE,∴△BEF是等边三角形,∴BF=EF,∵DF∥BE且DF=BE,∴四边形DEBF是平行四边形,∴DE=BF,∴DE=EF,故③正确;④在直角△BOE中∵∠3=30°,∴BE=2OE,∵∠OAE=∠AOE=30°,∴AE=OE,∴BE=2AE,∴S△AOE:S△BCM=S△AOE:S△BOE=1:2,故④错误;所以其中正确结论的个数为3个;故选B【分析】①利用线段垂直平分线的性质的逆定理可得结论;②证△OMB≌△OEB得△EOB≌△CMB;③先证△BEF是等边三角形得出BF=EF,再证▱DEBF得出DE=BF,所以得DE=EF;④由②可知△BCM≌△BEO,则面积相等,△AOE和△BEO属于等高的两个三角形,其面积比就等于两底的比,即S△AOE:S△BOE=AE:BE,由直角三角形30°角所对的直角边是斜边的一半得出BE=2OE=2AE,得出结论S△AOE:S△BOE=AE:BE=1:2.本题综合性比较强,既考查了矩形的性质、等腰三角形的性质,又考查了全等三角形的性质和判定,及线段垂直平分线的性质,内容虽多,但不复杂;看似一个选择题,其实相当于四个证明题,属于常考题型.15、【答案】B【考点】菱形的判定与性质,翻折变换(折叠问题),等腰直角三角形【解析】【解答】解:∵四边形ABCD是正方形,∴∠GAD=∠ADO=45°,由折叠的性质可得:∠ADG= ∠ADO=22.5°,故①正确.∵由折叠的性质可得:AE=EF,∠EFD=∠EAD=90°,∴AE=EF<BE,∴AE<AB,∴>2,故②错误.∵∠AOB=90°,∴AG=FG>OG,△AGD与△OGD同高,∴S△AGD>S△OGD,故③错误.∵∠EFD=∠AOF=90°,∴EF∥AC,∴∠FEG=∠AGE,∵∠AGE=∠FGE,∴∠FEG=∠FGE,∴EF=GF,∵AE=EF,∴AE=GF,故④正确.∵AE=EF=GF,AG=GF,∴AE=EF=GF=AG,∴四边形AEFG是菱形,∴∠OGF=∠OAB=45°,∴EF=GF= OG,∴BE= EF= ×OG=2OG.故⑤正确.∵四边形AEFG是菱形,∴AB∥GF,AB=GF.∵∠BAO=45°,∠GOF=90°,∴△OGF时等腰直角三角形.∵S△OGF=1,∴OG2=1,解得OG= ,∴BE=2OG=2 ,GF= = =2,∴AE=GF=2,∴AB=BE+AE=2 +2,∴S正方形ABCD=AB2=(2 +2)2=12+8 ,故⑥错误.∴其中正确结论的序号是:①④⑤.故选B.【分析】①由四边形ABCD是正方形,可得∠GAD=∠ADO=45°,又由折叠的性质,可求得∠ADG的度数;②由AE=EF<BE,可得AD>2AE;③由AG=GF>OG,可得△AGD的面积>△OGD的面积;④由折叠的性质与平行线的性质,易得△EFG是等腰三角形,即可证得AE=GF;⑤易证得四边形AEFG是菱形,由等腰直角三角形的性质,即可得BE=2OG;⑥根据四边形AEFG是菱形可知AB∥GF,AB=GF,再由∠BAO=45°,∠GOF=90°可得出△OGF时等腰直角三角形,由S△OGF=1求出GF的长,进而可得出BE及AE的长,利用正方形的面积公式可得出结论.此题考查的是四边形综合题,涉及到正方形的性质、折叠的性质、等腰直角三角形的性质以及菱形的判定与性质等知识.此题综合性较强,难度较大,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.16、【答案】B【考点】全等三角形的判定与性质,正方形的性质,翻折变换(折叠问题),相似三角形的判定与性质【解析】【解答】解:∵E,F分别是正方形ABCD边BC,CD的中点,∴CF=BE,在△ABE和△BCF中,,∴Rt△ABE≌Rt△BCF(SAS),∴∠BAE=∠CBF,AE=BF,故①正确;又∵∠BAE+∠BEA=90°,∴∠CBF+∠BEA=90°,∴∠BGE=90°,∴AE⊥BF,故②正确;根据题意得,FP=FC,∠PFB=∠BFC,∠FPB=90°∵CD∥AB,∴∠CFB=∠ABF,∴∠ABF=∠PFB,∴QF=QB,令PF=k(k>0),则PB=2k在Rt△BPQ中,设QB=x,∴x2=(x﹣k)2+4k2,∴x= ,∴sin=∠BQP= = ,故③正确;∵∠BGE=∠BCF,∠GBE=∠CBF,∴△BGE∽△BCF,∵BE= BC,BF= BC,∴BE:BF=1:,∴△BGE的面积:△BCF的面积=1:5,∴S四边形ECFG=4S△BGE,故④错误.故选:B.【分析】首先证明△ABE≌△BCF,再利用角的关系求得∠BGE=90°,即可得到①AE=BF;②AE⊥BF;△BCF沿BF对折,得到△BPF,利用角的关系求出QF=QB,解出BP,QB,根据正弦的定义即可求解;根据AA可证△BGE与△BCF相似,进一步得到相似比,再根据相似三角形的性质即可求解.本题主要考查了四边形的综合题,涉及正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质以及折叠的性质的知识点,解决的关键是明确三角形翻转后边的大小不变,找准对应边,角的关系求解.17、【答案】D【考点】二次函数的图象,二次函数的性质,菱形的判定【解析】【解答】解:①∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣2,0)、B(1,0),∴该抛物线的对称轴为x=﹣=﹣0.5,∴a=b,a﹣b=0,①正确;②∵抛物线开口向下,且抛物线与x轴交于点A(﹣2,0)、B(1,0),∴当﹣2<x<1时,y>0,②正确;③∵点A、B关于x=0.5对称,∴AM=BM,又∵MC=MD,且CD⊥AB,∴四边形ACBD是菱形,③正确;④当x=﹣3时,y<0,即y=9a﹣3b+c<0,④错误.综上可知:正确的结论为①②③.故选D.【分析】①由抛物线与x轴的两交点坐标即可得出抛物线的对称轴为x=﹣=﹣0.5,由此即可得出a=b,①正确;②根据抛物线的开口向下以及抛物线与x轴的两交点坐标,即可得出当﹣2<x<1时,y>0,②正确;③由AB关于x=0.5对称,即可得出AM=BM,再结合MC=MD以及CD⊥AB,即可得出四边形ACBD是菱形,③正确;④根据当x=﹣3时,y<0,即可得出9a﹣3b+c<0,④错误.综上即可得出结论.本题考查了二次函数的图象、二次函数的性质以及菱形的判定,解题的关键是逐条分析四条结论是否正确.本题属于中档题,难度不大,解决该题型题目时,根据给定的函数图象结合二次函数的性质逐条分析给定的结论是关键.18、【答案】D【考点】全等三角形的判定与性质,正方形的性质,翻折变换(折叠问题)【解析】【解答】解:∵正方形ABCD的边长为6,CE=2DE,∴DE=2,EC=4,∵把△ADE沿AE折叠使△ADE落在△AFE的位置,∴AF=AD=6,EF=ED=2,∠AFE=∠D=90°,∠FAE=∠DAE,在Rt△ABG和Rt△AFG中,∴Rt△ABG≌Rt△AFG(HL),∴GB=GF,∠BAG=∠FAG,∴∠GAE=∠FAE+∠FAG= ∠BAD=45°,所以①正确;设BG=x,则GF=x,C=BC﹣BG=6﹣x,在Rt△CGE中,GE=x+2,EC=4,CG=6﹣x,∵CG2+CE2=GE2,∴(6﹣x)2+42=(x+2)2,解得x=3,∴BG=3,CG=6﹣3=3∴BG=CG,所以②正确;∵EF=ED,GB=GF,∴GE=GF+EF=BG+DE,所以③正确;∵GF=GC,∴∠GFC=∠GCF,又∵Rt△ABG≌Rt△AFG,∴∠AGB=∠AGF,而∠BGF=∠GFC+∠GCF,∴∠AGB+∠AGF=∠GFC+∠GCF,∴∠AGB=∠GCF,∴CF∥AG,所以④正确;过F作FH⊥DC∵BC⊥DH,∴FH∥GC,∴△EFH∽△EGC,∴,EF=DE=2,GF=3,∴EG=5,∴△EFH∽△EGC,∴相似比为:= ,∴S△FGC=S△GCE﹣S△FEC= ×3×4﹣×4×(×3)= =3.6,所以⑤正确.故正确的有①②③④⑤,故选:D.【分析】先计算出DE=2,EC=4,再根据折叠的性质AF=AD=6,EF=ED=2,∠AFE=∠D=90°,∠FAE=∠DAE,然后根据“HL”可证明Rt△ABG≌Rt△AFG,则GB=GF,∠BAG=∠FAG,所以∠GAE= ∠BAD=45°;GE=GF+EF=BG+DE;设BG=x,则GF=x,CG=BC﹣BG=6﹣x,在Rt△CGE中,根据勾股定理得(6﹣x)2+42=(x+2)2,解得x=3,则BG=CG=3,则点G为BC的中点;同时得到GF=GC,根据等腰三角形的性质得∠GFC=∠GCF,再由Rt△ABG≌Rt△AFG得到∠AGB=∠AGF,然后根据三角形外角性质得∠BGF=∠GFC+∠GCF,易得∠AGB=∠GCF,根据平行线的判定方法得到CF∥AG;过F作FH⊥DC,则△EFH∽△EGC,△EFH∽△EGC,由相似比为,可计算S△FGC.本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了三角形全等的判定与性质、勾股定理和正方形的性质.19、【答案】C【考点】垂径定理,圆周角定理,相似三角形的判定与性质,解直角三角形【解析】【解答】解:①∵AB是⊙O的直径,弦CD⊥AB,∴,DG=CG,∴∠ADF=∠AED,∵∠FAD=∠DAE(公共角),∴△ADF∽△AED;故①正确;②∵= ,CF=2,∴FD=6,∴CD=DF+CF=8,∴CG=DG=4,∴FG=CG﹣CF=2;故②正确;③∵AF=3,FG=2,∴AG= = ,∴在Rt△AGD中,tan∠ADG= = ,∴tan∠E= ;故③错误;④∵DF=DG+FG=6,AD= = ,∴S△ADF= DF•AG= ×6×=3 ,∵△ADF∽△AED,∴=()2,∴= ,∴S△AED=7 ,∴S△DEF=S△AED﹣S△ADF=4 ;故④正确.故选C.【分析】①正确.由AB是⊙O的直径,弦CD⊥AB,根据垂径定理可得:,DG=CG,继而证得△ADF∽△AED;②正确.由= ,CF=2,可求得DF的长,继而求得CG=DG=4,则可求得FG=2;③错误.由勾股定理可求得AG的长,即可求得tan∠ADF的值,继而求得tan∠E= .④首先求得△ADF的面积,由相似三角形面积的比等于相似比的平方,即可求得△ADE的面积,继而求得S△DEF=4 .20、【答案】D【考点】垂径定理,圆周角定理,相似三角形的判定与性质【解析】【解答】解:∵在⊙O中,点C是的中点,∴= ,∴∠CAD=∠ABC,故①正确;∵≠ ,∴≠ ,∴AD≠BC,故②错误;∵AB是⊙O的直径,∴∠ACB=90°,又∵CE⊥AB,∴∠ACE+∠CAE=∠ABC+∠CAE=90°,∴∠ACE=∠ABC,又∵C为的中点,∴= ,∴∠CAP=∠ABC,∴∠ACE=∠CAP,∴AP=CP,∵∠ACQ=90°,∴∠ACP+∠PCQ=∠CAP+∠PQC=90°,∴∠PCQ=∠PQC,∴PC=PQ,∴AP=PQ,即P为Rt△ACQ斜边AQ的中点,∴P为Rt△ACQ的外心,故③正确;∵AB是⊙O的直径,∴∠ACB=90°,又∵CE⊥AB∴根据射影定理,可得AC2=AE•AB,故④正确;如图,连接BD,则∠ADG=∠ABD,∵≠ ,∴≠ ,∴∠ABD≠∠BAC,∴∠ADG≠∠BAC,又∵∠BAC=∠BCE=∠PQC,∴∠ADG≠∠PQC,∴CB与GD不平行,故⑤错误.故答案为:D.【分析】在同圆或等圆中,同弧或等弧所对的圆周角相等,据此推理可得①正确,②错误;通过推理可得∠ACE=∠CAP,得出AP=CP,再根据∠PCQ=∠PQC,可得出PC=PQ,进而得到AP=PQ,即P为Rt△ACQ斜边AQ的中点,故P为Rt△ACQ的外心,即可得出③正确;连接BD,则∠ADG=∠ABD,根据∠ADG≠∠BAC,∠BAC=∠BCE=∠PQC,可得出∠ADG≠∠PQC,进而得到CB与GD不平行,可得⑤错误.。
