7自由度机械臂底座计算
7轴机械臂运动学方程

7轴机械臂运动学方程机械臂是一种能够模拟人类手臂运动的机械装置,广泛应用于工业生产线、医疗手术、空间探测等领域。
而机械臂的运动学方程则是描述机械臂运动的数学模型,通过解析运动学方程,可以准确计算机械臂的位置、速度和加速度等运动参数。
7轴机械臂是指机械臂由7个关节驱动,具有7个自由度。
每个关节都可以旋转或者转动,从而实现机械臂在空间中的各种姿态和位置变化。
为了描述机械臂的运动学特性,需要建立一套运动学方程。
机械臂的运动学方程可以分为正向运动学和逆向运动学两部分。
正向运动学是指已知机械臂各关节的角度,如何计算机械臂末端的位置和姿态。
逆向运动学则是指已知机械臂末端的位置和姿态,如何逆推出各关节的角度。
对于7轴机械臂的正向运动学方程,可以通过连续的坐标变换来实现。
首先,我们需要定义机械臂的基座坐标系和末端执行器的坐标系。
然后,通过一系列的旋转和平移变换,将基座坐标系转换到末端执行器的坐标系。
最后,通过坐标变换矩阵,可以得到机械臂末端的位置和姿态。
对于7轴机械臂的逆向运动学方程,可以通过逆解正向运动学方程来实现。
首先,已知机械臂末端的位置和姿态,我们可以通过逆变换矩阵,将末端执行器的坐标系转换到基座坐标系。
然后,通过逆解旋转和平移变换,可以得到各关节的角度。
在实际应用中,机械臂的运动学方程可以用于路径规划、碰撞检测、动力学分析等方面。
通过对机械臂的运动学进行建模和分析,可以提高机械臂的精度和效率。
然而,机械臂的运动学方程并不是一个简单的问题。
由于机械臂的关节之间存在复杂的几何约束,以及关节之间的耦合效应,导致运动学方程的求解变得困难。
因此,在实际应用中,通常会借助计算机辅助设计软件来求解机械臂的运动学方程。
总结起来,7轴机械臂的运动学方程是描述机械臂运动的重要数学模型。
通过正向运动学和逆向运动学两部分的分析,可以准确计算机械臂的位置、速度和加速度等参数。
机械臂的运动学方程不仅在工业自动化领域有着广泛的应用,还对于机器人技术的发展起着重要的推动作用。
七自由度柔性机械臂机构说明.

七自由度柔性机械臂机构说明设计目标由于人工成本的不断提升,人们的刚性需求也不断的扩大,生产自动化越来越被人们所重视。
也是社会发展的必然。
让机器人去完成一些高危、肮脏、重复、精度高的工作。
由此,设计一款高精度,高灵活性的机器臂显得更为重要。
设计的目标:高精度仿人工业机器人。
运用先进的仿生理论与柔性设计为基础,设计开发用二次式运动反馈来实现其高精度控制,合理的仿人机构来完成动动。
机械臂整体设计方案一、功能需求:满足实现模仿人类手臂的基本功能,自由度包括手臂的肩部的抬起,摆动,旋转,肘部的弯曲,腕部的旋转,弯曲,摆动共7个自由度。
(图一)图一图二二、优化后确定的构型:自由度包括手臂的肩部的摆动,抬起,大臂旋转,肘部的弯曲,小臂的旋转,腕部的弯曲,摆动共7个自由度。
(图二)三、驱动模块示意设计:(图三)胡克定律是力学基本定律之一。
适用于一切固体材料的弹性定律,它指出:在弹性限度内,物体的形变跟引起形变的外力成正比。
这样增加了力的反馈测量。
在弹性材料在弹性限度内形变时,测得其形变量,从而计算出受力与关节下方所处的位置。
1.先进行测试图三四、机械臂的具体设计方案,(图四)五、各关节的受力分析:基本尺寸图(图五)图五L1=426mm,L2=293mm,L3=108mm,L4=442mm。
六、马达的初选谐波减速器的优点:Harmonic减速器结构简单,体积小,重量轻、啮合的齿数多、承载能力大、运动精度高、运动平稳、间隙可以调整、传动效率高、同轴性好、可实现向密闭空间传递运动及动力。
瑞士Maxon电机优点:轴向窜动和径向跳动小、温度范围大、回差小等,并且电机型号全编码器与抱闸与控制器配套全面。
瑞士Maxon电机与日本Harmonic谐波减速器选型需求示例图片:图六马达1:EC90flat 90W扭力:4.67 nm 0.387nm;转速:3190rpm;重量:648g减速器1:CSG-25-160 减速比:1:160;最大扭力:314nm;正常:176nm;重量:420g马达2:EC-4pole max30 200W 扭力:3.18 nm 0.112nm;转速:17000rpm;重量:300g减速器2:CSG-25-160 减速比:1:160;最大扭力:314nm;正常:176nm;重量:420g马达3:EC max40 170W 扭力:2.66nm0.16nm;转速:9840rpm;重量:580g减速器3:CSG-17-120 减速比:1:120;扭力最大:112nm;正常:70nm;重量:150g马达4:EC45flat 70W 扭力:0.82nm0.13nm;转速:4840rpm;重量:110g减速器4:CSG-20-160 减速比:1:160;最大扭力:191nm;正常:120nm;重量:280g马达5:EC-4pole max30 100W 扭力:1.24nm 0.0 63nm;转速:17800rpm;重量:210g减速器5:CSD SHD-17-100 减速比:1:100;最大扭力:71nm;正常:37nm;重量:100g 马达6:EC45flat 70W 扭力:0.13 nm 0.17nm;转速:4840rpm重量:110g减速器6:CSF-11-100 减速比:1:100;最大扭力:25nm;正常:11nm;重量:50g马达7:EC-4pole max30 100W 扭力:1.24nm 0.0 63nm;转速:17800rpm;重量:210g减速器7:CSF-11-100 最大扭力:25nm;正常:11nm;重量:50g说明:EC45flat 70W要更换为EC-I40 70W+MR七、受力分析:有效扭力计算公式:(堵转-连续)*0.3+连续质量分配:设大臂小臂均为,外径D=110mm,假设主体为外壁壁厚为L=5mm的铝壳,长度为H=250mm,则体积为:412cm3,铝的密度2.7g/cm3,外壳质量为1.1kg大臂部分质量有马达3(580g)减速器(150g),外壳(1.1kg);小臂部分有马达4567(110g,210g,110g,210g),减速器4567(280g,100g,50g,50g),外壳(1.1kg);手部主要是灵巧手的质量设为1kg;外加假设载荷6kg。
七自由度仿人机械臂设计与分析.pptx

首先对人体上肢运动机理进行研究分析,以人体手臂完成动作类 型区分自由度,分析各自由度运动所需的人体上肢骨骼和肌肉。 结合机械臂的设计要求,对机械臂各关节进行结构设计,并根据 各关节运动特点进行驱动匹配和选型。
对机械臂完成指定任务所需要的传感器进行选配。对液压驱动 关节铰接位置参数进行了优化分析,完善了机械臂结构。
最后使用拉格朗日法得到了机械臂的动力学方程,使用ADAMS和 MATLAB联合仿真,将关节转角、角速度与关节力矩建立闭环关系, 建立一个完整虚拟样机完成机械臂的动力学仿真,得到了各关节 仿真力矩变化图。
对机械臂进行运动学计算,通过机械臂的D-H参数的确定,建立各 关节之间位置关系,完成正逆运动学方程的求解,采用五次多项 式插值表示机械臂运动轨迹;基于MATLAB开展仿真分析,验证机 械臂运动学理论正逆解,得到机械臂工作空间及到达指定位置机 械臂各关节角位移变化,为后续机械臂的动力学分析提供基础。 对机械臂关键部件进行拓扑轻量化设计及强度校核,借助ANSYS Workbench平台对机械臂关键部件进行形状拓扑优化设计,对优 化前后机械臂关键部件位移变形进行对比分析,并对优化后的结 构进行强度校核。
七自由度仿人机械臂设计与分析
在《中国制造2025》趋势的影响下,服务型机器人进入了快速发 展的浪潮,其中具有多功能的辅助机械臂逐渐成为极具广阔应用 前景的研究热点。本文针对老龄残疾人士及大型工程设备装配 两个对象,提出了一种基于人体解剖学的七自由度机械臂的设计 方案,解决大型工程设备装配需要多名工程师在相对狭小环境下 协同配合及服务老龄残疾人士成本较高的问题,特点在于:(1)全 刚体结构的机械臂可以保证末端强稳定性;(2)具有冗余自由度 机械臂使得服务老龄残疾人士时,末端固定时其余关节可根据实 际空间情况自由活动达到避免碰到受帮助者的目的;(3)同人体 上肢相似的尺寸、相似的驱动效果的机械臂可以直接应用在为 人类设计的工作场景。
7自由度工业机器人机械结构设计说明书

摘要7自由度工业机器人以工作范围大、动作灵活、结构紧凑、能抓取靠近机座的物体等特点备受设计者和使用者的青睐。
由于有一个冗余自由度,很容易在确保最佳焊接姿势的同时,避免工件以及夹具对机器人工作臂的干扰。
本论文首先根据机器人持重3、工作范围1434、本体重量150,确立kg mm kg机器人为S腰部回转、L小臂摆动、E大臂回转、U臂部俯仰、R腕部扭转、B 腕部俯仰、T腕部回转的7自由度关节型弧焊机器人的总体结构;分析机器人的各个关节在转动惯量、角速度、加速度等技术指标下的工作状况,确定7个关节都采用交流电机驱动、机器人手臂专用减速器传动,同时B、T腕部关节还用到同步带传动。
通过计算各关节所需电机的功率和转矩、减速器的减速比、同步带的要求并选型;用UG NX6.0画出机器人的各关节三维仿真模型,并装配成型。
本课题研究具有广泛的实际意义和应用前景。
设计的7自由度工业机器人为后续的机器人动力学分析和运动控制提供了参考依据,并可以做进一步的研发。
关键词:7自由度,工业机器人,机械结构Abstract7 dof industrial robots with large scope of work, flexible, compact structure, can grab the object near the base are famous among so much designers and users. Because there is a redundant freedom, it is easy to ensure the best welding position at the same time, avoid workpiece and fixture work on the robot arm interference.In this thesis, according to the robot puts up , the scope of work is ,3kg1434mm body weight is ,establish 7 dof150kg joint structure of arc-welding robot including S waist, L arm swing, E arm rotation, U pitching arm, R wrist turn, B wrist pitch, T wrist rotation. Analysis of the various robot joints in moment of inertia, angular velocity, acceleration and other technical indicators of the work under the conditions identified seven joints driven by AC motor, the robot arm dedicated reducer drive, while B, T wrist joint is also used in synchronous belt drive. Required by calculating the joint motor power and torque, reduction ratio reducer, belt requirements and selection; robot with UG NX6.0 draw three-dimensional simulation model of each joint, and assembly molding.This research has extensive practical significance and application prospect. 7 dof industrial robots designed for the follow-up dynamics analysis and motion control and provide a reference, and can do further research and development.Key words: 7 dof, industrial robot, mechanical structure目录摘要 (I)Abstract (II)目录 (III)第一章绪论 (1)1.1 课题背景 (1)1.2 国内外工业机器人的发展概况 (2)1.2.1 国内外工业机器人的发展现状 (2)1.2.2 工业机器人的发展趋势 (4)1.3 课题来源 (5)1.4 主要研究内容 (6)第二章7自由度工业机器人总体方案设计 (7)2.1 机器人机械设计的特点 (7)2.2 与机器人有关的概念 (7)2.3 机器人的基本技术要求 (9)2.4 机器人手臂结构型式 (10)2.5 机器人结构方案的分析 (12)2.5.1 7自由度工业机器人的外形结构设计 (12)2.5.2 7自由度工业机器人的关节结构设计 (15)2.6 机器人的驱动方式的选择 (19)2.7 7自由度机器人的控制系统 (20)2.7.1 7自由度工业机器人控制系统硬件部分 (20)2.7.2 7自由度工业机器人控制系统软件部分 (21)2.8 本章小结 (21)第三章7自由度工业机器人结构设计 (22)3.1 引言 (22)3.2 减速器类型选择 (23)3.3 同步带类型选择 (24)3.4 机器人结构设计 (25)3.4.1 T腕部回转关节交流伺服电机和减速器、同步带的选择 (25)3.4.2 B腕部摆动关节交流伺服电机和减速器、同步带的选择 (30)3.4.3 R回转关节交流伺服电机和减速器的选择 (36)3.4.4 U回转关节交流伺服电机和减速器的选择 (38)3.4.5 E回转关节交流伺服电机和减速器的选择 (40)3.4.6 L摆动关节交流伺服电机和减速器的选择 (42)3.4.7 S腰部回转关节交流伺服电机和减速器的选择 (44)3.4.8 电机、减速器、同步带选型总表 (47)3.5 电机型号 (48)3.5.1 SGMGH系列1500转电机 (48)3.5.2 SGMPH系列3000转电机 (49)3.6 本章小结 (51)第四章7自由度工业机器人三维结构设计 (52)4.1 机器人各个关节三维图 (52)4.1.1 底座造型图 (52)4.1.2 S腰部回转关节造型图 (53)4.1.3 L小臂摆动关节造型图 (56)4.1.4 E大臂回转关节造型图 (60)4.1.5 U臂部俯仰关节造型图 (60)4.1.6 R腕部扭转关节造型图 (61)4.1.7 B腕部俯仰关节造型图 (62)4.2 机器人装配图 (65)4.3 本章小结 (66)第五章结论和展望 (67)5.1 结论 (67)5.2 技术经济分析报告 (68)5.2.1 技术可行性分析 (69)5.2.2 技术优越性分析 (69)5.3 展望 (69)参考文献 (71)致谢 (73)声明 (74)第一章绪论1.1 课题背景机器人是典型的机电一体化装备,除了在制造业、农业、医疗、海洋开发、航天工程等方面得到了越来越广泛的应用之外,也渗透到人们生活的各个方面,随着工业机器人向更深、更广方向的发展以及机器人智能化水平的提高,机器人的应用范围还在不断地扩大。
基于旋量理论的7自由度机械臂运动学建模与分析

基金项目:山西省自然科学基金项目(201801D121183)ꎻ山西省重点研发计划项目(201803D421028ꎻ201903D421051)第一作者简介:李冠琦(1996 )ꎬ男ꎬ山西吕梁人ꎬ硕士研究生ꎬ研究方向为康复机器人机构ꎮDOI:10.19344/j.cnki.issn1671-5276.2022.01.027基于旋量理论的7自由度机械臂运动学建模与分析李冠琦ꎬ武建德ꎬ李瑞琴(中北大学机械工程学院ꎬ山西太原030051)摘㊀要:机械臂模仿人手臂的7自由度会拥有冗余自由度ꎮ基于旋量理论计算7自由度机械臂的正向运动学解ꎬ从数值上验证矩阵指数先分块展开比直接泰勒展开准确ꎮ用Newton-Raphson数值迭代法求逆解ꎮ通过编写Matlab程序对正逆解互相验证ꎮ研究发现逆解的求解有适用范围ꎬ较之传统的D-H法ꎬ使用0螺距的螺旋轴ꎬ会使建模更加简洁ꎮ关键词:旋量ꎻ机械臂ꎻNewton-Raphson数值迭代法中图分类号:TP241㊀㊀文献标志码:A㊀㊀文章编号:1671 ̄5276(2022)01 ̄0105 ̄03KinematicsModelingandAnalysisofSeven-degree-freedomRoboticArmBasedonSpinorTheoryLIGuanqiꎬWUJiandeꎬLIRuiqin(InstituteofMechanicalEngineeringꎬNorthUniversityofChinaꎬTaiyuan030051ꎬChina)Abstract:Theroboticarmmimickingthe7DOFofthehumanarmwillhaveredundantdegreesoffreedom.Theforwardkinematicsolutionoftheseven-DOFroboticarmiscalculatedbasedonthespinortheoryꎬanditisverifiednumericallythatthematrixexponentialfirstblockexpansionismoreaccuratethanthedirectTaylorexpansion.TheNewton-Raphsonnumericaliterationmethodisusedtofindtheinversesolution.Theforwardandinversesolutionsareverifiedagainsteachotherbywritingamatlabprogram.Itisfoundthatthereisarangeofapplicabilityfortheinversesolutionꎬandtheuseofa0-pitchspiralaxisresultsinamoreconcisemodelingthanthetraditionalD-Hmethod.Keywords:spinortheoryꎻroboticarmꎻNewton-Raphsonnumericaliterativemethod0㊀引言机械臂是机器人技术领域中应用最为广泛的自动化装置ꎬ在工业制造㊁医疗康复等领域都有其应用实例ꎬ拟人化机械臂技术也逐渐成熟[1-4]ꎮ匹兹堡大学生物医学团队在BCI机械臂假肢里引入实时触觉反馈ꎬ使完成任务的时间减少一半ꎮ波士顿动力开发Stretch移动式7R机械臂已应用于仓库运输ꎮ20世纪80年代学者们开始讨论将旋转轴从数学中引入机器人研究的可行性ꎬ旋量理论[5-9]日益成熟ꎬ然而对其的应用介绍却鲜见报道ꎮ本文建模7自由度串联机械臂ꎬ着重对螺旋轴这一单位矢量在运动学的应用加以详细描述ꎮ6自由度逆解有通用公式ꎬ7R逆解包含32个实根ꎬ出现虚空间或自运动歧ꎮ7R逆解可结合Newton-Raphson数值迭代法求解[10]ꎮ使用Matlab进行正解中的化简与直接展开等运算过程的比较ꎬ并且同时使用开源Python对结果进行比较ꎮ使用基于空间(space简称s)坐标系的空间雅可比矩阵ꎬ找出数值迭代法求逆解的适用范围ꎬ基于正解的前提下ꎬ验证逆解的准确性ꎮ1㊀旋量理论螺旋(旋量 旋转向量)理论在正运动学中的应用ꎮ1.1㊀M矩阵(0位置㊁起始位置)M矩阵为当所有的关节转角都为0的时候ꎬ操作空间坐标系(body简称b)在s坐标系中的位置和姿态矩阵ꎮ1.2㊀旋转向量Sң与指数积公式将每一个转动关节视为0螺距的轴ꎬ假设除了最后一个关节转动θʎ外ꎬ其他关节都是固定的ꎮ在s坐标系里ꎬ关节7上螺旋轴的向量形式如式(1)所示ꎬ在高维度上ꎬRn是n维的欧几里得空间ꎬS7ңɪR6㊁ω7ңɪR3ꎬV7ңɪR3ꎮ螺旋轴的矩阵形式S7如式(2)所示ꎮS7ң=ωң7Vң7éëêêùûúú(1)S7=ω7Vң700éëêêùûúú(2)T07=eS7θ7M(3)501 博看网 . All Rights Reserved.特殊正交群是所有有效的3ˑ3旋转矩阵的集合群SO(3):包括R㊁ω㊁eωθꎮ特殊的欧几里得集合群或刚体运动群或R3中的同质变换矩阵Se(3)表示位姿:包括M㊁eSθ㊁T07ꎮeSθ=I+Sθ+S2θ22!+S3θ33!+ =eωθf(θ)ν01éëêêùûúú(4)式(4)中ꎬ可利用特性ω3=-ω来化简ꎬ且eωθ有Rodrigues公式:f(θ)=Iθ+(1-cosθ)ω+(θ-sinθ)ω2(5)eωθ=I+sinθω+(1-cosθ)ω2(6)依次解锁一个角度ꎬ往前代值ꎬ得到T07=eS1θ1 eS7θ7M(7)2㊀数值法逆解使用非线性寻根的Newton-Raphson方法ꎬ有寻根㊁不存在根时寻找近似解㊁存在多个解时寻找最优解的优势ꎮ给定一个初始值ꎬ然后代入迭代式求解直到出现误差范围内的解ꎮ设正向运动学函数为f(θd)ꎬ末端执行器的位置向量为νꎬ非线性寻根Newton-Raphson是找到目标函数的解ꎮ几何视角如图1所示ꎻ式(8)是解析视角ꎮ式(9)-式(11)是计算雅可比矩阵ꎮ图1㊀迭代法几何过程Δθ=J-1(θ0)[vd-f(θi)](8)JS(θ)=JS1(θ1)ңJS2(θ2)ң JSn(θn)ң[](9)JS1(θ1)ң=S1ң(10)JSi(θi)ң=[eS1θ1 eSi-1θi-1]∗Siң(11)式中∗为其伴随矩阵ꎮ对这种算法的进一步改进:1)末端执行器的位置描述f(θd)变更为正运动学计算出的矩阵T07ꎮ2)误差调整ꎮ用螺旋轴SMTң两分量的模代替末端执行器每次迭代的位置变化ꎮ3)引进伪逆矩阵J†避免求解奇异时无解的情况ꎮ在Matlab里编程为pinv(J)ꎮ当前基于b坐标系ꎬ变换为基于s坐标系:SMTbң=log(TMT07(θi))(12)SMTsң=(Tsb)∗SMTbң(13)式中:Tsb是坐标转移矩阵ꎻ∗为求其伴随矩阵ꎮ改进算法的流程图如图2所示ꎮ图2㊀改进的数值迭代法流程图3㊀验证正逆解3.1㊀正运动学方程㊀绘制三维模型图ꎬ并建立7R示意图(图3)进行验证ꎮ如图3(b)所示的坐标平面ꎬy方向定义为a并依次标号ꎬz方向定义为b也依次序标号ꎮ标示7个螺距为0的右手螺旋轴S1ң-S7ңꎮM=1000010240000100001éëêêêêùûúúúú(14)S7ң=[0㊀0㊀1㊀-a7㊀0㊀0]T=[0㊀0㊀1㊀-300㊀0㊀0]T(15)U a U 7Rb 7R .图3㊀三维模型图及7R示意图根据式(3)ꎬ使用矩阵分块后化简的运算过程ꎬ编程并计算结果ꎮT(θ)=c7-s70-2700s7s7c702700c7-30000100000éëêêêêùûúúúú(16)根据式(3)ꎬ发现将矩阵指数直接泰勒展开(采用了3种计算方法:Pada法㊁特征值法㊁6次的泰勒展开)得出的601结果虽然一致ꎬ但是它是虚数形式ꎬ增加了计算量ꎮ结果:TM_pada(θ)=c7-s70-2700s7s7c701350e-θ7i+1350eθ7i-30000100001éëêêêêùûúúúú(17)使用先进行矩阵分块然后利用特性化简的运算方法ꎬ该结果更准确㊁后期的运算量更小ꎮ代入式(7)ꎬ使用该方法分别在Matlab和Python中运算ꎬ得出的结果一致:T=c5-6c1234c7-s1234c7-s1234c7-c5-6c1234s7-s5-6c1234r1c1234s7+c5-6s1234c7c1234c7-c5-6s1234s7-s5-6s1234r2s5-6c7-s5-6s7c5-6r30001éëêêêêêùûúúúúúr1=150s1234-5-1350s12347-300s123-675s123457-6-675s123467-5-150s12345-1350s1234-7+600s1234+300s12+675s12345-6-7+675s12346-5-7-300s1+750s12345-6-750s12346-5r2=150c1234-5+1350c12347+300c123+675c123457-6+675c123467-5-150c1234-5+1350c1234-7-600c1234-300c12-675c12345-6-7-675c12346-5-7+300c1-750c12345-6+750c12346-5r3=2700s7c5s6-s5c6-1500s5s6-c5(1500c6-1500)-1200c5+12003.2㊀逆运动学方程1)第一次验证设初始位置为正解的0位置ꎬ转动角度为θlistꎮθlist=πꎻπ2ꎻπ3ꎻπ4ꎻπ5ꎻπ6ꎻπ7[]=[3.142ꎻ1.571ꎻ1.047ꎻ0.785ꎻ0.628ꎻ0.524ꎻ0.449]给逆解的初始值[3ꎬ1.5ꎬ1ꎬ0.6ꎬ0.5ꎬ0.4ꎬ0.3]ꎮ解得[3.161ꎬ1.563ꎬ1.059ꎬ0.762ꎬ0.628ꎬ0.523ꎬ0.449]ꎮ2)第二次验证因发现误差较大:1)改用角度制ꎻ2)迭代次数增加到1000次ꎻ3)精度调整为eω<0.0001ꎬev<0.0001ꎮ经过多组数据实验发现ꎬ相差3ʎ以内ꎬ位置完全重现ꎻ相差10ʎ以内ꎬ第一角度有0.1ʎ的偏差ꎻ相差15ʎ以上的逆运算ꎬ第一个角度有1ʎ以上的偏差ꎮ所以ꎬ该方法求逆解有完全重现的适用范围ꎬ需要把初始解猜测在真实解的附近15ʎ以内(表1)ꎮ表1㊀正逆解互相验证单位:(ʎ)㊀验证项目θ1θ2θ3θ4θ5θ6θ7Δθ初始角度10203040506070 猜测角度7172737475767计算的逆解102030405060700猜测角度6162636465666计算的逆解10.00120.00129.99939.9995060700.001猜测角度1112131415161计算的逆解10.0620.03229.94939.9595060700.060猜测角度0102030405060计算的逆解10.120.05329.91639.9325060700.100猜测角度-551525354555计算的逆解10.7420.40329.37339.4845060700.740续表1验证项目θ1θ2θ3θ4θ5θ6θ7Δθ猜测角度-641424344454计算的逆解11.0320.56629.12839.2765060701.030猜测角度-13-3717273747计算的逆解26.72824.46724.37534.4295060706.728猜测角度-15-5515253545计算的逆解24.46633.10318.25724.17350607014.466猜测角度-16-7414243444计算的逆解63.432-26.264-22.72585.55750607053.4324㊀结语本文重点介绍了如何使用形如螺旋楼梯的转向量计算正逆解ꎮ结合旋量与Newton-Raphson数值法求逆解ꎮ为涵盖转动机构可能出现的问题ꎬ采用目前串联机构中最复杂的7R机构并且使机构尽可能复杂ꎬ但是设计中没有涵盖helical螺旋和cylindrical圆筒等机构ꎮ在比较了不同的运算方法后ꎬ计算正解ꎬ得出先将矩阵分块㊁再利用特性化简的方法更好的结论ꎮ在计算逆解的过程中ꎬ发现当初始猜测的第一个角度超过真实解20ʎꎬNewton-Raphson数值法不会重现正解ꎮ验证结果表明旋量形式美观ꎬ建模快捷ꎬ编程明了ꎬ适用于机械臂中的串联机构㊁并联机构㊁转动关节㊁平动关节㊁螺旋关节等的运动学㊁动力学特性建模和分析ꎮ参考文献:[1]FLESHERSNꎬDOWNEYJEꎬWEISSJMꎬetal.Abrain-computerinterfacethatevokestactilesensationsimprovesroboticarmcontrol[J].Scienceꎬ2021ꎬ372(6544):831 ̄836.[2]KEVINMLꎬFRANKCP.Modernrobotics:mechanicsplanningandcontrol[M].Illinois:CambridgeUniversityPressꎬ2017.[3]刘世平ꎬ曹俊峰ꎬ孙涛ꎬ等.基于BP神经网络的冗余机械臂逆运动学分析[J].中国机械工程ꎬ2019ꎬ30(24):2974 ̄2977ꎬ2985.[4]赵京ꎬ王鑫ꎬ张自强ꎬ等.基于肘部自运动的主从异构7自由度机械臂运动映射及其几何逆解[J].机械工程学报ꎬ2020ꎬ56(15):181 ̄190.[5]YOUWSꎬLEEYHꎬOHHSꎬetal.Designofa3D-printableꎬrobustanthropomorphicrobothandincludingintermetacarpaljoints[J].IntelligentServiceRoboticsꎬ2019ꎬ12(1):1 ̄16.[6]BINDURAꎬNELOYAAꎬALAMSꎬetal.Sigma-3:Integrationandanalysisofa6DOFroboticarmconfigurationinarescuerobot[C]//20194thInternationalConferenceonRoboticsandAutomationEngineering(ICRAE).Singapore:IEEEꎬ2019:6 ̄11.[7]常健ꎬ王亚珍ꎬ李斌.基于力/位混合算法的7自由度机械臂精细操控方法[J].机器人ꎬ2016ꎬ38(5):531 ̄539.[8]张昌ꎬ武玉强.基于P-Rob六自由度机械臂运动学建模与仿真[J].包装工程ꎬ2020ꎬ41(11):166 ̄173.[9]WIEDMEYERWꎬALTOÉPꎬAUBERLEJꎬetal.Areal-time-capableclosed-formmulti-objectiveredundancyresolutionschemeforseven-DoFserialmanipulators[J].IEEERoboticsandAutomationLettersꎬ2021ꎬ6(2):431 ̄438.收稿日期:20210401701 博看网 . All Rights Reserved.。
如何求解七自由度机械臂运动学

如何求解七自由度机械臂运动学机械臂是一种典型的多自由度机械系统,七自由度机械臂是指机械臂有七个独立运动自由度。
七自由度机械臂广泛应用于工业生产、医疗手术和科学研究等领域。
在机械臂的运动控制中,运动学是一个重要的研究方向,其目的是通过运动学模型求解机械臂的位置、速度和加速度等参数。
下面介绍如何求解七自由度机械臂的运动学问题。
一、建立机械臂运动学模型机械臂的运动学模型包括正运动学和逆运动学两种。
正运动学是指已知机械臂各个关节的角度和长度,求解机械臂末端的位置和姿态;逆运动学是指已知机械臂末端的位置和姿态,求解机械臂各个关节的角度和长度。
对于七自由度机械臂,需要建立其正逆运动学模型。
二、正运动学求解正运动学求解的方法有多种,其中最常用的是解析法和数值法。
解析法是指通过代数求解机械臂的位置和姿态解析解的方法。
数值法是指通过迭代求解机械臂的位置和姿态数值解的方法。
对于七自由度机械臂,解析法比较困难,通常采用数值法求解。
数值法的实现需要运用矩阵转换和旋转矩阵等数学方法。
三、逆运动学求解逆运动学求解是指已知机械臂末端的位置和姿态,求解机械臂各个关节的角度和长度。
逆运动学求解的方法有多种,其中最常用的是解析法和数值法。
解析法是指通过代数求解机械臂各个关节的角度和长度解析解的方法。
数值法是指通过迭代求解机械臂各个关节的角度和长度数值解的方法。
对于七自由度机械臂,解析法比较困难,通常采用数值法求解。
数值法的实现需要运用牛顿-拉夫森方法和LM法等数学方法。
四、结论通过上述方法,可以求解七自由度机械臂的运动学问题。
在实际应用中,根据具体问题的不同,可以选择适合的求解方法。
机械臂的运动学问题是机械臂控制研究中的重要问题,其解决对于机械臂的运动控制和精度提高具有重要意义。
七自由度机械臂逆解方案设计

七自由度机械臂逆解方案设计七自由度机械臂是一种具有七个关节的机械臂,每个关节都可以独立运动,因此具有较大的灵活性和自由度。
逆解是指根据机械臂末端执行器的位置和姿态,计算出各个关节的角度,从而实现目标位置和姿态的精确控制。
本文将提出一种七自由度机械臂的逆解方案设计。
1.确定目标姿态和位置首先,需要明确机械臂末端执行器的目标姿态和位置。
可以通过现实需求或者希望的机械臂运动轨迹来确定。
姿态通常由旋转矩阵或四元数表示,位置由三维坐标表示。
2.建立正解模型将机械臂的关节角度和末端执行器的位置姿态联系起来,建立正向运动学模型。
正向运动学模型是一种从关节角度到末端位置姿态的映射关系。
可以使用Denavit-Hartenberg(DH)参数法来描述机械臂的运动学模型。
3.建立逆解模型根据所建立的正向运动学模型,可以反过来建立逆向模型,即从末端执行器的位置姿态到关节角度的映射关系。
逆向模型可以使用数值方法或解析方法求解。
数值方法包括迭代方法(如牛顿迭代法)和优化方法(如遗传算法、粒子群算法等);解析解则是通过数学推导直接得到关节角度的表达式。
4.选择逆解方法根据具体情况选择适合的逆解方法。
如果机械臂结构简单且准确性要求不高,可以选择数值方法求解。
如果机械臂结构复杂且准确性要求高,可以选择解析解。
对于七自由度机械臂,由于其自由度较高,复杂度较高,建议选择解析解。
5.实现逆解算法根据所选择的逆解方法,编写相应的逆解算法。
如果选择解析解,将所建立的逆解模型转化为MATLAB或其他编程语言的代码实现。
如果选择数值方法,编写相应的数值算法。
6.仿真验证通过建立的逆解算法,进行机械臂的姿态和位置逆解计算,并进行仿真验证。
在仿真软件中输入机械臂末端执行器的目标姿态和位置,运行逆解算法得到关节角度,然后通过正解模型将关节角度转化为末端执行器的实际位置和姿态,比较与目标值的差异,验证逆解算法的正确性。
7.实际控制在进行了仿真验证之后,可以将逆解算法应用到实际机械臂控制中。
如何求解七自由度机械臂动力学

如何求解七自由度机械臂动力学如何求解七自由度机械臂动力学机械臂是一种能够模拟人类手臂运动的机器人,它可以在工业生产、医疗、军事等领域发挥重要作用。
机械臂的运动学和动力学是机械臂控制的基础,其中动力学是指机械臂在运动过程中所受到的力和力矩的关系。
本文将介绍如何求解七自由度机械臂动力学。
一、机械臂动力学模型机械臂动力学模型是指机械臂在运动过程中所受到的力和力矩的关系。
机械臂动力学模型可以分为两种:欧拉-拉格朗日动力学模型和牛顿-欧拉动力学模型。
欧拉-拉格朗日动力学模型是通过拉格朗日方程来描述机械臂的动力学,而牛顿-欧拉动力学模型是通过牛顿定律和欧拉定理来描述机械臂的动力学。
二、机械臂动力学求解方法机械臂动力学求解方法可以分为两种:解析方法和数值方法。
解析方法是指通过解析式来求解机械臂的动力学,而数值方法是指通过数值计算来求解机械臂的动力学。
1. 解析方法解析方法是指通过解析式来求解机械臂的动力学。
解析方法的优点是计算速度快,精度高,但是只适用于简单的机械臂模型。
解析方法的具体步骤如下:(1)建立机械臂动力学模型。
(2)求解机械臂的运动学方程。
(3)求解机械臂的动力学方程。
(4)求解机械臂的运动学和动力学方程的解析解。
2. 数值方法数值方法是指通过数值计算来求解机械臂的动力学。
数值方法的优点是适用于复杂的机械臂模型,但是计算速度较慢,精度有限。
数值方法的具体步骤如下:(1)建立机械臂动力学模型。
(2)将机械臂的运动学和动力学方程转化为数值计算的形式。
(3)通过数值计算求解机械臂的运动学和动力学方程。
(4)对数值计算结果进行分析和验证。
三、总结机械臂动力学是机械臂控制的基础,求解机械臂动力学是机械臂控制的重要环节。
本文介绍了机械臂动力学模型和求解方法,包括欧拉-拉格朗日动力学模型、牛顿-欧拉动力学模型、解析方法和数值方法。
在实际应用中,需要根据具体情况选择合适的动力学模型和求解方法,以达到最佳的控制效果。
机械臂自由度计算

机械臂自由度计算机械臂自由度计算随着工业自动化的普及,机器人在制造、装配、加工等领域的应用越来越广泛。
而机械臂作为机器人的重要组成部分,其自由度的计算方法也成为研究的重要方向之一。
机器人的自由度指的是机器人在操作空间内可以运动的自由程度,也称“自由度”。
机械臂的自由度数是指机械臂每个关节的参考点在操作空间内所能运动的自由度的总和。
在机械臂的设计和控制系统开发中,自由度数的计算往往是非常重要的一步。
正确计算出机械臂的自由度数,可以为后续设计和操作提供参考,避免在实际应用中出现错误和不必要的风险。
机械臂的自由度数计算方法主要包括几何法和运动学法两种方法,下面我们分别介绍一下。
一、几何法几何法主要依据机械臂机构结构进行计算,是一种简单易行的计算方法。
首先,我们需要对机械臂结构进行简化,将机械臂的每个关节看做是一个球关节。
然后,利用“球的约束度”来计算。
对于每个球关节,由于其轴线可沿任意方向转动,因此其约束度为2。
而对于连接两个球关节的连杆,其约束度为1,因为连接点只能在该连杆上移动,而不能旋转。
根据以上分析,我们可以得到机械臂自由度的计算公式如下:自由度数 = 6 - Σ(约束度)其中,“约束度”指的是机械臂每个关节及连接连杆所约束的自由度数。
例如,一个由 6 个旋转关节构成的机械臂,其自由度数为:自由度数 = 6 - (2+2+2+2+2+1) = -1计算结果为-1,说明这个机械臂的结构无法实现运动,需要考虑重新设计。
二、运动学法运动学法通常是使用向量和矩阵进行计算。
在机械臂中,关节的运动受到多个因素的影响,包括机械臂的结构设计、工作负载、传动系统以及控制算法等。
这些因素的相互作用很难进行分析,因此运动学法的计算比几何法更为精准和复杂。
在运动学法中,机械臂通常被建模为一系列坐标系,其中每个关节都有一个坐标系,整个机械臂也有一个基坐标系。
通过计算关节坐标系的相对位置和方向,可以推导出机械臂的自由度数。
7自由度机械臂底座计算
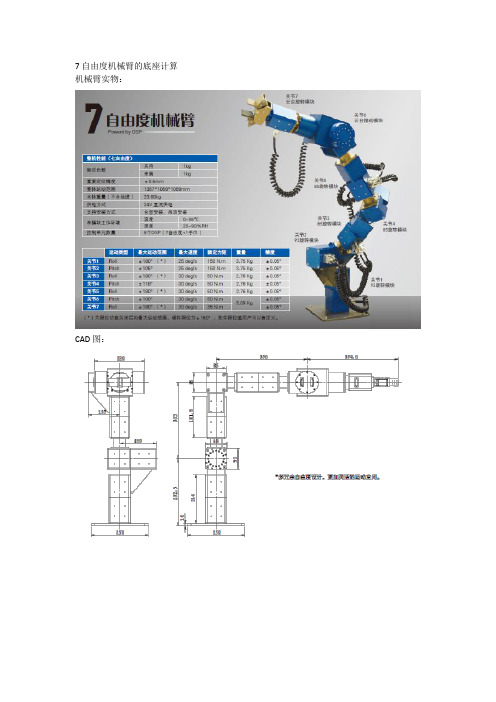
7自由度机械臂的底座计算机械臂实物:CAD图:重心简化模型:最大伸展状态下最大扭矩时负重{关节2作为输出力矩最大的旋转关节,额定力矩150N*M,力矩tol和负载m函数:G=mg=1KG*10N/kg(9.8N/kg)=10N(9.8N)Tol= 65mm*3.5kg*10N/kg*0.001m/mm+311*2.7/100+675*10/100+m*858/100= 78.1720+m*8.58<150 :仅考虑关节2不全面m<8.3716 (最大扭矩安全系数一般安全系数可取1.05)但是关节1会受到同等大小的力矩,产生的对应剪切力矩,轴向上剪切力的估计值3500N+} 当额定载荷1kg时,同样算法的估计值78.1720+1*8.58)*1000/42.5约2000N(3关节末端10kg,6关节末端2kg,随着的末端力臂的增长,负载减少)最大伸展半径为857.6,额定载荷1kg,得到此临界条件下,底座半径x与底座质量M的关系:质量M=-((x-65)*3.5+(x-311)*2.7+(x-675)*10+7.5*x+(x-858)*1)/x底座半径在100至200间时:工作空间所需高度与人机工程学共同决定底座高度参考402机械臂参数:末端伸展长度70cm~80cm,底座尺寸,与机械臂相连处45*40,与地面通过螺栓连接,尺寸(45+9*2)*(40+9*2),底座半径最小处29.机械臂高度:1.2m~1.3m,底座高度22+,但是有木地板,提升了水平地面的高度。
情况1:最低(掉电?直流供电?有断电保护功能,有软硬件限位功能):293-395-396=-498;减少地面干涉对工作空间干涉,同时也是地面夹取最大高度最高:333+293+396+395=1417情况2:333+293=626,关节4最大高度333+293+396= 1022,关节4最大高度满足需求:能从地面拿物件,常用工作空间在合适的位置上(站着使用的工作表面的最舒适高度是低于人的肘部高度7.6cm,约1m)。
机械臂运动空间计算公式

机械臂运动空间计算公式机械臂是一种能够模拟人类手臂运动的机械装置,它可以在工业生产中完成各种复杂的任务,如搬运、装配、焊接等。
在机械臂的设计和控制过程中,运动空间的计算是非常重要的一部分。
本文将介绍机械臂运动空间的计算公式,帮助读者更好地理解和应用机械臂技术。
机械臂的运动空间可以用数学模型来描述,通常采用笛卡尔坐标系或关节坐标系。
在笛卡尔坐标系中,机械臂的位置可以用三维直角坐标系来表示,而在关节坐标系中,机械臂的位置可以用各个关节的角度来表示。
下面将分别介绍这两种坐标系下的机械臂运动空间计算公式。
1. 笛卡尔坐标系下的机械臂运动空间计算公式。
在笛卡尔坐标系中,机械臂的位置可以用三维直角坐标系来表示。
假设机械臂有n个自由度,即可以在三维空间中运动的自由度为n。
那么机械臂的位置可以用一个n维向量来表示,即:P = (x1, x2, ..., xn)。
其中,x1, x2, ..., xn分别表示机械臂在各个方向上的位移。
在实际应用中,我们通常会将机械臂的位置表示为其末端执行器的位置,即机械臂末端的位置可以用一个三维向量来表示,即:P = (x, y, z)。
其中,x, y, z分别表示机械臂末端在x、y、z方向上的位移。
机械臂的运动空间可以通过运动学模型来计算,即通过机械臂各个关节的运动学参数来计算机械臂末端的位置。
机械臂的运动学模型通常可以表示为一个矩阵乘法的形式,即:P = T1 T2 ... Tn P0。
其中,T1, T2, ..., Tn分别表示机械臂各个关节的运动学参数,P0表示机械臂的起始位置,P表示机械臂的末端位置。
通过这个公式,我们可以计算出机械臂在笛卡尔坐标系中的运动空间。
2. 关节坐标系下的机械臂运动空间计算公式。
在关节坐标系中,机械臂的位置可以用各个关节的角度来表示。
假设机械臂有n个自由度,即可以在各个关节上运动的自由度为n。
那么机械臂的位置可以用一个n维向量来表示,即:Q = (q1, q2, ..., qn)。
一种7DOF机械臂逆运动学解析算法及其应用

一种7DOF机械臂逆运动学解析算法及其应用一种7自由度(7DOF)机械臂逆运动学解析算法是指通过给定末端执行器的位置和姿态,计算出机械臂各关节角度的算法。
逆运动学问题是机械臂控制的重要问题之一,解决了逆运动学问题,就能够实现机械臂在特定位置和姿态下的精准控制。
7DOF机械臂是指拥有7个关节的机械臂,每个关节都可以进行旋转运动。
这类机械臂在工业自动化、医疗设备、物流等领域有着广泛的应用。
由于关节数量较多,其逆运动学解析解的求解通常较为复杂。
一种常用的逆运动学解析算法是解析几何法。
该算法通过求解方程组来计算机械臂的关节角度。
具体而言,通过将机械臂的几何特性转化为数学方程,然后利用数学方法求解方程组,从而得到机械臂的关节角度。
解析几何法的基本原理是通过利用机械臂的几何关系,将终端执行器的位置和姿态转换为表示关节角度的方程,然后通过求解这些方程得到关节角度。
具体而言,可以通过三角函数、旋转矩阵等数学方法进行计算。
逆运动学解析算法的应用有很多,以下是几个常见的应用场景:1.工业自动化:机械臂在工业生产线上的应用非常广泛,可以实现对物体的抓取、搬运、装配等任务。
逆运动学解析算法可以帮助机械臂精确地完成这些任务,提高生产效率。
2.医疗设备:机械臂在医疗设备中的应用越来越多,可以用于手术辅助、病人抬床、康复训练等。
逆运动学解析算法可以确保机械臂在操作过程中的精确性和安全性。
3.物流:机械臂在仓储物流系统中的应用也越来越普遍,可以实现货物的分拣、装载、搬运等任务。
逆运动学解析算法可以帮助机械臂快速准确地完成这些物流任务,提高物流效率。
总之,7DOF机械臂逆运动学解析算法是机械臂控制中的关键技术之一、解决了逆运动学问题,可以实现机械臂在特定位置和姿态下的精确控制。
随着机械臂技术的不断发展和应用的扩大,7DOF机械臂的逆运动学解析算法将继续得到广泛的研究和应用。
机械臂 解算 -回复

机械臂解算-回复机械臂解算是指通过计算机算法来确定机械臂运动的位置和朝向,以实现精确的运动控制。
本文将分步骤回答机械臂解算的相关问题,从基本原理到具体实现。
第一步:理解机械臂的运动学模型机械臂运动学模型是机械臂解算的基础,它描述了机械臂的关节和末端执行器之间的几何关系。
机械臂一般由多个关节组成,每个关节都可以控制自身的角度或位置。
常见的机械臂运动学模型有两种:正解和逆解。
正解是根据每个关节的角度或位置,计算机械臂末端执行器的位置和朝向。
逆解则是根据末端执行器的位置和朝向,计算机械臂各个关节的角度或位置。
第二步:正解解算正解解算的基本原理是通过一系列的几何变换,从机械臂基座的坐标系开始,逐级计算每个关节的坐标系,最终得到末端执行器的位置和朝向。
具体步骤如下:1. 确定机械臂的DH参数:DH参数描述了机械臂各个关节的相对位置和沿着关节旋转轴的方向。
根据机械臂的结构,可以确定每个关节的旋转轴和相邻关节之间的位移。
2. 建立机械臂的坐标系:根据DH参数,可以确定每个关节的坐标系。
通常选择其中一个坐标系作为基座坐标系,其他关节的坐标系依次相对于基座坐标系建立。
3. 计算关节的转换矩阵:根据DH参数,可以构建每个关节之间的转换矩阵。
每个转换矩阵包含了旋转和位移的信息。
4. 级联转换矩阵:将各个关节的转换矩阵相乘,得到从基座坐标系到末端执行器坐标系的整体转换矩阵。
5. 提取位置和朝向信息:从整体转换矩阵中提取出末端执行器的位置和朝向。
第三步:逆解解算逆解解算的基本原理是通过已知的末端执行器的位置和朝向,计算每个关节的角度或位置,使得机械臂能够达到目标位置和朝向。
具体步骤如下:1. 确定机械臂的DH参数:与正解解算相同,需要确定机械臂的DH参数。
2. 建立机械臂的坐标系:根据DH参数,建立机械臂各个关节的坐标系。
3. 计算逆解:根据末端执行器的位置和朝向,计算每个关节的角度或位置。
这是一个反推问题,需要使用数值求解或迭代求解的方法。
机械臂 解算 -回复

机械臂解算-回复机械臂解算是指根据给定的输入参数,计算机械臂的运动轨迹和关节角度的过程。
机械臂解算是机械臂控制的关键步骤,它决定了机械臂的精度和灵活性。
本文将从机械臂的基本结构开始,逐步介绍机械臂解算的原理和方法。
第一部分:机械臂结构和坐标系机械臂是由多个关节相互连接组成的机械系统。
通常情况下,机械臂有6个自由度,分别对应于机械臂的6个关节。
每个关节都可以旋转或转动,从而实现机械臂的运动。
为了方便解算,机械臂通常使用笛卡尔坐标系和关节坐标系来描述位置和姿态。
笛卡尔坐标系是一个三维直角坐标系,用来描述机械臂末端执行器的位置。
关节坐标系是一个相对于机械臂基座标识每个关节的坐标系。
第二部分:机械臂运动学解算机械臂的运动学解算是通过给定末端执行器的位置和姿态,计算机械臂各个关节的角度的过程。
机械臂的运动学解算可以分为正解和逆解两种。
正解是指根据关节的角度,计算机械臂末端执行器的位置和姿态。
逆解则是指根据末端执行器的位置和姿态,计算机械臂各个关节的角度。
正解的过程可以使用迭代方法或者解析方法来实现。
其中,迭代方法是指从初始猜测开始,通过迭代计算出最接近目标位置和姿态的关节角度。
解析方法则是指直接通过代数方程求解来得到关节角度。
逆解的过程可以使用几何方法、代数方法或者数值方法来实现。
几何方法是指通过几何关系推导出关节角度的方程,然后求解这些方程来得到关节角度。
代数方法则是使用代数运算推导出关节角度的方程,然后求解这些方程。
数值方法则是使用数值计算求解逆解问题。
第三部分:机械臂动力学解算机械臂的动力学解算是指根据给定的关节角度和关节速度,计算机械臂末端执行器的加速度和关节力矩的过程。
机械臂的动力学解算可以分为正解和逆解两种。
正解是指根据关节的角度和速度,计算机械臂末端执行器的加速度和关节力矩。
逆解则是指根据末端执行器的加速度和关节力矩,计算机械臂各个关节的角度和速度。
机械臂的动力学解算可以使用牛顿-欧拉方法、拉格朗日方法或者遗传算法来实现。
七自由度机械臂逆解方案设计

七自由度机械臂逆解方案设计
七自由度机械臂逆解方案设计是指在已知机械臂末端位置和姿态的情况下,求解出机械臂各关节的角度,从而实现机械臂的运动。
以下是一种常用的七自由度机械臂逆解方案设计的步骤:
1. 机械臂建模:确定机械臂的结构和参数,包括关节类型(如旋转关节、滑动关节等)、关节长度和转动轴的方向。
2. 坐标系设定:确定机械臂的坐标系,包括基座的坐标系和末端执行器的坐标系。
通常选择一个固定的参考坐标系作为基座坐标系,然后依次定义各关节坐标系和末端执行器坐标系。
3. 正运动学求解:根据机械臂的结构和参数,使用正运动学方程求解出末端执行器的位置和姿态。
正运动学方程将末端执行器的坐标表示为各关节角度的函数。
4. 逆运动学求解:根据末端执行器的位置和姿态,使用逆运动学方程求解出机械臂的关节角度。
逆运动学方程将关节角度表示为末端执行器的位置和姿态的函数。
5. 解的求解:使用数值方法求解逆运动学方程的解。
由于逆运动学方程往往是非线性的,一般使用数值迭代方法(如牛顿法)求解。
6. 解的优化:对求解得到的关节角度进行优化,以满足机械臂
运动的限制条件,如关节角度限制、关节速度限制等。
7. 控制指令生成:将求解得到的关节角度转化为机械臂的控制指令,发送给机械臂控制系统,实现机械臂的运动。
8. 可视化和验证:将求解得到的关节角度应用到机械臂模型中,进行可视化和验证,确保逆解方案设计的正确性。
以上是一种常用的七自由度机械臂逆解方案设计的步骤,具体的设计过程还需要根据具体的机械臂结构和要求进行调整和优化。
七自由度机械臂逆运动学

七自由度机械臂逆运动学引言:机械臂是一种重要的工业自动化设备,在许多领域中发挥着重要的作用。
为了实现机械臂的精确控制,我们需要了解机械臂的逆运动学。
本文将介绍七自由度机械臂的逆运动学问题,并探讨其解决方法。
一、机械臂的七自由度七自由度机械臂是指具有七个独立自由度的机械臂。
这意味着机械臂可以在七个不同的方向上进行运动,包括三个平移自由度和四个旋转自由度。
平移自由度使机械臂能够在三维空间中进行定位,而旋转自由度则使机械臂能够在各个方向上进行转动。
二、逆运动学问题的定义逆运动学问题是指已知机械臂的末端位置和姿态,求解机械臂各个关节角度的问题。
通过解决逆运动学问题,我们可以实现对机械臂的精确控制,使其能够达到预定位置和姿态。
三、逆运动学问题的求解方法1. 几何方法几何方法是最常用的求解逆运动学问题的方法之一。
它基于机械臂的几何特性和坐标变换原理,通过解析几何方法求解机械臂的关节角度。
这种方法的优点是简单直观,容易理解和实现。
然而,对于复杂的机械臂结构和运动学模型,几何方法可能会导致复杂的数学计算和多解性问题。
2. 数值方法数值方法是一种基于数值计算的求解逆运动学问题的方法。
它通过迭代计算的方式逼近机械臂的关节角度,直到满足末端位置和姿态的要求。
数值方法的优点是适用于各种复杂的机械臂结构和运动学模型,可以得到较为精确的解。
然而,数值方法的计算量较大,可能需要较长的计算时间。
四、七自由度机械臂逆运动学问题的求解对于七自由度机械臂的逆运动学问题,可以采用几何方法或数值方法进行求解。
其中,几何方法可以通过解析几何的方式求解机械臂的关节角度,而数值方法则可以通过迭代计算的方式逼近机械臂的关节角度。
在具体求解过程中,需要根据机械臂的运动学模型和几何特性建立逆运动学模型。
然后,通过解析几何或数值计算的方法求解机械臂的关节角度。
最后,通过控制器将计算得到的关节角度发送给机械臂,实现对机械臂的精确控制。
五、总结七自由度机械臂的逆运动学是机械臂控制中的重要问题。
机械臂 解算

机械臂解算机械臂是一种模仿人体臂膀的机械装置,通过电力、气动、液压等驱动方式实现运动。
机械臂在工业生产线上广泛应用,可完成复杂的操作任务,提高生产效率。
解算是机械臂中的一个重要环节,它能够确定机械臂执行器的位置,从而控制机械臂的运动。
机械臂的解算可以分为运动学解算和动力学解算两个方面。
运动学解算是通过机械臂的构型关系和运动规律来确定机械臂各个关节的位置和姿态。
动力学解算则是在已知机械臂的构型和负载条件下,计算各个关节的动力学性能,确定机械臂运动过程中的力、力矩和加速度等参数。
在机械臂的运动学解算中,有两种主要的方法:正解法和逆解法。
正解法是根据给定的关节角度和机械臂的几何参数,计算末端执行器的位置和姿态。
逆解法则是已知末端执行器的位置和姿态,求解关节角度。
正解法可以使用几何模型和旋转矩阵等方法来计算,逆解法则需要使用解析法或迭代法等计算方式。
机械臂解算的重要性在于它能够使机械臂实现精确定位和精确运动。
在工业生产线上,精确位置和稳定运动是保证产品质量和生产效率的关键因素。
通过解算,机械臂可以按照预定规划的路径和轨迹进行运动,完成需求的操作任务。
另外,在机械臂的动力学解算中,可以利用牛顿欧拉法和拉格朗日法等方法来计算机械臂各个关节的动力学参数。
这些参数包括关节的负载、力、力矩和加速度等,对于机械臂的控制和优化至关重要。
动力学解算可以帮助机械臂进行自适应控制和力控制,在处理复杂任务和不确定环境下具有重要的应用价值。
机械臂解算中的一种常用方法是DH法(Denavit-Hartenberg方法)。
DH法是一种通过坐标系变换来描述机械臂各个关节之间的运动关系和坐标关系的方法。
DH法通过为机械臂建立坐标系,定义坐标系的原点、坐标轴和坐标变换关系,从而实现机械臂的运动学和动力学分析。
除了DH法,还有一些其他的解算方法,如工具框法、束法和广义反解法等。
这些方法通过建立不同的数学模型和算法,来实现机械臂的解算和控制。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7自由度机械臂的底座计算机械臂实物:
CAD图:
重心简化模型:
最大伸展状态下最大扭矩时负重
{关节2作为输出力矩最大的旋转关节,额定力矩150N*M,力矩tol和负载m函数:
G=mg=1KG*10N/kg(9.8N/kg)=10N(9.8N)
Tol= 65mm*3.5kg*10N/kg*0.001m/mm+311*2.7/100+675*10/100+m*858/100
= 78.1720+m*8.58<150 :仅考虑关节2不全面
m<8.3716 (最大扭矩安全系数一般安全系数可取1.05)
但是关节1会受到同等大小的力矩,产生的对应剪切力矩,轴向上剪切力的估计值3500N+} 当额定载荷1kg时,同样算法的估计值78.1720+1*8.58)*1000/42.5约2000N
(3关节末端10kg,6关节末端2kg,随着的末端力臂的增长,负载减少)
最大伸展半径为857.6,额定载荷1kg,得到此临界条件下,底座半径x与底座质量M的关系:质量M=-((x-65)*3.5+(x-311)*2.7+(x-675)*10+7.5*x+(x-858)*1)/x
底座半径在100至200间时:
工作空间所需高度与人机工程学共同决定底座高度
参考402机械臂参数:
末端伸展长度70cm~80cm,底座尺寸,与机械臂相连处45*40,与地面通过螺栓连接,尺寸(45+9*2)*(40+9*2),底座半径最小处29.
机械臂高度:1.2m~1.3m,底座高度22+,但是有木地板,提升了水平地面的高度。
情况1:最低(掉电?直流供电?有断电保护功能,有软硬件限位功能):
293-395-396=-498;减少地面干涉对工作空间干涉,同时也是地面夹取最大高度
最高:333+293+396+395=1417
情况2:333+293=626,关节4最大高度
333+293+396= 1022,关节4最大高度
满足需求:能从地面拿物件,常用工作空间在合适的位置上(站着使用的工作表面的最舒适高度是低于人的肘部高度7.6cm,约1m)。
尺寸类似实验室的6自由度移动机械手,该机械手底座60cm,大关节一60cm,大关节二60cm。
工作高度与402机械臂类似,基本符合人机工程学。
情况3:从地面水平夹持所需最低高度396-292.5=100,情况1+3:100~500mm之间
综合情况2,水平夹取100+工件高度1000,仍需要工作台配合: 300?~400?之间
工作半径和加工难易程度选择底座形状,底座体积和所需重量决定选材,考虑安全系数1.圆盘
接地半径30cm,表面积(pi*0.3^2+0.3^2+0.3*0.35*2)*7.9*10=46 (kg/cm),厚度1cm,密度7.9g/cm^3,质量46kg,安全系数。
