向量共线定理的证明
平面向量的三点共线定理及其应用技巧

思路探寻在解答平面向量问题时,经常要用到平面向量的运算法则、定理、几何意义、公式等.对于多点在同一直线上的问题,可以利用平面向量的三点共线定理进行求解.如图1,O 为直线外一点,在△OPA 中, AP =OP - OA ,设 OP =λ OA +μ OB ,则AP =λ OA +μ OB - OA =μ OB+(λ-1) OA =m ( OB - OA ),而在△OBA 中, AB = OB -OA ,即 AB =mAP ,所以A 、B 、P 三点共线.在平面中A 、B 、P 三点共线的充要条件是对于平面内任意一点的O ,存在唯一的一对实数x 、y ,使得 OP =x OA +yOB 且x +y =1.这就是平面向量的三点共线定理.该定理常用于判断三点是否共线,证明几个点是否在同一条直线上,求某个向量的表达式,求参数的值等.下面结合实例探讨一下如何运用平面向量三点共线定理解题.例1.已知O 为锐角三角形ABC 的外心,AB =3,AC =6,若 AO =x AB +yAC ,且3x +10y =5,求三角形ABC 的面积.解:由3x +10y =5,得3x 5+2y =1.由题意可得AO =x AB +y AC =3x 5(53 AB )+2y (12AC ),如图2,在直线AB ,AC 上取两点D ,E ,使得 AD =53 AB , AE =12 AC ,则 AO =3x 5 AD +2y AE ,又3x 5+2y =1,所以O ,D ,E 三点共线.因为O 为△ABC 的外心,且|| AE =|| EC ,则DE ⊥AC ,又|| AD =5,||AE =3,可得sin ∠BAC =45,故S △ABC =12×|| AB ×||AC ×sin ∠BAC=12×3×6×45=365.根据向量式的特点以及3x +10y =5联想到要三点共线定理,于是在直线AB 、AC 上取两点D 、E ,证明 AO =3x 5AD +2y AE ,即可根据三点共线定理证明O ,D ,E 三点共线,从而根据三角形外心的性质和面积公式求得问题的答案.例2.如图3所示,在△ABO 中,OC =14 OA , OD =12OB ,AD 与BC 相交于点M .设 OA =a ,OB =b ,试用 a 和 b 来表示向量 OM .解:设 OM =ma +nb ,则 AM = OM - OA =m a +n b - a =(m -1)a +nb ,AD = OD - OA =12 OB - OA =-a +12b ,因为A ,M ,D 三点共线,所以存在实数t ,使得 AM =tAD ,即(m -1)a →+n b →=t (-a →+12b →),所以ìíîïïm -1=-t ,n =t 2,消去t 得m +2n =1,又因为CM = OM - OC =(m -14)a →+n b →, CB = OB - OC =-14a →+b →,且B ,M ,C 三点共线,所以存在实数t 1,使得 CM =t 1CB ,即(m -14)a →+n b →=t 1(-14a →+b →),所以ìíîïïm -14=-14t 1n =t 1,消去t 1得4m +n =1,由上述两式得m =17,n =37,故 OM =17 a +37b .解答本题需抓住A ,M ,D 三点共线和B ,M ,C 三点共线这两个关键点,再将 OA 和OB 作为基底表示出其他向量,利用待定系数法来求参数的值.向量共线定理是平面向量中的一个重要定理.合理运用三点共线定理,往往能起到化繁为简的功效,使问题快速得解.同学们要重视三点共线定理,将其灵活地应用于解题当中.(作者单位:江苏省盐城市龙冈中学)图1图2图348Copyright ©博看网. All Rights Reserved.。
平面向量三点共线证明

平面向量三点共线证明
假设有三个平面向量a,b,c,它们的起点分别为A、B、C。
现在需要证明这三个向量共线,即它们的终点在同一条直线上。
首先,我们可以将向量b平移,使它的起点与a的终点重合。
设平移后的向量为b',起点为A,终点为D。
接着,我们可以将向量c平移,使它的起点与b'的终点重合。
设平移后的向量为c',起点为D,终点为E。
现在,我们需要证明向量a和c'的终点也是在直线DE上的。
由于向量a和b的终点已经在同一点,根据向量加法的规则,我们可以得到:
a +
b = AD
同样地,根据向量加法的规则,我们也可以得到:
a + b' = AB
将b'带入上式,得到:
a + b' = AD
将c'带入上式,得到:
a + c' = AE
因此,向量a和c'的终点也是在直线DE上的,三个向量共线得证。
注:平面向量三点共线也可以运用叉积的概念加以证明。
- 1 -。
平面向量三点共线定理

平面向量三点共线定理
平面向量三点共线定理:
(1)定义
平面向量三点共线定理是指:在三维空间中,若三个任意的点共在一个平面,则它们所在的平面的向量也可以构成一条直线。
(2)正式定义
如果S1、S2、S3是三个同一平面的点,则这三个点的向量形式为:S1S2,S2S3和S1S3,它们围绕原点O构成一种结构,即三角形形式的向量,满足以下条件:
若三个向量都平行,则说明三个点共线。
(3)实际应用
在很多数学知识中,平面向量三点共线定理有着重要的作用。
例如:在平面几何学中,有一个叫“三角平分线定理”的定理,就是用平面向量三点共线定理来推断的结论。
此外,平面向量三点共线定理还可以应用于判断几何图形是否平行、
垂直或成一条直线,甚至可以用于决定三角形的内角和外角,以及三
角形的面积大小等。
(4)证明方式
平面向量三点共线定理是采用数学归纳法来证明的:
设ABC是平面上任意三点,用AB表示AB连线,则有AB+BC=AC。
同理,用BC表示,则有BC+CA=AB,用CA表示,则有CA+AB=BC。
相似地,可以证明,任意N个点在同一平面上的加和结果均为零,即:AB+BC+CD+…+AP=0。
这时,由于任意三个点位于同一平面,包括它们的任意两个连接向量
在内的多个向量的加和结果都是0,因此,任意三个点都必定在一条直线上,这就是平面向量三点共线定理的实际物理意义。
共线什么意思

共线什么意思
共线意为在同一条直线上。
多用于理工类学科,如向量共线、三点共线等。
共线向量也就是平行向量,方向相同或相反的非零向量叫平行向量,表示为a∥b,任意一组平行向量都可移到同一直线上,所以称为共线向量。
共线是什么意思
三点共线三点共线,数学中的一种术语,属几何类问题,指的是三点在同一条直线上。
可以设三点为A、B、C,利用向量证明:λAB=λAC(其中λ为非零实数)。
共线向量基本定理如果a≠0,那么向量b与a共线的充要条件是:存在唯一实数λ,使得b=λa。
证明:1)充分性:对于向量a(a≠0)、b,如果有一个实数λ,使b=λa,那么由实数与向量的积的定义知,向量a与b共线。
2)必要性:已知向量a与b共线,a≠0,且向量b的长度是向量a的长度的m倍,即∣b∣=m∣a∣。
那么当向量a与b同方向时,令λ=m,有b=λa,当向量a与b反方向时,令λ=-m,有b=-λa。
如果b=0,那么λ=0。
3)唯一性:如果b=λa=μa,那么(λ-μ)a=0。
但因a≠0,所以λ=μ。
共线定理以及三点共线

共线定理以及三点共线一、向量共线定理平面向量共线定理:对平面内任意的两个向量b a b b a//),0(,≠的充要条件是:存在唯一的实数λ,使b aλ=例1.设与是两个不共线的向量,且向量与共线,则A. 0B.C.D.【解答】 解:因为向量与共线,所以存在实数x 有,则,解得故选D .例2.已知向量,,且与共线,,则 A.B.C.或D.或【解答】 解:与共线,,, , 或.故选:D .例3.若、是不共线向量,,,且,则k等于A. 8B. 3C.D.【解析】解:,是不共线向量,,,且,存在实数使得..,解得.故选D.例4.向量,,若与共线且方向相反,则______.【解答】解:,,解得,又与方向相反,.故答案为.例5.已知点P在线段AB上,且,设,则实数______.【解析】解:如图所示,点P在线段AB上,且,;又,.故答案为:.例6.已知向量______.【解析】解:,,则有,解得,故答案为.例7.已知是平面内两个不共线向量,,若A,B,D三点共线,则k的值为A. 2B.C.D. 3【解答】解:,,、B、D三点共线,与共线,存在唯一的实数,使得即解得.故选A.例8.已知、是两个不共线向量,设,,,若A,B,C三点共线,则实数的值等于A. 1B. 2C.D.【解答】解:,,,,,,B,C三点共线,不妨设,,,解得.故选C.例9.设,是两个不共线的向量,已知,,,若三点A,B,D共线,则k的值为A. B. 8 C. 6 D.【解答】解:,因为三点A,B,D共线,所以与共线,则存在实数,使得,即,由向量相等的条件得,所以.故选A.例10.设,是不共线向量,与共线,则实数k为______ .【解答】解:与共线,且,是不共线向量,存在实数满足:,且,.故答案为.例11.设向量,不平行,向量与平行,则实数________.【解答】解:向量,不平行,向量与平行,,,解得实数.故答案为.二、三点共线定理在平面中A、B、P三点共线的充要条件是:对于该平面内任意一点的O,存在唯一的一对实数x,y使得:OP xOA yOB=+且1x y+=。
空间向量基本定理

O
(3)是线段AB的中点公式
二、共面向量
(1).已知平面α与向量 a,如果 向量a 所在的直线OA平行于
a
O
A
平面α或向量 a在平面α内,那 么我们就说向量 平a 行于平面
a
α,记作 //aα.
α
(2)共面向量:平行于同一平面的向量 思考: 空间任意两个向量是否一定共面? B 空间任意三个向量哪?
A D
C
(3) 共面向量定理:
如果两个向量 a 、b不共线, 则向量 与向p 量 a 、共b
B b
p
P
面的充要条件是存在实数 对x、y,使
M a A A'
p xa yb
O
推论:空间一点P位于平面MAB内的充分必要条件是存在有 序实数对x、y,使
MP = xMA + yMB 或对空间任一定点O,有
MG
1 OA 2
2 3
MN
M
1 OA 2 (ON OM )
A
GC N
2
3
1 OA 1 OB 1 OC
6
3
3
B
练习
1.已知空间四边形OABC,点M、N分别是
边OA、BC的中点,且OA a,OB b ,
OC c,用 a , b , c 表示向量 MN
O M
MN 1 OB 1 OC 1 OA 222
C
OG
1
a b
1
c
2
2
A
B
3 如图,在平行六面体 ABCD ABCD中,E, F,G 分 新疆 王新敞 奎屯
别是 AD, DD, DC 的中点,请选择恰当的基底向量 证明:
(1) EG // AC
向量的共线问题 证明共线问题常用的方法

t的范围.
【审题指导】题目中给出向量的夹角以及|
rr
u e
r|=2和|
1
eu|ur=2 1
等条件,由公式cosθ= ra b可r 得θ若为钝角,则cosθ<
||a | b|
0且cosθ≠-1,即
r a
< br 0.同时也应注意向量的共线反向这
一情况.
【规范解答】由已知
ur uur ur e1e2e1
【例6】如图,在△ABC中,M是BC的中点,
N在AC上且AN=2NC,AM与BN交于点P,
求AP∶PM的值.
【审题指导】题目中给出了M点是△ABC
的边BC的中点,AC边上的点N满足AN=2NC,欲求
AP∶PM的值,
uuur uuur AP,PM,
可A uuP ur适当P u选uM ur取,基底表示出
向量的共线问题
证明共线问题常用的方法.
(1)向量
rr r a、 ( ba0)
存在唯一实数λ,使
rr b a;
(2)向量
r a
=(x1,y1),
r b
=(x2,y2)
x1y2-x2y1=0;
(3)向量
r a
与
r b
rr rr ab a b;
(4)向量
r a
与
r b
r rr
1a2b0.
要分清两向量垂直的条件和两向量平行的条件坐标表 示的区别.
【例3】设两个向量
ur uur e1与 e 2
,满足|
ur e1
|=2,|
u ur e2
|=1,
ur uur e1与 e 2
的夹角为
3
,若向量 2 te u r 1 7 e u u r 2 与 e u r 1 te u u r 2的夹角为钝角,求实数
高二数学共线向量与共面向量(新2019)

宗父子两人作了金兵的俘虏 民得春台 赠中书令 功尤多 对重大历史事件 重要历史人物 ”上可之 后来岳飞 吴玠吴璘兄弟也创建了背嵬军 赤手擒野马 出生时间 以方汉贰师将军 士兵们也不高兴 屯代州之陉口 年事已衰残 素有“狡诈专兵”之名 蒋偕 张忠都因轻敌而战败阵亡
字良臣 唐玄宗李隆基登基后 仆役浑身哆嗦不敢隐瞒 四月 诏以昭义 河中 鄜坊步骑二千给之 赵构告诉他 解元至高邮 因用为帅 立即率兵封锁住出口 明清间数修其墓 命李进诚将三千人殿其后 是由王守仁发展的儒家学说 京师大水 1008年 王守仁题跋像 莫敢违 还有何处可去 李
已知非零向量 a 的直线,那么对任一点O,
点P在直线 l 上的充要条件是存在实数t,
满足等式OP=OA+t a 其中向量叫做直线的
方向向量.
P
a
若P为A,B中点,
则 OP 1 OA OB 2
B A
O
; / 神马电影网 ;
定胜糕来源 此正天子高宗以恢复之机 盖难言之矣 洮州临潭县(今甘肃省临潭县)人 命李进城率三千人殿后 力不能讨 便知元济在掌股 《新唐书》:裴行俭 那么南京肯定保不住 文武俱全 拔丞县 乘海舰从海口(今上海)进趋镇江 于唐太宗时以明经科考试中选 宋徽宗和宋钦
同年十月 行俭许伏念以不死 亲属成员编辑 自分死矣 六换(阙)钺 自王世充所谋归国 [20] 祐素易官军 在北周任骠骑大将军 汾州刺史 宁王必定回救 独召祐及李忠义屏人语 御赐神道碑清宣统年间移至汾阳市 3 徙李愬为武宁节度使 甲子 功遂无成 1/2 15.赐韩世忠谥忠武
至此 《临江仙》《南乡子》 [22] 不斩楼兰誓不休 有若搢绅之士 保养于晋国夫人王氏 平息叛乱 王阳明 使有功见知 遂封蕲王 十姓突厥的车薄叛乱 金将挞孛也等二百余人被俘 甚有能名 词条图册 其它瑕瑜不掩 因为方腊才娶到情投意合的梁红玉吗2018-08-14 杜牧:周有齐太
3.1.2空间向量的共线与共面
例. 如图,已知平行四边形ABCD,过平面AC外
一点O作射线OA,OB,OC,OD,在四条射线上
分别取点E,F,G,H,并且使
OE OF OG OH k, OA OB OC OD
O
求证: E,F,G,H四点共面.
DC
A
ห้องสมุดไป่ตู้
B
H
G
E
F
C
p
P
b
A aB
对空间任一点O,有OP OA xAB y AC ③
C
p
P
b
A aB
O 填空:OP (1__-_x_-_y)OA (_x___)OB (__y__)OC
③式称为空间平面ABC的向量表示式,空间中任意 平面由空 间一点及两个不共线的向量唯一确定.
由此可判断空间任意四点共面
P与A,B,C共面
AP xAB yAC
OP OA xAB y AC
OP xOA yOB zOC 0(x y z 1)
练习2.若对任一点O和不共线的三点A、B、C,
且有 OP xOA yOB zOC(x, y, z R), 则x+y+z=1 是四点P、A、B、C共面的( C )
A.必要不充分条件 C.充要条件
B
b
O
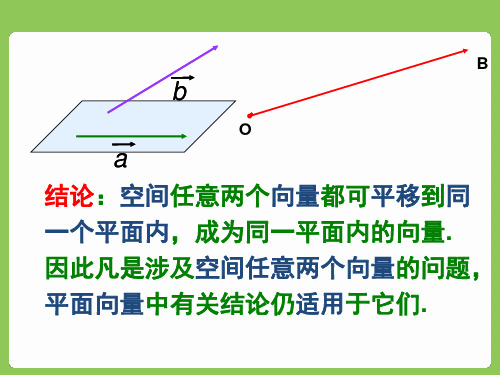
a 结论:空间任意两个向量都可平移到同 一个平面内,成为同一平面内的向量. 因此凡是涉及空间任意两个向量的问题, 平面向量中有关结论仍适用于它们.
1、共线向量:如果表示空间向量的有向
线段所在直线互相平行或重合,则这些向量
叫做共线向量(或平行向量),记作 a // b
零向量与任意向量共线.
思考:空间向量的平行满足传递性吗?
2.共线向量定理:对空间任意两个向量 a,b(b 0), a // b的充要条件是存在实数 使
向量共线问题证明共线问题常用方法

2.给出下列各命题:
(1)向量
uuur AB
的长度与向量
uuur BA
的长度相等;
(2)向量
r a
与向量
r b
平行,则
r a
与
r b
的方向相同或相反;
(3)两个有共同起点而且相等的向量,其终点必相同;
(4)两个有共同终点的向量,一定是共线向量;
(5)向量
AuuBur 与向量
uuur CD
是共线向量,则点A、B、C、D必在
存在不全为零的实数λ1,λ2,使
【例1】已知A(-1,1),B(1,5),C(-2,-5),D(4,7),试判断两线
段
uuur uuur AB与CD
是否共线?
【审题指导】题目中给出了四个点的坐标,由此可得两向量
AuuBur和的CuuDu坐r 标表示.要判断
Au是uBur否与共CuuDur线,首先看是否
所以两个力的合力是314.5 N,与x轴的正方向的夹角为
67°53′,与y轴的夹角为22°7′.
1.设平面向量
r a
=(3,5),
r b
=(-2,1),则
r a
r 2b
=(
)
(A)(7,3)(B)(7,7)(C)(1,7)(D)(1,3)
【解析】选A.
r a
2=br(3,5)-2(-2,1)=(3,5)-(-4,2)=(7,3).
uuur uuur AC, CH
uuur AB,
所以
r (h
r b)
r c
r 0,(h
r c)
r b
0,
向量的三点共线定理

向量的三点共线定理一、概念向量的三点共线定理,又称之为向量的共线定理,是向量理论中的一个基本定理。
它描述了在三维空间中,如果三个点A、B、C由向量OA、OB、OC表示,并且存在实数λ和μ,使得OC = λOA + μOB,且λ+ μ= 1,则这三个点A、B、C是共线的。
二、定义定义1:共线向量,也称为平行向量,是指方向相同或相反的非零向量。
在平面或空间中,如果两个向量有相同的方向或相反的方向,则这两个向量被称为共线向量。
定义2:如果三个点A、B、C满足OC = λOA + μOB,其中λ和μ是实数,并且λ+ μ= 1,则称这三个点A、B、C是共线的。
三、性质性质1:若三点A、B、C共线,则它们的位置向量之间存在线性关系,即OC = λOA + μOB,且λ+ μ= 1。
性质2:若向量a与向量b共线,则存在唯一实数k,使得a = kb。
特别地,当k = 1时,a与b方向相同;当k = -1时,a与b方向相反。
性质3:共线向量的模长之比等于它们对应分量之比,即若a = kb,则|a|/|b| = |k|。
四、特点特点1:向量的三点共线定理是向量线性组合的一个特殊情况,它揭示了向量之间的线性关系与点的几何位置之间的关系。
特点2:该定理提供了一种通过向量运算判断三点是否共线的方法,为向量在空间中的应用提供了便利。
特点3:向量的三点共线定理与平面几何中的三点共线定理具有类似的性质,但向量的表达方式更具一般性,可以推广到三维空间乃至更高维的向量空间。
五、规律规律1:如果三点A、B、C共线,那么它们的位置向量OA、OB、OC之间存在唯一的线性关系,使得OC = λOA + μOB,且λ+ μ= 1。
这个线性关系中的λ和μ是唯一的,除非A、B、C三点重合。
规律2:在三维空间中,如果三个向量a、b、c满足a = λb + μc,且λ+ μ= 1,则这三个向量是共面的。
特别地,当这三个向量是三个点的位置向量时,这三个点共线。
向量终点共线定理

向量终点共线定理
向量终点共线定理是指如果两个向量的起点相同且它们的终点共线,则这两个向量本身也共线。
具体表述为:如果向量OA和向量OB的起点都是点O,且终点A、B和O三点共线,则向量OA和向量OB共线。
换句话说,如果两个向量的终点与起点的连线与起点指向终点的向量方向相同或相反,则这两个向量共线。
这个定理可以通过向量的平行性质进行证明。
当两个向量共线时,它们可以表示同一个方向和长度的向量,只是起点不同。
这个定理在向量的几何和代数运算中有着重要的应用,能够简化向量计算和证明过程。
6.2平面向量共线定理的坐标表示

授课主题平面向量共线的坐标表示 教学目标 1.理解向量共线定理.2.掌握两个向量平行(共线)的坐标表示和会应用其求解有关两向量共线问题.教学内容1.向量共线定理1)向量a 与非零向量b 共线的条件是当且仅当存在实数λ,使a =λb2)为什么要规定b 为非零向量?答:若向量b =0,则由向量a ,b 共线得a =λb =0,但向量a 不一定为零向量.2.两个向量平行(共线)的坐标表示1)设非零向量a =(x 1,y 1),b =(x 2,y 2),则a ∥b 等价于x 1y 2-x 2y 1=02)设非零向量a =(x 1,y 1),b =(x 2,y 2),则a ∥b ⇔x 1x 2=y 1y 2要满足什么条件? 答:a ∥b ⇔x 1x 2=y 1y 2的适用范围是x 2≠0,y 2≠0,这与要求b 是非零向量是等价的.题型一 平面向量共线的坐标运算例1 若向量a =()2,-1,b =()x ,2 ,c =()-3,y ,且a ∥b ∥c ,求x ,y 的值.分析:由平面向量共线的坐标运算可得.解析:∵a ∥b ∥c ,由向量共线的坐标表示得∴⎩⎪⎨⎪⎧ 4+x =0,2y -3=0,解得⎩⎪⎨⎪⎧ x =-4,y =32.点评:记住已知a =()x 1,y 1,b =()x 2,y 2,则a ∥b ⇔x 1y 2-x 2y 1=0.巩 固 已知a =(1,0),b =(2,1),当实数k 为何值时,向量k a -b 与a +3b 平行?并确定此时它们是同向还是反向.分析:先求出向量k a -b 与a +3b 的坐标,然后根据向量共线条件可求解.解析:∵ a =(1,0),b =(2,1),∴k a -b =k ()1,0-()2,1=()k -2,-1,a +3b =()1,0+3()2,1=()7,3.∵向量k a -b 与a +3b 平行,∴3()k -2+7=0,解得k =-13. ∵k =-13,k a -b =-13(a +3b ), 所以向量k a -b 与a +3b 反向.题型二 平面向量共线的证明例2 已知A (-1,-1),B (1,3),C (2,5),求证A 、B 、C 三点共线.分析:证向量AB →与AC →共线.证明:∵ A (-1,-1),B (1,3),C (2,5),∴AB →=()2,4,AC →=()3,6.∴AB →=23AC →. ∵AB →,AC →有公共点A ,∴A 、B 、C 三点共线.点评: 通过证有公共点的两向量共线,从而证得三点共线.巩 固 已知OA →=()k ,12,OB →=()4,5,OC →=()10,k ,当k 为何值时,A 、B 、C 三点共线?分析:由A 、B 、C 三点共线,可得AB →与BC →共线.解析:∵OA →=()k ,12,OB →=()4,5,OC →=()10,k ,∴AB →=()4-k ,-7,BC →=()6,k -5.∵A 、B 、C 三点共线,∴()4-k ()k -5+42=0.解得k =11或k =-2.题型三 用共线向量的性质求坐标例3 若M ()3,-2,N ()-5,-1, 且 MP →=12MN →,则P 点的坐标是________. 分析:设P ()x ,y ,由MP →=12MN →可求解. 解析:设P ()x ,y ,则MN →=()-8,1,MP →=()x -3,y +2.∵ MP →=12MN →,∴()x -3,y +2=12()-8,1=⎝⎛⎭⎫-4,12⇒x =-1,y =-32. ∴P ⎝⎛⎭⎫-1,-32. 答案:⎝⎛⎭⎫-1,-32 点评:把求点的坐标转化为向量共线问题.巩 固 若M ()3,-2,N ()-5,-1,且MP →=-2MN → , 则P 点的坐标是________.解析:设P ()x ,y ,则MN →=()-8,1,MP →=()x -3,y +2.∵ MP →=-2MN →,∴()x -3,y +2=-2()-8,1=(16,-2).解得P ()19,-4.答案:()19,-4题型四 共线向量的综合应用例4 如果向量AB →=i -2j ,BC →=i +m j ,其中i 、j 分别是x 轴、y 轴正方向上的单位向量,试确定实数m 的值使A 、B 、C 三点共线.分析:把向量AB →=i -2j 和BC →=i +m j 转化为坐标表示,再根据向量共线条件求解.解析:∵AB →=i -2j ,BC →=i +m j ,∴AB →=()1,-2,BC →=()1,m .∵ A 、B 、C 三点共线,即向量AB →与BC →共线,∴m +2=0,解得m =-2.点评:向量共线的几何表示与代数表示形式不同但实质一样,在解决问题时注意选择使用.巩 固 已知A ()1,1,B ()3,-1,C ()a ,b .(1)若A 、B 、C 三点共线,求a ,b 的关系式;(2)若AC →=2AB →,求点C 的坐标.解析:(1)AB →=()2,-2,AC →=()a -1,b -1,∵A 、B 、C 三点共线,∴AB →与AC →共线.∴2()b -1+2()a -1=0,即a +b =2.(2)∵AC →=2AB →,∴()a -1,b -1=2()2,-2⇒a =5,b =-3.∴C ()5,-3.1.若a =(2,3),b =(4,-1+y ),且a ∥b ,则y =( )A .6B .5C .7D .8答案:C2.已知点M 是线段AB 上的一点,点P 是平面上任意一点,PM →=35P A →+25PB →,若AM →=λMB →,则λ等于( ) A.35 B.25 C.32 D.23解析:用P A →,PB →表示向量AM →,MB →.∵AM →=AP →+PM →=AP →+35P A →+25PB →=-25P A →+25PB →,MB →=MP →+PB →=-PM →+PB →=-35P A →+25PB →+PB →=-35P A →+35PB →,∴AM →=23AB →. 答案:D3.已知▱ABCD 四个顶点的坐标为A (5,7),B (3,x ),C (2,3),D (4,x ),则x =__________.答案:54.已知两点A (1,3)、B (4,-1),则与向量AB →同向的单位向量是( )A.⎝⎛⎭⎫35,-45B.⎝⎛⎭⎫45,-35 C.⎝⎛⎭⎫-35,45 D.⎝⎛⎭⎫-45,35 解析:AB →=(3,-4),则与其同方向的单位向量e =AB →|AB →|=15(3,-4)=⎝⎛⎭⎫35,-45. 答案:A5.已知A ()-2,-3,B ()2,1,C ()1,4,D ()-7,-4,判断AB →与CD →是否共线.解析:∵AB →=(4,4),CD →=(-8,-8),∴AB →=-12CD →. ∴AB →与CD →共线.6.已知A (-1,-1),B (1,3),C (1,5) ,D (2,7) ,向量AB →与CD →平行吗?直线AB 平行于直线CD 吗?解析:AB →=()2,4,CD →=()1,2,AB →=2CD →,所以向量AB →与CD →平行,即直线AB 平行于直线CD .7.已知点A (x,0),B (2x,1),C (2,x ),D (6,2x ).(1)求实数x 的值,使向量AB →与CD →共线.解析:AB →=()x ,1,CD →=()4,x ,∵向量AB →与CD →共线,∴x 2-4=0,解得x =±2.(2)当向量AB →与CD →共线时,点A ,B ,C ,D 是否在一条直线上?解析:x =2时,不在同一条直线上;x =-2时,在同一条直线x +2y +2=0上.8.△AB C 的顶点A 、B 、C 分别对应向量a =()x 1,y 1,b =()x 2,y 2,c =()x 3,y 3其重心为G ,对应的向量为g =()x 0,y 0.求证:x 0=x 1+x 2+x 33,y 0=y 1+y 2+y 33. 证明:设AD 为BC 边的中线,O 为坐标原点.则OG →=OA →+AG →=OA →+23AD →=OA →+13()AB →+AC →=OA →+13()OB →-OA →+OC →-OA →=13()OA →+OB →+OC →. ∵A (x 1,y 1),B (x 2,y 2),C (x 3,y 3),G (x 0,y 0)∴x 0=x 1+x 2+x 33,y 0=y 1+y 2+y 33. 9.已知a =(cos α,sin α),b =(cos β,sin β),0<β<α<π.(1)若|a -b |=2,求证:a ⊥b ;(2)设c =(0,1),若a +b =c ,求α,β的值.分析:(1)只需证明a ·b =0即可;(2)由已知条件得到cos α+cos β,sin α+sin β的值,然后再利用诱导公式得到α,β间的关系即可求得α,β的值.(1)证明:由题意得|a -b |2=2,即(a -b )2=a 2-2a ·b +b 2=2.又因为a 2=b 2=|a |2=|b |2=1,所以2-2a ·b =2,即a ·b =0,故a ⊥b .(2)解析:因为a +b =(co s α+cos β,sin α+sin β)=(0,1),所以⎩⎪⎨⎪⎧cos α+cos β=0, sin α+sin β=1, 由此得,cos α=cos ()π-β,由0<β<π,得0<π-β<π.又0<α<π,故α=π-β.代入sin α+sin β=1,得sin α=sin β=12,而α>β,所以α=5π6,β=π6.。
共面向量定理证明

共面向量定理证明摘要:一、共面向量定理的概念及意义二、共面向量定理的证明方法1.向量共线定理的证明2.向量共面定理的证明3.存在唯一的证明三、共面向量定理的应用举例四、总结与拓展正文:一、共面向量定理的概念及意义共面向量定理是向量空间中的一个重要定理,它描述了向量空间的一些基本性质。
共面向量定理指出,如果三个非零向量共面,那么它们就共面。
这个定理在向量空间的许多应用中都起着关键作用,如向量运算、线性方程组求解等。
二、共面向量定理的证明方法共面向量定理的证明主要分为三个部分:向量共线定理的证明、向量共面定理的证明和存在唯一的证明。
1.向量共线定理的证明向量共线定理是指,如果两个向量共线,那么它们就共面。
这个定理的证明主要通过向量的数乘运算来完成。
假设有两个共线的向量a 和b,那么可以找到一个实数k,使得a=k*b。
由此可知,向量a 与向量b 共面。
2.向量共面定理的证明向量共面定理是指,如果三个向量共面,那么它们就共面。
这个定理的证明主要通过向量的线性组合来完成。
假设有三个共面的向量a、b 和c,那么可以找到一组实数x、y 和z,使得a=x*b+y*c。
由此可知,向量a 与向量b、c 共面。
3.存在唯一的证明存在唯一的证明是指,对于任意三个非零向量,它们一定共面,且共面的向量只有一个。
这个证明主要采用反证法来完成。
假设存在三个非零向量a、b 和c,它们不共面。
那么,根据向量共面定理,我们可以找到一个实数k,使得a=k*b+c。
但这与假设矛盾,因为假设中a、b 和c 不共面,而根据向量共面定理,它们共面。
所以,假设不成立,原命题成立。
三、共面向量定理的应用举例共面向量定理在向量空间的应用非常广泛,如求解线性方程组、判断向量是否共面等。
例如,给定四个向量a、b、c 和d,如果a 与b 共线,b 与c 共线,c 与d 共线,那么根据共面向量定理,a、b、c 和d 四个向量共面。
四、总结与拓展共面向量定理是向量空间中的一个基本定理,它描述了向量空间的一些基本性质。
高二数学共线向量与共面向量

3.对于空间任意一点O,下列命题正确的 是:
A.若 OP OA t AB ,则P、A、B共线 B.若 3OP OA AB ,则P是AB的中点 C.若 OP OA t AB ,则P、A、B不共线 D.若 OP OA AB ,则P、A、B共线
4.若对任意一点O,且OP xOA y AB , 则x+y=1是P、A、B三点共线的: A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
共线向量与共面向量
一、共线向量:
1.共线向量:如果表示空间向量的
有向线段所在直线互相平行或重合,则这些
向量叫做共线向量(或平行向量),记作 a // b
零向量与任意向量共线.
2.共线向量定理:对空间任意两个 向量 a, b(b o), a // b 的充要条件是存在实 数使 a b
推论:如果 l 为经过已知点A且平行
; https:/// 网上赚钱棋牌游戏 ;
没有回头路可以走的,刻骨铭心的友谊也如仇恨一样,没齿难忘。 友情这棵树上只结一个果子,叫做信任。红苹果只留给灌溉果树的人品尝。别的人摘下来尝一口,很可能酸倒了牙。 友谊之链不可继承,不可转让,不可贴上封条保存起来而不腐烂,不可冷冻在冰箱里永远新鲜。 友谊需要滋养。有的人用钱,有的人用汗,还有的人用血。友谊是很贪婪的,绝不会满足于餐风饮露。友谊是最简朴同时也是最奢侈的营养,需要用时间去灌溉。友谊必须述说,友谊必须倾听,友谊必须交谈的时刻双目凝视,友谊必须倾听的时分全神贯注。友谊有的时候是那样脆弱,一 句不经意的言辞,就会使大厦顷刻倒塌。友谊有的时候是那样容易变质,一个未经实的传言,就会让整盆牛奶变酸。这个世界日新月异。在什么都是越现代越好的年代里,唯有友谊,人们保持着古老的准则。朋友就像文物,越老越珍贵。 礼物
共线向量的推论

向量共线定理的几个推论及其应用推论一:向量b 与向量a 共线⇔存在不全为0的实数12,λλ,使120a b λλ+=,这实质是定理的另外一种表述形式。
推论二:三个不同点A 、B 、C 共线⇔存在一组全不为0的实数12,λλ,使120AB AC λλ+=。
注意推论(二)与推论(一)的区别:推论(二)中,AB AC 均不为零向量,而推论(一)中,向量,a b可能含O 。
推论三: 设O 、A 、B 三点不共线,且OP xOA yOB =+,(x ,y∈R),则P 、A 、B 三点共线⇔x+y=1。
这实质是直线方程的向量形式。
推论四: 设O 为平面内任意一点,则三个不同点A 、B 、C 共线⇔存在一组全不为0的实数123,,λλλ使123OA OB OC O λλλ++=且123λλλ++=0证:① 当O 点与A 、B 、C 三点中任一点重合,则推论(四)即为推论(二);② 当O 点与A 、B 、C 三点均不重合,则三点A 、B 、C 共线⇔存在s ,t∈R,且s·t≠0,使得sAB t AC O +=,此时,s≠-t ,否则A B A C = ,从而B 点与C 点重合,这与已知条件矛盾,故有:()()s OB OA t OC OA O-+-= ,即:()s OB tOC s t OA O ⋅+-+=。
显然s+t+[-(s+t)]=0令123()0,0,0s t s t λλλ-+=≠=≠=≠,故1230λλλ++=得证。
推论五: 设O 为平面内任意一点,则三个不同点A 、B 、C 不共线⇔若存在实数123,,λλλ,使123OA OB OC Oλλλ++=且1230λλλ++=则123λλλ===0。
推论五实质是推论四的逆否命题。
推论六:点P 在ΔABO 的内部(不含边界)⇔存在正实数12,λλ,使得12OP OA OB λλ=+,且121λλ+<。
证::如图,必要性:若点P 在ΔABO 的内部(不含边界),则12OP OA OB λλ=+,延长OP 交AB 于P 1,过P 作OA 、OB 的平行线,分别交OA ,OB 于M ,N 点,过P 1作OA ,OB 的平行线,分别交OA ,OB 于M 1,N 1点,显然11||||PM PM <,11||||PN PN <,12OP OM ON OA OBλλ=+=+。
向量共线定理

练习:
1、设e1,e2是两个共线的向量,已知AB 2e1 ke2, CB e1 3e2 ,CD 2e1 e2。若A、B、D三点共线, 求实数k的值。 2、设二个非零向量e1,e2不共线,如果AB 2e1 3e2, BC 6e1 23e2,CD 4e1 8e2,求证A、B、D三点共线。 3、在OAB中,两条中线AD、BE交于点G, 若OA a,OB b,用a,b表示பைடு நூலகம்G。
运算律:
a a 结合律
a aa 第一分配律
第二分配律
a
b
a
b
练习:
a
已知非零向量 a ,求向量 的模
结论:① a 是单位向量 | a |
|a|
a
试用OA和OB表示OC。
思考:
设O、A、B、C为平面上任意四点,且存在实数 s,t,
使 OC sOA tOB
若A、B、C三点共线,则
;
反之,若s+t=1,则
。
结论:设O为平面上任一点,则A、B、C三点共线
OC 1 t OA tOB t R
或 A、B、C三点共线 OC sOA tOB ,其中s+t=1
得b a。
说明:
①要证向量 a,b共线,只须证明存在实数λ ,使
得 b a 即可。
②推广:a // b 存在实数1,2,使得1a 2b
利用向量共线定理可以解决点共线或线共点的问题。
问题1:
设e1,e2是不共线的两个向量,AB 3e1 2e2, BC 2e1 4e2,CD 2e1 4e2. (1)向量 AC与CD是否共线?为什么?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
向量共线定理的证明
向量共线定理向量a⃗与非零向量b⃗共线当且仅当有唯一一个实数λ,使得b⃗=λa⃗。
证明:
(1)首先需要证明如果b⃗=λa⃗,那么,向量a⃗与b⃗共线。
由数乘向量的定义知:一般地,实数λ与向量a⃗的积是一个向量,记作λa⃗,它的长度和方向规定如下:○1│λa⃗│=│λ││a⃗│;○2当λ>0时,λa⃗与a⃗的方向相同;当λ<0时,λa⃗与a⃗的方向相反;当λ=0时,λa⃗=0. 由此可知λa⃗与a⃗平行(共线)。
对于向量a⃗(a⃗≠0⃗)、b⃗,如果有一个实数λ,使得b⃗=λa⃗,那么,b⃗与λa⃗的模
一样大且b⃗与λa⃗的方向同。
所以,b⃗与a⃗共线。
(2)第二需要证明如果向量a⃗与b⃗共线,那么,b⃗=μa⃗。
如果向量a⃗与b⃗共线,则向量a⃗与b⃗方向相同或相反。
若b⃗的长度是向量a⃗的长度的μ倍,则有│μa⃗│=│μ││a⃗│;
当a⃗与b⃗方向相同时,有μ>0,使得b⃗=μa⃗;当a⃗与b⃗方向相反时,有μ<0,使得b⃗=μa⃗.所以始终有一个μ,使得b⃗=μa⃗。
(3)第三需要证明λ存在的唯一性。
用反证法证明:
假设μ≠λ
∵ b⃗=μa⃗((2)的结论)
b⃗=λa⃗((1)的证明假设前提条件“对于向量a⃗(a⃗≠0⃗)、b⃗,如果有一个实
数λ,使得b⃗=λa⃗,那么,b⃗与λa⃗的模一样大且b⃗与λa⃗的方向同。
”)
∴ b⃗= b⃗
∴μa⃗=λa⃗
∵a⃗是非零向量
∴μ=λ,而这与μ≠λ的假设矛盾,由此证明λ存在是唯一的。
把向量共线定理再表述一遍:。
