第一章电磁场的媒质边界条件
媒质的电磁性质和边界条件

磁导率
表示物质在磁场中导磁能力的物理量,单位为亨利/米(H/m)。
磁导
表示磁场中物质磁导能力的物理量,单位为亨利(H)。
电容率和电感率
电容率
表示电场中物质储存电荷能力的物理 量,单位为法拉/米(F/m)。
电感率
表示磁场中物质储存磁能能力的物理 量,单位为亨利/米(H/m)。
介电常数和磁导率
要点一
介电常数和磁导率的应用案例
介电常数:表示电介质极化程度的物 理量,单位为法拉(F)。
磁导率:表示磁性材料对磁场的影响 能力的物理量,单位为亨利(H)。
应用案例:在电磁波传播和微波工程 中,介电常数和磁导率的应用十分重 要。介电常数决定了电磁波在介质中 的传播速度和波长,而磁导率则影响 微波器件的性能。例如,在天线设计 和微波传输线中,需要选择具有适当 介电常数和磁导率的材料以确保电磁 波的正常传播和有效辐射。此外,介 电常数和磁导率的变化还可以用于制 造电磁波吸收材料和隐身技术等。
THANKS FOR WATCHING
感谢您的观看
06 结论
研究成果总结
媒质的电磁性质对电磁波的传播和散射具有重 要影响,研究媒质的电磁性质有助于深入理解 电磁波与物质相互作用的过程。
边界条件是描述媒质交界处电磁场行为的条件, 对于电磁波的传播和散射具有关键作用。
不同媒质的电磁性质和边界条件会导致电磁波 传播和散射的差异,这在实际应用中具有重要 的意义。
同一媒质间的边界条件
01
在同一媒质中,由于存在不均匀性或异常情况,电磁波的传播 也会受到限制或影响。
02
同一媒质间的边界条件描述了波在媒质中的传播行为,如吸收、
散射、折射等。
这些边界条件通常由物理定律和数学公式来描述,如波动方程、
电磁场与电磁波媒质的电磁性质和边界条件

6.介质的击穿
介质的击穿: 当电介质上的外加电场足够大时 ,束缚电荷有可能克服原子结构的吸引力,成 为自由电荷。此时,介质呈现导体特性。
击穿场强: 介质所能承受的最大电场强度。它 在高压技术中是一个表征材料性能的重要参数。
三、磁介质
1.磁介质的磁化
? 磁偶极矩
r pm
?
r IdS
I —分子电流
Am 2
3. 极化电荷(束缚电荷)
由于电场作用产生极化 ,从而使介质内部出
现极化体电荷 ,介质表面出现极化面电荷 .我们
定义:
极化体电荷密度 极化面电荷密度
r
?P ? ??? P
? Ps
?
r P
?
r a
n
若电介质中还存在自由电荷分布时,电介质中 一点总的电位为:
? ? ?A
?
1
4π?0
?V ? ? P dV?? 1
? 磁介质的磁化现象:
还有一些材料对磁场较敏感,例如螺丝刀在 磁铁上放一会儿,螺丝刀就具有一定的磁性, 能吸起小螺钉。这种现象称为 磁化现象。能产 生磁化现象的材料称为 磁介质。
一、导体
1. 导体的定义: 含有大量可以自由移动的带电粒子 的物质。
导体分为两种 金属导体:由自由电子导电 电解质导体:由带电离子导电
2. 极化强度
为了描述介质极化的状态, 引入极化强度 矢量.定义单位体积内的电偶极矩为 极化强度 矢量(Polarization Intensity Vector), 即
ur
r P?
lim ?
p
?V? 0 ? V
C / m2
式中 ?为p体积元 内?电V偶极矩的矢量和,
pr的方向从负极化电荷指向正极化电荷。
电磁场边界条件的推导

电磁场边界条件的推导
电磁场边界条件的推导
1、电荷边界条件
电荷边界条件指的是在一个给定时刻,电场空间分布的边界处,电荷的分布应符合一定的规律,常表示为
E(r,t)=ρ(r,t)/ε
其中,E(r,t)为电场在位置r处和时刻t时的电场强度,ρ(r,t)为该位置处以及时刻t时的电荷密度,ε为真空介质的介电常数。
2、磁荷边界条件
磁荷边界条件指的是在一个给定时刻,磁场空间分布的边界处,磁荷的分布应符合一定的规律,常表示为
B(r,t)=μ㎡(r,t)
其中,B(r,t)为磁场在位置r处和时刻t时的磁场强度,μ㎡(r,t)为该位置处以及时刻t时的磁荷密度,μ为真空介质的磁导率。
3、电流边界条件
电流边界条件指的是在一个给定时刻,电流空间分布的边界处,电流密度的分布应符合一定的规律,常表示为
j(r,t)=σ(r,t)/ε
其中,j(r,t)为电流密度在位置r处和时刻t时的电流密度,σ(r,t)为该位置处以及时刻t时的电荷密度,ε为真空介质的介电常数。
4、磁流边界条件
磁流边界条件指的是在一个给定时刻,磁流空间分布的边界处,磁流密度的分布应符合一定的规律,常表示为
m(r,t)=μφ(r,t)
其中,m(r,t)为磁流密度在位置r处和时刻t时的磁流密度,φ(r,t)为该位置处以及时刻t时的磁荷密度,μ为真空介质的磁导率。
电磁场的媒质边界条件

ur ur
ÑS D d S V dV S SdS
r D1
Snr
r D2
Snr
S S
Dn1 S Dn2 S SS
4 电通密度的关系
nr
rr D1 D2
0S
• 两种媒质界面处,电通量密度的法向分量有条件连续。 •当媒质界面上没有自由电荷分布时,电通量密度的法向 分量有条件连续。 • 电场强度法向分量总是不连续的,除非两种介质的介 电常数相等。
Et1 Et2
电场强度的切向连续变化,而法向量不连续变化。
7 静电场位函数的边界条件
1
1
n
2
2
n
1 2
绝缘不导电介质
1
1
n
2
2
n
1 2
导电介质
p1
p2
lim
p1 p2
p2 p1
E
dl
lim
h0
E0
h
0
1.1 磁场的边界条件
uur
Ñl H
d
r l
s
ur (J
ur
ur D t
蜒L Er
r dl
V
B t
dV
,
rr
S J dS 0
nr
rr J2 J1
rr
0, J E
nr
rr E2 E1
0
2 c tg2 1 c tg1
电场强度的切向连续变化,而法向量不连续变化。
rr
ÑrL Er
dl r
0 r
E1 l E2 l 0,
Et1l Et2l 0
H2t H1t J l
在两种媒质界面处,磁场强度的切向分量是
电磁场问题边界条件及求解

d
x
π k x E0 ez sin( z ) cos(t k x x) (A/m) 0 d
(2) z = 0 处导体表面的电流密度为 πE0 J S ez H ey sin(t k x x) z 0 0 d
(A/m)
z = d 处导体表面的电流密度为
媒质1 媒质2 分界面上的电流面密度
电磁场与电磁波
第2章
电磁场的基本规律
5
1.2 两种常见的情况
1. 两种理想介质分界 面上的边界条件 在两种理想介质 分界面上,通常没有 电荷和电流分布,即 JS=0、ρS=0,故
媒质1 媒质2
en
媒质1 媒质2
en
、 D B的法向分量连续
E、 的切向分量连续 H
en (D1 D2 ) S
或
D1n D2n S
en (B1 B2 ) 0 或 B1n B2n
同理 ,由
S
B dS 0
电磁场与电磁波
第2章
电磁场的基本规律
3
(2)电磁场量的切向边界条件 在介质分界面两侧,选取如图所示的小环路,令Δh →0,则
或
S e n (J1 J 2 ) t
J J en 1 2 0 1 2
1
J1t
2
J 2t
或
电磁场与电磁波
第2章
电磁场的基本规律
8
例 场强度
在两导体平板(z = 0 和 z = d)之间的空气中,已知电
π E ey E0 sin( z ) cos(t k x x) V/m d 试求:(1)磁场强度 H;(2)导体表面的电流密度 J S 。 H , 有 解 (1)由 E 0 z t H 1 E y t 0 d 1 E y E y O ( e x ez ) 0 z x
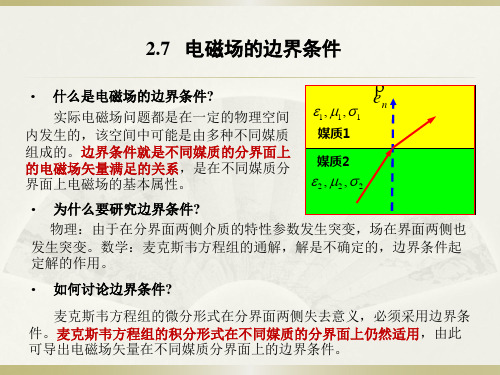
2.7电磁场的边界条件解析

第2章
电磁场的基本规律
1
2.7 电磁场的边界条件
en
媒质1 媒质2
• 什么是电磁场的边界条件?
et
实际电磁场问题都是在一定的物理空
间内发生的,该空间中可能是由多种不同
媒质组成的。边界条件就是不同媒质的分 界面两侧的电磁场物理量满足的关系。
中国矿业大学
电磁场与电磁波
第2章
电磁场的基本规律
en ( H1 H 2 ) J S en ( E1 E2 ) 0 en (B1 B2 ) 0 en (D1 D2 ) S
中国矿业大学
en
媒质1 媒质2
et
en en en en
H1 J S E1 0 B1 0 D1 S
H1t J s E 0 1t 或 B1n 0 D1n S
电磁场与电磁波
第2章
电磁场的基本规律
11
H1t J s E 0 1t B1n 0 D1n S
理想导体表面上的电流密度等于H 的切向分量 理想导体表面上 E 的切向分量为0 理想导体表面上 B 的法向分量为0 理想导体表面上的电荷密度等于 D的法向分量
D 右边 = J dS dS S S t
0 s 0
J S dl J S e p l
l
故得: [en (H1 H 2 )] ep l J S e p l
中国矿业大学
en (H1 H 2 ) J S 或H1t H 2t J S
电磁场与电磁波
第2章
电磁场的基本规律
媒质1 Δl
(完整版)电磁场的边界条件

电磁场的边界条件姓名:学号:专业:班级:提交日期:桑薇薇0990*******通信工程电工 1401 2016.5.28成绩:电磁场的边界条件1.引言2.边界条件分类3.边界条件的作用4.结束语5.参考文献1. 引言在两种不同媒质的分界面上,场矢量E,D,B,H 各自满足的关系,称为电磁场的边界条件。
在实际的电磁场问题中, 总会遇到两种不同媒质的分界面 (例如: 空气与玻璃的分界面、导体与空气的分界面等) ,边界条件在处理电磁场问题中占据十分重要的地位。
2. 边界条件分类1、电场法向分量的边界条件如图 3.9 所示的两种媒质的分界面, 第一种媒质的介电常数、磁导率和电导率分别为1,1和1,第二种媒质的介电常数、磁导率和电导率分别为2,2和 2 。
在这两种媒质分界面上取一个小的柱形闭合面,图 3.9 电场法向分量的边界条件如图 3.9 所示,其高h 为无限小量,上下底面与分界面平行,并分别在分界面两侧, 且底面积 S 非常小,可以认为在 S 上的电位vv v移矢量 D和面电荷密度S是均匀的。
n 1 n 2分别为上下底面的外法线单位矢量, , 在柱形闭合面上应用电场的高斯定律? v vv v S v vSSD gdS n 1 gD 1 n 2 gD 2 SS故v v v vn 1gD 1 n 2 gD 2S(3.48a)vv vvv若规定 n 为从媒质Ⅱ指向媒质Ⅰ为正方向,则 n 1 n ,n2n,式 (3.48a) 可写为v vvng(D 1D 2 )S(3.48b)或D1nD2nS(3.48c)式 (3.48 ) 称为电场法向分量的边界条件。
vvv 因为 DE ,所以式 (3.48) 可以用 E 的法向分量表示v v v v1n 1gE 12 n 2 gE 2S(3.49a)或1E 1n2 E 2nS(3.49b)若两种媒质均为理想介质时, 除非特意放置, 一般在分界面上不存在自由面电荷,即S,所以电场法向分量的边界条件变为D1nD2n(3.50a)或1E1n 2E2 n(3.50b)若媒质Ⅰ为理想介质,媒质Ⅱ为理想导体时, 导体内部电场为零,即E2,D2,在导体表面存在自由面电荷密度,则式(3.48) 变为v vn 1 gD 1 D 1nS(3.51a)或1E1ns(3.51b)2 、电场切向分量的边界条件在两种媒质分界面上取一小的矩形闭合回路 abcd ,如图 3.10 所示,该回路短边 h 为无限小量,其两个长边为l ,且平行于分界面,并分别在分界面两侧。
电磁场的边界条件

1)麦克斯韦方程组可以应用于任何连续的介质内部。
2)在两种介质界面上,介质性质有突变,电磁场也会突变。
3)分界面两边按照某种规律突变,称这种突变关系为电磁场的边值关系或边界条件。
4)推导边界条件的依据是麦克斯韦方程组的积分形式。
一、边界条件的一般形式 1、B 的边界条件:2、D 的边界条件结论:电位移矢量 在不同媒质分界面两侧的法向分量不连续,其差值等于分界面上自由电荷面密度。
3. H 的边界条件h∆→n-2B11220B dS B dS ⇒⋅+⋅=120B n B n ⇒⋅-⋅=210lim S h D H l H l J sl t→∂⇒⋅-⋅=⋅-⋅∂2t t SH H J⇒-=12()S n H H J⇒⨯-=21,S H l H l J s l n s⇒⋅-⋅=⋅=⨯()C sD H dl J dSt∂=+∂⎰⎰μ1μ2Hn1Hh →ls12()S n H H J⨯-=12()D D n σ-⋅=⇒2εε2D 1D n S∆n-n12n n D D σ⇔-=0S B dS ⋅=⎰12()0n B B ⋅-=21n nB B⇒=SD dS q =⋅⎰⇒⇒式中: S J 为介质分界面上的自由电流面密度。
结论:磁场强度 D 在不同媒质分界面两侧的切向分量不连续,其差值等于分界面上的电流面密度S J4.E 的边界条件结论:电场强度E 在不同每只分界面两侧的切向分量连续。
二、理想介质是指电导率为零的媒质,0=γ2)在理想介质内部和表面上,不存在自由电荷和自由电流。
结论:在理想介质分界面上,E 、H 矢量切向连续; 在理想介质分界面上,B 、D 矢量法向连续。
三、理想导体表面上的边界条件1)理想介质是指电导率为无穷大的导体,12t t E E⇒=12()0n E E ⇒⨯-= 2ε1ε2En1E2θl sl S BE dl d St∂⋅=-⋅∂⎰⎰12()0n E E ⨯-=⇒12t t EE=0s J =0ρ=12t t H H =⇒12n n D D=12()0n D D ⋅-=⇒12()0n B B ⋅-=12n n B B=⇒12()0n H H ⨯-=2)电场强度和磁感应强度均为零。
电磁场课件--第一章电磁场的媒质边界条

汇报人:
01
02
03
04
05
06
电磁场与媒质的相互作用是电 磁场理论的重要内容
媒质边界条件是描述电磁场与 媒质相互作用的重要工具
媒质边界条件包括电边界条件 和磁边界条件
媒质边界条件在电磁场计算和 工程应用中具有重要意义
理想边界条件:假设边界上不存在任何电磁场
非理想边界条件:假设边界上存在电磁场,但场强和场矢量满 足一定的条件
电场强度:在媒质分界面上,电场 强度必须连续
电荷密度:在媒质分界面上,电荷 密度必须连续
添加标题添加标题来自添加标题添加标题磁场强度:在媒质分界面上,磁场 强度必须连续
电流密度:在媒质分界面上,电流 密度必须连续
电场强度:在媒质分界面上,电场强度必须连续 磁场强度:在媒质分界面上,磁场强度必须连续 电荷密度:在媒质分界面上,电荷密度必须连续 电流密度:在媒质分界面上,电流密度必须连续
边界条件:描述媒质分界面上的电磁场性质 连续性条件:描述媒质分界面上电磁场的连续性 数学表达形式:通过数学公式表示边界条件 应用实例:在电磁场课件中,通过实例讲解边界条件的数学表达形式
理想导体:电场 强度为零,电流 密度无穷大
绝缘体:电场强 度不为零,电流 密度为零
边界条件:理想 导体与绝缘体之 间的边界上,电 场强度和电流密 度必须满足连续 性条件
数据采集:记录实验过程中的 数据,包括电磁场强度、温度、 湿度等
实验设计:选择合适的实验 设备,设计实验方案
数据分析:对采集到的数据进 行处理和分析,验证边界条件
的准确性
应用实例:介绍边界条件在实 际应用中的案例,如电磁屏蔽、
电磁兼容等
边界条件是电 磁场理论中的 重要概念,用 于描述电磁场 在媒质边界上
电磁场与电磁波--电磁场的边界条件
cos(15
108
t)
20
cos(15108
t)]
erx80cos(15108t) V/m
r E2
(0,
t
r ex
80
cos(15
108t)r exAcos(15
108
t)
)
V/m
V/m
z=0
r ez 媒质2
r ex
媒质1
2.7 电磁场的边界条件
利用两种电介质分界面上电场强度的切向分量连续的边界条件
电介质与自由空间 的分界面
rr r
r
rrr
ez {ex E1x ey E1y ez E1z [ex 2 y ey 5x ez (3 z)]} z0
r
r
ey (E1x 2 y) ex (E1y 5x) 0
则得
E1x 2 y, E1y 5x
r E2
r ex
2y
r ey 5z
r ez
r D
的法向分量连续
r B 的法向分量连续
r E 的切向分量连续
r H
的切向分量连续
1=0
ern
媒质1
媒质2
2
r D
、Br
的法向分量连续
2.7 电磁场的边界条件
2. 理想导体表面上的边界条件
D
• 理想导体:电导率为无限大的导电媒质 • 特征:电磁场不可能进入理想导体内 • 理想导体表面上的边界条件
r
r
l
rr H1 H2
r et
dl
r D
r
lim
h0
J dS
S
S
t
dS
媒质1
r r en Δl
电磁场电磁场的媒质边界条件

ars
nr S S
环路围面法向
3 电场强度的关系
rr r nnErrr 2EElrrr 22aErrnrs1
rr
l 0,l
nr r
r E1
r as
nr
r as
0
rE1 0
n E2 n E1 0 E2t E1t
两种媒质界面处电场强度的切向分量相等 (无条件连续)
4 电通密度的关系
以理想导体为边界的区域中,空间电磁场 可以看成是源电荷、电流激发场与导体表面 感应电荷,电流激发场(散射场)的叠加。 在一定条件下,散射场可以等效为位于导体 区域内等效像电荷、电流激发的场,等效像 电荷、电流的分布决定于导体的边界条件。 这种通过寻找像电荷电流求解空间区域电磁 场分布的方法称为镜像法。
l r
Hr2
H1 l
r as
r
nr
Jrl ,
rH1
l
r
ars
as
r Jl
n
r as
n H2 n H1 Jl
H2t H1t J l
在两种媒质界面处,磁场强度的切向分量是 有条件连续的。
4 磁通密度的关系
nr
rr B2 B1
0 Bn2 Bn1 0
在两种媒质的界面处,磁通密度矢量的法向分量 无条件连续。
T? ? 1 f
3 理想导体内部的电磁场
• 理想导体内部不存在电场,只要电场不为 零,在电场的作用下就会有自由电荷分布, 另外导体内的电流密度会成为无穷大,这是 不符合物理的。
• 由麦克斯韦第二方程可得理想导体中的时变 磁场也必为零。
r E
0,
r B
0,
r
Bt
r B
电磁场的边界条件

也可以表示为标量形式:
可见, 的切向分量在不同的媒质分界面上不连续, H 与分界面上的传导电流面密度有关。
②、E 的边界条件
en
(E1 E2 ) 0 E E 1t 2t
结论: E 切向连续。
③ D 的边界条件
1
dv
n
D2
D1 h 0
D dS
s
2
电磁场的边界条件
1 什么是边界条件?
2 为什么要研究边界条件? 3 如何讨论边界条件?
在两种不同媒质的分界面上,场矢量E, D, B, H
各自满足的关系,称为电磁场的边界条件。
在实际的电磁场问题中,总会遇到两种不
同媒质的分界面(例如:空气与玻璃的分界面、 导体与空气的分界面等),边界条件在处理电 磁场问题中占据着十分重要的地位。
或
B 1n B 2n D 1n D 2n
2.理想导体与介质的分界面,电导率 , 假设I为介质,II为理想导体。 此时
E 2 0 , B 2 0, D 2 0, H 2 0
en en en en
H1 Js E1 0 B1 0 D 1 ρ s
dS )
由于
D t
有限,故 lim S
h 0
D t
dS 0
而 lim
h 0
J dS
s
h 0
lim
(J S )
h 0
lim
( J e p l h ) J s e p l
en ( H 1
H2) Js
H 1t H 2t J s
数
, ,
节 媒质电磁性质和边界条件PPT学习教案

D t
E B
t
D V
B 0
JC
V t
D E B H
第21页/共31页
五、电磁场的边界条件
决定分界面两侧电磁场变化关系的方程称为边界条件。
1. 电场法向分量的边界条件
如图所示,在柱形闭合面 上应用电场的高斯定律
S D dS nˆ1 D1S nˆ2 D2S S S
故: nˆ1 D1 nˆ2 D2 S
☺磁介质的磁化现象: 还有一些材料对磁场较敏感,例如螺丝刀在磁铁上放
一会儿,螺丝刀就具有一定的磁性,能吸起小螺钉。这种 现象称为磁化现象。能产生磁化现象的材料称为磁介质。
第2页/共31页
一、导体
1. 导体的定义:含有大量可以自由移动的带电粒子的物质。 金属导体: 由自由电子导电。
导体分为两种 电解质导体:由带电离子导电。
aˆR
R1 R R2 : D 0r E
E2
Q
4π0r R2
aˆR
第13页/共31页
极化强度:
P
D
0E
(1
1
r
)
Q 4πR2
aˆR
电位:
R
E dl
R2
E1RdR
R
R2 E2RdR
Q 1 1 1
4π 0
(1
r
)
R2
r
R
D
r
Q R1
R2
E
O R
R1 R2
P
O
R
R1 R2
第14页/共31页
(1)无极分子的极化:位移极化演示 在外电场作用下,由无极分子组成的电介质中,分子的
正负电荷“重心”将发生相对位移,形成等效电偶极子。
电磁场边界条件

解:(1)磁场强度
r
Q
r E
0
H t
ex
E y z
ez
Ey x
0
H t
可求得
r
H t
E0
0
r [ex
d
cos(
d
z)
cos(t
kx)
r ez
k
sin(
d
z)sin(t kx)]
r H
r ex
0d
E0
cos(
d
z) sin(t
r kx) ez
k
0
E0
sin(
d
z) cos(t
kx)
2)两导体表面的面电流密度
D2 )
0
s
相应的标量形式为
H1t H2t B1n B2n
E1t E2t D1n D2n
2.7.2 两种特殊情况的边界条件
1、理想导体表面上的边界条件
理想导体是指σ→∞,所以在理想导体内部不存在电场
。此外,理想导体内部也不存在磁场。理想导体内部不存 在电磁场,即所有场量为零。设 e是n 理想导体的外法向矢
θ1=1.09°,B1 / B2=0.052。由此可见,铁磁材料内部的磁感应强 度远大于外部的磁感应强度,同时外部的磁感应线几乎与铁磁 材料表面垂直。
例1、在两导体平板(z=0和z=d)之间的空气中传播的
电磁波,已知其电场强度为
r E
ery E0
sin(
d
z) cos(t
kx)
式中k为常数,求:(1)磁场强度;(2)两导体表面的面电流 密度和面电荷密度。
s
en
D |zd
ez
D |zd
媒质分界面条件和边界条件

媒质分界面连接条件和媒质界限条件1.2.1 媒质分界面连接条件在求解电磁场问题时,在不一样媒质分界面上场的解答一定般配,已学过的有:电场:n E2E10n D2D1磁场:n H2H1J Sn B2B10电流场(恒定电场 )n E2E10n J2J10下边进一步剖析媒质分界面上场矢量发生突变的一般状况。
1.面散度场源可能惹起场磁量法向重量的突变:在电场中,散度场源D b( r ) 存在。
设电场中两种媒质之间存在一个过渡层,媒质性能参数由、、连续变化为、、1112 22 ,厚度h很小,取h 为一扁盒圆柱面的高,为过渡层内体自由电荷密度。
如下图,规定分界面上的正法向方向。
由高斯通量定理n 1D 2D ds D 2s 2 D 1s 1S2nD 2 D 1 sVD dVh s2、2、 2hn (D 2 D 1 )h1、 1、1s议论:D 11(1) 若为有限值,则当 h0,即n 2媒质参数发生跃变时,扁盒内的电荷量q = h 0n D 2 D 1 0D 2 n D 1 n 6(2) 若当 h 0 时, q 保持定值不变,即 h 0 , 不停增大,使 h 保持定值,定义它为面自由电荷密度lim ( h)h 0上边的界限条件式变成:n ( D 2 D 1 ) lim ( h)lim ( hD )h 0hD 的法向重量突变,也可用标量电位表示为n2 2 1 1将以上结论引伸到一般矢量场 F 中,当 h 0 时成为一广泛性界限条件公式:n F 2 F 1lim (hb)lim ( hF )h 0h 0称上述极限突变值为 面散度源 ,可知“矢量场的面散度源可能惹起场的法向重量改变,无散场的法向重量必定连续 (假如没有偶极矩阵 )”。
2. 面旋度源可能惹起场矢量切向重量的突变由斯托克斯定理:F dlF dsc(r ) dsn lSS设磁场中两种媒质间存在一过H 2n渡层,其厚为 h 很小,如下图。
l n跨分界面作矩形闭合曲线 l ,其长、 22 Jt边为 l ,宽边为 h ,且 n 、 t和1、1hsn 呈右旋关系 tn n ,有lH 1H dlH 2 l 2 H 1 l 1lH 2 H 1 t l(H ) dsSc ( r ) dsc ( r ) n h lSt H 2H 1 n n H 2 H 1n nH 2 H 1 n c r hn [n ( H 2 H 1 ) c(r )h]因 l 回路设定的随意性,上式建立,在 h →0 时,必有:n ( H 2H 1 ) lim [ hc ( r )] lim [ h(H )]h 0h 0lim [ h( JD)]ht式中 D D 老是有限的, h0 , h D0 。
电磁场的边界条件(一)

1. 电场法向分量的边界条件 2. 电场切向分量的边界条件 3. 标量电位的边界条件
决定分界面两侧电磁场变化关系的方程称为边界条件。
1.电场法向分量的边界条件
如图所示,在柱形闭合面上应 用电场的高斯定律
= & •0A5 +爲・Z)2冨= Qs勇 故: 疋占1兰対.刀2二用
风=01.小=(葯久+歯a y+歯a)
“=廁=顷2 ” a + 弟 a y + 弟 a z)
E、t = E、_E\
=(—a -
124 ay+95 az)
n
50 a 50
y 50
得:
EH = E,t
"l 3 n = S0E2 n
D\n — D2n = 0
E2n = (279 八aa + 372人ay + 465 az) 50 50 50
Ez= E2, + "5.72% + 4.960, + 11乓
小结:
1. 电场法向分量的边界条件Dm -D2n = PS
2. 电场切向分量的边界条件EH = At
域 。 3. 标量电位的边界条件
|s =
2I
-f 愛dS = _^MAh = 0 Js d t
dt
故: Eit = E2t 或 n x (瓦-瓦)=0
因为:D = sE
该式表明,在分界面上电场强度的切向分量总是连续的。
D\t _ D2t ^2
若媒质□为理想导体时:E1t = 0
面上取两点,分别 为爾站,如图,从标量电位的物理意 义出 发
例1:试求两个平行板电容器的电场强度。 解:
第一章电磁场的媒质边界条件

D
LHdl
S
J
t
dS
S BdS 0
2 积分环路和通量曲面的选择
• 在两种媒质界面上,作一跨越界面的矩形闭合路径,
• 令此矩形路径长边与界面平行,其短边h→0,
n
2 , 2
Jl
h
1,1
l
l 0,h 0
LHdl SJD tdS
3 磁场强度的关系
H2lH1l Jl,l asn nH2asnH1asJlas
5 电力线折射定律
tan 1
E t1 E n1
1
E t1 D n1
n 2
E2
tan 2
E t2 E n2
2
E t2 D n2
S0
tan 1 1 tan 2 2
1
E1
n D 1D 2 0 1En12En2 1E1cos12E2cos2
nE1nE20 E1t E2t E1sin1E2sin2
Dt 2
Dn1 Dt1
S0,h~0
l 0,h 0 S 0 ,h0
S D d S V d V SS d S D 1 S n D 2 S n S S
D n 1 S D n 2 SS S
4 电通密度的关系
n D1 D2 0S
• 两种媒质界面处,电通量密度的法向分量有条件连续。 •当媒质界面上没有自由电荷分布时,电通量密度的法向 分量有条件连续。 • 电场强度法向分量总是不连续的,除非两种介质的介 电常数相等。
s ( J
D t
)d S
L
E
d
l
S
B t
d
S
D d S S
V ef d V
S B d S 0
电磁场三类边界条件

电磁场三类边界条件介绍在电磁学中,边界条件是解决电磁场问题时的重要问题之一。
电磁场三类边界条件指的是麦克斯韦方程组在不同介质之间的边界上的满足条件。
这些条件在电磁场问题的求解中起到了关键的作用。
在本文中,我们将详细探讨电磁场三类边界条件的定义和应用。
一、第一类边界条件第一类边界条件也称为电磁场的法向边界条件。
其主要定义了电场和磁场在边界上的法向分量之间的关系。
具体表达如下:1.在介质边界上,电场的法向分量E n1和E n2满足:E n1=E n2;2.在介质边界上,磁场的法向分量H n1和H n2满足:H n1=H n2。
第一类边界条件体现了介质边界上的电场和磁场的连续性。
二、第二类边界条件第二类边界条件也称为电磁场的切向边界条件。
其主要定义了电场和磁场在边界上的切向分量之间的关系。
具体表达如下:1.在介质边界上,电场的切向分量E t1和E t2满足:E t1ϵ1=E t2ϵ2;2.在介质边界上,磁场的切向分量H t1和H t2满足:H t1μ1=H t2μ2。
其中,ϵ1和ϵ2分别为两个介质的介电常数,μ1和μ2分别为两个介质的磁导率。
第二类边界条件体现了介质边界上的电场和磁场的连续性和切向分量之间的比例关系。
三、第三类边界条件第三类边界条件也称为电磁场的混合边界条件。
其主要定义了电场和磁场在边界上的法向分量和切向分量之间的关系。
具体表达如下:1.在介质边界上,电场的法向分量E n1和E n2满足:E n1=E n2;2.在介质边界上,磁场的法向分量H n1和H n2满足:H n1=H n2;3.在介质边界上,电场的切向分量E t1和E t2满足:E t1ϵ1=E t2ϵ2;4.在介质边界上,磁场的切向分量H t1和H t2满足:H t1μ1=H t2μ2。
第三类边界条件综合了第一类和第二类边界条件,体现了介质边界上的电场和磁场的连续性以及法向分量和切向分量之间的比例关系。
四、应用举例电磁场三类边界条件在电磁学中的应用非常广泛,下面我们以几个实际问题为例,说明其应用方法:例一:平行板电容器考虑一对平行金属板构成的电容器,两板之间填充了介电常数为ϵ的均匀介质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
14
4 电通密度的关系
n D1 D2 0S
• 两种媒质界面处,电通量密度的法向分量有条件连续。 •当媒质界面上没有自由电荷分布时,电通量密度的法向 分量有条件连续。 • 电场强度法向分量总是不连续的,除非两种介质的介 电常数相等。
15
5 电力线折射定律
tan 1
E t1 E n1
1
E t1 D n1
n 2
E2
tan 2
E t2 E n2
2
E t2 D n2
S0
tan 1 1 tan 2 2
1
E1
n D 1D 2 0 1En12En2 1E1cos12E2cos2
nE1nE20 E1t E2t E1sin1E2sin2
边界处电力线不再连续变化,变化规律类似于光线的折射。
Maxwell's Equations
全电流定律
lH
dl
s(J
D t
)d
S
电磁感应定律
L
E
d
l
S
B t
d
S
D d S S
V ef dV
磁通连续性原理 S B d S 0
H J D t
E B t
D B 0
1
§1.3 电磁场的媒质边界条件
• 边界条件问题的由来; • 什么是边界条件; • 边界条件如何求得; • 具体边界条件形式; • 边界条件工程应用。 一、电磁场的边界条件 二、电像法
S h
S0,h 0 SBdS 0
25
4 磁通密度的关系
n B 2 B 1 0 B n 2 B n 1 0
在两种媒质的界面处,磁通密度矢量的法向分量 无条件连续。
26
5 磁力线折射定律
H2t H1t Jl
Bn2 Bn1 0
2Hn2 1hn1 0
tan 1 1 tan 2 2
n 2
n H 2 n H 1Jl H2t H1t Jl
在两种媒质界面处,磁场强度的切向分量是 有条件连续的。
n(H1H2)J0l , ,沿 界界 面面 上有 无电 电流 流存在24
• 跨越两种媒质界面作一高为h的柱形闭合面,
• 使其上下端面与界面平行,
• 令h→0
Bn2
2,2
Bt2
n
1,1
Bn1 Bt1
L E dl
S
B t
dS
S D d S V d V
8
2 积分环路和通量曲面的选择
• 在两种媒质界面上,作一跨越界面的矩形闭合路径,
• 令此矩形路径长边与界面平行,其短边h→0,
n
2 , 2
h
En2
Et 2
1,1
l
En1 Et1
l0,h~0
S0,h 0
9
l0,h 0 S0,h 0
LEdl SB tdS0
2
2
n
1 2
导电介质
p 1p 2 p l1 p i2m p p 1 2E d l lh 0 iE 0 m h 0
20
1.1 磁场的边界条件
lH
d l
s ( J
D t
)d S
L
E
d
l
S
B t
d
S
D d S S
V ef d V
S B d S 0
21
1.2磁场的边界条件
1 磁场的环量和通量
E1l1E2l2 0, E1l E2l 0,l asn
环路为面法向
10
n
2 , 2
1,1
l
l0,h~0
h
En2
Et 2
En1 Et1
S0,h 0
11
3 电场强度的关系
E1 l E2 l 0, E t1l E t2l 0 E t1 E t2
两种媒质界面处电场强度的切向分量相等 (无条件连续)
H2
1
H1
边界处磁力线(H线)不再连续变化,变化规律类似 于光线的折射。
27
1.3理想导体与介质分界面上的边界条件
• 媒质1为理想介质,其介电常数为ε1,导磁系数为µ1, 而导电系数σ1=0。 • 媒质2为理想导体,其介电常数ε0,导磁系数为µ2, 而导电系数σ2→∞。
•理想导体中E=0,J= σ E,否则电流密度无限大。
理想导体
理想介质
2 , ( 0 ); 2
2, (0 ); 2 0
n
28
由麦克斯韦第二方程
E B t
E2 0
E2
B2 t
0
• 在理想导体中不能存在电场和时变磁场。
L H dl
S
J
DtdSS B NhomakorabeaS 022
2 积分环路和通量曲面的选择
• 在两种媒质界面上,作一跨越界面的矩形闭合路径,
• 令此矩形路径长边与界面平行,其短边h→0,
n
2 , 2
Jl
h
1,1
l
l0,h 0
LHdl SJD tdS
23
3 磁场强度的关系
H2l H1l Jl,l asn nH2asnH1as Jl as
2 c tg2 1 c tg1
电场强度的切向连续变化,而法向量不连续变化。
18
LE dl 0
E1 l E2 l 0, E t1l E t2l 0 E t1 E t2
电场强度的切向连续变化,而法向量不连续变化。
19
7 静电场位函数的边界条件
1
1
n
2
2
n
1 2
绝缘不导电介质
1
1
n
16
6两种导电介质恒流电场的边界条件
S JdS 0
J dS n S
J1 J2
Jn1S Jn2S 0
Jn1 Jn2 0
电流密度法向连续变化
17
6两种导电介质恒流电场的边界条件
LE d l V B td V , SJd S0
n J2 J1 0, J E n E2 E1 0
2
• 边界条件问题的由来:实际问题所涉及的 场域中往往会有几种不同的介质,在介质
边界处场量会发生跃变( 、、 ),不
再满足麦克斯韦方程的微分形式,需要对 边界附近场量施以一定限制条件。
3
• 什么是边界条件:把两种媒质界面两侧电 场或磁场的关系叫做媒质分界面上的边界 条件。
4
• 边界条件如何求得:可以用积分形式的麦 克斯韦方程导出。
n(E 1E2)0
12
界面两侧电场法向分量的关系
• 跨越两种媒质界面作一高为h的柱形闭合面,
• 使其上下端面与界面平行,
• 令h→0 n
2 , 2 1,1
S
Dn 2
h
Dt 2
Dn1 Dt1
S0,h~0
13
l0,h 0 S0,h 0
S D d S Vd V SS d S
D 1 S n D 2 S n S S
5
一、电磁场的边界条件
1.1 电场的边界条件 1.2 磁场的边界条件 1.3 理想导体与介质分界面上的边界条件
6
1.1 电场的边界条件
lH
d l
s ( J
D t
)d S
L
E
d
l
S
B t
d
S
D d S S
V ef d V
S B d S 0
7
1.1 电场强度的边界条件
1 电场的通量和环量
