渐近线及函数作图共25页
例析函数图象的渐近线
.
4
. . . O 1 . . 3 2 1 、
_ - ●●:j 2
3
4
4
图4
3 函数 ) + ( ∈R, k ) = k 且 ≠0
-
( ) k 0时即为所谓 的双勾 函数 , 1当 > 它有两条 渐近 线 : , = , 中 Y= 0Y X其 显得更加特殊 , 关注它 以 Y= 应
y
J
C
, -
C
两条渐近线 =一 , 准确地 锁定 了图象 的位置 , Y= 再加之单调性辅 助 , 运用 其解 决一 类分 式 函数 的值 域 、 最 值 问题 极 为 方 便 , 可 巧妙避 开运 用不 等式性 质 进 行 的繁 琐 变 形 , 准 确 率 较 高 , 类 函数 极 此 具“ 工具 ” 功能 .
1 2
推广 : 函数 )=
( ,,, ER, c ,c 0 b cd 且 ≠o b ≠
1- “
b一
图3
0 ) 用分离常数法将 函数 变为 , )=兰 + d, (
C
, 中 其
十 “
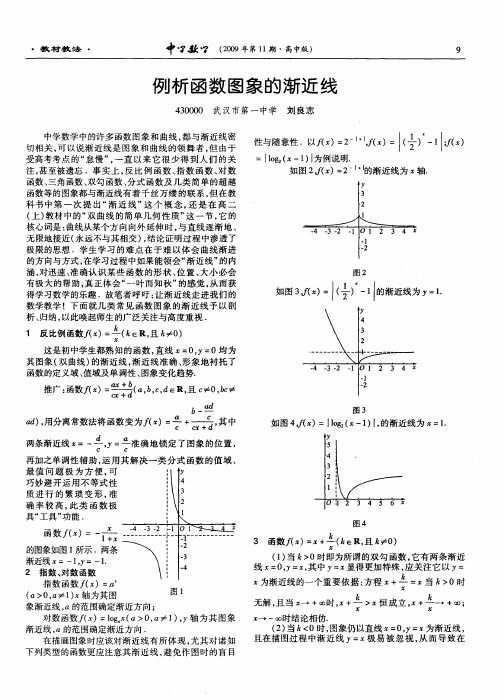
如图4 ) l 2 1 I =J g( o 一 ), 的渐近线为 = . 1
・ 教材教法 ・
综合应用知识的过程 中出现偏差 .以函数 厂 )= + 1 ( z
线之间的图象恰 好 是一个单 调 区间的图象 等等 . 切 余 曲线也有类似的性质 , 学生就更容易记忆.
和(= ÷ 图 加 说 , 它 还 双 线 5 函数 ,) 一的 象 以 明 实 们 是 曲 , 其
性随性以 2 )l)1 ) 与意., =l =号 - ( _ ) ( l
=
受高考考点 的 “ 怠慢 ” 一直 以来 它 很少 得 到人 们 的关 ,
4[1].6函数作图
![4[1].6函数作图](https://img.taocdn.com/s3/m/2a85901ffc4ffe473368abeb.png)
y′ = 2 xe
x2
y′′ = 2e
x2
(2 x 1)
2
驻点: 令 y′ = 0 驻点:x = 0
令 y′′ = 0
1 x=± 2
1 1 1 1 1 1 x ( ∞, ) ( ,0) 0 ( 0 , ) ( ,+∞ ) 2 2 2 2 2 2
y′ y′′
+ +
+
0
0 +
x
y′ y′′
曲线
( ∞ ,1) 1
+
极大值
4 3
0 +
0
拐点
2 (0, ) 3
( 1 ,0 )
0
(0,1)
1
(1,+∞ )
0
+
0
+ +
极小值
y
4 (4) 取辅助点: 2,),2, ); 取辅助点: 0 ( ( 3
显然,函数无水平渐近线和垂直渐近线. 显然,函数无水平渐近线和垂直渐近线. 曲线图象如下图: 曲线图象如下图:
+
0
极 大
y
下凸
1 e
上凸
1
上凸
1 e
下凸
y
2 2
o
2 2
x
例9
1 3 2 的图形. 作函数 y = x x + 的图形. 3 3
解 (1) 函数的定义域为 R, 该函数为非奇非偶函数 ; ( 2) y′ = x 2 1, y′′ = 2 x;
令 y′ = 0, 得 x = ±1; 令 y′′ = 0, 得 x=0; 确定函数的单 ( 3) 列表讨论 y′, y′′ 的符号, 的符号, 调区间和极值,凹凸区间和拐点. 调区间和极值,凹凸区间和拐点.
函数的凹凸与曲线的凸向、拐点和渐近线、函数作图

10
2.8.3-5 函数的凹凸与曲线的凸向、拐点和渐近线及函数作图
二、曲线的拐点
1. 定义:连续曲线上曲线向上凸与向下凸的分界点 称为曲线的拐点。
2£ Õ ã Ä Ð ¨· ® ¹ µ µ Ŷ¨
与极值点判断类似 , f ( x ) 0 的点和 f ( x ) 不存在 的点,是拐点横坐标 的可疑点。
2(1 x 2 ) 2x (2) y 2 , y 2 , 2 ( x 1) x 1
(3)令 y 0 ,得 x 1 , x 1 。
x y
曲线 y
Hale Waihona Puke (, 1)-1 0拐点 (-1,ln2)
(-1, 1) +
1 0
拐点 (1,ln2)
(1, )
例如: f ( x ) x 4 , f ( x ) 12 x 2 ,有 f (0) 0 ,但 (0,0)不是拐点。
12
2.8.3-5 函数的凹凸与曲线的凸向、拐点和渐近线及函数作图
例 2.求曲线 y ln( x 1) 的凸向和拐点。
2
解: (1)函数的定义域为 (,) ;
则称函数 f 为区间 I 上的凸函数; 若总有 f ( p1 x1 p2 x2 ) p1 f ( x1 ) p1 f ( x2 ) ,则称函数 f 为区间 I 上的凹函数。
3
2.8.3-5 函数的凹凸与曲线的凸向、拐点和渐近线及函数作图
y
y f ( x)
y
A
o a x1
D B
C
x
x2 b x
2
x2 x x x1 令 p1 , p2 , 则 p1 0 , p2 0 且 p1 p2 1 , x2 x1 x2 x1
函数三种渐近线的求法公式

函数三种渐近线的求法公式渐近线是指函数图像在无穷远处的趋势线,它可以帮助我们更好地理解和分析函数的性质。
在数学中,常见的渐近线有水平渐近线、垂直渐近线和斜渐近线。
下面将分别介绍这三种渐近线的求法公式。
一、水平渐近线当函数f(x)在无穷远处的函数值趋近于一个常数L时,我们称L为f(x)的水平渐近线。
水平渐近线通常是y=L的形式。
求法公式:1. 若极限lim[x→∞]f(x)存在且等于L,则y = L是f(x)的水平渐近线。
2. 若极限lim[x→-∞]f(x)存在且等于L,则y = L是f(x)的水平渐近线。
注:若f(x)在无穷大处不存在极限,则没有水平渐近线。
例题1:求函数f(x)=(3x^2+2)/(x^2+1)的水平渐近线。
解:由于当x趋近于无穷大时,常数项对于分子和分母的影响越来越小,因此该函数的水平渐近线应为y=3/1=3二、垂直渐近线当函数f(x)在一些点x=a处的函数值趋近于无穷大或负无穷大时,我们称x=a为f(x)的垂直渐近线。
求法公式:对于函数f(x):1. 若lim[x→a]f(x)存在且为无穷大或负无穷大,则x = a是f(x)的垂直渐近线。
2. 若lim[x→a+]f(x)存在且为无穷大或负无穷大,则x = a+是f(x)的垂直渐近线。
3. 若lim[x→a-]f(x)存在且为无穷大或负无穷大,则x = a-是f(x)的垂直渐近线。
注:若f(x)在特定点附近没有无穷大的极限值,则没有垂直渐近线。
例题2:求函数f(x)=1/(x-1)的垂直渐近线。
解:由于当x趋近于1时,分母趋向0,因此该函数在x=1处有垂直渐近线。
三、斜渐近线当函数f(x)在无穷远处的函数值趋近于一个斜线L时,我们称L为f(x)的斜渐近线。
斜渐近线通常是y = mx + b的形式。
求法公式:1.对于函数f(x):若lim[x→∞][f(x) - (mx + b)] = 0,则y = mx + b是f(x)的斜渐近线。
函数渐近线及函数图形的描绘

使用图形计算器绘制函数图形
简单易用、无需额外设置
图形计算器的操作通常非常简单,只需要选择相应的函数 类型或输入函数表达式,就可以自动绘制出相应的图形。 用户无需进行复杂的设置或调整参数,使得绘图过程更加 快速和简便。
使用图形计算器绘制函数图形
功能相对有限
VS
相对于数学软件,图形计算器的功能 相对有限。它们通常只能绘制基本的 函数图形,如直线、二次函数、三角 函数等,而无法绘制更复杂的函数图 形或进行高级的图形定制。
功能强大、精确度高
数学软件如Matlab、Mathematica和Maple等,提供了强大的绘图工具和函数 库,可以绘制各种复杂的函数图形,包括三维图形和极坐标图形。这些软件通常 具有高精度的计算和绘图能力,能够准确地表示函数的形状和变化趋势。
使用数学软件绘制函数图形
操作简便、可视化效果好
这些软件通常具有直观的用户界面和易于操作的命令语言,使得用户可以轻松地绘制函数图形。同时,这些软件还提供了丰 富的颜色、线条样式和标记工具,使得绘制的图形更加生动和易于理解。
验证模型
通过比较函数渐近线和实际数据,可以验证数学模型的准确 性和可靠性。
在科学计算中的应用
数据拟合
在科学实验中,利用函数渐近线可以 对实验数据进行拟合,得到更准确的 结论。
理论推导
在理论推导中,函数渐近线可以作为 理论依据,帮助推导出新的科学理论。
04 函数图形的描绘工具和技 术
使用数学软件绘制函数图形
平移变换
对称变换
将函数图像沿x轴或y轴方向平移一定 的距离。
将函数图像关于原点、x轴或y轴进行 对称。
伸缩变换
将函数图像在x轴或y轴方向上伸缩一 定的比例。
函数凹凸性

2) 根据拐点的定义, 可得拐点的判别法如下:
若曲线
或不存在,
但 f (x) 在 x0 两侧异号, 则点(x0 , f (x0 )) 是曲线
的一个拐点.
求拐点的步骤见教材P162.
机动 目录 上页 下页 返回 结束
例4. 求曲线
的上(下)凸区间及拐点.
解: 1) 求 y
y 12x3 12x2,
36x(x 32)
机动 目录 上页 下页 返回 结束
(2) 若恒有
则称
图形是上凸的; 或称f (x)为I上的上凸函数。
弦在弧的下方;切线在曲线的上方。
下凸也称为凸,上凸也称为凹。 y
o
x1 x1 x2 x2 x
2
机动 目录 上页 下页 返回 结束
等价定义:
定义1´:设函数 在区间 I 上连续 ,
(1) 若恒有
则称
f (1) f (0) f ( ) (0 1)
机动 目录 上页 下页 返回 结束
作业
P168 1(3,6);2 ; 3; 5(1,3) 6(3,4);7(2)
第七节 目录 上页 下页 返回 结束
例如, 双曲线
L PN
o
x
有渐近线
x y0
y
ab
但抛物线
无渐近线 .
ox
机动 目录 上页 下页 返回 结束
1. 水平与铅直渐近线
若
则曲线
有水平渐近线 y b.
(或x )
若
则曲线
有垂直渐近线 x x0 .
(或x x0 )
例1. 求曲线
的渐近线 .
解: lim ( 1 2) 2
2
x x 1
证明:
令
第8讲 函数图像的渐近线及其应用(教师版)

§8 函数图像的渐近线及其应用秒杀知识点①②知识点1:(渐近线的定义与类型)1.若曲线C 上的动点P 沿着曲线无限地远离原点时,点P 与某一固定直线l 的距离趋于零,则称直线l 为曲线C 的渐近线.2.渐近线分类:共分三类:水平渐近线(0α=),垂直渐近线π2α⎛⎫= ⎪⎝⎭和斜渐近线(0πα<<),其中α为渐近线的倾斜角.知识点2:(渐近线的求法)设曲线()y f x =有斜渐近线y kx b =+.如图所示,曲线上动点P 到渐近线的距离()()cos PN PM f x kx b α==-+.① 根据渐近线定义,当x →+∞(对x →-∞的情形也有相应结果)时,0PN →,从而应有()()lim 0x f x kx b →+∞-+=⎡⎤⎣⎦,②或()lim x f x kx b →+∞-⎡⎤⎦=⎣,③ 又由()()()1lim lim 00x x f x k f x kx b x x→+∞→+∞⎛⎫-=-=⋅=⎪⎝⎭. 得()limx f x k x→+∞=.④于是,若曲线()y f x =有斜渐近线y kx b =+,则k ,b 可由③,④确定,反之,若由④和③式求得k ,b ,再由②和①式得0PN →,从而直线y kx b =+为曲线()y f x =的渐近线.即斜渐近线问题就是③和④的极限问题.若曲线()y f x =存在水平渐近线y b =,则有()lim x f x b →+∞=或()lim x f x b →-∞=,反之,则y b =是曲线()y f x =的水平渐近线.若曲线()y f x =存在垂直渐近线0x x =,则有()0lim x x f x →=∞或()0lim x x f x +→=∞,()0lim x x f x -→=∞,反之,则说明0x x =是曲线()y f x =的垂直渐近线.知识点3:(正确认识渐近线——关于渐近线的几点注记)第一,并不是所有无限伸展或远离原点的曲线都有渐近线,如2y x =,sin y x =等都没有渐近线. 第二,在定义“无限地远离原点”中的原点,也未必是原点,可以是任意一个给定的点,两者是等价的,只不过原点比较有名且明确而已.如1x =是()211y x =-的垂直渐近线,“无限地远离原点”和无限地远离点()1,0,甚至点(),a b 没有本质区别.第三,定义中,当曲线上的动点无限地远离原点时,只需要以某种方式远离即可,不需要以任意方式都远离.如0y =是2x y =的水平渐近线,动点P 无限地远离原点,即这只是当x →-∞时,2x y =无限接近于x 轴,而当x →+∞时,2x y =无限远离x 轴.第四,若曲线存在渐近线,则当x 充分大(或充分小),或无限趋于0x (0x x =是其垂直渐近线)时,曲线基本就像相应渐近线那样近似于一条直线,如,双曲线存在渐近线,而抛物线则没有,从渐近线的角度很容易明白两者的区别.第五,曲线与其渐近线是可以相交的,甚至曲线在“渐近”的过程中与其渐近线可无限次地穿过来穿过去. 高中教材唯一一次挑明渐近线身份是学习双曲线时,给出指示性定义后教材补充一句“也就是说,双曲线与它的渐近线无限接近,但永不相交”.因此可能会给学生造成一般的渐近线都不能与曲线相交的错误认识.如sin x y x =,因为sin lim 0x x x →∞=,所以0y =是该偶函数的水平渐近线,但sin x y x =在区间()0,+∞内有无数个零点,如图所示.第六,曲线与其渐近线可以是相切的,而且可以有无数个切点.如sin 1x y x +=,因为sin 1lim 0x x x →∞+=,0sin 1lim x x x→+=∞,所以0y =,0x =分别是该函数的水平渐近线和垂直渐近线.但该函数与其水平渐近线0y =有无数个切点3π2π,02k ⎛⎫+ ⎪⎝⎭,()k +∈N ,如图所示.第七,根据以上讨论知,曲线并不都是一直“单调”接近渐近线的.知识点4:(求渐近线举例)【示例】求曲线()3223x f x x x =+-的渐近线. 【解析】由④()33223f x x xx x x=+-,所以332lim 123x x x x x →∞=+-,即1k =. 由③及1k =得:()()32lim lim 223x x x f x kx x x x →∞→∞⎛⎫-=-=- ⎪+-⎝⎭,即2b =-. 从而曲线的渐近线方程为2y x =-.又()3223x f x x x =+-,得()3lim x f x →-=∞,()1lim x f x →=∞.所以垂直渐近线为3x =-和1x =.(如上图所示)秒杀思路分析一般用渐近线分析函数性质,常见的有()b f x ax x =+和()()f x yg x =(其中()f x ,()g x 都是关于x 的非零多项式)两种类型.(1)关于型如()b f x ax x =+的分析:当0a =,0b ≠时,()b f x x=为反比例函数;当0a ≠,0b =时,()f x ax =为正比例函数(一次函数); 当0ab ≠时,0lim x b ax x →⎛⎫+=∞ ⎪⎝⎭,则0x =是其一条垂直渐近线. 又lim x b ax x a x →∞⎛⎫+ ⎪= ⎪ ⎪⎝⎭,lim 0x b ax ax x →∞⎛⎫+-= ⎪⎝⎭,则y ax =是其一条斜渐近线,即()b f x ax x =+的图像是夹在两条渐近线0x =和y ax =之间的双曲线,具体情况如下图所示.(2)对于有理分式函数()()f x yg x =的渐近线有如下一般结论:第一,若0x 是方程()0g x =的实数解,且()00f x ≠,则有理分式函数图像存在垂直渐近线0x x =; 第二,若多项式()f x 和()g x 的次数相等,且它们的最高次项系数分别为a ,b ,则该函数图像存在水平渐近线a y b=;第三,若多项式()f x 的次数小于()g x 的次数,则0y =为该函数图像的水平渐近线;第四,若多项式()f x 的次数比()g x 的次数大1,则该函数图像存在斜渐近线,可用公式④和③求解. 【示例】讨论下列三个函数图像的渐近线.(1)()2221x x f x x x +=-+; (2)()221x g x x x =+-; (3)()3221x x h x x x +=+-. 【解析】(1)函数()f x 的定义域为R ,图像如图(1)所示,存在水平渐近线12y =.(2)函数()g x 的定义域为{}112x x x ≠-≠且,图像如图(2)所示,存在水平渐近线0y =和垂直渐近线1x =-,12x =.(3)函数()h x 的定义域为{}112x x x ≠-≠且,图像如图(3)所示,存在垂直渐近线1x =-,12x =和斜渐近线1124y x =-.方法对比【例1】(2015年安徽卷理9)函数()()2ax b f x x c +=+的图像如图所示,则下列结论成立的是( )A .0a >,0b >,0c <B .0a <,0b >,0c >C .0a <,0b >,0c <D .0a <,0b <,0c <【例2】(2002年全国卷)函数111y x =--的图像是(如图所示)( )A .B .C .D .【例3】(2004年湖北卷文)已知52x ≥,则()24524x x f x x-+=-有( )A .最大值5B .最小值5C .最大值1D .最小值1秒杀训练【试题1】曲线()1ln 1e x y x =++渐近线的条数为( )A .0B .1C .2D .3【解析】()001lim lim ln 1e x x x y x →→⎡⎤=++=∞⎢⎥⎣⎦,则0x =是垂直渐近线;()1lim lim ln 1e 0x x x y x →-∞→-∞⎡⎤=++=⎢⎥⎣⎦,则0y =是曲线的水平渐近线; ()2ln 1e 1lim lim 1x x x y x x x →+∞→+∞⎡⎤+⎢⎥+=⎢⎥⎣⎦=,则y x =是其斜渐近线. 综上,共有3条渐近线,故选D . 【试题2】已知函数()321x y x =-,求函数图像的渐近线. 【解析】()321lim 1x x x →=+∞-,1x =是垂直渐近线. ()22lim lim 11x x y x x x →∞→∞==-,且()()32lim lim 21x x x y x x x →∞→∞⎡⎤-=-=⎢⎥-⎢⎥⎣⎦. 从而2y x =+是图像的斜渐近线.【试题3】如图所示的是一个函数的图像,在下面的四个函数中,其图像是所给图像的是( )A .ln y x x =+B .ln y x x =-C .ln y x x =-+D .ln y x x =--【解析】易知选择B .真题回放【试题1】(2017年全国卷Ⅲ文7)函数2sin 1x y x x=++的部分图像大致为(如图所示)( )A .B .C .D .【解析】31sin limlim 11x x y x x x x →+∞→+∞⎛⎫=++= ⎪⎝⎭.()2sin lim lim 11x x x y x x →+∞→+∞⎛⎫-=+= ⎪⎝⎭. 所以1y x =+是其斜渐近线,排除C ,B .又20sin lim 1x x x x +→⎛⎫++=+∞ ⎪⎝⎭,故选择D . 【试题2】(2010福建卷理10)对于具有相同定义域D 的函数()f x 和()g x ,若存在函数()h x kx b =+(k ,b 为常数),对任给的正数m ,存在相应的0x D ∈,使得当x D ∈且0x x >时,总有()()()()00f x h x mh x g x m⎧<-<⎪⎨<-<⎪⎩,则称直线:l y kx b =+为曲线()y f x =和()y g x =的“分渐近线”.给出定义域均为{}1D x x =>的四组函数如下:①()2f x x =,()g x = ②()102x f x -=+,()23x g x x-=;③()21x f x x +=,()ln 1ln x x g x x +=; ④()221x f x x =+,()()21e x g x x -=--. 其中,曲线()y f x =和()y g x =存在“分渐近线”的是( )A .①④B .②③C .②④D .③④【解析】①两个函数图像都没有渐近线;②当x →+∞时,()f x 从直线2y =上方趋近2,而()g x 从直线2y =下方趋近2,故2y =是两函数图像的“分渐近线”;③()f x 是双曲线型函数,存在渐近线0x =,y x =,而()g x 存在渐近线1x =,y x =.但是,当x →+∞时,()f x x >,()g x x >.即()f x 和()g x 都是从直线y x =上方趋于渐近线y x =,故不满足题意. ④当x →+∞时,()()()221211f x x x x =-+→-+,()()()22121e x g x x x =--→-.并且()()21f x x >-,()()21g x x <-.所以()21y x =-是()f x 和()g x 的斜渐近线且分别从两侧趋于()21y x =-.故选C .。
数学解函数渐近线问题

数学解函数渐近线问题一、问题描述与分析在解决数学问题中,我们经常会遇到函数渐近线的问题。
函数的渐近线是指当自变量趋于无穷大时,函数曲线与该直线无限接近,但并不会与其相交的直线。
在解题过程中,我们需要确定函数的渐近线的类型和方程,以便更好地理解和分析函数的性质。
二、概念和原理1. 水平渐近线:当函数f(x)的极限lim(x→±∞) f(x)存在时,若极限lim(x→±∞) f(x) = a,则直线y=a为函数f(x)的水平渐近线。
2. 垂直渐近线:当函数f(x)的极限lim(x→c) f(x)存在或者lim(x→c^+) f(x) = ±∞(或lim(x→c^-) f(x) = ±∞)时,若x=c为函数f(x)的垂直渐近线。
3. 斜渐近线:当函数f(x)的极限lim(x→±∞) f(x)/x存在时,若极限lim(x→±∞) f(x)/x = k,则直线y=kx为函数f(x)的斜渐近线。
三、问题求解我们以一个具体的函数为例进行讲解。
例题:求函数f(x)=3x^3+2x^2-4x-1的渐近线。
1. 水平渐近线的求解:首先我们需要求出函数f(x)当x趋于无穷大时的极限。
由于函数中最高次项为3x^3,所以当x趋于无穷大时,3x^3的影响会主导。
根据极限的性质,lim(x→±∞) f(x) = lim(x→±∞) (3x^3+2x^2-4x-1) = ±∞。
因此,函数f(x)=3x^3+2x^2-4x-1不存在水平渐近线。
2. 垂直渐近线的求解:接下来我们需要寻找函数f(x)的垂直渐近线。
我们可以通过求函数在某些点的极限来确定是否存在垂直渐近线。
a) 当x趋于正无穷大时,函数f(x)的极限为lim(x→∞) f(x) =lim(x→∞) (3x^3+2x^2-4x-1) = ∞。
因此,x=c为函数f(x)的垂直渐近线,其中c为正无穷大。
利用导数求解函数的渐近线与曲线段问题

利用导数求解函数的渐近线与曲线段问题在微积分中,导数是一种重要的工具,可以帮助我们研究函数的性质与行为。
在本文中,我们将探讨如何利用导数来求解函数的渐近线与曲线段问题。
一、渐近线渐近线是指函数曲线在无限远处逐渐趋近的直线。
具体来说,对于函数f(x),如果当x趋于无穷大或负无穷大时,函数值f(x)与一条直线L的距离趋近于0,那么该直线L就是函数f(x)的水平渐近线。
类似地,如果当x趋于无穷大或负无穷大时,函数值f(x)在某个方向上无限趋近于正无穷大或负无穷大,那么该方向上的直线L就是函数f(x)的斜渐近线。
要求解函数的渐近线,我们可以通过计算函数的导数来进行推导。
具体步骤如下:步骤1:首先计算函数f(x)的导数f'(x)。
步骤2:对于水平渐近线的情况,我们需要将f(x)的导数f'(x)置为0,并求出x的值。
然后将x带入原函数f(x)中,得到相应的y值。
这个点(x,y)即为水平渐近线与曲线的交点。
步骤3:对于斜渐近线的情况,我们需要将f(x)的导数f'(x)在无穷大或负无穷大的极限中求出。
然后根据极限的定义,我们可以得到斜渐近线的方程。
二、曲线段曲线段问题是指给定函数f(x),我们需要找出在某个特定区间上与x轴或y轴相交的曲线段。
通过求解导数,我们可以找到函数的最值点,进而确定曲线段的起点和终点。
具体步骤如下:步骤1:计算函数f(x)的导数f'(x)。
步骤2:求解f'(x)=0的解,得到函数f(x)的极值点。
步骤3:确定曲线段的起点和终点。
根据问题的要求,我们可以分别将特定区间的两端点带入函数f(x)中,得到相应的函数值。
这两个点即为曲线段的起点和终点。
通过以上步骤,我们可以利用导数有效地求解函数的渐近线与曲线段问题。
这为我们研究函数的行为和特性提供了有力工具。
函数的微分法作图

渐近线和函数作图
一、曲线的渐近线
1.水平渐近线 (平行于x轴的渐近线)
如果
x
lim f ( x ) b 或 lim f ( x ) b (b 为常数)
x
那么 y b 就是 y f ( x ) 的一条水平渐近线 . y 例如 y arctan x,
有两条水平渐近线: y , y . 2 2
13
5.设某产品的需求函数为
P 10 0.2Q,
成本函数为
C 50 2Q,
求产量为多少时利润最大?
14
6.某商店每周购进一批商品, 进价 为每件 6 元 , 如零售价定为每件 10元, 可售出120件; 当售价降低 0.5元时,销量增加 20件, 问售价 定为多少和每周进货多少时利 润最大,其值为何?
x2 2
,
( x )
( x 1)( x 1) 2
e
x2 2
.
令 ( x ) 0, 得驻点 x 0,
令 ( x ) 0, 得特殊点 x 1, x 1.
1 lim ( x ) lim e x x 2
x2 2
0, 得水平渐近线 y 0.
间和拐点;
第四步 讨论渐近线方程;
第五步 讨论一些特殊点(与坐标轴的交点等).
3
4( x 1) 2 的图形. 例2 作函数 f ( x ) 2 x
解
D : x 0, 非奇非偶函数.
4( x 2) f ( x) , 3 x
列 表
8( x 3) f ( x ) . 4 x
6
列表确定函数升降区间,凹凸区间及极值点与拐点:
x ( ,1) 1 ( 1,0) 0
求高等数学中函数渐近线的求法

求高等数学中函数渐近线的求法垂直渐近线:就是指当x→C时,y→∞。
一般来说,满足分母为0的x的值C,就是所求的渐进线。
x=C就是垂直渐进线。
水平渐近线:就是指在函数f(x)中,x→+∞或-∞时,y→c,y=c就是f(x)的水平渐近线。
所以我们需要考虑的是x无限变大或者变小后,y 的变化情况。
斜渐近线:这种渐近线的形式为y=kx+b,反映函数在无穷远点的性态,先求k,k=limf(x)/x,再求b,b=limf(x)-kx。
极限过程都是x趋向于无穷大综上所述,我们在算渐近线的时候:1.判断其要求的是水平渐近线还是垂直渐近线。
2.垂直渐近线就是求出使得函数表达式无意义的x取值,即为所求垂直渐近线。
3.水平渐近线需要简化等式,然后判断随着x的无限变大或变小,y 值的变化情况。
扩展资料:结论:1.与x^2/a^2-y^2/b^2=1渐近线相同的双曲线的方程,有无数条(且焦点可能在x轴或y轴上);2.与x^2/a^2-y^2/b^2=1渐近线相同的双曲线可设为x^2/a^2-y^2/b^2=N,进行求解;3.x^2/a^2-y^2/b^2=1的渐近线方程为b/a*x=y;4.x^2/b^2-y^2/a^2=1的渐近线方程为a/b*x=y。
求渐近线,可以依据以下结论:双曲线两渐近线夹角一半的余弦等于a/c且2c为两焦点的距离,2a 为轨迹上的点到焦点的距离差。
若极限存在,且极限lim[f(x)-ax,x→∞]=b也存在,那么曲线y=f(x)具有渐近线y=ax+b。
例:求渐近线。
解:(1)x=-1为其垂直渐近线。
(2),即a=1;,即b=-1;所以y=x-1也是其渐近线。
函数渐近线的求法

函数渐近线的求法
函数渐近线是数学建模中常用的概念,它是函数表示的一个特殊状态,主要用于反映函数中某种特定性质的变化趋势。
它具有很强的抽象意义和综合意义,可以用于分析不同数据,并对比不同现象和状态。
本文主要介绍函数渐近线中求解法的概念和方法。
函数渐近线的定义:在函数F(x)的上下两个值之间,存在一个y 值,使得F(x)在x趋近于某一值的时候,y的值趋于某一值。
函数渐近线的求解:函数渐近线的求解方法通常有以下几种:
(1)利用解析方法:利用函数F(x)的参数关系,求解函数渐近线y值;
(2)利用数值方法:根据函数F(x)的定义、参数取值范围,利用计算机求函数渐近线的(x,y)点;
(3)利用拟合方法:对每一个F(x)取值,拟合其y值,以此绘制函数渐近线;
(4)利用归纳方法:根据函数F(x)的取值及数据的变化趋势,求出函数渐近线的范围及趋势;
(5)利用特殊函数求解:利用特殊函数求解函数渐近线,如对数函数等。
函数渐近线的应用:函数渐近线可以用于许多数学领域,如物理、经济、地质学等。
在物理学中,它可以用来研究物体的运动变化规律;在经济学中,它可以用来分析物价和收入的变化趋势;在地质学中,它可以用来描述地球表面的变化规律等。
总而言之,函数渐近线可以
提供科学家对自然界和社会状况的宏观分析和指导,为科学技术的发展和社会管理提供诸多依据。
综上所述,函数渐近线是一个重要的数学概念,可以用来描述不同数据之间的变化趋势,为科学研究提供综合分析方法和实用工具。
学习、应用和研究函数渐近线的方法,可以帮助我们更加深入地了解自然界及社会状况,从而更好地改善生活质量。
数学——4.6 渐近线和函数作图

x2
2e
3
x2
2 2 x x 2 2
x2
y 4 xe
1 2 x e
2
x2
2 x 4 x 6 x e
3 3 4 xe x x 2 2 2 函数无不可导点,其驻点为x 0.71, y | x 2 2 1 e 2 0.43; 2
y
因函数在 , 上的定义,还要考虑曲线的渐近线,
lim xe
x
x2
lim
x
x e
x2
0,
lim
x
f x x
lim e
x
x2
0
故y 0,即x轴是曲线的水平渐近线;曲线无竖直和斜的渐近线。 .
函数y xe 的图形如图4 16所示。 .
2
y
x
2
1
2.竖直渐近线 (垂直于x轴的渐近线)
如果
x x0
lim f ( x ) 或 lim f ( x )
x x0
那么 x x0 就是 y f ( x ) 的一条竖直渐近线 .
1 , 例如 y ( x 2)( x 3)
y
有两条竖直渐近线:
e
x2 2
, ( x )
e
.
令 ( x ) 0, 得驻点 x 0,
令 ( x ) 0, 得特殊点 x 1, x 1.
lim ( x ) lim
x x x2 2
1 2
e
0, 得水平渐近线 y 0.
13
列表确定函数升降区间,凹凸区间及极值点与拐点:
3.6曲线的渐近线及其函数作图

1. 水平渐近线 2. 垂直渐近线 3. 斜渐近线
-1-
定义3.3 . 若曲线 C上的点M 沿着曲线无限地远离原点
时, 点 M 与某一直线 L 的距离趋于 0, 则称直线 L为
曲线C 的渐近线 .
例如, 双曲线
或为“纵坐标差” y
y f (x)
C M y kxb
L PN
有渐近线 但抛物线
4 (拐3点)
2 3
(极小)
3
-10-
例2 描绘函数
的图形.
解 1) 定义域为
图形对称于 y 轴.
2) 求关键点
y
1
x
e
x2 2
,
2
y
1
2
e
x2 2
(1
x2
)
令 y 0得 x 0; 令 y 0得x 1
3) 判别曲线形态
x 0 (0, 1) 1 (1, )
y 0
y
0
y
1
2
1
2 e
于确定函数位置的点,描绘函数图形 .
-9-
例1 描绘
的图形.
解 1) 定义域为
无对称性及周期性.
2) y x2 2x xx 2
y 2x 2 2x 1
令 y 0,
令 y 0,
1 1 2 3
3) x (,0) 0 (0,1) 1 (1, 2) 2 (2, )
y 0
0
y
0
y
2
x 1 3 (极大) 4) y 2 2
a lim [ f (x) b ],
x x
x
a lim f (x) , x x
(或x )
渐近线的数学性质

渐近线的数学性质渐近线是函数图像中的一种特殊线性。
当函数逐渐无限趋近于某个数值时,其图像与该数值所对应的水平或垂直线之间的距离逐渐缩小,直至无限接近于零。
这时,该水平或垂直线即为渐近线,是函数图像在该点附近的重要特征。
一个比较容易理解的例子是 y = 1/x 。
当x趋向于正或负无穷时,y趋向于零,而图像同时逐渐接近于y轴和x轴。
因此,该函数的水平渐近线是y=0,垂直渐近线是x=0。
下面,我们将对渐近线的数学性质进行详细探讨。
渐近线的类型根据函数图像与渐近线的相对位置关系,可以将渐近线分为以下几类:1. 水平渐近线当函数趋于正或负无穷时,函数曲线会与水平线(y = k)无限接近,而这条水平线即为该函数的水平渐近线。
例如,当函数为y = 1/x时,其水平渐近线为y = 0。
2. 垂直渐近线当函数曲线在某一点处斜率趋于无穷大或无穷小时,函数曲线无法通过该点,而该点处对应的垂直线(x = k)即为该函数的垂直渐近线。
例如,当函数为y = tanx时,其垂直渐近线为x =(n+1/2)π,其中n为任意整数。
3. 斜渐近线当函数曲线趋向于某一斜线(y = kx+b)时,该斜线即为该函数的斜渐近线。
例如,当函数为y = x + 1/x时,其斜渐近线为y = x,因为当x趋向于正或负无穷时,y/x趋向于1,x和1/x的和趋向于y = x。
渐近线的求法一般来说,求一条函数曲线的渐近线需要考虑以下几个因素:1. 极限存在性渐近线的存在需要保证函数在趋于无穷大或无穷小的过程中具有特定的性质,例如函数存在有理函数或三角函数等,否则无法通过数学方法求出其渐近线。
2. 斜率、截距的计算对于斜渐近线,需要计算斜率和截距,而对于垂直渐近线和水平渐近线,只需要确定其方程形式。
3. 定义域的限定有些函数在定义域内存在一个或多个不属于趋近范围的点,这些点不应该纳入渐近线的求解范围内,否则可能会导致错误结果。
应用实例渐近线在实际生活中有广泛的应用,以下将介绍其中几个典型例子:1. 电路设计电路中的信号波形通常与某个参考电平或时间轴之间存在一定的关系,而这种关系就可以通过斜、水平或垂直渐近线来表示。
极限计算与函数的渐近线

极限计算与函数的渐近线在数学学科中,极限是一个重要的概念,用来描述函数在无穷接近某一点时的行为。
而函数的渐近线则与极限紧密相关,是指函数图像在无穷远处逐渐趋近的一条直线。
一、极限的定义和性质在介绍函数的渐近线之前,我们先回顾一下极限的定义和性质。
对于函数f(x),当自变量x无限接近某一点a时,如果存在一个常数L,使得对于任意给定的正数ε,总存在对应的正数δ,使得当|x - a| < δ时,有|f(x) - L| < ε成立,则称L为函数f(x)当x趋于a时的极限,记作lim┬(x→a)〖f(x) = L〗。
在极限的计算中常用的方法有代数运算法则、夹逼定理、洛必达法则等。
二、函数的渐近线函数的渐近线指的是函数图像在无穷远处逐渐趋近的一条直线。
根据函数图像的特点,可以将渐近线分为三类:水平渐近线、垂直渐近线和斜渐近线。
1. 水平渐近线:当函数f(x)当x趋于正无穷或负无穷时,若存在一条水平直线y=k(k为常数),使得函数f(x)的图像无限趋近于该水平直线,则该直线称为函数f(x)的水平渐近线。
2. 垂直渐近线:当函数f(x)当x趋于某一实数a时,若函数在x=a处无定义或极限不存在,但其左右极限有至少一个是无穷大,则直线x=a称为函数f(x)的垂直渐近线。
3. 斜渐近线:当函数f(x)当x趋于正无穷或负无穷时,若存在一条斜直线y=kx+b(k为非零常数,b为常数),使得函数f(x)的图像无限趋近于该斜直线,则该直线称为函数f(x)的斜渐近线。
可以通过求出函数的极限来判断函数的渐近线的存在以及具体方程。
三、极限计算与渐近线的关系极限计算是判断函数是否有渐近线的重要方法,也是求出渐近线方程的关键。
以水平渐近线为例,若要判断函数f(x)在x趋于正无穷或负无穷时是否有水平渐近线y=k,需要计算lim┬(x→±∞)〖f(x)〗,若极限存在且等于k,则函数f(x)有水平渐近线y=k;若极限不存在或极限存在但不等于k,则函数f(x)无水平渐近线。
正切函数渐近线

正切函数渐近线正切函数渐近线是基本的数学函数,它在实际的应用中发挥着重要的作用。
首先,我们应该了解什么是正切函数渐近线。
正切函数渐近线是指二元函数的函数图的那一部分,沿着图形的右边界或左边界从某一点开始,从正无穷处到负无穷处的连续曲线部分,正切函数渐近线为抛物线。
正切函数渐近线是由两个独立变量确定的函数,即x和y,其形式为y=tanx,可以根据它的定义,推导出它的图形特征。
由此可见,正切函数的渐近线的图形是右手和左手的抛物线,抛物线的右边界是从正无穷到负无穷,左边界是从负无穷到正无穷,且抛物线围绕着起点周期性地往右和往左伸展,沿着它的周期性变化,到达无穷远处。
正切函数渐近线在实际应用中非常广泛,它可以用来解决各种数学问题,如方程求解、曲线拟合等。
正切函数渐近线可以用于求解曲线上的某一点的纵坐标。
例如,假定一个抛物线的给定的任意的一个横坐标为x,此时此抛物线的纵坐标y可以通过正切函数渐近线来求得。
另外,正切函数渐近线还可以用于求解曲线与直线的交点坐标,以及求解曲线最小值和最大值。
此外,正切函数渐近线还可以应用到工程和物理等多个领域,例如物理学家计算运动物体的轨迹、绘制压力体积曲线、推导某种物质的温度随压强变化的关系等等,都可以用正切函数渐近线来实现。
正切函数渐近线的应用不仅仅体现在实际的数学问题的解决上,同时也极为重要地体现出了数学的拓展能力。
它可以用于提升软件开发、机器人控制,甚至是某些具有一定复杂度的游戏中。
比如赛车游戏,玩家可以利用正切函数渐近线来更加准确地控制车辆,模拟真实的赛车过程。
由以上介绍可知,正切函数渐近线的应用非常广泛,它可以解决数学问题、应用到工程领域,也可以应用到游戏等多个领域。
可以看出,正切函数渐近线在实际应用中具有重要的作用,而且它本身也是数学的一个分支,它反映了数学发展的趋势,也反映了数学拓展能力的强大。
函数渐近线的求法

函数渐近线的求法
函数渐近线是数学中一种重要的概念,它可以用来表示函数在无穷大时的极限值。
它的求法有多种,主要有三种:一是通过函数的导数求渐近线;二是通过函数的定义域和值域求渐近线;三是通过函数的定义域和函数值的极限求渐近线。
首先,通过函数的导数求渐近线,即通过函数的导数来确定函数的渐近线。
具体的求法是:当函数的导数值接近于0时,函数的渐近线就是函数的图象的水平线;当函数的导数值不接近于0时,则函数的渐近线为函数的图象的斜率为函数的导数值的直线。
其次,通过函数的定义域和值域求渐近线,即通过函数的定义域和值域来确定函数的渐近线。
具体的求法是:当函数的定义域和值域都是有限的时,函数的渐近线就是定义域和值域的边界线;当函数的定义域和值域都是无限的时,函数的渐近线就是定义域和值域的极限线。
最后,通过函数的定义域和函数值的极限求渐近线,即通过函数定义域和函数值的极限来确定函数的渐近线。
具体的求法是:当函数的定义域和函数值的极限都是有限的时,函数的渐近线就是定义域和函数值的极限边界线;当函数的定义域和函数值的极限都是无限的时,函数的渐近线就是定义域和函数值的极限极限线。
综上所述,函数渐近线的求法有三种:通过函数的导数求渐近线;通过函数的定义域和值域求渐近线;通过函数的定义域和函数值的极限求渐近线。
每种求法都有其特定的规律,要求我们熟练掌握,以便在解决实际问题时能够灵活运用。
