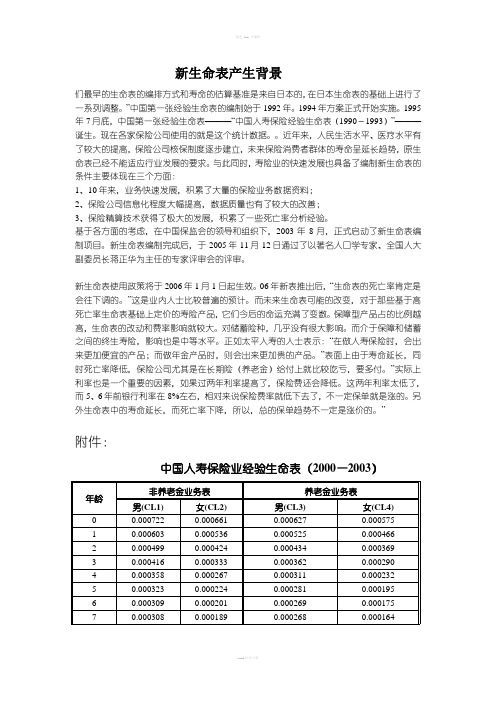
中国人寿保险业生命表(2000-2003)非养老金业务表(女)
第一章 生命表

从数学的角度,生存状况是一个简单的过程。这个过程有如下的 特征: 1. 存在两种状态:生存和死亡。 2. 单个的人──经常称作生命个体──可被划分为生存者或死亡者, 也就是说,我们可说出他们所处的状态。 3. 生命个体可从“生存”状态到“死亡”状态,但不能相反。 4. 任何个体的未来生存时间都是未知的,所以我们应从生存或死亡概 率的探讨而着手生存状况的研究。 5. 生存模型就是对此过程建立的一个数学模型,用数学公式进行清晰 的描述,从而对死亡率的问题作出了一些解释
本章结构
寿命分布
生命表
生命表 各年龄内的寿命分布
1.1
寿命分布
主要内容
寿命X的分布(分布函数和生存分布) 未来寿命(余命)的分布 死力(瞬时死亡率) 重点掌握: a. 各函数的符号表示及理解其涵义 b. 各种函数之间的关系
1.1.1
寿命X的分布函数
连续型死亡年龄
1. X: 死亡年龄(从生存到死亡的时间长度) 是一连续型随机变量
含义:
(x)生存t 年后,在x+t岁与x+t+u岁之间死亡的概率 (x)在活过 t 年后的u年内死亡的概率等于(x)在x+t岁时 仍活着的条件概率与(x+t)在以后的u年内死亡的概率之积。
1.1.3
未来寿命T的分布
t u
其他特殊符号b 特别地
p x t p x u p x t
平均余命
ex E[T ( x)]
0
0
tfT (t ) dt
t
0
p x dt
1.1.3
未来寿命T的分布
其他特殊符号a
s( x t ) s( x t u ) t T ( x) t u ] t | u q x Pr[ s ( x) t u qx t qx t px t u px t px u qx t
关于2000-2003新生命表出台对寿险业的影响分析

表 的变 化( 国外生命表。 般每l年重新评估。 次) 以及新,命表对j ‘ 0 ‘ , 上 品定价 的影响等 问题, 已成为寿险业迫切 需要研究的课题. 整体米说 新生命表将使寿险责任为主 的J 品价格略
有‘ 降, 两全险价格影响不大; 卜 对 但对 年金险 价格 影响较 大, 价格将会有较 一定程度 的提 升. 本文将重点对年金 险生命表进行研究, 究其变动趋势, 研 及其对定价 的影响. 次生命 本
维普资讯
用 概率 统 计 第 . p 咨 十 q 第 ・ 2 0 q.J 划 0 8 - 'q 2
Chie e J ur lo p id Pr ba lt n s o na fA pl o bi y e i an t t s i s V0 . 4 No. b. 00 d S a itc 12 1 Fe 2 8
§ . 引 1
言
近年米, 随着生活水平 、 医疗水平 的提高: 的寿命呈延长趋势: ,命表 已经不能适 人 原上 应行业发展 的要求, 一方面, 0 另一 1年米 国内保 险业务快速 发展, 保险公司的核保制度 、 精算 制度 、 信息化制度均 已逐步建立且得到了较大幅度 的提高 数据 的数量有 了 定程度的积 累, 数据 的质量也有 了较大程度改善. 0 3 月, 20 年8 保监会正式启动 了新,命表编制项 目: 上 组 织 收集 了数家保险公司的数据, 包括 L 国人寿 、 安、 平 洋、 } J 平 新华 、 泰康 、 友邦等人寿保 险公司的业务数据 , 了近2 时间完成 了新 生命表 的初稿 花 年 保监会于20 年l 月l 日’ 发 05 2 9 卜
究背景, 二 第一 部分对死1= L 效力( rai re进 行模拟 , motly f c) t o 并进 行 J可靠忡检验.第三部分结合中罔人 ,
新生命表相关

新生命表产生背景们最早的生命表的编排方式和寿命的估算基准是来自日本的,在日本生命表的基础上进行了一系列调整。
”中国第一张经验生命表的编制始于1992年。
1994年方案正式开始实施。
1995年7月底,中国第一张经验生命表———“中国人寿保险经验生命表(1990-1993)”———诞生。
现在各家保险公司使用的就是这个统计数据。
近年来,人民生活水平、医疗水平有了较大的提高,保险公司核保制度逐步建立,未来保险消费者群体的寿命呈延长趋势,原生命表已经不能适应行业发展的要求。
与此同时,寿险业的快速发展也具备了编制新生命表的条件主要体现在三个方面:1、10年来,业务快速发展,积累了大量的保险业务数据资料;2、保险公司信息化程度大幅提高,数据质量也有了较大的改善;3、保险精算技术获得了极大的发展,积累了一些死亡率分析经验。
基于各方面的考虑,在中国保监会的领导和组织下,2003年8月,正式启动了新生命表编制项目。
新生命表编制完成后,于2005年11月12日通过了以著名人口学专家、全国人大副委员长蒋正华为主任的专家评审会的评审。
新生命表使用政策将于2006年1月1日起生效。
06年新表推出后,“生命表的死亡率肯定是会往下调的。
”这是业内人士比较普遍的预计。
而未来生命表可能的改变,对于那些基于高死亡率生命表基础上定价的寿险产品,它们今后的命运充满了变数。
保障型产品占的比例越高,生命表的改动和费率影响就较大。
对储蓄险种,几乎没有很大影响。
而介于保障和储蓄之间的终生寿险,影响也是中等水平。
正如太平人寿的人士表示:“在做人寿保险时,会出来更加便宜的产品;而做年金产品时,则会出来更加贵的产品。
”表面上由于寿命延长,同时死亡率降低,保险公司尤其是在长期险(养老金)给付上就比较吃亏,要多付。
”实际上利率也是一个重要的因素,如果过两年利率提高了,保险费还会降低。
这两年利率太低了,而5、6年前银行利率在8%左右,相对来说保险费率就低下去了,不一定保单就是涨的。
新生命表相关
新生命表产生背景们最早的生命表的编排方式和寿命的估算基准是来自日本的,在日本生命表的基础上进行了一系列调整。
”中国第一张经验生命表的编制始于1992年。
1994年方案正式开始实施。
1995年7月底,中国第一张经验生命表———“中国人寿保险经验生命表(1990-1993)”———诞生。
现在各家保险公司使用的就是这个统计数据。
近年来,人民生活水平、医疗水平有了较大的提高,保险公司核保制度逐步建立,未来保险消费者群体的寿命呈延长趋势,原生命表已经不能适应行业发展的要求。
与此同时,寿险业的快速发展也具备了编制新生命表的条件主要体现在三个方面:1、10年来,业务快速发展,积累了大量的保险业务数据资料;2、保险公司信息化程度大幅提高,数据质量也有了较大的改善;3、保险精算技术获得了极大的发展,积累了一些死亡率分析经验。
基于各方面的考虑,在中国保监会的领导和组织下,2003年8月,正式启动了新生命表编制项目。
新生命表编制完成后,于2005年11月12日通过了以著名人口学专家、全国人大副委员长蒋正华为主任的专家评审会的评审。
新生命表使用政策将于2006年1月1日起生效。
06年新表推出后,“生命表的死亡率肯定是会往下调的。
”这是业内人士比较普遍的预计。
而未来生命表可能的改变,对于那些基于高死亡率生命表基础上定价的寿险产品,它们今后的命运充满了变数。
保障型产品占的比例越高,生命表的改动和费率影响就较大。
对储蓄险种,几乎没有很大影响。
而介于保障和储蓄之间的终生寿险,影响也是中等水平。
正如太平人寿的人士表示:“在做人寿保险时,会出来更加便宜的产品;而做年金产品时,则会出来更加贵的产品。
”表面上由于寿命延长,同时死亡率降低,保险公司尤其是在长期险(养老金)给付上就比较吃亏,要多付。
”实际上利率也是一个重要的因素,如果过两年利率提高了,保险费还会降低。
这两年利率太低了,而5、6年前银行利率在8%左右,相对来说保险费率就低下去了,不一定保单就是涨的。
生命表

国内的生命表
10年来,业务快速发展,积累了大量的保险业务数据资料; 2、保险公司信息化程度大幅提高,数据质量也有了较大 的改善; 3、保险精算技术获得了极大的发展,积累了一些死亡率 分析经验。 基于各方面的考虑,在中国保监会的领导和组织下, 2003年8月,正式启动了新生命表编制项目。新生命表编 制完成后,于2005年11月12日通过了以著名人口学专家、 全国人大副委员长蒋正华为主任的专家评审会的评审。于 2006年1月1日正式启用。
X=年龄 lx=在X岁生存的人数 dx=年龄在岁的人在一年内死亡的人数=lx-lx+1 qx=年龄在岁的人在一年内死亡的概率=dx/lx px=年龄在岁的人活过一年的概率 =lx+1/lx
生命表的分类
以死亡统计的对象为标准,生命表可分为 国民生命表和经验生命表。 国民生命表是根据全体国民或某一特定地 区人口的死亡资料编制而成的。 经验生命表是根据保险机构有关人寿保险、 社会保险的死亡记录编制而成的。
生命表概述
2009年10月
原理
现代保险学是建立在概率论和大数定律的基础上 大数法则:是用来说明大量的随机现象由于偶然性相互抵消所呈现的必然数 量规律的一系列定理的统称. 切比雪夫大数法则:在承保标的数量足够大时,被保险人所交纳的纯保费与 其所能获得的赔款期望值相等。 贝努力定理大数法则:利用统计资料来估计损失概率是极其重要的。 泊松大数法则:平均概率与观察结果所得的比例将无限接近。
国内的生命表
新生命表包括非养老金业务男女表和养老金业务男女表共 两套四张表,简称“CL(2000-2003)”。其结构与原生命表 相同,但取消了混合表。 之所以非养老金业务与养老金业务用表不同,是因为整体 而言,投保养老金的人群死亡的概率比投保非养老金的人 群要小。 本次非养老金业务表男性平均寿命为76.7岁,较原生命表 提高了3.1岁,女性平均寿命为80.9岁,较原生命表提高 了3.1岁。养老金业务表男性平均寿命为79.7岁,较原生 命表提高了4.8岁,女性平均寿命为83.7岁,较原生命表 提高了4.7岁。
中国保险监督管理委员会关于修订精算规定中生命表使用有关事项的通知-保监发[2005]118号
![中国保险监督管理委员会关于修订精算规定中生命表使用有关事项的通知-保监发[2005]118号](https://img.taocdn.com/s3/m/3fed652b5b8102d276a20029bd64783e09127df2.png)
中国保险监督管理委员会关于修订精算规定中生命表使用有关事项的通知正文:---------------------------------------------------------------------------------------------------------------------------------------------------- 中国保险监督管理委员会关于修订精算规定中生命表使用有关事项的通知(2005年12月19日保监发[2005]118号)各寿险公司、各养老保险公司、各健康保险公司:为了更好地使用《中国人寿保险业经验生命表(2000~2003)》,现对精算规定中有关生命表事项修订如下:一、《关于下发有关精算规定的通知》(保监发[1999]90号)之“人寿保险精算规定”第二部分“保险费”中第三条(二)“预定死亡率”修改为:“保险公司在厘定保险费时,自行决定采用的预定死亡率。
”二、《关于下发有关精算规定的通知》(保监发[1999]90号)之“人寿保险精算规定”第四部分“法定责任准备金”中第九条(二)“评估死亡率”修改为:“采用《中国人寿保险业经验生命表(2000~2003)》所提供的数据。
保险公司应根据产品特征,对于同一产品的全部保单整体考虑,按照审慎性原则在非养老金业务表和养老金业务表之间选择采用较为保守的评估死亡率。
”三、《关于印发人身保险新型产品精算规定的通知》(保监发[2003]67号)之“个人分红保险精算规定”第二部分“保险费”中第三条(二)“预定死亡率”修改为:“保险公司在厘定保险费时,自行决定采用的预定死亡率。
”四、《关于印发人身保险新型产品精算规定的通知》(保监发[2003]67号)之“个人分红保险精算规定”第五部分“法定责任准备金”中第十四条(二)“评估死亡率”修改为:“采用《中国人寿保险业经验生命表(2000~2003)》所提供的数据。
保险公司应根据产品特征,对于同一产品的全部保单整体考虑,按照审慎性原则在非养老金业务表和养老金业务表之间选择采用较为保守的评估死亡率。
保险理论与实务项目八

任务二 认识人寿保险
• 5. 复效条款 • 复效条款规定, 保险合同单纯因投保人不按期缴纳保费而失效后,
投保人保有一定时间 申请复效权。 复效是对原合同效力的恢复, 并 不改变原合同的各项权利和义务。 可申请复效的期间一般为2 年, 投保人在此期间内有权申请合同复效。 • 复效可分为体检复效和简易复效两种。 • (1)体检复效 • (2)简易复效
上一页 下一页 返回
任务二 认识人寿保险
• 2. 人寿保险的特征 • 人寿保险除了具有人身保险的一般特征之外, 还具有以下四个主要
特征: • (1)风险的特殊性 • (2)长期险种的储蓄型 • (3)保险的长期性 • (4)保费计算的均衡性
上一页 下一页 返回
任务二 认识人寿保险
• 二、人寿保险的主要类型
放弃了可以主张的权 利, 以后不可以再主张。 该条款规定, 保单生 效一定时期(通常为2 年) 后, 就成为不可争议的文件, 保险人不 能以投保人在投保时违反诚实信用原则, 没有履行告知义务等为由, 否定保单的有效性。
上一页 下一页 返回
任务二 认识人寿保险
• 2. 年龄误告条款 • 年龄误告条款通常规定了投保人在投保时误报被保险人年龄情况下的
上一页 下一页 返回
任务二 认识人寿保险
• 6. 不丧失价值任选条款 • 寿险保单除短期的定期险外, 投保人缴满一定期间 (一般为2 年)
的保费后, 如果合 同期满前解约或终止, 保单所具有的现金价值并 不丧失, 投保人或被保险人有权选择有利于自己的方式来处理保单 所具有的现金价值。 为了方便投保人或被保险人了解保单现金价值 的 数额与计算方法, 保险公司往往在保单上附上现金价值表。
• 1. 普通型人寿保险 • 按照保险责任, 普通型人寿保险分为死亡保险、 生存保险和两全保
浙教版数学九年级上册同步课件:概率的简单应用

答:他活到62岁的概率约为0.8969.
例3 小亮和小芳都想参加学校杜团组织的暑假实践活动,但只 有一个名额,小亮提议用如下的办法决定谁去参加活动:将一 个转盘9等分,分别标上1至9九个号码,随便转动转盘,若转到 2的倍数,小亮去参加活动;转到3的倍数,小芳去参加活动; 转到其它号码则重新转动转盘. (1)转盘转到2的倍数的概率是多少? (2)你认为这个游戏公平吗?请说明理由.
解:1 P 转动一次获得购物券 = 10 = 1,
20 2
2 200 1 +100 3 +50 6 =40元
20
20
20
40 30,
选择转动转盘对顾客更合算.
2.如图所示,一个转盘被平均分成六个扇形,并在上面依 次写上数字1、2、3、4、5、6;若自由转动转盘,当它停 止转动时,求: (1)指针指向4的概率_____;(直接写出答案) (2)指针指向数字是奇数的概率____;(直接写出答案) (3)指针指向数字不小于5的概率_____;(直接写出答案)
奖项 一等奖 二等奖 三等奖
|x| |x|=4 |x|=3 1≤|x|<3 (1)用列表或画树状图的方法求出甲同学抽奖一次获得一等奖的概率; (2)是否每次图如下:
∵共有20种等可能的情况,甲同学抽奖一次获得一等奖的有2
种情况,
2
∴甲同学抽奖一次获得一等奖的概率为 20
第2章 简单事件的概率
2.4 概率的简单应用
买彩票的人一定希望知道 中奖的概率有多大.怎样来估计 彩票中奖的概率呢?
例题讲授
例1 某商场举行有奖销售活动,每张奖券获奖的可能性相同. 以每10000张奖券为一个开奖单位,设特等奖1个,一等奖10 个,二等奖100个.问1张奖券中一等奖的概率是多少?中奖的 概率是多少?
