高考总复习三角恒等变换专题习题附解析
高考数学专题复习四-4.2三角恒等变换-高考真题练习(附答案)

4.2三角恒等变换考点三角恒等变换1.(2017课标Ⅲ文,4,5分)已知sinα-cosα=43,则sin2α=()A.-79 B.-29C.29D.79答案A ∵(sinα-cosα)2=169,∴sin2α=-79.解后反思涉及sinα±cosα,sinαcosα的问题,通常利用公式(sinα±cosα)2=1±2sinαcosα进行转换.2.(2017山东文,4,5分)已知cosx=34,则cos2x=()A.-14 B.14C.-18D.18答案D 本题考查二倍角余弦公式.因为cosx=34,所以cos2x=2cos 2-1=18.3.(2016课标Ⅲ文,6,5分)若tanθ=-13,则cos2θ=()A.-45 B.-15C.15D.45答案D 解法一:cos2θ=cos 2θ-sin 2θ=cos 2θ-sin 2θcos 2θ+sin 2θ=1−tan 2θ1+tan 2θ=45.故选D.解法二:由tanθ=-13,可得因而cos2θ=1-2sin 2θ=45.评析本题考查化归与转化的能力.属中档题.4.(2015课标Ⅰ理,2,5分)sin20°cos10°-cos160°sin10°=()C.-12D.12答案D 原式=sin20°cos10°+cos20°sin10°=sin(20°+10°)=sin30°=12,故选D.5.(2015重庆理,9,5分)若tanα=2tan π5,)A.1B.2C.3D.4答案C=sinvos π5+cosLin π5sinvos π5-cosLin π5=tanrtan π5tanttan π5,∵tanα=2tanπ5,∴=3tanπ5tanπ5=3.故选C.6.(2015重庆文,6,5分)若tanα=13,tan(α+β)=12,则tanβ=()A.17B.16C.57D.56答案A tanβ=tan[(α+β)-α]=tan(rp-tan1+tan(rp·tan=12-131+12×13=17,故选A.7.(2013课标Ⅱ文,6,5分)已知sin2α=23,则cos2)A.16B.13C.12D.23答案A cos2=1−sin22,把sin2α=23代入,原式=16.选A.评析本题考查了三角函数的化简求值,考查了降幂公式、诱导公式的应用.8.(2016课标Ⅱ,9,5分)若-α=35,则sin2α=()A.725B.15C.-15D.-725答案D解法一:因为-α=35,所以-2α=cos2-α=2cos-α-1=-725.故选D.解法二-α(cosα+sinα)=35⇒1+sin2α=1825,∴sin2α=-725.故选D. 9.(2021全国乙文,6,5分)cos2π12−cos25π12=()A.12答案D解析解法一:cos2π5π12=π=cos2π12−sin2π12=cosπ6=解法二:cos2π12−cos25π12cos2−cos2=cosπ4π6π4π4π6sinπ4×10.(2021全国甲理,9,5分)若α∈tan2α=cos2−sin,则tanα=()答案A 解题指导:先将切化弦,再将分式化为整式,利用两角差的余弦公式及二倍角公式将异角化为同角,最后利用同角三角函数的基本关系求解.解析∵tan 2α=cos 2−sin ,且α∈0,∴sin2cos2=cos2−sin ,∴2sin 2α=cos αcos 2α+sin αsin 2α,即4sin αcos α=cos (2α-α)=cos α,又cos α≠0,∴4sin α=1,∴sin α=14,∴cos αtan αA .疑难突破将tan 2α转化为sin2cos2是本题的突破口.11.(2021新高考Ⅰ,6,5分)若tan θ=-2,则sino1+sin2psinrcos=()A.-65B.−25C.25D.65答案Csino1+sin2psinrcos=sinosin 2rcos 2r2sinbcospsinrcos=sinosinrcosp 2sinrcos=sin θ(sin θ+cos θ)=sin 2θ+sin θ·cosθ=sin 2rsinbcos sin 2rcos 2=tan 2rtan tan 2r1=(−2)2−2(−2)2+1=25.故选C .12.(2022新高考Ⅱ,6,5分)若sin (α+β)+cos (α+β)=22cos β,则()A.tan (α-β)=1B.tan (α+β)=1C.tan (α-β)=-1D.tan (α+β)=-1答案C 因为sin (α+β)+cos (α+β)=sin αcos β+cos αsin β+cos αcos β-sin αsin β,22cos β=(2cosα-2sin α)sin β=2cos αsin β-2sin αsin β,所以sin αcos β+cos αsin β+cos αcos β-sin αsin β=2cos αsin β-2sin αsin β,即sin αcos β-cos αsin β+cos αcos β+sin αsin β=0,进而得sin (α-β)+cos (α-β)=0,又知cos (α-β)≠0,所以tan (α-β)=-1,故选C .13.(2022浙江,13,6分)若3sin α-sin β=10,α+β=π2,则sin α=,cos 2β=.答案45解析设a =sin α,b =sin β=cos α,则3−=10,21,解得a b∴sin α=a cos 2β=1-2sin 2β=1-2b 2=45.14.(2020课标Ⅱ文,13,5分)若sinx=-23,则cos2x=.答案19解析∵sinx=-23,∴cos2x=1-2sin2x=1-2×=19.15.(2018课标Ⅱ文,15,5分)已知tan t=15,则tanα=.答案32解析本题主要考查两角差的正切公式.tan t=tanttan5π41+tanMan5π4=tant11+tan=15,解得tanα=32.16.(2017课标Ⅰ文,15,5分)已知α∈则cos t=.答案解析因为α∈且tanα=sin cos=2,所以sinα=2cosα,又sin2α+cos2α=1,所以则cos t=cosαcosπ4+sinαsinπ4=易错警示在求三角函数值时,常用到sin2α+cos2α=1和tanα=sin cos,同时要注意角的范围,以确定三角函数值的正负.17.(2017江苏,5,5分)若tan t=16,则tanα=.答案75解析本题考查两角和的正切公式.因为tan=16,所以tanα=tan=16+11−16×1=75.18.(2016浙江,理10,文10,5分)已知2cos2x+sin2x=Asin(ωx+φ)+b(A>0),则A=,b=.答案2;1解析∵2cos2x+sin2x=1+cos2x+sin2x=2sin2+1,∴A=2,b=1.评析本题主要考查三角恒等变换,熟练利用两角和的正弦公式及二倍角公式是解题关键. 19.(2016课标Ⅰ文,14,5分)已知θ是第四象限角,且sin=35,则tan t=.答案-43解析解法一:∵sin×(sinθ+cosθ)=35,∴sinθ+cosθ=①,∴2sinθcosθ=-725.∵θ是第四象限角,∴sinθ<0,cosθ>0,∴sinθ-cosθ=-1−2sinvos=-由①②得,∴tanθ=-17,∴tan=tant11+tan=-43.解法二:∵-θ=π2,∴sin=35,又2kπ-π2<θ<2kπ,k∈Z,∴2kπ-π4<θ+π4<2kπ+π4,k∈Z,∴cos=45,∴sin-θ=45,-θ=43,∴tan=-43.评析本题主要考查了三角恒等变换,熟练掌握同角三角函数关系式及诱导公式是解题的关键.20.(2016四川理,11,5分)cos2π8-sin2π8=.答案解析由二倍角公式易得cos2π8-sin2π8=cosπ4=21.(2015江苏,8,5分)已知tanα=-2,tan(α+β)=17,则tanβ的值为.答案3解析tanβ=tan[(α+β)-α]=tan(rp-tan1+tan(rptan=17-(-2)1+17×(−2)=3.22.(2015四川理,12,5分)sin15°+sin75°的值是.答案解析sin15°+sin75°=sin15°+cos15°=2sin(15°+45°)=2sin60°=23.(2014课标Ⅱ理,14,5分)函数f(x)=sin(x+2φ)-2sinφcos(x+φ)的最大值为.答案1解析f(x)=sin[(x+φ)+φ]-2sinφcos(x+φ)=sin(x+φ)cosφ+cos(x+φ)sinφ-2sinφcos(x+φ)=sin(x+φ)cosφ-sinφcos(x+φ)=sin(x+φ-φ)=sinx,∴f(x)的最大值为1.24.(2014课标Ⅱ文,14,5分)函数f(x)=sin(x+φ)-2sinφcosx的最大值为.答案1解析f(x)=sin(x+φ)-2sinφcosx=sinxcosφ+cosxsinφ-2sinφcosx=sinxcosφ-cosxsinφ=sin(x-φ)≤1,所以f(x)max=1.25.(2015广东文,16,12分)已知tanα=2.(1)求tan;(2)求sin2sin2α+sinvostcos2t1的值.解析(1)因为tanα=2,所以tan=tanrtanπ41−tan·tanπ4=2+11−2×1=-3.(2)因为tanα=2,所以sin2sin2α+sinvostcos2t1=2sinvossin2α+sinvost(cos2α-sin2α)-(sin2α+cos2α)=2sinvostan2α+tant2=2×222+2−2=1.sin2α+sinvost2cos2α=2tan26.(2014江苏,15,14分)已知,π(1)求α的值;(2)求-2α.解析(1)因为2,π所以cosα=-1−sin2α=-故α=sinπ4cosα+cosπ4sinα×(2)由(1)知-=-45,cos2α=1-2sin2=35,所以-2α=cos5π6cos2α+sin5π6sin2α=×35+12×评析本题主要考查三角函数的基本关系式、两角和与差的正、余弦公式及二倍角公式,考查运算求解能力.。
(完整word)高中数学高考总复习简单的三角恒等变换习题及详解

高考总复习高 中 数 学 高 考 总 复习 简 单 的 三 角 恒 等 变 换 习 题 及 详 解一、选择题π π ,x ∈ R ,则函数 f(x) 是()1. (文 )(2010 山·师大附中模考 )设函数 f(x)= cos 2(x + )- sin 2(x + )44A .最小正周期为π的奇函数B .最小正周期为 π的偶函数πC .最小正周期为 2的奇函数πD .最小正周期为 2的偶函数 [答案]Aπ2π[分析]f(x)= cos(2x + 2)=- sin2x 为奇函数,周期T = 2 = π.( 理)(2010 辽·宁锦州 )函数 y = sin 2x + sinxcosx 的最小正周期T = ()π π A . 2π B . πC.2D.3[答案] B[分析]y = sin 2x + sinxcosx = 1- cos2x 12+ sin2x2 = 1+ 2π,∴最小正周期T = π.2 2 sin 2x - 4232. (2010 重·庆一中 )设向量 a = (cos α, 2 )的模为2 ,则 cos2α= ()111 3 A .-4 B .- 2C.2D. 2[答案] B[分析]∵ |a|2= cos 2α+22= cos 2α+ 1= 3,22 4∴ cos 2α=1,∴ cos2α= 2cos 2α- 1=- 1.42α3.已知 tan 2= 3,则 cos α= ()444 3A. 5 B .- 5C.15D .-5[答案]Bα αα α cos 2- sin 222 2含详解答案高考总复习1- tan 2α= 2=1- 9=- 4,应选 B. 1+ tan 2α1+9522C4.在△ABC 中,若 sinAsinB = cos 2 ,则△ABC 是 ()A .等边三角形B .等腰三角形C .直角三角形D .既非等腰又非直角的三角形 [答案]B[ 分析 ] ∵ sinAsinB = cos 2C,211∴ 2[cos(A - B)- cos(A + B)] = 2(1+ cosC), ∴ cos(A - B)-cos( π-C)= 1+ cosC ,∴ cos(A - B)=1,∵- π<A -B<π,∴ A - B = 0,∴△ ABC 为等腰三角形.π5. (2010 ·阳市诊疗绵 )函数 f(x)= 2sin(x - 2) +|cosx|的最小正周期为( )πA. 2B .πC . 2πD . 4π[答案]C[ 分析 ] f(x)=- 2cosx + |cosx|- cosx cosx ≥ 0=,画出图象可知周期为2π.- 3cosx cosx<016. (2010 揭·阳市模考 )若 sinx + cosx = 3, x ∈ (0, π),则 sinx - cosx 的值为 ()17171 17 A .± 3 B .- 3C.3D. 3[答案] D[分析]11 ,∴ sin2x =- 8π 由 sinx + cosx =两边平方得, 1+ 2sinxcosx = <0,∴ x ∈ , π,39 9 2∴ (sinx - cosx)2= 1- sin2x =17且 sinx>cosx ,9∴ sinx -cosx =17,应选 D.3高考总复习7. (文 )在锐角△ABC 中,设 x = sinA ·sinB , y = cosA ·cosB ,则 x , y 的大小关系是 ( )A . x ≤yB . x < yC . x ≥ yD . x >y[答案]Dπ[分析] ∵ π>A + B > ,∴ cos(A + B)<0,即 cosAcosB - sinAsinB < 0,∴ x > y ,故应选 D.2( 理)(2010 皖·南八校 )在△ABC 中,角 A 、B 、 C 的对边分别为 a 、b 、 c ,假如 cos(2B + C)+ 2sinAsinB<0,那么a 、b 、c 知足的关系是 ()A . 2ab>c 2B . a 2+ b 2<c 2C . 2bc>a 2D . b 2+ c 2<a 2[答案]B[ 分析 ] ∵ cos(2B +C)+ 2sinAsinB<0,且 A +B + C = π,∴ cos( π- A +B)+ 2sinA ·sinB<0,∴ cos( π- A)cosB - sin( π- A)sinB + 2sinAsinB<0,∴- cosAcosB + sinAsinB<0 ,即 cos(A + B)>0,π π∴ 0<A + B< ,∴ C> ,22a 2+b 2-c 2由余弦定理得,cosC =<0,2ab∴ a 2+ b 2- c 2<0,故应选 B.8. (2010 ·林省调研吉 )已知 a = (cosx ,sinx),b = (sinx ,cosx),记 f(x)=a ·b ,要获得函数 y = sin 4x - cos 4x 的图象,只要将函数 y = f( x)的图象 ()πA .向左平移 2个单位长度πB .向左平移 4个单位长度πC .向右平移 2个单位长度πD .向右平移 4个单位长度[答案] D[分析]y = sin 4x - cos 4 x =(sin 2x + cos 2x)(sin 2x - cos 2x)=- cos2x ,π π π π将 f( x)= a ·b = 2sinxcosx = sin2x ,向右平移 4 个单位得, sin2 x -4 = sin 2x -2 =- sin - 2x=- cos2x ,故2选 D.高考总复习π 29. (2010 浙·江金华十校模考 )已知向量 a = (cos2α, sin α), b = (1,2sin α- 1), α∈ 4, π,若 a ·b =5,π 则 tan α+4 的值为 ( )12 1 2 A.3 B.7C.7D.3[答案] C[分析]a ·b = cos2α+ 2sin 2α-sin α= 1- 2sin 2α+ 2sin 2α- sin α= 1- sin α=2,∴ sin α= 3,55π∵ <α<π,∴ cos α=- 4,∴ tan α=- 3,454π 1+ tan α 1 .∴ tan α+ ==41- tan α 75π 7π10. (2010 湖·北黄冈模拟 )若 2 ≤ α≤ 2 ,则 1+ sin α+ 1- sin α等于 ()α α A .- 2cos 2 B . 2cos 2α α C .- 2sin 2 D . 2sin 2[答案]C5π7π 5π α 7π[分析] ≤ α≤,∴4≤ ≤4.∵ 2 2 2∴ 1+ sin α+ 1- sin α=1+ 2sinα α 1- 2sin α α2 cos +cos222=α αα α2sin + cos2 +sin - cos2 222αα α α=- (sin + cos )- (sin - cos )2222α=- 2sin 2. 二、填空题π 311. (2010 广·东罗湖区调研 )若 sin 2+ θ= 5,则 cos2θ= ________.[答案] 7 - 25π 3,∴ cos θ= 3,[分析] ∵ sin + θ=25 5∴ cos2θ= 2cos2θ- 1=- 257.高考总复习tanx- tan3 x12. (2010 江·苏无锡市调研 )函数 y=的最大值与最小值的积是 ________.1+ 2tan2x+tan4x[答案]1-16[分析]y=tanx- tan3x tanx 1- tan2x2 4=2 21+ 2tan x+ tan x1+ tan x=tanx1- tan2x=sinxcosx cos2x- sin2x 2·22 2 +22 1+ tan x 1+ tan x cos x+ sin x cos x+ sin x 11=2sin2x·cos2x=4sin4x,1所以最大与最小值的积为-16.13. (2010 ·江杭州质检浙)函数 y= sin(x+ 10°)+ cos(x+ 40°),( x∈R )的最大值是 ________.[答案]1[ 分析 ]y= sinxcos10 °+ cosxsin10 +°cosxcos40 °- sinxsin40 =°(cos10 -°sin40 )sinx°+ (sin10 +°cos40 °)cosx,其最大值为=2+ 2 sin10 °cos40°- cos10°sin40 °=2+ 2sin - 30°= 1.θ14.(文 )如图, AB 是半圆 O 的直径,点 C 在半圆上, CD⊥ AB 于点 D ,且 AD= 3DB ,设∠COD =θ,则 tan22=________.[答案]1 3[分析]3r,∴ OD=r,∴ CD =3CD =3,设 OC= r,∵ AD = 3DB,且 AD+ DB=2r,∴ AD =222 r ,∴ tanθ=OD θ∵ tanθ=2tan2θ3,∴ tan =1- tan2θ23 (负值舍去 ),2θ1∴tan22=3.( 理)3tan12 -°3= ________. 4cos212°- 2 sin12 °[答案]- 43[分析]3tan12 -°3= 3 sin12 -°3cos12 °4cos212°-2 sin12° 2cos24 sin12°cos12° °2 3sin 12°- 60°3.=1=- 4三、解答题15. (文 )(2010 北·京理 )已知函数f(x)=2cos2x + sin 2x - 4cosx.π(1) 求 f(3)的值;(2) 求 f(x)的最大值和最小值.[分析]π 2π π π 3 9 (1) f( )= 2cos+ sin 2- 4cos =- 1+-2=- .333344(2) f(x)=2(2cos 2 x - 1)+(1 -cos 2x)- 4cosx= 3cos 2x - 4cosx - 1= 3(cosx -23)2-73, x ∈ R由于 cosx ∈ [ - 1,1] ,所以当 cosx =- 1 时, f(x)取最大值 6;当 cosx =2时, f(x)取最小值-733.( 理)(2010 广·东罗湖区调研 )已知 a =(cosx +sinx , sinx), b = (cosx - sinx,2cosx),设 f(x)= a ·b. (1) 求函数 f(x)的最小正周期;(2) 当 x ∈ 0,π时,求函数 f(x)的最大值及最小值.2[ 分析 ] (1) f(x)= a ·b = (cosx + sinx) ·(cosx - sinx)+ sinx ·2cosx = cos 2x -sin 2x + 2sinxcosx= cos2x + sin2x = 2222 cos2x + 2 sin2xπ = 2sin 2x +4 .∴ f(x)的最小正周期T = π.πππ 5π(2) ∵ 0≤ x ≤ ,∴ ≤ 2x + ≤ 4,2 4 4π π ππ 5π π∴当 2x +4= 2,即 x =8时, f(x)有最大值2;当 2x + 4= 4 ,即 x =2 时, f(x)有最小值- 1.π 16. (文 )设函数 f(x)= cos 2x + 3 + sin 2x.(1) 求函数 f(x)的最大值和最小正周期;1C1(2) 设 A 、 B 、 C 为△ABC 的三个内角,若 cosB =3, f(2 )=- 4,且 C 为锐角,求 sinA 的值.[分析] (1) f(x)= cos 2x + π π π 1- cos2x 1 - 3+ sin 2x = cos2xcos - sin2xsin + = 2sin2x ,3 3 3 2 2 所以函数 f(x)的最大值为1+ 3,最小正周期为π.2(2) f(C )=1- 3sinC =-1,所以 sinC =3π由于 C 为锐角,所以C = 3,在△ ABC 中, cosB =13,所以 sinB =2 3 2,所以 sinA = sin(B + C)= sinBcosC + cosBsinC=2 2 1 1 ×3 = 22+ 33 × + 26.2 3→ → → →( 理)已知角 A 、B 、 C 为△ABC 的三个内角, OM = (sinB + cosB , cosC), ON = (sinC , sinB - cosB), OM ·ON =1- 5.(1) 求 tan2A 的值;2A(2) 2cos 2- 3sinA - 1的值.求π2sin A +4[分析]→ →(1) ∵OM ·ON = (sinB + cosB)sinC +1cosC(sinB - cosB)= sin(B + C)- cos(B + C) =- 5,∴ sinA + cosA =- 1①5两边平方并整理得: 2sinAcosA =- 24,25∵-24π, π ,25<0,∴ A ∈ 2∴ sinA - cosA = 1-2sinAcosA = 75②联立①②得: sinA = 3,cosA =- 4,∴ tanA =- 3, 5 5 4- 3∴ tan2A =2tanA2=224 .A=- 1-tan 1- 9 7163(2) ∵ tanA =- 4,A2cos 22 - 3sinA - 1 cosA -3sinA 1- 3tanA ∴ π= cosA +sinA =1+ tanA 2sin A +43=1-3× -4 =13.-341+π点之间的距离为2.(1) 求 m 和 a 的值;π(2) 若点 A(x 0, y 0) 是 y = f( x)图象的对称中心,且 x 0∈ 0, 2 ,求点 A 的坐标.[ 分析 ] (1) f(x)= sin 2ax - 3sinaxcosax1- cos2ax3π 1= 2 - 2 sin2ax =- sin 2ax + 6 + 2,由题意知, m 为 f(x)的最大值或最小值,所以 m =- 12或 m =32,π 由题设知,函数f(x)的周期为,∴ a = 2,2所以 m =- 1或 m =3, a = 2. 2 2(2) ∵ f(x)=- sin 4x + π+1,6 2ππ∴令 sin 4x + 6 =0,得 4x +6= k π(k ∈ Z) ,∴ x = k π π-424(k ∈ Z),由 0≤ k π π π(k ∈ Z),得 k = 1 或 k = 2, 4 -24≤2所以点 A 的坐标为5π 1 或 11π1, ,24 224 2 .( 理)(2010 广·东佛山顺德区检测)设向量 a = (sinx,1), b = (1, cosx),记 f(x)= a ·b , f ′ (x)是 f( x)的导函数.(1) 求函数 F(x)= f(x)f ′ (x)+ f 2(x)的最大值和最小正周期;(2) 若 f(x)= 2f ′ (x),求1+ 2sin 2x的值.cos 2x - sinxcosx[ 分析 ] (1) f(x)= sinx +cosx ,∴ f ′( x)= cosx -sinx ,∴ F(x)= f(x)f ′ (x)+ f 2(x) = cos 2x -sin 2x + 1+2sinxcosx= cos2x + sin2x + 1= 1+ 2sin π2x +4 ,π π π∴当 2x + = 2k π+ ,即 x = k π+ (k ∈ Z)时, F( x)max =1 + 2.42 8最小正周期为 T =2π= π.2(2) ∵ f(x)= 2f ′ (x),∴ sinx+ cosx= 2cosx- 2sinx,∴cosx= 3sinx,∴ tanx=1,3∴1+ 2sin2x= 3sin2x+ cos2x= 3tan2x+ 1=2.cos2x-sinxcosx cos2x-sinxcosx1- tanx。
高三数学三角函数三角恒等变换解三角形试题答案及解析

高三数学三角函数三角恒等变换解三角形试题答案及解析1.已知函数的图象上关于轴对称的点至少有3对,则实数的取值范围是()A.B.C.D.【答案】A【解析】原函数在轴左侧是一段正弦型函数图象,在轴右侧是一条对数函数的图象,要使得图象上关于轴对称的点至少有对,可将左侧的图象对称到轴右侧,即,应该与原来轴右侧的图象至少有个公共点如图,不能满足条件,只有此时,只需在时,的纵坐标大于,即,得.【考点】分段函数,函数图象,正弦型函数,对数函数2.若,则函数的最大值是___________.【答案】【解析】由题意因为,所以,所以函数的最大值是.【考点】求最大值.3.已知,,则下列不等式一定成立的是A.B.C.D.【答案】D【解析】,【考点】三角函数的性质4.若,且为第二象限角,则()A.B.C.D.【答案】B【解析】由得又为第二象限角,所以,选B.【考点】两角差余弦公式5.设函数对任意的,都有,若函数,则的值是()A.1B.-5或3C.-2D.【答案】C【解析】根据题意有是函数图像的对称轴,从而有,所以有,故选C.【考点】三角函数的性质.6.设的最小值为,则.【答案】【解析】,根据题意,结合二次函数在某个区间上的最值问题,对参数进行讨论,当时,其最小值为,所以不合题意,当时,其最小值为,解得,当时,其最小值为,无解,所以.【考点】倍角公式,二次函数在给定区间上的最值问题.7.设函数对任意的,都有,若函数,则的值是()A.1B.-5或3C.D.-2【答案】D【解析】根据题意有是函数图像的对称轴,从而有,所以有,故选D.【考点】三角函数的性质.8.下列函数中,以为最小正周期的偶函数是()A.y=sin2x+cos2xB.y=sin2xcos2xC.y=cos(4x+)D.y=sin22x﹣cos22x【答案】D【解析】因为A项为非奇非偶函数,B项是奇函数,C项是奇函数,只有D项是符合题意的,故选D.【考点】诱导公式,倍角公式,三角函数的奇偶性和周期.9.函数的最大值为.【答案】【解析】解析式表示过的直线的斜率,由几何意义,即过定点(4,3)与单位圆相切时的切线斜率为最值.所以设切线得斜率为k,则直线方程为,即 ,【考点】三角函数最值【方法点睛】本题主要考查三角函数最值问题及转化的思想,解决问题的根据是根据所给函数式子转化为直线与圆的位置关系问题,即将所给式子看做定点与单位圆上点的连线的斜率的范围问题,通过模型转化使问题定点巧妙解决,属于经典试题.10.(本题满分12分)如图,在中,边上的中线长为3,且,.(1)求的值;(2)求边的长.【答案】(1)(2)4【解析】(1)利用角的关系,再结合两角差正弦公式展开就可求解(2)先在三角形ABD中,由正弦定理解出BD长,即CD长:由正弦定理,得,即,解得…故;再在三角形ADC中由余弦定理解出AC:;AC= 4试题解析:(1)(2)在中,由正弦定理,得,即,解得…故,从而在中,由余弦定理,得;AC= 4 ;【考点】正余弦定理11.中,,则的最大值为.【答案】【解析】设,由余弦定理的推论,所以,设,代入上式得,,故,当时,此时,符合题意,因此最大值为,故答案为:.【考点】解三角形.【思路点睛】首先假设,然后再根据余弦定理的推论,可得,找到与的关系,再设,代入上式得,利用根的判别式,进而求出结果.本题的关键是利用余弦定理的推论.12.已知函数的部分图象如图所示.(1)求函数的解析式;(2)若,求函数在区间上的单调减区间.【答案】(1);(2),.【解析】(1)由图象中的最高点和最低点的纵坐标得到关于的方程组求得,再利用图象得到函数的周期,进而得到值,最后代入最低点坐标或最高点坐标结合的范围求出,即得到函数的解析式;(2)先求出,利用两角和差的正弦公式将其化为的形式,再利用整体思想求其单调递减区间.试题解析:(1)由图知,解得,又,所以,所以,将点代入,得,再由,得,所以;(2)因为由,解得;又,故所求的单调减区间为,.【考点】1.三角函数的图象与性质;2.三角恒等变形.13.已知角的终边经过点(-4,3),则= ,= ;【答案】;【解析】由题意可得.【考点】任意角三角函数的定义.14.在△ABC中,a、b、c分别是角A、B、C的对边,且.(Ⅰ)求角B的大小;(Ⅱ)若,求△ABC的面积.【答案】(Ⅰ);(Ⅱ).【解析】(Ⅰ)在解三角形的背景下,考查正弦定理,余弦定理,知值求值.(Ⅱ)综合余弦定理,求三角形的面积公式,需要把作为整体求之.试题解析:(Ⅰ)由正弦定理得将上式代入已知即,即.∵∵∵B为三角形的内角,∴.(Ⅱ)由余弦定理得,结合,可得,所以△ABC的面积.【考点】正弦定理,余弦定理,三角形的面积公式.15.在△中,角,,所对的边分别为,,,表示△的面积,若,,则.【答案】【解析】∵,∴,∴,∴,.∵,∴,∴,∴,∴.【考点】解三角形.【思路点睛】先利用余弦定理和三角形的面积公式可得,可得,再用正弦定理把中的边换成角的正弦,利用两角和公式化简整理可求得,最后根据三角形内角和,进而求得.16.中,角A,B,C的对边分别为a,b,c,若的面积,则 .【答案】【解析】由余弦定理,,又,,,即,,.【考点】1、余弦定理;2、同角三角函数的基本关系;3、三角形面积公式.【思路点睛】本题主要考查的是余弦定理、同角三角函数基本关系、三角形的面积公式,属于容易题.因为题目求,且的面积,边的平方的形式一般想到余弦定理,面积展开后利用余弦定理即可求得与的关系,从而利用同角三角函数的基本关系求得.17.(2012•安徽)设△ABC的内角A、B、C所对边的长分别为a、b、c,且有2sinBcosA=sinAcosC+cosAsinC.(Ⅰ)求角A的大小;(Ⅱ)若b=2,c=1,D为BC的中点,求AD的长.【答案】(Ⅰ);(Ⅱ)【解析】(Ⅰ)根据2sinBcosA=sinAcosC+cosAsinC,可得2sinBcosA=sin(A+C),从而可得2sinBcosA=sinB,由此可求求角A的大小;(Ⅱ)利用b=2,c=1,A=,可求a的值,进而可求B=,利用D为BC的中点,可求AD的长.解:(Ⅰ)∵2sinBcosA=sinAcosC+cosAsinC∴2sinBcosA=sin(A+C)∵A+C=π﹣B∴sin(A+C)=sinB>0∴2sinBcosA=sinB∴cosA=∵A∈(0,π)∴A=;(Ⅱ)∵b=2,c=1,A=∴a2=b2+c2﹣2bccosA=3∴b2=a2+c2∴B=∵D为BC的中点,∴AD=.【考点】余弦定理;三角函数的恒等变换及化简求值.18.在中,已知.(Ⅰ)求sinA与角B的值;(Ⅱ)若角A,B,C的对边分别为的值.【答案】(Ⅰ);(Ⅱ),.【解析】(I)给出了关于角的两个三角函数值,利用诱导公式和同角三角函数的基本关系式可求得其正弦、余弦,再根据三角形的性质可求得的值;(II)在第一问的基础上,利用正弦定理可求得边,再由余弦定理求边,注意利用三角形基本性质舍解.试题解析:(Ⅰ)∵,,又∵,.∵,且,.(Ⅱ)由正弦定理得,,另由得,解得或(舍去),,.【考点】三角函数的诱导公式,同角三角函数的基本关系式及利用正、余弦定理在解三角形.19.已知,则的值为.【答案】.【解析】,故填:.【考点】三角恒等变形.20.在中,角A,B,C的对边分别为,,,若,则角的值为()A.或B.或C.D.【答案】A.【解析】,,∴或,故选A.【考点】余弦定理.【思路点睛】由已知条件,可先将切化弦,再结合正弦定理,将该恒等式的边都化为角,然后进行三角函数式的恒等变形,找出角之间的关系;或将角都化成边,然后进行代数恒等变形,可一题多解,多角度思考问题,从而达到对知识的熟练掌握.21.为了得到函数的图象,只需把函数图象上的所有点()A.横坐标缩短到原来的倍,纵坐标不变B.横坐标伸长到原来的2倍,纵坐标不变C.纵坐标缩短到原来的倍,横坐标不变D.纵坐标缩短到原来的2倍,横坐标不变【答案】A【解析】这是一个三角函数的图象变换问题,一般的为了得到函数的图象,只需把函数的图象上所有点的横坐标伸长()或缩短()到原来的倍(纵坐标不变)即可,因此为了得到函数的图象,只需把函数图象上的所有点横坐标缩短到原来的倍,纵坐标不变,故选A.【考点】三角函数的图象变换.【方法点睛】本题是一个三角函数的图象变换问题,属于容易题.一般的要得到函数(其中)的图像可按以下步骤进行:先把的图象向左()或向右()平移个单位,再将所得函数的图象上各点的横坐标扩大()或缩小()为原来的(纵坐标不变),再把所得函数图象上各点的纵坐标扩大()或缩小()为原来的倍(横坐标不变),最后再将所得图像向上()或向下()平移个单位,即可得到函数的图象.22.如图,在中,,,点在边上,且,.(I)求;(II)求的长.【答案】(Ⅰ);(Ⅱ),.【解析】(Ⅰ)由图可知,所以,又,所以,再由两角差的正弦公式可求得;(Ⅱ)由题意可用正弦定理、余弦定理即可求出、的长,在中,有,又从而可求得;在中,由余弦定理得,,从而可求出.试题解析:(Ⅰ)在中,因为,所以,所以(Ⅱ)在中,由正弦定理得,在中,由余弦定理得,所以【考点】1.解三角形;2.两角差的正弦公式.23.设的内角对边分别为,已知,且.(1)求角的大小;(2)若向量与共线,求的值.【答案】(1);(2)。
三角恒等变换专题复习带答案

三角恒等变换专题复习教学目标:1、能利用单位圆中的三角函数线推导出 απαπ±±,2的正弦、余弦、正切的诱导公式;2、理解同角三角函数的基本关系式:;3、可熟练运用三角函数见的基本关系式解决各种问题; 教学重难点:可熟练运用三角函数见的基本关系式解决各种问题 基础知识一、同角的三大关系:① 倒数关系 tan α•cot α=1 ② 商数关系 sin cos αα= tan α ; cos sin αα= cot α ③ 平方关系 22sin cos 1αα+=温馨提示:1求同角三角函数有知一求三规律,可以利用公式求解,最好的方法是利用画直角三角形速解;来源:学+科+网2利用上述公式求三角函数值时,注意开方时要结合角的范围正确取舍“±”号;二、诱导公式口诀:奇变偶不变,符号看象限用诱导公式化简,一般先把角化成,2k z α+∈的形式,然后利用诱导公式的口诀化简如果前面的角是90度的奇数倍,就是 “奇”,是90度的偶数倍,就是“偶”;符号看象限是,把α看作是锐角,判断角2k πα+在第几象限,在这个象限的前面三角函数的符号是 “+”还是“--”,就加在前面;用诱导公式计算时,一般是先将负角变成正角,再将正角变成区间0(0,360)的角,再变到区间00(0,180)的角,再变到区间00(0,90)的角计算;三、和角与差角公式 :sin()sin cos cos sin αβαβαβ±=±; cos()cos cos sin sin αβαβαβ±=;tan tan tan()1tan tan αβαβαβ±±=变 用 tan α±tan β=tan α±β1 tan αtan β四、二倍角公式:sin 2α= 2sin cos αα.2222cos 2cos sin 2cos 112sin ααααα=-=-=-.22tan tan 21tan ααα=-五、注意这些公式的来弄去脉这些公式都可以由公式cos()cos cos sin sin αβαβαβ±=推导出来;六、注意公式的顺用、逆用、变用;如:逆用sin cos cos sin sin()αβαβαβ±=± 1sin cos sin 22ααα=变用22cos 1cos 2αα+=22cos 1sin 2αα-= 21cos 4cos 22αα+= 七、合一变形辅助角公式把两个三角函数的和或差化为“一个三角函数,一个角,一次方”的 B x A y ++=)sin(ϕϖ形式;()22sin cos αααϕA +B =A +B +,其中tan ϕB=A. 八、万能公式ααα2tan 1tan 22sin += ααα22tan 1tan 12cos +-= ααα2tan 1tan 22tan -=九、用αsin ,αcos 表示2tanααααααsin cos 1cos 1sin 2tan-=+=十、积化和差与和差化积积化和差 )]sin()[sin(cos sin βαβαβα-++=; )]sin()[sin(sin cos βαβαβα--+=;)]cos()[cos(cos cos βαβαβα-++=; )]cos()[cos(sin sin βαβαβα--+=.和差化积 2cos2sin2sin sin ϕθϕθϕθ-+=+2sin 2cos 2sin sin ϕθϕθϕθ-+=- 2cos 2cos 2cos cos ϕθϕθϕθ-+=+ 2sin 2sin 2cos cos ϕθϕθϕθ-+=-十一、方法总结1、三角恒等变换方法观察角、名、式→三变变角、变名、变式1 “变角”主要指把未知的角向已知的角转化,是变换的主线,如α=α+β-β=α-β+β, 2α=α+β+ α-β, 2α=β+α-β-α,α+β=2·错误! , 错误! = α-错误!-错误!-β等.2“变名”指的是切化弦正切余切化成正弦余弦sin cos tan ,cot cos sin αααααα==, 3“变式’指的是利用升幂公式和降幂公式升幂降幂,利用和角和差角公式、合一变形公式展开和合并等; 2、恒等式的证明方法灵活多样①从一边开始直接推证,得到另一边,一般地,如果所证等式一边比较繁而另一边比较简时多采用此法,即由繁到简.②左右归一法,即将所证恒等式左、右两边同时推导变形,直接推得左右两边都等于同一个式子. ③比较法, 即设法证明: "左边-右边=0" 或" 错误! =1";④分析法,从被证的等式出发,逐步探求使等式成立的充分条件,一直推到已知条件或显然成立的结论成立为止,则可以判断原等式成立.例题精讲例1 已知α为第四象限角,化简:ααααααcos 1cos 1sin sin 1sin 1cos +-++-解:1因为α为第四象限角所以原式=αααααα2222cos 1)cos 1(sin sin 1)sin 1(cos --+-- ()ααααααααααsin cos cos 1sin 1sin cos 1sin cos sin 1cos -=---=--+-=例2 已知360270<<α,化简α2cos 21212121++ 解:360270<<α,02cos,0cos <>∴αα所以原式2111cos211cos 22222αα++=+21cos cos cos 222ααα+===- 例3 tan20°+4sin20°解:tan20°+4sin20°=0020cos 40sin 220sin +=0sin(6040)2sin 40cos 20-+00003340sin 403cos 20223cos 20+=== 例4 05天津已知727sin()2425παα-==,求sin α及tan()3πα+.解:解法一:由题设条件,应用两角差的正弦公式得)cos (sin 22)4sin(1027ααπα-=-=,即57cos sin =-αα ①由题设条件,应用二倍角余弦公式得)sin (cos 57)sin )(cos sin (cos sin cos 2cos 25722ααααααααα+-=+-=-== 故51sin cos -=+αα ② 由①和②式得53sin =α,54cos -=α因此,43tan -=α,由两角和的正切公式11325483343344331433tan 313tan )3tan(-=+-=+-=-+=+ααπα 解法二:由题设条件,应用二倍角余弦公式得αα2sin 212cos 257-==, 解得 259sin 2=α,即53sin ±=α 由1027)4sin(=-πα可得57cos sin =-αα由于0cos 57sin >+=αα,且057sin cos <-=αα,故α在第二象限于是53sin =α,从而5457sin cos -=-=αα 以下同解法一小结:1、本题以三角函数的求值问题考查三角变换能力和运算能力,可从已知角和所求角的内在联系均含α进行转换得到.2、在求三角函数值时,必须灵活应用公式,注意隐含条件的使用,以防出现多解或漏解的情形. 例 5 已知,,A B C 为锐角ABC ∆的三个内角,两向量(22sin ,cos sin )p A A A =-+,(sin cos ,q A A =-1sin )A +,若p 与q 是共线向量.1求A 的大小;2求函数232sin cos()2C By B -=+取最大值时,B 的大小. 解:122// 2(1)(1+)- p q sinA sinA sin A cos A ∴-=22220 120cos A cos A cos A ∴+=∴+= 1cos 2A 2∴=-0<2A<π,002A 120 A=60∴=∴200A=60 B+C=120∴ 2013y=2sin B+cos(602B)1cos 2B+cos 2B sin 2B 22-=-+31 =sin 2B cos 2B+1=sin(2B )1226π--+ , 2B B 623πππ-=当时,即=. 小结:三角函数与向量之间的联系很紧密,解题时要时刻注意例6 设关于x 的方程sinx +3cosx +a =0在0, 2π内有相异二解α、β.1求α的取值范围; 2求tan α+β的值. 解: 1∵sinx +3cosx =221sinx +23cosx =2 sinx +3π, ∴方程化为sinx +3π=-2a.∵方程sinx +3cosx +a =0在0, 2π内有相异二解, ∴sinx +3π≠sin 3π=23 .又sinx +3π≠±1 ∵当等于23和±1时仅有一解, ∴|-2a |<1 . 且-2a≠23. 即|a |<2且a ≠-3.∴ a 的取值范围是-2, -3∪-3, 2.2 ∵α、 β是方程的相异解, ∴sin α+3cos α+a =0 ①. sin β+3cos β+a =0 ②. ①-②得sin α- sin β+3 cos α- cos β=0. ∴ 2sin2βα-cos2βα+-23sin2βα+sin2βα-=0, 又sin2βα+≠0, ∴tan2βα+=33.∴tan α+β=2tan22tan22βαβα+-+=3.小结:要注意三角函数实根个数与普通方程的区别,这里不能忘记0, 2π这一条件. 例7 已知函数()x x m x f cos sin 2-=在区间⎪⎭⎫⎝⎛2,0π上单调递减,试求实数m 的取值范围.解:已知条件实际上给出了一个在区间⎪⎭⎫⎝⎛2,0π上恒成立的不等式. 任取∈21,x x ⎪⎭⎫⎝⎛2,0π,且21x x <,则不等式()()21x f x f >恒成立,即>-11cos sin 2x x m 22cos sin 2x x m -恒成立.化简得()()2112sin 2cos cos x x x x m ->- 由2021π<<<x x 可知:0cos cos 12<-x x ,所以()1221cos cos sin 2x x x x m --<上式恒成立的条件为:()上的最小值,在区间⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛--<20cos cos sin 21221πx x x x m . 由于()2sin 2cos 22sin 2sin 22cos 2sin4cos cos sin 22121212121211221x x x x x x x x x x x x x x x x +-=-+--=-- 2sin2cos 2cos 2sin 2sin 2sin 2cos 2cos 221212121x x x x x x x x +⎪⎭⎫ ⎝⎛+=2tan2tan 2tan 2tan 122121x x x x +⎪⎭⎫ ⎝⎛+=且当2021π<<<x x 时,42,2021π<<x x ,所以 12tan ,2tan 021<<x x , 从而 02tan 12tan 12tan 2tan 2tan 2tan1212121>⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+x x x x x x , 有 22tan2tan 2tan 2tan 122121>+⎪⎭⎫ ⎝⎛+x x x x , 故 m 的取值范围为]2,(-∞.基础精练1.已知α是锐角,且sin 错误!=错误!,则sin 错误!的值等于A.错误! B .-错误! C.错误! D .-错误!2.若-2π<α<-错误!,则 错误!的值是A .sin 错误!B .cos 错误!C .-sin 错误!D .-cos 错误!3.错误!·错误!等于A.-sinαB.-cosαC.sinαD.cosα4.已知角α在第一象限且cosα=错误!,则错误!等于A.错误!B.错误!C.错误!D.-错误!5.定义运算错误!=ad -bc.若cosα=错误!,错误!=错误!,0<β<α<错误!,则β等于A.错误!B.错误!C.错误!D.错误!6.已知tanα和tan 错误!-α是方程ax 2+bx +c =0的两个根,则a 、b 、c 的关系是A.b =a +cB.2b =a +cC.c =b +aD.c =ab7.设a =错误!sin56°-cos56°,b =cos50°cos128°+cos40°cos38°,c =错误!,d =错误!cos80°-2cos 250°+1,则a,b,c,d 的大小关系为A.a >b >d >cB.b >a >d >cC.d >a >b >cD.c >a >d >b8.函数y =错误!sin2x +sin 2x,x ∈R 的值域是A.错误!B.错误!C.错误!D.错误!9.若锐角α、β满足1+错误!tanα1+错误!tanβ=4,则α+β= .10.设α是第二象限的角,tanα=-错误!,且sin 错误!<cos 错误!,则cos 错误!= .11.已知sin-4πx=135,0<x<4π,求)4cos(2cos x x +π的值;12.若),0(,πβα∈,31tan ,507cos -=-=βα,求α+2β;拓展提高1、设函数fx =sin 错误!-错误!-2cos 2错误!+11求fx 的最小正周期.2若函数y =gx 与y =fx 的图像关于直线x =1对称,求当x ∈0,错误!时y =gx 的最大值2.已知向量a =cosα,sinα,b =cosβ,sinβ,|a -b|=错误!1求cosα-β的值;2若0<α<错误!,-错误!<β<0,且sinβ=-错误!,求sinα.3、求证:αβαsin 2sin )(+-2cos α+β=αβsin sin .基础精练参考答案4.C 解析原式=错误!=错误!=错误!=2×cosα+sinα=2×错误!+错误!=错误!. 5.D 解析依题设得:sinα·cosβ-cosα·sinβ=sin α-β=错误!.∵0<β<α<错误!,∴cosα-β=错误!. 又∵cosα=错误!,∴sinα=错误!.sinβ=sinα-α-β=sinα·cosα-β-cosα·sinα-β =错误!×错误!-错误!×错误!=错误!,∴β=错误!.6.C 解析tan tan()4,tan tan(),4b a c a πααπαα⎧+-=-⎪⎪⎨⎪-=⎪⎩∴tan 错误!=tan 错误!-α+α=错误!=1,∴-错误!=1-错误!,∴-b =a -c,∴c =a +b.7.B 解析a =sin56°-45°=sin11°,b =-sin40°cos52°+cos40°sin52°=sin52°-40°=sin12°,c =错误!=cos81°=sin9°,d =错误!2cos 240°-2sin 240°=cos80°=sin10°∴b >a >d >c.8.C 解析y =错误!sin2x +sin 2x =错误!sin2x -错误!cos2x +错误!=错误!sin 错误!+错误!,故选择C. 9. 错误!解析由1+错误!tanα1+错误!tanβ=4,可得错误!=错误!,即tanα+β=错误!. 又α+β∈0,π,∴α+β=错误!.10. -错误!解析:∵α是第二象限的角,∴错误!可能在第一或第三象限,又sin 错误!<cos 错误!,∴错误!为第三象限的角, ∴cos 错误!<0.∵tanα=-错误!,∴cosα=-错误!,∴cos 错误!=- 错误!=-错误!.12.解析∵),0(,πβα∈,507cos -=α∴),0,33(71tan -∈-=α),0,33(31tan -∈-=β∴),65(,ππβα∈,α+2β)3,25(ππ∈,又tan2β=43tan 1tan 22-=-ββ,12tan tan 12tan tan )2tan(-=-+=+βαβαβα,来源:Zxxk ∴α+2β=411π拓展提高参考答案1、解析 1fx =sin 错误!cos 错误!-cos 错误!sin 错误!-cos 错误!x =错误!sin 错误!x -错误!cos 错误!x=错误!sin 错误!x -错误!,故fx 的最小正周期为T =错误!=82法一:在y =g x 的图象上任取一点 x,gx,它关于x =1的对称点2-x,gx.由题设条件,点2-x ,gx 在y =fx 的图象上,从而gx =f2-x =错误!sin 错误!2-x -错误! =错误!sin 错误!-错误!x -错误!=错误!cos 错误!x +错误!,当0≤x≤错误!时, 错误!≤错误!x +错误!≤错误!,因此y =gx 在区间0,错误!上的最大值为gx max =错误!cos 错误!=错误!.法二:因区间0,错误!关于x =1的对称区间为错误!,2,且y =gx 与y =fx 的图象关于x =1对称,故y =gx 在0,错误!上的最大值为y =fx 在错误!,2上的最大值,由1知fx =错误!sin 错误!x -错误!, 当错误!≤x ≤2时,-错误!≤错误!x -错误!≤错误!,因此y =gx 在0,错误!上的最大值为gx max =错误!sin 错误!=错误!.2、解析1∵a =cos α,sinα,b =cosβ,sinβ, ∴a -b =cosα-cosβ,sinα-sinβ. ∵|a -b|=错误!,∴错误!=错误!, 即2-2cosα-β=错误!,∴cosα-β=错误!.2∵0<α<错误!,-错误!<β<0,∴0<α-β<π,∵cosα-β=错误!,∴sinα-β=错误! ∵sin β=-错误!,∴cosβ=错误!,∴sinα=sinα-β+β=sinα-βcosβ+cosα-βsinβ=错误!·错误!+错误!·-错误!=错误!。
高三数学三角函数三角恒等变换解三角形试题答案及解析

高三数学三角函数三角恒等变换解三角形试题答案及解析1.已知函数。
(Ⅰ)求的最小正周期;(Ⅱ)把的图像向右平移个单位后,在是增函数,当最小时,求的值【答案】(I)…………………4分∴…………………6分(II) …………………8分单调递增区间为周期为,则,,…………………10分当最小时,。
【解析】略2.若函数的图像向右平移个单位后所的图像关于轴对称,则的值可以是()A.7B.8C.9D.10【答案】B【解析】化简后得,向右平移个单位后得到的函数是,关于轴对称,所以当时,函数取得最值,所以,那么,所以时,.【考点】1.三角函数的化简;2.三角函数的性质;3三角函数的图像变换.3.已知函数的图象与y轴交于P,与x轴的相邻两个交点记为A,B,若△PAB的面积等于π,则ω=________.【答案】【解析】由题意得:,因此【考点】三角函数性质4.把函数图象上各点向右平移个单位,得到函数的图象,则的最小值为.【答案】【解析】,平移后的解析式为,所以,故有的最小值为.【考点】函数图像的平移,倍角公式,辅助角公式.5.已知,,且,,则的值是()A.B.C.D.【答案】C【解析】根据,可知,所以,结合,从而求得,根据和角公式,可知,所以有,从而有,从而得到只有符合题意,故选C.【考点】已知函数值求角.6.若函数f(x)=sin(φ∈[0,2π])是偶函数,则φ=()A.B.C.D.【答案】C【解析】函数f(x)是偶函数,所以f(0)=1或-1,所以.又因φ∈[0,2π],所以,k=0时,.故选C.【考点】由函数的奇偶性求参数值.7.若,,则的值为.【解析】把已知条件的等式两边都乘以,得到关于的方程,求出方程的解,根据的范围即可得到满足题意的值,然后把所求的式子利用两角和的正弦函数公式及特殊角的三角函数值化简后,再利用同角三角函数间的基本关系把分母中“1”化为正弦与余弦函数的平方和的形式,分子利用二倍角的正弦、余弦函数公式化简,然后给分子分母都除以,变为关于的关系式,把求出的的值,然后根据条件计算即可.或,,.【考点】两角和的正弦函数公式;同角三角函数间的基本关系化简求值;二倍角8.(本题满分12分)已知,,函数.(1)求的最小正周期,并求其图像对称中心的坐标;(2)当时,求函数的值域.【答案】(1)的最小正周期为,其对称中心的坐标为()();(2)的值域为.【解析】(1)先用降幂公式和辅助角公式,将进行化简整理得到,然后根据正弦函数的周期公式可得函数的最小正周期,进而求出函数的零点,即为函数的图像对称中心的坐标;(2)根据可得到,最后结合正弦函数的图像与性质可得函数的值域.试题解析:(1)因为=,所以的最小正周期为,令,得,∴故所求对称中心的坐标为()().(2)∵,∴,∴,即的值域为.【考点】1、三角函数中的恒等变换;2、三角函数的周期性及其求法;3、正弦函数的图像及其性质.【方法点晴】本题考查了三角函数中的恒等变换、三角函数的周期性及其求法和正弦函数的图像及其性质,重点考查学生对三角函数的基本概念、基本性质和基本原理,属中档题.解决这类问题最关键的一步是运用降幂公式、倍角公式及三角函数的和差公式等将函数的表达式化简为同角的正弦或余弦形式.因此需要大家应熟练掌握相关公式并结合三角函数的图像及其性质进行求解.9.在△ABC中,内角的对边分别为,已知,且,角为锐角.(1)求角的大小;(2)若,且△ABC的面积为,求的值.【答案】(1);(2).【解析】(1)首先运用正弦定理即可将已知等式转化为只函数角的正弦和余弦的形式,然后运用两角和或差的正弦和余弦公式即可得到,再结合三角形的内角和为即可得出,最后结合已知即可得出角的大小;(2)由(1)并结合三角形的面积公式可得出的值,再由余弦定理的计算公式即可得出的值.试题解析:(1)由正弦定理得,即,即有,即, 又,所以,因为角为锐角,所以.(2)由(1)得,所以,所以,又,由余弦定理可得:,所以.【考点】1、正弦定理的应用;2、余弦定理的应用.【方法点睛】本题以三角形为背景,主要考查三角恒等变形、正弦定理和余弦定理在解三角形中的应用,属中档题.对于第一问的解题的关键是能够熟练运用正弦定理将已知的边角等式关系转化为角角关系或边边关系;对于第二问的解题的关键是应注意三角形的面积公式的正确使用.10.已知,则=_______________.【答案】【解析】由余弦函数的周期性知函数的周期为4,且,所以…=.【考点】周期函数.11.对于函数,现有下列命题:①函数是奇函数;②函数的最小正周期是;③点是函数的图象的一个对称中心;④函数在区间上单调递增,其中是真命题的为()A.②④B.①④C.②③D.①③【答案】B【解析】因为,所以函数是奇函数,故①正确;因为,,,故②错;因为,,,故③错;因为,当时,,,所以,所以函数在区间上单调递增,故④正确,故选B.【考点】1、命题真假的判定;2、函数的奇偶性;3、利用导数研究函数的单调性;4、函数的图象与性质.12.将函数的图象沿轴向左平移个单位后,得到一个偶函数的图象,则的一个可能取值为()A.B.C.D.【答案】B【解析】将函数的图象沿轴向左平移个单位得,又是一个偶函数,所以,根据选项可知的一个可能取值为,故选B.【考点】三角函数的图像.13.已知函数f(x)=sin+sin-2cos2x.(1)求函数f(x)的值域及最小正周期;(2)求函数y=f(x)的单调增区间.【答案】(1),;(2).【解析】(1)根据两角和差的正弦公式及二倍角公式的变形可得:,再根据辅助角公式得:,所以可得函数值域及周期;(2)根据正弦型函数的性质,令,可解得函数单增区间.试题解析:(1)f(x)=sin2x+cos2x+sin2x-cos2x-(cos2x+1)=2-1=2sin-1.由-1≤sin≤1得,-3≤2sin-1≤1.可知函数f(x)的值域为[-3,1].且函数f(x)的最小正周期为π.(2)由2kπ-≤2x-≤2kπ+(k∈Z)解得,kπ-≤x≤kπ+(k∈Z).所以y=f(x)的单调增区间为[kπ-,kπ+](k∈Z).【考点】1、正弦定理;2、三角形的面积公式;3、两角差的正弦公式.14.(2014•朝阳区校级一模)函数是()A.非奇非偶函数B.仅有最小值的奇函数C.仅有最大值的偶函数D.既有最大值又有最小值的偶函数【答案】D【解析】利用函数的奇偶性的定义判断后,再利用升幂公式,将f(x)化为f(x)=2﹣,利用余弦函数的性质与二次函数的性质即可求得答案.解:∵f(x)=cos2x+cosx,f(﹣x)=cos(﹣2x)+cos(﹣x)=cos2x+cosx=f(x),∴f(x)=cos2x+cosx是偶函数;又f(x)=cos2x+cosx=2cos2x+cosx﹣1=2﹣,当cosx=1时,f(x)取得最大值2;当cosx=﹣时,f(x)取得最小值﹣;故选:D.【考点】三角函数中的恒等变换应用.15.(2015秋•锦州校级期中)在△ABC中,角A,B,C的对应边分别为a,b,c,若,则角C的值为()A.B.C.或D.或【答案】A【解析】利用余弦定理表示出cosC,将已知等式代入求出cosC的值,即可确定出C的度数.解:∵△ABC中,a2+b2﹣c2=ab,∴cosC==,则C=,故选:A.【考点】余弦定理.16.已知函数的最小正周期为,且,则的一个对称中心坐标是A.B.C.D.【答案】A【解析】由的最小正周期为,得.因为,所以,由,得,故.令,得,故的对称中心为,当时,的对称中心为,故选A.【考点】三角函数的图像与性质.17.已知直线与圆相交于,两点,设,分别是以,为终边的角,则()A.B.C.D.【答案】D.【解析】作直线的中垂线,交圆于,两点,再将轴关于直线对称,交圆于点,则,如图所示,,而,故,故选D.【考点】1.直线与圆的位置关系;2.三角恒等变形.18.已知,则()A.B.C.D.【答案】C【解析】,,解得:,从而.故选C.【考点】1.三角函数的和角公式;2.倍角公式;3.同角三角函数的基本关系式.19.的内角所对的边分别为,已知,.(1)求的值;(2)求的值.【答案】(1)(2)【解析】(1)由正弦定理,将条件转化为边的关系,又,有,再利用余弦定理得的值(2)首先由同角三角函数关系得,再利用二倍角公式得,,最后根据两角差的余弦公式得的值.试题解析:解:(1)在三角形中,由及,可得,又,有,所以.(2)在三角形中,由,可得,于是,,所以.【考点】正余弦定理,同角三角函数关系,二倍角公式20.已知函数的最小正周期为,把的图象向左平移个单位,得到函数的图象.则的解析式为()A.B.C.D.【答案】C【解析】,因为最小正周期,,把的图象向左平移个单位,得到函数,故选C.【考点】三角函数的图象与性质.21.如图,在梯形中,已知,,,,.求:(1)的长;(2)的面积.【答案】(1)(2)【解析】(1)在三角形ADC中,已知两角和一边,求一边,应用正弦定理求解:先利用三角形内角和为,以及两角和正弦公式求CD对应角的正弦值,再根据正弦定理解出CD(2)在三角形BDC中,已知BD,CD,以及由平行条件得的正切值,进而可求其余弦值,再由余弦定理得BC,最后根据三角形面积公式得试题解析:(1)因为,所以.所以,在△中,由正弦定理得.(2)因为,所以.在△中,由余弦定理,得,解得,所以.【考点】正余弦定理22.在中,角所对的边分别为.若,且,则的最大值是()A.B.C.D.【答案】B【解析】由得,又,由,得,所以,,所以当时,取得最大值,且为.【考点】正弦定理、诱导公式、二倍角公式、二次函数最值.【思路点睛】本题主要考查正弦定理、三角函数恒等变换及二次函数的应用,综合性较强.通过边角互化,将转化为,可得,由诱导公式,结合,可进而得出,故,由知,当时,取得最大值,且为.23.已知函数的定义域为,值域为,则的值不可能是()A.B.C.D.【答案】A【解析】当函数在是单调函数时有最小值,当函数在不是单调函数时有最大值,所以的取值范围为.故选A.【考点】1、三角函数的图象和性质;2、三角函数的最值.24.选修4-1:几何证明选讲中,,,,,点在上,且.求证:(I);(II).【答案】(I)详见解析(II)详见解析【解析】(I)条件为比例关系时,多往三角形相似上化简:易得,因此,从而.(II)同(I)条件为比例关系时,多往三角形相似上化简:易得,因此,从而试题解析:证明:设,则,.(I),.又为公共角,故,由,,.(II)由(I)得,故,,.,,.【考点】三角形相似25.为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的“弹射型”气候仪器,这种仪器可以弹射到空中进行气候观测,如图所示,三地位于同一水平面上,这种仪器在地进行弹射实验,观测点两地相距100米,,在地听到弹射声音的时间比地晚秒,在地测得该仪器至最高点处的仰角为.(1)求两地的距离;(2)求这种仪器的垂直弹射高度(已知声音的传播速度为340米/秒).【答案】(1)420米;(2)米.【解析】(1)先利用在地听到弹射声音的时间比地晚秒设出和AC,再利用余弦定理进行求解;(2)利用是直角三角形和正弦定理进行求解.试题解析:(Ⅰ)设,由条件可知在中,由余弦定理,可得,即,解得所以(米)故两地的距离为420米.(Ⅱ)在中,米,由正弦定理,可得,即所以(米),故这种仪器的垂直弹射高度为米.【考点】1.正弦定理;2.余弦定理;3.解直角三角形.26.在中,角的对边分别为,若成等差数列,且.(1)求角;(2)求.【答案】(1);(2).【解析】(1)利用三角形内角和为可将化为只有角与角的式子,进而利用两角和的正弦公式化简得到角;(2)利用成等差数列及正弦定理可得三角形三边的关系,再利用第一问中的角和余弦定理即可得到的值.试题解析:(1)由可得,由可得,又,所以,所以;(6分)(2)由成等差数列及正弦定理可得,所以①由余弦定理可得,所以②把①代入②并整理可得,又,∴,即.(12分)【考点】两角和与差三角恒等变换公式、正余弦定理的应用、等差数列的概念.27.已知函数,将函数的图象上所有点的横坐标伸长为原来的倍,纵坐标不变,再将所得函数图象向右平移个单位,得到函数的图象,则函数的一个单调递增区间为()A.B.C.D.【答案】B【解析】函数的图象上所有点的横坐标伸长为原来的倍,纵坐标不变,得,再将所得函数图象向右平移个单位,得,,,得,,所以符合.故应选B.【考点】1、三角函数的平移变换;2、正弦函数的单调性.28.如图,在四边形中,.(1)求;(2)求及的长.【答案】(1)(2),【解析】(1)因为,所以利用二倍角余弦公式得,解得(2)在等腰中,由余弦定理得,或利用直角三角形为与交点.在中,利用正弦定理得,而,利用两角和正弦公式可得试题解析:(1).(2),由正弦定理得:,在等腰中,,由余弦定理得:,即(负根舍去),(或由亦可求得).【考点】二倍角公式,正余弦定理【方法点睛】解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系,从而达到解决问题的目的.其基本步骤是:第一步:定条件即确定三角形中的已知和所求,在图形中标出来,然后确定转化的方向.第二步:定工具即根据条件和所求合理选择转化的工具,实施边角之间的互化.第三步:求结果.29.函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图,则其解析式为__________________.【答案】【解析】由图象可知:A=1,…可得:T=2×(﹣)=π=,∴解得:ω=2,…∵函数的图象经过(,1),∴1=sin(2×+φ),∵φ=2kπ+,|φ|<,∴φ=…∴函数的解析式y=sin(2x+).30.将函数的图象向左平移个单位,再将所有点的横坐标伸长到原来的倍,得到函数的图象,则函数的图象与直线轴围成的图形面积为()A.B.C.D.以上都不对【答案】C【解析】的图象向左平移个单位得到的图象,再将所有点的横坐标伸长到原来的2倍,得到函数g(x)=2sinx的图象,所以函数g(x)=2sinx与直线,x轴所围成的图形面积为S=.【考点】三角函数的图象变换,微积分基本定理.31.若,,则角的终边在______象限.【答案】第四【解析】,所以为第四象限角.【考点】三角恒等变换.【思路点晴】要判断一个角终边所在象限,需要我们判断其正弦值和余弦值的正负.本题中,知道了半角的三角函数值,我们就利用半角的函数值求出单倍角的函数值,由单倍角的函数值我们就可以判断出角的终边所在的象限了.在利用二倍角公式的过程中,有,也可以有,只要角的倍数是两倍的关系就可以.32.若函数的最小正周期为,则的值是 .【答案】【解析】【考点】三角函数周期【方法点睛】已知函数的图象求解析式(1).(2)由函数的周期求(3)利用“五点法”中相对应的特殊点求.33.若函数的部分图象如图所示,则关于描述中正确的是()A.在上是减函数B.在上是减函数C.在上是增函数D.在上是增函数【答案】C.【解析】由题意得,,,又∵过最高点,∴,,不妨取,∴,∴,从而可知C正确,故选C.【考点】三角函数的图象和性质.34.的值为()A.B.C.D.【答案】C【解析】,化简得,即.【考点】三角恒等变换.35.已知中,分别是角所对的边,若,则角的大小为()A.B.C.D.【答案】C【解析】由已知和正弦定理得展开化简得,由于为三角形内角,所以,所以,,选C.【考点】1.正弦定理;2.两角和的正弦公式;3.已知三角函数值求角.36.已知函数的三个零点成等比数列,则.【答案】【解析】设函数在区间上的三个零点从小到大位次为,又因为三个零点成等比数列,则,解之得,,,所以,.【考点】三角函数的图象与性质,等比数列的性质,对数运算.【名师】本题考查三角函数的图象与性质、等比数列的性质、对数运算法则,属中档题.把等比数列与三角函数的零点有机地结合在一起,命题立意新,同时考查数形结合基本思想以及学生的运算能力、应用新知识解决问题的能力,是一道优质题.37.(原创)已知,其导函数的部分图象如图所示,则下列对的说法正确的是()A.最大值为4且关于直线对称B.最大值为4且在上单调递增C.最大值为2且关于点中心对称D.最大值为2且在上单调递减【答案】A【解析】由,得,由图可得,,即,得,,将点代入得,得,故最大值为,故关于直线对称,故选A.【考点】(1)三角函数的图象;(2)三角函数的性质.38.已知中,分别为内角所对的边长,且,则的面积为()A.B.C.D.【答案】C【解析】由题设可得,则,所以.由余弦定理可得,即,解之得,所以,故应选C.【考点】1.三角变换公式;2.余弦定理的应用;3.三角形的面积公式.【方法点晴】本题设置的目的是考查三角变换中两角和的正切公式,余弦定理,三角形的面积公式等基础知识和基本方法.解答时先依据题设中的求出,继而求出和,再运用余弦定理求出边,最后应用三角形的面积公式求该三角形的面积为.39.在中,内角对应的边分别为,若,则角等于()A.30°B.60°C.30°或150°D.60°或120°【答案】C【解析】由于,故为.【考点】解三角形.40.已知顶点在单位圆上的△,角,,所对的边分别是,,,且.(1)求的值;(2)若,求的取值范围.【答案】(1);(2).【解析】(1)由正弦定理可得:;(2)由,由,.试题解析:(1)因为,由正弦得,,所以.因为,且,所以.(2)由,得,由,得,,所以.因为,所以,即,所以.【考点】1、解三角形;2、三角恒等变换.41.已知角的顶点与原点重合,始边与轴的非负半轴重合,是角终边上的一点,则的值为()A.B.C.D.【答案】C【解析】因为是角终边上的一点,所以,所以=,故选C.【考点】1、任意角的三角函数的定义;2、两角和的正切函数.42.若,则()A.B.C.D.【答案】C【解析】由得,故,故选C.【考点】(1)诱导公式;(2)两角差的正弦.43.在中,,,,则的角平分线的长为()A.B.C.D.【答案】C【解析】由余弦定理得,再由角平分线定理得,最后根据余弦定理得,选C.【考点】余弦定理44.在中,角所对的边分别为,已知,,为的外接圆圆心. (1)若,求的面积;(2)若点为边上的任意一点,,求的值.【答案】(1)(2)【解析】(1)根据三角形面积公式,只需由求,这只需根据同角三角函数关系及三角形内角范围可求,(2)根据向量减法由得,再根据向量投影得,因此由得,即,最后根据正弦定理得试题解析:(1)由得,∴.(2)由,可得,于是,即,①又O为△ABC的的外接圆圆心,则,=,②将①代入②得到解得.由正弦定理得,可解得.【考点】向量投影,正弦定理【思路点睛】三角函数和平面向量是高中数学的两个重要分支,内容繁杂,且平面向量与三角函数交汇点较多,向量的平行、垂直、夹角、数量积等知识都可以与三角函数进行交汇.不论是哪类向量知识与三角函数的交汇试题,都会出现交汇问题中的难点,对于此类问题的解决方法就是利用向量的知识将条件转化为三角函数中的“数量关系”,再利用三角函数的相关知识进行求解.45.的部分图象如图所示,把的图象向右平移个单位长度得到的图象,则的单调递增区间为()A.B.C.D.【答案】C【解析】试题分析:由题设所提供的图象信息可得,即,将代入可得,即,则,所以,向右平移后可得,由可得,即,故函数的单调递增区间是,应选C.【考点】正弦函数的图象和性质及综合运用.【易错点晴】三角函数的图象和性质是中学数学中的重要内容和工具,也高考和各级各类考试的重要内容和考点.本题以函数的解析式所对应的图象为背景,考查的是正弦函数的图象和性质及数形结合的数学思想等有关知识和方法的综合运用.解答本题时要充分利用题设中提供的条件信息和图形信息,求出,进而确定函数解析式,然后借助平移求出,然后确定其单调递增区间,从而使得问题获解.46.在中,角,,的对边分别为,,,已知,,且.(1)求角的大小;(2)求的面积.【答案】(1);(2).【解析】(1)由,化简题设条件得,求得,即可求解角的值;(2)由余弦定理得,得到,再由条件,可化简求得,即可求解三角形的面积.试题解析:(1)∵,由,得,∴,整理得,解得,∵,∴.(2)由余弦定理得,即,∴,由条件,得,解得,∴.【考点】余弦定理及三角恒等变换.47.已知为锐角,若,则.【答案】【解析】试题分析:由于,因为锐角,若,故,所以,故应填答案.【考点】诱导公式及正弦二倍角公式的综合运用.【易错点晴】三角变换是高中数学的重要内容之一,也是高考必考的重要考点.本题以锐角满足的等式为背景,考查的是诱导公式和三角变换中的变角的技巧.变角是三角变换的精髓,也解决问题的难点,本题先用诱导公式将化为,进而运用倍角公式化为,从而使得问题巧妙获解,体现了角变换的要义.48.已知中,角,,的对边分别为,,,且.(Ⅰ)求角;(Ⅱ)若,求的取值范围.【答案】(Ⅰ)(Ⅱ)的取值范围是.【解析】(1)由正弦定理化简已知,整理可得:,由余弦定理可得,结合范围即可得解的值.(2)由正弦定理可得,,又,则求得的范围即可得解的取值范围试题解析:(Ⅰ)根据正弦定理可得,即,即,根据余弦定理得,所以.(Ⅱ)根据正弦定理,所以,,又,所以,因为,所以,所以,所以,即的取值范围是.【考点】正弦定理,余弦定理49.已知,且,则.【答案】【解析】由题可知,因为所以,则,故,则,故答案为.【考点】1、同角三角函数之间的关系;2、两角和的正切公式及二倍角的正切公式.50.在△中,角,,的对边分别为,,,且满足条件,,则△的周长为.【答案】【解析】中,即又,解得,其中为外接圆半径;,解得,,,的周长为,故答案为.【考点】1、正弦定理和余弦定理;2、诱导公式及两角和的余弦公式.【方法点睛】本题主要考查正弦定理和余弦定理、诱导公式及两角和的余弦公式,属于难题.以三角形为载体,三角恒等变换为手段,正弦定理、余弦定理为工具,对三角函数及解三角形进行考查是近几年高考考查的一类热点问题,一般难度不大,但综合性较强.解答这类问题,两角和与差的正余弦公式、诱导公式以及二倍角公一定要熟练掌握并灵活应用,特别是二倍角公式的各种变化形式要熟记于心. 解三角形时,有时可用正弦定理,有时也可用余弦定理,应注意用哪一个定理更方便、简捷.如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果遇到的式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到.51.函数的图象可由函数的图象至少向右平移个单位长度得到.【答案】【解析】,故应至少向右平移个单位.【考点】1、三角恒等变换;2、图象的平移.52.在中,角所对边分别为,已知向量,且.(1)求角的大小;(2)若,求的周长的最大值.【答案】(1);(2).【解析】(1);(2)由(1)及的周长的最大值.试题解析:(1)因为,所以,即,..................................2分故.................4分又,所以.............................6分(2)由(1)及,得,所以,....................................9分所以,..........................11分故的周长的最大值..................12分【考点】1、解三角形;2、基本不等式.53.在中,分别为角的对边,已知且,则__________.【答案】1【解析】由射影定理,可得a=2b=2,解得b=1【点睛】对于解三角形问题,一般利用正余弦定理,统一边或统一角做,同时要注意使用身影定理。
新高考数学计算题型精练 三角恒等变换(解析版)

新高考数学计算题型精练三角恒等变换1.cos70cos20sin70sin160︒︒-︒︒=()A.0B.12C D.1【答案】A【详解】cos20cos70sin160sin70︒︒-︒︒()cos20cos70sin18020sin70=︒︒-︒-︒︒cos20cos70sin20sin70=︒︒-︒︒()cos2070cos900=︒+︒=︒=.故选:A.2.sin40°cos10°+cos140°sin10°=()A B C.﹣12D.12【答案】D【详解】sin40°cos10°+cos140°sin10°,=sin40°cos10°-cos40°sin10°,=sin(40°-10°),=sin30°=12.故选:D3.sin20cos40cos20sin140︒︒︒︒+=A.B.2C.12-D.12【答案】B【详解】sin20cos40cos20sin140sin20cos40cos20sin40sin(2040)sin60︒︒+︒︒=︒︒+︒︒=︒+︒=︒故选B4.已知π1cos63α⎛⎫-=⎪⎝⎭,则πsin26α⎛⎫+=⎪⎝⎭()A.79-B.79C.3-D.3【答案】A【详解】因为π1 cos63α⎛⎫-=⎪⎝⎭,故2πππππ27sin 2sin 2()cos 2()2cos ()116626699αααα⎛⎫⎡⎤+=-+=-=--=-=- ⎪⎢⎥⎝⎭⎣⎦,故选:A 5.若cos tan 3sin ααα=-,则sin 22πα⎛⎫+= ⎪⎝⎭()A .23B .13C .89D .79【答案】D【详解】因为cos tan 3sin ααα=-,所以sin cos cos 3sin αααα=-,即223sin sin cos ααα-=,所以223sin sin cos 1ααα=+=,即1sin 3α=,所以27sin 2cos212sin 2π9ααα⎛⎫+==-= ⎪⎝⎭,故选:D .6.sin 20cos 40sin 70sin 40︒︒+︒︒=()AB .12C.2D .1【答案】A【详解】已知可化为:()sin 20cos 40cos 20sin 40sin 20402︒︒︒+︒=︒+︒=.故选:A7.若πtan 28α⎛⎫-= ⎪⎝⎭,则πtan 24α⎛⎫-= ⎪⎝⎭()A .34B .34-C .43D .43-【答案】D【详解】由2π2tan()π448tan 2π41431tan ()8ααα-⎛⎫-===- ⎪-⎝⎭--.故选:D8.已知π0,2α⎛⎫∈ ⎪⎝⎭π2sin 4αα⎛⎫=+ ⎪⎝⎭,则sin 2α=()A .34-B .34C .1-D .1【答案】B【详解】π2sin(4αα=+Q,)22(sin cos )2cos sin αααα=+-Q,1(cos sin )(cos sin )02αααα∴+--=,又π0,2α⎛⎫∈ ⎪⎝⎭,则sin 0,cos 0αα>>,即cos sin 0αα+>所以1cos sin 2αα-=,因为π0,2α⎛⎫∈ ⎪⎝⎭,所以2(0,π)α∈,sin 20α>.由1cos sin 2αα-=平方可得11sin 24α-=,即3sin 24α=,符合题意.综上,3sin 24α=.故选:B.9.已知5π4sin 125θ⎛⎫+= ⎪⎝⎭,则πsin 23θ⎛⎫+= ⎪⎝⎭()A .2425-B .725-C .725D .2425【答案】C【详解】5ππππ4sin sin cos 12212125θθθ⎡⎤⎛⎫⎛⎫⎛⎫+=--=-= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,所以22πππ47cos 2cos 22cos 1216612525θθθ⎛⎫⎛⎫⎛⎫⎛⎫-=-=--=⨯-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,得ππππ7sin 2sin 2cos 2326625θθθ⎡⎤⎛⎫⎛⎫⎛⎫+=+-=-= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦.故选:C.10.已知tan 2α=,则213cos sin2αα-=()A .12B .14C .2D .4【答案】A【详解】因为tan 2α=,所以222213cos sin 2cos tan 221sin22sin cos 2tan 42αααααααα---====,故选:A.11.化简:()22sin πsin 22cos 2ααα-+=()A .sin αB .sin 2αC .2sin αD .sin2α【答案】C【详解】根据题意可知,利用诱导公式可得()222sin πsin 22sin sin 22cos 2cos 22αααααα-++=再由二倍角的正弦和余弦公式可得()()222sin 1cos 2sin 1cos 2sin sin 22sin 1cos 2cos2cos22αααααααααα+++===+,即()22sin πsin 22sin 2cos2αααα-+=.故选:C12.cos78cos18sin 78sin18︒︒+︒︒的值为()A .12B .13CD【答案】A【详解】依题意由两角差的余弦公式可知,()1cos78cos18sin 78sin18cos 7818cos602︒︒+︒︒=︒-︒==.故选:A13.若tan 2θ=-,则()()()πsin 1sin22sin πcos πθθθθ⎛⎫+- ⎪⎝⎭=-++____________【答案】35-/-0.6【详解】()()()()22πsin 1sin2cos sin cos 2cos sin cos sin πcos πsin cos θθθθθθθθθθθθ⎛⎫+- ⎪-⎝⎭==--++-22222tan 1213cos sin 1tan 1(2)5cossin cos θθθθθθ-=---===-+++-,故答案为:35-14.已知ππ2θ<<,且4cos 5θ=-,则tan 2θ=______.【答案】247-【详解】4cos 5θ=-,3sin 5θ==±,ππ2θ<< ,3sin 5θ∴=.sin 3tan cos 4θθθ∴==-,232tan 242tan 291tan 7116θθθ-===---.故答案为:247-.15.已知cos 24π7sin 4αα=⎛⎫+ ⎪⎝⎭,则sin 2α的值是______.【答案】4149【详解】22cos 2442cos sin π777sin 422αααα=⇒⇒-=⎛⎫+ ⎪⎝⎭228841cos 2sin cos sin 1sin 2sin 2494949αααααα⇒-+=⇒-=⇒=,故答案为:414916.已知()0,απ∈,若sin 6πα⎛⎫-= ⎪⎝⎭cos 26πα⎛⎫+= ⎪⎝⎭_________.【答案】3±【详解】因为sin 63πα⎛⎫-= ⎪⎝⎭,()0,απ∈,所以cos 6πα⎛⎫-== ⎪⎝⎭所以sin 2=2sin cos =6663πππααα⎛⎫⎛⎫⎛⎫---±⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭所以cos 2cos 2cos 2sin 2=6326263ππππππαααα⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+=-+=-+=--± ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦.故答案为:17.若3,0,sin 25⎛⎫∈-=- ⎪⎝⎭x x π,则tan 2x =________.【答案】247-【详解】343,0,sin cos ,tan 2554x x x x π⎛⎫∈-=-∴==-⎪⎝⎭Q 232tan 242tan 291tan 7116x x x -∴===---故答案为:247-18.已知(),2αππ∈,cos 3sin 1αα-=,则cos 2α=_______________________.【答案】【详解】因为(),2αππ∈,所以,22αππ⎛⎫∈ ⎪⎝⎭,由cos 3sin 1αα-=可得212sin 6sin cos 1222ααα--=,整理可得sin 3cos 22αα=-,22sin 3cos 22sin cos 12222ααααπαπ⎧=-⎪⎪⎪+=⇒⎨⎪⎪<<⎪⎩cos 2α=故答案为:19.若πcos 0,,tan 22sin αααα⎛⎫∈= ⎪⎝⎭,则α=__________.【答案】6π/16π【详解】依题意,πcos 0,,tan 22sin αααα⎛⎫∈= ⎪⎝⎭,所以2222tan 1,2tan 1tan 1tan tan ααααα==--,21tan 3α=,而α为锐角,所以πtan 6αα=.故答案为:π620.已知tan 3α=,则sin 2α=______.【答案】35【详解】22222sin cos 2tan 233sin 2sin cos tan 1315ααααααα⨯====+++.故答案为:3521.已知α是第二象限的角,1cos24α=,则tan α=________.【答案】5/【详解】因为21cos 212sin 4αα=-=,又α是第二象限的角,所以6sin 4α=,cos 4α=,所以5tan α=-.故答案为:5-22.已知22cos 5sin 10αα-+=,则cos 2=α______.【答案】12/0.5【详解】解:已知()2222cos 5sin 121sin 5sin 12sin 5sin 30αααααα-+=--+=--+=,即()()22sin 5sin 32sin 1sin 30αααα+-=-+=,解得1sin 2α=或sin 3α=-(舍),211cos 212sin 1242αα∴=-=-⨯=,故答案为:12.23.若tan 2θ=,则sin cos 2cos sin θθθθ=-_________.【答案】65/1.2/115【详解】()()22sin cos sin sin cos 2sin cos sin cos sin cos sin θθθθθθθθθθθθ-==+--222222sin cos sin tan tan 246sin cos sin sin cos tan 155θθθθθθθθθθθ+++=+====++.故答案为:65.24.函数()sin 2sin 1cos x xf x x=+的值域__________.【答案】14,2⎛⎤- ⎥⎝⎦【详解】因为()()222221cos cos sin 2sin 2sin cos 11=2cos 2cos 2cos 1cos 1cos 1cos 22x x x x x x f x x x x x x x -⎛⎫===-+=--+ ⎪+++⎝⎭,因为1cos 1x -≤≤,当1cos 2x =时,()f x 取得最大值12,当cos 1x =-时,()f x 取得最小值4-,又因为1cos 0x +≠,所以()f x 的值域为14,2⎛⎤- ⎝⎦.故答案为:14,2⎛⎤- ⎥⎝⎦.25.已知sin 2cos αα=,π0,2α⎛⎫∈ ⎪⎝⎭,tan α=________.【详解】sin 2cos 2sin cos αααα==,π0,2α⎛⎫∈ ⎪⎝⎭,则cos 0α≠,1sin 2α=,π6α=,故tan α=26.(1)计算:cos157sin 97sin 60cos 97︒+︒︒︒;(2)已知tan 1α=-,求2cos 2sin cos 1ααα--的值.【答案】(1)12;(2)12【详解】(1)cos157sin 97sin 60cos97︒+︒︒︒()cos 9760sin 97sin 60cos 97︒+︒+︒︒=︒cos 97cos 60sin 97sin 60sin 97sin 60cos 97︒︒-︒︒+︒︒=︒cos 60=︒12=.(2)2cos 2sin cos 1ααα--222cos 2sin cos 1cos sin ααααα-=-+212tan 11tan αα-=-+()()2121111-⨯-=-+-12=.。
三角函数恒等变换含答案及高考题

三角函数恒等变形的基本策略。
(1)常值代换:特别是用“1”的代换,如1=cos 2θ+sin 2θ=tanx ·cotx=tan45°等。
(2)项的分拆与角的配凑。
如分拆项:sin 2x+2cos 2x=(sin 2x+cos 2x)+cos 2x=1+cos 2x ;配凑角:α=(α+β)-β,β=2βα+-2βα-等。
(3)降次与升次。
(4)化弦(切)法。
(4)引入辅助角。
asin θ+bcos θ=22b a +sin(θ+ϕ),这里辅助角ϕ所在象限由a 、b 的符号确定,ϕ角的值由tan ϕ=ab确定。
1.已知tan x =2,求sin x ,cos x 的值. 解:因为2cos sin tan ==xxx ,又sin 2x +cos 2x =1, 联立得⎩⎨⎧=+=,1cos sin cos 2sin 22x x xx 解这个方程组得.55cos 552sin ,55cos 552sin ⎪⎪⎩⎪⎪⎨⎧-=-=⎪⎪⎩⎪⎪⎨⎧==x x x x 2.求)330cos()150sin()690tan()480sin()210cos()120tan(----的值.解:原式)30360cos()150sin()30720tan()120360sin()30180cos()180120tan(o--+---++-= .3330cos )150sin (30tan )120sin )(30cos (60tan -=---=3.若,2cos sin cos sin =+-xx xx ,求sin x cos x 的值.解:法一:因为,2cos sin cos sin =+-xx xx所以sin x -cos x =2(sin x +cos x ),得到sin x =-3cos x ,又sin 2x +cos 2x =1,联立方程组,解得 ,,⎪⎪⎩⎪⎪⎨⎧=-=⎪⎪⎩⎪⎪⎨⎧-==1010cos 10103sin 1010cos 10103sin x x x x 所以⋅-=103cos sin x x 法二:因为,2cos sin cos sin =+-xx xx 所以sin x -cos x =2(sin x +cos x ),所以(sin x -cos x )2=4(sin x +cos x )2, 所以1-2sin x cos x =4+8sin x cos x , 所以有⋅-=103cos sin x x 4.求证:tan 2x ·sin 2x =tan 2x -sin 2x .证明:法一:右边=tan 2x -sin 2x =tan 2x -(tan 2x ·cos 2x )=tan 2x (1-cos 2x )=tan 2x ·sin 2x ,问题得证. 法二:左边=tan 2x ·sin 2x =tan 2x (1-cos 2x )=tan 2x -tan 2x ·cos 2x =tan 2x -sin 2x ,问题得证. 5.求函数)6π2sin(2+=x y 在区间[0,2π ]上的值域. 解:因为0≤x ≤2π,所以,6π76π26π,π20≤+≤≤≤x x 由正弦函数的图象, 得到],1,21[)6π2sin(-∈+x所以y ∈[-1,2]. 6.求下列函数的值域.(1)y =sin 2x -cos x +2; (2)y =2sin x cos x -(sin x +cos x ). 解:(1)y =sin 2x -cos x +2=1-cos 2x -cos x +2=-(cos 2x +cos x )+3,令t =cos x ,则,413)21(413)21(3)(],1,1[222++-=++-=++-=-∈t t t t y t利用二次函数的图象得到].413,1[∈y (2)y =2sin x cos x -(sin x +cos x )=(sin x +cos x )2-1-(sin x +cos x ),令t =sin x +cos x 2=,)4πsin(+x ,则]2,2[-∈t 则,,12--=t t y 利用二次函数的图象得到].21,45[+-∈y7.若函数y =A sin(ωx +φ)(ω>0,φ>0)的图象的一个最高点为)2,2(,它到其相邻的最低点之间的图象与x 轴交于(6,0),求这个函数的一个解析式.解:由最高点为)2,2(,得到2=A ,最高点和最低点间隔是半个周期,从而与x 轴交点的间隔是41个周期,这样求得44=T ,T =16,所以⋅=8πω又由)28πsin(22ϕ+⨯=,得到可以取).4π8πsin(2.4π+=∴=x y ϕ8.已知函数f (x )=cos 4x -2sin x cos x -sin 4x .(Ⅰ)求f (x )的最小正周期; (Ⅱ)若],2π,0[∈x 求f (x )的最大值、最小值. 数xxy cos 3sin 1--=的值域.解:(Ⅰ)因为f (x )=cos 4x -2sin x cos x -sin4x =(cos 2x -sin 2x )(cos 2x +sin 2x )-sin2x )4π2sin(2)24πsin(22sin 2cos 2sin )sin (cos 22--=-=-=--=x x x x x x x所以最小正周期为π.(Ⅱ)若]2π,0[∈x ,则]4π3,4π[)4π2(-∈-x ,所以当x =0时,f (x )取最大值为;1)4πsin(2=--当8π3=x 时,f (x )取最小值为.2-1. 已知2tan =θ,求(1)θθθθsin cos sin cos -+;(2)θθθθ22cos 2cos .sin sin +-的值.解:(1)2232121tan 1tan 1cos sin 1cos sin 1sin cos sin cos --=-+=-+=-+=++θθθθθθθθθ; (2) θ+θθ+θθ-θ=θ+θθ-θ222222cos sin cos 2cos sin sin cos 2cos sin sin 324122221cos sin 2cos sin cos sin 222-=++-=+θθ+θθ-θθ=. 说明:利用齐次式的结构特点(如果不具备,通过构造的办法得到),进行弦、切互化,就会使解题过程简化。
高中数学三角函数及三角恒等变换精选题目(附解析)

高中数学三角函数及三角恒等变换精选题目(附解析) 一、三角函数的定义若角α的终边上任意一点P (x ,y )(原点除外),r =|OP |=x 2+y 2,则sin α=y r ,cos α=x r ,tan α=y x (x ≠0).1.已知角α的终边过点P (-3cos θ,4cos θ),其中θ∈⎝ ⎛⎭⎪⎫π2,π,则sin α=________,tan α=________.[解析] ∵θ∈⎝ ⎛⎭⎪⎫π2,π,∴cos θ<0,∴r =x 2+y 2=9cos 2θ+16cos 2θ=-5cosθ,故sin α=y r =-45,tan α=y x =-43.[答案] -45 -43 注:利用三角函数定义求函数值的方法当已知角的终边所经过的点或角的终边所在的直线时,一般先根据三角函数的定义求这个角的三角函数值,再求其他.但当角经过的点不固定时,需要进行分类讨论.求与正切函数有关问题时,不要忽略正切函数自身的定义域.2.已知点M ⎝ ⎛⎭⎪⎫13,a 在函数y =log 3x 的图象上,且角θ的终边所在的直线过点M ,则tan θ=( )A .-13 B .±13 C .-3D .±3解析:选C 因为点M ⎝ ⎛⎭⎪⎫13,a 在函数y =log 3x 的图象上,所以a =log 313=-1,即M ⎝ ⎛⎭⎪⎫13,-1,所以tan θ=-113=-3,故选C.3.已知角θ的顶点与原点重合,始边与x 轴的正半轴重合,终边在直线y =2x 上,则cos 2θ=( )A .-45B .-35 C.35D.45解析:选B 在角θ的终边上任取一点P (a,2a )(a ≠0). 则r 2=|OP |2=a 2+(2a )2=5a 2. 所以cos 2θ=a 25a 2=15,cos 2θ=2cos 2 θ-1=25-1=-35.4.若θ是第四象限角,则点P (sin θ,tan θ)在第________象限. 解析:∵θ是第四象限角,则sin θ<0,tan θ<0, ∴点P (sin θ,tan θ )在第三象限. 答案:三二、同角三角函数的基本关系及诱导公式①牢记两个基本关系式sin 2α+cos 2α=1及sin αcos α=tan α,并能应用两个关系式进行三角函数的求值、化简、证明.②诱导公式可概括为k ·π2±α(k ∈Z)的各三角函数值的化简公式.记忆规律是:奇变偶不变,符号看象限.其中的奇、偶是指π2的奇数倍或偶数倍,变与不变是指函数名称的变化.5.已知2+tan (θ-π)1+tan (2π-θ)=-4,求(sin θ-3cos θ)(cos θ-sin θ)的值.[解] 法一:由已知得2+tan θ1-tan θ=-4,∴2+tan θ=-4(1-tan θ), 解得tan θ=2.∴(sin θ-3cos θ)(cos θ-sin θ ) =4sin θcos θ-sin 2θ-3cos 2θ =4sin θcos θ-sin 2θ-3cos 2θsin 2θ+cos 2θ=4tan θ-tan2θ-3tan2θ+1=8-4-34+1=15.法二:由已知得2+tan θ1-tan θ=-4,解得tan θ=2.即sin θcos θ=2,∴sin θ=2cos θ.∴(sin θ-3cos θ)(cos θ-sin θ)=(2cos θ-3cos θ)(cos θ-2cos θ)=cos2θ=cos2θsin2θ+cos2θ=1tan2θ+1=15.注:三角函数式的求值、化简、证明的常用技巧(1)化弦:当三角函数式中三角函数名称较多时,往往把三角函数化为弦,再化简变形.(2)化切:当三角函数式中含有正切及其他三角函数时,有时可将三角函数名称都化为正切,再变形化简.(3)“1”的代换:在三角函数式中,有些会含有常数1,常数1虽然非常简单,但有些三角函数式的化简却需要利用三角函数公式将“1”代换为三角函数式.6.若sin(π+α)=35,且α是第三象限角,则sin⎝⎛⎭⎪⎫π2+α-cos⎝⎛⎭⎪⎫π2+αsin⎝⎛⎭⎪⎫π2-α-cos⎝⎛⎭⎪⎫π2-α=()A.1B.7 C.-7 D.-1解析:选B由sin(π+α)=35,得sin α=-35.又α是第三象限角,所以cos α=-4 5,所以sin⎝⎛⎭⎪⎫π2+α-cos⎝⎛⎭⎪⎫π2+αsin⎝⎛⎭⎪⎫π2-α-cos⎝⎛⎭⎪⎫π2-α=cos α+sin αcos α-sin α=-45+⎝ ⎛⎭⎪⎫-35-45-⎝ ⎛⎭⎪⎫-35=7.7.已知sin θ+cos θ=43,且0<θ<π4,则sin θ-cos θ的值为( )A.23 B .-23 C.13D .-13解析:选B ∵sin θ+cos θ=43,∴1+2sin θcos θ=169,则2sin θcos θ=79.又0<θ<π4,所以sin θ-cos θ<0,故sin θ-cos θ=-(sin θ-cos θ)2=-1-2sin θcos θ=-23,故选B.8.已知α为第三象限角,且sin α+cos α=2m,2sin αcos α=m 2,则m 的值为________.解析:由(sin α+cos α)2=1+2sin αcos α,得4m 2=1+m 2,即m 2=13.又α为第三象限角,所以sin α<0,cos α<0,则m <0,所以m =-33.答案:-339.已知sin(3π-α)=2cos ⎝ ⎛⎭⎪⎫3π2+β,cos(π-α)=63cos(π+β),且0<α<π,0<β<π,求sin α和cos β的值.解:由已知,得sin α=2sin β,① 3cos α=2cos β,②由①2+②2,得sin 2α+3cos 2α=2, 即sin 2α+3(1-sin 2α)=2,所以sin 2α=12. 又0<α<π,则sin α=22. 将sin α=22代入①,得sin β=12.又0<β<π,故cos β=±32.三、简单的三角恒等变换两角和与差的正弦、余弦、正切公式 ①sin(α±β)=sin αcos β±cos αsin β; ②cos(α±β)=cos αcos β∓sin αsin β; ③tan(α±β)=tan α±tan β1∓tan αtan β.二倍角的正弦、余弦、正切公式 ①sin 2α=2sin αcos α;②cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α; ③tan 2α=2tan α1-tan 2α.10.已知tan α=2. (1)求tan ⎝ ⎛⎭⎪⎫α+π4的值;(2)求sin 2αsin 2α+sin αcos α-cos 2α-1的值.[解] (1)tan ⎝ ⎛⎭⎪⎫α+π4=tan α+tan π41-tan αtan π4=2+11-2×1=-3.(2)sin 2αsin 2α+sin αcos α-cos 2α-1=2sin αcos αsin 2α+sin αcos α-2cos 2α=2tan αtan 2α+tan α-2=2×24+2-2=1.注:条件求值的解题策略(1)分析已知角和未知角之间的关系,正确地用已知角来表示未知角. (2)正确地运用有关公式将所求角的三角函数值用已知角的三角函数值来表示.(3)求解三角函数中给值求角的问题时,要根据已知求这个角的某种三角函数值,然后结合角的取值范围,求出角的大小.11.若θ∈⎣⎢⎡⎦⎥⎤π4,π2,sin 2θ=378,则sin θ=( )A.35 B.45 C.74D.34解析:选D 因为θ∈⎣⎢⎡⎦⎥⎤π4,π2,所以2θ∈⎣⎢⎡⎦⎥⎤π2,π,所以cos 2θ<0,所以cos 2θ=-1-sin 22θ=-18.又cos 2θ=1-2sin 2θ=-18,所以sin 2θ=916,所以sin θ=34.12.已知sin ⎝ ⎛⎭⎪⎫α+π3+sin α=-435,-π2<α<0,则cos ⎝ ⎛⎭⎪⎫α+8π3等于( )A .-45 B .-35 C.35D.45解析:选D 因为sin ⎝ ⎛⎭⎪⎫α+π3+sin α=-435,所以sin ⎝ ⎛⎭⎪⎫α+π3+sin ⎝ ⎛⎭⎪⎫α+π3-π3=-435,所以sin ⎝ ⎛⎭⎪⎫α+π3+sin ⎝ ⎛⎭⎪⎫α+π3cos π3-cos ⎝ ⎛⎭⎪⎫α+π3sin π3=-435,所以32sin ⎝ ⎛⎭⎪⎫α+π3-32cos ⎝ ⎛⎭⎪⎫α+π3=-435,所以-3⎣⎢⎡⎦⎥⎤12cos ⎝ ⎛⎭⎪⎫α+π3-32sin ⎝ ⎛⎭⎪⎫α+π3=-435,即-3cos ⎝ ⎛⎭⎪⎫α+π3+π3=-435,cos ⎝ ⎛⎭⎪⎫α+2π3=45,所以cos ⎝ ⎛⎭⎪⎫α+8π3=cos ⎝ ⎛⎭⎪⎫α+2π3=45,故选D.13.(2017·全国卷Ⅲ)已知sin α-cos α=43,则sin 2α=( )A .-79B .-29 C.29D.79解析:选A 将sin α-cos α=43的两边进行平方,得sin 2 α-2sin αcos α+cos 2α=169,即sin 2α=-79.14.已知向量a =(1,-3),b =⎝ ⎛⎭⎪⎫sin x ,2cos 2x 2-1,函数f (x )=a ·b .(1)若f (θ)=0,求2cos 2θ2-sin θ-12sin ⎝ ⎛⎭⎪⎫θ+π4的值;(2)当x ∈[0,π]时,求函数f (x )的值域.解:(1)∵a =(1,-3),b =⎝ ⎛⎭⎪⎫sin x ,2cos 2x 2-1,∴f (x )=a ·b =sin x -3⎝ ⎛⎭⎪⎫2cos 2x 2-1=sin x -3cos x .∵f (θ)=0,即sin θ-3cos θ=0,∴tan θ=3,∴2cos 2θ2-sin θ-12sin ⎝ ⎛⎭⎪⎫θ+π4=cos θ-sin θsin θ+cos θ=1-tan θtan θ+1=1-33+1=-2+ 3.(2)由(1)知f (x )=sin x -3cos x =2sin ⎝ ⎛⎭⎪⎫x -π3,∵x ∈[0,π],∴x -π3∈⎣⎢⎡⎦⎥⎤-π3,2π3,当x -π3=-π3,即x =0时,f (x )min =-3; 当x -π3=π2,即x =5π6时,f (x )max =2,∴当x ∈[0,π]时,函数f (x )的值域为[-3,2].。
高三数学三角函数三角恒等变换解三角形试题答案及解析

高三数学三角函数三角恒等变换解三角形试题答案及解析1.命题P:实数x满足其中a<0,命题q:实数x满足或且是的必要不充分条件,求a的取值范围【答案】或【解析】本试题主要是考查了充分条件的判定和运用。
由于不等式的解集的关系可知q是P的必要不充分条件,然后利用集合的包含关系得到参数a的范围。
2.已知的图象与直线的两个交点的最短距离是,要得到的图象,只需要把的图象A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向右平移个单位【答案】A【解析】由于的图象与直线的两个交点的最短距离是,,,即,将的图象向左平移个单位得到,故答案为A.【考点】函数图象的平移.3.在中,若,则此三角形形状是A.等腰三角形B.直角三角形C.等边三角形D.等腰直角三角形【答案】B【解析】由得则原式可化为,整理得即此三角形为直角三角形【考点】解三角形4.在中,角的对边分别为,,,,则_______.【答案】【解析】由正弦定理得:即,∴,∵,∴.【考点】正弦定理.5.已知,,则下列不等式一定成立的是()A.B.C.D.【答案】D【解析】设函数,所以.显然,时,,即此时函数为增函数.易知函数为偶函数,所以在时,函数单调递减.又因,所以即,所以,故.选D.【考点】构造函数法并利用单调性解不等式.【方法点睛】题目中条件,启发我们构造函数,而选项从整体上看,是比较与的大小关系的.以上两点结合考虑,应判断函数的单调性,而函数是偶函数,由及单调性直接判断变量与的大小比较难,应利用偶函数的性质得到,从而得到.这样显然答案选D.本题综合性较强、难度较大,要有构造函数的意识,同时要灵活运用函数性质.6.(本题满分12分)已知函数(1)求函数的最小正周期和最大值;(2)求函数单调递增区间【答案】(1)最小正周期为,最大值为;(2)【解析】三角函数问题,一般利用两角和与差的正弦、余弦公式、二倍角公式化为一个角的一个三角函数,然后利用正弦函数(或余弦函数)的性质得出结论.试题解析:(1)函数的最小正周期为,函数的最大值为(2)由得函数的单调递增区间为【考点】三角函数的周期、最值、单调区间.7.如图,正五边形的边长为2,甲同学在中用余弦定理解得,乙同学在中解得,据此可得的值所在区间为()A.B.C.D.【答案】C【解析】由题意有,即,整理得:,构造函数,因为,,且函数在定义域内为增函数,所以函数有唯一零点在区间上,即方程的解在区间上,所以的值所在区间为,故选C.【考点】1.诱导公式;2.函数与方程;3.零点存在定理.【名师】本题主要考查零点存在定理、函数与方程思想以用诱导公式,属难题.求方程解所在区间通常转化为求函数零点所在区间问题求解,解决函数零点所在区间是通过零点存在定理来实现的,需要注意的是零点存在定理只能解决变号零点的问题.本题由求一个数的了以值区间问题转化为求一个方程的近似解的问题,进一步转化为求函数零点所在区间,体现数学中的转化转化思想.8.已知函数的部分图象如图所示.(Ⅰ)求函数的解析式;(Ⅱ)在△中,角的对边分别是,若,求的取值范围.【答案】(Ⅰ);(Ⅱ).【解析】(Ⅰ)观察图像可知函数的一条对称轴为,进而求出其最小正周期,于是运用公式可求出的值,再将点代入的解析式即可求出,即可求出函数的解析式;(Ⅱ)运用正弦定理并结合已知,可得,再由三角形的内角和为可得出角的值,进而得出的大小,即可得出的取值范围.试题解析:(Ⅰ)由的一条对称轴为,从而的最小正周期,故.将点代入的解析式得,又,故,将点代入的解析式得,所以.(Ⅱ)由得,所以,因为,所以,,,,.【考点】1、由函数的图像求函数的解析式;2、正弦定理的应用;3、三角函数的图像及其性质.【易错点睛】本题主要考查了由函数的图像求函数的解析式、正弦定理的应用和三角函数的图像及其性质,属中档题.其解题过程中容易出现以下两处错误:其一是不能仔细观察函数图像,并结合已知条件求出函数的解析式,尤其是求的时候不知道怎么合理取点代值计算,不知道怎么舍去增根,导致出现增根;其二是未能将正弦定理与三角恒等变换结合起来综合运用并准确地进行化简求值.9.设函数,则该函数的最小正周期为,在的最小值为.【答案】,【解析】由题意可知,;,所以,所以在的最小值为.【考点】函数的性质.10.在锐角中,角的对边分别为,已知依次成等差数列,且求的取值范围.【答案】.【解析】由三角形内角和定理和等差中项易求,,根据正弦定理把边,用角的三角函数表示出来,通过三角恒等变换构造正弦型函数,把问题转化为求正弦型函数在给定区间上的值域问题,求角的取值范围时,不要忽略为锐角三角形.试题解析:解:角成等差数列根据正弦定理的又为锐角三角形,则【考点】等差中项、正弦定理、三角恒等变换及正弦型函数值域.11.如图,D,C,B三点在地面同一直线上,,从C,D两点测得A点仰角分别是,则A点离地面的高度AB等于()A.B.C.D.【答案】A【解析】由题意,即,即.故选A.【考点】解三角形.12.将函数的图象沿轴向左平移个单位后,得到一个偶函数的图象,则的一个可能取值为()A.B.C.D.【答案】B【解析】将函数的图象沿轴向左平移个单位得,又是一个偶函数,所以,根据选项可知的一个可能取值为,故选B.【考点】三角函数的图像.13.在中,内角的对边分别为,且,则的面积最大值为.【答案】【解析】由余弦定理得:,代入得解得,那么根据三角形面积公式所以当时,面积取得最大值.【考点】1.余弦定理;2.三角形面积公式.【方法点睛】考察到了解三角形的最值问题,属于中档题型,解决此问题的关键是面积的表达公式,,将这样的三个量用一个量表示,尤其是,但不可用正弦定理,而要用余弦定理,用表示出,再转化为,最后代入面积公式,将面积表示为的函数关系求最值.14.同时具有性质“①最小周期是;②图象关于直线对称;③在上是增函数”的一个函数是()A.B.C.D.【答案】C【解析】故A不正确.对于选项B,如果为对称轴.则但在上是减函数不满足题意,对于选项C,因为为对称轴.所以,在上是增函数满足题意,故选C.【考点】正弦函数的图像15.已知,则()A.B.C.D.【答案】B【解析】因为,所以,又,所以,从而,因此,选B.【考点】同角三角函数关系16.若点在角的终边上,则的值为()A.B.C.D.【答案】D【解析】因为,所以,故选D.【考点】任意角的三角函数值.17.中,分别为的重心和外心,且,则的形状是()A.锐角三角形B.钝角三角形C.直角三角形D.上述均不是【答案】B【解析】,而,∴.,故为钝角.【考点】平面向量的运算及余弦定理解三角形.【方法点晴】本题主要考查了平面向量的线性运算和数量积运算及利用余弦定理判断三角形的形状问题,属于中档题.解答本题的关键是:选择三角形的两边表示的向量作为平面的基底,通过向量的线性运算把转化为基底的关系,结合平面向量数量积的运算律得到,进而利用余弦定理得到问题的答案.18.若点在直线上,则的值等于()A.B.C.D.【答案】A【解析】由题意得,所以,故选B.【考点】三角函数的化简求值.19.已知函数向右平移个单位后,所得的图像与原函数图像关于轴对称,则的最小正值为()A.B.C.D.【答案】D【解析】原函数向右平移个单位后所得函数为其与原函数关于轴对称,则必有,由三角函数诱导公式可知的最小正值为,故本题的正确选项为D.【考点】函数的平移,对称,以及三角函数的诱导公式.20.若、,且,则下面结论正确的是()A.B.C.D.【答案】D【解析】因为函数,,,所以函数是偶函数,,当时,,所以在上是增函数,由知,所以,即,故选D.【考点】1、函数的奇偶性;2、利用导数研究函数的单调性.21.已知中,,,分别是角,,的对边,且,是关于的一元二次方程的两根.(1)求角的大小;(2)若,设,的周长为,求的最大值.【答案】(1);(2).【解析】(1)根据韦达定理得到三边所满足的一个关系式,进而利用余弦定理的变式求解;(2)利用正弦定理得到的解析式,再利用三角恒等变形将其化简,利用三角函数的性质求其最值.试题解析:(1)在中,依题意有:,∴,又∵,∴;(2)由,及正弦定理得:,∴,,故,即,由得:,∴当,即时,. .【考点】1.正余弦定理解三角形;2.三角恒等变形;3.韦达定理;4.三角函数的性质.22.已知函数f(x)=(sin x+ cos x)cos x一(x R,>0).若f(x))的最小止周期为4.( I)求函数f(x)的单调递增区间;(II)在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.【答案】(Ⅰ);(Ⅱ).【解析】( I)先利用二倍角公式和配角公式化简函数解析式,再利用三角函数的周期公式确定参数值和函数的解析式,进而利用整体思想求其单调递增区间; (II)先利用正弦定理将边角关系转化为角角关系,再利用三角形的内角和定理和两角和的正弦公式进行求解.(I).,.由,得.∴的单调递增区间为(Ⅱ)由正弦定理得,,∴.∵,∴或:,,∴.又,..【考点】1.三角恒等变换;2.正弦定理.23.已知函数,.(1)求函数的图像的对称轴方程;(2)求函数的最小正周期和值域.【答案】(1);(2),值域.【解析】(1)用二倍角公式将函数降幂,根据余弦函数的对称轴公式可求得此函数的对称轴方程. (2)根据(1)中所得函数的解析式与相加,用化一公式将其化简变形可得,根据周期公式可得其周期,根据正弦的值域可得其值域.试题解析:(1)由题设知.令,所以函数图像对称轴的方程为.(2).所以最小正周期是,值域.【考点】1三角函数的化简;2三角函数的周期,对称轴,值域.24.已知是锐角三角形,则点在()A.第一象限B.第二象限C.第三象限D.第四象限【答案】B【解析】是锐角三角形,则,,同理可得,故选B.【考点】诱导公式.25.关于函数(),下列命题正确是()A.由可得是的整数倍;B.的表达式可改写成;C.的图象关于点对称;D.的图象关于直线对称.【答案】C【解析】,,,因此,A错;,但时,,B错,事实上;,,时,,因此是其对称中心,C正确;,,不含,D错.故选C.【考点】函数的性质.26.已知函数, 先将的图象上所有点的横坐标缩短到原来的倍(纵坐标不变),再将得到的图象上所有点向右平行移动()个单位长度,得到的图象关于直线x=对称,则的最小值为()A.B.C.D.【答案】A【解析】,将的图象上所有点的横坐标缩短到原来的倍(纵坐标不变),得,再将得到的图象上所有点向右平行移动()个单位长度,得,则,,,因为,最小值为.故选A.【考点】三角函数图象变换,三角函数的对称轴.27.已知函数对称,现将的图象向左平移个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数的图象,则的表达式为()A.B.C.D.【答案】B【解析】设上一点与上点关于对称,则有,,,,,现将的图象向左平移个单位后,得到再将得到的图象上各点的横坐标伸长到原来的倍,纵坐标不变,得到函数的图象,故选B.【考点】三角函数图象的变换.28.同时具有性质“①最小正周期是,②图象关于直线对称;③在上是增函数”的一个函数是()A.B.C.D.【答案】C【解析】由题意得,函数的最小周期为,则,又函数图象关于直线对称,则函数为函数的最小值,则只有B、C满足,由当时,,则函数是单调递增函数,故选C.【考点】三角函数的性质.29.在中,内角的对边边长分别为,且.若,则的面积最大值为________.【答案】【解析】设三角形面积为,所以,又,两式相除得,同理,因为,所以,化简得,故,,,,故.【考点】解三角形.【思路点晴】本题属于一个综合性的题目背景是解三角形,设计三角形面积公式、余弦定理,同脚三角函数关系,基本不等式的知识.已知条件中关键的突破口在,我们由同角三角函数关系,结合余弦定理,就可以求出,然后代入三角形的面积公式,最后利用基本不等式来求面积的最大值.注意运算不要出错.30.在中,AC=6,(1)求AB的长;(2)求的值.【答案】(1)(2)【解析】(1)利用同角三角函数的基本关系求再利用正弦定理求AB的长;(2)利用诱导公式及两角和与差正余弦公式分别求,然后求试题解析:解(1)因为,,所以由正弦定理知,所以(2)在中,,所以,于是又故因为,所以因此【考点】同角三角函数的基本关系、正余弦定理、两角和与差的正余弦公式【名师】三角函数是以角为自变量的函数,因此解三角函数题,首先应从角进行分析,善于用已知角表示所求角,即注重角的变换.角的变换涉及诱导公式、同角三角函数的基本关系、两角和与差的三角公式、二倍角公式、配角公式等,选用恰当的公式是解决三角问题的关键,同时应明确角的范围、开方时正负的取舍等.31.△ABC的内角A,B,C的对边分别为a,b,c,若,,a=1,则b=____________.【答案】【解析】因为,且为三角形的内角,所以,,又因为,所以.【考点】正弦定理,两角和、差的三角函数公式【名师】在解有关三角形的题目时,要有意识地考虑用哪个定理更合适,或是两个定理都要用,要抓住能够利用某个定理的信息.一般地,如果式子中含有角的余弦或边的二次式时,要考虑用余弦定理;如果式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到.32.如图,平面四边形中,,则的面积为_____________.【答案】【解析】在中,由正弦定理得:,在中,由余弦定理得:,所以.因为,所以.因为.所以.故答案为.【考点】1、正弦定理、余弦定理的应用;2、两角和的正弦公式及三角形面积公式.【方法点睛】以三角形和平面向量为载体,三角恒等变换为手段,正弦定理、余弦定理为工具,对三角函数及解三角形进行考查是近几年高考考查的一类热点问题,一般难度不大,但综合性较强.解答这类问题,两角和与差的正余弦公式、诱导公式以及二倍角公一定要熟练掌握并灵活应用,特别是二倍角公式的各种变化形式要熟记于心,此外,解三角形时三角形面积公式往往根据不同情况选用下列不同形式能简化计算过程,.33.函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图,则其解析式为__________________.【答案】【解析】由图象可知:A=1,…可得:T=2×(﹣)=π=,∴解得:ω=2,…∵函数的图象经过(,1),∴1=sin(2×+φ),∵φ=2kπ+,|φ|<,∴φ=…∴函数的解析式y=sin(2x+).34.设的内角的对边分别为,且,则____.【答案】【解析】,.【考点】解三角形、正余弦定理.35.等于()A.B.C.D.【答案】D【解析】因,故,故应选D.【考点】两角和的余弦公式及运用.36.已知函数,则要得到其导函数的图象,只需将函数的图象()A.向右平移个单位B.向左平移个单位C.向右平移个单位D.左平移个单位【答案】B【解析】函数,所以函数,所以将函数函数的图象上所有的点向左平移个单位长度得到,故选B.【考点】函数的图象变换.37.已知,则 .【答案】【解析】.【考点】三角恒等变换.38.函数的部分图象如图所示,则 .【答案】【解析】,,,即,,又,∴.【考点】函数的图象与性质.39.设当时,函数取得最大值,则__________.【答案】【解析】,其中,故当函数取得最大值时,【考点】辅助角公式,三角函数的最值和值域【名师】本题考查三角函数的辅助角公式以及取得最大值时的值,属中档题.解题时正确确定函数在取得最大值时的值是解题的关键40.如图,在凸四边形中,,,,.设.(1)若,求的长;(2)当变化时,求的最大值.【答案】(1);(2).【解析】(1)由余弦定理可得,解得.从而,解得;(2)设,,由余弦定理得,再由正弦定理得.从而.再由得:当,时取到最大值.试题解析:(1)在中,,∴,∴.在中,,∴.(2)设,,在中,,.∵,∴.在中,.∵,∴,当,时取到最大值.【考点】解三角形.41.已知函数的最小正周期是,将函数图象向左平移个单位长度后所得的函数图象过点,则函数()A.在区间上单调递减B.在区间上单调递增C.在区间上单调递减D.在区间上单调递增【答案】B【解析】依题, ,平移后得到的函数是,其图象过(0,1),∴,因为,∴,,故选B.【考点】三角函数的图象与性质.42.海上有三个小岛,,,则得,,,若在,两岛的连线段之间建一座灯塔,使得灯塔到,两岛距离相等,则,间的距离为()A.B.C.D.【答案】B【解析】设由余弦定理可得,,故选B.【考点】解三角形.43.已知角为第四象限角,且,则()A.B.C.D.【答案】A【解析】,,又,得出.因为角为第四象限角, ,;.故选A.【考点】同角三角函数的运算.44.如图,某广场中间有一块边长为2百米的菱形状绿化区ABCD,其中BMN是半径为1百米的扇形,.管理部门欲在该地从M到D修建小路:在弧MN上选一点P(异于M、N两点),过点P修建与BC平行的小路PQ.问:点P选择在何处时,才能使得修建的小路与PQ及QD的总长最小?并说明理由.【答案】当时,总路径最短.【解析】借助题设条件建立函数关系,再运用三角变换的公式求解和探求.试题解析:连接, 过作垂足为 , 过作垂足为设,…………………2分若,在中,若则若则…………………………4分在中,…………………………6分所以总路径长……………………10分………………12分令,当时,当时,…………………………14分所以当时,总路径最短.答:当时,总路径最短. ……16分【考点】解三角形及三角变换的公式等有关知识的综合运用.【易错点晴】应用题是高考必考的重要题型之一,也是检测数学知识在实际问题中的的运用的一种重要题型之一.求解这类问题的一般步骤是先仔细阅读题设中的文字信息.再将问题中的数量关系找出来,通过构造数量关系构建数学模型.最后运用数知识求解数学模型,依据题设写出答案.本题是以绿化过程中的一个实际问题为背景设置了一道最值问题,求解时,先,然后建立以为变量的函数关系式从而将问题进行转化求函数的最值问题.最后通过求该函数的最值,从而使得问题简捷巧妙获解.45.已知,则__________.【答案】【解析】试题分析: ,故应填答案.【考点】诱导公式及同角关系的综合运用.46.已知,且,则()A.B.C.D.【答案】C【解析】因为,所以,又因为,所以,故选C.【考点】1、诱导公式的应用;2、同角三角函数之间的关系.47.方程在区间内的解是.【答案】【解析】因为,所以,,即或,,,故答案为.【考点】1、特殊角的三角函数;2、简单的三角方程.【思路点睛】本题主要考查特殊角的三角函数、简单的三角方程,属于中档题.由于近年来高考对三角函数考查难度的降低,对三角方程的考查也以容易题和中档题为主,该题型往往根据特殊角的三角函数解答.本题首先将原方程变形为,然后根据的余弦值为,确定或,再根据确定方程的解.48.若,则的值为______.【答案】【解析】由,解得,又.【考点】三角函数的化简求值.49.在中,角的对边分别是,若,,则面积是_______.【答案】1【解析】在中,,,当且仅当时取等号, ,又,故,则面积是1【考点】正弦定理,基本不等式【易错点睛】在利用基本不等式求最值时,要特别注意“拆、拼、凑”等技巧,使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用,否则会出现错误.50.已知函数(,,)的最大值为3,的图象与轴的交点坐标为,其相邻两条对称轴间的距离为2,则的值为()A.2468B.3501C.4032D.5739【答案】C【解析】∵已知函数的最大值为,故.的图象与轴的交点坐标为,∵,∴,,即.再根据其相邻两条对称轴间的距离为,可得,,故函数的周期为.∵,∴,故选C.【考点】(1)三角函数中的恒等变换应用;(2)余弦函数的图象.51.在△中,,,所对的边分别是,,,,且,则的值为()A.B.C.D.【答案】B【解析】∵,∴,即.又∵,∴,∴,即,解得,故选B.【考点】余弦定理.52.若,则()A.1B.2C.3D.4【答案】B【解析】.【考点】三角恒等变换.53.在中,角,,的对边分别为,,,已知,,且.(1)求角的大小;(2)求的面积.【答案】(1);(2).【解析】(1)由,化简题设条件得,求得,即可求解角的值;(2)由余弦定理得,得到,再由条件,可化简求得,即可求解三角形的面积.试题解析:(1)∵,由,得,∴,整理得,解得,∵,∴.(2)由余弦定理得,即,∴,由条件,得,解得,∴.【考点】余弦定理及三角恒等变换.54.已知函数的最小正周期为,为了得到函数的图象,只要将的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度【答案】C【解析】∵函数的最小正周期为,∴,得,,故将的图象向左平移个单位长度可得,故选C.【考点】三角函数图象的变换.55.在三角形中,角,,所对的边分别是,,.已知,.(1)若,求的值;(2)若,求的值.【答案】(Ⅰ)(Ⅱ)【解析】(Ⅰ)已知两边一角求第三边,一般利用余弦定理,将角化为边的条件:,代入条件即得,(Ⅱ)同(Ⅰ)可先利用余弦定理,将角化为边的条件:,代入,可得,再利用余弦定理求,也可先利用正弦定理,将边的条件转化为角的关系,再根据正弦定理求的值试题解析:(1)由余弦定理,,…………………3分将,代入,解得:.…………………6分(2)由正弦定理,,化简得:,则,…………………8分因为,,所以,,所以或(舍去),则.………………10分由正弦定理可得,,将,代入解得.……………………14分【考点】正余弦定理【方法点睛】解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系,从而达到解决问题的目的.其基本步骤是:第一步:定条件,即确定三角形中的已知和所求,在图形中标出来,然后确定转化的方向.第二步:定工具,即根据条件和所求合理选择转化的工具,实施边角之间的互化.第三步:求结果.56.已知函数.⑴求的最小正周期和单调递增区间;⑵求在区间上的最大值和最小值.【答案】(1),增区间为;(2) 最大值为,最小值为.【解析】(1)借助题设条件余弦二倍角公式及余弦函数单调性求解;(2)依据题设运用余弦函数的有界性进行探求.试题解析:⑴由已知,有,所以的最小正周期,当时,单调递增,解得:,所以的单调递增区间为,⑵由⑴可知,在区间上是减函数,在区间上是增函数,而,,所以在区间上的最大值为,最小值为.【考点】余弦二倍角公式及余弦函数的图象和性质等有关知识的综合运用.57.已知,,分别为的三个内角,,所对边的边长,且满足.(Ⅰ)求;(Ⅱ)若,的面积为,求,.【答案】(Ⅰ);(Ⅱ).【解析】(Ⅰ)由正弦定理将条件中的边换为角的正弦,利用三角变换公式,化简可得,从而可求得角的值;(Ⅱ)由余弦定理及三角形面积公式列出关于的方程组,解之即可.试题解析:(Ⅰ),由正弦定理得:,…(2分),,…………(3分),,…(5分),…(6分)(Ⅱ),所以,……(7分),,则(或),……(8分)解得:.………(10分)【考点】1.正弦定理与余弦定理;2.三角恒等变换.【名师】本题考查正弦定理与余弦定理、三角恒等变换,属中档题;解三角形问题实质是附加条件的三角变换,因此在解三角形问题的处理中,正弦定理、余弦定理就起到了适时、适度转化边角的作用,分析近几年的高考试卷,有关的三角题,大部分以三角形为载体考查三角变换.58.已知函数与函数的部分图像如右图所示,则____________.【答案】【解析】令.【考点】1、三角函数的图象与性质;2、一次函数.59.要得到函数的图象,只需将函数的图象()A.向左平移个单位B.向左平移个单位C.向右平移个单位D.向右平移个单位【答案】C【解析】由题意得,,因此只需要将函数的图象向右平移个单位即可得到函数的图象,故选C.60.已知函数相邻两条对称轴之间的距离为.(I)求的值及函数的单调递减区间;(Ⅱ)已知分别为中角的对边,且满足,,求的面积.【答案】(I);(II).【解析】(I)利用降幂公式将函数化为,再由函数的图象相邻两条对称轴之间的距离为,求出,结合三角函数的单调性可得其单调区间;(Ⅱ)将代入函数解析式,结合的范围可求出的值,由正弦定理和余弦定理可求出边,故而可得三角形的面积.试题解析:解:(Ⅰ).因为相邻两条对称轴之间的距离为,所以,即,所以.所以.令,解得.所以的单调递减区间为.(Ⅱ)由得,因为.所以,.已知及正弦定理得.由余弦定理得,代入得,解得,所以.61. (江淮十校2017届高三第一次联考文数试题第7题)《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式为:弧田面积=1/2(弦矢+矢2).弧田(如图),由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为,半。
高考数学专题《三角恒等变换》习题含答案解析

专题5.4 三角恒等变换1.(2021·四川德阳市·高三二模(文))在平面直角坐标系中,已知点()2cos80,2sin80A︒︒,()2cos20,2sin20B︒︒,那么AB=()A.2 B.C.D.4【答案】A【解析】利用利用两点间的距离公式求得AB.【详解】AB==2====.故选:A2.(2018·全国高考真题(文))(2018年全国卷Ⅲ文)若sinα=13,则cos2α=()A.89B.79C.−79D.−89【答案】B【解析】cos2α=1−2sin2α=1−29=79故答案为B.3.(2021·商丘市第一高级中学高三月考(文))已知2sin21sin22πθθ⎛⎫-=+⎪⎝⎭,则tanθ的所有取值之和为()A.-5 B.-6 C.-3 D.2【答案】D练基础利用诱导公式和二倍角公式化简已知式,得到sin cos θθ=-或sin 3cos θθ=,即得tan θ的可能取值,求和即可. 【详解】依题意得,2cos21sin 2θθ-=+,即()()2222sincos sin cos θθθθ-=+,即()()()22sin cos sin cos sin cos θθθθθθ+-=+, 故sin cos 0θθ+=或()2sin cos sin cos θθθθ-=+,所以sin cos θθ=-或sin 3cos θθ=,可得tan 1θ=-或tan 3θ=, 所以tan θ的所有取值之和为2. 故选:D.4.(2021·北京北大附中高三其他模拟)已知()0,απ∈,且1cos 23α=,则sin α=( )A .3B .23C .13D .9【答案】A 【解析】由余弦的二倍角公式,先求出2sin α的值,结合角α的范围可得答案. 【详解】由21cos 212sin 3αα=-=,可得21sin 3α=又()0,απ∈,则sin α= 故选:A5.(2022·河南高三月考(理))若,2παπ⎛⎫∈ ⎪⎝⎭,且23cos sin 210αα-=,则tan α=( )A .-7B .13 C .17-D .-7或13【答案】A 【解析】利用二倍角公式及同角三角函数的基本关系将弦化切,再解方程即可;解:因为23cos sin 210αα-=, 所以2222cos sin 2cos 2sin cos 31sin cos 10ααααααα--==+,所以212tan 3tan 110αα-=+, 得23tan 20tan 70αα+-=, 则tan 7=-α或1tan 3α=, 又,2παπ⎛⎫∈⎪⎝⎭, 所以tan 7=-α. 故选:A6.(2021·江苏淮安市·高三三模)设2sin 46a =︒,22cos 35sin 35b =︒-︒,2tan321tan 32c ︒=-︒,则a ,b ,c 的大小关系为( )A .b c a <<B .c a b <<C .a b c <<D .b a c <<【答案】D 【解析】根据正弦函数的单调性,结合不等式性质,可得到a 的范围;利用二倍角公式化简b 、c ,结合函数单调性,可得到b 、c 的大致范围;从而,可以比较a 、b 、c 的大小. 【详解】因为sin 45sin 46sin 60︒<︒<︒,所以有222sin 45sin 46sin 60︒<︒<︒,即222(sin 46(22<︒<,所以1324a <<; 因为222cos 35sin 3512sin 35︒-︒=-︒,而sin30sin35sin 45︒<︒<︒, 所以有211sin 3542<︒<,所以21012sin 352<-︒<,即102b <<;因为22tan 3212tan 321tan 641tan 3221tan 322︒︒=⨯=︒-︒-︒,而tan 64tan 60︒>︒=所以2c >;显然,b a <,而22233()44c >=>,所以34c >,即c a > 所以b a c << 故选:D7.(2020·河北高三其他模拟(文))已知函数()22sin cos f x x x x ωωω=+(0>ω)的最小正周期为π,关于函数()f x 的性质,则下列命题不正确的是( ) A .1ω=B .函数()f x 在R 上的值域为[]1,3-C .函数()f x 在,63ππ⎡⎤-⎢⎥⎣⎦上单调递增 D .函数()f x 图象的对称轴方程为3x k ππ=+(k ∈Z )【答案】D 【解析】首先把函数的关系式进行恒等变换,把函数的关系式变形成正弦型函数,进一步利用函数的性质的应用求出结果. 【详解】解:函数()22sincos f x x x x ωωω=+1cos 222sin 216x x x πωωω⎛⎫=-+=-+ ⎪⎝⎭,由于函数()f x 的最小正周期为π,即22ππω=,所以1ω=,故A 正确; 故()2sin 216f x x π⎛⎫=-+ ⎪⎝⎭. 对于B :由于x ∈R ,所以函数()f x 的最小值为1-,函数的最大值为3,故函数的值域为[]1,3-,故B 正确; 对于C :当,63x ππ⎡⎤∈-⎢⎥⎣⎦时,2,622πππ⎡⎤-∈-⎢⎥⎣⎦x ,故函数在该区间上单调递增,故C 正确;对于D :当262x k πππ-=+,()k Z ∈时,整理得23k x ππ=+(k ∈Z )为函数的对称轴,故D 错误. 故选:D .8.(2020·全国高考真题(文))若2sin 3x =-,则cos2x =__________. 【答案】19【解析】22281cos 212sin 12()1399x x =-=-⨯-=-=.故答案为:19.9.(2021·贵溪市实验中学高二期末)tan 42tan1842tan18︒+︒︒︒的值是___________.【解析】由()tan18tan 42tan 60tan 18421tan18tan 42︒+︒︒=︒+︒==-︒⋅︒.【详解】解:由()tan18tan 42tan 60tan 18421tan18tan 42︒+︒︒=︒+︒==-︒⋅︒)tan18tan 421tan18tan 42∴︒+︒=-︒⋅︒tan18tan 42tan 42∴︒+︒︒⋅︒=10.(2021·山东高三其他模拟)若tan()4πα-=,则3cos 22απ⎛⎫+ ⎪⎝⎭=__________________. 【答案】﹣817【解析】先用诱导公式化简,再根据二倍角及22sin cos 1a a +=变形,再求值即可.【详解】解:因为tan (π﹣α)=﹣tan α=4, 所以tan α=﹣4, 则cos (2α+32π)=sin2α=2sin αcos α=222sin cos sin cos a a a a +=22tan 1tan a a +=﹣817. 故答案为:﹣817.1.(2021·广东佛山市·高三其他模拟)()sin 40tan103-=( ) A .2 B .-2C .1D .-1【答案】D 【解析】利用切化弦,三角恒等变换,逆用两角差的正弦公式,二倍角公式,诱导公式化简求值. 【详解】()sin 40tan103sin10=sin40(cos10sin10sin 40cos1012(sin10)22sin 40cos102(cos 60sin10sin 60cos10)sin 40cos102sin(1060)sin 40cos102sin 50sin 40cos102sin -︒︒⋅-︒︒︒=︒⋅︒︒︒=︒⋅︒︒⋅︒-︒⋅︒=︒⋅︒︒-︒=︒⋅︒-︒=︒⋅︒-=⋅40cos 40cos10sin 80cos101︒⋅︒︒-︒=︒=-2.(2021·沈阳市·辽宁实验中学高三二模)攒尖是古代中国建筑中屋顶的一种结构形式,宋代称为撮尖,清练提升代称攒尖.攒尖建筑的屋面在顶部交汇为一点,形成尖顶,依其平面有圆形攒尖、三角攒尖、四角攒尖、八角攒尖.也有单檐和重檐之分,多见于亭阁式建筑、园林建筑.辽宁省实验中学校园内的明心亭,为一个八角攒尖,它的主要部分的轮廓可近似看作一个正八棱锥,设正八棱锥的侧面等腰三角形的顶角为2θ,它的侧棱与底面内切圆半径的长度之比为( ). A.1sin θB.1cos θCD【答案】A 【解析】分别用SA 和θ表示出AB 的一半,得出侧棱与底面边长的比,再根据正八边形的结构特征求出底面内切圆的半径与边长的关系,即可求出结果. 【详解】设O 为正八棱锥S ABCDEFGH -底面内切圆的圆心,连接OA ,OB , 取AB 的中点M ,连接SM 、OM ,则OM 是底面内切圆半径R ,如图所示:设侧棱长为x ,底面边长为a ,由题意知2ASB θ∠=,ASM θ∠=,则12sin axθ=,解得2sin a x θ=;由底面为正八边形,其内切圆半径OM 是底面中心O 到各边的距离,AOB 中,45AOB ∠=︒,所以22.5AOM ∠=︒,由22tan 22.5tan 4511tan 22.5︒︒==-︒,解得tan 22.51︒=,所以12tan 22.512aa R R==︒=,所以2sin 12x R θ=,解得x R =,.故选:A .3.(2020·海南枫叶国际学校高一期中)若3cos 22sin()4παα=-,(,)2παπ∈则sin 2α的值为( )A.9-B.9-C .79-D .79【答案】C 【解析】因为3cos 22sin()4παα=-,所以3cos 22(sincos cossin )sin )44ππααααα=-=-,223(cos sin )sin )αααα-=-,3(cos sin )(cos sin )sin )αααααα+-=-,因为(,)2παπ∈,所以cos sin 0αα-≠,所以3(cos sin )αα+=所以cos sin 3αα+=, 两边平方得,212cos sin 9αα+= 所以7sin 29α=-, 故选:C4.(2019·江苏高考真题)已知tan 2π3tan 4αα=-⎛⎫+ ⎪⎝⎭,则πsin 24α⎛⎫+ ⎪⎝⎭的值是_____.【答案】10. 【解析】由()tan 1tan tan tan 2tan 1tan 13tan 1tan 4αααααπααα-===-++⎛⎫+ ⎪-⎝⎭,得23tan 5tan 20αα--=, 解得tan 2α=,或1tan 3α=-. sin 2sin 2cos cos 2sin 444πππααα⎛⎫+=+ ⎪⎝⎭)22222sin cos cos sin sin 2cos 2=22sin cos αααααααα⎛⎫+-=+ ⎪+⎝⎭222tan 1tan =2tan 1ααα⎫+-⎪+⎝⎭, 当tan 2α=时,上式222212==22110⎛⎫⨯+- ⎪+⎝⎭ 当1tan 3α=-时,上式=22112133=210113⎛⎫⎛⎫⎛⎫⨯-+--⎪ ⎪ ⎪⎝⎭⎝⎭⎪ ⎪⎛⎫-+ ⎪ ⎪⎝⎭⎝⎭综上,sin 2410πα⎛⎫+= ⎪⎝⎭ 5.(2021·全国高三其他模拟(理))已知函数2ππ()sin 6212x f x x ⎛⎫⎛⎫=+++- ⎪ ⎪⎝⎭⎝⎭[0,]m 上恰有10个零点,则m 的取值范围是________________. 【答案】55π61π,66⎡⎫⎪⎢⎣⎭【解析】先用降幂公式和辅助角公式化简()f x ,再转化为图象与x 轴交点个数问题. 【详解】 ∵()2ππππsin sin 1cos 621266x f x x x x ⎤⎛⎫⎛⎫⎛⎫⎛⎫=+++=+-+ ⎪ ⎪ ⎪ ⎪⎥⎝⎭⎝⎭⎝⎭⎝⎭⎦ π2sin 6x ⎛⎫=- ⎪⎝⎭,∴π()02sin 06f x x ⎛⎫=⇔-= ⎪⎝⎭,∵()f x 在[0,]m 上恰有10个零点, ∴πsin 06x ⎛⎫-= ⎪⎝⎭在[0,]m 上恰有10个解, ∴π9π10π6m -<,解得55π61π66m <, 故答案为:55π61π,66⎡⎫⎪⎢⎣⎭. 6.(2021·上海复旦附中高三其他模拟)已知函数()3sin 24cos2f x x x =+.若存在0x R ∈,对任意x ∈R ,都有()()0f x f x ≥成立.给出下列两个命题: (1)对任意x ∈R ,不等式()02f x f x π⎛⎫+⎪⎝⎭≤都成立. (2)存在512πθ>-,使得()f x 在005,12x x πθ⎛⎫-+ ⎪⎝⎭上单调递减. 则其中真命题的序号是__________.(写出所有真命题的序号) 【答案】(1)(2) 【解析】由辅助角公式可得()5sin(2)f x x ϕ=+,由题意可得0x 是()f x 的最小值点,()f x 关于0x x =对称,由三角函数的性质逐个分析各个选项,即可求得结论. 【详解】解:函数()3sin 24cos 25sin(2)f x x x x ϕ=+=+,其中ϕ为锐角,且3cos 5ϕ=, 由题意,0x 是()f x 的最小值点,所以()f x 关于0x x =对称, 因为()f x 的最小正周期22T ππ==,所以0()2f x π+为最大值,所以任意x ∈R ,0()()2f x f x π+,故(1)正确;因为函数()f x 在()00,2x k x k k Z πππ⎛⎫-++∈ ⎪⎝⎭上单调递减, 取4πθ=-,则00005,,1242x x x x πππ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭,所以()f x 即在005,124x x ππ⎛⎫-- ⎪⎝⎭内单调递减,故(2)正确;故答案为:(1)(2)7.(2021·全国高三其他模拟(文))已知角0,4πα⎛⎫∈ ⎪⎝⎭,,2πβπ⎛⎫∈⎪⎝⎭,若3sin 35πα⎛⎫-=- ⎪⎝⎭,1cos 32πβ⎛⎫-=- ⎪⎝⎭,则()cos αβ-=___________.【答案】410+- 【解析】根据,αβ的范围确定,33ππαβ--的范围,然后求出cos 3πα⎛⎫- ⎪⎝⎭和sin 3πβ⎛⎫- ⎪⎝⎭,将()cos αβ-变形为cos 33ππαβ⎡⎤⎛⎫⎛⎫-++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,结合两角和的余弦公式即可求解.【详解】 ∵0,4πα⎛⎫∈ ⎪⎝⎭,,2πβπ⎛⎫∈⎪⎝⎭, ∴3312πππα-<-<-,2336πππβ-<-<-, 又3sin 35πα⎛⎫-=- ⎪⎝⎭,1cos 032πβ⎛⎫-=-< ⎪⎝⎭,∴2332πππβ-<-<-∴4cos 35πα⎛⎫-=== ⎪⎝⎭,sin 32πβ⎛⎫-===-⎪⎝⎭ ∴()cos cos 33ππαβαβ⎡⎤⎛⎫⎛⎫-=-++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦cos cos sin sin 3333ππππαβαβ⎛⎫⎛⎫⎛⎫⎛⎫=----- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭413525⎛⎛⎫⎛⎫=⨯---⨯ ⎪ ⎪ ⎝⎭⎝⎭⎝⎭410+=-.故答案为:410+-. 8.(2021·江西新余市·高一期末(理))已知单位圆上第三象限内的一点P 沿圆周逆时针旋转4π到点Q ,若点Q 的横坐标为35,则点P 的横坐标为___________.【答案】10- 【解析】首先设(cos ,sin )2P πθθπθ⎛⎫-<<-⎪⎝⎭,根据题意得到cos ,sin 44ππθθ⎛⎫⎛⎫⎛⎫++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,从而得到3cos 45πθ⎛⎫+= ⎪⎝⎭,4sin 45πθ⎛⎫+=- ⎪⎝⎭,再根据cos cos 44ππθθ⎡⎤⎛⎫=+- ⎪⎢⎥⎝⎭⎣⎦求解即可.【详解】由题意设(cos ,sin )2P πθθπθ⎛⎫-<<-⎪⎝⎭, 从而点P 沿圆周逆时针旋转4π到点Q ,即Q 点坐标为cos ,sin 44ππθθ⎛⎫⎛⎫⎛⎫++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,所以3cos 45πθ⎛⎫+= ⎪⎝⎭,3,444πππθ⎛⎫+∈-- ⎪⎝⎭, ∵3cos 045πθ⎛⎫+=> ⎪⎝⎭,∴,424πππθ⎛⎫+∈-- ⎪⎝⎭,则4sin 45πθ⎛⎫+=- ⎪⎝⎭,所以cos cos cos cos sin sin 444444ππππππθθθθ⎡⎤⎛⎫⎛⎫⎛⎫=+-=+++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦34525210=⨯-⨯=-.所以点P 的横坐标为10-.故答案为:10-9.(2020·浙江吴兴�湖州中学高三其他)已知02πα<<,4sin 5α,1tan()3αβ-=-,则tan β=_______;sin())4βππβ+=+__.【答案】3 32【解析】 因为02πα<<,4sin 5α,所以3cos 5α===, 所以sin 4tan cos 3ααα==, 因为1tan()3αβ-=-所以tan tan()tan tan[()]1tan tan()ααββααβααβ--=--=+-415()33334151()339--===+⨯-,所以sin()sin tan 33cos sin 1tan 132)4βπββπββββ+---====---+,故答案为:3;32. 10.(2021·聊城市·山东聊城一中高三其他模拟)在①6x π=-是函数()f x 图象的一条对称轴,②12π是函数()f x 的一个零点,③函数()f x 在[],a b 上单调递增,且b a -的最大值为2π,这三个条件中任选一个,补充在下面问题中,并解答. 已知函数1()2sin cos (02)62f x x x πωωω⎛⎫=--<< ⎪⎝⎭,__________,求()f x 在,22ππ⎡⎤-⎢⎥⎣⎦上的单调递减区间.注:如果选择多个条件分别解答,按第一个解答计分. 【答案】选择见解析;单调递减区间为,26ππ⎡⎤--⎢⎥⎣⎦,,32ππ⎡⎤⎢⎥⎣⎦.【解析】利用三角函数恒等变换的应用化简函数解析式可得()sin(2)6f x x πω=-,若选①,利用正弦函数的对称性可得362k πωπππ--=+,k Z ∈,得32k ω=--,k Z ∈,又02ω<<,可得ω,可求()sin(2)6f x x π=-;若选②,由题意可得2126k ππωπ⨯-=,可得61k ω=+,k Z ∈,又02ω<<,可得ω,可求()sin(2)6f x x π=-;若选③,可求22T ππω==,可得1ω=,可得()sin(2)6f x x π=-,利用正弦函数的单调性,结合22xππ-,即可求解()f x 在[2π-,]2π上的单调递减区间.【详解】解:11()2sin cos 2sin cos cos sin sin 62662f x x x x x x πππωωωωω⎛⎫⎛⎫=--=+- ⎪ ⎪⎝⎭⎝⎭21sin sin 2x x x ωωω=+-12cos 222x x ωω=- sin x π⎛⎫=ω- ⎪⎝⎭26.①若6x π=-是函数()f x 图象的一条对称轴,则362k πωπππ--=+,k Z ∈,即233k πωππ-=+,k Z ∈, 得32k ω=--,k Z ∈,又02ω<<,∴当1k =-时,1ω=,()sin 26f x x π⎛⎫=- ⎪⎝⎭. ②若12π是函数()f x 的一个零点,则2126k ππωπ⨯-=,即66k ππωπ=+,k Z ∈,得61k ω=+,k Z ∈.又02ω<<,∴当0k =时,1ω=,所以,()sin 26f x x π⎛⎫=- ⎪⎝⎭. ③若()f x 在[],a b 上单调递增,且b a -的最大值为2π. 则22T ππω==,故1ω=,所以()sin 26f x x π⎛⎫=- ⎪⎝⎭.由3222262k x k πππππ+≤-≤+,k Z ∈, 得536k x k ππππ+≤≤+,k Z ∈, 令0k =,得536x ππ≤≤,令1k =-,得236k ππ-≤≤-, 又22x ππ-≤≤,所以()f x 在,22ππ⎡⎤-⎢⎥⎣⎦上的单调递减区间为,26ππ⎡⎤--⎢⎥⎣⎦,,32ππ⎡⎤⎢⎥⎣⎦.1.(2021·全国高考真题(文))函数()sin cos 33x xf x =+的最小正周期和最大值分别是( ) A .3π B .3π和2C .6πD .6π和2【答案】C 【解析】利用辅助角公式化简()f x ,结合三角函数最小正周期和最大值的求法确定正确选项. 【详解】由题,()34x f x π⎛⎫=+ ⎪⎝⎭,所以()f x 的最小正周期为2613T .故选:C .2.(2021·北京高考真题)函数()cos cos2f x x x =-,试判断函数的奇偶性及最大值( ) A .奇函数,最大值为2B .偶函数,最大值为2练真题C .奇函数,最大值为98D .偶函数,最大值为98【答案】D 【解析】由函数奇偶性的定义结合三角函数的性质可判断奇偶性;利用二倍角公式结合二次函数的性质可判断最大值. 【详解】由题意,()()()()cos cos 2cos cos2f x x x x x f x -=---=-=,所以该函数为偶函数,又2219()cos cos 22cos cos 12cos 48f x x x x x x ⎛⎫=-=-++=--+ ⎪⎝⎭, 所以当1cos 4x =时,()f x 取最大值98. 故选:D.3.(2019·全国高考真题(文))tan255°=( ) A .-2B .-C .2D .【答案】D 【解析】000000tan 255tan(18075)tan 75tan(4530)=+==+=0001tan 45tan 3021tan 45tan 30+==+- 4.(2019·全国高考真题(文理))已知a ∈(0,π2),2sin2α=cos2α+1,则sinα=( ) A .15 B.5C.3D.5【答案】B 【解析】2sin 2cos21α=α+,24sin cos 2cos .0,,cos 02π⎛⎫∴α⋅α=αα∈∴α> ⎪⎝⎭.sin 0,2sin cos α>∴α=α,又22sin cos 1αα+=,2215sin 1,sin 5∴α=α=,又sin 0α>,sin 5α∴=,故选B . 5.(2020·全国高考真题(理))已知2tan θ–tan(θ+π4)=7,则tan θ=( ) A .–2 B .–1C .1D .2【答案】D 【解析】2tan tan 74πθθ⎛⎫-+= ⎪⎝⎭,tan 12tan 71tan θθθ+∴-=-,令tan ,1t t θ=≠,则1271tt t+-=-,整理得2440t t -+=,解得2t =,即tan 2θ=. 故选:D.6.(2020·全国高考真题(文))已知πsin sin =31θθ⎛⎫++ ⎪⎝⎭,则πsin =6θ⎛⎫+ ⎪⎝⎭( )A .12B C .23D 【答案】B 【解析】由题意可得:1sin sin 122θθθ++=,则:3sin cos 122θθ+=,1cos 223θθ+=,从而有:sin coscos sin66ππθθ+=,即sin 6πθ⎛⎫+= ⎪⎝⎭故选:B.。
高三数学三角恒等变换试题答案及解析

高三数学三角恒等变换试题答案及解析1.已知,则()A.B.C.D.【答案】B【解析】将两边平方得,,可得,故选B.【考点】同角基本关系以及二倍角公式.2.已知cos(α-)+sinα=,则sin(α+)的值是()A.-B.C.-D.【答案】C【解析】cos(α-)+sinα=⇒sinα+cosα=⇒sin(α+)=,所以sin(α+)=-sin(α+)=-.3.已知函数f(x)=cos2ωx+sinωxcosωx-(ω>0)的最小正周期为π.(1)求ω值及f(x)的单调递增区间;(2)在△ABC中,a,b,c分别是角A,B,C的对边,已知a=1,b=,f()=,求角C 的大小.【答案】(1)增区间为[kπ-,kπ+](k∈Z)(2)当B=时,C=π--=;当B=时,C=π--=.【解析】解:(1)f(x)=+sin2ωx-=sin(2ωx+).∵T=π,∴ω=1,∴f(x)=sin(2x+),增区间为[kπ-,kπ+](k∈Z).(2)∵f()=sin(A+)=,角A为△ABC的内角且a<b,∴A=.又a=1,b=,∴由正弦定理得=,也就是sinB==×=.∵b>a,∴B=或B=,当B=时,C=π--=;当B=时,C=π--=.4.已知α,β∈(0,),满足tan(α+β)=4tanβ,则tanα的最大值是()A.B.C.D.【答案】B【解析】tanα=tan[(α+β)-β]==≤=,当且仅当tanβ=时等号成立.5.在中,若分别为的对边,且,则有()A.a、c、b成等比数列B.a、c、b成等差数列C.a、b、c成等差数列D.a、b、c成等比数列【答案】D【解析】由已知得,,故,又,而,故,所以,故,从而a、b、c成等比数列.【考点】1、两角和与差的余弦公式;2、二倍角公式;3、正弦定理.6.在△ABC中,角A,B,C的对边分别为a,b,c,已知,b sin=a+c sin,则C= .【答案】【解析】由已知得,所以,由,应用正弦定理,得,.整理得,即,由于,从而,又,故.【考点】1正弦定理;2正弦两角和差公式。
专题5.5 三角恒等变换(解析版)

专题5.5三角恒等变换(一)两角和与差的正弦、余弦、正切公式1.C (α-β):cos(α-β)=cos αcos β+sin αsin β;C (α+β):cos(α+β)=cos αcos_β-sin_αsin β;S (α+β):sin(α+β)=sin αcos β+cos αsin β;S (α-β):sin(α-β)=sin_αcos_β-cos αsin β;T (α+β):tan(α+β)=tan α+tan β1-tan αtan β;T (α-β):tan(α-β)=tan α-tan β1+tan αtan β.2.变形公式:tan α±tan β=tan(α±β)(1∓tan αtan β);4sin(2cos sin πααα±=±.sin αsin β+cos(α+β)=cos αcos β,cos αsin β+sin(α-β)=sin αcos β,3.辅助角公式:函数f(α)=acos α+bsin α(a ,b 为常数),可以化为f(α)=a 2+b 2sin(α+φ)或f(α)=a 2+b 2cos(α-φ),其中φ可由a ,b 的值唯一确定.(二)二倍角的正弦、余弦、正切公式1.S 2α:sin 2α=2sin αcos α;C 2α:cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α;T 2α:tan 2α=2tan α1-tan 2α2.变形公式:(1)降幂公式:cos 2α=1+cos 2α2,sin 2α=1-cos 2α2,sin αcos α=12sin 2α.(2)升幂公式1+cos α=2cos 2α2;1-cos α=2sin 2α2;1+sin αα2+cos ;1-sin αα2-cos .(3)配方变形:1+sin 2α=(sin α+cos α)2,1-sin 2α=(sin α-cos α)21±sin αsin α2±cos 1+cos α=2cos 2α2,1-cos α=2sin 2α2(4)sin 2α=2sin αcos αsin 2α+cos 2α=2tan α1+tan 2α;cos 2α=cos 2α-sin 2αcos 2α+sin 2α=1-tan 2α1+tan 2α.tanα2=sin α1+cos α=1-cos αsin α.(三)常见变换规律(1)角的变换:明确各个角之间的关系(包括非特殊角与特殊角、已知角与未知角),熟悉角的变换技巧,及半角与倍角的相互转化,如:2α=(α+β)+(α-β),α=(α+β)-β=(α-β)+β,40°=60°-20°=π2,α2=2×α4等.(2)名的变换:明确各个三角函数名称之间的联系,常常用到同角关系、诱导公式,把正弦、余弦化为正切,或者把正切化为正弦、余弦.一、单选题1.sin 40sin 50cos 40cos50︒︒-︒︒等于()A .1-B .1C .0D .cos10-︒【答案】C【解析】由两角和的余弦公式得:()()sin 40sin 50cos 40cos50cos 40cos50sin 40sin 50cos 4050cos900︒︒-︒︒=-︒︒-︒︒=-+=-=故选:C2.已知()5cos 2cos 22παπα⎛⎫-=+ ⎪⎝⎭,且()1tan 3αβ+=,则tan β的值为()A .7-B .7C .1D .1-【答案】D【解析】:因为()5cos 2cos 22παπα⎛⎫-=+ ⎪⎝⎭,所以sin 2cos αα=,所以sin tan 2cos ααα==,又()1tan 3αβ+=,所以()()()12tan tan 3tan tan 111tan tan 123αβαβαβααβα-+-=+-===-⎡⎤⎣⎦+++⨯.故选:D3.已知,αβ均为锐角,且1sin 2sin ,cos cos 2αβαβ==,则()sin αβ-=()A .35B .45C.3D .23【答案】A【解析】:因为1sin 2sin ,cos cos 2αβαβ==,所有22221sin cos 4sin cos 14ααββ+=+=,则2153sin 44β=,又,αβ均为锐角,所以sin β=cos β=所以sin αα==所以()3sin sin cos cos sin 5αβαβαβ-=-=.故选:A.4.已知()1sin 5αβ+=,()3sin 5αβ-=,则tan tan αβ的值为()A .2B .2-C .12D .12-【答案】B【解析】()()1sin sin cos cos sin 53sin sin cos cos sin 5αβαβαβαβαβαβ⎧+=+=⎪⎪⎨⎪-=-=⎪⎩,解得2sin cos 51cos sin 5αβαβ⎧=⎪⎪⎨⎪=-⎪⎩,所以tan sin cos 2tan cos sin ααββαβ==-.故选:B5.已知sin sin 13πθθ⎛⎫++= ⎪⎝⎭,则tan 6πθ⎛⎫+= ⎪⎝⎭()ABC .D .±22【答案】D【解析】sin sin()13πθθ++=,则1sin sin cos 122θθθ++=,即3sin 122θθ+=,故1sin cos 223θθ+=,所以sin 6πθ⎛⎫+= ⎪⎝⎭cos 63πθ⎛⎫+=± ⎪⎝⎭,所以tan 62πθ⎛⎫+=± ⎪⎝⎭故选:D6.下面公式正确的是()A .3sin cos 2πθθ⎛⎫+= ⎪⎝⎭B .2cos212cos θθ=-C .3cos sin 2πθθ⎛⎫+=- ⎪⎝⎭D .cos()sin 2πθθ-=【答案】D 【解析】对A ,3sin cos 2πθθ⎛⎫+=- ⎪⎝⎭,故A 错误;对B ,2cos 22cos 1θθ=-,故B 错误;对C ,3cos sin 2πθθ⎛⎫+= ⎪⎝⎭,故C 错误;对D ,cos()sin 2πθθ-=,故D 正确;故选:D7.已知2tan()5αβ+=,1tan()44πβ-=,则tan()4πα+的值为()A .16B .322C .2213D .1318【答案】B【解析】:因为2tan()5αβ+=,1tan()44πβ-=,所以()tan()tan 44ππααββ⎡⎤⎛⎫+=+-- ⎪⎢⎥⎝⎭⎣⎦()()tan tan 41tan tan 4παββπαββ⎛⎫+-- ⎪⎝⎭=⎛⎫++- ⎪⎝⎭213542122154-==+⨯.故选:B 8.设1cos1022a =-,22tan131tan 13b =+,c =,则a ,b ,c 大小关系正确的是()A .a b c <<B .c b a <<C .a c b <<D .b c a<<【答案】C【解析】()1cos10cos 6010cos 70sin 202a =︒=︒+︒=︒=︒,2222sin132tan13cos132sin13cos13sin 26sin 131tan 131cos 13b ︒︒︒===︒︒=︒︒+︒+︒,sin 25c =,因为函数sin y x =在0,2π⎛⎫⎪⎝⎭上是增函数,故sin 20sin 25sin 26<<,即a c b <<.故选:C.9.已知sin()63πα+=-,则2cos(2)3πα-=()A .23-B .13-C .23D .13【答案】B 【解析】:因为sin()6πα+=2cos 2cos 263παππα⎡⎤⎛⎫⎛⎫-=-⎪ ⎪⎢⎥⎝⎭⎣+⎭⎝⎦6cos 2πα⎪+⎛⎫=- ⎝⎭212n 6si πα⎡⎤⎛⎫=-- ⎪⎢⎥⎭⎣+⎝⎦21123⎡⎤⎛⎢⎥=--=- ⎢⎥⎝⎭⎣⎦故选:B 10.若11tan ,tan()72βαβ=+=,则tan =α()A .115B .112C .16D .13【答案】D【解析】:因为11tan ,tan()72βαβ=+=,所以()()()11tan tan 127tan =tan 111tan tan 3127αββααββαββ-+-+-===⎡⎤⎣⎦+++⨯.故选:D.11.已知3cos 16παα⎛⎫--= ⎪⎝⎭,则sin 26πα⎛⎫+= ⎪⎝⎭()A .13-B .13C.3-D.3【答案】B【解析】:因为3cos 16παα⎛⎫--= ⎪⎝⎭,即3cos cos sin sin 166ππααα⎛⎫-+= ⎪⎝⎭,即13cos sin 122ααα⎫-+=⎪⎪⎝⎭3sin 12αα-=1cos 123πααα⎫⎛⎫=+=⎪ ⎪⎪⎝⎭⎭,所以cos 3πα⎛⎫+= ⎪⎝⎭所以sin 2cos 2662πππαα⎛⎫⎛⎫+=-++ ⎪ ⎪⎝⎭⎝⎭2cos 22cos 133ππαα⎡⎤⎛⎫⎛⎫=-+=-+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦21213⎡⎤⎢⎥=--=⎢⎥⎝⎭⎣⎦.故选:B 12.已知4sin 5α=,π5,π,cos ,213αββ⎛⎫∈=- ⎪⎝⎭是第三象限角,则()cos αβ-=()A .3365-B .3365C .6365D .6365-【答案】A【解析】由4sin 5α=,π,π2α⎛⎫∈ ⎪⎝⎭,可得3cos 5α=-由5cos ,13ββ=-是第三象限角,可得12sin 13β=-则()3541233cos cos cos sin sin 51351365αβαβαβ⎛⎫⎛⎫⎛⎫-=+=-⨯-+⨯-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭故选:A13.若sin 25α=,()sin 10βα-=,且,4απ⎡⎤∈π⎢⎥⎣⎦,3,2βππ⎡⎤∈⎢⎥⎣⎦,则αβ+的值是()A .54πB .74πC .54π或74πD .54π或94π【答案】B【解析】,,2,242ππαπαπ⎡⎤⎡⎤∈∴∈⎢⎥⎢⎥⎣⎦⎣⎦,又∵sin 2,2,,,242πππααπα⎡⎤⎡⎤=∴∈∈⎢⎥⎢⎥⎣⎦⎣⎦,∴cos 25α==-.又∵35,,,224πππβπβα⎡⎤⎡⎤∈∴-∈⎢⎥⎢⎥⎣⎦⎣⎦,∴()cos βα-==,于是()()()()cos cos 2cos 2cos sin 2sin αβαβααβααβα+=+-=---⎡⎤⎣⎦5105102⎛⎛⎫=---= ⎪ ⎪⎝⎭⎝⎭,易得5,24αβπ⎡⎤+∈π⎢⎥⎣⎦,则74αβπ+=.故选:B.14.)sin20tan50=()A .12B .2C D .1【答案】D【解析】原式()()()()sin20sin 50cos502sin 20sin 50602sin 20sin 9020cos50cos50cos 9050++===-2sin 20cos 20sin 401sin 40sin 40===.故选:D.15.若1cos ,sin(),0722ππααβαβ=+=<<<<,则角β的值为()A .3πB .512πC .6πD .4π【答案】A 【解析】∵0,022ππαβ<<<<,0αβπ∴<+<,由1cos 7α=,()sin αβ+=,得sin α=11cos()14αβ+=±,若11cos()14αβ+=,则sin sin[()]βαβα=+-sin()cos cos()sin αβααβα=+-+1110714=-<,与sin 0β>矛盾,故舍去,若11cos()14αβ+=-,则cos cos[()]βαβα=+-cos()cos sin()sin αβααβα=+++111147147=-⨯+⨯12=,又(0,)2πβ∈,3πβ∴=.故选:A.16.若7171212ππα<<,且7cos 268πα⎛⎫+=- ⎪⎝⎭,则5cos 12πα⎛⎫-=⎪⎝⎭()A .B .CD .14-【答案】A【解析】由27cos 212sin 6128ππαα⎛⎫⎛⎫+=-+=- ⎪ ⎪⎝⎭⎝⎭,得215sin 1216πα⎛⎫+= ⎪⎝⎭.因为7171212ππα<<,所以233122πππα<+<,所以sin 122πα⎛⎫⎛⎫+∈- ⎪ ⎪ ⎪⎝⎭⎝⎭,所以15sin 124πα⎛⎫+= ⎪⎝⎭所以5cos cos sin 1221212ππππααα⎛⎫⎛⎫⎛⎫⎛⎫-=-+=+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭故选:A17.已知sin cos αα-=0απ≤≤,则sin 23πα⎛⎫-= ⎪⎝⎭()A B .34410-C .D 【答案】D【解析】:因为sin cos αα-=()22sin cos αα-=⎝⎭,即222sin 2sin cos cos 5αααα-+=,即21sin 25α-=,所以3sin 25α=,又sin cos 45πααα⎛⎫-=-=⎪⎝⎭,即2sin 42πα⎛⎫-= ⎪⎝⎭,因为0απ≤≤,所以3444πππα-≤-≤,所以044ππα<-≤,即42ππα<≤,所以22παπ<≤,所以4cos 25α==-,所以sin 2sin 2cos cos 2sin333πππααα⎛⎫-= ⎪⎝⎭23145252⎛⎫=⨯--⨯ ⎪⎝⎭故选:D18.若10,0,cos ,cos 2243423ππππβαβα⎛⎫⎛⎫<<-<<+=-= ⎪ ⎪⎝⎭⎝⎭,则cos 2βα⎛⎫+= ⎪⎝⎭()A B .C D .【答案】C 【解析】cos cos cos cos sin sin 2442442442βππβππβππβαααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+=+--=+-++- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,因为0,022ππαβ<<-<<所以3,444πππα⎛⎫+∈ ⎪⎝⎭,,4242πβππ⎛⎫-∈ ⎪⎝⎭,因为1cos 43πα⎛⎫+= ⎪⎝⎭,cos 423πβ⎛⎫-= ⎪⎝⎭所以sin 4πα⎛⎫+ ⎪⎝⎭sin 42πβ⎛⎫-= ⎪⎝⎭则122cos 233βα⎛⎫+=+ ⎪⎝⎭C 19.已知π43cos sin 65αα⎛⎫-+= ⎪⎝⎭,则2πcos 3α⎛⎫+ ⎪⎝⎭的值是()A .45-B .45C .5-D .5【答案】A【解析】由πcos sin 6αα⎛⎫-+= ⎪⎝⎭ππ3πcos cossin sin sin sin 6623αααααα⎛⎫++=+=-=⎪⎝⎭,所以,π4cos 35α⎛⎫-= ⎪⎝⎭,所以,2πππ4cos cos πcos 3335ααα⎛⎫⎛⎫⎛⎫⎛⎫+=--=--=-⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.故选:A.20.已知,2παπ⎛⎫∈ ⎪⎝⎭,且2sin 45πα⎛⎫+= ⎪⎝⎭,则cos()α-=()A .10B .10C .10-D .222110【答案】C【解析】因为,2παπ⎛⎫∈ ⎪⎝⎭,所以35,444πππα⎛⎫+∈ ⎪⎝⎭.又2sin 45πα⎛⎫+= ⎪⎝⎭,所以cos 45πα⎛⎫+==- ⎪⎝⎭,cos()cos cos cos cos sin sin 44444410ππππππααααα⎡⎤⎛⎫⎛⎫⎛⎫-==+-=+++=⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦故选:C.二、多选题21.对于函数()sin 22f x x x =,下列结论正确的是()A .()f x 的最小正周期为πB .()f x 的最小值为2-C .()f x 的图象关于直线6x π=-对称D .()f x 在区间,26ππ⎛⎫-- ⎪⎝⎭上单调递增【答案】AB【解析】()1sin 222(sin 2cos 2)2sin(2)223f x x x x x x π=+=+=+,22T ππ==,A 正确;最小值是2-,B 正确;(2sin()0633f πππ-=-+=,C 错误;(,26x ππ∈--时,22(,0)33x ππ+∈-,232x ππ+=-时,()f x 得最小值2-,因此函数不单调,D 错误,故选:AB .22)A .222cos2sin 1212ππ-B .1tan151tan15+︒-︒C .cos 75︒︒D .cos15︒︒【答案】ABC【解析】A :222cos 2sin 2cos 12126πππ-==B :1tan15tan 45tan15tan 601tan151tan 45tan15+︒︒+︒==︒=-︒-︒︒C :cos 754sin15230︒︒=︒︒=︒=D :cos152sin(3015)2sin15︒︒=︒-︒=︒.故选:ABC23.已知函数2()sin 222x x xf x =-,则下列结论正确的有()A .()f x 的最小正周期为4πB .直线23x π=-是()f x 图象的一条对称轴C .()f x 在0,2π⎛⎫⎪⎝⎭上单调递增D .若()f x 在区间,2m π⎡⎤-⎢⎥⎣⎦上的最大值为12,则3m π≥【答案】BD【解析】:()21cos 1cos sin sin 222262x x x xf x x x π-⎛⎫=-=-=+- ⎪⎝⎭,所以()f x 的最小正周期为2,π故A 不正确;因为2362πππ-+=-,所以直线23x π=-是()f x 图象的一条对称轴,故B 正确;当02x π<<时,2+663x πππ<<,而函数sin y x =在2,63ππ⎛⎫⎪⎝⎭上不单调,故C 不正确;当2x m π-≤≤时,++366x m πππ-≤≤,因为()f x 在区间,2m π⎡⎤-⎢⎥⎣⎦上的最大值为12,即11sin 622x π⎛⎫+-≤ ⎪⎝⎭,所以sin 16x π⎛⎫+≤ ⎪⎝⎭,所以+62m ππ≥,解得3m π≥,故D 正确.故选:BD.24.已知函数22()cos cos sin (0)f x x x x x ωωωωω=+->的周期为π,当π[0]2x ∈,时,()f x 的()A .最小值为2-B .最大值为2C .零点为5π12D .增区间为π06⎡⎤⎢⎥⎣⎦,【答案】BCD【解析】22()cos cos sin (0)f x x x x x ωωωωω=+->2cos 2x xωω=+2sin 26x πω⎛⎫=+ ⎪⎝⎭,因为()f x 的周期为π,所以22ππω=,得1ω=,所以()2sin 26f x x π⎛⎫=+ ⎪⎝⎭,当π[0]2x ∈,时,72,666x πππ⎡⎤+∈⎢⎥⎣⎦,所以1sin 2126x π⎛⎫-≤+≤ ⎪⎝⎭,所以12sin 226x π⎛⎫-≤+≤ ⎪⎝⎭,所以()f x 的最小值为1-,最大值为2,所以A 错误,B 正确,由()2sin 206f x x π⎛⎫=+= ⎪⎝⎭,72,666x πππ⎡⎤+∈⎢⎥⎣⎦,得26x ππ+=,解得512x π=,所以()f x 的零点为5π12,所以C 正确,由2662x πππ≤+≤,得06x π≤≤,所以()f x 的增区间为π06⎡⎤⎢⎣⎦,,所以D 正确,故选:BCD25.关于函数()cos 2cos f x x x x =-,下列命题正确的是()A .若1x ,2x 满足12πx x -=,则()()12f x f x =成立;B .()f x 在区间ππ,63⎡⎤-⎢⎥⎣⎦上单调递增;C .函数()f x 的图象关于点π,012⎛⎫⎪⎝⎭成中心对称;D .将函数()f x 的图象向左平移7π12个单位后将与2sin 2y x =的图象重合.【答案】ACD 【解析】()1cos 2cos cos 222cos 222f x x x x x x x x ⎛⎫=-== ⎪ ⎪⎝⎭π2cos 23x ⎛⎫=+ ⎪⎝⎭,对于A ,若1x ,2x 满足12πx x -=,则()()()1222ππ2cos 2π2cos 233f x x x f x ⎡⎤⎛⎫=++=+= ⎪⎢⎥⎣⎦⎝⎭成立,故A 正确;对于B ,由ππ2π22π2π,3k x k k Z +≤+≤+∈,得:π5πππ,36k x k k +≤≤+∈Z ,即()f x 在区间π5π,36⎡⎤⎢⎣⎦上单调递增,故B 错误;对于C ,因为πππ2cos 2012123f ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭,所以函数()f x 的图象关于点π,012⎛⎫⎪⎝⎭成中心对称,故C 正确;对于D ,将函数()f x 的图象向左平移7π12个单位后得到7π7ππ3π2cos 22cos 22sin 2121232y f x x x x ⎡⎤⎛⎫⎛⎫⎛⎫=+=++=+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,其图象与2sin 2y x =的图象重合,故D 正确.故选:ACD 三、解答题26.求下列各式的值(1)cos54cos36sin54sin36⋅-⋅(2)sin7cos37cos(7)sin(37)⋅+-⋅-(3)ππcos sin 1212⋅(4)22ππsincos 88-【答案】(1)0;(2)12-;(3)14;(4)2-.【解析】(1)cos54cos36sin54sin36cos(5436)cos900⋅-⋅=+==.(2)sin7cos37cos(7)sin(37)sin7cos37cos7sin37⋅+-⋅-=⋅-⋅1sin(737)sin(30)2=-=-=-.(3)ππ1π1cossin 1212264⋅==.(4)22πππsin cos cos 8842-=-=-.27.已知3sin 5α=,其中2απ<<π.(1)求tan α;(2)若0,cos 2πββ<<=()sin αβ+的值.【答案】(1)34-(2)5-【解析】(1)由3sin 5α=可得4cos 5α=±,因为2απ<<π,故4cos 5α=-,进而sin 3tan cos 4ααα==-(2)π0,cos 2ββ<<=,故sin β==;()34sin =sin cos cos sin 55αβαβαβ++==28.已知角α为锐角,2πβαπ<-<,且满足1tan23=α,()sin 10βα-=(1)证明:04πα<<;(2)求β.【答案】(1)证明见解析(2)3.4πβ=【解析】(1)证明:因为1tan23α=,所以2122tan332tan 1tan 1441tan 129απαα⨯===<=--,因为α为锐角且函数tan y x =在0,2π⎛⎫⎪⎝⎭上单调递增,所以04πα<<(2)由22sin 3tan cos 4sin cos 1ααααα⎧==⎪⎨⎪+=⎩,结合角α为锐角,解得3sin 5α=,4cos 5α=,因为2πβαπ<-<,且()sin 10βα-=所以()cos βα-==()()()sin sin sin cos cos sin βαβααβααβα⎡⎤=+-=-+-⎣⎦3247225105102⎛=⨯-+⨯ ⎝⎭又5224πππαβπα<+<<+<,所以3.4πβ=29.已知α,β为锐角,π33sin 314α⎛⎫-=⎪⎝⎭,()11cos 14αβ+=-.(1)求cos α的值;(2)求角β.【答案】(1)17(2)π3【解析】(1)因为π0,2α⎛⎫∈ ⎪⎝⎭,所以ππ336πα⎛⎫-∈ ⎪⎝⎭-,,又π33sin 314α⎛⎫-=⎪⎝⎭所以π13cos 314α⎛⎫-== ⎪⎝⎭所以ππcos =cos +33αα⎡⎤⎛⎫- ⎪⎢⎥⎝⎭⎣⎦ππππ1cos cos sin sin =33337αα⎛⎫⎛⎫=--- ⎪ ⎪⎝⎭⎝⎭(2)因为α,β为锐角,所以0αβ<+<π,则()sin 0αβ+>,因为()11cos 14αβ+=-,所以()sin 14αβ+==.又α为锐角,1cos 7α=,所以sin α==,故()()()sin sin sin cos cos sin βαβααβααβα=+-=+-+⎡⎤⎣⎦111714=+=因为β为锐角,所以π3β=.30.已知sincos22αα-=(1)求sin α的值;(2)若αβ,都是锐角,()3cos 5αβ+=,求sin β的值.【答案】(1)12【解析】(1)解:2221sin cos sin 2sin cos cos 1sin 2222222a αααααα⎛⎫-=-+=-= ⎪⎝⎭,1sin 2a =.(2)因为αβ,都是锐角,所以0αβ<+<π,()4sin 5αβ+==,13sin cos 22a a =⇒=,()()()43sin cos c 0s 13si o 55n sin sin 221αβααβααββα-=-+=+-=+-=⨯⨯⎡⎤⎣⎦31.已知tan ,tan αβ是方程23570x x +-=的两根,求下列各式的值:(1)()tan αβ+(2)()()sin cos αβαβ+-;(3)()cos 22αβ+.【答案】(1)12-(2)54(3)35【解析】(1)由题意可知:57tan tan ,tan tan 33αβαβ+=-=-()5tan tan 13tan 71tan tan 213αβαβαβ-++===--+(2)()()5sin sin cos cos sin tan tan 537cos cos cos sin sin 1tan tan 413αβαβαβαβαβαβαβαβ-+++====-++-(3)()22222211cos ()sin ()1tan ()34cos 221cos ()sin ()1tan ()514αβαβαβαβαβαβαβ-+-+-++====++++++。
高考真题与模拟训练 专题07 三角恒等变换(解析版)

专题7 三角恒等变换第一部分 近3年高考真题一、选择题1.(2021·浙江高考真题)已知,,αβγ是互不相同的锐角,则在sin cos ,sin cos ,sin cos αββγγα三个值中,大于12的个数的最大值是( )A .0B .1C .2D .3【答案】C【解析】法1:由基本不等式有22sin cos sin cos 2αβαβ+≤,同理22sin cos sin cos 2βγβγ+≤,22sin cos sin cos 2γαγα+≤,故3sin cos sin cos sin cos 2αββγγα++≤,故sin cos ,sin cos ,sin cos αββγγα不可能均大于12.取6πα=,3πβ=,4πγ=,则1111sin cos ,sin cos ,sin cos 424242αββγγα=<=>=>,故三式中大于12的个数的最大值为2,故选:C.法2:不妨设αβγ<<,则cos cos cos ,sin sin sin αβγαβγ>><<,由排列不等式可得:sin cos sin cos sin cos sin cos sin cos sin cos αββγγααγββγα++≤++,而()13sin cos sin cos sin cos sin sin 222αγββγαγαβ++=++≤,故sin cos ,sin cos ,sin cos αββγγα不可能均大于12.取6πα=,3πβ=,4πγ=,则1111sin cos ,sin cos ,sin cos 424242αββγγα=<=>=>,故三式中大于12的个数的最大值为2,故选:C.2.(2021·全国高考真题(理))2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为8848.86(单位:m ),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,现有A ,B ,C 三点,且A ,B ,C 在同一水平面上的投影,,A B C '''满足45A C B ∠'''=︒,60A B C ''∠'=︒.由C 点测得B 点的仰角为15︒,BB '与CC '的差为100;由B 点测得A 点的仰角为45︒,则A ,C 两点到水平面A B C '''的高度差AA CC ''- 1.732≈)( )A .346B .373C .446D .473【答案】B【解析】过C作'CH BB ⊥,过B作'BD AA ⊥,故()''''''100100AA CC AA BB BH AA BB AD -=--=-+=+,由题,易知ADB △为等腰直角三角形,所以AD DB =.所以''100''100AA CC DB A B -=+=+.因为15BCH ∠=︒,所以100''tan15CH C B ==︒在'''A B C 中,由正弦定理得:''''100100sin 45sin 75tan15cos15sin15A B C B ===︒︒︒︒︒,而sin15sin(4530)sin 45cos30cos 45sin 304︒=︒-︒=︒︒-︒︒=,所以1004''1)273A B ⨯⨯==≈,所以''''100373AA CC A B -=+≈.故选:B .3.(2020·全国高考真题(理))已知2tan θ–tan(θ+π4)=7,则tan θ=( )A .–2B .–1C .1D .2【解析】2tan tan 74πθθ⎛⎫-+= ⎪⎝⎭ ,tan 12tan 71tan θθθ+∴-=-,令tan ,1t t θ=≠,则1271tt t+-=-,整理得2440t t -+=,解得2t =,即tan 2θ=.故选:D.4.(2020·全国高考真题(文))已知πsin sin =31θθ⎛⎫++ ⎪⎝⎭,则πsin =6θ⎛⎫+ ⎪⎝⎭( )A .12B .3C .23D .2【答案】B【解析】由题意可得:1sin sin cos 122θθθ++=,则:3sin cos 122θθ+=,1sin cos 223θθ+=,从而有:sin coscos sin 663ππθθ+=,即sin 63πθ⎛⎫+= ⎪⎝⎭.故选:B.5.已知α ∈(0,π2),2sin2α=cos2α+1,则sinα=A .15B .5C .3D .5【解析】2sin 2cos 21α=α+ ,24sin cos 2cos .0,,cos 02π⎛⎫∴α⋅α=αα∈∴α> ⎪⎝⎭.sin 0,2sin cos α>∴α=α,又22sin cos 1αα+=,2215sin 1,sin 5∴α=α=,又sin 0α>,sin 5α∴=,故选B .6.已知函数()222cos sin 2f x x x =-+,则( )A .()f x 的最小正周期为π,最大值为3B .()f x 的最小正周期为π,最大值为4C .()f x 的最小正周期为2π,最大值为3D .()f x 的最小正周期为2π,最大值为4【答案】B【解析】根据题意有()1cos2x 35cos212cos2222f x x x -=+-+=+,所以函数()f x 的最小正周期为22T ππ==,且最大值为()max 35422f x =+=,故选B.7.已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点()1A a ,,()2B b ,,且2cos23α=,则a b -=( )A .15B .5C .5D .1【答案】B 【解析】由,,O A B三点共线,从而得到2b a=,因为222cos22cos 1213αα⎛⎫=-=⋅-=,解得215a =,即5a =,所以25a b a a -=-=,故选B.二、填空题8.(2020·全国高考真题(文))若2sin 3x =-,则cos 2x =__________.【答案】19【解析】22281cos 212sin 12(1399x x =-=-⨯-=-=.故答案为:19.9.(2020·江苏高考真题)已知2sin ()4πα+ =23,则sin 2α的值是____.【答案】13【解析】221sin ()(cos sin )(1sin 2)4222παααα+=+=+Q121(1sin 2)sin 2233αα∴+=∴=故答案为:1310.(2020·北京高考真题)若函数()sin()cos f x x xϕ=++的最大值为2,则常数ϕ的一个取值为________.【答案】2π(2,2k k Zππ+∈均可)【解析】因为()()()cos sin sin 1cos f x x x x ϕϕθ=++=+,2=,解得sin 1ϕ=,故可取2ϕπ=.故答案为:2π(2,2k k Zππ+∈均可).11.已知tan 2π3tan 4αα=-⎛⎫+ ⎪⎝⎭,则πsin 24α⎛⎫+ ⎪⎝⎭的值是_____.【答案】10.【解析】由()tan 1tan tan tan 2tan 1tan 13tan 1tan 4αααααπααα-===-++⎛⎫+ ⎪-⎝⎭,得23tan 5tan 20αα--=,解得tan 2α=,或1tan 3α=-.sin 2sin 2cos cos 2sin444πππααα⎛⎫+=+ ⎪⎝⎭)22222sin cos cos sin sin 2cos 2=22sin cos αααααααα⎛⎫+-=+ ⎪+⎝⎭222tan 1tan =2tan 1ααα⎛⎫+- ⎪+⎝⎭,当tan 2α=时,上式222212==22110⎛⎫⨯+- ⎪+⎝⎭当1tan 3α=-时,上式=22112133=210113⎛⎫⎛⎫⎛⎫⨯-+-- ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪ ⎪⎛⎫-+ ⎪ ⎪⎝⎭⎝⎭综上,sin 2.410πα⎛⎫+= ⎪⎝⎭12.函数3π()sin(2)3cos 2f x x x =+-的最小值为___________.【答案】4-.【解析】23()sin(23cos cos 23cos 2cos 3cos 12f x x x x x x x π=+-=--=--+23172(cos )48x =-++,1cos 1x -≤≤ ,∴当cos 1x =时,min ()4f x =-,故函数()f x 的最小值为4-.三、解答题13.(2020·全国高考真题(文))ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知B =150°.(1)若a c ,b ,求ABC 的面积;(2)若sin A sin C =2,求C .【答案】(1;(2)15︒.【解析】(1)由余弦定理可得2222282cos1507b a c ac c ==+-⋅︒=,2,c a ABC ∴==∴△的面积1sin 2S ac B ==;(2)30A C +=︒ ,sin sin(30)A C C C ∴+=︒-+1cos sin sin(30)222C C C =+=+︒=,030,303060C C ︒<<︒∴︒<+︒<︒ ,3045,15C C ∴+︒=︒∴=︒.14.设常数R a ∈,函数()2sin 22cos f x a x x =+.(1)若()f x 为偶函数,求a 的值;(2)若π14f ⎛⎫= ⎪⎝⎭,求方程()1f x =[]ππ-,上的解.【答案】(1)0a =;(2)5π24x =-或19π24x =或13π11π2424x x 或==-.【解析】(1)∵()2sin22cos f x a x x=+,∴()2sin22cos f x a x x-=-+,∵()f x为偶函数,∴()() f x f x-=,∴22 sin22cos sin22cosa x x a x x -+=+,∴2sin20 a x=,∴0 a=;(2)∵π14f⎛⎫=⎪⎝⎭,∴2ππsin2cos11 24a a⎛⎫+=+=⎪⎝⎭,∴a=,∴()2π2cos cos212sin216f x x x x x x⎛⎫=+=++=++⎪⎝⎭,∵()1 f x=∴π2sin2116x⎛⎫++=⎪⎝⎭,∴πsin262x⎛⎫+=-⎪⎝⎭,∴ππ22π64x k+=-+,或π52π2πZ64x k k+=+∈,,∴5ππ24x k=-+,或13ππZ24x k k=+∈,,∵[]ππx∈-,,∴5π24x =-或19π24x =或13π11π2424x x 或==-15.已知,αβ为锐角,4tan 3α=,cos()5αβ+=-.(1)求cos 2α的值;(2)求tan()αβ-的值.【答案】(1)725-;(2)211-【解析】(1)因为4tan 3α=,sin tan cos ααα=,所以4sin cos 3αα=.因为22sin cos 1αα+=,所以29cos 25α=,因此,27cos22cos 125αα=-=-.(2)因为,αβ为锐角,所以()0,παβ+∈.又因为()cos 5αβ+=-,所以()sin 5αβ+==,因此()tan 2αβ+=-.因为4tan 3α=,所以22tan 24tan21tan 7ααα==--,因此,()()()()tan2tan 2tan tan 21+tan2tan 11ααβαβααβααβ-+⎡⎤-=-+==-⎣⎦+.16.已知函数()2sin cos f x x x x =+.(Ⅰ)求()f x 的最小正周期;(Ⅱ)若()f x 在区间,3m π⎡⎤-⎢⎥⎣⎦上的最大值为32,求m 的最小值.【答案】(Ⅰ)π ;(Ⅱ)π3.【解析】(Ⅰ)()1cos211π1sin2sin2cos2sin 22222262x f x x x x x -⎛⎫=+=-+=-+ ⎪⎝⎭,所以()f x 的最小正周期为2ππ2T ==.(Ⅱ)由(Ⅰ)知()π1sin 262f x x ⎛⎫=-+⎪⎝⎭.因为π,3x m ⎡⎤∈-⎢⎥⎣⎦,所以π5ππ2,2666x m ⎡⎤-∈--⎢⎥⎣⎦.要使得()f x 在π,3m ⎡⎤-⎢⎥⎣⎦上的最大值为32,即πsin 26x ⎛⎫- ⎪⎝⎭在π,3m ⎡⎤-⎢⎥⎣⎦上的最大值为1.所以ππ262m -≥,即π3m ≥.所以m 的最小值为π3.17.在ABC 中,角,,A B C 所对的边分别为,,a b c .已知5,a b c ===.(Ⅰ)求角C的大小;(Ⅱ)求sin A 的值;(Ⅲ)求sin 24A π⎛⎫+ ⎪⎝⎭的值.【答案】(Ⅰ)4C π=;(Ⅱ)sin 13A =;(Ⅲ)sin 2426A π⎛⎫+= ⎪⎝⎭.【解析】(Ⅰ)在ABC中,由5,a b c ===及余弦定理得222cos 22a b c C ab +-===,又因为(0,)C π∈,所以4C π=;(Ⅱ)在ABC中,由4C π=,a c ==及正弦定理,可得sin sin a C A c ⨯===13;(Ⅲ)由a c <知角A为锐角,由sin 13A =,可得cos A ==13,进而2125sin 22sin cos ,cos 22cos 11313A A A A A ===-=,所以125sin(2)sin 2cos cos2sin 444132132A A A πππ+=+=⨯+⨯=26.第二部分 模拟训练1.已知ABC 的内角A ,B ,C 成等差数列,若()3sin sin 5B αα+=+,则()sin 300α+︒=( )A .35B .45-C .45D .35-【答案】D【解析】解:∵A,B,C成等差数列,∴2B A C=+,又180A B C ++=︒,∴60B =︒,由()3sin 60sin 5αα︒+=+得,13cos sin 225αα-=,∴()3cos 305α︒+=,则()()()3sin 300sin 27030cos 305ααα+︒=︒+︒+=-︒+=-,故选:D .2.已知函数()()cos 0f x x x ωωω=->在0,2π⎡⎤⎢⎥⎣⎦内有且仅有1个最大值点和3个零点,则ω的取值范围是( )A .1316,33⎛⎤⎥⎝⎦B .1316,33⎡⎫⎪⎢⎣⎭C .1417,33⎛⎤⎥⎝⎦D .1417,33⎡⎫⎪⎢⎣⎭【答案】B【解析】()2sin(),0cos 62f x x x x x ππωωω=-≤≤-=,6626x ππωππω∴-≤-≤-,1322635162623ωπππωωπππω⎧⎧-≥≥⎪⎪⎪⎪⇒⎨⎨⎪⎪-<<⎪⎪⎩⎩,则ω的取值范围是1316,33⎡⎫⎪⎢⎣⎭.故选:B.3.将函数()sin 22f x x x=+的图象沿x 轴向左平移()0ϕϕ>个单位后得到函数()g x ,若()g x 为偶函数,则ϕ的最小值为( )A .12πB .6πC .4πD .512π【答案】A【解析】函数sin 222sin(23y x x x π=+=+,将函数sin 22y x x =+的图象沿x 轴向左平移ϕ个单位后,得到函数2sin(22)3y x πϕ=++,因为函数是偶函数,∴2()()32212k k k Z k Z ππππϕπϕ+=+∈∴=+∈.当0k =时,12πϕ=.故选:A 4.设ABC的内角A ,B ,C 满足2A C B+=,则函数()2sin()cos sin2f x x B x x=+-图象的对称轴方程是( )A .ππ,32k x k =+∈Z B .ππ,122k x k =+∈Z C .5ππ,122k x k =+∈Z D .ππ,62k x k =+∈Z 【答案】C【解析】因为()A C B π-+=,2A+C =B ,所以3B π=,()2sin cos sin 23f x x x xπ⎛⎫=+- ⎪⎝⎭(sin )cos sin 2x x x x=+-1sin 2cos 2222x x =-++sin 232x π⎛⎫=--+⎪⎝⎭.由232x kx ππ-=+,k ∈Z ,得5122k x ππ=+,k ∈Z .故选:C.5.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,满足()2cos b c A acosC -=.(1)求角A ;(2)若a =,5b c +=,求△ABC 的面积.【答案】(1)A 3π=;(2).【解析】(1)在三角形ABC 中,()2cos acos b c A C-= ,由正弦定理得:()2sin cos sin cos B sinC A A C -=,化为:()2sin cos sin cos sin cos sin sin B A C C A C A C B=+=+= ,三角形中sin 0B ≠,解得cos A12=,()0,A π∈,∴A 3π=.(2)由余弦定理得2222cos a b c bc A=+-,a =5bc +=,()2213353b c cb bc ∴=+-=-,化为4bc =,所以三角形ABC 的面积S 12=sin bc A 12=⨯42=6.在锐角ABC中,内角A,B,C所对的边分别为a ,b ,c ,且直线x A=为函数()222sin f x x x=+图象的一条对称轴.(1)求A ;(2)若4a =,求ABC 面积的最大值.【答案】(1)3A π=;(2).【解析】(1)()222sin 2cos 212sin 216πx x x x x f x ⎛⎫=+=-+=-+ ⎪⎝⎭,∴直线x A =为函数()f x 图像的一条对称轴,∴262ππA kπ-=+(k ∈Z ),即132πA kπ=+(k ∈Z ),又02A π<<,∴当0k =时,3A π=.(2)∵3A π=,4a =,∴由余弦定理得,2222162cos23πb c bc b c bc bc bc bc=+-=+-≥-=,即16bc ≤,当且仅当b=c=4时等号成立∴111sin sin 1622322ABC πbc A bc S ==≤⨯⨯=△,故ABC 面积的最大值为7.在ABC 中,角,,A B C 的对边分别为,,a b c ,已知45b c B ==∠=.(1)求边BC 的长﹔(2)在边BC 上取一点D ,使得4cos 5ADB Ð=,求sin DAC ∠的值.【答案】(1)3BC =;(2)25.【解析】在ABC 中,因为b =,c =,45B ∠= ,由余弦定理2222cos b a c ac B=+-,得25222a a =+-⨯所以2230a a --=解得:3a =或1a =-(舍)所以3BC =.(2)在ABC 中,由正弦定理sin sin b cB C =,得sin 45sin C =.所以sin C =在ADC 中,因为()4cos 180cos cos 5ADB ADB ADC -∠=-∠∠=-= ,所以ADC∠为钝角.而180ADC C CAD ∠+∠+∠=,所以C ∠为锐角故cos 5C ==因为4cos 5ADC ∠=-,所以35sin ADC ∠===,()sin sin 180sin()DAC ADC C ADC C ∠=-∠-∠=∠+∠ ,sin cos cos sin ADC C ADC C =∠∠+∠∠34555525=⨯-⨯=8.已知函数2()cos cos 1f x x x x =++.(1)求()f x 的最小正周期和值域;(2)若对任意x ∈R ,2()()20f x k f x -⋅-≤的恒成立,求实数k 的取值范围.【答案】(1)最小正周期π,值域为15,22⎡⎤⎢⎥⎣⎦;(2)1710k ≥.【解析】解:(1)2()cos cos 1f x x x x =++cos21133sin 21sin 2cos2sin 22222262x x x x x π+⎛⎫=++=++=++ ⎪⎝⎭∴()f x 的为最小正周期22T ππ==,值域为15(),22f x ⎡⎤∈⎢⎥⎣⎦;(2)记()f x t =,则15,22t ⎡⎤∈⎢⎥⎣⎦,由2()()20f x k f x -⋅-≤恒成立,知220t kt --≤恒成立,即22kt t ≥-恒成立,∵0t >∴222t t t k t -=-≥.∵2()g t t t =-在15,22t ⎡⎤∈⎢⎥⎣⎦时单调递增max 55417()22510g t g ⎛⎫==-=⎪⎝⎭∴k 的取值范围是1710k ≥9.已知函数2()2cos 12x f x x =-+.(Ⅰ)若()6f παα⎛⎫=+ ⎪⎝⎭,求tan α的值;(Ⅱ)若函数()f x 图象上所有点的纵坐标保持不变,横坐标变为原来的12倍得函数()g x 的图象,求函数()g x 在0,2π⎡⎤⎢⎥⎣⎦得的值域.【答案】(Ⅰ)9-;(Ⅱ)[]1,2-.【解析】解:(Ⅰ)2()2cos 12x f x x =-+cos 2sin 6x x x π⎛⎫=-=- ⎪⎝⎭,因为()6f παα⎛⎫=+ ⎪⎝⎭,所以sin 6παα⎛⎫-= ⎪⎝⎭,即1sin cos 22ααα-=,所以cos αα-=,所以tan 9α=-;(Ⅱ)()f x 图象上所有点横坐标变为原来的12倍得到函数()g x 的图象,所以()g x 的解析式为()(2)2sin 26g x f x x π⎛⎫==- ⎪⎝⎭,因为02x π≤≤,所以52666x πππ-≤-≤,则1sin 2126x π⎛⎫-≤-≤ ⎪⎝⎭,所以1()2g x -≤≤故()g x 在0,2π⎡⎤⎢⎥⎣⎦上的值域为[]1,2-.10.已知函数()2cos 2cos 1222x x x f x =-+.(1)求函数()f x 的最小正周期;(2)将函数()f x 图象上所有点的横坐标都缩短到原来的12倍(纵坐标不变),再向左平移6π个单位得到函数()g x 图象,求函数()g x 的单调增区间.【答案】(1)最小正周期2π;(2)单调增区间是(),36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦.【解析】(1)()2cos 2cos 1cos 2sin 2226x x x f x x x x π⎛⎫=-+=-=- ⎪⎝⎭,所以函数()f x 的最小正周期为2π;(2)将函数()f x 图象上所有点的横坐标都缩短到原来的12倍(纵坐标不变),得到()2sin 26h x x π⎛⎫=- ⎪⎝⎭,再向左移动6π个单位得()2sin 22sin 2666g x x x πππ⎡⎤⎛⎫⎛⎫=+-=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,由()222262k x k k ππππ-≤+≤π+∈Z ,解得()36k x k k πππ-≤≤π+∈Z .函数()g x 的单调增区间是(),36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦.。
(完整word)高中数学高考总复习简单的三角恒等变换习题及详解.doc

高考总复习高 中 数 学 高 考 总 复习 简 单 的 三 角 恒 等 变 换 习 题 及 详 解一、选择题π π ,x ∈ R ,则函数 f(x) 是()1. (文 )(2010 山·师大附中模考 )设函数 f(x)= cos 2(x + )- sin 2(x + )44A .最小正周期为 π的奇函数B .最小正周期为 π的偶函数πC .最小正周期为 2的奇函数πD .最小正周期为 2的偶函数 [ 答案 ] Aπ2π[ 解析 ] f(x)= cos(2x + 2)=- sin2x 为奇函数,周期 T = 2 = π. ( 理)(2010 辽·宁锦州 )函数 y = sin 2x + sinxcosx 的最小正周期 T = ()π π A . 2π B . πC.2D.3[ 答案 ] B[ 解析 ] y = sin 2x + sinxcosx = 1- cos2x 12+ sin2x2 = 1+ 2π,∴最小正周期 T = π.2 2 sin 2x - 4232. (2010 重·庆一中 )设向量 a = (cos α, 2 )的模为 2 ,则 cos2α= ()111 3 A .- 4 B .- 2C.2D. 2[ 答案 ] B[ 解析 ] ∵ |a|2= cos 2α+ 2 2= cos 2α+ 1= 3,2 2 4∴ cos 2α=1,∴ cos2α= 2cos 2α- 1=- 1.42α3.已知 tan 2= 3,则 cos α= ()444 3A. 5 B .- 5C.15D .- 5[ 答案 ] Bαααα cos2- sin2222含详解答案高考总复习1- tan 2α= 2 =1- 9=- 4,故选 B. 1+ tan 2α 1+ 9522C4.在△ABC 中,若 sinAsinB = cos 2 ,则△ABC 是 ()A .等边三角形B .等腰三角形C .直角三角形D .既非等腰又非直角的三角形 [ 答案 ] B[ 解析 ] ∵ sinAsinB = cos 2C,211∴ 2[cos(A - B)- cos(A + B)] = 2(1+ cosC), ∴ cos(A - B)-cos( π-C)= 1+ cosC ,∴ cos(A - B)=1,∵- π<A -B<π,∴ A - B = 0,∴△ ABC 为等腰三角形.π5. (2010 ·阳市诊断绵 )函数 f(x)= 2sin(x - 2) +|cosx|的最小正周期为( )πA. 2B .πC . 2πD . 4π[ 答案 ] C[ 解析 ] f(x)=- 2cosx + |cosx|- cosx cosx ≥ 0=,画出图象可知周期为2π.- 3cosx cosx<016. (2010 揭·阳市模考 )若 sinx + cosx = 3, x ∈ (0, π),则 sinx - cosx 的值为 ()17171 17 A . ± 3 B .- 3C.3D. 3[ 答案 ] D[ 解析 ]11 ,∴ sin2x =- 8π 由 sinx + cosx = 两边平方得, 1+ 2sinxcosx = <0,∴ x ∈ , π,3 99 2∴ (sinx - cosx)2= 1- sin2x =17且sinx>cosx , 9∴ sinx -cosx =17,故选 D.3高考总复习7. (文 )在锐角△ABC 中,设 x = sinA ·sinB , y = cosA ·cosB ,则 x , y 的大小关系是 ( )A . x ≤yB . x < yC . x ≥ yD . x >y[ 答案 ] Dπ[ 解析 ] ∵ π>A + B > ,∴ cos(A + B)<0,即 cosAcosB - sinAsinB < 0,∴ x > y ,故应选 D.2( 理)(2010 皖·南八校 )在△ABC 中,角 A 、B 、 C 的对边分别为 a 、b 、 c ,如果 cos(2B + C)+ 2sinAsinB<0,那么 a 、 b 、 c 满足的关系是 ()A . 2ab>c 2B . a 2+ b 2<c 2C . 2bc>a 2D . b 2+ c 2<a 2[ 答案 ] B[ 解析 ] ∵ cos(2B +C)+ 2sinAsinB<0,且 A +B + C = π,∴ cos( π- A +B)+ 2sinA ·sinB<0,∴ cos( π- A)cosB - sin( π- A)sinB + 2sinAsinB<0,∴- cosAcosB + sinAsinB<0 ,即 cos(A + B)>0,π π∴ 0<A + B< ,∴ C> ,22a 2+b 2-c 2由余弦定理得,cosC =<0,2ab∴ a 2+ b 2- c 2<0,故应选 B.8. (2010 ·林省调研吉 )已知 a = (cosx ,sinx),b = (sinx ,cosx),记 f(x)=a ·b ,要得到函数 y = sin 4x - cos 4x 的图象,只需将函数 y = f( x)的图象 ()πA .向左平移 2个单位长度πB .向左平移 4个单位长度πC .向右平移 2个单位长度πD .向右平移 4个单位长度[ 答案 ] D[ 解析 ] y = sin 4x - cos 4 x =(sin 2x + cos 2x)(sin 2x - cos 2x)=- cos2x ,π π π π将 f( x)= a ·b = 2sinxcosx = sin2x ,向右平移 4 个单位得, sin2 x -4 = sin 2x -2 =- sin - 2x=- cos2x ,故2 选 D.高考总复习π 29. (2010 浙·江金华十校模考 )已知向量 a = (cos2α, sin α), b = (1,2sin α- 1), α∈ 4, π,若 a ·b =5,π 则 tan α+4 的值为 ( )12 1 2 A.3 B.7C.7D.3[ 答案 ] C[ 解析 ]a ·b = cos2α+ 2sin 2α-sin α= 1- 2sin 2α+ 2sin 2α- sin α= 1- sin α= 2,∴ sin α= 3,5 5 π∵ <α<π,∴ cos α=- 4,∴ tan α=- 3,454π 1+ tan α 1 .∴ tan α+ = =4 1- tan α 75π 7π10. (2010 湖·北黄冈模拟 )若 2 ≤ α≤ 2 ,则 1+ sin α+ 1- sin α等于 ()α α A .- 2cos 2 B . 2cos 2α α C .- 2sin 2 D . 2sin 2[ 答案 ]C5π7π 5π α 7π[ 解析 ] ≤ α≤,∴4≤ ≤4.∵ 2 2 2∴ 1+ sin α+ 1- sin α=1+ 2sin α α 1- 2sin α α2 cos + cos22 2 =α α α α2sin + cos2 +sin - cos2 2 22αα α α=- (sin + cos )- (sin - cos )2222α=- 2sin 2. 二、填空题π 311. (2010 广·东罗湖区调研 )若 sin 2+ θ=5,则 cos2θ= ________. [ 答案 ] 7 - 25π 3,∴ cos θ= 3,[ 解析 ] ∵ sin + θ=2 5 5∴ cos2θ= 2cos2θ- 1=- 257.高考总复习tanx- tan3 x12. (2010 江·苏无锡市调研 )函数 y=的最大值与最小值的积是 ________.1+ 2tan 2x+tan4x[ 答案 ]1 -16[ 解析 ] y=tanx- tan3x tanx 1- tan2x2 4=2 21+ 2tan x+ tan x 1+ tan x=tanx 1- tan2x=sinxcosx cos2x- sin2x2 · 2 2 2 + 2 2 1+ tan x 1+ tan x cos x+ sin x cos x+ sin x 1 1=2sin2x·cos2x=4sin4x,1所以最大与最小值的积为-16.13. (2010 ·江杭州质检浙)函数 y= sin(x+ 10°)+ cos(x+ 40°),( x∈R )的最大值是 ________.[ 答案 ] 1[ 解析 ]y= sinxcos10 °+ cosxsin10 +°cosxcos40 °- sinxsin40 =°(cos10 -°sin40 )sinx°+ (sin10 +°cos40 °)cosx,其最大值为=2+ 2 sin10 °cos40°- cos10°sin40 °=2+ 2sin - 30°= 1.θ14.(文 )如图, AB 是半圆 O 的直径,点 C 在半圆上, CD⊥ AB 于点 D ,且 AD= 3DB ,设∠COD =θ,则 tan22=________.[ 答案 ] 1 3[ 解析 ]3r,∴ OD=r,∴ CD = 3 CD =3,设 OC= r,∵ AD = 3DB,且 AD+ DB=2r,∴ AD =2 2 2 r ,∴ tanθ=OD θ∵ tanθ=2tan2 θ3,∴ tan =1- tan2θ 2 3 (负值舍去 ),2θ1∴tan22=3.( 理)3tan12 -°3= ________. 4cos212 °- 2 sin12 °[ 答案 ] - 4 3[ 解析 ]3tan12 -°3 = 3 sin12 -°3cos12 °4cos212°-2 sin12 ° 2cos24 sin12°cos12° °2 3sin 12 °- 60°3. = 1 =- 4三、解答题15. (文 )(2010 北·京理 )已知函数f(x)=2cos2x + sin 2x - 4cosx.π(1) 求 f(3)的值;(2) 求 f(x)的最大值和最小值.[ 解析 ] π 2π π π 3 9 (1) f( )= 2cos+ sin2- 4cos =- 1+-2=- .3 33344(2) f(x)=2(2cos 2 x - 1)+(1 -cos 2x)- 4cosx= 3cos 2x - 4cosx - 1= 3(cosx -23)2-73, x ∈ R因为 cosx ∈ [ - 1,1] ,所以当 cosx =- 1 时, f(x)取最大值 6;当 cosx =2时, f(x)取最小值-733.( 理)(2010 广·东罗湖区调研 )已知 a =(cosx +sinx , sinx), b = (cosx - sinx,2cosx),设 f(x)= a ·b. (1) 求函数 f(x)的最小正周期;(2) 当 x ∈ 0,π时,求函数 f(x)的最大值及最小值.2[ 解析 ] (1) f(x)= a ·b = (cosx + sinx) ·(cosx - sinx)+ sinx ·2cosx = cos 2x -sin 2x + 2sinxcosx= cos2x + sin2x = 2222 cos2x + 2 sin2xπ = 2sin 2x +4 .∴ f(x)的最小正周期 T = π.πππ 5π(2) ∵ 0≤ x ≤ ,∴ ≤ 2x + ≤ 4 ,2 4 4π π ππ 5π π∴当 2x +4= 2,即 x =8时, f(x)有最大值 2;当 2x + 4= 4 ,即 x =2 时, f(x)有最小值- 1.π16. (文 )设函数 f(x)= cos 2x + 3 + sin 2x.(1) 求函数 f(x)的最大值和最小正周期;1C1(2) 设 A 、 B 、 C 为△ABC 的三个内角,若 cosB =3, f(2 )=-4,且 C 为锐角,求 sinA 的值. [ 解析 ] (1) f(x)= cos 2x + π π π 1- cos2x 1 - 3 + sin 2x = cos2xcos - sin2xsin + = 2 sin2x ,3 3 3 2 2所以函数 f(x)的最大值为1+ 3,最小正周期为π.2(2) f(C )= 1- 3sinC =- 1,所以 sinC = 3π因为 C 为锐角,所以C = 3,在△ ABC 中, cosB =13,所以 sinB =2 3 2,所以 sinA = sin(B + C)= sinBcosC + cosBsinC= 2 2 1 1 × 3 = 22+ 33 × + 26 .2 3→ → → →( 理)已知角 A 、B 、 C 为△ABC 的三个内角, OM = (sinB + cosB , cosC), ON = (sinC , sinB - cosB), OM ·ON =1- 5.(1) 求 tan2A 的值;2A(2) 2cos 2- 3sinA - 1 的值.求π2sin A +4[ 解析 ]→ →(1) ∵OM ·ON = (sinB + cosB)sinC +1cosC(sinB - cosB)= sin(B + C)- cos(B + C) =- 5,∴ sinA + cosA =- 1①5两边平方并整理得: 2sinAcosA =- 24,25∵-24π, π ,25<0,∴ A ∈ 2∴ sinA - cosA = 1-2sinAcosA = 75②联立①②得: sinA = 3,cosA =- 4,∴ tanA =- 3, 5 5 4- 3∴ tan2A =2tanA2=224 . A =- 1-tan 1- 9 7163(2) ∵ tanA =- 4,A2cos 22 - 3sinA - 1 cosA -3sinA 1- 3tanA ∴ π= cosA +sinA =1+ tanA 2sin A +43=1-3× -4 = 13.-341+π点之间的距离为2.(1) 求 m 和 a 的值;π(2) 若点 A(x 0, y 0) 是 y = f( x)图象的对称中心,且 x 0∈ 0, 2 ,求点 A 的坐标. [ 解析 ] (1) f(x)= sin 2ax - 3sinaxcosax1- cos2ax3π 1= 2 - 2 sin2ax =- sin 2ax + 6 + 2,由题意知, m 为 f(x)的最大值或最小值,所以 m =- 12或 m =32,π 由题设知,函数f(x)的周期为,∴ a = 2,2所以 m =- 1或 m =3, a = 2. 2 2(2) ∵ f(x)=- sin 4x + π+1,6 2ππ∴令 sin 4x + 6 =0,得 4x +6= k π(k ∈ Z) ,∴ x = k π π-424(k ∈ Z),由 0≤ k π π π(k ∈ Z),得 k = 1 或 k = 2,4 -24≤2 因此点 A 的坐标为 5π 1 或 11π1 , ,24 2 24 2.( 理)(2010 广·东佛山顺德区检测 )设向量 a = (sinx,1), b = (1, cosx),记 f(x)= a ·b , f ′ (x)是 f( x)的导函数.(1) 求函数 F(x)= f(x)f ′ (x)+ f 2(x)的最大值和最小正周期;(2) 若 f(x)= 2f ′ (x),求1+ 2sin 2x的值.cos 2x - sinxcosx[ 解析 ] (1) f(x)= sinx +cosx ,∴ f ′( x)= cosx -sinx ,∴ F(x)= f(x)f ′ (x)+ f 2(x) = cos 2x -sin 2x + 1+2sinxcosx= cos2x + sin2x + 1= 1+ 2sin π2x +4 ,π π π ∴当 2x + = 2k π+ ,即 x = k π+ (k ∈ Z)时, F( x)max =1 + 2.428最小正周期为 T = 2π= π.2(2) ∵ f(x)= 2f ′ (x),∴ sinx+ cosx= 2cosx- 2sinx,∴cosx= 3sinx,∴ tanx=1,3∴1+ 2sin2x = 3sin2x+ cos2x = 3tan2x+ 1=2.cos2x-sinxcosx cos2x-sinxcosx 1- tanx。
方法技巧专题19 三角恒等变换(解析版)
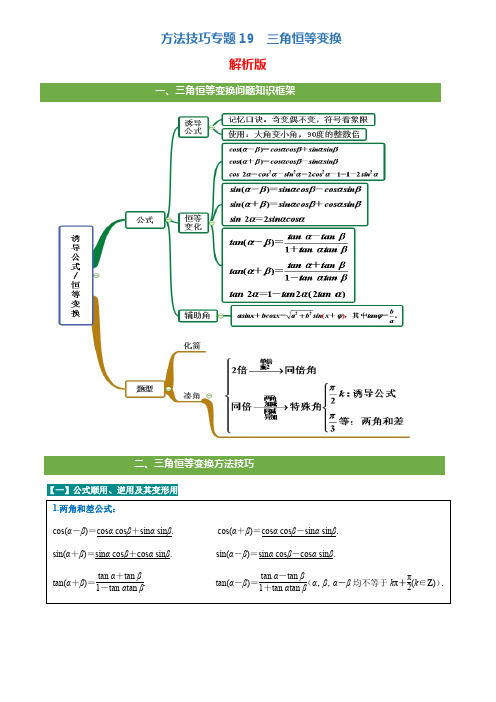
方法技巧专题19 三角恒等变换解析版一、三角恒等变换问题知识框架【一】公式顺用、逆用及其变形用1.例题 【例1】计算:(1)cos(-15°); (2)cos 15°cos 105°+sin 15°sin 105°. 【解析】(1)方法一 原式=cos(30°-45°)=cos 30°cos 45°+sin 30°sin 45°=32×22+12×22=6+24. 方法二 原式=cos 15°=cos(45°-30°)=cos 45°cos 30°+sin 45°sin 30°=22×32+22×12=6+24. (2)原式=cos(15°-105°)=cos(-90°)=cos 90°=0. 【例2】(1)计算:cos 2π12-sin 2π12; 【解析】原式=cos π6=32.(2)计算:1-tan 275°tan 75°;【解析】 1-tan 275°tan 75°=2·1-tan 275°2tan 75°=2·1tan 150°=-2 3.(3)计算:cos 20°cos 40°cos 80°.【解析】原式=12sin 20°·2sin 20°cos 20°cos 40°cos 80°=12sin 20°·sin 40°·cos 40°cos 80°=122sin 20°sin 80°cos 80°=123sin 20°·sin 160°=sin 20°23sin 20°=18.【例3】(1)1+tan 15°1-tan 15°=________.【解析】3 原式=tan 45°+tan 15°1-tan 45°tan 15°=tan(45°+15°)=tan 60°= 3.(2)化简:tan 23°+tan 37°+3tan 23°tan 37°. 【解析】方法一 tan 23°+tan 37°+3tan 23°tan 37° =tan(23°+37°)(1-tan 23°tan 37°)+3tan 23°tan 37° =tan 60°(1-tan 23°tan 37°)+3tan 23°tan 37°= 3. 方法二 ∵tan(23°+37°)=tan 23°+tan 37°1-tan 23°tan 37°,∴3=tan 23°+tan 37°1-tan 23°tan 37°,∴3-3tan 23°tan 37°=tan 23°+tan 37°, ∴tan 23°+tan 37°+3tan 23°tan 37°= 3. (3)已知sin θ=45,5π2<θ<3π,求cos θ2和tan θ2.【解析】 ∵sin θ=45,且5π2<θ<3π,∴cos θ=-1-sin 2θ=-35.由cos θ=2cos 2θ2-1,得cos 2θ2=1+cos θ2=15.∵5π4<θ2<3π2,∴cos θ2=- 1+cos θ2=-55. tan θ2=sin θ1+cos θ=2.2.巩固提升综合练习【练习1】化简cos 15°cos 45°+cos 75°sin 45°的值为( )A.12B.32 C .-12 D .-32【解析】Bcos 15°cos 45°+cos 75°sin 45°=cos 15°cos 45°+sin 15°sin 45°=cos(15°-45°)=cos(-30°)=32.【练习2】1-3tan 75°3+tan 75°=________.【解析】-1原式=33-tan 75°1+33tan 75°=tan 30°-tan 75°1+tan 30°tan 75°=tan(30°-75°)=-tan 45°=-1.【练习3】在△ABC 中,A +B ≠π2,且tan A +tan B +3=3tan A tan B ,则角C 的值为( )A.π3B.2π3C.π6D.π4 【解析】A∵tan A +tan B +3=3tan A tan B ⇔tan(A +B )·(1-tan A tan B )=3(tan A tan B -1).(*) 若1-tan A tan B =0,则cos A cos B -s in A sin B =0,即cos(A +B )=0. ∵0<A +B <π,∴A +B =π2与题设矛盾.∴由(*)得tan(A +B )=-3,即tan C = 3.又∵0<C <π,∴C =π3.【练习4】若sin α+cos α=13,则sin 2α= .【解析】由题意,得(sin α+cos α)2=19,∴1+2sin αcos α=19,即1+sin 2α=19,∴sin 2α=-89.1.例题【例1】已知31)3sin(=-πα,则)6cos(πα+ 的值为( ) A .-13 B.13 C.223 D .-223【答案】A 【解析】∵sin )3(πα-=13,∴cos )6(πα+=cos )]3(2[παπ-+=-sin )3(πα-=-13.【例2】已知角α的顶点与原点O 重合,始边与x 轴的非负半轴重合,它的终边过点⎪⎭⎫⎝⎛--54,53P . 若角β满足sin(α+β)=513,则cos β的值为________.【答案】 -5665或1665【解析】 由角α的终边过点⎪⎭⎫⎝⎛--54,53P ,得sin α=-45,cos α=-35. 由sin(α+β)=513,得cos(α+β)=±1213.由β=(α+β)-α,得cos β=cos(α+β)cos α+sin(α+β)sin α, 所以cos β=-5665或cos β=1665.【例3】若1sin 63πα⎛⎫-= ⎪⎝⎭,则2cos 23πα⎛⎫+= ⎪⎝⎭( ) A .13 B .13-C .79D .79-【答案】D 【解析】222πππcos 22cos 12cos 13326πααα⎡⎤⎛⎫⎛⎫⎛⎫+=+-=--- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦2π272sin 11699α⎛⎫=--=-=- ⎪⎝⎭2.巩固提升综合练习 【练习1】已知33)6tan(=-απ,则=+)65tan(απ________. 【答案】-33【解析】tan )65(απ+=tan )6(αππ+-=tan )]6([αππ--=-tan )6(απ-=-33. 【练习2】若1027)4sin(=+πA ,A ∈),4(ππ,则sin A 的值为( ) A.35 B.45C.35或45D.34【答案】B 【解析】∵A ∈),4(ππ,∴A +π4∈)45,2(ππ, ∴cos (A +π4)=-1-sin 2⎝⎛⎭⎫A +π4=-210, ∴sin A =sin[(A +π4)- π4]=sin (A +π4)cos π4-cos (A +π4)sin π4=45.【练习3】已知sin(α−3π10)=35,则cos(α+π5)=( ) A.−45 B.45C.−35D.35【答案】C【解析】因为sin(α−3π10)=35,则cos(α+π5)=cos[π2+(α−3π10)]=−sin(α−3π10)=−35.故应选C . 【练习4】若sin (3x π-)=23,则cos (23x π+)=( )A .79B .19C .19-D .79-【答案】C 【解析】令3x πθ=-,则223x ππθ+=-,所以()21cos 2cos 2cos 22sin 139x ππθθθ⎛⎫+=-=-=-=- ⎪⎝⎭,故选C .【练习5】已知3sin 245x π⎛⎫-= ⎪⎝⎭,则sin 4x 的值为( ) A .1825B .1825±C .725D .725±【答案】C【解析】由题意得:297cos 412sin 212242525x x ππ⎛⎫⎛⎫-=--=-⨯=⎪ ⎪⎝⎭⎝⎭7sin 4cos 4225x x π⎛⎫∴=-= ⎪⎝⎭本题正确选项:C1.例题【例1】已知02απ<<,cos()4απ+= (1)求tan()4απ+的值; (2)求sin(2)3απ+的值.【解析】(1)∵02απ<<,cos()4απ+= ∴sin()4απ+==, ∴sin()4tan()24cos()4αααπ+π+==π+. (2)∵tan 1tan()241tan αααπ++==-,∴1tan 3α=, ∴2222sin cos 2tan 3sin 2sin cos tan 15ααααααα===++,2222cos sin cos 2sin cos ααααα-=+221tan 4tan 15αα-==+,3sin(2)sin 2cos cos 2sin 33310αααπππ++=+=.【例2】已知△ABC 中,137cos sin -=+A A ,则tanA= . 【解析】解法一:列出方程组⎪⎩⎪⎨⎧=+-=+1cos sin 137cos sin 22A A A A由第一个方程得,A A sin 137cos --=,代入第二个方程得1)sin 137(sin 22=--+A A , 即016960sin 137sin 2=-+A A , 解得135sin =A 或1312sin -=A , 因为△ABC 中0<A<π, 所以sinA>0,135sin =A ,1312cos -=A ,所以125tan -=A . 答案:125-. 解法二:由已知得sinA>0, cosA<0, |sin A|<|cos A|, tanA>-1, 由137cos sin -=+A A 两边平方,整理得16960cos sin -=⋅A A ,即16960cos sin cos sin 22-=+⋅A A A A , 分子分母同除以A 2cos 得169601tan tan 2-=+A A , 解得125tan -=A .2.巩固提升综合练习【练习1】已知a ∈R ,sina +2cosa =√102,则tan2a =( )A .−34或−35 B .−34C .34D .−35【答案】B 【解析】因为sina +2cosa =√102,所以(sina +2cosa )2=52,所以sin 2a +4cos 2a +4sinacosa =52, 所以sin 2a+4cos 2a+4sin acosasin 2a+cos 2a=52,即tan 2a+4+4tanatan 2a+1=52,解得tana =3或者tana =−13,当tana =3时,tan2a =2tana1−tan 2a =−34,当tana =−13时,tan2a =2tana 1−tan 2a =−34, 综上所述,tan2a =−34,故选B 。
高三复习数学32_三角恒等变换(有答案)

3.2 三角恒等变换一、解答题。
1. 和、差角公式:sin(α±β)=________;cos(α±β)=________;tan(α±β)=________.2. 二倍角公式:sin2α=________;cos2α=________=________=________;tan2α=________.当tanα、tanβ或tan(α±β)的值不存在时,不能使用公式Tα±β处理有关问题,应改用诱导公式或其它方法来解.3. 如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为√210,2√5 5.求tan(α+β)的值;求α+2β的值.4. 已知sin(α−π4)=√55,α∈(π2,5π4),则sinα=()A.3√1010B.−√1010C.±√1010D.−√1010或3√10105. 已知α∈(0,π2),2sin2α=cos2α+1,则sinα=()A.1 5B.√55C.√33D.2√556. 设α∈(0,π2),β∈(0,π4),且tanα=1+sin2βcos2β,则下列结论中正确的是()A.α−β=π4B.α+β=π4C.2α−β=π4D.2α+β=π47. sin40∘(tan10∘−√3)=________.8. 在锐角△ABC中,若sin A=2sin B sin C,则tan A tan B tan C的最小值是________.9. 已知函数f(x)=2cos2x−sin2x+2,则()A.f(x)的最小正周期为π,最大值为3B.f(x)的最小正周期为π,最大值为4C.f(x)的最小正周期为2π,最大值为3D.f(x)的最小正周期为2π,最大值为410. 若cos(π4−α)=35,则sin2α=()A.7 25B.15C.−15D.−72511. 若tanα=34,则cos2α+2sin2α=()A.64 25B.4825C.1D.162512. 设函数f(x)=sin2x+b sin x+c,则f(x)的最小正周期()A.与b有关,且与c有关B.与b有关,但与c无关C.与b无关,且与c无关D.与b无关,但与c有关13. 已知α为第二象限角,sinα+cosα=√33,则cos2α=()A.−√53B.−√59C.√59D.√5314. 2cos10∘−sin20∘sin70∘的值是( )A.1 2B.√32C.√2D.√315. 函数f(x)=4cos x sin(x+π6)−1在区间[−π6,π4]上值域为________.16. 已知α,β∈(3π4,π),sin(α+β)=−35,sin(β−π4)=1213,则cos(α+π4)=________.17. 已知sin(π6−α)=√23,那么cos2α+√3sin2α=________.18. 在△ABC中,角A,B,C的对边分别为a,b,c,且2cos2A−B2cos B−sin(A−B)sin B+cos(A+C)=−35.求cos A的值.19. 求函数y=7−4sin x cos x+4cos2x−4cos4x的最大值与最小值.20. 在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b+c=2a cos B.证明:A=2B;若△ABC的面积S=a 24,求角A的大小.参考答案与试题解析3.2 三角恒等变换一、解答题。
三角恒等变换大题(含详细解答)

三角恒等变换1.已知0<α<π4,0<β<π4且3sin β=sin(2α+β),4tan α2=1-tan 2α2,求α+β的值. 2.化简:(1-sinα)(1-sinβ)-⎝⎛⎭⎫sin α+β2-cos α-β2 2. 3.已知sin(2α-β)=35,sinβ=-1213,且α∈⎝⎛⎭⎫π2,π,β∈⎝⎛⎭⎫-π2,0,求sinα 4.若cos(α+β)cos(α-β)=13,求cos2α-sin2β 5.函数y =12sin2x +sin2x ,x ∈R ,求y 的值域 6.已知0<α<π4,0<β<π4且3sinβ=sin(2α+β),4tan α2=1-tan2α2,求α+β的值. 7.化简:(1-sinα)(1-sinβ)-⎝⎛⎭⎫sin α+β2-cos α-β2 2. 8.已知函数()sin()cos()f x x x θθ=+++的定义域为R ,(1)当0θ=时,求()f x 的单调区间;(2)若(0,)θπ∈,且sin 0x ≠,当θ为何值时,()f x 为偶函数. 9 已知sin sin sin 0,cos cos cos 0,αβγαβγ++=++=求cos()βγ-的值 10 若,22sin sin =+βα求βαcos cos +的取值范围 11 求值:0010001cos 20sin10(tan 5tan 5)2sin 20-+-- 12 已知函数.,2cos 32sinR x x x y ∈+=(1)求y 取最大值时相应的x 的集合;(2)该函数的图象经过怎样的平移和伸变换可以得到)(sin R x x y ∈=的图象参考答案1. 解:由4tan α2=1-tan 2α2得tan α=2tan α21-tan 2α2=12. 由3sin[(α+β)-α]=sin[(α+β)+α],得3sin(α+β)cos α-3cos(α+β)sin α=sin(α+β)cos α+cos(α+β)sin α,∴2sin(α+β)cos α=4cos(α+β)sin α.∴tan(α+β)=2tan α.∴tan(α+β)=1.又∵0<α<π4,0<β<π4,∴0<α+β<π2,∴α+β=π4评析:首先由4tan α2=1-tan 2α2的形式联想倍角公式求得tan α,再利用角的变换求tan(α+β),据α、β的范围确定角α+β.求角的问题的关键是恰当地选择一个三角函数值,再依据范围求角,两步必不可少.2. 分析:本题由于α+β2+α-β2=α,α+β2-α-β2=β,因此可以从统一角入手,考虑应用和差化积公式. 解:原式=1-(sin α+sin β)+sin αsin β-⎝⎛ sin 2α+β2-⎭⎫2sin α+β2cos α-β2+cos 2α-β2 =1-2sin α+β2cos α-β2+sin αsin β-⎣⎡⎦⎤1-cos(α+β)2+1+cos(α-β)2-2sin α+β2cos α-β2 =sin αsin β+12[cos(α+β)-cos(α-β)]=sin αsin β+12·(-2)sin αsin β=0. 评析:(1)必须是同名三角函数才能和差化积;(2)若是高次函数必须用降幂公式降为一次.3. 解:∵π2<α<π,∴π<2α<2π.又-π2<β<0,∴0<-β<π2.∴π<2α-β<5π2.而sin(2α-β)=35>0,∴2π<2α-β<5π2,cos (2α-β)=45.又-π2<β<0且sin β=-1213,∴cos β=513, ∴cos2α=cos[(2α-β)+β]=cos(2α-β)cos β-sin(2α-β)sin β=45×513-35×⎝⎛⎭⎫-1213=5665. 又cos2α=1-2sin 2α,∴sin 2α=9130,又α∈⎝⎛⎭⎫π2,π,∴sin α=3130130. 评析:由sin(2α-β)求cos(2α-β)、由sin β求cos β,忽视2α-β、β的范围,结果会出现错误.另外,角度变换在三角函数化简求值中经常用到,如:α=(α+β)-β,2α=(α-β)+(α+β),⎝⎛⎭⎫π4+α+⎝⎛⎭⎫π4-α=π2等. 4. 解析:∵cos(α+β)cos(α-β)=13, ∴12(cos2α+cos2β)=13, ∴12(2cos 2α-1+1-2sin 2β)=13, ∴cos 2α-sin 2β=13. 5. 解析:y =12sin2x +sin 2x =12sin2x -12cos2x +12=22sin ⎝⎛⎭⎫2x -π4+12 评析:本题是求有关三角函数的值域的一种通法,即将函数化为y =A sin(ωx +φ)+b 或y =A cos(ωx +φ)+b 的模式.一般地,a cos x +b sin x =a 2+b 2⎝ ⎛⎭⎪⎫a a 2+b 2cos x +b a 2+b 2sin x =a 2+b 2(sin φcos x +cos φsin x )=a 2+b 2sin(x +φ),其中tan φ=a b,也可以变换如下:a cos x +b sin x =a 2+b 2(cos φcos x +sin φsin x )=a 2+b 2cos(x -φ),其中tan φ=b a. 6. 解:由4tan α2=1-tan 2α2 得tan α=2tan α21-tan 2α2=12. 由3sin[(α+β)-α]=sin[(α+β)+α],得3sin(α+β)cos α-3cos(α+β)sin α=sin(α+β)cos α+cos(α+β)sin α, ∴2sin(α+β)cos α=4cos(α+β)sin α. ∴tan(α+β)=2tan α. ∴tan(α+β)=1.又∵0<α<π4,0<β<π4,∴0<α+β<π2, ∴α+β=π4. 评析:首先由4tan α2=1-tan 2α2的形式联想倍角公式求得tan α,再利用角的变换求tan(α+β),据α、β的范围确定角α+β.求角的问题的关键是恰当地选择一个三角函数值,再依据范围求角,两步必不可少.7. 分析:本题由于α+β2+α-β2=α,α+β2-α-β2=β,因此可以从统一角入手,考虑应用和差化积公式. 解:原式=1-(sin α+sin β)+sin αsin β-⎝⎛sin 2α+β2- ⎭⎫2sin α+β2cos α-β2+cos 2α-β2 =1-2sin α+β2cos α-β2+sin αsin β- ⎣⎡⎦⎤1-cos(α+β)2+1+cos(α-β)2-2sin α+β2cos α-β2 =sin αsin β+12[cos(α+β)-cos(α-β)]=sin αsin β+12·(-2)sin αsin β=0. 评析:(1)必须是同名三角函数才能和差化积;(2)若是高次函数必须用降幂公式降为一次.8. 解:(1)当0θ=时,()sin cos )4f x x x x π=+=+ 322,22,24244k x k k x k πππππππππ-≤+≤+-≤≤+()f x 为递增; 3522,22,24244k x k k x k πππππππππ+≤+≤++≤≤+()f x 为递减 ()f x ∴为递增区间为 3[2,2],44k k k Z ππππ-+∈; ()f x 为递减区间为5[2,2],44k k k Z ππππ++∈。
高中数学高考总复习简单的三角恒等变换习题及详解

高中数学高考总复习简单的三角恒等变换习题及详解一、选择题1.(文)(2010·山师大附中模考)设函数f (x )=cos 2(x +π4)-sin 2(x +π4),x ∈R ,则函数f (x )是( )A .最小正周期为π的奇函数B .最小正周期为π的偶函数C .最小正周期为π2的奇函数D .最小正周期为π2的偶函数[答案] A[解析] f (x )=cos(2x +π2)=-sin2x 为奇函数,周期T =2π2=π.(理)(2010·辽宁锦州)函数y =sin 2x +sin x cos x 的最小正周期T =( ) A .2πB .πC.π2D.π3[答案] B[解析] y =sin 2x +sin x cos x =1-cos2x 2+12sin2x =12+22sin ⎝⎛⎭⎫2x -π4,∴最小正周期T =π. 2.(2010·重庆一中)设向量a =(cos α,22)的模为32,则cos2α=( ) A .-14B .-12C.12D.32[答案] B[解析] ∵|a |2=cos 2α+⎝⎛⎭⎫222=cos 2α+12=34,∴cos 2α=14,∴cos2α=2cos 2α-1=-12.3.已知tan α2=3,则cos α=( )A.45B .-45C.415D .-35[答案] B[解析] cos α=cos 2α2-sin 2α2=cos 2α2-sin 2α2cos 2α2+sin2α2=1-tan 2α21+tan 2α2=1-91+9=-45,故选B.4.在△ABC 中,若sin A sin B =cos 2C2,则△ABC 是( )A .等边三角形B .等腰三角形C .直角三角形D .既非等腰又非直角的三角形 [答案] B[解析] ∵sin A sin B =cos 2C2,∴12[cos(A -B )-cos(A +B )]=12(1+cos C ), ∴cos(A -B )-cos(π-C )=1+cos C , ∴cos(A -B )=1,∵-π<A -B <π,∴A -B =0, ∴△ABC 为等腰三角形.5.(2010·绵阳市诊断)函数f (x )=2sin(x -π2)+|cos x |的最小正周期为( )A.π2B .πC .2πD .4π[答案] C[解析] f (x )=-2cos x +|cos x |=⎩⎪⎨⎪⎧-cos x cos x ≥0-3cos x cos x <0,画出图象可知周期为2π. 6.(2010·揭阳市模考)若sin x +cos x =13,x ∈(0,π),则sin x -cos x 的值为( )A .±173B .-173C.13D.173[答案] D[解析] 由sin x +cos x =13两边平方得,1+2sin x cos x =19,∴sin2x =-89<0,∴x ∈⎝⎛⎭⎫π2,π, ∴(sin x -cos x )2=1-sin2x =179且sin x >cos x , ∴sin x -cos x =173,故选D. 7.(文)在锐角△ABC 中,设x =sin A ·sin B ,y =cos A ·cos B ,则x ,y 的大小关系是( )高考总复习含详解答案A .x ≤yB .x <yC .x ≥yD .x >y[答案] D[解析] ∵π>A +B >π2,∴cos(A +B )<0,即cos A cos B -sin A sin B <0,∴x >y ,故应选D.(理)(2010·皖南八校)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,如果cos(2B +C )+2sin A sin B <0,那么a 、b 、c 满足的关系是( )A .2ab >c 2B .a 2+b 2<c 2C .2bc >a 2D .b 2+c 2<a 2[答案] B[解析] ∵cos(2B +C )+2sin A sin B <0,且A +B +C =π, ∴cos(π-A +B )+2sin A ·sin B <0,∴cos(π-A )cos B -sin(π-A )sin B +2sin A sin B <0, ∴-cos A cos B +sin A sin B <0,即cos(A +B )>0, ∴0<A +B <π2,∴C >π2,由余弦定理得,cos C =a 2+b 2-c 22ab <0,∴a 2+b 2-c 2<0,故应选B.8.(2010·吉林省调研)已知a =(cos x ,sin x ),b =(sin x ,cos x ),记f (x )=a ·b ,要得到函数y =sin 4x -cos 4x 的图象,只需将函数y =f (x )的图象( )A .向左平移π2个单位长度B .向左平移π4个单位长度C .向右平移π2个单位长度D .向右平移π4个单位长度[答案] D[解析] y =sin 4x -cos 4x =(sin 2x +cos 2x )(sin 2x -cos 2x )=-cos2x ,将f (x )=a ·b =2sin x cos x =sin2x ,向右平移π4个单位得,sin2⎝⎛⎭⎫x -π4=sin ⎝⎛⎭⎫2x -π2=-sin ⎝⎛⎭⎫π2-2x =-cos2x ,故选D.9.(2010·浙江金华十校模考)已知向量a =(cos2α,sin α),b =(1,2sin α-1),α∈⎝⎛⎭⎫π4,π,若a ·b =25,则tan ⎝⎛⎭⎫α+π4的值为( ) A.13B.27C.17D.23[答案] C[解析] a ·b =cos2α+2sin 2α-sin α=1-2sin 2α+2sin 2α-sin α=1-sin α=25,∴sin α=35,∵π4<α<π,∴cos α=-45,∴tan α=-34, ∴tan ⎝⎛⎭⎫α+π4=1+tan α1-tan α=17. 10.(2010·湖北黄冈模拟)若5π2≤α≤7π2,则1+sin α+1-sin α等于( ) A .-2cos α2B .2cos α2C .-2sin α2D .2sin α2[答案] C[解析] ∵5π2≤α≤7π2,∴5π4≤α2≤7π4.∴1+sin α+1-sin α =1+2sin α2cos α2+1-2sin α2cos α2=(sin α2+cos α2)2+(sin α2-cos α2)2 =-(sin α2+cos α2)-(sin α2-cos α2)=-2sin α2.二、填空题11.(2010·广东罗湖区调研)若sin ⎝⎛⎭⎫π2+θ=35,则cos2θ=________. [答案] -725[解析] ∵sin ⎝⎛⎭⎫π2+θ=35,∴cos θ=35, ∴cos2θ=2cos 2θ-1=-725.12.(2010·江苏无锡市调研)函数y =tan x -tan 3x1+2tan 2x +tan 4x的最大值与最小值的积是高考总复习含详解答案________.[答案] -116[解析] y =tan x -tan 3x 1+2tan 2x +tan 4x =tan x (1-tan 2x )(1+tan 2x )2=tan x 1+tan 2x ·1-tan 2x 1+tan 2x =sin x cos xcos 2x +sin 2x +cos 2x -sin 2x cos 2x +sin 2x=12sin2x ·cos2x =14sin4x , 所以最大与最小值的积为-116. 13.(2010·浙江杭州质检)函数y =sin(x +10°)+cos(x +40°),(x ∈R )的最大值是________. [答案] 1[解析] y =sin x cos10°+cos x sin10°+cos x cos40°-sin x sin40°=(cos10°-sin40°)sin x +(sin10°+cos40°)cos x ,其最大值为(cos10°-sin40°)2+(sin10°+cos40°)2 =2+2(sin10°cos40°-cos10°sin40°) =2+2sin (-30°)=1.14.(文)如图,AB 是半圆O 的直径,点C 在半圆上,CD ⊥AB 于点D ,且AD =3DB ,设∠COD =θ,则tan 2θ2=________.[答案] 13[解析] 设OC =r ,∵AD =3DB ,且AD +DB =2r ,∴AD =3r 2,∴OD =r 2,∴CD =32r ,∴tan θ=CDOD=3,∵tan θ=2tanθ21-tan 2θ2,∴tan θ2=33(负值舍去),∴tan 2θ2=13.(理)3tan12°-3(4cos 212°-2)sin12°=________.[答案] -4 3 [解析] 3tan12°-3(4cos 212°-2)sin12°=3(sin12°-3cos12°)2cos24°sin12°cos12°=23sin (12°-60°)12sin48°=-4 3.三、解答题15.(文)(2010·北京理)已知函数f (x )=2cos2x +sin 2x -4cos x . (1)求f (π3)的值;(2)求f (x )的最大值和最小值.[解析] (1)f (π3)=2cos 2π3+sin 2π3-4cos π3=-1+34-2=-94.(2)f (x )=2(2cos 2x -1)+(1-cos 2x )-4cos x =3cos 2x -4cos x -1 =3(cos x -23)2-73,x ∈R因为cos x ∈[-1,1],所以当cos x =-1时,f (x )取最大值6;当cos x =23时,f (x )取最小值-73. (理)(2010·广东罗湖区调研)已知a =(cos x +sin x ,sin x ),b =(cos x -sin x,2cos x ),设f (x )=a ·b .(1)求函数f (x )的最小正周期;(2)当x ∈⎣⎡⎦⎤0,π2时,求函数f (x )的最大值及最小值. [解析] (1)f (x )=a ·b =(cos x +sin x )·(cos x -sin x )+sin x ·2cos x =cos 2x -sin 2x +2sin x cos x =cos2x +sin2x =2⎝⎛⎭⎫22cos2x +22sin2x=2sin ⎝⎛⎭⎫2x +π4. ∴f (x )的最小正周期T =π. (2)∵0≤x ≤π2,∴π4≤2x +π4≤5π4,∴当2x +π4=π2,即x =π8时,f (x )有最大值2;当2x +π4=5π4,即x =π2时,f (x )有最小值-1.16.(文)设函数f (x )=cos ⎝⎛⎭⎫2x +π3+sin 2x .高考总复习含详解答案(1)求函数f (x )的最大值和最小正周期;(2)设A 、B 、C 为△ABC 的三个内角,若cos B =13,f (C 2)=-14,且C 为锐角,求sin A 的值.[解析] (1)f (x )=cos ⎝⎛⎭⎫2x +π3+sin 2x =cos2x cos π3-sin2x sin π3+1-cos2x 2=12-32sin2x , 所以函数f (x )的最大值为1+32,最小正周期为π.(2)f (C 2)=12-32sin C =-14,所以sin C =32,因为C 为锐角,所以C =π3,在△ABC 中,cos B =13,所以sin B =223,所以sin A =sin(B +C )=sin B cos C +cos B sin C =223×12+13×32=22+36. (理)已知角A 、B 、C 为△ABC 的三个内角,OM →=(sin B +cos B ,cos C ),ON →=(sin C ,sin B -cos B ),OM →·ON →=-15.(1)求tan2A 的值;(2)求2cos 2A2-3sin A -12sin ⎝⎛⎭⎫A +π4的值.[解析] (1)∵OM →·ON →=(sin B +cos B )sin C + cos C (sin B -cos B )=sin(B +C )-cos(B +C )=-15,∴sin A +cos A =-15①两边平方并整理得:2sin A cos A =-2425,∵-2425<0,∴A ∈⎝⎛⎭⎫π2,π, ∴sin A -cos A =1-2sin A cos A =75②联立①②得:sin A =35,cos A =-45,∴tan A =-34,∴tan2A =2tan A 1-tan 2A=-321-916=-247. (2)∵tan A =-34,∴2cos 2A2-3sin A -12sin ⎝⎛⎭⎫A +π4=cos A -3sin A cos A +sin A =1-3tan A1+tan A=1-3×⎝⎛⎭⎫-341+⎝⎛⎭⎫-34=13.17.(文)(2010·厦门三中阶段训练)若函数f (x )=sin 2ax -3sin ax cos ax (a >0)的图象与直线y =m 相切,相邻切点之间的距离为π2.(1)求m 和a 的值;(2)若点A (x 0,y 0)是y =f (x )图象的对称中心,且x 0∈⎣⎡⎦⎤0,π2,求点A 的坐标. [解析] (1)f (x )=sin 2ax -3sin ax cos ax =1-cos2ax 2-32sin2ax =-sin ⎝⎛⎭⎫2ax +π6+12, 由题意知,m 为f (x )的最大值或最小值, 所以m =-12或m =32,由题设知,函数f (x )的周期为π2,∴a =2,所以m =-12或m =32,a =2.(2)∵f (x )=-sin ⎝⎛⎭⎫4x +π6+12, ∴令sin ⎝⎛⎭⎫4x +π6=0,得4x +π6=k π(k ∈Z ), ∴x =k π4-π24(k ∈Z ),由0≤k π4-π24≤π2 (k ∈Z ),得k =1或k =2,因此点A 的坐标为⎝⎛⎭⎫5π24,12或⎝⎛⎭⎫11π24,12.(理)(2010·广东佛山顺德区检测)设向量a =(sin x,1),b =(1,cos x ),记f (x )=a ·b ,f ′(x )是f (x )的导函数.高考总复习含详解答案(1)求函数F (x )=f (x )f ′(x )+f 2(x )的最大值和最小正周期; (2)若f (x )=2f ′(x ),求1+2sin 2xcos 2x -sin x cos x 的值.[解析] (1)f (x )=sin x +cos x , ∴f ′(x )=cos x -sin x , ∴F (x )=f (x )f ′(x )+f 2(x ) =cos 2x -sin 2x +1+2sin x cos x=cos2x +sin2x +1=1+2sin ⎝⎛⎭⎫2x +π4, ∴当2x +π4=2k π+π2,即x =k π+π8(k ∈Z )时,F (x )max =1+ 2.最小正周期为T =2π2=π.(2)∵f (x )=2f ′(x ),∴sin x +cos x =2cos x -2sin x , ∴cos x =3sin x ,∴tan x =13,∴1+2sin 2x cos 2x -sin x cos x =3sin 2x +cos 2x cos 2x -sin x cos x =3tan 2x +11-tan x =2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角恒等变换专题习题
一、选择题(本大题共6小题,每小题5分,共30分)
1.已知α为锐角,cosα=,则tan=( )
A.-3 B.-
C.-D.-7
解析依题意得,sinα=,故tanα=2,tan2α==-,所以tan==-.
答案 B
2.已知cos=-,则cos x+cos的值是( )
A.-B.±
C.-1 D.±1
解析cos x+cos=cos x+cos x+sin x=cos x+sin x==cos=-1.
答案 C
3.已知cos2θ=,则sin4θ+cos4θ的值为( )
A. B.
C. D.-1
解析∵cos2θ=,∴sin22θ=,∴sin4θ+cos4θ=1-2sin2θcos2θ=1-(sin2θ)2=.
答案 B
4.已知α+β=,则(1+tanα)(1+tanβ)的值是( )
A.-1 B.1
C.2 D.4
解析∵α+β=,tan(α+β)==1,
∴tanα+tanβ=1-tanαtanβ.
∴(1+tanα)(1+tanβ)=1+tanα+tanβ+tanαtanβ
=1+1-tanαtanβ+tanαtanβ=2.
答案 C
5.
(2014·成都诊断检测)如图,在平面直角坐标系xOy中,角α,β的顶点与坐标原点重合,始边与x轴的非负半轴重合,它们的终边分别与单位圆相交于A,B两点,若点A,B的坐标为和,则cos(α+β)的值为( ) A.-B.-
C.0 D.
解析cosα=,sinα=,cosβ=-,sinβ=,cos(α+β)=cosαcosβ-sinαsinβ=·(-)-·=-.选A.
答案 A
6.若=-,则sinα+cosα的值为( )
A.-B.-
C. D.
解析∵(sinα-cosα)=-(cos2α-sin2α),
∴sinα+cosα=.
答案 C
二、填空题(本大题共3小题,每小题5分,共15分)
7.若tan=,则tanα=________.
解析∵tan==,
∴5tanα+5=2-2tanα.
∴7tanα=-3,∴tanα=-.
答案-
8.(2013·江西卷)函数y=sin2x+2sin2x的最小正周期T为________.
解析y=sin2x+2sin2x=sin2x-cos2x+
=2sin(2x-)+,所以T=π.
答案π
9.(2013·新课标全国卷Ⅰ)设当x=θ时,函数f(x)=sin x-2cos x取得最大值,则cosθ=________.
解析f(x)=sin x-2cos x=(sin x-cos x)=sin(x-φ)而sinφ=,cosφ=,当x-φ=+2kπ(k∈Z)时,f(x)取最大值,即θ=φ++2kπ时,f(x)取最大值.cosθ=cos(φ++2kπ)=-sinφ=-=-.
答案-
三、解答题(本大题共3小题,每小题10分,共30分)
10.已知tan2θ=(<θ<π),求的值.
解∵tan2θ==,
∴tanθ=-3或tanθ=.
又θ∈(,π),∴tanθ=-3.
∴==
==-.
11.已知函数f(x)=2cos(其中ω>0,x∈R)的最小正周期为10π.
(1)求ω的值;
(2)设α,β∈,f=-,
f=,求cos(α+β)的值.
解(1)∵T=10π=,∴ω=.
(2)由(1)得f(x)=2cos,
∵f=2cos=-2sinα=-.
∴sinα=,cosα=.
∵f=2cosβ=,
∴cosβ=,sinβ=.
∴cos(α+β)=cosαcosβ-sinαsinβ
=×-×=-.
12.(2013·重庆卷)在△ABC中,内角A,B,C的对边分别是a,b,c,且a2+b2+ab=c2.
(Ⅰ)求C;
(Ⅱ)设cos A cos B=,=,求tanα的值.
解(Ⅰ)因为a2+b2+ab=c2,
由余弦定理有cos C===-.
故C=.
(Ⅱ)由题意得
=.
因此(tanαsin A-cos A)(tanαsin B-cos B)=,
tan2αsin A sin B-tanα(sin A cos B+cos A sin B)+cos A cos B=,tan2αsin A sin B-tanαsin(A+B)+cos A cos B=.①
因为C=,A+B=,所以sin(A+B)=,
因为cos(A+B)=cos A cos B-sin A sin B,即-sin A sin B=,解得sin A sin B=-=.
由①得tan2α-5tanα+4=0,解得tanα=1或tanα=4.。
