《信号与系统》陈生潭第二版西安电子科技大学出版社课后答案
《信号与系统》课后习题参考答案

《信号与系统》课后习题参考答案第二章 连续信号与系统的时域分析2-9、(1)解:∵系统的微分方程为:)(2)(3)(t e t r t r '=+',∴r(t)的阶数与e(t) 的阶数相等,则h(t)应包含一个)(t δ项。
又∵系统的特征方程为:03=+α,∴特征根3-=α∴)()(2)(3t u Ae t t h t -+=δ∴)]()(3[)(2)(33t e t u e A t t h t t δδ--+-+'=')()(3)(23t A t u Ae t t δδ+-'=-将)(t h 和)(t h '代入微分方程(此时e(t)= )(t δ),得:)()(3)(23t A t u Ae t t δδ+-'-+3)(2)]()(2[3t t u Ae t t δδ'=+-∴A=-6则系统的冲激响应)(6)(2)(3t u et t h t --=δ。
∴⎰⎰∞--∞--==t td ue d h t g τττδτττ)](6)(2[)()(3⎰∞-=t d ττδ)(2⎰∞---t d u e τττ)(63 )()(6)(203t u d e u t t ⎰-∞--=τττ )()3(6)(203t u e t u t --=-τ)()1(2)(23t u e t u t -+=- )(23t u e t -=则系统的阶跃响应)(2)(3t u et g t -=。
2-11、解:①求)(t r zi : ∵系统的特征方程为:0)3)(2(652=++=++αααα,∴特征根:21-=α,32-=α ∴t t zi e C eC t r 3221)(--+= (t ≥0) ②求)(t r zs :t t e A eA t h 3221)(--+= (t ≥0),可求得:11=A ,12-=A (求解过程略) ∴)()()(32t u e e t h t t ---=∴)(*)()(*)()]()[(*)()(*)()(3232t u e t u e t u e t u e t u e e t u e t h t e t r t t t t t t t zs --------=-==)()2121()()(21)()(3232t u e e e t u e e t u e e t t t t t t t -------+-=---= ③求)(t r :)(t r =)(t r zi +)(t r zs ++=--)(3221t te C e C )2121(32t t t e e e ---+- t tt e C e C e 3221)21()1(21---++-+= (t ≥0) ∵)()(t u Ce t r t -=,21=C 21=C ∴ 011=-C , ∴ 11=C0212=+C 212-=C ∴=-)0(r 21211)0(21=-=+=+C C r zi , ='-)0(r 2123232)0(21-=+-=--='+C C r zi 2-12、解:(1)依题意,得:)(2)(*)()(t u e t h t u t r tzi -=+)()()(t t h t r zi δ=+∴)(2)]()([*)()(t u e t r t t u t r t zi zi -=-+δ)(2)()()()1(t u e t r t u t r t zi zi --=-+∴)()12()()()1(t u e t r t r t zi zi -=---,两边求导得:)()12()(2)()(t e t u e t r t r t t zi ziδ-+-=-'-- )(2)()()(t u e t t r t r t zi zi--=-'δ ∴)(11)(112)()()1(t p p t p t t r p zi δδδ+-=+-=- ∴)()(11)(t u e t p t r t zi -=+=δ (2)∵系统的起始状态保持不变,∴)()(t u e t r t zi -=∵)()()(t t h t r zi δ=+,∴)()()(t u e t t h t--=δ∴)]()([*)()()(*)()()(33t u e t t u e t u e t h t e t r t r t t t zi ----+=+=δ )()()(t u te t u e t u e tt t ----+=)()2(t u e t t --= 2-16、证:∑∑∞-∞=--∞-∞=--=-=k k t k t k t u e k t t u e t r )3()3(*)()()3(δ∑∞-∞=--=k k t k t u e e )3(3 ∵当t-3k>0即3t k <时:u(t-3k)为非零值 又∵0≤t ≤3,∴k 取负整数,则:3003311)(---∞=∞=----===∑∑e e e e e et r t k k k t k t 则t Ae t r -=)(,且311--=e A 。
信号与系统--完整版答案--纠错修改后版本
1)
3)
5)
3.8、求下列差分方程所描述的离散系统的单位序列响应。
2)5)
3.9、求图所示各系统的单位序列响应。
(a)
(c)
3.10、求图所示系统的单位序列响应。
3.11、各序列的图形如图所示,求下列卷积和。
(1)(2)(3)(4)
4.34 某LTI系统的频率响应,若系统输入,求该系统的输出。
4.35 一理想低通滤波器的频率响应
4.36 一个LTI系统的频率响应
若输入,求该系统的输出。
4.39 如图4-35的系统,其输出是输入的平方,即(设为实函数)。该系统是线性的吗?
(1)如,求的频谱函数(或画出频谱图)。
(2)如,求的频谱函数(或画出频谱图)。
(1) (2) (3) (4) (5)
4.19 试用时域微积分性质,求图4-23示信号的频谱。
图4-23
4.20 若已知,试求下列函数的频谱:
(1)(3) (5)
(8)(9)
4下列方式求图4-25示信号的频谱函数 (1)利用xx和线性性质(门函数的频谱可利用已知结果)。
(1)
5-18 已知系统函数和初始状态如下,求系统的零输入响应。
(1),
(3),
5-22 如图5-5所示的复合系统,由4个子系统连接组成,若各子系统的系统函数或冲激响应分别为,,,,求复合系统的冲激响应。
5-26 如图5-7所示系统,已知当时,系统的零状态响应,求系数a、b、c。
5-28 某LTI系统,在以下各种情况下起初始状态相同。已知当激励时,其全响应;当激励时,其全响应。
(7)(8)
1-7 已知序列的图形如图1-7所示,画出下列各序列的图形。
信号与系统(第三版)陈生潭第一章课后答案

信号与系统 电子教案
1.3 阶跃信号与冲激信号
n
f ( n)
©西安电子科技大学电路与系统教研中心
k
第1-16页
■
信号与系统 电子教案
1.3 阶跃信号与冲激信号
1.3 阶跃信号与冲激信号
一 序列函数定义
1.阶跃信号
(t )
A (t t 0 )
1
ε (t)
∆→0
0 t
2
1 o t
A
0
t0
t
0 (t ) t 1
广义函数:为避开变量点上没有确定函数值的情况, 广义函数采用它与另一个函数相互作用(如相乘后积 分)后的效果来定义:
第1-20页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
1.3 阶跃信号与冲激信号
g (t )(t )dt Ng[(t )]
可理解为:在试验函数集{(t)}中,对每一函数 (t),按一定规则Ng,分配一个函数值Ng[(t)]. 注意: (t)是普通函数,满足连续、有任意阶导数。 且(t)及各阶导数在|t|时要比|t|的任意次幂更 快的趋于零;
f (t) 1 o 1 t
反转 t → - t
1 -1
f (- t )
o
t
第1-9页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
1.2 信号的运算
2.平移
将 f (t) → f (t – t0) , f (k) → f (t – k0)称为对信号f (· )的 平移或移位。若t0 (或k0) >0,则将f (· )右移;否则左移。 如: f (t- 1)
信号与系统课后答案(第二版)+曾禹村+第二章作业参考答案

i1(t) = i2 (t) + i3 (t) , i2 (t) R2 − L 有 8i2 `(t) + 3i2 (t) = 2e`(t) ˆ ˆ 由 h`(t) + 3h(t) = 2δ (t)
0
h
(−1) t 3
T
t
t 3E − τ E (t) = ∫ δ (τ )dτ − ∫ e 8 u(τ )dτ −∞ 4 −∞ 32
x(t)
1
2 t
yx(t)
1 2 3 4 t
0
1
0
Qh(0) = 0, t ≤ 0, 有 0 ≤ t <1 , h(t) + h(t −1) + h(t − 2) = h(t) = t 时 1≤ t < 2时 h(t) + h(t −1) + h(t − 2) = h(t) + h(t −1) =1 , h(t) =1− h(t −1) =1− (t −1) = 2 −t 2 ≤ t < 3 , h(t) + h(t −1) + h(t − 2) =1 时 h(t) =1− h(t −1) − h(t − 2) =1− (2 − (t −1)) − (t − 2) = 0 3 ≤ t < 4时 h(t) = 4 − t − h(t −1) − h(t − 2) =4 −t − 0 − (2 − (t − 2)) = 0 , t, 0 ≤ t < 1 ∴h(t) = 2 − t, 1 ≤ t ≤ 2 0, t < 0,2 < t
解: (e) 特征方程为 λ2+4λ+4=0 得 λ1=-2, λ2=-2。 则 h(t)= (c1eλ1 t+ c2eλ2t)u(t)=( c1e- 3 t+ c2e-2 t)u(t) h`(t)= (c1+ c2)δ(t)+(-3c1e- 3 t-2c2e- 2t)u(t) h``(t)= (c1+ c2)δ`(t)+(-3c1-2c2) δ(t)+ (9c1e- 3 t+4c2e- 2t)u(t) 将x(t)= δ(t), y(t)=h(t)代入原方程得:
信号与系统课后习题参考答案.pdf

-5
-4 -3 -2
-1
2 1
2
3
-1
x(-t+4)
t
45
6
2 1
4
6
-1
x(-t/2+4)
t 8 10 12
(e)[x(t)+x(-t)]u(t)
-2
-1
2
x(-t)
1
t
01
2
-1
(f)
x(t)[δ(t +
3) − δ(t - 3)]
2
2
3
[x(t)+x(-t)]u(t)
1 t
01
2
-1
-3/2 (-1/2)
x(t)[δ(t + 3) − δ(t - 3)]
2
2
3/2
t
0 (-1/2)
6
1.22
(a)x[n-4]
x[n-4]
11 1 1
1/2 1/2
1/2 n
0 1 23 4 5 6 7 8
-1/2
-1
(b)x[3-n]
x[n+3]
11 1 1
1/2 1/2
1/2 n
-7 -6 -5 -4 -3 -2 -1 0 1
=
2π 4
=π 2
则:整个信号的周期为:T = LCM{T1,T2} = π
1.11
j 4πn
解: e 7
→
ω1
=
4πn 7
,则:
2π ω1
=
2π 4π
=7= 2
N1 k
,⇒
N1
=
7
7
j 2πn
e5
→ ω2
信号与系统第二版课后答案

则有
相加得
即
可见
即满足可加性,齐次性是显然的。故系统为线性的。
1-8若有线性时不变系统的方程为
若在非零f(t)作用下其响应 ,试求方程
的响应。
解因为f(t) ,由线性关系,则
由线性系统的微分特性,有
故响应
第2章习题解析
2-1如图2-1所示系统,试以uC(t)为输出列出其微分方程。
2-10对图示信号,求f1(t) *f2(t)。
题2-10图
解(a)先借用阶跃信号表示f1(t)和f2(t),即
f1(t)= 2(t)2(t1)
f2(t)=(t)(t2)
故
f1(t) *f2(t) = [2(t)2(t1)] * [(t)(t2)]
因为
(t) *(t)= =t(t)
故有
f1(t) *f2(t) = 2t(t)2(t1)(t1)2(t2)(t2)+ 2(t3)(t3)
解因方程的特征根=3,故有
当h(t) =(t)时,则冲激响应
阶跃响应
2-9试求下列卷积。
(a)(t+ 3 ) *(t5 )
(b)(t) * 2
(c)tet(t)*(t)
解(a)按定义
(t+ 3 ) *(t5 )=
考虑到<3时,(+ 3 )= 0;>t5时,(t5 )= 0,故
(t+ 3 ) *(t5 )=
试证明:
(1)
(2)利用(1)的结果,证明阶跃响应
证(1)因为
y(t)=f(t)h(t)
由微分性质,有
y(t)=f(t)h(t)
再由积分性质,有
(2)因为
《信号与系统(第2版》【附录+习题答案】

附 录 A 常 用 数 学 公 式A.1 三角函数公式j e cos jsin t t t ωωω=+ j e e (cos jsin )t t t σωσωω+=+j j 1cos (e e )2t t t ωωω-=+j j 1sin (e e )2jt t t ωωω-=-sin()sin cos cos sin αβαβαβ±=± cos()cos cos sin sin αβαβαβ±=sin22sin cos ααα=2222cos2cos sin 12sin 2cos 1ααααα=-=-=-1sin sin [cos()cos()]2αβαβαβ=--+1cos cos [cos()cos()]2αβαβαβ=-++1sin cos [sin()sin()]2αβαβαβ=-++双曲正弦:e e sh 2x xx --=双曲余弦:e e ch 2x xx -+=A.2 微积分公式d()d Cu C u =,C 为常数(下同)d()d d u v u v ±=±,u 、v 为t 的函数(下同) d()d d uv v u u v =+ 2d d d u v u u v v v -⎛⎫= ⎪⎝⎭d d Cu t C u t =⎰⎰()d d d u v t u t v t ±=±⎰⎰⎰信号与系统288d d u v uv v u =-⎰⎰()d ()()()()d ()bb baaau t v t u t v t v t u t =-⎰⎰A.3 数列求和公式(1)等比数列123,,,,N a a a a 的通项为11n n a a q -=,q 为公比,前n 项的和为 111(1)11NN N N n n a a q a q S a q q =--===--∑(2)等差数列123,,,,N a a a a 的通项为1(1)n a a n d =+-,d 为公差,前n 项的和为111()(1)22NN N n n N a a N N dS a Na =+-===+∑附 录 B 常 用 信 号 与 系 统 公 式B.1 连续时间信号的卷积121221()()()()d ()()d x t x t x x t x x t ττττττ∞∞-∞-∞*=-=-⎰⎰B.2 离散时间信号的卷积121221()()()()()()m m x n x n x m x n m x m x n m ∞∞=-∞=-∞*=-=-∑∑B.3 连续时间三角形式的傅里叶级数0000011()[cos()sin()]cos()kk kkk k x t a ak t b k t A A k t ωωωϕ∞∞===++=++∑∑0000001()d t T t a A x t t T +==⎰000002()cos()d 1,2,t T k t a x t k t t k T ω+==⎰, 000002()sin()d 1,2,t T k t b x t k t t k T ω+==⎰,1,2,k A k = arctan 1,2,k k k b k a ϕ⎛⎫=-=⎪⎝⎭,B.4 连续时间指数形式的傅里叶级数FS000j 01()e d t T k t k t X x t t T ω+-=⎰0j 0()()ek tk x t X k ωω∞=-∞=∑信号与系统290B.5 连续时间傅里叶变换FTj (j )()e d t X x t t ωω∞--∞=⎰j 1()(j )e d 2πt x t X ωωω∞-∞=⎰B.6 双边拉普拉斯变换()()e d st X s x t t ∞--∞=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰B.7 单边拉普拉斯变换0()()e d st X s x t t ∞--=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰,0t ≥B.8 离散时间傅里叶级数DFS2πj 1()()ekn NN N n N X k x n N -=<>=∑,0,1,2,k =±±2πj()()ekn NN N k N x n X k =<>=∑,0,1,2,n =±±B.9 离散时间傅里叶变换DTFTj j (e )()enn X x n ΩΩ∞-=-∞=∑j j 2π1()(e )e d 2πn x n X ΩΩΩ=⎰B.10 离散傅里叶变换DFT1()()01N knNn X k x n Wk N -==-∑≤≤,附 录 B 常 用 信 号 与 系 统 公 式29111()()01N kn Nk x n X k Wn N N--==-∑≤≤,B.11 双边Z 变换b ()()nn X z x n z∞-=-∞=∑11()()2n cx n X z z dzj π-=⎰B.12 单边Z 变换s 0()()nn X z x n z∞-==∑11()()2n cx n X z z dzj π-=⎰习题参考答案第1章1.1(a)确定信号、连续时间信号、非周期信号、能量信号、非因果信号。
2023年大学_信号与系统第二版(陈生潭著)课后答案下载

2023年信号与系统第二版(陈生潭著)课后答案下载2023年信号与系统第二版(陈生潭著)课后答案下载第1章信号与系统的基本概念1.0 信号与系统1.1 信号的描述和分类1.1.1 信号的描述1.1.2 信号的分类1.2 信号的基本特性1.3 信号的基本运算1.3.1 相加和相乘1.3.2 翻转、平移和展缩1.3.3 信号的导数和积分1.3.4 信号的差分和迭分1.4 阶跃信号和冲激信号1.4.1 连续时间阶跃信号1.4.2 连续时间冲激信号1.4.3 广义函数和艿函数性质1.4.4 阶跃序列和脉冲序列1.5 系统的描述1.5.1 系统模型1.5.2 系统的输入输出描述1.5.3 系统的状态空间描述1.5.4 系统的框图表示1.6 系统的特性和分类1.6.1 线性特性1.6.2 时不变特性1.6.3 因果性1.6.4 稳定性1.6.5 系统的分类1.7 信号与系统的分析方法习题一第2章连续信号与系统的`时域分析 2.0 引言2.1 连续时间基本信号2.1.1 奇异信号2.1.2 正弦信号2.1.3 指数信号2.2 卷积积分2.2.1 卷积的定义2.2.2 卷积的图解机理2.2.3 卷积性质2.2.4 常用信号的卷积公式2.3 系统的微分算子方程2.3.1 微分算子和积分算子2.3.2 LTI系统的微分算子方程2.3.3 电路系统算子方程的建立2.4 连续系统的零输入响应2.4.1 系统初始条件2.4.2 零输入响应算子方程2.4.3 简单系统的零输入响应2.4.4 一般系统的零输入响应2.5 连续系统的零状态响应2.5.1 连续信号的艿(£)分解2.5.2 基本信号d(£)激励下的零状态响应 2.5.3 一般信号厂(£)激励下的零状态响应2.5.4 零状态响应的另一个计算公式2.6 系统微分方程的经典解法2.6.1 齐次解和特解2.6.2 响应的完全解习题二第3章连续信号与系统的频域分析3.0 引言3.1 信号的正交分解3.1.1 矢量的正交分解3.1.2 信号的正交分解3.2 周期信号的连续时间傅里叶级数3.2.1 三角形式的傅里叶级数3.2.2 指数形式的傅里叶级数3.3 周期信号的频谱3.3.1 周期信号的频谱3.3.2周期信号频谱的特点3.3.3周期信号的功率3.4 非周期信号的连续时IⅫ傅里叶变换 3.4.1 傅里叶变换3.4.2 非周期信号的频谱函数3.4.3 典型信号的傅里叶变换3.5 傅里叶变换的性质3.6 周期信号的傅里叶变换3.7 连续信号的抽样定理3.7.1 信号的时域抽样定理3.7.2 周期脉冲抽样……第4章连续信号与系统的S域分析第5章离散信号与系统的时域分析第6章离散信号与系统的频域分析第7章离散信号与系统的Z域分析第8章系统的状态空间分析第9章随机信号通过线性系统分析第10章 MATLAB在信号与系统分析中的应用附录各章习题参考答案信号与系统第二版(陈生潭著):内容提要本书可作为高等学校电子信息工程、通信工程、计算机科学与技术、测控技术与仪器、光信息科学与技术、电气工程及自动化等专业“信号与系统”课程的教材,也可供相关专业科技工作人员参考。
信号与系统课后题答案

《信号与系统》课程习题与解答第二章习题(教材上册第二章p81-p87)2-1,2-4~2-10,2-12~2-15,2-17~2-21,2-23,2-24第二章习题解答2-1 对下图所示电路图分别列写求电压的微分方程表示。
图(a):微分方程:11222012()2()1()()()2()()()()2()()()c cc di t i t u t e t dtdi t i t u t dtdi t u t dt du t i t i t dt ⎧+*+=⎪⎪⎪+=⎪⇒⎨⎪=⎪⎪⎪=-⎩图(b ):微分方程:⎪⎪⎪⎩⎪⎪⎪⎨⎧-==+++=+++⎰⎰2021'2'21'2'11)(01)(1Ri t v Ri Mi Li dt i Ct e Ri Mi Li dt i C)()(1)(2)()2()(2)()(33020022203304422t e dtd MR t v C t v dt d C R t v dt d C L R t v dt d RL t v dt d M L =+++++-⇒ 图(c)微分方程:dt i C i L t v ⎰==211'101)(⎪⎪⎪⎩⎪⎪⎪⎨⎧===⇒⎰dt t v L i t v L i dtdt v L i dt d)(1)(1)(10110'1122011∵ )(122111213t i dt d L C i i i i +=+=)(0(1]1[][101011022110331t e dt dR t v RL v dt d RR L C v dt d R C R C v dt d CC μ=+++++⇒图(d)微分方程:⎪⎩⎪⎨⎧+-=++=⎰)()()()()(1)()(11111t e t Ri t v t v dt t i C t Ri t e μRC v dt d 1)1(1+-⇒μ)(11t e V CR = ∵)()(10t v t v μ=)()(1)1(0'0t e R v t v R Cv v =+-⇒2-4 已知系统相应的其次方程及其对应的0+状态条件,求系统的零输入响应。
【电子信息类】课后习题答案大全

【电子信息类】课后习题答案大全第9类【一共15类】【电子信息类课后习题答案大全】▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆第9类【一共15类】【电子信息类课后习题答案大全】▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆《模拟电子技术基础》详细习题答案(童诗白,华成英版,高教版)/viewthread.php?tid=42&fromuid=1000《电工学》课后习题答案(第六版,上册,秦曾煌主编)/viewthread.php?tid=232&fromuid=1000《数字电子技术基础》习题答案(阎石,第五版)/viewthread.php?tid=90&fromuid=1000《电路》习题答案上(邱关源,第五版)/viewthread.php?tid=137&fromuid=1000《电工学》习题答案(第六版,秦曾煌)/viewthread.php?tid=112&fromuid=1000《模拟电子技术基础》课后习题答案(共10章)/viewthread.php?tid=21&fromuid=1000《模拟电子技术基础简明教程》课后习题答案(杨素行第三版)/viewthread.php?tid=41&fromuid=1000《信号与线性系统分析》习题答案及辅导参考(吴大正版)/viewthread.php?tid=74&fromuid=1000《通信原理》课后习题答案及每章总结(樊昌信,国·防工业出版社,第五版)/viewthread.php?tid=203&fromuid=1000《电力电子技术》习题答案(第四版,王兆安,王俊主编)/viewthread.php?tid=164&fromuid=1000《自动控制原理》课后题答案(胡寿松,第四版)/viewthread.php?tid=52&fromuid=1000《信号与系统》习题答案(第四版,吴大正)/viewthread.php?tid=268&fromuid=1000《电工学——电子技术》习题答案(下册)/viewthread.php?tid=237&fromuid=1000《微机原理及应用》习题答案/viewthread.php?tid=261&fromuid=1000《信息论与编码》辅导PPT及部分习题答案(曹雪虹,张宗橙,北京邮·电大学出版社)/viewthread.php?tid=136&fromuid=1000《数字电子技术基础》课后习题答案(完整答案版)/viewthread.php?tid=197&fromuid=1000《单片机原理及应用》课后习题答案(张毅刚主编,高教版)/viewthread.php?tid=36&fromuid=1000《高频电子线路》习题参考答案(第四版)/viewthread.php?tid=142&fromuid=1000《信号与系统》习题详解(奥本海姆版)/viewthread.php?tid=79&fromuid=1000《电路分析》课后答案及学习指导(第二版,胡翔骏,高教版)/viewthread.php?tid=177&fromuid=1000《数字电路与逻辑设计》课后习题答案,讲解详细/viewthread.php?tid=233&fromuid=1000《电路》第五版课后答案/viewthread.php?tid=1678&fromuid=1000自动控制原理习题集(自学辅导推荐)/viewthread.php?tid=53&fromuid=1000《现代通信原理》习题答案(曹志刚版)/viewthread.php?tid=44&fromuid=1000《数字信号处理》课后答案及详细辅导(丁美玉,第二版)/viewthread.php?tid=58&fromuid=1000《控制工程基础》课后习题解答(清华版)/viewthread.php?tid=127&fromuid=1000《信息论与编码》学习辅导及习题详解(傅祖芸版)/viewthread.php?tid=238&fromuid=1000《自动控制原理》习题答案/viewthread.php?tid=117&fromuid=1000《微机原理》作业答案(李继灿版)/viewthread.php?tid=218&fromuid=1000《电力电子技术》习题答案(第4版,西安交通·大学)/viewthread.php?tid=130&fromuid=1000《通信原理》习题答案/viewthread.php?tid=190&fromuid=1000《控制工程基础》习题答案(第二版,燕山·大学)/viewthread.php?tid=126&fromuid=1000《自动控制原理》课后习题答案———胡寿松,第五版/viewthread.php?tid=1740&fromuid=1000《数字电子技术基础》详细习题答案(阎石第四版)/viewthread.php?tid=167&fromuid=1000《数字信号处理——基于计算机的方法》习题答案(第二版)/viewthread.php?tid=174&fromuid=1000《电力拖动自动控制系统》习题答案/viewthread.php?tid=115&fromuid=1000《自动控制原理》课后题答案(卢京潮主编,西北工业·大学出版社)/viewthread.php?tid=128&fromuid=1000《电路分析》习题答案(第2版,高等教育出版社,胡翔俊)/viewthread.php?tid=250&fromuid=1000《信号与系统》习题解析(燕庆明,第3版)非常详细/viewthread.php?tid=71&fromuid=1000《信号与系统》课后习题答案/viewthread.php?tid=198&fromuid=1000《电磁场与电磁波》习题答案(第4版,谢处方编,高教版)/viewthread.php?tid=2514&fromuid=1000《信号与系统》习题答案详解(郑君莉,清·华大学,牛逼完整版)/viewthread.php?tid=257&fromuid=1000《高频电子线路》课后答案(第四版,张肃文)/viewthread.php?tid=3392&fromuid=1000《通信电路》课后习题答案(沈伟慈,西安电子科技·大学出版社)/viewthread.php?tid=259&fromuid=1000《数字信号处理》完整习题答案(程佩青,英文版)/viewthread.php?tid=223&fromuid=1000《数字信号处理教程》习题解答(第二版)/viewthread.php?tid=65&fromuid=1000《电子线路-非线性部分》课后答案(谢嘉奎高等教育出版社)/viewthread.php?tid=192&fromuid=1000《数字信号处理》习题答案/viewthread.php?tid=111&fromuid=1000《数字逻辑》(第二版)习题答案(欧阳明星主编)/viewthread.php?tid=26&fromuid=1000《数字逻辑电路与系统设计》习题答案/viewthread.php?tid=234&fromuid=1000数字信号处理程佩青第三版清·华大学出版社/viewthread.php?tid=2264&fromuid=1000《信息论与编码》曹雪虹-张宗橙清·华大学出版社可配北邮版本/viewthread.php?tid=1956&fromuid=1000《数字通信》习题答案(第四版,Proakis)/viewthread.php?tid=275&fromuid=1000电子技术数字和模拟部分答案(第四版,康华光)/viewthread.php?tid=100&fromuid=1000《单片机及接***术》课后答案(梅丽凤,王艳秋,清·华大学出版社)/viewthread.php?tid=159&fromuid=1000《信号与线性系统》习题详解(管致中,第四版)/viewthread.php?tid=858&fromuid=1000《信号与系统》习题及精解/viewthread.php?tid=108&fromuid=1000《电路与电子学》习题解答与实验指导(电子工业出版社出版,第3版)/viewthread.php?tid=2788&fromuid=1000《信号与系统》课后习题答案(西安电子科·技大学)/viewthread.php?tid=106&fromuid=1000《测控电路》习题答案(机械出版社)/viewthread.php?tid=166&fromuid=1000《数字逻辑》第四版习题答案/viewthread.php?tid=11&fromuid=1000《高频电子线路》习题集参考答案(曾兴雯版,高等教育出版社)/viewthread.php?tid=1502&fromuid=1000电工学(第6版)上册(电工技术)秦曾煌主编高教出版社/viewthread.php?tid=2655&fromuid=1000《数字电子技术》课后习题答案详解(阎石,第四版)/viewthread.php?tid=97&fromuid=1000模拟电子技术课后习题答案/viewthread.php?tid=1145&fromuid=1000《电工学》习题答案(高教版,第六版)/viewthread.php?tid=1621&fromuid=1000《信号与系统》课后习题答案(于慧敏著)/viewthread.php?tid=107&fromuid=1000《电子电路分析与设计》课后题答案(英文版)/viewthread.php?tid=135&fromuid=1000《电工学》课后习题答案(第六版,上册,秦曾煌主编)/viewthread.php?tid=2076&fromuid=1000《基础电子技术》习题解答(哈工大,蔡惟铮)/viewthread.php?tid=266&fromuid=1000《现代控制系统》答案(英文版)730页/viewthread.php?tid=98&fromuid=1000奥本海姆《信号与系统》第二版习题详解/viewthread.php?tid=1343&fromuid=1000《数字电路》习题答案(龚之春,电子科·技大学出版社)/viewthread.php?tid=2342&fromuid=1000《热工测量与自动控制》习题及答案/viewthread.php?tid=248&fromuid=1000简明电路分析基础李瀚荪高教版/viewthread.php?tid=6218&fromuid=1000传感器与检测技术+课后习题答案/viewthread.php?tid=2175&fromuid=1000《信息论基础教程》习题答案(李亦农,李梅版)/viewthread.php?tid=2159&fromuid=1000传感器期末考试复习资料大全/viewthread.php?tid=5262&fromuid=1000《IBM-PC汇编语言》课后习题答案/viewthread.php?tid=67&fromuid=1000《信号与系统》课后习题答案(郑君里,第二版)/viewthread.php?tid=2682&fromuid=1000化工原理第三版答案(清晰版)(缺三七章)陈敏恒等化学工业出版社/viewthread.php?tid=3523&fromuid=1000电磁场与电磁波(第二版)课后题答案/viewthread.php?tid=1705&fromuid=1000自动控制原理习题答案/viewthread.php?tid=1944&fromuid=1000电力电子技术+第四版+王兆安/viewthread.php?tid=6306&fromuid=1000数字逻辑与数字系统设计课后答案王永军/viewthread.php?tid=2050&fromuid=1000信号与系统(第三版)陈生潭西安电子科·技大学出版社/viewthread.php?tid=1525&fromuid=1000《信息论与编码》习题答案(高等教育出版社)仇佩亮编/viewthread.php?tid=99&fromuid=1000《电磁场与电磁波》课后习题答案(冯恩信)/viewthread.php?tid=3863&fromuid=1000模拟电子技术期末复习/viewthread.php?tid=7366&fromuid=1000工厂供电习题答案/viewthread.php?tid=1929&fromuid=1000《电路与模拟电子技术》习题答案/viewthread.php?tid=2861&fromuid=1000(新)图像处理2008(A卷)及答案!/viewthread.php?tid=5533&fromuid=1000面向21世纪课程教材电子电路基础/viewthread.php?tid=3261&fromuid=1000《16/32位微机原理、汇编语言及接***术》答案1~10章钱晓婕版机械工业出版社/viewthread.php?tid=3655&fromuid=1000《高频电路原理与分析》西电出版社第三版习题答案/viewthread.php?tid=2649&fromuid=1000《自动控制理论》第2版_夏德钤翁贻方机械工业出版社习题答案/viewthread.php?tid=2716&fromuid=1000电工电子技术-王鼎等主编/viewthread.php?tid=7946&fromuid=1000模拟电子技术基础(第3版华成英主编)习题答案/viewthread.php?tid=2125&fromuid=1000哈工大(威海)电工学期末试题/viewthread.php?tid=3408&fromuid=1000《C语言程序设计》习题参考答案(罗朝盛版)/viewthread.php?tid=4561&fromuid=1000高教版计算方法(施吉林,刘淑珍,陈桂芝编)课后习题答案/viewthread.php?tid=7088&fromuid=1000《电路与电子技术基础》习题参考解答/viewthread.php?tid=856&fromuid=1000固体物理习题答案/viewthread.php?tid=7715&fromuid=1000通信原理课件第五版/viewthread.php?tid=7716&fromuid=1000《数字电路》习题解答(余孟尝,第3版)/viewthread.php?tid=444&fromuid=1000《微电子器件与IC设计》习题答案(科学出版社)/viewthread.php?tid=116&fromuid=1000高频电子线路答案/viewthread.php?tid=1501&fromuid=1000《数字逻辑》PPT课件/viewthread.php?tid=673&fromuid=1000高频电路/viewthread.php?tid=1683&fromuid=1000数电实验报告/viewthread.php?tid=5501&fromuid=1000信息论与编码学习辅导及习题详解/viewthread.php?tid=4557&fromuid=1000《固体物理》习题答案(黄昆版)/viewthread.php?tid=1319&fromuid=1000电工电子学第二版课后答案/viewthread.php?tid=7322&fromuid=1000电气控制与可编程序控制器习题解答/viewthread.php?tid=6907&fromuid=1000微积分II复习/viewthread.php?tid=5875&fromuid=1000《Visual foxpro 程序设计》课后答案(重`庆大学出版社)/viewthread.php?tid=610&fromuid=1000传感器与传感器技术第二版何道清习题解答/viewthread.php?tid=6815&fromuid=1000微观经济学/viewthread.php?tid=5876&fromuid=1000《传感器与检测技术》陈杰高教版高等教育出版社课后答案/viewthread.php?tid=3173&fromuid=1000信息安全数学基础(陈恭亮)课后习题答案/viewthread.php?tid=5948&fromuid=1000量子力学/viewthread.php?tid=4488&fromuid=1000数据处理模拟练习题参考答案(14张word)/viewthread.php?tid=820&fromuid=1000C++语言学习质料/viewthread.php?tid=7889&fromuid=1000模拟电子技术基础部分答案/viewthread.php?tid=8499&fromuid=1000计算机操作系统期末复习题/viewthread.php?tid=5996&fromuid=1000电力电子技术练习及参考解/viewthread.php?tid=7123&fromuid=1000《传感器与检测技术》课后答案,陈杰编著,高等教育出版社。
信号与系统课后答案(PDF)
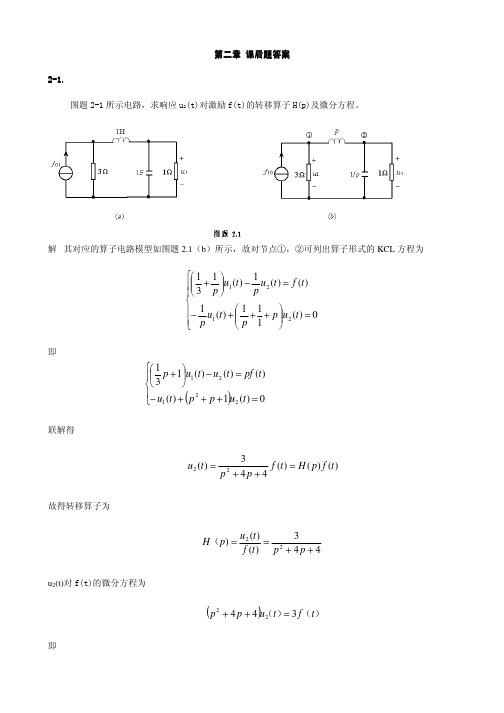
第二章第二章 课后题答案课后题答案2-1.1.图题2-1所示电路,求响应u 2(t)对激励f(t)的转移算子H(p)及微分方程。
解 其对应的算子电路模型如图题2.1(b )所示,故对节点①,②可列出算子形式的KCL 方程为= +++−=−+0)(111)(1)()(1)(1312121t u p p t u p t f t u p t u p即()=+++−=−+0)(1)()()()(13122121t u p p t u t pf t u t u p联解得)()()(443)(22t f p H t f p p t u =++=故得转移算子为443)()()22++==p p t f t u p H (u 2(t)对f(t)的微分方程为())()(t f t u p p 34422=++即)(t f t u t u dt d t u dt d 3)(4)(4)(22222=++2-2图题2-2所示电路,求响应i(t)对激励f(t)的转移算子H(p)及微分方程。
解 其对应的算子电路模型如图2.2(b)所示。
故得)()(t f p p p p pp t f t i 3011101022221.01)(2+++=+×++=故得转移算子为30111010)()()(2+++==p p p t f t i p Hi(t)对f(t)的微分方程为)()1010()()3011(2t f p t i p p +=++即)(10)(10)(30)(11)(22t f t f dt d t i t i dt d t i dt d +=++2-3图题2-3所示电路,已知u C (0-)=1 V, i(0-)=2 A。
求t>0时的零输入响应i(t)和u C (t)。
解 其对应的算子电路模型如图题2.3(b)所示。
故对节点N 可列写出算子形式的KCL 方程为0)(2312= ++t u p p C又有uc(t)=pi(t),代入上式化简,即得电路的微分方程为=====++−+−+1)0()0(2)0()0(0)()23(2c cu u i i t i p p电路的特征方程为0232=++p p故得特征根(即电路的自然频率)为p 1=-1,p 2=-2。
信号与系统课后习题答案(西安电子科技大学)

(7)
所以, cos(8kπ
/ 7)
=
cos⎢⎣⎡87π
(k
+
N )⎥⎦⎤
,即 8π 7
N
=
2πn ,则有:
N
=
7 4
n
=
7(取n
=
4)
1.5 已知连续时间信号 x(t)和 y(t)分别如题图 1.2(a)、(b)所示,试画出下列各信号 的波形图:
解:
1.6 已知离散时间信号 x(k)和 y(k)分别如题图 1.3(a)、(b)所示,试画出下列序列 的图形:
+
Cuc′
(t
)
+
1 2
u(t)
----⑴
对回路①,有:
⎧− ⎪ ⎨ ⎪⎩iL
uR (t) + LiL′ (t) + u(t) =
(t)
=
CuC′
(t)
+
1 2
u(t)
0
⇒
u
R
(t
)
=
u
′′(t
)
+
1 2
u′(t
)
+
u(t
)
----⑵
⑴、⑵式联合求解得:
is
(t)
=
1 3
u′′(t)
+
1 6
u′
(t)
1
∞
解: f (t)δT (t) = t ∑δ (t − nT ) n=−∞
∴ f1 (t) = [ f (t)δT (t)]* gτ (t) f2 (t) = f (t)[δT (t) * gτ (t)]
解: 利用卷积的微积分性质
∫ [ ] y(t) =
《信号与系统》习题参考答案

《信号与系统》习题参考答案(1)2—1(1) 01()()()()(1)()ta at x t h t x u t d e d e u t aτττττ∞---∞*=⋅-==-⎰⎰ (2) 00()()(cos sin )()x t h t t d ωτωτδττ∞-∞*=+⋅-⎰0000(cos sin )()cos sin t t t d t t ωωδττωω∞-∞=+⋅-=+⎰(3) 当0t <时 ()()0x t h t *=当01t ≤<时 20()()(1)2tt x t h t d t ττ*=+=+⎰当12t ≤<时 13()()(1)2x t h t d ττ*=+=⎰ 当23t ≤<时 12213()()(1)22t x t h t d t t ττ-*=+=-++⎰ 当3t ≥时 ()()0x t h t *= (4) 当0t <时 ()()0x t h t *=当0t ≥时 01()()sin 2(1cos 2)2tx t h t d t ττ*==-⎰ (5) 22222(2)2(4)241()()(2)2t t t t t t t x t h t e d e d e ee ττττ-----*=-=-+⎰⎰ (6)()x t at b =+11212()()()()()(2)3363tt x t h t a b d a tb t a t a bττδ-*=+++*--=++⎰2—2(1) [][][][2](2)[2]x n h n nu n n n u n δ*=*-=--(2) 10[][](2)[](21)[]nin i x n h n u n u n +=*==-∑(3) 当0n ≥时 1111[][]2()()232i n in i x n h n --=-∞*==∑ 当0n <时 111[][]2()223n i n i n i x n h n --=-∞*==⋅∑ (4) 当0n <时 [][]0x n h n *=当0n ≥时 110[][]()[]n n nin ii x n h n u n βααββα++-=-*==-∑(5) 当07n ≤≤时 071[][](1)[1(1)]2in i n x n h n -=-*=-=--∑ 当70n -≤≤时 71[][](1)[(1)1]2ni n i x n h n -=-*=-=--∑ 2—3(1) 12()()[(1)(1)][(5)(5)]x t x t u t u t t t δδ*=+--*++- (6)(4)(4)(6)u t u t u t u t =++--+-- (2) 123()()()x t x t x t **{[(6)(4)][(4)(6)]}*[u t u t u t u t =+-++---11()()]22t t δδ++- ( 6.5)( 4.5)( 5.5)( 3.5)( 3.5)( 5.5)u t u t u t u t u t u t =+-+++-++--- ( 4.5)( 6.5)u t u t +---(3) 1311()()[(1)(1)][()()]22x t x t u t u t t t δδ*=+--*++- ( 1.5)(0.5)(0.5)( 1.5)u t u t u t u t =+--++-- 2—4 0(3)331()(3)1t k k t tk k y t eu t k e e e e∞-----=-∞=-∞=-=⋅=-∑∑311A e-=- 2—5(1) 当2t ≥时 ()()0x t h t *= 当20t -<<时 11()()2t x t h t d t τ+-*==+⎰当02t <<时 11()()2t x t h t d t τ-*==-⎰(2) 当01t <<时 1()()22(1)tx t h t d t τ*==-⎰ 当10t -<<时 01()()22(1)2t tx t h t d d t t t ττ+*=+=-++=+⎰⎰当21t -<<-时 11()()2t x t h t d t τ+-*==+⎰当 1t ≥ 或 2t <-时 ()()0x t h t *=此题也可利用性质,先对()x t 积分,对()h t 微分,'()()()y t x t dt h t =*⎰(3) 当0t <时 (1)1()()1t x t h t e dt +∞--*==⎰当0t ≥时 1(1)(1)11()()22t t t t t x t h t e dt e dt e ++∞-----+*=+=-⎰⎰(4) 当t π< 或 5t π>时 ()()0x t h t *= 当3t ππ<<时 0()()sin 1cos t x t h t d t πττ-*==+⎰当35t ππ<<时 23()()sin 1cos t x t h t d t ππττ-*==--⎰(5) 当01t <<时 2211()()222()22x t h t t t t *=-=--当12t <≤时 2231()()264[2()]22x t h t t t t *=-+-=---()()x t h t *是以2为周期的周期函数 2—7(1) 111[][1]()[]()[1]22nn h n Ah n u n A u n ---=--111()[()()][1]()22nn n A u n n δδ-=+--=12A =(2) 111[][][][1][][]h n h n Ah n h n h n n δ---*-*-=*11[][][1]2h n n n δδ-∴=-- (3) 11[][][]2[[][1]][]nx n h n h n u n u n h n --**=--* 2[]2[[][4]]2[[1][5]]nn x n u n u n u n u n -∴=------2—8(1) 0()3()y t y t =(2) 00()()(2)y t y t y t =-- (3) 0()(1)y t y t =- (4) 0()()y t y t =-(5) 0()()dy t y t dt=(6) 202()()d y t y t dt =2—9 12111[][]()[]()[1]222n n x n h n u n u n -*=-+--1()([][1])[]2nu n u n n δ=---=1221[][][][]([][])*[]y n x n h n h n x n h n h n =**=* []*([][])[][]n n n n n u n u n u n u n δαβαβ=+=+ 2—10(1) 341201[][]((0.5))[3]2(1())[3]2n nn n x n x n u n u n ++=*=+=-+∑ (2) 4123[][][]2(1(0.5))[3]([][1])n x n x n x n u n n n δδ+**=-+*-- 43312(1(0.5))[3]2(1(0.5))[2]()[3]2n n n u n u n u n +++=-+--+=+ (3) 23[][][3]([][1])[3][2][3]x n x n u n n n u n u n n δδδ*=+*--=+-+=+ 2—11(1) 12345[][]([][][])[]h n h n h n h n h n h n =*-*+ (2) 34[][][1]h n h n nu n *=- 234[][][](1)[][1][]h n h n h nn u n n u n u n -*=+--= 12345[][]([][][])[]h n h n h n h n h n h n =*-*+514()([][3])*[][]2nu n u n u n hn =--+ 4[]6[1]7[2][]4[3]5[]6[1]7[2]4[3]n n u n n n n n u n n δδδδδδδ=+-+-++-=+-+---(1)'()()(2)(2)()(2)tt y t e x d x t y t x t τττ---∞=--+-=-+-⎰(2)()(2)t h t eu t --=- (2)当1t ≤时 ()0y t =当14t <≤时 1(2)(1)2()1t t y t e d e ττ+----==-⎰当4t >时 1(2)(4)(1)2()t t t t y t e d e e ττ+-------==-⎰2—13(1)213()()()()(1)[()](1)[()](1)h t h t h t u t t t u t t u t δδδ**=*-*-=-*-=-- 1213()()()()()()(1)h t h t h t h t h t u t u t =+**=--(2)1(10)1(02)()3(23)0t t t y t t t +-<<⎧⎪<<⎪=⎨-<<⎪⎪⎩其余2—14(1)因果、稳定 (2)非因果、非稳定 (3)非因果、稳定 (4)非因果、稳定 (5)非因果、稳定 (6)因果、稳定 (7)因果、非稳定 2—15(1)因果、稳定 (2)非因果、稳定 (3)非因果、非稳定 (4)非因果、稳定 (5)因果、非稳定 (6)非因果、稳定 (7)因果、稳定 2—16(1)对 (2)对()h t dt ∞-∞=+∞⎰(3)错 例如单位冲激响应(1)t δ-是因果的,但LTI 系统的逆系统(1)t δ+不是因果的。
信号与系统课后习题参考答案

1试分别指出以下波形是属于哪种信号?题图1-11-2试写出题1-1图中信号的函数表达式。
1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示,试作出下列各信号的波形图,并加以标注。
题图1-3⑴)2(1-t x ⑵)1(1t x -⑶)22(1+t x⑷)3(2+t x ⑸)22(2-t x ⑹)21(2t x - ⑺)(1t x )(2t x -⑻)1(1t x -)1(2-t x ⑼)22(1t x -)4(2+t x 1-4已知信号)(1n x 与)(2n x 波形如题图1-4中所示,试作出下列各信号的波形图,并加以标注。
题图1-4⑴)12(1+n x ⑵)4(1n x -⑶)2(1n x ⑷)2(2n x -⑸)2(2+n x ⑹)1()2(22--++n x n x⑺)2(1+n x )21(2n x -⑻)1(1n x -)4(2+n x ⑼)1(1-n x )3(2-n x1-5已知信号)25(t x -的波形如题图1-5所示,试作出信号)(t x 的波形图,并加以标注。
题图1-51-6试画出下列信号的波形图:⑴)8sin()sin()(t t t x ΩΩ=⑵)8sin()]sin(211[)(t t t x ΩΩ+= ⑶)8sin()]sin(1[)(t t t x ΩΩ+=⑷)2sin(1)(t tt x = 1-7试画出下列信号的波形图:⑴)(1)(t u e t x t -+=⑵)]2()1([10cos )(---=-t u t u t e t x t π⑶)()2()(t u e t x t --=⑷)()()1(t u e t x t --=⑸)9()(2-=t u t x ⑹)4()(2-=t t x δ1-8试求出以下复变函数的模与幅角,并画出模与幅角的波形图。
⑴)1(1)(2Ω-Ω=Ωj e j X ⑵)(1)(Ω-Ω-Ω=Ωj j e e j X ⑶Ω-Ω---=Ωj j e e j X 11)(4⑷21)(+Ω=Ωj j X 1-9已知信号)]()([sin )(π--=t u t u t t x ,求出下列信号,并画出它们的波形图。
信号与系统(陈生潭)习题答案1-4章部分1

信号与系统(陈生潭)习题答案1-4章部分1第一章,第二章,第三章,第四章,第一章:1.找两个表示信号的例子,并指出信号表示的信息(消息)。
1.1(1),1.1(5),1.1(9);1.2(4),1.2(6) ;1.3(a);1()(1)0.5*() 2.5*(1)(3)f t t t t t εεεε=++--+-1.4(6), (1)6()j t f t eπ-=, 周期信号,周期为22T ππ==1.5(10);1.6(4);1.11(3),[]00000()()()()1j t j t j t j t j t e t t t dte t dt e t t dt e e e ωωωωωδδδδ∞--∞∞∞---∞-∞----=--=-=-⎰⎰⎰1.19 解:(1) 线性、时不变、因果、稳定;(2) 非线性(零输入响应12(0)(0)x x 为非线性响应)、时不变、因果、不稳定(响应中0()t f d ττ⎰,例如信号()()f t t ε=时,随时间增长变为无穷大。
); (3) 非线性(输出响应sin[()]f t 为非线性响应)、时不变、因果、稳定;(4) 线性、时变(响应(2)f t 和初始时间有关系)、非因果(响应(1)f t +,0t =时刻的响应和之后的时刻1t =有关系)、稳定;(5) 非线性(响应()(2)f k f k -为非线性响应)、时不变、因果、稳定; (6) 线性、时变(响应11(0)2kx ⎛⎫⎪⎝⎭为和初始时刻有关系的响应)、非因果(响应(1)(2)k f k -+,0k =时刻的响应和之后的时刻2k =有关系)、不稳定(响应中(1)(2)k f k -+,例如信号()()f k k ε=时,随k 增长变为无穷大。
);1.21 解:零输入线性,包括零输入齐次性和零输入可加性。
因为激励()0f t =,故系统零状态响应()0fyt =。
对于零输入响应,已知3121(0)1,(0)0()23,0ttx x x y t e e t ----==→=+≥3122(0)0,(0)1()42,0t t x x x y t e e t ----==→=-≥ 根据零输入线性,可得12123(0)5,(0)3()5()3()229,0x x x t tx x y t y t y t e e t ----==→=+=+≥响应;3()()229,0tt xy t y t ee t --==+≥1.23 解: 设初始状态12(0)1,(0)2x x --==时,系统的零输入响应为1()x y t ;输入()()f t t ε=时,系统的零状态响应为 1()f y t ,则有11231231()()65()3()87t tx f t t x f y t y t e e y t y t e e----⎧+=-⎪⎨+=-⎪⎩联立,解方程组得12312354t t x t t f y e e y e e----⎧=-⎪⎨=-⎪⎩根据系统的线性特性,求得 (1)23154,0t t x x y y e e t --==-≥(2)输入为()2()f t t ε=时的零状态响应12322(),0ttff y y e e t --==-≥# 离散信号()f n : # (3)()()(3)t t t t εεεε-=-- # )()()()(02t d d e d e tttεττδττδττδτ===⎰⎰⎰∞-∞-∞--1.4(6), (1)6()j t f t eπ-=, 周期信号,周期为22T ππ==# 系统结构框图如图所示,该系统的单位冲激响应h(t) 满足的方程式为dh t dt h t t ()()()+=δ)()()()()()()()();()()()()()()()()()()()()()()()('''''t t h dtt dh t t h t h t t x t h t y t x t y t y t y t x t s t x t s t y t s t y t s t x t s δδδ=+=+===+-=-===-=代入第二章:2.3(3)()434()()()(1)()(1)f t f t f t t t t δδδ*=*+++-444(1)()(1)(2)(1)(1)(2)f t f t f t t t t t εεεε=+++-=+++----2.3(4) 45()()((1)(1))((1)(4))f t f t t t t t εεεε*=+--*---235()|()|()|()|t t t t t t t t t t t t t t t t εεεε→→-→-→-=--+()(2)(2)(3)(3)(5)(5)t t t t t t t t εεεε=------+--2.4(4)122200()()()()()()11()22ttf t f t t t t t d d t t εετετετττττε∞-∞*=*=-===⎰⎰2.4(8)122()()(1)(2)(2)(1)(1)t f t f t t e t e t d e t d ττεεετεττεττ∞-∞-∞*=-*-=---=--⎰⎰当 12t -< 即 3t <时 1112()()t t f t f t e d e ττ---∞*==⎰当 12t -≥ 即 3t ≥时 2212()()f t f t e d e ττ-∞*==⎰故 21(3)(1)(2)(3)tt e t t e t et εε-⎧≥-*-=⎨<⎩2.4(9) 2312()()(1)(3)tt f t f t et e t εε--*=-*+22(1)93(3)(1)(3)t t e e t e e t εε----+=-*+72(1)3(3)723137232724362331((1)(3))(()())|()()|()(2)()(2)t t t t t t t t t t t t t t e e t e t e e t e t e e e t e e e t e e t εεεεεεε---+--→-+--→+-----+-+=-*+=*=-=-+=-+2.612013111()()53()123323t or t t t f t f t t t t t <->⎧⎪+-≤<⎪⎪*=⎨--≤<⎪⎪-≤≤⎪⎩ 2.7(1)112222[(2)(1)]2[(2)(1)]23t t t d d εετετετττττ∞-∞--*+--=+--===-⎰⎰ 2.7(2)11()()()()1t tn n n n t t t d d t t n εετεττττε+-∞*===+⎰⎰ [()0]ε-∞=2.7(3)''()()()()[()()]tt et t t e t t t εδεεδε--**=** [()0]ε-∞='()[()()]()[()()]()()()t t tte t t t e t t t e t t e t εδεεδδεδε----=**=**=*=2.7(4)由于 ()0t t t ε=-∞=2"2'2'22()()()()()[()()]()()()()()()()t t ttte t t t t e t t t t t e t t t e t t t e t εδεεδεδεδεεδδε-----**=**+=**=**=2.8123()()[(2)2(1)](1)(2)(1)2(1)(1)()2()(3)(3)2()t t t t f t f t t t t t t t t t t t t t t t t εεεεεεεεεεε→+→*=-++-*+=-+*++-*+=-+=-+++(1)(13)2f -=--+=-;(0)(03)03f =-++=- (1)(13)2112f =-++⋅⋅=-2.9 由图可知 1()(2)(3)f t t t εε=---,(1)2()(1)t f t et ε-+=+因此(1)(1)12213112(1)(2)(1)(1)()()()(2)(1)(3)(1)[()()][()()](1)()(1)()(1)(1)(1)(2)01112(t t t t t t t t t t t t t t t t t t f t f t f t t e t t e t t e t t e t e t e t e t e t t e t e e εεεεεεεεεεεε-+-+----→-+→-+→-→---------=*=-*+--*+=*-*=---=-----<=-≤<1)2t ⎧⎪⎨⎪-≥⎩# ()()()()t f t t f t δδ**= # ())()(2121t t t f tt t t f --=-*-δ# 已知函数()f t ,则函数0()f tat -可以把函数()f at -右移0t a 得到。
