4-4-1 圆与扇形(一).教师版
六年级奥数第8次课:圆与扇形(教师版)

【我生命中最最最重要的朋友们,请你们仔细听老师讲而且随着老师的思想走。
学业的成功重在于考点的不停过滤,相信我赠予你们的是你们学业成功的过滤器。
感谢使用!!!】圆与扇形一、考点、热门回首五年级已经学习过三角形、矩形、平行四边形、梯形以及由它们形成的组合图形的有关问题,这一讲学习与圆有关的周长、面积等问题。
圆的周长、面积计算公式:c d 或 c 2 r s r 2半圆的周长、面积计算公式:c rd s 1 r 22扇形的周长、面积:c ad 2r s a r 2360 360如无特别说明,圆周率都取π=3.14 。
二、典型例题:例 1、以下列图所示,200 米赛跑的起点和终点都在直跑道上,中间的弯道是一个半圆。
已知每条跑道宽 1.22 米,那么外道的起点在内道起点前方多少米?(精准到0.01 米)剖析与解:半径越大,周长越长,因此外道的弯道比内道的弯道长,要保证内、外道的人跑的距离相等,外道的起点就要向前移,移的距离等于外道弯道与内道弯道的长度差。
固然弯道的各个半径都不知道,但是两条弯道的中心线的半径之差等于一条跑道之宽。
设外弯道中心线的半径为R,内弯道中心线的半径为r ,则两个弯道的长度之差为πR- π r =π( R-r )= 3.14 ×1.22 ≈ 3.83 (米)。
即外道的起点在内道起点前方 3.83 米。
例 2、有七根直径 5 厘米的塑料管,用一根橡皮筋把它们勒紧成一捆(如左下列图),此时橡皮筋的长度是多少厘米?剖析与解:由右上图知,绳长等于 6 个线段 AB 与 6 个 BC弧长之和。
将图中与BC弧近似的6 个弧所对的圆心角平移拼补,获得 6 个角的和是 360°,因此 BC弧所对的圆心角是 60°,6 个 BC弧等于直径 5 厘米的圆的周长。
而线段AB等于塑料管的直径,由此知绳长=5× 6+ 5×3.14 = 45.7 (厘米)。
例 3 、左下列图中四个圆的半径都是 5 厘米,求暗影部分的面积。
4-4-1-圆与扇形(一).教师版

研究圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,通过变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形来计算它们的面积.圆的面积2πr =;扇形的面积2π360n r =⨯; 圆的周长2πr =;扇形的弧长2π360n r =⨯. 一、跟曲线有关的图形元素:①扇形:扇形由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形,扇形是圆的一部分.我们经常说的12圆、14圆、16圆等等其实都是扇形,而这个几分之几表示的其实是这个扇形的圆心角占这个圆周角的几分之几.那么一般的求法是什么呢?关键是360n . 比如:扇形的面积=所在圆的面积360n ⨯; 扇形中的弧长部分=所在圆的周长360n ⨯ 扇形的周长=所在圆的周长+360n ⨯2⨯半径(易错点是把扇形的周长等同于扇形的弧长) ②弓形:弓形一般不要求周长,主要求面积.一般来说,弓形面积=扇形面积-三角形面积.(除了半圆) ③”弯角”:如图:弯角的面积=正方形-扇形④”谷子”:如图:“谷子”的面积=弓形面积2⨯二、常用的思想方法:①转化思想(复杂转化为简单,不熟悉的转化为熟悉的)②等积变形(割补、平移、旋转等)③借来还去(加减法)④外围入手(从会求的图形或者能求的图形入手,看与要求的部分之间的”关系”)板块一 平移、旋转、割补、对称在曲线型面积中的应用【例 1】 如图,圆O 的直径AB 与CD 互相垂直,AB =10厘米,以C 为圆心,CA 为半径画弧。
求月牙形ADBEA (阴影部分)的面积。
【考点】圆与扇形 【难度】3星 【题型】解答【关键词】华杯赛,决赛,第9题,10分【解析】 ①月牙形ADBEA (阴影部分)的面积=半圆的面积+△ABC 的面积-扇形CAEBC 的面积②月牙形ADBEA 的面积=211π525π502524⨯⨯+-⨯⨯=(平方厘米),所以月牙形ADBEA 的面积是25平方厘米。
《圆形和方形》教案

《圆形和方形》教案《圆形和方形》教案1活动目标:1.初步认识圆形、正方形,并辨识生活中圆形和正方形的物品。
2.通过游戏发展幼儿的动手能力和对图形初步的概括力3.能积极参与游戏活动,体会集体活动的快乐。
4.引发幼儿学习图形的兴趣。
5.培养幼儿的尝试精神,发展幼儿思维的敏捷性、逻辑性。
活动重点:能从生活物品中辨认出圆形和正方形活动准备:圆形和方形各2个、魔法袋,;大嘴娃娃2个、圆形,方形饼干若干、ppt、鱼竿和小鱼若干,呼啦圈2个。
活动过程:(一)变魔术(认识图形)1.教师演示变魔术,出示圆形和正方形2.分别介绍圆形和正方形3.请一名幼儿变魔术,其他幼儿辨认图形(二)送饼干(图形配对)1.出示大嘴娃娃,请幼儿观察其异同(圆形与正方形的嘴巴)2.给大嘴娃娃送上对应图形的饼干(三)小熊开店(联系生活,对图形进行辨识分类)1.引导幼儿说出生活中圆形和正方形的物品2.尝试在活动室找圆形和正方形的物品3.引出小熊开店并帮小熊整理货架(四)游戏钓鱼(巩固练习)1.引出钓鱼话题,和幼儿一起去钓鱼2.介绍钓鱼注意事项:圆形的鱼要放进圆形的鱼缸里,正方形的鱼要放进正方形的鱼缸里。
3.活动结束,幼儿随教师走出活动室。
教学反思当我进行实际教学过程时,我从孩子们身上看到了这样的现象:1.幼儿对各种图形非常感兴趣,幼儿对身边的事物有着敏锐的观察力,有渴望了解图形宝宝的欲望2. 在活动中,幼儿的情绪很活跃,能把自己发现的主动地告诉老师和周边的小伙伴,使幼儿的表达能力、反应能力和观察能力都得到了发展。
我还从孩子们的操作中1. 在这次活动中孩子乐于参与,积极发现。
2. 孩子们兴致浓厚,也愿意主动去探索,主动去参与。
我觉得我原来的设计可以这样的调整:幼儿自我操作时间不足,没有创设幼儿合作交流的机会,语言还要精炼等,在以后组织活动的过程中我应加以改进,为幼儿传递良好的语感,培养幼儿善于表达的能力。
《圆形和方形》教案2一、活动目标1、引导幼儿发展初步的观察与分辨能力。
【研】第1讲 圆与方程-教师版

个性化教学辅导教案【学习目标】1、熟练掌握圆的方程的两种形式及其特点;2、会利用代数法、几何法求圆的方程,注意圆的方程形式的选择;3、比较直线到圆心距离与圆半径的大小关系,判定直线与圆的位置关系、直线与圆相交弦长;4、通过解直线与圆方程组成的方程,根据解的个数,判定直线与圆的位置关系;5、利用圆心距和半径判断圆之间的位置关系,会求相交圆的公共弦所在的直线,公共弦长;6、圆与直线对称问题。
【达标运用】1、圆(x﹣2)2+(y+3)2=2的圆心和半径分别是()A.(﹣2,3),1 B.(2,﹣3),3 C.(﹣2,3),D.(2,﹣3),解:∵圆的标准方程为(x﹣2)2+(y+3)2=2∴圆的圆心坐标和半径长分别是(2,﹣3),故选:D.2、圆x2+y2﹣4x+2y+4=0的半径和圆心坐标分别为()A.r=1;(﹣2,1)B.r=2;(﹣2,1)C.r=1;(2,﹣1)D.r=2;(2,﹣1)解:由x2+y2﹣4x+2y+4=0,得(x﹣2)2+(y+1)2=1,∴圆x2+y2﹣4x+2y+4=0的半径为r=1;圆心坐标为(2,﹣1),故选:C.3、已知圆的半径为2,圆心在x轴的正半轴上,且与y轴相切,则圆的方程是()A.x2+y2﹣4x=0 B.x2+y2+4x=0 C.x2+y2﹣2x﹣3=0 D.x2+y2+2x﹣3=0解:∵圆的半径为2,圆心在x轴的正半轴上,且与y轴相切,∴圆的圆心坐标为(2,0),∴圆的方程为(x﹣2)2+y2=4,即x2+y2﹣4x=0.故选:A.4、圆(x﹣1)2+(y﹣2)2=1关于直线x﹣y﹣2=0对称的圆的方程为()A.(x﹣4)2+(y+1)2=1 B.(x+4)2+(y+1)2=1C.(x+2)2+(y+4)2=1 D.(x﹣2)2+(y+1)2=1解:由于圆心(1,2)关于直线x﹣y﹣2=0对称的点的坐标为(4,﹣1),半径为1,故选:A.5、圆心为(3,0)且与直线x相切的圆的方程为()A.(x﹣)2+y2=1 B.(x﹣3)2+y2=3 C.(x﹣)2+y2=3 D.(x﹣3)2+y2=9解:圆心到直线的距离d=r===,则圆的标准方程为(x﹣3)2+y2=3,故选:B.6、已知以点A(﹣1,2)为圆心的圆与直线m:x+2y+7=0相切,过点B(﹣2,0)的动直线l与圆A 相交于M、N两点(1)求圆A的方程.(2)当|MN|=2时,求直线l方程.解:(1)意知A(﹣1,2)到直线x+2y+7=0的距离为圆A半径r,∴,∴圆A方程为(x+1)2+(y﹣2)2=20(5分)(2)垂径定理可知∠MQA=90°.且,在Rt△AMQ中由勾股定理易知设动直线l方程为:y=k(x+2)或x=﹣2,显然x=﹣2合题意.由A(﹣1,2)到l距离为1知.∴3x﹣4y+6=0或x=﹣2为所求l方程.7、已知圆O:x2+y2﹣10x﹣10y=0和圆C:x2+y2﹣6x+2y﹣40=0相交于A、B两点,求公共弦AB的长.解:圆O:x2+y2﹣10x﹣10y=0的圆心为(5,5),半径为5;圆C:x2+y2﹣6x+2y﹣40=0的圆心为(3,﹣1),半径为5,由圆O:x2+y2﹣10x﹣10y=0和圆C:x2+y2﹣6x+2y﹣40=0得方程可得直线AB的方程为:x+3y﹣10=0.圆心C(3,﹣1)到直线x+3y﹣10=0的距离为d=.∴AB=2=4.8、已知圆C1:x2+y2﹣6x﹣6=0,圆C2:x2+y2﹣4y﹣6=0(1)试判断两圆的位置关系;(2)求公共弦所在的直线的方程;(3)求公共弦的长度.解:(1)圆C1:x2+y2﹣6x﹣6=0,化为(x﹣3)2+y2=15,圆心坐标为(3,0),半径为;圆C2:x2+y2﹣4y﹣6=0化为x2+(y﹣2)2=10,圆心坐标(0,2),半径为.圆心距为:=,因为﹣<<+,所以两圆相交.(2)将两圆的方程相减,得﹣6x+4y=0,化简得:3x﹣2y=0,∴公共弦所在直线的方程是3x﹣2y=0;(3)由(2)知圆C1的圆心(3,0)到直线3x﹣2y=0的距离d==,由此可得,公共弦的长l=2=.1、利用圆的标准方程、一般方程求圆心、半径;2、圆的标准方程与一般方程互化;3、利用几何法、待定系数法求圆的方程;4、求点关于直线对称的步骤;5、圆的弦长公式(勾股定理);6、求两圆相交得到的公共弦长与弦所在直线的方程基本方法与步骤。
圆与扇形.题库教师版.doc

圆与扇形精选题【例 1】 图中的4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?【解析】 如下图所示:可以将每个圆内的阴影部分拼成一个正方形,每个正方形的面积为11240.542⨯÷⨯=⨯=()(平方厘米),所以阴影部分的总面积为248⨯=(平方厘米).【巩固】如图所示,四个全等的圆每个半径均为2m ,阴影部分的面积是 .或【解析】 我们虽没有学过圆或者圆弧的面积公式,但做一定的割补后我们发现其实我们并不需要知道这些公式也可以求出阴影部分面积.如图,割补后阴影部分的面积与正方形的面积相等,等于222216m ⨯=()().【例 2】 如图中三个圆的半径都是5cm ,三个圆两两相交于圆心.求阴影部分的面积和.(圆周率取3.14)【解析】 将原图割补成如图,阴影部分正好是一个半圆,面积为255 3.14239.25(cm )⨯⨯÷=【巩固】如图,大圆半径为小圆的直径,已知图中阴影部分面积为1S ,空白部分面积为2S ,那么这两个部分的面积之比是多少?(圆周率取3.14)【解析】 如图添加辅助线,小圆内部的阴影部分可以填到外侧来,这样,空白部分就是一个圆的内接正方形.设大圆半径为r ,则222S r =,221π2S r r =-,所以()12: 3.142:257:100S S =-=.移动图形是解这种题目的最好方法,一定要找出图形之间的关系. 【例 3】 请计算图中阴影部分的面积.【解析】 法一:为了求得阴影部分的面积,可以从下图的整体面积中扣掉一个圆的面积,就是要求的面积了.=-要扣掉圆的面积,如果按照下图把圆切成两半后,从两端去扣掉也是一样.如此一来,就会出现一个长方形的面积.O半圆半圆103-=因此,所求的面积为210330cm ⨯=(). 【例 4】 求如图中阴影部分的面积.(圆周率取3.14)44【解析】 可将左下橄榄型的阴影部分剖开,两部分分别顺逆时针90︒,则阴影部分转化为四分之一圆减去一个等腰直角三角形,所以阴影部分的面积为211π444 4.5642⨯⨯-⨯⨯=.【巩固】如图,四分之一大圆的半径为7,求阴影部分的面积,其中圆周率π取近似值227.【解析】 原题图中的左边部分可以割补至如右上图位置,这样只用先求出四分之一大圆的面积,再减去其内的等腰直角三角形面积即为所求.因为四分之一大圆的半径为7,所以其面积为:2211227π738.5447⨯⨯≈⨯⨯=.四分之一大圆内的等腰直角三角形ABC 的面积为17724.52⨯⨯=,所以阴影部分的面积为38.524.514-=. 【例 5】 (华校2005~2006年度第一学期期中测试第6题)大圆半径为R ,小圆半径为r ,两个同心圆构成一个环形.以圆心O 为顶点,半径R 为边长作一个正方形:再以O 为顶点,以r 为边长作一个小正方形.图中阴影部分的面积为50平方厘米,求环形面积.(圆周率取3.14)【解析】 环形的面积应该用大圆的面积减去小圆的面积,但分别求出两个圆的面积显然不可能.题中已知阴影部分的面积,也就是2250R r -=平方厘米,那么环形的面积为:2222πππ()π50=157R r R r -=-=⨯(平方厘米).【巩固】图中阴影部分的面积是225cm ,求圆环的面积.【解析】 设大圆半径为R ,小圆半径为r ,依题有222522R r -=,即2250R r -=.则圆环面积为:22222πππ()50π157(cm )R r R r -=-==.【例 6】 (2008年101中学考题)已知图中正方形的面积是20平方厘米,则图中里外两个圆的面积之和是 .(π取3.14)【解析】 设图中大圆的半径为r ,正方形的边长为a ,则小圆的直径等于正方形的边长,所以小圆的半径为2a ,大圆的直径2r 等于正方形的对角线长,即222(2)r a a =+,得222a r =.所以,大圆的面积与正方形的面积之比为:22π:π:2r a =,所以大圆面积为:202π10π÷⨯=;小圆的面积与正方形的面积之比为:22π():π:42aa =,所以小圆的面积为:204π5π÷⨯=;两个圆的面积之和为:10π5π15π15 3.1447.1+==⨯=(平方厘米).【巩固】图中小圆的面积是30平方厘米,则大圆的面积是 平方厘米.(π取3.14)【解析】 设图中大圆的半径为r ,正方形的边长为a ,则小圆的直径等于正方形的边长,所以小圆的半径为2a ,大圆的直径2r 等于正方形的对角线长,即222(2)r a a =+,得222a r =.所以,大圆的面积与小圆的面积之比为:222222π:π()::2:12424a a a a r r ===, 即大圆的面积是小圆面积的2倍,大圆的面积为30260⨯=(平方厘米).【巩固】(2008年四中考题)图中大正方形边长为a ,小正方形的面积是 .【解析】 设图中小正方形的边长为b ,由于圆的直径等于大正方形的边长,所以圆的直径为a ,而从图中可以看出,圆的直径等于小正方形的对角线长,所以22222a b b b =+=,故2212b a =,即小正方形的面积为212a .【例 1】 如图,两个正方形摆放在一起,其中大正方形边长为12,那么阴影部分面积是多少?(圆周率取3.14)AFEAFE【解析】 方法一:设小正方形的边长为a ,则三角形ABF 与梯形ABCD 的面积均为()122a a +⨯÷.阴影部分为:大正方形+梯形-三角形ABF -右上角不规则部分=大正方形-右上角不规则部分=14圆.因此阴影部分面积为:3.1412124113.04⨯⨯÷=. 方法二:连接AC 、DF ,设AF 与CD 的交点为M ,由于四边形ACDF 是梯形,根据梯形蝴蝶定理有ADM CMF S S =△△,所以DCF S S =阴影扇形 3.1412124113.04=⨯⨯÷=【巩固】如右图,两个正方形边长分别是10和6,求阴影部分的面积.(π取3)【解析】 (法1)观察可知阴影部分面积等于三角形ACD 的面积减去月牙BCD 的面积,那么求出月牙BCD 的面积就成了解题的关键.月牙BCD 的面积为正方形BCDE 的面积减去四分之一圆:166π6694⨯-⨯⨯⨯=; 则阴影部分的面积为三角形ACD 的面积减去月牙BCD 的面积,为:()110669392S =⨯+⨯-=阴影.(法2)观察可知AF 和BD 是平行的,于是连接AF 、BD 、DF .则ABD ∆与BDF ∆面积相等,那么阴影部分面积等于BDF ∆与小弓形的面积之和,也就等于DEF ∆与扇形BED 的面积之和,为:211(106)6π63924-⨯⨯+⨯⨯=.【例 2】 如图,ABC 是等腰直角三角形,D 是半圆周的中点,BC 是半圆的直径.已知10AB BC ==,那么阴影部分的面积是多少?(圆周率取3.14)DD【解析】 连接PD 、AP 、BD ,如图,PD 平行于AB ,则在梯形ABDP 中,对角线交于M 点,那么ABD ∆与ABP ∆面积相等,则阴影部分的面积转化为ABP ∆与圆内的小弓形的面积和.ABP ∆的面积为:()10102225⨯÷÷=;弓形面积: 3.145545527.125⨯⨯÷-⨯÷=; 阴影部分面积为:257.12532.125+=.【例 3】 图中给出了两个对齐摆放的正方形,并以小正方形中右上顶点为圆心,边长为半径作一个扇形,按图中所给长度阴影部分面积为 ;(π 3.14=)A【解析】 连接小正方形AC ,有图可见ACD ABC S S S S =+-△△阴影扇形∵211144222AC ⨯=⨯⨯ ∴232AC =同理272CE =,∴48AC CE ⨯= ∴148242ACD S =⨯=△290π412.56360S =⨯=扇形,14482ABC S =⨯⨯=△ ∴2412.56828.56S =+-=阴影【例 4】 如图,ABCD 是边长为a 的正方形,以AB 、BC 、CD 、DA 分别为直径画半圆,求这四个半圆弧所围成的阴影部分的面积.(π取3)DCBADCBA【解析】 这道题目是很常见的面积计算问题.阴影部分是一个花瓣状的不规则图形,不能直接通过面积公式求解,观察发现阴影部分是一个对称图形,我们只需要在阴影部分的对称轴上作两条辅助线就明了了.如图,这样阴影部分就划分成了4个半圆减去三角形,我们可以求得,()4S S S =⨯-阴影半圆三角形 21142222a a a π⎡⎤⎛⎫=⨯⨯⨯-⨯⨯⎢⎥ ⎪⎝⎭⎢⎥⎣⎦212a =【巩固】如图,正方形ABCD 的边长为4厘米,分别以B 、D 为圆心以4厘米为半径在正方形内画圆.求阴影部分面积.(π取3)DBADB【解析】 由题可知,图中阴影部分是两个扇形重叠的部分,我们可以利用容斥原理从图形整体上考虑来求阴影部分面积;同样,我们也可以通过作辅助线直接求阴影部分的面积. 解法一:把两个扇形放在一起得到1个正方形的同时还重叠了一块阴影部分. 则阴影部分的面积为=21π44482⋅⋅-⨯=; 解法二:连接AC ,我们发现阴影部分面积的一半就是扇形减去三角形的面积, 所以阴影部分面积=212π444284⨯⋅⋅-⨯÷=().【例 5】 (2008年四中考题)已知三角形ABC 是直角三角形,4cm AC =,2cm BC =,求阴影部分的面积.【解析】 从图中可以看出,阴影部分的面积等于两个半圆的面积和与直角三角形ABC 的面积之差,所以阴影部分的面积为:2214121ππ42 2.5π4 3.8522222⎛⎫⎛⎫⨯+⨯-⨯⨯=-= ⎪ ⎪⎝⎭⎝⎭(2cm ).【例 6】 如图,矩形ABCD 中,AB =6厘米,BC =4厘米,扇形ABE 半径AE =6厘米,扇形CBF 的半径CB =4厘米,求阴影部分的面积.(π取3)A【解析】 方法一:观察发现,阴影部分属于一个大的扇形,而这个扇形除了阴影部分之外,还有一个不规则的空白部分ABFD 在左上,求出这个不规则部分的面积就成了解决这个问题的关键.我们先确定ABFD 的面积,因为不规则部分ABFD 与扇形BCF 共同构成长方形ABCD ,所以不规则部分ABFD 的面积为2164π4124⨯-⨯⨯=(平方厘米), 再从扇形ABE 中考虑,让扇形ABE 减去ABFD 的面积, 则有阴影部分面积为21π612154⨯⨯-=(平方厘米).方法二:利用容斥原理2211π6π4461544EAB BCF ABCD S S S S =+-=⨯+⨯-⨯=阴影扇形扇形长方形(平方厘米)【巩固】求图中阴影部分的面积.【解析】 阴影部分面积=半圆面积+扇形面积-三角形面积22211211π()π121241.042282=⨯+⨯-⨯=.【巩固】如右图,正方形的边长为5厘米,则图中阴影部分的面积是 平方厘米,(π 3.14=)C【解析】 观察可知阴影部分是被以AD 为半径的扇形、以AB 为直径的半圆形和对角线BD 分割出来的,分头求各小块阴影部分面积明显不是很方便,我们发现如果能求出左下边空白部分的面积,就很容易求出阴影部分的面积了,我们再观察可以发现左下边空白部分的面积就等于三角形ABD 的面积减去扇形ADE 的面积,那么我们的思路就很清楚了.因为45ADB ∠=︒,所以扇形ADE 的面积为:224545π 3.1459.8125360360AD ⨯⨯=⨯⨯=(平方厘米), 那么左下边空白的面积为:1559.8125 2.68752⨯⨯-=(平方厘米),又因为半圆面积为:215π9.812522⎛⎫⨯⨯= ⎪⎝⎭(平方厘米),所以阴影部分面积为:9.8125 2.68757.125-=(平方厘米).【例 7】 已知半圆所在的圆的面积为62.8平方厘米,求阴影部分的面积.(π 3.14=)B【解析】 由于阴影部分是一个不规则图形,所以要设法把它转化成规则图形来计算.从图中可以看出,阴影部分的面积是一个45°的扇形与一个等腰直角三角形的面积差. 由于半圆的面积为62.8平方厘米,所以262.8 3.1420OA =÷=. 因此:22210AOB S OA OB OA =⨯÷=÷=△(平方厘米). 由于AOB ∆是等腰直角三角形,所以220240AB =⨯=. 因此:扇形ABC 的面积24545ππ4015.7360360AB =⨯⨯=⨯⨯=(平方厘米). 所以,阴影部分的面积等于:15.710 5.7-=(平方厘米).【例 8】 如图,等腰直角三角形ABC 的腰为10;以A 为圆心,EF 为圆弧,组成扇形AEF ;两个阴影部分的面积相等.求扇形所在的圆面积.【解析】 题目已经明确告诉我们ABC 是等腰直角三角形,AEF 是扇形,所以看似没有关系的两个阴影部分通过空白部分联系起来.等腰直角三角形的角A 为45度,则扇形所在圆的面积为扇形面积的8倍. 而扇形面积与等腰直角三角形面积相等,即11010502S =⨯⨯=扇形, 则圆的面积为508400⨯=【例 9】 如图,直角三角形ABC 中,AB 是圆的直径,且20AB =,阴影甲的面积比阴影乙的面积大7,求BC 长.(π 3.14=)【解析】 因为两块阴影部分都是不规则图形,单独对待它们无法运用面积公式进行处理,而解题的关键就是如何把它们联系起来,我们发现把两块阴影加上中间的一块,则变成1个半圆和1个直角三角形,这个时候我们就可以利用面积公式来求解了. 因为阴影甲比阴影乙面积大7,也就是半圆面积比直角三角形面积大7. 半圆面积为:21π101572⨯⨯=,则直角三角形的面积为157-7=150,可得BC =2⨯150÷20=15.【巩固】三角形ABC 是直角三角形,阴影I 的面积比阴影II 的面积小225cm ,8cm AB =,求BC 的长度.I IABCI【解析】 由于阴影I 的面积比阴影II 的面积小225cm ,根据差不变原理,直角三角形ABC 面积圆与扇形精选题11 减去半圆面积为225cm ,则直角三角形ABC 面积为218π258π2522⎛⎫⨯+=+ ⎪⎝⎭(2cm ), BC 的长度为()8π25282π 6.2512.53+⨯÷=+=(cm ).【巩固】 如图,三角形ABC 是直角三角形,阴影部分①比阴影部分②的面积小28平方厘米,AB 长40厘米.求BC 的长度?(π取3.14)【解析】 图中半圆的直径为AB ,所以其面积为2120π200 3.146282⨯⨯≈⨯=. 有空白部分③与①的面积和为628,又②-①28=,所以②、③部分的面积和62828656+=.有直角三角形ABC 的面积为12AB BC ⨯⨯=1406562BC ⨯⨯=.所以32.8BC =厘米.【例 10】 如图,求阴影部分的面积.(π取3)43【解析】 如图,图中阴影部分为月牙儿状,月牙儿形状与扇形和弓形都不相同,目前我们还不能直接求出 它们的面积,那么我们应该怎么来解决呢?首先,我们分析下月牙儿状是怎么产生的,观察发现月牙儿形是两条圆弧所夹部分,再分析可以知道,两条圆弧分别是不同圆的圆周的一部分,那么我们就找到了解决问题的方法了.阴影部分面积=12小圆面积+12中圆面积+三角形面积-12大圆面积=2221111π3π434π52222⋅⋅+⋅⋅+⨯⨯-⋅⋅ =6【例 11】 (2009年十三分入学测试题)图中的长方形的长与宽的比为8:3,求阴影部分的面积.204【解析】 如下图,设半圆的圆心为O ,连接OC .。
全国通用六年级下册数学奥数:几何之圆与扇形(解析版)
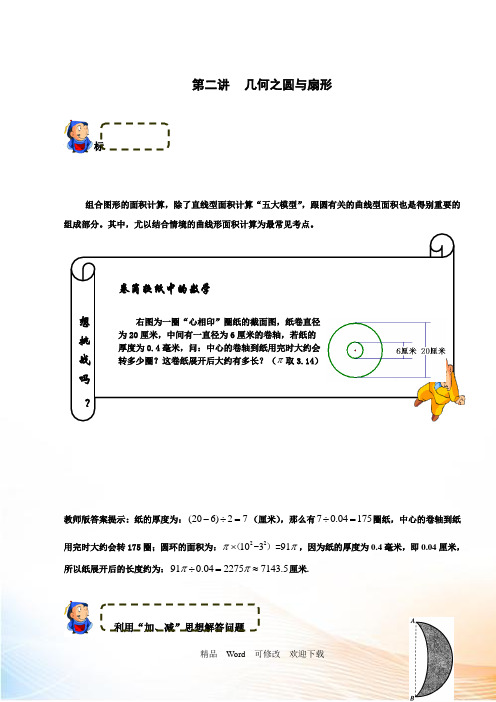
第二讲 几何之圆与扇形教学目标组合图形的面积计算,除了直线型面积计算“五大模型”,跟圆有关的曲线型面积也是得别重要的组成部分。
其中,尤以结合情境的曲线形面积计算为最常见考点。
教师版答案提示:纸的厚度为:(206)27-÷=(厘米),那么有70.04175÷=圈纸,中心的卷轴到纸用完时大约会转175圈;圆环的面积为:2210391ππ⨯(-)=,因为纸的厚度为0.4毫米,即0.04厘米,所以纸展开后的长度约为:910.0422757143.5ππ÷=≈厘米.利用“加、减”思想解答问题想挑 战 吗 ? 卷筒软纸中的数学右图为一圈“心相印”圈纸的截面图,纸卷直径 为20厘米,中间有一直径为6厘米的卷轴,若纸的 厚度为0.4毫米,问:中心的卷轴到纸用完时大约会 转多少圈?这卷纸展开后大约有多长?(π取3.14)【例1】 如图,一个“月牙”形屏幕在屏幕上随意平行移动(不许发生转动也不越过屏幕边界),已知线段AB 是月牙外半圆弧的直径,长为2厘米。
初始时,A 、B 两点在矩形屏幕的一条边上。
屏幕的长和宽分别为30厘米和20厘米。
问:屏幕上“月牙”擦不到的部分的面积是多少平方厘米?(π取3)分析:由于“月牙”形屏幕在屏幕上只能平行移动(不许发生转动也不越过屏幕边界),所以它擦不到的地方只是屏幕的右上角和右下角两部分,如右下图中斜线所示区域,其面积为0.5平方厘米。
[前铺]如右图所示,等腰直角三角形ABC 的高AD=4厘米,以AD 为直径作圆分别交AB 、AC 与E 、F ,求阴影部分的面积。
(π取3) 分析:连接EF ,那么有BED ABD EOD S S S =-阴影三角形扇形,计算可得阴影部分面积为6平方厘米。
[巩固]一个长方形的长为9,宽为6,一个半径为l 的圆在这个长方形内任意运动,在长方形内这圆无法运动到的部分,面积的和是多少?(π取3)分析:圆无法运动到的部分是右下图中角处的阴影部分面积的4倍,114111π⨯⨯-⨯⨯=[拓展]如右图所示,用一块面积为36平方厘米铝板下料,可裁出七个同样大小的圆铝板。
4-1-2_图形找规律[1].题库教师版.doc(2021年整理精品文档)
![4-1-2_图形找规律[1].题库教师版.doc(2021年整理精品文档)](https://img.taocdn.com/s3/m/bbc4abea581b6bd97e19ea17.png)
4-1-2_图形找规律[1].题库教师版.doc编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(4-1-2_图形找规律[1].题库教师版.doc)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为4-1-2_图形找规律[1].题库教师版.doc的全部内容。
找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力。
一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题:⑴图形数量的变化;⑵图形形状的变化;⑶图形大小的变化;⑷图形颜色的变化;⑸图形位置的变化;⑹图形繁简的变化。
对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题。
板块一数量规律【例 1】请找出下面哪个图形与其他图形不一样。
【解析】这组图形的共同特征是,连接各边上一点,组成一个复合图形.所不同的是,第四个图形是一个六边形,而其它几个都是四边形,这样,只有(4)与其它不一样【例 2】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【解析】横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变。
因为圆形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个圆形.【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形??【解析】(方法一)横着看,每行三角形的个数依次减少,而正方形的个数依次增加,但每行图形的总个数不变.因为三角形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个三角形△。
(方法二)竖着看,三角形由左而右依次减少,而正方形由左而右依次增加,三角形按照4、?、2、1的顺序变化,也可以看出“?”处应是三角形△。
【上海初中数学讲义】预初(上)第14讲:圆与扇形的面积 教师版

第14讲 圆与扇形的面积1. 圆的面积公式:设圆的半径长为r ,面积为S ,那么圆的面积2==S r r r ππ⨯ 2. 圆环面积圆环的计算公式(r 表示小圆半径,R 表示大圆半径)22=S R r ππ-圆环 3. 扇形面积公式:设组成扇形的半径为r ,圆心角为o n ,弧长为l ,那么21==3602n S r lr π扇形 特别地:360S nS=扇 4. 组合图形面积(1)计算图形面积时,经常用到割补法,要善于添加辅助线,把图形分割成几个基本图形,再分别求出它们的面积.(2)一些复杂的图形,要经常用到平移、翻转等方法,把复杂图形转化为基本图形,再分别计算它们的面积.【例题1】填空:1. 在一个正方形里面画一个最大的圆,这个圆的周长是6.28厘米,这正方形的面积是_________平方厘米.剩下的面积是__________平方厘米.2. 大圆半径是3分米,小圆半径是2分米,小圆面积是大圆面积的__________.3. 已知外圆的半径为2cm ,内圆半径为1cm ,圆环的面积为 .4.小圆的半径为2,大圆的直径为8,那么大圆的面积是小圆的__________倍.5. 甲圆的半径是乙圆的43,则甲圆与乙圆的周长之比为 面积之比为_______ 6. A B 两圆的周长之比为2:3,其中一个大圆的面积是18,另外一个圆的面积为:______ 7. 若两圆的周长和为87.92cm ,并且大圆的直径是小圆直径的3倍,则小圆的面积为______【例题2】(圆的面积)已知甲圆的半径长等于乙圆的直径长,且它们的面积之和是100平方厘米,那么甲圆的面积是多少?【例题3】(圆环面积)已知一个圆形花坛的直径是4米,沿它的外侧铺一条1米宽的小路,求这条小路的面积。
【例题4】(扇形面积)已知圆心角为60 ,OC=6厘米,AC=2厘米,求阴影部分的面积.【例题5】(组合图形问题)求图中阴影部分的面积.【例题6】如图,长方形ABCD的长AD=8cm,宽AB=6cm,求阴影部分的周长和面积.【例题7】有一只狗被拴在建筑物的墙角上,这个建筑物是边长600厘米的正方形,拴狗的绳子长20米,现在狗从A点出发,将绳子拉紧顺时针跑,求狗跑过的图形面积【练习1】填空:1. 有相同周长的长方形、正方形、圆,它们的面积从大到小是_________________________.2. 如果一个扇形所含圆弧的长是相同半径圆周长的51,那么这个扇形的面积是这个圆面积的 .3. 如图,三个同心圆的半径分别为2、6、10,则图中阴影部分占大圆面积的____________%.(第3题)(第4题)(第5题)4. 如图,大小两个圆重叠部分的面积是20平方厘米,是大圆面积的18,是小圆面积的16,则大圆面积比小圆面积多__________平方厘米.5. 如图所示,圆1O 、圆2O 、圆3O 的半径均为1厘米,则阴影部分的面积为_______平方厘米.【练习2】 两个圆的周长之比是3∶2,面积之差是10平方厘米,两个圆的面积之和是多少?【练习3】如图中两个相连的正方形的边长分别是8厘米、3厘米,求阴影部分的面积.【练习4】求阴影部分的面积.【练习5】某已知直角三角形三边长为12、16、20,求阴影部分的面积.【练习6】如图,已知AB=10cm,以AB为直径的半圆绕A点旋转了30 ,求阴影部分的面积.(结果保留π)【练习7】如图A与B两个圆(只有14)的圆心,那么两个阴影部分的面积相差多少平方厘米?【练习8】如图,小杨将自家宠物A栓在墙角,若绳长为3米,求小狗在地面活动的最大区域面积.【练习1】如图所示,Rt△ABC中,∶C=90°,AB=10,那么图中两个扇形(即阴影部分)的面积之和为___________.【练习2】已知正方形的边长为2,求右图中阴影部分的面积.A B【练习3】求下列阴影部分的面积.(1) (2)【练习4】已知小正方形的边长是2,大正方形的边长是4,求阴影部分的面积.【练习5】如图是以边长为40米的正方形ABCD 的顶点A 为圆心,AB 长为半径的弧与以CD 、BC 为直径的半圆构成的花坛(图中阴影部分).小杰沿着这个花坛边以相同的速度跑了6圈,用去了8分钟,求小杰平均每分钟跑多少米?A BCD【例题精讲】【例题1】(1)4、0.86 (2)49(3)3π (4)4 (5)3:4、9:16 (6)8 (7)494π 【例题2】280cm 【例题3】5π2m 【例题4】143π2cm 【例题5】(1)32 (2)816-π 【例题6】()10cm π+8、2(2648)cm -π 【例题7】166π2m【学习巩固】【练习1】(1)圆、正方形、长方形 (2)15(3)33 (4)40 (5)2π【练习2】26【练习3】9(214-π)2cm【练习4】()88-π 【练习5】96 【练习6】253π2cm 【练习7】()238cm -π 【练习8】52π2m【家庭作业】 【练习1】254π 【练习2】24-π【练习3】(1)8π (2)24-π 【练习4】2+π【练习5】()6030/min m +π。
初三数学培优第10讲- 圆(圆与圆位置关系+圆与正多边形) (教师版)

圆与圆的位置关系圆与正多边形考点解读模块考点水平层级图形与几何相关定义Ⅱ两圆位置关系及圆与正多边形的位置关系备注理解性理解水平(记为Ⅱ)探究性理解水平(记为Ⅲ)知识梳理一、相关定义:1.外离:两个圆没有公共点,并且每个圆上的点都在另一个圆的外部,叫做这两个圆外离.2.外切:两个圆有唯一的公共点,并且除了这个公共点以外,每个圆上的点都在另一个圆的外部,叫做这两个圆外切.这个唯一的公共点叫做切点.3.相交:两个圆有两个公共点,叫做这两个圆相交.4.内切:两个圆有唯一的公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的内部,叫做这两个圆内切,这个唯一的公共点叫做切点.5.内含:两个圆没有公共点,并且一个圆上的点都在另一个圆的内部,叫做这两个圆内含.当两个圆的圆心重合时,称它们为同心圆.6.圆心距:两个圆的圆心之间的距离叫做圆心距.7.各边相等,各角也相等的多边形叫做正多边形.n )就称作正n边形.8.有n条边的正多边形(n是正整数,且39.正多边形的外接圆(或内切圆)的圆心叫做正多边形的中心.10.正多边形的外接圆的半径叫做正多边形的半径.11.正多边形的内切圆的半径长叫做正多边形的边心距.12.正多边形一边所对的关于外接圆的圆心角叫做正多边形的中心角.【注意】1.正n边形,若n是奇数,则正n边形是轴对称图形;若n是偶数,则正n边形既是轴对称图形,又是中心对称图形.2.正n边形的条对称轴交于一点,其外接圆和内切圆的圆心都是这个正n边形的对称轴的交点.这个交点到正n边形的各顶点的距离相等,到正n边形各边的距离也相等.二、两圆位置关系:1.半径不等的两圆的位置关系:半径不等的两圆的半径分别为1R 和2R ,圆心距为d ,则两圆的位置关系可用1R 、2R 和d 之间的 数量关系表达,具体表达如下: ①两圆外离12d R R ⇔>+; ②两圆外切12d R R ⇔=+;③两圆相交1212R R d R R ⇔-<<+; ④两圆内切12d R R ⇔=-; ⑤两圆内含120d R R ⇔≤<-.2.半径相等的两圆的位置关系有:外离、外切、相交、重合.【总结】1.半径不等两圆的位置关系用数轴表示:2.从两圆公共点个数考虑:交点个数 半径不等 半径相等两圆无交点 两圆外离两圆内含(同心圆)两圆外离 两圆有一个交点 两圆外切两圆内切两圆外切 两圆有两个交点 两圆相交 两圆相交 两圆有无数个交点 ——两圆重合三、相关定理:1.相交两圆的连心线垂直平分两圆的公共弦. 2.相切两圆的连心线经过切点.典型例题1. 下列判断错误的是( C )A. 对角线互相垂直且相等的平行四边形是正方形B. 对角线互相垂直平分的四边形是菱形C. 对角线相等的四边形是矩形D. 对角线互相平分的四边形是平行四边形 2. 已知1O 与2O 外离,1O 半径是5,圆心距127O O =,那么2O 半径可以是( D )A. 4B. 3C. 2D. 13.已知⊙1O 的半径16r =,⊙2O 的半径为2r ,圆心距123O O =,如果⊙1O 与⊙2O 有交点,那么2r 的 取值范围是( D )A. 23r ≥B. 29r ≤C. 239r <<D. 239r ≤≤4. 圆O 是正n 边形12n A A A ⋅⋅⋅的外接圆,半径长为18,若12A A 长为π,那么边数n 为( C ) A. 5 B. 10 C. 36 D. 725.若⊙1O 与⊙2O 相交于两点,且圆心距125O O cm =,则下列哪一选项中的长度可能为此两圆的 半径?( D )A. 1cm ,2cmB. 2cm ,3cmC. 10cm ,15cmD. 2cm ,5cm 6.如图,A 、B 的半径分别为1cm 、2cm ,圆心距AB 为5cm .将A 由图示位置沿直线AB 向右平移,当该圆与B 内切时,A 平移的距离是 4或6 .(黄浦2015二模5) 如果两圆的半径长分别为6与2,圆心距为4,那么这两个圆的位置关系是(A )内含; (B )内切; (C )外切; (D )相交. 【答案】B(奉贤2015二模5)相交两圆的圆心距是5,如果其中一个圆的半径是3,那么另外一个圆的半径可以是( )A .2;B .5;C .8;D .10. 【参考答案】B(虹口2015二模5)下列多边形中,中心角等于内角的是( )A .正三角形;B .正四边形;C .正六边形;D .正八边形. 【参考答案】B(奉贤2015二模14)如果正n 边形的中心角是40°,那么n = ; 【参考答案】9(黄浦2015二模17)当两个圆有两个公共点,且其中一个圆的圆心在另一圆的圆内时,我们称此两圆的 位置关系为“内相交”.如果⊙1O 、⊙2O 半径分别为3和1,且两圆“内相交”,那么两圆的圆心距d 的 取值范围是 .【参考答案】23d <<.(黄浦2016二模5)如果两圆的半径长分别为1和3,圆心距为3,那么这两个圆的位置关系是( ) A. 内含 B. 内切 C. 外切 D. 相交【参考答案】D(奉贤2016二模6)已知1O 与2O 外离,1O 半径是5,圆心距127O O =,那么2O 半径可以是( )A. 4B. 3C. 2D. 1【参考答案】D(松江2016二模6)已知⊙1O 的半径16r =,⊙2O 的半径为2r ,圆心距123O O =,如果⊙1O 与⊙2O 有交点,那么2r 的取值范围是( )A. 23r ≥B. 29r ≤C. 239r <<D. 239r ≤≤【参考答案】D(闸北2016二模6)若⊙1O 与⊙2O 相交于两点,且圆心距125O O cm =,则下列哪一选项中的长度可能为此两圆的半径?( )A. 1cm ,2cmB. 2cm ,3cmC. 10cm ,15cmD.2cm ,5cm【参考答案】D(嘉定、宝山2016二模15)已知A 的半径长为1、B 的半径长为2、C 的半径长为3,如果这三个圆两两外切,那么cos B 的值是______________.【参考答案】35(虹口2016二模16)若两圆的半径分别为1cm 和5cm ,圆心距为4cm ,则这两圆的位置关系是________.【参考答案】内切(静安、青浦2016二模17)已知⊙1O 、⊙2O 的半径分别为3、2,且⊙1O 上的点都在⊙2O 的外部,那么圆心距d 的取值范围是________________.【参考答案】5d >或01d ≤<变式训练1.如图,已知AB 是⊙O 的直径,16AB =,点P 是AB 所在直线上一点,10OP =,点C 是⊙O 上 一点,PC 交⊙O 于点D ,3sin 5BPC ∠=,求CD 的长;【答案】 CD =;22. 如图①,三个直径为a 的等圆⊙P 、⊙Q 、⊙O 两两外切,切点分别是A 、B 、C ; (1)那么OA 的长是 (用含a 的代数式表示);(2)探索:现有若干个直径为a 的圆圈分别按如图②所示的方案一和如图③所示的方案二的方式排放,那么这两种方案中n 层圆圈的高度n h = ,n h '= (用含n 、a 的代数式表示);(3)应用:现有一种长方体集装箱,箱内长为6米,宽为2.5米,高为2.5米,用这种集装箱装运长 为6米,底面直径(横截面的外圆直径)为0.1米的圆柱形铜管,你认为采用第(2)题中的哪种方案 在这种集装箱中装运铜管数多?通过计算说明理由;1.41≈ 1.73≈】【答案】22.(1;(2)na (1a +-;(3)方案②;(闸北2016二模17)在平面直角坐标系xOy 中,⊙C 的半径为r ,点P 是与圆心C 不重合的点,给出如下定义:若点P '为射线CP 上一点,满足2CP CP r '⋅=,则称点P '为点P 关于⊙C 的反演点,如图为点P 及其关于⊙C 的反演点P '的示意图,写出点1(,0)2M 关于以原点O 为圆心,1为半径的⊙O 反演点M '的坐标_____________.【参考答案】(2,0)课后训练(崇明2016二模5)如图,正六边形ABCDEF 内接于圆O ,半径为4,那么这个正六边形的边心距OM 和弧BC 的长分别为( )A. 2、3πB. πC. 、23πD. 43π【参考答案】D(普陀2016二模6)如果圆形纸片的直径是8cm ,用它完全覆盖正六边形,那么正六边形的边长最大不能超过( )A. 2cmB.C. 4cmD.【参考答案】C(杨浦2016二模6)圆O 是正n 边形12n A A A ⋅⋅⋅的外接圆,半径长为18,若12A A 长为π,那么边数n 为( )A. 5B. 10C. 36D. 72【参考答案】C(黄浦2016二模15)中心角为60°的正多边形有 条对称轴.【参考答案】6(长宁、金山2016二模17)已知AB 、AC 分别是同一个圆的内接正方形和内接正六边形的边,那么BAC ∠的度数是 度【参考答案】15或105(虹口2016二模17)设正n 边形的半径为R ,边心距为r ,如果我们将Rr的值称为正n 边形的“接近度”, 那么正六边形的“接近度”是 (结果保留根号)【参考答案】3(崇明2016二模5)如图,正六边形ABCDEF 内接于圆O ,半径为4,那么这个正六边形的边心距OM 和弧BC 的长分别为( )A. 2、3πB. πC. 、23πD. 43π【参考答案】D(普陀2016二模6)如果圆形纸片的直径是8cm ,用它完全覆盖正六边形,那么正六边形的边长最大不能超过( )A. 2cmB.C. 4cmD.【参考答案】C(杨浦2016二模6)圆O 是正n 边形12n A A A ⋅⋅⋅的外接圆,半径长为18,若12A A 长为π,那么边数n 为( )A. 5B. 10C. 36D. 72【参考答案】C(黄浦2016二模15)中心角为60°的正多边形有 条对称轴.【参考答案】6(长宁、金山2016二模17)已知AB 、AC 分别是同一个圆的内接正方形和内接正六边形的边,那么BAC ∠的度数是 度【参考答案】15或105(虹口2016二模17)设正n边形的半径为R,边心距为r,如果我们将Rr的值称为正n边形的“接近度”,那么正六边形的“接近度”是(结果保留根号)【参考答案】3。
2021年上海市六年级数学期末复习-第4章《圆和扇形》考点分类复习导学案(教师版)

沪教版六年级上册第4章《圆和扇形》考点分类复习导学案【考点1:圆周率的概念】例题1.下列说法中错误的是( )A.圆周率π的值等于3.14B.圆周率π的值是圆周长与直径的比值C.圆周率π的值与元的大小无关D.圆周率π是一个无限不循环小数【答案】A【变式1】(金山2017期末15)下列说法正确的是( )(A )圆的周长÷圆的直径=圆周率; (B )两个奇数一定互素;(C )1,2,3,4 能组成比例; (D )因为42.18.4=÷,所以4.8能被1.2整除.【答案】A【考点2:圆的周长及半圆周长】例题1.如图1所示,已知半圆的半径为3厘米,那么半圆形的周长为多少厘米?分析:由题意知3厘米,所以. 反思: 封闭图形的四周长称为周长,求得半圆的长度与直径的长度之和即可.计算的时候不要忘了直径.图1=r 厘米)63(323r 2r 221C +π=⨯+⨯π=+π⨯=【变式1】.用一张边长为5分米的正方形纸片见一个最大的圆,求这个圆的周长.分析:由题意知d=5分米,所以.反思:要求出这个圆的周长应该知道这个圆与正方形的位置关系,从而找到圆的半径,再求出圆的周长.如图3所示,可知圆的直径是正方形的边长,即d=5分米.如果在长方形纸上剪一个最大的圆,直径即为长方形的宽.【变式2】.(闵行2018期末17)如图是由两个正方形和两个扇形组成的组合图形,那么阴影部分的周长为 cm .【答案】33.98【变式3】如果圆的周长为12.56厘米,那么这个圆的半径是 厘米.【答案】2【变式4】小丽家钟的分针长为5cm ,时针的长度是分针长度的35,从下午1点到下午5点,时针针尖走过 cm.【答案】6.28【变式4】(金山2017期末12)如果圆的直径是6米,那么这个圆的周长为___________米.【变式5】如图是由一个半径为r 的半圆和一条直径所组成的图形,那么这个图形的周长可表示为 (结果保留π)图3(分米)15.753.14d C =⨯=π=【答案】2r r π+【考点3:圆环】例题1.如图2所示,圆环的外圆周长C 1=250厘米,内周长C 2=150厘米,求圆环的宽度d (保留π).分析:设外圆的半径是R 1,内圆的半径是R 2,则d = R 1-R 2,因为,, 所以1257550d πππ=-=(厘米)反思:圆环的宽度就是两圆半径之差,利用两圆的周长可分别求得两圆半径.【变式1】.(普陀2017期末29)求图中阴影部分的周长和面积.(单位:cm )【答案】25.12cm ; 25.122cm ;(第20题图)π=π=1252250R 1π=π=752150R 2【考点4:扇形与圆之间的关系】例题1.求图1中扇形的周长和面积.分析: 26,(36060)300,360n R cm n S r π==-==扇,2300663094.2360S cm ππ=⨯⨯=≈扇. 反思:扇形面积公式2360n S r π=⋅扇中,圆心角n 指的是所求弧所对的圆心角,所以图中弧所对的圆心角应该是n =(360-60)=300°.例题2.求图中阴影部分的面积.分析:设∠A 、∠B 、∠C 所对的弧长分别为123l l l 、、,由题意知,∠A+∠B+∠C=180°,半径r=15毫米, 则1180A l r π=,2180B l r π=,3180C l r π=. 所以三段弧长之和为123()15180180180180A B C r l l l l r r r A B C r ππππππ=++=++=++==(毫米) 反思:本例涉及弧长计算,弧长与圆的半径和圆心角有关。
1.教师版:圆的方程

圆的方程专项复习(教师版)一、知识点归纳: 1.圆的标准方程平面内与定点距离等于定长的点的集合(轨迹)是圆。
定点是圆心,定长是半径。
如果圆心坐标为(a ,b ),半径等于r ,根据两点间距离公式可得圆的标准方程(x -a )2+(y -b )2=r 2。
如果圆心恰好为原点时,方程为x 2+y 2=r 2。
圆心在原点(0,0),半径为1的圆称为单位圆,其方程为x 2+y 2=1,由圆心坐标(a ,b )及半径r 的值,可以直接写出圆的标准方程。
由圆的标准方程也可直接读出圆心坐标和半径r 的大小。
2.圆的一般式方程任何一个圆的方程都可以写成下面形式:x 2+y 2+Dx+Ey+F=0,但方程x 2+y 2+Dx+Ey+F=0不一定表示圆方程。
一般方程x 2+y 2+Dx +Ey +F=0,配方22224()()224D E D E Fx y +-+++=(1)当D 2+E 2-4F >0时,方程表示圆,称为圆的一般式方程,其圆心(,)22D E --.(2)当D 2+E 2-4F =0时,方程仅表示一个点;(3)当D 2+E 2-4F <0时,方程没有实数解,方程不表示任何图形。
3.参数方程的概念在取定的坐标系中,如果曲线上任意一点的坐标x ,y 都是某个变数t 的函数,即(),()x f t y g t =⎧⎨=⎩且对于t 的每一个允许值,由方程组所确定的点M (x ,y )都在这条曲线上,则此方程组就叫这条曲线的参数方程,联系x ,y 之间关系的变数叫做参数。
相对于参数方程而言,直接给出曲线上点的坐标关系的方程叫做曲线的普通方程。
4.圆的参数方程:若圆心坐标为C (a ,b ),半径为r ,则cos ,sin x a r y b r θθ=+⎧⎨=+⎩称为圆的参数方程。
其中θ是以x 轴正方向为始边方向,CP 方向为终边方向的角。
C 是圆心,P 是圆上与θ对应的点。
特别地,以(0,0)为圆心,以r 为半径的圆的参数方程为)(sin cos 为参数θθθ⎩⎨⎧==r y r x5.点与圆的位置关系几何法——利用距离来判断:设点到圆心的距离为d ,圆的半径为r .(1)点在圆外;r d >⇔ (2)点在圆上;r d =⇔ (3)点在圆内;r d <⇔ 代数法——利用方程来判断:设点),,(00y x P 圆的方程为(x -a)2+(y -b)2=r 2(r>0)(1)点P 在圆外22020)()(r b y a x >-+-⇔;(2)点P 在圆上;)()(22020r b y a x =-+-⇔;(3)点P 在圆内22020)()(r b y a x <-+-⇔; 6. 求圆的切线方法(1)已知圆x 2+y 2+Dx +Ey +F=0.①若已知切点(x 0,y 0)在圆上,则切线只有一条,其方程是02)(2)(0000=++++++F y y E x x D y y x x 当),(00y x 在圆外时,0)2()2(000=++++++F y y E x x D y y x x 表示过两个切点的切点弦方程. ②若已知切线过圆外一点(x 0,y 0),则设切线方程为y -y 0=k(x -x 0),再利用相切条件求k ,这时必有两条切线,注意不要漏掉平行于y 轴的切线.③若已知切线斜率为k ,则设切线方程为y=kx +b ,再利用相切条件求b ,这时必有两条切线. (2)已知圆x 2+y 2=r 2.①若已知切点P 0(x 0,y 0)在圆上,则该圆过P 0点的切线方程为x 0x +y 0y=r 2.②已知圆的切线的斜率为k ,圆的切线方程为12+±=k r kx y . 7.几种特殊位置的圆的方程(1)圆心在原点:222(0)x y r r +=≠ (2)圆心在x 轴上:222()(0)x a y r r -+=≠ (3)圆心在y 轴上:222()(0)x y b r r +-=≠ (4)与x 轴相切:222()()(0)x a y b b b -+-=≠ (5)与y 轴相切:222()()(0)x a y b a a -+-=≠ (6)圆心在x 轴上且过原点:222()(0)x a y a a -+=≠ (7)圆心在y 轴上且过原点:222()(0)x y b b b +-=≠(8)过原点:222222()()(0)x a y b a b a b -+-=++≠ (9)与两坐标轴都相切:222()()(||||0)x a y b a a b -+-==≠ 8.重要结论:(1)已知:一个圆的直径端点是A(x 1,y 1)、B(x 2,y 2).则圆的方程是(x-x 1)(x-x 2)+(y-y 1)(y-y 2)=0. (2)过圆外一点00(,)P x y 的圆的切线方程的求解方法:设切线方程为00()y y k x x -=-,与圆的方程联立,根据=0∆即可求出k 的值;也可以根据圆心到直线的距离等于半径求出k 的值。
(完整版)初中数学教材章节-人教版

七年级上册(人教版)第一章有理数1、正数和负数2、有理数(有理数、数轴、相反数、绝对值)3、有理数的加减法(加法法则、交换律、结合律)4、有理数的乘除(倒数、交换律、结合律、分配律)5、有理数的乘方(幂、近似数)第二章整式的加减1、整式(单项式、多项式)2、整式的加减(同类项、合并同类项)第三章一元一次方程1、从算式到方程(一元一次方程、等式的性质)2、解一元一次方程-合并同类项与移项3、解一元一次方程-去括号去分母4、实际问题与一元一次方程第四章几何图形的初步1、几何图形(立体图形、平面图形、三视图、点线面体)2、直线、射线、线段(相交)3、角(度、分、秒、角的比较与运算、角平分线、余角、补角)4、课题设计-设计制作长方形形状的包装纸盒七年级下册第五章相交线与平行线1、相交线(邻补角、对顶角、垂线、同位角、内错角、同旁内角)2、平行线及其判定(3个判定)3、平行线的性质(3个性质、命题、定理、证明)4、平移第六章实数1、平方根(算术平方根);2、立方根;3、实数(无理数)第七章平面直角坐标系1、平面直角坐标系(有序数对、坐标系、原点、横轴、纵轴)2、坐标方法的简单应用(位置、平移)第八章二元一次方程组1、二元一次方程组2、消元-解二元一次方程组3、实际问题与二元一次方程组4、三元一次方程组的解法第九章不等式1、不等式(解集、不等式的性质3个)2、一元一次不等式3、一元一次不等式组第十章数据的收集、整理与描述1、统计调查(全面调查、抽样调查、简单随机抽样)2、直方图(组距、频数);3、课题学习-从数据谈节水八年级上册第十一章 三角形1、与三角形有关的线段(三边关系、高、中线、角平分线、重心、稳定性)2、与三角形有关的角(内角和、外角)3、多边形及其内角和(多边形、内角和、外角和360°)第十二章 全等三角形1、全等三角形(全等形、性质、)2、三角形全等的判定(SSS 、SAS 、AAS 、ASA 、HL )3、角的平分线的性质第十三章 轴对称1、轴对称(对称点、垂直平分线、对称轴、垂直平分线的性质)2、画轴对称图形3、等腰三角形(性质、等边三角形、30°的直角三角形)4、课题学习-最短路径的问题第十四章 整式的乘法与因式分解1、整式的乘法(同底数幂的乘法、幂的乘方、积的乘方、单项式/多项式×单项式/多项式)2、乘法公式(平方差、完全平方公式)3、因式分解(分解因式、提公因式法、公式法)第十五章 分式1、分式(分数-分式、性质、约分、最简分式、通分、最简公分母)2、分式的运算(乘除法则、加减法则、整数指数幂)3、分式的方程(检验)八年级下册第十六章 二次根式1、二次根式(()的区别与22a a 、代数式)2、二次根式的乘除(最简二次根式)3、二次根式的加减(同类二次根式)第十七章 勾股定理1、勾股定理2、勾股定理的逆定理第十八章 平行四边形1、平行四边形(性质、判定、三角形中位线)2、特殊的平行四边形(矩形、直角三角形的中线、菱形、正方形) 第十九章 一次函数1、函数(变量、函数、解析式、图像)2、一次函数(正比例函数、一次函数、待定系数法、一次函数与方程/不等式)3、课题学习-选择方案第二十章 数据的分析1、数据的集中趋势(平均数、中位数、众数)2、数据的波动程度(方差)3、课题学习-体质健康测试中的数据分析九年级上册第二十一章一元一次方程1、一元一次方程(定义、根)2、解一元一次方程(配方法、公式法、判别式、因式分解法、根与系数的关系)3、实际问题与一元二次方程第二十二章二次函数1、二次函数的图象和性质2、二次函数与一元一次方程3、实际问题与二次函数第二十三章旋转1、图形的旋转2、中心对称(关于原点对称的点的坐标)3、课题学习-图形设计第二十四章圆1、圆的有关性质(圆心、半径、弦、等圆、垂直弦的直径、圆心角、圆周角)2、点和圆、直线和圆的位置关系3、正多边形和圆4、弧形和扇形面积第二十五章概率初步1、随机事件与概率2、用列举法求概率3、用频率估计概率九年级下册第二十六章反比例函数1、反比例函数(图像、性质)2、实际问题与反比例函数第二十七章相似1、图形的相似(相似比)2、相似三角形(判定、性质、应用)3、位似(位似图形、位似中心)第二十八章锐角三角函数1、锐角三角函数2、解直角三角形及其应用第二十九章投影与视图1、投影(平行投影、中心投影、正投影)2、三视图3、课题学习-制作立体模型。
九年级数学圆单元知识点总结及习题练习教师版

九年级数学《圆》知识点祥解及习题检测一、圆的概念集合形式的概念: 1、 圆可以看作是到定点的距离等于定长的点的集合; 2、圆的外部:可以看作是到定点的距离大于定长的点的集合; 3、圆的内部:可以看作是到定点的距离小于定长的点的集合 轨迹形式的概念:1、圆:到定点的距离等于定长的点的轨迹就是以定点为圆心,定长为半径的圆;(补充)2、垂直平分线:到线段两端距离相等的点的轨迹是这条线段的垂直平分线(也叫中垂线);3、角的平分线:到角两边距离相等的点的轨迹是这个角的平分线;4、到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线;5、到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直线距离都相等的一条直线。
二、点与圆的位置关系1、点在圆内 ⇒ d r < ⇒ 点C 在圆内;2、点在圆上 ⇒ d r = ⇒ 点B 在圆上;3、点在圆外 ⇒ d r > ⇒ 点A 在圆外; 三、直线与圆的位置关系1、直线与圆相离 ⇒ d r > ⇒ 无交点;2、直线与圆相切 ⇒ d r = ⇒ 有一个交点;3、直线与圆相交 ⇒ d r < ⇒ 有两个交点;四、圆与圆的位置关系外离(图1)⇒ 无交点 ⇒ d R r >+; 外切(图2)⇒ 有一个交点 ⇒ d R r =+;相交(图3)⇒ 有两个交点 ⇒ R r d R r -<<+; 内切(图4)⇒ 有一个交点 ⇒ d R r =-; 内含(图5)⇒ 无交点 ⇒ d R r <-;rdd CBAO五、垂径定理垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。
推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧; (2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其它3个结论,即:①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧AD中任意2个条件推出其他3个结论。
冀教版六年级数学上册知识点汇总

第一单元圆和扇形1、圆各部分的名称:(1)圆(中心)的一点叫圆心,用字母(o)来表示。
(2)从(圆心)到圆上(任意一点)的线段叫半径,用字母(r)来表示。
(3)过(圆心0),且两端都在(圆上)的线段,叫直径,用字母(d)来表示。
2、在同一个圆中:(1)有(无数)条半径,有(无数)条直径。
(2)所有的半径都(相等),所以的直径都(相等)。
(3)直径是半径的(两)倍,半径是直径的(一半)。
3、圆的画法:(1)先确定(圆心)的位置,(2)再确定半径的(长度)。
(3)以(圆心)为定点,以(圆规的另一脚)为动点,旋转(一周)。
4、沿着一条直线对折,两边能(能完全重合)的图形,叫轴对称图形。
5、我们学过的轴对称图形有哪些?各有几条对称轴?被除数÷除数=分子÷分母=前项÷后项被除数/除数=分子/分母=前项/后项4、最简比:比的前项和后项互质(公因数只有1)最简分数:分子和分母互质(公因数只有1)5、如何化简比?整数比:比的前后项同时除以一个数(公因数),使比的前项和后项互质。
分数比:比的前后项同时乘一个相同的数(公倍数),使分数比变成整数比,再化成最简比。
小数比:比的前后项同时乘一个相同的数,使小数比变成整数比,再化成最简比。
另外也可以用求比值的方法来化简比。
可以先求出比值,再写成最简比。
6、按比例分配:如按a :b分配平均分法:平均分成a+b 份分数法:a占几分之几,b占几分之几。
第三单元百分数1、(表示一个数是另一个数的百分之几的数)叫百分数,又叫(百分率),又叫(百分比)。
2、百分数表示两个数的(倍数)关系,(不能)带单位。
3、百分数的读法:先读(分之),再读(分母)。
(写语文数)。
4、百分数的写法:先写(数据),后写(百分号)。
5、小数化百分数的方法:把小数点向(右)移动(两)位,再添上(百分号)。
6、百分数化小数的方法是:先去掉(百分号),再把小数点向(左)移动(两)位。
五年级下册数学试题-培优专题训练:03圆与扇形(5年级培优)教师版

圆✧ 任意一个圆,它的周长除以直径的商总是一个固定的数,这个数叫圆周率。
如果用C 表示圆周的长度,d 表示这个圆的直径,r 表示它的半径,π表示圆周率,就有:d c =π或rc 2=。
π是一个无限不循环小数:Λ89793238461415926535.3=π, 我们在做题时,通常取14.3=π。
✧ 圆的周长:r C π2=或d C π= ✧ 圆的面积:2r S π=扇形✧ 扇形是圆的一部分,它是由圆心角的两条半径和圆心角所对弧围成的图形,扇形的大小由它的半径和弧所对的圆心角的大小决定,因为扇形是圆的一部分,所以扇形的弧长和面积的计算方法就是从圆周长和面积的计算方法中引申出来的。
✧ 如右图所示,设扇形的圆心角是n 度,利用圆的周长计算公式可知扇形的弧长计算公式是r n r n l ππ⨯=⨯=1802360 扇形的面积计算公式是lr r n S 213602=⨯=π ✧ 一些特殊角的扇形可以看作是ΛΛ43314161、、、的圆来计算。
重难点:圆和扇形的面积公式一个圆形的铁环,直径是40厘米,做这样一个铁环需要用多长的铁条?【答案】125.6厘米 【知识点】圆的周长 【难度】A 【出处】底稿 【分析】6.12514.340=⨯(厘米)小明在一条路上滚铁环,铁环的直径是50厘米,滚动了78.5米,求铁环滚动了几圈?【答案】50圈 【知识点】圆的周长 【难度】A 【出处】底稿 【分析】()5014.35.05.78=⨯÷(圈)有两根长188.4厘米的铁丝,分别围成一个正方形和一个圆,哪个面积大?大多少?【答案】圆的面积大 【知识点】圆的面积 【难度】B 【出处】底稿【分析】正方形的面积:1.4744.188=÷(厘米) 41.22181.471.47=⨯(平方厘米) 圆的面积:3014.324.188=÷÷(厘米) 2826303014.3=⨯⨯(平方厘米) 所以圆的面积大。
初三数学.圆与三角形和四边形.教师版
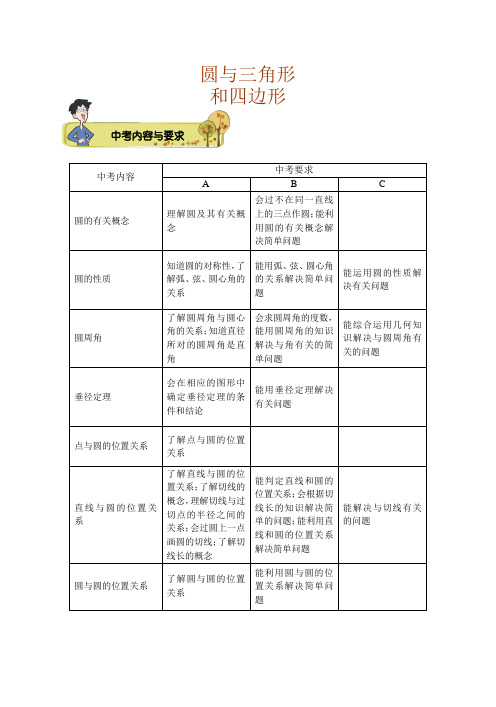
中考内容中考要求A B C圆的有关概念理解圆及其有关概念会过不在同一直线上的三点作圆;能利用圆的有关概念解决简单问题圆的性质知道圆的对称性,了解弧、弦、圆心角的关系能用弧、弦、圆心角的关系解决简单问题能运用圆的性质解决有关问题圆周角了解圆周角与圆心角的关系;知道直径所对的圆周角是直角会求圆周角的度数,能用圆周角的知识解决与角有关的简单问题能综合运用几何知识解决与圆周角有关的问题垂径定理会在相应的图形中确定垂径定理的条件和结论能用垂径定理解决有关问题点与圆的位置关系了解点与圆的位置关系直线与圆的位置关系了解直线与圆的位置关系;了解切线的概念,理解切线与过切点的半径之间的关系;会过圆上一点画圆的切线;了解切线长的概念能判定直线和圆的位置关系;会根据切线长的知识解决简单的问题;能利用直线和圆的位置关系解决简单问题能解决与切线有关的问题圆与圆的位置关系了解圆与圆的位置关系能利用圆与圆的位置关系解决简单问题中考内容与要求圆与三角形和四边形弧长会计算弧长能利用弧长解决有关问题扇形会计算扇形面积能利用扇形面积解决有关问题圆锥的侧面积和全面积会求圆锥的侧面积和全面积能解决与圆锥有关的简单实际问题圆是北京中考的必考内容,主要考查圆的有关性质与圆的有关计算,每年的第20题都会考查,第1小题一般是切线的证明,第2小题运用圆与三角形相似、解直角三角形等知识求线段长度问题,有时也以阅读理解、条件开放、结论开放探索题作为新的题型。
要求同学们重点掌握圆的有关性质,掌握求线段、角的方法,理解概念之间的相互联系和知识之间的相互转化,理解直线和圆的三种位置关系,掌握切线的性质和判定方法,会根据条件解决圆中的动态问题。
年份2011年2012年2013年题号20,25 8,20,25 8,20,25分值13分17分17分考点圆的有关证明,计算(圆周角定理、切线、等腰三角形、相似、解直角三角形);直线与圆的位置关系圆的基本性质,圆的切线证明,圆同相似和三角函数的结合;直线与圆的位置关系圆中的动点函数图像,圆的基本性质(垂径定理、圆周角定理),圆同相似和三角函数的结合;直线与圆的位置关系中考考点分析图1ODB A图2EABC DO【例1】 已知AD 是O ⊙的直经,AB AC 、是弦,若232AD AB AC ===,,,求由A B C D 、、、四点构成的四边形的周长.【解析】 ⑴ 如图1,弦AB AC 、在直径AD 的异侧,连结BD CD 、.∵AD 是直径,∴90B C ∠=∠=︒, 在Rt ABD △中,222BD AD AB =-, 则()22231BD =-=,在Rt ACD ∆中,222CD AD AC =-, 则()22222CD =-=,∴四边形周长为31221322AB BD CD AC +++=+++=++. ⑵ 如图2,弦AB AC 、在直径AD 的同侧,连结CB BD CD 、、,过C 点作CE AB ⊥于E .∵AD 是直径,∴90ACD ABD ∠=∠=︒ 在Rt ABD ∆中,222BD AD AB =-, 则()22231BD =-=,在Rt ACD △中,222CD AD AC =-, 则()22222CD =-=,∴AC CD =,∴45CAD CDA ∠=∠=︒,∴45ABC ADC ∠=∠=︒, ∵CE AB ⊥,∴90CEB ∠=︒,∴45ECB ∠=︒,∴CE EB =.设CE EB x ==,则3AE x =-, 在Rt ACE △中,222AE CE AC +=, 即()()22232x x -+=,整理得222310xx -+=,解得31x ±=, ∵CE AE <,∴31CE -=, ∴622BC CE -==, ∴四边形周长62622123AC CB BD AD -++++=+++=+.典题精练【例2】 如图所示,圆O 是ABC △的外接圆,BAC ∠与ABC ∠的平分线相交于点I ,延长AI 交圆O 于点D ,连结BD CD 、.⑴ 求证:BD CD DI ==;⑵ 若圆O 的半径为10cm ,120BAC ∠=︒,求BDC △的面积.【解析】 ⑴ ∵AD 平分BAC ∠,∴BAD CAD ∠=∠,∴BD CD =,∴BD CD =.∵DBC DAC ∠=∠,∴BAD DBC ∠=∠, ∵BI 平分ABC ∠,∴ABI CBI ∠=∠, ∴BAD ABI DBC CBI ∠+∠=∠+∠,∵BAD ABI BID ∠+∠=∠,∴DBI BID ∠=∠, ∴BD DI =,∴BD CD DI ==. ⑵ 连结BO DO 、∵120BAC ∠=︒,∴60BAD ∠=︒,∴120BOD ∠=︒,∴60BCD ∠=︒, ∵BD CD =,∴BCD △是等边三角形 , ∵10cm BODO ==,∴BD =,∴(22BCD S ==△.【例3】 在ABC △中,AC BC >,M 是它的外接圆上包含点C 的AB 的中点,AC 上的点X 使得MX AC ⊥,求证:AX XC CB =+.【解析】 解法一:过点M 作MN AC ∥交O ⊙于N ,过点N 作NE AC ⊥于E .∴AN CM =,AE CX =,∵AM BM =,∴MN BC =∴MN BC =,∴BC EX =,∴AX XC CB =+解法二:如图,在XA 上取一点D ,使得XD XC =, 连接MC ,MB ,MD ,MA由XC XD =,XM CD ⊥,∴MD MC = 又∵M 是圆上包含点C 的弧AB 的中点 ∴MA MB =又MBC MAD ∠=∠,MDC MCD BAM ∠=∠=∠, ∴AMD BMC ∠=∠,∴MAD MBC △≌△,∴AD BC = ∵AX AD DX =+,∴AX XC BC =+解法三:如图,过M 点作ME BC ⊥交BC 延长线于E , 连结MA MB MC 、、,∵M 是圆上包含点C 的弧AB 的中点, ∴MA MB =, ∵MX AC ME BC ⊥⊥,, ∴90AXM BEM ∠=∠=︒,又∵MAX MBE ∠=∠,∴AM X BM E △≌△, ∴MX ME AX BE ==,.∵MCE MAB MBA MCA ∠=∠=∠=∠, ∴MCX MCE △≌△, ∴CX CE =,∴AX BE BC CE BC CX ==+=+.(类似此方法还可以“延长BC 到E ,使CE CX =,连结ME ”) 解法四:如图,延长AC 到F ,使FX AX =,连结MA MB MC MF 、、、, ∵M 是圆上包含点C 的弧AB 的中点, ∴MA MB =,MAB MBA ∠=∠, ∵MX AC AX FX ⊥=,, ∴MA MF =,∴MB MF =,M AF M FA ∠=∠,∵MAC MBC ∠=∠,∴MBC MFC ∠=∠,∵MCA MFC CMF ∠=∠+∠,MCA MBA MAB ∠=∠=∠, ∴MAB MFC CMF ∠=∠+∠, ∵BAC BMC CBM CAM ∠=∠∠=∠,,∴MAB BAC CAM BMC CBM ∠=∠+∠=∠+∠, ∴MFC CMF BMC CBM ∠+∠=∠+∠, ∴BMC CMF ∠=∠,∴MBC MFC △≌△,∴CF BC =, ∴AX FX XC CF XC BC ==+=+.此法还可以连接FB ,利用等腰三角形的性质可以证得结论.【点评】 此题还有很多种不同的解法,老师们可以引导学生拓展思维,多总结方法.【例4】 已知四边形ABCD 内接于O ,对角线AC BD ⊥,F 为线段AB 的中点.求证:12OF CD =.【解析】 证法一:如图,设四边形ABCD 内接于圆O ,且AC BD ⊥,OF 为AB之弦心距.作CD 的弦心距OE ,连接OB 、OC .显然190902OCE EOC DC ∠=︒-∠=︒-的度数.∵AC BD ⊥,∴180AB DC +=︒,∴12m OCE AB ∠=.又12m BOF AB ∠=,∴OCE BOF ∠=∠.∵OC BO =,∴Rt Rt OCE BOF △≌△.∴CE OF =,即12OF DC =.证法二:如图,作直径AE ,连接BE 、CE . ∵O 、F 为中点,∴2BE OF =.∵CE AC ⊥,BD AC ⊥,∴CE BD ∥,∴BE DC =,∴BE DC =.A EFOCBDAEFOC BDA即2OF DC =,∴12OF DC =. 证法三:如图,设AC 、BD 交于P ,E 为DC 之中点.连接EP 延长垂直AB 于G .连接FP 延长必垂直DC 于H .连接OE . ∵OE DC ⊥,FH DC ⊥,∴FH OE ∥,同理EG OF ∥.∴PFOE 为平行四边形,∴OF EP =.而12EP DC =(∵EP 是Rt CDP △斜边上的中线),∴12OF DC =.【例5】 已知:如图,O ⊙的内接ABC △中,45BAC ∠=︒,15ABC ∠=︒,AD OC ∥并交BC 的延长线于D ,OC 交AB 于E . ⑴ 求D ∠的度数;⑵ 求证:2AC AD CE =⋅;⑶ 求BC CD的值.(西城初三上期末) 【解析】 ⑴ 连结OB ,∵O ⊙的内接ABC △中,45BAC ∠=︒, ∴290BOC BAC ∠=∠=︒,∵OB OC =,∴45OBC OCB ∠=∠=︒, ∵AD OC ∥,∴45D OCB ∠=∠=︒. ⑵ ∵4545BAC D ∠=︒∠=︒,,∴BAC D ∠=∠, ∵AD OC ∥,∴ACE DAC ∠=∠,∴ACE DAC △∽△,∴AC CEDA AC=, ∴2AC AD CE =⋅.⑶ 解法一:延长BO 交DA 延长线于F ,连结OA . ∵AD OC ∥,∴90F BOC ∠=∠=︒,∵15ABC ∠=︒,∴30OBA OBC ABC ∠=∠-∠=︒. ∵OA OB =,∴6030FOA OBA OAB OAF ∠=∠+∠=︒∠=︒,,∴12OF OA =,∵AD OC ∥,∴BOC BFD △∽△,∴BC BOBD BF=, ∴2BC BO OA CD OF OF ===,即BCCD的值为2. 解法二:作OM BA ⊥于M ,设O ⊙的半径为r ,易得30OBM∠=︒,2rBM OM ==,,且30MOE ∠=︒,tan30ME OM =︒=,G EHFOCBDA则BE BM ME=+,AE AB BE =-=, ∵AD OC ∥,∴2BC BECD AE==.【例6】 如图,Rt ABC △内接于O ⊙,AC BC =,BAC ∠的平分线AD 与O ⊙交于点D ,与BC交于点E ,延长BD 与AC 的延长线交于点F ,连结CD ,G 是CD 的中点,连结OG . ⑴ 判断OG 与CD 的位置关系,写出你的结论并证明; ⑵ 求证:AE BF =; ⑶ 若(32OG DE ⋅=,求O ⊙的面积.(四川成都中考)【解析】 ⑴ OG CD ⊥连结OC OD 、∵OC OD =,G 是CD 的中点, ∴OG CD ⊥.⑵ ∵ABC ∆是直角三角形,且AC BC =, ∴90ACB ∠=︒∵CAD CBF ∠=∠,∴ACE BCF ∆∆≌, ∴AE BF =.⑶ 由⑴可知12COG COD ∠=∠,12CG DG CD ==,∵12EBD COD ∠=∠,∴EBD COG ∠=∠,∵90BDE OGC ∠=∠=︒,∴BDE OGC ∆∆∽, ∴DE BDCG OG=,即OG DE BD CG ⋅=⋅, ∵AD 是BAC ∠的平分线,∴CD BD =, ∴212BD CG BD⋅=,∵(32OG DE⋅=,∴(21322BD =,∴(262BD =设O ⊙的半径为r ,∵AB 是O ⊙的直径,∴2AB r =,∵90AC BC ACB =∠=︒,,∴AC BC =,∵90BAD CAD ADB ∠=∠∠=︒,,∴ABF ∆是等腰三角形,∴2AF AB r ==,12DF BD BF ==,∴(2CF AF AC r =-=,∴)((222222242BF BC CF r r ⎡⎤=+=+=⎣⎦,OIABCQ PFEDCBAOI H FE DCB A I O∵12BD BF =,∴2214BD BF =,∴()()222622r -=-,解得26r =, ∴O ⊙的面积为2π6πS r ==.【例7】 如图,不等边ABC △内接于O ⊙,I 是其内心,且AI OI ⊥,求证:2AB AC BC +=.【解析】 解法一:过I 点分别作AB BC CA 、、的垂线ID IE IF 、、,垂足分别为D E F 、、,再过O 点作OP AB OQ AC ⊥⊥,,垂足分别为P Q 、,连结IP IQ 、.∵I 是ABC ∆内切圆圆心,∴D E F 、、是内切圆与三角形三边的切点,ID IE IF ==,∴AD AF BD BE CE CF ===,,, ∵O 是ABC △外接圆圆心,∴P Q 、分别是AB AC 、的中点, 即1122BP AB CQ AC ==,, ∴1122AB AC BP CQ BD DP CF FQ +=+=++- BE CE DP FQ BC DP FQ =++-=+-,∵90APO AQO ∠=∠=︒,∴A P O Q 、、、四点共圆,且AO 为该圆直径, ∵AI OI ⊥,∴90AIO ∠=︒,∴I 点在A P O Q 、、、四点确定的圆上,即A P I O Q 、、、、五点共圆,∴IPO IQO ∠=∠,又ID OP IF OQ ∥,∥,∴DIP IPO FIQ IQO ∠=∠∠=∠,, ∴DIP FIQ ∠=∠,∴IPD IQF △≌△,∴DP FQ =,∴1122AB AC BC +=,∴2AB AC BC +=.解法二:过I 点分别作AB BC CA 、、的垂线ID IE IF 、、,垂足分别为D E F 、、,延长AI 交O ⊙于G ,连结OG BG BI 、、. ∵I 是ABC △内切圆圆心, ∴D E F 、、是内切圆与三角形三边的切点,ID IE IF ==,∴AD AF BD BE CE CF ===,,, ∴AB AC BC AB BD AF CF BE CE +-=+++--2AD AF AD =+=,又∵AI 平分BAC ∠,∴G 是BC 的中点,∴OG BC ⊥,BAG CBG ∠=∠, ∴H 是BC 中点,即2BC BH =, ∵OI AG ⊥,∴AI IG =, ∵GBI GBC IBC BIG ABI BAI ∠=∠+∠∠=∠+∠,,且ABI IBC CBG BAG ∠=∠∠=∠,, ∴GBI IBG ∠=∠,∴BG IG AI ==, ∴()AAS ADI BHG △≌△,∴AD BH =,∴2AD BC =,∴AB AC BC BC +-=,即2AB AC BC +=.训练1. 如图,已知O ⊙是ABC △的外接圆,D 为劣弧BC 的中点,H 为劣弧AB 的中点.连接CH ,交AB 于点E ,连接AD ,交CH 于点G ,延长CH 到点M ,使MH HG =,延长DA 到点K ,使AK AG =,CA 的延长线交MK 于点F .求证:⑴ MGK MKG ∠=∠;⑵ ME MF =.O MKHGE DCBAA BCDEG H K MO【解析】 连接AH∵GH MH =,AG AK =,∴AH M K ∥, ∴HAG MKG ∠=∠,∵D 是劣弧BC 的中点,H 是劣弧AB 的中点,∴CD BD =,BH AH =,∴CAD BAD ∠=∠,BCH ACH BAH ∠=∠=∠, ∴MGK ACH CAD BAD BAH HAG MKG ∠=∠+∠=∠+∠=∠=∠. ∵CAD FAK BAD ∠=∠=∠,∴AEG AFK △≌△, ∴EG FK =,∴MG EG MK FK -=-,即ME MF =.思维拓展训练(选讲)训练2. 如图,以线段AB 为直径作半圆,点O 为圆心,C 是AB 上一点,G 是半圆上一点,且ACG ∠为锐角.作CE CG ∥交AB 于D ,交半圆于点E ,且满足2DO DB DE ⋅=,连接EO ,再作CF OE ∥交半圆于点F .求证:13FCG ACG ∠=∠.【解析】 连接BE由CG DE ∥,CF OE ∥可得FCG OED ∠=∠,ACG ADE ∠=∠∵2DO DB DE ⋅=,ODE ∠是公共角,∴ODE EDB △∽△, ∴OED OBE OEB ∠=∠=∠,∴3ADE DEB DBE OED ∠=∠+∠=∠,∴3ACG FCG ∠=∠,即13FCG ACG ∠=∠.训练3. 如图,已知:在O ⊙中,直径4AB =,点E 是OA 上任意一点,过E 作弦CD AB ⊥,点F是BC 上一点,连接AF 交CE 于H ,连接AC CF BD OD 、、、.⑴ 求证:ACH AFC △∽△;⑵ 猜想:AH AF ⋅与AE AB ⋅的数量关系,并说明你的猜想; ⑶ 探究:当点E 位于何处时,:1:4AEC BOD S S =△△?并加以说明.(湖北襄樊中考)【解析】 ⑴ ∵AB 是直径,且AB CD ⊥, ∴AC AD =,∴AFC ACD ∠=∠, ∵CAH FAC ∠=∠,∴ACH AFC △∽△. ⑵ AH AF AE AB ⋅=⋅解法一:由⑴ACH AFC △∽△可得:2AC AH AF =⋅, 连结BC ,∵C 在O ⊙上,∴90ACB ∠=︒, 又CD AB ⊥,∴2AC AE AB =⋅, ∴AH AF AE AB ⋅=⋅. 解法二:连结FB∵F 在O ⊙上,∴90AFB ∠=︒,又EAH FAB ∠=∠,∴AEH AFB △∽△,∴AE AHAF AB =,即AH AF AE AB ⋅=⋅. ⑶ 12AEC S AE CE ∆=⋅,12BOD S BO DE ∆=⋅,∵:1:4AEC BOD S S ∆∆=,∴112142AEC BODAE CES AE S BO BO DE ∆∆⋅===⋅,∵4AB =,∴122OB AB ==, ∴1142AE OB ==,∴当12AE =时,:1:4AEC BOD S S ∆∆=.1193D C BA【练习1】 已知圆内接四边形ABCD 中1193AB BC CD ===,,,如图,AB CD BC AD +=+,则AD =__________. 【解析】 连接AC ,BD ,由AB CD BC AD +=+,知180AB CD +=︒,AC BD ⊥,因而2222AD BC AB CD +=+,22221139497AD AD =+-==,.【练习2】 如图,O ⊙的内接四边形ABMC 中,AB AC >,点M 是弧BC 的中点,MH AB ⊥于点H .求证:()12BH AB AC =-.H M CBANABCMH【解析】 在AH 上截取NH BH =,连接AM MN 、,∵MH AB ⊥,NH BH =,∴BM MN =, ∴B BNM ∠=∠,∵M 是BC 的中点,∴BM CM =,∴BM CM =,BAM CAM ∠=∠, ∴AMN AMC △≌△,∴AN AC =,∴2BH BN AB AN AB AC ==-=-,即()12BH AB AC =-.【练习3】 如图,ABC △的两个顶点B C 、在圆上,顶点A 在圆外,AB AC 、分别交圆于E D 、两点,连结EC BD 、.⑴ 求证:ABD ACE △∽△;⑵ 若BEC △与BDC △的面积相等,试判定ABC △的形状.(山东潍坊中考) 【解析】 ⑴ ∵ABD ACE ∠=∠,∴ABD ACE △∽△.⑵ 方法一:连接DE∵BEC BDC S S =△△,∴DE BC ∥,∴BE CD =,∴四边形BCDE 是等腰梯形,∴ABC ACB ∠=∠,∴AB AC =,∴ABC △是等腰三角形. 方法二:∵BEC BDC S S =△△,∴ABD ACE S S =△△, 复习巩固EDCBA由⑴可知ABD △和ACE △的相似比为1, ∴AB AC =,∴ABC △是等腰三角形.【练习4】 如图,AB CD ,是O ⊙的两条弦,它们相交于点P ,连结AD BD 、,已知4AD BD ==,6PC =,求CD 的长. 【解析】 连结AC∵AD BD =,∴AD BD =, ∴ACD ABD BAD ∠=∠=∠,∴APD CAD △∽△,∴AD PDCD AD=,即2AD PD CD =⋅, ∴16PD CD ⋅=,又6PC CD PD =-=,∴6PD CD =-, ∴26160CD CD --=,解得8CD =(舍负).【练习5】 如图,半径为O ⊙内有互相垂直的两条弦AB CD 、相交于P 点. ⑴ 求证:PA PB PC PD ⋅=⋅;⑵ 设BC 的中点为F ,连结FP 并延长交AD 于E ,求证:EF AD ⊥; ⑶ 若86AB CD ==,,求OP 的长. (湖北荆门中考)【解析】 ⑴ ∵DAP BCP APD CPB ∠=∠∠=∠,, ∴APD CPB △∽△,∴AP PDCP PB=, ∴PA PB PC PD ⋅=⋅.⑵ ∵AB CD ⊥,∴90BPD BPC ∠=∠=︒,∵F 是BC 中点,∴12PF BC BF ==,∴BPF PBF ∠=∠,∵ADC PBC ∠=∠,∴ADP BPF ∠=∠∵90DPE BPF ∠+∠=︒,∴90ADP DPE ∠+∠=︒, ∴90DEP ∠=︒,即EF AD ⊥. ⑶ 过O 点作OM AB ON CD ⊥⊥,,垂足分别为M N 、 由垂径定理得43AM CN ==,,∴2OM ON =,,易证得四边形OMPN 是矩形,∴OP。
2-1 圆(教师版)2021-2022学年九年级数学上册讲义(苏科版)

第2章对称图形----圆2.1 圆课程标准课标解读1、理解圆的定义(圆的描述概念和圆的集合概念);2、掌握点和圆的三种位置关系;3、会利用点到圆心的距离和圆的半径之间的数量关系判定点和圆的位置关系;4、初步会运用圆的定义证明四个点在同一个圆上1、理解圆的描述概念和圆的集合概念;2、理解半径、直径、弧、弦、弦心距、圆心角、同心圆、等圆、等弧的概念;3、经历探索点与圆的位置关系的过程,会运用点到圆心的距离与圆的半径之间的数量关系判断点与圆的位置关系;4、了解不在同一直线上的三点确定一个圆,了解三角形的外接圆、三角形的外心、圆的外接三角形的概念.知识点01 圆的定义1.圆的描述概念如图,在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫圆,固定的端点O叫做圆心,线段OA叫做半径. 以点O为圆心的圆,记作“⊙O”,读作“圆O”【微点拨】①圆心确定圆的位置,半径确定圆的大小;确定一个圆应先确定圆心,再确定半径,二者缺一不可;②圆是一条封闭曲线.2.圆的集合概念圆心为O,半径为r的圆是平面内到定点O的距离等于定长r的点的集合.平面上的一个圆,把平面上的点分成三类:圆上的点,圆内的点和圆外的点.目标导航知识精讲圆的内部可以看作是到圆心的距离小于半径的的点的集合;圆的外部可以看成是到圆心的距离大于半径的点的集合.【微点拨】①定点为圆心,定长为半径;②圆指的是圆周,而不是圆面;③强调“在一个平面内”是非常必要的,事实上,在空间中,到定点的距离等于定长的点的集合是球面,一个闭合的曲面.【即学即练1】1.圆形的井盖怎么放都不会掉到井里,并且能恰好盖住井口,这是利用了圆特征中的()A.圆是曲线图形B.同一圆中所有直径都相等C.圆有无数多条对称轴D.圆心决定圆的位置,半径决定圆的大小【答案】B【分析】根据同圆的直径都相等即可解答.【详解】解:圆形的井盖怎么放都不会掉到井里,并且能恰好盖住井口,这是利用了同一圆中所有直径都相等.故选:B.知识点02 点与圆的位置关系点和圆的位置关系有三种:点在圆内,点在圆上,点在圆外.若⊙O的半径为r,点P到圆心O的距离为d,那么:点P在圆内⇔d < r ;点P在圆上⇔d = r ;点P在圆外⇔d >r.“⇔”读作“等价于”,它表示从左端可以推出右端,从右端也可以推出左端.【微点拨】点在圆上是指点在圆周上,而不是点在圆面上;PO=,则点P与O的位置关系是()【即学即练2】2.已知O的直径为8,点P在同一平面内,6A.点P在O内B.点P在O上C.点P在O外D.无法判断【答案】C【分析】先求出⊙O的半径,再根据点与圆的位置关系即可求解.【详解】解:⊙⊙O的直径为8,⊙⊙O的半径为4,⊙PO=6>4,⊙点P在⊙O外.故选:C.知识点03 与圆有关的概念1.弦弦:连结圆上任意两点的线段叫做弦.直径:经过圆心的弦叫做直径.弦心距:圆心到弦的距离叫做弦心距.【微点拨】直径是圆中通过圆心的特殊弦,也是圆中最长的弦,即直径是弦,但弦不一定是直径.为什么直径是圆中最长的弦?如图,AB是⊙O的直径,CD是⊙O中任意一条弦,求证:AB≥CD.证明:连结OC、OD∵AB=AO+OB=CO+OD≥CD(当且仅当CD过圆心O时,取“=”号)∴直径AB是⊙O中最长的弦.2. 弧弧:圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作,读作“圆弧AB”或“弧AB”. 半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆;优弧:大于半圆的弧叫做优弧;劣弧:小于半圆的弧叫做劣弧.【微点拨】①半圆是弧,而弧不一定是半圆;②无特殊说明时,弧指的是劣弧.3.等弧在同圆或等圆中,能够完全重合的弧叫做等弧.【微点拨】①等弧成立的前提条件是在同圆或等圆中,不能忽视;②圆中两平行弦所夹的弧相等.4.同心圆与等圆圆心相同,半径不等的两个圆叫做同心圆.圆心不同,半径相等的两个圆叫做等圆.【微点拨】同圆或等圆的半径相等.5.圆心角顶点在圆心的角叫做圆心角.【微点拨】在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,反之也成立.【即学即练3】3.对于圆周率 的研究,我国古代数学家们也做出了巨大贡献,如东汉初年的一本著作中就有“径一周三”的古率记载,这本著作是()A .《九章算术》B .《海岛算径》C .《周髀算经》D .《孙子算径》【答案】C 【分析】根据数学史实解答即可. 【详解】解:历史上,对于圆周率π的研究是古代数学一个经久不衰的话题.在我国,东汉初年的《周髀算经》就有“径一周三”的古率记载. 故选C .知识点04 确定圆的条件(1)经过一个已知点能作无数个圆;(2)经过两个已知点A 、B 能作无数个圆,这些圆的圆心在线段AB 的垂直平分线上; (3)不在同一直线上的三个点确定一个圆.(4)经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.如图:⊙O 是△ABC 的外接圆, △ABC 是⊙O 的内接三角形,点O 是△ABC 的外心.外心的性质:外心是△ABC 三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等. 【微点拨】(1)不在同一直线上的三个点确定一个圆.“确定”的含义是“存在性和唯一性”. (2)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定.【即学即练4】4.已知AB 是O 的弦,O 的半径为r ,下列关系式一定成立的是( ) A .AB r > B .AB r <C .2AB r <D .2AB r ≤【答案】D根据“直径是最长的弦”进行解答即可. 【详解】解:若AB 是O 的直径时,2AB r =,若AB 不是O 的直径时2AB r <,无法判定AB 与r 的大小关系. 观察选项,只有选项D 符合题意. 故选D .考法01 判断点和圆的位置关系点和圆的位置关系有三种:点在圆内,点在圆上,点在圆外. 若⊙O 的半径为r ,点P 到圆心O 的距离为d ,那么: 点P 在圆内 ⇔d < r ; 点P 在圆上 ⇔d = r ; 点P 在圆外 ⇔d >r.“⇔”读作“等价于”,它表示从左端可以推出右端,从右端也可以推出左端.【典例1】如图,线段OA 绕点O 旋转,线段OB 的位置保持不变,在AB 的上方作等边PAB △,若1OA =,3OB =,则在线段OA 旋转过程中,线段OP 的最大值是( )A.10 B .4C .25D .5【答案】B 【分析】首先构造以OB 为边的等边⊙'OO B ,再证明'OBA O BP ,证明AO=O’P ,因为OA 的长度不变,所以动点A 在以O 为圆心,半径为1的圆上运动,因为O’P 的长度不变,O’不动,所以动点P 在以O’为圆心,半径为1的圆上运动,当三点O,O’,P 共线时,OP 最大,即可求得.能力拓展如图,以OB 为边作等边'OO B △,连接O’P ,⊙OB=O’B,⊙⊙PAB 为等边三角形, ⊙AB=BP,⊙1+⊙2=23∠+∠=60°, ⊙⊙1=⊙3,在⊙OBA 和'O BP 中'12OB OB AB BP =⎧⎪∠=∠⎨⎪=⎩⊙'()OBA O BP SAS⊙OA=O’P ,点A 在以O 为圆心,半径的1的圆上运动,P 在以O’为圆心,半径为1的圆上运动, 当O,O’,P 三点共线时,OP 最大, 此时OP''314OO O P ,故选:B .考法02 已知圆内一点求过该点的最长弦直径是圆中最长的弦,我们可以将圆中的弦分为两类:一类是经过圆心的弦(即直径);另一类是不经过圆心的弦,如图1,AB 是⊙O 中的任意一条不经过圆心的弦,连结OA ,OB ,根据三角形的三边关系都有OA+OB>AB ,即,直径的长大于非直径的弦长,所以直径是圆中最长的弦。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
研究圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,通过变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形来计算它们的面积.圆的面积2πr =;扇形的面积2π360nr =⨯;圆的周长2πr =;扇形的弧长2π360nr =⨯.一、跟曲线有关的图形元素:①扇形:扇形由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形,扇形是圆的一部分.我们经常说的12圆、14圆、16圆等等其实都是扇形,而这个几分之几表示的其实是这个扇形的圆心角占这个圆周角的几分之几.那么一般的求法是什么呢?关键是360n.比如:扇形的面积=所在圆的面积360n⨯;扇形中的弧长部分=所在圆的周长360n⨯扇形的周长=所在圆的周长+360n⨯2⨯半径(易错点是把扇形的周长等同于扇形的弧长)②弓形:弓形一般不要求周长,主要求面积.一般来说,弓形面积=扇形面积-三角形面积.(除了半圆)③”弯角”:如图:弯角的面积=正方形-扇形④”谷子”:如图:“谷子”的面积=弓形面积2⨯二、常用的思想方法:①转化思想(复杂转化为简单,不熟悉的转化为熟悉的) ②等积变形(割补、平移、旋转等) ③借来还去(加减法)④外围入手(从会求的图形或者能求的图形入手,看与要求的部分之间的”关系”)板块一 平移、旋转、割补、对称在曲线型面积中的应用【例 1】 如图,圆O 的直径AB 与CD 互相垂直,AB =10厘米,以C 为圆心,CA 为半径画弧。
求月牙形ADBEA (阴影部分)的面积。
例题精讲圆与扇形D【考点】圆与扇形 【难度】3星 【题型】解答 【关键词】华杯赛,决赛,第9题,10分 【解析】 ①月牙形ADBEA (阴影部分)的面积=半圆的面积+△ABC 的面积-扇形CAEBC 的面积②月牙形ADBEA 的面积=211π525π502524⨯⨯+-⨯⨯=(平方厘米),所以月牙形ADBEA 的面积是25平方厘米。
【答案】25【例 2】 三个半径为100厘米且圆心角为60º的扇形如图摆放;那么,这个封闭图形的周长是________厘米.(π取3.14)【考点】圆与扇形 【难度】3星 【题型】填空 【关键词】迎春杯,六年级,初赛,4题【解析】 三个扇形的弧长相当于半径100厘米,圆心角为1800的扇形的弧长,1802 3.14314360⨯⨯=厘米; 【答案】314【例 3】 分别以一个边长为2厘米的等边三角形的三个顶点为圆心,以2厘米为半径画弧,得到右图;那么,阴影图形的周长是_______【考点】圆与扇形 【难度】3星【关键词】迎春杯,六年级,初赛,试题【解析】 每段弧长为16C 圆,所以166C C C =⨯=圆圆阴影C 阴影=6×16C 圆= C 圆,所以12.56C =阴影【答案】12.56【例 4】 下图中每一个小正方形的面积是1平方厘米,那么格线部分的面积是多少平方厘米?【考点】圆与扇形 【难度】3星 【题型】解答 【解析】 割补法.如右图,格线部分的面积是36平方厘米. 【答案】36【巩固】下图中每一个小正方形的面积是1平方厘米,那么格线部分的面积是多少平方厘米?【考点】圆与扇形 【难度】3星 【题型】解答 【解析】 割补法.如右图,格线部分的面积是36平方厘米. 【答案】36【例 5】 如图,在18⨯8的方格纸上,画有1,9,9,8四个数字.那么,图中的阴影面积占整个方格纸面积的几分之几?【考点】圆与扇形 【难度】3星 【题型】解答【解析】 我们数出阴影部分中完整的小正方形有8+15+15+16=54个,其中部分有6+6+8=20个,部分有6+6+8=20(个),而1个 和1个 正好组成一个完整的小正方形,所以阴影部分共包含54+20=74(个)完整小正方形,而整个方格纸包含8⨯18=144(个)完整小正方形.所以图中阴影面积占整个方格纸面积的74144,即3772.【答案】3772【巩固】在4×7的方格纸板上面有如阴影所示的”6”字,阴影边缘是线段或圆弧.问阴影面积占纸板面积的几分之几?【考点】圆与扇形 【难度】3星 【题型】解答 【解析】 矩形纸板共28个小正方格,其中弧线都是14圆周,非阴影部分有3个完整的小正方形,其余部分可拼成6个小正方格.因此阴影部分共28-6-3=19个小正方格.所以,阴影面积占纸板面积的1928.【答案】1928【例 6】 在一个边长为2厘米的正方形内,分别以它的三条边为直径向内作三个半圆,则图中阴影部分的面积为 平方厘米.【考点】圆与扇形 【难度】3星 【题型】填空 【关键词】西城实验 【解析】 采用割补法.如果将阴影半圆中的2个弓形移到下面的等腰直角三角形中,那么就形成两个相同的等腰直角三角形,所以阴影部分的面积等于两个等腰直角三角形的面积和,即正方形面积的一半,所以阴影部分的面积等于21222⨯=平方厘米.【答案】2【巩固】如图,在一个边长为4的正方形内,以正方形的三条边为直径向内作三个半圆.求阴影部分的面积.【考点】圆与扇形 【难度】3星 【题型】解答 【解析】 阴影部分经过切割平移变成了一个面积为正方形一半的长方形,则阴影部分面积为 4428⨯÷=. 【答案】8【例 7】 如图,正方形边长为1,正方形的4个顶点和4条边分别为4个圆的圆心和半径,求阴影部分面积.(π取3.14)【考点】圆与扇形 【难度】4星 【题型】解答 【关键词】人大附中,分班考试 【解析】 把中间正方形里面的4个小阴影向外平移,得到如右图所示的图形,可见,阴影部分的面积等于四个正方形面积与四个90︒的扇形的面积之和,所以,221444441π14π7.14S S S S S =⨯+⨯=⨯+=⨯+⨯=+=圆阴影圆.【答案】7.14【例 8】 图中的4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?【考点】圆与扇形 【难度】4星 【题型】解答 【解析】 如下图所示:可以将每个圆内的阴影部分拼成一个正方形,每个正方形的面积为11240.542⨯÷⨯=⨯=()(平方厘米),所以阴影部分的总面积为248⨯=(平方厘米).【答案】8【巩固】如图所示,四个全等的圆每个半径均为2m ,阴影部分的面积是 .或【考点】圆与扇形 【难度】3星 【题型】填空 【解析】 我们虽没有学过圆或者圆弧的面积公式,但做一定的割补后我们发现其实我们并不需要知道这些公式也可以求出阴影部分面积.如图,割补后阴影部分的面积与正方形的面积相等,等于222216m ⨯=()().【答案】16【例 9】 如右图,有8个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心.则花瓣图形的面积是多少平方厘米? (π取3)【考点】圆与扇形 【难度】4星 【题型】解答 【解析】 本题直接计算不方便,可以利用分割移动凑成规则图形来求解.如右上图,连接顶角上的4个圆心,可得到一个边长为4的正方形.可以看出,与原图相比,正方形的每一条边上都多了一个半圆,所以可以把原花瓣图形的每个角上分割出一个半圆来补在这些地方,这样得到一个正方形,还剩下4个14圆,合起来恰好是一个圆,所以花瓣图形的面积为224π119+⨯=(平方厘米).【总结】在求不规则图形的面积时,我们一般要对原图进行切割、移动、补齐,使原图变成一个规则的图形,从而利用面积公式进行求解.这个切割、移动、补齐的过程实际上是整个解题过程的关键,我们需要多多练习,这样才能快速找到切割拼补的方法、【答案】19【例 10】 如图中三个圆的半径都是5cm ,三个圆两两相交于圆心.求阴影部分的面积和.(圆周率取3.14)【考点】圆与扇形 【难度】4星 【题型】解答 【解析】 将原图割补成如图,阴影部分正好是一个半圆,面积为255 3.14239.25(cm )⨯⨯÷= 【答案】39.25【巩固】如图,大圆半径为小圆的直径,已知图中阴影部分面积为1S ,空白部分面积为2S ,那么这两个部分的面积之比是多少?(圆周率取3.14)【考点】圆与扇形 【难度】4星 【题型】解答 【解析】 如图添加辅助线,小圆内部的阴影部分可以填到外侧来,这样,空白部分就是一个圆的内接正方形.设大圆半径为r ,则222S r =,221π2S r r =-,所以()12: 3.142:257:100S S =-=. 移动图形是解这种题目的最好方法,一定要找出图形之间的关系.【答案】57:100【例 11】 计算图中阴影部分的面积(单位:分米).A A【考点】圆与扇形 【难度】3星 【题型】解答 【解析】 将右边的扇形向左平移,如图所示.两个阴影部分拼成—个直角梯形. ()5105275237.5+⨯÷=÷=(平方分米). 【答案】37.5【巩固】如图,阴影部分的面积是多少?224【考点】圆与扇形 【难度】3星 【题型】解答 【解析】 首先观察阴影部分,我们发现阴影部分形如一个号角,但是我们并没有学习过如何求号角的面积,那么我们要怎么办呢?阴影部分我们找不到出路,那么我们不妨考虑下除了阴影部分之外的部分吧!观察发现,阴影部分左侧是一个扇形,而阴影部分右边的空白部分恰好与左边的扇形构成一个边长为4的正方形,那么阴影部分的面积就等于大的矩形面积减去正方形面积.则阴影部分面积(222)4(22)48++⨯-+⨯=【答案】8【例 12】 请计算图中阴影部分的面积.【考点】圆与扇形 【难度】4星 【题型】解答 【解析】 法一:为了求得阴影部分的面积,可以从下图的整体面积中扣掉一个圆的面积,就是要求的面积了.=-要扣掉圆的面积,如果按照下图把圆切成两半后,从两端去扣掉也是一样.如此一来,就会出现一个长方形的面积.半圆半圆-=因此,所求的面积为210330cm ⨯=(). 法二:由于原来的月牙形很难直接计算,我们可以尝试构造下面的辅助图形:如左上图所示,我们也可以这样来思考,让图形往右侧平移3cm 就会得到右上图中的组合图形,而这个组合图形中右端的月牙形正是我们要求的面积.显然图中右侧延伸出了多少面积,左侧就会缩进多少面积. 因此,所求的面积是210330cm ⨯=(). 【答案】30【例 13】 求图中阴影部分的面积.12C B12CB 【考点】圆与扇形 【难度】3星 【题型】解答【解析】 如图,连接BD ,可知阴影部分的面积与三角形BCD 的面积相等,即为1112123622⨯⨯⨯=.【答案】36【例 14】 求如图中阴影部分的面积.(圆周率取3.14)【考点】圆与扇形 【难度】2星 【题型】解答 【解析】 可将左下橄榄型的阴影部分剖开,两部分分别顺逆时针90︒,则阴影部分转化为四分之一圆减去一个等腰直角三角形,所以阴影部分的面积为211π444 4.5642⨯⨯-⨯⨯=.【答案】4.56【巩固】如图,四分之一大圆的半径为7,求阴影部分的面积,其中圆周率π取近似值227.【考点】圆与扇形 【难度】3星 【题型】解答【解析】 原题图中的左边部分可以割补至如右上图位置,这样只用先求出四分之一大圆的面积,再减去其内的等腰直角三角形面积即为所求.因为四分之一大圆的半径为7,所以其面积为: 2211227π738.5447⨯⨯≈⨯⨯=. 四分之一大圆内的等腰直角三角形ABC 的面积为17724.52⨯⨯=,所以阴影部分的面积为38.524.514-=. 【答案,14【例 15】 求下列各图中阴影部分的面积.(1)1010(2)ba【考点】圆与扇形 【难度】3星 【题型】解答 【解析】 在图(1)中,阴影部分经过切割平移变成了一个底为10,高为5的三角形,利用三角形面积公式可以求得110102522S =⨯⨯=阴影;在图(2)中,阴影部分经过切割平移变成了一个长为b ,宽为a 的长方形,利用长方形面积公式可以求得S a b ab =⨯=阴影. 【答案】25,ab【巩固】求下列各图中阴影部分的面积(图中长度单位为cm ,圆周率按3计算):⑴3⑵4⑶111⑷2⑸2⑹【考点】圆与扇形 【难度】3星 【题型】解答 【解析】 ⑴4.5 ⑵4 ⑶1 ⑷2 ⑸1.5 ⑹4.5 【答案】⑴4.5 ⑵4 ⑶1 ⑷2 ⑸1.5 ⑹4.5【例 16】 如图,ABCD 是正方形,且1FA AD DE ===,求阴影部分的面积.(取π3=)【考点】圆与扇形 【难度】3星 【题型】解答 【解析】 方法一:两个分割开的阴影部分给我们求面积造成了很大的麻烦,那么我们把它们通过切割、移动、补齐,使两块阴影部分连接在一起,这个时候我们再来考虑,可能会有新的发现. 由于对称性,我们可以发现,弓形BMF 的面积和弓形BND 的面积是相等的,因此,阴影部分面积就等于不规则图形BDWC 的面积.因为ABCD 是正方形,且F A =AD =DE =1,则有CD =DE .那么四边形BDEC 为平行四边形,且∠E =45°.我们再在平行四边形BDEC 中来讨论,可以发现不规则图形BDWC 和扇形WDE 共同构成这个平行四边形,由此,我们可以知道阴影部分面积=平行四边形BDEC -扇形DEW 245511π13608=⨯-⨯⨯=.方法二:先看总的面积为14的圆,加上一个正方形,加上一个等腰直角三角形,在则阴影面积为总面积扣除一个等腰直角三角形,一个14圆,一个45︒的扇形.那么最终效果等于一个正方形扣除一个45︒的扇形.面积为215113188⨯-⨯⨯=.【答案】58【巩固】求图中阴影部分的面积(单位:cm ).2【考点】圆与扇形 【难度】2星 【题型】解答 【解析】 从图中可以看出,两部分阴影的面积之和恰好是梯形的面积,所以阴影部分面积为21(24)39cm 2⨯+⨯=.【答案】9【例 17】 如图,长方形ABCD 的长是8cm ,则阴影部分的面积是 2cm .(π 3.14=)【考点】圆与扇形 【难度】2星 【题型】填空 【解析】 阴影部分的面积实际上是右上图阴影部分面积的一半,所以求出右上图中阴影部分面积再除以2即可.长方形的长等于两个圆直径,宽等于1个圆直径,所以右图的阴影部分的面积等于:()2882822π2 6.88⨯÷-÷÷⨯⨯=所以左图阴影部分的面积等于6.882 3.44÷=平方厘米.【答案】3.44【例 18】 如图所示,在半径为4cm 的图中有两条互相垂直的线段,阴影部分面积A 与其它部分面积B 之差(大减小)是 2cm .【考点】圆与扇形 【难度】3星 【题型】填空 【关键词】西城实验,期末考试 【解析】 如图,将圆对称分割后,B 与A 中的部分区域能对应,B 仅比A 少了一块矩形,所以两部分的面积差为:()()222128cm ⨯⨯⨯=.【答案】8【巩固】一块圆形稀有金属板平分给甲、乙二人.但此金属板事先已被两条互相垂直的弦切割成如图所示尺寸的四块.现甲取②、③两块,乙取①、④两块.如果这种金属板每平方厘米价值1000元,问:甲应偿付给乙多少元?5cm 7.5cm3cm 2cm ④③②①【考点】圆与扇形 【难度】3星 【题型】解答 【解析】 如右上图所示,④的面积与Ⅰ的面积相等,①的面积等于②与Ⅱ的面积之和.可见甲比乙多拿的部分为中间的长方形,所以甲比乙多拿的面积为:2537.522 5.511cm -⨯-=⨯=()()(),而原本应是两人平分,所以甲应付给乙:11100055002⨯=(元).【答案】5500【例 19】 求右图中阴影部分的面积.(π取3)【考点】圆与扇形【难度】3星【题型】解答【解析】看到这道题,一下就会知道解决方法就是求出空白部分的面积,再通过作差来求出阴影部分面积,因为阴影部分非常不规则,无法入手.这样,平移和旋转就成了我们首选的方法.(法1)我们只用将两个半径为10厘米的四分之一圆减去空白的①、②部分面积之和即可,其中①、②面积相等.易知①、②部分均是等腰直角三角形,但是①部分的直角边AB的长度未知.单独求①部分面积不易,于是我们将①、②部分平移至一起,如右下图所示,则①、②部分变为一个以AC 为直角边的等腰直角三角形,而AC为四分之一圆的半径,所以有AC=10.两个四分之一圆的面积和为150,而①、②部分的面积和为11010502⨯⨯=,所以阴影部分的面积为15050100-=(平方厘米).(法2)欲求图①中阴影部分的面积,可将左半图形绕B点逆时针方向旋转180°,使A与C重合,从而构成如右图②的样子,此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.所以阴影部分面积为21110101010022π⨯⨯-⨯⨯=(平方厘米).A【答案】100【例20】如图,边长为3的两个正方形BDKE、正方形DCFK并排放置,以BC为边向内侧作等边三角形,分别以B、C为圆心,BK、CK为半径画弧.求阴影部分面积.(π 3.14=)EE【考点】圆与扇形【难度】4星【题型】解答【关键词】走美,决赛【解析】根据题意可知扇形的半径r恰是正方形的对角线,所以223218r=⨯=,如右图将左边的阴影翻转右边阴影下部,S S S=-阴影扇形柳叶1118π2(18π33)34=⨯-⨯-⨯183π8.58=-=【答案】8.58。
