控制工程基础第二版课后复习题答案
机械控制工程基础第二版课后答案

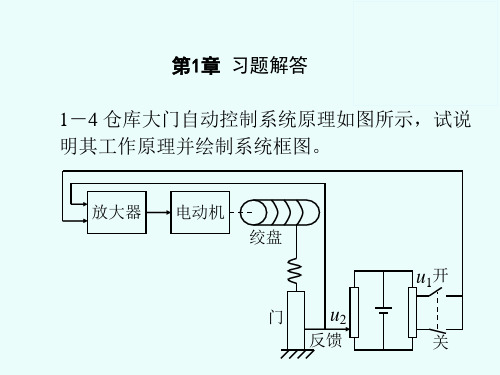
机械控制工程基础第二版课后答案【篇一:《控制工程基础》王积伟_第二版_课后习题解答(完整)】解:1)工作原理:电压u2反映大门的实际位置,电压u1由开(关)门开关的指令状态决定,两电压之差△u=u1-u2驱动伺服电动机,进而通过传动装置控制大门的开启。
当大门在打开位置,u2=u上:如合上开门开关,u1=u上,△u=0,大门不动作;如合上关门开关,u1=u下,△u0,大门逐渐关闭,直至完全关闭,使△u=0。
当大门在关闭位置,u2=u下:如合上开门开关,u1=u上,△u0,大门执行开门指令,直至完全打开,使△u=0;如合上关门开关,u1=u下,△u=0,大门不动作。
2)控制系统方框图4解:1)控制系统方框图2)工作原理:a)水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球顶杆的长度给定,杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),通过杠杆机构是进水阀的开度增大(减小),进入水箱的水流量增加(减小),水位升高(降低),浮球也随之升高(降低),进水阀开度增大(减小)量减小,直至达到新的水位平衡。
此为连续控制系统。
b) 水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球拉杆的长度给定。
杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),到一定程度后,在浮球拉杆的带动下,电磁阀开关被闭合(断开),进水阀门完全打开(关闭),开始进水(断水),水位升高(降低),浮球也随之升高(降低),直至达到给定的水位高度。
随后水位进一步发生升高(降低),到一定程度后,电磁阀又发生一次打开(闭合)。
此系统是离散控制系统。
2-1解:(c)确定输入输出变量(u1,u2)u1?i1r1?i2r2u2?i2r2u1?u2?1c?(idt2?i1)dt得到:cr2du2?(1?r2r1)u2?cr2du1dt?r2r1u1一阶微分方程(e)确定输入输出变量(u1,u2)u1?ir1?ir2? i? u1?u2r1c?idt消去i得到:(r1?r2)一阶微分方程du2dt?u2c?r2du1dt?u1c第二章2-2解:1)确定输入、输出变量f(t)、x2f(t)?fk1(t)?fb1(t)?fb3(t)?m1fb3?f?f?m2dx2(t)dtdx1dt22dx1(t)dt222)对各元件列微分方程:k2b2fk1?k1x1;fb1?b1fb3?b3d(x1?x2)dt;fk2?k2x223)拉氏变换:f(s)?k1x1(s)?b1sx1(s)?b3s[x1(s)?x2(s)]?m1sx1(s)b3s[x1(s)?x2( s)]?k2x2(s)?b2sx2(s)?m2sx2(s)24)消去中间变量:f(s)?b3sx2(s)?(b1s?k1?b3s?m1s)2b3s?k2?b3s?m2sb3s2x2(s)5)拉氏反变换:m1m2dx2dt44?(b1m2?b2m1?bsm2?b3m1)dx2dtdx2dt33?(b1b3?b1b2?bsb2?k1m2?m1k2)dfdtdx2dt22?(k1b2?k1b3?k2b1?k2b3)?k1k2x2?b32-3 解:(2)2s?1?1s?22e?t?e?2t (4)199s?4e?4t?19119s?1?t?1123(s?1)?t?e?13te1(s?1)2(5)?2(s?2)?2(s?1)??2e?2t?2e?t?te?t (6)?0.25?2ss?42?0.5?2?2s?42?2s?1?2.5s?t?0.5cos2t?sin2t?2e?2.52-5解:1)d(s)=0,得到极点:0,0,-2,-5m(s)=0,得到零点:-1,??,??,?? 2) d(s)=0,得到极点:-2,-1,-2 m(s)=0,得到零点:0,0,-1 3) d(s)=0,得到极点:0, ?1?j3,?1?j32m(s)=0,得到零点:-2,??,??4) d(s)=0,得到极点:-1,-2,?? m(s)=0,得到零点:??2-8解:1)a)建立微分方程??mx(t)?f(t)?fk1(t)?fk2(t)f(t)?abfi(t)fk1(t)?k1x0(t)fk2(t)?k2(x0(t)?x(t))fk2(t)?fb(t)?bdx(t)dtb)拉氏变换msx0(s)?f(s)?ff(s)?abfi(s)2k1(s)?fk2(s)fk1(s)?k1x0(s)fk2(s)?k2(x0(s)?x(s))fk2(s)?bsx(s)c)画单元框图(略)d)画系统框图??mx0(t)?fk(t)?fb1(t)?fb2(t)fk(t)?k(xi(t)?x0(t))2)a)建立微分方程:fb1(t)?b1fb2(t)?b2d(xi(t)?xo(t))dtdxo(t)dtmsxo(s)?fk(s)?fb1(s)?fb2(s)2b)拉氏变换:fk(s)?k(xi(s)?xo(s))fb1(s)?b1s(xi(s)?xo(s))fb2(s)?b2sx0(s)c)绘制单元方框图(略)4)绘制系统框图【篇二:机械工程控制基础第二版答案】p> 234【篇三:2机械控制工程基础第二章答案】是线性系统?其最重要的特性是什么?下列用微分方程表示的系统中,xo表示系统输出,xi表示系统输入,哪些是线性系统? (1) ??o?2x (3) ??o?2x??2x?2x (2) ???2x??2tx?2x xxxoooioooi??2x?2x(4) ???2xx??2tx?2x xxooiooooi解: 凡是能用线性微分方程描述的系统就是线性系统。
《控制工程基础》第二版 (董景新 著)课后习题答案 清华出版社

Xi
G1 G2
1+G1 H1+ G2 H2 +G1G2 H3 +G1G2H1H2 )
X0
G (s) =
G 1G 2 1 + G 1 H 1 + G 2 H 2 + G 1G 2 H 3 + G 1G 2 H 1 H 2
第二章习题解
2-7: 求X0(s) 和Xi2(s) (s)之间的闭环传递函数; 求X0(s) 和Xi1(s (s)之间的闭环传递函数;
G (s) =
G1G 2G 3G 4G 5 H 1 1 + G 4 + G1G 2 + G1G 2G 4 − G1G 4G 5 H 1H 2
第二章习题解
4):求出
X 02 ( s ) X i1 ( s )
-
解:第一步,方框图整理
-
G2 G1
Xi1 +
+
+
①
H2 H1
+
② G4 ③
X02 G5 G6
( g )解:设中间变量 : xa (t ) Q k ′ = (Ds + k1 )
x 0(t) k1 k2 m x a(t) (t)
(t) fi(t)
k ′x0 (t ) = k 2 [xa (t ) − x0 (t )] k ′ + k2 D x0 (t ) ∴ xa (t ) = k2 x 又:f i (t ) = m&&a (t ) + k 2 [xa (t ) − x0 (t )] k2 ∴ G (s ) = mDs 3 + m(k1 + k 2 )s 2 + k 2 Ds + k1k 2
控制工程基础第二版(徐立)课后习题答案整理版

二到四章答案2-1试建立题2-1图所示各系统的微分方程[其中外力的),位移x(f)和电压为输入量;位移y⑺和电压顽)为输出量;k(弹性系数),"(阻尼系数),R(电阻),C(电容)和m(质量)均为常数]。
////////m/(O M(a)题2-1图系统原理图解:2-l(a)取质量m为受力对象,如图,取向下为力和位移的正方向。
作用在质量块m上的力有外力f(t),重力mg,这两个力向下,为正。
有弹簧恢复力4X0+Jo]和阻尼力〃也也,这两个力向上,为负。
其中,光为at扣)=0、物体处于静平衡位置时弹簧的预伸长量。
A A dtmv v7(0哗根据牛顿第二定理£F=ma,有f(t)+mg一灯yQ)+为]—#«')=/花』,?)其中:mg=ky0代入上式得f(t)-ky(f)-r顿')=m"半)at dt整理成标准式:d2y(t)dyit)...…..m-—以—ky(t)=/(0dt dt或也可写成:H顷)~dT m at m m它是一个二阶线性定常微分方程。
2-l(b)如图,取A点为辅助质点,设该点位移为x A(t),方向如图。
再取B点也为辅助质点,则该点位移即为输出量X0,方向如图A 点力平衡方程:4M 。
一%“)] = //[竺史一¥]at atB 点力平衡方程:k 2y(t}= 〃[也也—也£1]dt dt由①和②:^[%(z)-x A (O] = k 2y(t}得:xA (t) = x(t)-^y(t)二边微分,办a ") _办⑺ *2 ©(,)dt将③代入②:①dt 、 dt整理成标准式:k 、+ k 2 dy(t) * k 2 y(Q _ dx(t)k 、 dt 〃 dt或也可写成:dy(t)工 k x k 2+ ,,仰)=灯如)dt /u(k\ + 幻) k x +k 2 dt它是一个一阶线性定常微分方程。
控制工程基础课后习题解答
(R1
R2
)C
d dt
uo
(t
)
uo
(t
)
R2C
d dt
ui
(t
)
ui
(t)
xi
xo
K1 K2 B f)
K1(
xi
xo
)
K2
(
xo
x)
B
dx dt
(K1
K2)B
d dt
xo
(t)
K1K 2 xo
(t)
K1B
d dt
xi
(t)
K1K 2 xi
(t)
易见:a)与b)、c)与d)、e)与f)为相似系统。
第2章 习题解答
dx2 dt
B2
dx2 dt
K 2 x2
m2
d 2x2 dt 2
第2章 习题解答
m1m2
d 4x2 dt 4
(m1B2
m1B3
m2 B1
m2 B3 )
d 3x2 dt3
(m1K2
m2 K1
B1B2
B1B3
B2 B3 )
d 2x2 dt 2
( K1B2
K1B3
K 2 B1
K 2 B3 )
dx2 dt
故:G2 (s)
X o (s) Xi (s)
(B1s K1)(B2s K2 ) (B2s K2 )(B1s K1) K1B1s
B1 K1 s 1 B2 K2 s 1
B1 K1 s 1 B2 K2 s 1 B1 K2 s
显然:两系统具有相同形式的传递函数。
第2章 习题解答
2-8 按信息传递和转换过程,绘出图示两机械系 统的方框图。
机械控制工程基础第二版课后答案

机械控制工程基础第二版课后答案机械控制工程基础第二版课后答案【篇一:《控制工程基础》王积伟_第二版_课后习题解答(完整)】解:1)工作原理:电压u2反映大门的实际位置,电压u1由开(关)门开关的指令状态决定,两电压之差△u=u1-u2驱动伺服电动机,进而通过传动装置控制大门的开启。
当大门在打开位置,u2=u 上:如合上开门开关,u1=u上,△u=0,大门不动作;如合上关门开关,u1=u下,△u0,大门逐渐关闭,直至完全关闭,使△u=0。
当大门在关闭位置,u2=u下:如合上开门开关,u1=u上,△u0,大门执行开门指令,直至完全打开,使△u=0;如合上关门开关,u1=u下,△u=0,大门不动作。
2)控制系统方框图4解:1)控制系统方框图2)工作原理:a)水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球顶杆的长度给定,杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),通过杠杆机构是进水阀的开度增大(减小),进入水箱的水流量增加(减小),水位升高(降低),浮球也随之升高(降低),进水阀开度增大(减小)量减小,直至达到新的水位平衡。
此为连续控制系统。
b) 水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球拉杆的长度给定。
杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),到一定程度后,在浮球拉杆的带动下,电磁阀开关被闭合(断开),进水阀门完全打开(关闭),开始进水(断水),水位升高(降低),浮球也随之升高(降低),直至达到给定的水位高度。
随后水位进一步发生升高(降低),到一定程度后,电磁阀又发生一次打开(闭合)。
此系统是离散控制系统。
2-1解:(c)确定输入输出变量(u1,u2)u1?i1r1?i2r2u2?i2r2u1?u2?1c(idt2i1)dt得到:cr2du2(1?r2r1)u2?cr2du1dtr2r1u1一阶微分方程(e)确定输入输出变量(u1,u2)u1?ir1?ir2? i? u1?u2r1cidt消去i得到:(r1?r2)一阶微分方程du2dtu2cr2du1dtu1c第二章2-2解:1)确定输入、输出变量f(t)、x2 f(t)?fk1(t)?fb1(t)?fb3(t)?m1fb3?f fm2dx2(t)dtdx1dt22dx1(t)dt222)对各元件列微分方程:k2b2fk1?k1x1;fb1?b1fb3?b3d(x1?x2)dt;fk2?k2x223)拉氏变换:f(s)?k1x1(s)?b1sx1(s)?b3s[x1(s)?x2(s)]?m1sx1(s)b3s[x1(s)?x2( s)]?k2x2(s)?b2sx2(s)?m2sx2(s)24)消去中间变量:f(s)?b3sx2(s)?(b1s?k1?b3s?m1s)2b3s?k2?b3s?m2sb3s2x2(s)5)拉氏反变换:m1m2dx2dt44(b1m2?b2m1?bsm2?b3m1)dx2dtdx2dt33(b1b3?b1b2?bsb2?k1m2?m1k2)dfdtdx2dt22(k1b2?k1b3?k2b1?k2b3)?k1k2x2?b32-3 解:(2)2s?11s?22e?t?e?2t (4)199s?4e4t19119s?1t1123(s?1)te?13te1(s?1)2(5)?2(s?2)2(s?1)2e?2t?2e?t?te?t (6)0.25?2ss?420.5?2?2s?422s?12.5st0.5cos2t?sin2t?2e?2.52-5解:1)d(s)=0,得到极点:0,0,-2,-5m(s)=0,得到零点:-1,??,??,?? 2) d(s)=0,得到极点:-2,-1,-2 m(s)=0,得到零点:0,0,-1 3) d(s)=0,得到极点:0, ?1?j3,1?j32m(s)=0,得到零点:-2,??,??4) d(s)=0,得到极点:-1,-2,?? m(s)=0,得到零点:??2-8解:1)a)建立微分方程mx(t)?f(t)?fk1(t)?fk2(t)f(t)?abfi(t)fk1(t)?k1x0(t)fk2(t)?k2(x0(t)?x(t))fk2(t)?fb(t)?bdx(t)dtb)拉氏变换msx0(s)?f(s)?ff(s)?abfi(s)2k1(s)?fk2(s)fk1(s)?k1x0(s)fk2(s)?k2(x0(s)?x(s))fk2(s)?bsx(s)c)画单元框图(略)d)画系统框图mx0(t)?fk(t)?fb1(t)?fb2(t)fk(t)?k(xi(t)?x0(t))2)a)建立微分方程:fb1(t)?b1fb2(t)?b2d(xi(t)?xo(t))dtdxo(t)dtmsxo(s)?fk(s)?fb1(s)?fb2(s)2b)拉氏变换:fk(s)?k(xi(s)?xo(s))fb1(s)?b1s(xi(s)?xo(s))fb2(s)?b2sx0(s)c)绘制单元方框图(略)4)绘制系统框图【篇二:机械工程控制基础第二版答案】p> 234【篇三:2机械控制工程基础第二章答案】是线性系统?其最重要的特性是什么?下列用微分方程表示的系统中,xo表示系统输出,xi表示系统输入,哪些是线性系统? (1) ??o?2x (3) ??o?2x2x?2x (2) 2x??2tx?2x xxxoooioooi2x?2x(4) 2xx??2tx?2x xxooiooooi解: 凡是能用线性微分方程描述的系统就是线性系统。
《控制工程基础》参考复习题及答案

】 】
7.闭环系统前向传递函数是【 】 A.输出信号的拉氏变换与输入信号的拉氏变换之比 B.输入信号的拉氏变换与输出信号的拉氏变换之比 C.输出信号的拉氏变换与误差信号的拉氏变换之比 D.误差信号的拉氏变换与输出信号的拉氏变换之比 8.一阶系统的时间常数为 T,其脉冲响应为【 】 A. 1 e
t T
B. t T Te
t
T
C.
1 tT e T
】
D. T Te
t
T
8-1.一阶系统的时间常数为 T,其单位阶跃响应为【 A. 1 e
t T
B. t T Te
t
T
C.
1 tT e T
】
D. T Te
t
T
8-2.一阶系统的时间常数为 T,其单位斜坡响应为【 A. 1 e
D.线性控制系统
A.2 B.1 C.0 D. 不确定 28.一阶系统的单位阶跃响应在 t=0 处的斜率越大,系统的【 】 A.响应速度越快 B.响应速度越慢 C.响应速度不变 D.响应速度趋于零 29.临界阻尼二阶系统的单位阶跃稳态响应为【 】 A.零 B.常数 C.单调上升曲线 D.等幅衰减曲线 30.欠阻尼二阶系统的输出信号振幅的衰减速度取决于【 】 A. n B. C. g 】 D. D. c
t T
B. t T Te
t
T
C.
1 tT e T
t T
D. T Te
t
T
8-3.一阶系统的时间常数为 T,其单位阶跃响应的稳态误差为【 A.0 B. T C.
】
1 T 1 T
D. T Te
8-4.一阶系统的时间常数为 T,其单位斜坡响应的稳态误差为【 A.0 B. T C. D. T Te
《控制工程基础》第二版课后习题答案
第一章习题解笞U]>U2 U\ U2第二章习题解答2-1a) b)d)f)L^f| 忙d)f\ — fl =^2X O严(f)=$(M+E ⑴虑 如(f) =iQ)RRC^-u o (t)^u o (t) = RC^-u^t) at at fs (r)=B 低[xi (f) -曲(幼 j/B (t)=fK (t) = KXo(t) B dB d 『八10602斤不%()+%©二斤击可()占dR^c —% (0+ (*i + 心)% ⑴=邛应 ~u i (0+ R 2u t (0 atati =i R +,C u o =IR?:R R 严冃3宙 % =gR\ +u oa)=K ](旳一兀)+」:dx o ](J?l + J?2)C —«c (!)+ %("■ R Q C — Wj(O + tti (Oat at(K[ + K2)B — x o (t)+ K\K2X o (t)= K\R 〒曲(f)+ 琦心再(f)dt at10602a) b) c) Q © f)U Q —1/?2 + — j icit— Z/?| + iR-f H —J idte)dxK\% K i (兀 _ %) = K 》(兀)—x)=号二dtoB 2+ (®K° ++ B'B? + 场*3 + 水2〃?)& 2+ (K }B 2+K }B 3 + 心汝 + KM 巴2 + K }K 2X 2 dt3J S + 2用 + 8S-丘($ + 2)($戈+2$十4)广、■炉+ 5,2+9用+7E ($+恥 + 2)乡一rn\fU2K 2rdx { dx 2< dt dt ;/(O™-坷罕~_叭 dtdxj … 一 —- - K?x^ = m dtdx l dx 2dt dt护d 2x 2 2~d^ k,用典2+ (的+创坷+用2创+加2*3);?7皿乔对)13173 G($)= --------------- —(£+。
控制工程基础(第二版)答案_董景新_赵长德等pdf

Ms 2 X o (s) = k1 X o ( s) + D1sX o ( s) + k 2 ( X o ( s) − X i (s)) + D2 (sX o ( s) − sX i (s))
(b).根据力平衡方程,直接列写系统的方程 k1 Ds ( X i ( s) − X o (s)) = k2 X o ( s) k1 + Ds
(0) = 1, x(0) = 0 带入得: 将已知条件 x
对上式进行拉氏反变换的微分方程的解:
x(t ) =
1 7 −2t 7 −4 t + e − e 8 4 8
2-9 试求机械系统的传递函数 参考答案: (a). 根据牛顿定律,列写系统微分方程为:
进行拉氏变换得:
ms 2Yo ( s ) = f i − k1Yo ( s ) o − k 2 Yo ( s ) − DsYo ( s )
X (s) =
1 s
s 2 + 6s + 1 s ( s 2 + 6 s + 8) 1 7 = − 2 s s ( s + 6s + 8) = 1 ⎛1 1 1 1 1 1 ⎞ − 7⎜ ⋅ − ⋅ + ⋅ ⎟ s ⎝8 s 4 s + 2 8 s + 4⎠ 1 1 7 1 7 1 = ⋅ + ⋅ − ⋅ 8 s 4 s+2 8 s+4
整理得: X o (s) D1s D1 = = 2 X i ( s ) ms + ( D1 + D2 ) s ms + ( D1 + D2 )
(f). 根据牛顿定律,列写系统微分方程为:
o = k1 xo + D1 x o + k 2 ( xo − xi ) + D2 ( x o − x i ) M x
《控制工程基础》参考复习题及答案

《控制工程基础》参考复习题及习题解答第一部分 单项选择题1.闭环控制系统的主反馈取自【 D 】A.给定输入端B.干扰输入端C.控制器输出端D.系统输出端2.不同属性的物理系统可以有形式相同的【 A 】A.数学模型B.被控对象C.被控参量D.结构参数3.闭环控制系统的开环传递函数为G(s)H(s),其中H(s)是反馈传递函数,则系统的误差信号为【 A 】A.X i (s )-H (s)X 0(s )B.X i (s )-X 0(s )C.X or (s )-X 0(s )D.X or (s )-H (s )X 0(s )3-1闭环控制系统的开环传递函数为G(s)H(s),其中H(s)是反馈传递函数,则系统的偏差信号为【 A 】A.X i (s )-H (s)X 0(s )B.X i (s )-X 0(s )C.X or (s )-X 0(s )D.X or (s )-H (s )X 0(s )4.微分环节使系统【 A 】A.输出提前B.输出滞后C.输出大于输入D.输出小于输入5.当输入量发生突变时,惯性环节的输出量不能突变,只能按【 B 】A.正弦曲线变化B.指数曲线变化C.斜坡曲线变化D.加速度曲线变化6.PID 调节器的微分部分可以【 A 】A.提高系统的快速响应性B.提高系统的稳态性C.降低系统的快速响应性D.降低系统的稳态性6-1.PID 调节器的微分部分可以【 A 】A.提高系统的稳定性B.提高系统的稳态性C.降低系统的稳定性D.降低系统的稳态性7.闭环系统前向传递函数是【 C 】A.输出信号的拉氏变换与输入信号的拉氏变换之比B.输入信号的拉氏变换与输出信号的拉氏变换之比C.输出信号的拉氏变换与误差信号的拉氏变换之比D.误差信号的拉氏变换与输出信号的拉氏变换之比8.一阶系统的时间常数为T ,其脉冲响应为【 C 】 A.T t e --1 B.T t Te T t -+- C.T t e T-1 D.T t Te T -+ 8-1.一阶系统的时间常数为T ,其单位阶跃响应为【 C 】 A.T t e --1 B.T t Te T t -+- C.T t e T-1 D.T t Te T -+ 8-2.一阶系统的时间常数为T ,其单位斜坡响应为【 C 】 A.T t e --1 B.T t Te T t -+- C.T t e T-1 D.T t Te T -+ 8-3.一阶系统的时间常数为T ,其单位阶跃响应的稳态误差为【C 】A.0B.TC.1TD.T t Te T -+ 8-4.一阶系统的时间常数为T ,其单位斜坡响应的稳态误差为【 C 】A.0B.TC.1TD.T t Te T -+ 9.过阻尼二阶系统的单位阶跃稳态响应为【 】A.零B.常数C.单调上升曲线D.等幅衰减曲线10.干扰作用下,偏离原来平衡状态的稳定系统在干扰作用消失后【 】A.将发散离开原来的平衡状态B.将衰减收敛回原来的平衡状态C.将在原平衡状态处等幅振荡D.将在偏离平衡状态处永远振荡11.单位脉冲函数的拉普拉斯变换是【 】 A.1/s B.1 C. 21s D.1+1/s12.线性控制系统的频率响应是系统对输入【 】A.阶跃信号的稳态响应B.脉冲信号的稳态响应C.斜坡信号的稳态响应D.正弦信号的稳态响应13.积分环节的输出比输入滞后【 】A.090-B.090C.0180-D.018014.奈魁斯特围线中所包围系统开环传递函数)(s G 的极点数为3个,系统闭环传递函数的极点数为2个,则映射到)(s G 复平面上的奈魁斯特曲线将【 】A.逆时针围绕点(0,j0)1圈B.顺时针围绕点(0,j0)1圈C.逆时针围绕点(-1,j0)1圈D.顺时针围绕点(-1,j0)1圈15.最小相位系统稳定的条件是【 】A.γ>0和g L <0B.γ<0和g K >1C.γ>0和)(g L ω<0D.γ<0和)(g L ω>016.若惯性环节的时间常数为T ,则将使系统的相位【 】A.滞后1tan ()T ω-B.滞后1tan ω--C.超前1tan ()T ω-D.超前1tan ω-- 17.控制系统的误差是【 】A.期望输出与实际输出之差B.给定输入与实际输出之差C.瞬态输出与稳态输出之差D.扰动输入与实际输出之差18.若闭环系统的特征式与开环传递函数的关系为)()(1)(s H s G s F +=,则【 】A.)(s F 的零点就是系统闭环零点B.)(s F 的零点就是系统开环极点C.)(s F 的极点就是系统开环极点D.)(s F 的极点就是系统闭环极点19.要使自动调速系统实现无静差,则在扰动量作用点的前向通路中应含有【 】A.微分环节B.积分环节C.惯性环节D.比例环节20.积分器的作用是直到输入信号消失为止,其输出量将【 】A.直线上升B.垂直上升C.指数线上升D.保持水平线不变21.自动控制系统的控制调节过程是以偏差消除【 】A.偏差的过程B.输入量的过程C.干扰量的过程D.稳态量的过程22.系统输入输出关系为i o o o x x x x cos =++,则该系统为【 】 A.线性系统 B.非线性系统 C.线性时变系统 D.线性定常系统23.线性定常二阶系统的输出量与输入量之间的关系是【 】A.振荡衰减关系B.比例线性关系C.指数上升关系D.等幅振荡关系24. 微分环节可改善系统的稳定性并能【 】A.增加其固有频率B.减小其固有频率C.增加其阻尼D.减小其阻尼25.用终值定理可求得)8)(5(4)(++=s s s s F 的原函数f (s )的稳态值为【 】 A.∞ B .4 C.0.1 D.026.可以用叠加原理的系统是【 】A.开环控制系统B.闭环控制系统C.离散控制系统D.线性控制系统27.惯性环节含有贮能元件数为【 】A.2B.1C.0D.不确定28.一阶系统的单位阶跃响应在t =0处的斜率越大,系统的【 】A.响应速度越快B.响应速度越慢C.响应速度不变D.响应速度趋于零29.临界阻尼二阶系统的单位阶跃稳态响应为【 】A.零B.常数C.单调上升曲线D.等幅衰减曲线30.欠阻尼二阶系统的输出信号振幅的衰减速度取决于【 】A.n ξωB.ξωC.g ξωD.c ξω31.单位加速度信号的拉氏变换为【 】 A.1 B. s 1 C. 21s D. 31s32.线性系统的输入信号为t t x i ωsin )(=,则其输出信号响应频率为【 】A.ωB.n ωC.ωjD.n j ω33.微分环节的输出比输入超前【 】A.090-B.090C.0180-D.018034.若闭环系统的特征式与开环传递函数的关系为)()(1)(s H s G s F +=,则【 】A.)(s F 的极点就是系统开环零点B.)(s F 的零点就是系统开环极点C.)(s F 的零点就是系统闭环极点D.)(s F 的极点就是系统闭环极点35.系统开环传递函数为)11.0()14.0()(2++=s s s K s G 不用计算或作图,凭思考就能判断该闭环系统的稳定状况是【】A.稳定B.不稳定C.稳定边界D.取决于K 的大小36.为了保证系统有足够的稳定裕量,在设计自动控制系统时应使穿越频率附近)(ωL 的斜率为【 】A.-40 dB/decB.-20 dB/decC.+40 dB/decD.+20 dB/dec37.线性定常系统的偏差信号就是误差信号的条件为【 】A.反馈传递函数H(s)=1B.反馈信号B(s)=1C.开环传递函数G(s) H(s)=1D.前向传递函数G(s)=138.降低系统的增益将使系统的【 】A.稳定性变差B.稳态精度变差C.超调量增大D.稳态精度变好39.含有扰动顺馈补偿的复合控制系统可以显著减小【 】A.超调量B.开环增益C.扰动误差D.累计误差40.PID 调节器的微分部分可以【 】A.改善系统的稳定性B.调节系统的增益C.消除系统的稳态误差D.减小系统的阻尼比41.一般情况下开环控制系统是【 】A.不稳定系统B.稳定系统C.时域系统D.频域系统42.求线性定常系统的传递函数条件是【 】A.稳定条件B.稳态条件C.零初始条件D.瞬态条件43.单位负反馈系统的开环传递函数为G(s),则其闭环系统的前向传递函数与【 】A.反馈传递函数相同B.闭环传递函数相同C.开环传递函数相同D.误差传递函数相同44.微分环节是高通滤波器,将使系统【 】A.增大干扰误差B.减小干扰误差C.增大阶跃输入误差D.减小阶跃输入误差45.控制框图的等效变换原则是变换前后的【 】A.输入量和反馈量保持不变B.输出量和反馈量保持不变C.输入量和干扰量保持不变D.输入量和输出量保持不变46.对于一个确定的系统,它的输入输出传递函数是【 】A.唯一的B.不唯一的C.决定于输入信号的形式D.决定于具体的分析方法47.衡量惯性环节惯性大小的参数是【 】A.固有频率B.阻尼比C.时间常数D.增益系数48.三个一阶系统的时间常数关系为T2<T1<T3,则【 】A.T2系统响应快于T3系统B.T1系统响应快于T2系统C.T2系统响应慢于T1系统D.三个系统响应速度相等49.闭环控制系统的时域性能指标是【 】A.相位裕量B.输入信号频率C.最大超调量D.系统带宽50.输入阶跃信号稳定的系统在输入脉冲信号时【 】A .将变成不稳定系统 B.其稳定性变好 C.其稳定性不变 D.其稳定性变差51.二阶欠阻尼系统的阶跃响应为【 】A.单调上升曲线B.等幅振荡曲线C.衰减振荡曲线D.指数上升曲线52.单位斜坡信号的拉氏变换为【 】 A.1 B.s 1 C.21s D.31s53.线性控制系统【 】A.一定是稳定系统B.是满足叠加原理的系统C.是稳态误差为零的系统D.是不满足叠加原理的系统54.延迟环节Ts e s G -=)(的幅频特性为【 】A.)(ωA =1B.)(ωA =0C.)(ωA <1D.)(ωA >155.闭环系统稳定的充分必要条件是其开环极坐标曲线逆时针围绕点(-1,j0)的圈数等于落在S 平面右半平面的【】 A.闭环极点数 B.闭环零点数 C.开环极点数 D.开环零点数56.频率响应是系统对不同频率正弦输入信号的【 】A.脉冲响应B.阶跃响应C.瞬态响应D.稳态响应57.传递函数的零点和极点均在复平面的左侧的系统为【 】A.非最小相位系统B.最小相位系统C.无差系统D.有差系统58.零型系统跟踪阶跃信号的稳态误差为【 】A.0B.∞C.常数D. )()(lim 0s H s G s→ 59.降低系统的增益将使系统的【 】A.稳定性变差B.快速性变差C.超调量增大D.稳态精度变好60.把系统从一个稳态过渡到新的稳态的偏差称为系统的【 】A.静态误差B.稳态误差C.动态误差D.累计误差61.闭环控制系统除具有开环控制系统所有的环节外,还必须有【 】A.给定环节B.比较环节C.放大环节D.执行环节62.同一系统由于研究目的的不同,可有不同的【 】A.稳定性B.传递函数C.谐波函数D.脉冲函数63.以同等精度元件组成的开环系统和闭环系统其精度比较为【 】A.开环高B.闭环高C.相差不多D.一样高64.积分环节的积分时间常数为T ,其脉冲响应为【 】A.1B.1/TC.TD.1+1/T65.串联环节的对数频率特性为各串联环节的对数频率特性的【 】A.叠加B.相乘C.相除D.相减66.非线性系统的最主要特性是【 】A.能应用叠加原理B.不能应用叠加原理C.能线性化D.不能线性化67.理想微分环节的输出量正比于【 】A.反馈量的微分B.输入量的微分C.反馈量D.输入量68.若二阶系统的阻尼比和固有频率分别为ξ和n ω,则其共轭复数极点的实部为【 】A.n ξωB.n ξω-C.d ξω-D.d ξω69.控制系统的时域稳态响应是时间【 】A.等于零的初值B.趋于零的终值C.变化的过程值D.趋于无穷大时的终值70.一阶系统的时间常数T 越小,系统跟踪斜坡信号的【 】A.稳定性越好B.稳定性越差C.稳态性越好D.稳态性越差71.二阶临界阻尼系统的阶跃响应为【 】A.单调上升曲线B.等幅振荡曲线C.衰减振荡曲线D.指数上升曲线72.线性系统的输入信号为t A t x i ωsin )(=,则其稳态输出响应相位【 】A.等于输入信号相位B.一般为输入信号频率ω的函数C.大于输入信号相位D.小于输入信号相位73.延迟环节Ts es G -=)(的相频特性为【 】 A.T ωωϕ1tan )(--= B.T ωωϕ1tan )(-=C. T ωωϕ=)(D. T ωωϕ-=)(74.Ⅱ型系统的开环传递函数在虚轴上从右侧环绕其极点的无穷小圆弧线所对应的开环极坐标曲线是半径为无穷大,且按顺时针方向旋转【 】A.π2的圆弧线B.πv 的圆弧线C.-π2的圆弧线D.π的圆弧线75.闭环系统稳定的充要条件是系统开环对数幅频特性过零时,对应的相频特性【 】A. 180)(-<c ωϕB. 180)(->c ωϕC. 180)(>c ωϕ 180)(<c ωϕ76.对于二阶系统,加大增益将使系统的【 】A.稳态性变差B.稳定性变差C.瞬态性变差D.快速性变差77.Ⅰ型系统跟踪阶跃信号的稳态误差为【 】A.0B.∞C.常数D. )()(lim 0s H s G s → 78.控制系统含有的积分个数多,开环放大倍数大,则系统的【 】A.稳态性能愈好B.动态性能愈好C.稳定性愈好D.稳态性能愈差79.控制系统的稳态误差主要取决于系统中的【 】A.微分和比例环节B.惯性和比例环节C.比例和积分环节D.比例和延时环节80.比例积分微分(PID)校正对应【 】A.相位不变 B .相位超前校正 C .相位滞后校正 D .相位滞后超前校正81.闭环控制系统必须通过【 】A.输入量前馈参与控制B.干扰量前馈参与控制C.输出量反馈到输入端参与控制D.输出量局部反馈参与控制82.不同属性的物理系统可以有形式相同的【 】A.传递函数B.反函数C.正弦函数D.余弦函数83.输出信号对控制作用有影响的系统为【 】A.开环系统B.闭环系统C.局部反馈系统D.稳定系统84.比例环节能立即地响应【 】A.输出量的变化B.输入量的变化C.误差量的变化D.反馈量的变化85.满足叠加原理的系统是【 】A.定常系统B.非定常系统C.线性系统D.非线性系统86.弹簧-质量-阻尼系统的阻尼力与两相对运动构件的【 】A.相对位移成正比B.相对速度成正比C.相对加速度成正比D.相对作用力成正比87.当系统极点落在复平面S 的虚轴上时,其系统【 】A.阻尼比为0B.阻尼比大于0C.阻尼比小于1大于0D.阻尼比小于088.控制系统的最大超调量【 】A.只与阻尼比有关B.只与固有频率有关C.与阻尼比和固有频率都有关D.与阻尼比和固有频率都无关89.过阻尼的二阶系统与临界阻尼的二阶系统比较,其响应速度【 】A.过阻尼的小于临界阻尼的B.过阻尼的大于临界阻尼的C.过阻尼的等于临界阻尼的D.过阻尼的反比于临界阻尼的90.二阶过阻尼系统的阶跃响应为【 】A.单调衰减曲线B.等幅振荡曲线C.衰减振荡曲线D.指数上升曲线91.一阶系统在时间为T 时刻的单位阶跃响应为【 】A. 1B. 0.98C. 0.95D. 0.63292.线性系统的输出信号完全能复现输入信号时,其幅频特性【 】A.)(ωA ≥1B.)(ωA <1C. 0<)(ωA <1D.)(ωA ≤093.Ⅱ型系统是定义于包含有两个积分环节的【 】A.开环传递函数的系统B.闭环传递函数的系统C.偏差传递函数的系统D.扰动传递函数的系统94.系统的幅值穿越频率是开环极坐标曲线与【 】A.负实轴相交处频率B.单位圆相交处频率C.Bode 图上零分贝线相交处频率D.Bode 图上-180°相位线相交处频率94-1.系统的幅值穿越频率是对数频率特性曲线与【 】A.负实轴相交处频率B.单位圆相交处频率C.Bode 图上零分贝线相交处频率D.Bode 图上-180°相位线相交处频率95.系统的穿越频率越大,则其【 】A.响应越快B.响应越慢C.稳定性越好D.稳定性越差96. 最小相位系统传递函数的【 】A.零点和极点均在复平面的右侧B.零点在复平面的右侧而极点在左侧C.零点在复平面的左侧而极点在右侧D.零点和极点均在复平面的左侧97.Ⅰ型系统能够跟踪斜坡信号,但存在稳态误差,其稳态误差系数等于【 】A.0B.开环放大系数C.∞D.时间常数98.把系统扰动作用后又重新平衡的偏差称为系统的【 】A.静态误差B.稳态误差C.动态误差D.累计误差99.0型系统跟踪斜坡信号的稳态误差为【 】A.0B.∞C.常数D. )()(lim 0s H s G s → 100.PID 调节器的比例部分主要调节系统的【 】A.增益B.固有频率C.阻尼比D.相频特性101.随动系统要求系统的输出信号能跟随【 】A.反馈信号的变化B.干扰信号的变化C.输入信号的变化D.模拟信号的变化102.传递函数的量纲是【 】A.取决于输入与反馈信号的量纲B.取决于输出与输入信号的量纲C.取决于干扰与给定输入信号的量纲D.取决于系统的零点和极点配置103.对于抗干扰能力强系统有【 】A.开环系统B.闭环系统C.线性系统D.非线性系统104.积分调节器的输出量取决于【 】A.干扰量对时间的积累过程B.输入量对时间的积累过程C.反馈量对时间的积累过程D.误差量对时间的积累过程105.理想微分环节的传递函数为【 】 A.Ts+11 B.s 1 C.s D.1+Ts 105.一阶微分环节的传递函数为【 】A.Ts +11B.s 1C.sD.1+Ts106.实际系统传递函数的分母阶次【 】A.小于分子阶次B.等于分子阶次C.大于等于分子阶次D.大于或小于分子阶次107.当系统极点落在复平面S 的负实轴上时,其系统【 】A.阻尼比为0B.阻尼比大于0C.阻尼比大于或等于1D.阻尼比小于0108.欠阻尼二阶系统的输出信号的衰减振荡角频率为【 】A.无阻尼固有频率B.有阻尼固有频率C.幅值穿越频率D.相位穿越频率109.反映系统动态精度的指标是【 】A.超调量B.调整时间C.上升时间D.振荡次数110.典型二阶系统在欠阻尼时的阶跃响应为【 】A.等幅振荡曲线B.衰减振荡曲线C.发散振幅曲线D.单调上升曲线111.一阶系统时间常数为T ,在单位阶跃响应误差范围要求为±0.05时,其调整时间为【】 A.T B.2T C.3T D.4T112.比例环节的输出能不滞后地立即响应输入信号,其相频特性为【 】A.00)(=ωϕB.0180)(-=ωϕC.090)(-=ωϕD.090)(=ωϕ113.实际的物理系统)(s G 的极点映射到)(s G 复平面上为【 】A.坐标原点B.极点C.零点D.无穷远点114.系统的相位穿越频率是开环极坐标曲线与【 】A.负实轴相交处频率B.单位圆相交处频率C.Bode 图上零分贝线相交处频率D.Bode 图上-180°相位线相交处频率114-1.系统的相位穿越频率是对数频率特性曲线与【 】A.负实轴相交处频率B.单位圆相交处频率C.Bode 图上零分贝线相交处频率D.Bode 图上-180°相位线相交处频率115.比例微分环节(时间常数为T )使系统的相位【 】A.滞后1tan T ω-B.滞后1tan ω-C.超前1tan T ω-D.超前1tan ω-116.系统开环频率特性的相位裕量愈大,则系统的稳定性愈好,且【 】A.上升时间愈短B.振荡次数愈多C.最大超调量愈小D.最大超调量愈大117.Ⅱ型系统跟踪阶跃信号的稳态误差为零,其静态位置误差系数等于【 】A.0B.开环放大系数C.∞D.时间常数118.PID 调节器的积分部分消除系统的【 】A.瞬态误差B.干扰误差C.累计误差D.稳态误差119.Ⅰ型系统跟踪斜坡信号的稳态误差为【 】A.0B.∞C.常数D. )()(lim 0s H s G s → 120.比例微分校正将使系统的【 】A.抗干扰能力下降B.抗干扰能力增加C.稳态精度增加D.稳态精度减小120-1.比例微分校正将使系统的【 】A.稳定性变好B.稳态性变好C.抗干扰能力增强D.阻尼比减小121.若反馈信号与原系统输入信号的方向相反则为【 】A.局部反馈B.主反馈C.正反馈D.负反馈122.实际物理系统微分方程中输入输出及其各阶导数项的系数由表征系统固有特性【 】A.结构参数组成B.输入参数组成C.干扰参数组成D.输出参数组成123.对于一般控制系统来说【 】A.开环不振荡B.闭环不振荡C.开环一定振荡D.闭环一定振荡124.积分环节输出量随时间的增长而不断地增加,增长斜率为【 】A.TB.1/TC.1+1/TD.1/T 2125.传递函数只与系统【 】A.自身内部结构参数有关B.输入信号有关C.输出信号有关D.干扰信号有关126.闭环控制系统的开环传递函数是【 】A.输出信号的拉氏变换与输入信号的拉氏变换之比B.输入信号的拉氏变换与输出信号的拉氏变换之比C.反馈信号的拉氏变换与误差信号的拉氏变换之比D.误差信号的拉氏变换与反馈信号的拉氏变换之比127.当系统极点落在复平面S 的Ⅱ或Ⅲ象限内时,其系统【 】A.阻尼比为0B.阻尼比大于0C.阻尼比大于0而小于1D.阻尼比小于0128.欠阻尼二阶系统是【 】A .稳定系统 B. 不稳定系统 C.非最小相位系统 D.Ⅱ型系统129.二阶无阻尼系统的阶跃响应为【 】A.单调上升曲线B.等幅振荡曲线C.衰减振荡曲线D.指数上升曲线130.二阶系统总是【 】A.开环系统B.闭环系统C.稳定系统D.非线性系统131.一阶系统时间常数为T ,在单位阶跃响应误差范围要求为±0.02时,其调整时间为【 】A.TB.2TC.3TD.4T132.积分环节Ts s G 1)(=的幅值穿越频率为【 】 A.T 1 B.-T 1 C. 20T 1lg D. -20T 1lg132-1.微分环节()G s Ts =的幅值穿越频率为【 】 A.T 1B.-T 1C. 20T 1lgD. -20T 1lg132-2.积分环节21()G s Ts =的幅值穿越频率为【 】 A.T 1 B.-T 1133.实际的物理系统)(s G 的零点映射到)(s G 复平面上为【 】A.坐标原点B.极点C.零点D.无穷远点134.判定系统稳定性的穿越概念就是开环极坐标曲线穿过实轴上【 】A.(-∞,0)的区间B.(-∞,0]的区间C.(-∞,-1)的区间D.(-∞,-1]的区间135.控制系统抗扰动的稳态精度是随其前向通道中【 】A.微分个数增加,开环增益增大而愈高B.微分个数减少,开环增益减小而愈高C.积分个数增加,开环增益增大而愈高D.积分个数减少,开环增益减小而愈高136.若系统无开环右极点且其开环极座标曲线只穿越实轴上区间(-1,+∞),则该闭环系统一定【】 A.稳定 B.临界稳定 C. 不稳定 D.不一定稳定137.比例环节的输出能不滞后地立即响应输入信号,其相频特性为【 】A.00)(=ωϕB.0180)(-=ωϕC.090)(-=ωϕD.090)(=ωϕ138.控制系统的跟随误差与前向通道【 】A.积分个数和开环增益有关B.微分个数和开环增益有关C.积分个数和阻尼比有关D.微分个数和阻尼比有关139.Ⅰ型系统跟踪阶跃信号的稳态误差为【 】A.0B.∞C.常数D.)()(lim 0s H s G s→ 140.Ⅱ型系统跟踪斜坡信号的稳态误差为零,其静态位置误差系数等于【 】A.0B.开环放大系数C. ∞D.时间常数141.实际物理系统的微分方程中输入输出及其各阶导数项的系数由表征系统固有特性【 】A.特征参数组成B.输入参数组成C.干扰参数组成D.输出参数组成142.输出量对系统的控制作用没有影响的控制系统是【 】A.开环控制系统B.闭环控制系统C.反馈控制系统D.非线性控制系统143.传递函数代表了系统的固有特性,只与系统本身的【 】A. 实际输入量B.实际输出量C.期望输出量D.内部结构,参数144.惯性环节不能立即复现【 】A.反馈信号B.输入信号C.输出信号D.偏差信号145.系统开环传递函数为)(s G ,则单位反馈的闭环传递函数为【 】 A.)(1)(s G s G + B.)()(1)()(s H s G s H s G + C.)()(1)(s H s G s G + D.)()(1)(s H s G s H + 146.线性定常系统输出响应的等幅振荡频率为n ω,则系统存在的极点有【 】A.n j ω±1B.n j ω±C.n j ω±-1D.1-147.开环控制系统的传递函数是【 】A.输出信号的拉氏变换与输入信号的拉氏变换之比B.输入信号的拉氏变换与输出信号的拉氏变换之比C.反馈信号的拉氏变换与误差信号的拉氏变换之比D.误差信号的拉氏变换与反馈信号的拉氏变换之比147-1.闭环控制系统的开环传递函数是【 】A.输出信号的拉氏变换与输入信号的拉氏变换之比B.输入信号的拉氏变换与输出信号的拉氏变换之比C.反馈信号的拉氏变换与误差信号的拉氏变换之比D.误差信号的拉氏变换与反馈信号的拉氏变换之比148.欠阻尼二阶系统的单位阶跃稳态响应为【 】A.零B.常数C.等幅振荡曲线D.等幅衰减曲线149.一阶系统是【 】A.最小相位系统B.非最小相位系统C.Ⅱ型系统D.不稳定系统150.单位阶跃函数的拉普拉斯变换是【 】 A.1/s B.1 C.21s D.1+1/s151.一阶系统的响应曲线开始时刻的斜率为【 】A.TB.TC.T 1D.T1 152.惯性环节11)(+=Ts s G 的转折频率越大其【 】 A.输出响应越慢 B.输出响应越快C.输出响应精度越高D.输出响应精度越低153.对于零型系统的开环频率特性曲线在复平面上【 】A.始于虚轴上某点,终于坐标原点B.始于实轴上某点,终于实轴上另一点C.始于坐标原点,终于虚轴上某点D.始于虚轴上某点,终于虚轴上另一点153-1.对于Ⅰ型系统的开环频率特性曲线在复平面上【 】A.始于(0)180G j =∞∠-的点,终于坐标原点B.始于(0)90G j =∞∠-的点,终于坐标原点C.始于(0)180G j =∞∠-的点,终于实轴上任意点D.始于(0)90G j =∞∠-的点,终于虚轴上任意点154.相位裕量是当系统的开环幅频特性等于1时,相应的相频特性离【 】A.负实轴的距离B.正实轴的距离C.负虚轴的距离D.正虚轴的距离155.对于二阶系统,加大增益将使系统的【 】A.动态响应变慢B.稳定性变好C.稳态误差增加D.稳定性变差155-1.对于二阶系统,加大增益将使系统的【 】A.动态响应变慢B.稳态误差减小C.稳态误差增加D.稳定性变好156.惯性环节使系统的输出【 】A.幅值增大B.幅值减小C.相位超前D.相位滞后156-1.惯性环节使系统的输出随输入信号频率增加而其【 】A.幅值增大B.幅值减小C.相位超前D.相位滞后157.无差系统是指【 】A.干扰误差为零的系统B.稳态误差为零的系统C.动态误差为零的系统D.累计误差为零的系统158.Ⅱ型系统跟踪加速度信号的稳态误差为【 】A.0B.常数C.∞D.时间常数159.控制系统的稳态误差组成是【 】A.跟随误差和扰动误差B.跟随误差和瞬态误差C.输入误差和静态误差D.扰动误差和累计误差160.Ⅰ型系统的速度静差系数等于【 】A.0B.开环放大系数C.∞D.时间常数161.线性定常系统输入信号导数的时间响应等于该输入信号时间响应的【 】A. 傅氏变换B.拉氏变换C.积分D.导数162.线性定常系统输入信号积分的时间响应等于该输入信号时间响应的【 】A.傅氏变换B.拉氏变换C.积分D.导数第一部分 单项选择题1.D2.A3.A4.A5.B6.A7.C8.C9.B 10.B 11.B 12.D 13.B 14.C 15.C 16.A 17.A 18.C19.B 20.A 21.A 22.B 23.B 24.C 25.C 26.D 27.B 28.A 29.B 30.A 31.D 32.A 33.B 34.C 35.A 36.B37.A 38.B 39.C 40.A 41.B 42.C 43.C 44.A 45.D 46.A 47.C 48.A 49.C 50.C 51.C 52.C 53.B54.A 55.C 56.D 57.B 58.C 59.B 60.B 61.B 62.B 63.B 64.B 65.A 66.B 67.B 68.B 69.D 70.C71.A 72.B 73.D 74.A 75.B 76.B 77.A 78.A 79.C 80.D 81.C 82.A 83.B 84.B 85.C 86.B 87.A88.A 89.A 90.D 91.D 92.A 93.A 94.B 95.A 96.D 97.B 98.B 99.B 100.A 101.C 102.B 103.B 104.B 105.C 106.C 107.C 108.B 109.A 110.B 111.C 112.A 113.D 114.A 115.C 116.C 117.C 118.D 119.C 120.A 121.D 122.A 123.A 124.B 125.A 126.C 127.C 128.A 129.B 130.C 131.D 132.A 133.A 134.D 135.C 136.A 137.A 138.A 139.A 140.C 141.A 142.A 143.D 144.B 145.A 146.B 147.A 148.B 149.A 150.A 151.C 152.B 153.B 154.A 155.D 156.D 157.B 158.B 159.A 160.B第二部分 填空题1.积分环节的特点是它的输出量为输入量对 时间 的积累。
机械控制工程基础第二版课后答案

机械控制工程基础第二版课后答案【篇一:《控制工程基础》王积伟_第二版_课后习题解答(完整)】解:1)工作原理:电压u2反映大门的实际位置,电压u1由开(关)门开关的指令状态决定,两电压之差△u=u1-u2驱动伺服电动机,进而通过传动装置控制大门的开启。
当大门在打开位置,u2=u上:如合上开门开关,u1=u上,△u=0,大门不动作;如合上关门开关,u1=u下,△u0,大门逐渐关闭,直至完全关闭,使△u=0。
当大门在关闭位置,u2=u下:如合上开门开关,u1=u上,△u0,大门执行开门指令,直至完全打开,使△u=0;如合上关门开关,u1=u下,△u=0,大门不动作。
2)控制系统方框图4解:1)控制系统方框图2)工作原理:a)水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球顶杆的长度给定,杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),通过杠杆机构是进水阀的开度增大(减小),进入水箱的水流量增加(减小),水位升高(降低),浮球也随之升高(降低),进水阀开度增大(减小)量减小,直至达到新的水位平衡。
此为连续控制系统。
b) 水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球拉杆的长度给定。
杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),到一定程度后,在浮球拉杆的带动下,电磁阀开关被闭合(断开),进水阀门完全打开(关闭),开始进水(断水),水位升高(降低),浮球也随之升高(降低),直至达到给定的水位高度。
随后水位进一步发生升高(降低),到一定程度后,电磁阀又发生一次打开(闭合)。
此系统是离散控制系统。
2-1解:(c)确定输入输出变量(u1,u2)u1?i1r1?i2r2u2?i2r2u1?u2?1c?(idt2?i1)dt得到:cr2du2?(1?r2r1)u2?cr2du1dt?r2r1u1一阶微分方程(e)确定输入输出变量(u1,u2)u1?ir1?ir2? i? u1?u2r1c?idt消去i得到:(r1?r2)一阶微分方程du2dt?u2c?r2du1dt?u1c第二章2-2解:1)确定输入、输出变量f(t)、x2f(t)?fk1(t)?fb1(t)?fb3(t)?m1fb3?f?f?m2dx2(t)dtdx1dt22dx1(t)dt222)对各元件列微分方程:k2b2fk1?k1x1;fb1?b1fb3?b3d(x1?x2)dt;fk2?k2x223)拉氏变换:f(s)?k1x1(s)?b1sx1(s)?b3s[x1(s)?x2(s)]?m1sx1(s)b3s[x1(s)?x2( s)]?k2x2(s)?b2sx2(s)?m2sx2(s)24)消去中间变量:f(s)?b3sx2(s)?(b1s?k1?b3s?m1s)2b3s?k2?b3s?m2sb3s2x2(s)5)拉氏反变换:m1m2dx2dt44?(b1m2?b2m1?bsm2?b3m1)dx2dtdx2dt33?(b1b3?b1b2?bsb2?k1m2?m1k2)dfdtdx2dt22?(k1b2?k1b3?k2b1?k2b3)?k1k2x2?b32-3 解:(2)2s?1?1s?22e?t?e?2t (4)199s?4e?4t?19119s?1?t?1123(s?1)?t?e?13te1(s?1)2(5)?2(s?2)?2(s?1)??2e?2t?2e?t?te?t (6)?0.25?2ss?42?0.5?2?2s?42?2s?1?2.5s?t?0.5cos2t?sin2t?2e?2.52-5解:1)d(s)=0,得到极点:0,0,-2,-5m(s)=0,得到零点:-1,??,??,?? 2) d(s)=0,得到极点:-2,-1,-2 m(s)=0,得到零点:0,0,-1 3) d(s)=0,得到极点:0, ?1?j3,?1?j32m(s)=0,得到零点:-2,??,??4) d(s)=0,得到极点:-1,-2,?? m(s)=0,得到零点:??2-8解:1)a)建立微分方程??mx(t)?f(t)?fk1(t)?fk2(t)f(t)?abfi(t)fk1(t)?k1x0(t)fk2(t)?k2(x0(t)?x(t))fk2(t)?fb(t)?bdx(t)dtb)拉氏变换msx0(s)?f(s)?ff(s)?abfi(s)2k1(s)?fk2(s)fk1(s)?k1x0(s)fk2(s)?k2(x0(s)?x(s))fk2(s)?bsx(s)c)画单元框图(略)d)画系统框图??mx0(t)?fk(t)?fb1(t)?fb2(t)fk(t)?k(xi(t)?x0(t))2)a)建立微分方程:fb1(t)?b1fb2(t)?b2d(xi(t)?xo(t))dtdxo(t)dtmsxo(s)?fk(s)?fb1(s)?fb2(s)2b)拉氏变换:fk(s)?k(xi(s)?xo(s))fb1(s)?b1s(xi(s)?xo(s))fb2(s)?b2sx0(s)c)绘制单元方框图(略)4)绘制系统框图【篇二:机械工程控制基础第二版答案】p> 234【篇三:2机械控制工程基础第二章答案】是线性系统?其最重要的特性是什么?下列用微分方程表示的系统中,xo表示系统输出,xi表示系统输入,哪些是线性系统? (1) ??o?2x (3) ??o?2x??2x?2x (2) ???2x??2tx?2x xxxoooioooi??2x?2x(4) ???2xx??2tx?2x xxooiooooi解: 凡是能用线性微分方程描述的系统就是线性系统。
《控制工程基础》参考复习题及答案

《控制工程基础》参考复习题及习题解答第一部分 单项选择题1.闭环控制系统的主反馈取自【 D 】A.给定输入端B.干扰输入端C.控制器输出端D.系统输出端2.不同属性的物理系统可以有形式相同的【 A 】A.数学模型B.被控对象C.被控参量D.结构参数3.闭环控制系统的开环传递函数为G(s)H(s),其中H(s)是反馈传递函数,则系统的误差信号为【 A 】A.X i (s )-H (s)X 0(s )B.X i (s )-X 0(s )C.X or (s )-X 0(s )D.X or (s )-H (s )X 0(s )3-1闭环控制系统的开环传递函数为G(s)H(s),其中H(s)是反馈传递函数,则系统的偏差信号为【 A 】A.X i (s )-H (s)X 0(s )B.X i (s )-X 0(s )C.X or (s )-X 0(s )D.X or (s )-H (s )X 0(s )4.微分环节使系统【 A 】A.输出提前B.输出滞后C.输出大于输入D.输出小于输入5.当输入量发生突变时,惯性环节的输出量不能突变,只能按【 B 】A.正弦曲线变化B.指数曲线变化C.斜坡曲线变化D.加速度曲线变化6.PID 调节器的微分部分可以【 A 】A.提高系统的快速响应性B.提高系统的稳态性C.降低系统的快速响应性D.降低系统的稳态性6-1.PID 调节器的微分部分可以【 A 】A.提高系统的稳定性B.提高系统的稳态性C.降低系统的稳定性D.降低系统的稳态性7.闭环系统前向传递函数是【 C 】A.输出信号的拉氏变换与输入信号的拉氏变换之比B.输入信号的拉氏变换与输出信号的拉氏变换之比C.输出信号的拉氏变换与误差信号的拉氏变换之比D.误差信号的拉氏变换与输出信号的拉氏变换之比8.一阶系统的时间常数为T ,其脉冲响应为【 C 】 A.T t e --1 B.T t Te T t -+- C.T t e T-1 D.T t Te T -+ 8-1.一阶系统的时间常数为T ,其单位阶跃响应为【 C 】 A.T t e --1 B.T t Te T t -+- C.T t e T-1 D.T t Te T -+ 8-2.一阶系统的时间常数为T ,其单位斜坡响应为【 C 】 A.T t e --1 B.T t Te T t -+- C.T t e T-1 D.T t Te T -+ 8-3.一阶系统的时间常数为T ,其单位阶跃响应的稳态误差为【C 】A.0B.TC.1TD.T t Te T -+ 8-4.一阶系统的时间常数为T ,其单位斜坡响应的稳态误差为【 C 】A.0B.TC.1TD.T t Te T -+ 9.过阻尼二阶系统的单位阶跃稳态响应为【 】A.零B.常数C.单调上升曲线D.等幅衰减曲线10.干扰作用下,偏离原来平衡状态的稳定系统在干扰作用消失后【 】A.将发散离开原来的平衡状态B.将衰减收敛回原来的平衡状态C.将在原平衡状态处等幅振荡D.将在偏离平衡状态处永远振荡11.单位脉冲函数的拉普拉斯变换是【 】 A.1/s B.1 C. 21s D.1+1/s12.线性控制系统的频率响应是系统对输入【 】A.阶跃信号的稳态响应B.脉冲信号的稳态响应C.斜坡信号的稳态响应D.正弦信号的稳态响应13.积分环节的输出比输入滞后【 】A.090-B.090C.0180-D.018014.奈魁斯特围线中所包围系统开环传递函数)(s G 的极点数为3个,系统闭环传递函数的极点数为2个,则映射到)(s G 复平面上的奈魁斯特曲线将【 】A.逆时针围绕点(0,j0)1圈B.顺时针围绕点(0,j0)1圈C.逆时针围绕点(-1,j0)1圈D.顺时针围绕点(-1,j0)1圈15.最小相位系统稳定的条件是【 】A.γ>0和g L <0B.γ<0和g K >1C.γ>0和)(g L ω<0D.γ<0和)(g L ω>016.若惯性环节的时间常数为T ,则将使系统的相位【 】A.滞后1tan ()T ω-B.滞后1tan ω--C.超前1tan ()T ω-D.超前1tan ω-- 17.控制系统的误差是【 】A.期望输出与实际输出之差B.给定输入与实际输出之差C.瞬态输出与稳态输出之差D.扰动输入与实际输出之差18.若闭环系统的特征式与开环传递函数的关系为)()(1)(s H s G s F +=,则【 】A.)(s F 的零点就是系统闭环零点B.)(s F 的零点就是系统开环极点C.)(s F 的极点就是系统开环极点D.)(s F 的极点就是系统闭环极点19.要使自动调速系统实现无静差,则在扰动量作用点的前向通路中应含有【 】A.微分环节B.积分环节C.惯性环节D.比例环节20.积分器的作用是直到输入信号消失为止,其输出量将【 】A.直线上升B.垂直上升C.指数线上升D.保持水平线不变21.自动控制系统的控制调节过程是以偏差消除【 】A.偏差的过程B.输入量的过程C.干扰量的过程D.稳态量的过程22.系统输入输出关系为i o o o x x x x cos =++,则该系统为【 】 A.线性系统 B.非线性系统 C.线性时变系统 D.线性定常系统23.线性定常二阶系统的输出量与输入量之间的关系是【 】A.振荡衰减关系B.比例线性关系C.指数上升关系D.等幅振荡关系24. 微分环节可改善系统的稳定性并能【 】A.增加其固有频率B.减小其固有频率C.增加其阻尼D.减小其阻尼25.用终值定理可求得)8)(5(4)(++=s s s s F 的原函数f (s )的稳态值为【 】 A.∞ B .4 C.0.1 D.026.可以用叠加原理的系统是【 】A.开环控制系统B.闭环控制系统C.离散控制系统D.线性控制系统27.惯性环节含有贮能元件数为【 】A.2B.1C.0D.不确定28.一阶系统的单位阶跃响应在t =0处的斜率越大,系统的【 】A.响应速度越快B.响应速度越慢C.响应速度不变D.响应速度趋于零29.临界阻尼二阶系统的单位阶跃稳态响应为【 】A.零B.常数C.单调上升曲线D.等幅衰减曲线30.欠阻尼二阶系统的输出信号振幅的衰减速度取决于【 】A.n ξωB.ξωC.g ξωD.c ξω31.单位加速度信号的拉氏变换为【 】 A.1 B. s 1 C. 21s D. 31s32.线性系统的输入信号为t t x i ωsin )(=,则其输出信号响应频率为【 】A.ωB.n ωC.ωjD.n j ω33.微分环节的输出比输入超前【 】A.090-B.090C.0180-D.018034.若闭环系统的特征式与开环传递函数的关系为)()(1)(s H s G s F +=,则【 】A.)(s F 的极点就是系统开环零点B.)(s F 的零点就是系统开环极点C.)(s F 的零点就是系统闭环极点D.)(s F 的极点就是系统闭环极点35.系统开环传递函数为)11.0()14.0()(2++=s s s K s G 不用计算或作图,凭思考就能判断该闭环系统的稳定状况是【】A.稳定B.不稳定C.稳定边界D.取决于K 的大小36.为了保证系统有足够的稳定裕量,在设计自动控制系统时应使穿越频率附近)(ωL 的斜率为【 】A.-40 dB/decB.-20 dB/decC.+40 dB/decD.+20 dB/dec37.线性定常系统的偏差信号就是误差信号的条件为【 】A.反馈传递函数H(s)=1B.反馈信号B(s)=1C.开环传递函数G(s) H(s)=1D.前向传递函数G(s)=138.降低系统的增益将使系统的【 】A.稳定性变差B.稳态精度变差C.超调量增大D.稳态精度变好39.含有扰动顺馈补偿的复合控制系统可以显著减小【 】A.超调量B.开环增益C.扰动误差D.累计误差40.PID 调节器的微分部分可以【 】A.改善系统的稳定性B.调节系统的增益C.消除系统的稳态误差D.减小系统的阻尼比41.一般情况下开环控制系统是【 】A.不稳定系统B.稳定系统C.时域系统D.频域系统42.求线性定常系统的传递函数条件是【 】A.稳定条件B.稳态条件C.零初始条件D.瞬态条件43.单位负反馈系统的开环传递函数为G(s),则其闭环系统的前向传递函数与【 】A.反馈传递函数相同B.闭环传递函数相同C.开环传递函数相同D.误差传递函数相同44.微分环节是高通滤波器,将使系统【 】A.增大干扰误差B.减小干扰误差C.增大阶跃输入误差D.减小阶跃输入误差45.控制框图的等效变换原则是变换前后的【 】A.输入量和反馈量保持不变B.输出量和反馈量保持不变C.输入量和干扰量保持不变D.输入量和输出量保持不变46.对于一个确定的系统,它的输入输出传递函数是【 】A.唯一的B.不唯一的C.决定于输入信号的形式D.决定于具体的分析方法47.衡量惯性环节惯性大小的参数是【 】A.固有频率B.阻尼比C.时间常数D.增益系数48.三个一阶系统的时间常数关系为T2<T1<T3,则【 】A.T2系统响应快于T3系统B.T1系统响应快于T2系统C.T2系统响应慢于T1系统D.三个系统响应速度相等49.闭环控制系统的时域性能指标是【 】A.相位裕量B.输入信号频率C.最大超调量D.系统带宽50.输入阶跃信号稳定的系统在输入脉冲信号时【 】A .将变成不稳定系统 B.其稳定性变好 C.其稳定性不变 D.其稳定性变差51.二阶欠阻尼系统的阶跃响应为【 】A.单调上升曲线B.等幅振荡曲线C.衰减振荡曲线D.指数上升曲线52.单位斜坡信号的拉氏变换为【 】 A.1 B.s 1 C.21s D.31s53.线性控制系统【 】A.一定是稳定系统B.是满足叠加原理的系统C.是稳态误差为零的系统D.是不满足叠加原理的系统54.延迟环节Ts e s G -=)(的幅频特性为【 】A.)(ωA =1B.)(ωA =0C.)(ωA <1D.)(ωA >155.闭环系统稳定的充分必要条件是其开环极坐标曲线逆时针围绕点(-1,j0)的圈数等于落在S 平面右半平面的【】 A.闭环极点数 B.闭环零点数 C.开环极点数 D.开环零点数56.频率响应是系统对不同频率正弦输入信号的【 】A.脉冲响应B.阶跃响应C.瞬态响应D.稳态响应57.传递函数的零点和极点均在复平面的左侧的系统为【 】A.非最小相位系统B.最小相位系统C.无差系统D.有差系统58.零型系统跟踪阶跃信号的稳态误差为【 】A.0B.∞C.常数D. )()(lim 0s H s G s→ 59.降低系统的增益将使系统的【 】A.稳定性变差B.快速性变差C.超调量增大D.稳态精度变好60.把系统从一个稳态过渡到新的稳态的偏差称为系统的【 】A.静态误差B.稳态误差C.动态误差D.累计误差61.闭环控制系统除具有开环控制系统所有的环节外,还必须有【 】A.给定环节B.比较环节C.放大环节D.执行环节62.同一系统由于研究目的的不同,可有不同的【 】A.稳定性B.传递函数C.谐波函数D.脉冲函数63.以同等精度元件组成的开环系统和闭环系统其精度比较为【 】A.开环高B.闭环高C.相差不多D.一样高64.积分环节的积分时间常数为T ,其脉冲响应为【 】A.1B.1/TC.TD.1+1/T65.串联环节的对数频率特性为各串联环节的对数频率特性的【 】A.叠加B.相乘C.相除D.相减66.非线性系统的最主要特性是【 】A.能应用叠加原理B.不能应用叠加原理C.能线性化D.不能线性化67.理想微分环节的输出量正比于【 】A.反馈量的微分B.输入量的微分C.反馈量D.输入量68.若二阶系统的阻尼比和固有频率分别为ξ和n ω,则其共轭复数极点的实部为【 】A.n ξωB.n ξω-C.d ξω-D.d ξω69.控制系统的时域稳态响应是时间【 】A.等于零的初值B.趋于零的终值C.变化的过程值D.趋于无穷大时的终值70.一阶系统的时间常数T 越小,系统跟踪斜坡信号的【 】A.稳定性越好B.稳定性越差C.稳态性越好D.稳态性越差71.二阶临界阻尼系统的阶跃响应为【 】A.单调上升曲线B.等幅振荡曲线C.衰减振荡曲线D.指数上升曲线72.线性系统的输入信号为t A t x i ωsin )(=,则其稳态输出响应相位【 】A.等于输入信号相位B.一般为输入信号频率ω的函数C.大于输入信号相位D.小于输入信号相位73.延迟环节Ts es G -=)(的相频特性为【 】 A.T ωωϕ1tan )(--= B.T ωωϕ1tan )(-=C. T ωωϕ=)(D. T ωωϕ-=)(74.Ⅱ型系统的开环传递函数在虚轴上从右侧环绕其极点的无穷小圆弧线所对应的开环极坐标曲线是半径为无穷大,且按顺时针方向旋转【 】A.π2的圆弧线B.πv 的圆弧线C.-π2的圆弧线D.π的圆弧线75.闭环系统稳定的充要条件是系统开环对数幅频特性过零时,对应的相频特性【 】A. 180)(-<c ωϕB. 180)(->c ωϕC. 180)(>c ωϕ 180)(<c ωϕ76.对于二阶系统,加大增益将使系统的【 】A.稳态性变差B.稳定性变差C.瞬态性变差D.快速性变差77.Ⅰ型系统跟踪阶跃信号的稳态误差为【 】A.0B.∞C.常数D. )()(lim 0s H s G s → 78.控制系统含有的积分个数多,开环放大倍数大,则系统的【 】A.稳态性能愈好B.动态性能愈好C.稳定性愈好D.稳态性能愈差79.控制系统的稳态误差主要取决于系统中的【 】A.微分和比例环节B.惯性和比例环节C.比例和积分环节D.比例和延时环节80.比例积分微分(PID)校正对应【 】A.相位不变 B .相位超前校正 C .相位滞后校正 D .相位滞后超前校正81.闭环控制系统必须通过【 】A.输入量前馈参与控制B.干扰量前馈参与控制C.输出量反馈到输入端参与控制D.输出量局部反馈参与控制82.不同属性的物理系统可以有形式相同的【 】A.传递函数B.反函数C.正弦函数D.余弦函数83.输出信号对控制作用有影响的系统为【 】A.开环系统B.闭环系统C.局部反馈系统D.稳定系统84.比例环节能立即地响应【 】A.输出量的变化B.输入量的变化C.误差量的变化D.反馈量的变化85.满足叠加原理的系统是【 】A.定常系统B.非定常系统C.线性系统D.非线性系统86.弹簧-质量-阻尼系统的阻尼力与两相对运动构件的【 】A.相对位移成正比B.相对速度成正比C.相对加速度成正比D.相对作用力成正比87.当系统极点落在复平面S 的虚轴上时,其系统【 】A.阻尼比为0B.阻尼比大于0C.阻尼比小于1大于0D.阻尼比小于088.控制系统的最大超调量【 】A.只与阻尼比有关B.只与固有频率有关C.与阻尼比和固有频率都有关D.与阻尼比和固有频率都无关89.过阻尼的二阶系统与临界阻尼的二阶系统比较,其响应速度【 】A.过阻尼的小于临界阻尼的B.过阻尼的大于临界阻尼的C.过阻尼的等于临界阻尼的D.过阻尼的反比于临界阻尼的90.二阶过阻尼系统的阶跃响应为【 】A.单调衰减曲线B.等幅振荡曲线C.衰减振荡曲线D.指数上升曲线91.一阶系统在时间为T 时刻的单位阶跃响应为【 】A. 1B. 0.98C. 0.95D. 0.63292.线性系统的输出信号完全能复现输入信号时,其幅频特性【 】A.)(ωA ≥1B.)(ωA <1C. 0<)(ωA <1D.)(ωA ≤093.Ⅱ型系统是定义于包含有两个积分环节的【 】A.开环传递函数的系统B.闭环传递函数的系统C.偏差传递函数的系统D.扰动传递函数的系统94.系统的幅值穿越频率是开环极坐标曲线与【 】A.负实轴相交处频率B.单位圆相交处频率C.Bode 图上零分贝线相交处频率D.Bode 图上-180°相位线相交处频率94-1.系统的幅值穿越频率是对数频率特性曲线与【 】A.负实轴相交处频率B.单位圆相交处频率C.Bode 图上零分贝线相交处频率D.Bode 图上-180°相位线相交处频率95.系统的穿越频率越大,则其【 】A.响应越快B.响应越慢C.稳定性越好D.稳定性越差96. 最小相位系统传递函数的【 】A.零点和极点均在复平面的右侧B.零点在复平面的右侧而极点在左侧C.零点在复平面的左侧而极点在右侧D.零点和极点均在复平面的左侧97.Ⅰ型系统能够跟踪斜坡信号,但存在稳态误差,其稳态误差系数等于【 】A.0B.开环放大系数C.∞D.时间常数98.把系统扰动作用后又重新平衡的偏差称为系统的【 】A.静态误差B.稳态误差C.动态误差D.累计误差99.0型系统跟踪斜坡信号的稳态误差为【 】A.0B.∞C.常数D. )()(lim 0s H s G s → 100.PID 调节器的比例部分主要调节系统的【 】A.增益B.固有频率C.阻尼比D.相频特性101.随动系统要求系统的输出信号能跟随【 】A.反馈信号的变化B.干扰信号的变化C.输入信号的变化D.模拟信号的变化102.传递函数的量纲是【 】A.取决于输入与反馈信号的量纲B.取决于输出与输入信号的量纲C.取决于干扰与给定输入信号的量纲D.取决于系统的零点和极点配置103.对于抗干扰能力强系统有【 】A.开环系统B.闭环系统C.线性系统D.非线性系统104.积分调节器的输出量取决于【 】A.干扰量对时间的积累过程B.输入量对时间的积累过程C.反馈量对时间的积累过程D.误差量对时间的积累过程105.理想微分环节的传递函数为【 】 A.Ts+11 B.s 1 C.s D.1+Ts 105.一阶微分环节的传递函数为【 】A.Ts +11B.s 1C.sD.1+Ts106.实际系统传递函数的分母阶次【 】A.小于分子阶次B.等于分子阶次C.大于等于分子阶次D.大于或小于分子阶次107.当系统极点落在复平面S 的负实轴上时,其系统【 】A.阻尼比为0B.阻尼比大于0C.阻尼比大于或等于1D.阻尼比小于0108.欠阻尼二阶系统的输出信号的衰减振荡角频率为【 】A.无阻尼固有频率B.有阻尼固有频率C.幅值穿越频率D.相位穿越频率109.反映系统动态精度的指标是【 】A.超调量B.调整时间C.上升时间D.振荡次数110.典型二阶系统在欠阻尼时的阶跃响应为【 】A.等幅振荡曲线B.衰减振荡曲线C.发散振幅曲线D.单调上升曲线111.一阶系统时间常数为T ,在单位阶跃响应误差范围要求为±0.05时,其调整时间为【】 A.T B.2T C.3T D.4T112.比例环节的输出能不滞后地立即响应输入信号,其相频特性为【 】A.00)(=ωϕB.0180)(-=ωϕC.090)(-=ωϕD.090)(=ωϕ113.实际的物理系统)(s G 的极点映射到)(s G 复平面上为【 】A.坐标原点B.极点C.零点D.无穷远点114.系统的相位穿越频率是开环极坐标曲线与【 】A.负实轴相交处频率B.单位圆相交处频率C.Bode 图上零分贝线相交处频率D.Bode 图上-180°相位线相交处频率114-1.系统的相位穿越频率是对数频率特性曲线与【 】A.负实轴相交处频率B.单位圆相交处频率C.Bode 图上零分贝线相交处频率D.Bode 图上-180°相位线相交处频率115.比例微分环节(时间常数为T )使系统的相位【 】A.滞后1tan T ω-B.滞后1tan ω-C.超前1tan T ω-D.超前1tan ω-116.系统开环频率特性的相位裕量愈大,则系统的稳定性愈好,且【 】A.上升时间愈短B.振荡次数愈多C.最大超调量愈小D.最大超调量愈大117.Ⅱ型系统跟踪阶跃信号的稳态误差为零,其静态位置误差系数等于【 】A.0B.开环放大系数C.∞D.时间常数118.PID 调节器的积分部分消除系统的【 】A.瞬态误差B.干扰误差C.累计误差D.稳态误差119.Ⅰ型系统跟踪斜坡信号的稳态误差为【 】A.0B.∞C.常数D. )()(lim 0s H s G s → 120.比例微分校正将使系统的【 】A.抗干扰能力下降B.抗干扰能力增加C.稳态精度增加D.稳态精度减小120-1.比例微分校正将使系统的【 】A.稳定性变好B.稳态性变好C.抗干扰能力增强D.阻尼比减小121.若反馈信号与原系统输入信号的方向相反则为【 】A.局部反馈B.主反馈C.正反馈D.负反馈122.实际物理系统微分方程中输入输出及其各阶导数项的系数由表征系统固有特性【 】A.结构参数组成B.输入参数组成C.干扰参数组成D.输出参数组成123.对于一般控制系统来说【 】A.开环不振荡B.闭环不振荡C.开环一定振荡D.闭环一定振荡124.积分环节输出量随时间的增长而不断地增加,增长斜率为【 】A.TB.1/TC.1+1/TD.1/T 2125.传递函数只与系统【 】A.自身内部结构参数有关B.输入信号有关C.输出信号有关D.干扰信号有关126.闭环控制系统的开环传递函数是【 】A.输出信号的拉氏变换与输入信号的拉氏变换之比B.输入信号的拉氏变换与输出信号的拉氏变换之比C.反馈信号的拉氏变换与误差信号的拉氏变换之比D.误差信号的拉氏变换与反馈信号的拉氏变换之比127.当系统极点落在复平面S 的Ⅱ或Ⅲ象限内时,其系统【 】A.阻尼比为0B.阻尼比大于0C.阻尼比大于0而小于1D.阻尼比小于0128.欠阻尼二阶系统是【 】A .稳定系统 B. 不稳定系统 C.非最小相位系统 D.Ⅱ型系统129.二阶无阻尼系统的阶跃响应为【 】A.单调上升曲线B.等幅振荡曲线C.衰减振荡曲线D.指数上升曲线130.二阶系统总是【 】A.开环系统B.闭环系统C.稳定系统D.非线性系统131.一阶系统时间常数为T ,在单位阶跃响应误差范围要求为±0.02时,其调整时间为【 】A.TB.2TC.3TD.4T132.积分环节Ts s G 1)(=的幅值穿越频率为【 】 A.T 1 B.-T 1 C. 20T 1lg D. -20T 1lg132-1.微分环节()G s Ts =的幅值穿越频率为【 】 A.T 1B.-T 1C. 20T 1lgD. -20T 1lg132-2.积分环节21()G s Ts =的幅值穿越频率为【 】 A.T 1 B.-T 1133.实际的物理系统)(s G 的零点映射到)(s G 复平面上为【 】A.坐标原点B.极点C.零点D.无穷远点134.判定系统稳定性的穿越概念就是开环极坐标曲线穿过实轴上【 】A.(-∞,0)的区间B.(-∞,0]的区间C.(-∞,-1)的区间D.(-∞,-1]的区间135.控制系统抗扰动的稳态精度是随其前向通道中【 】A.微分个数增加,开环增益增大而愈高B.微分个数减少,开环增益减小而愈高C.积分个数增加,开环增益增大而愈高D.积分个数减少,开环增益减小而愈高136.若系统无开环右极点且其开环极座标曲线只穿越实轴上区间(-1,+∞),则该闭环系统一定【】 A.稳定 B.临界稳定 C. 不稳定 D.不一定稳定137.比例环节的输出能不滞后地立即响应输入信号,其相频特性为【 】A.00)(=ωϕB.0180)(-=ωϕC.090)(-=ωϕD.090)(=ωϕ138.控制系统的跟随误差与前向通道【 】A.积分个数和开环增益有关B.微分个数和开环增益有关C.积分个数和阻尼比有关D.微分个数和阻尼比有关139.Ⅰ型系统跟踪阶跃信号的稳态误差为【 】A.0B.∞C.常数D.)()(lim 0s H s G s→ 140.Ⅱ型系统跟踪斜坡信号的稳态误差为零,其静态位置误差系数等于【 】A.0B.开环放大系数C. ∞D.时间常数141.实际物理系统的微分方程中输入输出及其各阶导数项的系数由表征系统固有特性【 】A.特征参数组成B.输入参数组成C.干扰参数组成D.输出参数组成142.输出量对系统的控制作用没有影响的控制系统是【 】A.开环控制系统B.闭环控制系统C.反馈控制系统D.非线性控制系统143.传递函数代表了系统的固有特性,只与系统本身的【 】A. 实际输入量B.实际输出量C.期望输出量D.内部结构,参数144.惯性环节不能立即复现【 】A.反馈信号B.输入信号C.输出信号D.偏差信号145.系统开环传递函数为)(s G ,则单位反馈的闭环传递函数为【 】 A.)(1)(s G s G + B.)()(1)()(s H s G s H s G + C.)()(1)(s H s G s G + D.)()(1)(s H s G s H + 146.线性定常系统输出响应的等幅振荡频率为n ω,则系统存在的极点有【 】A.n j ω±1B.n j ω±C.n j ω±-1D.1-147.开环控制系统的传递函数是【 】A.输出信号的拉氏变换与输入信号的拉氏变换之比B.输入信号的拉氏变换与输出信号的拉氏变换之比C.反馈信号的拉氏变换与误差信号的拉氏变换之比D.误差信号的拉氏变换与反馈信号的拉氏变换之比147-1.闭环控制系统的开环传递函数是【 】A.输出信号的拉氏变换与输入信号的拉氏变换之比B.输入信号的拉氏变换与输出信号的拉氏变换之比C.反馈信号的拉氏变换与误差信号的拉氏变换之比D.误差信号的拉氏变换与反馈信号的拉氏变换之比148.欠阻尼二阶系统的单位阶跃稳态响应为【 】A.零B.常数C.等幅振荡曲线D.等幅衰减曲线149.一阶系统是【 】A.最小相位系统B.非最小相位系统C.Ⅱ型系统D.不稳定系统150.单位阶跃函数的拉普拉斯变换是【 】 A.1/s B.1 C.21s D.1+1/s151.一阶系统的响应曲线开始时刻的斜率为【 】A.TB.TC.T 1D.T1 152.惯性环节11)(+=Ts s G 的转折频率越大其【 】 A.输出响应越慢 B.输出响应越快C.输出响应精度越高D.输出响应精度越低153.对于零型系统的开环频率特性曲线在复平面上【 】A.始于虚轴上某点,终于坐标原点B.始于实轴上某点,终于实轴上另一点C.始于坐标原点,终于虚轴上某点D.始于虚轴上某点,终于虚轴上另一点153-1.对于Ⅰ型系统的开环频率特性曲线在复平面上【 】A.始于(0)180G j =∞∠-的点,终于坐标原点B.始于(0)90G j =∞∠-的点,终于坐标原点C.始于(0)180G j =∞∠-的点,终于实轴上任意点D.始于(0)90G j =∞∠-的点,终于虚轴上任意点154.相位裕量是当系统的开环幅频特性等于1时,相应的相频特性离【 】A.负实轴的距离B.正实轴的距离C.负虚轴的距离D.正虚轴的距离155.对于二阶系统,加大增益将使系统的【 】A.动态响应变慢B.稳定性变好C.稳态误差增加D.稳定性变差155-1.对于二阶系统,加大增益将使系统的【 】A.动态响应变慢B.稳态误差减小C.稳态误差增加D.稳定性变好156.惯性环节使系统的输出【 】A.幅值增大B.幅值减小C.相位超前D.相位滞后156-1.惯性环节使系统的输出随输入信号频率增加而其【 】A.幅值增大B.幅值减小C.相位超前D.相位滞后157.无差系统是指【 】A.干扰误差为零的系统B.稳态误差为零的系统C.动态误差为零的系统D.累计误差为零的系统158.Ⅱ型系统跟踪加速度信号的稳态误差为【 】A.0B.常数C.∞D.时间常数159.控制系统的稳态误差组成是【 】A.跟随误差和扰动误差B.跟随误差和瞬态误差C.输入误差和静态误差D.扰动误差和累计误差160.Ⅰ型系统的速度静差系数等于【 】A.0B.开环放大系数C.∞D.时间常数161.线性定常系统输入信号导数的时间响应等于该输入信号时间响应的【 】A. 傅氏变换B.拉氏变换C.积分D.导数162.线性定常系统输入信号积分的时间响应等于该输入信号时间响应的【 】A.傅氏变换B.拉氏变换C.积分D.导数第一部分 单项选择题1.D2.A3.A4.A5.B6.A7.C8.C9.B 10.B 11.B 12.D 13.B 14.C 15.C 16.A 17.A 18.C19.B 20.A 21.A 22.B 23.B 24.C 25.C 26.D 27.B 28.A 29.B 30.A 31.D 32.A 33.B 34.C 35.A 36.B37.A 38.B 39.C 40.A 41.B 42.C 43.C 44.A 45.D 46.A 47.C 48.A 49.C 50.C 51.C 52.C 53.B54.A 55.C 56.D 57.B 58.C 59.B 60.B 61.B 62.B 63.B 64.B 65.A 66.B 67.B 68.B 69.D 70.C71.A 72.B 73.D 74.A 75.B 76.B 77.A 78.A 79.C 80.D 81.C 82.A 83.B 84.B 85.C 86.B 87.A88.A 89.A 90.D 91.D 92.A 93.A 94.B 95.A 96.D 97.B 98.B 99.B 100.A 101.C 102.B 103.B 104.B 105.C 106.C 107.C 108.B 109.A 110.B 111.C 112.A 113.D 114.A 115.C 116.C 117.C 118.D 119.C 120.A 121.D 122.A 123.A 124.B 125.A 126.C 127.C 128.A 129.B 130.C 131.D 132.A 133.A 134.D 135.C 136.A 137.A 138.A 139.A 140.C 141.A 142.A 143.D 144.B 145.A 146.B 147.A 148.B 149.A 150.A 151.C 152.B 153.B 154.A 155.D 156.D 157.B 158.B 159.A 160.B第二部分 填空题1.积分环节的特点是它的输出量为输入量对 时间 的积累。
《控制工程基础》参考复习题及答案

《控制工程基础》参考复习题及习题解答第一部分 单项选择题1.闭环控制系统的主反馈取自【 】A.给定输入端B.干扰输入端C.控制器输出端D.系统输出端2.不同属性的物理系统可以有形式相同的【 】A.数学模型B.被控对象C.被控参量D.结构参数3.闭环控制系统的开环传递函数为G(s)H(s),其中H(s)是反馈传递函数,则系统的误差信号为【】 (s )-H (s)X 0(s ) (s )-X 0(s ) (s )-X 0(s ) (s )-H (s )X 0(s )3-1闭环控制系统的开环传递函数为G(s)H(s),其中H(s)是反馈传递函数,则系统的偏差信号为【】(s )-H (s)X 0(s ) (s )-X 0(s ) (s )-X 0(s ) (s )-H (s )X 0(s )4.微分环节使系统【 】A.输出提前B.输出滞后C.输出大于输入D.输出小于输入5.当输入量发生突变时,惯性环节的输出量不能突变,只能按【 】A.正弦曲线变化B.指数曲线变化C.斜坡曲线变化D.加速度曲线变化调节器的微分部分可以【 】A.提高系统的快速响应性B.提高系统的稳态性C.降低系统的快速响应性D.降低系统的稳态性6-调节器的微分部分可以【 】A.提高系统的稳定性B.提高系统的稳态性C.降低系统的稳定性D.降低系统的稳态性7.闭环系统前向传递函数是【 】A.输出信号的拉氏变换与输入信号的拉氏变换之比B.输入信号的拉氏变换与输出信号的拉氏变换之比C.输出信号的拉氏变换与误差信号的拉氏变换之比D.误差信号的拉氏变换与输出信号的拉氏变换之比8.一阶系统的时间常数为T ,其脉冲响应为【 】 A.T t e --1 B.T t Te T t -+- C.T t e T -1 D.Tt Te T -+8-1.一阶系统的时间常数为T ,其单位阶跃响应为【 】 A.T t e --1 B.T t Te T t -+- C.T t e T -1 D.Tt Te T -+8-2.一阶系统的时间常数为T ,其单位斜坡响应为【 】 A.T t e --1 B.T t Te T t -+- C.T t e T -1 D.Tt Te T -+8-3.一阶系统的时间常数为T ,其单位阶跃响应的稳态误差为【 】B.TC.1TD.T tTe T -+8-4.一阶系统的时间常数为T ,其单位斜坡响应的稳态误差为【 】B.TC.1TD.T t Te T -+ 9.过阻尼二阶系统的单位阶跃稳态响应为【 】A.零B.常数C.单调上升曲线D.等幅衰减曲线10.干扰作用下,偏离原来平衡状态的稳定系统在干扰作用消失后【 】A.将发散离开原来的平衡状态B.将衰减收敛回原来的平衡状态C.将在原平衡状态处等幅振荡D.将在偏离平衡状态处永远振荡11.单位脉冲函数的拉普拉斯变换是【 】s C. 21s +1/s12.线性控制系统的频率响应是系统对输入【 】A.阶跃信号的稳态响应B.脉冲信号的稳态响应C.斜坡信号的稳态响应D.正弦信号的稳态响应13.积分环节的输出比输入滞后【 】A.090-B.090C.0180-D.018014.奈魁斯特围线中所包围系统开环传递函数)(s G 的极点数为3个,系统闭环传递函数的极点数为2个,则映射到)(s G 复平面上的奈魁斯特曲线将【 】A.逆时针围绕点(0,j0)1圈B.顺时针围绕点(0,j0)1圈C.逆时针围绕点(-1,j0)1圈D.顺时针围绕点(-1,j0)1圈15.最小相位系统稳定的条件是【 】A.γ>0和g L <0B.γ<0和g K >1C.γ>0和)(g L ω<0D.γ<0和)(g L ω>016.若惯性环节的时间常数为T ,则将使系统的相位【 】A.滞后1tan ()T ω-B.滞后1tan ω--C.超前1tan ()T ω-D.超前1tan ω-- 17.控制系统的误差是【 】A.期望输出与实际输出之差B.给定输入与实际输出之差C.瞬态输出与稳态输出之差D.扰动输入与实际输出之差18.若闭环系统的特征式与开环传递函数的关系为)()(1)(s H s G s F +=,则【 】A.)(s F 的零点就是系统闭环零点B.)(s F 的零点就是系统开环极点C.)(s F 的极点就是系统开环极点D.)(s F 的极点就是系统闭环极点19.要使自动调速系统实现无静差,则在扰动量作用点的前向通路中应含有【 】A.微分环节B.积分环节C.惯性环节D.比例环节20.积分器的作用是直到输入信号消失为止,其输出量将【 】A.直线上升B.垂直上升C.指数线上升D.保持水平线不变21.自动控制系统的控制调节过程是以偏差消除【 】A.偏差的过程B.输入量的过程C.干扰量的过程D.稳态量的过程22.系统输入输出关系为i o o o x x x x cos =++,则该系统为【 】 A.线性系统 B.非线性系统 C.线性时变系统 D.线性定常系统23.线性定常二阶系统的输出量与输入量之间的关系是【 】A.振荡衰减关系B.比例线性关系C.指数上升关系D.等幅振荡关系24. 微分环节可改善系统的稳定性并能【 】A.增加其固有频率B.减小其固有频率C.增加其阻尼D.减小其阻尼25.用终值定理可求得)8)(5(4)(++=s s s s F 的原函数f (s )的稳态值为【 】A.∞ B .426.可以用叠加原理的系统是【 】A.开环控制系统B.闭环控制系统C.离散控制系统D.线性控制系统27.惯性环节含有贮能元件数为【 】D.不确定28.一阶系统的单位阶跃响应在t =0处的斜率越大,系统的【 】A.响应速度越快B.响应速度越慢C.响应速度不变D.响应速度趋于零29.临界阻尼二阶系统的单位阶跃稳态响应为【 】A.零B.常数C.单调上升曲线D.等幅衰减曲线30.欠阻尼二阶系统的输出信号振幅的衰减速度取决于【 】A.n ξωB.ξωC.g ξωD.c ξω31.单位加速度信号的拉氏变换为【 】B. s 1C. 21sD. 31s32.线性系统的输入信号为t t x i ωsin )(=,则其输出信号响应频率为【 】A.ωB.n ωC.ωjD.n j ω33.微分环节的输出比输入超前【 】A.090-B.090C.0180-D.018034.若闭环系统的特征式与开环传递函数的关系为)()(1)(s H s G s F +=,则【 】A.)(s F 的极点就是系统开环零点B.)(s F 的零点就是系统开环极点C.)(s F 的零点就是系统闭环极点D.)(s F 的极点就是系统闭环极点35.系统开环传递函数为)11.0()14.0()(2++=s s s K s G 不用计算或作图,凭思考就能判断该闭环系统的稳定状况是【】A.稳定B.不稳定C.稳定边界D.取决于K 的大小36.为了保证系统有足够的稳定裕量,在设计自动控制系统时应使穿越频率附近)(ωL 的斜率为【 】A.-40 dB/decB.-20 dB/decC.+40 dB/decD.+20 dB/dec37.线性定常系统的偏差信号就是误差信号的条件为【 】A.反馈传递函数H(s)=1B.反馈信号B(s)=1C.开环传递函数G(s) H(s)=1D.前向传递函数G(s)=138.降低系统的增益将使系统的【 】A.稳定性变差B.稳态精度变差C.超调量增大D.稳态精度变好39.含有扰动顺馈补偿的复合控制系统可以显著减小【 】A.超调量B.开环增益C.扰动误差D.累计误差调节器的微分部分可以【 】A.改善系统的稳定性B.调节系统的增益C.消除系统的稳态误差D.减小系统的阻尼比41.一般情况下开环控制系统是【 】A.不稳定系统B.稳定系统C.时域系统D.频域系统42.求线性定常系统的传递函数条件是【 】A.稳定条件B.稳态条件C.零初始条件D.瞬态条件43.单位负反馈系统的开环传递函数为G(s),则其闭环系统的前向传递函数与【 】A.反馈传递函数相同B.闭环传递函数相同C.开环传递函数相同D.误差传递函数相同44.微分环节是高通滤波器,将使系统【 】A.增大干扰误差B.减小干扰误差C.增大阶跃输入误差D.减小阶跃输入误差45.控制框图的等效变换原则是变换前后的【 】A.输入量和反馈量保持不变B.输出量和反馈量保持不变C.输入量和干扰量保持不变D.输入量和输出量保持不变46.对于一个确定的系统,它的输入输出传递函数是【 】A.唯一的B.不唯一的C.决定于输入信号的形式D.决定于具体的分析方法47.衡量惯性环节惯性大小的参数是【 】A.固有频率B.阻尼比C.时间常数D.增益系数48.三个一阶系统的时间常数关系为T2<T1<T3,则【 】系统响应快于T3系统 系统响应快于T2系统系统响应慢于T1系统 D.三个系统响应速度相等49.闭环控制系统的时域性能指标是【 】A.相位裕量B.输入信号频率C.最大超调量D.系统带宽50.输入阶跃信号稳定的系统在输入脉冲信号时【 】A .将变成不稳定系统 B.其稳定性变好 C.其稳定性不变 D.其稳定性变差51.二阶欠阻尼系统的阶跃响应为【 】A.单调上升曲线B.等幅振荡曲线C.衰减振荡曲线D.指数上升曲线52.单位斜坡信号的拉氏变换为【 】B.s 1C.21sD.31s53.线性控制系统【 】A.一定是稳定系统B.是满足叠加原理的系统C.是稳态误差为零的系统D.是不满足叠加原理的系统54.延迟环节Ts e s G -=)(的幅频特性为【 】A.)(ωA =1B.)(ωA =0C.)(ωA <1D.)(ωA >155.闭环系统稳定的充分必要条件是其开环极坐标曲线逆时针围绕点(-1,j0)的圈数等于落在S 平面右半平面的【】A.闭环极点数B.闭环零点数C.开环极点数D.开环零点数56.频率响应是系统对不同频率正弦输入信号的【 】A.脉冲响应B.阶跃响应C.瞬态响应D.稳态响应57.传递函数的零点和极点均在复平面的左侧的系统为【 】A.非最小相位系统B.最小相位系统C.无差系统D.有差系统58.零型系统跟踪阶跃信号的稳态误差为【 】B.∞C.常数D. )()(lim 0s H s G s →59.降低系统的增益将使系统的【 】A.稳定性变差B.快速性变差C.超调量增大D.稳态精度变好60.把系统从一个稳态过渡到新的稳态的偏差称为系统的【 】A.静态误差B.稳态误差C.动态误差D.累计误差61.闭环控制系统除具有开环控制系统所有的环节外,还必须有【 】A.给定环节B.比较环节C.放大环节D.执行环节62.同一系统由于研究目的的不同,可有不同的【 】A.稳定性B.传递函数C.谐波函数D.脉冲函数63.以同等精度元件组成的开环系统和闭环系统其精度比较为【 】A.开环高B.闭环高C.相差不多D.一样高64.积分环节的积分时间常数为T ,其脉冲响应为【 】T +1/T65.串联环节的对数频率特性为各串联环节的对数频率特性的【 】A.叠加B.相乘C.相除D.相减66.非线性系统的最主要特性是【 】A.能应用叠加原理B.不能应用叠加原理C.能线性化D.不能线性化67.理想微分环节的输出量正比于【 】A.反馈量的微分B.输入量的微分C.反馈量D.输入量68.若二阶系统的阻尼比和固有频率分别为ξ和n ω,则其共轭复数极点的实部为【 】A.n ξωB.n ξω-C.d ξω-D.d ξω69.控制系统的时域稳态响应是时间【 】A.等于零的初值B.趋于零的终值C.变化的过程值D.趋于无穷大时的终值70.一阶系统的时间常数T 越小,系统跟踪斜坡信号的【 】A.稳定性越好B.稳定性越差C.稳态性越好D.稳态性越差71.二阶临界阻尼系统的阶跃响应为【 】A.单调上升曲线B.等幅振荡曲线C.衰减振荡曲线D.指数上升曲线72.线性系统的输入信号为t A t x i ωsin )(=,则其稳态输出响应相位【 】A.等于输入信号相位B.一般为输入信号频率ω的函数C.大于输入信号相位D.小于输入信号相位73.延迟环节Ts es G -=)(的相频特性为【 】 A.T ωωϕ1tan )(--= B.T ωωϕ1tan )(-=C. T ωωϕ=)(D. T ωωϕ-=)(74.Ⅱ型系统的开环传递函数在虚轴上从右侧环绕其极点的无穷小圆弧线所对应的开环极坐标曲线是半径为无穷大,且按顺时针方向旋转【 】A.π2的圆弧线B.πv 的圆弧线C.-π2的圆弧线D.π的圆弧线75.闭环系统稳定的充要条件是系统开环对数幅频特性过零时,对应的相频特性【 】A. 180)(-<c ωϕB. 180)(->c ωϕC. 180)(>c ωϕ 180)(<c ωϕ76.对于二阶系统,加大增益将使系统的【 】A.稳态性变差B.稳定性变差C.瞬态性变差D.快速性变差77.Ⅰ型系统跟踪阶跃信号的稳态误差为【 】B.∞C.常数D. )()(lim 0s H s G s → 78.控制系统含有的积分个数多,开环放大倍数大,则系统的【 】A.稳态性能愈好B.动态性能愈好C.稳定性愈好D.稳态性能愈差79.控制系统的稳态误差主要取决于系统中的【 】A.微分和比例环节B.惯性和比例环节C.比例和积分环节D.比例和延时环节80.比例积分微分(PID)校正对应【 】A.相位不变 B .相位超前校正 C .相位滞后校正 D .相位滞后超前校正81.闭环控制系统必须通过【 】A.输入量前馈参与控制B.干扰量前馈参与控制C.输出量反馈到输入端参与控制D.输出量局部反馈参与控制82.不同属性的物理系统可以有形式相同的【 】A.传递函数B.反函数C.正弦函数D.余弦函数83.输出信号对控制作用有影响的系统为【 】A.开环系统B.闭环系统C.局部反馈系统D.稳定系统84.比例环节能立即地响应【 】A.输出量的变化B.输入量的变化C.误差量的变化D.反馈量的变化85.满足叠加原理的系统是【 】A.定常系统B.非定常系统C.线性系统D.非线性系统86.弹簧-质量-阻尼系统的阻尼力与两相对运动构件的【 】A.相对位移成正比B.相对速度成正比C.相对加速度成正比D.相对作用力成正比87.当系统极点落在复平面S 的虚轴上时,其系统【 】A.阻尼比为0B.阻尼比大于0C.阻尼比小于1大于0D.阻尼比小于088.控制系统的最大超调量【 】A.只与阻尼比有关B.只与固有频率有关C.与阻尼比和固有频率都有关D.与阻尼比和固有频率都无关89.过阻尼的二阶系统与临界阻尼的二阶系统比较,其响应速度【 】A.过阻尼的小于临界阻尼的B.过阻尼的大于临界阻尼的C.过阻尼的等于临界阻尼的D.过阻尼的反比于临界阻尼的90.二阶过阻尼系统的阶跃响应为【 】A.单调衰减曲线B.等幅振荡曲线C.衰减振荡曲线D.指数上升曲线91.一阶系统在时间为T 时刻的单位阶跃响应为【 】A. 1B.C.D.92.线性系统的输出信号完全能复现输入信号时,其幅频特性【 】A.)(ωA ≥1B.)(ωA <1C. 0<)(ωA <1D.)(ωA ≤093.Ⅱ型系统是定义于包含有两个积分环节的【 】A.开环传递函数的系统B.闭环传递函数的系统C.偏差传递函数的系统D.扰动传递函数的系统94.系统的幅值穿越频率是开环极坐标曲线与【 】A.负实轴相交处频率B.单位圆相交处频率图上零分贝线相交处频率 图上-180°相位线相交处频率94-1.系统的幅值穿越频率是对数频率特性曲线与【 】A.负实轴相交处频率B.单位圆相交处频率图上零分贝线相交处频率 图上-180°相位线相交处频率95.系统的穿越频率越大,则其【 】A.响应越快B.响应越慢C.稳定性越好D.稳定性越差96. 最小相位系统传递函数的【 】A.零点和极点均在复平面的右侧B.零点在复平面的右侧而极点在左侧C.零点在复平面的左侧而极点在右侧D.零点和极点均在复平面的左侧97.Ⅰ型系统能够跟踪斜坡信号,但存在稳态误差,其稳态误差系数等于【 】B.开环放大系数C.∞D.时间常数98.把系统扰动作用后又重新平衡的偏差称为系统的【 】A.静态误差B.稳态误差C.动态误差D.累计误差型系统跟踪斜坡信号的稳态误差为【 】B.∞C.常数D. )()(lim 0s H s G s→ 调节器的比例部分主要调节系统的【 】A.增益B.固有频率C.阻尼比D.相频特性101.随动系统要求系统的输出信号能跟随【 】A.反馈信号的变化B.干扰信号的变化C.输入信号的变化D.模拟信号的变化102.传递函数的量纲是【 】A.取决于输入与反馈信号的量纲B.取决于输出与输入信号的量纲C.取决于干扰与给定输入信号的量纲D.取决于系统的零点和极点配置103.对于抗干扰能力强系统有【 】A.开环系统B.闭环系统C.线性系统D.非线性系统104.积分调节器的输出量取决于【 】A.干扰量对时间的积累过程B.输入量对时间的积累过程C.反馈量对时间的积累过程D.误差量对时间的积累过程105.理想微分环节的传递函数为【 】 A.Ts +11B.s 1+Ts105.一阶微分环节的传递函数为【 】 A.Ts +11B.s 1+Ts106.实际系统传递函数的分母阶次【 】A.小于分子阶次B.等于分子阶次C.大于等于分子阶次D.大于或小于分子阶次107.当系统极点落在复平面S 的负实轴上时,其系统【 】A.阻尼比为0B.阻尼比大于0C.阻尼比大于或等于1D.阻尼比小于0108.欠阻尼二阶系统的输出信号的衰减振荡角频率为【 】A.无阻尼固有频率B.有阻尼固有频率C.幅值穿越频率D.相位穿越频率109.反映系统动态精度的指标是【 】A.超调量B.调整时间C.上升时间D.振荡次数110.典型二阶系统在欠阻尼时的阶跃响应为【 】A.等幅振荡曲线B.衰减振荡曲线C.发散振幅曲线D.单调上升曲线111.一阶系统时间常数为T ,在单位阶跃响应误差范围要求为±时,其调整时间为【】112.比例环节的输出能不滞后地立即响应输入信号,其相频特性为【 】A.00)(=ωϕB.0180)(-=ωϕC.090)(-=ωϕD.090)(=ωϕ113.实际的物理系统)(s G 的极点映射到)(s G 复平面上为【 】A.坐标原点B.极点C.零点D.无穷远点114.系统的相位穿越频率是开环极坐标曲线与【 】A.负实轴相交处频率B.单位圆相交处频率图上零分贝线相交处频率 图上-180°相位线相交处频率114-1.系统的相位穿越频率是对数频率特性曲线与【 】A.负实轴相交处频率B.单位圆相交处频率图上零分贝线相交处频率 图上-180°相位线相交处频率115.比例微分环节(时间常数为T )使系统的相位【 】A.滞后1tan T ω-B.滞后1tan ω-C.超前1tan T ω-D.超前1tan ω-116.系统开环频率特性的相位裕量愈大,则系统的稳定性愈好,且【 】A.上升时间愈短B.振荡次数愈多C.最大超调量愈小D.最大超调量愈大117.Ⅱ型系统跟踪阶跃信号的稳态误差为零,其静态位置误差系数等于【 】B.开环放大系数C.∞D.时间常数调节器的积分部分消除系统的【 】A.瞬态误差B.干扰误差C.累计误差D.稳态误差119.Ⅰ型系统跟踪斜坡信号的稳态误差为【 】B.∞C.常数D. )()(lim 0s H s G s→ 120.比例微分校正将使系统的【 】A.抗干扰能力下降B.抗干扰能力增加C.稳态精度增加D.稳态精度减小120-1.比例微分校正将使系统的【 】A.稳定性变好B.稳态性变好C.抗干扰能力增强D.阻尼比减小121.若反馈信号与原系统输入信号的方向相反则为【 】A.局部反馈B.主反馈C.正反馈D.负反馈122.实际物理系统微分方程中输入输出及其各阶导数项的系数由表征系统固有特性【】 A.结构参数组成 B.输入参数组成 C.干扰参数组成 D.输出参数组成123.对于一般控制系统来说【 】A.开环不振荡B.闭环不振荡C.开环一定振荡D.闭环一定振荡124.积分环节输出量随时间的增长而不断地增加,增长斜率为【 】T +1/T T 2125.传递函数只与系统【 】A.自身内部结构参数有关B.输入信号有关C.输出信号有关D.干扰信号有关126.闭环控制系统的开环传递函数是【 】A.输出信号的拉氏变换与输入信号的拉氏变换之比B.输入信号的拉氏变换与输出信号的拉氏变换之比C.反馈信号的拉氏变换与误差信号的拉氏变换之比D.误差信号的拉氏变换与反馈信号的拉氏变换之比127.当系统极点落在复平面S 的Ⅱ或Ⅲ象限内时,其系统【 】A.阻尼比为0B.阻尼比大于0C.阻尼比大于0而小于1D.阻尼比小于0128.欠阻尼二阶系统是【 】A .稳定系统 B. 不稳定系统 C.非最小相位系统 D.Ⅱ型系统129.二阶无阻尼系统的阶跃响应为【 】A.单调上升曲线B.等幅振荡曲线C.衰减振荡曲线D.指数上升曲线130.二阶系统总是【 】A.开环系统B.闭环系统C.稳定系统D.非线性系统131.一阶系统时间常数为T ,在单位阶跃响应误差范围要求为±时,其调整时间为【】132.积分环节Ts s G 1)(=的幅值穿越频率为【 】 A.T 1B.-T 1C. 20T 1lg D. -20T 1lg132-1.微分环节()G s Ts =的幅值穿越频率为【 】 A.T 1B.-T 1C. 20T 1lgD. -20T 1lg132-2.积分环节21()G s Ts =的幅值穿越频率为【 】 A.T 1B.-T 1C.D.133.实际的物理系统)(s G 的零点映射到)(s G 复平面上为【 】A.坐标原点B.极点C.零点D.无穷远点134.判定系统稳定性的穿越概念就是开环极坐标曲线穿过实轴上【 】A.(-∞,0)的区间B.(-∞,0]的区间C.(-∞,-1)的区间D.(-∞,-1]的区间135.控制系统抗扰动的稳态精度是随其前向通道中【 】A.微分个数增加,开环增益增大而愈高B.微分个数减少,开环增益减小而愈高C.积分个数增加,开环增益增大而愈高D.积分个数减少,开环增益减小而愈高136.若系统无开环右极点且其开环极座标曲线只穿越实轴上区间(-1,+∞),则该闭环系统一定【】A.稳定B.临界稳定C. 不稳定D.不一定稳定137.比例环节的输出能不滞后地立即响应输入信号,其相频特性为【 】A.00)(=ωϕB.0180)(-=ωϕC.090)(-=ωϕD.090)(=ωϕ138.控制系统的跟随误差与前向通道【 】A.积分个数和开环增益有关B.微分个数和开环增益有关C.积分个数和阻尼比有关D.微分个数和阻尼比有关139.Ⅰ型系统跟踪阶跃信号的稳态误差为【 】B.∞C.常数D.)()(lim 0s H s G s→ 140.Ⅱ型系统跟踪斜坡信号的稳态误差为零,其静态位置误差系数等于【 】B.开环放大系数C. ∞D.时间常数141.实际物理系统的微分方程中输入输出及其各阶导数项的系数由表征系统固有特性【 】A.特征参数组成B.输入参数组成C.干扰参数组成D.输出参数组成142.输出量对系统的控制作用没有影响的控制系统是【 】A.开环控制系统B.闭环控制系统C.反馈控制系统D.非线性控制系统143.传递函数代表了系统的固有特性,只与系统本身的【 】A. 实际输入量B.实际输出量C.期望输出量D.内部结构,参数144.惯性环节不能立即复现【 】A.反馈信号B.输入信号C.输出信号D.偏差信号145.系统开环传递函数为)(s G ,则单位反馈的闭环传递函数为【 】 A.)(1)(s G s G + B.)()(1)()(s H s G s H s G + C.)()(1)(s H s G s G + D.)()(1)(s H s G s H +146.线性定常系统输出响应的等幅振荡频率为n ω,则系统存在的极点有【 】A.n j ω±1B.n j ω±C.n j ω±-1D.1-147.开环控制系统的传递函数是【 】A.输出信号的拉氏变换与输入信号的拉氏变换之比B.输入信号的拉氏变换与输出信号的拉氏变换之比C.反馈信号的拉氏变换与误差信号的拉氏变换之比D.误差信号的拉氏变换与反馈信号的拉氏变换之比147-1.闭环控制系统的开环传递函数是【 】A.输出信号的拉氏变换与输入信号的拉氏变换之比B.输入信号的拉氏变换与输出信号的拉氏变换之比C.反馈信号的拉氏变换与误差信号的拉氏变换之比D.误差信号的拉氏变换与反馈信号的拉氏变换之比148.欠阻尼二阶系统的单位阶跃稳态响应为【 】A.零B.常数C.等幅振荡曲线D.等幅衰减曲线 149.一阶系统是【 】A.最小相位系统B.非最小相位系统C.Ⅱ型系统D.不稳定系统 150.单位阶跃函数的拉普拉斯变换是【 】s C.21s +1/s151.一阶系统的响应曲线开始时刻的斜率为【 】A.TB.TC.T 1 D.T 1 152.惯性环节11)(+=Ts s G 的转折频率越大其【 】 A.输出响应越慢 B.输出响应越快C.输出响应精度越高D.输出响应精度越低153.对于零型系统的开环频率特性曲线在复平面上【 】A.始于虚轴上某点,终于坐标原点B.始于实轴上某点,终于实轴上另一点C.始于坐标原点,终于虚轴上某点D.始于虚轴上某点,终于虚轴上另一点 153-1.对于Ⅰ型系统的开环频率特性曲线在复平面上【 】A.始于(0)180G j =∞∠-的点,终于坐标原点B.始于(0)90G j =∞∠-的点,终于坐标原点C.始于(0)180G j =∞∠-的点,终于实轴上任意点D.始于(0)90G j =∞∠-的点,终于虚轴上任意点154.相位裕量是当系统的开环幅频特性等于1时,相应的相频特性离【 】A.负实轴的距离B.正实轴的距离C.负虚轴的距离D.正虚轴的距离 155.对于二阶系统,加大增益将使系统的【 】A.动态响应变慢B.稳定性变好C.稳态误差增加D.稳定性变差 155-1.对于二阶系统,加大增益将使系统的【 】A.动态响应变慢B.稳态误差减小C.稳态误差增加D.稳定性变好 156.惯性环节使系统的输出【 】A.幅值增大B.幅值减小C.相位超前D.相位滞后156-1.惯性环节使系统的输出随输入信号频率增加而其【 】A.幅值增大B.幅值减小C.相位超前D.相位滞后157.无差系统是指【 】A.干扰误差为零的系统B.稳态误差为零的系统C.动态误差为零的系统D.累计误差为零的系统158.Ⅱ型系统跟踪加速度信号的稳态误差为【 】B.常数C.∞D.时间常数159.控制系统的稳态误差组成是【 】A.跟随误差和扰动误差B.跟随误差和瞬态误差C.输入误差和静态误差D.扰动误差和累计误差160.Ⅰ型系统的速度静差系数等于【 】B.开环放大系数C.∞D.时间常数161.线性定常系统输入信号导数的时间响应等于该输入信号时间响应的【 】A. 傅氏变换B.拉氏变换C.积分D.导数162.线性定常系统输入信号积分的时间响应等于该输入信号时间响应的【 】A.傅氏变换B.拉氏变换C.积分D.导数第一部分 单项选择题第二部分 填空题1.积分环节的特点是它的输出量为输入量对 的积累。
《控制工程基础》王积伟_第二版_课后习题解答

d)画系统框图
2)a)建立微分方程:
b)拉氏变换:
c)绘制单元方框图(略)
4)绘制系统框图
2-11
解:a)
b)
2-14
解:(1)
(2)由于扰动产生的输出为:
要消除扰动对输出的影响,必须使
得到:
得到:
第三章
3-1
解:1)法一:一阶惯性环节的调整时间为4T,输出达稳态值的98%,故:
3-8
解:闭环传递函数
1)K=200:
最大超调量
峰值时间
调整时间
上升时间
振动次数
2)K=150,得到:
依次得到的动态性能指标:0、54,0037s,0、175s,0、02s,2、34。
3)K=13、5,得到:
此时,系统为过阻尼系统,为两个惯性环节串联。
4)对于二阶系统传递函数化为标准形式后,只要 不变,系统调整时间ts不变;随着 增大,过渡过程在缩短(tp,tr),但总过渡时间(调整时间ts)不变;而随着 的减小,振动幅度在加剧,振动次数N、超调量Mp都在加大。
3)单位加速度输入稳态误差;
法二:
3-11
解:开环传递函数 ,此系统为 型系统。
1)稳态误差系数
2)输入信号为阶跃信号、速度信号与加速度信号的组合,它们的系数分别为:
根据信号线性叠加的原理,系统的稳定误差为:
a)当 时,
b)当 时,
c)当 时,
3-12
解:
1)仅有输入信号作用下的稳态误差
偏差传递函数
4T=1min,得到:T=15s
法二:求出一阶惯性环节的单位阶跃时间响应,代入,求出。
2)法一:输入信号 ,就是速度信号;
控制工程基础王积伟_第二版_课后复习题解答(完整)
d)画系统框图
2)a)建立微分方程:
b)拉氏变换:
c)绘制单元方框图(略)
4)绘制系统框图
2-11
解:a)
b)
2-14
解:(1)
(2)由于扰动产生的输出为:
要消除扰动对输出的影响,必须使
得到:
得到:
第三章
3-1
解:1)法一:一阶惯性环节的调整时间为4T,输出达稳态值的98%,故:
拉氏反变换:
3-4
解:闭环传递函数为:
(1)单位阶跃函数的拉氏变换:
部分分式展开:
系数比较得到:4A+3B=0
A-3C=0
A=1
得到:A=1,B=-4/3,C=1/3
拉氏反变换:
(2)法一、利用微分关系,把结果(1微分)
法二、单位脉冲函数的拉氏变换:
部分分式展开:
系数比较得到:A+B=0
4A+B=4
法二:a0=1,a1=10,a2=16,a3=160;
因为三阶系统,a0,a1,a2,a3均大于0,且a1×a2=160=a0×a3=160,
所以该三阶系统临界稳定。
3-16
(2)解:劳思阵列
系统稳定的条件,劳思阵列第一列元素全为正号,即:
由式1)得:k>0
式2)得:k>10/99
式3)得:k<99/10
第四章
4-4
解:闭环传递函数
频率特性
幅频特性
相频特性
1) ,稳态输出
2)
稳态输出
3)
稳态输出
4-9
解:1)
;
2)
、
;
4-12
1)解a)典型环节:放大环节:2
