粘性流体力学
4-粘性流体力学与层流流动

4-粘性流体力学与层流流动粘性流体力学是研究粘性流体运动规律的一门学科,可根据流体的不同分为牛顿流体和非牛顿流体。
层流流动是流体流动方式的一种,指流体流动时粒子之间的运动具有良好的有序性,且互相之间影响很小,层流流动的特性和规律是粘性流体力学研究的一部分。
粘性流体力学中,我们用一种称为“粘度”的物理量来描述流体的内部阻力。
粘度描述了流体粒子之间难以滑动的程度,粘度越大,表明流体相对运动的内阻力越大。
在粘性流体中,如果微观粒子的速度变化较大,则会产生较大的粘性阻力。
层流流动中,流体按照一定的竖直方向上的速度分布进行平稳流动。
由于粘度的存在,不同速度层面上的流体在相互掠过时,会因相对速度而受到阻力,这就形成了一种剪切应力。
在一定条件下,流体会形成种类众多、形态各异的流动类型,如平面层流,管道层流等等。
在粘性流体力学里,层流流动是一种非常稳定的流动现象,诸如颗粒的路径稳定、流速和压力分布稳定等。
层流流动中流体中各个流层都是并行流动的,并且相邻流层间的速度差别通常不大,这使得层流流动中的流动失稳和湍动现象较少出现,从而能够获得相当准确的数学描述和解析解。
然而,尽管层流流动在粘性流体力学中处于重要地位,但并不是所有流体流动都能达到层流状态。
在实际生产和生活中,许多流体常常处于层流与湍流的过渡状态,这就需要进行深入的研究来对这些过渡状态进行理解和把控。
研究粘性流体力学和层流流动有着重要的理论意义和实际价值。
这些研究成果广泛应用在化工、高分子材料、土壤水动力学、生物医学等诸多领域,如液态塑料的注塑工艺、血液的流动、河流的径流等等。
以上是简单介绍粘性流体力学与层流流动的相关知识,希望能帮助大家对这两个概念有一个更深入的理解。
粘性流体力学与层流流动的研究充满了挑战,需要我们用严谨的科学态度和持续的努力去不断深化研究,推动这一门学科的进步。
在现代物理科学与工程技术中,粘性流体力学与层流流动的研究定会有更广阔的应用前景,值得我们进一步探索和研究。
工程流体力学 第4章 粘性流体动力学基础

沿程损失水头 (hf):
hf
LV2 D 2g
达西(Darcy)公式
λ:为沿程损失系数,与流动状态、管壁的粗糙度等有关
hf不仅与管段长度成正比,还与管道直径成反比
2020年1月10日
FESTO气动中心
局部阻力水头损失 :当流体在运动中遇到局部障 碍(半开阀门、管道弯头、粗细管接口、滤网等)时, 流线会发生局部变形,并且由于流动分离、二次流等 原因产生漩涡运动,从而耗散一部分机械能,造成水 头损失。
2020年1月10日
FESTO气动中心
解 :(1)求管中心最大流速 umax 2V 2 6.35 12.7cm/s
(2)离管中心 r=20mm 处的流速
u
umax
p
4L
r2
当r=50mm时,管轴处u=0,则有
0 12.7 p 52
4L
p 0.51
4L
则r=20mm在处的流速 u 12.7 0.51 22 10.7cm/s
LV2
d 2g
64 / Re
2020年1月10日
FESTO气动中心
克服沿程阻力而消耗的功率
W
ghf Q
pQ
128 LQ 2 d 4
动能修正系数
1
R2
R u 32rdr 2
0 V
2020年1月10日
FESTO气动中心
例: 设有一恒定有压均匀管流,已知管径d=20mm,管长l=20m, 管 中 水 流 流 速 V=0.12m/s , 水 温 t=10℃ 时 水 的 运 动 粘 度 ν=1.306×10-6m2/s。求沿程阻力损失
流体力学中的流体粘性分析

流体力学中的流体粘性分析流体力学是机械工程领域中一个重要的分支,研究的是流体的运动和力学行为。
其中,流体的粘性是流体力学中一个重要的参数,对于流体的运动状况和性质具有显著影响。
本文将深入探讨流体粘性的分析及其在流体力学中的应用。
首先,我们需要了解粘性的概念。
粘性是指流体内部分子之间的相互作用力所导致的内摩擦力,是流体流动阻力的基本成因。
粘性较高的流体具有较大的内摩擦力,因此在流动过程中更容易形成无穷小的剪切应力。
而粘性较低的流体则具有较小的内摩擦力,流动时相对容易滑动,形成较小的剪切应力。
要分析流体粘性,我们可以通过研究流体的运动方式和流动特性来进行。
在流体力学中,粘性的分析通常依赖于牛顿第二定律和流体连续性方程,通过这些方程我们可以推导出粘性流体的运动方程。
在这个过程中,维度分析和相似性理论是非常重要的工具,可以帮助我们得到流体粘性的定量描述。
流体粘性的分析结果在工程实践中具有广泛的应用。
比如,在汽车设计中,对于车辆的阻力和燃油消耗有着直接影响的就是气体的粘性。
如果能减小气体的粘性,车辆的阻力将减小,从而提高燃油效率。
另外,粘性在计算机模拟和工艺设计中也有着重要的应用。
例如,在模拟油管输送过程中,对于油管内部流体的粘性分析能够直接影响输油速度和整个过程的效率。
流体粘性的研究对于我们理解自然界中的很多现象也非常重要。
例如,水滴落在玻璃上时的展开形状、液体在管道中的流动特性等等,这些现象都与流体的粘性密切相关。
另外,流体粘性的研究对于生物学和医学领域也有着重要意义。
比如,血液的流动过程和心血管系统的研究,需要考虑血液的粘性以及血管内部流体的行为。
流体力学中的流体粘性分析是一个复杂的课题,需要深入理解流体运动规律和力学原理。
通过数学模型的建立和实验数据的分析,我们可以得到流体粘性的定性和定量描述。
这为工程应用和科学研究提供了重要的依据。
同时,未来的研究也需要进一步深入挖掘流体粘性的实质,提出更加准确和可靠的粘性模型,为流体力学领域的发展做出更多贡献。
八章粘性流体力学基础

任意平面上应力 pn n P = ni pijej
n是该平面单位法向量 nx cos(n,i),ny cos(n, j),nz cos(n,k) 重规例复定Pn的:ip量用ijpije,e1nie,1e表jp21,e示j 3代该n替2P量pi 2i,各jj,pki,项jne3j下相p3 j标加用1,n2i,e3j代pij替xn,1nnyne32,1jz(((p,eee1111jppp一132111n项2eeee中22j2pppp1下232222j 标eene33符33pepp1j32号33p3)))3 j
2
第八章 粘性流体力学基础
8.1.3 应力张量分析
Sx sxx sxy sxz
变形速率张量 S iSx jSy kSz S y syx syy syz
Sz
szx
szy
szz
即:S sijeiej
式 中:
sij
牛顿流体平行平板层流流动实验: xy
du dy
(三)偏应力τ与变形速率S的线性关系式
aS b ij aS ij b ij
牛顿流体平行平板层流流动实验: xy
du dy
xy
a (u 2 y
v x
)
0
xy
a 2
u y
a
2
又: pm ( p11 p22 p33 ) / 3 3 pm pii 0
第八章 粘性流体力学基础 1.粘性流体动力学问题的建立; 2.粘性流动的基本特性; 3.粘性流体运动的相似律; 4.几个典型问题的解析求解和近似求解:
粘性流体力学第一章

有关三维边界层和边界层分离计算仍在不断发展。
有关湍流计算的模式理论等仍适用边界层的计算, 有关边界层流动的研究也是这些理论和方法发展的动 力。
ቤተ መጻሕፍቲ ባይዱ
边界层的实验测量
在湍流边界层计算的发展中,边界层的实验测量, 其中最主要的是对速度分布规律的研究,这方面的 成果有普朗特(Prandtl 1933年)的内层律,卡门 的外层律(Karman 1930年),克劳塞(Clauser 1954年,1956年)压力梯度对外层律影响的修正, 科尔斯(Coles)的尾迹律, 以及1960年代克兰 (Kline)开始用氢气泡技术观察到的边界层猝发 (burst)现象。
粘性流体力学的发展 两种基本流态——层流、湍流 和雷诺数 流体的传输性质 应变率张量和应力张量 广义牛顿定律
第一节 粘性流体力学的发展
1、研究流体粘性的意义
流体存在着粘性,粘性是流体阻止其本身流动 的性质。当流场中存在速度梯度时,流体就会 产生阻力,这就是粘性。
在求解运动物体在流体中的阻力,以及涡旋的 扩散、热量的传递等问题时,粘性会起主导作 用不能忽略。
D. Catherall et al(1966)首先提出了二维边界层 积分型逆解法。在二维边界层上主要应用East(1977)的 逆解法。
三维边界层在分离现象、判别和模拟方面比二维复杂, J. Cousteix(1981)提出了三维边界层的逆解法。以后Le Ballear(1981),Delery J and Formery(1983), Radwan S. F. (1984)和Edwards D.E.(1987)等都进 行边界层逆解法的计算,并取得了满意的结果。
粘性流体力学讲解

z
-px
、v、px、p y、pz、f
牛顿第二定律:
x -py
z
M
z
y
py
p y y
y
ma F
x
y
px
p x x
x
-pz
Dv Dt
x
y
z
f
x
y
z
p x
y
z
(p x
p x x
x)
y
z
p y
x
z
(p
y
p y y
y)
x
z
Dv Dt
fy
1
p y
2v
Dw Dt
fz
1
p z
2w
Discussion:
Dv f 1 p 2 v v
Dt
3
1. 物理意义:单位质量流体惯性力、质量力、压力合力和 粘性力平衡。粘性力包括剪应力与附加法向应力。
0
du
dy
yh
dp h dx
y
h
o -h
umax x
dp 0 dx
压力梯度使速度剖面为抛物型——层流运动的特征。
7.3.2往复振荡平板引起的层流流动
平板运动引起粘性效应的扩散。 流场速度分布:
y o u=Ucos t
u U eky cosky t ——粘性扰动波。 y 2
dp 0 dx
速度分布: (Couette流动)
《工程流体力学》第七章 粘性流体动力学
x方向 : 1)表面力:作用在左右两面上力的合力:
作用在上下两面上力的合力:
作用在前后两面上力的合力:
作用在整个六面体上表面力沿x轴方向的合力:
2) x方向质量力 : 单位质量流体受到的质量力分量:X;
六面体受到的质量力: Xrdxdydz
牛顿第二定律:
—— 以应力形式表示的粘性流体运动微分方程 再把表面应力和变形率之间关系代入上3式:
应力:各向同性
运动粘性流体:存在法向、切向表面力 应力:各向异性
流体中:任一点c :绕c任意方位
c点应力定义: 要计算两个向量的比值
用作用在dAx, dAy, dAz上的dFx, dFy, dFz:定义c上的应力
需要2个下标表示:9个应力分量
第1个下标i:应力作用方向 第2个下标j:作用面方向
第七章 粘性流体动力学
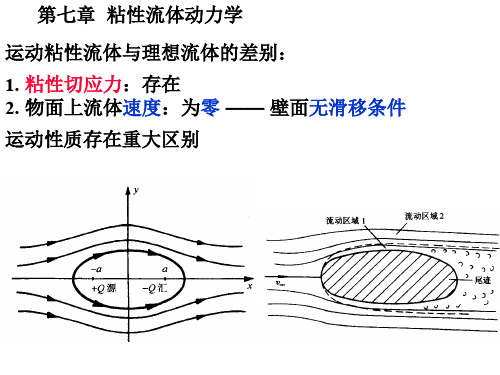
运动粘性流体与理想流体的差别: 1. 粘性切应力:存在 2. 物面上流体速度:为零 —— 壁面无滑移条件 运动性质存在重大区别
第一节 粘性流体中作用力
一、粘性应力: 1.质量力:与流体质量有关
与流体粘性无关 粘性流体中质量力考虑方法:和理想流体相同
2. 表面力: 静止和运动理想流体:仅存在指向作用面法向表面力
由于外部无粘流:受到分离流的排挤 明显改变:其中压强分布 实际计算:用实测物面压力分布计算分离点前附面层流动 附面层分离:使流体一部分机械能损失在涡流中
绕流物体阻力增加 流体机械效率降低 甚至产生不稳定流动 导致机器损坏 防止或推迟附面层分离现象发生:是工程上一个重要问 题
边界层分离后:形成尾涡区 尾涡区压强:基本上等于分离点压强 压强:上下对称 若将压强在圆柱面上积分:则得压差阻力
流体在y+l层时均速度:
《工程流体力学》第七章 粘性流体动力学

2.附面层位移厚度d*: 设物面P点附面层厚度d ,在垂直于纸面方向取单位宽度,
则该处通过附面层的质量流量:
通过同一面积理想流体流量:
ro, Vo —— 附面层外边界处理想
流体的密度和速度
以d*高度作一条线平行于物面,
使两块阴影处面积相同:
即在流量相等条件下将理想流体流动区从物面向外移动了
流体绕物体流动,整个流场分为三个区域:
1)附面层: 流速:由壁面上零值急剧增加到自由来流速度同数量级值 沿物面法线方向:速度梯度很大
即使流体粘性系数小:粘性应力仍可达到一定数值
由于速度梯度很大: 使得通过附面层物体 涡旋强度很大,流体 是有旋的
2)尾迹流: 附面层内流体:离开物体流入下游,在物体后形成尾迹流
各物理量都是统计平均值, \ 瞬时物理量=平均物理量+脉动物理量, 对整个方程进行时间平均的运算。
一、常用时均运算关系式:
时均运算规律:
推论:脉动量对空间坐标各阶导数的时均值=0。
二、连续方程:对二维流动,瞬态运动连续方程 进行时均运算:
\ 可压缩紊流运动连续方程:
进行时均运算: 上两式相减:
\ 附加法向应力
法向应力: l: 比例系数,与体积变化率有关
三个法向应力平均值的负值:为粘性流体在该点压强
最后得表面应力与变形率之间的关系:
第二节 粘性流体运动的基本方程
一、连续方程:
粘性流体运动:服从质量守恒定律 连续方程:不涉及力的作用 仍能得出与理想流体相同形式的方程
二、运动微分方程: 粘性流体中:微元六面体 微元六面体中心:c
三、雷诺方程: 二维不可压缩粘性流,不考虑质量力,N-S为:
对上式进行时均运算:
粘性流体力学

∂n w
式中 T w 是物面上的温度。 q w 为通过单位面积传递给流体 的热量。 ∂T / ∂n 为沿物面外法线方向的温度梯度。
5.粘性流体运动的涡量传输方程
为了讨论漩涡在粘性流体中运动的性质和规律, 有必要建立涡量传输方程。涡量传输方程是从运动 方程派生出来的,便于说明粘性流体中涡旋的产生、 发展和衰减的现象。 根据数学中的场论知识,速度矢量V的随体导数 2 可写为 DV ∂V ∂V V
不可压缩粘性流体的N-S方程在柱坐标系下形式为
∂vr ∂vr vθ ∂vr vθ2 ∂vr vr 2 ∂vθ 1 ∂p 2 + vr + − + vz = fr − +ν ∇ vr − 2 − 2 ∂t ∂r r ∂θ r ∂z ρ ∂r r r ∂θ ∂vθ ∂vθ vθ ∂vθ vr vθ ∂vθ vθ 2 ∂vr 1 1 ∂p 2 + vr + + + vz = fθ − +ν ∇ vθ − 2 + 2 ∂t ∂r r ∂θ r ∂z ρ r ∂θ r r ∂θ ∂vz ∂vz vθ ∂vz ∂vz 1 ∂p + vr + + vz = fz − +ν∇2 vz ∂t ∂r r ∂θ ∂z ρ ∂z
同理,可分别计算沿y方向和z方向净流出控 制体的质量分别为 ∂ ( ρ v) δ xδ yδ zδ t
∂y ∂(ρw)
∂z
(1.2 )
δ xδ yδ zδ t
(1.3 )
Байду номын сангаас
同时,在δ t 时间内控制体内的流体质量减少 了
∂ρ - δ xδ yδ zδ t ∂t
粘性流体力学基本方程组

牛顿流体具有剪切应力和剪切速率成线性关系的特性,这种 关系可以用本构方程来表示。
牛顿流体的本构方程
本构方程
本构方程是描述流体应力与应变之间 关系的方程,对于牛顿流体,其本构 方程为剪切应力等于粘性系数乘以剪 切速率。
本构方程的意义
本构方程是粘性流体力学中的基本方 程之一,它描述了流体在受到外力作 用时内部应力的产生和分布情况。
有限差分法
将流场离散化为网格,用差分表达式近似代 替微分方程中的导数项,从而将微分方程转 化为差分方程进行求解。
有限元法
将流场离散化为单元,用有限元近似表示流场中的 物理量,通过求解有限元方程得到流场中的数值解 。
有限体积法
将流场离散化为体积,每个体积单元上的物 理量通过中心值或平均值表示,通过求解离 散方程得到流场中的数值解。
VS
详细描述
非牛顿流体在剪切力作用下不会表现出恒 定的剪切粘度,其流动行为受到许多因素 的影响,如温度、压力、浓度、分子间相 互作用等。
非牛顿流体的本构方程
总结词
本构方程是描述非牛顿流体在剪切力作用下 的应力与应变率之间关系的数学模型。
详细描述
非牛顿流体的本构方程通常由实验数据确定, 并可以用来预测流体在不同剪切力作用下的 流动行为。常见的本构方程包括幂律模型、 Carreau模型、Bingham模型等。
理论分析方法
01
02
03
数学建模
通过建立数学模型来描述 粘性流体的运动规律,包 括连续性方程、动量方程、 能量方程等。
解析求解
对建立的数学模型进行解 析求解,得到流体运动的 解析解,用于分析流体运 动的特性。
近似方法
在某些情况下,可以采用 近似方法来求解数学模型, 如摄动法、匹配渐近展开 等。
流体力学1.3 流体的粘性、牛顿切应力公式、理想流体

课堂习题
0.1m 0.2m
流体力学第一章
F
已知条件: 0.2N s / m2 ,V 5m / s, A 0.8m2
求需要多大的力?
[μ]=牛顿·秒/米2=N·s/m2
[ ] m2 / s
1.3.3 理想流体
粘性系数等于零的流体称作理想流体。
流体力学第一章
例题
流体力学第一章
如图所示,一块木板底面积 A 0.05m2 ,重量 G 3.5N 沿倾角 300 的斜面以等速度 V 0.2m / s 下滑,
流体力学第一章
流体力学第一章
1.3 流体的粘性、牛顿切 应力公式、理想流体
1.3.1流体的粘性、牛顿切应力公式
流体力学第一章
流体具有粘性。粘性是当流体微团发生相对运动时,产生的 一种抵抗变形、阻碍运动的性质。
流体力学第一章
由试验发现,流动具有下列特点:
u
U b
y,
F A
U b
式中μ为比例系数,通常称作粘性系数或动力粘性系数,或 绝对粘性系数,它是一个与流体物性有关的系数。
p yx
F A
yx
Pyx
U b
du dy
流体力学第一章
进一步实验证明,可以把这个结果推广到流体作任意层流直线 运动中去。
pyx
udu dyu
u y
牛顿切应力公式
流体力学第一章
应当特别指出,牛顿公式只能应用于或推广应用于流体作层 状运动的情况,即所谓层流情况。
1.3.2 粘性系数
斜面上涂有厚度 1.5mm 的润滑油。 试求润滑油的粘度 。
流体力学中的流体的黏滞性分布

流体力学中的流体的黏滞性分布流体力学是研究流体运动和力学性质的一门学科。
在流体力学中,黏性是流体的一种重要性质,它描述了流体内部分子间的摩擦力大小。
本文将详细介绍流体的黏性分布及其在流体力学中的应用。
一、黏性的定义和原理黏性是指流体内部分子间相对运动的阻力。
它是流体的基本性质之一,与流体分子的相互作用力有关。
当两个相邻的流体分子相对运动时,由于分子之间的相互作用力,会产生阻力,这就是黏性的体现。
黏性的大小与流体分子间的作用力有关,流体分子间的作用力越大,黏性也越大。
在低温下,分子间作用力较强,黏性较大;在高温下,分子间作用力较弱,黏性较小。
此外,流体的浓度、压力和流速等因素也会影响黏性的大小。
二、流体黏性的分布在流体力学中,流体的黏性分布可以分为均匀分布和非均匀分布两种情况。
1. 均匀分布均匀分布指的是在流体中,黏性是均匀分布的,即任意位置的流体分子之间的黏性相同。
这种情况下,流体的黏性可以通过测量黏度来描述。
黏度是指单位面积上流体流动一单位速度所需施加的力。
当黏度在整个流体中保持不变时,黏性分布呈均匀分布。
2. 非均匀分布非均匀分布指的是流体中的黏性不是均匀分布的,即流体分子之间的阻力不同。
这种情况下,流体的黏性随位置的不同而变化,称为非均匀黏性分布。
非均匀黏性分布常出现在流体在受外力作用下存在强烈的流动或者涡旋情况下。
三、流体黏性分布的应用流体的黏性分布在实际应用中起着重要作用,特别是在流体力学和工程领域。
1. 流体力学研究黏性分布对于流体力学研究具有重要影响。
通过研究流体黏性分布特征,可以深入了解流体在不同条件下的流动规律,从而为流体力学理论的建立和计算模型的优化提供依据。
2. 工程应用在工程中,了解流体的黏性分布对于流体的输送和控制具有重要意义。
例如,在石油输送领域,了解流体的黏性分布可以优化管道布局和输送速度,提高输送效率和减少能源消耗。
另外,在飞机和汽车设计中,黏性分布也是重要考虑因素之一,可以影响飞行和行驶的稳定性和能效。
流体力学中的流体粘性和黏滞性

流体力学中的流体粘性和黏滞性流体力学中的流体粘性和黏性流体力学是研究流体运动和流体力学性质的科学领域。
在流体力学中,流体粘性和黏性是两个重要的概念。
本文将详细介绍流体粘性和黏性的概念、特点以及其在不同领域的应用。
一、流体粘性的概念和特点流体粘性是指流体内部分子间相互摩擦的性质。
当一个力作用于流体时,流体分子会相互移动并产生内部的相对运动,即流体内部会产生剪切应力。
而流体粘性就是流体对剪切应力的抵抗能力。
1. 流体的黏性流体的黏性是流体粘性的一种表现形式。
黏性是指流体内部分子的相互作用力导致的粘滞效应。
当流体受到外力作用时,分子之间会互相摩擦并产生内部的扰动。
流体的黏性可以通过流动的阻力和黏滞系数来描述。
黏滞系数越大,流体的黏性越大,流动受阻越明显。
2. 流体的牛顿性和非牛顿性根据流体黏性的不同特性,流体可以分为牛顿流体和非牛顿流体。
牛顿流体是指在剪切应力作用下,流体的黏滞系数保持不变的流体。
在牛顿流体中,流体的黏滞系数与流体的剪切速率无关。
水和空气是典型的牛顿流体。
非牛顿流体是指在剪切应力作用下,流体的黏滞系数随剪切速率的变化而变化的流体。
在非牛顿流体中,流体的黏滞系数会随着剪切应力的增加而减小或增加。
例如,墨汁和牛奶都是非牛顿流体。
二、流体粘性和黏性的应用流体的粘性和黏性在多个领域都有着广泛的应用。
1. 工程领域的应用在工程领域中,流体粘性和黏性的研究对于设计和优化各种结构和系统至关重要。
例如,汽车工程师需要考虑空气对车辆运动的阻力,以及黏性对车辆行驶稳定性的影响。
同时,在船舶和飞机设计中,黏性的考虑也是十分重要的。
2. 传热领域的应用流体的粘性和黏性对于传热过程有着明显的影响。
在传热装置中,如换热器和冷却剂管道中,黏滞系数决定了热传递的速率和传热效率。
而流体的黏性也直接影响着粘弹性材料的应用,如胶水、涂料等。
3. 地球科学中的应用流体粘性和黏性的研究对于地球科学领域的地壳运动、地震活动以及火山喷发等现象的解释和预测具有重要意义。
粘性流体的基本概念

14
湍流的数值模拟方法
湍流研究方法
直接法(DNS) 统计平均法 大涡模拟(LES)
谱方法 伪谱法 涡动力学法 雷诺平均法(RANS) 统计法
Recr' = 8000~12000。
24
2、粘性的影响
均匀流动流过一个二维圆柱(半径为R)的理想流
动的解是一个均匀流U∞与一个偶极子叠加而得到的势
流解。
y
U P
B
r R
A
C
ur
U
21
B
图1-1 雷诺试验
G
K
T
如果试管内流速逐渐提高,可以看出颜色流束逐渐波动, 但还与周围流体没发生混杂。随着流速的进一步提高,颜色流 束开始断开,发生了局部混杂。当到某一流速Vcr'(上临界流 速)时,颜色流体在尖针出口即与周围流体发生混杂,整个玻 璃管呈淡的颜色流。可以认为此时层流流态已完全破坏,流体 微团间发生强烈的动量交换,液流呈不规律的湍乱状态,称为 湍流。
格子 Boltzmann 法(LBM)
15
雷诺平均湍流模式理论
Reynolds 平均理论
代数涡粘模型
涡粘性模型
单方程模型 双方程模型
标准k 重整化群k
Reynolds 应力模型
二阶矩应力方程模型 代数应力方程模型(ASM)
16
小尺度湍流分量的描述
研究原因:初始条件的微小扰动,经过一段时间 的发展可以完全改变湍流运动的细节;但是高雷诺数 的完全发展湍流的统计平均行为是稳定的。完全发展 湍流的这一特征决定了统计理论在湍流研究中的地位。
《高等流体力学》第7章 粘性流体力学基础

1 v2 ∂v + ∇ + Ω × v= f + ∇ ⋅ P ∂t ρ 2
2 P = − pδ + τ = − p + µ∇ ⋅ v δ + 2 µε 3
v2 1 1 ∂v 1 2 + ∇ + Ω × v= f − ∇p − ∇( µ∇ ⋅ v ) + ∇ ⋅ (2 µε ) ∂t ρ ρ 3 ρ 2
对初始条件的极度敏感性目前只解决了低维系统中的几种转捩方式而湍流场是时间与空间的函数对于每一空间点可看成一维混沌所以湍流是无穷维混沌现有的低维系统理论只能对湍流作定性描述说明湍流是ns方程内在特性的表现从理论上证明了ns方程对湍流的适用性
第七章 粘性流体力学基础
主 讲:刘全忠 单 位:能源科学与工程学院 流体机械及工程研究所 Email:liuquanzhong@
Lamb型方程变为
对上式两边取旋度,得到
整理后得到
这是最一般的涡量输运方程。该式清楚地表明:流 体的粘性、非正压性和质量力无势,是破坏旋涡守 恒的根源。在这三者中,最常见的是粘性作用。
1 2 1 ∂Ω 1 + ∇ × (Ω × v ) = ∇ × f − ∇ × ( ∇p ) − ∇ × ∇( µ∇ ⋅ v ) + ∇ × ∇ ⋅ (2 µε ) ρ ∂t ρ 3 ρ
λδ ijδ kl + µ (δ ik δ jl + δ ilδ jk ) ε kl τ ij = Cijkl ε kl = = λδ ij ε kk + µ ( ε ij + ε ji = ) λδ ijε kk + 2µε ij
流体力学5.4 粘性流体运动的一般性质

所以,无旋运动速度场的解只能满足理想流体的边界条 件,无法满足粘性流体的边界条件。即同时满足N-S方 程和无滑移条件的无旋运动不存在,所以粘性流体流动 一定是有旋的。
5.4.2粘性流动的能量耗散性
流体力学第五章
粘性流体运动时,部分机械能转化为热能的现象称为机 械能的耗散性,这部分机械能用于克服粘性力做功。单 位体积内耗散的动能由耗散函数表示
有限体积内耗散能量为 E=d
5.4.3粘性流动的旋涡扩散性
流体力学第五章
在理想流体中,无旋运动及有旋运动都是大量存在的。 而粘性流体则都是有旋运动。
在粘性流体中存在着旋涡的扩散现象。即旋涡强的地方 向旋涡弱的地方输送涡量。直至涡量相等为止。
流体力学第五章
第五章 粘性流体动力学
流体力学第五章
5.4 粘性流体运动的一般性质
5.4.1粘性流动的有旋性
流体力学第五章
在理想流体中,无旋运动及有旋运动都是大量存在的。
(无旋)有势、正压,初始无旋,则一直无旋;定常流动, 某截面无旋,则整个流动无旋。 (有旋)无势或斜压,流 动有旋,气象学中大量存在。
在不可压缩粘性流体中,情形就不同了。
V 0
dV dt
F
1
p
若流动为无旋,则
ห้องสมุดไป่ตู้
V 0
dV dt
F
1
p
可见无旋运动的速度场同时满足欧拉方程和N-S方程。
流体力学第五章
考虑边界条件
理想流体 Vn 0,Vt 0 粘性流体 Vn 0,Vt 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d 2g
d
,
Re umd
o
水泵 1 水池
局部损失(局部范围流动旋涡、转向或撞击引起)
h
um2 2g
—局部损失系数
阀门
2 2
z 1
o
水泵 1 水池
3.管路计算
简单管路:——查到 ,后 应用能量方程
串联管路:直径或粗糙度不同的简单管路串在一起
7.7.2 圆管内的湍流速度分布(5个区域)
1.层流底层 (y d ):
du
dy
u
y
0
(y从壁面算起)
u 0 y
u yu u
( u
0
— 壁面剪应力速度)
记 u u , y yu ,无因次速度分布:
u
u y ( y 5)
2.过渡层(5 y 30) :
u
11arctan
y 11
3.
水力光滑管湍流核心区
e
(
u
4, y
30):
e
d
Prandtl 近壁假设:核心区 0 常数,l ky
(
t )
du dy
l2 ( du )2
dy
0
对数定律:
u 1 ln yu c
u k
k 0.4 , c 5.5
(Nikuradse实验)
u 2.5ln y 5.5, ( y 30) ——水力光滑管
rh 湿润周长
液
a
充满
充满 面
水力半径
流体与管壁接触 的边界长度
a×a 矩形
rh
a 2
a×b 矩形
rh
ab ab
充液面积 a×b
2ab rh 2a b
非圆截面管的当量直径 d e
de 2rh ,
e e;
de 2rh
f (Re,e
de
)
(Re um 2rh )
以圆管计算或查Moody图得出非圆直管的阻力系数。
u umax
y a
1
7
,
Re
105
根据比值
um umax
测定管中最大流速求平均流速、流量。
管流速度剖面 层流:抛物型
Re=106
Re=104 Re<2000
湍流:指(对)数型(丰满)。Re愈大愈接近于平均速度。
4. 水力粗糙管湍流核心区速度分布 (e u 60)
Nikuradse实验:k=0.4 、c=8.5,得到
Nikuradse管流实验曲线:
f (Re, e )
d
1. 层流区 (Re 2300) 1次方阻力区
64
Re
hf um1
人工粗糙度
2.过渡区 (2300 Re 4000) 流动不稳定,可能是层流,也可能是湍流。
3.流水力光滑区
4000 Re 26.98d
e
8
7
(1.75次方阻力区)
1. 能量方程
umi Q / Ai
轴线位置
p1
1
u
2 m1
2g
z1 H T
p2
2
u
2 m
2
2g
z2 h
动能修正系数:
2 1
(层流) (湍流)
动力源的功率: N QH T
2.流动损失
h h f h
扬程
流动损失
2 2
沿程损失(管路粘性摩擦损失)
z
1
hf
l um2 , f (Re, e )
最大速度: 平均速度:
umax 2.5 ln au 5.5
u
um umax 3.75u
y a
亏损定律: umax u 2.5ln a ——水力光滑和水力粗糙管
u
y
指数定律: u
u
cn
yu
n
u y n umax a
Re 3.2106 光滑管
Blasuis
1/7次方规律:
Re
e
3.71d
(经验公式)
5.湍流粗糙管平方阻力区
Re 4160 d
2e
0.85
1 2.0 lg d 1.74
2e
hf um2 (与Re无关)
Moody图: f (Re, e )
d
7.7.4 非圆管中的摩擦阻力系数
经验方法计算:把非圆截面管化为当量的等截面圆管。
当量圆管
2A 2 过流截面积
湍流运动方程组的封闭性:
方程数:4个
未知量:ui , p, pij (6个)共10个 补充方程:湍流应力与平均速度之间的关系式——湍流模式。
7.6 Prandtl 混合长度理论(半经验)
基本思想:把湍流中微团的脉动与气体分子的运动相比拟。
层流:
l
du dy
(分子运动)
湍流: t
u v
t
du(微团脉动)
dy
湍流粘性系数
涡粘性系数
y
l' l' y1
o
v ' u+δu u
δA u-δu
x
平面平行定常湍流的摩擦剪应力:
l
t
(
t )
du dy
t
l2
du dy
du , dy
t
l2
du dy
l ——混合长度(由假定及实验确定),湍流中 t 。
7.7 圆管内的(充分发展)湍流
7.7.1 引言
1.充分发展流
u 2.5 ln y 8.5
u
e
um 2.5 ln a 4.75
e
d
u
e
7.7.3 圆管中的摩擦阻力系数
0
1 8
um2
8
u um
2
um
速度分布公式
层流:解析解
f (Re, e )
d
光滑管或粗糙管湍流:理论方法、经验或半径公式(实验)。
五个区域——层流区、临界区、光滑管区、过渡区、完全湍 流粗糙区。
7.8 管路的计算
工程管路:通常包括
• 管道
• 动力源(水泵、风机、轮机)
z
• 各种部件(弯头、阀门、突缩结构、
1
扩张结构和分叉等)。
o
2 2
水泵 1 水池
三类问题: • 给定管路尺寸和流量,确定管路压降(损失),选择动力头; • 给定管路尺寸和压降(动力头),确定流量; • 根据给定的流量和压降,设计管路尺寸(管径)。
d
层流:
L d
0.057 Re。L
114dRecr
2000
湍流:L=(25-50)d
L
2.管内湍流结构
3.水力光滑与水力粗造 “水力光滑管”d: e
“水力粗糙管”:d e
湍流核心区
过渡区
层流底层 d
d
34.2 Re 0.875
e ——管壁的绝对粗糙度
e
e ——相对粗糙度
d
de (a)
d (b)
4000 Re 105: 0.3164
Re0.25
h f
u
1.75 m
(1/7次方规律)
4000
Reቤተ መጻሕፍቲ ባይዱ
26.98
d
e
8
7
:
1 2.0 lg Re
0.8
(Karman-Prandtl公式)
4.湍流粗糙管过渡区
26.98 d
e 8 7
Re 4160d
2e
0.85
1
2
lg
2.51
ui
t
(ui
u
j
)
x j
p
xi
2ui
x j
(
uiuj )
2ui ——平均运动的粘性应力
uu pij uiuj vu
wu
uv vv wv
uw
vw ww
湍流应力 Reynolds应 力
pij 是p对ji 称张量,六个独立量。它源于湍流脉动引起 的动量输运。因此,湍流应力 uiu是j 和平均流关联的。
