第十五章 复数复习纲要
复数知识点复习总结

复数知识点复习总结复数知识点复习总结「篇一」眼下即将进入炎热的暑期,繁重的学习压力,酷热的环境对每位考研的学生来讲都是一个不小的挑战。
如何在如此考验耐力的条件下保证有效地复习?跨考教育公共课教研室张老师认为,非但科学的学习方法还得有颗坚韧的心,信心决不动摇,努力决不松懈,策略决不疏忽,做到三个“绝不”,暑期备考方能一路过关斩将。
演讲大师齐格勒曾经讲到,世界上牵引力最大的火车头停在铁轨上,为了防滑,只需在它的8个驱动轮前面塞一块1英寸见方的木块,这个庞然大物就无法动弹。
然而,一旦这个巨型火车头开始启动,这小小的木块就再也挡不住它了;当它的时速达到100英里时,一堵5英尺厚的钢筋混凝土墙也能轻而易举被它撞穿。
从一块小木块令其无法动弹,到能撞穿一堵钢筋水泥墙,火车头威力变得如此巨大,原因不是别的,就是因为火车头的潜力已经被挖掘出来了。
而潜能之所以被挖掘出来,在于它受到了激励,打开了潜能释放的阀门。
每个人都有巨大的潜能,然而这潜能却往往惨遭埋没,因为释放潜能的阀门没有激励,无法开启。
一句话、一件事、一个灵感、一次邂逅都可以成为释放潜能的钥匙。
信心决不动摇,努力决不松懈,策略决不疏忽,考研路上离不开精神动力。
信心决不动摇,在信念上坚如磐石,“任尔东西南北风,咬住青山不放松”;努力决不松懈,在行动上勇往直前,“努力才是硬道理”,空有信心必然心虚,只有扎实苦干,才是成功的捷径;策略决不疏忽,在考虑问题时决不轻敌,正所谓“战略上藐视,战术上重视”,力求认认真真做好考研复习的每一件事情。
然而,如果我们要想主宰自己的命运,我们就不能完全寄希望于来自外界的激励,而必须学会自我激励,自己开启内在潜能的阀门。
这在考研过程中尤为重要,考研往往是孤独的,往往很难获得来自朋友亲人等外界的激励,因此需要我们把自我激励化为生活的一部分,不断激发自己的信心,沉着冷静地扎实前行!考研过程会有很多意外,会有很多的意想不到的打击,比如课程设计,专业实习,感冒发烧等;或者在复习中出现瓶颈,个人学习遇到难题,复试面试时遇到自己从没有接触过的知识点这个时候,学会痛并快乐着的忍耐,不断激励自己“信心决不动摇,努力绝不松懈,策略绝不疏忽!”,大声唱响自己的人生之歌,生命之歌,站在金色的起跑线上,向着理想,以最快的速度,奔跑!也许下一站,就会柳暗花明!复数知识点复习总结「篇二」1.图象题。
复数高二知识点

复数高二知识点复数是英语中的一种重要的语法形式,它用于表示两个或两个以上的人、事物或概念。
在高二英语学习中,复数的使用是一个重要的知识点。
本文将从名词的变化规则、特殊名词以及复数的用法等方面详细介绍高二英语复数的知识点。
一、名词的变化规则1. 一般情况下,将名词变为复数的方法是在词尾加上-s。
例如:- book → books- pen → pens- student → students2. 以s、x、ch、sh结尾的名词,在词尾加-es构成复数。
例如:- bus → buses- box → boxes- watch → watches- brush → brushes3. 以辅音字母+y结尾的单词,将y变为i,再加-es构成复数。
例如:- baby → babies- lady → ladies- city → cities4. 以元音字母+y结尾的名词,直接加-s构成复数。
例如:- boy → boys- day → days5. 以“辅音字母+o”结尾的名词,在词尾加-es构成复数。
例如:- tomato → tomatoes- potato → potatoes6. 以“元音字母+o”结尾的名词,直接加-s构成复数。
例如:- radio → radios- zoo → zoos7. 以“辅音字母+f或fe”结尾的名词,将f或fe变为v,再加-es 构成复数。
例如:- wife → wives- wolf → wolves二、特殊名词的复数形式1. 一些名词的复数形式需要记忆,它们的复数形式不遵循一般的变化规则。
例如:- man → men- woman → women- child → children- tooth → teeth- foot → feet2. 有些名词的复数形式与单数形式相同。
例如:- sheep → sheep- fish → fish- deer → deer三、复数的用法1. 复数可以用来表示多个人或物。
复数知识点总结ppt

复数知识点总结ppt一、基本概念复数是指表示两个或两个以上的名词或代词的数量。
在英语语法中,复数形式通常通过在名词或代词后面加上-s或-es来表示。
复数形式的使用是英语语法的重要部分,因此掌握复数知识点对于学习和运用英语非常重要。
二、名词的复数形式1. 一般情况下,在名词后面加上-s来表示复数形式,如:book-books, cat-cats, dog-dogs 等。
2. 以-s, -x, -sh, -ch结尾的名词,复数形式加-es,如:box-boxes, bus-buses, brush-brushes, church-churches等。
3. 以辅音字母+y结尾的名词,将y变为i,再加-es表示复数形式,如:baby-babies, city-cities, party-parties等。
4. 以-f或-fe结尾的名词,将f或fe变为v,再加-es表示复数形式,如:leaf-leaves, wolf-wolves, wife-wives等。
5. 不规则名词的复数形式,如:man-men, woman-women, child-children, tooth-teeth等。
6. 复合名词的复数形式,在最后一个名词后面加上-s或-es表示复数形式,如:brother-in-law-brothers-in-law, son-in-law-sons-in-law等。
三、代词的复数形式1. 人称代词的复数形式,如:I-we, you-you, he-they, she-they等。
2. 物主代词的复数形式,如:my-our, your-your, his-their, her-their等。
3. 不定代词的复数形式,如:some-some, any-any, both-both等。
四、复数形式的用法1. 表示两个或两个以上的人或物时,使用复数形式,如:There are three apples on the table.2. 表示一个整体的多个部分时,使用复数形式,如:The team are practicing for the match.3. 在可数名词的数量前面使用数词表示复数,如:ten books, five cats等。
高考数学考前知识要点复习十五复数.doc

高中数学第十五章复数考试内容:复数的概念. 复数的加法和减法. 复数的乘法和除法. 数系的扩充. 考试要求:(1) 了解复数的有关概念及复数的代数表示和几何意义(2) 掌握复数代数形式的运算法则,能进行复数代数形式的加法、减法、乘法、除法运算. (3) 了解从自然数系到复数系的关系及扩充的基本思想.§ 15. 复数知识要点1. ⑴复数的单位为i ,它的平方等于一 1,即 i 2= J.⑵复数及其相关概念:① 复数一形如a +bi 的数(其中a, b e R ); ② 实数一当b = 0 时的复数a + b i, 即a ;③ 虚数一当b^O 时的复数a+ bi ;④ 纯虚数一当a 二0且13工0吋的复数a+ bi ,即bi.⑤ 复数a+ bi 的实部与虚部一a 叫做复数的实部,b 叫做虚部(注意a, b 都是实数) ⑥ 复数集C —全体复数的集合,一般用字母 C 表示.⑶两个复数相等的定义:a +bi =c+di = a =c 且 d d (其中,a, b, c, R )特别地 a+ bi= 0= a= b= 0 ・⑷两个复数,如果不全是实数,就不能比较大小注:①若Zl,Z2为复数,则厂若Z1 + Z2 > 0 ,则Z1A_Z2・(X ) [ Zl , Z 2为复数,而不是实数] 2 喏 Z1 Y Z2,则 Z1 Z2 Y °・(厂)2 b c c a 2+ — 2 + — =()()0 是2(a b)€②若 a, b, c C ,a b c 的必要不充分条件.(当(b c) 21,()0时,上式成立)2. (1)复平面内的两点间距离公式:d zi z2・其中Z1, Z2是复平面内的两点Z1和Z2所对应的复数,d表示Z1和Z2间的距离・由丄可得:复平面内以z为圆心,r为半径的圆的复数方程:z zo r (r 0).—= o⑵曲线方程的复数形式:I - I =| ■ J①z zo r表示以zo为圆心,r为半径的圆的方程・②Z乙Z Z2表示线段乙Z2的垂直平分线的方程3. 尹轨复数的性质:=Z1 Z2 Z1 Z2I)表示以2aa 0 2a z z1 2为焦点,长半轴长为a 的椭圆的方程z22aII IzIH 此方梅表示线陵 Zil Z 2I). 1 2=| I④ z Z1 Z Z22a (0 2a ziz 2),表示以Zi, Z2为焦点,实半轴长为a 的双曲线方程(若2a z z ,此方程表示两条射线)・ 1 2\卜ul<i +丨勻州丨⑶缆对值木馨式:设Z1, Z2是不等于零的复数人则① |zi|-|z2 | 伞-Z2 | 伞 | +上2 |.左边取等号的条件是 Z2 =/Zi ( /u € R?且A 0),右边取等号的条件是42/.乙R,. Y 0).②Z1 Z 茅 Zf £2 •孕・・£2・左边取等号的条件是 Z2 Z1 ( R,0),右边取等号的条件是Z2 Z1 ( R,0).注:Ai A2 A2A3 A3A4An 1 AnAl An •z =11+ + +=-1 1 = = 一 = 一 2 i4 2 )1 1就会得到1 1的错误结论・ ( 2 2|x| X •当X 为虚数时,|x| X ,所以复数集内解方程不能采用两边平方 法.⑵常用的结论:j 2I n I I 11| n414243②在实数集成立的z 2 , ★ z 、 a仁」 Z1z z 2bi (z a + bi )Z1 Z2 Z1 Z2Z 1 Z 2(Z2 0 )注:两个共轨复数之差是纯虚数(X[之差可能为零,此时两个复数是相等的 ]4 (1)①复数的乘方:z 乙・.z(nn②对任倔b zr Z1 ,Z 2一、 m -7 -7m n ③ Z Znz n z n*1 2注:①以上结论不能拓 展到分数指数幕的形式, 否则会得到荒谬的结果,如 U 4 1若由1 1 1 5 5 1 ,n, n +1 j n+2Jn 、 (1+ ± 2= ±4—i = i) 2i, rj3 0,( 4^+ = -.4 +・I1 I的 立 方+虚+数 根 如如=◎如 划 = €5.32⑴复数z 是实数纯z R z z.,10,+_ = n n Z 20(贏数的充要条件: ① ②若z 0 z 是纯虚数⑵模相等亀方向相同的向量,不管它的起点在哪里,都认为是相等的,而相等的向量表屈 一复数•特例:零向量的方囘是任轡P 其停为零 .|Z| |z|9注: 6.⑴复数的三角形式:z辐角主值: 适合于0< 注:①至为塚时,angz②辐角是多值的,都相差 的整数倍・ r(cos i sin )・7t< 2 的值,iferg z . 可取TO,2:;)内任意屛.、 ______ 3 ③率 则 0 -prg a 6 0,arg^ a) ^,arg ai 步逼g( ai)6⑵复数的代数形式与三角形式的互化:a bi a©os 0i sin ) ,扌a b,sin色儿类三夢輕的标樓住式:n +07T +0r (cos - 0i sin ) r[cos( ) i sin( +)1n -8r(cos0 + i sin ) 6 = r[cos( -- 8 1 iSiL e )]r( cosi sin ) r[cos( )i sin()]r (sin cos ) r[cos( 2 7.复数集申解一元二绳方程: isin (2+ )[=工 ±v A 在复数朋解关眨x 的一元二次方程 2 ax bx 6內,应注意下同题 ①当a,b,c R 时,若 >0, X1 ,2 b 8 ;+若 0 0,则有二相蒂复i 数根 2a ,2 a,b,c 不全为实数时,不能 方程根的情况・ X1 ,2 2a ;若 =0,则有二相等实数根 2a 1 h o (牟,3为共觑复数百+6 ② 当 ③ 不玲b,c 为何复数,都可用求根公式求根,并且韦达定理也成 8.复数的三角形式运算:H i sin ) r i r r i )](COS 1 2 2 (COS 2 sin 2) 1 2 [cos( 1 2) 1 2sin(=_0 -0 +j si"%—i"1[cos( )吟 01=e +2n n棣莫弗定理:[r(cos isin )] r (cosn i sin n )r (cosO +i sin 8 )~r (cos i sin )2 2 2-4-。
复数全章知识点

复数全章知识点一、知识概述《复数》①基本定义:复数就是把实数和虚数合在一起的数。
比如,3是实数,但如果写成3 + 0i,这就是复数了。
其中i是虚数单位,规定i的平方等于-1。
就好像有一个神秘的数字世界,原本只有像1、2、3这些实实在在能看到摸到的实数,但科学家为了解决一些问题,发现还得有像i这么个神奇的东西,当它和实数组合起来就成了复数。
②重要程度:在数学学科里可是非常重要的,很多数学问题,特别是和方程、函数相关的,如果没有复数的概念,就没办法完整解决。
像在高等数学、物理学中的交流电计算等领域它可都是大功臣。
③前置知识:要掌握好实数的知识,像有理数、无理数,它们的运算规则,四则运算这些基本功。
因为复数也会用到实数的运算规则。
④应用价值:在电工学里,计算交流电的时候,如果只考虑实数,很多计算是没办法进行的。
因为交流电是有相位差的,而这个相位差就是复数里虚数部分在现实中的体现。
在信号处理里,也经常用到复数,把信号分解成实部和虚部来分别处理。
二、知识体系①知识图谱:复数在数学学科里算是数系扩充后的内容,它是实数系的扩展。
如果我们把数系比作一个家族,实数是家族的一大部分,那复数就是把这个家族又扩大了一些,把像i这种很奇怪的成员也包含进来了。
②关联知识:和方程、函数特别是多项式函数有很大联系。
许多多项式方程在实数范围内无解,但在复数范围内就有解了。
还和向量有点联系。
可以把复数看成一种特殊的向量,实部和虚部分别是向量的两个分量。
③重难点分析:- 掌握难度:我刚学的时候觉得有点难的就是虚数单位i这个概念,有点抽象。
它不像实数那么直观。
- 关键点:理解复数的实部、虚部,还有i的平方等于-1这条铁律。
能熟练进行复数的四则运算。
④考点分析:- 在考试中,如果是基础数学考试,会重点考查复数的基本运算,像加、减、乘、除。
比如出一道题让你计算(2 + 3i)+(1 - 2i),这种简单的计算。
如果是稍难一点的或者高等数学考试,会考查复数在方程中的应用,比如解一个在实数内无解的二次方程在复数范围内的解。
高三数学高考第一轮复习第十五章教案复数的概念

第七节 复数的的概念一、复习目标:1、了解数系的扩充过程,体会实际需求与数学内部的矛盾(数的运算规则、方程理论)在数系扩充过程中的作用;2、理解复数的基本概念以及复数相等的充要条件。
二、重难点:1.重点:理解并掌握复数的有关概念(复数集、代数形式、虚数、纯虚数、实部、虚部、复数相等)。
2.难点:复数的有关概念的应用。
三、教学方法:探析归纳,讲练结合四、教学过程(一)、谈新考纲要求及新课标高考命题考查情况,促使积极参与复数部分考查的重点是复数的有关概念、复数的代数形式、运算及运算的几何意义,一般是选择题、填空题,难度不大,预计今后的高考还会保持这个趋势。
预测2010年高考对本讲的试题难度不会太大,重视对基本问题诸如:复数的四则运算的考查,题目多以选择、填空为主。
(二)、知识梳理,方法定位(学生完成复资P148页填空题,教师准对问题讲评)1、复数的定义:形如(,)a bi a b R +∈的数叫复数,a 叫复数的实部,b 叫复数的虚部.全体复数所成的集合叫做复数集,用字母C 表示2、复数的代数形式: 复数通常用字母z 表示,即(,)z a bi a b R =+∈,把复数表示成a bi +的形式,叫做复数的代数形式.3、复数与实数、虚数、纯虚数及0的关系:对于复数(,)a bi a b R +∈,当且仅当0b =时,复数(,)a bi a b R +∈是实数a ;当0b ≠时,复数z a bi =+叫做虚数;当0a =且0b ≠时,z bi =叫做纯虚数;当且仅当0a b ==时,z 就是实数04、复数集与其它数集之间的关系:N Z Q R C 苘苘5、两个复数相等的定义:如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.这就是说,如果a ,b ,c ,d R ∈,那么a bi c di +=+⇔a c =,b d =6、复数的模:设oz =bi a +,则向量oz 的长度叫做复数bi a +的模(或绝对值),记作bi a +. (1)22b a bi a z +=+=;(2)1212Z Z Z Z ∙=∙;(3)2121z z z z =;7.共扼复数:如果两个复数的实部相等,而虚部互为相反数,则这两个复数互为共扼复数。
数学复数知识点提纲

数学复数知识点提纲数学复数知识点提纲复数的概念:形如a+bi(a,b∈R)的数叫复数,其中i叫做虚数单位。
全体复数所成的集合叫做复数集,用字母C表示。
复数的表示:复数通常用字母z表示,即z=a+bi(a,b∈R),这一表示形式叫做复数的代数形式,其中a叫复数的实部,b叫复数的虚部。
复数的几何意义:(1)复平面、实轴、虚轴:点Z的横坐标是a,纵坐标是b,复数z=a+bi(a、b∈R)可用点Z(a,b)表示,这个建立了直角坐标系来表示复数的平面叫做复平面,x轴叫做实轴,y轴叫做虚轴。
显然,实轴上的点都表示实数,除原点外,虚轴上的点都表示纯虚数(2)复数的几何意义:复数集C和复平面内所有的点所成的集合是一一对应关系,即这是因为,每一个复数有复平面内惟一的一个点和它对应;反过来,复平面内的每一个点,有惟一的一个复数和它对应。
这就是复数的一种几何意义,也就是复数的另一种表示方法,即几何表示方法。
复数的模:复数z=a+bi(a、b∈R)在复平面上对应的点Z(a,b)到原点的距离叫复数的模,记为|Z|,即|Z|=虚数单位i:(1)它的平方等于-1,即i2=-1;(2)实数可以与它进行四则运算,进行四则运算时,原有加、乘运算律仍然成立(3)i与-1的关系:i就是-1的一个平方根,即方程x2=-1的一个根,方程x2=-1的另一个根是-i。
(4)i的周期性:i4n+1=i,i4n+2=-1,i4n+3=-i,i4n=1。
复数模的性质:复数与实数、虚数、纯虚数及0的关系:对于复数a+bi(a、b∈R),当且仅当b=0时,复数a+bi(a、b∈R)是实数a;当b≠0时,复数z=a+bi叫做虚数;当a=0且b≠0时,z=bi叫做纯虚数;当且仅当a=b=0时,z就是实数0。
两个复数相等的定义:如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等,即:如果a,b,c,d∈R,那么a+bi=c+di a=c,b=d。
特殊地,a,b∈R时,a+bi=0a=0,b=0.复数相等的充要条件,提供了将复数问题化归为实数问题解决的途径。
高三数学高考第一轮复习第十五章教案复数的运算

第八课时 复数的运算一、复习目标:1、了解复数的代数表示法及其几何意义,能进行复数代数形式的四则运算;2、了解复数代数形式的加、减运算的几何意义;3、掌握复数的运算法则,并熟练地进行运算。
二、重难点:1.重点:掌握复数的运算法则,复数加减法的几何意义及应用。
2.难点:复数相关问题的综合应用。
三、教学方法:探析归纳,讲练结合 四、教学过程 (一)、谈新考纲要求及新课标高考命题考查情况,促使积极参与复数部分考查的重点是复数的有关概念、复数的代数形式、运算及运算的几何意义,一般是选择题、填空题,难度不大,预计今后的高考还会保持这个趋势。
预测2010年高考对本讲的试题难度不会太大,重视对基本问题诸如:复数的四则运算的考查,题目多以选择、填空为主。
(二)、知识梳理,方法定位(学生完成复资P149页填空题,教师准对问题讲评) 1、复数1z 与2z 的和的定义:12z z +=()()a bi c di +++=()()a c b d i +++ 2、复数1z 与2z 的差的定义:12z z -=()()a bi c di +-+=()()a c b d i -+-3、乘法运算规则: 设1z a bi =+,2z c di =+(a 、b 、c 、d R ∈)是任意两个复数,那么它们的积2()()()()a bi c di ac bci adi bdi ac bd ad bc i ++=+++=-++4、复数除法定义:满足()()()c di x yi a bi ++=+的复数x yi +(x 、y R ∈)叫复数a bi +除以复数c di +的商,记为:()()a bi c di +÷+或者di c bia ++则2222()()()()()()a bi a bi c di ac bd bc ad a bi c di i c di c di c di c d c d ++-+-+÷+===+++-++5、复数加、减法的几何意义 (1)加法的几何意义复数21z z + 是以→1oz 、→2oz 为两邻边的平行四边形对角线→oz 所对应的复数. (2)复数减法的几何意义复数21z z -是连接向量1OZ 、2OZ 的终点,并指向被减数的向量21z z 所对应的复数. 6、 重要结论对复数z 、1z 、2z 和自然数m 、n ,有n m n m z z z +=∙,mn n m z z =)(,nn n z z z z 2121)(∙=∙(2) i i =1,12-=i ,i i -=3,14=i ; 114=+n i,124-=+n i ,i i n -=+34,14=n i .(3) i i 2)1(2±=±,i i i -=+-11,i i i =-+11。
2020届高三数学一轮总复习 第十五章 复 数(文)(教师用书)
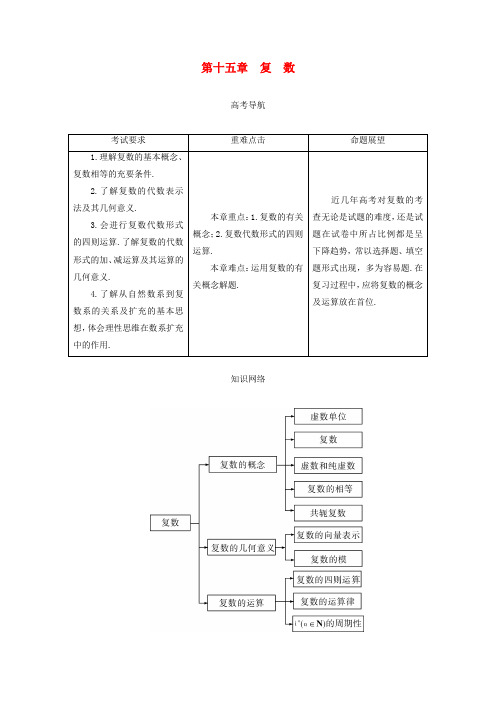
第十五章复数高考导航考试要求重难点击命题展望1.理解复数的基本概念、复数相等的充要条件.2.了解复数的代数表示法及其几何意义.3.会进行复数代数形式的四则运算.了解复数的代数形式的加、减运算及其运算的几何意义.4.了解从自然数系到复数系的关系及扩充的基本思想,体会理性思维在数系扩充中的作用.本章重点:1.复数的有关概念;2.复数代数形式的四则运算.本章难点:运用复数的有关概念解题.近几年高考对复数的考查无论是试题的难度,还是试题在试卷中所占比例都是呈下降趋势,常以选择题、填空题形式出现,多为容易题.在复习过程中,应将复数的概念及运算放在首位.知识网络15.1 复数的概念及其运算典例精析题型一 复数的概念【例1】 (1)如果复数(m 2+i)(1+m i)是实数,则实数m = ;(2)在复平面内,复数1+i i对应的点位于第 象限; (3)复数z =3i +1的共轭复数为z = .【解析】 (1)(m 2+i)(1+m i)=m 2-m +(1+m 3)i 是实数⇒1+m 3=0⇒m =-1.(2)因为1+i i =i(1+i)i 2=1-i ,所以在复平面内对应的点为(1,-1),位于第四象限. (3)因为z =1+3i ,所以z =1-3i.【点拨】 运算此类题目需注意复数的代数形式z =a +b i(a ,b ∈R ),并注意复数分为实数、虚数、纯虚数,复数的几何意义,共轭复数等概念.【变式训练1】(1)如果z =1-a i 1+a i 为纯虚数,则实数a 等于( ) A.0 B.-1C.1D.-1或1 (2)在复平面内,复数z =1-i i(i 是虚数单位)对应的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限【解析】(1)设z =x i ,x ≠0,则x i =1-a i 1+a i ⇔1+ax -(a +x )i =0⇔⎩⎨⎧=+=+0,01x a ax ⇔⎩⎨⎧-==1,1x a 或⎩⎨⎧=-=.1,1x a 故选D. (2)z =1-i i=(1-i)(-i)=-1-i ,该复数对应的点位于第三象限.故选C. 题型二 复数的相等【例2】(1)已知复数z 0=3+2i ,复数z 满足z ·z 0=3z +z 0,则复数z = ;(2)已知m1+i=1-n i ,其中m ,n 是实数,i 是虚数单位,则m +n i = ; (3)已知关于x 的方程x 2+(k +2i)x +2+k i =0有实根,则这个实根为 ,实数k 的值为 .【解析】(1)设z =x +y i(x ,y ∈R ),又z 0=3+2i ,代入z ·z 0=3z +z 0得(x +y i)(3+2i)=3(x +y i)+3+2i ,整理得 (2y +3)+(2-2x )i =0,则由复数相等的条件得⎩⎨⎧=-=+,022,032x y 解得⎪⎩⎪⎨⎧-==,23,1y x 所以z =1-i 23. (2)由已知得m =(1-n i)(1+i)=(1+n )+(1-n )i.则由复数相等的条件得⎩⎨⎧==⇒⎩⎨⎧-=+=,1,210,1n m n n m 所以m +n i =2+i.(3)设x =x 0是方程的实根,代入方程并整理得0,i )2()2(0020=++++k x kx x 由复数相等的充要条件得⎪⎩⎪⎨⎧=+=++.02,020020k x kx x 解得⎪⎩⎪⎨⎧-==22,20k x 或⎪⎩⎪⎨⎧=-=.22,20k x 所以方程的实根为x =2或x =-2,相应的k 值为k =-22或k =2 2.【点拨】复数相等须先化为z =a +b i(a ,b ∈R )的形式,再由相等得实部与实部相等、虚部与虚部相等.【变式训练2】(1)设i 是虚数单位,若1+2i 1+i=a +b i(a ,b ∈R ),则a +b 的值是( ) A.-12 B.-2 C.2 D.12(2)若(a -2i)i =b +i ,其中a ,b ∈R ,i 为虚数单位,则a +b = .【解析】(1)C.1+2i 1+i =(1+2i)(1-i)(1+i)(1-i)=3+i 2,于是a +b =32+12=2. (2)3.2+a i =b +i ⇒a =1,b =2.题型三 复数的运算【例3】 (1)若复数z =-12+32i , 则1+z +z 2+z 3+…+z 2 008= ; (2)设复数z 满足z +|z |=2+i ,那么z = .【解析】 (1)由已知得z 2=-12-32i ,z 3=1,z 4=-12+32i =z . 所以z n 具有周期性,在一个周期内的和为0,且周期为3.所以1+z +z 2+z 3+…+z2 008 =1+z +(z 2+z 3+z 4)+…+(z 2 006+z 2 007+z 2 008)=1+z =12+32i. (2)设z =x +y i(x ,y ∈R ),则x +y i +x 2+y 2=2+i , 所以⎪⎩⎪⎨⎧==++,1,222y y x x 解得⎪⎩⎪⎨⎧==,1,43y x 所以z =43+i. 【点拨】 解(1)时要注意x 3=1⇔(x -1)(x 2+x +1)=0的三个根为1,ω,ω-,其中ω=-12+32i ,ω-=-12-32i , 则 1+ω+ω2=0, 1+ω-+ω-2=0 ,ω3=1,ω-3=1,ω·ω-=1,ω2=ω-,ω-2=ω.解(2)时要注意|z |∈R ,所以须令z =x +y i.【变式训练3】(1)复数11+i +i 2等于( ) A.1+i 2 B.1-i 2 C.-12 D.12(2)(2020江西鹰潭)已知复数z =23-i 1+23i+(21-i )2 010,则复数z 等于( ) A.0 B.2 C.-2i D.2i【解析】(1)D.计算容易有11+i +i 2=12. (2)A.总结提高复数的代数运算是重点,是每年必考内容之一,复数代数形式的运算:①加减法按合并同类项法则进行;②乘法展开、除法须分母实数化.因此,一些复数问题只需设z =a +b i(a ,b ∈R )代入原式后,就可以将复数问题化归为实数问题来解决.。
高考数学一轮复习 第十五章复数课件 新人教版选修2

4.zm·zn=zm+n ,(zm)n= zmn ,(z1·z2)n=
;(其中
七、常见的运算规律
1.i的周期性:i4n+1= i ,i4n+2= -1,i4n+3= -i ,
i4n= 1 ;(n∈Z)
2.(a+bi)(a-bi)=a2+b2 ;
3.(1±i)2= ±2i ; 4. 5.( = i , )2= ±i ; = -i ;
命题预测:从2009年高考来看,复数仍是高考的必考 内容,主要考查复数的概念和复数代数形式的运算. 1.复数概念的考查,高考命题仍以考查基本概念为 主,题型为选择题、填空题,一般为容易题.
2.复数运算的考查,高考命题主要以复数的代数形
式为主,考查复数的加、减、乘、除运算,考查学生的运 算能力.了解从自然数系到复数系扩充的基本思想,为上 大学后的学习做准备.所以复数仍然是高考命题中必有的 部分.
备考指南:我们可以看到高考常以考查复数的代数运 算为主兼顾考查复数概念,估计这一命题趋势还将继续下 去,所以复习时, 1 .掌握好复数的基本概念及形如 a + bi(a , b∈R) 的 复数表示实数、虚数、纯虚数的充要条件.要注意 a + bi 表示纯虚数时,不要忽略a=0且b≠0这一条件. 2.在进行复数运算时,不能把实数集的某些法则和 性质搬到复数集上来,如不等式的性质、绝对值的定义, 偶次方非负等,要熟练掌握复数加、减、乘、除的运算法 则. 3.在复习中需注意的两点:一是注意练习难度不要 过大,以中低档题为主,要求做到熟练准确.二是注意转 化思想方法的训练、善于将复数向实数转化.
“b≠0”.对照各选项,故选A.2+4i C.2+4i 解析: 答案:A
= B.-2-4i D.2-4i
(
)
3 . (2009· 北京 ) 在复平面内,复数 z = i(1 + 2i) 对应的 点位于 A.第一象限 C.第三象限 B.第二象限 D.第四象限 ( )
复数知识点复习

复数知识点复习复数是数学中的一个重要概念,在许多领域都有着广泛的应用。
下面咱们就来好好复习一下复数的相关知识。
一、复数的定义形如 a + bi 的数叫做复数,其中 a 和 b 均为实数,i 为虚数单位,满足 i²=-1。
a 被称为实部,记作 Re(z);b 被称为虚部,记作 Im(z)。
当 b = 0 时,复数 a + bi 就变成了实数 a;当 a = 0 且b ≠ 0 时,复数就称为纯虚数 bi。
二、复数的表示形式1、代数形式就是咱们最常见的 a + bi 这种形式。
2、几何形式在平面直角坐标系中,以 x 轴为实轴,y 轴为虚轴,复数 a + bi 可以用坐标(a, b) 来表示。
3、三角形式复数 a + bi 可以表示为r(cosθ +isinθ),其中 r =√(a²+ b²),θ是复数的辐角。
4、指数形式根据欧拉公式 e^(iθ) =cosθ +isinθ,复数又可以写成 r e^(iθ) 的形式。
三、复数的运算1、加法和减法(a + bi) ±(c + di) =(a ± c) +(b ± d)i2、乘法(a + bi)(c + di) =(ac bd) +(ad + bc)i3、除法(a + bi) ÷(c + di) =(ac + bd) /(c²+ d²) +(bc ad) /(c²+ d²)i四、复数的模和辐角1、复数的模复数 z = a + bi 的模记作|z|,|z| =√(a²+ b²)模的几何意义就是复数对应的点到原点的距离。
2、复数的辐角以 x 轴正半轴为始边,向量 OZ 所在的射线为终边的角θ 叫做复数z = a + bi 的辐角。
辐角主值通常用 arg z 表示,并且规定在0 ≤ arg z <2π 的范围内。
五、复数的性质1、共轭复数两个实部相等,虚部互为相反数的复数互为共轭复数。
华师一2011届高三第一轮复习教案(第十五章)第1讲--复数的概念

课 题: 复数的有关概念教学内容: 复数的概念教学目的: 了解复数的有关概念及复数的代数表示和几何意义;掌握复数代数形式的运算法则,能进行复数代数形式的加法、减法、乘法、除法运算.教学重点: 掌握复数代数形式的运算法则,能进行复数代数形式的加法、减法、乘法、除法运算. 教学过程:一、知识概要教学要求:了解复数的有关概念及复数的代数表示和几何意义;掌握复数代数形式的运算法则,能进行复数代数形式的加法、减法、乘法、除法运算;了解从自然数系到复数系的关系及扩充的基本思想知识点1 复数的概念形如(,)a bi a b R +∈的数叫复数,a 叫复数的实部,b 叫复数的虚部全体复数所成的集合叫做复数集,用字母C 表示。
指出:(1)关于虚数单位i : ① 它的平方等于-1,即 21i =-; ②实数可以与它进行四则运算,进行四则运算时,原有加、乘运算律仍然成立(2)i 与-1的关系: i 是-1的一个平方根,即方程x 2=-1的一个根,方程x 2=-1的另一个根是-i(3)i 的周期性:i 4n+1=i, i 4n+2=-1, i 4n+3=-i, i 4n =1知识点2 复数的分类复数a+bi(a 、b ∈R ),当b=0时,就是实数;当b≠0时,叫做虚数;当a=0, b≠0时,叫做纯虚数. 指出:(1)① 复数是实数的充要条件:z=a+bi ∈R ⇔b=0, a ∈R ;z ∈R ⇔z=z ; z ∈R ⇔z 2≥0. ② 复数是纯虚数的充要条件:z=a+bi 是纯虚数⇔a=0且b≠0(a 、b ∈R );z 是纯虚数⇔z+z =0, 且z≠0; z 是纯虚数⇔z 2<0.(2)数的概念扩展为复数后,实数集中的一些运算性质、概念、关系就不一定适用了.如不等式的性质、绝对值的定义、偶次方非负等.知识点3 复数的相等如果两个复数a+bi(a 、b ∈R )与c+di(c 、d ∈R )的实部与虚部分别相等,就说这两个复数相等.指出:一般地,两个复数只能说相等或不相等,而不能比较大小如果两个复数都是实数,就可以比较大小 也只有当两个复数全是实数时才能比较大小知识点4 共轭复数当两个复数的实部相等,虚部互为相反数时,这两个复数互为共轭复数(当虚部不为0时又可说成互为共轭虚数).指出:两个复数和、差、积、商的共轭等于其共轭的和、差、积、商. 即).0()(,)(,)(,)(22121212*********≠=⋅=⋅-=-+=+z z z z z z z z z z z z z z z z z 知识点5 复平面建立直角坐标系来表示复数的平面叫做复平面,x 轴叫做实轴、y 轴叫做虚轴.显然,实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数.知识点6 复数的模设z=a+bi, (a, b ∈R ),则r=22b a +叫做z 的模,记作|z|,即|z|=|a+bi|=22b a +,显然r≥0,几何意义是复平面上的点Z(a, b)到原点的距离.指出:(1) 两个实数可以比较大小,但两个复数,如果不全是实数,就不能比较它们的大小.但两个复数的模可以比较大小(2) ①)|||(|2||||2221221221z z z z z z +=-++; ②22||||z z z z ==⋅;二、典例解析例1 已知m ∈R, 复数z=i m m m m m )32(1)2(2-++--当,当m 为何值时: (1)z ∈R ; (2)z 是纯虚数; (3)z 对应的点位于复平面第二象限;(4)z 对应的点在直线x+y+3=0上。
高中总复习第一轮数学 第十五章复数(理)15.1 复数的概念与运算

第十五章 复数(理)网络体系总览考点目标定位1.复数的概念.2.复数的加法和减法.3.复数的乘法和除法.4.数系的扩充.复习方略指南本章主要内容是复数的有关概念、代数形式、向量表示以及复数的运算法则.从近几年的高考试题看,对复数的要求呈下降趋势,试题考查的重点仍是基本概念和运算,为此建议复习中注意以下几点:1.在复习中,应注意理解和掌握复数的基本概念,特别是虚数、纯虚数、共轭复数、两复数相等及复数的模等.2.应重视数形结合的思想方法在解题中的应用.3.所选习题应突出概念、运算,以中、低档难度的选择题和解答题为主,并注意转化思想的应用.复数问题常转化为实数问题处理.15.1 复数的概念与运算巩固·夯实基础一、自主梳理1.i 叫虚数单位,满足(1)i 2=-1;(2)实数可以与i 进行四则运算,原有的加、乘运算律仍然成立,它具有周期性,表现为i 4n =1,i 4n+1=i,i 4n+2=-1,i 4n+3=-i(n ∈Z).2.形如a+bi(a 、b ∈R)叫复数,a 叫实部,b 叫虚部,当b=0时,a+bi(a 、b ∈R)是实数;当b ≠0时,a+bi 是虚数;当a=0,b ≠0时,a+bi(a 、b ∈R)是纯虚数.3.复数可以用向量表示.用点Z(a,b)表示复数z=a+bi(a 、b ∈R),复数与复平面上的点一一对应,这是复数的几何意义.4.a 、b 、c 、d ∈R 时,a+bi=c+di ⇔a=c 且b=d,两个虚数不能比较大小.5.两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数,用z 表示,当z ∈R ⇔z=z ;当z ≠0时,z 为纯虚数⇔z+z =0;对于任意复数z 均有z+z ∈R,|z|2=|z |2=z ·z .利用这些结论,往往可以使问题得到简洁明快的解决.6.z=a+bi(a 、b ∈R),则|z|=22b a +叫复数的模.它的几何意义是复数z 对应的点到原点的距离.二、点击双基1.(2005北京春季高考)i-2的共轭复数是( )A.2+iB.2-iC.-2+iD.-2-i解析:由共轭复数的定义知选D.答案:D2.(2005全国高考卷Ⅰ)复数ii 2123--等于( ) A.i B.-i C.22-i D.-22+i 解析:原式=i i 212-+=i. 答案:A3.(2005天津高考,理)若复数ii a 213++(a ∈R)是纯虚数,则实数a 的值为( ) A.-2 B.4 C.-6 D.6解析:i i a 213++=41)21)(3(+-+i i a =51(a+6)+51(3-2a)i. ∵i i a 213++是纯虚数, ∴⎩⎨⎧≠-=+.023,06a a ∴a=-6.答案:C4.在复平面内,z=(m 2-m-2)+(m 2-3m+2)i 所对应的点在实轴负半轴上,则实数m 的取值为______ _____________.解析:由题意知z ∈R 且z<0,∴⎪⎩⎪⎨⎧=+-<--.023,0222m m m m ∴m=1. 答案:15.下列命题中:①任意两个确定的复数都不能比较大小;②若|z |≤1,则-1≤z ≤1;③若z 12+z 22=0,则z 1=z 2=0;④z+z =0⇔z 为纯虚数;⑤z=z ⇔z ∈R.其中正确的命题是_________________________.解析:①中的两个实数可比较大小,②中的z 可为虚数,③中的z 1=i,z 2=1,④中的z=0. 答案:⑤诱思·实例点拨【例1】 设关于x 的方程是x 2-(tan θ+i)x-(2+i)=0.(1)若方程有实数根,求锐角θ和实数根;(2)证明对任意θ≠k π+2π(k ∈Z),方程无纯虚数根. 剖析:(1)对于复数方程存在实根的问题,一般可先设出实根,然后再利用复数相等的条件求解.(2)直接证明有困难时,可用反证法.(1)解:设实数根为α,则α2-(tan θ+i)α-2(2+i)=0,即α2-tan θ·α-2-(α+1)i=0.∴⎩⎨⎧=-=.1tan ,1θα 又θ∈(0,2π),∴θ=4π,α=-1. (2)证明:若方程有纯虚数根βi(β∈R,β≠0),则(βi)2-(tan θ+i)·(βi)-(2+i)=0.∴⎩⎨⎧=-∙-=-+-.01tan ,022θβββ此方程组无解,∴原方程没有纯虚数根.讲评:对于虚系数一元二次方程,不可用判别式Δ来判断方程根的实虚,而应该用复数相等的条件转化为实数方程进行讨论.【例2】设复数z=l g(m2-2m-2)+(m2+3m+2)i,试求实数m 取何值时,(1)z 是纯虚数;(2)z 是实数;(3)z 对应的点位于复平面的第二象限?剖析:利用复数的有关概念易求得.解:(1)由⎪⎩⎪⎨⎧≠++=--,023,0)22lg(22m m m m 得m=3. (2)由m2+3m+2=0,得m=-1或m=-2.(3)由⎪⎩⎪⎨⎧>++<--,023,0)22lg(22m m m m 得-1<m<1-3或1+3<m<3.讲评:对复数的分类条件要注意其充要性,对复数相等、共轭复数的概念的运用也是这样. 链接·聚焦若复数z 对应的向量,逆时针旋转90°是纯虚数,求实数m 的值.提示:设复数z 对应的点为Z 1(lg(m 2-2m-2),m 2+3m+2),向量1OZ 逆时针旋转90°对应的点为Z 2,易知Z 2(-(m 2+3m+2),lg(m 2-2m-2)).由题意得⎪⎩⎪⎨⎧≠--=++-.0)22lg(,0)23(22m m m m解得m=-2.【例3】设z ∈C,求满足z+z1∈R 且|z-2|=2的复数z. 剖析:设z=a+bi(a 、b ∈R),代入条件,把复数问题转化为实数问题,易得a 、b 的两个方程. 解法一:设z=a+bi,则z+z 1=a+bi+bi a +1=a+bi+22b a bi a +- =a+22b a a ++(b-22b a b +)i ∈R. ∴b=22b a b +. ∴b=0或a 2+b 2=1.当b=0时,z=a,∴|a-2|=2.∴a=0或4.a=0不合题意舍去,∴z=4.当b ≠0时,a 2+b 2=1.又∵|z-2|=2,∴(a-2)2+b 2=4.解得a=41,b=±415, ∴z=41±415i. 综上,z=4或z=41±415i. 解法二:∵z+z1∈R, ∴z+z 1=z +z 1. ∴(z-z )-zz z z -=0,(z-z )·22||1||z z -=0. ∴z=z 或|z|=1,下同解法一.讲评:解法一设出复数的代数形式,把复数问题转化为实数问题来研究;解法二利用复数是实数的条件复数问题实数化.这些都是解决复数问题的常用方法.链接·提示试探究z ∈C,z+z 1是实数的充要条件. 提示:z+z1是实数的充要条件是|z|=1且z ≠0.【例4】已知z 1=x 2+12+x i,z 2=(x 2+a)i 对于任意x ∈R 均有|z 1|>|z 2|成立,试求实数a 的取值范围.剖析:求出|z 1|及|z 2|,利用|z 1|>|z 2|问题转化为x ∈R 时不等式恒成立问题. 解:∵|z 1|>|z 2|,∴x 4+x 2+1>(x 2+a)2.∴(1-2a)x 2+(1-a 2)>0对x ∈R 恒成立. 当1-2a=0,即a=21时,不等式成立; 当1-2a ≠0时,⎩⎨⎧<--->-0)1)(21(40212a a a ⇒-1<a<21. 综上,a ∈(-1,21]. 讲评:本题利用复数的性质求模之后,转化为求含参数的二次不等式的参数取值范围.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
第十五章 复数复习纲要
一.基本概念
1.复数的有关概念:
1>.复数:①形如a+bi(a,b∈R)的数叫复数.a叫复数的实部,记作:Re(z),b叫复数的虚部,记作:Im(z).i是虚数单位. ②全体复数构成的集合叫复数集,用C表示. z=a+bi(a,b∈R)叫复数的代数形式. 2>.复平面:建立平面直角坐标系来表示复数的平面,叫复平面.x轴叫实轴,y轴除去原点的部分叫虚轴.
3>.实数集与复数集的关系:实数集是复数集的真子集.即:R⊂C. 2.复数的分类:
()
()()0,
00.00.00b a bi a b R b a a a bi a b a bi a b =+∈≠⎧⎧⎪⎪⎨⎪⎪⎪
⎩⎨⎪⎧=≠⎪⎪⎨⎪+≠≠⎪⎩⎩
正实数:>0实数 :=0
负实数:<0复数纯虚数: 且虚数非纯虚数: 且a=0是z=a+bi 为纯虚数的必要非充分条件.
3.两虚数相等的充要条件:
a c
a bi c di
b d
=⎧+=+⇔⎨
=⎩
注:两个复数不能比较大小,即当且仅当两个复
数都是实数时,才能比较大小. 4.虚数单位i的幂的性质:
2441
42
43
1.1.. 1..n
n n n i i
i
i i
i
i i +++=-===-=-①② 叫的周期性.
5.复数的几何意义:
①任何一个复数z=a+bi.(a,b∈R)与复平面内的一点Z(a,b)一一对应. ②任何一个复数z=a+bi.(a,b∈R)与
以原点为起点,点Z(a,b)为终点的向量OZ
一一对应.
6.复数的模.z=a+bi.则z OZ =
二.复数的代数形式及运算
1.复数代数形式的四则运算:
()()()()()()()()()121212122222,.,,,z a bi z c di a b c d R z z a bi c di a c b d i z z a bi c di ac bd ad bc i z a bi ac bd bc ad
i z c di c d c d
=+=+∈±=+±+=±+±⋅=+⋅+=-++++-==++++设 则 2.复数加减法的几何意义:
12z z +是向量12OZ OZ +
所对应的复数.
12z z -是向量12OZ OZ - 即向量21Z Z
所对应的复数.
3.复数加法,乘法的运算律
()()()()()()()1221123123123123
123121312121212.,n
m
m n m n m m n m m
z z z z z z z z z z z z z z z z z z z z z z z z z z z m n N z z z z z z z z z *+⋅+=+++=++⋅⋅=⋅⋅⋅+=⋅+⋅⋅=⋅∈⋅==⋅=⋅⑴①.②③④⑤⑵若,则
①.②.③注意:m,n是正整数,不是分数. 4.模运算性质:
(
)11
121222
2
2
22
121212121212
2z z z z z z z z z z z z z z z z z z z z ⋅=⋅=++-=+-≤+≤+①.②
③④
5.共轭复数
(1)①定义:实部相等,虚部互为相反数的两个复数,叫共轭复数.
②复数z=a+bi的共轭复数, 记作z ,即:z a bi =-.
(2)共轭复数的性质:
①实数的共轭复数是它本身.特别的时
()2
2
22
1212121211
222
2.2.1,1
..0z z a z z bi z z z z z z
z
a b
z z z z z z z z z z z z z z z z +=-==⋅===+=⋅=±=±⋅=⋅⎛⎫=≠
⎪⎝⎭②③④⑤=z ⑥特别的时⑦⑧⑨
6.常用运算技巧 (1)i的周期性:
()()()
44142431231231.. 1..0.1.n n n n n n n n n n n n i i i i i i n N i i i i n N i i i i n N +++++++++
===-=-∈+++=∈⋅⋅⋅=∈***① ② ③
(2)技巧:
()()2
111 2...
111i i
i
i i i i i
a
bi a bi b ai i b ai
+-±=±==--+++=-+-①②③④=-i.⑤=i.⑥i
(3)设12ω=-
,则有: ()
322121..10.n n n n N ωωωωωωωω++==++=+∈*①②③④+=0.ω与ω统称为1的立方虚根,即若x3=1则:
x=1,ω.ω.而且对ω也有类似上面的等式。
7﹡.复数的三角形式:
(1)定义:辐角主值:0≤argθ<2π.
()cos sin .,sin a b z r i r r r
θθθθ=+==
= (2)运算:尼莫佛定理
()()()()()()1212121211121222
cos sin :cos sin cos sin cos sin 22cos sin 0,1,2,n
n z z r r i r i r n i n z r i z r k k i n n k n
θθθθθθθθθθθθθπ
θπ⋅=⋅+++⎡⎤⎣⎦+=+⎡⎤⎣⎦
=-+-⎡⎤⎣⎦++⎫+⎪
⎭= ①.
②尼莫佛定理③8.数集的关系:N Z Q R Z ⊂⊂⊂⊂ 9.实系数方程复根成对定理.。
