MatlabPDE工具箱有限元法求解偏微分方程

合集下载

偏微分方程Matlab数值解法(补充4)

偏微分方程Matlab 数值解法（补充4）Matlab 可以求解一般的偏微分方程，也可以利用偏微分方程工具箱中给出的函数求解一些偏微分方程。

1 偏微分方程组求解Matlab 语言提供了pdepe()函数，可以直接求解偏微分方程(,,,)[(,,,)](,,,)m mu u u u C x t u x x f x t u s x t u x t x x x-∂∂∂∂∂=+∂∂∂∂∂ （4.1）这样，偏微分方程可以编写为以下函数的描述，其入口为[,,](,,,)x c f s pdefun x t u u =其中：pdefun 为函数名。

由给定输入变量可计算出,,c f s 这三个函数。

边界条件可以用下面的函数描述(,,)(,,).*(,,,)0up x t u q x t u f x t u x∂+=∂ （4.2）这样的边值函数可以写为Matlab 函数[,,,](,,,)a a b b x p q p q pdebc x t u u =初始条件数学描述为00(,)u x t u =，编写一个简单的函数即可0()u pdeic x =还可以选择x 和t 的向量，再加上描述这些函数，就可以用pdepe （）函数求解次偏微分方程，需要用如下格式求解(,@,@,@,,)sol pdepe m pdefun pdeic pdebc x t =【例1】试求下列偏微分方程2111222221220.024()0.17()u u F u u t x u u F u u tx ⎧∂∂=--⎪⎪∂∂⎨∂∂⎪=+-⎪∂∂⎩ 其中： 5.7311.46()xx F x e e -=-，且满足初始条件1(,0)1u x =，2(,1)0u x =及边界条件1221(0,)0,(0,)0,(1,)1,(1,)0u u t u t u t t x x∂∂====∂∂解：对照给出的偏微分方程和（4.1），可将原方程改写为111222120.024/()1.*10.17/()u u x F u u u u x F u u t x ∂∂--⎡⎤⎡⎤⎡⎤⎡⎤∂∂=+⎢⎥⎢⎥⎢⎥⎢⎥∂∂-∂∂⎣⎦⎣⎦⎣⎦⎣⎦可知0m =，且1122120.024/()1,,10.17/()u x F u u c f s u x F u u ∂∂--⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥∂∂-⎣⎦⎣⎦⎣⎦编写下面的Matlab 函数function [c,f,s]=c7mpde(x,t,u,du)c=[1;1];y=u(1)-u(2);F=exp(5.73*y)-exp(-11.46*y);s=F*[-1;1]; f=[0.024*du(1);0.17*du(2)];套用（4.2）中的边界条件，可以写出如下的边值方程左边界2010.*00f u ⎡⎤⎡⎤⎡⎤+=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦，右边界1100.*100u f -⎡⎤⎡⎤⎡⎤+=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ 编写下面的Matlab 函数function [pa,qa,pb,qb]=c7mpbc(xa,ua,xb,ub,t) pa=[0;ua(2)];qa=[1;0];pb=[ub(1)-1;0];qb=[0,1]; 另外，描述初值的函数function u0=c7mpic(x) u0=[1;0];有了这三个函数，选定x 和t 向量，则可以由下面的程序直接求此微分方程，得出解1u 和2u 。

Matlab求解微分方程(组)及偏微分方程(组)

第四讲 Matlab 求解微分方程（组）理论介绍：Matlab 求解微分方程（组）命令求解实例：Matlab 求解微分方程（组）实例实际应用问题通过数学建模所归纳得到的方程，绝大多数都是微分方程，真正能得到代数方程的机会很少.另一方面，能够求解的微分方程也是十分有限的，特别是高阶方程和偏微分方程（组）.这就要求我们必须研究微分方程（组）的解法：解析解法和数值解法. 一．相关函数、命令及简介1.在Matlab 中，用大写字母D 表示导数，Dy 表示y 关于自变量的一阶导数，D2y 表示y 关于自变量的二阶导数，依此类推.函数dsolve 用来解决常微分方程（组）的求解问题，调用格式为：X=dsolve(‘eqn1’,’eqn2’,…)函数dsolve 用来解符号常微分方程、方程组，如果没有初始条件，则求出通解，如果有初始条件，则求出特解.注意，系统缺省的自变量为t2.函数dsolve 求解的是常微分方程的精确解法，也称为常微分方程的符号解.但是，有大量的常微分方程虽然从理论上讲，其解是存在的，但我们却无法求出其解析解，此时，我们需要寻求方程的数值解，在求常微分方程数值解方面，MATLAB 具有丰富的函数，我们将其统称为solver ，其一般格式为：[T,Y]=solver(odefun,tspan,y0)说明：(1)solver 为命令ode45、ode23、ode113、ode15s 、ode23s 、ode23t 、ode23tb 、ode15i 之一.(2)odefun 是显示微分方程'(,)y f t y =在积分区间tspan 0[,]f t t =上从0t 到ft 用初始条件0y 求解.(3)如果要获得微分方程问题在其他指定时间点012,,,,f t t t t 上的解，则令tspan 012[,,,]f t t t t =(要求是单调的).(4)因为没有一种算法可以有效的解决所有的ODE 问题，为此，Matlab 提供了多种求解器solver ，对于不同的ODE 问题，采用不同的solver.表1 Matlab中文本文件读写函数说明：ode23、ode45是极其常用的用来求解非刚性的标准形式的一阶微分方程（组）的初值问题的解的Matlab常用程序，其中：ode23采用龙格-库塔2阶算法，用3阶公式作误差估计来调节步长，具有低等的精度.ode45则采用龙格-库塔4阶算法，用5阶公式作误差估计来调节步长，具有中等的精度.3．在matlab命令窗口、程序或函数中创建局部函数时，可用内联函数inline，inline函数形式相当于编写M函数文件，但不需编写M-文件就可以描述出某种数学关系.调用inline函数，只能由一个matlab表达式组成，并且只能返回一个变量，不允许[u,v]这种向量形式.因而，任何要求逻辑运算或乘法运算以求得最终结果的场合，都不能应用inline函数，inline函数的一般形式为：FunctionName=inline(‘函数内容’, ‘所有自变量列表’)例如：（求解F(x)=x^2*cos(a*x)-b ,a,b是标量；x是向量）在命令窗口输入:Fofx=inline(‘x .^2*cos(a*x)-b ’ , ‘x ’,’a ’,’b ’); g= Fofx([pi/3 pi/3.5],4,1) 系统输出为：g=-1.5483 -1.7259注意：由于使用内联对象函数inline 不需要另外建立m 文件，所有使用比较方便，另外在使用ode45函数的时候，定义函数往往需要编辑一个m 文件来单独定义，这样不便于管理文件，这里可以使用inline 来定义函数. 二．实例介绍1.几个可以直接用Matlab 求微分方程精确解的实例例1 求解微分方程2'2x y xy xe -+=程序：syms x y; y=dsolve(‘Dy+2*x*y=x*exp(-x^2)’,’x ’)例 2 求微分方程'0x xy y e +-=在初始条件(1)2y e =下的特解并画出解函数的图形.程序：syms x y; y=dsolve(‘x*Dy+y-exp(1)=0’,’y(1)=2*exp(1)’,’x ’);ezplot(y)例 3 求解微分方程组530tdx x y e dtdy x y dt⎧++=⎪⎪⎨⎪--=⎪⎩在初始条件00|1,|0t t x y ====下的特解并画出解函数的图形.程序：syms x y t[x,y]=dsolve('Dx+5*x+y=exp(t)','Dy-x-3*y=0','x(0)=1','y(0)=0','t')simple(x); simple(y)ezplot(x,y,[0,1.3]);axis auto2.用ode23、ode45等求解非刚性标准形式的一阶微分方程（组）的初值问题的数值解（近似解）例 4 求解微分方程初值问题2222(0)1dy y x xdx y ⎧=-++⎪⎨⎪=⎩的数值解，求解范围为区间[0,0.5].程序：fun=inline('-2*y+2*x^2+2*x','x','y'); [x,y]=ode23(fun,[0,0.5],1); plot(x,y,'o-')例 5 求解微分方程22'2(1)0,(0)1,(0)0d y dyy y y y dt dtμ--+===的解，并画出解的图形.分析：这是一个二阶非线性方程，我们可以通过变换，将二阶方程化为一阶方程组求解.令12,,7dyx y x dtμ===，则 121221212,(0)17(1),(0)0dx x x dtdx x x x x dt⎧==⎪⎪⎨⎪=--=⎪⎩ 编写M-文件vdp.m function fy=vdp(t,x)fy=[x(2);7*(1-x(1)^2)*x(2)-x(1)]; end在Matlab 命令窗口编写程序 y0=[1;0][t,x]=ode45(@vdp,[0,40],y0);或[t,x]=ode45('vdp',[0,40],y0); y=x(:,1);dy=x(:,2); plot(t,y,t,dy)练习与思考：M-文件vdp.m 改写成inline 函数程序？ 3.用Euler 折线法求解Euler 折线法求解的基本思想是将微分方程初值问题00(,)()dyf x y dxy x y ⎧=⎪⎨⎪=⎩ 化成一个代数(差分)方程，主要步骤是用差商()()y x h y x h +-替代微商dydx，于是00()()(,())()k k k k y x h y x f x y x h y y x +-⎧=⎪⎨⎪=⎩记1,(),k k k k x x h y y x +=+=从而1(),k k y y x h +=+于是0011(),,0,1,2,,1(,).k k k k k k y y x x x h k n y y hf x y ++=⎧⎪=+=-⎨⎪=+⎩例 6 用Euler 折线法求解微分方程初值问题22(0)1dyx y dxy y ⎧=+⎪⎨⎪=⎩的数值解（步长h 取0.4），求解范围为区间[0,2].分析：本问题的差分方程为00110,1,0.4,0,1,2,,1(,).k k k k k k x y h x x h k n y y hf x y ++===⎧⎪=+=-⎨⎪=+⎩程序：>> clear >> f=sym('y+2*x/y^2'); >> a=0; >> b=2; >> h=0.4; >> n=(b-a)/h+1; >> x=0; >> y=1;>> szj=[x,y];%数值解 >> for i=1:n-1y=y+h*subs(f,{'x','y'},{x,y});%subs ，替换函数 x=x+h;szj=[szj;x,y]; end>>szj>> plot(szj(:,1),szj(:,2))说明：替换函数subs 例如：输入subs(a+b,a,4) 意思就是把a 用4替换掉，返回 4+b ，也可以替换多个变量，例如：subs(cos(a)+sin(b),{a,b},[sym('alpha'),2])分别用字符alpha 替换a 和2替换b ，返回 cos(alpha)+sin(2)特别说明：本问题可进一步利用四阶Runge-Kutta 法求解，Euler 折线法实际上就是一阶Runge-Kutta 法，Runge-Kutta 法的迭代公式为001112341213243(),,(22),6(,),0,1,2,,1(,),22(,),22(,).k k k k k k k k k k k k y y x x x h h y y L L L L L f x y k n h h L f x y L h h L f x y L L f x h y hL ++=⎧⎪=+⎪⎪=++++⎪⎪=⎪=-⎨⎪=++⎪⎪⎪=++⎪⎪=++⎩相应的Matlab 程序为：>> clear >> f=sym('y+2*x/y^2'); >> a=0; >> b=2; >> h=0.4; >> n=(b-a)/h+1; >> x=0; >> y=1;>> szj=[x,y];%数值解 >> for i=1:n-1l1=subs(f, {'x','y'},{x,y});替换函数 l2=subs(f, {'x','y'},{x+h/2,y+l1*h/2}); l3=subs(f, {'x','y'},{x+h/2,y+l2*h/2}); l4=subs(f, {'x','y'},{x+h,y+l3*h});y=y+h*(l1+2*l2+2*l3+l4)/6; x=x+h;szj=[szj;x,y]; end >>szj>> plot(szj(:,1),szj(:,2))练习与思考：(1)ode45求解问题并比较差异. (2)利用Matlab 求微分方程(4)(3)''20y y y -+=的解.(3)求解微分方程''2',2(1)0,030,(0)1,(0)0y y y y x y y --+=≤≤==的特解. (4)利用Matlab 求微分方程初值问题2''''00(1)2,|1,|3x x x y xy y y ==+===的解. 提醒：尽可能多的考虑解法三．微分方程转换为一阶显式微分方程组Matlab 微分方程解算器只能求解标准形式的一阶显式微分方程（组）问题，因此在使用ODE 解算器之前，我们需要做的第一步，也是最重要的一步就是借助状态变量将微分方程（组）化成Matlab 可接受的标准形式.当然，如果ODEs 由一个或多个高阶微分方程给出，则我们应先将它变换成一阶显式常微分方程组.下面我们以两个高阶微分方程组构成的ODEs 为例介绍如何将它变换成一个一阶显式微分方程组.Step 1 将微分方程的最高阶变量移到等式左边，其它移到右边，并按阶次从低到高排列.形式为：()'''(1)'''(1)()'''(1)'''(1)(,,,,,,,,,,)(,,,,,,,,,,)m m n n m n x f t x x x x y y y y y g t x x x x y y y y ----⎧=⎨=⎩Step 2 为每一阶微分式选择状态变量，最高阶除外'''(1)123'''(1)123,,,,,,,,,m m n m m m m n x x x x x x x x x y x y x y x y--++++========注意：ODEs 中所有是因变量的最高阶次之和就是需要的状态变量的个数，最高阶的微分式不需要给它状态变量.Step 3 根据选用的状态变量，写出所有状态变量的一阶微分表达式''''122334123''12123,,,,(,,,,,),,(,,,,,)m m n m m m nm n x x x x x x x f t x x x x xx xg t x x x x +++++======练习与思考：(1)求解微分方程组**'''3312*'''3312()()22x x x y x r r y y y x y r r μμμμμμ⎧+-=+--⎪⎪⎨⎪=+--⎪⎩其中2r =1r =*1,μμ=-1/82.45,μ=(0) 1.2,x =(0)0,y ='(0)0,x ='(0) 1.049355751y =-(2)求解隐式微分方程组''''''''''''2235x y x y x y x y xy y ⎧+=⎨++-=⎩ 提示：使用符号计算函数solve 求'''',x y ，然后利用求解微分方程的方法四．偏微分方程解法Matlab 提供了两种方法解决PDE 问题，一是使用pdepe 函数，它可以求解一般的PDEs,具有较大的通用性，但只支持命令形式调用；二是使用PDE 工具箱，可以求解特殊PDE 问题，PDEtoll 有较大的局限性，比如只能求解二阶PDE 问题，并且不能解决片微分方程组，但是它提供了GUI 界面，从复杂的编程中解脱出来，同时还可以通过File —>Save As 直接生成M 代码.1.一般偏微分方程（组）的求解(1)Matlab 提供的pdepe 函数，可以直接求解一般偏微分方程（组），它的调用格式为：sol=pdepe(m,@pdefun,@pdeic,@pdebc,x,t)@pdefun 是PDE 的问题描述函数，它必须换成标准形式：(,,)[(,,,)](,,,)m m u u u uc x t x x f x t u s x t u x t x x x-∂∂∂∂∂=+∂∂∂∂∂ 这样，PDE 就可以编写入口函数：[c,f,s]=pdefun(x,t,u,du)，m,x,t 对应于式中相关参数，du 是u 的一阶导数，由给定的输入变量可表示出c,f,s 这三个函数.@pdebc 是PDE 的边界条件描述函数，它必须化为形式：(,,)(,,).*(,,,)0up x t u q x t u f x t u x∂==∂ 于是边值条件可以编写函数描述为：[pa,qa,pb,qb]=pdebc(x,t,u,du),其中a 表示下边界，b 表示上边界.@pdeic 是PDE 的初值条件，必须化为形式：00(,)u x t u =，故可以使用函数描述为：u0=pdeic(x)sol 是一个三维数组，sol(:,:,i)表示i u 的解，换句话说，k u 对应x(i)和t(j)时的解为sol(i,j,k)，通过sol ，我们可以使用pdeval 函数直接计算某个点的函数值.(2)实例说明求解偏微分2111222221220.024()0.17()u u F u u t xu u F u u tx ⎧∂∂=--⎪⎪∂∂⎨∂∂⎪=+-⎪∂∂⎩ 其中， 5.7311.46()xx F x e e -=-且满足初始条件12(,0)1,(,0)0u x u x ==及边界条件1(0,)0,u t x ∂=∂221(0,)0,(1,)1,(1,)0uu t u t t x∂===∂ 解：(1)对照给出的偏微分方程和pdepe 函数求解的标准形式，原方程改写为111221220.024()1.*()10.17u u F u u x u F u u u t x x ∂⎡⎤⎢⎥--⎡⎤⎡⎤⎡⎤∂∂∂=+⎢⎥⎢⎥⎢⎥⎢⎥-∂∂∂⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥∂⎣⎦可见1121220.024()10,,,()10.17u F u u x m c f s F u u u x ∂⎡⎤⎢⎥--⎡⎤⎡⎤∂====⎢⎥⎢⎥⎢⎥-∂⎣⎦⎣⎦⎢⎥⎢⎥∂⎣⎦%目标PDE 函数function [c,f,s]=pdefun(x,t,u,du) c=[1;1];f=[0.024*du(1);0.17*du(2)];temp=u(1)-u(2);s=[-1;1].*(exp(5.73*temp)-exp(-11.46*temp)) end(2)边界条件改写为：下边界2010.*00f u ⎡⎤⎡⎤⎡⎤+=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦上边界1110.*000u f -⎡⎤⎡⎤⎡⎤+=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦%边界条件函数function [pa,qa,pb,qb]=pdebc(xa,ua,xb,ub,t) pa=[0;ua(2)]; qa=[1;0]; pb=[ub(1)-1;0]; qb=[0;1]; end(3)初值条件改写为：1210u u ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦%初值条件函数 function u0=pdeic(x) u0=[1;0]; end(4)编写主调函数 clcx=0:0.05:1; t=0:0.05:2; m=0;sol=pdepe(m,@pdefun,@pdeic,@pdebc,x,t); subplot(2,1,1) surf(x,t,sol(:,:,1)) subplot(2,1,2) surf(x,t,sol(:,:,2))练习与思考： This example illustrates the straightforward formulation, computation, and plotting of the solution of a single PDE.2()u u t x xπ∂∂∂=∂∂∂ This equation holds on an interval 01x ≤≤ for times 0t ≥. The PDE satisfies the initial condition (,0)sin u x x π= and boundary conditions(0,)0;(1,)0t u u t e t xπ-∂=+=∂ 2.PDEtool 求解偏微分方程 (1)PDEtool （GUI ）求解偏微分方程的一般步骤在Matlab 命令窗口输入pdetool ，回车，PDE 工具箱的图形用户界面(GUI)系统就启动了.从定义一个偏微分方程问题到完成解偏微分方程的定解，整个过程大致可以分为六个阶段Step 1 “Draw 模式”绘制平面有界区域Ω，通过公式把Matlab 系统提供的实体模型：矩形、圆、椭圆和多边形，组合起来，生成需要的平面区域.Step 2 “Boundary 模式”定义边界，声明不同边界段的边界条件.Step 3 “PDE 模式”定义偏微分方程，确定方程类型和方程系数c,a,f,d ，根据具体情况，还可以在不同子区域声明不同系数.Step 4 “Mesh 模式”网格化区域Ω，可以控制自动生成网格的参数，对生成的网格进行多次细化，使网格分割更细更合理.Step 5 “Solve 模式”解偏微分方程，对于椭圆型方程可以激活并控制非线性自适应解题器来处理非线性方程；对于抛物线型方程和双曲型方程，设置初始边界条件后可以求出给定时刻t 的解；对于特征值问题，可以求出给定区间上的特征值.求解完成后，可以返回到Step 4，对网格进一步细化，进行再次求解.Step 6 “View 模式”计算结果的可视化，可以通过设置系统提供的对话框，显示所求的解的表面图、网格图、等高线图和箭头梯形图.对于抛物线型和双曲线型问题的解还可以进行动画演示.(2)实例说明用法求解一个正方形区域上的特征值问题：12|0u u u u λ∂Ω⎧-∆-=⎪⎨⎪=⎩ 正方形区域为：11,1 1.x x -≤≤-≤≤(1)使用PDE工具箱打开GUI求解方程(2)进入Draw模式，绘制一个矩形，然后双击矩形，在弹出的对话框中设置Left=-1,Bottom=-1,Width=2,Height=2,确认并关闭对话框(3)进入Boundary模式，边界条件采用Dirichlet条件的默认值(4)进入PDE模式，单击工具栏PDE按钮，在弹出的对话框中方程类型选择Eigenmodes,参数设置c=1,a=-1/2,d=1,确认后关闭对话框(5)单击工具栏的按钮，对正方形区域进行初始网格剖分，然后再对网格进一步细化剖分一次(6)点开solve菜单，单击Parameters选项，在弹出的对话框中设置特征值区域为[-20,20](7)单击Plot菜单的Parameters项，在弹出的对话框中选中Color、Height(3-D plot)和show mesh项，然后单击Done确认(8)单击工具栏的“=”按钮，开始求解。

MATLAB pde tool偏微分方程数值解

The Partial Differential Equation T oolbox extends the MATLAB® technical computing environment with tools for the study and solution of partial differential equations (PDEs) in two-space dimensions (2-D) and time. A set of command-line functions and a graphical user interface let you preprocess, solve, and postprocess generic 2-D PDEs using the Finite Element Method (FEM).Partial Differential Equation Toolbox 1 Solve and analyze partial differential equationsWorking With the Partial Differential Equation ToolboxThe Partial Differential Equation T oolbox lets you work in six modes from the graphi-cal user interface or the command line. Each mode corresponds to a step in the process of solving PDEs using the Finite Element Method.• D raw mode lets you create Ω, the geometry, using the constructive solid geometry (CSG) model paradigm. The graphical interface provides a set of solid building blocks (square, rectangle, circle, ellipse, and polygon) that can be combined to define complex geometries.•B oundary mode lets you specify conditions on different boundaries or remove sub d omain borders.• P DE mode lets you select the type of PDE problem and the coefficientsc, a, f, and d . By specifying the coefficients for each subdomain independently, you can represent different material properties.• M esh mode lets you control the fully automated mesh generation and refinement process.• S olve mode lets you invoke and control the nonlinear and adaptive solver for elliptic problems. For parabolic and hyperbolic PDEproblems, you can specify the initial values and obtain solutions at specific times. For the eigenvalue solver, you can define the interval over which to search for eigenvalues.• P lot mode lets you select from different plot types, including surface, mesh, and contour. Y ou can simultaneously visualize multiple solution properties using color, height, and vector fields. The FEM mesh can be overlaid on all plots and shown in the displaced position. For parabolic and hyperbolic equations, you can animatethe solution as it changes with time.Defining and Solving Partial Differential EquationsWith the Partial Differential Equation T oolbox, you can define and numerically solve different types of PDEs, including elliptic, parabolic, hyperbolic, eigenvalue, nonlinear elliptic, and systems of PDEs with multiple variables.Elliptic PDEThe basic scalar equation of the toolbox is the elliptic PDEwhere is the vector (∂/∂x ,∂/∂y ), and c is a 2-by-2 matrix function on Ω, the bounded planar domain of interest. c, a, and f can be complex valued functions of x and y.Nonlinear Elliptic PDEA nonlinear Newton solver is available for the nonlinear elliptic PDEwhere the coefficients defining c, a, and fcan be functions of x, y, and the unknown solution u. All solvers can handle the PDE system with multiple dependent variablesY ou can handle systems of dimensiontwo from the graphical user interface.An arbitrary number of dimensions canbe handled from the command line.The toolbox also provides an adaptivemesh refinement algorithm for ellipticand nonlinear elliptic PDE problems.Using the graphical user interfaceto define the complex geometryof a wrench, generate a mesh,and analyze it for a given loadconfiguration.Toolbox Application ModesThe Partial Differential Equation T oolbox graphical interface includes a set ofappli c ation modes for common engineeringand science problems. When you select a mode, PDE coefficients are replaced with appli c ation-specific parameters, such asY oung’s modulus for problems in structural mechanics. Available modes include:• Structural Mechanics - Plane Stress• Structural Mechanics - Plane Strain• Electrostatics• Magnetostatics• AC Power Electromagnetics• Conductive Media DC• Heat Transfer• DiffusionThe boundary conditions are alteredto reflect the physical meaning of the different boundary condition coefficients. The plotting tools lets you visualizethe relevant physical variables for the selected application.Required ProductsMATLABRelated ProductsOptimization Toolbox. Solve standardand large-scale optimization problems.Statistics Toolbox. Apply statistical algorithms and probability models.Symbolic Math Toolbox andExtended Symbolic Math Toolbox. Perform computations using symbolic mathematics and variable-precision arithmetic.Platform and System RequirementsFor platform and system requirements, visit /products/pde ■8557v02 10/03For demos, application examples,tutorials, user stories, and pricing:•Visit •Contact The MathWorks directlyUS & Canada 508-647-7000Benelux +31 (0)182 53 76 44France +33 (0)1 41 14 67 14Germany +49 (0)241 470 750Italy +39 (011) 2274 700Spain +34 93 362 13 00Switzerland +41 (0)31 954 20 20UK +44 (0)1223 423 200Visit to obtaincontact information for authorizedMathWorks representatives in countriesthroughout Asia Pacific, Latin America,the Middle East, Africa, and the restof Europe.Visualization tools provide multiple ways to plot results. A contourplot with gradient arrows shows the temperature and heat flux.The temperature gradient is displayed using 3-D plotting tools.T el: 508.647.7000 info@ © 2003 by The MathWorks, Inc. MATLAB, Simulink, Stateflow, Handle Graphics, and Real-Time Workshop are registered trademarks, and TargetBox is a trademark of The MathWorks, Inc. Other product or brand names are trademarks or registered trademarks of their respective holders.。

偏微分方程(PDEs)的MATLAB数值解法

偏微分方程的MATLAB求解精讲©MA TLAB求解微分/偏微分方程，一直是一个头大的问题，两个字，“难过”，由于MA TLAB对LaTeX的支持有限，所有方程必须化成MA TLAB可接受的标准形式，不支持像其他三个数学软件那样直接傻瓜式输入，这个真把人给累坏了！不抱怨了，还是言归正传，回归我们今天的主体吧！MA TLAB提供了两种方法解决PDE问题，一是pdepe()函数，它可以求解一般的PDEs，据用较大的通用性，但只支持命令行形式调用。

二是PDE工具箱，可以求解特殊PDE问题，PDEtool有较大的局限性，比如只能求解二阶PDE问题，并且不能解决偏微分方程组，但是它提供了GUI界面，从繁杂的编程中解脱出来了，同时还可以通过File->Save As直接生成M代码一、一般偏微分方程组(PDEs)的MA TLAB求解 (3)1、pdepe函数说明 (3)2、实例讲解 (4)二、PDEtool求解特殊PDE问题 (6)1、典型偏微分方程的描述 (6)（1）椭圆型 (6)（2）抛物线型 (6)（3）双曲线型 (6)（4）特征值型 (7)2、偏微分方程边界条件的描述 (8)（1）Dirichlet条件 (8)（2）Neumann条件 (8)3、求解实例 (9)一、一般偏微分方程组(PDEs)的MATLAB 求解1、pdepe 函数说明MA TLAB 语言提供了pdepe()函数，可以直接求解一般偏微分方程(组)，它的调用格式为sol=pdepe(m,@pdefun,@pdeic,@pdebc,x,t)【输入参数】@pdefun ：是PDE 的问题描述函数，它必须换成下面的标准形式(,,)[(,,,)](,,,)()m m u u u uc x t x x f x t u s x t u x t x x x−∂∂∂∂∂=+∂∂∂∂∂式1 这样，PDE 就可以编写下面的入口函数 [c,f,s]=pdefun(x,t,u,du)m,x,t 就是对应于(式1)中相关参数，du 是u 的一阶导数，由给定的输入变量即可表示出出c,f,s 这三个函数@pdebc ：是PDE 的边界条件描述函数，必须先化为下面的形式(,,)(,,).*(,,,)0up x t u q x t u f x t u x∂+=∂ 于是边值条件可以编写下面函数描述为 [pa,qa,pb,qb]=pdebc(x,t,u,du)其中a 表示下边界，b 表示下边界@pdeic ：是PDE 的初值条件，必须化为下面的形式00(,)u x t u =我们使用下面的简单的函数来描述为 u0=pdeic(x)m,x,t ：就是对应于(式1)中相关参数【输出参数】sol ：是一个三维数组，sol(:,:,i)表示u i 的解，换句话说u k 对应x(i)和t(j)时的解为sol(i,j,k)通过sol ，我们可以使用pdeval()直接计算某个点的函数值2、实例讲解试求解下面的偏微分2111222221220.024()0.17()u u F u u t xu u F u u tx ∂∂=−− ∂∂ ∂∂ =−− ∂∂ 其中， 5.7311.46()x x F x e e −=−，且满足初始条件12(,0)1,(,0)0u x u x ==及边界条件1221(0,)0,(0,)0,(1,)1,(1,)0u ut u t u t t x x∂∂====∂∂【解】（1）对照给出的偏微分方程，根据标注形式，则原方程可以改写为111222120.024()1.*1()0.17u u F u u x u u F u u t t x ∂−−∂∂∂=+ ∂−∂∂∂可见m=0，且1122120.024()1,,1()0.17u F u u x c f s u F u u x ∂−− ∂===∂−∂%% 目标PDE 函数function [c,f,s]=pdefun (x,t,u,du) c=[1;1];f=[0.024*du(1);0.17*du(2)]; temp=u(1)-u(2);s=[-1;1].*(exp(5.73*temp)-exp(-11.46*temp));（2）边界条件改写为12011010.*.*00000u f f u −+=+=下边界上边界%% 边界条件函数function [pa,qa,pb,qb]=pdebc(xa,ua,xb,ub,t) %a 表示下边界，b 表示上边界 pa=[0;ua(2)];qa=[1;0]; pb=[ub(1)-1;0]; qb=[0;1];（3）初值条件改写为1210u u =%% 初值条件函数function u0=pdeic(x) u0=[1;0];（4）最后编写主调函数 clcx=0:0.05:1; t=0:0.05:2; m=0;sol=pdepe(m,@pdefun,@pdeic,@pdebc,x,t);figure('numbertitle','off','name','PDE Demo ——by Matlabsky') subplot(211)surf(x,t,sol(:,:,1)) title('The Solution of u_1') xlabel('X') ylabel('T') zlabel('U') subplot(212)surf(x,t,sol(:,:,2)) title('The Solution of u_2') xlabel('X') ylabel('T') zlabel('U')二、PDEtool 求解特殊PDE 问题MATLAB 的偏微分工具箱(PDE toolbox)可以比较规范的求解各种常见的二阶偏微分方程，但是惋惜的是只能求解特殊二阶的PDE 问题，并且不支持偏微分方程组！PDE toolbox 支持命令行形式求解PDE 问题，但是要记住那些命令以及调用形式真的很累人，还好MATLAB 提供了GUI 可视交互界面pdetool ，在pdetool 中可以很方便的求解一个PDE 问题，并且可以帮我们直接生成M 代码(File->Save As)。

《应用matlab的pdetoolbox求解偏微分方程综合实验》

2011届信计专业学生综合实验题目（要求按照所附开题报告表的格式填写提交开题报告。

一个小组选做一题，小组全体成员共同完成，每个小组只提交一份实验报告，按照出力多少排名。

提交时间在本学期18周以前。

）3 应用Matlab 的PDE Toolbox 求解偏微分方程熟悉Matlab 的PDE 工具箱的功能，并用其求解具有工程背景的偏微分方程，要求分别对三种类型方程：抛物型、椭圆形和双曲型。

阐述清楚如下方法：1、这里我们先脱离问题所含有的工程背景，分别举三个例子，大致的说明一下如何使用Matlab 的PDE 工具箱来求解三种类型的偏微分方程。

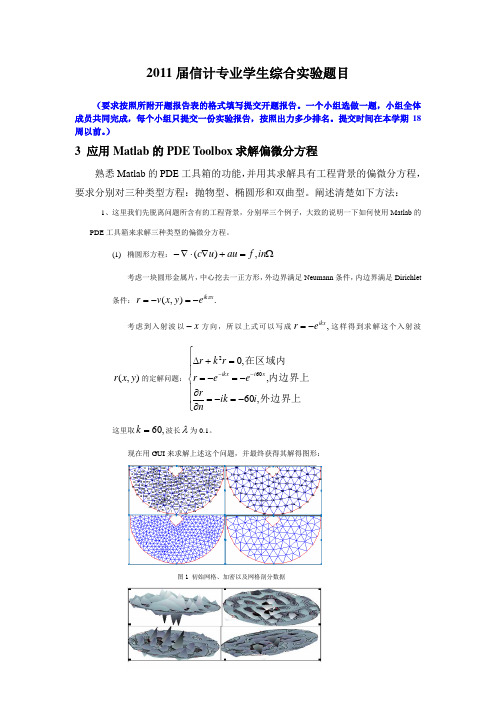
(1) 椭圆形方程：考虑一块圆形金属片，中心挖去一正方形，外边界满足Neumann 条件，内边界满足Dirichlet 条件：考虑到入射波以方向，所以上式可以写成这样得到求解这个入射波的定解问题：这里取波长为0.1。

现在用GUI 来求解上述这个问题，并最终获得其解得图形：图1 初始网格、加密以及网格剖分数据图2 解的三维图形Ω=+∇⋅∇-in f au u c ,)(.),(xik e y x v r π-=-=x -,ikxe r -=),(y x r ⎪⎪⎩⎪⎪⎨⎧-=-=∂∂-=-==+∆--外边界上内边界上在区域内,60,,0602i ik n ree r r k r xi ikx ,60=kλ图3 解的二维动画图附录1：二维动画的Matlab程序(2) 抛物型方程：考虑一个圆柱形放射性杆，其左端供热，右端保持常温，侧面与环境有热交换。

由于放性作用，热量均匀地产生。

初始温度为。

于是可以用如下方程描述：其中为密度，为杆的热容量，为导热系数，为放射性热源密度。

这一金属杆的密度取为热容量为导热系数为热源密度为右端恒温为侧面环境温度为热交换系数为左端的热流为边界条件(如右图4)：在杆的左端(): 在杆的右端():Ω=+∇⋅∇-∂in f au u c t d,)(C 0f u k tuc=∇⋅∇-∂∂)(ρρc k fρ,/78003m kg c ,/5000C kg ws k ,/400C m w f,/200003m w ,1000C ,1000C ,/5002C m w ./50002m w 处5.1-=z r u c n 5000)(=∇处5.1=z100=u在杆的侧面()：在杆的轴心():初始温度：现在用GUI 来求解上述这个问题，并最终获得其解得图形：图5 解的2维动画图形图6 解的3维动画图形处2.0=r 1005050)(⋅=⋅+∇⋅r u r u c n 处0=r 0)(=∇⋅u c n 0|0==t tu图7 解的动画图形比较图(3)双曲型方程：考虑如下二维波动方程的定界问题，并最终获得其解得图形：现在用GUI 来求解上述这个问题，并最终获得其解得图形：图8 解的3维动画图形附录2：双曲线三维动画的Matlab 程序 Ω=+∇⋅∇-∂∂in f au u c t ud ,)(22{}⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=∂∂===∂∂=<<-<<-=Ω∈=∆-∂∂--+=+=)2sin(1122)sin(3)),2(arctan(cos ,00|0|11,11|),(),(,0y y xx e x t ux u t n uu y x y x y x u tuπππ求解三种类型的偏微分方程。

偏微分方程matlab

MATLAB是一款广泛使用的数学软件，它提供了强大的工具来解决偏微分方程（PDE）。

偏微分方程是描述物理现象的数学模型，例如热传导、波动、流体动力学等。

在MATLAB中，你可以使用PDE工具箱（PDE Toolbox）来解决偏微分方程。

这个工具箱提供了一系列的函数和工具，用于建模、求解和分析偏微分方程。

下面是一个简单的例子，演示如何使用MATLAB的PDE工具箱求解一个简单的二维热传导方程：
首先，打开MATLAB并输入以下命令来启动PDE工具箱：
matlab
pdetool
在PDE工具箱界面中，选择"New"来创建一个新的PDE模型。

选择"2D"作为问题的维度，并选择"Heat Transfer"作为问题的类型。

在新创建的模型中，你可以定义问题的几何形状、边界条件、初始条件等。

接下来，使用工具箱中的求解器来求解PDE。

选择适当的求解器和参数，并运行求解过程。

求解完成后，你可以使用工具箱中的可视化工具来查看结果。

例如，你可以绘制温度分布图、等值线图等。

这只是一个简单的例子，MATLAB的PDE工具箱提供了更多的功能和选项来解决更复杂的偏微分方程。

你可以查阅MATLAB的文档和教程来了解更多关于PDE工具箱的详细信息和用法。

需要注意的是，使用PDE工具箱需要一定的数学和物理知识来理解偏微分方程和其相关概念。

因此，在使用MATLAB解决偏微分方程之前，建议先学习相关的数学和物理基础知识。

偏微分方程的MATLAB解法

引言微分方程定解问题有着广泛的应用背景。

人们用偏微分方程来描述、解释或者预见各种自然现象，并用于科学和工程技术的各个领域fll。

然而，对于广大应用工作者来说，从偏微分方程模型出发，使用有限元法或有限差分法求解都要耗费很大的工作量，才能得到数值解。

现在，MATLAB PDEToolbox已实现对于空间二维问题高速、准确的求解过程。

偏微分方程果一个微分方程中出现的未知函数只含一个自变量，这个方程叫做常微分方程，也简称微分方程；如果一个微分方程中出现多元函数的偏导数，或者说如果未知函数和几个变量有关，而且方程中出现未知函数对几个变量的导数，那么这种微分方程就是偏微分方程。

用的方法有变分法和有限差分法。

变分法是把定解问题转化成变分问题，再求变分问题的近似解；有限差分法是把定解问题转化成代数方程，然后用计算机进行计算；还有一种更有意义的模拟法，它用另一个物理的问题实验研究来代替所研究某个物理问题的定解。

虽然物理现象本质不同，但是抽象地表示在数学上是同一个定解问题，如研究某个不规则形状的物体里的稳定温度分布问题，由于求解比较困难，可作相应的静电场或稳恒电流场实验研究，测定场中各处的电势，从而也解决了所研究的稳定温度场中的温度分布问题。

着物理科学所研究的现象在广度和深度两方面的扩展，偏微分方程的应用范围更广泛。

从数学自身的角度看，偏微分方程的求解促使数学在函数论、变分法、级数展开、常微分方程、代数、微分几何等各方面进行发展。

从这个角度说，偏微分方程变成了数学的中心。

一、MATLAB方法简介及应用1.1 MATLAB简介ATLAB是美国MathWorks公司出品的商业数学软件，用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境，主要包括MATLAB和Simulink两大部分。

1.2 Matlab主要功能数值分析数值和符号计算工程与科学绘图控制系统的设计与仿真数字图像处理数字信号处理通讯系统设计与仿真财务与金融工程1.3 优势特点1) 高效的数值计算及符号计算功能，能使用户从繁杂的数学运算分析中解脱出来；2) 具有完备的图形处理功能，实现计算结果和编程的可视化；3) 友好的用户界面及接近数学表达式的自然化语言，使学者易于学习和掌握；4) 功能丰富的应用工具箱(如信号处理工具箱、通信工具箱等) ，为用户提供了大量方便实用的处理工具。

matlab偏微分方程工具箱使用手册

MATLAB偏微分方程工具箱使用手册一、Matlab偏微分方程工具箱介绍Matlab偏微分方程工具箱是Matlab中用于求解偏微分方程（PDE）问题的工具。

它提供了一系列函数和工具，可以用于建立、求解和分析PDE问题。

PDE是许多科学和工程领域中的重要数学模型，包括热传导、扩散、波动等现象的数值模拟、分析和优化。

Matlab偏微分方程工具箱为用户提供了丰富的功能和灵活的接口，使得PDE问题的求解变得更加简单和高效。

二、使用手册1. 安装和启用在开始使用Matlab偏微分方程工具箱前，首先需要确保Matlab已经安装并且包含了PDE工具箱。

确认工具箱已经安装后，可以通过以下命令启用PDE工具箱：```pdetool```这将打开PDE工具箱的图形用户界面，用户可以通过该界面进行PDE 问题的建立、求解和分析。

2. PDE建模在PDE工具箱中，用户可以通过几何建模工具进行PDE问题的建立。

用户可以定义几何形状、边界条件、初值条件等，并选择适当的PDE方程进行描述。

PDE工具箱提供了各种几何建模和PDE方程描述的选项，用户可以根据实际问题进行相应的设置和定义。

3. 求解和分析一旦PDE问题建立完成，用户可以通过PDE工具箱提供的求解器进行求解。

PDE工具箱提供了各种数值求解方法，包括有限元法、有限差分法等。

用户可以选择适当的求解方法，并进行求解。

求解完成后，PDE工具箱还提供了丰富的分析功能，用户可以对结果进行后处理、可视化和分析。

4. 结果导出和应用用户可以将求解结果导出到Matlab环境中，并进行后续的数据处理、可视化和分析。

用户也可以将结果导出到其他软件环境中进行更进一步的处理和应用。

三、个人观点和理解Matlab偏微分方程工具箱是一个非常强大的工具，它为科学和工程领域中的PDE问题提供了简单、高效的解决方案。

通过使用PDE工具箱，用户可以快速建立、求解和分析复杂的PDE问题，从而加快科学研究和工程设计的进程。

matlab 求解偏微分方程组

一、介绍Matlab是一种强大的数学计算工具，用于解决各种数学问题，包括求解偏微分方程组。

偏微分方程组是描述自然界中许多物理现象的数学模型，其求解对于科学研究和工程应用具有重要意义。

在Matlab中，可以通过多种方法来求解偏微分方程组，包括有限差分方法、有限元方法、谱方法等。

本文将对Matlab中求解偏微分方程组的方法进行介绍和讨论。

二、有限差分方法有限差分方法是一种常用的求解偏微分方程组的数值方法。

其基本思想是将连续的变量离散化为有限个点，并利用差分逼近来近似偏微分方程的导数。

在Matlab中，可以通过编写相应的差分方程组来求解偏微分方程组。

对于二维热传导方程，可以将偏导数用中心差分逼近，并构建相应的差分方程来求解温度分布。

通过循环迭代的方式，可以逐步逼近偏微分方程的解，并得到数值解。

三、有限元方法有限元方法是另一种常用的求解偏微分方程组的数值方法。

其基本思想是将求解区域离散化为有限个单元，并在每个单元内建立近似函数来逼近原始方程。

在Matlab中，可以利用有限元建模工具箱来构建离散化的网格，并编写相应的有限元方程来求解偏微分方程组。

对于弹性力学方程，可以利用有限元方法来求解结构的位移和应力分布。

通过求解线性方程组，可以得到离散化网格上的数值解。

四、谱方法谱方法是一种利用特定基函数展开偏微分方程解的方法。

其基本思想是选取适当的基函数，并通过展开系数来得到偏微分方程的数值解。

在Matlab中，可以通过谱方法工具箱来实现对偏微分方程组的求解。

对于波动方程，可以利用正交多项式展开来逼近波函数，通过选取适当的基函数和展开系数，可以得到偏微分方程的数值解。

五、总结在Matlab中，有多种方法可以用来求解偏微分方程组，包括有限差分方法、有限元方法、谱方法等。

这些方法各有特点，适用于不同类型的偏微分方程和求解问题。

通过合理地选择方法和编写相应的数值算法，可以在Matlab中高效地求解偏微分方程组，为科学研究和工程应用提供重要支持。

二阶偏微分方程的Matlab有限元法求解

二阶偏微分方程的 Matlab有限元法求解摘要：本文基于偏微分方程有限元法求解原理，运用Matlab中的偏微分方程工具箱（PDE Toolbox）对三类典型的二阶偏微分方程：椭圆型方程、双曲线型方程和抛物线型方程算例进行求解，为求解偏微分方程的提供参考。

关键词：偏微分方程，有限元，Matlab偏微分方程工具箱0引言偏微分方程定解问题是描述许多自然现象或工程问题的最重要的数学模型，应用非常广泛[1]。

解析法只能求解非常简单的偏微分方程，远远不能满足科学研究和工程实际的需要。

随着计算机技术和科学计算的迅速发展，数值解法成为求解偏微分方程的重要工具[2-3]。

数值解法将连续问题离散化，最后将偏微分方程化成线性代数方程组。

根据离散化方法不同，偏微分方程数值解法主要有差分法和有限元法。

有限元法是分片定义试函数与变分原理相结合的产物。

它能适应各种形状的区域，且通用性强，现已成为求解偏微分方程定解问题的一种有效数值方法[4]。

本文首先简述了偏微分方程有限元法原理，然后，对Matlab中的偏微分方程工具箱（Partial Differential Equations Toolbox）的功能和求解思路进行了阐述[5-6]，最后，给出了用PDE Toolbox求解椭圆方程、、双曲线方程和抛物线方程的计算实例。

1偏微分方程有限元法原理偏微分方程有限元法的基本思想是将实际上连续的整个求解域进行离散化处理，即用一些假想的面或线将求解域分割为一系列的单元，各个单元之间仅在有限个节点处相互连接。

取未知函数的节点值作为基本未知量，在每个单元上选取一个近似的插值函数表示单元中场函数的分布规律。

利用变分原理来获得单元的刚度方程，然后按一定的规则把所有单元的刚度方程组集合起来，经适当的边界条件处理，便得到整个系统的总体方程组。

这样，偏微分方程便转化为一组常微分方程。

最后，求解总体方程组，得到节点值和用插值函数确定整个求解域上的场函数。

利用Matlab中的PDE工具箱进行偏微分方程求解！

利用Matlab中的PDE工具箱进行偏微分方程求解！在科学技术各领域中，有很多问题都可以归结为偏微分方程问题。

在物理专业的力学、热学、电学、光学、近代物理课程中都可遇见偏微分方程。

偏微分方程，再加上边界条件、初始条件构成的数学模型，只有在很特殊情况下才可求得解析解。

随着计算机技术的发展，采用数值计算方法，可以得到其数值解。

下面的几个简单例子，将为大家介绍如何利用Matlab中的PDE 工具箱进行偏微分方程的求解！抛物线型受热金属块的热传导问题：一块受热的有矩形裂纹的金属块。

金属块的左侧被加热到100℃，右侧热量则以恒定速率降低到周围空气的温度，所有其他边界都是独立的，于是边界条件为：初始温度为0℃。

指定起始时间为0，研究5s的热扩散问题。

求解结果如下：具体步骤：1.建模。

先画一个起点为(-0.5,-0.8)，终点为(0.5,0.8)的矩形，再建另一个矩形，起点(-0.05,-0.4)，终点(0.05,0.4)，然后在设置公式中输入R1-R2；2.设置边界条件；3.PDE中设置参数，d=1,c=1,a=0,f=0；4.初始化网格并细化一次；5.在Solve Parameter中，设置u0=0，时间为[0:0.5:5]，然后求解。

注意到金属块的温度升高很快，可试着改变时间列表的表达式为logspace(-2,0.5,20)以便观察。

双曲线型方形薄膜横向波动问题（波动方程）：薄膜左侧和右侧固定（u=0），上端和下端自由：满足边界条件的初值为：求解结果如下：具体步骤：1.建模，画出起点(-1,-1)，终点(1,1)的矩形；2.确定边界条件；3.PDE Specification对话框中选择双曲线型，参数设为c=1,a=0,f=0,d=1；4.初始化网格，并细化一次；5.在Solve Parameters对话框的时间中输入linspace(0,5,31)，u的初值为atan(cos(pi/2*x))，一次偏导的初值为3*sin(pi*x).*exp(sin(pi/2*y))，然后求解。

偏微分方程的matlab解法

图 22.2 定解问题的边界
第四步：设置方程类型
选择PDE菜单中PDE Mode命令，进入PDE模式，再单击PDE菜单中PDE Secification选项，打开 PDE Secification对话框，设置方程类型．本例取抛物型方程 d
u (cu ) au f , t
故参数c,a,f,d,分别是l，0，10，1．第五步：选择Mesh菜单中Initialize Mesh命令，进行网格剖分，选择Mesh菜单中Refine Mesh命令，使网格密集化，
例如，对于细杆导热，虽然是一维问题，可以将宽度y虚拟出来，对应于y的边界条件和初始条件按照题意制定
Boundary Mode

PDE Mode
PDE Specification，确定偏微分方程类型共有四种：
椭圆形Elliptic

抛物型Parabolic

双曲型Hyperbolic

如图22.3．
图 22.3 网格密集化
第六步：解偏微分方程并显示图形解选择Solve菜单中Solve PDE命令，解偏微分方程并显示图形解，如图 2.4 所示
第七步：单击Plot菜单中Parameter选项，打开Plot Selection对话框，选中Color,Height(3D plot)和 Show mesh三项.再单击Polt按钮，显示三维图形解，如图22.5所示.
例：解热传导方程 ut u f 边界条件是齐次类型，定解区域自定。
【解】第一步：启动MATLAB，键入命令pdetool并回车，就进入GUI．在Options菜单下选择Gid命令，打开栅格，栅格使用户容易确定所绘图形的大小．第二步：选定定解区域本题为自定区域：自拟定解区域如图22 1所示：E1-E2+R1-E3．具体用快捷工具分别画椭圆E1、圆E2、矩形R1、圆E3．然后在Set formula栏中进行编辑并用算术运算符将图形对象名称连接起来(或删去默认的表达式，直接键入E1E2+R1-E3)

MATLAB中的偏微分方程数值解法

MATLAB中的偏微分方程数值解法偏微分方程（Partial Differential Equations，PDEs）是数学中的重要概念，广泛应用于物理学、工程学、经济学等领域。

解决偏微分方程的精确解往往非常困难，因此数值方法成为求解这类问题的有效途径。

而在MATLAB中，有丰富的数值解法可供选择。

本文将介绍MATLAB中几种常见的偏微分方程数值解法，并通过具体案例加深对其应用的理解。

一、有限差分法（Finite Difference Method）有限差分法是最为经典和常用的偏微分方程数值解法之一。

它将偏微分方程的导数转化为差分方程，通过离散化空间和时间上的变量，将连续问题转化为离散问题。

在MATLAB中，使用有限差分法可以比较容易地实现对偏微分方程的数值求解。

例如，考虑一维热传导方程（Heat Equation）：∂u/∂t = k * ∂²u/∂x²其中，u为温度分布随时间和空间的变化，k为热传导系数。

假设初始条件为一段长度为L的棒子上的温度分布，边界条件可以是固定温度、热交换等。

有限差分法可以将空间离散化为N个节点，时间离散化为M个时刻。

我们可以使用中心差分近似来计算二阶空间导数，从而得到以下差分方程：u(i,j+1) = u(i,j) + Δt * (k * (u(i+1,j) - 2 * u(i,j) + u(i-1,j))/Δx²)其中，i表示空间节点，j表示时间步。

Δt和Δx分别为时间和空间步长。

通过逐步迭代更新节点的温度值，我们可以得到整个时间范围内的温度分布。

而MATLAB提供的矩阵计算功能，可以大大简化有限差分法的实现过程。

二、有限元法（Finite Element Method）有限元法是另一种常用的偏微分方程数值解法，特点是适用于复杂的几何形状和边界条件。

它将求解区域离散化为多个小单元，通过构建并求解代数方程组来逼近连续问题。

在MATLAB中，我们可以使用Partial Differential Equation Toolbox提供的函数进行有限元法求解。

matlab中求解偏微分方程

文章标题：深入探讨 Matlab 中求解偏微分方程的方法和应用一、引言在现代科学和工程中，偏微分方程是一种重要的数学工具，用于描述各种自然现象和物理过程，如热传导、流体力学、电磁场等。

Matlab 是一个用于科学计算和工程应用的强大工具，提供了丰富的数值计算和数据可视化功能，其中包括求解偏微分方程的工具箱，本文将深入探讨在Matlab中求解偏微分方程的方法和应用。

二、基本概念偏微分方程（Partial Differential Equation, PDE）是关于多个变量的函数及其偏导数的方程。

在物理学和工程学中，PDE广泛应用于描述空间变量和时间变量之间的关系。

在Matlab中，求解PDE通常涉及到确定PDE类型、边界条件、初始条件和求解方法等步骤。

三、求解方法1. 有限差分法（Finite Difference Method）有限差分法是求解PDE的常用数值方法之一，它将PDE转化为差分方程组，并通过迭代求解得到数值解。

在Matlab中，可以使用pdepe 函数来求解具有一维、二维或三维空间变量的PDE，该函数可以直接处理边界条件和初始条件。

2. 有限元法（Finite Element Method）有限元法是另一种常用的数值方法，它将求解区域离散化为有限数量的单元，并通过单元之间的插值来逼近PDE的解。

Matlab提供了pdenonlin函数来求解非线性PDE，该函数支持各种复杂的几何形状和非线性材料参数。

3. 特征线法（Method of Characteristics）特征线法适用于一维双曲型PDE的求解，该方法基于特征线方程的性质来构造数值解。

在Matlab中，可以使用pdegplot函数来展示特征线，并通过构造特征线网格来求解PDE。

四、实际应用1. 热传导方程的求解假设我们需要求解一个长条形的材料中的热传导方程，可以通过在Matlab中定义边界条件和初始条件，然后使用pdepe函数来求解得到温度分布和热流线。

matlab解偏微分方程

matlab解偏微分方程偏微分方程（PDE）是描述物理系统和工程问题中的变化和变形的基本方程之一。

它们是数学方程，可以用来解决流体力学、热传递、电磁场和结构分析等领域的问题。

在MATLAB中，可以使用PDE工具箱来求解偏微分方程。

PDE工具箱是MATLAB中的一个工具箱，用于求解偏微分方程。

它提供了多种方法来求解PDE，如有限元方法、有限差分方法、谱方法等。

PDE工具箱还提供了可视化工具，可以帮助用户更好地理解方程的解。

以下是PDE工具箱的使用步骤：1. 创建偏微分方程使用PDE工具箱，可以通过选择预定义的模型或手动创建方程来定义偏微分方程。

预定义的模型包括泊松方程、热传导方程、斯托克斯方程等。

手动创建方程要求用户提供方程的系数和初始条件。

2. 定义边界条件通过定义边界条件，可以限制方程的解在特定区域内。

通常，边界条件与实际问题的物理特征有关。

例如，泊松方程的边界条件可以是Dirichlet、Neumann或Robin条件。

3. 离散化空间和时间PDE工具箱使用离散化方法来计算偏微分方程的解。

在离散化过程中，空间和时间被分割成小的网格。

离散化方法的选择取决于所使用的数值方法。

4. 求解方程完成离散化后，PDE工具箱可以求解偏微分方程。

求解器的选取依赖于方程的类型和分析目的。

例如，稳态问题可以使用静态求解器，而动态问题可以使用显式和隐式求解器。

5. 可视化解PDE工具箱提供了多种工具来可视化解。

用户可以使用等值线、箭头和图形等来显示解的不同方面。

此外，PDE工具箱还提供了交互式工具，使用户可以更改参数以观察不同的解。

总之，MATLAB的PDE工具箱提供了一个方便的方式来解决偏微分方程。

通过使用这个工具箱，用户可以创建、定义、求解和可视化偏微分方程。

《应用matlab的pdetoolbox求解偏微分方程综合实验》

pderect([-0.1 0.1 0.2 0.9],'R2')
pderect([0 1 0 1],'SQ1')
③单击Boundary菜单下的Boundary Mode选项，进入边界模式.选择Boundary菜单中的Show Subdomain Labels命令，显示区域编号(如图10所示)，再单击所要删去的线段或弧段，执行Boundary菜单中Remove Subdomain Border命令，则可以得到图11.
%取复数解的实部
h=newplot;set(get(h,'Parent'),'Renderer','zbuffer')
pdeplot(p,e,t,'xydata',real(u),'zdata',real(u),...
'mesh','off');
colormap(cool)
clc
%制作反射波的动画程序
②在PDE Toolbox面板中依次拖出圆双击所绘制的圆，将圆心设置为(0,0),半径分别为1,0.8,0.6,0.5,0.4；依次拖出矩形双击所绘制的矩形，分别设置Left为-0.2、-0.1，Bottom分别为0.2、0.1,Width分别为0.2、0.2，Height分别为0.9、0.9.这样便可以得到图9所示的平面图.
for j=1:m,...
uu=real(exp(-j*2*pi/m*sqrt(-1))*u);...
fprintf('%d',j);...
pdeplot(p,e,t,'xydata',uu,'colorbar','off',...

matlab用有限元法求解偏微分方程组

matlab用有限元法求解偏微分方程组使用有限元法求解偏微分方程组是一种常见的数值计算方法，它在工程领域和科学研究中广泛应用。

本文将介绍如何利用MATLAB软件进行有限元法求解偏微分方程组的基本步骤和注意事项。

我们需要了解有限元法的基本原理。

有限元法是一种将连续问题离散化为有限个小区域，通过在每个小区域内建立适当的数学模型，然后将这些小区域连接起来形成整个问题的数学模型的方法。

在有限元法中，我们通常将问题的域分割成许多小的有限元，每个有限元都具有简单的几何形状，如线段、三角形或四边形。

然后，在每个有限元上建立适当的近似函数，通过对这些函数的系数进行求解，我们可以得到问题的近似解。

在MATLAB中，有限元法的求解过程可以分为以下几个步骤：1. 离散化域：根据问题的几何形状，将问题的域进行离散化处理。

离散化可以采用三角剖分法或四边形剖分法，将域分割成许多小的有限元。

2. 建立数学模型：在每个有限元上建立适当的数学模型。

这通常涉及选择适当的近似函数，并在每个有限元上求解这些函数的系数。

3. 组装方程：将每个有限元上的数学模型组装成整个问题的数学模型。

这涉及到将有限元之间的边界条件进行匹配，并建立整个问题的刚度矩阵和载荷向量。

4. 求解方程：利用线性代数求解方法，求解得到问题的近似解。

MATLAB提供了各种求解线性方程组的函数，如“\”运算符、LU 分解和共轭梯度法等。

5. 后处理：对求解结果进行后处理，包括绘制解的图形、计算问题的误差等。

在进行有限元法求解偏微分方程组时，需要注意以下几点：1. 网格剖分的合理性：网格剖分的精细程度对结果的精确性有很大影响。

网格过于粗糙可能导致结果的不准确，而网格过于细小则会增加计算的复杂性。

因此，需要根据问题的特点和计算资源的限制选择合适的网格剖分。

2. 近似函数的选择：近似函数的选择直接影响到结果的准确性和计算的效率。

一般情况下，近似函数的阶数越高，结果的准确性越高，但计算的复杂性也越大。

matlab 求解偏微分方程

matlab 求解偏微分方程使用MATLAB求解偏微分方程摘要：偏微分方程(partial differential equation, PDE)是数学中重要的一类方程，广泛应用于物理、工程、经济、生物等领域。

MATLAB 是一种强大的数值计算软件，提供了丰富的工具箱和函数，可以用来求解各种类型的偏微分方程。

本文将介绍如何使用MATLAB来求解偏微分方程，并通过具体案例进行演示。

引言：偏微分方程是描述多变量函数的方程，其中包含了函数的偏导数。

一般来说，偏微分方程可以分为椭圆型方程、双曲型方程和抛物型方程三类。

求解偏微分方程的方法有很多，其中数值方法是最常用的一种。

MATLAB作为一种强大的数值计算软件，提供了丰富的工具箱和函数，可以用来求解各种类型的偏微分方程。

方法：MATLAB提供了多种求解偏微分方程的函数和工具箱，包括pdepe、pdetoolbox和pde模块等。

其中，pdepe函数是用来求解带有初始条件和边界条件的常微分方程组的函数，可以用来求解一维和二维的偏微分方程。

pdepe函数使用有限差分法或有限元法来离散化偏微分方程，然后通过求解离散化后的常微分方程组得到最终的解。

案例演示：考虑一维热传导方程的求解，偏微分方程为：∂u/∂t = α * ∂^2u/∂x^2其中，u(x,t)是温度分布函数，α是热扩散系数。

假设初始条件为u(x,0)=sin(pi*x)，边界条件为u(0,t)=0和u(1,t)=0。

我们需要定义偏微分方程和边界条件。

在MATLAB中，可以使用匿名函数来定义偏微分方程和边界条件。

然后，我们使用pdepe函数求解偏微分方程。

```matlabfunction [c,f,s] = pde(x,t,u,DuDx)c = 1;f = DuDx;s = 0;endfunction u0 = uinitial(x)u0 = sin(pi*x);endfunction [pl,ql,pr,qr] = uboundary(xl,ul,xr,ur,t)pl = ul;ql = 0;pr = ur;qr = 0;endx = linspace(0,1,100);t = linspace(0,0.1,10);m = 0;sol = pdepe(m,@pde,@uinitial,@uboundary,x,t);u = sol(:,:,1);surf(x,t,u);xlabel('Distance x');ylabel('Time t');zlabel('Temperature u');```在上述代码中，我们首先定义了偏微分方程函数pde，其中c、f和s分别表示系数c、f和s。