全等三角形的识别案例(SSS)
全等三角形判定经典

11.2三角形全等的判定ABC DEF(1)三边对应相等的两个三角形全等,简写为“边边边”或“SSS ”。
表示方法:如图所示,在△ABC 和△DEF 中,AB DEAC DF BC EF=⎧⎪=⎨⎪=⎩,∴△ABC ≌△DEF (SSS )。
例1. 如图所示,AB =CD ,AC =DB 。
求证:△ABC ≌△DCB 。
A BCD分析:由已知可得AB =CD ,AC =DB ,又因为BC 是两个三角形的公共边,所以根据SSS 可得出△ABC ≌△DCB 。
证明:在△ABC 和△DCB 中,∵⎩⎨⎧AB =CD AC =DB BC =CB,∴△ABC ≌△DCB (SSS )评析:证明格式:①点明要证明的两个三角形;②列举两个三角形全等的条件(注意写在前面的三角形,条件也放在前面),用大括号括起来;③条件按照“SSS ”顺序排序;④得出结论,并把判断的依据注在后面。
“ASA ”。
表示方法:如图所示,在△ABC 和△DEF 中,B E BC EF C F∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ABC ≌△DEF (ASA )。
例2. 如图所示,AB ∥CD ,AF ∥DE ,BE =CF ,求证:AB =CD 。
ABEFCD分析:要证明AB =CD ,由于AB 、CD 分别是△ABF 和△DCE 的边,可尝试证明△ABF ≌△DCE ,由已知易证:∠B =∠C ,∠AFB =∠DEC ,下面只需证明有一边对应相等即可。
事实上,由BE =CF 可证得BF =CE ,由ASA 即可证明两三角形全等。
证明:∵AB ∥CD ,∴∠B =∠C (两直线平行,内错角相等) 又∵AF ∥DE ,∴∠AFC =∠DEB (同上) ∴∠AFB =∠CED (等角的补角相等)又∵BE =CF ,∴BE -EF =CF -EF ,即BF =CE 在△ABF 和△DCE 中,()()()B C BF CE AFB CED ∠=∠⎧⎪=⎨⎪∠=∠⎩已证已证已证∴△ABF ≌△DCE (ASA )∴AB =CD (全等三角形对应边相等)角边”或“AAS ”。
12.2全等三角形的判定(sss)(公开课)

八年级数学组
第1页,共18页。
知识回顾
1、 什么叫全等三角形?
2、 全等三角形有什么性质?
A
D
B
C
E
F
第2页,共18页。
探究一: 动手操作:
1.满足一个条件:
①一边:
可以发现按这些条
件画的三角形不 一定全等。
②一角:
60°
60°
第3页,共18页。
60°
动手操作:
第12页,共18页。
2、如图,已知AB=CD,AD=CB,
求证:∠B=∠D
A
B
能说明∠A=∠C吗?
A
D
B
C
数学转化思想:四
边形转化成三角形
第13页,共18页。
D C
3.如图,D、F是线段BC上的两点,AB=CE,AF=DE,
请添加一个条件
,使△ABF≌△ECD。
BF=DC 或 BD=FC
A
E
B DFC
第14页,共18页。
A
D
B
E
C
F
第15页,共18页。
归纳总结:
证明三角形全等的步骤:
(1)准备条件:证全等时要用的间接条件要先证好; (2)证明三角形全等书写三步骤:
①写出在哪两个三角形中 ②摆出三个条件用大括号括起来
③写出全等结论
第16页,共18页。
作业布置:
v基础训练: P22课堂练习1—5题
2.满足两个条件:
①一边一角:
30°
②两角:
30°50° ③两边:
2cm 4cm
30°
30°
同样可以发现按 这些条件画的三
全等三角形的判定(sss)

A
A’
B
C B’
C’
图一
图二
AB=A’B’
∠A=∠A’ ΔABC ≌ ∆A’ B’ C’ (SAS) AC=A’C’
A
A’
B
C
B’
C’
∠A=∠A’
AB=A’B’
ΔABC ≌ ∆A’ B’ C’
∠B=∠B’
(ASA)
A
A’
B
C
B’
C’
∠A=∠A’
∠B=∠B’ ΔABC ≌ ∆A’ B’ C’(AAS)
AD=AD(公共边)
∴ △ABD≌ACD(SAS)
总结 上题中应用了哪些性质及定理
性质一:等腰三角形的两底角相等 性质二:等腰三角形的中线、角平分线、高线互相重合。 定理三:在两个三角形中,如果有三条边相等,那么这两个三角形全等。 定理四:在两个三角形中,如果有两个角相等及一条边相等,那么这两个三角形 全等。 定理五:在两个三角形中,如果有两个角相等及所夹的边相等,那么这两个三角 形全等。 定理六:在两个三角形中,如果有两条边相等及所夹的角相等,那么这两个三角 形全等。
作业:课后习题
AC=A’C’
定理的引入 A
C
E
F
B
D
思考
已知:AC=DE AB=DF BC=FE 求证:△ABC≌ △DFE
定理的引入 A
C
D
已知:AC=DC AB=DB 求证:△ABC≌ △DBC
B
证明:连接AD, ∵AC=DC
∴∠CAD= ∠CDA
同理, ∠BAD= ∠BDA
∴ ∠BAC= ∠BDC
∵ AC=DC
答:图中有△ABE≌ACE,△BDE≌CDE △ABD≌ACD。
初中数学《三角形全等的判定——SSS》教学案例分析

探索三角形全等的条件——边边边(sss)教学案例一、案例背景本节课是2019-2020学年第一学期,人教版数学八年级上册第十二章探索三角形全等的第一节,教科书把研究三角形全等条件的重点就放在了第一个条件“边边边”上,使学生以“边边边”条件为例,理解什么是全等三角形的判定,怎样判定。
在掌握了“边边边”条件的基础上,使学生学会运用“边边边”条件进行推理论证,正确的表达全等三角形的证明过程。
本节课是笔者在农村寄宿制初中上的一节组内公开课。
课堂上数学成绩绝对优秀生人数不足五分之一,后进生人数较多。
二、案例主题本节课是在学习了第十一章三角形和第十二章第一节全等三角形后,对全等三角形条件探索的第一节,鉴于农村学生学情的实际情况,本节课以“动手实践、自主探索、合作交流、表达应用”为主题开展课堂教学,以学生“看得到、感受得到”的基本素材创设问题情境,引导学生活动,并在活动中认真探索、积极思考、主动获取数学知识,从而促进学生研究性学习方式的形成。
三、案例教学目标1、教学目标:学生在教师引导下,积极主动的经历探索三角形全等的条件的过程中,体会利用操作归纳获得数学的过程。
掌握三角形全等的“边边边”的判定方法,了解三角形的稳定性,能用三角形的全等解决一些实际问题。
培养学生推理能力,发展有条理地表达能力,积累数学活动经验。
2、教学重点与难点:重点:三角形全等条件的探索过程和运用“边边边”规律解决问题。
难点:三角形全等条件的探索过程,特别是创设出问题后,学生面对开放性问题,要作出全面、正确的分析,并对各种情况进行讨论,对学生来说有一定难度。
3、学习方式:为了使学生更好地掌握这一部分内容,遵循启发式教学的原则,用设问形式创设问题情景,涉及一系列实践活动,引导学生操作、观察、探索、交流、发现、思维,使学生经历从现实世界抽象出几何模型并运用所学知识解决实际问题,真正把学生放在主体位置。
4、课前准备:教师准备一张画有两个全等三角形的白纸四、案例教学过程(一)、创设情境,导入新课师:我们先来看几幅图片(投影出示)部分生:这些图片都是由三角形组成的。
三角形全等的判定(SSS、SAS) 习题
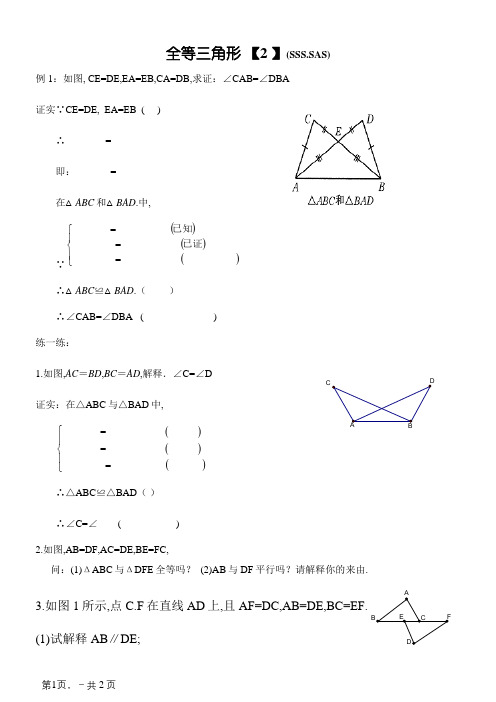
全等三角形 【2 】(SSS.SAS)例1:如图, CE=DE,EA=EB,CA=DB,求证:∠CAB=∠DBA 证实∵CE=DE, EA=EB ( )∴________=________ 即:_______=________ 在△ABC 和△BAD .中,∵()()()⎪⎩⎪⎨⎧===___________________________________________已证已知∴△ABC ≌△BAD .( ) ∴∠CAB=∠DBA ( ) 练一练:1.如图,AC =BD ,BC =AD ,解释.∠C=∠D证实:在△ABC 与△BAD 中,()()()______________________________________________= ⎧⎪= ⎨⎪=⎩ ∴△ABC ≌△BAD ( ) ∴∠C=∠___ ( ) 2.如图,AB=DF,AC=DE,BE=FC,问:(1)ΔABC 与ΔDFE 全等吗? (2)AB 与DF 平行吗?请解释你的来由.3.如图1所示,点C.F 在直线AD 上,且AF=DC,AB=DE,BC=EF.(1)试解释AB ∥DE;ABDFDCE(2)不雅察图2,图3,指出它们是如何由图1变换得到的? (3)在知足已知前提的情形下依据图2,试证实BC ∥EF .4.已知AB ⊥BD,ED ⊥BD,AB=CD,BC=DE,点B.C.D 在一条直线上,求证:AC ⊥CE.5.(多变题)已知AB=CD,AD=CB,求证:∠A=∠C一变:已知AD ∥BC,AD=CB,试证实:△ADC ≌△CBA二变:已知AD ∥BC,AD=CB,AE=CF.试证:△AFD ≌△CEB6.(现实应用)有一湖的湖岸在A.B 之间呈不规矩外形,A.B 之间的距离不能直接测量,你能用已学过的常识或办法设计测量计划并求出A.B 之间的距离吗?做一做:7.如图所示,有一块三角形的镜子,小明不当心弄决裂成1.2两块,现需配成同样 大小的一块.为了便利起见,需带上________块,其来由是__________.8.如图所示,AB ,CD 订交于O ,且AO =OB ,不雅察图形,图中已具备的另一相等 的前提是________,联想到SAS,只需补充前提________,则有△AOC ≌△_______ 9.如图,已知CA=CB,AD=BD,E,F 分离为CB,CA 的中点,求证:DE=DF10.如图,已知AB =AE,∠B =∠E,BC =ED,点F 是CD 的中点.求证:AF ⊥CD.11.已知△ABE 和三角形DEC 均为等边三角形,衔接BD,AC,求证:AC =BD图3图2图1F E D C B A E DF C B AE D CFABD EBACDCB A DCB A F E CB DAFEDCBADBAEFCF C。
【数学课件】三角形全等的判定(SSS)

如 何 用 符 号 语 言 来 表 达 呢
A
D
B
C
E
F
在△ABC与△DEF中 AB=DE AC=DF BC=EF ∴△ABC≌△DEF(SSS)
思考:你能 用“边边边” 解释三角形 具有稳定性 吗?
例1 已知:如图,AB=AD,BC=CD, 求证:△ABC≌ △ADC
A B D
证明:在△ABC和△ADC中 AB=AD (已知) BC=CD (已知) AC = AC (公共边)
失 败
(2)一个角 (1)两边 4cm
6cm 4cm 6cm
2.给定两个条件: (2)一边一角
30º 6cm
失 败
30º 6cm
(3)两角
30º 20º 30º 20º
俗话说:失败是成功之母! 我们继续探究: 千万别泄气哦! 探究二
(1)三边 给定三个条件: (2)两边一角 (3)一边两角 (4)三角 [动手画一画]
画出一个三角形,使它的三边长分别为3cm、 4cm、6cm , 把你画的三角形与小组内画的进 行比较,它们一定全等吗?
画法: 1.画线段AB=3㎝; 2.分别以A、B为圆心,4㎝和6㎝长为半径画弧,两 弧交于点C; 3. 连接线段AC、BC.
结论:三边对应相等的两个三角形全等. 可ቤተ መጻሕፍቲ ባይዱ写为”边边边”或SSS
课堂小测
2.如图,已知 AB DC,AC DB .求证: △ABC≌△DCB.
A
D
O B C
1.课本P15习题11.2的第1、2题(一号本)
能力提升题:
课本16页第9题(一号本)
1、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之毁灭。——卢梭 2、教育人就是要形成人的性格。——欧文 3、自我教育需要有非常重要而强有力的促进因素——自尊心、自我尊重感、上进心。——苏霍姆林斯基 4、追求理想是一个人进行自我教育的最初的动力,而没有自我教育就不能想象会有完美的精神生活。我认为,教会学生自己教育自己,这是一种 最高级的技巧和艺术。——苏霍姆林斯基 5、没有时间教育儿子——就意味着没有时间做人。——(前苏联)苏霍姆林斯基 6、教育不是注满一桶水,而且点燃一把火。——叶芝 7、教育技巧的全部奥秘也就在于如何爱护儿童。——苏霍姆林斯基 8、教育的根是苦的,但其果实是甜的。——亚里士多德 9、教育的目的,是替年轻人的终生自修作准备。——R.M.H. 10、教育的目的在于能让青年人毕生进行自我教育。——哈钦斯 11、教育的实质正是在于克服自己身上的动物本能和发展人所特有的全部本性。——(前苏联)苏霍姆林斯基 12、教育的唯一工作与全部工作可以总结在这一概念之中——道德。——赫尔巴特 13、教育儿童通过周围世界的美,人的关系的美而看到的精神的高尚、善良和诚实,并在此基础上在自己身上确立美的品质。——苏霍姆林斯基 14、教育不在于使人知其所未知,而在于按其所未行而行。——园斯金 15、教育工作中的百分之一的废品,就会使国家遭受严重的损失。——马卡连柯 16、教育技巧的全部诀窍就在于抓住儿童的这种上进心,这种道德上的自勉。要是儿童自己不求上进,不知自勉,任何教育者就都不能在他的身 上培养出好的品质。可是只有在集体和教师首先看到儿童优点的那些地方,儿童才会产生上进心。——苏霍姆林斯基 17、教育能开拓人的智力。——贺拉斯 18、作为一个父亲,最大的乐趣就在于:在其有生之年,能够根据自己走过的路来启发教育子女。——蒙田 19、教育上的水是什么就是情,就是爱。教育没有了情爱,就成了无水的池,任你四方形也罢、圆形也罢,总逃不出一个空虚。班主任广博的爱 心就是流淌在班级之池中的水,时刻滋润着学生的心田。——夏丐尊 20、教育不能创造什么,但它能启发儿童创造力以从事于创造工作。——陶行知
全等三角形SSS

全等三角形SSS在初中数学的几何世界里,全等三角形是一个非常重要的概念,而其中的“SSS”(边边边)判定定理更是基础且关键的一部分。
今天,咱们就来好好聊聊这个“SSS”。
首先,咱们得搞清楚啥是全等三角形。
简单说,就是两个三角形的形状和大小完全一样。
这就好比两个一模一样的模具,无论是角度还是边长,都分毫不差。
那怎么判断两个三角形是不是全等呢?这就轮到“SSS”登场啦。
“SSS”说的是,如果两个三角形的三条边都分别相等,那么这两个三角形就是全等的。
这听起来好像挺简单,但要真正理解它,还得深入琢磨琢磨。
咱们来举个例子。
假设有三角形 ABC 和三角形 DEF,AB 的长度等于 DE,BC 的长度等于 EF,AC 的长度等于 DF。
那咱们就能肯定地说,三角形 ABC 和三角形 DEF 是全等的。
那为什么三条边相等就能判定两个三角形全等呢?这其实是可以通过一些逻辑推理来证明的。
想象一下,咱们已经知道了三条边的长度,那么三角形的形状和大小基本上就被固定住了。
就好比咱们用三根固定长度的棍子去搭一个架子,不管怎么搭,最后搭出来的形状都是唯一的。
再从实际应用的角度来看,“SSS”在解决很多几何问题的时候都特别有用。
比如说,要证明两个三角形对应的角相等,或者要计算某个角度的大小,如果能先证明这两个三角形是全等的,那就会让问题变得简单很多。
而且,“SSS”在生活中也有不少应用呢。
比如说建筑师在设计建筑的时候,需要确保一些结构中的三角形部件是完全一样的,这时候就可以用“SSS”来进行判断和设计。
咱们再深入探讨一下“SSS”的一些特点和需要注意的地方。
在使用“SSS”判定两个三角形全等的时候,一定要保证测量的边长是准确无误的。
哪怕有一点点的误差,都可能导致判定错误。
另外,有时候题目可能不会直接告诉我们三条边的长度相等,而是需要我们通过一些已知条件去推导和计算得出。
这就需要我们灵活运用所学的几何知识和定理,进行一步步的推理。
全等三角形的判定含答案(SSS)
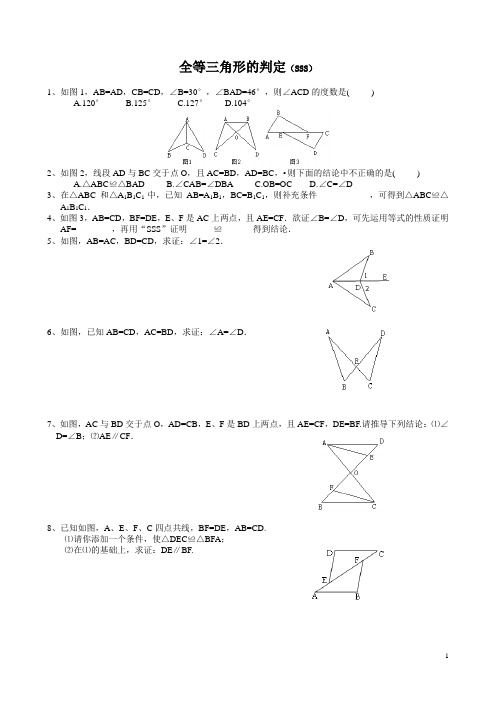
全等三角形的判定(SSS)1、如图1,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )A.120°B.125°C.127°D.104°2、如图2,线段AD与BC交于点O,且AC=BD,AD=BC,•则下面的结论中不正确的是( )A.△ABC≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D3、在△ABC和△A1B1C1中,已知AB=A1B1,BC=B1C1,则补充条件____________,可得到△ABC≌△A1B1C1.4、如图3,AB=CD,BF=DE,E、F是AC上两点,且AE=CF.欲证∠B=∠D,可先运用等式的性质证明AF=________,再用“SSS”证明______≌_______得到结论.5、如图,AB=AC,BD=CD,求证:∠1=∠2.6、如图,已知AB=CD,AC=BD,求证:∠A=∠D.7、如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导下列结论:⑴∠D=∠B;⑵AE∥CF.8、已知如图,A、E、F、C四点共线,BF=DE,AB=CD.⑴请你添加一个条件,使△DEC≌△BFA;⑵在⑴的基础上,求证:DE∥BF.答案1.C;2.C. 3、AC=A1C1 4、CE,△ABF≌△CDE.5、证明△ABE≌△ACE.6、连接BC,证明△ABC≌△DCB.7、⑴证明△ADE≌△CBF;⑵证明∠AEF=∠CFE.8、⑴可添加AE=CF或添加AF=CE,证明△DEC≌△BFA;⑵由⑴得∠BFA=∠DEC,∴DE∥BF.。
2.5 第5课时 全等三角形的判定(SSS)

BH=CH, BD=CD, DH=DH,
△ABD≌△ACD(SSS)
A
△ABH≌△ACH(SSS) B
△BDH≌△CDH(SSS)
D HC
课堂小结
三角形全等的“SSS”判定:三 边分别相等的两个三角形全等.
三边分别相等 的两个三角形
三角形的稳定性:三角形三边 长度确定了,这个三角形的形 状和大小就完全确定了.
课后作业
见《名师学案》本课时练习
A
E
A×
D
= ×× =
B D FC
=
=
O
B
×C
2.如图,AB=CD,AD=BC, 则下列结论:
①△ABC≌△CDB;②△ABC≌△CDA;③△ABD
≌△CDB;④BA∥DC. 正确的个数是
( C)
A . 1个 B. 2个 C. 3个 D. 4个
3.如图,桥梁的斜拉钢索是三角形的结构,主要是
为了
(C )
2.如图,工人师傅砌门时,常用木条EF固定门框
ABCD,使其不变形,这种做法的根据是(D )
A.两点之间线段最短
B.三角形两边之和大于第三边
C.长方形的四个角都是直角 A D.三角形的稳定性
E
D
F
B
C
当堂练习
1.如图,D、F是线段BC上的两点,AB=CE,AF=DE,
要使△ABF≌△ECD,还需要条件 BF=CD(答__案_不唯一. )
你能举出一些现实生活中的应用了三角形 稳定性的例子吗?
讨论
观察上面这些图片,你发现了什么? 发现这些物体都用到了三角形,为什么呢?
这说明三角形有它所独有的性质,是什 么呢?我们通过实验来探讨三角形的特性.
12.2三角形全等的判定(一)(SSS、SAS)(原卷版)

八年级上册数学《第十二章 全等三角形》1.2.2 三角形全等的判定(一)“边边边”与“边角边”◆利用“SSS ”判定两个三角形全等文字语言:三边分别相等的两个三角形全等,简写为“边边边”或“SSS”.几何语言:在△ABC 和△DEF 中,AB =DE BC =EF CA =FD∴△ABC ≌△DEF (SSS).◆利用“SAS ”判定两个三角形全等1、文字语言:两边和它们的夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”.2、几何语言:在△ABC 和△DEF 中,AB =DE ∠B =∠E BC =EF∴△ABC ≌△DEF (SSS).3、方法:(1)已知两边,可以找“夹角”;(2)已知一角和这角的一夹边,可找这角的另一夹边【注意】1. 有两边和其中一边的对角对应相等的两个三角形不一定全等.2. 说明两三角形全等所需的条件应按对应边的顺序书写.3. 结论中所出现的边必须在所证明的两个三角形中.【例题1】如图,△ABC 中,AB =AC ,EB =EC ,则由“SSS ”可以判定( )A.△ABE≌△ACE B.△ABD≌△ACDC.△BDE≌△CDE D.以上答案都不对【变式1-1】如图,在△ACE和△BDF中,AE=BF,CE=DF,要利用“SSS”证明△ACE≌△BDF,需添加的一个条件可以是( )A.AB=BC B.DC=BC C.AB=CD D.以上都不对【变式1-2】下列四个三角形中,与图中的△ABC全等的是( )A.B.C .D .【变式1-3】如图,已知点A 、D 、B 、F 在一条直线上,AC =EF ,AD =FB ,要使△ABC ≌△FDE ,还需添加一个条件,这个条件可以是( )A .AC ∥EFB .∠E =∠C C .∠ABC =∠FDED .AB =DF【变式1-4】如图,已知∠1=∠2,若用“SAS ”证明△BDA ≌△ACB ,还需加上条件( )A .AD =BCB .BD =AC C .∠D =∠C D .OA =OB【例题2】如图,已知点B ,C ,D ,E 在同一直线上,且AB =AE ,AC =AD ,BD =CE .求证:△ABC ≌△AED.【变式2-1】(2023•云南)如图,C是BD的中点,AB=ED,AC=EC.求证:△ABC≌△EDC.【变式2-2】如图,AB=DE,AC=DF,BF=EC,△ABC和△DEF全等吗?请说明理由.【变式2-3】(2023•永善县三模)如图,AB=DE,AC=DF,BE=CF,求证:△ABC≌△DEF.【例题3】11.(2018秋•庆云县校级月考)请仔细观察用直尺和圆规作一个角等于已知角的示意图,请你根据所学的三角形全等有关的知识,说明画出∠A ′O ′B ′=∠AOB 的依据是 .【变式3-1】小聪在用直尺和圆规作一个角等于已知角时,具体过程是这样的:已知:∠AOB .求作:∠A ′O ′B ′,使∠A ′O ′B ′=∠AOB .作法:(1)如图,以点O 为圆心,任意长为半径画弧,分别交OA ,OB 于点C ,D ;(2)画一条射线O ′A ′,以点O ′为圆心,OC 长为半径画弧,交O ′A ′于点C ′;(3)以点C '为圆心,CD 长为半径画弧,与第(2)步中所画的弧相交于点D ′;(4)过点D '画射线O ′B ′,则∠A ′O ′B ′=∠AOB .小聪作法正确的理由是( )A .由SSS 可得△O ′C ′D′≌△OCD ,进而可证∠A ′O ′B ′=∠AOBB .由SAS 可得△O ′C ′D ′≌△OCD ,进而可证∠A ′O ′B ′=∠AOBC .由ASA 可得△O ′C ′D ′≌△OCD ,进而可证∠A ′O ′B ′=∠AOBD .由“等边对等角”可得∠A ′O ′B ′=∠AOB【变式3-2】(2023春•白银期中)已知∠AOB ,点C 是OB 边上的一点.用尺规作图画出经过点C 与OA 平行的直线.【变式3-3】如图,以△ABC 的顶点A 为圆心,以BC 长为半径作弧,再以顶点C 为圆心,以AB 长为半径作弧,两弧交于点D ;连接AD 、CD ,若∠B =56°,则∠ADC 的大小为 度.【例题4】(2023•官渡区一模)如图,点A ,B ,C ,D 在同一直线上,AF =DE ,∠A =∠D ,AC =DB .求证:△ABF ≌△DCE.【变式4-1】(2023•从化区二模)为了制作燕子风筝,燕子风筝的骨架图如图所示,AB=AE,AC=AD,∠BAD=∠EAC,证明:△ABC≌△AED.【变式4-2】(2023•祥云县模拟)已知:如图,点F、C在线段BE上,AB=DE,∠B=∠E,BF=EC,求证:△ABC≌△DEF.【变式4-3】(2023•乾安县四模)已知:如图,BA=BD,BE=BC,∠ABD=∠CBE,求证:△ABE≌△DBC.【变式4-4】(2023•宁江区二模)如图,△ABC 中,D 是BC 延长线上一点,满足CD =AB ,过点C 作CE ∥AB 且CE =BC ,连接DE 并延长,分别交AC 、AB 于点F 、G ,求证:△ABC ≌△DCE .【变式4-5】(2023•五华区校级模拟)如图,已知AB ∥DE ,AB =DE ,AF =DC .求证:△ABC ≌△DEF .【例题5】如图,点D 在AB 上,点E 在AC 上,CD 与BE 相交于点O ,且AD =AE ,∠B =∠C ,若BE =4,则CD = .【变式5-1】(2022春•成华区期末)如图,在等腰△ABC 中,∠ACB =90°,点D 是AC 的中点,过点A 作直线BD 的垂线交BC 的延长线于点E ,若BC =4,则CE 的长为 .【变式5-2】茗茗用同种材料制成的金属框架如图所示,已知∠B =∠E ,AB =DE ,BF =EC ,其中△ABC 的周长为24cm ,CF =3cm ,则制成整个金属框架所需这种材料的长度为 cm .【变式5-3】(2023•青海一模)在△ABC 中,D 是BC 边的中点,若AB =9,AC =5,则△ABC 的中线AD 长的取值范围是( )A .5<AD <9B .4<AD <9C .2<AD <14D .2<AD <7【例题6】如图,已知OA =OB ,OC =OD ,∠O =50°,∠D=35°,则∠OBC =( )A.95°B.120°C.50°D.105°【变式6-1】(2022春•福山区期中)如图,AC是四边形ABCD的对角线,∠1=∠B,点E、F分别在AB、BC上,BE=CD,BF=CA,连接EF.(1)求证:∠D=∠2;(2)若EF∥AC,∠D=76°,求∠BAC的度数.【变式6-2】(2023春•青羊区期末)如图在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.(1)求证:△ABE≌△DBE;(2)若∠A=100°,∠C=40°,求∠DEC的度数.【变式6-3】(2022秋•湟中区校级期末)如图,在△ABC中,D为AB上一点,E为AC中点,连接DE 并延长至点F,使得EF=ED,连CF.(1)求证:CF∥AB(2)若∠ABC=50°,连接BE,BE平分∠ABC,AC平分∠BCF,求∠A的度数.【例题7】(2022秋•甘井子区校级月考)如图,点C、E、B、F在同一直线上,AC∥DF,AC=DF,BF =CE,试判断AB和DE的关系,并说明理由.【变式7-1】(2023春•罗湖区校级期末)已知:如图,点A、F、C、D在同一直线上,AF=DC,AB=DE,AB∥DE,连接BC,BF,CE.求证:(1)△ABC≌△DEF;(2)BC∥EF.【变式7-2】(2023春•萍乡期末)如图,已知:AB⊥BD,ED⊥BD,AB=CD,BC=DE,那么AC与CE 有什么关系?写出你的猜想并说明理由.【变式7-3】如图,在△ABC中,D为AB的中点,F为BC上一点,DF∥AC,延长FD至E,且DE=DF,联结AE、AF.(1)求证:∠E=∠C;(2)如果DF平分∠AFB,求证:AC⊥AB.【例题8】如图,AC =DC ,BC =EC ,请你添加一个适当的条件: ,使得△ABC ≌△DEC .【变式8-1】如图,已知在△ABC 和△DEF 中,∠B =∠E ,BF =CE ,点B 、F 、C 、E 在同一条直线上,若使△ABC ≌△DEF ,则还需添加的一个条件是 (只填一个即可).【变式8-2】如图,AB =AE ,AC=AD,要使△ABC ≌△AED ,应添加一个条件是 .【变式8-3】问题:如图,在△ABC 和△DEF 中,B ,E ,C ,F 在同一条直线上,AB =DE ,若 .求证:△ABC ≌△DEF .在①AC =DF ,②∠ABC =∠DEF ,③BE =CF 这三个条件中选择其中两个,补充在上面的问题中,并完成解答.【例题9】(2022春•包头期末)如图,已知点A ,C 在线段BD 两侧,AB =AD ,CB =CD ,线段AC ,BD 相交A 于点O .下列结论:①∠ABC =∠ADC ;②AC ⊥BD ;③AC 平分∠BAD ;④OB =OD .其中正确的是 (填写所有正确结论的序号).【变式9-1】(2023•禅城区校级一模)如图,已知AB=AC,AD=AE,∠BAC=∠DAE,且B、D、E三点共线,(1)证明:△ABD≌△ACE;(2)证明:∠3=∠1+∠2.【变式9-2】(2022春•沙坪坝区校级期中)如图,点C在线段AB上,AD∥BE,AC=BE,AD=BC,CF 平分∠DCE.求证:△DCF≌△ECF【变式9-3】(2023春•浦东新区校级期末)如图,已知AB=AE,AC=AD,∠BAD=∠EAC,AD∥BC.(1)△ADE与△ACB是否全等?说明理由;(2)如果∠B=30°,∠D=40°,求∠BAE的度数.【变式9-4】(2022秋•自流井区校级期末)如图,在△ABC和△ADE中,AB=AD,AC=AE,∠1=∠2,AD、BC相交于点F.(1)求证:∠B=∠D;(2)若AB∥DE,AE=3,DE=4,求△ACF的周长.【变式9-5】如图,AD=CB,E、F是AC上两动点,且有DE=BF.(1)若点E、F运动至如图(1)所示的位置,且有AF=CE,求证:△ADE≌△CBF;(2)若点E、F运动至如图(2)所示的位置,仍有AF=CE,则△ADE≌△CBF还成立吗?为什么?(3)若点E、F不重合,则AD和CB平行吗?请说明理由.。
全等三角形判定(SSS)

E
F
用 数学语言表述:
在△ABC和△ DEF中
∴ △ABC ≌△ DEF(SSS)
AB=DE BC=EF CA=FD
结论:三边分别都相等的两个三角形全等(SSS)
例1. 如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架。 求证:△ ABD≌ △ ACD
添加标题
小结
添加标题
知道三角形三条边的长度怎样画三角形。
添加标题
①只给一条边:
②只给一个角:
60°
60°
60°
探究:
只给出一个条件时不能保证所画的两个三角形一定全等.
2.给出两个条件:
①一边一内角:
②两内角:
③两边:
30°
30°
30°
30°
30°
50°
50°
2cm
2cm
4cm
4cm
可以发现按两个条件画的两个三角形也不能保证一定全等。
已知一个三角形的三个内角是80°、60°、40°,它们全等吗?
∴ △ ABD≌ △ACD(SSS)
A
B
C
D
证明:∵D是BC的中点 ∴BD=CD 在△ABD和△ACD中,
AB=AC(已知) AD=AD(公共边) DB=DC
∴ △ ABD≌ △ACD(SSS)
∴∠1= ∠2(全等三角形对应角相等) ∵ ∠1+∠2=180º
∴∠1= ∠BDC=90º
结论:三个内角对应相等的两个三角形不一定全等。
A
B
C
60°
80°
40°
D
E
F
60°
40°
80°
3、给出三个条件:(三个角相等)
三角形全等的判定(SSS)全面版

小结:四边形问题转化为三角形问题解决。 D
问:此题添加辅助线,若连结BD行吗? 在原有条件下,还能推出什么结论? B 答:∠ABC=∠ADC,AB∥CD,AD∥BC
C
练一练 工人师傅常用角尺平分一个任意角,做法如下: 如图,∠AOB是一个任意角,在边OA,OB上分别取 OM=ON,移动角尺,使角尺两边相同的刻度分别与M、 N重合,过角尺顶点C的射线OC便是∠AOB的平分线。 为什么?
∠C=、三组对应角 六个条件分别相等。
问题1:若两个三角形三组对应边、三组对应角分别 相等,则这两个三角形是否一定全等? 两个三角形全等 三组对应边、三组对应角 六个条件分别相等。
问题2:两个三角形满足六个条件中的几个条件才能 确保这两个三角形全等呢?
探究一 (1)一条边 1.给定一个条件:
D
若要求证: ∠B=∠C, 你会吗?
∴∠B=∠C(全等三角形的对应角相等)
归纳:
证明全等的书写步骤:
①准备条件:证全等时要用的间接 条件要先证好; ②三角形全等书写三步骤:
写出在哪两个三角形中 摆出三个条件用大括号括起来 写出全等结论
练习1
如图,AB=CD,AC=BD,△ABC和△DCB 是否全等?试说明理由。 A D
C
B
∴ ∠ A= ∠ C (全等三角形的对应角相等)
变形题: 已知AB=CD,AD=CB,求证:∠B=∠D
证明:连接AC, A 在△ABC和△ ADC中 AB=CD(已知) BC=AD(已知) AC=AC(公共边) ∴ △ ABC≌ △ CDA(SSS) D
B
C
∴ ∠B=∠D(全等三角形对应角相等)
失 败
(2)一个角 (1)两边 4cm
6cm 4cm 6cm
初中数学教学课例《三角形全等的判定(SSS)》教学设计及总结反思

2 所示的残片,•你对图中的残片作哪些测量,就可以
割取符合规格的三角形玻璃,与同伴交流.
【学生活动】观察,思考,回答教师的问题.方法
如下:可以将图 1•的玻璃碎片放在一块纸板上,然后
用直尺和铅笔或水笔画出一块完整的三角形.如图 2,
教学过程 •剪下模板就可去割玻璃了.
【理论认知】
如果△ABC≌△A′B′C′,那么它们的对应边相
三角形全等. 【评析】通过学生全过程的画图、观察、比较、交
流等,逐步探索出最后的结论──边边边,在这个过程 中,学生不仅得到了两个三角形全等的条件,同时增强 了数学体验.
二、范例点击,应用所学 【例 1】如课本图 11.2─3 所示,△ABC 是一个钢 架,AB=AC,AD 是连接点 A 与 BC 中点 D 的支架,求证 △ABD≌△ACD.(教师板书) 【教师活动】分析例 1,分析:要证明 △ABD≌△ACD,可看这两个三角形的三条边是否对应相 等. 证明:∵D 是 BC 的中点, ∴BD=CD 在△ABD 和△ACD 中 ∴△ABD≌△ACD(SSS). 【评析】符号“∵”表示“因为”,“∴”表示“所 以”;从例 1 可以看出,•证明是由题设(已知)出发, 经过一步步的推理,最后推出结论(求证)正确的过 程.书写中注意对应顶点要写在同一个位置上,哪个三 角形先写,哪个三角形的边就先写. 三、实践应用,合作学习
12.2.1全等三角形的判定(sss)

三边
两边一角
两角一边
300
500
300
500
满足下列条件的两个三角形是一定否全等:
(1)一个条件
× 一边
只有一个条件对应相等的
× 一角
两个三角形不一定全等。
(2)两个条件
一边一角 × 两角 ×
两边
三角
(3)三个条件
三边 两边一角
两角一边
8cm
8cm
满足下列条件的两个三角形是一定否全等:
(1)一个条件 (2)两个条件 (3)三个条件
(2)两个条件 (3)三个条件
一边一角 × 两角 × 两边 × 三角 ×
三边
只有两个条件对应相 等的两个三角形不一 定全等。
两边一角
两角一边
8cm
8cm
满足下列条件的两个三角形是否一定全等:一个条件× 一边
只有一个条件对应相等的
× 一角
两个三角形不一定全等。
两个条件 三个条件
一边一角 × 两角 × 两边 × 三角 × 三边 √
A
B D
C
E
F
判断两个三角形全等的推理过程,叫做证明三角 形全等。
例1. 如下图,△ABC是一个钢架,
AB=AC,AD是连接A与BC中点D的 支架。求证:△ABD≌ △ACD
A
B
D
C
例2.已知AC=FE,BC=DE,点A, D,B,F在一条直线上,AD=FB,证 明△ABC ≌△ FDE
A
C
DB
E
F
A
C
B
D
E
F
证明三角形全等的步骤:
(1)准备条件:证全等时要用的间接条 件 要先证好; (2)证明三角形全等书写三步骤:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题全等三角形的识别(1)重庆市长寿中学数学组袁家秀教材的地位和作用本节课是华师版九年级数学(上)《图形的全等》一章第二节第一课时内容,它是几何学习的重要内容。
三角形全等是说明线段、角相等的重要依据。
本年级学生已学习了“图形全等的定义”及“平行四边形的认识”,但由于没有“三角形全等的识别”这部分知识储备,因此解题时常感到力不从心、无从下手,所以本备课组集体研究决定把“三角形全等的识别”提到本期末来上,“三角形全等的识别”是研究全等图形的基础,也是说理推理的基础。
以本节的知识探求活动为裁体,让学生体会分析问题的一种方法,积累数学活动的经验,逐渐树立推理的意识,发展有条理地思考和表达能力,在此基础上进一步研究,三角形全等的其他条件及其应用,为以后研究其它几何图形,指明研究的方法、方向奠定一定的基础。
教案目标▲知识目标:经历探索三角形的全等条件,掌握用“边边边”条件识别三角形全等的方法。
▲能力目标:体会利用操作,归纳获得数学结论的过程,在探索三角形全等条件及其运用的过程中,获得一种研究问题的方法(由简单的情形出发、分类等),能够进行有条理的思考并进行简单的推理。
▲情感目标:由边边边的应用,体会数学与现实生活中的联系,树立学好数学的信心。
教案重点、难点:▲重点:掌握三角形全等的识别方法“SSS”,并能用它来判定两个三角形是否全等。
▲难点:探索三角形全等的识别方法“SSS ”及应用。
教案方法与手段探究式教案,遵循以学生为主体,教师为主导,发展为主旨的现代教育原则,以问题的提出,问题的解决为主线,引导学生探索新知,归纳总结,以学定教。
采用多媒体铺助教案,增大教案容量,提高课堂效率。
教具、学具:教具:多媒体课件学具:三角板、量角器、圆规、小剪刀。
教案媒体:大屏幕、实物投影。
教案程序设计一、创设问题情境,激发学生学习兴趣(帮帮小明)。
小明不小心把一块三角形的玻璃打碎成了三块,他现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带哪一块去呢?(由问题的引入,学生非常想帮助小明解决困难,自然进入问题情境,激起探究动机.)学生回答①、②、③的都有,对于学生的回答给予鼓励,然后引导学生思考:要想配一块完全一样的玻璃,需作一个与原三角形玻璃全等的三角形,就要探究三角形全等的方法,你知道从那个角度去探究吗?二、回顾1.怎样的两个三角形全等?(学生在已有的知识基础上能回答:) ③ ② ①①能够完全重合的两个三角形全等。
②边、角分别对应相等的两个三角形全等。
2.试一试:如图,△ABC 是等腰三角形,AD 是底边上的高,△ABD 和△ACD 全等吗?试根据等腰三角形的有关知识说明理由。
解:∵△ABC 是等腰三角形,AD 是底边BC 上的高.∴AB=AC ,BD=CD ,∠B=∠C ,∠BAD=∠CAD ,∠ADB=∠ADC=90°.又 AD=AD (公共边)(等腰三角形底边上的高线、中线和顶角的平分线三线合一.)∴△ABD ≌△ACD从上面问题我们知道:若两个三角形能够完全重合或所有边、角分别对应相等,则这两个三角形全等。
除了这个方法外,我们能不能找到一些较为简便的方法,用来识别三角形的全等呢?能否减少一些条件也能识别两个三角形全等呢?自然引入“课题:全等三角形的识别(1)”(从生活情境及解题需要入手,让学生感受到探索三角形全等识别方法的必要性,实用性,由问题的引入,引出课题同时也体现了生活中蕴含数学,数学溶于生活这一理念,培养用数学的意识。
选择新旧知识的切入点,通过启发提问,构设问题悬念,激发学生兴趣。
明确本节课的学习目的。
)三、指导探索研究1.教师引导学生将条件由少到多地逐步探索全等的条件。
2.组织小组交流3.最后小组对所有问题的意见达成共识后,推举一代表发布研究成果。
教师巡视,融入不同的学生小组,指导学生有效地完成实┓ B A验。
和学生一起归纳,总结出结论:只给出一个条件或两个条件时,都不能保证所画出的三角形一定全等自主探索研究学生按条件由少到多的过程,画图,观察,各自所画的三角形形状。
学生充分交流,比较后小组代表把讨论结果和所画图形在实物投影仪上展示。
(时间关系最好让学生课前按要求将三角形画好、剪下。
)结论对于两个三角形的三条对应边、三个对应角中,只满足其中一个条件或两个条件相等,两个三角形不一定全等。
营造自主探索空间,提供合作交流的场所以学生的探求活动为主体,让学生参与经历,体验,感悟,“三角形全等条件”的形成与发展过程。
让学生通过画图,观察比较,推理,交流,在条件由少到多的过程中逐步探索三角形全等的条件,初步体会分类的思想。
4.如果两个三角形有三组量分别对应相等,那么有哪几种可能的情况?让学生通过充分思考、讨论后答出:(1) 三边 (S.S.S.)(2) 三角 (A.A.A.)(3)两边一角①夹角 (S.A.S.)②不是夹角 (S.S.A.)(4)一边两角①夹边 (A.S.A.)②不是夹边 (A.A.S.)然后挑选本节课主题提问:如果两个三角形的三条边分别对应相等,那么这两个三角形会全等吗?(师生共同完成)做一做:请按照下面的方法,用刻度尺和圆规画△ABC,使其三边长分别为4cm,3cm和4.8cm.在经历画图的过程后,请学生把所画的三角形剪下来与其他同学所画的三角形进行比较。
(进行小组交流、讨论,并归纳出三角形全等判定条件。
)1)画一线段AB使它的长度等于 c(4.8cm).2)以点A为圆心,以线段b(3cm)的长为半径画圆弧。
以点B为圆心,以线段a(4cm)的长为半径画圆弧。
两弧交于点C.3)连结AC、BC.△ABC即为所求.想一想:①把你画的三角形与其他同学画的三角形相比较,他们全等吗?②它们重合满足几个条件?换三条线段,再试试看,是否有同样的结论.通过刚才的“做一做”中问题的解决,尝试用自己的语言归纳三角形全等的条件,并与你的同伴交流在学生充分思考、交流的基础上,让学生归纳出识别三角形全等的“SSS”方法。
发现:给定三条线段,如果它们能组成三角形,那么所画的三角形都是全等的.引导学生说一说:识别三角形全等的一种简便的方法:如果两个三角形的三条边分别对应相等,那么这两个三角形全等. 简写为(“边边边”或“S.S.S.”).在△ABC和△DEF中AB=DE(已知) ∵AC=DF(已知)BC=EF(已知)DE FCBA(通过“做一做”让学生在动手画图,动脑思考,动口交流的丰富情境中经历具体实例的抽象概括过程,使学生明确三边对应相等的两个三角形完重合。
通过“说一说”培养学生归纳表达能力,从中培养成果意识,感受成功体验。
在这个相对宽松的环境气围中,培养了学生相互学习,相互合作的品质,有效地发挥余地和空间,充分调动学生的积极性,参与性,力求达到不仅让学生掌握基础知识和技能的目的,更能让学生在享受探索成果的同时,学到一种探究学习的方法,积累数学活动的经验。
)练一练:学生完成课后练习P83第一题。
(同桌之间互相交流,并进一步体会用“SSS”来判定三角形全等。
)在这个相对宽松的环境气围中,培养了学生相互学习,相互合作的品质,有效地发挥余地和空间,充分调动学生的积极性,参与性,力求达到不仅让学生掌握基础知识和技能的目的,更能让学生在享受探索成果的同时,学到一种探究学习的方法,积累数学活动的经验。
参与总结提炼鼓励学生用自己的语言归纳知识上的收获,过程与方法上的收获,情感与态度上的感受。
4.范例例1如图,四边形ABCD中,AD=BC,AB=CD,△ABC≌△CDA 吗?试说明理由。
解:在△ABC和△CDA中,CB=AD(已知)∵AB=CD (已知)AC= CA (公共边),BC DA1.由实践知,对于两个三角形的三条对应边、三个对应角中,只满足其中一个条件或两个条件相等,两个三角形不一定全等.2.可用(S.S.S.)来识别两个三角形全等.思考 三个角对应相等的两个三角形全等吗?四、反思总结提高不同的学生谈自己不同的收获和感受。
五、练习教材 P82-83 练习题六、作业1.课本上P90 习题1补充:(1) 已知△ABC 中,AD=AE ,AB=AC=BE=CD ,试说明△ABD ≌△ACE.第(1)题 第(2)题(2)如图,AB=CD ,BE=DF,AF=CE,试判断BE 与DF 的位置关系.2.探索与研究:能否用两角一边,二边一角“来判定三角形全等,说明你的理由,下节课展示你的探索结果。
3.收集三角形全等和三角形的稳定性在生活中的实例或图片,并展示你的结果EA DB E BCD A F教案设计说明1.教育理念数学教案不仅要教给学生数学知识,而且还要揭示获取知识的思维过程。
本节的重点是归纳、总结三角形全等的(S.S.S.)识别方法,而如何科学地、合理地向学生展示识别方法的产生、发展过程尤其重要。
如果直接以“三角形全等的识别方法—例题—习题”组成的纯数学体系展现在学生面前,这样呈现给学生的是数学冰冷的美丽。
这种方式在一定程度上颠倒了数学的发现过程,掩盖了数学发现、发明、创造和数学应用的火热思考过程,扼杀了学生的学习兴趣和求知欲望。
若改为“从实际问题的需要出发,启发学生为什么要引入三角形的全等的识别方法,再让学生亲身经历探索三角形的全等的条件过程分类等数学思想,从而归纳总结出识别方法。
”就可使数学冰冷的美丽变为火热的思考,就能达到启发式教育的目的,同时让学生形成良好的认知结构。
本节课还运用了讲练结合的方法,有意让学生暴露一些片面或错误的认识,能使学生更深刻地获取知识。
2.我采用的教案模式是创设..交流讨..问题情境—指导..探索研究—组织论—引导总结提炼3.针对评价方式的说明,根据新课标的评价理念,教师在教案中关注的不仅仅是结果,同时也要关注学生对待学习的态度是否积极,关注的是学生的参与意识,关注的是能否从数学的角度思考问题,归根到底教师关注的是整个教案的过程。
在课堂教案中,我尽量给学生更多的展示自己的机会,鼓励与欣赏学生,帮助学生认识自我,建立自信,争取最大限度地发挥评价的激励功能。
4.有效的学习活动是学生要能充分有效地参与到数学探究活动之中。
这就要求教师要有效地组织引导学生的活动。
这节课,我设计了试一试、做一做、想一想、说一说、练一练活动,并以小组合作学习的形式进行。
先在小组内进行交流,再以小组为单位在全班进行交流,并引入竞争机制,从而有效地调动了学生参与的积极性。
5.不足之处是感觉有些仓促,时间把握不好。
