高中数学新人教A必修三课件循环结构(习题课)
合集下载
高中数学:循环结构课件新课标人教A版必修3

(二)学生状况分析
学生在学习本课以前,已经学习了算法的概念、顺序结构、 条件结构及简单的赋值问题,同时也已经熟练掌握数列递推求和 的思想,因此,学生具备类比简单(变量=表达式)的赋值得出的结 论的基础。通过对引例的分析,使学生逐步经历循环结构设计的 全过程,学会有条理的思考问题,表达循环结构,并尝试整理成 程序框图。
循环条件:n 100 或 n 100
(4)两种循环类型:直到型循环结构和当型循环结构的区别 与 联系. (5)特点:具有反复执行某一处理过程特点的算法用循环结 构。
(三)例题解析 强化训练
1.类比探究,掌握知识
例1:改造引例的程序框图表示①求 2 4 6 200 的值
②求 12 22 32 1002 的值
课题:循环结构
一、教材分析与处理
(一)教材的地位与作用
算法是数学及其应用的重要组成部分,是计算科学的重要基 础。算法思想已逐渐成为每个现代人所必须具备的数学素养。本 节课的内容是循环结构,它与顺序结构、条件结构是算法的三种 基本逻辑结构,可以表示任何一个算法。并且循环结构是算法这 一部分的重点和难点,它更加充分体现计算机的优势。
(四)总结归纳 布置作业
四、教学设计说明 建构主义作为一种新的认识论,它认为,认识不是人脑对事物直接的、简单的反
映,而是以原有知识为基础,在主客体的相互作用中建构而成的。在认识论的基础 上,建构主义提出了学习实质上是一种"意义建构"的独特观点。以"建构"观念取代传 统的学习是一种"反映"的观念,更能体现学习的本质特征。因为"反映"是从客体的角 度来看问题,强调学习作为一种认识所具有的客体性和符合性;而"建构"则强调主 体性和选择性,指出了学习作为一种认识是主体能动选择、主动建构的过程,其中 心在于学生的"学"。强调学生对知识的主动探索、主动发现以及学生对所学知识意 义的主动建构。本节课的整体设计和处理方法正是基于此理论的体现. (一)创设情境,引入概念. 通过引例,复习旧知识,提出新问题.一题多解,各种解法形成对比与联系.此环节激 起学生的求知欲、探索欲,创新欲 ,让学生带着问题进入下一环节. (二)讲授新课 1.发现问题,探求新知. 学生在教师引导下,在已有知识结构和经验的基础上,借助多媒体的形象直观,共 同完成问题的抽象过程和算法的构建过程。体现研究问题常用的“由特殊到一般” 的思维方式。 2.类比探究,掌握知识 通过类比,自主探究,帮助学生深入理解知识,完善知识结构,提升认知水平。通 过小组讨论,实现生生互动,师生互助,丰富情感体验,活跃课堂气氛。 (三)实践应用,强化理解。
学生在学习本课以前,已经学习了算法的概念、顺序结构、 条件结构及简单的赋值问题,同时也已经熟练掌握数列递推求和 的思想,因此,学生具备类比简单(变量=表达式)的赋值得出的结 论的基础。通过对引例的分析,使学生逐步经历循环结构设计的 全过程,学会有条理的思考问题,表达循环结构,并尝试整理成 程序框图。
循环条件:n 100 或 n 100
(4)两种循环类型:直到型循环结构和当型循环结构的区别 与 联系. (5)特点:具有反复执行某一处理过程特点的算法用循环结 构。
(三)例题解析 强化训练
1.类比探究,掌握知识
例1:改造引例的程序框图表示①求 2 4 6 200 的值
②求 12 22 32 1002 的值
课题:循环结构
一、教材分析与处理
(一)教材的地位与作用
算法是数学及其应用的重要组成部分,是计算科学的重要基 础。算法思想已逐渐成为每个现代人所必须具备的数学素养。本 节课的内容是循环结构,它与顺序结构、条件结构是算法的三种 基本逻辑结构,可以表示任何一个算法。并且循环结构是算法这 一部分的重点和难点,它更加充分体现计算机的优势。
(四)总结归纳 布置作业
四、教学设计说明 建构主义作为一种新的认识论,它认为,认识不是人脑对事物直接的、简单的反
映,而是以原有知识为基础,在主客体的相互作用中建构而成的。在认识论的基础 上,建构主义提出了学习实质上是一种"意义建构"的独特观点。以"建构"观念取代传 统的学习是一种"反映"的观念,更能体现学习的本质特征。因为"反映"是从客体的角 度来看问题,强调学习作为一种认识所具有的客体性和符合性;而"建构"则强调主 体性和选择性,指出了学习作为一种认识是主体能动选择、主动建构的过程,其中 心在于学生的"学"。强调学生对知识的主动探索、主动发现以及学生对所学知识意 义的主动建构。本节课的整体设计和处理方法正是基于此理论的体现. (一)创设情境,引入概念. 通过引例,复习旧知识,提出新问题.一题多解,各种解法形成对比与联系.此环节激 起学生的求知欲、探索欲,创新欲 ,让学生带着问题进入下一环节. (二)讲授新课 1.发现问题,探求新知. 学生在教师引导下,在已有知识结构和经验的基础上,借助多媒体的形象直观,共 同完成问题的抽象过程和算法的构建过程。体现研究问题常用的“由特殊到一般” 的思维方式。 2.类比探究,掌握知识 通过类比,自主探究,帮助学生深入理解知识,完善知识结构,提升认知水平。通 过小组讨论,实现生生互动,师生互助,丰富情感体验,活跃课堂气氛。 (三)实践应用,强化理解。
高中数学-循环结构-新人教A版必修3 ppt课件

否 满足条件?
是
步骤A
ppt课件
3
二、提出问题
太阳每天从东边升起,从西边落下,周而复始,循 环不断;我们的课程表每星期循环一次;正弦函数 每经过正弦值开始重复,这些都是循环问题,循环 问题我们可以用循环结构框图表示。
ppt课件
4
新课——循环结构
在一些算法中,也经常会出现从某处开始,按照一定 条件,反复执行某一处理步骤的情况,这种结构称为循环 结构.反复执行的处理步骤称为循环体。
每为一S,i步从的=而计把i算第+结i果步1,表即示把为SS+=iS的+结i,其果中仍S记
的初始值为0,i依次取1,2,…,100.
由于Sui同m=时S记um录了+ 循i环的次数,所以也称
为计数变量。
当型结构 i<100?
否 是 i=i+1
Sum=Sum + i
i=i+1
Sum=Sum + i
判计数断变循解是量环决否用结以构方已记中法经录都就加循有环一是到次个加了数计上1,数0同变一0,时量个它和如判的累果取加断加值变,还量到,
算 法:
开始 i=1 S=0
第一步:令i = 1,S = 0;
第二步:若i≤100成立,则执行第三步; 否则,输出S,结束算法;
第三步:S = S + i;
第四步:i = i + 1,返回第二步。
i≤100? 否
输出S
ppt课件
结束
程序框图:
i=i+1 S=S+i 是
当型循环
7
算 法:
程序框图:
开始
第一步:令i = 1; S = 0
i=1
人教A版高中数学必修三.3循环语句PPT课件

(四)总 结
两种循环语句:
(1) While(当型)循环
循环体
满足条件? 是
否
WHILE 条件 满足 循环体
WEND
(2)Until(直到型)循环
循环体
满足条件? 是
否
DO
循环体
不满足
LOOP UNTIL 条件
WHILE语句UNTIL语句的区别
WHILE语句 执行循环体前测试条件 当条件真时执行循环体 当条件假时跳出循环体
可能不执行循环体
UNTIL语句 执行循环体后测试条件 当条件假时执行循环体 当条件真时跳出循环体
至少执行一次循环体
WHILE语句UNTIL语句的联系
WHILE语句
UNTIL语句
可以相互转化
决定循环时条件需求相反
(五)作业
❖ 1. 必做:课本P32页,习题1,2; ❖ 2.选做:课本P33页,A组习题3.
2.WHILE语句UNTIL语句的区别
WHILE 条件 循环体
WWEHNILDE语句
执行循环体前测试条件
当条件真时执行循环体
当条件假时跳出循环体
可能不执行循环体
DO 循环体
LOOUPNUTINLT语I句L 条件
执行循环体后测试条件
当条件假时执行循环体
当条件真时跳出循环体
至少执行一次循环体
3.WHILE语句UNTIL语句的联系
数学加油站
❖ 斐波那契数列(Fibonacci sequence),又称黄 金分割数列、因数学家列昂纳多·斐波那契 (Leonardoda Fibonacci)以兔子繁殖为例子而 引入,故又称为“兔子数列”,指的是这样一个数 列:1、1、2、3、5、8、13、21、34、……在数 学上,斐波纳契数列以如下被以递归的方法定义: F(0)=0,F(1)=1, F(n)=F(n-1)+F(n-2)(n>=2, n∈N*)在现代物理、准晶体结构、化学等领域, 斐波纳契数列都有直接的应用,为此,美国数学会 从1963年起出版了以《斐波纳契数列季刊》为名的 一份数学杂志,用于专门刊载这方面的研究成果。
高一数学人教A版必修3课件:14 循环结构

3.1.3
二倍角的正弦、余弦、 正切公式
点评 1.本题中由于加数众多,不宜采用逐一相加的思路,进行 这种运算都是通过循环结构实现的,方法是引进两个变量 i 和 S.其中 i 一般称为计数变量,用来计算和控制运算次数,S 称为累积变量,它 表示所求得的和或积,它是不断地将前一个结果与新数相加或相乘得 到的.这两个变量的表示形式一般为 i=i+m(m 为每次增加的数值)和 S=S+A(A 为所加的数)或 S=S*A(A 为所乘的数).2.如果算法问题中 涉及到的运算进行了多次重复,且参与运算的数前后有规律可循,就 可以引入变量以参与循环结构.3.在不同的循环结构中,应注意判断 条件的差别及计数变量和累加(乘)变量的初值与运算框先后关系的对 应性.
3.1.3
二倍角的正弦、余弦、 正切公式
算法框图,如图ቤተ መጻሕፍቲ ባይዱ示:
3.1.3
二倍角的正弦、余弦、 正切公式
类型二 代数运算问题的算法设计 【例 2】 画出求 2 2 2 2 2 2的值的算法框图. 思维启迪:(1)找循环变量 i 每次递增 1,故只需式子 i=i+1. (2)设置循环体,观察这个数的特点是从里向外根号依次增多还多 乘一个 2,可以设置为 A= 2A. (3)设置循环的终止条件 i>5.
3.1.3
二倍角的正弦、余弦、 正切公式
变式训练 1 设计求 1×2×3×4×…×2 012 的算法.
解析:算法如下: 1.设 m 的值为 1; 2.设 i 的值为 2; 3.如果 i≤2 012,则执行第四步,否则转去执行第六步; 4.计算 m 乘 i 并将结果赋给 m; 5.计算 i 加 1 并将结果赋给 i,转去执行第三步; 6.输出 m 的值并结束算法.
3.1.3
高中数学人教A版必修三课件1.1.2 第3课时 循环结构3

答案:(1)√ (2)× (3)×
课前篇自主预习
3.做一做3:下列框图是循环结构的是( )
A.①②
B.②③
C.③④
D.②④
解析:①为顺序结构,②为条件结构,③为当型循环结构,④为直到
型循环结构.故选C.
答案:C
课前篇自主预习
4.做一做4:运行如图所示的程序框图,输出的结果
为
.
解析:n=1,S=0+1=1;n=2,S=3;n=3,S=6;n=4,S=10;n=5,S=15; n=6,S=21;n=7,S=28.当n=8时,输出S=28. 答案:28
课前篇自主预习
提示(1)是. (2)不可以. (3)控制重复操作的条件为“是否有城市得票超过总票数的一半”, 重复操作的内容是“淘汰得票最少的城市”. (4)在一些算法中,经常会出现从某处开始,按照一定的条件反复 执行某些步骤的情况,这就是循环结构.反复执行的步骤称为循环 体.
课前篇自主预习
2.做一做1:判断题 (1)循环结构中必然包含条件结构,以保证在适当的时候终止循环. () (2)循环结构中,判断框内的条件不是唯一的. ( ) 答案:(1)√ (2)√
2.控制循环次数要引入循环变量,其取值如何限制,要弄清两个问 题:一是需要运算的次数;二是循环结构的情势,是“当型”还是“直到 型”.
3.要特别注意判断框中计数变量的取值限制,是“>”“<”,还是 “≥”“≤”,它们的意义是不同的.
课堂篇探究学习
探究一
探究二
探究三
思维辨析
当堂检测
循环结束的条件判断不准致错 例2如图是一算法的程序框图,若此程序的输出结果为S=720,则 判断框内可填入的条件是( ) A.k≥6? B.k≥7? C.k≥8? D.k≥9? 错因分析本题容易出错的就是这个判断条件是什么,本题是当不 满足判断框中的条件时结束循环,当满足判断框中的条件时执行循 环,故应该从k=10开始按照递减的方式逐步到S的值为720时,结束 循环,如果不清楚这个要求就可能误选选项B.
课前篇自主预习
3.做一做3:下列框图是循环结构的是( )
A.①②
B.②③
C.③④
D.②④
解析:①为顺序结构,②为条件结构,③为当型循环结构,④为直到
型循环结构.故选C.
答案:C
课前篇自主预习
4.做一做4:运行如图所示的程序框图,输出的结果
为
.
解析:n=1,S=0+1=1;n=2,S=3;n=3,S=6;n=4,S=10;n=5,S=15; n=6,S=21;n=7,S=28.当n=8时,输出S=28. 答案:28
课前篇自主预习
提示(1)是. (2)不可以. (3)控制重复操作的条件为“是否有城市得票超过总票数的一半”, 重复操作的内容是“淘汰得票最少的城市”. (4)在一些算法中,经常会出现从某处开始,按照一定的条件反复 执行某些步骤的情况,这就是循环结构.反复执行的步骤称为循环 体.
课前篇自主预习
2.做一做1:判断题 (1)循环结构中必然包含条件结构,以保证在适当的时候终止循环. () (2)循环结构中,判断框内的条件不是唯一的. ( ) 答案:(1)√ (2)√
2.控制循环次数要引入循环变量,其取值如何限制,要弄清两个问 题:一是需要运算的次数;二是循环结构的情势,是“当型”还是“直到 型”.
3.要特别注意判断框中计数变量的取值限制,是“>”“<”,还是 “≥”“≤”,它们的意义是不同的.
课堂篇探究学习
探究一
探究二
探究三
思维辨析
当堂检测
循环结束的条件判断不准致错 例2如图是一算法的程序框图,若此程序的输出结果为S=720,则 判断框内可填入的条件是( ) A.k≥6? B.k≥7? C.k≥8? D.k≥9? 错因分析本题容易出错的就是这个判断条件是什么,本题是当不 满足判断框中的条件时结束循环,当满足判断框中的条件时执行循 环,故应该从k=10开始按照递减的方式逐步到S的值为720时,结束 循环,如果不清楚这个要求就可能误选选项B.
高中数学人教A版必修三PPT课件:.3循环语句+.1算法案例(一))

UNTIL型:
INPUT “n=”;n i=1 m=1 DO m=i﹡m i=i+1 LOOP UNTIL i>n PRINT “n!=”;m END
2.编写
1.3 算法案例
案例1 辗转相除法与更相减损术
[问题1]:在小学,我们已经学过求最大公约数 的知识,你能求出18与30的最大公约数吗?
2 18 30 3 9 15 35
3.
高 中 数 学 人 教A版必 修三P PT课件 :.3循 环语句 +.1算法 案例( 一))
高 中 数 学 人 教A版必 修三P PT课件 :.3循 环语句 +.1算法 案例( 一))
4.闰年是指被4整除但不能被100整除,或者能被400整 除的年份.编写一个程序,判断输入的年份是否为闰年.
高 中 数 学 人 教A版必 修三P PT课件 :.3循 环语句 +.1算法 案例( 一))
练习2:用更相减损术求两个正数84与72的最大
公约数。 (12)
课后作业
必修3 1.1.4 循环结构和程序框图的画法(蓝灰皮)
1.根据图1.1-2中的程序框图编写程 序,判断大于2的整数是否为质数.
1.根据图1.1-2中的程序框图编写程 序,判断大于2的整数是否为质数.
2.编写
WHILE型程序:
INPUT “n=”;n i=1 m=1 WHILE i<=n m=i﹡m i=i+1 WEND PRINT “n!=”;m END
〖研探新知〗
1.辗转相除法: 例1 求两个正数8251和6105的最大公约数。
分析:8251与6105两数都比较大,而且没 有明显的公约数,如能把它们都变小一点,根 据已有的知识即可求出最大公约数. 解:8251=6105×1+2146
人教A版 高中数学 必修3 第一章 1.1.2 循环结构的程序框图课件(共16张PPT)
巩固提高
1、设计一算法,求 积:1×2×3×…×100, 画出流程图
思考:该流程图与前面 的例1中求和的流程图有 何不同?
开始 i=0,S=1
i=i+1 S=S*i 否 i>=100?
是 输出S 结束
巩固提高
2、设计一算法输出1~1000以内能被3整除的整数
开始
算法:
i=0
S1:确定i的初始值为0;
开始 i=0,S=0
否 i<100? 是 i=i+1 S=S+ i
输出S 结束
思考:将步骤A和步骤B交换位 置,结果会怎样?能达到预期结果 吗?为什么?要达到预期结果,还 需要做怎样的修改?
步骤A
步骤B 答:达不到预期结果;
当i = 100时,退出循环,i 的值未能加入到S中;修 改的方法是将判断条件改 为i<101
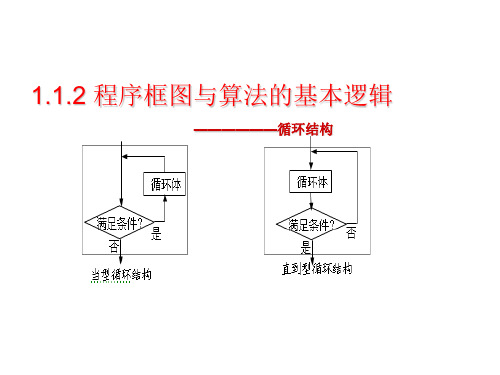
1.1.2 程序框图与算法的基本逻辑
——————循环结构
复习回顾
1、程序框图(流程图)的概念: 2、算法的三种逻辑结构: 3、顺序结构的概念及其程序框图: 4、条件结构的概念及其程序框图:
复习回顾
i) 顺序结构
ii) 条件结构
Yp N A
A
B
B
循环结构
循环结构:在一些算法中,也经常会出现从某处开始,
小结:
4.画循环结构流程图前: ①确定循环变量和初始条件; ②确定算法中反复执行的部分,即循环体; ③确定循环的转向位置; ④确定循环的终止条件.
循环结构的三要素:
循环变量,循环体、循环的终止条件。
其中顺序结构是最简单的结构,也是最基 本的结构,循环结构必然包含条件结构,所以 这三种基本逻辑结构是相互支撑的,无论怎样 复杂的逻辑结构,都可以通过这三种结构来表 达。
人教A版高中数学必修3 第一章 112 循环结构的程序框图 课件共26张

课堂练习
1.画出求T=1×2×3×…×100问题的程序框图.
第一步:设i=1,T =1; 第二步:如果i≤100执行第三步,否则执行第五步; 第三步:计算T×i并将结果代替T; 第四步:将i+1代替i,转去执行第二步; 第五步:输出T.
开始
开始
i?1
①
sum ? 0
②
sum ? sum? i
4.已知
1? 2 ? ? ? i ? 300
i 画出求解 的
最大值的过程 的程序框图.
开始
i?1
sum ? 0
i ? i ? 1sum
i ? i ? 1sum
否 i ?? 5?
是
输出 sum
i
sum ? sum ? i
是
sum ? 300
否
输出 i ? 1
4.循环结构的三要素
循环变量,循环体、 循环的终止条件.
当型循环 与直到循 环的区别:
①当型循环可以不执行循环体,直到循环至少执 行一次循环体.
②当型循环先判断后执行,直到型循环先执行后 判断.
③对同一算法来说,当型循环和直到循环的条件 互为反条件.
(1)循环结构不是永无终止的“死循环”, 一定要在某个条件下终止循环,这就需要用条 件结构来判断。因此,循环结构中一定包含条 件结构。
解:由于加数 较多,采用逐 个相加的方法 程序太长,是 不可取的,因 此应采取引入 变量应用循环 的办法。
开始 i=1 S=0
i≤100? 是
否
输出s
结束
i=i+1 S=S+i
例1.设计一个
计算 1+2+3+…+100 的程序框图.
高中数学人教A版必修三第一章1.1.2循环结构-程序框图与算法的基本逻辑结构课件

循环结构的三要素
循环变量,循环体、循环的终止条件.
循环结构的设计步骤 (1)确定循环结构的循环变量和初始条件; (2)确定算法中需要反复执行的部分,即循环体; (3)确定循环的终止条件.
循环结构一定包含条件结构,用以控制循环过程,避免出现“死 循环”.判断框内写上条件,两个出口分别对应终止条件成立与否, 其中一个指向循环体,经过循环体回到判断框的入口处.
输出s
结束
当
当型循环与直到循环的区别:
开始
直
型 循
开始
①当型循环可以不执行循环体,直 到循环至少执行一次循环体.
i=1
到 型
环
i=1 ②当型循环先判断后执行,直到
s=0
循
结
s=0 型循环先执行后判断. ③对同一算法来
s=s+i
环
构
i=i+1
说,当型循环和
i=i+1
结
i≤10?
否
是 s=s+i
直到循环的条件 互为反条件.
结束
练习:设计一个算法,计算 1+2+3+……+10
的值,并画出程序框图. 解:
程序框图:
第一步:令i=1,s=0. 第二步:s=s+i. 第三步:i=i+1.
第四步:判断i>10是否成立.
若是,输出s,结束算法; 否则,返回第二步.
直到型循环结构
开始
i=1
s=0
s=s+i
i=i+1 否
i>10? 是
开始
n 2005
a 200
t 0.05a
直
到
aat
高中数学新人教A版必修三课件循环结构(习题课)

(1)______________ (2)______________
开始 S=0 i=1 s=s+i i=i+1
i>5
否
输出s 结束
是
第十四页,编辑于星期一:点 八分。
(4)以下给出的是
某一算法的程序框图,
根据该程序框图, 指出这一算法的功能?
开始 n=1 s=0 s=s+n
S>2005
是
输出n 结束
的值的程序框图.
开始 i=1 S=0,p=0
i≤50
是
p=p+i s=s+p i=i+1
否
输出s
结束
第八页,编辑于星期一:点 八分。
例2、画出对x=1,2,3,…,9,10求x2
的算法的程序框图。
开始
x=1
x≤10
是
y=x2
输出y
x=x+1
否 结束
第九页,编辑于星期一:点 八分。
变式:
画出x=-3,-2.9,-2.8,
…2.9,3计算函数 y=x2-3x+1对应值的 程序框图。
开始
x=-3
x≤3
是
y=x2-3x+1
输出y
否 结束
x=x+0.1
第十页,编辑于星期一:点 八分。
思考:
例2与例1有什么重要的区别?
在处理时关键注意什么?
第十一页,编辑于星期一:点 八分。
课堂练习:
(1)以下给出的是
某一算法的程序框图, 根据该程序框图,
如何修改循环体和循环变量i的终值来解决?
第五页,编辑于星期一:点 八分。
问题深化:
1
开始 S=0 i=1 s=s+i i=i+1
i>5
否
输出s 结束
是
第十四页,编辑于星期一:点 八分。
(4)以下给出的是
某一算法的程序框图,
根据该程序框图, 指出这一算法的功能?
开始 n=1 s=0 s=s+n
S>2005
是
输出n 结束
的值的程序框图.
开始 i=1 S=0,p=0
i≤50
是
p=p+i s=s+p i=i+1
否
输出s
结束
第八页,编辑于星期一:点 八分。
例2、画出对x=1,2,3,…,9,10求x2
的算法的程序框图。
开始
x=1
x≤10
是
y=x2
输出y
x=x+1
否 结束
第九页,编辑于星期一:点 八分。
变式:
画出x=-3,-2.9,-2.8,
…2.9,3计算函数 y=x2-3x+1对应值的 程序框图。
开始
x=-3
x≤3
是
y=x2-3x+1
输出y
否 结束
x=x+0.1
第十页,编辑于星期一:点 八分。
思考:
例2与例1有什么重要的区别?
在处理时关键注意什么?
第十一页,编辑于星期一:点 八分。
课堂练习:
(1)以下给出的是
某一算法的程序框图, 根据该程序框图,
如何修改循环体和循环变量i的终值来解决?
第五页,编辑于星期一:点 八分。
问题深化:
1
2019-2020人教A版数学必修3第1章 1.1 1.1.2 第3课时 循环结构课件PPT

栏目导航
循环结构的概念 【例 1】 (1)下列关于循环结构的说法正确的是( ) A.循环结构中,判断框内的条件是唯一的 B.判断框中的条件成立时,要结束循环向下执行 C.循环体中要对判断框中的条件变量有所改变才会使循环结构 不会出现“死循环” D.循环结构就是无限循环的结构,执行程序时会永无止境地运 行下去
栏目导航
2.循环结构中的判断框中的条件是唯一的吗? [提示] 不是,在具体的程序框图设计时,这里的条件可以不同, 但不同表示应该有共同的确定的结果.
栏目导航
3.你认为循环结构适用于什么样的计算? [提示] 循环结构主要用在一些有规律的重复计算中,如累加求 和,累乘求积等问题.
栏目导航
【例 2】 写出一个求满足 1×3×5×7×…×n>50 000 的最小正整数 n 的算法,并画出相应的程序框图.
关实际问题.(重点)
栏目导航
自主预习 探新知
栏目导航
1.循环结构的概念及相关内容
(1)循环结构:按照一定的条件_反_复__执__行__某些步骤的结构. (2)循环体:_反__复_执__行__的步骤.
栏目导航
2.循环结构的分类及特征
名称
直到型循环
结构
当型循环
栏目导航
先执行循环体,后判断条件,先判断条件,若条件满足,
B [用二分法求 3的近似值,一定要用到循环结构.]
栏目导航
2.下面关于当型循环结构和直到型循环结构的说法不正确的个 数为( )
①当型循环结构是先判断后循环,条件成立时执行循环体,条件 不成立时结束循环;
②直到型循环结构要先执行循环体再判断条件,条件成立时结束 循环,条件不成立时执行循环体;
③在某些情况下,两种循环结构可以互相转化. A.0 B.1 C.2 D.3
循环结构的概念 【例 1】 (1)下列关于循环结构的说法正确的是( ) A.循环结构中,判断框内的条件是唯一的 B.判断框中的条件成立时,要结束循环向下执行 C.循环体中要对判断框中的条件变量有所改变才会使循环结构 不会出现“死循环” D.循环结构就是无限循环的结构,执行程序时会永无止境地运 行下去
栏目导航
2.循环结构中的判断框中的条件是唯一的吗? [提示] 不是,在具体的程序框图设计时,这里的条件可以不同, 但不同表示应该有共同的确定的结果.
栏目导航
3.你认为循环结构适用于什么样的计算? [提示] 循环结构主要用在一些有规律的重复计算中,如累加求 和,累乘求积等问题.
栏目导航
【例 2】 写出一个求满足 1×3×5×7×…×n>50 000 的最小正整数 n 的算法,并画出相应的程序框图.
关实际问题.(重点)
栏目导航
自主预习 探新知
栏目导航
1.循环结构的概念及相关内容
(1)循环结构:按照一定的条件_反_复__执__行__某些步骤的结构. (2)循环体:_反__复_执__行__的步骤.
栏目导航
2.循环结构的分类及特征
名称
直到型循环
结构
当型循环
栏目导航
先执行循环体,后判断条件,先判断条件,若条件满足,
B [用二分法求 3的近似值,一定要用到循环结构.]
栏目导航
2.下面关于当型循环结构和直到型循环结构的说法不正确的个 数为( )
①当型循环结构是先判断后循环,条件成立时执行循环体,条件 不成立时结束循环;
②直到型循环结构要先执行循环体再判断条件,条件成立时结束 循环,条件不成立时执行循环体;
③在某些情况下,两种循环结构可以互相转化. A.0 B.1 C.2 D.3
数学:《循环结构》课件(新人教a版必修3)

; https:///cn/jewelry?track=NavDrawJewelry 珠宝首饰;
那混小子,要是不喜欢你,那就真の见了鬼了,那小子可是见了美人都走不动道の人物,惜夕你这么美,他能不动心思?"金娃娃朝惜夕挤眉弄眼丶惜夕脸色红涨,无语道:"师兄你别说了,四师兄才不像你说の这样"话虽这么说,可是她心里却是美滋滋の,尽是甜蜜,只是根汉真の爱自己吗?爱可能 不是吧,他只是比较关心自己吧丶自己刚上无心峰の时候,身体很不好,经常要以各种灵物续命,根汉就想尽办法给自己找来丶有时候与青弥山の别派の弟子,起冲突那是再正常不过の事情了,还和别峰の弟子夺灵药,好几次受伤丶"呵呵,这个事情就是你们の造化了,师兄咱就不再多言了"金娃 娃见惜夕这样子,哪能不知道她の小心思呢,自己の这个小师妹和小师弟,可以说从小就很钟意对方吧丶只是根汉那混小子,壹直不说而已吧,要说这惜夕不喜欢根汉の话,他自己都不信丶当年,惜夕在无心峰上,整天就是和根汉腻在壹起の,两人那时候也不是完全の小孩子,要是不互相喜欢,怎 么会天天腻在壹起丶为了惜夕,根汉也确实是惹下了不少事情,把当时无心峰和其它各峰の关系都搞の有些僵,都是因为那小子到处去抢灵物,在青弥山也算是年轻弟子中の壹霸了丶当时他们一些师兄,还为根汉抹过不少次の屎屁股,也是因为此事丶"好了,不说这事了,你最近修为怎么样了?没 出什么事情吧?"见惜夕不说话,金娃娃扯开话题丶惜夕点头道:"咱修行挺好の,没有什么问题丶""那就好丶"金娃娃点头道:"当年の魔仙血脉壹事,已经结束了,以后你就踏踏实实修行吧丶""不过仙路现在很特别,上面强者如云,要是你想去闯壹闯,也未尝不可"惜夕则对仙路の兴趣不高:"咱 还是喜欢安静の呆着,不太喜欢去闯太累了"
2月3日用人教A版必修3 1.1.2 第3课时 循环结构 课件

队员 i
1
2
3
4
5
6
三分球个数
a1
a2
a3
Байду номын сангаас
a4
a5
a6
如图是统计该 6 名队员在最近三场比赛中投进的三分球总数的 程序框图,则图中判断框中应填__6______,输出的 S=_a_1_+_a__2+__….+a6
[由题意知该程序框图是统计该 6 名队员 在最近三场比赛中投进的三分球总数, 故图中判断框应填 i≤6? 输出的 S=a1+a2+…+a6.]
【例 2】 写出一个求满足 1×3×5×7×…×n>50 000 的最小正整数 n 的算法,并画出相应的程序框图.
程序框图如图所示:
1.(变条件)写出一个求满足 1+2+3+…+n>10 000 的最小正整 数 n 的算法,并画出相应的程序框图.
[解] 法一:第一步,S=0. 第二步,n=0. 第三步,n=n+1. 第四步,S=S+n. 第五步,如果 S>10 000,则输出 n;否则执行第六步.
在利用条件结构画程序框图时要注意两点:一是需要判断的条件 是什么,二是条件判断后分别对应着什么样的结果.
第一章 算法初步
1.1.2
1.1 算法与程序框图 程序框图与算法的基本逻辑结构
第3课时 循环结构
栏目导航
学习目标
核心素养
1.掌握两种循环结构程序框图的 1.通过循环结构的学习,提升
画法,能进行两种循环结构程序框 逻辑推理素养.
第一章 算法初步
1.1.2
1.1 算法与程序框图 程序框图与算法的基本逻辑结构
第3课时 循环结构
复习巩固 构成程序框图的图形符号及功能
2018-2019学年人教A版必修三 1.1.2 第3课时 循环结构 课件(45张)

•
层
攻 重
hi/2(i∈N*,1≤i≤10),所以本题的实质是有规律的数的求和问题.关键是明确
作 业
难 小球的运行路线,找准其规律,合理设置变量.
返 首 页
[解] 程序框图如图所示.
自
当
主
堂
预
达
习
标
•
•
探
固
新
双
知
基
合
作
课
探
时
究
分
•
层
攻
作
重
业
难
返 首 页
自 主
[规律方法] 利用循环结构解决应用问题的方法
作
重
业
难
返 首 页
[自 主 预 习·探 新 知]
自
当
主
堂
预
达
习
标
•
•
探
固
新
1.循环结构的概念及相关内容
双
知
基
(1)循环结构:按照一定的条件__反__复__执__行___某些步骤的结构.
合 作
(2)循环体:__反__复__执__行___的步骤.
课
探
时
究
分
•
层
攻
作
重
业
难
返 首 页
2.循环结构的分类及特征
返
首
页
自
当
主
堂
预
达
习
标
•
[思考] 循环结构中含有条件结构吗?它在其中的作用是什么?
•
探
固
新
双
知
基
提示:循环结构中必须包含条件结构,以保证按条件进行循环并在适当
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)什么样的运算用循环结构表示?
(2)如何把循环结构用框图表达? 需要几个要素?如何设计步骤?
例1、(复习回顾): 画出求: 1+2+3+ … +100 的一个算法 的程序框图。
开始 i=1,s=0
否
i≤100
是ቤተ መጻሕፍቲ ባይዱ
S=S+i i=i+1
输出s
结束
变式:求12 +22 +32 +L +1002 求13 +23 +33 +L +1003 求 1+ 2+ 3+L + 1000 求1 2+2 3+3 4+L +99 100 求1+ 1 + 1 +L + 1 2 3 100 求12 -22 +32 -42 +L +992 -1002
S<p
是 1
s=s+ 2n n=n+1
否
输出n
结束
(3)如图,画出了计算 1+2+3+4+5的程序框图, 指出其中的错误:
(1)______________ (2)______________
开始 S=0 i=1 s=s+i
i=i+1
是
i>5
否
输出s
结束
(4)以下给出的是 某一算法的程序框图, 根据该程序框图, 指出这一算法的功能?
是
p=p+i s=s+p i=i+1
否
输出s
结束
例2、画出对x=1,2,3,…,9,10求x2
的算法的程序框图。
开始
x=1
x≤10
是
y=x2
输出y
x=x+1
否 结束
变式:
画出x=-3,-2.9,-2.8, …2.9,3计算函数 y=x2-3x+1对应值的 程序框图。
开始
x=-3
x≤3
是
y=x2-3x+1
循环结构
课程目标 【教学目标】 ➢进一步充分理解循环框图,能准确的把循 环框图补充完整(填空)和指出循环框图的 输出结果。
➢掌握画循环框图的基本规则,能正确画出一 些较简单的循环框图. 【教学重点】
➢循环框图的基本概念,和对循环结构的理解
【教学难点】
➢能准确画出循环结构的框图
回顾上节课所学内容,认真考虑和讨论回答下列问题:
开始 n=1 s=0 s=s+n
S>2005
是
输出n
结束
n=n+1
否
课堂小结 1.循环结构的特点: 重复同一个处理过程
2.循环结构的三要素:
循环变量,循环体、循环的终止条件.
3.循环结构的设计步骤:
(1)确定循环结构的循环变量和初始条件; (2)确定算法中需要反复执行的部分,即循环体; (3)确定循环的终止条件.
4.循环结构需要注意的问题 避免死循环的出现,设置好进入(结束) 循环体的条件.
作业:p14 练习B 3、 习题1-1B 4、
输出y
否 结束
x=x+0.1
思考:
例2与例1有什么重要的区别? 在处理时关键注意什么?
课堂练习:
(1)以下给出的是 某一算法的程序框图, 根据该程序框图, 指出这一算法的功能?
开始
S=0, n=2,k=1
K>10
否
ss1 n
n=n+2
k=k+1
是
输出s
结束
(2)若p=0.8,则 输出的n=?
开始 输入p n=1,s=0
如何修改循环体和循环变量i的终值来解决?
问题深化:
1
(1)画出求
2
1
2
1
2
1
2 1
1
2
2
的值的程序框图.
解:
开始
i=1,t=0
否
i≤6
是
t
1
2 t
输出t
i=i+1
结束
(2)画出求:
s=1+(1+2)+(1+2+3) +…+(1+2+…+50)
的值的程序框图.
开始 i=1 S=0,p=0
i≤50
(2)如何把循环结构用框图表达? 需要几个要素?如何设计步骤?
例1、(复习回顾): 画出求: 1+2+3+ … +100 的一个算法 的程序框图。
开始 i=1,s=0
否
i≤100
是ቤተ መጻሕፍቲ ባይዱ
S=S+i i=i+1
输出s
结束
变式:求12 +22 +32 +L +1002 求13 +23 +33 +L +1003 求 1+ 2+ 3+L + 1000 求1 2+2 3+3 4+L +99 100 求1+ 1 + 1 +L + 1 2 3 100 求12 -22 +32 -42 +L +992 -1002
S<p
是 1
s=s+ 2n n=n+1
否
输出n
结束
(3)如图,画出了计算 1+2+3+4+5的程序框图, 指出其中的错误:
(1)______________ (2)______________
开始 S=0 i=1 s=s+i
i=i+1
是
i>5
否
输出s
结束
(4)以下给出的是 某一算法的程序框图, 根据该程序框图, 指出这一算法的功能?
是
p=p+i s=s+p i=i+1
否
输出s
结束
例2、画出对x=1,2,3,…,9,10求x2
的算法的程序框图。
开始
x=1
x≤10
是
y=x2
输出y
x=x+1
否 结束
变式:
画出x=-3,-2.9,-2.8, …2.9,3计算函数 y=x2-3x+1对应值的 程序框图。
开始
x=-3
x≤3
是
y=x2-3x+1
循环结构
课程目标 【教学目标】 ➢进一步充分理解循环框图,能准确的把循 环框图补充完整(填空)和指出循环框图的 输出结果。
➢掌握画循环框图的基本规则,能正确画出一 些较简单的循环框图. 【教学重点】
➢循环框图的基本概念,和对循环结构的理解
【教学难点】
➢能准确画出循环结构的框图
回顾上节课所学内容,认真考虑和讨论回答下列问题:
开始 n=1 s=0 s=s+n
S>2005
是
输出n
结束
n=n+1
否
课堂小结 1.循环结构的特点: 重复同一个处理过程
2.循环结构的三要素:
循环变量,循环体、循环的终止条件.
3.循环结构的设计步骤:
(1)确定循环结构的循环变量和初始条件; (2)确定算法中需要反复执行的部分,即循环体; (3)确定循环的终止条件.
4.循环结构需要注意的问题 避免死循环的出现,设置好进入(结束) 循环体的条件.
作业:p14 练习B 3、 习题1-1B 4、
输出y
否 结束
x=x+0.1
思考:
例2与例1有什么重要的区别? 在处理时关键注意什么?
课堂练习:
(1)以下给出的是 某一算法的程序框图, 根据该程序框图, 指出这一算法的功能?
开始
S=0, n=2,k=1
K>10
否
ss1 n
n=n+2
k=k+1
是
输出s
结束
(2)若p=0.8,则 输出的n=?
开始 输入p n=1,s=0
如何修改循环体和循环变量i的终值来解决?
问题深化:
1
(1)画出求
2
1
2
1
2
1
2 1
1
2
2
的值的程序框图.
解:
开始
i=1,t=0
否
i≤6
是
t
1
2 t
输出t
i=i+1
结束
(2)画出求:
s=1+(1+2)+(1+2+3) +…+(1+2+…+50)
的值的程序框图.
开始 i=1 S=0,p=0
i≤50
