(完整)全等三角形的判定专题
全等三角形的判定专题

全等三角形的判定专题1.如图,点A,F,C,D在一条直线上,AB∥DE,AB=DE,AF=DC.求证:BC∥EF.2.如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.(1)求证:△ABC≌△DEF;(2)若∠A=55°,∠B=88°,求∠F的度数.3.已知:如图,点A,F,E,C在同一直线上,AB∥DC,AB=CD,∠B=∠D.(1)求证:△ABE≌△CDF;(2)若点E,G分别为线段FC,FD的中点,连接EG,且EG=5,求AB的长.4.如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:OB=OC.5.如图,已知∠1=∠2,∠B=∠D,求证:CB=CD.6.如图,已知AB=AD,AC=AE,∠BAE=∠DAC.求证:∠C=∠E.7.如图,已知CA=CD,∠1=∠2(1)请你添加一个条件使△ABC≌△DEC,你添加的条件是;(2)添加条件后请证明△ABC≌△DEC.8.如图,AB与CD相交于点E,AE=CE,DE=BE.求证:∠A=∠C.9.如图,四边形ABCD是正方形,M为BC上一点,连接AM,延长AD至点E,使得AE=AM,过点E 作EF⊥AM,垂足为F,求证:AB=EF.10.如图,在△ABC中,∠C=90°,点D是AB边上的一点,DM⊥AB,且DM=AC,过点M作ME ∥BC交AB于点E.求证:△ABC≌△MED.11.如图,∠ACB=90°,AC=BC,AD⊥CE于点D,BE⊥CE于点E.(1)求证:△ACD≌△CBE;(2)已知AD=4,DE=1,求EF的长.12.如图,点E、F分别是矩形ABCD的边AD、AB上一点,若AE=DC=2ED,且EF⊥EC.(1)求证:点F为AB的中点;(2)延长EF与CB的延长线相交于点H,连结AH,已知ED=2,求AH的值.13.如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.(1)求证:△ABE≌△ACF;(2)若∠BAE=30°,则∠ADC=°.14.如图,AB∥CD,E、F分别为AB、CD上的点,且EC∥BF,连接AD,分别与EC、BF相交于点G,H,若AB=CD,求证:AG=DH.15.已知:如图,点A 、D 、C 、B 在同一条直线上,AD =BC ,AE =BF ,CE =DF ,求证:AE ∥FB .16.如图,△ABC 中,D 是BC 边上一点,E 是AD 的中点,过点A 作BC 的平行线交BE 的延长线于F ,且AF =CD ,连接CF .(1)求证:△AEF ≌△DEB ;(2)若AB =AC ,试判断四边形ADCF 的形状,并证明你的结论.17.如图,点B 、F 、C 、E 在一条直线上,FB =CE ,AB ∥ED ,AC ∥FD ,AD 交BE 于O .求证:AD 与BE 互相平分.18.如图,在四边形ABCD 中,E 是AB 的中点,AD ∥EC ,∠AED =∠B . (1)求证:△AED ≌△EBC . (2)当AB =6时,求CD 的长.19.如图,正方形ABCD 中,E 是BC 上的一点,连接AE ,过B 点作BH ⊥AE ,垂足为点H ,延长BH 交CD 于点F ,连接AF .(1)求证:AE =BF .(2)若正方形边长是5,BE =2,求AF 的长.20.已知:在△ABC 中,AB =AC ,D 为AC 的中点,DE ⊥AB ,DF ⊥BC ,垂足分别为点E ,F ,且DE =DF .求证:△ABC 是等边三角形.21.如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.(1)求证:AF=DC;(2)若AC⊥AB,试判断四边形ADCF的形状,并证明你的结论.22.如图所示,在四边形ABCD中,AE⊥BD于点E,CF⊥BD于点F,AE=CF,BE=DF.求证:(1)△ABE≌△CDF;(2)四边形ABCD是平行四边形.23.如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.(1)求证:AC=CD;(2)若AC=AE,求∠DEC的度数.24.已知:如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,且CD =AB,点E是CD的中点,过点C作CF∥AB交AE的延长线于点F.(1)求证:△ADE≌△FCE;(2)若∠DCF=120°,DE=2,求BC的长.25.如图,△ABC、△CDE均为等边三角形,连接BD、AE交于点O,BC与AE交于点P.求证:∠AOB =60°.26.如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.(1)求证:DE=DF,DE⊥DF;(2)连接EF,若AC=10,求EF的长.27.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.(1)求证:△AEC≌△BED;(2)若∠1=42°,求∠BDE的度数.28.如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.(1)求证:△ABC≌△AED;(2)当∠B=140°时,求∠BAE的度数.29.如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知∠ABC=60°,EF⊥AB,垂足为F,连接DF.(1)求证:△ABC≌△EAF;(2)试判断四边形EFDA的形状,并证明你的结论.30.如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F分别在AC,BC上,求证:DE=DF.31.如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD.32.如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.(1)求证:AB=AC;(2)若AD=2,∠DAC=30°,求AC的长.33.四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E、F.(1)求证:△ADE≌△CBF;(2)若AC与BD相交于点O,求证:AO=CO.34.如图,在△ABC中,CD是AB边上的中线,F是CD的中点,过点C作AB的平行线交BF的延长线于点E,连接AE.(1)求证:EC=DA;(2)若AC⊥CB,试判断四边形AECD的形状,并证明你的结论.35.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E.AD⊥CE于点D.求证:△BEC≌△CDA.36.如图,在▱ABCD中,点E,F在AC上,且∠ABE=∠CDF,求证:BE=DF.37.如图,四边形ABCD、BEFG均为正方形,连接AG、CE.(1)求证:AG=CE;(2)求证:AG⊥CE.38.已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.(1)求证:△ABD≌△CAE;(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请证明你的结论.39.如图,⊙O的直径为AB,点C在⊙O上,点D,E分别在AB,AC的延长线上,DE⊥AE,垂足为E,∠A=∠CDE.(1)求证:CD是⊙O的切线;(2)若AB=4,BD=3,求CD的长.40.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,交AC于点E,AC的反向延长线交⊙O于点F.(1)求证:DE是⊙O的切线;(2)若DE+EA=8,⊙O的半径为10,求△OAF的面积.。
(完整版)全等三角形证明方法(最新整理)

全等三角形的证明方法一、三角形全等的判定:(1)三组对应边分别相等的两个三角形全等(SSS);(2)有两边及其夹角对应相等的两个三角形全等(SAS) ;(3)有两角及其夹边对应相等的两个三角形全等(ASA) ;(4)有两角及一角的对边对应相等的两个三角形全等(AAS) ;(5)直角三角形全等的判定:斜边及一直角边对应相等的两个直角三角形全等(HL).二、全等三角形的性质:(1)全等三角形的对应边相等;全等三角形的对应角相等;(2)全等三角形的周长相等、面积相等;(3)全等三角形的对应边上的高对应相等;(4)全等三角形的对应角的角平分线相等;(5)全等三角形的对应边上的中线相等;三、找全等三角形的方法:(1)可以从结论出发,看要证明相等的两条线段(或角)分别在哪两个可能全等的三角形中;(2)可以从已知条件出发,看已知条件可以确定哪两个三角形相等;(3)从条件和结论综合考虑,看它们能一同确定哪两个三角形全等;(4)若上述方法均不行,可考虑添加辅助线,构造全等三角形。
三角形全等的证明中包含两个要素:边和角。
①积极发现隐含条件:公共角对顶角公共边②观察发现等角等边:等边对等角同角的余角相等同角的补角相等等角对等边等角的余角相等等角的补角相等③推理发现等边等角:图1:平行转化图2 :等角转化图3:中点转化图4 :等量和转化图5:等量差转化图6:角平分线性质转化图7:三线合一转化图8:等积转化图9:中垂线转化图10:全等转化图11:等段转化四、构造辅助线的常用方法:1、关于角平分线的辅助线:当题目的条件中出现角平分线时,要想到根据角平分线的性质构造辅助线。
角平分线具有两条性质:①角平分线具有对称性;②角平分线上的点到角两边的距离相等。
关于角平分线常用的辅助线方法:(1)截取构造全等:如下左图所示,OC是∠AOB的角平分线,D为OC上一点,F为OB上一点,若在OA上取一点E,使得OE=OF,并连接DE,则有△OED≌△OFD,从而为我们证明线段、角相等创造了条件。
三角形全等的判定(含例题)

1.判定两个三角形全等的基本事实:边边边(SSS)(1)基本事实:三边分别相等的两个三角形全等,简写成“__________”或“SSS”.(2)这个基本事实告诉我们:当三角形的三边确定后,其形状、大小也随之确定.这也是三角形具有稳定性的原因.2.判定两个三角形全等的基本事实:边角边(SAS)(1)基本事实:两边和它们的夹角分别相等的两个三角形全等,简写成“边角边”或“__________”.(2)此方法包含“边”和“角”两种元素,必须是两边夹一角才行,而不是两边及一边对角分别相等,一定要注意元素的“对应”关系.【注意】(1)此方法是证明两个三角形全等最常用的方法之一,应用时,可以从图形上直接观察到三个对应元素必须符合“两边夹角”,即“SAS”,不要误认为有两边一角就能判定两个三角形全等.(2)在书写时也要按照“边→角→边”的顺序排列条件,必须牢记“边边角”不能作为判定两个三角形全等的条件.3.判定两个三角形全等的基本事实:角边角(ASA)(1)基本事实:两角和它们的夹边分别相等的两个三角形全等,简写成“角边角”或“__________”.(2)用“ASA”来判定两个三角形全等,一定要证明这两个三角形有两个角以及这两个角的夹边分别相等,证明时要加强对夹边的认识.4.判定两个三角形全等的基本事实:角角边(AAS)(1)基本事实:两角和其中一个角的对边分别相等的两个三角形全等,简写成“角角边”或“__________”.(2)这一结论很容易由“ASA”推得,将这一结论与“ASA”结合起来,即可得出:两个三角形如果具备两角和一条边对应相等,就可判定其全等.5.直角三角形全等的判定方法:斜边、直角边(HL)(1)基本事实:斜边和一条直角边分别相等的两个直角三角形全等,简写成“斜边、直角边”或“________”.(2)“HL ”定理是直角三角形所独有的,对于一般三角形不成立. 【归纳】判定两个三角形全等常用的思路方法如下: HL SAS SSS AAS SAS ASA AAS ASA AAS ⎧⎧⎪⎪⎨⎪⎪⎪⎩⎪⎪⎧⎪⎪⎪⎧⎪⎨⎨⎪⎨⎪⎪⎪⎪⎪⎩⎩⎪⎪⎧⎪⎨⎪⎩⎪⎩一直角边一斜边—已知两边找夹角—找另一边—边为角的对边—找任一角—找夹角的另一边—已知一边一角边为角的邻边找夹边的另一角—找边的对角—找夹边—已知两角找任一角的对边—K 知识参考答案:1.(1)边边边2.(1)SAS 3.(1)ASA4.(1)AAS5.(1)HLK —重点 三角形全等的判定K —难点 三角形全等的判定和性质的综合运用 K —易错三角形全等的判定一、用边边边(SSS )证明三角形全等明确要证明全等的两个三角形,在书写两个三角形全等时,“≌”左边三角形的三边与“≌”右边三角形的三边的前后顺序要保持一致.【例1】如图,ABC △中,AB AC =,EB EC =,则由“SSS ”可判定A .ABD △≌ACD △B .ABE △≌ACE △△D.以上答案都不对C.BDE△≌CDE【答案】B二、用边角边(SAS)证明三角形全等此方法包含“边”和“角”两种元素,必须是两边夹一角才行,而不是两边及一边对角分别相等,一定要注意元素的“对应”关系.【例2】如图,AB=AC,添加下列条件,能用SAS判断△ABE≌△ACD的是A.∠B=∠C B.∠AEB=∠ADC C.AE=AD D.BE=DC【答案】C【解析】∵AB=AC(已知),∠A=∠A(公共角),∴只需要AE=AD,∴△ABE≌△ACD,故选C.三、用角边角、角角边(ASA、AAS)证明三角形全等1.不能说“有两角和一边分别相等的两个三角形全等”,这是因为:假设这条边是两角的夹边,则根据角边角可知正确;假设一个三角形的一边是两角的夹边,而与另一个三角形相等的边是其中一等角的对边,则两个三角形不一定全等.2.有三个角对应相等的两个三角形不一定全等.【例3】如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长,就得出AB的长,判定△EDC≌△ABC的理由是A.SSS B.SASC.SAA D.ASA【答案】D【解析】∵BF⊥AB,DE⊥BD,∴∠ABC=∠BDE.又∵CD=BC,∠ACB=∠DCE,∴△EDC≌△ABC(ASA).故选D.【例4】如图,已知点B、C、F、E在同一直线上,∠A=∠D,BF=EC,AB∥DE,若∠1=80°,求∠BFD 的度数.四、用斜边、直角边(HL)证明直角三角形全等1.当证明两个直角三角形全等时,若不适合应用“HL”,也可考虑用“SAS”“ASA”或“AAS”来证明.2.在用一般方法证明时,因为两个直角三角形中已具备一对直角相等的条件,故只需找另外两个条件即可,在实际证明中可根据条件灵活选用不同的方法.【例5】如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌△Rt△DCF,则还需要添加一个条件是A.AE=DF B.∠A=∠D C.∠B=∠C D.AB=DC【答案】D五、全等三角形的判定和性质的综合寻找解决问题的思路方法可以从求证的结论出发,结合已知条件,逐步寻求解决问题所需要的条件.同时要注意对图形本身隐含条件的挖掘,如对顶角、公共角、公共边等.【例6】如图,AB与CD交于点O,OA=OC,OD=OB,∠A=50°,∠B=30°,则∠D的度数为A.50°B.30°C.80°D.100°【答案】B【解析】∵OA=OC,OD=OB,∠AOD=∠COB,∴△AOD≌△COB(SAS),∴∠D=∠B=30°.故选B.【例7】如图,已知∠CAB=∠DBA,∠CBD=∠DAC.求证:BC=AD.【解析】∵∠CAB=∠DBA,∠CBD=∠DAC,∴∠DAB=∠CBA.在△ADB与△BCA中,CAB DBA AB ABDAB CBA ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ADB≌△BCA(ASA),∴BC=AD.。
全等三角形判定-专题复习50题(含答案)

全等三角形判定一、选择题:1.如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是()A.SSS B.SAS C.AAS D.ASA2.方格纸中,每个小格顶点叫做一个格点,以格点连线为边的三角形叫做格点三角形.如图,在4×4的方格纸中,有两个格点三角形△ABC、△DEF,下列说法中成立的是()A.∠BCA=∠EDF B.∠BCA=∠EFDC.∠BAC=∠EFD D.这两个三角形中,没有相等的角3.如图所示,△ABD≌△CDB,下面四个结论中,不正确的是()A.△ABD和△C DB的面积相等B.△ABD和△CDB的周长相等C.∠A+∠ABD=∠C+∠CBD D.AD∥BC,且AD=BC4.下列判断中错误..的是()A.有两角和一边对应相等的两个三角形全等B.有两边和一角对应相等的两个三角形全等C.有两边和其中一边上的中线对应相等的两个三角形全等D.有一边对应相等的两个等边三角形全等5.使两个直角三角形全等的条件是()A.一个锐角对应相等B.两个锐角对应相等C.一条边对应相等 D.两条边对应相等6.如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则∠ACB等于()A.∠EDB B.∠BED C.∠AFB D.2∠ABF7.在△ABC和△A/B/C/中,已知∠A=∠A/,AB=A/B/,在下面判断中错误的是( )A.若添加条件AC=A/C/,则△ABC≌△△A/B/C/B.若添加条件BC=B/C/,则△ABC≌△△A/B/C/C.若添加条件∠B=∠B/,则△ABC≌△△A/B/C/D.若添加条件∠C=∠C/,则△ABC≌△△A/B/C/8.如图,△ABC和△DEF中,AB=DE、∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF()A.AC∥DF B.∠A=∠D C.AC=DF D.∠ACB=∠F9.如图,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是()A.4cm B.6cm C.8cm D.9cm10.在如图所示的5×5方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),则与△ABC有一条公共边且全等的所有格点三角形个数是()A.1 B.2 C.3 D.411.如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为()A. a2B. a2C. a2D. a212.在连接A地与B地的线段上有四个不同的点D、G、K、Q,下列四幅图中的实线分别表示某人从A 地到B地的不同行进路线(箭头表示行进的方向),则路程最长的行进路线图是()A.B.C.D.二、填空题:13.如图所示,有一块三角形的镜子,小明不小心弄破裂成1、2两块,现需配成同样大小的一块.为了方便起见,需带上块,其理由是.14.如图示,点B在AE上,∠CBE=∠DBE,要使ΔABC≌ΔABD, 还需添加一个条件是__________.(填上你认为适当的一个条件即可)15.如图,已知∠1=∠2,AC=AD,请增加一个条件,使△ABC≌△AED,你添加的条件是.16.如图,∠1=∠2,要使△ABD≌△ACD,需添加的一个条件是(只添一个条件即可).17.如图,在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角形对.18.如图,△ABD≌△BAC,若AD=BC,则∠BAD的对应角是.19.如图,已知AB⊥BD,垂足为B,ED⊥BD,垂足为D,AB=CD,BC=DE,则∠ACE= 度.20.如图,如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三边所对的角的关系是.三、解答题:21.如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A.B.试说明AD+AB=BE.22.如图,E、A.C三点共线,AB∥CD,∠B=∠E,,AC=CD。
全等三角形复习专题

全等三角形复习专题一、全等三角形基本概念与性质全等三角形是指能够完全重合的两个三角形,即形状相同和大小相等的三角形。
全等三角形的性质是全等三角形的边、角及其对应线段之间具有一些特殊的数量关系和位置关系。
如全等三角形的对应边相等,对应角相等,对应线段相等,以及全等三角形的中点连线等于其一边。
二、全等三角形的判定全等三角形的判定是全等三角形研究的核心内容,主要有以下五个判定方法:1、边角边定理(SAS):若两个三角形的两边及其夹角对应相等,则这两个三角形全等。
2、角边角定理(ASA):若两个三角形的两个角及其夹边对应相等,则这两个三角形全等。
3、边边边定理(SSS):若两个三角形的三边对应相等,则这两个三角形全等。
4、角角边定理(AAS):若两个三角形的两个角及其一边对应相等,则这两个三角形全等。
5、斜边直角边定理(HL):若两个直角三角形的斜边和一条直角边对应相等,则这两个直角三角形全等。
三、全等三角形的应用全等三角形在数学、几何、物理等领域中都有广泛的应用。
如证明线段相等、角相等、平行四边形、矩形、菱形、正方形等几何图形的性质和判定,以及解决一些实际问题等。
四、全等三角形的复习策略1、掌握全等三角形的基本概念和性质,理解判定方法的意义和适用范围。
2、熟练掌握全等三角形的判定方法,能够根据题目条件选择合适的判定方法解决问题。
3、熟悉全等三角形的应用,能够将全等三角形的知识应用到实际问题和数学问题中。
4、多做练习题,熟悉各种题型和解题方法,提高解题能力和思维水平。
5、注意对易错点和难点进行重点复习和强化训练,避免出现常见的错误和失误。
全等三角形动点专题在数学的世界里,全等三角形和动点问题是两个重要的概念。
全等三角形是指两个或两个以上的三角形,它们的边长和角度都相等,可以完全重合。
动点问题则涉及到在给定的图形或轨迹上移动的点,以及这些点的变化和规律。
将这两个概念结合起来,我们可以研究一类非常有趣的数学问题,即全等三角形动点专题。
三角形全等的判定专题训练50题

三角形全等的判定专题训练题1、如图(1):AD ⊥BC ,垂足为D ,BD=CD 。
求证:△ABD ≌△ACD 。
2、如图(2):AC ∥EF ,AC=EF ,AE=BD 。
求证:△ABC ≌△EDF 。
3、 如图(3):DF=CE ,AD=BC ,∠D=∠C 。
求证:△AED ≌△BFC 。
4、 如图(4):AB=AC ,AD=AE ,AB ⊥AC ,AD ⊥AE 。
求证:(1)∠B=∠C ,(2)BD=CE.(图1)D CBA F E (图2)DCB A F E (图3)DCB A E (图4)D C B A5、如图(5):AB ⊥BD ,ED ⊥BD ,AB=CD ,BC=DE 。
求证:AC ⊥CE 。
6、如图(6):CG=CF ,BC=DC ,AB=ED ,点A 、B 、C 、D 、E 在同一直线上。
求证:(1)AF=EG ,(2)BF ∥DG 。
7、如图(7):AC ⊥BC ,BM 平分∠ABC 且交AC 于点M ,N 是AB 的中点且BN=BC 。
求证:(1)MN 平分∠AMB ,(2)∠A=∠CBM 。
8、如图(8):A 、B 、C 、D 四点在同一直线上,AC=DB ,BE ∥CF ,AE ∥DF 。
求证:△ABE ≌△DCF 。
GF E(图6)D CBA N M(图7)CBA F E (图8)D CBA E (图5)DC B A9、如图(9)AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
10、如图(10)∠BAC=∠DAE ,∠ABD=∠ACE ,BD=CE 。
求证:AB=AC 。
11、如图(11)在△ABC 和△DBC 中,∠1=∠2,∠3=∠4,P 是BC 上任一点。
求证:PA=PD 。
12、如图(12)AB ∥CD ,OA=OD ,点F 、D 、O 、A 、E 在同一直线上,AE=DF 。
求证:EB ∥CF 。
专题12.2 三角形全等的判定(解析版)

专题12.2 三角形全等的判定全等三角形的判定定理(1)边边边(SSS):三边对应相等的两个三角形全等.(2)边角边(SAS):两边和它们的夹角对应相等的两个三角形全等.(3)角边角(ASA):两角和它们的夹边对应相等的两个三角形全等.(4)角角边(AAS):两角和其中一个角的对边对应相等的两个三角形全等.(5)斜边、直角边(HL):斜边和一条直角边对应相等的两个直角三角形全等. (只适用两个直角三角形)【例题1】如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD()A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD【答案】D.【解析】欲使△ABE≌△ACD,已知AB=AC,可根据全等三角形判定定理AAS、SAS、ASA添加条件,逐一证明即可.∵AB=AC,∠A为公共角,A.如添加∠B=∠C,利用ASA即可证明△ABE≌△ACD;B.如添AD=AE,利用SAS即可证明△ABE≌△ACD;C.如添BD=CE,等量关系可得AD=AE,利用SAS即可证明△ABE≌△ACD;D.如添BE=CD,因为SSA,不能证明△ABE≌△ACD,所以此选项不能作为添加的条件.【点拨】欲使△ABE≌△ACD,已知AB=AC,可根据全等三角形判定定理AAS、SAS、ASA添加条件,逐一证明即可.【例题2】如图,点E、F分别是矩形ABCD的边AB、CD上的一点,且DF=BE.求证:AF=CE.【答案】见解析。
【解析】证明:∵四边形ABCD是矩形,∴∠D=∠B=90°,AD=BC,在△ADF和△BCE中,,∴△ADF≌△BCE(SAS),∴AF=CE.【点拨】由SAS证明△ADF≌△BCE,即可得出AF=CE.【例题3】如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F.求证:BD=2CE.【答案】见解析。
(完整)全等三角形和角平分线专题讲解和练习题

C EODBA21C EDB A21OA全等三角形专题讲解专题一 全等三角形判别方法的应用专题概说:判定两个三角形全等的方法一般有以下4种: 1.三边对应相等的两个三角形全等(简写成“SSS ”)2.两边和它们的夹角对应相等的两个三角形全等(简写成“SAS") 3.两角和它们的夹边对应相等的两个三角形全等(简写成“ASA ”)4.两个角和其中一个角的对边对应相等的两个三角形全等(简写成“AAS")而在判别两个直角三角形全等时,除了可以应用以上4种判别方法外,还可以应用“斜边、直角边”,即斜边和一条直角边对应相等的两个直角三角形全等(简写成“HL ”).也就是说“斜边、直角边”是判别两个直角三角形全等的特有的方法,它仅适用于判别两个直角三角形全等.三角形全等是证明线段相等,角相等最基本、最常用的方法,这不仅因为全等三角形有很多重要的角相等、线段相等的特征,还在于全等三角形能把已知的线段相等、角相等与未知的结论联系起来.那么我们应该怎样应用三角形全等的判别方法呢?(1)条件充足时直接应用在证明与线段或角相等的有关问题时,常常需要先证明线段或角所在的两个三角形全等,而从近年的中考题来看,这类试题难度不大,证明两个三角形的条件比较充分.只要同学们认真观察图形,结合已知条件分析寻找两个三角形全等的条件即可证明两个三角形全等.例1 已知:如图1,CE ⊥AB 于点E ,BD ⊥AC 于点D ,BD 、CE 交于点O,且AO 平分∠BAC .那么图中全等的三角形有___对.图1(2)条件不足,会增加条件用判别方法此类问题实际是指条件开放题,即指题中没有确定的已知条件或已知条件不充分,需要补充使三角形全等的条件.解这类问题的基本思路是:执果索因,逆向思维,逐步分析,探索结论成立的条件,从而得出答案.例2 如图2,已知AB=AD ,∠1=∠2,要使△ABC ≌△ADE,还需添加的条件是(只需填一个)_____. 图2(3)条件比较隐蔽时,可通过添加辅助线用判别方法在证明两个三角形全等时,当边或角的关系不明显时,可通过添加辅助线作为桥梁,沟通边或角的关系,使条件由隐变显,从而顺利运用全等三角形的判别方法证明两个三角形全等.例3 已知:如图3,AB=AC,∠1=∠2. 求证:AO 平分∠BAC .分析:要证AO 平分∠BAC ,即证∠BAO=∠BCO,要证∠BAO=∠BCO,只需证∠BAO 和∠BCO 所在的两个三角形全等.而由已知条件知,只需再证明BO=CO 即可.图3GABF DEC ODA CBFCEDBA(4)条件中没有现成的全等三角形时,会通过构造全等三角形用判别方法有些几何问题中,往往不能直接证明一对三角形全等,一般需要作辅助线来构造全等三角形.例4 已知:如图4,在Rt △ABC 中,∠ACB=90º,AC=BC ,D 为BC 的中点,CE ⊥AD 于E ,交AB 于F ,连接DF .求证:∠ADC=∠BDF .说明:常见的构造三角形全等的方法有如下三种:①涉及三角形的中线问题时,常采用延长中线一倍的方法,构造出一对全等三角形;②涉及角平分线问题时,经过角平分线上一点向两边作垂线,可以得到一对全等三角形;③证明两条线段的和等于第三条线段时,用“截长补短”法可以构造一对全等三角形.(5)会在实际问题中用全等三角形的判别方法新课标强调了数学的应用价值,注意培养同学们应用数学的意识,形成解决简单实际问题的能力﹒在近年中考出现的与全等三角形有关的实际问题,体现了这一数学理念,应当引起同学们的重视.例5 要在湖的两岸A 、B 间建一座观赏桥,由于条件 限制,无法直接度量A ,B 两点间的距离﹒请你用学过的数 学知识按以下要求设计一测量方案﹒(1)画出测量图案﹒(2)写出测量步骤(测量数据用字母表示)﹒ 图5 (3)计算A 、B 的距离(写出求解或推理过程,结果用字母表示)﹒分析:可把此题转化为证两个三角形全等.第(1)题,测量图案如图5所示.第(2)题,测量步骤:先在陆地上找到一点O ,在AO 的延长线上取一点C ,并测得OC=OA ,在BO 的延长线上取一点D ,并测得OD=OB,这时测得CD 的长为a ,则AB 的长就是a .第(3)题易证△AOB ≌△COD ,所以AB=CD ,测得CD 的长即可得AB 的长.解:(1)如图6示.(2)在陆地上找到可以直接到达A 、B 的一点O,在AO 的延长线上取一点C ,并测得OC =OA ,在BO 的延长线上取一点D ,并测得OD =OB,这时测出CD 的长为a ,则AB 的长就是a .(3)理由:由测法可得OC=OA ,OD=OB . 又∠COD=∠AOB ,∴△COD ≌△AOB .∴CD=AB=a . 图6评注:本题的背景是学生熟悉的,提供了一个学生动手操作的机会,重点考查了学生的操作能力,培养了 学生用数学的意识﹒练习:1.已知:如图7,D 是△ABC 的边AB 上一点,AB ∥FC ,DF 交AC 于点E ,DE=FE . 求证:AE=CE .C ED B AAO Q M CPBN A D C PBHF EGAD CBADCFBEA2.如图8,在△ABC 中,点E 在BC 上,点D 在AE 上,已知∠ABD=∠ACD ,∠BDE=∠CDE .求证:BD=CD .3.用有刻度的直尺能平分任意角吗?下面是一种方法:如图9所示,先在∠AOB 的两边上取OP=OQ ,再取PM=QN,连接PN 、QM,得交点C ,则射线OC 平分∠AOB .你能说明道理吗?4.如图10,△ABC 中,AB=AC,过点A 作GE ∥BC ,角平分线BD 、CF 相交于点H ,它们的延长线分别交GE 于点E 、G .试在图10中找出3对全等三角形,并对其中一对全等三角形给出证明.5.已知:如图11,点C 、D 在线段AB 上,PC=PD .请你添加一个条件,使图中存在全等三角形,并给予证明.所添条件为__________,你得到的一对全等三角形是△_____≌△_____.6.如图12,∠1=∠2,BC=EF ,那么需要补充一个直接条件_____(写出一个即可),才能使△ABC ≌△DEF .7图13,在△ABD 和△ACD 中,AB=AC,∠B=∠C .求证:△ABD ≌△ACD .AODCBAFCGBEAF DCB EOED218.如图14,直线AD与BC相交于点O,且AC=BD,AD=BC.求证:CO=DO.9.已知△ABC,AB=AC,E、F分别为AB和AC延长线上的点,且BE=CF,EF交BC于G.求证:EG=GF.10.已知:如图16,AB=AE,BC=ED,点F是CD的中点,AF⊥CD.求证:∠B=∠E.11.如图17,某同学把一把三角形的玻璃打碎成了三块,现在要到玻璃店去配一块大小形状完全一样的玻璃,那么最省事的办法是()﹒(A)带①和②去 (B)带①去(C)带②去(D)带③去12.有一专用三角形模具,损坏后,只剩下如图18中的阴影部分,你对图中做哪些数据度量后,就可以重新制作一块与原模具完全一样的模具,并说明其中的道理.13.如图19,将两根钢条AA’、BB’的中点O连在一起,使AA’、BB’可以绕着点O自由转动,就做成了一个测量工件,则A' B'的长等于内槽宽AB,那么判定△OAB≌△OAB的理由是( )(A)边角边(B)角边角(C)边边边(D)角角边专题二角的平分线从一个角的顶点出发,把一个角分成相等的两个角的射线,叫做这个角的平分线.角的平分线有着重要的作用,它不仅把角分成相等的两部分,而且角的平分线上的点到角两边的距离相等,到一个角的两边距离相等的点在这个角的平分线上,再加上角的平分线所在的直线是角的对称轴.因此当题目中有角的平分线时,可根据角的平分线性质证明线段或角相等,或利用角的平分线构造全等三角形或等腰三角形来寻找解题思路.(1)利用角的平分线的性质证明线段或角相等F ED CB A 21A FH DCGBEADCBE AF DC BE C E D例6 如图20,∠1=∠2,AE ⊥OB 于E , BD ⊥OA 于D ,交点为C .求证:AC=BC .说明:本题若用全等方法证明点C 到OA 、OB 距离相等,浪费时间和笔墨,不如直接应用角平分线性质证明,原因在于同学们已经习惯了用全等的方法,不善于直接应用定理,仍去找全等三角形,结果相当于重新证明了一次定理,以后再学新定理,应用时要注意全等定势的干扰,注意采用简捷证法. 例7 已知:如图21,△ABC 中, BD=CD ,∠1=∠2.求证:AD 平分∠BAC .说明:遇到有关角平分线的问题时,可引角的两边的垂线,先证明三角形全等,然后根据全等三角形的性质得出垂线段相等,再利用角的平分线性质得出两角相等.(2)利用角的平分线构造全等三角形 ①过角平分线上一点作两边的垂线段例8 如图22,AB ∥CD ,E 为AD 上一点,且BE 、CE 分别平分∠ABC 、∠BCD . 求证:AE=ED .分析:由于角平分线上一点到角的两边的距离相等,而点E 是两条角平分线的交点,因此我们自然想到过点E 分别作AB 、BC 、CD 的垂线段.②以角的平分线为对称轴构造对称图形例9 如图23,在△ABC 中,AD 平分∠BAC,∠C=2∠B .求证:AB=AC+CD .分析:由于角平分线所在的直线是这个角的对称轴,因此在AB 上截取AE=AC,连接DE ,我们就能构造出一对全等三角形,从而将线段AB 分成AE 和BE 两段,只需证明BE=CD 就可以了.③延长角平分线的垂线段,使角平分线成为垂直平分线 例10 如图24,在△ABC 中,AD 平分∠BAC ,CE ⊥AD 于E . 求证:∠ACE=∠B+∠ECD .分析:注意到AD 平分∠BAC ,CE ⊥AD ,于是可延长CE 交AB 于点F,即可构造全等三角形..(3)利用角的平分线构造等腰三角形如图25,在△ABC 中,AD 平分∠BAC ,过点D 作DE ∥AB ,DE 交AC 于点E .易证△AED 是等腰三角形. 因此,我们可以过角平分线上一点作角的一边的平行线,构造等腰三角形.CF E BADQPCBACB AD EA例11 如图26,在△ABC 中,AB=AC,BD 平分∠ABC ,DE ⊥BD 于D ,交BC 于点E .求证:CD=21BE .分析:要证CD=21BE ,可将BE 分成两条线段,然后再证明CD 与这两条线段都相等.练习:1.如图27,在△ABC 中,∠B=90º,AD 为∠BAC 的平分线,DF ⊥AC 于F,DE=DC .求证:BE=CF .2.已知:如图28,AD 是△ABC 的中线,DE ⊥AB 于E ,DF ⊥AC 于F ,且BE=CF .求证:(1)AD 是∠BAC 的平分线;(2)AB=AC .3.在△ABC 中,∠BAC=60º,∠C=40º,AP 平分∠BAC 交BC 于P,BQ 平分∠ABC 交AC 于Q . 求证:AB+BP=BQ+AQ .4.如图30,在△ABC 中,AD 平分∠BAC ,AB=AC+CD . 求证:∠C=2∠B .5.如图31,E 为△ABC 的∠A 的平分线AD 上一点,AB >AC . 求证:AB —AC >EB-EC .CB AD 4321C E BADF CE BAD CEBADCBADACBD6.如图32,在四边形ABCD 中,BC >BA ,AD=CD ,BD 平分∠ABC . 求证:∠A+∠C=180º.7.如图33所示,已知AD ∥BC ,∠1=∠2,∠3=∠4,直线DC 过点E 作交AD 于点D ,交BC 于点C .求证:AD+BC=AB .8.已知,如图34,△ABC 中,∠ABC=90º,AB=BC,AE 是∠A 的平分线,CD ⊥AE 于D .求证:CD=21AE .9.△ABC 中,AB=AC,∠A=100º,BD 是∠B 的平分线.求证:AD+BD=BC .10.如图36,∠B 和∠C 的平分线相交于点F ,过点F 作DE ∥BC 交AB 于点D ,交AC 于点E ,若BD+CE=9,则线段DE 的长为( )A .9B .8C .7D .611.如图37,△ABC 中,AD 平分∠BAC ,AD 交BC 于点D ,且D 是BC 的中点.求证:AB=AC .A CF E B M D12.已知:如图38,△ABC 中,AD 是∠BAC 的平分线,E 是BC 的中点,EF ∥AD ,交AB 于M ,交CA 的延长线于F .求证:BM=CF .。
三角形全等的判定方法(5种)例题+练习(全面)

三角形全等的判定方法(5种)例题+练习(全面)本文讲述了全等三角形的判定方法,重点是边角边和角边角。
边角边指两边及其夹角分别相等的两个三角形全等,可以简写成“SAS”。
需要注意的是,必须是两边及其夹角,不能是两边和其中一边的对角。
例如,在图中的△ABC和△ABD中,虽然有一个角和两边相等,但是这两个三角形不全等。
但是在例1中,如果AC=AD,且∠CAB=∠DAB,则可以证明△ACB≌△ADB。
在例2中,如果AD∥BC,且∠ABC=∠DCB,AB=DC,AE=DF,则可以证明BF=CE。
角边角是指两角及其夹边分别相等的两个三角形全等,可以简写成“ASA”。
例如,在例2中,如果AD平分∠BAC,且∠ABD=∠ACD,则可以直接判定△ABD≌△ACD。
在例3中,如果在Rt△ABC中,BC=2cm,CD⊥AB,且EC=BC,EF=5cm,则可以求出AE的长度。
除了边角边和角边角外,还有三种判定全等三角形的条件。
在例5中,如果在△ABC和△DEF中,AB=DE,BC=EF,且有一个角相等,则可以证明△ABC≌△DEF。
在例6中,如果AB∥DE,AB=DE,BF=CE,则可以证明△ABC≌△DEF。
在例7和例8中,分别是通过角平分线和垂线的判定方法来证明两个三角形全等。
总之,掌握全等三角形的判定方法对于解决几何问题非常重要。
1.如图所示,在三角形ABC中,已知AB=DC,∠ABC=∠DCB。
根据角角边相等可知,∠ACB=∠DCB。
又因为AB=DC,所以BC=AC。
因此,根据SSS(边边边)相等可知,△ABC≌△DCB。
同时,∠ACB=∠DCB,AC=BC=DC。
2.如图所示,在三角形ABD和ABF中,已知AD=AE,∠1=∠2,BD=CE。
根据角角边相等可知,∠ABD=∠BCE。
又因为AD=CE,所以BD=BE。
因此,根据SAS(边角边)相等可知,△ABD≌△BCE。
同时,∠ABD=∠BCE,AD=CE=BE。
(完整版)全等三角形知识总结和经典例题

全等三角形复习[ 知识要点 ]一、全等三角形1.判定和性质一般三角形直角三角形边角边( SAS)、角边角( ASA)具备一般三角形的判定方法判定斜边和一条直角边对应相等( HL )角角边( AAS)、边边边( SSS)对应边相等,对应角相等性质对应中线相等,对应高相等,对应角平分线相等注:①判定两个三角形全等必须有一组边对应相等;② 全等三角形面积相等.2.证题的思路:找夹角( SAS)已知两边找直角( HL )找第三边( SSS)若边为角的对边,则找任意角( AAS)找已知角的另一边(SAS)已知一边一角边为角的邻边找已知边的对角(AAS)找夹已知边的另一角(ASA)找两角的夹边(ASA)已知两角找任意一边(AAS)性质1、全等三角形的对应角相等、对应边相等。
2、全等三角形的对应边上的高对应相等。
3、全等三角形的对应角平分线相等。
4、全等三角形的对应中线相等。
5、全等三角形面积相等。
6、全等三角形周长相等。
( 以上可以简称 : 全等三角形的对应元素相等)7、三边对应相等的两个三角形全等。
(SSS)8、两边和它们的夹角对应相等的两个三角形全等。
(SAS)9、两角和它们的夹边对应相等的两个三角形全等。
(ASA)10、两个角和其中一个角的对边对应相等的两个三角形全等。
(AAS)11、斜边和一条直角边对应相等的两个直角三角形全等。
(HL)运用1、性质中三角形全等是条件,结论是对应角、对应边相等。
而全等的判定却刚好相反。
2、利用性质和判定,学会准确地找出两个全等三角形中的对应边与对应角是关键。
在写两个三角形全等时,一定把对应的顶点,角、边的顺序写一致,为找对应边,角提供方便。
3,当图中出现两个以上等边三角形时,应首先考虑用 SAS找全等三角形。
4、用在实际中,一般我们用全等三角形测等距离。
以及等角,用于工业和军事。
有一定帮助。
5、角平分线的性质及判定性质:角平分线上的点到这个角的两边的距离相等判定:到一个角的两边距离相等的点在这个角平分线上做题技巧一般来说考试中线段和角相等需要证明全等。
(完整版)全等三角形的性质及判定

全等三角形第1节全等三角形的性质和判定【知识梳理】1、全等图形:能够完全重合的两个图形就是全等图形.2、全等三角形的概念与表示:能够完全重合的两个三角形叫作全等三角形.能够相互重合的顶点、边、角分别叫作对应顶点、对应边、对应角.全等符号为“≌”.3、全等三角形的性质:对应角相等,对应边相等,对应边上的中线相等,对应边上的高相等,对应角的角平分线相等,面积相等.4、全等三角形的判定方法:(1) 边角边定理(SAS):两边和它们的夹角对应相等的两个三角形全等.(2) 角边角定理(ASA):两角和它们的夹边对应相等的两个三角形全等.(3) 边边边定理(SSS):三边对应相等的两个三角形全等.(4) 角角边定理(AAS):两个角和其中一个角的对边对应相等的两个三角形全等.(5) 斜边、直角边定理(HL):斜边和一条直角边对应相等的两个直角三角形全等.【诊断自测】1、如果ΔABC≌ΔDBC,则AB的对应边是_____,AC的对应边是_____,∠DBC的对应角是_____,∠DCB的对应角是_____.2、如图,已知△ABE≌△DCE,AE=2 cm,BE=1.5 cm,∠A=25°,∠B=48°;那么DE=_____cm,EC=_____cm,∠C=_____°;∠D=_____°.3、如果△ABC和△DEF这两个三角形全等,点C和点E,点B和点D分别是对应点,则另一组对应点是,对应边是,对应角是,表示这两个三角形全等的式子是.【考点突破】类型一:全等形例1、由同一张底片冲洗出来的两张五寸照片的图案_____全等图案,而由同一张底片冲洗出来的五寸照片和七寸照片____全等图形。
(填“是”或者“不是”)类型二:全三角形的定义和性质例2、如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=()A.∠B B.∠A C.∠EMF D.∠AFB例3、如图,△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的,若∠BAC:∠ABC:∠BCA=28:5:3,则∠α的度数为()A.90°B.85°C.80°D.75°类型三:全等三角形的判定(SSS)例4、用直尺和圆规作一个角等于己知角的作图痕迹如图所示,则作图的依据是()A.SSS B.SAS C.ASA D.AAS例5、已知:如图2-1,△RPQ中,RP=RQ,M为PQ的中点.求证:RM平分∠PRQ.分析:要证RM平分∠PRQ,即∠PRM=______,只要证______≌______证明:∵ M 为PQ 的中点(已知),∴______=______在△______和△______中,⎪⎩⎪⎨⎧===),______(____________,),(PM RQ RP 已知 ∴______≌______( ).∴ ∠PRM =______(______).即RM .例6.已知:如图,AD =BC .AC =BD .试证明:∠CAD =∠DBC .类型四:全等三角形的判定(SAS )例7. 已知:如图3-1,AB 、CD 相交于O 点,AO =CO ,OD =OB .求证:∠D =∠B .分析:要证∠D =∠B ,只要证______≌______证明:在△AOD 与△COB 中,⎪⎩⎪⎨⎧=∠=∠=),______(),______(______),(OD CO AO∴ △AOD ≌△______ ( ).∴ ∠D =∠B (______).例8、小红家有一个小口瓶(如图所示),她很想知道它的内径是多少?但是尺子不能伸在里边直接测,于是她想了想,唉!有办法了.她拿来了两根长度相同的细木条,并且把两根长木条的中点固定在一起,木条可以绕中点转动,这样只要量出AB的长,就可以知道玻璃瓶的内径是多少,你知道这是为什么吗?请说明理由.(木条的厚度不计)例9、如图,将两个一大、一小的等腰直角三角尺拼接(A、B、D三点共线,AB=CB,EB=DB,∠ABC=∠EBD=90°),连接AE、CD,试确定AE与CD的位置与数量关系,并证明你的结论.类型五:全等三角形的判定(AAS和ASA)例10、某同学把一块三角形的玻璃打碎成了3块,现要到玻璃店去配一块完全一样的玻璃,同学小明知道只要带③去就行了,你知道其中的道理是()A.SAS B.SSA C.ASA D.HL例11. 如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中和△ABC 全等的图形是例12、已知:如图,PM=PN,∠M=∠N.求证:AM=BN.分析:∵PM =PN ,∴ 要证AM =BN ,只要证PA =______,只要证______≌______.证明:在△______与△______中,⎪⎩⎪⎨⎧∠=∠=∠=∠),______(______),______(______),______(______ ∴ △______≌△______ ( ).∴PA =______ ( ).∵PM =PN ( ),∴PM -______=PN -______,即AM =______.例13、已知:AB ⊥AE ,AD ⊥AC ,∠E=∠B ,DE=CB .求证:AD=AC ..例14、如图,在△ABC 中,∠ACB =90°,AC =BC ,BE ⊥CE 于点E .AD ⊥CE 于点D .求证:△DEC ≌△CDA .类型六:全等三角形的判定(HL ) 例15.已知在△ABC 和△DEF 中,∠A=∠D=90°,则下列条件中不能判定△ABC 和△DEF 全等的是( )A.AB=D E,AC=DFB.AC=EF,BC=DFC.AB=DE,BC=EFD.∠C=∠F,BC=EF例16、如图所示,在△ABC中,∠C=90°,DE⊥AB于点D,BD=BC,若AC=6,则AE+DE=_____【易错精选】1、如图所示,△ABC≌△DEC,则不能得到的结论是()A.AB=DE B.∠A=∠D C.BC=CD D.∠ACD=∠BCE2、如图,梯形ABCD中,AD∥BC,点M是AD的中点,且MB=MC,若AD=4,AB=6,BC=8,则梯形ABCD的周长为()A.22 B.24 C.26 D.283、如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=__________度A CBED【精华提炼】判定三角形全等的基本思路:SAS SS HLSSS →⎧⎪→⎨⎪→⎩找夹角已知两边 找直角 找另一边 AAS ASA SA AASSAS ⎧⎪⎧⎪⎨⎪⎨⎪⎪⎪⎩⎩边为角的对边→找任意一角→ 找这条边上的另一角→已知一边一角 边就是角的一条边 找这条边上的对角→ 找该角的另一边→ ASA AA AAS →⎧⎨→⎩找两角的夹边已知两角 找任意一边 备注:寻找对应边和对应角,常用到以下方法:(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边.(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角.(3)有公共边的,公共边常是对应边.(4)有公共角的,公共角常是对应角.(5)有对顶角的,对顶角常是对应角.(6)两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角),一对最短边(或最小角)是对应边(或对应角).要想正确地表示两个三角形全等,找出对应的元素是关键. 全等三角形的图形归纳起来有以下几种典型形式:⑴ 平移全等型⑵ 对称全等型⑶ 旋转全等型【本节训练】训练【1】如图,E为线段BC上一点,AB⊥BC,△ABE≌△ECD,判断AE与DE的关系,并证明你的结论.训练【2】如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:BC∥EF.训练【3】已知图中的两个三角形全等,则∠1等于度.【训练4】.如图,∠BAC=∠DAE,∠ABD=∠ACE,AB=AC.求证:BD=CE.基础巩固一、选择题1、下列说法:①有两条直角边对应相等的两个直角三角形全等;②有斜边对应相等的两个等腰直角三角形全等;③有一条直角边和斜边上的高对应相等的两个直角三角形全等;④有一条边相等的两个等腰直角三角形全等.其中正确的有().A、1个B、2个C、3个D、4个2、如图,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画出 [ ].A.2个 B.4个 C.6个 D.8个3、下列说法正确的是()A、全等三角形是指周长和面积都一样的三角形;B、全等三角形的周长和面积都一样 ;C、全等三角形是指形状相同的两个三角形;D、全等三角形的边都相等4、下列两个三角形中,一定全等的是()A. 两个等边三角形B. 有一个角是40°,腰相等的两个等腰三角形C. 有一条边相等,有一个内角相等的两个等腰三角形D. 有一个角是100°,底相等的两个等腰三角形5、如图,△ABC与△BDE都是等边三角形,AB<BD,若△ABC不动,将△BDE绕点B旋转,则在旋转过程中,AE与CD的大小关系为 ( )A.AE=CD B.AE>CD C.AE<CD D.无法确定6、如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是()A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°二、填空题6、如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与B E相交于点F,若BF=AC,则∠ABC=_______7、如图,等腰直角三角形ABC的直角顶点B在直线PQ上,AD⊥PQ于D,CE⊥PQ 于E,且AD=2cm,DB=4cm,则梯形ADEC的面积是 _____.A8、(动手操作实验题)如图所示是小明自制对顶角的“小仪器”示意图:(1)将直角三角板ABC的AC边延长且使AC固定;(2)另一个三角板CDE•的直角顶点与前一个三角板直角顶点重合;(3)延长DC,∠PCD与∠ACF就是一组对顶角,已知∠1=30°,∠ACF为多少?三、简答题9、如图,已知AB=AC,∠1=∠2,AD=AE,求证:∠C=∠B.10、如图,在△ABC中,AD是∠BAC的平分线,DE、DF分别是△ABD和△ACD的高线,求证:AD⊥EF。
全等三角形的判定精选练习题(分专题)
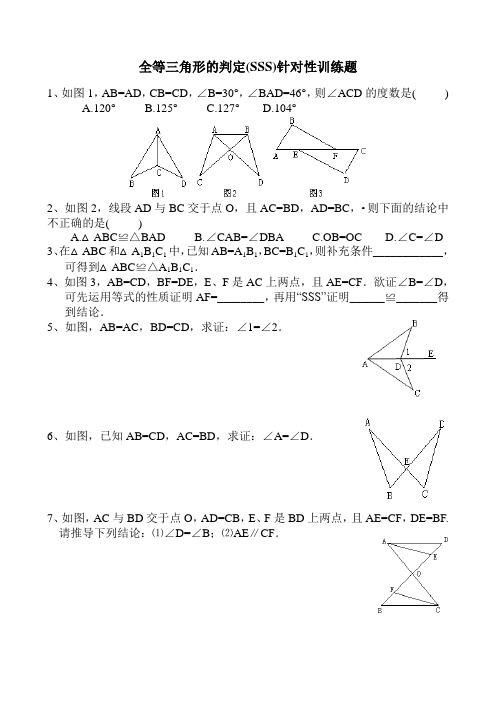
全等三角形的判定(SSS)针对性训练题1、如图1,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )A.120°B.125°C.127°D.104°2、如图2,线段AD与BC交于点O,且AC=BD,AD=BC,•则下面的结论中不正确的是( )A.△ABC≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D3、在△ABC和△A1B1C1中,已知AB=A1B1,BC=B1C1,则补充条件____________,可得到△ABC≌△A1B1C1.4、如图3,AB=CD,BF=DE,E、F是AC上两点,且AE=CF.欲证∠B=∠D,可先运用等式的性质证明AF=________,再用“SSS”证明______≌_______得到结论.5、如图,AB=AC,BD=CD,求证:∠1=∠2.6、如图,已知AB=CD,AC=BD,求证:∠A=∠D.7、如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导下列结论:⑴∠D=∠B;⑵AE∥CF.8、已知如图,A、E、F、C四点共线,BF=DE,AB=CD.⑴请你添加一个条件,使△DEC≌△BFA;⑵在⑴的基础上,求证:DE∥BF.全等三角形的判定(SAS)针对性训练题1、如图1,AB∥CD,AB=CD,BE=DF,则图中有多少对全等三角形( )A.3B.4C.5D.62、如图2,AB=AC,AD=AE,欲证△ABD≌△ACE,可补充条件( )A.∠1=∠2B.∠B=∠CC.∠D=∠ED.∠BAE=∠CAD3、如图3,AD=BC,要得到△ABD和△CDB全等,可以添加的条件是( )A.AB∥CDB.AD∥BCC.∠A=∠CD.∠ABC=∠CDA4、如图4,AB与CD交于点O,OA=OC,OD=OB,∠AOD=________,•根据_________可得到△AOD≌△COB,从而可以得到AD=_________.5、如图5,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程说明△ABD≌△ACD的理由.∵AD平分∠BAC,∴∠________=∠_________(角平分线的定义).在△ABD和△ACD中,∵____________________________,∴△ABD≌△ACD()DC BA 6、如图6,已知AB=AD ,AC=AE ,∠1=∠2,求证∠ADE=∠B.7、如图,已知AB=AD ,若AC 平分∠BAD ,问AC 是否平分∠BCD ?为什么?8、如图,在△ABC 和△DEF 中,B 、E 、F 、C ,在同一直线上,下面有4个条件,请你在其中选3个作为题设,余下的一个作为结论,写一个真命题,并加以证明.①AB=DE ; ②AC=DF ; ③∠ABC=∠DEF ; ④BE=CF.9、如图⑴,AB ⊥BD ,DE ⊥BD ,点C 是BD 上一点,且BC=DE ,CD=AB .⑴试判断AC 与CE 的位置关系,并说明理由. ⑵如图⑵,若把△CDE 沿直线BD 向左平移,使△CDE 的顶点C 与B 重合,此时第⑴问中AC 与BE 的位置关系还成立吗?(注意字母的变化)全等三角形的判定(AAS)和(ASA)针对性训练题 【典型例题】例1.如图,AB ∥CD ,AE=CF ,求证:AB=CD例2.如图,已知:AD=AE ,ABE ACD ∠=∠,求证:BD=CE.例3.如图,已知:ABD BAC D C ∠=∠∠=∠.,求证:OC=OD.例4.如图已知:AB=CD ,AD=BC ,O 是BD 中点,过O 点的直线分别交DA和BC 的延长线于E ,F.求证:AE=CF. 例5.如图,已知321∠=∠=∠,AB=AD.求证:BC=DE.例6.如图,已知四边形ABCD 中,AB=DC ,AD=BC ,点F 在AD 上,点E 在BC 上,AF=CE ,EF 的对角线BD 交于O ,请问O 点有何特征?AEABDC EO12 3 AFDOBECABCDO【经典练习】1.△ABC 和△C B A '''中,C B C B A A ''='∠=∠,',C C '∠=∠则△ABC 与△C B A ''' .2.如图,点C ,F 在BE 上,,,21EF BC =∠=∠请补充一个条件,使△ABC ≌DFE,补充的条件是 .3.在△ABC 和△C B A '''中,下列条件能判断△ABC 和△C B A '''全等的个数有( ) ①A A '∠=∠ B B '∠=∠,C B BC ''= ②A A '∠=∠,B B '∠=∠,C A C A ''=' ③A A '∠=∠ B B '∠=∠,C B AC ''= ④A A '∠=∠,B B '∠=∠,C A B A ''='A . 1个B. 2个C. 3个D. 4个4.如图,已知MB=ND ,NDC MBA ∠=∠,下列条件不能判定是△ABM ≌△CDN 的是( )A .N M ∠=∠ B. AB=CDC . AM=CND. AM ∥CN5.如图所示, ∠E =∠F =90°,∠B =∠C ,AE =AF , 给出下列结论①∠1=∠2 ②BE=CF ③△ACN ≌△ABM④CD=DN ,其中正确的结论是_________。
(完整版)全等三角形题型总结

全等三角形的判定题型类型一、全等三角形的判定1——“边边边”例题、已知:如图,AD =BC ,AC =BD.试证明:∠CAD =∠DBC.(答案)证明:连接DC , 在△ACD 与△BDC 中()AD BC AC BDCD DC ⎧=⎪=⎨⎪=⎩公共边∴△ACD ≌△BDC (SSS )∴∠CAD =∠DBC (全等三角形对应角相等)类型二、全等三角形的判定2——“边角边”例题、已知,如图,在四边形ABCD 中,AC 平分∠BAD ,CE ⊥AB 于E ,并且AE =12(AB +AD ),求证:∠B +∠D =180°.(答案)证明:在线段AE 上,截取EF =EB ,连接FC ,∵CE ⊥AB ,∴∠CEB =∠CEF =90°在△CBE 和△CFE 中,CEB CEF EC =EC EB EF =⎧⎪∠=∠⎨⎪⎩∴△CBE 和△CFE (SAS )∴∠B =∠CFE ∵AE =12(AB +AD ),∴2AE = AB +AD ∴AD =2AE -AB ∵AE =AF +EF ,∴AD =2(AF +EF )-AB =2AF +2EF -AB =AF +AF +EF +EB -AB =AF +AB -AB ,即AD =AF在△AFC 和△ADC 中(AF AD FAC DAC AC AC =⎧⎪∠=∠⎨⎪=⎩角平分线定义)∴△AFC ≌△ADC (SAS )∴∠AFC =∠D∵∠AFC +∠CFE =180°,∠B =∠CFE.∴∠AFC +∠B =180°,∠B +∠D =180°. 类型三、全等三角形的判定3——“角边角”例题、已知:如图,在△MPN 中,H 是高MQ 和NR 的交点,且MQ =NQ .求证:HN =PM.证明:∵MQ 和NR 是△MPN 的高, ∴∠MQN =∠MRN =90°, 又∵∠1+∠3=∠2+∠4=90°,∠3=∠4 ∴∠1=∠2在△MPQ 和△NHQ 中,12MQ NQ MQP NQH ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△MPQ ≌△NHQ (ASA ) ∴PM =HN类型四、全等三角形的判定4——“角角边”例题、已知Rt △ABC 中,AC =BC ,∠C =90°,D 为AB 边的中点,∠EDF =90°,∠EDF 绕D 点旋转,它的两边分别交AC 、CB 于E 、F .当∠EDF 绕D 点旋转到DE ⊥AC 于E 时(如图1),易证12DEF CEF ABC S S S +=△△△;当∠EDF 绕D 点旋转到DE 和AC 不垂直时,在图2情况下,上述结论是否成立?若成立,请给予证明;若不成立,请写出你的猜想,不需证明.解:图2成立; 证明图2:过点D 作DM AC DN BC ⊥⊥,则90DME DNF MDN ∠=∠=∠=°在△AMD 和△DNB 中,AMD=DNB=90A B AD BD ∠∠︒⎧⎪∠=∠⎨⎪=⎩∴△AMD ≌△DNB (AAS )∴DM =DN∵∠MDE +∠EDN =∠NDF +∠EDN =90°,∴∠ MDE =∠NDF在△DME 与△DNF 中,90EMD FDN DM DN MDE NDF ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩∴△DME ≌△DNF (ASA )∴DME DNF S S =△△∴DEF CEF DMCN DECF S =S =S S .+△△四边形四边形可知ABC DMCN 1S =S 2△四边形,∴12DEF CEF ABC S S S +=△△△类型五、直角三角形全等的判定——“HL ”下列说法中,正确的画“√”;错误的画“×”,并举出反例画出图形.(1)一条直角边和斜边上的高对应相等的两个直角三角形全等.( ) (2)有两边和其中一边上的高对应相等的两个三角形全等.( ) (3)有两边和第三边上的高对应相等的两个三角形全等.( )(答案)(1)√;(2)×;在△ABC 和△DBC 中,AB =DB ,AE 和DF 是其中一边上的高,AE =DF(3)×. 在△ABC 和△ABD 中,AB =AB ,AD =AC ,AH 为第三边上的高,如下图:1、已知:如图,DE ⊥AC ,BF ⊥AC ,AD =BC ,DE =BF.求证:AB ∥DC.(答案与解析)证明:∵DE ⊥AC ,BF ⊥AC ,∴在Rt △ADE 与Rt △CBF 中.AD BC DE BF ⎧⎨⎩=,=∴Rt △ADE ≌Rt △CBF (HL ) ∴AE =CF ,DE =BF∴AE +EF =CF +EF ,即AF =CE在Rt △CDE 与Rt △ABF 中,DE BFDEC BFA EC FA =⎧⎪∠=∠⎨⎪=⎩∴Rt △CDE ≌Rt △ABF (SAS )∴∠DCE =∠BAF ∴AB ∥DC. (点评)从已知条件只能先证出Rt △ADE ≌Rt △CBF ,从结论又需证Rt△CDE ≌Rt △ABF.我们可以从已知和结论向中间推进,证出题目.2、如图,△ABC 中,∠ACB =90°,AC =BC ,AE 是BC 边上的中线, 过C 作CF ⊥AE ,垂足为F ,过B 作BD ⊥BC 交CF 的延长线于D. (1)求证:AE =CD ;(2)若AC =12cm ,求BD 的长.(答案与解析)(1)证明:∵DB ⊥BC ,CF ⊥AE ,∴∠DCB +∠D =∠DCB +∠AEC =90°.∴∠D =∠AEC .又∵∠DBC =∠ECA =90°,且BC =CA ,∴△DBC ≌△ECA (AAS ).∴AE =CD . (2)解:由(1)得AE =CD ,AC =BC ,∴△CDB ≌△AEC (HL ) ∴BD =EC =12BC =12AC ,且AC =12. ∴BD =6cm .(点评)三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件三角形角平分线的性质三角形三条角平分线交于三角形内部一点,此点叫做三角形的内心且这一点到三角形三边的距离相等.三角形的一内角平分线和另外两顶点处的外角平分线交于一点.这点叫做三角形的旁心.三角形有三个旁心.所以到三角形三边所在直线距离相等的点共有4个.如图所示:△ABC 的内心为1P ,旁心为234,,P P P ,这四个点到△ABC 三边所在直线距离相等.角的平分线的性质及判定1、如图,AD 是∠BAC 的平分线,DE ⊥AB ,交AB 的延长线于点E ,DF ⊥AC 于点F ,且DB =DC.求证:BE =CF.(答案)证明:∵DE ⊥AE ,DF ⊥AC ,AD 是∠BAC 的平分线, ∴DE =DF ,∠BED =∠DFC =90°在Rt △BDE 与Rt △CDF 中,DB DCDE DF =⎧⎨=⎩,∴Rt △BDE ≌Rt △CDF (HL ) ∴BE =CF2、如图,AC=DB ,△PAC 与△PBD 的面积相等.求证:OP 平分∠AOB .(答案与解析)证明:作PM ⊥OA 于M ,PN ⊥OB 于N12PAC S AC PM =△∵,12PBD S BD PN =△,且PAC S =△PBD S △ ∴ 12AC PM 12BD PN =又∵AC =BD ∴PM =PN又∵PM⊥OA,PN⊥OB ∴OP平分∠AOB(点评)观察已知条件中提到的三角形△PAC与△PBD,显然与全等无关,而面积相等、底边相等,于是自然想到可得两三角形的高线相等,联系到角平分线判定定理可得.跟三角形的高结合的题目,有时候用面积会取得意想不到的效果.3、如图,DC∥AB,∠BAD和∠ADC的平分线相交于E,过E的直线分别交DC、AB于C、B两点. 求证:AD=AB+DC.(答案)证明:在线段AD上取AF=AB,连接EF,∵AE是∠BAD的角平分线,∴∠1=∠2,∵AF=AB AE=AE,∴△ABE≌△AFE,∴∠B=∠AFE由CD∥AB又可得∠C+∠B=180°,∴∠AFE+∠C=180°,又∵∠DFE+∠AFE=180°,∴∠C=∠DFE,∵DE是∠ADC的平分线,∴∠3=∠4,又∵DE=DE,∴△CDE≌△FDE,∴DF=DC,∵AD=DF+AF,∴AD=AB+DC.类型一、全等三角形的性质和判定如图,已知:AE⊥AB,AD⊥AC,AB=AC,∠B=∠C,求证:BD=CE.(答案)证明:∵AE⊥AB,AD⊥AC,∴∠EAB=∠DAC=90°∴∠EAB+∠DAE=∠DAC+∠DAE ,即∠DAB=∠EAC.在△DAB与△EAC中,DAB EACAB ACB C∠=∠⎧⎪=⎨⎪∠=∠⎩∴△DAB≌△EAC (SAS)∴BD=CE.类型二、巧引辅助线构造全等三角形(1).作公共边可构造全等三角形:1、在ΔABC中,AB=AC.求证:∠B=∠C(答案)证明:过点A作AD⊥BC在Rt△ABD与Rt△ACD中AB AC AD AD=⎧⎨=⎩∴Rt△ABD≌Rt△ACD(HL)∴∠B=∠C.(2).倍长中线法:1、已知:如图所示,CE、CB分别是△ABC与△ADC的中线,且∠ACB=∠ABC.求证:CD=2CE.(答案)证明:延长CE至F使EF=CE,连接BF.∵EC为中线,∴AE=BE.在△AEC与△BEF中,,,,AE BEAEC BEFCE EF=⎧⎪∠=∠⎨⎪=⎩∴△AEC≌△BEF(SAS).∴AC=BF,∠A=∠FBE.(全等三角形对应边、角相等)又∵∠ACB=∠ABC,∠DBC=∠ACB+∠A,∠FBC=∠ABC+∠A.∴AC=AB,∠DBC=∠FBC.∴AB=BF.又∵BC为△ADC的中线,∴AB=BD.即BF=BD.在△FCB与△DCB中,,,,BF BDFBC DBC BC BC=⎧⎪∠=∠⎨⎪=⎩∴△FCB≌△DCB(SAS).∴CF=CD.即CD=2CE.2、若三角形的两边长分别为5和7, 则第三边的中线长x的取值范围是( )A.1 <x<6B.5 <x<7C.2 <x<12D.无法确定(答案)A ;提示:倍长中线构造全等三角形,7-5<2x<7+5,所以选A选项.(3).作以角平分线为对称轴的翻折变换构造全等三角形:如图,AD 是ABC ∆的角平分线,H ,G 分别在AC ,AB 上,且HD =BD. (1)求证:∠B 与∠AHD 互补;(2)若∠B +2∠DGA =180°,请探究线段AG 与线段AH 、HD 之间满足的等量关系,并加以证明.(答案)证明:(1)在AB 上取一点M, 使得AM =AH, 连接DM.∵ ∠CAD =∠BAD, AD =AD, ∴ △AHD ≌△AMD. ∴ HD =MD, ∠AHD =∠AMD. ∵ HD =DB, ∴ DB = MD. ∴ ∠DMB =∠B.∵ ∠AMD +∠DMB =180︒,∴ ∠AHD +∠B =180︒. 即 ∠B 与∠AHD 互补. (2)由(1)∠AHD =∠AMD, HD =MD, ∠AHD +∠B =180︒.∵ ∠B +2∠DGA =180︒,∴ ∠AHD =2∠DGA. ∴ ∠AMD =2∠DGM.∵ ∠AMD =∠DGM +∠GDM. ∴ 2∠DGM =∠DGM +∠GDM. ∴ ∠DGM =∠GDM. ∴ MD =MG.∴ HD = MG.∵ AG = AM +MG, ∴ AG = AH +HD. (3).利用截长(或补短)法作构造全等三角形:1、如图,AD 是△ABC 的角平分线,AB >AC,求证:AB -AC >BD -DC (答案)证明:在AB 上截取AE =AC,连结DE∵AD 是△ABC 的角平分线,∴∠BAD =∠CAD在△AED 与△ACD 中⎪⎩⎪⎨⎧=∠=∠=AD AD CAD BAD ACAE∴△AED ≌△ADC (SAS )∴DE =DC 在△BED 中,BE >BD -DC即AB -AE >BD -DC ∴AB -AC >BD -DCM G HDCBAEDC BA2、如图所示,已知△ABC中AB>AC,AD是∠BAC的平分线,M是AD上任意一点,求证:MB-MC<AB-AC.(答案与解析)证明:∵AB>AC,则在AB上截取AE=AC,连接ME.在△MBE中,MB-ME<BE(三角形两边之差小于第三边).在△AMC和△AME中,()()()AC AECAM EAMAM AM=⎧⎪∠=∠⎨⎪=⎩所作,角平分线的定义,公共边,∴△AMC≌△AME(SAS).∴MC=ME(全等三角形的对应边相等).又∵BE=AB-AE,∴BE=AB-AC,∴MB-MC<AB-AC.(点评)因为AB>AC,所以可在AB上截取线段AE=AC,这时BE=AB-AC,如果连接EM,在△BME中,显然有MB-ME<BE.这表明只要证明ME=MC,则结论成立.充分利用角平分线的对称性,截长补短是关键.(4).在角的平分线上取一点向角的两边作垂线段.1、如图所示,已知E为正方形ABCD的边CD的中点,点F在BC上,且∠DAE=∠FAE.求证:AF=AD+CF.(答案与解析)证明:作ME⊥AF于M,连接EF.∵四边形ABCD为正方形,∴∠C=∠D=∠EMA=90°.又∵∠DAE=∠FAE,∴AE为∠FAD的平分线,∴ME=DE.在Rt△AME与Rt△ADE中,()()AE AEDE ME=⎧⎨=⎩公用边,已证,∴Rt△AME≌Rt△ADE(HL).∴AD=AM(全等三角形对应边相等).又∵E为CD中点,∴DE=EC.∴ME=EC.在Rt△EMF与Rt△ECF中,()(ME CEEF EF=⎧⎨=⎩已证,公用边),∴Rt△EMF≌Rt△ECF(HL).∴MF=FC(全等三角形对应边相等).由图可知:AF=AM+MF,∴AF=AD+FC(等量代换).(点评)与角平分线有关的辅助线:在角两边截取相等的线段,构造全等三角形;在角的平分线上取一点向角的两边作垂线段. 四边形ABCD为正方形,则∠D=90°.而∠DAE=∠FAE说明AE为∠FAD的平分线,按常规过角平分线上的点作出到角两边的距离,而E到AD的距离已有,只需作E到AF的距离EM即可,由角平分线性质可知ME=DE.AE=AE.Rt△AME与Rt△ADE全等有AD=AM.而题中要证AF=AD+CF.根据图知AF=AM+MF.故只需证MF=FC即可.从而把证AF=AD+CF转化为证两条线段相等的问题.2、如图所示,在△ABC中,AC=BC,∠ACB=90°,D是AC上一点,且AE垂直BD的延长线于E,12AE BD=,求证:BD是∠ABC的平分线.(答案与解析)证明:延长AE和BC,交于点F,∵AC⊥BC,BE⊥AE,∠ADE=∠BDC(对顶角相等),∴∠EAD+∠ADE=∠CBD+∠BDC.即∠EAD=∠CBD.在Rt△ACF和Rt△BCD中.所以Rt△ACF≌Rt△BCD(ASA).则AF=BD(全等三角形对应边相等).∵AE=BD,∴AE=AF,即AE=EF.在Rt△BEA和Rt△BEF中,则Rt△BEA≌Rt△BEF(SAS).所以∠ABE=∠FBE(全等三角形对应角相等),即BD是∠ABC的平分线.(点评)如果由题目已知无法直接得到三角形全等,不妨试着添加辅助线构造出三角形全等的条件,使问题得以解决.平时练习中多积累一些辅助线的添加方法.类型三、全等三角形动态型问题解决动态几何问题时要善于抓住以下几点:(1)变化前的结论及说理过程对变化后的结论及说理过程起着至关重要的作用;(2)图形在变化过程中,哪些关系发生了变化,哪些关系没有发生变化;原来的线段之间、角之间的位置与数量关系是否还存在是解题的关键;(3)几种变化图形之间,证明思路存在内在联系,都可模仿与借鉴原有的结论与过程,其结论有时变化,有时不发生变化1、已知:在△ABC中,∠BAC=90°,AB=AC,点D为射线BC上一动点,连结AD,以AD 为一边且在AD的右侧作正方形ADEF.(1)当点D在线段BC上时(与点B不重合),如图1,求证:CF=BD(2)当点D 运动到线段BC 的延长线上时,如图2,第(1)问中的结论是否仍然成立,并说明理由.(答案)证明:(1)∵正方形ADEF ∴AD =AF ,∠DAF =90°∴∠DAF -∠DAC =∠BAC -∠DAC ,即∠BAD =∠CAF在△ABD 和△ACF 中,AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△ACF (SAS ) ∴BD =CF(2)当点D 运动到线段BC 的延长线上时,仍有BD =CF此时∠DAF +∠DAC =∠BAC +∠DAC ,即∠BAD =∠CAF在△ABD 和△ACF 中,AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△ACF (SAS ) ∴BD =CF2、如图(1),△ABC 中,BC =AC ,△CDE 中,CE =CD ,现把两个三角形的C 点重合,且使∠BCA =∠ECD ,连接BE ,AD .求证:BE =AD .若将△DEC 绕点C 旋转至图(2),(3)所示的情况时,其余条件不变,BE 与AD 还相等吗?为什么?(答案)证明:∵∠BCA =∠ECD , ∴∠BCA -∠ECA =∠ECD -∠ECA ,即∠BCE =∠ACD在△ADC 与△BEC 中ACD=BCE AC BC CD CE =⎧⎪∠∠⎨⎪=⎩∴△ADC ≌△BEC(SAS) ∴BE =AD .若将△DEC 绕点C 旋转至图(2),(3)所示的情况时,其余条件不变,BE 与AD 还相等,因为还是可以通过SAS 证明△ADC ≌△BEC.。
三角形全等的判定方法(5种)例题+练习(全面)

教学内容全等三角形的判定教学目标掌握全等三角形的判定方法重点全等三角形的判定探索三角形全等的条件(5种)1 边角边(重点)两边及其夹角分别分别相等的两个三角形全等,可以简写成“边角边”或“SAS”. 注:必须是两边及其夹角,不能是两边和其中一边的对角.原因:如图:在∆ABC和∆ABD中,∠A=∠A,AB=AB,BC=BD,显然这两个三角形不全等. 例1 如图,AC=AD,∠CAB=∠DAB,求证:∆ACB≌∆ADB.例2 如图,在四边形ABCD中,AD∥BC,∠ABC=∠DCB,AB=DC,AE=DF求证:BF=CE.例3.(1)如图①,根据“SAS”,如果BD=CE, = ,那么即可判定△BDC≌△CEB;(2) 如图②,已知BC=EC,∠BCE=ACD,要使△ABC≌△DEC,则应添加的一个条件为例4.如图,已知AD=AE,∠1=∠2,BD=CE,则有△ABD≌,理由是;△ABE≌,理由是.例5.如图,在△ABC和△DEF中,如果AB=DE,BC=EF,只要找出∠ =∠或∥,就可得到△ABC≌△DEF.例6.如图,已知AB∥DE,AB=DE,BF=CE,求证:△ABC≌△DEF.例7.如图,点B在线段AD上,BC∥DE,AB=ED,BC=DB.求证:∠A=∠E例8.如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.2.角边角两角及其夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”)例1.如图,在△ABC中,点D是BC的中点,作射线AD,线段AD及其延长线上分别取点E,F,连接CE,BF.添加一个条件,使得△BDF≌△CDE,你添加的条件是:.(不添加辅助线)例2.如图,已知AD平分∠BAC,且∠ABD=∠ACD,则由“AAS”可直接判定△≌△.例3.如图,在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,那么AE= cm.例4.如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为.例5.如图,已知EC=AC,∠BCE=∠DCA,∠A=∠E.求证:BC=DC.例6.如图,在△ABC中,D是BC边上的点 (不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE.请你添加一个条件,使△BDE≌△CDF (不再添加其他线段,不再标注或使用其他字母),并给出证明.(1) 你添加的条件是:;(2) 证明:例7.如图,A在DE上,F在AB上,且BC=DC,∠1=∠2=∠3,则DE的长等于 ( ) A.DC B.BCC.AB D.AE+AC【基础训练】1.如图,已知AB=DC,∠ABC=∠DCB,则有△ABC≌_______,理由是_______;且有∠ACB=_______,AC=_______.2.如图,已知AD=AE,∠1=∠2,BD=CE,则有△ABD≌_______,理由是_______;△ABF≌_______,理由是_______.3.如图,在△ABC和△BAD中,因为AB=BA,∠ABC=∠BAD,_______=_______,根据“SAS”可以得到△ABC≌△BAD.4.如图,要用“SAS”证△ABC≌△ADE,若AB=AD,AC=AE,则还需条件( ).A.∠B=∠D B∠C=∠EC.∠1=∠2 D.∠3=∠45.如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠AEC等于( ).A.60°B.50°C.45°D.30°6.如图,如果AE=CF,AD∥BC,AD=CB,那么△ADF和ACBE全等吗?请说明理由.7.如图,已知AD与BC相交于点O,∠CAB=∠DBA,AC=BD.求证:(1)∠C=∠D;(2)△AOC≌△BOD.8.如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交DC于F,BD分别交CE、AE于点G、H.试猜测线段AE和BD的位置和数量关系,并说明理由.9.如图,在△ABC中,AB=AC,AD平分∠BAC.求证:∠DBC=∠DCB.10.如图,△ABC是等边三角形,D是AB边上的一点,以CD为边作等边三角形CDE,使点E、A在直线DC的同侧,连接AE.求证:AE∥BC.A BC DEF角角边两角分别相等且其中一组等角的对边相等的两个三角形全等,可以简写成“角角边”或“AAS ”. 例1、如图,在△ABC 中,∠ABC =45°,H 是高AD 和高BE 的交点,试说明BH =AC .例2、如图,∠ACB=90°,AC=BC ,BE ⊥CE ,AD ⊥CE 于D ,AD=2.5cm ,DE=1.7cm . 求BE 的长.例3、如图, 在△ABC 中, AC ⊥BC, CE ⊥AB 于E, AF 平分∠CAB 交CE 于点F, 过F 作FD ∥BC 交AB 于点D. 求证:AC =AD.例4、如图, 在ABC中, ∠A=90°, BD平分B, DE⊥BC于E, 且BE=EC,(1)求∠ABC与∠C的度数;(2)求证:BC=2AB.边边边三边分别相等的两个三角形全等,可以简写成“边边边”或“SSS”.例1、如图,在四边形ABCD中,AB=CB,AD=CD.你能说明∠C=∠A吗? 试一试.例2、如图,在四边形ABCD中,AB=AD,BC=DC,E为AC上的一动点(不与A重合),在E移动过程中.BE和DE是否相等? 若相等,请写出证明过程;若不相等,请说明理由.例3.如图,AB=CD ,AE=CF ,BO=DO ,EO=FO .求证:OC=OA .斜边、直角边斜边和一条直角边分别相等的两个直角三角形全等,可以简写成“斜边、直角边”或“HL ”。
全等三角形判定-专题复习50题(含答案)

A.一个锐角对应相等C.一条边对应相等B.两个锐角对应相等全等三角形判定、选择题:1-如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全样的三角形,那么这两个三角形完全一样的依据是()A.SSSB.SASC.AASD.ASA2•方格纸中,每个小格顶点叫做一个格点,以格点连线为边的三角形叫做格点三角形。
如图,在4X4的方格纸中,有两个格点三角形△ABC、ADEF,下列说法中成立的是()A.ZBCA=ZEDF CoZBAC=ZEFDB.ZBCA=ZEFDD.这两个三角形中,没有相等的角3•如图所示,△ABD9ACDB,下面四个结论中,不正确的是()A.△ABD和厶CDB的面积相等B.AABD和厶CDB的周长相等C.ZA+ZABD=ZC+ZCBDD.AD〃BC,且AD=BC4.下列判断中错误的是()A.有两角和一边对应相等的两个三角形全等B.有两边和一角对应相等的两个三角形全等C.有两边和其中一边上的中线对应相等的两个三角形全等D.有一边对应相等的两个等边三角形全等5-使两个直角三角形全等的条件是()6•如图,在AABC和厶BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则Z AACB等于(B.ZBEDC.寺ZAFBD.2ZABFA.ZEDBBA B C DB.ZA=ZDC.AC=DD.ZACB=ZF7.在AABC 和厶A /B /C /中,已知ZA=ZA /,AB=A /B /,在下面判断中错误的是()A. 若添加条件AC=A /C /,则厶ABC^^^A /B /C /B. 若添加条件BC=B /C /,则厶ABC^^^A /B /C /C 。
若添加条件ZB=ZB /,则△ABC^^^A /B /C /D 。
若添加条件ZC=ZC /,则△ABC^^^A /B /C /8•如图,AABC 和厶DEF 中,AB=DE 、ZB=ZDEF,添加下列哪一个条件无法证明厶ABC^^DEF ()9•如图,在△ABC 中,ZABC=45°,AC=8cm,F 是高AD 和BE 的交点,则BF 的长是()A.4cmB.6cmC.8cmD.9cm1°.在如图所示的5X5方格中,每个小方格都是边长为1的正方形,AABC 是格点三角形(即顶点恰好是正方形的顶点),则与△ABC 有一条公共边且全等的所有格点三角形个数是()11.如图,点E 在正方形ABCD 的对角线AC 上,且EC=2AE ,直角三角形FEG 的两直角边EF 、EG 分别交BC 、DC 于点M 、N.若正方形ABCD 的边长为a,则重叠部分四边形EMCN 的面积为( A.AC 〃DF12-在连接A地与B地的线段上有四个不同的点D、G、K、Q,下列四幅图中的实线分别表示某人从A 地到B地的不同行进路线(箭头表示行进的方向),则路程最长的行进路线图是(C、填空题:I3•如图所示,有一块三角形的镜子,小明不小心弄破裂成1、2两块,现需配成同样大小的一块.为了方便起见,需带上—块,其理由是.14.如图示,点B在AE上,ZCBE=ZDBE,要使AABC^AABD,还需添加一个条件是,(填上你认为适当的一个条件即可)15•如图,已知Z1=Z2,AC=AD,请增加一个条件,使△ABC9AAED,你添加的条件是16-如图,Z1=Z2,要使△ABD9AACD,需添加的一个条件是(只添一个条件即可).17•如图,在△ABC中,AB=AC,AD丄BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角形对.18•如图,△ABD9ABAC,若AD=BC,则ZBAD的对应角是.19-如图,已知AB丄BD,垂足为B,ED丄BD,垂足为D,AB=CD,BC=DE,则ZACE=_度.2°・如图,如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三边所对的角的关系是.三、解答题:21•如图,ZDCE=90°,CD=CE,AD丄AC,BE丄AC,垂足分别为A.B.试说明AD+AB=BE.22.如图,E、A.C三点共线,AB〃CD,ZB=ZE,,AC=CD。
三角形全等的判定(SSS)全面版

小结:四边形问题转化为三角形问题解决。 D
问:此题添加辅助线,若连结BD行吗? 在原有条件下,还能推出什么结论? B 答:∠ABC=∠ADC,AB∥CD,AD∥BC
C
练一练 工人师傅常用角尺平分一个任意角,做法如下: 如图,∠AOB是一个任意角,在边OA,OB上分别取 OM=ON,移动角尺,使角尺两边相同的刻度分别与M、 N重合,过角尺顶点C的射线OC便是∠AOB的平分线。 为什么?
∠C=、三组对应角 六个条件分别相等。
问题1:若两个三角形三组对应边、三组对应角分别 相等,则这两个三角形是否一定全等? 两个三角形全等 三组对应边、三组对应角 六个条件分别相等。
问题2:两个三角形满足六个条件中的几个条件才能 确保这两个三角形全等呢?
探究一 (1)一条边 1.给定一个条件:
D
若要求证: ∠B=∠C, 你会吗?
∴∠B=∠C(全等三角形的对应角相等)
归纳:
证明全等的书写步骤:
①准备条件:证全等时要用的间接 条件要先证好; ②三角形全等书写三步骤:
写出在哪两个三角形中 摆出三个条件用大括号括起来 写出全等结论
练习1
如图,AB=CD,AC=BD,△ABC和△DCB 是否全等?试说明理由。 A D
C
B
∴ ∠ A= ∠ C (全等三角形的对应角相等)
变形题: 已知AB=CD,AD=CB,求证:∠B=∠D
证明:连接AC, A 在△ABC和△ ADC中 AB=CD(已知) BC=AD(已知) AC=AC(公共边) ∴ △ ABC≌ △ CDA(SSS) D
B
C
∴ ∠B=∠D(全等三角形对应角相等)
失 败
(2)一个角 (1)两边 4cm
6cm 4cm 6cm
全等三角形判定-专题练习

全等三角形判定经典练习1、如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A.B.试说明(1) △ABD≌△BAC(2)AD+AB=BE.2、如图,E、A.C三点共线,AB∥CD,∠B=∠E,,AC=CD。
求证:BC=ED。
3、如图:AD是△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD。
求证:(1)△FBD≌△CAD (2)BE⊥AC。
4、如图,已知△ABC中,∠1=∠2,AE=AD,求证:△ABE≌△ACD.5、如图所示,已知AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.6、如图,已知D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE.求证:△ABC≌△DAE.7、已知:如图AC,BD相交于点O,∠A=∠D,AB=CD,求证:△AOB≌△DOC.8、如图,点D,E在△ABC的边BC上,AB=AC,BD=CE.求证:AD=AE.9、如图,已知点B、E、C、F在同一条直线上,BE=CF,AB∥DE,∠A=∠D.求证:AB=DE.11、如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB.求证:AE=CE.12、如图,点A.C、D、B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF.求证:DE=CF.13、如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.求证:BD=CE.14、如图,AB=DC,AC=DB,求证:AB∥CD.15、如图,点D,E分别在AB,AC上,且AD=AE,∠BDC=∠CEB.求证:BD=CE.16、如图,AB=AE,∠1=∠2,∠C=∠D.求证:△ABC≌△AED.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形的判定证明专题
一、全等三角形的性质
①全等三角形的对应边相等.
②全等三角形的对应角相等。
二、全等三角形的判定定理
①角边角公理:有两角和它们的夹边对应相等的两个三角形全等(ASA)。
②边角边公理:有两边和它们的夹角对应相等的两个三角形全等(SAS)。
③边边边公理:有三边对应相等的两个三角形全等(SSS)。
④角角边定理:有两个角和其中一个角的对边对应相等的两个三角形全等(AAS)。
三、一般思考方法
1、已知两边对应相等—1。
第三边;2。
夹角;3。
直角
2、一角及邻边对应相等—1。
角的另一边;2.边的另一角;3。
边的对角
3、一角及对边对应相等—1.另一角
4、两角相等-1。
夹边;2。
一已知角的对边
第一部分简单证明
例题分析
例1:已知:如图AC=BD,∠CAB=∠DBA.求证:∠CAD=∠DBC。
例2:已知:AB=CD,AB∥DC,求证:△ABC≌△CDB
例3:已知:在△ABC中,AD为BC边上的中线,CE⊥AD,BF⊥AD.求证:CE=BF
例4.已知:如图AB=AC,AD=AE,BE和CD相交于G。
求证:AG平分∠BAC.
例5:已知:△ABC中,D、E、F分别是AB、AC、BC上的点,连结DE、EF,∠ADE=∠EFC,∠AED=∠ACB,DE=FC.求证:△ADE≌△EFC
例6:已知:△ABC是等边三角形,∠GAB=∠HBC=∠DCA,∠GBA=∠HCB=∠DAC。
求证:△ABG≌△BCH≌△CAD。
自我检测
1、已知:△ABC中,AB=AC,D、E分别为AB、AC的中点。
求证:∠ABE=∠ACD.
2、已知:AB=DC,AC=BD ,AC 交BD 于E.求证:AE=DE.
3、已知:如图,AB=CD ,BE=DF ,AF=EC.求证:BF=DE
4、如图,在△ABE 中,AB =AE ,AD =AC ,∠BAD =∠EAC , BC 、DE 交于点O. 求证:(1) △ABC ≌△AED ; (2) OB =OE 。
5、如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直
线CE 交BA 的延长线于F . 求证:BD =2CE .
O
C E
B
D
A
F
E D
C
B A
第二部分 辅助线证全等三角形
三角形辅助线做法
图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连. 要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线.
常见辅助线的作法有以下几种:
1) 遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”. 2) 遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等
变换中的“旋转”.
3) 遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的
“对折”,所考知识点常常是角平分线的性质定理或逆定理.
4) 过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻转折
叠”
5) 截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是之与
特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目.
特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答.
有三角形中线时,常延长加倍中线,构造全等三角形。
1、如图,AD 为 △ABC 的中线,求证:AB +AC >2AD 。
截长补短法作辅助线
1、如图,ABC ∆中,AB=2AC ,AD 平分BAC ∠,且AD=BD,求证:CD ⊥AC
A
B
C
D
E C
D
B
A
C
B
A
C
B
A
2、如图,AC ∥BD,EA,EB 分别平分∠CAB,∠DBA ,CD 过
点E,求证;AB =AC+BD
3、如图,已知在ABC 内,0
60BAC ∠=,040C ∠=,P ,Q 分别在BC,CA 上,并且AP ,BQ 分别是BAC ∠,ABC ∠的角平分线。
求证:BQ+AQ=AB+BP
4、如图,在四边形ABCD 中,BC >BA ,AD =CD ,BD 平分ABC ∠,
求证: 0180=∠+∠C A
5、如图在△ABC 中,AB >AC,∠1=∠2,P 为AD 上任意一点,求证;AB —AC >PB-PC
延长已知边构造三角形:
1、如图,已知AC =BD ,AD ⊥AC 于A ,BC ⊥BD 于B,
求证:AD =BC
连接四边形的对角线,把四边形的问题转化成为三角形来解决。
1、如图,AB ∥CD ,AD ∥BC 。
求证:AB=CD 。
连接已知点,构造全等三角形.
1、已知,如图,AC 、BD 相交于O 点,且AB =DC ,AC =BD ,求证:∠A =∠D 。
取线段中点构造全等三有形。
1、如图,AB =DC ,∠A =∠D 求证:∠ABC =∠DCB.
A B
C
D E O A
B C
D 1
2
3
4
D
B A
O D
C
B A M
N
F
E
D C
B
A
C
B
A
借助角平分线造全等
1、如图,已知在△ABC 中,∠B=60°,△ABC 的角平分线AD,CE 相交于点
O ,求证:OE=OD
2、如图,△ABC 中,AD 平分∠BAC ,DG ⊥BC 且平分BC ,DE ⊥AB 于E,DF ⊥AC 于F. (1)说明BE=CF 的理由;(2)如果AB=a ,AC=b ,求AE 、BE 的长.
旋转
1、正方形ABCD 中,E 为BC 上的一点,F 为CD 上的一点,BE+DF=EF ,求∠EAF 的度数.
2、D 为等腰Rt ABC ∆斜边AB 的中点,DM ⊥DN ,DM,DN 分别交BC,CA 于点E ,F.
(1) 当MDN ∠绕点D 转动时,求证DE=DF 。
(2) 若AB=2,求四边形DECF 的面积.
E
D
G
F
C B
A
E
D C
B A
3、已知:2,以AB 为一边作正方形ABCD ,使P 、D 两点落在直线AB 的两侧.
(1)如图,当∠APB=45°时,求AB 及PD 的长;
(2)当∠APB 变化,且其它条件不变时,求PD 的最大值,及相应∠APB 的大小.
平移变换
1、AD 为△ABC 的角平分线,直线MN ⊥AD 于A 。
E 为MN 上一点,△ABC 周长记为A P ,△EBC 周长记为B P 。
求证B P >A P .
2、如图,在△ABC 的边上取两点D 、E,且BD=CE ,求证:AB+AC 〉AD+AE 。
