2020-2021成都市高二数学上期末模拟试题(带答案)

合集下载

2020-2021成都市第二十中学校高二数学上期末一模试题(及答案)

2020-2021成都市第二十中学校高二数学上期末一模试题(及答案)一、选择题1．如图，ABC ∆和DEF ∆都是圆内接正三角形，且//BC EF ，将一颗豆子随机地扔到该圆内，用A 表示事件“豆子落在ABC ∆内”，B 表示事件“豆子落在DEF ∆内”，则(|)P B A =（）A ．33B ．3 C ．13D ．232．已知一组数据的茎叶图如图所示，则该组数据的平均数为（）A ．85B ．84C ．83D ．813．已知回归方程$21y x =+，而试验得到一组数据是(2,5.1)，(3,6.9)，(4,9.1)，则残差平方和是（） A ．0.01B ．0.02C ．0.03D ．0.044．把五个标号为1到5的小球全部放入标号为1到4的四个盒子中，并且不许有空盒，那么任意一个小球都不能放入标有相同标号的盒子中的概率是（） A ．320B ．720C ．316D ．255．执行如图所示的程序框图，若输入8x =，则输出的y 值为（）A ．3B ．52C ．12D ．34-6．随着人民生活水平的提高，对城市空气质量的关注度也逐步增大，下图是某城市1月至8月的空气质量检测情况，图中一、二、三、四级是空气质量等级，一级空气质量最好，一级和二级都是质量合格天气，下面四种说法正确的是（）．①1月至8月空气合格天数超过20天的月份有5个 ②第二季度与第一季度相比，空气合格天数的比重下降了 ③8月是空气质量最好的一个月 ④6月的空气质量最差 A ．①②③B ．①②④C ．①③④D ．②③④7．在半径为2圆形纸板中间，有一个边长为2的正方形孔，现向纸板中随机投飞针，则飞针能从正方形孔中穿过的概率为（） A ．4π B ．3πC ．2πD ．1π8．某校从高一(1)班和(2)班的某次数学考试(试卷满分为100分)的成绩中各随机抽取了6份数学成绩组成一个样本，如茎叶图所示.若分别从(1)班、(2)班的样本中各取一份，则(2)班成绩更好的概率为( )A ．1636B ．1736C ．12D ．19369．在R 上定义运算：A()1B A B =-，若不等式()x a -()1x a +<对任意的实数x ∈R 恒成立，则实数a 的取值范围是( ) A ．11a -<<B ．02a <<C ．1322a -<< D ．3122a -<< 10．设数据123,,,,n x x x x L 是郑州市普通职工*(3,)n n n N ≥∈个人的年收入，若这n 个数据的中位数为x ，平均数为y ，方差为z ，如果再加上世界首富的年收入1n x +，则这1n +个数据中，下列说法正确的是（）A ．年收入平均数大大增大，中位数一定变大，方差可能不变B ．年收入平均数大大增大，中位数可能不变，方差变大C ．年收入平均数大大增大，中位数可能不变，方差也不变D ．年收入平均数可能不变，中位数可能不变，方差可能不变11．定义运算a b ⊗为执行如图所示的程序框图输出的S 值，则式子π2πtan cos 43⎛⎫⎛⎫⊗ ⎪ ⎪⎝⎭⎝⎭的值是A ．－1B ．12C ．1D ．3212．如图，边长为2的正方形有一内切圆.向正方形内随机投入1000粒芝麻，假定这些芝麻全部落入该正方形中，发现有795粒芝麻落入圆内，则用随机模拟的方法得到圆周率π的近似值为( )A ．3.1B ．3.2C ．3.3D ．3.4二、填空题13．若正方形ABCD 的边长为4, E 为四边形上任意一点,则AE 的长度大于5的概率等于______14．某同学同时掷两颗骰子，得到点数分别为a ，b ，则双曲线2222x y 1a b -=的离心率e 5>的概率是______．15．执行如图所示的程序框图，若输入的1,7s k ==则输出的k 的值为_______．16．下图给出了一个程序框图，其作用是输入x 的值，输出相应的y 值．若要使输入的x 值与输出的y 值满足关系式y=-2x+4，则这样的x 值___个．17．某班60名学生参加普法知识竞赛，成绩都在区间[40100]，上，其频率分布直方图如图所示，则成绩不低于60分的人数为___．18．某公司的广告费支出x 与销售额y （单位：万元）之间有下列对应数据：由资料显示y 对x 呈线性相关关系。

2020-2021成都市高二数学上期中模拟试题(带答案)

2020-2021成都市高二数学上期中模拟试题(带答案)一、选择题1．某学校为了解1 000名新生的身体素质，将这些学生编号为1，2，…，1 000，从这些新生中用系统抽样方法等距抽取100名学生进行体质测验，若46号学生被抽到，则下面4名学生中被抽到的是 A ．8号学生B ．200号学生C ．616号学生D ．815号学生2．已知某样本的容量为50，平均数为70，方差为75．现发现在收集这些数据时，其中的两个数据记录有误，一个错将80记录为60，另一个错将70记录为90．在对错误的数据进行更正后，重新求得样本的平均数为x ，方差为2s ，则 A ．270,75x s =<B ．270,75x s =>C ．270,75x s ><D ．270,75x s <>3．在含有3件次品的50件产品中，任取2件，则至少取到1件次品的概率为 ( )A ．11347250C C C B ．20347250C C C C ．1233250C C C +D ．1120347347250C C C C C + 4．“三个臭皮匠，赛过诸葛亮”，这是我们常说的口头禅，主要是说集体智慧的强大. 假设李某智商较高，他独自一人解决项目M 的概率为10.3P =；同时，有n 个水平相同的人也在研究项目M ，他们各自独立地解决项目M 的概率都是0.1.现在李某单独研究项目M ，且这n 个人组成的团队也同时研究项目M ，设这个n 人团队解决项目M 的概率为2P ，若21P P ≥，则n 的最小值是( ) A ．3B ．4C ．5D ．65．在本次数学考试中，第二大题为多项选择题.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得5分，部分选对的得3分，有选错的得0分，小明因某原因网课没有学习，导致题目均不会做，那么小明做一道多选题得5分的概率为（） A ．115B ．112C ．111D ．146．在去年的足球甲A 联赛上，一队每场比赛平均失球数是1.5，全年比赛失球个数的标准差为1.1；二队每场比赛平均失球数是2.1，全年失球个数的标准差是0.4，你认为下列说法中正确的个数有（）①平均来说一队比二队防守技术好；②二队比一队防守技术水平更稳定；③一队防守有时表现很差，有时表现又非常好；④二队很少不失球. A ．1个B ．2个C ．3个D ．4个7．我国数学家陈景润在哥德巴赫猜想的研究中做出了重大贡献，哥德巴赫猜想是：“任一大于2的偶数都可以写成两个质数之和”，如32=13+19．在不超过32的质数中，随机选取两个不同的数，其和等于30的概率为（） A ．111B ．211C ．355D ．4558．下列命题：①对立事件一定是互斥事件；②若A ，B 为两个随机事件，则P(A∪B)＝P(A)＋P(B)；③若事件A ，B ，C 彼此互斥，则P(A)＋P(B)＋P(C)＝1；④若事件A ，B 满足P(A)＋P(B)＝1，则A 与B 是对立事件．其中正确命题的个数是( ) A ．1B ．2C ．3D ．49．将三枚质地均匀的骰子各掷一次，设事件A =“三个点数之和等于15”，B =“至少出现一个5点”，则概率()|P A B 等于（） A ．5108B ．113C ．17D ．71010．如图所示是为了求出满足122222018n +++>L 的最小整数n ，和两个空白框中，可以分别填入（）A ．2018S >？，输出1n -B ．2018S >？，输出nC ．2018S ≤？，输出1n -D ．2018S ≤？，输出n11．下列说法正确的是（）A ．若残差平方和越小，则相关指数2R 越小B ．将一组数据中每一个数据都加上或减去同一常数，方差不变C ．若2K 的观测值越大，则判断两个分类变量有关系的把握程度越小D ．若所有样本点均落在回归直线上，则相关系数1r =12．某厂家为了解销售轿车台数与广告宣传费之间的关系，得到如表统计数据表：根据数据表可得回归直线方程y bx a =+$$$，其中ˆ 2.4b=，$a y bx =-$，据此模型预测广告费用为9万元时，销售轿车台数为（）广告费用x （万元） 2 3 4 5 6 销售轿车y （台数）3461012A ．17B ．18C ．19D ．20二、填空题13．若x 是从区间[0,3]内任意选取的一个实数，y 也是从区间[0,3]内任意选取的一个实数，则221x y +<的概率为__________． 14．执行如图所示的框图，输出值______．15．如图所示，程序框图(算法流程图)的输出值x ＝________.16．以下说法正确的是_____________ . ①类比推理属于演绎推理.②设有一个回归方程ˆ23yx =- ，当变量每增加1个单位，y 平均增加3个单位. ③样本相关系数r 满足以下性质：1r ≤，并且r 越接近1，线性相关程度越强；r 越接近0，线性相关程度越弱.④对复数12,z z 和自然数n 有()1212nn n z z z z ⋅=⋅.17．为了对某课题进行研究，用分层抽样方法从三所高校,,A B C 的相关人员中，抽取若干人组成研究小组，有关数据见表（单位：人）若从高校,B C抽取的人中选2人作专题发言，则这2人都来自高校C的概率P=__________．18．执行如图所示的流程图，则输出的x值为______．19．如图程序框图的输出结果是_________.1.5,4，则丢失的数20．已知,x y之间的一组数据不小心丢失一个，但已知回归直线过点()据是__________．x0123y135三、解答题21．中国神舟十一号载人飞船在酒泉卫星发射中心成功发射，引起全国轰动．开学后，某校高二年级班主任对该班进行了一次调查，发现全班60名同学中，对此事关注的占13，他们在本学期期末考试中的物理成绩如下面的频率分布直方图：（1）求“对此事关注”的同学的物理期末平均分（以各区间的中点代表该区间的均值）．（2）若物理成绩不低于80分的为优秀，请以是否优秀为分类变量， ①补充下面的22⨯列联表：物理成绩优秀物理成绩不优秀合计对此事关注对此事不关注合计②是否有95%以上的把握认为“对此事是否关注”与物理期末成绩是否优秀有关系？参考公式：22()()()()()n ad bc k a b c d a c b d -=++++，其中n a b c d =+++.参考数据：20()P K k ≥ 0.150.10 0.05 0.025 0.010 0.005 0.001 0k2.0722.7063.8415.0246.6357.87910.82822．为保护农民种粮收益，促进粮食生产，确保国家粮食安全，调动广大农民生产粮食的积极性，从2014年开始，国家实施了对种粮农民直接补贴的政策通过对2014~2018年的数据进行调查，发现某地区发放粮食补贴额x （单位：亿元）与该地区粮食产量y （单位：万亿吨）之间存在着线性相关关系，统计数据如下表：年份 2014 2015 2016 2017 2018 补贴额x /亿元 9 10 12 11 8 粮食产量y /万亿2526313721（1）请根据上表所给的数据，求出y 关于x 的线性回归直线方程ˆˆybx a =+；（2）通过对该地区粮食产量的分析研究，计划2019年在该地区发放粮食补贴7亿元，请根据（1）中所得到的线性回归直线方程，预测2019年该地区的粮食产量.参考公式：()()()121ˆniii nii x x y y bx x ==--=-∑∑，ˆˆay bx =-. 23．光伏发电是将光能直接转变为电能的一种技术，具有资源的充足性及潜在的经济性等优点，在长期的能源战略中具有重要地位，2015年起，国家能源局、国务院扶贫办联合在6省的30个县开展光伏扶贫试点，在某县居民中随机抽取50户，统计其年用量得到以下统计表.以样本的频率作为概率.(Ⅰ)在该县居民中随机抽取10户，记其中年用电量不超过600度的户数为X ，求X 的数学期望；(Ⅱ)在总结试点经验的基础上，将村级光伏电站稳定为光伏扶贫的主推方式.已知该县某自然村有居民300户.若计划在该村安装总装机容量为300千瓦的光伏发电机组，该机组所发电量除保证该村正常用电外，剩余电量国家电网以0.8元/度的价格进行收购.经测算每千瓦装机容量的发电机组年平均发电1000度，试估计该机组每年所发电量除保证正常用电外还能为该村创造直接受益多少元？24．某校高二八班学生每周用于数学学习的时间x （单位：h ）与数学成绩y （单位：分）之间有如下数据：某同学每周用于数学学习的时间为18小时，试预测该生数学成绩.（保留小数点后两位）参考数据17.4x = 74.9y =10213182ii x==∑ 102158375i i y ==∑ 10113578i i i x y ==∑，参考公式：回归直线的方程$y bx a =+，其中()()()1122211,n niii ii i nniii i x x y y x y nx yb a y bx x x xnx====---===---∑∑∑∑.25．近年来，我国许多省市雾霾天气频发，为增强市民的环境保护意识，某市面向全市征召n 名义务宣传志愿者，成立环境保护宣传组织，现把该组织的成员按年龄分成5组第1组[20,25)，第2组[25,30)，第3组[30,35)，第4组[35,40)，第5组[40,45]，得到的频率分布直方图如图所示，已知第2组有35人.（1）求该组织的人数；（2）若在第3,4,5组中用分层抽样的方法抽取6名志愿者参加某社区的宣传活动，应从第3,4,5组各抽取多少名志愿者？（3）在（2）的条件下，该组织决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验，求第3组至少有1名志愿者被抽中的概率.26．某保险公司有一款保险产品的历史收益率（收益率=利润÷保费收入）的频率分布直方图如图所示：（1）试估计这款保险产品的收益率的平均值；（2）设每份保单的保费在20元的基础上每增加x 元，对应的销量为y （万份）．从历史销售记录中抽样得到如下5组x 与y 的对应数据：x 元25 30 38 45 52 销量为y （万份）7.57.16.05.64.8由上表，知x 与y 有较强的线性相关关系，且据此计算出的回归方程为10.0ˆybx =-．（ⅰ）求参数b 的值；（ⅱ）若把回归方程10.0ˆybx =-当作y 与x 的线性关系，用（1）中求出的收益率的平均值作为此产品的收益率，试问每份保单的保费定为多少元时此产品可获得最大利润，并求出最大利润．注：保险产品的保费收入=每份保单的保费⨯销量．【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【解析】【分析】等差数列的性质．渗透了数据分析素养．使用统计思想，逐个选项判断得出答案．【详解】详解：由已知将1000名学生分成100个组，每组10名学生，用系统抽样，46号学生被抽到，所以第一组抽到6号，且每组抽到的学生号构成等差数列{}n a ，公差10d =，所以610n a n=+()n *∈N ，若8610n =+，则15n =，不合题意；若200610n =+，则19.4n =，不合题意；若616610n =+，则61n =，符合题意；若815610n =+，则80.9n =，不合题意．故选C ．【点睛】本题主要考查系统抽样.2．A解析：A 【解析】【分析】分别根据数据的平均数和方差的计算公式，求得2,x s 的值，即可得到答案．【详解】由题意，根据平均数的计算公式，可得7050806070907050x ⨯+-+-==，设收集的48个准确数据分别记为1248,,,x x x L ，则()()()()()2222212481757070706070907050x x x ⎡⎤=-+-++-+-+-⎣⎦L ()()()2221248170707050050x x x L ⎡⎤=-+-++-+⎣⎦， ()()()()()222222124817070708070707050s x x x ⎡⎤=-+-++-+-+-⎣⎦L ()()()222124817070701007550x x x ⎡⎤=-+-++-+<⎣⎦L ，故275s <．选A ．【点睛】本题主要考查了数据的平均数和方差的计算公式的应用，其中解答中熟记数据的平均数和方差的公式，合理准确计算是解答的关键，着重考查了推理与运算能力，数基础题．3．D解析：D 【解析】【分析】由题意，恰好两件都是次品，共有23C 种不同的取法，恰好两件中一件是次品、一件是正品，共有11347C C 种不同的取法，即可求解．【详解】由题意，从含有3件次品的50件产品中，任取2件，共有250C 种不同的取法，恰好两件都是次品，共有20347C C 种不同的取法，恰好两件中一件是次品、一件是正品，共有11347C C 种不同的取法，所以至少取到1件次品的概率为1120347347250C C C C C +，故选D ．【点睛】本题主要考查了古典概型及其概率的计算，其中解答中正确理解题意，合理分类讨论，利用组合数的公式是解答的关键，着重考查了分类讨论思想，以及推理与运算能力，属于基础题．4．B解析：B 【解析】【分析】设这个n 人团队解决项目M 的概率为2P ，则021(0.9)n n P C =-，由21P P …，得10.90.3n-…，由此能求出n 的最小值．【详解】Q 李某智商较高，他独自一人解决项目M 的概率为10.3P =，有n 个水平相同的人也在研究项目M ，他们各自独立地解决项目M 的概率都是0.1，现在李某单独研究项目M ，且这n 个人组成的团队也同时研究M ，设这个n 人团队解决项目M 的概率为2P ，则021(0.9)n nP C =-， 21P P Q …，10.90.3n∴-…，解得4n ≥．n ∴的最小值是4．故选B ．【点睛】本题考查实数的最小值的求法，考查n次独立重复试验中事件A恰好发生k次的概率的计算公式等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．5．C解析：C【解析】【分析】根据题意结合组合的知识可知，总的答案的个数为11个，而正确的答案只有1个，根据古典概型的计算公式，即可求得结果.【详解】总的可选答案有：AB，AC，AD，BC，BD，CD，ABC，ABD，ACD，BCD，ABCD，共11个，而正确的答案只有1个，即得5分的概率为111 p .故选：C.【点睛】本题考查了古典概型的基本知识，关键是弄清一共有多少个备选答案，属于中档题. 6．D解析：D【解析】在（1）中，一队每场比赛平均失球数是1.5，二队每场比赛平均失球数是2.1，∴平均说来一队比二队防守技术好，故（1）正确；在（2）中，一队全年比赛失球个数的标准差为1.1，二队全年比赛失球个数的标准差为0.4，∴二队比一队技术水平更稳定，故（2）正确；在（3）中，一队全年比赛失球个数的标准差为1.1，二队全年比赛失球个数的标准差为0.4，∴一队有时表现很差，有时表现又非常好，故（3）正确；在（4）中，二队每场比赛平均失球数是2.1，全年比赛失球个数的标准差为0.4，∴二队很少不失球，故（4）正确.故选：D．7．C解析：C【解析】【分析】利用列举法求得基本事件的总数，再得出选取两个不同的数且和等于30，所包含的基本事件的个数，利用古典概型的概率计算公式，即可求解.【详解】由题意，不超过32的质数有2，3，5，7，11，13，17，19，23，29，31，共有11个，其中随机选取两个不同的数且和等于30的有30=7+23=11+19=13+17，共有3组，所以所求概率为2113355C =，故选：C. 【点睛】本题主要考查了古典概型及其概率的计算，其中解答中利用列举法求得基本事件的总数是解答的关键，着重考查了推理与计算能力.8．A解析：A 【解析】【分析】根据互斥之间和对立事件的概念，及互斥事件和对立事件的关系和概率的计算，即可作出判断，得到答案．【详解】由题意①中，根据对立事件与互斥事件的关系，可得是正确；②中，当A 与B 是互斥事件时，才有P(A∪B)＝P(A)＋P(B)，对于任意两个事件A ，B 满足P(A∪B)＝P(A)＋P(B)－P(AB)，所以是不正确的；③也不正确．P(A)＋P(B)＋P(C)不一定等于1，还可能小于1；④也不正确．例如：袋中有大小相同的红、黄、黑、绿4个球，从袋中任摸一个球，设事件A ＝{摸到红球或黄球}，事件B ＝{摸到黄球或黑球}，显然事件A 与B 不互斥，但P(A)＋P(B)＝＋＝1. 【点睛】本题主要考查了互斥事件和对立事件的基本概念、互斥事件与对立时间的关系及其应用，其中熟记互斥事件和对立事件的概念和关系是解答的关键，着重考查了推理与论证能力，属于基础题．9．B解析：B 【解析】【分析】根据条件概率的计算公式即可得出答案. 【详解】3311166617()216A P AB C C C +==Q ，11155561116691()1216C C C P B C C C =-= ()()()72161|2169113P AB P A B P B ∴==⨯= 故选：B 【点睛】本题主要考查了利用条件概率计算公式计算概率，属于中档题.10．A解析：A 【解析】【分析】通过要求122222018n +++>L 时输出且框图中在“是”时输出确定“”内应填内容；再通过循环体确定输出框的内容．【详解】因为要求122222018n +++>L 时输出，且框图中在“是”时输出，所以“”内输入“2018S >？”，又要求n 为最小整数，所以“”中可以填入输出1n -，故选：A ．【点睛】本题考查了程序框图的应用问题，是基础题．11．B解析：B 【解析】【分析】由残差平方和越小，模型的拟合效果越好，可判断A ；由方差的性质可判断B ；由的随机变量2K 的观测值的大小可判断C ；由相关系数r 的绝对值趋近于1，相关性越强，可判断D .【详解】对于A ，可用残差平方和判断模型的拟合效果，残差平方和越小，模型的拟合效果越好，相关指数2R 越大，故A 错误；对于B ，将一组数据的每一个数据都加上或减去同一常数后，由方差的性质可得方差不变，故B 正确；对于C ，对分类变量X 与Y ，它们的随机变量2K 的观测值越大，“X 与Y 有关系”的把握程度越大，故C 错误；对于D ，若所有样本点均落在回归直线上，则相关系数1r =，故D 错误. 故选：B. 【点睛】本题考查命题的真假判断，主要是线性回归直线的特点和线性相关性的强弱、样本数据的特征值和模型的拟合度，考查判断能力，属于基础题．12．C解析：C 【解析】由题意4,7, 2.4,7 2.44 2.6,9,ˆˆˆˆˆˆ 2.49 2.619 x y b a y bx x y bx a===∴=-=-⨯=-∴==+=⨯-=,故选C.二、填空题13．【解析】分析：不等式组表示的是正方形区域面积为满足的平面区域为阴影部分的面积利用几何概型概率公式可得结果详解：根据题意画出图形如图所示则不等式组表示的是正方形区域面积为其中满足的平面区域为阴影部分的解析：36p【解析】分析：不等式组0303xy≤≤⎧⎨≤≤⎩表示的是正方形区域，面积为339⨯=，满足221x y+<的平面区域为阴影部分的面积21144ππ⋅=，利用几何概型概率公式可得结果.详解：根据题意，画出图形，如图所示，则不等式组0303xy≤≤⎧⎨≤≤⎩表示的是正方形区域，面积为339⨯=，其中满足221x y+<的平面区域为阴影部分的面积21144ππ⋅=，故所求的概率为4936Pππ==，故答案为36p.点睛：对于几何概型的概率公式中的“测度”要有正确的认识，它只与大小有关，而与形状和位置无关，在解题时，要掌握“测度”为长度、面积、体积、角度等常见的几何概型的求解方法．14．-1【解析】【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量a的值模拟程序的运行过程分析循环中各变量值的变化情况可得答案【详解】模拟程序的运行可得a=2i=1不满足条件i≥2解析：【解析】【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量a 的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．【详解】模拟程序的运行，可得，不满足条件，执行循环体，，不满足条件，执行循环体，，不满足条件，执行循环体，，观察规律可知a 的取值周期为3，由于，可得：不满足条件，执行循环体，，此时，满足条件，退出循环，输出a 的值为．故答案为：．【点睛】本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．15．12【解析】试题分析：第一圈是x=2;第二圈否x=4否x=5；第三圈是x=6否x=8否x=9；第四圈是x=10否x=12是输出x=12故答案为12考点：程序框图功能识别点评：简单题程序框图功能识别一解析：12 【解析】试题分析：第一圈，是，x=2; 第二圈，否，x=4,否，x=5，；第三圈，是，x=6,否，x=8，否，x=9；第四圈，是，x=10，否，x=12,是，输出x=12．故答案为12 ．考点：程序框图功能识别点评：简单题，程序框图功能识别，一般按程序逐次运行即可．16．③④【解析】分析：①根据类比推理与演绎推理的定义即可判断；②根据回归方程的表达式即可判断；③利用线性相关指数的意义即可判断；④根据复数的乘法运算律即可判断详解：对于①类比推理是合情推理的重要形式则不解析：③④ 【解析】分析：①根据类比推理与演绎推理的定义即可判断；②根据回归方程的表达式，即可判断；③利用线性相关指数r 的意义即可判断；④根据复数的乘法运算律即可判断. 详解：对于①，类比推理是合情推理的重要形式，则不属于演绎推理，故①错误；对于②，根据回归方程为ˆ23yx =-，可得当变量每增加1个单位，y 平均减少3个单位，故②错误；对于③，在回归分析中，r 具有以下性质：1r ≤，并且r 越接近1，线性相关程度越强；r 越接近0，线性相关程度越弱，故③正确；对于④，根据复数的乘法运算律，对复数12,z z 和自然数n 有()1212nn n z z z z ⋅=⋅，故④正确.故答案为③④.点睛：本题考查了命题的真假判断与应用，考查相关关系及复数的运算，是一个考查的知识点比较多的题目，解题本题的关键是理解概念及掌握运算公式，如在回归分析中，r 具有的性质，复数遵循的运算律等．17．【解析】根据分层抽样的方法可得解得所以若从高校抽取的人中选人作专题发言共有种情况则这二人都来自高校共有种情况所以概率为点睛：本题主要考查了分层抽样和古典概型及其概率的计算问题其中解答中涉及分层抽样的解析：310【解析】根据分层抽样的方法，可得2361854x y ==，解得1,3x y ==，所以若从高校,B C 抽取的人中选2人作专题发言，共有10种情况，则这二人都来自高校C 共有3种情况，所以概率为3()10P C =．点睛：本题主要考查了分层抽样和古典概型及其概率的计算问题，其中解答中涉及分层抽样的方法的计算，古典概型及其概率计算的公式的应用，试题比较基础，属于基础题，解答中牢记古典概型及其概率的求解是解答的关键．18．4【解析】循环依次为循环结束输出解析：4 【解析】循环依次为0120,21,1;1,22,2;2,24,3;x x k x x k x x k ============424,216,4;16,log 164,55;x x k x x k ========≥循环结束,输出4x =19．【解析】执行程序框图第一次循环；第二次循环；第三次循环；第十五次循环；退出循环输出故答案为【方法点睛】本题主要考查程序框图的循环结构流程图属于中档题解决程序框图问题时一定注意以下几点：(1)不要混淆解析：15S =【解析】执行程序框图，第一次循环，1S = ；第二次循环，2S = ；第三次循环，3S = ；... 第十五次循环，15S = ；退出循环，输出15S =，故答案为15.【方法点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.20．7【解析】设丢失的数据是点睛：函数关系是一种确定的关系相关关系是一种非确定的关系事实上函数关系是两个非随机变量的关系而相关关系是非随机变量与随机变量的关系如果线性相关则直接根据用公式求写出回归方程回解析：7【解析】设丢失的数据是,m 344413572x y m m =∴=∴⨯=+++⇒=Q 点睛：函数关系是一种确定的关系，相关关系是一种非确定的关系.事实上，函数关系是两个非随机变量的关系，而相关关系是非随机变量与随机变量的关系.如果线性相关，则直接根据用公式求ˆˆ,ab ，写出回归方程，回归直线方程恒过点(),x y . 三、解答题21．（1）75.5；（2）列联表见解析，没有. 【解析】试题分析：（1）各小矩形中点横坐标与纵坐标的乘积的和即是对此事关注的同学的物理期末平均分；（2）根据直方图求出列联表所需数据，即可完成22⨯列联表，利用公式()()()()()22n ad bc k a b c d a c b d -=++++求得2K ，与邻界值比较，即可得到结论.试题解析：（1）对此事关注的同学的物理期末平均分为(450.005550.005650.020⨯+⨯+⨯ 750.030850.030+⨯+⨯ 950.010)1075.5+⨯⨯=（分）．（2）①补充的22⨯列联表如下：()()()()()22n ad bc k a b c d a c b d -=++++ ()26083281216442040⨯⨯-⨯=⨯⨯⨯ 302.733.84111=≈<，所以没有95%以上的把握认为“对此事是否关注”与物理期末成绩是否优秀有关系．【方法点睛】本题主要考查频率分布直方图的应用以及独立性检验，属于中档题.独立性检验的一般步骤：（1）根据样本数据制成22⨯列联表；（2）根据公式()()()()()22n ad bc K a b a d a c b d -=++++计算2K 的值；(3) 查表比较2K 与临界值的大小关系，作统计判断.（注意：在实际问题中，独立性检验的结论也仅仅是一种数学关系，得到的结论也可能犯错误.）22．（1）ˆ 2.24yx =+（2）大约为19.4万亿吨【解析】【分析】（1）分别求出x 和y ，根据公式，求出ˆb和ˆa ，即可得出线性回归方程；（2）由（1）得ˆ 2.24yx =+，可估计出2019年该地区的粮食产量. 【详解】解：（1）由表中所给数据可得，91012118105x ++++==，2526312721265y ++++==，代入公式()()()51521ˆiii ii x x y y bx x ==--=-∑∑，解得ˆ 2.2b=，所以ˆˆ4ay bx =-=. 故所求的y 关于x 的线性回归直线方程为ˆ 2.24yx =+. （2）由题意，将7x =代入回归方程ˆ 2.24y x =+，可得，ˆ19.4y=. 所以预测2019年该地区的粮食产量大约为19.4万亿吨. 【点睛】本题考查求线性回归方程，以及根据回归方程解决实际问题，考查计算能力. 23．（Ⅰ）6；(Ⅱ)1?15200元. 【解析】试题分析：（1）频率近似概率及古典概型可求得()3P A 5=，由样本估计总体和，可知X 服从二项分布，EX=np.(2)由样本期望估计总体期望，得该自然村年均用电量约156 000度.由剩余电量可求得收益．试题解析：(Ⅰ)记在抽取的50户居民中随机抽取1户，其年用电量不超过600度为事件A ，则()3P A 5=. 由已知可得从该县山区居民中随机抽取10户，记其中年用电量不超过600度的户数为X ，X 服从二项分布，即3X ~B 10,5⎛⎫ ⎪⎝⎭，故()3E X 1065=⨯=. (Ⅱ)设该县山区居民户年均用电量为()E Y ，由抽样可得()78151371003005007009005205050505050E Y =⨯+⨯+⨯+⨯+⨯=则该自然村年均用电量约156 000度. 又该村所装发电机组年预计发电量为300000度，故该机组每年所发电量除保证正常用电外还能剩余电量约144 000度，能为该村创造直接收益1440000.8115200⨯＝元.24．77.02【解析】【分析】根据公式计算得到 3.53b ≈，13.48a =，$3.5313.48y x =+，再代入数据计算得到答案. 【详解】12221135781017.474.9545.43.5331821017.4154.4ni ii ni i x y nx yb x nx==--⨯⨯===≈-⨯-∑∑，故74.9 3.5317.413.48a y bx =-=-⨯=，故$3.5313.48y x =+. 当18x =时，$3.531813.4877.02y =⨯+=. 【点睛】本题考查了线性回归方程，意在考查学生的计算能力和应用能力. 25．（1）100（2）应从第3,4,5组中分别抽取3人，2人，1人. （3）45【解析】试题分析：（1）由题意第2组的人数为3550.07n =⨯⨯，即可求解该组织人数. （2）根据频率分布直方图，求得第3组，第4组，，第5组的人数，再根据分层抽样的方法，即可求解再第3,4,5组所抽取的人数.（3）记第3组的3名志愿者为123,,A A A ，第4组的2名志愿者为12,B B ，第5组的1名志愿者为1C ，列出所有基本事件的总数，得出事件所包含的基本事件的个数，利用古典概型，即可求解概率. 试题解析：（1）由题意第2组的人数为3550.07n =⨯⨯，得到100n =，故该组织有100人. （2）第3组的人数为0.06510030⨯⨯=，第4组的人数为0.04510020⨯⨯=，第5组的人数为0.02510010⨯⨯=，所以第3,4,5组共有名志愿者，所以利用分层抽样的方法在60名志愿者中抽取6名志愿者，每组抽取的人数分别为：第3组306360⨯=；第4组。

四川省成都市2020-2021学年高二上学期期末调研考试数学(理)试题

四川省成都市2020-2021学年高二上学期期末调研考试数学（理）试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．抛物线28y x =的准线方程是（）A ．2x =-B ．4x =-C ．2y =-D ．4y =-2．从某中学甲班随机抽取9名男同学测量他们的体重(单位：kg)，获得体重数据如茎叶图所示，对这些数据，以下说法正确的是A ．中位数为62B ．中位数为65C ．众数为62D ．众数为643．命题“0200,2x x R x ∃∈≤”的否定是 A ．不存在0200,2x x R x ∈>B ．0200,2x x R x ∃∈>C ．2(100)(80)7644x x x --+=D ．2,2x x R x ∀∈>4．容量为100的样本，其数据分布在[2]18,，将样本数据分为4组：[2,6),[6,10),[10,14),[14,18]，得到频率分布直方图如图所示，则下列说法不正确的是（）A ．样本数据分布在[6,10)的频率为0.32B ．样本数据分布在[10,14)的频数为40C ．样本数据分布在[2,10)的频数为40D ．估计总体数据大约有10%分布在[10,14)5．“46k <<”是“22164x y k k +=--为椭圆方程”是( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件6．已知函数2()log (3)f x x =+，若在[2,5]-上随机取一个实数0x ，则0()1f x ≥的概率为（） A ．37B ．47C ．57D ．677．在平面内，已知两定点,A B 间的距离为2，动点P 满足||||4PA PB +=.若060APB ∠=，则APB ∆的面积为A ．2B C ．D ．8．在2021年3月15日，某物价部门对本市5家商场某商品一天的销售额及其价格进行调查，5家商场的价格x 与销售额y 之间的一组数据如下表所示：由散点图可知，销售额y 与价格x 之间有较好的线性相关关系，且回归直线方程是3.2ˆˆy x a =-+，则ˆa =（）A ．24-B ．35.6C ．40D ．40.59．已知双曲线C ：22221(0,0)x y a b a b-=>>的左焦点为F ，右顶点为E ，过点F 且垂直于x 轴的直线与双曲线C 相交于不同的两点,A B ，若ABE ∆为锐角三角形，则双曲线C 的离心率的取值范围为（） A ．(1,2)B ．(1,2]C ．(2,3]D ．[2,3)10．阅读如图所示的程序，若执行循环体的次数为5，则程序中a 的取值范围是( )A ．56a ≤≤B ．56a <<C ．56a <≤D ．56a ≤<11．已知椭圆22:11612x y C +=的右焦点为F ，点(),P x y 在椭圆C 上.若点Q 满足1QF =且0QP QF ⋅=，则PQ 的最小值为( )A ．3B ．125CD ．112．设抛物线2:2C y x =的焦点为F ，过点()2,0M 的直线与抛物线C 相交于不同的两点A ，B ，与抛物线C 的准线相交于N 点，且3BF =，记ANF 与BNF 的面积分别为1S ，2S ，则12S S =( ) A ．710B ．45C ．47D ．23二、填空题13．若直线()0y kx k =>为双曲线221x y -=的一条渐近线，则k =____________. 14．我校共有师生2400人，现用分层抽样的方法，从所有师生中抽取一个容量为160的样本，已知从学生中抽取的人数为150，那么该学校的教师人数是 . 15．如图所示的程序框图的算法思路源于宋元时期数学名著《算法启蒙》中的“松竹并生”问题.若输入的a ，b 的值分别为7，3，则输出的n 的值为____________.16．若经过坐标原点O 的直线l 与圆22430x y y +-+=相交于不同的两点A ，B ，则弦AB 的中点M 的轨迹方程为____________.三、解答题17．甲袋中有1只黑球，3只红球；乙袋中有2只黑球，1只红球. (1)从甲袋中任取两球，求取出的两球颜色不相同的概率； (2)从甲，乙两袋中各取一球，求取出的两球颜色相同的概率.18．已知命题p ：若关于x 的方程x 2＋2mx －4m －3＝0无实数根，则－3＜m ＜－1；命题q ：若关于x 的方程x 2＋tx ＋1＝0有两个不相等的正实数根，则t ＜－2. (1)写出命题p 的否命题r ，并判断命题r 的真假； (2)判断命题“p 且q”的真假，并说明理由． 19．阅读如图所示的程序框图，解答下列问题：(Ⅰ)求输入的x 的值分别为1-，2时，输出的()f x 的值．(Ⅱ)根据程序框图，写出函数()()f x x R ∈的解析式，并求当关于x 的方程()0f x k -=有三个互不相等的实数解时，实数k 的取值范围．20．已知以坐标原点O 为圆心的圆与抛物线C ：22(0)y px p =>相交于不同的两点,A B ，与抛物线C 的准线相交于不同的两点,D E ，且4AB DE ==.（1）求抛物线C 的方程；（2）若不经过坐标原点O 的直线l 与抛物线C 相交于不同的两点,M N ，且满足OM ON ⊥.证明直线l 过x 轴上一定点Q ，并求出点Q 的坐标.21．一网站营销部为统计某市网友2021年12月12日在某网店的网购情况，随机抽查了该市60名网友在该网店的网购金额情况，如下表：若将当日网购金额不小于2千元的网友称为“网购达人”，网购金额小于2千元的网友称为“网购探者”.已知“网购达人”与“网购探者”人数的比例为2：3.（1）确定,,,x y p q 的值，并补全频率分布直方图；（2）试根据频率分布直方图估算这60名网友当日在该网店网购金额的平均数和中位数；若平均数和中位数至少有一个不低于2千元，则该网店当日被评为“皇冠店”，试判断该网店当日能否被评为“皇冠店”.22．已知动点M 到定点()F 的距离和它到直线:3m x =-M 的轨迹为曲线C . (1)求曲线C 的方程；(2)若直线11:l y kx t =+与曲线C 相交于不同的两点A ，B ，直线()2212:l y kx t t t =+≠与曲线C 相交于不同的两点D ，E ，且AB DE =，求以A ，B ，D ，E 为顶点的凸四边形的面积S 的最大值.参考答案1．A【解析】抛物线28y x =,满足22y px =，所以4p =，则22p=. 所以准线方程是22px =-=-. 故选A. 2．C 【解析】∵由茎叶图得到所有数据从小到大排为53,55,62,62,64,65,71,72,73 ∴中位数为64，众数为62 故选C 3．D 【解析】命题0200,2x x R x ∃∈≤的否定是2,2x x R x ∀∈>故选D 4．D 【分析】根据频率分布直方图对给出的四个选项逐一分析、判断后可得结果．【详解】对于A ，由图可得样本数据分布在[)6,10的频率为0.0840.32⨯=，所以A 正确．对于B ，由图可得样本数据分布在[)10,14的频数为()1000.1440⨯⨯=，所以B 正确．对于C ，由图可得样本数据分布在[)2,10的频数为()1000.020.08440⨯+⨯=，所以C 正确.对于D ，由图可估计总体数据分布在[)10,14的比例为0.140.440%⨯==，故D 不正确．故选D ．【点睛】本题考查频率分布直方图的应用，考查识图和用图解题的能力，解题时容易出现的错误是误认为图中小长方形的高为频率，求解时要注意这一点．5．B 【解析】若22164x y k k +=--表示椭圆，则60,40k k ->->，且64k k -≠- ∴45k <<或者56k故46k <<是22164x y k k +=--为椭圆方程的必要不充分条件故选B 6．D 【解析】令()1f x ≥得32x +≥，即1x ≥-，由几何概型性质可知概率()()516527P --==-- 故选D 7．B 【解析】在平面内，已知两定点A ，B 间的距离为2，动点P 满足4PA PB +=，所以动点P 在以A,B 为焦点的椭圆上，其中24,22,2,1a c a c ==∴== 由余弦定理可得：22222()3AB PA PB PAPB cos APB PA PB PAPB =+-∠=+-，整理得:4163PA PB =-，解得：4PAPB =.则APB 的面积为11422PAPBsin APB ∠=⨯=故选B. 8．C 【解析】由题可知89.51010.512105x ++++==121086485y ++++==∵ 3.2ˆy x a=-+ ∴ 3.2 3.2ˆ10840ax y =+=⨯+= 故选C点睛：本题看出回归分析的应用，本题解题的关键是求出样本中心点，根据样本中心点代入求出ˆa的值，本题是一个基础题；求回归直线方程的一般步骤：①作出散点图（由样本点是否呈条状分布来判断两个量是否具有线性相关关系），若存在线性相关关系；②求回归系数；③写出回归直线方程，并利用回归直线方程进行预测说明. 9．A 【解析】双曲线2222:1(0,0)x y C a b a b-=>>右顶点为E ，左焦点为F ，EF a c =+，过点F 作垂直于x 轴的直线与双曲线相交于,A B 两点，则212b AB a= ∵若EAB ∆为锐角三角形，只要FEA ∠为锐角，即12AB EF < ∴2b a c a<+，即222c a a ac -<+即220e e --< ∴()1,2e ∈ 故选A点睛：解决双曲线的离心率的求值及范围问题其关键就是确立一个关于,,a b c 的方程或不等式，再根据,,a b c 的关系消掉b 得到,a c 的关系式，而建立关于,,a b c 的方程或不等式，要充分利用双曲线的几何性质、点的坐标的范围等. 10．D 【解析】执行程序：0,1,01,2,2S i S i a ===+=≤； 3,3,3S i a ==≤； 6,44S i a ==≤，；10,5,5S i a ==≤； 15,6,6S i a ==>，共执行了5次循环体，结束循环，所以56a ≤<. 故选D. 11．C 【解析】根据题意得：()2,0F ,由0QP QF ⋅=，得QP QF ⊥，所以PQ PF ==又因为422PF ≥-=.所以4PQ ≥-=故选C. 12．A 【解析】抛物线22y x =的焦点为F (12,0),准线方程为x =−12, 分别过A . B 作准线的垂线，垂足分别为D .E ，连结AD 、BE 、AF .genju设()()1122,,A x y B x y 、、,直线AB 的方程为()2y k x =-,与22y x =联立消去y ，得()22224240k x k x k -++=,所以212122424k x x x x k++==，，∵|BF |=2,∴根据抛物线的定义,得|BF |=|BE |=2x +12=3,解得2x =52. 由此可得12485x x ==,所以|AD |=1x +12=2110， ∵△CAD 中,BE ∥AD ,∴1221710310S AN AD S BN BE ====.故选A.点睛：1.凡涉及抛物线上的点到焦点距离时，一般运用定义转化为到准线距离处理． 2．若()00,P x y 为抛物线22(0)y px p =>上一点，由定义易得02pPF x =+；若过焦点的弦AB AB 的端点坐标为()()1122,,,A x y B x y ，则弦长为1212,AB x x p x x =+++可由根与系数的关系整体求出,本题212y y p =-就是由韦达定理得到；若遇到其他标准方程，则焦半径或焦点弦长公式可由数形结合的方法类似地得到． 13．1 【解析】∵双曲线221x y -= ∴1,1a b == ∴渐近线方程为by x x a=±=± ∵直线(0)y kx k =>为双曲线221x y -=的一条渐近线∴1k = 故答案为1 14．150 【解析】试题分析：该校教师人数为2400×160150160-＝150(人)．考点：分层抽样方法. 15．3 【解析】输入7,3,1a b n ===进入循环，21,2622a a ab b =+===，不满足a b ≤ 执行循环，6312,,21224a n n a ab b =+==+===，不满足a b ≤ 执行循环，18913,,22428a n n a ab b =+==+===，满足a b ≤，输出3n = 故答案为316．()2231122x y y ⎛⎫+-=<≤⎪⎝⎭【解析】设当直线l 的方程为()()1122,,y kx A x y B x y =、、，与圆联立方程组,消去y 可得：()221430k xkx +-+=，由()22164130k k=-+⨯>,可得23k>.由韦达定理,可得12241kx x k +=+， ∴线段AB 的中点M 的轨迹C 的参数方程为2222121k x k k y k ⎧=⎪⎪+⎨⎪=⎪+⎩,其中23k >， ∴线段AB 的中点M 的轨迹C 的方程为：()2211x y +-=,其中322y <≤. 故答案为()22311(2)2x y y +-=<≤. 点睛：求轨迹方程的常用方法：（1）直接法：直接利用条件建立x ，y 之间的关系F (x ，y )＝0．（2）待定系数法：已知所求曲线的类型，求曲线方程．（3）定义法：先根据条件得出动点的轨迹是某种已知曲线，再由曲线的定义直接写出动点的轨迹方程．（4）代入(相关点)法：动点P (x ，y )依赖于另一动点Q (x 0，y 0)的变化而运动，常利用代入法求动点P (x ，y )的轨迹方程．17．(1) 从甲袋中任取两球，取出的两球颜色不相同的概率为12;(2) 从甲，乙两袋中各取一球，取出的两球颜色相同的概率为512. 【解析】试题分析：（1）先求出取出两球的种数，再根据分类和分步计数原理求出一只黑球一只红球的种数，根据概率公式计算即可；（2）分为同是黑色，红色，根据分类和分步计数原理即可求出取得两球颜色相同的种数，根据概率公式计算即可．试题解析：（1）将甲袋中的1只黑球，3只红球分别记为123,,,a b b b .从甲袋中任取两球，所有可能的结果有{}{}{}{}{}{}123121323,,,,,,,,,,,a b a b a b b b b b b b 共6种.其中两球颜色不相同的结果有{}{}{}123,,,,,a b a b a b 共3种.记“从甲袋中任取两球，取出的两球的颜色不相同”为事件A ，则()3162P A == ∴从甲袋中任取两球，取出的两球的颜色不相同的概率为12. （2）将甲袋中的1只黑球，3只红球分别记为123,,,a b b b ，将乙袋中的2只黑球，1只红球分别记为121,,A A B 从甲、乙两袋中各取一球的所有可能结果有{}{}{}{}{}{}121111211,,,,,;,,,,,;a A a A a B b A b A b B{}{}{}212221,,,,,;b A b A b B {}{}{}313231,,,,,b A b A b B 共12种.其中两球颜色相同的结果有{}{}{}{}{}12112131,,,,,,,,,a A a A b B b B b B 共5种记“从甲、乙两袋中各取一球，取出的两球的颜色相同”为事件B ，则()512P B = ∴从甲、乙两袋中各取一球，取出的两球的颜色相同的概率为512. 18．（1）见解析；（2）见解析【分析】（1）若命题p 为真命题，解得实数m 的取值范围，对其求补集.（2）命题“p 且q”为真，需要p ，q 都是真命题，当p ，q 一真一假或都假时，则“p 且q”为假．【详解】(1)命题p 的否命题r ：若关于x 的方程x 2＋2mx －4m －3＝0有实数根，则m≤－3或m≥－1.∵关于x 的方程x 2＋2mx －4m －3＝0有实数根，∴Δ≥0.∵Δ＝(2m)2－4×(－4m －3)＝4m 2＋16m ＋12≥0，化简，得m 2＋4m ＋3≥0. 解得m≤－3或m≥－1. ∴命题r 为真命题．(2)对于命题p ：若关于x 的方程x 2＋2mx －4m －3＝0无实数根，则Δ＝(2m)2－4×(－4m －3)＝4m 2＋16m ＋12＜0. 化简，得m 2＋4m ＋3＜0.解得－3＜m ＜－1. ∴命题p 为真命题．对于命题q ：关于x 的方程x 2＋tx ＋1＝0有两个不相等的正实数根，有240t t ⎧->⎨->⎩，解得t＜－2.∴命题q 为真命题． ∴命题“p 且q”为真命题．【点睛】本题考查四种命题关系及复合命题真假的判断，属于基础题. 19．（1）见解析（2）(0,1). 【解析】试题分析：（1）根据框图中条件语句，判断变量执行哪个函数，计算求解即可；（2）由框图可知()22,02,021,0x x f x x x x x ⎧<⎪==⎨⎪-+>⎩，分析分段函数的单调性，进而可得解. 试题解析：(1)当输入的x 的值为1-时，输出的()1122f x -==. 当输入的x 的值为2时，输出的()222211f x =-⨯+=.(2)根据程序框图，可得()22,02,021,0x x f x x x x x ⎧<⎪==⎨⎪-+>⎩，当0x <时，()2xf x =，此时()f x 单调递增，且()01f x <<；当0x =时，()2f x =；当0x >时，()()22211f x x x x =-+=-在()0,1上单调递减，在()1,+∞上单调递增，且()0f x ≥.结合图象，知当关于x 的方程()0f x k -=有三个不同的实数解时，实数k 的取值范围为()0,1.20．（1）24y x =；（5.2) 直线l 过定点()4,0Q .【解析】试题分析：（1）由AB DE =，得,A B 两点所在的直线方程为2px =，进而根据长度求得p ；（2）设直线l 的方程为()0x my n n =+≠，()()1122,,,M x y N x y ，与抛物线联立得2440y my n --=，由OM ON ⊥得12120x x y y +=，进而利用韦达定理求解即可.试题解析：（1）由已知，4AB DE ==，则,A B 两点所在的直线方程为2p x = 则24AB p ==，故2p = ∴抛物线C 的方程为24y x =.（2）由题意，直线l 不与y 轴垂直，设直线l 的方程为()0x my n n =+≠，()()1122,,,M x y N x y .联立24x my n y x=+⎧⎨=⎩消去x ，得2440y my n --=.∴216160m n ∆=+>，124y y m +=，124y y n =-，∵OM ON ⊥，∴12120x x y y +=又2211224,4y x y x ==，∴22121216y y x x =∴222121212124016y y x x y y y y n n +=+=-=解得0n =或4n =而0n ≠，∴4n =（此时216160m n ∆=+>） ∴直线l 的方程为4x my =+，故直线l 过x 轴上一定点()4,0Q .点睛：定点、定值问题通常是通过设参数或取特殊值来确定“定点”是什么、“定值”是多少，或者将该问题涉及的几何式转化为代数式或三角问题，证明该式是恒定的. 定点、定值问题同证明问题类似，在求定点、定值之前已知该值的结果，因此求解时应设参数，运用推理，到最后必定参数统消，定点、定值显现. 21．(1)见解析（2）见解析【解析】试题分析：(1)由频数之和为60，“网购达人”与“网购探者”人数的比例为2：3，列出关于,x y 的方程组，由此能求出,,,x y p q 的值，并补全频率分布直方图；（2）根据频率分布直方图分别计算平均数和中位数，再与题设条件做比较，即可判断.试题解析：(1)由题意，得3915186018239153x y y x +++++=⎧⎪+⎨=⎪+++⎩化简，得1523x y x y+=⎧⎨=⎩，解得9,6x y == ∴0.15,0.1p q ==补全的频率分布直方图如图所示：（2）设这60名网友的网购金额的平均数为x ，则0.250.050.750.15 1.250.15 1.750.25 2.250.3 2.750.1 1.7x =⨯+⨯+⨯+⨯+⨯+⨯=（千元）又∵0.050.150.150.35++=，0.150.30.5=， ∴这60名网友的网购金额的中位数为1.5+0.3=1.8（千元） ∵平均数1.72<，中位数1.82<，∴根据估算判断，该网店当日不能被评为“皇冠店”.22．（1）曲线C 的方程为2214x y +=；（2）四边形ABDE 的面积S 的最大值为4. 【解析】试题分析：（1）设(),M x y ，根据题意，动点M的轨迹为集合{|MF P M d==，=，化简求解即可；（2）联立122440y kx t x y =+⎧⎨+-=⎩消去y ，得()22211148440k x kt x t +++-=，利用两点距离公式及韦达定理求得AB=，同理可得DE =，由AB DE =得120t t +=，设两平行线,AB DE 间的距离为r =S AB r =⋅代入求解即可.试题解析：（1）设(),M x y ，动点到直线m：3x =-的距离为d ，根据题意，动点M的轨迹为集合{|MF P M d==2=化简，得2214x y +=∴曲线C 的方程为2214x y +=.（2）设()()1122,,,A x y B x y 联立122440y kx t x y =+⎧⎨+-=⎩消去y ，得()22211148440kxkt x t +++-=.∴()221112221122164108144414k t kt x x k t x x k ⎧∆=-+>⎪⎪⎪+=-⎨+⎪⎪-=-⎪+⎩， ∴AB ==同理可得DE =∵AB DE =，∴2212t t =又12t t ≠，∴120t t +=由题意，以,,,A B D E 为顶点的凸四边形为平行四边形设两平行线,AB DE 间的距离为r ，则 ∵120t t +=，∴r =则S AB r =⋅==∵()2221124128414kt t S k -+=≤=+（当且仅当221142k t +=时取等号，此时满足21160t ∆=>），∴四边形ABDE 的面积S 的最大值为4.。

2020-2021成都七中(高新校区)高二数学上期末第一次模拟试题含答案

2020-2021成都七中(高新校区)高二数学上期末第一次模拟试题含答案一、选择题1．在区间[]0,1上随机取两个数x ，y ，记P 为事件“23x y +≤”的概率，则(P = ) A ．23B ．12C ．49 D ．292．如图，ABC ∆和DEF ∆都是圆内接正三角形，且//BC EF ，将一颗豆子随机地扔到该圆内，用A 表示事件“豆子落在ABC ∆内”，B 表示事件“豆子落在DEF ∆内”，则(|)P B A =（）A ．334πB ．32πC ．13D ．233．已知一组数据的茎叶图如图所示，则该组数据的平均数为（）A ．85B ．84C ．83D ．814．执行如图所示的程序框图，若输入8x =，则输出的y 值为（）A ．3B ．52C ．12D ．34-5．如果数据121x +、221x +、、21n x +的平均值为5，方差为16，则数据：153x -、253x -、、53n x -的平均值和方差分别为（）A ．1-，36B ．1-，41C ．1，72D ．10-，1446．若执行如图所示的程序框图，则输出S 的值为( )A ．10072015B ．10082017C ．10092019D ．101020217．如果数据12,,,n x x x 的平均数为x ，方差为28，则152x +，252x +，…，52n x +的平均数和方差分别为（）A ．x ，28B ．52x +，28C ．52x +，2258⨯D ．x ，2258⨯8．已知具有线性相关的两个变量,x y 之间的一组数据如下表所示：x0 1 2 3 4 y 2.24.34.54.86.7若,x y 满足回归方程 1.5ˆˆyx a =+，则以下为真命题的是（） A ．x 每增加1个单位长度，则y 一定增加1.5个单位长度 B ．x 每增加1个单位长度，y 就减少1.5个单位长度 C ．所有样本点的中心为(1,4.5) D ．当8x =时，y 的预测值为13.59．运行如图所示的程序框图，若输出的S 的值为480，则判断框中可以填( )A ．60i >B ．70i >C ．80i >D ．90i >10．从0，1，2，3这四个数中任取两个不同的数组成一个两位数，则这个两位数是偶数的概率为（） A ．27B ．57C ．29D ．5911．如图，在圆心角为直角的扇形OAB 中，分别以,OA OB 为直径作两个半圆，在扇形OAB 内随机取一点，则此点取自阴影部分的概率是（）A ．21π-B ．122π- C ．2πD ．1π12．袋中装有红球3个、白球2个、黑球1个，从中任取2个，则互斥而不对立的两个事件是( )A ．至少有一个白球；都是白球B ．至少有一个白球；至少有一个红球C ．至少有一个白球；红、黑球各一个D ．恰有一个白球；一个白球一个黑球二、填空题13．已知实数]9[1x ∈，，执行如图所示的流程图，则输出的x 不小于55的概率为________．14．某同学同时掷两颗骰子，得到点数分别为a ，b ，则双曲线2222x y 1a b -=的离心率e 5>的概率是______．15．某单位有职工900人，其中青年职工450人，中年职工270人，老年职工180人，为了了解该单位职工的健康情况，用分层抽样的方法从中抽取样本.若样本中的青年职工为10人，则样本容量为________．16．某公司的广告费支出x 与销售额y （单位：万元）之间有下列对应数据：由资料显示y 对x 呈线性相关关系。

2020-2021成都市高三数学上期末模拟试题(带答案)

24．等差数列{an}的前n项和为Sn，且 =9，S6=60．
（I）求数列{an}的通项公式；
（II）若数列{bn}满足bn+1﹣bn= （n∈N+）且b1=3，求数列的前n项和Tn．
25．设为等差数列的前项和，公差，，且 .
（1）求的通项公式；
（2）设数列的前项和为，若，对恒成立，求 .
解析：
【解析】
【分析】
根据题意，化简得，利用式相加，得到，进而得到，即可求解结果.
【详解】
因为，所以，
所以，
将以上各式相加，得，
又，所以，解得或 .
【点睛】
本题主要考查了数列的递推关系式应用，其中解答中利用数列的递推关系式，得到关于数列首项的方程求解是解答的关键，着重考查了推理与运算能力，属于中档试题.
10．B
解析：B
【解析】
【分析】
作出不等式对应的可行域，当目标函数过点时，取最小值，即，可求得的值，当目标函数过点时，取最大值，即可求出答案.
【详解】
作出不等式对应的可行域，如下图阴影部分，目标函数可化为，
联立，可得，当目标函数过点时，取最小值，则，解得，
联立，可得，即，当目标函数过点时，取最大值， .
故选：A．
【点睛】
本题主要考查了等差数列的性质．考查了学生的推理能力和运算能力．
3．D
解析：D
【解析】
【分析】
作出不等式组所表示的可行域，根据目标函数的几何意义，利用直线斜率的几何意义以及数形结合进行求解即可.
【详解】
目标函数，
设，则的几何意义是区域内的点与定点连线的斜率，

2020-2021成都七中初中学校高二数学上期末一模试卷含答案

2020-2021成都七中初中学校高二数学上期末一模试卷含答案一、选择题1．如图，一个边长为2的正方形里有一个月牙形的图案，为了估算这个月牙形图案的面积，向这个正方形里随机投入500粒芝麻，经过统计，落在月牙形图案内的芝麻有150粒，则这个月牙图案的面积约为（）A ．35B ．45C ．1D ．652．已知一组数据的茎叶图如图所示，则该组数据的平均数为（）A ．85B ．84C ．83D ．813．下面的程序框图表示求式子32×35×311×323×347×395的值, 则判断框内可以填的条件为（）A ．90?i ≤B ．100?i ≤C ．200?i ≤D ．300?i ≤4．《九章算术》是我国古代的数学名著，体现了古代劳动人民的数学智慧，其中第六章“均输”中，有一竹节容量问题，某教师根据这一问题的思想设计了如图所示的程序框图，若输出m 的值为67，则输入a 的值为( )A ．7B ．4C ．5D ．115．下列赋值语句正确的是( ) A ．s ＝a ＋1 B ．a ＋1＝s C ．s －1＝a D ．s －a ＝16．预测人口的变化趋势有多种方法，“直接推算法”使用的公式是()0 1nn P P k =+（1k >-），n P 为预测人口数，0P 为初期人口数，k 为预测期内年增长率，n 为预测期间隔年数．如果在某一时期有10k -<<，那么在这期间人口数 A ．呈下降趋势B ．呈上升趋势C ．摆动变化D ．不变 7．执行如图所示的程序框图，若输入的a ，b ，c 依次为()sin sin αα，()cos sin αα，()sin cos αα，其中,42ππα⎛⎫∈⎪⎝⎭，则输出的x 为( )A ．()cos cos ααB ．()sin sin ααC ．()cos sin ααD ．()sin cos αα8．为了解某社区居民的家庭年收入和年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：收入x 万 8.3 8.6 9.9 11.1 12.1 支出y 万5.97.88.18.49.8根据上表可得回归直线方程ˆˆˆybx a =+，其中0.78b ∧=，a y b x ∧∧=-元，据此估计，该社区一户收入为16万元家庭年支出为（） A ．12.68万元B ．13.88万元C ．12.78万元D ．14.28万元9．已知具有线性相关的两个变量,x y 之间的一组数据如下表所示：x0 1 2 3 4 y 2.24.34.54.86.7若,x y 满足回归方程 1.5ˆˆyx a =+，则以下为真命题的是（） A ．x 每增加1个单位长度，则y 一定增加1.5个单位长度 B ．x 每增加1个单位长度，y 就减少1.5个单位长度 C ．所有样本点的中心为(1,4.5) D ．当8x =时，y 的预测值为13.510．“微信抢红包”自2015年以来异常火爆，在某个微信群某次进行的抢红包活动中，若所发红包的总金额为8元，被随机分配为1.72元，1.83元，2.28元，1.55元，0.62元， 5份供甲、乙等5人抢，每人只能抢一次，则甲、乙二人抢到的金额之和不低于3元的概率是（） A ．310B ．25C ．12D ．3511．运行如图所示的程序框图，若输出的S 的值为480，则判断框中可以填( )A ．60i >B ．70i >C ．80i >D ．90i >12．根据表中提供的全部数据，用最小二乘法得出y 关于x 的线性回归方程是9944y x =+$，则表中m 的值为( ) x 8 10 1112 14 y2125m2835A ．26B ．27C ．28D ．29二、填空题13．若正方体1111ABCD A B C D -的棱长为3，E 为正方体内任意一点，则AE 的长度大于3的概率等于_________.14．若正方形ABCD 的边长为4, E 为四边形上任意一点,则AE 的长度大于5的概率等于______15．北京市某银行营业点在银行大厅悬挂着不同营业时间段服务窗口个数的提示牌，如图所示. 设某人到达银行的时间是随机的，记其到达银行时服务窗口的个数为X ，则()E X =______________．16．已知2件次品和3件正品放在一起，现需要通过检测将其区分，每次随机检测一件产品，检测后不放回，直到检测出2件次品或者检测出3件正品时检测结束，则恰好检测四次停止的概率为_____（用数字作答）．17．已知实数]9[1x ∈，，执行如图所示的流程图，则输出的x 不小于55的概率为________．18．在[1,1]-上随机地取一个数k ，则事件“直线y kx =与圆22(5)9x y -+=相离”发生的概率为_______。

2020-2021成都武侯外国语学校高二数学上期末模拟试题(及答案)

2020-2021成都武侯外国语学校高二数学上期末模拟试题(及答案)一、选择题1．将A，B，C，D，E，F这6个字母随机排成一排组成一个信息码，则所得信息码恰好满足A，B，C三个字母连在一起，且B在A与C之间的概率为（）A．112B．15C．115D．2152．我国古代数学著作《九章算术》中，其意是：“今有器中米，不知其数，前人取半，中人三分取一，后人四分取一，余米一斗五升．问：米几何？右图是源于其思想的一个程序框图，若输出的2S （单位：升），则输入k的值为A．6 B．7 C．8 D．93．《九章算术》是我国古代的数学名著，体现了古代劳动人民的数学智慧，其中第六章“均输”中，有一竹节容量问题，某教师根据这一问题的思想设计了如图所示的程序框图，若输出m的值为67，则输入a的值为()A．7B．4C．5D．114．把化为五进制数是（）A．B．C．D．5．在长为10cm 的线段AB 上任取一点C ，作一矩形，邻边长分別等于线段AC 、CB 的长，则该矩形面积小于216cm 的概率为（） A ．23B ．34C ．25D ．136．为了解某社区居民的家庭年收入和年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：收入x 万 8.3 8.6 9.9 11.1 12.1 支出y 万5.97.88.18.49.8根据上表可得回归直线方程ˆˆˆybx a =+，其中0.78b ∧=，a y b x ∧∧=-元，据此估计，该社区一户收入为16万元家庭年支出为（） A ．12.68万元B ．13.88万元C ．12.78万元D ．14.28万元7．按照程序框图（如图所示）执行，第3 个输出的数是（）A ．6B ．5C ．4D ．38．设数据123,,,,n x x x x L 是郑州市普通职工*(3,)n n n N ≥∈个人的年收入，若这n 个数据的中位数为x ，平均数为y ，方差为z ，如果再加上世界首富的年收入1n x +，则这1n +个数据中，下列说法正确的是（）A ．年收入平均数大大增大，中位数一定变大，方差可能不变B ．年收入平均数大大增大，中位数可能不变，方差变大C ．年收入平均数大大增大，中位数可能不变，方差也不变D ．年收入平均数可能不变，中位数可能不变，方差可能不变9．如图，边长为2的正方形有一内切圆.向正方形内随机投入1000粒芝麻，假定这些芝麻全部落入该正方形中，发现有795粒芝麻落入圆内，则用随机模拟的方法得到圆周率π的近似值为( )A ．3.1B ．3.2C ．3.3D ．3.410．甲、乙两位同学在高一年级的5次考试中，数学成绩统计如茎叶图所示，若甲、乙两人的平均成绩分别是12,x x ，则下列叙述正确的是（）A ．12x x >，乙比甲成绩稳定B ．12x x >，甲比乙成绩稳定C ．12x x <，乙比甲成绩稳定D ．12x x <，甲比乙成绩稳定11．我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”，如40337=+.（注：如果一个大于1的整数除1和自身外无其他正因数，则称这个整数为素数.）在不超过11的素数中，随机选取2个不同的数，其和小于等于10的概率是（） A ．12B ．13C ．14D ．1512．已知某班级部分同学一次测验的成绩统计如图，则其中位数和众数分别为( )A ．92，94B ．92，86C ．99，86D ．95，91二、填空题13．小明通过做游戏的方式来确定接下来两小时的活动，他随机地往边长为1的正方形内扔一颗豆子，若豆子到各边的距离都大于14，则去看电影；若豆子到正方形中心的距离大于12，则去打篮球；否则，就在家写作业则小明接下来两小时不在家写作业的概率为______.(豆子大小可忽略不计)14．我国元朝著名数学家朱世杰在《四元玉鉴》中有一首诗：“我有一壶酒，携着游春走，遇店添一倍，逢友饮一斗，店友经三处，没有壶中酒，借问此壶中，当原多少酒？”用程序框图表达如图所示，即最终输出的0x=，问一开始输入的x=______斗.遇店添一倍，逢友饮一斗，意思是碰到酒店就把壶里的酒加1倍，碰到朋友就把壶里的酒喝一斗，店友经三处，意思是每次都是遇到店后又遇到朋友，一共是3次．15．已知某产品连续4个月的广告费i x（千元）与销售额i y（万元）（1,2,3,4i=）满足4115 iix ==∑，4112 iiy ==∑，若广告费用x和销售额y之间具有线性相关关系，且回归直线方程为^y bx a=+，0.6b=，那么广告费用为5千元时，可预测的销售额为___万元. 16．如图所示的程序框图，输出的S的值为()A．12B．2C．1-D．12-17．如图是一个算法的流程图，则输出的a的值是__________．18．某公司的班车在8:00，8:30发车，小明在7:50至8:30之间到达发车站乘坐班车，且到达发车站的时刻是随机的，则他等车时间不超过10分钟的概率是__________19．为了了解2100名学生早晨到校时间，计划采用系统抽样的方法从全体学生中抽取容量为100栋样本，则分段间隔为__________．20．向面积为20的ABC ∆内任投一点M ，则使MBC ∆的面积小于5的概率是__________．三、解答题21．近期，某公交公司分别推出支付宝和徽信扫码支付乘车活动，活动设置了一段时间的推广期，由于推广期内优惠力度较大，吸引越来越多的人开始使用扫码支付．某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次，用x 表示活动推出的天数，y 表示每天使用扫码支付的人次(单位：十人次)，统计数据如表l 所示：表1根据以上数据，绘制了如右图所示的散点图．(1)根据散点图判断，在推广期内，(c ，d 均为大于零的常数)哪一个适宜作为扫码支付的人次y 关于活动推出天数x 的回归方程类型?(给出判断即可，不必说明理由)；(2)根据(1)的判断结果及表1中的数据，求y 关于x 的回归方程，并预测活动推出第8天使用扫码支付的人次；参考数据：其中参考公式：对于一组数据，其回归直线的斜率和截距的最小二乘估计公式分别为：.22．为了了解某省各景区在大众中的熟知度，随机从本省1565:岁的人群中抽取了n 人，得到各年龄段人数的频率分布直方图如图所示，现让他们回答问题“该省有哪几个国家AAAAA 级旅游景区？”，统计结果如下表所示：组号分组回答正确的人数回答正确的人数占本组的频率第1组 [)1525， a0.5第2组 [)2535， 18x第3组 [)3545， b 0.9 第4组 [)4555， 9 0.36第5组[)5565，3y（1）分别求出,,,a b x y 的值；（2）从第2,3,4组回答正确的人中用分层抽样的方法抽取6人，求第2,3,4组每组抽取的人数；（3）在（2）中抽取的6人中随机抽取2人，求所抽取的人中恰好没有年龄段在[)3545，的概率23．为了减轻家庭困难的高中学生的经济负担，让更多的孩子接受良好的教育，国家施行高中生国家助学金政策，普通高中国家助学金平均资助标准为每生每年1500元，具体标准由各地结合实际在1000元至3000元范围内确定，可以分为两或三档.各学校积极响应政府号召，通过各种形式宣传国家助学金政策.为了解某高中学校对国家助学金政策的宣传情况，拟采用随机抽样的方法抽取部分学生进行采访调查.（1）若该高中学校有2000名在校学生，编号分别为0001，0002，0003，…，2000，请用系统抽样的方法，设计一个从这2000名学生中抽取50名学生的方案.（写出必要的步骤）（2）该校根据助学金政策将助学金分为3档，1档每年3000元，2档每年2000元，3档每年1000元，某班级共评定出3个1档，2个2档，1个3档，若从该班获得助学金的学生中选出2名写感想，求这2名同学不在同一档的概率.24．一个袋中装有四个形状大小完全相同的球，球的编号分别为1，2，3，4. （1）从袋中随机抽取两个球，求取出的球的编号之和不大于4的概率；（2）先从袋中随机取一个球，该球的编号为m ，将球放回袋中，然后再从袋中随机取一个球，该球的编号为n ，求2n m <+的概率25．从某校随机抽取100名学生，获得了他们一周课外阅读时间（单位：小时）的数据，整理得到数据分组及频数分布表和频率分布直方图：（1）从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于12小时的概率；（2）求频率分布直方图中的a ，b 的值；（3）假设同一组中的每个数据可用该组区间的中点值代替，试估计样本中的100名学生该周课外阅读时间的平均数在第几组（只需写出结论）26．某校高一举行了一次数学竞赛，为了了解本次竞赛学生的成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100）作为样本（样本容量为n ）进行统计，按照[)50,60，[)60,70，[)70,80，[)80,90，[]90,100的分组作出频率分布直方图，已知得分在[)50,60，[]90,100的频数分别为8，2．（1）求样本容量n 和频率分布直方图中的,x y 的值；（2）估计本次竞赛学生成绩的中位数；（3）在选取的样本中，从竞赛成绩在80分以上（含80分）的学生中随机抽取2名学生，求所抽取的2名学生中至少有一人得分在[]90,100内的概率．【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【解析】【分析】将A ，B ，C 三个字捆在一起，利用捆绑法得到答案. 【详解】由捆绑法可得所求概率为242466A A 1A 15P ==. 故答案为C 【点睛】本题考查了概率的计算，利用捆绑法可以简化运算.2．C解析：C 【解析】分析：执行程序框图，得到输出值4k S =，令24k=，可得8k =. 详解：阅读程序框图，初始化数值1,n S k ==，循环结果执行如下：第一次：14n =<成立，2,22k k n S k ==-=；第二次：24n =<成立，3,263k k k n S ==-=；第三次：34n =<成立，4,3124k k k n S ==-=；第四次：44n =<不成立，输出24kS ==，解得8k =. 故选C.点睛：解决循环结构程序框图问题的核心在于：第一，要确定是利用当型还是直到型循环结构；第二，要准确表示累计变量；第三，要注意从哪一步开始循环，弄清进入或终止的循环条件、循环次数.3．C【解析】模拟程序框图的运行过程，如下：输入a ，23m a =-，1i =，()223349m a a =--=-；2i =，()2493821m a a =--=-； 3i =，()282131645m a a =--=-；4i =，()2164533293m a a =--=-；输出3293m a =-，结束；令329367a -=，解得5a =. 故选C.4．B解析：B 【解析】【分析】利用倒取余数法可得化为五进制数.【详解】因为所以用倒取余数法得323，故选：B. 【点睛】本题考查十进制数和五进制数之间的转化，利用倒取余数法可解决此类问题.5．C解析：C 【解析】【分析】根据几何概型的概率公式，设AC ＝x ，则BC ＝10﹣x ，由矩形的面积S ＝x （10﹣x ）＜16可求x 的范围，利用几何概率的求解公式求解．【详解】设线段AC 的长为xcm ，则线段CB 长为(10)cm x -，那么矩形面积为(10)16x x -<，2x <或8x >，又010x <<，所以该矩形面积小于216cm 的概率为42105=. 故选：C 【点睛】本题考查几何概型，考查了一元二次不等式的解法，明确测度比为长度比是关键，是中档题．解析：A 【解析】【分析】由已知求得 x ， y ，进一步求得$ a，得到线性回归方程，取16x =求得y 值即可．【详解】8.38.69.911.1512.1 10x +++=+=， 5.97.88.18.49.858y ++++==．又 0.78b =$，∴$ 80.78100.2a y bx --⨯===$． ∴$ 0.780.2y x =+．取16x =，得$ 0.78160.212.68y ⨯+==万元，故选A ．【点睛】本题主要考查线性回归方程的求法，考查了学生的计算能力，属于中档题．7．B解析：B 【解析】第一次输出1,A =第二次输出123A =+=，第三次输出325A =+= ，选B.8．B解析：B 【解析】∵数据x 1，x 2，x 3，…，x n 是郑州普通职工n (n ⩾3,n ∈N ∗)个人的年收入，而x n +1为世界首富的年收入则x n +1会远大于x 1，x 2，x 3，…，x n ，故这n +1个数据中，年收入平均数大大增大，但中位数可能不变，也可能稍微变大，但由于数据的集中程序也受到x n +1比较大的影响，而更加离散，则方差变大. 故选B9．B解析：B 【解析】【分析】由圆的面积公式得：S π=圆，由正方形的面积公式得：4S =正，由几何概型中的面积型结合随机模拟试验可得：7951000S S =圆正，得解．【详解】由圆的面积公式得：S π=圆，由正方形的面积公式得：4S =正，由几何概型中的面积型可得：7951000S S =圆正，所以79543.21000π⨯=≈，故选：B ．【点睛】本题考查了圆的面积公式、正方形的面积公式及几何概型中的面积型，属简单题．10．C解析：C 【解析】甲的平均成绩11(7378798793)825x =++++=，甲的成绩的方差22222211[(7382)(7882)(7982)(8782)(9382)]50.45s =-+-+-+-+-=；乙的平均成绩21(7989899291)885x =++++=，乙的成绩的方差22222221[(7988)(8988)(8988)(9288)(9188)]21.65s =-+-+-+-+-=.∴12x x <，乙比甲成绩稳定. 故选C .11．A解析：A 【解析】【分析】先列出不超过11的素数,再列举出随机选取2个不同的数的情况,进而找到和小于等于10的情况,即可求解【详解】不超过11的素数有:2,3,5,7,11,共有5个, 随机选取2个不同的数可能为:()2,3,()2,5,()2,7,()2,11,()3,5,()3,7,()3,11,()5,7,()5,11,()7,11,共有10种情况, 其中和小于等于10的有:()2,3,()2,5,()2,7,()3,5,()3,7,共有5种情况, 则概率为51102P ==, 故选:A 【点睛】本题考查列举法求古典概型的概率,属于基础题解析：B 【解析】由茎叶图可知，中位数为92，众数为86. 故选B.二、填空题13．【解析】【分析】根据题意画出图形求出写作业所对应的区域面积利用得到结果【详解】由题意可知当豆子落在下图中的空白部分时小明在家写作业大正方形面积；阴影正方形面积空白区域面积：根据几何概型可知小明不在家解析：5π4- 【解析】【分析】根据题意画出图形，求出写作业所对应的区域面积，利用()()1P A P A =-得到结果. 【详解】由题意可知，当豆子落在下图中的空白部分时，小明在家写作业∴大正方形面积111S =⨯=；阴影正方形面积1111224S =⨯= 空白区域面积：22111244S ππ-⎛⎫=⨯-= ⎪⎝⎭根据几何概型可知，小明不在家写作业的概率为：2514S P S π-=-= 本题正确结果：54π- 【点睛】本题考查几何概型中的面积型，属于基础题.14．【解析】【分析】模拟执行程序框图只要按照程序框图规定的运算方法逐次计算直到达到输出条件输出令即可得结果【详解】第一次输入执行循环体执行循环体执行循环体输出的值为0解得：故答案为【点睛】本题主要考查程解析：78【解析】模拟执行程序框图，只要按照程序框图规定的运算方法逐次计算，直到达到输出条件输出87x -，令870x -=即可得结果. 【详解】第一次输入x x =，1i =执行循环体，21x x =-，2i =，执行循环体，()221143x x x =--=-，3i =，执行循环体，()243187x x x =--=-，43i =>，输出87x -的值为0，解得：78x =，故答案为78．【点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.15．75【解析】【分析】计算然后将代入回归直线得从而得回归方程然后令x ＝5解得y 即为所求【详解】∵∴∵∴∴样本中心点为（3）又回归直线过（3）即3＝06×+解得＝所以回归直线方程为y ＝06x+令x ＝5时解析：75 【解析】【分析】计算x ，y ，然后将x ，y 代入回归直线得a ，从而得回归方程，然后令x ＝5解得y 即为所求．【详解】 ∵4115i i x ==∑，∴154x =， ∵4112i i y ==∑，∴1234y ==， ∴样本中心点为（154，3），又回归直线0.6ˆyx a =+过（154，3），即3＝0.6×154+a ，解得a ＝34，所以回归直线方程为y ＝0.6x +34，令x ＝5时，y ＝0.6×5+34＝3.75万元故答案为：3.75．【点睛】本题考查线性回归方程的应用，以及利用线性回归方程进行预测，要注意回归直线必过样本中心点.16．A 【解析】【分析】模拟执行程序框图依次写出每次循环得到的k 的值当k=2012时不满足条件退出循环输出的值为【详解】模拟执行程序框图可得满足条件满足条件满足条件满足条件由此可见S 的周期为3故当k=20解析：A 【解析】【分析】模拟执行程序框图，依次写出每次循环得到的k ，S 的值，当k=2012时不满足条件2011k ≤ ，退出循环，输出S 的值为12.【详解】模拟执行程序框图，可得 2,1S k ==满足条件2011k ≤，1,22S k ==，满足条件2011k ≤，1,3S k =-=，满足条件2011k ≤，2,4S k ==，满足条件2011k ≤，1,52S k ，== 由此可见S 的周期为3，20113670...1,÷= 故当k=2012时不满足条件2011k ≤ ，退出循环，输出S 的值为12. 故选A. 【点睛】本题主要考查了循环结构的程序框图，属于基础题．17．7【解析】执行程序框图当输入第一次循环；第二次循环；第三次循环；第四次循环；第五次循环结束循环输出故答案为【方法点睛】本题主要考查程序框图的循环结构流程图属于中档题解决程序框图问题时一定注意以下几点解析：7 【解析】执行程序框图，当输入2,10a b ==，第一次循环，3,9==a b ；第二次循环，4,8a b ==；第三次循环，5,7a b ==；第四次循环，6,6a b ==；第五次循环，7,5a b ==，结束循环输出7a =，故答案为7.【方法点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.18．【解析】【分析】求出小明等车时间不超过10分钟的时间长度代入几何概型概率计算公式可得答案【详解】设小明到达时间为当在7：50至8：00或8：20至8：30时小明等车时间不超过10分钟故故答案为【点睛解析：1 2【解析】【分析】求出小明等车时间不超过10分钟的时间长度，代入几何概型概率计算公式，可得答案．【详解】设小明到达时间为y，当y在7：50至8：00，或8：20至8：30时，小明等车时间不超过10分钟，故201402P==．故答案为12．【点睛】本题考查的知识点是几何概型，难度不大，属于基础题．19．【解析】【分析】根据系统抽样的特征求出分段间隔即可【详解】根据系统抽样的特征得：从2100名学生中抽取100个学生分段间隔为故答案是21【点睛】该题所考查的是有关系统抽样的组距问题应用总体除以样本容解析：21【解析】【分析】根据系统抽样的特征，求出分段间隔即可.【详解】根据系统抽样的特征，得：从2100名学生中抽取100个学生，分段间隔为210021 100=，故答案是21.【点睛】该题所考查的是有关系统抽样的组距问题，应用总体除以样本容量等于组距，得到结果，属于简单题目.20．【解析】分析：在内任投一点要使的面积小于5根据几何关系求解出它们的比例即可详解：记事件{的面积大于5}基本事件是的面积如图：事件A的几何度量为图中阴影部分的面积（DE分别是三角形的边上的四等分点）且解析：716【解析】分析：在ABC∆内任投一点M，要使MBC∆的面积小于5，根据几何关系求解出它们的比例即可.详解：记事件A={MBC∆的面积大于5}，基本事件是ABC∆的面积，如图：事件A的几何度量为图中阴影部分的面积（D、E分别是三角形的边上的四等分点），ADE ABC∆~∆Q，且相似比为34，239416ADEABCSS∆∆⎛⎫∴==⎪⎝⎭，()916ADEABCSP AS∆∆∴==.∴MBC∆的面积小于5的概率是()97111616P A-=-=.故答案为：716.点睛：本题考查几何概型，解答此题的关键在于明确测度比是面积比，对于几何概型常见的测度是长度之比、面积之比、体积之比、角度之比，要根据题意合理的判断和选择是哪一种测度进行求解，属于中档题.三、解答题21．（1）（2）【解析】【分析】(1) 根据散点图判断，适宜；（2），两边同时取常用对数得：，根据公式得到均值和系数即可得到公式，再代入x=8可得到估计值. 【详解】（1）根据散点图判断，适宜作为扫码支付的人数关于活动推出天数的回归方程类型；（2），两边同时取常用对数得：；设，，把样本中心点代入,得: ，，，关于的回归方程式：；把代入上式，；活动推出第天使用扫码支付的人次为；【点睛】本题考查回归分析，考查线性回归直线过样本中心点，在一组具有相关关系的变量的数据间，这样的直线可以画出许多条，而其中的一条能最好地反映x 与Y 之间的关系，这条直线过样本中心点．线性回归方程适用于具有相关关系的两个变量，对于具有确定关系的两个变量是不适用的, 线性回归方程得到的预测值是预测变量的估计值，不是准确值. 22．（1）5a =，27b =，0.9x =，0.2y =；（2）分边抽取2,3,1人；（3）15. 【解析】【分析】（1）根据数据表和频率分布直方图可计算得到第4组的人数和频率，从而可得总人数；根据总数、频率和频数的关系，可分别计算得到所求结果；（2）首先确定第2,3,4组的总人数，根据分层抽样原则计算即可得到结果；（3）首先计算得到基本事件总数；再计算出恰好没有年龄段在[)3545，包含的基本事件个数，根据古典概型概率公式可求得结果. 【详解】（1）第4组的人数为：9250.36=人，第4组的频率为：0.025100.25⨯＝ 251000.25n ∴== Q 第一组的频率为0.010100.1⨯= ∴第一组的人数为：0.110010⨯=100.55a ∴=⨯=Q 第二组的频率为0.020100.2⨯= ∴第二组的人数为：0.210020⨯=180.920x ∴== Q 第三组的频率为0.030100.3⨯= ∴第三组的人数为：0.310030⨯=300.927b ∴=⨯=Q 第五组的频率为0.015100.15⨯= ∴第五组的人数为：0.1510015⨯=30.215y ∴== （2）第2,3,4组的总人数为：1827954++=人∴第2组抽取的人数为：186254⨯=人；第3组抽取的人数为：276354⨯=人；第4组抽取的人数为：96154⨯=人（3）在（2）中抽取的6人中随机抽取2人，基本事件总数为：2615n C ==所抽取的人中恰好没有年龄段在[)3545，包含的基本事件个数为：233m C == ∴所抽取的人中恰好没有年龄段在[)3545，的概率：31155m p n === 【点睛】本题考查利用频率分布直方图计算总数、频数和频率、分层抽样基本方法的应用、古典概型计算概率问题；关键是熟练掌握频率分布直方图的相关知识，能够通过频率分布直方图准确计算出各组数据对应的频率. 23．（1）见解析；（2）()1115P A = 【解析】【分析】（1）第一步编号分组，第二步抽样；（2）先用枚举法确定从6名学生选2名的总事件数，再从中确定2名同学不在同一档的事件数，最后根据古典概型概率公式求结果. 【详解】（1）第一步：分组.将2000名学生分成50组，每组40人，编号是0001～0040的为第1组，编号为0041～0080的为第2组，…，编号为1961～2000为第50组；第二步：抽样.在第1组中用简单随机抽样方法（抓阄）抽取一个编号为m 的学生，则在第k 组抽取编号为()401k m -+的学生.每组抽取一人，共计抽取50名学生.（2）记该班3个1档的学生为1A ，2A ，3A ，2个2档的学生为1B ，2B ，1个3档的学生为1C ，从该班获得助学金的同学中选择2名同学不在同一档为事件A .基本事件：12A A ，13A A ，11A B ，11A B ，11A C ，23A A ，21A B ，22A B ，21A C ，31A B ，32A B ，31A C ，12B B ，11B C ，21B C ，共计15个.事件A 包含的基本事件共有11个，则()1115P A = 【点睛】本题考查系统抽样以及古典概型概率公式，考查基本分析求解能力，属基础题. 24．（1），（2）【解析】【分析】【详解】（1）从袋子中随机取两个球，其一切可能的结果组成的基本事件有1和2,1和3,1和4,2和3,2和4,3和4，共6个，从袋中随机取出的球的编号之和不大于4的事件共有1和2,1和3两个．因此所求事件的概率为.（2）先从袋中随机取一个球，记下编号为m ，放回后，在从袋中随机取一个球，记下编号为n ，其中一切可能的结果（m ，n ）有：（1,1）（1,2），（1,3），（1,4），（2,1），（2,2），（2,3），（2,4），（3,1）（3， 2），（3,3）（3,4），（4,1），（4,2），（4,3），（4,4），共16个．所有满足条件n≥m ＋2的事件为（1,3）（1,4）（2,4），共3个，所以满足条件n≥m ＋2的事件的概率为P1＝316故满足条件n ＜m ＋2的事件的概率为1－P1＝1－316＝.25．（1）0.9；（2）0.085a =，0.125b =；（3）第4组. 【解析】试题分析：（1）由频率分布表知，100人中有10人阅读时间不少于12小时，所以由对立事件的概率计算公式得p=；（2）由频率分表知，阅读时间在[4，6）的共17人，所以样本落在该组的概率为0．17，则频率分布直方图中样本落在[4，6）的小矩形的面积为0．17，从而求出矩形的高即a 的值，同理得到b 的值；（3）可以通过频率分布表或频率分布直方图求出平均数即可知平均数在那一组．试题解析：（1）根据频数分布表，100名学生中课外阅读时间不少于12小时的学生共有6+2+2=10名，所以样本中的学生课外阅读时间少于12小时的频率是；（2）课外阅读时间落在[4，6）的有17人，频率为0．17，所以，课外阅读时间落在[8，10）的有25人，频率为0．25，所以，（3）估计样本中的100名学生课外阅读时间的平均数在第4组．考点：频率分布表和频率分布直方图的应用．【方法点睛】频率分布直方图的几个常用结论：（1）所有小矩形的面积和为1；（2）小矩形的高等于样本落在该组的概率除以组距；（3）最高的小矩形的所在组的区间的中点值即为众数；（4）每个组的区间中点值乘以所在组的概率之和即为平均数；（4）样本取值m，两侧的样本数据的概率相等且为，则m即为中位数．26．(1)；(2)；(3).【解析】【分析】【详解】试题分析：(1)借助题设条件运用频率分布直方图求解；(2)借助题设条件运用频率分布直方图中提供的数据信息求解；(3)运用列举法和古典概型计算公式求解.试题解析：（1）由题意可知，样本容量n=80.01610⨯=50，，x=0.100﹣0.004﹣0.010﹣0.016﹣0.040=0.030；（2）设本次竞赛学生成绩的中位数为m，平均分为x，则[0.016+0.03]×10+（m﹣70）×0.040 =0.5，解得71m=，x=（55×0.016+65×0.030+75×0.040+85×0.010+95×0.004]×10=70.6，（3）由题意可知，分数在[80，90）内的学生有5人，记这5人分别为a1，a2，a3，a4，a5，分数在[90，100]内的学生有2人，记这2人分别为b1，b2．抽取的2名学生的所有情况有21种，分别为：（a1，a2），（a1，a3），（a1，a4），（a1，a5），（a1，b1），（a1，b2），（a2，a3），（a2，a4），（a2，a5），（a2，b1），（a2，b2），（a3，a4），（a3，a5），（a3，b1），（a3，b2），（a4，a5），（a4，b1），（a4，b2），（a5，b1），（a5，b2），（b1，b2）．其中2名同学的分数都不在[90，100]内的情况有10种，分别为：（a1，a2），（a1，a3），（a1，a4），（a1，a5），（a2，a3），（a2，a4），（a2，a5），（a3，a4），（a3，a5），（a4，a5）．∴所抽取的2名学生中至少有一人得分在[90，100]内的概率101112121 p=-=.考点：频率分布直方图、频率与频数的关系及古典概型的计算公式等有关知识的综合运用．【易错点晴】本题以学校中的数学竞赛的数学成绩的抽样统计的频率分布直方图为背景,设置了三个较为平常的数学问题.解答时一定要充分利用题设中提供的频率分布直方图所提供的数据信息,结。

四川省成都市2020学年高二数学上学期期末调考模拟试题试卷(4)

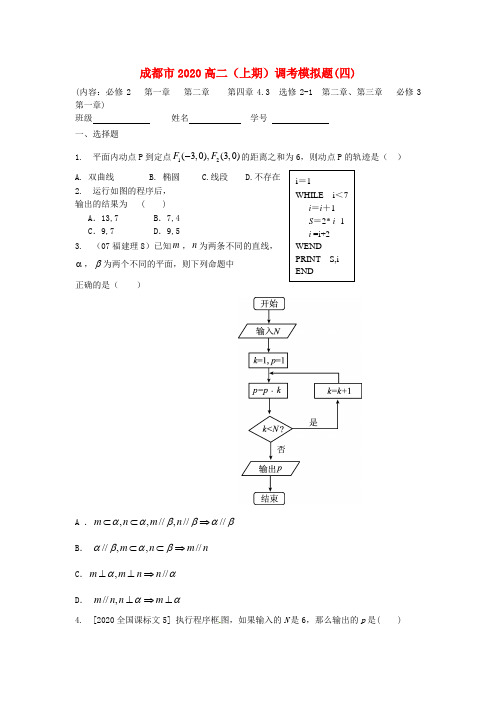
i ＝1WHILE i ＜7 i ＝i ＋1 S ＝2* i -1 i =i+2 WEND PRINT S,i END成都市2020高二（上期）调考模拟题(四)(内容：必修2 第一章第二章第四章4.3 选修2-1 第二章、第三章必修3第一章)班级姓名学号一、选择题1. 平面内动点P 到定点12(3,0),(3,0)F F -的距离之和为6，则动点P 的轨迹是（） A. 双曲线 B. 椭圆 C.线段 D.不存在2. 运行如图的程序后，输出的结果为 ( ) A ．13,7 B ．7,4 C ．9,7 D ．9,53. （07福建理8）已知m ，n 为两条不同的直线，α，β为两个不同的平面，则下列命题中正确的是（）A ．,,//,////m n m n ααββαβ⊂⊂⇒B ． //,,//m n m n αβαβ⊂⊂⇒C ．,//m m n n αα⊥⊥⇒D ． //,m n n m αα⊥⇒⊥4. [2020全国课标文5] 执行程序框图，如果输入的N 是6，那么输出的p 是( )A ．120B ．720C ．1440D ．50405. （07浙江理6）若P 是两条异面直线,l m 外的任意一点，则（）A ．过点P 有且仅有一条直线与,l m 都平行B ．过点P 有且仅有一条直线与,l m 都垂直C ．过点P 有且仅有一条直线与,l m 都相交D ．过点P 有且仅有一条直线与,l m 都异面6. （2020全国1理9)已知1F 、2F 为双曲线C:221x y -=的左、右焦点，点P 在C 上，∠1F P 2F =060，则P 到x 轴的距离为3636 7. (2020北京6)如图，在正方体ABCD A B C D -1111中，P 是侧面BB C C 11内一动点，若P 到直线BC 与直线C D 11的距离相等，则动点P 的轨迹所在的曲线是（） A. 直线 B. 圆C. 双曲线D. 抛物线8. （2020广东文7）若一个椭圆长轴的长度、短轴的长度和焦距成等差数列，则该椭圆的离心率是（）A.54 B.53 C. 52D. 519. [2020·广东卷7] 如，某几何体的正视图(主视图)是平行四边形，侧视图(左视图)和俯视图都是矩形，则该几何体的体积为( )A ．6 3B ．9 3C ．12 3D ．18 310. （2020全国卷2文（12））已知椭圆C ：22221x y a b+=（a>b>03D C 1A 1B 1P D CA B过右焦点F 且斜率为k （k>0）的直线于C 相交于A 、B 两点，若3AF FB =u u u r u u u r。

四川省成都市2020学年高二数学上学期期末调考模拟试题试卷(3)

成都市2020高二（上期）调考模拟题(三)(内容：必修2 第一章第二章第四章4.3 选修2-1 第二章、第三章必修3第一章)班级姓名学号一、选择题1. 四进制数201(4)表示的十进制数的是 ( ) A ．31 B ．32 C ．33 D ．34 2. [2020·北京文5] 某四棱锥的三视图如图所示，该四棱锥的表面积是( )A ．32B ．16＋16 2C ．48D ．16＋32 2 3. 若{a 、b 、c }为空间的一组基底，则下列各项中，能构成基底的一组向量是 ( )A ．a ，a ＋b ，a －bB ．b ，a ＋b ，a －bC ．c ，a ＋b ，a －bD ．a ＋b ，a －b ，a ＋2b 4. （2020浙江理（4））下列命题中错误的是（）（A ）如果平面αβ⊥平面，那么平面α内一定存在直线平行于平面β （B ）如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β（C ）如果平面αγ⊥平面，平面βγ⊥平面，=l αβ⋂，那么l γ⊥平面（D ）如果平面αβ⊥平面，那么平面α内所有直线都垂直于平面β5. 双曲线13622=-y x 的渐近线与圆)0()3(222>=+-r r y x 相切，则r=（）（A ）3 （B ）2 （C ）3 （D ）66. (2020·福建理6)如图，若Ω是长方体ABCD —A 1B 1C 1D 1被平面EFGH 截去几何体EFGHB 1C 1后得到的几何体，其中E 为线段A 1B 1上异于B 1的点，F 为线段BB 1上异于B 1的点，且EH ∥A 1D 1，则下列结论中不正确的是 ( ) A ．EH ∥FG B ．四边形EFGH 是矩形 C ．Ω是棱柱 D ．Ω是棱台7. 已知E 、F 分别为正四面体ABCD 棱AD 、BC 的中点，则异面直线AC 与EF 所成的角为( ) A ．30° B ．45° C ．60° D ．90°8. [2020·北京卷6.] 执行如图所示的程序框图，若输入A 的值为2，则输出的P 值为( ) A ．2 B ．3 C ．4 D ．5 9. 设22,,26,x y x y x y ∈+=+R 则的最小值是（）A ．22-B ．335-C ．－3D ．27-10. （06年全国I ）抛物线2y x =-上的点到直线4380x y +-=距离的最小值是 A ．43 B ．75 C ．85D ．3 11. 已知PA ，PB ，PC 是从P 引出的三条射线，每两条的夹角都是60º，则直线PC 与平面PAB 所成的角的余弦值为（）A ．123 6 312. （08全国二11）设ABC △是等腰三角形，120ABC ∠=o，则以A B ，为焦点且过点C的双曲线的离心率为（） A ．221+ B ．231+ C ． 21+ D ．31+二、填空题13. 已知向量(1,1,0),(1,0,2)a b ==r r，a r 在b r 方向上的投影是____________.14. 右边程序执行后输出的结果是________．i ＝11s ＝1DOs ＝s*ii ＝i －1LOOP UNTIL i ＜9PRINT s END15. 有一块多边形的菜地，它的水平放置的平面图形的斜二测直观图是直角梯形(如图)，∠ABC ＝45°，AB ＝AD ＝1，DC ⊥BC ，则这块菜地的面积为________．16. 过椭圆14922=+y x 内一点M (2,0)引椭圆的动弦AB , 则弦AB 的中点N 的轨迹方程是 . 三、解答题17. (2020·全国课标)如图，已知四棱锥P －ABCD 的底面为等腰梯形，AB ∥CD ，AC ⊥BD ，垂足为H ，PH 是四棱锥的高． (1)证明：平面PAC ⊥平面PBD ；(2)若AB ＝6，∠APB ＝∠ADB ＝60°，求四棱锥P －ABCD 的体积．18.(07安徽文18）设F是抛物线G:x2=4y的焦点.（Ⅰ）过点P（0，- 4）作抛物线G的切线，求切线方程：（Ⅱ）设A、B为抛物线G上异于原点的两点，且满足0· ,延长AF、BF分别交抛物线G于点C,D，求四边形ABCD面积的最小值.19. 如图4，在直角梯形ABCD 中，AD=DC,90ABC DAB ∠=∠=°．30CAB ∠=°，1BC =，把DAC ∆沿对角线AC 折起后如图5所示 (点D 记为点P )．点P 在平面ABC 上的正投影E 落在线段AB 上，连接PB ． (1) 求直线PC 与平面PAB 所成的角的大小；(2) 求二面角P AC B --的大小的余弦值．20. 直线12:1:22=-+=y x C kx y l 与双曲线的右支交于不同的两点A 、B.（I ）求实数k 的取值范围；（II ）是否存在实数k ，使得以线段AB 为直径的圆经过双曲线C 的右焦点F ？若存在，求出k 的值；若不存在，说明理由.高2020级高二期末综合复习(三)(内容：必修2 第一章第二章第四章4.3 选修2-1 第二章、第三章必修3第一章)班级姓名学号一、选择题（12×5=60）1. 四进制数201(4)表示的十进制数的是( C ) A ．31 B ．32 C ．33 D ．34 2. [2020·北京文5] 某四棱锥的三视图如图所示，该四棱锥的表面积是( B )A ．32B ．16＋16 2C ．48D ．16＋32 2 3. 若{a 、b 、c }为空间的一组基底，则下列各项中，能构成基底的一组向量是 ( ) A ．a ，a ＋b ，a －b B ．b ，a ＋b ，a －b C ．c ，a ＋b ，a －b D ．a ＋b ，a －b ，a ＋2b解析：若c 、a ＋b 、a －b 共面，则c ＝λ(a ＋b )＋m (a －b )＝(λ＋m )a ＋(λ－m )b ，则a 、b 、c为共面向量，此与{a 、b 、c }为空间向量的一组基底矛盾，故c ，a ＋b ，a －b 可构成空间向量的一组基底．答案：C4. （2020浙江理（4））下列命题中错误的是（ D ）（A ）如果平面αβ⊥平面，那么平面α内一定存在直线平行于平面β （B ）如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β（C ）如果平面αγ⊥平面，平面βγ⊥平面，=l αβ⋂，那么l γ⊥平面（D ）如果平面αβ⊥平面，那么平面α内所有直线都垂直于平面β5. （2020全国卷Ⅱ文）双曲线13622=-y x 的渐近线与圆)0()3(222>=+-r r y x 相切，则r=（ A ）（A ）3 （B ）2 （C ）3 （D ）66. (2020·福建理6)如图，若Ω是长方体ABCD —A 1B 1C 1D 1被平面EFGH 截去几何体EFGHB 1C 1后得到的几何体，其中E 为线段A 1B 1上异于B 1的点，F 为线段BB 1上异于B 1的点，且EH ∥A 1D 1，则下列结论中不正确的是 ( D ) A ．EH ∥FG B ．四边形EFGH 是矩形C ．Ω是棱柱D ．Ω是棱台 7. 已知E 、F 分别为正四面体ABCD 棱AD 、BC 的中点，则异面直线AC 与EF 所成的角为 ( B ) A ．30° B ．45° C ．60° D ．90° 8. [2020·北京卷6.] 执行如图所示的程序框图，若输入A 的值为2，则输出的P 值为( ) A ．2 B ．3 C ．4 D ．5【解析】C 第一步，P ＝1＋1＝2，S ＝1＋12＝32；第二步，P ＝2＋1＝3，S ＝32＋13＝116；第三步，P ＝3＋1＝4，S ＝116＋14＝2512>2，输出P ＝4，故选C. 9. 设22,,26,x y x y x y ∈+=+R 则的最小值是（ C ）A ．22-B ．335-C ．－3D ．27-10. （06年全国I ）抛物线2y x =-上的点到直线4380x y +-=距离的最小值是A ．43 B ．75 C ．85D ．3 抛物线上任意一点（t ，2t -）到直线的距离22|438||348|55t t t t d ---+==。

四川省成都市2020-2021学年高二上学期期末调研考试数学(理)试题

四川省2020-2021学年高二数学上学期期末模拟考试试题2套(含答案)

四川省高二上学期数学期末模拟试卷（含答案）第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.对变量,x y 有观测数据,1,2,,10i i x y i …，得散点图(1)；对变量,u v 有观测数据(,1,2,,10i iu v i …，得散点图(2)，由这两个散点图可以判断( )A.变量x 与y 正相关，u 与v 正相关B.变量x 与y 正相关，u 与v 负相关C.变量x 与y 负相关，u 与v 正相关D.变量x 与y 负相关，u 与v 负相关2.若圆22240x y x y 关于直线30x y a 对称，则a 的值为( ) A.1B.1C.3D.33.下列命题中的真命题是( ) A.x R ，使得3sin cos 5x x B.,0x ，21x C.x R ，21x xD.0,x，sin cos x x4.广安市某学校高一年级8个班参加合唱比赛的得分如茎叶图所示，则这组数据的中位数和平均数分别是A.91.5和91.5B.91.5和92C.91和91.5D.92和925.直线cos20x y 的倾斜角的范围是( )A.,44B.30,,44C.0,D.0,46.已知1,5,2AB ，3,1,BC z ，若AB BC ，1,,3BP x y ，且BP 平面ABC ，则实数,,x y z 分别为( ) A.3315,,477B.4015,,477C.40,2,47D.404,,1577.如图，矩形ABCD 中，点E 为边CD 的中点，若在矩形ABCD 内部随机取一个点Q ，则点Q 取自ABE △内部的概率等于( )A.14B.13C.12D.238.方程231310x y x 表示的曲线是( )A.两条直线B.两条射线C.两条线段D.一条直线和一条射线9.某高中在校学生2000人，为了响应“阳光体育运动”号召，学校举行了跑步和登山比赛活动，每人都参加而且只参加了其中一项比赛，各年级参与比赛人数情况如下表：高一年级高二年级高三年级跑步 a bc登山xyz其中::2:3:5a b c ，全校参与登山的人数占总人数的25，为了了解学生对本次活动的满意程度，从中抽取一个200人的样本进行调查，则高二年级参与跑步的学生中应抽取( ) A.36人B.60人C.24人D.30人10.若P ：直线l 与双曲线C 只有一个公共点，Q ：直线l 与双曲线C 相切，则P 是Q 的( ) A.充分不必要条件 B.必要不充分条件 C .充要条件 D.既不充分也不必要条件11.已知12,F F 是椭圆的两个焦点，满足120MF MF 的点M 总在椭圆内部，则椭圆离心率的取值范围是( ) A.0,1B.10,2C.20,D.2,112.到两互相垂直的异面直线的距离相等的点，在过其中一条直线且平行于另一条直线的平面内的轨迹是( ) A.直线B.椭圆C.抛物线D.双曲线第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.四进制数4123化为十进制数为 .14.动圆过点1,0，且与直线1x相切，则动圆的圆心的轨迹方程为. 15.执行如图所示的程序框图，如果输入的N 是5，那么输出的p 是.16.下列命题中，所有正确命题的序号是.①若1n ，2n 分别是平面,的法向量，则12n n ∥∥； ②若1n ，2n 分别是平面，的法向量，则120n n ；③若n 是平面的法向量，a 与共面，则0n a ； ④若两个平面的法向量不垂直，则这两个平面一定不垂直.三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.已知直线1l 的方程为34120x y . (1)若直线2l 与1l 平行，且过点1,3，求直线2l 的方程；(2)若直线2l 与1l 垂直，且2l 与两坐标轴围成的三角形面积为4，求直线2l 的方程. 18.分别抛掷两颗骰子各一次，观察向上的点数，求： (1)两数之和为5的概率；(2)以第一次向上的点数为横坐标x ，第二次向上的点数为纵坐标y 的点,x y 在圆2215x y 内部的概率.19.设p ：实数x 满足30x ax a，q ：实数x 满足31x .(1)若1a ，且p q 为真，求实数x 的取值范围；(2)若其中0a 且p 是q 的充分不必要条件，求实数a 的取值范围.20.如图所示，在棱长为2的正方体1111ABCD A B C D 中，,E F 分别为11A D 和1CC 的中点.(1)求证：EF ∥平面1ACD ；(2)在棱1BB 上是否存在一点P ，使得二面角P AC B 的大小为30°，若存在，求出BP 的长；若不存在，请说明理由.21.已知椭圆2222:10x y G a b a b 6右焦点为22,0，斜率为1的直线l 与椭圆G 交于,A B 两点，以AB 为底边作等腰三角形，顶点为3,2P .(1)求椭圆G 的方程；(2)M 为椭圆G 上任意一点，若,M m n ，求4n m 的最大值和最小值.(3)求PAB △的面积.22.已知动点P ，Q 都在曲线2cos :2sin x tC y t(t 为参数)上，对应参数分别为t与202t ，M 为PQ 的中点.(1)求曲线C的普通方程；(2)将M到坐标原点的距离d表示为的函数，并判断M的轨迹是否过坐标原点.23.已知0a b，证明：b，332a，0a b a b；(1)554(2)2a b.答案一、选择题1-5:CBCAB 6-10:BCDAB 11、12：CD二、填空题13.27 14.24y x 15.120 16.①②③④三、解答题17.解：(1)由直线2l 与1l 平行，可设2l 的方程为340x y m ，以1x，3y 代入，得3120m ，即得9m，∴直线2l 的方程为3490x y .(2)由直线2l 与1l 垂直，可设2l 的方程为430x y n ，令0y ，得4n x，令0x ，得3n y ，故三角形面积为14243n nS ，∴得296n ，即46n ，∴直线2l 的方程为43460x y 或43460x y .18.解：将一颗骰子先后抛掷2次，此问题中含有36个等可能基本事件.(1)记“两数之和为5“为事件A ，则事件A 中含有4个基本事件：1,4，2,3，3,2，4,1，所以41369P A. ∴两数之和为5的概率为19.(2)基本事件总数为36，点,x y 在圆2215x y 的内部记为事件C ，则C 包含8个事件C 中所含基本事件：1,1，1,2，1,3，2,1，2,2，2,3，3,1，3,2，所以82369P C ， ∴点,x y 在圆2215x y 内部的概率为29. 19.解：(1)由22430x ax a 得30x ax a ，当1a 时，13x ，即p 为真时实数x 的取值范围是13x ，由31x ，得131x ，得24x ，即q 为真时实数x 的取值范围是24x ，若p q 为真，则p 真且q 真， ∴实数x 的取值范围是23x . (2)若p 是q 的充分不必要条件，则p q ，∴qq ，由30x a x a ，0a ， ∴02a ，且34a， ∴实数a 的取值范围是423a.20.(1)证明：如图所示，分别以1,,DA DC DD 所在的直线为x 轴，y 轴，z 轴建立空间直角坐标系Dxyz ，由已知得0,0,0D ，2,0,0A ，2,2,0B ，0,2,0C ，12,2,2B ，10,0,2D ，1,0,2E ，0,2,1F ， ∵平面1ACD 的一个法向量是12,2,2DB ，又∵1,2,1EF ，∴12420EF DB ，∴1EFDB ，而EF 平面1ACD ，∴EF ∥平面1ACD .(2)解：设点2,2,02P tt ，平面ACP 的一个法向量为,,nx y z ，则n AC n AP ，∵0,2,AP t ，2,2,0AC ，∴20220y tz x y ，取1y ，则1x ，2zt，∴21,1,n t，平面ABC 的一个法向量10,0,2BB ，依题意知，1,30BB n°或1,150BB n°，∴1243cos ,422t BB nt ，即2243424t t ，解得6t或6t (舍)，0,2，∴在棱1BB 上存在一点P ，当BP P AC B 的大小为30°. 21.解：(1)由已知得22c ，6c a，解得23a ，又2224b a c ，所以椭圆G 的方程为221124x y .(2)设4,0C 则直线CM l 的方程为4kyx ，由2241124kyx x y ，得223840k y ky ①11k ，4n m 的最大值为1和最小值为1.(3)设直线l 的方程为y x m ，由221124y x m x y ，得22463120x mx m ①设,A B 的坐标分别为11,x y ，22,x y 12x x ，AB 中点为00,E x y ，则12324x x mx ，004m y x m，因为AB 是等腰PAB △的底边，所以PEAB ，所以PE 的斜率241334m km ，解得2m ，此时方程①为24120x x ，解得13x ，20x ，所以11y ，22y ，所以32AB ，此时，点3,2P 到直线:20AB x y 的距离3223222d，所以PAB △的面积1922S AB d . 22.解：(1)曲线C 的直角坐标方程：224x y .(2)依题意有2cos ,2sinP ，2cos 2,2sin 2Q ，因此coscos2,sin sin 2M ，M的轨迹的参数方程为cos cos 2sinsinx y (为参数，02)，M 点到坐标原点的距离2222cos 02dx y ，当时，0d ，故M 的轨迹过坐标原点.23.解：(1)由柯西不等式得： 222225522334a b a b aba ab b a b .(2)由332a b 及24a b ab得22223a b a b aba ba bab232344a ba b a b a b，∴2a b .四川省高二上学期数学期末模拟试卷（含答案）第一部分（选择题共60分）一、选择题：本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设命题:p x R ∀∈，||20x +>，则p ⌝为（）A ．0,||20x R x ∃∈+>B ．0,||20x R x ∃∈+≤C ．0,||20x R x ∃∈+<D ．,||20x R x ∀∈+≤2.将长方体截去一个四棱锥后得到的几何体如下图所示，则该几何体的侧视图为（）A ．B ．C ．D ．3.已知椭圆2221(0)16x y k k +=>的左焦点为1(7,0)F -，则k =（） A ．2 B ．3 C ．4 D ．94.一水平放置的平面四边形OABC ，用斜二测画法画出它的直观图''''O A B C ，如图所示，此直观图恰好是一个边长为1的正方形，则原平面四边形OABC 的面积为（）A ．1B 2 C.2 D ．225.“1m >且2m ≠”是“方程22121x y m m -=--表示双曲线”的（）A ．充分不必要条件B ．必要不充分条件C.充分必要条件 D ．既不充分也不必要条件6.若抛物线22x py =的焦点与椭圆22159x y +=的上焦点．．．重合，则该抛物线的准线方程为（） A ．1y =- B ．1y = C.2y =- D ．2y =7.设αβ、是两个不同的平面，l m 、是两条不同的直线，且l α⊂，m β⊂，则有（）A ．若l β⊥，则αβ⊥B ．若αβ⊥，则l m ⊥C.若//l β，则//αβ D ．若//αβ，则//l m8.已知椭圆22142x y +=的两个焦点是12F F 、，点P 在椭圆上，若12||||2PF PF -=，则12PF F ∆的面积是（）A ．3B ．31+ C.2 D ．21+9.已知直三棱柱111BCD B C D -中，BC CD =，BC CD ⊥，12CC BC =，则CD 与平面1BDC 所成角的正弦值为（）A ．23B ．23 C.33 D ．1310.已知点12F F 、分别是双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点，点P 是双曲线C 上异于12F F 、的另外一点，且12PF F ∆是顶角为120︒的等腰三角形，则该双曲线的离心率为（）A 31B ．312 C.212D ．312 11.在三棱锥P ABC -中，PA ⊥平面ABC ，AC BC ⊥，D 为侧棱PC 上的一点，它的正（主）视图和侧（左）视图如图所示，则下列命题正确的是（）A ．AD ⊥平面PBC 且三棱锥D ABC -的体积为83B ．BD ⊥平面PAC 且三棱锥D ABC -的体积为83C.AD ⊥平面PBC 且三棱锥D ABC -的体积为163D ．BD ⊥平面PAC 且三棱锥D ABC -的体积为163 12.椭圆22:12x C y +=的左、右顶点分别为12A A 、，点P 在C 上且直线1PA 斜率的取值范围是[1,2]，那么直线2PA 斜率的取值范围是（）A ．31[]2-B ．33[ C. 11[,]24-- D ．22[ 第二部分（非选择题共90分）二、填空题：本大题共4小题；每小题5分，共20分.13.抛物线214y x =-的焦点坐标是． 14.已知F 为双曲线22:1169x y C -=的左焦点，P Q 、为C 上的点.若PQ 的长等于虚轴长的2倍，点(5,0)A 在线段PQ 上，则PQF ∆的周长为．15.已知A B C 、、三点在球心为O ，半径为R 的球面上，120BAC ∠=︒，BC R =，则球心O 到平面ABC 的距离为．16.如图，在梯形ABCD 中，//AD BC ，90ABC ∠=︒，::2:3:4AD BC AB =，E F 、分别是AB CD 、的中点，将四边形ADFE 沿直线EF 进行翻折.给出四个结论：①DF BC ⊥；②BD FC ⊥；③平面BDF ⊥平面BFC ；④平面DCF ⊥平面BFC .在翻折过程中，可能成立的结论序号是．三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17.如图所示，在正方体1111ABCD A B C D -中，E F 、分别是AB BC 、的中点.（1）求异面直线1A D 与EF 所成的角的大小；（2）求证：1EF BD ⊥.18.已知双曲线的方程是224936x y -=.（1）求双曲线的焦点坐标、离心率和渐近线方程；（2）设1F 和2F 是双曲线的左、右焦点，点P 在双曲线上，且12||||16PF PF ⋅=，求12F PF ∠的大小.19.如图，四棱锥P ABCD -中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD 的中点.（1）证明：//PB 平面AEC ；（2）设1AP =，3AD =P ABD -的体积33V =，求A 到平面PBC 的距离.20.已知抛物线2:2(0)C y px p =>的焦点为F ，抛物线C 与直线1:l y x =-的一个交点的横坐标为4.（1）求抛物线C 的方程；（2）不过原点的直线2l 与1l 垂直，且与抛物线C 交于不同的两点A B 、，若线段AB 的中点为P ，且||||OP PB =，求FAB ∆的面积.21.如图，在等腰梯形ABCD 中，//AB CD ，1AD DC CB ===，60ABC ∠=︒，四边形ACFE 为矩形，平面ACFE ⊥平面ABCD ，1CF =.（1）求证：BC ⊥平面ACFE ；（2）点M 在线段EF 上运动，设平面MAB 与平面FCB 所成二面角的平面角为θ，试求cos θ的取值范围.22.如图，椭圆2222:1(0)x y C a b a b+=>>的离心率是2，点(0,1)P 在短轴CD 上，且1PC PD ⋅=-.（1）求椭圆C 的方程；（2）设O 为坐标原点，过点P 的动直线与椭圆交于A B 、两点.是否存在常数λ，使得OA OB PA PB λ⋅+⋅为定值？若存在，求λ的值；若不存在，请说明理由.试卷答案一、选择题1-5:BDBDB 6-10:CACAD 11、12：CC二、填空题13. (0,1)- 14.40 15.16. ②③ 三、解答题17.（1）解：连结11A C ，由题可知11//A C EF ，则1A D 与EF 所成的角即为11C A D ∠，连结1C D ，易知11AC D ∆为等边三角形，则160CA D ∠=︒，即直线1A D 与EF 所成的角为60︒.（2）证明：连结BD ，易知EF BD ⊥，又1D D ⊥面ABCD ，即1D D EF ⊥， ∴EF ⊥面1D DB ，则1EF BD ⊥，得证.18.（1）解：由224936x y -=得22194x y -=，所以3a =，2b =，c =，所以焦点坐标1(F，2F，离心率3e =，渐近线方程为23y x =±. （2）解：由双曲线的定义可知12||||||6PF PF -=， ∴22212121212||||||cos 2||||PF PF F F F PF PF PF +-∠=⋅ 2212121212(||||)2||||||2||||PF PF PF PF F F PF PF -+⋅-=⋅3632521322+-==，则1260F PF ∠=︒. 19.（1）证明：设BD 与AC 的交点为O ，连接EO .因为ABCD 为矩形，所以O 为BD 的中点，又E 为PD 的中点，所以//EO PB . 又因为EO ⊂平面AEC ，PB ⊄平面AEC ，所以//PB 平面AEC .（2）解：16V PA AB AD AB =⋅⋅=.由V =，可得2AB =. 作AH PB ⊥交PB 于H .由题设知AB BC ⊥，PA BC ⊥，且4PAAB =，所以BC ⊥平面PAB ，又AH ⊂平面PAB ，所以BC AH ⊥，又PB BC B =，做AH ⊥平面PBC . ∵PB ⊂平面PBC ，∴AH PB ⊥，在Rt PAB ∆中，由勾股定理可得5PB =，所以25PA PB AH PB ⋅==，所以A 到平面PBC 的距离为25.20.（1）解：易知直线与抛物线的交点坐标为(4,4)-，∴2(4)24p -=⨯，∴24p =，∴抛物线方程为24y x =.（2）解：直线2l 与1l 垂直，故可设直线2:l x y m =+，11(,)A x y ，22(,)B x y ，且直线2l 与x 轴的交点为M .由24y x x y m⎧=⎨=+⎩得2440y y m --=，16160m ∆=+>，∴2m >-.124y y +=，124y y m ⋅=-，∴222121216y y x x m ==. 由题意可知OA OB ⊥，即2121240x x y y m m +=-=，∴4m =或0m =（舍），∴直线2:4l x y =+，(4,0)M . 故FAB FMB FMA S S S ∆∆∆=+121||||2FM y y =⋅⋅-2121213()4652y y y y =⨯+-=21.（1）证明：在梯形ABCD 中，∵//AB CD ，1AD DC CB ===，60ABC ∠=︒，∴2AB =，∴2222cos603AC AB BC AB BC =+-⋅⋅︒=，∴222AB AC BC =+，∴BC AC ⊥.又平面ACFE ⊥平面ABCD ，平面ACFE平面ABCD AC =，BC ⊂平面ABCD ，∴BC ⊥平面ACFE . （2）由（1）知，可分别以,,CA CB CF 所在的直线为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系，令(03)FM λλ=≤≤，则(0,0,0)C，(3,0,0)A ，(0,1,0)B ，(,0,1)M λ， ∴(3,1,0)AB =-，(,1,1)BM λ=-.设1(,,)n x y z =为平面MAB 的法向量，由1100n AB n MB ⎧⋅=⎪⎨⋅=⎪⎩，得300x y x y z λ⎧-+=⎪⎨-+=⎪⎩，取1x =，则1(1,3,3)n λ=-为平面MAB 的一个法向量，易知2(1,0,0)n =是平面FCB 的一个法向量，∴12212||cos ||||13(3)n n n n θλ⋅==⋅++-2(3)4λ=-+. ∵03λ≤≤，∴当0λ=时，cos θ有最小值7，当3λ=时，cos θ有最大值12， ∴71cos [,]2θ∈22.解：（1）由已知，点,C D 的坐标分别为(0,)b -，(0,)b .又点P 的坐标为(0,1)，且1PC PD ⋅=-，于是211b -=-，2c a =，222a b c -=，解得2a =，2b =所以椭圆C 方程为22142x y +=. （2）当直线AB 的斜率存在时，设直线AB 的方程为1y kx =+，,A B 的坐标分别为11(,)x y ，22(,)x y .联立221421x y y kx ⎧+=⎪⎨⎪=+⎩，得22(21)420k x kx ++-=.其判别式22(4)8(21)0k k ∆=++>，所以122421k x x k +=-+，122221x x k =-+.从而，OA OB PA PB λ⋅+⋅12121212[(1)(1)]x x y y x x y y λ=+++--21212(1)(1)()1k x x k x x λ=+++++22(24)(21)21k k λλ--+--=+21221k λλ-=---+. 所以，当1λ=时，212321k λλ----=-+.此时，3OA OB PA PB λ⋅+⋅=-为定值.当直线AB 斜率不存在时，直线AB 即为直线CD ，此时OA OB PA PB λ⋅+⋅=OC OD PC PD ⋅+⋅213=--=-，故存在常数1λ=，使得OA OB PA PB λ⋅+⋅为定值-3.。

2020-2021成都七中实验学校高二数学上期末模拟试卷含答案

2020-2021成都七中实验学校高二数学上期末模拟试卷含答案一、选择题1．将1000名学生的编号如下：0001，0002，0003，…，1000，若从中抽取50个学生，用系统抽样的方法从第一部分0001，0002，…，0020中抽取的号码为0015时，抽取的第40个号码为（） A ．0795B ．0780C ．0810D ．08152．把五个标号为1到5的小球全部放入标号为1到4的四个盒子中，并且不许有空盒，那么任意一个小球都不能放入标有相同标号的盒子中的概率是（） A ．320B ．720C ．316D ．253．如图是把二进制的数11111化成十进制数的一个程序框图，则判断框内应填入的条件是( )A ．4i >？B ．5i >？C ．4i ≤？D ．5i ≤？4．学校为了解新课程标准提升阅读要求对学生阅读兴趣的影响情况，随机抽取了100名学生进行调查.根据调查结果绘制学生周末阅读时间的频率分布直方图如图所示：将阅读时间不低于30分钟的观众称为“阅读霸”，则下列命题正确的是（） A ．抽样表明，该校有一半学生为阅读霸 B ．该校只有50名学生不喜欢阅读 C ．该校只有50名学生喜欢阅读 D ．抽样表明，该校有50名学生为阅读霸5．某高校大一新生中,来自东部地区的学生有2400人、中部地区学生有1600人、西部地区学生有1000人.从中选取100人作样本调研饮食习惯,为保证调研结果相对准确,下列判断正确的有（）①用分层抽样的方法分别抽取东部地区学生48人、中部地区学生32人、西部地区学生20人；②用简单随机抽样的方法从新生中选出100人；③西部地区学生小刘被选中的概率为150； ④中部地区学生小张被选中的概率为15000A ．①④B ．①③C ．②④D ．②③ 6．把化为五进制数是（）A ．B ．C ．D ．7．在半径为2圆形纸板中间，有一个边长为2的正方形孔，现向纸板中随机投飞针，则飞针能从正方形孔中穿过的概率为（） A ．4π B ．3πC ．2πD ．1π8．已知具有线性相关的两个变量,x y 之间的一组数据如下表所示：x0 1 2 3 4 y 2.24.34.54.86.7若,x y 满足回归方程 1.5ˆˆyx a =+，则以下为真命题的是（） A ．x 每增加1个单位长度，则y 一定增加1.5个单位长度 B ．x 每增加1个单位长度，y 就减少1.5个单位长度 C ．所有样本点的中心为(1,4.5) D ．当8x =时，y 的预测值为13.59．如图，正方形ABNH 、DEFM 的面积相等，23CN NG AB ==，向多边形ABCDEFGH 内投一点，则该点落在阴影部分内的概率为（）A ．12B ．34C ．27D ．3810．从2名男生和2名女生中任意选择两人在星期六、星期日参加某公益活动，每天一人，则星期六安排一名男生、星期日安排一名女生的概率为( )A．13B．512C．12D．71211．我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”，如40337=+.（注：如果一个大于1的整数除1和自身外无其他正因数，则称这个整数为素数.）在不超过11的素数中，随机选取2个不同的数，其和小于等于10的概率是（）A．12B．13C．14D．1512．执行如图所示的程序框图，则输出s的值为（）A．10 B．17 C．19 D．36二、填空题13．根据党中央关于“精准脱贫”的要求，石嘴山市农业经济部门派3位专家对大武口、惠农2个区进行调研，每个区至少派1位专家，则甲，乙两位专家派遣至惠农区的概率为_____．14．小明通过做游戏的方式来确定接下来两小时的活动，他随机地往边长为1的正方形内扔一颗豆子，若豆子到各边的距离都大于14，则去看电影；若豆子到正方形中心的距离大于12，则去打篮球；否则，就在家写作业则小明接下来两小时不在家写作业的概率为______.(豆子大小可忽略不计)15．执行如图所示的伪代码，若输出的y的值为10，则输入的x的值是________．16．为长方形，，，为的中点，在长方形内随机取一点，取到的点到的距离大于1的概率为________．17．玉林市有一学校为了从254名学生选取部分学生参加某次南宁研学活动，决定采用系统抽样的方法抽取一个容量为42的样本，那么从总体中应随机剔除的个体数目为__________．，上，其频率分布直方图如18．某班60名学生参加普法知识竞赛，成绩都在区间[40100]图所示，则成绩不低于60分的人数为___．19．如图是一个算法流程图，则输出的S的值为______．20．为了了解2100名学生早晨到校时间，计划采用系统抽样的方法从全体学生中抽取容量为100栋样本，则分段间隔为__________．三、解答题21．冬季历来是交通事故多发期，面临着货运高危运行、恶劣天气频发、包车客运监管漏洞和农村交通繁忙等四个方面的挑战.全国公安交管部门要认清形势、正视问题，针对近期事故暴露出来的问题，强薄羽、补短板、堵漏洞，进一步推动五大行动，巩固扩大五大行动成果，全力确保冬季交通安全形势稳定.据此，某网站推出了关于交通道路安全情况的调查，通过调查年龄在[15,65)的人群，数据表明，交通道路安全仍是百姓最为关心的热点，参与调查者中关注此类问题的约占80%.现从参与调查并关注交通道路安全的人群中随机选出100人，并将这100人按年龄分组：第1组[15,25)，第2组[25,35)，第3组[35,45)，第4组[45,55)，第5组[55,65)，得到的频率分布直方图如图所示.（1）求这100人年龄的样本平均数（同一组数据用该区间的中点值作代表）和中位数（精确到小数点后一位）；（2）现在要从年龄较大的第1，2组中用分层抽样的方法抽取5人，再从这5人中随机抽取2人进行问卷调查，求第2组恰好抽到1人的概率；22．随着经济的发展，轿车已成为人们上班代步的一种重要工具.现将某人三年以来每周开车从家到公司的时间之和统计如图所示.6.5,7.5（时）内的频率；（1）求此人这三年以来每周开车从家到公司的时间之和在[)（2）求此人这三年以来每周开车从家到公司的时间之和的平均数（每组取该组的中间值作代表）；（3）以频率估计概率，记此人在接下来的四周内每周开车从家到公司的时间之和在[)4.5,6.5（时）内的周数为X ，求X 的分布列以及数学期望.23．“中国人均读书4.3本（包括网络文学和教科书），比韩国的11本、法国的20本、日本的40本、犹太人的64本少得多，是世界上人均读书最少的国家.”这个论断被各种媒体反复引用，出现这样的统计结果无疑是令人尴尬的，而且和其他国家相比，我国国民的阅读量如此之低，也和我国是传统的文明古国、礼仪之邦的地位不相符.某小区为了提高小区内人员的读书兴趣，特举办读书活动，准备进一定量的书籍丰富小区图书站，由于不同年龄段需看不同类型的书籍，为了合理配备资源，现对小区内看书人员进行年龄调查，随机抽取了一天40名读书者进行调查，将他们的年龄分成6段：[)20,30，[)30,40，[)40,50，[)50,60，[)60,70，[]70,80后得到如图所示的频率分布直方图.问：（1）估计在40名读书者中年龄分布在[)40,70的人数；（2）求40名读书者年龄的平均数和中位数；（3）若从年龄在[)20,40的读书者中任取2名，求这两名读书者年龄在[)30,40的人数X 的分布列及数学期望.24．一个袋中装有四个形状大小完全相同的球，球的编号分别为1，2，3，4. （1）从袋中随机抽取两个球，求取出的球的编号之和不大于4的概率；（2）先从袋中随机取一个球，该球的编号为m ，将球放回袋中，然后再从袋中随机取一个球，该球的编号为n ，求2n m <+的概率25．读书可以使人保持思想活力，让人得到智慧启发，让人滋养浩然正气书籍是文化的重要载体，读书是承继文化的重要方式某地区为了解学生课余时间的读书情况，随机抽取了n 名学生进行调查，根据调查得到的学生日均课余读书时间绘制成如图所示的频率分布直方图，将日均课余读书时间不低于40分钟的学生称为“读书之星”，日均课余读书时间低于40分钟的学生称为“非读书之星”:已知抽取的样本中日均课余读书时间低于10分钟的有10人(1)求,n p 的值;(2)根据已知条件完成下面的22⨯列联表，并判断是否有95%以上的把握认为“读书之星”与性别有关?非读书之星读书之星总计男女 10 55 总计(3)将上述调查所得到的频率视为概率，现从该地区大量学生中，随机抽取3名学生，每次抽取1名，已知每个人是否被抽到互不影响，记被抽取的“读书之星”人数为随机变量X ，求X 的分布列和期望()E X附：()()()()()22n ad bc K a b c d a c b d -=++++，其中n a b c d =+++.()20P K k ≥ 0.10 0.05 0.025 0.010 0.005 0.001 0k2.7063.8415.0246.6357.87910.82826．某班同学利用国庆节进行社会实践，对[25，55]岁的人群随机抽取人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：组数分组低碳族的人数占本组的频率第一组 [25，30) 120 0.6第二组 [30，35) 195 p第三组[35，40)1000.5第四组[40，45)a0.4第五组[45，50)300.3第六组[50，55]150.3(1)补全频率分布直方图并求,,n a p的值；(2)从年龄段在[40，50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动，其中选取2人作为领队，求选取的2名领队中恰有1人年龄在[40，45)岁的概率.【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【解析】分析：先确定间距，再根据等差数列通项公式求结果.详解：因为系统抽样的方法抽签，所以间距为100020 50=所以抽取的第40个数为1520(401)795+⨯-=选A.点睛：本题考查系统抽样概念，考查基本求解能力. 2．B解析：B【解析】【分析】由题意可以分两类，第一类第5球独占一盒，第二类，第5球不独占一盒，根据分类计数原理得到答案．【详解】解：第一类，第5球独占一盒，则有4种选择；如第5球独占第一盒，则剩下的三盒，先把第1球放旁边，就是2，3，4球放入2，3，4盒的错位排列，有2种选择，再把第1球分别放入2，3，4盒，有3种可能选择，于是此时有236⨯=种选择；如第1球独占一盒，有3种选择，剩下的2，3，4球放入两盒有2种选择，此时有236⨯=种选择，得到第5球独占一盒的选择有4(66)48⨯+=种，第二类，第5球不独占一盒，先放14-号球，4个球的全不对应排列数是9；第二步放5号球：有4种选择；9436⨯=，根据分类计数原理得，不同的方法有364884+=种．而将五球放到4盒共有2454240C A ⨯=种不同的办法，故任意一个小球都不能放入标有相同标号的盒子中的概率84724020P == 故选：B ．【点睛】本题主要考查了分类计数原理，关键是如何分步，属于中档题．3．C解析：C 【解析】【分析】根据程序框图依次计算得到答案. 【详解】根据程序框图：1,1S i ==；3,2S i ==；7,3S i ==；15,4S i ==；31,5S i ==，结束. 故选：C . 【点睛】本题考查了程序框图，意在考查学生的计算能力和理解能力.4．A解析：A 【解析】【分析】根据频率分布直方图得到各个时间段的人数，进而得到结果. 【详解】根据频率分布直方图可列下表：阅读时间（分）[0,10)[10,20)[20,30)[30,40)[40,50)[50,60]抽样人数（名）10182225205故选A.【点睛】这个题目考查了频率分布直方图的实际应用，以及样本体现整体的特征的应用，属于基础题.5．B解析：B【解析】分析：由题意逐一考查所给的说法是否正确即可.详解：逐一考查所给的说法：①由分层抽样的概念可知，取东部地区学生2400100240016001000⨯=++48人、中部地区学生1600100240016001000⨯=++32人、西部地区学生1000100240016001000⨯=++20人，题中的说法正确；②新生的人数较多，不适合用简单随机抽样的方法抽取人数，题中的说法错误；③西部地区学生小刘被选中的概率为1001 24001600100050=++，题中的说法正确；④中部地区学生小张被选中的概率为1001 24001600100050=++，题中的说法错误；综上可得，正确的说法是①③.本题选择B选项.点睛：本题主要考查分层抽样的概念，简单随机抽样的特征，古典概型概率公式等知识，意在考查学生的转化能力和计算求解能力.6．B解析：B【解析】【分析】利用倒取余数法可得化为五进制数.【详解】因为所以用倒取余数法得323，故选：B. 【点睛】本题考查十进制数和五进制数之间的转化，利用倒取余数法可解决此类问题.7．D解析：D 【解析】【分析】根据面积比的几何概型，即可求解飞针能从正方形孔中穿过的概率，得到答案. 【详解】由题意，边长为2的正方形的孔的面积为1224S =⨯=，又由半径为2的圆形纸板的面积为224S ππ=⨯=，根据面积比的几何概型，可得飞针能从正方形孔中穿过的概率为1414S P S ππ===，故选D. 【点睛】本题主要考查了面积比的几何概型的概率的计算，以及正方形的面积和圆的面积公式的应用，着重考查了推理与运算能力，属于基础题.8．D解析：D 【解析】【分析】利用回归直线过样本点中心可求回归方程，根据该方程可得正确的选项. 【详解】由$$1.5y x a=+，得x 每增一个单位长度，y 不一定增加1.5，而是大约增加1.5个单位长度，故选项,A B 错误；由已知表格中的数据，可知0123425x ++++==，2.2 4.3 4.5 4.8 6.74.55y ++++==，Q 回归直线必过样本的中心点()2,4.5，故C 错误；又4.5 1.52 1.5ˆˆa a =⨯+⇒=，∴回归方程为$1.5 1.5y x =+，当8x =时，y 的预测值为1.58 1.513.5⨯+=，故D 正确，故选：D. 【点睛】本题考查线性回归方程的性质及应用，注意回归直线过(),x y ，本题属于基础题.9．C解析：C【解析】【分析】由正方形ABNH 、DEFM 的面积相等，可得两正方形边长相等，设边长为3，由23CN NG AB ==，可得正方形MCNG 的边长为2，分别求出阴影部分的面积及多边形ABCDEFGH 的面积，由测度比为面积比得答案. 【详解】如图所示，由正方形ABNH 、DEFM 的面积相等，可得两正方形边长相等，设边长为3，由23CN NG AB ==，可得正方形MCNG 的边长为2，则阴影部分的面积为224⨯=，多边形ABCDEFGH 的面积为2332214⨯⨯-⨯=. 则向多边形ABCDEFGH 内投一点，则该点落在阴影部分内的概率为42147=. 故选：C.【点睛】本题主要考查了几何概型的概率的求法，关键是求出多边形ABCDEFGH 的面积，着重考查了推理与运算能力，以及数形结合的应用，属于基础题.10．A解析：A 【解析】设2名男生记为A 1,A 2,2名女生记为B 1,B 2,任意选择两人在星期六、星期日参加某公益活动,共有(A 1,A 2),(A 1,B 1),(A 1,B 2),(A 2,B 1),(A 2,B 2),(B 1,B 2),(A 2,A 1),(B 1,A 1),(B 2,A 1),(B 1,A 2),(B 2,A 2),(B 2,B 1)12种情况,而星期六安排一名男生、星期日安排一名女生共有(A 1,B 1),(A 1,B 2),(A 2,B 1),(A 2,B 2)4种情况,则发生的概率为P=41123=, 故选：A .11．A解析：A 【解析】【分析】先列出不超过11的素数,再列举出随机选取2个不同的数的情况,进而找到和小于等于10的情况,即可求解【详解】不超过11的素数有:2,3,5,7,11,共有5个, 随机选取2个不同的数可能为:()2,3,()2,5,()2,7,()2,11,()3,5,()3,7,()3,11,()5,7,()5,11,()7,11,共有10种情况, 其中和小于等于10的有:()2,3,()2,5,()2,7,()3,5,()3,7,共有5种情况, 则概率为51102P ==, 故选:A 【点睛】本题考查列举法求古典概型的概率,属于基础题12．C解析：C 【解析】试题分析：该程序框图所表示的算法功能为：235919S =+++=，故选C ．考点：程序框图．二、填空题13．【解析】【分析】将所有的基本事件全部列举出来确定基本事件的总数并确定所求事件所包含的基本事件数然后利用古典概型的概率公式求出答案【详解】所有的基本事件有：（甲乙丙）（乙甲丙）（丙甲乙）（甲乙丙）（甲解析：16【解析】【分析】将所有的基本事件全部列举出来，确定基本事件的总数，并确定所求事件所包含的基本事件数，然后利用古典概型的概率公式求出答案．【详解】所有的基本事件有：（甲、乙丙）、（乙，甲丙）、（丙、甲乙）、（甲乙、丙）、（甲丙、乙）、（乙丙、甲）（其中前面的表示派往大武口区调研的专家），共6个，因此，所求的事件的概率为16，故答案为16．【点睛】本题考查古典概型概率的计算，解决这类问题的关键在于确定基本事件的数目，一般利用枚举法和数状图法来列举，遵循不重不漏的基本原则，考查计算能力，属于基础题．14．【解析】【分析】根据题意画出图形求出写作业所对应的区域面积利用得到结果【详解】由题意可知当豆子落在下图中的空白部分时小明在家写作业大正方形面积；阴影正方形面积空白区域面积：根据几何概型可知小明不在家解析：5π4- 【解析】【分析】根据题意画出图形，求出写作业所对应的区域面积，利用()()1P A P A =-得到结果. 【详解】由题意可知，当豆子落在下图中的空白部分时，小明在家写作业∴大正方形面积111S =⨯=；阴影正方形面积1111224S =⨯= 空白区域面积：22111244S ππ-⎛⎫=⨯-= ⎪⎝⎭根据几何概型可知，小明不在家写作业的概率为：2514S P S π-=-= 本题正确结果：54π- 【点睛】本题考查几何概型中的面积型，属于基础题.15．3【解析】【分析】分析出算法的功能是求分段函数的值根据输出的值为10分别求出当时和当时的值即可【详解】由程序语句知：算法的功能是求的值当时解得(或不合題意舍去)；当时解得舍去综上的值为3故答案为3【解析：3 【解析】【分析】分析出算法的功能是求分段函数22,31,3x x y x x <⎧=⎨+≥⎩的值，根据输出的值为10 ,分别求出当3x <时和当3x ≥时的x 值即可. 【详解】由程序语句知：算法的功能是求22,31,3x x y x x <⎧=⎨+≥⎩的值，当3x ≥时，2110y x =+=，解得3x =(或3- ,不合題意舍去)；当3x <时，210y x ==,解得5x = ,舍去，综上，x 的值为3，故答案为3 . 【点睛】本题主要考查条件语句以及算法的应用，属于中档题 .算法是新课标高考的一大热点，其中算法的交汇性问题已成为高考的一大亮，这类问题常常与函数、数列、不等式等交汇自然，很好地考查考生的信息处理能力及综合运用知识解决问題的能力，解决算法的交汇性问题的方：（1）读懂程序框图、明确交汇知识，(2）根据给出问题与程序框图处理问题即可.16．1-π12【解析】【分析】由题意得长方形的面积为S=3×2=6以O 点为原型半径为1作圆此时圆在长方形内部的部分的面积为Sn=π2再由面积比的几何概型即可求解【详解】由题意如图所示可得长方形的面积为S 解析：【解析】【分析】由题意，得长方形的面积为，以O 点为原型，半径为1作圆，此时圆在长方形内部的部分的面积为，再由面积比的几何概型，即可求解.【详解】由题意，如图所示，可得长方形的面积为，以O 点为原型，半径为1作圆，此时圆在长方形内部的部分的面积为，所以取到的点到的距离大于1的表示圆的外部在矩形内部分部分，所以概率为.【点睛】本题主要考查了几何概型的概率的计算问题，解决此类问题的步骤：求出满足条件A 的基本事件对应的“几何度量”，再求出总的基本事件对应的“几何度量”，然后根据求解，着重考查了分析问题和解答问题的能力.17．2【解析】【分析】根据系统抽样的概念结合可得最后结果为2【详解】学生总数不能被容量整除根据系统抽样的方法应从总体中随机剔除个体保证整除∵故应从总体中随机剔除个体的数目是2故答案为2【点睛】本题主要考解析：2 【解析】【分析】根据系统抽样的概念结合2544262=⨯+，可得最后结果为2. 【详解】学生总数不能被容量整除，根据系统抽样的方法，应从总体中随机剔除个体，保证整除. ∵2544262=⨯+，故应从总体中随机剔除个体的数目是2，故答案为2. 【点睛】本题主要考查系统抽样，属于基础题；从容量为N 的总体中抽取容量为n 的样本，系统抽样的前面两个步骤是：（1）将总体中的N 个个体进行编号；（2）当Nn为整数时，抽样距即为N n ；当N n 不是整数时，从总体中剔除一些个体，使剩下的总体中的个体的个数N '能被n 整除．18．30【解析】由题意可得：则成绩不低于分的人数为人解析：30 【解析】由题意可得：()400.0150.0300.0250.0051030⨯+++⨯=则成绩不低于60分的人数为30人19．【解析】【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量S 的值模拟程序的运行过程分析循环中各变量值的变化情况可得答案【详解】模拟程序的运行可得满足条件执行循环体满足条件执行循解析：7【解析】【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量S 的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．【详解】模拟程序的运行，可得1S =，1i =满足条件4i <，执行循环体，2S =，2i = 满足条件4i <，执行循环体，4S =，3i = 满足条件4i <，执行循环体，7S =，4i =此时，不满足条件4i <，退出循环，输出S 的值为7．故答案为7．【点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.20．【解析】【分析】根据系统抽样的特征求出分段间隔即可【详解】根据系统抽样的特征得：从2100名学生中抽取100个学生分段间隔为故答案是21【点睛】该题所考查的是有关系统抽样的组距问题应用总体除以样本容解析：21【解析】【分析】根据系统抽样的特征，求出分段间隔即可. 【详解】根据系统抽样的特征，得：从2100名学生中抽取100个学生，分段间隔为210021100=，故答案是21. 【点睛】该题所考查的是有关系统抽样的组距问题，应用总体除以样本容量等于组距，得到结果，属于简单题目.三、解答题21．（1）平均数为41.5岁；中位数为42.1岁（2）35【解析】【分析】（1）先根据频率分布直方图求出a ，再求其平均值.（2）按照分层抽样的方式抽取的人数分别为2人，3人, 设第1组抽取的人员为12,a a ；第2组抽取的人员为123,,b b b .列举出随机抽取两人的情况，再求出概率. 【详解】解：（1）由10(0.0100.0150.0300.010)1a ⨯++++=，得0.035a =，平均数为200.1300.15400.35500.3600.141.5⨯+⨯+⨯+⨯+⨯=岁；设中位数为x ，则100.010100.015(35)0.0350.5⨯+⨯+-⨯=x ，∴42.1x ≈岁. （2）根据题意，第1，2组分的人数分别为1000.110⨯=人，1000.1515⨯=人，按照分层抽样的方式抽取的人数分别为2人，3人.设第1组抽取的人员为12,a a ；第2组抽取的人员为123,,b b b . 于是，在5人随机抽取两人的情况有：()12,a a ，()()()111213,, ,, ,a b a b a b ， ()()()212223,, ,, ,a b a b a b ， ()()()121323,,,,,b b b b b b 共10种.满足题意的有：()()()()()()111213212223,, ,, ,, ,, ,, ,a b a b a b a b a b a b 共6种. 所以第2组恰好抽到1人的概率63105p ==. 【点睛】本题考查频率分布直方图，求平均值，考查概率，属于中档题. 22．（1）0.35；（2）7；（3）分布列见解析；数学期望65. 【解析】【分析】（1）用1减去频率直方图中位于区间[)3.5,6.5和[]7.5,10.5的矩形的面积之和可得出结果；（2）将各区间的中点值乘以对应的频率，再将所得的积全部相加即可得出所求平均数；（3）由题意可知34,10X B ⎛⎫⎪⎝⎭:，利用二项分布可得出随机变量X 的概率分布列，并利用二项分布的均值可计算出随机变量X 的数学期望. 【详解】（1）依题意，此人这三年以来每周开车从家到公司的时间之和在[)6.5,7.5（时）内的频率为10.030.10.20.190.090.040.35------=；（2）所求平均数为40.0350.160.270.3580.1990.09100.047x =⨯+⨯+⨯+⨯+⨯+⨯+⨯=（时）；（3）依题意，34,10X B ⎛⎫ ⎪⎝⎭:.()47240101010000P X ⎛⎫=== ⎪⎝⎭，()314371029110102500P X C ⎛⎫⎛⎫=== ⎪⎪⎝⎭⎝⎭，()2224371323210105000P X C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭，()33437189310102500P X C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭，()438141010000P X ⎛⎫=== ⎪⎝⎭. 故X 的分布列为故()364105E X =⨯=. 【点睛】本题考查频率分布直方图中频率和平均数的计算，同时也考查了二项分布的概率分布列和数学期望的计算，考查计算能力，属于中等题. 23．(1)30;(2)54,55;(3) X 的分布列如下：数学期望3EX = 【解析】试题分析：（1）由频率分布直方图知年龄在[40，70）的频率为（0.020+0.030+0.025）×10，进而得出40 名读书者中年龄分布在[40，70）的人数．（2）40 名读书者年龄的平均数为25×0.05+35×0.1+45×0.2+55×0.3+65×0.25+75×0.1．计算频率为12处所对应的数据即可得出中位数．（3）年龄在[20，30）的读书者有2人，年龄在[30，40）的读书者有4人，所以X 的所有可能取值是0，1，2．利用超几何分布列计算公式即可得出．试题解析：（1）由频率分布直方图知年龄在[)40,70的频率为()0.0200.0300.025100.75++⨯=，所以40名读书者中年龄分布在[)40,70的人数为400.7530⨯=. （2）40名读书者年龄的平均数为250.05350.1450.2550.3⨯+⨯+⨯+⨯ 650.25750.154+⨯+⨯=.设中位数为x ，则()0.005100.01100.02100.03500.5x ⨯+⨯+⨯+⨯-= 解得55x =，即40名读书者年龄的中位数为55. （3）年龄在[)20,30的读书者有0.00510402⨯⨯=人，年龄在[)30,40的读书者有0.0110404⨯⨯=人，所以X 的所有可能取值是0,1,2，()2024241015C C P X C ===， ()1124248115C C P X C ===，()0224246215C C P X C ===， X 的分布列如下：X0 1 2P115815 615数学期望18640121515153EX =⨯+⨯+⨯=. 24．（1），（2）【解析】【分析】【详解】（1）从袋子中随机取两个球，其一切可能的结果组成的基本事件有1和2,1和3,1和4,2和3,2和4,3和4，共6个，从袋中随机取出的球的编号之和不大于4的事件共有1和2,1和3两个．因此所求事件的概率为.（2）先从袋中随机取一个球，记下编号为m ，放回后，在从袋中随机取一个球，记下编号为n ，其中一切可能的结果（m ，n ）有：（1,1）（1,2），（1,3），（1,4），（2,1），（2,2），（2,3），（2,4），（3,1）（3， 2），（3,3）（3,4），（4,1），（4,2），（4,3），（4,4），共16个．所有满足条件n≥m ＋2的事件为（1,3）（1,4）（2,4），共3个，所以满足条件n≥m ＋2的事件的概率为P1＝316故满足条件n ＜m ＋2的事件的概率为1－P1＝1－316＝.25．（1）0.01P =,n =100,（2）表见解析，没有95%以上的把握认为“读书之星”与性别有关（3）分布列见解析，()34E X = 【解析】【分析】（1）首先根据频率和为1求P ，再根据频率，频数和样本容量的关系求n ；（2）首先计算“读书之星”的人数，然后再依次填写22⨯列联表；并根据公式计算2K 和3.841比较大小，做出判断；（3）从该地区学生中抽取一名学生是“读书之星”的概率为14，由题意可知1~3,4X B ⎛⎫⎪⎝⎭并求分布列和数学期望. 【详解】（1）()0.0050.0180.0200.0220.025101P +++++⨯=。

2020-2021学年高二上学期期末考试数学试卷(含解析)

2020-2021学年高二上学期期末考试数学试卷学校:___________姓名：___________班级：___________考号：___________一、单选题1．若3324A 10A n n =，则n =（）A ．1B ．8C ．9D ．102．期末考试结束后，某班要安排6节课进行试卷讲评，要求课程表中要排入语文、数学、英语、物理、化学、生物共六节课，如果第一节课只能排语文或数学，最后一节不能排语文，则不同的排法共有（） A ．192种B ．216种C ．240种D ．288种3．一台X 型号自动机床在一小时内不需要工人照看的概率为0.8，有4台这种型号的自动机床各自独立工作，则在一小时内至多2台机床需要工人照看的概率是（） A ．0.1536B ．0.1808C ．0.5632D ．0.97284．某市气象部门根据2021年各月的每天最高气温平均值与最低气温平均值（单位：℃）数据，绘制如下折线图：那么，下列叙述错误的是（）A ．各月最高气温平均值与最低气温平均值总体呈正相关B ．全年中，2月份的最高气温平均值与最低气温平均值的差值最大C ．全年中各月最低气温平均值不高于10℃的月份有5个D ．从2021年7月至12月该市每天最高气温平均值与最低气温平均值都呈下降趋势5．若()2N 1,X σ~，则()0.6827P X μσμσ-<≤+=，(22)0.9545P X μσμσ-<≤+=，已知()21,3X N ~，则(47)P X <≤=（）A ．0.4077B ．0.2718C ．0.1359D ．0.04536．为了评价某个电视栏目的改革效果，在改革前后分别从居民点抽取了100位居民进行调查，经过计算()200.01P K k ≥=，根据这一数据分析，下列说法正确的是（）A ．有1%的人认为该栏目优秀；B ．有1%的把握认为该栏目是否优秀与改革有关系；C ．有99%的把握认为电视栏目是否优秀与改革有关系；D ．没有理由认为电视栏目是否优秀与改革有关系.7．若1021001210)x a a x a x a x =++++，则012310a a a a a -+-++的值为．A 1B 1C ．101)D ．101)8．关于()72x +的二项展开式，下列说法正确的是（） A ．()72x +的二项展开式的各项系数和为73B ．()72x +的二项展开式的第五项与()72x +的二项展开式的第五项相同C ．()72x +的二项展开式的第三项系数为4372CD ．()72x +的二项展开式第二项的二项式系数为712C9．如图，某建筑工地搭建的脚手架局部类似于一个3×2×3的长方体框架，一个建筑工人欲从A 处沿脚手架攀登至B 处，则其最近的行走路线中不连续向上攀登的概率为（）A ．528B ．514C ．29D ．1210．三棱锥P ABC -中P A ､PB ､PC 两两互相垂直，4PA PB +=，3PC =，则其体积（） A ．有最大值4B ．有最大值2C ．有最小值2D ．有最小值4二、填空题11．最小二乘法得到一组数据(),(1,2,3,4,5)i i x y i =的线性回归方程为ˆ23yx =+，若5125ii x==∑，则51i i y ==∑___________.12．某班举行的联欢会由5个节目组成,节目演出顺序要求如下: 节目甲不能排在第一个,并且节目甲必须和节目乙相邻.则该班联欢会节目演出顺序的编排方案共有____种. 13．若随机变量X 的概率分布如表，则表中a 的值为______.14．设随机变量ξ~B (2，p )，若P (ξ≥1)=59，则D (ξ)的值为_________.15．已知等差数列{}n a 中，33a =，则1a 和5a 乘积的最大值是______.16．某次知识竞赛规则如下：在主办方预设的5个问题中，选手若能连续正确回答出两个问题，即停止答题，晋级下一轮假设某选手正确回答每个问题的概率都是0.8，且每个问题的回答结果相互独立，则该选手恰好回答了5个问题就晋级下一轮的概率为___________.17．经统计，在银行一个营业窗口每天上午9点钟排队等候的人数及相应概率如下：则该营业窗口上午9点钟时，至少有2人排队的概率是_____．18．点A ，B ，C 在球O 表面上，2AB =，BC =90ABC ∠=︒，若球心O 到截面ABC的距离为___________.19．如图，在三棱柱111ABC A B C -中，四边形11AAC C 是边长为4的正方形，平面ABC ⊥平面11AAC C ，3AB =，5BC =.（℃）求证：1AA ⊥平面；（℃）若点E 是线段的中点，请问在线段是否存在点E ，使得面11AAC C ？若存在，请说明点E 的位置，若不存在，请说明理由；（℃）求二面角的大小.20．四根绳子上共挂有10只气球,绳子上的球数依次为1,2,3,4，每枪只能打破一只球,而且规定只有打破下面的球才能打上面的球,则将这些气球都打破的不同打法数是________.三、解答题21．已知集合(){}()12,,,|,1,2,,1nn i R x x x x R i n n =∈=≥，定义n R 上两点()12,,,n A a a a ，()12,,,n B b b b 的距离()1,ni i i d A B a b ==-∑.（1）当2n =时，以下命题正确的有__________（不需证明）： ℃若()1,2A ，()4,6B ，则(),7d A B =；℃在ABC 中，若90C =∠，则()()()222,,,d A C d C B d A B ⎡⎤⎡⎤⎡⎤+=⎣⎦⎣⎦⎣⎦； ℃在ABC 中，若()(),,d A B d A C =，则B C ∠=∠;（2）当2n =时，证明2R 中任意三点A B C ，，满足关系()()(),,,d A B d A C d C B ≤+；（3）当3n =时，设()0,0,0A ，()4,4,4B ，(),,P x y z ，其中x y z Z ∈，，，()()(),,,d A P d P B d A B +=.求满足P 点的个数n ，并证明从这n 个点中任取11个点，其中必存在4个点，它们共面或者以它们为顶点的三棱锥体积不大于83.22．今年4月，教育部办公厅印发了《关于加强义务教育学校作业管理的通知》，规定初中学生书面作业平均完成时长不超过90分钟．某市为了更好地贯彻落实“双减”工作要求，作教育决策，该市教育科学研究院就当前全市初三学生每天完成书面作业时长抽样调查，结果是学生书面作业时长（单位：分钟）都在区间[]50,100内，书面作业时长的频率分布直方图如下：(1)若决策要求：在国家政策范围内，若当前初三学生书面作业时长的中位数估计值大于或等于平均数（计算平均数时，同一组中的数据用该区间的中点值代表）估计值，则减少作业时长；若中位数估计值小于平均数，则维持现状．请问：根据这次调查，该市应该如何决策？(2)调查统计时约定：书面作业时长在区间[]90,100内的为A 层次学生，在区间[)80,90内的为B 层次学生，在区间[70,80)内的为C 层次学生，在其它区间内的为D 层次学生．现对书面作业时长在70分钟以上（含70分钟）的初三学生，按作业时长出现的频率用分层抽样的方法随机抽取8人，再从这8人中随机抽取3人作进一步调查，设这3人来自X 个不同层次，求随机变量X 的分布列及数学期望．23．国家文明城市评审委员会对甲､乙两个城市是否能入围“国家文明城市”进行走访调查.派出10人的调查组.先后到甲､乙两个城市的街道､社区进行问卷调查，然后打分（满分100分）.他们给出甲､乙两个城市分数的茎叶图如图所示：(1)请你用统计学的知识分析哪个城市更应该入围“国家文明城市”，请说明理由；(2)从甲､乙两个城市的打分中各抽取2个，在已知有大于80分的条件下，求抽到乙城市的分数都小于80分的概率；(3)从对乙城市的打分中任取2个，设这2个分数中不小于80分的个数为X，求X的分布列和期望.参考答案：1．B【分析】根据排列数的运算求解即可.【详解】由332A 10A n n =得，2(21)(22)10(1)(2)n n n n n n --=--，又3,n n *≥∈N ，所以2(21)5(2)n n -=-，解得8n =，所以正整数n 为8．故选：B. 2．B【分析】对第一节课的安排进行分类讨论，结合分步乘法计数原理和分类加法计数原理可得结果.【详解】分以下两种情况讨论：℃若第一节课安排语文，则后面五节课的安排无限制，此时共有55A 种；℃若第一节课安排数学，则语文可安排在中间四节课中的任何一节，此时共有444A 种.综上所述，不同的排法共有54544216A A +=种.故选：B. 3．D【详解】设在一个小时内有ξ台机床需要工人照看，则ξ～B (4,0.2)，所以P (ξ≤2)＝04C (0.8)4＋14C (0.8)3×0.2＋24C (0.8)2×(0.2)2＝0.972 8. 故选D 4．D【分析】利用折线图可以判断选项ABC 正确，从2021年7月至12月该市每天最高气温平均值与最低气温平均值，先上升后下降，所以选项D 错误.【详解】解：由2021年各月的每天最高气温平均值和最低气温平均值（单位：C)︒数据，绘制出的折线图，知：在A 中，各月最高气温平均值与最低气温平均值为正相关，故A 正确；在B 中，全年中，2月的最高气温平均值与最低气温平均值的差值最大，故B 正确；在C 中，全年中各月最低气温平均值不高于10C ︒的月份有1月，2月，3月，11月，12月，共5个，故C 正确；在D 中，从2021年7月至12月该市每天最高气温平均值与最低气温平均值，先上升后下降，故D 错误. 故选：D ． 5．C【分析】由题意，得(47)(2)P X P X μσμσ<≤=+<≤+，再利用3σ原则代入计算即可.【详解】℃()21,3X N ~，由()0.6827P X μσμσ-<≤+=，(22)0.9545P X μσμσ-<≤+=，℃1(47)(2)(0.95450.6827)0.13592P X P X μσμσ<≤=+<≤+=-=.故选：C 6．C【分析】利用独立性检验的基本原理即可求出答案．【详解】解：℃()200.01P K k ≥=表示“电视栏目是否优秀与改革没有关系”的概率，℃有99%的把握认为电视栏目是否优秀与改革有关系，故选：C ．【点睛】本题主要考查独立性检验的基本应用，准确的理解判断方法是解决本题的关键，属于基础题． 7．D【详解】分析：令1021001210())f x x a a x a x a x ==++++，再求f(-1)的值得解.详解：令1021001210())f x x a a x a x a x ==++++，1001210(1)1)f a a a a -==-+++．故答案为D ．点睛：（1）本题主要考查二项式定理中的系数求法问题，意在考查学生对这些基础知识的掌握水平.(2) 二项展开式的系数0123,,,,n a a a a a ⋅⋅⋅的性质：对于2012()?··n n f x a a x a x a x =++++，0123(1)n a a a a a f ++++⋅⋅⋅+=， 0123(1)(1)n n a a a a a f -+-+⋅⋅⋅+-=-.8．A【分析】利用赋值法求出展开式各项系数和，即可判断A ，根据二项式展开式的通项，即可判断B 、C 、D ；【详解】解：()72x +展开式的通项为7172rrr r T C x -+=⋅⋅，故第二项的二项式系数为177C =，故D 错误；第三项的系数为2572C ⋅，故C 错误；()72x +的展开式的第五项为43472C x ⋅⋅，()72x +的展开式的第五项为44372C x ⋅⋅，故B 错误；令1x =则()7723x +=，即()72x +的二项展开式的各项系数和为73，故A 正确；故选：A 9．B【解析】将问题抽象成“向左三次，向前两次，向上三次”，计算出总的方法数，然后利用插空法计算出最近的行走路线中不连续向上攀登的事件数，最后根据古典概型概率计算公式，计算出所求概率.【详解】从A 的方向看，行走方向有三个：左、前、上. 从A 到B 的最近的行走线路，需要向左三次，向前两次，向上三次，共8次.所以从A 到B 的最近的行走线路，总的方法数有88332332560A A A A =⋅⋅种. 不连续向上攀登的安排方法是：先将向左、向前的安排好，再对向上的方法进行插空.故方法数有：53563232200A C A A ⨯=⋅.所以最近的行走路线中不连续向上攀登的概率为200556014=. 故选：B【点睛】本小题主要考查古典概型的计算，考查有重复的排列组合问题，考查插空法，属于中档题. 10．B【分析】依题意可得1113332P ABC PABV PC SPA PB -=⋅=⨯⨯⋅再利用基本不等式计算可得；【详解】解：依题意21111132332222P ABCPABPA PB V PC S PA PB PA PB -+⎛⎫=⋅=⨯⨯⋅=⋅≤= ⎪⎝⎭，当且仅当2PA PB ==时取等号，所以()max 2P ABC V -=，故选：B11．65【分析】由最小二乘法得到的线性回归方程过点(),x y ，代入即可解决【详解】由5125i i x ==∑可知，数据的平均数2555x ==，又线性回归方程ˆ23yx =+过点(),x y ，所以25313y =⨯+=，故51551365i i y y ===⨯=∑故答案为：65 12．42【分析】由题意可知，甲可排在第二、三、四、五个，再根据甲、乙相邻，分别计算. 【详解】由题意可知，甲可排在第二、三、四、五个，当甲排在第二、三、四个时，甲乙相邻，有22A 种排法，将甲乙当做一个整体，剩下三个节目全排列，共3×22A ×33A =36种当甲排在第五个时，甲乙相邻，只有一种排法，剩下三个节目全排列，共33A =6种综上，编排方案共36+6=42种【点睛】本题考查了分类计数原理，分类时要注意不重不漏；解决排列问题时，相邻问题常用捆绑法，特殊位置要优先考虑. 13．0.2【解析】利用概率和为1可求出答案. 【详解】由随机变量X 的概率分布表得： 0.20.30.31a +++=，解得0.2a =. 故答案为：0.2【点睛】本题考查的是分布列的性质，较简单. 14．49【分析】由二项分布的特征，先求出13p =，套公式即可求出D (ξ). 【详解】因为随机变量ξ~B (2，p )，且P (ξ≥1)=59，所以P (ξ≥1)=()11P ξ-<= ()10P ξ-==()25119p --=. 解得：13p =. 所以D (ξ)()12412339np p =-=⨯⨯=.故答案为：4915．9【分析】设出公差，根据等差数列的性质，表示出15,a a ，再列式即可求得结果. 【详解】因为{}n a 是等差数列，设公差为d ，可得13532,2a a d a a d =-=+，于是得()()2153322949a a a d a d d =-+=-≤，当且仅当d =0，即153a a ==时，取得最大值. 故答案为：9.【点睛】本题考查等差数列的下标和性质，属基础题. 16．1443125##0.04608 【分析】认真分析该选手所有可能的答题情况，是本题的关键【详解】由该选手恰好回答了5个问题就晋级下一轮，说明他第4、第5两个问题是连续答对的，第3个问题没有答对，第1和第2两个问题也没有全部答对，即他答题结果可能有三种情况：⨯⨯⨯√√或⨯√⨯√√或√⨯⨯√√，根据独立事件同时发生的概率公式，可得该选手恰好回答了5个问题就晋级下一轮的概率为0.20.20.20.80.8+0.20.80.20.80.8+0.80.20.20.80.8=0.04608⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯故答案为：0.04608 17．0.74【详解】试题分析：x 表示人数，(2)(2)(3)(4)(5)P x P x P x P x P x ≥==+=+=+≥0.30.30.10.040.74=+++=.考点：互斥事件的概率.18．【分析】根据截面圆性质，先求出截面圆半径，然后由求得球半径，从而求得体积．【详解】因为2AB =，BC =90ABC ∠=︒，所以4AC ==，所以三角形外接圆半径22ACr ==，又球心O 到截面ABC 的距离为R =球体积为(334433V R ππ==⨯=．故答案为：．19．（℃）（℃）（℃）见解析【详解】试题分析：（℃）由正方形的性质得1AC AA ⊥，然后由面面垂直的性质定理可证得结果；（℃）当点E 是线段1AB 的中点时，利用中位线定理可得1DE AC ，进而得出DE 面11AAC C ；（℃）利用二面角的定义先确定11C AC ∠是二面角111C A B C --的平面角，易求得11tan C A C ∠，从而求得二面角的平面角为的度数．试题解析：（℃）因为四边形11AAC C 为正方形，所以1AC AA ⊥．因为平面ABC ⊥平面11AAC C ，且平面ABC ⋂平面11AAC C AC =，所以1AA ⊥平面ABC ．（℃）当点E 是线段1AB 的中点时，有DE 面11AAC C ，连结1AB 交1AB 于点E ，连结BC ，因为点E 是1AB 中点，点⊄是线段DE 的中点，所以1DE AC ．又因为BC ⊂面11AAC C ，11A C 面11AAC C ，所以DE 面11AAC C .（℃）因为1AA ⊥平面ABC ，所以.又因为，所以面11AAC C ，所以11A B ⊥面11AAC C ，所以11A B ⊥1A C ，11A B ⊥11A C ，所以11C AC ∠是二面角111C A B C --的平面角，易得，所以二面角111C A B C --的平面角为45°.考点：1、线面垂直的判定；2、线面平行的判定；2、二面角．【方法点睛】立体几何中的探索性问题主要是对平行、垂直关系的探究，对条件和结论不完备的开放性问题的探究．解决这类问题时一般根据探索性问题的设问，假设其存在并探索出结论，然后在假设下进行推理，若得到合乎情理的结论就肯定假设，若得到矛盾就否定假设． 20．12600【详解】问题等价于编号为1,2,3,10的10个小球排列，其中2,3号，4,5,6号，7,8,9,10号的排列顺序是固定的，据此可得：将这些气球都打破的不同打法数是101023423412600A A A A =⨯⨯. 21．（1）℃；（2）证明见解析；（3）125n =，证明见解析．【解析】（1）℃根据新定义直接计算．℃根据新定义，写出等式两边的表达式，观察它们是否相同，即可判断；℃由新定义写出等式()(),,d A B d A C =的表达式，观察有无AB AC =；（2）由新定义，写出不等式两边的表达式，根据绝对值的性质证明；（3）根据新定义，及绝对值的性质得P 点是以AB 为对角线的正方体的表面和内部的整数点，共125个，把它们分布在五个平面(0,1,2,3,4)z =上，这五个面一个面取3个点，相邻面上取一个点，以它们为顶点构成三棱锥（能构成时），棱锥的体积不超过83，然后任取11点中如果没有4点共面，但至少有一个平面内有3个点．根据这3点所在平面分类讨论可得．【详解】（1）当2n =时，℃若()1,2A ，()4,6B ，则(),41627d A B =-+-=，℃正确；℃在ABC 中，若90C =∠，则222AC BC AB +=，设112233(,),(,),(,)A x y B x y C x y ，所以222222131323231212()()()()()()x x y y x x y y x x y y -+-+-+-=-+-而()2221212121221212()()()2)),((x x y y x x y y d A x B x y y =⎡⎤⎣-+-+⎦=--+--， ()()22,,d A C d C B ⎡⎤⎡⎤+=⎣⎦⎣⎦22221313232313132323()()()()2()()2()()x x y y x x y y x x y y x x y y -+-+-+-+--+--，但1313232312122()()2()()2()()x x y y x x y y x x y y --+--=--不一定成立，℃错误； ℃在ABC 中，若()(),,d A B d A C =，在℃中的点坐标，有12121313x x y y x x y y -+-=-+-，但1212131322x x y y x x y y -⋅-=-⋅-不一定成立，因此AB AC =不一定成立，从而B C ∠=∠不一定成立，℃错误．空格处填℃（2）证明：设112233(,),(,),(,)A x y B x y C x y ，根据绝对值的性质有132312x x x x x x -+-≥-，132312y y y y y y -+-≥-，所以(,)(,)(,)d A C d B C d A B +≥．,（3）(,)12d A B =，44,44,44x x y y z z +-≥+-≥+-≥，所以(,)(,)12d A P d B P +≥，当且仅当以上三个等号同时成立，(,)(,)12d A P d B P +=又由已知()()(),,,d A P d P B d A B +=，℃04,04,04x y z ≤≤≤≤≤≤，又,,x y z Z ∈，℃,,0,1,2,3,4x y z =，555125⨯⨯=，点P 是以AB 为对角线的正方体内部（含面上）的整数点，共125个，125n =．这125个点在0,1,2,3,4z z z z z =====这五面内．这三个平面内，一个面上取不共线的3点，相邻面上再取一点构成一个三棱锥．则这个三棱锥的体积最大为118441323V =⨯⨯⨯⨯=，现在任取11个点，若有四点共面，则命题已成立，若其中无4点共面，但11个点分在5个平面上至少有一个平面内有3个点（显然不共线），若这三点在1,2,3z z z ===这三个平面中的一个上，与这个面相邻的两个面上如果有一点，那么这一点与平面上的三点这四点可构成三棱锥的四个顶点，其体积不超过83，否则还有8个点在平面0z =和4z =上，不合题意，若这三个点在平面0z =或5z =上，不妨设在平面0z =，若在平面1z =在一个点，则同样四点构成的三棱锥体积不超过83，否则剩下的8个点在2,3,4z z z ===三个平面上，只能是3，3，2分布，不管哪一种分布都有四点构成的三棱锥体积不超过83，综上，任取11个点，其中必存在4个点，它们共面或者以它们为顶点的三棱锥体积不大于83.【点睛】关键点点睛：本题新定义距离(,)d A B ，解题关键是利用新定义转化为绝对值，利用绝对值的性质解决一些问题．本题还考查了抽屉原理，11个放在5个平面上，至少有一个平面内至少有3点，由此分类讨论可证明结论成立． 22．(1)该市应该作出减少作业时长的决策； (2)分布列见解析；期望为167.【分析】（1）根据题意，结合频率分布直方图，分别求出中位数和平均数，即可求解；（2）根据题意，结合分层抽样以及离散型随机变量的分布列与期望求法，即可求解. (1)作业时长中位数的估计值为直方图中等分面积的线对立的值，设为x ．0.01100.01100.02100.5⨯+⨯+⨯<． 0.01100.01100.02100.03100.5⨯+⨯+⨯+⨯>，()0.01100.01100.02100.03800.5x ∴⨯+⨯+⨯+⨯-=．解得2503x =，即中位数的故计值2503分钟．又作业时长平均数估计值为0.0110550.0110650.021075⨯⨯+⨯⨯+⨯⨯ 2500.0310850.031095813+⨯⨯+⨯⨯=<．因为中位数的估计值2503分钟大于平均数估计值81分钟，所以，根据这次调查，该市应该作出减少作业时长的决策. (2)由题，作业时长在70分钟以上（含70分钟）为[90.100]，[80,90)，[70,80)三个区间，其频率比为3：3：2，分别对应A ，B ，C 三个层次．根据分层抽样的方法，易知各层次抽取的人数分别为3，3，2，因此X 的所有可能值为1，2，3．因为333821(1)28C P X C ⨯===，111233389(3)28C C C P X C ⋅⋅===， 121221333232382229(2)14C C C C C C P X C ⨯⋅+⨯⋅+⨯⋅===，所以X 的分在列为：故数学期望19916()1232814287E X =⨯+⨯+⨯=. 23．(1)乙城市更应该入围“国家文明城市”．理由见解析． (2)425； (3)分布列见解析，期望为1．【分析】（1）根据得分的平均值与方差说明，极差最值也可用来说明；（2）记抽到的数据中有大于80分为事件A ，甲城市抽到的分数有大于80分为事件B ，乙城市抽到的分数有大于80分为事件C ，由()()(|)()()P AC P C P C A P A P A ==计算；（2）X 的可能值是0,1,2，分别求得概率得概率分布列，由期望公式计算出期望． (1)乙城市更应该入围“国家文明城市”．理由如下：由茎叶图，计算两个城市的得分的均值为甲：6365987910x +++==，乙：6568927910y +++==，均值相等，方差为甲：222211[(16)(14)19]13610s =-+-++=，乙：222221[(14)(11)13]59.810s =-+-++=，甲的方差远大于乙的方差，说明乙的得分较稳定，甲极其不稳定，因此乙城市更应该入围“国家文明城市”． (2)记抽到的数据中有大于80分为事件A ，甲城市抽到的分数有大于80分为事件B ，乙城市抽到的分数有大于80分为事件C ，262102()13C P B C =-=，252107()19C P C C =-=，2725()1(1)(1)3927P A =--⨯-=，7()()9P AC P C ==，所以()()()()749(|)1(|)111252527P AC P C P C A P C A P A P A =-=-=-=-=；(3)乙城市10个人中5个大于80分，5个小于80，X 的可能是0,1,2，252102(0)9C P X C ===，11552105(1)9C C P X C ===，252102(2)9C P X C ===，所以X 的分布列为：52()12199E X =⨯+⨯=．。

2020-2021成都市高二数学上期末试卷含答案

2020-2021成都市高二数学上期末试卷含答案一、选择题1．口袋里装有大小相同的5个小球，其中2个白球，3个红球，现一次性从中任意取出3个，则其中至少有1个白球的概率为（）A．910B．710C．310D．1102．气象意义上的春季进入夏季的标志为连续5天的日平均温度不低于022C.现有甲、乙、丙三地连续5天的日平均气温的记录数据（记录数据都是正整数）：①甲地：5个数据是中位数为24，众数为22；②乙地：5个数据是中位数为27，总体均值为24；③丙地：5个数据中有一个数据是32，总体均值为26，总体方差为10.8则肯定进入夏季的地区有（）A．①②③B．①③C．②③D．①3．我国古代数学著作《九章算术》中，其意是：“今有器中米，不知其数，前人取半，中人三分取一，后人四分取一，余米一斗五升．问：米几何？右图是源于其思想的一个程序框图，若输出的2S （单位：升），则输入k的值为A．6 B．7 C．8 D．94．某高校大一新生中,来自东部地区的学生有2400人、中部地区学生有1600人、西部地区学生有1000人.从中选取100人作样本调研饮食习惯,为保证调研结果相对准确,下列判断正确的有（）①用分层抽样的方法分别抽取东部地区学生48人、中部地区学生32人、西部地区学生20人；②用简单随机抽样的方法从新生中选出100人；③西部地区学生小刘被选中的概率为1 50；④中部地区学生小张被选中的概率为1 5000A．①④B．①③C．②④D．②③5．按照程序框图（如图所示）执行，第3 个输出的数是（）A ．6B ．5C ．4D ．36．要从其中有50个红球的1000个形状相同的球中，采用按颜色分层抽样的方法抽取100个进行分析，则应抽取红球的个数为（） A ．5个B ．10个C ．20个D ．45个7．执行如图的程序框图，如果输出的是a=341，那么判断框（）A ．4k <B ．5k <C ．6k <D ．7k < 8．设数据123,,,,n x x x x 是郑州市普通职工*(3,)n n n N ≥∈个人的年收入，若这n 个数据的中位数为x ，平均数为y ，方差为z ，如果再加上世界首富的年收入1n x +，则这1n +个数据中，下列说法正确的是（）A ．年收入平均数大大增大，中位数一定变大，方差可能不变B ．年收入平均数大大增大，中位数可能不变，方差变大C ．年收入平均数大大增大，中位数可能不变，方差也不变D ．年收入平均数可能不变，中位数可能不变，方差可能不变9．从2名男生和2名女生中任意选择两人在星期六、星期日参加某公益活动，每天一人，则星期六安排一名男生、星期日安排一名女生的概率为( ) A ．13B ．512C ．12D ．71210．从1,2,3，…，9中任取两数，其中：①恰有一个偶数和恰有一个奇数；②至少有一个奇数和两个都是奇数；③至少有一个奇数和两个都是偶数；④至少有一个奇数和至少有一个偶数．在上述事件中，是对立事件的是 ( )． A ．①B ．②④C ．③D ．①③11．我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”，如40337=+.（注：如果一个大于1的整数除1和自身外无其他正因数，则称这个整数为素数.）在不超过11的素数中，随机选取2个不同的数，其和小于等于10的概率是（） A ．12B ．13C ．14D ．1512．袋中装有红球3个、白球2个、黑球1个，从中任取2个，则互斥而不对立的两个事件是( )A ．至少有一个白球；都是白球B ．至少有一个白球；至少有一个红球C ．至少有一个白球；红、黑球各一个D ．恰有一个白球；一个白球一个黑球二、填空题13．根据党中央关于“精准脱贫”的要求，石嘴山市农业经济部门派3位专家对大武口、惠农2个区进行调研，每个区至少派1位专家，则甲，乙两位专家派遣至惠农区的概率为_____．14．如图，在半径为1的圆上随机地取两点,B E ，连成一条弦BE ，则弦长超过圆内接正BCD ∆边长的概率是__________．15．在[1,1]-上随机地取一个数k ，则事件“直线y kx =与圆22(5)9x y -+=相离”发生的概率为_______。

2020-2021学年四川省成都市高二(上)期末数学试卷(文科)

2020-2021学年四川省成都市高二（上）期末数学试卷（文科）一、单选题（本大题共12小题，共60.0分）1.命题“∃x0>0，lnx0≥x0−1”的否定是()A. ∀x>0，lnx<x−1B. ∀x≤0，lnx<x−1C. ∀x>0，lnx≤x−1D. ∃x0>0，lnx0<x0−12.若双曲线x2−y2b2=1(b>0)的一条渐近线方程为y=x，则该双曲线的离心率为()A. 54B. √2 C. 32D. 23.在空间直角坐标系Oxyz中，点(2,−1,1)在xOy平面上的射影到坐标原点O的距离为()A. √2B. √3C. √5D. √64.如图是2021年至2025年我国5G宏基站建设投资额预算(单位：亿元)的折线图，则以下结论不正确的是()A. 5年比较，2023年投资额预算达到最大值B. 逐年比较，2022年投资额预算增幅最大C. 2021年至2023年，投资额预算逐年增加D. 2021年至2023年，投资额预算增幅逐年增加5.若圆(x−a)2+y2=1(a>0)与直线y=√33x只有一个公共点，则a的值为()A. 1B. √3C. 2D. 2√36.如图是某次文艺比赛中七位评委为其中一位选手所打分数(满分为100分)的茎叶图.在去掉一个最高分和一个最低分后，所剩5个分数的方差为()A. 2√2B. 8C. 15D. 207.一个不透明盒子里装有标号为1，2，3，4，5的五张标签，现从中随机无放回地抽取两次，每次抽一张，则两次抽取的标签号数均为奇数的概率为()A. 15B. 310C. 825D. 258.已知两点A(−3,0)，B(3,0).若动点M满足|MA|2+|MB|2=d(d>0)，则“d≥18”是“动点M的轨迹是圆”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件9.甲、乙两艘轮船都要在某个泊位停靠6小时，假定他们在一昼夜时间内随机到达，试求这两艘船中至少有一艘在停靠泊位时必须等待的概率是()A. 716B. 516C. 916D. 111610.为了解某地区的人口年龄分布情况，某机构从该地区年龄在[20,80]内的居民中随机抽取了100位进行调查，并将年龄按[20,30)，[30,40)，[40,50)，[50,60)，[60,70)，[70,80]分组，得到如图所示的频率分布直方图.则下列说法正确的是()A. 频率分布直方图中a的值为0.017B. 这100位居民中有50位居民的年龄不低于60岁C. 估计这100位居民的平均年龄为53岁D. 该地区人口年龄分布在[50,60)的人数与分布在[20,30)的人数分别记为m，n，则m=9n一定成立11.已知抛物线x2=4y的焦点为F，P为抛物线上一点，过点P向抛物线的准线作垂线，垂足为N.若∠PNF=30°，则△PNF的面积为()A. 2√39B. 12C. 4√39D. 8√3912. 执行如图所示的程序语句，若输入m 的值为306，输出结果为17，则输入n 的值可能为( )A. 98B. 102C. 105D. 119二、单空题（本大题共4小题，共20.0分）13. 一组数据8，7，3，7，6，9的极差为______ ．14. 已知命题p ：若x <y ，则x 2<y 2；命题q ：∀m ∈R ，直线x −my −1=0与椭圆x 22+y 2=1恒有两个公共点.在命题①p ；②p ∨(￢q)；③(￢p)∧q 中，所有真命题的序号是______ ．15. 某公司从A ，B ，C ，D 四个女孩中选两位担任该公司的两个秘书职位.假定每个女孩是否被选中是等可能的，则事件“女孩A 或女孩B 被选中”的概率为______ ． 16. 已知椭圆C ：x 2a2+y 28=1(a >2√2)的左，右焦点分别为F 1，F 2，点P 在椭圆C 上且位于第一象限，∠F 1PF 2的平分线交x 轴于点M ，若F 1M ⃗⃗⃗⃗⃗⃗⃗⃗ =2MF 2⃗⃗⃗⃗⃗⃗⃗⃗ ，则a 的取值范围为______ ．三、解答题（本大题共6小题，共70.0分）17. 已知双曲线C ：x 2a 2−y 2b 2=1(a >0,b >0)的两个焦点分别为F 1(−√3,0)，F 2(√3,0)，且过点M(√3,2)．(Ⅰ)求双曲线C 的虚轴长；(Ⅱ)求与双曲线C 有相同渐近线，且过点P(−2,4)的双曲线的标准方程．18. 已知圆E 经过点A(−6,0)，B(2,0)，且圆心E 在直线y =−x 上．(Ⅰ)求圆E 的一般方程；(Ⅱ)若圆O ：x 2+y 2=4和圆E 相交于点M ，N ，求线段MN 的长．19. 为统计某城市居民用水情况，利用随机抽取的100位居民某年的月均用水量(单位：t)为样本组距绘制成了如图1所示的频率分布直方图.将图中从左至右每个小长方形对应组的中间值x i (x i 为第i 组左右两个边界值的算术平均数，如x 1=0+0.52=0.25)与高y i 表示的有序数对(x i ,y i )作为样本数据，其中i =1，2，3，…，9.记Mo 表示y i 取最大值时所对应的x i 的值．(Ⅰ)根据频率分布直方图求Mo 的值；(Ⅱ)求图2程序框图的输出结果i 的值，令n =i −1，记Me =0.75+x n+1−∑y k n k=1.若Me <Mo ，则称样本数据符合“左偏分布”；否则不符合“左偏分布”.请问本题的样本数据是否符合“左偏分布”？20. 为做好传染病的防治工作，某部门收集了所辖5个地区一个月中的就诊人数x(单位：人)和参与治疗的医务人员人数y(单位：人)，相关数据如表：A 地B 地C 地D 地E 地就诊人数x(单位：人)8 2 5 9 1 参与治疗的医务人员人数y(单位：人)1237112(Ⅰ)研究发现y 与x 之间具有线性相关关系.试根据表中统计数据，求出y 关于x 的线性回归方程y ^=b ^x +a ^；(Ⅱ)若该部门将所辖5个地区按参与治疗的医务人员人数不超过5人和超过5人的标准分别划分为“甲类区域”和“乙类区域”.现采用分层抽样的方法在甲乙两类区域参与治疗的所有医务人员中共抽取14人进行培训，求所抽取的“甲类区域”的医务人员来自不同地区的概率．参考数据：∑(5i=1x i −x −)2=50，∑x i 5i=1y i −5x −y −=63．参考公式：b ̂=∑(n i=1x i −x −)(y i −y −)∑(n i=1x i −x −)2=∑x i n i=1y i −nx −y−∑x i 2n i=1−nx−2，a ̂=y −−b ̂x −．21. 如图，在圆O ：x 2+y 2=4上任取一点P ，过点P 作x 轴的垂线段PD ，D 为垂足．(Ⅰ)当点P 在圆上运动时，求线段PD 的中点M 的轨迹方程；(Ⅱ)过点E(2,0)的直线l 与动点M 的轨迹相交于A ，B 两点，求△OAB 面积的最大值．22. 如图，已知直线l ：x =−1，点F(1,0).H 为直线l 上任意一点，过点H 且与l 垂直的直线交线段HF 的垂直平分线于点M ，记动点M 的轨迹为曲线C ． (Ⅰ)求曲线C 的方程；(Ⅱ)若N 为线段HF 与曲线C 的交点，且HF ⃗⃗⃗⃗⃗⃗ =λNF ⃗⃗⃗⃗⃗⃗ ，其中λ∈R.求2λ−|HF⃗⃗⃗⃗⃗⃗ |的值．答案和解析1.【答案】A【解析】解：根据存在性命题的否定是全称命题，故命题“∃x0>0，lnx0≥x0−1”的否定是“∀x>0，lnx<x−1”．故选：A．利用含有一个量词的命题的否定进行求解即可．本题考查了含有量词的命题的否定，要掌握其否定方法：先改变量词，然后再否定结论，属于基础题．2.【答案】B【解析】解：双曲线x2−y2b2=1(b>0)的一条渐近线方程为y=x，可知b=1，所以该双曲线的离心率为：e=ca =√1+11=√2．故选：B．利用双曲线的渐近线方程求解b，然后求解离心率即可．本题考查双曲线的简单性质的应用，离心率的求法，是基础题．3.【答案】C【解析】解：在空间直角坐标系Oxyz中，点(2,−1,1)在xOy平面上的射影为(2,−1,0)，∴点(2,−1,1)在xOy平面上的射影到坐标原点O的距离为：d=√22+(−1)2=√5．故选：C．先求出点(2,−1,1)在xOy平面上的射影，再由两点间距离公式能求出点(2,−1,1)在xOy平面上的射影到坐标原点O的距离．本题考查点在xOy平面上的射影到坐标原点的距离的求法，考查两点间距离公式等基础知识，考查运算求解能力，是基础题．4.【答案】D【解析】解：对于A，由频率分布折线图知，5年比较，2023年投资额预算达到最大值为1400亿元，所以A正确；对于B，由频率分布折线图知，逐年比较，2022年投资额预算增幅最大，为1100−670=430(亿元)，所以B正确；对于C，由频率分布折线图知，2021年至2023年投资额预算逐年增加，所以C正确；对于A，由频率分布折线图知，2021年至2022年投资额增幅为430亿元，2022年至2023年投资额增幅为300亿元，不是逐年增加，所以D错误．故选：D．利用频率分布折线图，逐项分析选项中的命题是否正确即可．本题考查了频率分布折线图的应用问题，也考查了数据分析与识图、用图能力，是基础题．5.【答案】C【解析】解：圆(x −a)2+y 2=1(a >0)与直线y =√33x 只有一个公共点，可得：|√33a|1+(√33)=1，解得a =2．故选：C ．利用直线与圆相切，通过圆心到直线的距离等于半径，列出方程求解即可．本题考查直线与圆的位置关系的应用，考查转化思想以及计算能力，是基础题． 6.【答案】B【解析】解：去掉一个最高分95和一个最低分79后，这组数据的平均数是x −=15×(84+85+86+88+92)=87，方差是s 2=15×[(84−87)2+(85−87)2+(86−87)2+(88−87)2+(92−87)2]=8．故选：B ．由题意计算这组数据的平均数和方差即可．本题考查了利用茎叶图求平均数和方差的应用问题，是基础题． 7.【答案】B【解析】解：一个不透明盒子里装有标号为1，2，3，4，5的五张标签，现从中随机无放回地抽取两次，每次抽一张，基本事件总数n =5×4=20，两次抽取的标签号数均为奇数包含的基本事件个数m =3×2=6，则两次抽取的标签号数均为奇数的概率为P =m n=620=310．故选：B ．从中随机无放回地抽取两次，每次抽一张，求出基本事件总数和两次抽取的标签号数均为奇数包含的基本事件个数，由此能求出两次抽取的标签号数均为奇数的概率．本题考查概率的求法，考查古典概型等基础知识，考查运算求解能力，是基础题． 8.【答案】B【解析】解：因为两点A(−3,0)，B(3,0)，设动点M(x,y)，则由足|MA|2+|MB|2=d ，可得(x +3)2+(x −3)2+2y 2=d ，所以x 2+y 2=d −18，当d =18时，x 2+y 2=0，故点M 为定点(0,0)，不是圆，所以充分性不成立，当动点M 的轨迹是圆，则d >18，故必要性成立，所以“d ≥18”是“动点M 的轨迹是圆”的必要不充分条件．故选：B ．先求出点M 满足的关系式，然后利用圆的方程满足的条件结合充分条件与必要条件的定义进行判断即可．本题考查了充分条件与必要条件的判断，解题的关键是掌握充分条件与必要条件的判断方法，属于基础题． 9.【答案】A【解析】解：设甲到达的时刻为x ，乙到达的时刻为y ，则所有的基本事件构成的区域 Ω={(x,y)|{0≤x ≤240≤y ≤24 }，这两艘船中至少有一艘在停靠泊位时必须等待包含的基本事件构成的区域A =A ={(x,y)|{0≤x ≤240≤y ≤24|x −y|≤6},这两艘船中至少有一艘在停靠泊位时必须等待的概率P(A)=S 阴S Ω=1−18×1824×24=716．故选A ．设出甲、乙到达的时刻，列出所有基本事件的约束条件同时列出这两艘船中至少有一艘在停靠泊位时必须等待约束条件，利用线性规划作出平面区域，利用几何概型概率公式求出概率．本题考查利用线性规划作出事件对应的平面区域，再利用几何概型概率公式求出事件的概率． 10.【答案】C【解析】解：对于A ，由频率分布直方图得：(0.004+0.010+a +0.036+a +0.006)×10=1，解得a =0.022，故A 错误；对于B ，这100位居民中年龄不低于60岁的有：(0.022+0.006)×10×100=28位，故B 错误；对于C ，估计这100位居民的平均年龄为：25×0.04+35×0.10+45×0.22+55×0.36+65×0.22+75×0.06=53岁，故C 正确；对于D ，频率分布图中，人口年龄分布在[50,60)的人数与分布在[20,30)的人数分别记为m ，n ，则m =0.036×10×100=36，n =0.004×10×100=4，但是利用校本估计总体时会有误差，故m =9n 不一定成立，故D 错误．故选：C ．利用频率分布直方图的性质直接求解．本题考查命题真假的判断，考查频率分布直方图的性质等基础知识，考查运算求解能力，是基础题． 11.【答案】C【解析】解：由抛物线的方程可得：F(0,1)，准线方程为：y =−1，设准线与y 轴的交点为B ，在直角三角形NBF 中，因为BF//PN 且∠PNF =30°，所以∠NFB =30°，而BF =2，所以NB =BFtan30°=2√33，NF =2NB =4√33，设点P 的坐标为(m,n)，不妨设点P 在第一象限，则m =2√33，代入抛物线方程可得：n =13，所以点P 的坐标为(2√33,13)，则PN =13+1=43，所以三角形PNF 的面积为S =12⋅NF ⋅PN ⋅sin∠PNF =12×4√33×43×12=4√39，故选：C ．画出图象，设准线与y 轴的交点为B ，在直角三角形NBF 中，因为BF//PN 且∠PNF =30°，由此即可求出NB ，NF ，然后再求出点P 的坐标，由此求出PN 的长，利用三角形面积公式即可求解．本题考查了抛物线的性质，涉及到求解三角形面积的问题，考查了学生的数形结合的能力，属于中档题． 12.【答案】D【解析】解：模拟程序的运行，可得该程序的功能是利用辗转相除法求输入的两个数的最大公约数，对于A ，m =306，n =98，最大公约数为2，错误；对于B ，m =306，n =102，最大公约数为102，错误；对于C ，m =306，n =105，最大公约数为3，错误；对于D ，m =306，n =119，最大公约数为17，正确．故选：D ．模拟程序的运行，可得该程序的功能是利用辗转相除法求输入的两个数的最大公约数，逐项验证即可得解．本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，属于基础题 13.【答案】6【解析】解：数据8，7，3，7，6，9的极差为9−3=6．故答案为：6．利用极差的定义直接求解．本题考查极差的定义，考查运算求解能力，是基础题． 14.【答案】③【解析】解：对于命题p ：若0<x <y ，则x 2<y 2；故命题p 为假命题；对于命题q ：∀m ∈R ，直线x −my −1=0恒过点(1,0)，由于点(1,0)在椭圆x 22+y 2=1内，所以直线恒与椭圆有两个公共点，故该命题q 为真命题；①p 为假命题；②p ∨(￢q)为假命题；③(￢p)∧q 为真命题；故选：③．直接利用不等式的性质，直线和椭圆的关系，真值表的应用判断命题①②③的真假．本题考查的知识要点：不等式的性质，直线和椭圆的关系，真值表，主要考查学生的运算能力和转换能力及思维能力，属于基础题．15.【答案】56【解析】解：从A ，B ，C ，D 四个女孩中选两位担任该公司的两个秘书职位，共有AB ，AC ，AD ，BC ，BD ，CD 6种选法，女孩A 或女孩B 被选中共有AB ，AC ，AD ，BC ，BD 5种情况，故事件“女孩A 或女孩B 被选中”的概率为P =56，故答案为：56．求出所有的基本事件，再求出满足条件的基本事件，作商即可．本题考查了古典概型问题，考查列举法的应用，是基础题． 16.【答案】(3,+∞)【解析】解：由F 1M ⃗⃗⃗⃗⃗⃗⃗⃗ =2MF 2⃗⃗⃗⃗⃗⃗⃗⃗ ，则|F 1M|=2|MF 2|，在三角形△MF 1F 2中，由角平分线定理可得，|MF 1|：|MF 2|=|PF 1|：|PF 2|=2：1…①，又因|PF 1|+|PF 2|=2a …②，设|PF 2|=m ，由①②联立得m =2a 3，又因点P 在椭圆C 上且位于第一象限， ∴2a 3>a −c ，即13a <c =√a 2−8，∴a >3，故答案为：(3,+∞)．由椭圆的性质，角平分线的性质，可以直接求解．本题考查了椭圆的性质，角平分线的性质，属于基础题．17.【答案】解：(Ⅰ)由题意，易知|MF 2|=2，|F 1F 2|=2√3，MF 2⊥F 1F 2．在Rt △MF 2F 1中，|MF 1|=√|MF 2|2+|F 1F 2|2=4．由双曲线的定义可知，|MF 1|−|MF 2|=2a ，∴2a =2，即a =1． ∵双曲线C 的两个焦点分别为F 1(−√3,0)，F 2(√3,0)， ∴半焦距c =√3．又∵a 2+b 2=c 2，∴b =√2．故双曲线C 的虚轴长为2√2． (Ⅱ)由(Ⅰ)知双曲线C 的方程为x 2−y 22=1．设与双曲线C 有相同渐近线的双曲线的方程为x 2−y 22=λ(λ≠0)．将点P(−2,4)的坐标代上述方程，得λ=−4．故所求双曲线的标准方程为y 28−x 24=1．【解析】(Ⅰ)由双曲线的定义可知，|MF 1|−|MF 2|=2a ，又∵2+b 2=c 2，求得b =√2即可． (Ⅱ)设与双曲线C 有相同渐近线的双曲线的方程为x 2−y 22=λ(λ≠0)，将点P(−2,4)的坐标代上述方程得λ即可．．本题考查了双曲线的方程、渐近线，属于基础题．18.【答案】解：(Ⅰ)由圆E 经过点A(−6,0)，B(2,0)，得圆心E 在直线x =−2上．又∵圆心E 在直线y =−x 上， ∴圆心E 的坐标为(−2,2)．设圆E 的半径为r ，则r =|EB|=√[2−(−2)]2+(0−2)2=2√5．故圆E 的方程为(x +2)2+(y −2)2=20．化成一般方程为x 2+y 2+4x −4y −12=0．(Ⅱ)圆O 与圆E 的方程联立，得到方程组{x 2+y 2−4=0,⋯①x 2+y 2+4x −4y −12=0.⋯②①−②，得x −y −2=0，即为直线MN 的方程．原点O 到直线MN 的距离d =√12+12=√2=√2．又圆O 的半径为2，∴由勾股定理，得|MN|2=√22−(√2)2=√2．故|MN|=2√2．【解析】(Ⅰ)由已知条件推知该圆的圆心是直线x =−2与直线y =−x 的交点，求得圆心坐标，再由两点间的距离公式求得半径，则圆的方程可求；(Ⅱ)由方程x 2+y 2=4与x 2+y 2+4x −4y −12=0消去二次项得，x −y −2=0，再求得圆心O 到直线x −y −2=0的距离，由圆弦长、圆心距和圆的半径之间关系得线段MN 的长．本题主要考查直线与圆的位置关系及其方程的应用，主要涉及了直线与圆相交，由圆心距，半径和圆的弦长构成的直角三角形，是中档题．19.【答案】解：(Ⅰ)根据频率分布直方图，得y i 的最大值为y 5=0.50，该值所对应小长方形左右两个边界值分别为2和2.5． ∴对应组的中间值x 5=2+2.52=2.25，即Mo 的值为2.25．(Ⅱ)执行程序框图，输入y 1=0.08，得S =0+0.5×0.08=0.04≤0.5；输入y 2=0.16，得S =0.04+0.5×0.16=0.12≤0.5；输入y 3=0.30，得S =0.12+0.5×0.30=0.27≤0.5；输入y 4=0.44，得S =0.27+0.5×0.44=0.49≤0.5；输入y 5=0.50，得S =0.49+0.5×0.50=0.74>0.5．故输出结果i 的值为5.∴n =5−1=4，Me =0.75+x n+1−∑y k n ℎ=1=0.75+x 5−∑y k 4ℎ=1=0.75+2.25−0.98=2.02．而Mo =2.25，即有Me <Mo ． ∴本题样本数据符合“左偏分布”．【解析】(Ⅰ)根据频率分布直方图，得y i 的最大值为y 5=0.50，该值所对应小长方形左右两个边界值分别为2和2.5.求出对应组的中间值即可．(Ⅱ)执行程序框图，得到Mo =2.25，由Me <Mo ，可知本题样本数据符合“左偏分布”．本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，得出正确的结论，是基础题．20.【答案】解：(Ⅰ)由题意，得x −=15(8+2+5+9+1)=5，y −=15(12+3+7+11+2)=7．由参考数据∑(5i=1x i −x −)2=50，∑x i 5i=1y i −5x −y −=63．得b ̂=6350=1.26．又x −=5，y −=7，∴a ̂=y −−b ̂x −=7−5×1.26=0.7．故所求线性回归方程为y ̂=1.26x +0.7．(Ⅱ)依题意B 地和E 地属于“甲类区域”，两地共计5名医务人员参与治疗，总共有35位医务人员参与治疗，所以应从“甲类区域”的5名医务人员抽取14×535=2名．记B 地三名医务人员分别为B 1，B 2，B 3，E 地两名医务人员分别为E 1，E 2．则所抽两名医务人员所有可能结果为：(B 1,B 2)，(B 1,B 3)，(B 2,B 3)，(B 1,E 1)，(B 1,E 2)，(B 2,E 1)， (B 2,E 2)，(B 3,E 1)，(B 3,E 1)，(B 3,E 2)，(E 1,E 2)，共计10种．这两名医务人员分别来自不同地区的结果有：(B 1,E 1)，(B 1,E 2)，(B 2,E 1)，(B 2,E 2)，(B 3,E 1)，(B 3,E 2)，共计6种．故所抽取的“甲类区域”的医务人员来自不同地区的概率为35．【解析】(Ⅰ)求出样本中心坐标，求出回归直线方程的系数，得到回归直线方程．(Ⅱ)记B 地三名医务人员分别为B 1，B 2，B 3，E 地两名医务人员分别为E 1，E 2.列出所抽两名医务人员所有可能结果，这两名医务人员分别来自不同地区的结果，然后求解概率即可．本题考查回归直线方程的求法，古典概型概率的求法，是基础题． 21.【答案】解：(Ⅰ)设M(x,y)，P(x P ,y P )，则D(x P ,0)． ∵M 为线段PD 的中点， ∴{x =x Py =y P +02，即x P =x ，y P =2y ．又点P 在圆O ：x 2+y 2=4上， ∴x 2+(2y)2=4，即x 24+y 2=1．故点M 的轨迹方程为x 24+y 2=1．(Ⅱ)解法一：∵直线l 过点E(0,2)，设l ：y =kx +2(k ≠0)，设A(x 1,y 1)，B(x 2,y 2)，由{y =kx +2x 24+y 2=1，消去y 得(1+4k 2)x 2+16kx +12=0，由△=(16k)2−48(1+4k 2)>0，得4k 2−3>0，即k 2>34．则x 1+x 2=−16k1+4k 2，x 1x 2=121+4k 2，∴|AB|=√1+k 2⋅√(x 1+x 2)2−4x 1x 2=√1+k 2⋅√(−16k1+4k 2)2−4⋅121+4k 2=4√1+k 2⋅√4k 2−31+4k 2．又原点O 到直线l 的距离为d =√1+k 2，故△OAB 面积S =12|AB|⋅d =4√4k2−31+4k 2．设t =4k 2−3，则t >0，所以S =4√t(t+4)2=4√1t+16t+8≤1，当且仅当t =4，即k 2=74时等号成立．此时k 2=74>34，符合题意．∴△OAB 面积的最大值为1．解法二：∵直线l 过点E(0,2)，设l ：y =kx +2(k ≠0)．由{y =kx +2x 24+y 2=1，消去y 得(1+4k 2)x 2+16kx +12=0，由△=(16k)2−48(1+4k 2)>0，得4k 2−3>0，即k 2>34．设A(x 1,y 1)，B(x 2,y 2)，则x 1+x 2=−16k 1+4k 2，x 1x 2=121+4k 2．∴|AB|=√1+k 2⋅√(x 1+x 2)2−4x 1x 2=√1+k 2⋅√(−16k 1+4k 2)2−4⋅121+4k 2=4√1+k 2⋅√4k 2−31+4k 2．又原点O 到直线l 的距离为d =2√1+k 2，故△OAB 面积S =12|AB|⋅d =4√4k2−31+4k 2，∵4√4k 2−31+4k 2=2×2×√4k 2−31+4k 2≤22+(√4k 2−3)21+4k 2=1，当且仅当2=√4k 2−3，即k 2=74时等号成立．此时k 2=74>34，符合题意． ∴△OAB 面积的最大值为1．【解析】(Ⅰ)设M(x,y)，P(x P ,y P )，得到D 的坐标，利用M 为线段PD 的中点，得到P 点坐标与动点M 坐标之间的关系，将P 点坐标用M 点坐标表示，然后代入圆的方程即可得到动点M 的轨迹方程；(Ⅱ)解法一：设直线l 的方程以及点A ，B 的坐标，然后联立直线与椭圆的方程，得到韦达定理，由△>0解得k 的范围，利用弦长公式求出|AB|，然后求出点O 到直线l 的距离，将三角形的面积用k 表示出来，令t =4k 2−3，然后再利用基本不等式求解最值即可；解法二：设直线l 的方程以及点A ，B 的坐标，然后联立直线与椭圆的方程，得到韦达定理，由△>0解得k 的范围，利用弦长公式求出|AB|，然后求出点O 到直线l 的距离，将三角形的面积用k 表示出来，直接利用基本不等式求解最值即可．本题考查了动点轨迹方程的求解，直线与椭圆位置关系的应用、点到直线距离公式的应用、弦长公式的应用、基本不等式求最值的应用，涉及知识点多，综合性强，对逻辑推理能力和化简运算能力有较高的要求，属于中档题．22.【答案】解：(Ⅰ)根据线段垂直平分线的性质，知|MH|=|MF|． ∴动点M 的轨迹是以F(1,0)为焦点，x =−1为准线的抛物线．故曲线C 的方程为y 2=4x ．(Ⅱ)解法一：由题意，直线HF 的斜率一定存在．设点N(x N ,y N ).①若直线HF 的斜率为0，则2λ−|HF⃗⃗⃗⃗⃗⃗ |=4−2=2． ②若直线HF 的斜率不为0，设直线HF ：y =k(x −1)，且由题意知x N ∈(0,1)．由{y =k(x −1)y 2=4x ，消去y ，得k 2x 2−(2k 2+4)x +k 2=0． ∵k ≠0，△=16(k 2+1)>0，则x N =k2+2−2√k 2+1k 2．又H(−1,−2k)，∴|HF ⃗⃗⃗⃗⃗⃗ |=2√k 2+1． ∴λ=|HF⃗⃗⃗⃗⃗⃗ ||NF⃗⃗⃗⃗⃗⃗ |=21−x N=√k 2+1+1．∴2λ−|HF ⃗⃗⃗⃗⃗⃗ |=2(√k 2+1+1)−2√k 2+1=2.即2λ−|HF ⃗⃗⃗⃗⃗⃗ |的值为2．解法二：设点N(x N ,y N )，H(−1,y H ).当y H =0，即H(−1,0)时，易得2|HF⃗⃗⃗⃗⃗⃗ ||NF ⃗⃗⃗⃗⃗⃗ |−|HF ⃗⃗⃗⃗⃗⃗ |=2．当y H ≠0时，设直线HF ：x =my +1(m ≠0)．由{x =my +1y 2=4x ，消去x ，得y 2−4my −4=0．在直线HF ：x =my +1中，由y H =−1，得y H =−2m ． ①m <0，则y N >0.∴y N =4m+√(4m)2+162=2m +2√m 2+1.，∴2λ−|HF ⃗⃗⃗⃗⃗⃗ |=2⋅y H yN−√1+m 2y H =2⋅m(2m+2√m 2+1)+2√1+m 2m=(−2)×√m 2+1−mm+2√1+m 2m=2．②若m >0，则y N <0． ∴y N =4m−√(4m)2+162=2m −2√m 2+1．∴2λ−|HF ⃗⃗⃗⃗⃗⃗ |=2⋅yH yN−√1+m 2y H =2⋅m(2m−2√m 2+1)−2√1+m 2m=(−2)×√m 2+1+mm−2√1+m 2m=2．综上所述，2λ−|HF⃗⃗⃗⃗⃗⃗ |的值为2．解法三：如图，易知直线l ：x =−1为抛物线C 的准线，过点N 作NN′⊥l ，交直线l 于点N′，记点(−1,0)为F′，则有△HN′N∽△HF′F ． ∴|HN||HF|=|N′N||F′F|．又|F′F|=2，且根据抛物线的定义知|N′N|=|NF|， ∴|HN||HF|=|N′N||F′F|=|NF|2，则有|HF|⋅|NF|=2|HN|，故2λ−|HF|=2|HF||NF|−|HF|=2|HF|−|HF|⋅|NF||NF|=2|HF|−2|HN||NF|=2|NF||NF|=2．【解析】(Ⅰ)由题意|MH|=|MF|，所以动点M的轨迹是以F(1,0)为焦点，x=−1为准线的抛物线，即可求曲线C的方程；(Ⅱ)解法一：由题意，直线HF的斜率一定存在．设点N(x N,y N).分两种情况解答：①若直线HF的斜率为0、②若直线HF的斜率不为0；解法二：设点N(x N,y N)，H(−1,y H).分两种情况解答：y H=0和y H≠0；解法三：如图，易知直线l：x=−1为抛物线C的准线，过点N作NN′⊥l，交直线l于点N′，记点(−1,0)为F′，则有△HN′N∽△HF′F.由相似三角形的性质和抛物线的性质解答．本题考查了抛物线的标准方程及其性质、直线与抛物线相交问题，考查了推理能力与计算能力，属于难题．。

2020-2021成都树德中学高二数学上期末模拟试卷附答案

2020-2021成都树德中学高二数学上期末模拟试卷附答案一、选择题1．将A ，B ，C ，D ，E ，F 这6个字母随机排成一排组成一个信息码，则所得信息码恰好满足A ，B ，C 三个字母连在一起，且B 在A 与C 之间的概率为（） A ．112B ．15C ．115D ．2152．如图，矩形ABCD 中，点E 为边CD 的中点，若在矩形ABCD 内部随机取一个点Q ，则点Q 取自△ABE 内部的概率等于A ．14B ．13C ．12D ．233．己知某产品的销售额y 与广告费用x 之间的关系如下表：若求得其线性回归方程为 6.5ˆˆyx a =+，其中ˆˆa y bx =-，则预计当广告费用为6万元时的销售额是（） A ．42万元B ．45万元C ．48万元D ．51万元4．高二某班共有学生60名，座位号分别为01, 02, 03，···, 60.现根据座位号，用系统抽样的方法，抽取一个容量为4的样本.已知03号、18号、48号同学在样本中，则样本中还有一个同学的座位号是（） A ．31号B ．32号C ．33号D ．34号5．预测人口的变化趋势有多种方法，“直接推算法”使用的公式是()0 1nn P P k =+（1k >-），n P 为预测人口数，0P 为初期人口数，k 为预测期内年增长率，n 为预测期间隔年数．如果在某一时期有10k -<<，那么在这期间人口数 A ．呈下降趋势 B ．呈上升趋势C ．摆动变化D ．不变6．为了解某社区居民的家庭年收入和年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：收入x 万 8.3 8.6 9.9 11.1 12.1 支出y 万5.97.88.18.49.8根据上表可得回归直线方程ˆˆˆybx a =+，其中0.78b ∧=，a y b x ∧∧=-元，据此估计，该社区一户收入为16万元家庭年支出为（） A ．12.68万元B ．13.88万元C ．12.78万元D ．14.28万元7．已知线段MN 的长度为6，在线段MN 上随机取一点P ，则点P 到点M ，N 的距离都大于2的概率为( ) A ．34B ．23C ．12D ．138．要从其中有50个红球的1000个形状相同的球中，采用按颜色分层抽样的方法抽取100个进行分析，则应抽取红球的个数为（） A ．5个B ．10个C ．20个D ．45个9．类比“赵爽弦图”，可类似地构造如图所示的图形，它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形，设2AD BD =，若在大等边三角形中随机取一点，则此点取自小等边三角形的概率是（）A ．14B ．13C ．17D ．41310．一位学生在计算20个数据的平均数时，错把68输成86，那么由此求出的平均数与实际平均数的差为 A ．B ．C ．D ．11．下表是某两个相关变量x ，y 的几组对应数据，根据表中提供的数据，求出y 关于x 的线性回归方程ˆ0.70.35yx =+，那么表中t 的值为（） x 3 4 5 6 y2.5t44.5A ．3B ．3.15C ．3.5D ．4.512．执行如图的程序框图，若输出的4n =，则输入的整数p 的最小值是（）A．4B．5C．6D．15二、填空题13．袋中装有大小相同的总数为5个的黑球、白球若从袋中任意摸出2个球，至少得到1个白球的概率是910，则从中任意摸出2个球，得到的都是白球的概率为______．14．某程序框图如图所示，若输入的4t=，则输出的k=______．15．如果执行如图的程序框图，那么输出的S=__________．16．执行如图所示的程序框图，若输入n的值为8，则输出的s的值为_____．17．如图所示的程序框图，输出的S的值为()A ．12B ．2C ．1-D ．12-18．已知集合{1,U =2，3，⋯，}n ，集合A 、B 是集合U 的子集，若A B ⊆，则称“集合A 紧跟集合B ”，那么任取集合U 的两个子集A 、B ，“集合A 紧跟集合B ”的概率为______．19．执行下面的程序框图，如果输入的0.02t =，则输出的n =_______________．20．如图，曲线sin32xy π=+把边长为4的正方形OABC 分成黑色部分和白色部分.在正方形内随机取一点，则此点取自黑色部分的概率是__________．三、解答题21．现有8名马拉松比赛志愿者，其中志愿者1A ，2A ，3A 通晓日语，1B ，2B ，3B 通晓俄语，1C ，2C 通晓英语，从中选出通晓日语、俄语和英语的志愿者各1名，组成一个小组．()1列出基本事件；()2求1A 被选中的概率；()3求1B和1C不全被选中的概率．22．随着经济的发展，轿车已成为人们上班代步的一种重要工具.现将某人三年以来每周开车从家到公司的时间之和统计如图所示.6.5,7.5（时）内的频率；（1）求此人这三年以来每周开车从家到公司的时间之和在[)（2）求此人这三年以来每周开车从家到公司的时间之和的平均数（每组取该组的中间值作代表）；（3）以频率估计概率，记此人在接下来的四周内每周开车从家到公司的时间之和在[)4.5,6.5（时）内的周数为X，求X的分布列以及数学期望.23．某学校艺术专业300名学生参加某次测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了100名学生，记录他们的分数，将数据分成7组：[20，30)，[30，40)，…，[80，90]，并整理得到如下频率分布直方图：(1)从总体的300名学生中随机抽取一人，估计其分数小于70的概率；(2)已知样本中分数小于40的学生有5人，试估计总体中分数在区间[40，50)内的人数；(3)已知样本中有一半男生的分数不小于70，且样本中分数不小于70的男女生人数相等．试估计总体中男生和女生人数的比例．24．某蔬果经销商销售某种蔬果，售价为每公斤25元，成本为每公斤15元.销售宗旨是当天进货当天销售.如果当天卖不出去，未售出的全部降价以每公斤10元处理完.根据以往的销售情况，得到如图所示的频率分布直方图：（1）根据频率分布直方图计算该种蔬果日需求量的平均数x（同一组中的数据用该组区间中点值代表）；（2）该经销商某天购进了250公斤这种蔬果，假设当天的需求量为x公斤≤≤，利润为y元.求y关于x的函数关系式，并结合频率分布直方图估计利润(0500)xy不小于1750元的概率.25．某高校在2017年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组，得到的频率分布表如表：组号分组频率160,1650.05第1组[)165,1700.35第2组[)170,175①第3组[)175,1800.20第4组[)180,1850.10第5组[]()1求出频率分布表中①处应填写的数据，并完成如图所示的频率分布直方图；()2根据直方图估计这次自主招生考试笔试成绩的平均数和中位数(结果都保留两位小数)．26．设关于x 的一元二次方程2220x bx a -+=，其中,a b 是某范围内的随机数，分别在下列条件下，求上述方程有实根的概率. （1）若随机数,{1,2,3,4}a b ∈；（2）若a 是从区间[0,4]中任取的一个数，b 是从区间[1,3]中任取的一个数.【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【解析】【分析】将A ，B ，C 三个字捆在一起，利用捆绑法得到答案. 【详解】由捆绑法可得所求概率为242466A A 1A 15P ==. 故答案为C 【点睛】本题考查了概率的计算，利用捆绑法可以简化运算.2．C解析：C 【解析】【分析】利用几何概型的计算概率的方法解决本题，关键要弄准所求的随机事件发生的区域的面积和事件总体的区域面积，通过相除的方法完成本题的解答．【详解】解：由几何概型的计算方法，可以得出所求事件的概率为P=．故选C ．【点评】本题考查概率的计算，考查几何概型的辨别，考查学生通过比例的方法计算概率的问题，考查学生分析问题解决问题的能力，考查学生几何图形面积的计算方法，属于基本题型．3．C解析：C【分析】由已知求得样本点的中心的坐标，代入线性回归方程求得ˆa，则线性回归方程可求，取6x =求得y 值即可．【详解】()10123425x =++++=，()11015203035225y =++++=，样本点的中心的坐标为()2,22，代入ˆˆa yb x =-，得22 6.529a =-⨯=．y ∴关于x 得线性回归方程为 6.59y x =+．取6x =，可得6.56948(y =⨯+=万元)．故选：C ．【点睛】本题考查线性回归方程的求法，考查计算能力，是基础题．4．C解析：C 【解析】【分析】根据系统抽样知，组距为604=15÷，即可根据第一组所求编号，求出各组所抽编号. 【详解】学生60名，用系统抽样的方法，抽取一个容量为4的样本,所以组距为604=15÷，已知03号，18号被抽取，所以应该抽取181533+=号，故选C. 【点睛】本题主要考查了抽样，系统抽样，属于中档题.5．A解析：A 【解析】【分析】可以通过n P 与0P 之间的大小关系进行判断．【详解】当10k -<<时，()011011nk k <+<<+<，，所以()001nn P P k P =+<，呈下降趋势．【点睛】判断变化率可以通过比较初始值与变化之后的数值之间的大小来判断．6．A【解析】【分析】由已知求得 x ， y ，进一步求得$ a，得到线性回归方程，取16x =求得y 值即可．【详解】8.38.69.911.1512.1 10x +++=+=， 5.97.88.18.49.858y ++++==．又 0.78b =$，∴$ 80.78100.2a y bx --⨯===$． ∴$ 0.780.2y x =+．取16x =，得$ 0.78160.212.68y ⨯+==万元，故选A ．【点睛】本题主要考查线性回归方程的求法，考查了学生的计算能力，属于中档题．7．D解析：D 【解析】【分析】根据题意画出图形，结合图形即可得出结论．【详解】如图所示，线段MN 的长度为6，在线段MN 上随机取一点P ，则点P 到点M ，N 的距离都大于2的概率为2163P ==．故选D ．【点睛】本题考查了几何概型的概率计算问题，是基础题．8．A解析：A 【解析】应抽取红球的个数为5010051000⨯= ，选A. 点睛：在分层抽样的过程中，为了保证每个个体被抽到的可能性是相同的，这就要求各层所抽取的个体数与该层所包含的个体数之比等于样本容量与总体的个体数之比，即n i ∶N i ＝n ∶N .9．C解析：C 【解析】【分析】由题意求出7AB BD =，所求概率即为DEFABCS P S =V V ，即可得解. 【详解】由题意易知120ADB ∠=o ，AF FD BD ==，由余弦定理得22222cos1207AB AD BD AD BD BD =+-⋅⋅=即7AB BD =，所以7AB FD =，则所求概率为217DEF ABC S FD P S AB ⎛⎫=== ⎪⎝⎭V V .故选：C. 【点睛】本题考查了几何概型概率的求法和余弦定理的应用，属于中档题.10．B解析：B 【解析】【分析】应用平均数计算方法，设出两个平均数表达式，相减，即可。

2020-2021学年四川省成都市蓉城名校联盟高二(上)期末数学试卷(文科)

2020-2021学年四川省成都市蓉城名校联盟高二（上）期末数学试卷（文科）一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．（5分）命题“若两条直线平行，则这两条直线在同一个平面内”和它的逆命题、否命题、逆否命题，这四个命题中真命题的个数为（）A．0B．2C．3D．42．（5分）袋中装有大小和材质均相同的红球4个，黄球2个，白球1个，记事件A为“取出的是红球”，事件B为“取出的是黄球”（）A．不互斥但对立B．不互斥也不对立C．互斥且对立D．互斥但不对立3．（5分）命题“∀x≥2，x2+x≥6”的否定是（）A．∀x≥2，x2+x＜6B．∃x0≥2，x02+x0＜6C．∀x＜2，x2+x＜6D．∃x0＜2，x02+x0＜64．（5分）平面内有两个定点A、B和一个动点M，|AB|＝5，|MA|+|MB|＝a（a为常数），q表示“点M的轨迹是椭圆”．则p是q的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件5．（5分）若方程x2+y2+2x﹣4ay﹣5a＝0表示圆，则下列四个数中a不能取的是（）A．﹣1B．﹣2C．1D．26．（5分）某校高二年级有980名同学，编号为1到980，采用系统抽样的方法从中抽出49人，则下列编号中没有被抽中的是（）A．82B．202C．372D．5627．（5分）圆M：（x+2）2+y2＝16与圆N：（x﹣4）2+（y+8）2＝36的位置关系为（）A．外离B．外切C．相交D．内切8．（5分）从1，2，3，4，5，6，7这七个数字中随机抽取一个，记事件A为“抽取的数字为偶数”，则事件A+B发生的概率为（）A．B．C．D．9．（5分）已知抛物线x2＝2ay的焦点在直线3x+2y﹣6＝0上，则a＝（）A．3B．4C．6D．210．（5分）把点M随机投入长为5，宽为4的矩形ABCD内，则点M与矩形ABCD四边的距离均不小于1的概率为（）A．B．C．D．11．（5分）已知曲线y＝﹣与直线x＝my+5只有一个交点，则实数m的值为（）A．﹣B．C．﹣D．12．（5分）已知椭圆M：+＝1的左、右焦点分别为F1、F2，过F2作y轴的平行线交椭圆M于A、B两点，O为坐标原点，双曲线N以F1、F2为顶点，以直线OA、OB为渐近线，则双曲线N的焦距为（）A．B．C．D．二、填空题：本题共4小题，每小题5分，共20分。