统计学第四章
统计学原理第四章

第二节 相对指标
(三)比较相对指标 比较相对指标是不同单位的同类现象数量对比而确定的相对指标, 用以说明某一同类现象在同一时间内各单位发展的不平衡程度,以 表明同类实物在不同条件下的数量对比关系。 甲单位某指标值 比较相对指标 乙单位同类指标值
比例指标与比较指标的区别?
比例相对指标和比较相对指标的区别是:⑴子项与母项的内容不同,比 例相对指标是同一总体内,不同组成部分的指标数值的对比;比较相对指 标是同一时间同类指标在空间上的对比。⑵说明问题不同,比例相对指标 说明总体内部的比例关系;比较相对指标说明现象发展的不均衡程度。 比较相对指标是不同单位的同类指标对比而确定的相对数,用以说明同类 现象在同一时期内各单位发展的不平衡程度。如:甲地职工平均收入是乙 地职工平均收入的1.3倍。
第二节 相对指标
例题4:某企业产值,计划完成程度指标为103%,比上期增长5%,试 问产值计划比上期增长多少? 解:设本期产值为a1,上期产a0,值为计划数为an, 则据题意有:a1/ an=103%, a1/ a0=105%, an/ a0=101.94%
选C
第三节 平均指标
一、平均指标的意义
第二节 相对指标
二、相对指标的种类及其计算方法
(一)结构相对指标 结构相对指标是在对总体分组的基础上,以总体总量作为比较标准, 求出各组总量占总体总量的比重,来反映总体内部组成情况的综合 指标。 各组(或部分)总量 结构相对指标 总体总量 计算结构相对指标能够反映总体内部结构和现象的类型特征,如各 工种的工人占全部工人的比重。 (二)比例相对指标 (轻重工业比例) 比例相对指标是总体中不同部分数量对比的相对指标,用以分析总 体范围内各个局部、各个分组之间的比例关系和协调平衡状况。 总体中某一部分数量 比例相对指标 总体中另一部分数值
统计学第四章

第四章 差异量教学目的:1.理解全距、四分位距、百分位距、平均差、方差、标准差和差异系数等概念;2.掌握各种差异量指标的计算方法。
数据的分布特征不仅有集中趋势,还有离中趋势。
以动态的眼光,从不同的角度看,数据是向中间变动的,也是向两端变动的。
两组数据可能平均水平相同,但两组数据的分布特征并不完全相同。
【如】:比较下列两组数据 A 组:88、82、73、76、81 B 组:92、86、70、72、80两组平均数,80==B A X X 但R A =88-73=15,R B=92-70=22。
即A 组较集中,B 组较分散。
因此,我们描述一组数据的分布特征,既要描述其集中趋势,也要描述其离中趋势。
差异量:表示一组数据的离中趋势或变异程度的量称为差异量。
常用的差异量指标有全距、四分位距、百分位距、平均差、方差、标准差和差异系数。
第一节全距、四分位距、百分位距一、全距全距:是一组数距中最大值与最小值之差。
优点:意义明确,计算方便。
缺点:反应不灵敏,易受极端值影响。
二、四分位距(一)四分位距的的概念四分位距:是指一组按大小顺序排列的数据中间部位50%个频数距离的一半。
)(1.4213Q Q QD -=QD :表示四分位距; Q 3:表示第三四分位数;Q 1:表示第一四分位数。
所以:四分位距的公式又为:22575P P QD -=(二)四分位数的计算方法 1、原始数据计算法(1)将数据由小到大进行排列; (2)分别求出三位四分位数(点); (3)代入公式计算。
【例如】:有以下16个数据25、22、29、12、40、15、14、39、37、31、33、19、17、20、35、30,其中四分位距的计算方法如下:(1)先将原始数据从小到大排列好;12、14、15、17、*19、20、22、25、*29、30、31、33、*35、37、39、40Q 1=18 Md =27 Q 3=34(2)求出Q 1、Md 、Q 3;(3)将Q 1、Md 、Q 3的得数代入公式(4.1)。
《统计学》第4章总体指标与相对指标

• (四)动态相对指标 • 动态相对指标又称发展速度,它是同类现象 在不同时间上变动程度的相对指标。其计算 公式为:
报告期指标数值 100% • 动态相对指标(%)= 基期指标数值
• 动态相对指标就是发展速度。
22
• 例:某大学在校生人数1990年10000人, 2000年为15000人,则该校在校生人数 2000年是1990年的150%。 • 即:动态相对指标= 15000 100% 150%
380 100 % 76% 单位成本的计划完成相对数= 500
32
(3)当计划任务数是比上期提高或降低百分 之几的形式出现时 • 计划完成程度(%)=
1 实际提高(降低)百分数 100% 1 计划提高(降低)百分数
• 该指标是用于考核社会经济现象的降低率、 增长率的计划完成程度。
25
[例3]某城市人口1000000人,零售商店3000个。则: • 该城市商业网点密度=
3000个 3个 / 千人 1000000人
• 计算结果表明,该城市每千人拥有3个商业网点, 指标数值越大,商业越发达,人民生活越方便, 表示强度越高,这是正指标。
26
• 如果把分子和分母对换,则: 1000000人 • 该城市商业网点密度= 3000个 333人 / 个 • 计算结果表明,该城市每个商业网点为333 人服务,指标数值越大,需要服务的人数 越多,商业欠发达,即表示强度越低,这 是逆指标。
• 相对指标的概念 把两个有联系的指标加 以对比而得到的统计指 标 • 相对指标的表现形式为 相对比率,相对指标也 通称为相对数。
相对指标的计量单位
无名 数 系数 或倍 数 成 百分 翻番 数 数或 千分 数
有名 将相对指标中的分子和 数 分母指标数值计量单位 同时使用的一种表示方 法,主要用于部分强度 相对指标。
统计学课件 第四章 时间数列

c a b
故对相对数或平均数时间数列计算平均发展水平,只需要对 其的分子、分母分别计算平均发展水平后再相除即可。即:
c a 分子代表分子数列的平均发展水平,分母代表分母数列的平均发展水平 b
(1)分子分母都是时期数列
某企业产值情况
时间
1月
2月
3月
产值计划完成程度(%) 105 100 109.1
计划产值(万)
某市财政收入情况
月份
1
2
3
4
5
6
财政收入 1(a0) 1.1(a1) 1.05(a2) 1.2(a3) 1.22(a4) 1.3(a5) (亿)
逐期增长量 ----
0.1
-0.05
0.15
0.02
0.08
(亿)
累计增长量 -----
0.1
0.05
0.2
0.22
0.3
(亿)
平均增长量=【0.1+(-0.05)+0.15+0.02+0.08】÷5 =0.3÷5=0.06(亿)
100 110 110
实际产值(万)
105 110 120
求该企业第一季度产值平均计划完成程度?
105110 120
c
3 100 110 110
104.69%
3
第二节 时间数列的水平指标
(2)分子分母都是时点数列
某企业员工情况
时间 1月初 2月初 3月初 4月初
男性比重 52
(%)
50.98 49.09 49.07
Ⅰ、资料逐日登记排列形成,用简单算术平均法。即:例:a a
某车间某月1到15日在册人数资料
n
日 期
统计学第四章总量指标和相对指标

第四章
以相对数形式计算计划完成程度相对指标
当计划任务以相对数的形式下达时,检查计划完成程度
就用相对数的形式检查。
实际完成程度(%)
公式:计划完成程度(%) = ————————————
计划规定的完成程度(%)
其中:
实际完成程度(%)=
本期实际完成数 ————————
上期实际完成数
计划规定的完成程度(%) = 上—本期—期实—计际—划完—任成—务数—数—
148.06 103.89
1、检查各月产量计划完成情况。 (计算结果见上表) 2、检查累计至二月份的产量计划完成程度情况。 3、简要说明一季度的计划完成情况。
累计至二成 月程 份 1度 2的 2 15 7计 2 10 0 % 划 05完 .5 4% 4 5400
21
作业2小题
第四章
第二节 相对指标(7)
(一)计划完成程度相对数
1、概念及基本计算公式 计划完成程度相对数(Relative number of
fulfilling plan)是现象在某一段时期内实际完 成数与计划任务数的对比,用以说明计划完成 的程度。 基本公式: 计划完成相对数=实际完成数÷计划任务数
11
第四章
第二节 相对指标(3)
1
作业2小题
第四章
•总量指标的含义、作用和种类 •相对指标的含义、种类和计算 •相对指标的运用
2
第四章
第四章 总量指标和相对指标
• 第一节 总量指标 • 第二节 相对指标 • 第三节 计算和运用相对指标的原则
3
第四章
第一节 总量指标(1)
• 一 总量指标的概念p.67
总量指标(Population quantity)是反映社会 经济现象发展的总规模、总水平的综合指标。
统计学第四章 总量指标与相对指标分析

4 - 13
2、时点指标
时点指标是反映社会经济现象在某一时点(瞬间)上所 处状况的总量指标。如某一时点上的人口数、商品库存 数、牲畜存栏数、土地面积数等。 时点指标的特点 第一,不能累计相加。时点指标是表明现象在某一 时点上的状况,只能按时点所表示的瞬间计数, 若累计相加,所得到的结果包含着大量重复计算, 不仅脱离实际而且也没有任何意义。 第二,时点指标的大小与时点的间隔长短无直接关 系。如资产负债表中年末资产总额并不一定大于 月末资产总额。
资金 占用
资金利 润率
500 3000 16.7% 万元 万元 不可比 不可比 可比 5000 万元 40000 12.5% 万元
乙企业
4 - 28
比较两厂经济效益
3、相对指标的表现形式
无名数 分母 为1 有名数
4 - 29
用倍数、系数、成数、﹪、‰等表示
分母为 1.00
分母 为10
分母 为100
4 - 14
第三,时点指标数值是间断计数的。
14
2014-4-23
时 点 指 标
2009年年末国家外汇储备23992亿美元,比上年末增加4531亿美元。
4 - 15
时期指标和时点指标的区别:
⑴时期指标连续计数,时点指标间断计数 ⑵时期指标具有累加性,时点指标不具有累加性 ⑶时期指标数值大小与时期长短有直接关系,时点 指标数值大小与时期长短无直接关系。
第四章 总量指标和相对指标分析
4-1
第一节
总量指标分析
一、总量指标的概念和作用
二、总量指标的分类 三、总量指标的计算方法
4-2
一、总量指标的概念和作用
1、总量指标的概念 总量指标又称统计绝对数:是用来反映社会 经济现象在一定条件下的总规模、总水平 或工作总量的统计指标。 总产值、总人数 、国民生产总值等
统计学第四章课后题及答案解析

统计学第四章课后题及答案解析第四章⼀、单项选择题1.由反映总体单位某⼀数量特征的标志值汇总得到的指标是()A.总体单位总量B.质量指标C.总体标志总量D.相对指标2.各部分所占⽐重之和等于1或100%的相对数()A.⽐例相对数B.⽐较相对数C.结构相对数D.动态相对数3.某企业⼯⼈劳动⽣产率计划提⾼5%,实际提⾼了10%,则提⾼劳动⽣产率的计划完成程度为()A.104.76%B.95.45%C.200%D.4.76%4.某企业计划规定产品成本⽐上年度降低10%实际产品成本⽐上年降低了14.5%,则产品成本计划完成程度()A.14.5%B.95%C.5%D.114.5%5.在⼀个特定总体内,下列说法正确的是( )A.只存在⼀个单位总量,但可以同时存在多个标志总量B.可以存在多个单位总量,但必须只有⼀个标志总量C.只能存在⼀个单位总量和⼀个标志总量D.可以存在多个单位总量和多个标志总量6.计算平均指标的基本要求是所要计算的平均指标的总体单位应是()A.⼤量的B.同质的C.有差异的D.不同总体的7.⼏何平均数的计算适⽤于求()A.平均速度和平均⽐率B.平均增长⽔平C.平均发展⽔平D.序时平均数8.⼀组样本数据为3、3、1、5、13、12、11、9、7这组数据的中位数是()A.3B.13C.7.1D.79.某班学⽣的统计学平均成绩是70分,最⾼分是96分,最低分是62分,根据这些信息,可以计算的测度离散程度的统计量是()A.⽅差B.极差C.标准差D.变异系数10.⽤标准差⽐较分析两个同类总体平均指标的代表性⼤⼩时,其基本的前提条件是( )A.两个总体的标准差应相等B.两个总体的平均数应相等C.两个总体的单位数应相等D.两个总体的离差之和应相等11.已知4个⽔果商店苹果的单价和销售额,要求计算4个商店苹果的平均单价,应采⽤()A.简单算术平均数B.加权算术平均数C.加权调和平均数D.⼏何平均数12.算术平均数、众数和中位数之间的数量关系决定于总体次数的分布状况。
统计学(第4章)

连续变动结果的总量指标,时期指标是
一个流量。
时间维度上
时期指标的三个特点 具有可加性
时期指标可以累计
时期指标数值大小与时期长短有直接关系
时期指标的数值一般为连续登记
2019/6/15
第四章 描述统计
5
统计学
2、时点指标
时点指标又叫存量指标,是指反映社 会经济现象在某一时点上的总量指标,
四 季度
1 500
计划完成百分数=
1400+1420+1470+1500 5000
=115.8%
注:2010年第一季度前的四个季度的累计量已达5000,说明五年计 划提前三个季度完成。
2019/6/15
第四章 描述统计
33
统计学
(2)累计法
如何确定提前 完成时间?
计算公式:
计划完成相对指标 长期计划期间实际累计完成数 长期计划规定的累计数
时点指标是一个存量。
时间维度上
时点指标的三个特点
不具可加性
不同时点指标数值是不能累加
时点指标数值大小与时点间隔长短无直 接关系
时点指标一般为间断统计
2019/6/15
第四章 描述统计
6
统计学
三、总量指标的计量单位
1、实物量单位(包括度量衡单位) 2、价值量单位 3、劳动量单位(工时和工日)
5 000 1 250 1 340 1 280
102.4
52.4
4 000 1 000 1 030 1 215
121.5
56.1
2 000 500 600 400
80.0
50.0
11 000 2 750 2 970 2 895 105.33
统计学4

用,掌握统计整理的方法,能够针对具体的调查资料
进行分类、汇总并编制统计表。
教学要求:
了解统计整理的概念和步骤,掌握统计分组、
分配数列及统计表的概念,重点掌握统计分组的
方法 、分配数列的编制,并学回会运用统计表来
表现统计资料。
4、1统计整理概述
检查数据是否真实反映客观实际情况,内 容是否符合实际 检查数据是否有错误,计算是否正确等
数据的审核—原始数据
(RAW DATA)
审核数据准确性的方法
1.
2.
逻辑检查 从定性角度,审核数据是否符合逻辑,内容 是否合理,各项目或数字之间有无相互矛盾 的现象 主要用于对分类和顺序据的审核 计算检查 检查调查表中的各项数据在计算结果和计算 方法上有无错误 主要用于对数值型数据的审核
饮料,就将这一饮料的品牌名字记录一次。
下面的表格是记录的原始数据。
顾客购买饮料的品牌名称
旭日升 露露 旭日升 可口可乐 百事可乐 可口可乐 汇源果汁 可口可乐 露露 可口可乐 可口可乐 旭日升 可口可乐 百事可乐 露露 旭日升 旭日升 百事可乐 可口可乐 旭日升 旭日升 可口可乐 可口可乐 旭日升 露露 旭日升 可口可乐 露露 百事可乐 百事可乐 汇源果汁 露露 百事可乐 可口可乐 百事可乐 汇源果汁 可口可乐 汇源果汁 可口可乐 汇源果汁 露露 可口可乐 旭日升 百事可乐 露露 汇源果汁 可口可乐 百事可乐 露露 旭日升
所以要选择组距式分组
第一步:确定组数。
K 1 lg 50 lg 2 7
第二步:确定各组的组距。 最大值为139,最小值为107,
统计学基础课件 第四章 总量指标和相对指标

❖ 作用
1. 反映总体内在的结构特征;
2. 用于不同对象的比较评价;
3. 反映事物发展变化的过程和趋势。
❖ 计量形式
1.有名数
2.无名数
第四章 总量指标和相对指标
二、相对指标的种类及计算方法
❖ 值
结构相对数
100%
总体全部数值
第四章 总量指标和相对指标
引例:
男性人口的 比重为50.8﹪
女性人口的 比重为49.2﹪
比1980年末的 9.9亿人增加
了28﹪
1999年末我国共有 总人口12.6亿人,其 中男性人口为6.4亿, 女性人口为6.2亿。
人口性别比 为1.03:1
人口出生率 为15.23‰
人口密度为 130人/平方公里
51.52﹪
特 ⒈为无名数,可用百分数或一比几或几比几表示; 点 ⒉分子分母可以互换;
3.用来反映组与组之间的联系程度或比例关系。
第四章 总量指标和相对指标
二、相对指标的种类及计算方法
3.比较相对指标 :比较相对数 某一总体的某指标数值
另一总体的该指标数值
例:某年某地区甲、乙两个公司商品销售额 分别为5.4亿元和3.6亿元。则
第四章 总量指标和相对指标
三、总量指标的计量单位 按计量单位分
实物量单位
价值量单位
劳动量单位
第四章 总量指标和相对指标
实物量单位
❖ 实物单位是根据事物的属性和特点而采用的计量单位,有 自然单位、度量衡单位和标准实物单位等。
1.自然单位 2.度量衡单位 3.复合计量单位 4.多重计量单位 3.标准实物单位
❖ 特点:
▪ 表现形式为绝对数 ▪ 总量指标反映了总体的规模信息 ▪ 只有有限总体才能准确计算总量指标
统计学 第四章 推断统计概述

第四章 推断统计概述第一部分 概率论基本知识← 一、概率的定义;二、概率的性质;三、概率的加法定理和乘法定理← 四、概率分布类型四、概率分布类型← 概率分布(probability distribution )是指对随机变量取不同值时的概率的描述,一般用概率分布函数进行描述。
← 依不同的标准,对概率分布可作不同的分类。
1、离散型分布与连续型分布← 依随机变量的类型,可将概率分布分为离散型概率分布与连续型概率分布。
← 教育统计学中最常用的离散型分布是二项分布,最常用的连续型分布是正态分布。
2、经验分布与理论分布← 依分布函数的来源,可将概率分布分为经验分布与理论分布。
← 经验分布(empirical distribution )是指根据观察或实验所获得的数据而编制的次数分布或相对频率分布。
← 理论分布(theoretical distribution )是按某种数学模型计算出的概率分布。
3、基本随机变量分布与抽样分布← 依所描述的数据的样本特性,可将概率分布分为基本随机变量分布与抽样分布(sampling distribution )。
← 基本随机变量分布是随机变量各种不同取值情况的概率分布,← 抽样分布是从同一总体内抽取的不同样本的统计量的概率分布。
第二部分 几种常见的概率分布← 一、二项分布← 二项分布(binomial distribution )是一种具有广泛用途的离散型随机变量的概率分布,它是由贝努里创始的,因此又称为贝努里分布。
← 2.二项分布函数← 二项分布是一种离散型随机变量的概率分布。
← 用 n 次方的二项展开式来表达在 n 次二项试验中成功事件出现的不同次数(X =0,1…,n )的概率分布,叫做二项分布函数。
← 二项展开式的通式(即二项分布函数):← ←← ← ←← 成功概率 p ;样本容量 n← 在成功概率为p 的总体中随机抽样,抽取样本容量为n 的样本中,有X 次为成()011111100q p C q p C q p C q p C q p n n n n n n n n n n n ++++=+---Λ()Xn X X n X q p C P -⋅⋅=()X n X q p X n X n -⋅-=!!!功的概率: ←(X =0,1…,n ) ←称X 服从参数为n ,p 的二项分布,记为: ←X ~B(n ,p ) 其中,0<p<1 ←二项分布的性质 ←二项分布有如下性质: ←①当p=q 时,图形是对称的。
统计学第四章 综合指标

3、计划完成百分数的计算
A、计划数为绝对数。
绝对数的计划完成百分数 实际绝对水平 100% 计划绝对水平
某工业企业总产值资料如下表:
车 名
间 称
总产值(万元) 计划Hale Waihona Puke 实际数计划完成百分数 (%)
(甲)
甲 乙 丙
(1)
50 110 140
(2)
80 100 140
(3)=(2)/(1)
160.00 90.91 100.00
时期指标与时点指标的联系:
1、二者都属于总量指标。 2、二者通常是相互影响的。
总量指标的计算
总量指标的单位一般有: 实物量单位 价值量单位 劳动量单位
1. 实物单位是根据事物的自然属性和特点采用的计 量单位。 实物单位的分类: ①自然单位:它是按照研究现象的自然状况来计量其 数量的一种计量单位。 ②度量衡单位:它是按照同意的度量衡制度的规定来 计量客观事物数量的一种计量单位。 ③双重单位和复合单位:是指在需要同时采用两个或 两个以上单位来计量事物时采用的单位。 ④标准实物单位:按照统一折算的标准来度量被研究 现象数量的一种计量单位。
相对指标在统计分析中的作用:
• 相对指标为人们深入认识事物发展的质 量与状况提供客观的依据,社会经济现 象总是相互联系、相互制约的关系。 • 计算相对指标可以使不能直接对比的现 象找到可以对比的基础,进行有效的分 析。
二、相对指标的种类及计算方法:
1、结构相对指标: • 定义:是在资料分组的基础上,以总体 总量作为比较标准,求出各组总量占总 体总量的比重,来反映总体内部组成情 况的综合指标。
合
计
300
320
106.67
要求:计算各车间和全厂总产值的计划完成百分数。
统计学第四章动态数列

动态数列
第一节 动态数列的编制
第二节 动态数列水平分析指标
第三节 动态数列速度分析指标
第四节 长期趋势的测定与预测 第五节 季节变动的测定与预测
第一节
动态数列的编制
动态数列的概念
动态数列的种类
动态数列的编制原则
一、动态数列的概念
社会经济现象总是随着时间度加权平均
一季 度初 二季 度初
90天
三季 度初
90天
y1
y2
y3
次年一 季度初
180天
y4
y1 y2 2
y 2 y3 2
y3 y 4 2
y2 y3 y3 y4 y1 y 2 1 1 2 2 2 2 11 2
y2 y3 y1 y 2 y N 1 y N f1 f2 f N 1 2 2 2 y f 1 f 2 f N 1
99.49 118 .28 118 .28 140 .71 83.50 99.49 3 2 3 则该省1994年-2006 年服务业平均从业人数: 2 2 2 140 .71 168 .51 168 .51 183 .75 2 2 2 2 y 3 2 3 2 2 12 8.52 万人
国有经济单位职 工工资总额所占 78.45 比重(%)
77.55
77.78
45.06
74.81
职工平均货币工 资(元)
2365
2677
3236
4510
5500
动态数列的作用
描述社会经济现象在不同时间的发展状态和 过程。(研究过去)
研究社会经济现象的发展趋势和速度以及掌
《统计学》第四章

•各个变量值与算术平均数的离差平方总和为最小 证 明 : 值。 设 x 为 不 等 于 x 的 任 意 值 , c = x − x
0 0
Σ ( x − x )2 = 最 小 值
x 0 = x − c , 则 以 x 0为 中 心 的 离 差 总 和 为 : Σ ( x − x0 )2 = Σ
[x − ( x − c ) ]
3、调和算术平均数:调和平均数是常 用的另一种平均指标,它是根据标志 值的倒数计算的,又称为倒数平均数。
m1 + m2 + ⋅⋅⋅ + mn H = m1 m2 = mn x1 + x2 + ⋅⋅⋅ + xn
∑m ∑
i =1 i =1 n mi xi
n
i
例、假定有A 例、假定有A、B两家公司员工的月工资资 料如下表所示:要求计算平均工资。
60 70 20 150
50 40 25 115
工资总额 平均工资 = ,但职工人数(分母)未知。 职工人数 各组工资总额 m 各组职工人数 = ,f = 各组工资水平 x H A公司 =
∑m ∑
i =1 i =1 3 mi xi
3
i
48000 + 70000 + 32000 = 48000 + 70000 + 32000 800 1000 1600
250
3.13
42 50 × 5 + 150 × 42 + 52.50 16 + 150 × 13 250 × 350 = + 200—300 16 5 + 42 + 16 + 132504 20.00 16900 = 300—400 13 16.25 350 80 =400以上 (百吨) 211 . 26 4 5.00 450 合计 80 100.00 —
统计学 第四章 参数估计

由样本数量特征得到关于总体的数量特征 统计推断(statistical 的过程就叫做统计推断 的过程就叫做统计推断 inference)。 统计推断主要包括两方面的内容一个是参 统计推断主要包括两方面的内容一个是参 数估计(parameter estimation),另一个 数估计 另一个 假设检验 。 是假设检验(hypothesis testing)。
ˆ P(θ )
无偏 有偏
A
B
θ
ˆ θ
估计量的无偏性直观意义
θ =µ
•
•
•
• •
• • • •
•
2、有效性(efficiency)
有效性:对同一总体参数的两个无偏点估计 有效性: 量,有更小标准差的估计量更有效 。
ˆ P(θ )
ˆ θ1 的抽样分布
B A
ˆ θ2 的抽样分布
θ
ˆ θ
பைடு நூலகம்
3、一致性(consistency)
置信区间与置信度
1. 用一个具体的样本 所构造的区间是一 个特定的区间, 个特定的区间,我 们无法知道这个样 本所产生的区间是 否包含总体参数的 真值 2. 我们只能是希望这 个区间是大量包含 总体参数真值的区 间中的一个, 间中的一个,但它 也可能是少数几个 不包含参数真值的 区间中的一个
均值的抽样分布
总体均值的区间估计(例题分析)
25, 95% 解 : 已 知 X ~N(µ , 102) , n=25, 1-α = 95% , zα/2=1.96。根据样本数据计算得: x =105.36 96。 总体均值µ在1-α置信水平下的置信区间为 σ 10 x ± zα 2 = 105.36 ±1.96× n 25 = 105.36 ± 3.92
统计学第四章的教材

几个直观的结论
1. 样本均值的均值(数学期望)等于总体均值(式中:M为样本 n 数目); xi 22 23 28 i 1 25 X M 16 2. 抽样误差是随样本不同而不同的随机变量。抽样误差均值 等于0; xX 0
3. 样本均值的方差等于总体方差的1/n。
3
(二)抽样估计的一般步骤 1、设计抽样方案 2、 随机抽取样本(从总体随机抽取部分单位构成样本) 3、搜集样本资料(对样本单位进行调查登记) 4、整理样本资料(审查、分组汇总、计算样本指标的
数值,即计算估计量的具体数值)
5、估计总体指标(即估计总体参数)
总体参数与样本估计量的关系——对于特定的目 的,总体是惟一的,所以参数也是惟一的;而由 于样本是随机的,所以样本估计量是随机变量。
(3)抽样方法。相同条件下,重复抽样的抽样平均误 差大比不重复抽样的抽样平均误差大。
(4)抽样组织方式。由于不同抽样组织方式有不同的 抽样误差,所以,在误差要求相同的情况下,不同抽 样组织方式所必需的抽样数目也不同。
21
不知道总体方差时如何计算
用样本方差代替计算 用过去(总体或样本)方差代替计算 用同类现象(当前 或过去、总体或样本) 方 代替计算 有若干个方差可选择时,选方差最大者 (注意:对比率,即选择最接近0.5的值所 得的方差最大)
进无偏估计量。
29
二、区间估计
(一)区间估计的原理 区间估计就是根据样本估计量以一定 可靠程度推断总体参数所在的区间范围。 特点:考虑了估计量的分布,所以它能 给出估计精度,也能说明估计结果的把握 程度(置信度)。
30
(一)总体均值的置信区间
(1)假定条件
总体服从正态分布,且总体方差(2)已知
统计学第四章统计分析指标
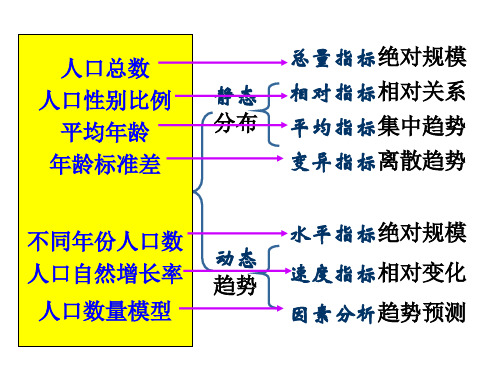
计划完成相对指标
产值计划完成程度若大于100%,说明超额完 成计划;若小于100%,说明没有完成计划, 为正指标。 单位成本计划完成程度若大于100%,说明成 本比计划高,没有完成计划;若小于100%, 说明超额完成计划,为逆指标。 计划完成相对数的分子分母不能互换,在指 标含义、计算范围、核算方法等方面要一致。
计划完成相对指标
长期(通常是五年)计划完成情况—水平法和累计法
总体的一部分单位 总体另一部分单位 比例相对数
人口性别比例 积累与消费比例 农轻重比例
…
…
比例相对指标
人口出生性别比正常值一般在103到107之间。但 我国人口的出生性别比自20世纪80年代中期以来 迅速攀升。 1995年,0岁~4岁人口性别比:118.38 2000年,0岁~4岁人口性别比:120.17 2003年,0岁~4岁人口性6
(1)计划数为绝对数
计划完成相对数=(实际完成数÷同期计划数)×100%
适用于研究分析社会经济现象的规模或水平的计划完成 程度。
计划完成相对指标
〔例〕 某公司2010年计划销售某种产品30万件, 实际销售32万件,则该公司2010年销售计划完成相对 指标是多少?超额完成计划多少?
销售计划完成相对指标 = (32/30)*100% = 106.7% 超额完成计划 = 106.7% - 100% = 6.7%
t1时段
t2时段
t3时段
时期指标的特点: 1. 不同时期的时期指标数值具有可加性; 2. 时期指标的数值大小与时期长短有直接关系; 3. 时期指标数值是连续登记、累计的结果。
时点指标的特点: 1. 不同时期的时点指标数值不具有可加性。 2. 时点指标的数值大小与时间间隔长短无关。 3. 时点指标的数值是间断计数的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12
Percentiles - Example
Listed below are the commissions earned last month by a sample of 15 brokers at Salomon Smith Barney’s Oakland, California, office. Salomon Smith Barney is an investment company with offices located throughout the United States.
13
Percentiles – Example (cont.)
Step 1: Organize the data from lowest to largest value
$1,460 $1,758 $2,047 $2,287 $1,471 $1,787 $2,054 $2,311 $1,637 $1,940 $2,097 $2,406 $1,721 $2,038 $2,205
Alternative ways of describing spread of data include determining the location of values that divide a set of observations into equal parts.
These measures include quartiles, deciles, and percentiles.
7
Stem-and-leaf: Another Example
Listed in Table 4–1 is the number of 30-second radio advertising spots purchased by each of the 45 members of the Greater Buffalo Automobile Dealers Association last year. Organize the data into a stem-and-leaf display. Around what values do the number of advertising spots tend to cluster? What is the fewest number of spots purchased by a dealer? The largest number purchased?
11
Percentile Computation
To formalize the computational procedure, let Lp refer to the location of a desired percentile. So if we wanted to find the 33rd percentile we would use L33 and if we wanted the median, the 50th percentile, then L50.
6
Stem-and-Leaf – Example
Suppose the seven observations in the 90 up to 100 class are: 96, 94, 93, 94, 95, 96, and 97.
The stem value is the leading digit or digits, in this case 9. The leaves are the trailing digits. The stem is placed to the left of a vertical line and the leaf values to the right. The values in the 90 up to 100 class would appear as Then, we sort the values within each stem from smallest to largest. Thus, the second row of the stemand-leaf display would appear as follows:
20
Skewness
In Chapter 3, measures of central location for a set of observations (the mean, median, and mode) and measures of data dispersion (e.g. range and the standard deviation) were introduced Another characteristic of a set of data is the shape. There are four shapes commonly observed:
Stem-and-leaf display is a statistical technique to present a set of data. Each numerical value is divided into two parts. The leading digit(s) becomes the stem and the trailing digit the leaf. The stems are located along the vertical axis, and the leaf values are stacked against each other along the horizontal axis. Advantage of the stem-and-leaf display over a frequency distribution - the identity of each observation is not lost.
3
Dot Plots - Examples
Reported below are the number of vehicles sold in the last 24 months at Smith Ford Mercury Jeep, Inc., in Kane, Pennsylvania, and Brophy Honda Volkswagen in Greenville, Ohio. Construct dot plots and repo small-town Auto USA lots.
Describing Data: Displaying and Exploring Data
Chapter 4
McGraw-Hill/Irwin
©The McGraw-Hill Companies, Inc. 2008
GOALS
Develop and interpret a dot plot. Develop and interpret a stem-and-leaf display. Compute and understand quartiles, deciles, and percentiles. Construct and interpret box plots. Compute and understand the coefficient of skewness. Draw and interpret a scatter diagram. Construct and interpret a contingency table.
4
Dot Plot – Minitab Example
5
Stem-and-Leaf
In Chapter 2, we showed how to organize data into a frequency distribution. The major advantage to organizing the data into a frequency distribution is that we get a quick visual picture of the shape of the distribution. One technique that is used to display quantitative information in a condensed form is the stem-and-leaf display.
$2,038 $2,097 $2,287 $2,406 $1,758 $2,047 $1,940 $1,471 $1,721 $1,637 $2,205 $1,787 $2,311 $2,054 $1,460
Locate the median, the first quartile, and the third quartile for the commissions earned.
8
Stem-and-leaf: Another Example
9
Stem-and-leaf: Another Example (Minitab)
10
Quartiles, Deciles and Percentiles
The standard deviation is the most widely used measure of dispersion.
2
Dot Plots
A dot plot groups the data as little as possible and the identity of an individual observation is not lost. To develop a dot plot, each observation is simply displayed as a dot along a horizontal number line indicating the possible values of the data. If there are identical observations or the observations are too close to be shown individually, the dots are “piled” on top of each other.
