拉船靠岸问题速度与加速度分析

合集下载

大学物理学(第三版)课后习题答案

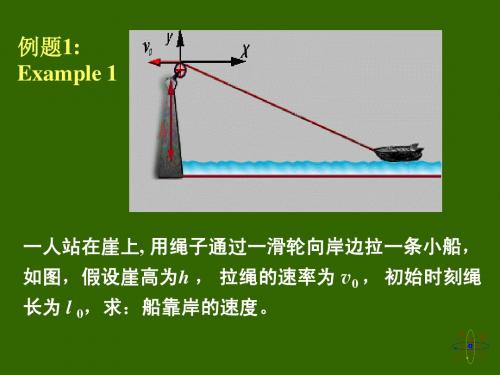
1-4 在离水面高h 米的岸上，有人用绳子拉船靠岸，船在离岸S 处，如题1-4图所示．当人以0v (m ·1-s )的速率收绳时，试求船运动的速度和加速度的大小．图1-4解：设人到船之间绳的长度为l ，此时绳与水面成θ角，由图可知222s h l +=将上式对时间t 求导，得tss t l ld d 2d d 2= 题1-4图根据速度的定义，并注意到l ,s 是随t 减少的， ∴ tsv v t l v d d ,d d 0-==-=船绳即 θcos d d d d 00v v s l t l s l t s v ==-=-=船或 sv s h s lv v 02/1220)(+==船将船v 再对t 求导，即得船的加速度1-6 已知一质点作直线运动，其加速度为 a ＝4+3t 2s m -⋅，开始运动时，x ＝5 m ，v=0，求该质点在t ＝10s 时的速度和位置．解：∵ t tva 34d d +==分离变量，得 t t v d )34(d +=积分，得 12234c t t v ++= 由题知，0=t ,00=v ,∴01=c故 2234t t v += 又因为 2234d d t t t x v +==分离变量， t t t x d )234(d 2+= 积分得 232212c t t x ++= 由题知 0=t ,50=x ,∴52=c故 521232++=t t x 所以s 10=t 时m70551021102s m 190102310432101210=+⨯+⨯=⋅=⨯+⨯=-x v1-10 以初速度0v ＝201s m -⋅抛出一小球，抛出方向与水平面成幔 60°的夹角，求：(1)球轨道最高点的曲率半径1R ；(2)落地处的曲率半径2R ．(提示：利用曲率半径与法向加速度之间的关系)解：设小球所作抛物线轨道如题1-10图所示．题1-10图 (1)在最高点，o 0160cos v v v x == 21s m 10-⋅==g a n又∵ 1211ρv a n =∴ m1010)60cos 20(22111=︒⨯==n a v ρ(2)在落地点，2002==v v 1s m -⋅,而 o60cos 2⨯=g a n∴ m 8060cos 10)20(22222=︒⨯==n a v ρ1-13 一船以速率1v ＝30km ·h -1沿直线向东行驶，另一小艇在其前方以速率2v ＝40km ·h -1 沿直线向北行驶，问在船上看小艇的速度为何?在艇上看船的速度又为何?解：(1)大船看小艇，则有1221v v v-=，依题意作速度矢量图如题1-13图(a)题1-13图由图可知 1222121h km 50-⋅=+=v v v方向北偏西 ︒===87.3643arctan arctan21v v θ (2)小船看大船，则有2112v v v-=，依题意作出速度矢量图如题1-13图(b)，同上法，得5012=v 1h km -⋅2-2 一个质量为P 的质点，在光滑的固定斜面（倾角为α）上以初速度0v 运动，0v 的方向与斜面底边的水平线AB 平行，如图所示，求这质点的运动轨道．解: 物体置于斜面上受到重力mg ，斜面支持力N .建立坐标：取0v方向为X 轴，平行斜面与X 轴垂直方向为Y 轴.如图2-2.题2-2图X 方向： 0=x F t v x 0= ①Y 方向： y y ma mg F ==αsin ②0=t 时 0=y 0=y v2sin 21t g y α=由①、②式消去t ，得220sin 21x g v y ⋅=α 2-4 质点在流体中作直线运动，受与速度成正比的阻力kv (k 为常数)作用，t =0时质点的速度为0v ，证明(1) t 时刻的速度为v ＝t mkev )(0-；(2) 由0到t 的时间内经过的距离为x ＝(k mv 0)［1-t m ke )(-］；(3)停止运动前经过的距离为)(0kmv ；(4)证明当k m t =时速度减至0v 的e1，式中m 为质点的质量．答: (1)∵ tvm kv a d d =-= 分离变量，得mtk v v d d -=即 ⎰⎰-=vv t mt k v v00d d m kte v v -=ln ln 0∴ tm k ev v -=0(2) ⎰⎰---===tttm k m ke kmv t ev t v x 000)1(d d (3)质点停止运动时速度为零，即t →∞，故有 ⎰∞-=='00d kmv t ev x tm k(4)当t=km时，其速度为 ev e v ev v km m k 0100===-⋅- 即速度减至0v 的e1. 2-10 一颗子弹由枪口射出时速率为10s m -⋅v ，当子弹在枪筒内被加速时，它所受的合力为F =(bt a -)N(b a ,为常数)，其中t 以秒为单位：(1)假设子弹运行到枪口处合力刚好为零，试计算子弹走完枪筒全长所需时间；(2)求子弹所受的冲量．(3)求子弹的质量．解: (1)由题意，子弹到枪口时，有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量⎰-=-=t bt at t bt a I 0221d )(将bat =代入，得 ba I 22=(3)由动量定理可求得子弹的质量202bv a v I m == 2-13 以铁锤将一铁钉击入木板，设木板对铁钉的阻力与铁钉进入木板内的深度成正比，在铁锤击第一次时，能将小钉击入木板内1 cm ，问击第二次时能击入多深，假定铁锤两次打击铁钉时的速度相同．解: 以木板上界面为坐标原点，向内为y 坐标正向，如题2-13图，则铁钉所受阻力为题2-13图ky f -=第一锤外力的功为1A⎰⎰⎰==-='=ssky ky y f y f A 112d d d ① 式中f '是铁锤作用于钉上的力，f 是木板作用于钉上的力，在0d →t 时，f 'f -=．设第二锤外力的功为2A ，则同理，有⎰-==21222221d y kky y ky A ② 由题意，有2)21(212kmv A A =∆== ③即222122k k ky =- 所以， 22=y于是钉子第二次能进入的深度为cm 414.01212=-=-=∆y y y2-15 一根劲度系数为1k 的轻弹簧A 的下端，挂一根劲度系数为2k 的轻弹簧B ，B 的下端一重物C ，C 的质量为M ，如题2-15图．求这一系统静止时两弹簧的伸长量之比和弹性势能之比．解: 弹簧B A 、及重物C 受力如题2-15图所示平衡时，有题2-15图Mg F F B A ==又 11x k F A ∆=22x k F B ∆=所以静止时两弹簧伸长量之比为1221k k x x =∆∆ 弹性势能之比为12222211121212k kx k x k E E p p =∆∆= 2-17 由水平桌面、光滑铅直杆、不可伸长的轻绳、轻弹簧、理想滑轮以及质量为1m 和2m 的滑块组成如题2-17图所示装置，弹簧的劲度系数为k ，自然长度等于水平距离BC ，2m 与桌面间的摩擦系数为μ，最初1m 静止于A 点，AB ＝BC ＝h ，绳已拉直，现令滑块落下1m ,求它下落到B 处时的速率．解: 取B 点为重力势能零点，弹簧原长为弹性势能零点，则由功能原理，有])(21[)(21212212l k gh m v m m gh m ∆+-+=-μ 式中l ∆为弹簧在A 点时比原长的伸长量，则h BC AC l )12(-=-=∆联立上述两式，得()()212221122m m khgh m m v +-+-=μ题2-17图2-19 质量为M 的大木块具有半径为R 的四分之一弧形槽，如题2-19图所示．质量为m 的小立方体从曲面的顶端滑下，大木块放在光滑水平面上，二者都作无摩擦的运动，而且都从静止开始，求小木块脱离大木块时的速度．解: m 从M 上下滑的过程中，机械能守恒，以m ，M ，地球为系统，以最低点为重力势能零点，则有222121MV mv mgR +=又下滑过程，动量守恒，以m ,M 为系统则在m 脱离M 瞬间，水平方向有0=-MV mv联立，以上两式，得()M m MgR v +=2习题八8-1 电量都是q 的三个点电荷，分别放在正三角形的三个顶点．试问：(1)在这三角形的中心放一个什么样的电荷，就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系?解: 如题8-1图示(1) 以A 处点电荷为研究对象，由力平衡知：q '为负电荷2220)33(π4130cos π412a q q a q '=︒εε解得 q q 33-=' (2)与三角形边长无关．题8-1图题8-2图8-2 两小球的质量都是m ，都用长为l 的细绳挂在同一点，它们带有相同电量，静止时两线夹角为2θ ,如题8-2图所示．设小球的半径和线的质量都可以忽略不计，求每个小球所带的电量．解: 如题8-2图示⎪⎩⎪⎨⎧===220)sin 2(π41sin cos θεθθl q F T mg T e解得θπεθtan 4sin 20mg l q =8-3 根据点电荷场强公式204r q E πε=，当被考察的场点距源点电荷很近(r →0)时，则场强→∞，这是没有物理意义的，对此应如何理解?解: 020π4r r q Eε=仅对点电荷成立，当0→r 时，带电体不能再视为点电荷，再用上式求场强是错误的，实际带电体有一定形状大小，考虑电荷在带电体上的分布求出的场强不会是无限大．8-4 在真空中有A ，B 两平行板，相对距离为d ，板面积为S ，其带电量分别为+q 和-q ．则这两板之间有相互作用力f ，有人说f =2024dq πε,又有人说，因为f =qE ,SqE 0ε=，所以f =Sq 02ε．试问这两种说法对吗?为什么? f到底应等于多少?解: 题中的两种说法均不对．第一种说法中把两带电板视为点电荷是不对的，第二种说法把合场强Sq E 0ε=看成是一个带电板在另一带电板处的场强也是不对的．正确解答应为一个板的电场为Sq E 02ε=，另一板受它的作用力Sq S qq f 02022εε==，这是两板间相互作用的电场力． 8-5一电偶极子的电矩为l q p=，场点到偶极子中心O 点的距离为r ,矢量r与l的夹角为θ,(见题8-5图)，且l r >>．试证P 点的场强E 在r 方向上的分量r E 和垂直于r 的分量θE 分别为r E =302cos r p πεθ,θE =304sin r p πεθ证: 如题8-5所示，将p 分解为与r平行的分量θsin p 和垂直于r的分量θsin p ．∵ l r >>∴ 场点P 在r 方向场强分量30π2cos r p E r εθ=垂直于r 方向，即θ方向场强分量300π4sin r p E εθ=题8-5图题8-6图8-6 长l =15.0cm的直导线AB 上均匀地分布着线密度λ=5.0x10-9C ·m -1的正电荷．试求：(1)在导线的延长线上与导线B 端相距1a =5.0cm 处P 点的场强；(2)在导线的垂直平分线上与导线中点相距2d =5.0cm 处Q 点的场强．解：如题8-6图所示(1)在带电直线上取线元x d ，其上电量q d 在P 点产生场强为20)(d π41d x a xE P -=λε222)(d π4d x a x E E l l P P -==⎰⎰-ελ]2121[π40l a l a +--=ελ)4(π220l a l-=ελ用15=l cm ，9100.5-⨯=λ1m C -⋅,5.12=a cm 代入得21074.6⨯=P E 1C N -⋅方向水平向右(2)同理2220d d π41d +=x xE Q λε 方向如题8-6图所示由于对称性⎰=l QxE 0d ，即Q E只有y 分量，∵22222220dd d d π41d ++=x x x E Qyλε 22π4d d ελ⎰==l QyQy E E ⎰-+2223222)d (d l l x x2220d4π2+=l lελ以9100.5-⨯=λ1cm C -⋅,15=l cm ,5d 2=cm 代入得21096.14⨯==Qy Q E E 1C N -⋅，方向沿y 轴正向8-7 一个半径为R 的均匀带电半圆环，电荷线密度为λ,求环心处O 点的场强．解: 如8-7图在圆上取ϕRd dl =题8-7图ϕλλd d d R l q ==，它在O 点产生场强大小为 20π4d d R R E εϕλ=方向沿半径向外则ϕϕελϕd sin π4sin d d 0RE E x ==ϕϕελϕπd cos π4)cos(d d 0RE E y -=-= 积分RR E x 000π2d sin π4ελϕϕελπ==⎰ 0d cos π400=-=⎰ϕϕελπRE y ∴RE E x 0π2ελ==，方向沿x 轴正向． 8-8 均匀带电的细线弯成正方形，边长为l ，总电量为q ．(1)求这正方形轴线上离中心为r 处的场强E ；(2)证明：在l r >>处，它相当于点电荷q 产生的场强E ．解: 如8-8图示，正方形一条边上电荷4q 在P 点产生物强P Ed 方向如图，大小为()4π4cos cos d 22021l r E P +-=εθθλ∵22cos 221l r l +=θ12cos cos θθ-=∴24π4d 22220l r l l r E P ++=ελP Ed 在垂直于平面上的分量βcos d d P E E =⊥∴424π4d 2222220l r rl r l r lE +++=⊥ελ题8-8图由于对称性，P 点场强沿OP 方向，大小为2)4(π44d 422220l r l r lrE E P ++=⨯=⊥ελ∵ lq 4=λ∴2)4(π422220l r l r qrE P ++=ε 方向沿OP8-9 (1)点电荷q 位于一边长为a 的立方体中心，试求在该点电荷电场中穿过立方体的一个面的电通量；(2)如果该场源点电荷移动到该立方体的一个顶点上，这时穿过立方体各面的电通量是多少?*(3)如题8-9(3)图所示，在点电荷q 的电场中取半径为R 的圆平面．q 在该平面轴线上的A 点处，求：通过圆平面的电通量．(xR arctan =α)解: (1)由高斯定理0d εqS E s ⎰=⋅立方体六个面，当q 在立方体中心时，每个面上电通量相等 ∴ 各面电通量06εq e=Φ．(2)电荷在顶点时，将立方体延伸为边长a 2的立方体，使q 处于边长a 2的立方体中心，则边长a 2的正方形上电通量06εqe=Φ对于边长a 的正方形，如果它不包含q 所在的顶点，则24εq e =Φ，如果它包含q 所在顶点则0=Φe．如题8-9(a)图所示．题8-9(3)图题8-9(a)图题8-9(b)图题8-9(c)图(3)∵通过半径为R 的圆平面的电通量等于通过半径为22x R +的球冠面的电通量，球冠面积*]1)[(π22222xR x x R S +-+=∴)(π42200x R Sq +=Φε02εq=[221xR x +-]*关于球冠面积的计算：见题8-9(c)图ααα⎰⋅=0d sin π2r r Sααα⎰⋅=02d sin π2r)cos 1(π22α-=r8-10 均匀带电球壳内半径6cm ，外半径10cm ，电荷体密度为2×510-C ·m -3求距球心5cm ，8cm ,12cm 各点的场强．解: 高斯定理0d ε∑⎰=⋅qS E s,02π4ε∑=qr E当5=r cm 时，0=∑q ,0=E8=r cm 时，∑q 3π4p=3(r )3内r - ∴()2023π43π4rr r E ερ内-=41048.3⨯≈1C N -⋅，方向沿半径向外．12=r cm时,3π4∑=ρq -3(外r ）内3r ∴()420331010.4π43π4⨯≈-=r r r E ερ内外 1C N -⋅ 沿半径向外.8-11 半径为1R 和2R (2R ＞1R )的两无限长同轴圆柱面，单位长度上分别带有电量λ和-λ,试求:(1)r ＜1R ；(2)1R ＜r ＜2R ；(3)r ＞2R 处各点的场强．解: 高斯定理0d ε∑⎰=⋅qS E s取同轴圆柱形高斯面，侧面积rl S π2= 则 rl E S E Sπ2d =⋅⎰对(1) 1R r <0,0==∑E q (2) 21R r R <<λl q =∑∴rE 0π2ελ=沿径向向外(3)2R r >0=∑q∴0=E题8-12图8-12 两个无限大的平行平面都均匀带电，电荷的面密度分别为1σ和2σ，试求空间各处场强．解: 如题8-12图示，两带电平面均匀带电，电荷面密度分别为1σ与2σ，两面间，n E)(21210σσε-= 1σ面外，n E )(21210σσε+-=2σ面外， n E)(21210σσε+=n：垂直于两平面由1σ面指为2σ面．8-13 半径为R 的均匀带电球体内的电荷体密度为ρ,若在球内挖去一块半径为r ＜R 的小球体，如题8-13图所示．试求：两球心O 与O '点的场强，并证明小球空腔内的电场是均匀的．解: 将此带电体看作带正电ρ的均匀球与带电ρ-的均匀小球的组合，见题8-13图(a)． (1)ρ+球在O 点产生电场010=E，ρ- 球在O 点产生电场'd π4π3430320OO r E ερ=∴O 点电场'd33030OO r E ερ= ； (2)ρ+在O '产生电场'd π4d 3430301OO E ερπ='ρ-球在O '产生电场002='E∴ O ' 点电场03ερ='E 'OO题8-13图(a) 题8-13图(b)(3)设空腔任一点P 相对O '的位矢为r'，相对O 点位矢为r (如题8-13(b)图)则3ερrE PO =，3ερr E O P '-=' ,∴003'3)(3ερερερd OO r r E E E O P PO P=='-=+='∴腔内场强是均匀的． 8-14 一电偶极子由q =1.0×10-6C的两个异号点电荷组成，两电荷距离d=0.2cm ，把这电偶极子放在1.0×105N ·C -1的外电场中，求外电场作用于电偶极子上的最大力矩．解: ∵电偶极子p在外场E 中受力矩E p M ⨯=∴qlE pE M ==max 代入数字4536max 100.2100.1102100.1---⨯=⨯⨯⨯⨯⨯=M m N ⋅8-15 两点电荷1q =1.5×10-8C ，2q =3.0×10-8C ，相距1r =42cm ，要把它们之间的距离变为2r =25cm ，需作多少功?解:⎰⎰==⋅=22210212021π4π4d d r r r r q q r r q q r F A εε )11(21r r - 61055.6-⨯-=J外力需作的功61055.6-⨯-=-='A A J题8-16图8-16 如题8-16图所示，在A ，B 两点处放有电量分别为+q ,-q 的点电荷，AB 间距离为2R ，现将另一正试验点电荷0q 从O 点经过半圆弧移到C 点，求移动过程中电场力作的功．解: 如题8-16图示0π41ε=O U 0)(=-RqR q 0π41ε=O U )3(R qR q -R q 0π6ε-= ∴Rqq U U q A o C O 00π6)(ε=-=8-17 如题8-17图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R ．试求环中心O 点处的场强和电势．解: (1)由于电荷均匀分布与对称性，AB 和CD 段电荷在O 点产生的场强互相抵消，取θd d R l =则θλd d R q =产生O 点Ed 如图，由于对称性，O 点场强沿y 轴负方向题8-17图θεθλππcos π4d d 2220⎰⎰-==R R E E yR 0π4ελ=［)2sin(π-2sin π-］ R0π2ελ-=(2)AB 电荷在O 点产生电势，以0=∞U⎰⎰===AB200012ln π4π4d π4d R R x x x x U ελελελ 同理CD 产生 2ln π402ελ=U 半圆环产生034π4πελελ==R R U∴ 0032142ln π2ελελ+=++=U U U U O8-18 一电子绕一带均匀电荷的长直导线以2×104m ·s -1的匀速率作圆周运动．求带电直线上的线电荷密度．(电子质量0m =9.1×10-31kg ，电子电量e =1.60×10-19C)解: 设均匀带电直线电荷密度为λ，在电子轨道处场强rE 0π2ελ=电子受力大小 re eE F e 0π2ελ== ∴ rv m r e 20π2=ελ得1320105.12π2-⨯==emv ελ1m C -⋅8-19 空气可以承受的场强的最大值为E =30kV ·cm -1，超过这个数值时空气要发生火花放电．今有一高压平行板电容器，极板间距离为d =0.5cm ，求此电容器可承受的最高电压．解: 平行板电容器内部近似为均匀电场∴ 4105.1d ⨯==E U V8-20根据场强E与电势U 的关系UE -∇= ，求下列电场的场强：(1)点电荷q 的电场；(2)总电量为q ，半径为R 的均匀带电圆环轴上一点；*(3)偶极子ql p =的l r >>处(见题8-20图)．解: (1)点电荷 rqU 0π4ε= 题 8-20 图∴200π4r rq r r U E ε=∂∂-= 0r为r 方向单位矢量．(2)总电量q ，半径为R 的均匀带电圆环轴上一点电势220π4xR q U +=ε∴()i x R qx i x U E2/3220π4+=∂∂-=ε(3)偶极子l q p=在l r >>处的一点电势200π4cos ])cos 21(1)cos 2(1[π4r ql llr q U εθθθε=+--=∴30π2cos r p r U E r εθ=∂∂-= 30π4sin 1r p U r E εθθθ=∂∂-=8-21 证明：对于两个无限大的平行平面带电导体板(题8-21图)来说，(1)相向的两面上，电荷的面密度总是大小相等而符号相反；(2)相背的两面上，电荷的面密度总是大小相等而符号相同．证: 如题8-21图所示，设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1σ，2σ，3σ，4σ题8-21图(1)则取与平面垂直且底面分别在A 、B 内部的闭合柱面为高斯面时，有0)(d 32=∆+=⋅⎰S S E s σσ∴+2σ03=σ说明相向两面上电荷面密度大小相等、符号相反； (2)在A 内部任取一点P ，则其场强为零，并且它是由四个均匀带电平面产生的场强叠加而成的，即0222204030201=---εσεσεσεσ 又∵+2σ03=σ ∴1σ4σ=说明相背两面上电荷面密度总是大小相等，符号相同． 8-22 三个平行金属板A ，B 和C 的面积都是200cm 2，A 和B 相距4.0mm ，A 与C 相距2.0 mm ．B ，C 都接地，如题8-22图所示．如果使A 板带正电3.0×10-7C ，略去边缘效应，问B 板和C 板上的感应电荷各是多少?以地的电势为零，则A 板的电势是多少? 解: 如题8-22图示，令A 板左侧面电荷面密度为1σ，右侧面电荷面密度为2σ题8-22图(1)∵ AB AC U U =，即 ∴ AB AB AC AC E E d d =∴2d d 21===ACABAB AC E E σσ 且 1σ+2σSq A =得 ,32Sq A=σSq A 321=σ而7110232-⨯-=-=-=A C q S q σCC10172-⨯-=-=S q B σ(2)301103.2d d ⨯===AC AC AC A E U εσV 8-23 两个半径分别为1R 和2R （1R ＜2R )的同心薄金属球壳，现给内球壳带电+q ，试计算：(1)外球壳上的电荷分布及电势大小；(2)先把外球壳接地，然后断开接地线重新绝缘，此时外球壳的电荷分布及电势；*(3)再使内球壳接地，此时内球壳上的电荷以及外球壳上的电势的改变量．解: (1)内球带电q +；球壳内表面带电则为q -,外表面带电为q +，且均匀分布，其电势题8-23图⎰⎰∞∞==⋅=22020π4π4d d R R Rqr r q r E U εε (2)外壳接地时，外表面电荷q +入地，外表面不带电，内表面电荷仍为q -．所以球壳电势由内球q +与内表面q -产生：0π4π42020=-=R q R q U εε(3)设此时内球壳带电量为q '；则外壳内表面带电量为q '-，外壳外表面带电量为+-q q ' (电荷守恒)，此时内球壳电势为零，且0π4'π4'π4'202010=+-+-=R q q R q R q U A εεε 得q R R q 21='外球壳上电势()22021202020π4π4'π4'π4'R qR R R q q R q R q U B εεεε-=+-+-=8-24 半径为R 的金属球离地面很远，并用导线与地相联，在与球心相距为R d 3=处有一点电荷+q ，试求：金属球上的感应电荷的电量．解: 如题8-24图所示，设金属球感应电荷为q '，则球接地时电势0=O U8-24图由电势叠加原理有：=O U 03π4π4'00=+Rq R q εε 得-='q 3q8-25 有三个大小相同的金属小球，小球1，2带有等量同号电荷，相距甚远，其间的库仑力为0F ．试求：(1)用带绝缘柄的不带电小球3先后分别接触1，2后移去，小球1，2之间的库仑力；(2)小球3依次交替接触小球1，2很多次后移去，小球1，2之间的库仑力．解: 由题意知2020π4r q F ε=(1)小球3接触小球1后，小球3和小球1均带电2q q =', 小球3再与小球2接触后，小球2与小球3均带电 q q 43='' ∴ 此时小球1与小球2间相互作用力00220183π483π4"'2F rqr q q F =-=εε (2)小球3依次交替接触小球1、2很多次后，每个小球带电量均为32q . ∴ 小球1、2间的作用力00294π432322F r q q F ==ε *8-26 如题8-26图所示，一平行板电容器两极板面积都是S ，相距为d ，分别维持电势A U =U ，B U =0不变．现把一块带有电量q 的导体薄片平行地放在两极板正中间，片的面积也是S ，片的厚度略去不计．求导体薄片的电势．解: 依次设A ,C ,B 从上到下的6个表面的面电荷密度分别为1σ，2σ，3σ，4σ,5σ,6σ如图所示．由静电平衡条件，电荷守恒定律及维持U U AB =可得以下6个方程题8-26图⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧++++==+=+-==+=+===+6543215432065430021001σσσσσσσσσσεσσσσεσσd US q S qdU U C S S q B A解得Sq 261==σσSq d U2032-=-=εσσ Sq dU2054+=-=εσσ所以CB 间电场S qd U E 00422εεσ+==)2d(212d 02Sq U E U U CB C ε+=== 注意：因为C 片带电，所以2U U C≠，若C 片不带电，显然2U U C =8-27 在半径为1R 的金属球之外包有一层外半径为2R 的均匀电介质球壳，介质相对介电常数为r ε，金属球带电Q ．试求： (1)电介质内、外的场强； (2)电介质层内、外的电势； (3)金属球的电势．解:利用有介质时的高斯定理∑⎰=⋅q S D Sd(1)介质内)(21R r R <<场强 303π4,π4r rQ E r r Q D r εε ==内;介质外)(2R r <场强303π4,π4r rQ E r Qr D ε ==外(2)介质外)(2R r >电势 rQE U 0r π4r d ε=⋅=⎰∞外介质内)(21R r R <<电势2020π4)11(π4R Q R r qr εεε+-=)11(π420R r Qr r -+=εεε (3)金属球的电势 r d r d 221⋅+⋅=⎰⎰∞R R RE E U 外内⎰⎰∞+=22220π44πdr R R Rr r Qdr r Q εεε)11(π4210R R Qr r-+=εεε 8-28 如题8-28图所示，在平行板电容器的一半容积内充入相对介电常数为r ε的电介质．试求：在有电介质部分和无电介质部分极板上自由电荷面密度的比值．解: 如题8-28图所示，充满电介质部分场强为2E，真空部分场强为1E，自由电荷面密度分别为2σ与1σ由∑⎰=⋅0d q S D得 11σ=D ，22σ=D 而101E D ε=,202E D r εε=d21U E E ==∴r D D εσσ==1212 r d r d ⋅+⋅=⎰⎰∞∞rrE E U 外内题8-28图题8-29图8-29 两个同轴的圆柱面，长度均为l ，半径分别为1R 和2R (2R ＞1R )，且l >>2R -1R ，两柱面之间充有介电常数ε的均匀电介质.当两圆柱面分别带等量异号电荷Q 和-Q 时，求： (1)在半径r 处(1R ＜r ＜2R ＝，厚度为dr ，长为l 的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量； (2)电介质中的总电场能量； (3)圆柱形电容器的电容．解: 取半径为r 的同轴圆柱面)(S 则rlD S D S π2d )(=⋅⎰当)(21R r R <<时，Q q =∑ ∴rlQD π2=(1)电场能量密度 22222π82lr Q D w εε== 薄壳中rlrQ rl r l r Q w W εευπ4d d π2π8d d 22222===(2)电介质中总电场能量 ⎰⎰===211222ln π4π4d d R R VR R l Q rl r Q W W εε(3)电容：∵CQ W 22=∴)/ln(π22122R R lW Q C ε== *8-30 金属球壳A 和B 的中心相距为r ，A 和B 原来都不带电．现在A 的中心放一点电荷1q ，在B 的中心放一点电荷2q ，如题8-30图所示．试求： (1)1q 对2q 作用的库仑力，2q 有无加速度；(2)去掉金属壳B ，求1q 作用在2q 上的库仑力，此时2q 有无加速度．解: (1)1q 作用在2q 的库仑力仍满足库仑定律，即2210π41r q q F ε=但2q 处于金属球壳中心，它受合力．．为零，没有加速度． (2)去掉金属壳B ，1q 作用在2q 上的库仑力仍是2210π41r q q F ε=，但此时2q 受合力不为零，有加速度．题8-30图题8-31图8-31 如题8-31图所示，1C =0.25μF ，2C =0.15μF ，3C =0.20μF．1C 上电压为50V ．求：AB U ．解: 电容1C 上电量111U C Q =电容2C 与3C 并联3223C C C += 其上电荷123Q Q = ∴355025231123232⨯===C U C C Q U 86)35251(5021=+=+=U U U AB V 8-321C 和2C 两电容器分别标明“200 pF 、500 V”和“300 pF、900 V”，把它们串联起来后等值电容是多少?如果两端加上1000 V 的电压，是否会击穿?解: (1)1C 与2C 串联后电容1203002003002002121=+⨯=+='C C C C C pF (2)串联后电压比231221==C C U U ，而100021=+U U∴6001=U V ,4002=U V即电容1C 电压超过耐压值会击穿，然后2C 也击穿． 8-33 将两个电容器1C 和2C 充电到相等的电压U 以后切断电源，再将每一电容器的正极板与另一电容器的负极板相联．试求：(1)每个电容器的最终电荷； (2)电场能量的损失．解: 如题8-33图所示，设联接后两电容器带电分别为1q ,2q题8-33图则⎪⎪⎩⎪⎪⎨⎧==-=-=+2122112121201021U U U C U C q q U C U C q q q q解得 (1)=1q UC C C C C q U C C C C C 21212221211)(,)(+-=+-(2)电场能量损失W W W -=∆0)22()2121(2221212221C q C q U C U C +-+= 221212U C C C C +=8-34 半径为1R =2.0cm 的导体球，外套有一同心的导体球壳，壳的内、外半径分别为2R =4.0cm 和3R =5.0cm ，当内球带电荷Q =3.0×10-8C 时，求：(1)整个电场储存的能量；(2)如果将导体壳接地，计算储存的能量； (3)此电容器的电容值．解: 如图，内球带电Q ，外球壳内表面带电Q -，外表面带电Q题8-34图(1)在1R r <和32R r R <<区域0=E在21R r R <<时301π4r r Q E ε =3R r >时302π4r r Q E ε =∴在21R r R <<区域⎰=21d π4)π4(21222001R R r r rQ W εε ⎰-==21)11(π8π8d 2102202R R R R Q r r Q εε 在3R r >区域⎰∞==32302220021π8d π4)π4(21R R Q r r rQ W εεε∴ 总能量)111(π83210221R R R Q W W W +-=+=ε41082.1-⨯=J(2)导体壳接地时，只有21R r R <<时30π4rrQ E ε=,02=W ∴4210211001.1)11(π8-⨯=-==R R Q W W ε J(3)电容器电容)11/(π422102R R Q W C -==ε 121049.4-⨯=F习题九9-1在同一磁感应线上，各点B的数值是否都相等?为何不把作用于运动电荷的磁力方向定义为磁感应强度B的方向?解: 在同一磁感应线上，各点B的数值一般不相等．因为磁场作用于运动电荷的磁力方向不仅与磁感应强度B的方向有关，而且与电荷速度方向有关，即磁力方向并不是唯一由磁场决定的，所以不把磁力方向定义为B的方向．9-2 (1)在没有电流的空间区域里，如果磁感应线是平行直线，磁感应强度B的大小在沿磁感应线和垂直它的方向上是否可能变化(即磁场是否一定是均匀的)?(2)若存在电流，上述结论是否还对?解: (1)不可能变化，即磁场一定是均匀的．如图作闭合回路abcd 可证明21B B=∑⎰==-=⋅0d 021I bc B da B l B abcdμ∴21B B=(2)若存在电流，上述结论不对．如无限大均匀带电平面两侧之磁力线是平行直线，但B方向相反，即21B B ≠.9-3 用安培环路定理能否求有限长一段载流直导线周围的磁场?答: 不能，因为有限长载流直导线周围磁场虽然有轴对称性，但不是稳恒电流，安培环路定理并不适用．9-4 在载流长螺线管的情况下，我们导出其内部nI B 0μ=，外面B =0，所以在载流螺线管外面环绕一周(见题9-4图)的环路积分⎰外B L·d l =0但从安培环路定理来看，环路L 中有电流I 穿过，环路积分应为⎰外B L·d l =I 0μ这是为什么?解: 我们导出nl B 0μ=内,0=外B 有一个假设的前提，即每匝电流均垂直于螺线管轴线．这时图中环路L 上就一定没有电流通过，即也是⎰∑==⋅LI l B 0d 0μ 外，与⎰⎰=⋅=⋅Ll l B 0d 0d外是不矛盾的．但这是导线横截面积为零，螺距为零的理想模型．实际上以上假设并不真实存在，所以使得穿过L 的电流为I ，因此实际螺线管若是无限长时，只是外B的轴向分量为零，而垂直于轴的圆周方向分量rIB πμ20=⊥,r 为管外一点到螺线管轴的距离．题 9 - 4 图9-5 如果一个电子在通过空间某一区域时不偏转，能否肯定这个区域中没有磁场?如果它发生偏转能否肯定那个区域中存在着磁场?解：如果一个电子在通过空间某一区域时不偏转，不能肯定这个区域中没有磁场，也可能存在互相垂直的电场和磁场，电子受的电场力与磁场力抵消所致．如果它发生偏转也不能肯定那个区域存在着磁场，因为仅有电场也可以使电子偏转．9-6 已知磁感应强度0.2=B Wb ·m -2的均匀磁场，方向沿x 轴正方向，如题9-6图所示．试求：(1)通过图中abcd 面的磁通量；(2)通过图中befc 面的磁通量；(3)通过图中aefd 面的磁通量．解：如题9-6图所示题9-6图(1)通过abcd 面积1S 的磁通是24.04.03.00.211=⨯⨯=⋅=S BΦWb(2)通过befc 面积2S 的磁通量022=⋅=S BΦ(3)通过aefd 面积3S 的磁通量24.0545.03.02cos 5.03.0233=⨯⨯⨯=θ⨯⨯⨯=⋅=S B ΦWb(或曰24.0-Wb )题9-7图9-7 如题9-7图所示，AB 、CD 为长直导线，C B为圆心在O 点的一段圆弧形导线，其半径为R ．若通以电流I ，求O 点的磁感应强度．解：如题9-7图所示，O 点磁场由AB 、C B、CD 三部分电流产生．其中AB 产生01=BCD 产生RIB 1202μ=，方向垂直向里CD 段产生)231(2)60sin 90(sin 24003-πμ=-πμ=︒︒R I R I B ，方向⊥向里 ∴)6231(203210ππμ+-=++=R I B B B B ，方向⊥向里． 9-8 在真空中，有两根互相平行的无限长直导线1L 和2L ，相距0.1m ，通有方向相反的电流，1I =20A,2I =10A ，如题9-8图所示．A ，B 两点与导线在同一平面内．这两点与导线2L 的距离均为5.0cm ．试求A ，B 两点处的磁感应强度，以及磁感应强度为零的点的位置．题9-8图解：如题9-8图所示,A B方向垂直纸面向里42010102.105.02)05.01.0(2-⨯=⨯+-=πμπμI I B A T(2)设0=B在2L 外侧距离2L 为r 处则02)1.0(220=-+rI r Iπμπμ 解得 1.0=r m题9-9图9-9 如题9-9图所示，两根导线沿半径方向引向铁环上的A ，B 两点，并在很远处与电源相连．已知圆环的粗细均匀，求环中心O 的磁感应强度．解：如题9-9图所示，圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生，但∞A 和∞B 在O 点产生的磁场为零。

浅谈连接体的关联加速度问题

GUAN ＧＤONG JIAO YU GAO ZHONG广东教育·高中2020年第1期图2v 0hv 兹A v //v 子图1v 0hv 兹A浅谈连接体的关联加速度问题■广东省佛山市南海区石门中学余建刚一、问题的由来在高中的习题中，常会见到如下题目：“如图1所示，在离水面高度为h 的岸边，有人用小车通过绳子拉船靠岸，若车的速度恒为v 0，试求：当绳子与竖直方向的夹角为兹时，船的速度为多少？”此题较为简单，由于绳子不可伸长，沿绳各点速率相等，如图2，我们可将船速正交分解为沿绳和垂直于绳；车的速率v 0等于船沿绳分速度v n .即v 0=v n =v cos 兹.既然绳物连接体的沿绳速度相等，那么，倘若小车的加速度为a 0，则船的加速度是否也满足a 0=a cos 兹.即绳物连接体的沿绳加速度是否也相等？不少学生想当然地以为，既然速度沿绳速度相同，则它们沿绳加速度也一定相同，并列出“充分的物理依据”：“根据a =驻v 驻t ，由于绳子不可伸长，则沿绳各点速率相等，又绳子上各点经历时间相等，所以沿绳各点的加速度也必然相等，故有a 0=a cos 兹”.持这一错误的观点的学生不在少数，当前有不少老师对这一的解答比较笼统，不能给学生一个信服的解释，以致学生一知不解，不知所以然.卢瑟福有一句名言：“只有当你能把一个理论讲得连女仆都能听懂，你才算真懂了.”为了给学生一个清晰透彻、有说服力的解答，于是笔者撰写此文，以达抛砖引玉之效.二、问题的分析我们首先来看看学生所认为的沿绳加速度相同，其求解小船所谓的“充分的物理依据”，中出现了概念错误，加速度的定义a 軆=驻v 軆驻t 应是对速度的求导，学生的解法的前提必须是绳与船前进方向间夹角保持不变才可能正确.但实际上船在前进过程中绳子与船前进方向间夹角会发生变化.下面列出二种解法.解法一：高等数学求导法加速度的基本思路：小船合运动是水平运动，先通过绳船速度关系得出小船速度的表达式，并小船实际速度进行求导a=dv dt 即可得小船加速度.由于船前进过程绳子与水平面夹角兹随时间变化，故求导时兹也是时间变量.具体求导如下：a=dv dt =d （v 0cos 兹）dt =a 01cos 兹+v 0·d （v 0cos 兹）dt =a 01cos 兹+v 0·（-1）-sin 兹cos 2兹·d 兹dt =a 0cos 兹+v 0sin 兹cos 2兹·d 兹dt又因为d 兹dt =棕=v 子L =v 0tan 兹L （注：v 子为船垂直于绳的速度分量），代入上式中，可得，小船加速度：a =a 0cos 兹+v 0sin兹cos 2兹·d 兹dt=a 0cos 兹+v 02sin 兹tan 兹L cos 2兹=a 0cos 兹+v 02tan 2兹L cos 兹由上式知：a =a 0cos 兹+v 02tan 2兹L cos 兹≠a 0cos 兹，可得：a cos 兹≠a 0，即小船加速度的沿绳分量不等于车的加速度，沿绳加速度不等！解法二：加速度叠加法如图3，以O 点为参考系，则小船相对于O 点作瞬时圆周运动，船A 相对于O 的径向心加速分量为a A 对O （径向）=v 子2L，v 子为船垂直于绳的速度分量v 子=v //tan 兹=v 0tan 兹；根据加速度关系：a 船对地（径向分量）=a 车对地+a 船对车（径向分量），由小车的对地加速度为a 车对地=a 0，船沿绳加速度分量：a 船对地（径向分量）=a cos 兹，可得：a cos 兹=a 0+v 子2L，将v 子=v 0tan 兹代入，整理，得a cos 兹=a 0+v 02tan 2兹L纵观此两种方法得出相同的结果，对比学生错解，我们不难发现，正解比错解，多出一项v 02tan 2兹L，此项的物理意义是由于船由于绕O 点转动而引起的向心加速度.结论：1.轻绳两端的两个物体沿绳的分速度一定相等，但沿绳方向的加速度不一定相等.当物体有转动的分运动时，绳上两物体体沿绳子方向的加速一定不相同.2.根据运动独立性原理，被牵引物体沿绳方向的加速度分量，可认为由两部分组成，一是牵引端物体加速度的沿绳分量，二是被牵引物体由于转动，由切向速度方向变化而所v 0a 0O hv 兹v 子A v //a图355广东教育·高中2020年第1期理综高参a軆AtA v軆Bt B v軆Anv軆Bn图4图5v軆Ata軆Bt A B a 軆Ana 軆Bnv 軆相L图7自軋CC a Cna C自軋Ba Ct BA 自軋CBD产生是径向加速度.牵引加速度和转动径向加速度二者叠加方为被牵引物的加速度.三、结论的深入与推广上面结论以从绳-物连接体推广到杆-物连接体.其理论分析如下.杆、绳物系关联共同特征是杆和绳都是不可伸长的.由于杆和绳都是不可伸长的，故其上的两个质点间的相对位置不发生变化.如图4所示，杆、绳子上AB 两点的速度，AB 两点的速度可以分解为两个方向的速度：沿杆或沿绳方向为径向速度，垂直于杆和绳子方向v n ，切向速度v 子.由于杆、绳子不可伸长，则AB 在法向的分速度相等v 1n =v 2n .即AB 的相对速度方向为切向方向，B 相对于A 的速度可以表示为：v軆B 对A =v 軆B -v 軆A .以A 为原点，建立参考系，B 相对于A 旋转，若设AB 长度为L ，B 绕A 旋转的角度为棕，B 相对于A 的速度大小可以表示为：v軆B 对A =v 軆B -v 軆A =棕Le 軆如图5所示，AB 两点的的加速度，可以分解为沿杆或绳方向的法向加速度和垂于于杆或绳的切向加速度，以A 为参考点，则B 相对旋转，产生一个法向加速度.若设AB 长度为L ，B 绕A 旋转的相对线速度为v軆B 对A =v 軆B -v 軆A ，则AB 的加速度关联，可以表示a軆Bn -a 軆An =-Le 軆n ，即沿杆或沿绳加速度分量不等.四、结论的应用实例在历届竞赛题中，经常会涉及到绳、杆速度关联和加速度关联，在24届全国中学生物理竞赛复赛题中，此法应用尤其淋漓尽致.【例题】如图6中所示为用三角形刚性细杆AB 、BC 、CD 连成的平面连杆结构图.AB 和CD 杆可分别绕过A 、D 的垂直于纸面的固定轴转动，A 、D 两点位于同一水平线上.BC 杆的两端分别与AB 杆和CD 杆相连，可绕连接处转动（类似铰链）.当AB 杆绕A 轴以恒定的角速度棕转到图中所示的位置时，AB 杆处于竖直位置.BC 杆与CD 杆都与水平方向成45°角，已知AB 杆的长度为l ，BC 杆和CD 杆的长度由图给定.求此时C 点加速度a c 的大小和方向（用与CD 杆之间的夹角表示）解析：因为B 点绕A 轴作圆周运动，其速度的大小为：自B =棕l (1)B 点的向心加速度的大小为a B =棕2l (2)因为是匀角速转动，B 点的切向加速度为0，故a B 也是B 点的加速度，其方向沿BA 方向.因为C 点绕D 轴作圆周运动，其速度的大小用自C 表示，方向垂直于杆CD ，在考察的时刻，由图可知，其方向沿杆BC 方向.因BC 是刚性杆，所以B 点和C 点沿BC 方向的速度必相等，故有自C =自B cos π4=2姨2棕l (3)此时杆CD 绕D 轴按顺时针方向转动，C 点的法向加速度a Cn =自CD (4)由图7可知CD =22姨l ，由（3）、（4）式得a Cn =2姨8棕2l (5)其方向沿CD 方向．下面来分析C 点沿垂直于杆CD 方向的加速度，即切向加速度a Ct .因为BC 是刚性杆，所以C 点相对B 点的运动只能是绕B 的转动，C 点相对B 点的速度方向必垂直于杆BC .令自CB 表示其速度的大小，根据速度合成公式有自軋CB =自軋C -自軋B 由几何关系得自CB =-姨=2姨2自B =2姨2棕l (6)由于C 点绕B 作圆周运动，相对B 的向心加速度a CB =B CB (7)因为CB =2姨l ，故有a CB =2姨4棕2l (8)其方向垂直杆CD .由（2）式及图可知，B 点的加速度沿BC 杆的分量为（a B ）BC =a B cos π4 (9)所以C 点相对A 点（或D 点）的加速度沿垂直于杆CD 方向的分量a Ct =a CB +（a B ）BC =32姨4棕2l (10)C 点的总加速度为C 点绕D 点作圆周运动的法向加速度a Cn 与切向加速度a Ct 的合加速度，即a C =+姨=74姨8棕2l (11)a C 的方向与杆CD 间的夹角兹=arctan a Ct a Cn=arctan6=80.54° (12)责任编辑李平安v 相2C 2自B 2自C 2自C 2a Cn 2a Ct 2llB 45°A45°CD图656。

运动学例题_

v 烟船 20 ( km h )
1
北 v船水
30

y
v风地
v风地
20 km h
1
O
v水地东
v水地
x
30

即在船上观察，烟以的速率向南偏西

30

v风船

30 飘去。
v船水
v v0 v
v
2
y´
x´
v0
x
1
v v0 tan 60 10 tan 60 17.3 m s
H 17.3
2
v
2g
2 9.80
15.3 m
v 60
v0
Example 2 河水自西向东流动,速度为10 kmh-1. 一轮船在水中航行, 船相对于河水的航向为北偏西30, 相对于河水的航速为20 kmh-1. 此时风向为由东向西，风速为10 kmh-1. 试求在船上观察到的烟囱冒出的烟缕的飘向(设烟离开烟囱后很快就获得与风相同的速度). Solution 根据相对速度公式北 y v船水 v 烟船 v 风船 v 风地 v 船地
v r r (2t 4) 0.4 m s 1 v 0.4et m s
2
1
a r 0.4 m s
2
an r 0.8 m s 2 a 0.8en 0.4 et m s
2
Example 2 一质点从静止出发作圆周运动，半径R=3.0m， 2 a 3.，求：（1）速度与时间的关 0 m s 切向加速度系；（2）经过多长时间，其加速度与由圆心至质点的矢径方向成 135 0 角？（3）在上述时间内，质点所经历的路程和角位移各为多少？ Solution （1） a

[绳拉船模型的速度分解及其应用]绳杆端速度分解模型

[绳拉船模型的速度分解及其应用]绳杆端速度分解模型■一、问题的由来大家经常会遇到这样的关于速度分解的题目：如图1所示，某人站在岸上通过绕过定滑轮的绳子向岸边拉船，他拉绳子的速率v保持不变，当拉船的绳子与水平面成θ角时，船前进速度u为多大？初次接触这道题目，学生最易出现的速度矢量分解图有两个，见图2、图3，两个图所得到的结论均为u=vcoθ.■二、问题的分析图2错误的原因是没有分清哪个是研究对象，哪个速度是合速度.而是把绳收缩的速度作为合速度，把它按水平和竖直方向正交分解，因小船是沿水平方向运动，所以这样的分解中竖直向上的分速度是没有物理意义的，结论自然也是错误的. 图3分解的虽是实际速度，即合速度，但没有正交分解，错误原因是其中的一个分运动并不是竖直向下的，而应是绳以定滑轮O为轴沿顺时针方向的转动，这个分运动的方向应垂直于绳. 另外，由刚才两图得到的结论都表明u＜v.倘若小船经过一个极短时间Δt从位置A运动到位置B，如图4所示，则AB线段表示小船在这段时间内的位移大小，而OA与OB之差则表示这段时间内绳子收缩的距离，也即人的位移大小，很显然OA与OB之差小于AB，同除以时间Δt应得到u＞v，这也与刚才的结论不符合. ■三、问题的解决其实，当认为绳子不可伸长时，对于用绳联结的两个物体，若速度沿绳方向，则两物体速度必相同，否则绳子就处于松弛状态或者被拉断了；若两物体速度不沿绳子方向，则两物体速度在沿绳方向的分量必定相同.本题中，人的速度全在沿绳方向上，因此，只要将小船速度沿绳方向和垂直绳子方向进行分解（垂直绳子方向的分量表示小船绕O点的转动），再令两物体沿绳方向的速度相等即可求出.作出速度矢量的平行四边形.由图5可知船的速度大小为：u=■.■四、模型的应用■例1如图6所示，物块A通过光滑的定滑轮用细绳与圆环B相连，A位于光滑的水平桌面上，B套在光滑的竖直杆上.当细绳与水平方向的夹角为θ时，A的速度为v，此时B的速度u为多少？■解析B的速度u为“实际速度”，即合速度.将B的速度分别沿绳的方向和垂直于绳的方向进行分解，如图7所示.由图可得：u=■.■例2如图8所示，在水平面上小车A通过光滑的定滑轮用细绳拉一物块B，小车A的速度为v1＝5m/.当细绳与水平方向的夹角分别为30°和60°时，物块B的速度v2为多少？■解析将A、B的速度v1、v2都分别沿绳的方向和垂直于绳的方向进行分解，在沿绳的方向上A、B的速度相等，即：v1co30°=v2co60°所以v2=5■m/.■例3如图9所示，杆OA长为R，可绕过O点的水平轴在竖直平面内转动，其端点A系着一跨过定滑轮B、C的不可伸长的轻绳，绳的另一端系一物块M.滑轮的半径可忽略，B在O的正上方，OB之间的距离为H.某一时刻，当绳的BA段与OB之间的夹角为α时，杆的角速度为ω，求此时物块M的速率vM. ■解析杆的端点A点绕O点做圆周运动，其速度vA的方向与杆OA垂直，在所考察时其速度大小为：vA=ωR.对于速度vA作如图10所示的正交分解，即沿绳BA方向和垂直于BA方向进行分解，沿绳BA方向的分量就是物块M的速率vM，因为物块只有沿绳方向的速度，所以vM=vAcoβ.由正弦定理知，■=■.由以上各式得vM=ωHinα.■五、模型的延伸上面的分解方法对于求解面接触物体的速度问题也是可以的. ■例4一个半径为R的半圆柱体沿水平方向向右以速度v0匀速运动.在半圆柱体上搁置一根竖直杆，此杆只能沿竖直方向运动，如图11所示.当杆与半圆柱体接触点P与柱心的连线与竖直方向的夹角为θ，求竖直杆运动的速度. ■解析将两物体的速度分别沿弹力的方向和垂直于弹力的方向进行分解，令两物体沿弹力方向的速度相等即可求出.设竖直杆运动的速度为v1，方向竖直向上，由于弹力方向沿OP方向，所以v0、v1在OP方向的投影相等，即有v0inθ=v1coθ，解得v1=v0tanθ.对于连接体中物体之间的速度关系分析思路是：把两物体的速度沿着某一共同的方向进行分解，如例2中的绳子方向，例4中的弹力方向，利用在该方向上的速度分量相等建立关系式进行求解.。

绳船模型中的速度和加速度关系深度分析

绳船模型中的速度和加速度关系深度分析摘要：速度合成和分解中，绳子两端绳上的点的速度沿绳子方向的分量才相等，而不是绳子两端的物体的速度沿绳子方向的分量相等。

同时，绳子两端的点的加速度沿绳子方向的分量也不是单纯意义上的相等，本文通过绳船模型定量给出速度及加速度的关系。

关键词：速度加速度分解相等绳杆端速度分解模型中，在绳子不松弛的情况下，在同一时刻必须具有相同的沿杆绳方向的分速度[1]。

这里的速度分量指，绳子两端点的速度沿绳子方向分量，而不是绳子两端物体的速度分量。

绳子两端点的速度与绳子两端物体的速度有很大的区别，如图1所示，数值方向的动滑轮模型，绳子端点C的速度是绳子两端物体（滑轮）速度的两倍。

本文将通过绳船模型详细说明速度关系。

图1在教学过程中，学生从速度关系直接类比加速度关系，绳子两端的点的加速度沿绳方向分量相等，这样的理解显然是不对的。

如图2所示，物体绕圆心o作匀速圆周运动，半径为r，速率为v，分析绳子两端的点的加速度沿绳方向分量的关系?绳子一端物体的加速度，这个加速度为物体的合加速度，此加速度沿半径方向的分量为，绳子一端圆心的加速度0，此加速度沿半径方向的分量为0，显然绳子两端的点的加速度沿绳方向的分量不相等。

本文将通过绳船模型详细说明加速度关系。

1、单绳船模型中速度关系如图3所示，人用轻质细绳通过定滑轮牵引小船靠岸，如果收绳的速度为，则在绳与水平方向夹角为的时刻，船头到滑轮的距离为，船的速度有多大[2]？分析：船在水面在直线运动，实际发生的运动就是合运动，这个合运动有两个运动效果，一是使小船沿绳拉力方向以速度运动，二是使小船随绳的一端绕滑轮做顺时针方向的圆周运动。

靠近船头绳上的速度和船的速度一样，由于绳子不松软，所以沿绳方向速度分量相等：①由①式变形得船的速度：②2、单绳船模型中加速度关系如图3所示，如果人拉绳子以恒定的加速度向前奔跑，则在绳与水平方向夹角为的时刻，船头到滑轮的距离为，船的速度有多大？错误的理解，由于绳子不松软，所以沿绳方向加速度分量相等。

拉船靠岸问题速度与加速度分析

两端对时间求导，得
2ldl02sdsl dl sds
dt
dt dt dt
l为绳长，按速度定义，ddtl 即为收绳
速度v 0 船只能沿s线在水面上行驶
逐渐靠近岸壁，因而ds 应为船速 v
dt
2021/2/4
1
3
将它们代入上式，得船速
v
l s
v0
整理得 v h2ss2v0(m/s)
由 advdvds dt ds dt
( s2
hh22s2v0)vhs2v302 (m/s)
202船速与船的加速度均与船的位置有关，它们是变化的，当船靠近岸时，船速与加速度都不断增大。
2021/2/4
1
5
携手共进，齐创精品工程
Thank You
世界触手可及
拉船靠岸问题速度与加速度分析
如图所示，在离水面高度为h（米）的岸上，有人用绳子拉船靠岸。假定绳长
为 l (米），船位于离岸壁（s米）处试的问速：度当，收加绳速速度度各为为多v0少(m？/s)时，船
v0
h
l
s
o
x
2021/2/4
1
2
解：l , h , s 三者构成了直角三角形由勾股定理得 l2h2s2

高中物理专题绳拉船模型的分析

绳拉船模型目标：1、进一步理解运动的合成和分解；2、运动分解的原则：按效果分解；3、绳拉船模型分析。

例1、如图所示，在河岸上利用定滑轮拉绳使小船靠岸，拉绳速度为v,当船头绳长方向与水平方向夹角为a 时，船的速度是多少？例2、如图所示，汽车沿水平路面以恒定速度v 前进，则当拉绳与水平方向成θ角时，被吊起的物体M 的速度为M v 为多大？变式1、A 、B 两物体通过一根跨过定滑轮的轻绳相连放在水平面上，现物体A 以v 1的速度向右匀速运动，当绳被拉成与水平面夹角分别是α、β时，如图所示．物体B 的运动速度v B 为(绳始终有拉力)( )A ．v 1sinα/sinβB ．v 1cosα/sinβC ．v 1sinα/cosβD ．v 1cosα/cosβ例3、如图所示，杆AB 的A 端靠在竖直墙上，B 端放在水平面上，此时杆与水平面的夹角为α，且B 端的滑动速度为B v ，求A 端的滑动速度A v .同步练习：1.如图所示，物体A和B的质量均为m，且分别用轻绳连接跨过定滑轮(不计绳与滑轮、滑轮与轴之间的摩擦)。

当用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中()A．物体A也做匀速直线运动B．绳子的拉力始终大于物体A所受的重力C．物体A的速率小于物体B的速率D．地面对物体B的支持力逐渐增大2.如图所示，一根长直轻杆AB在墙角沿竖直墙和水平地面滑动，当AB杆和墙的夹角为θ时，杆的A端沿墙下滑的速度大小为v1，B端沿地面滑动的速度大小为v2，则v1、v2的关系是()A．v1＝v2 B．v1＝v2cosθC．v1＝v2tanθD．v1＝v1sinθ3.如图所示，不计所有接触面之间的摩擦，斜面固定，两物体质量分别为m1和m2，且m1<m2。

若将m2从位置A由静止释放，当落到位置B时，m2的速度为v2，且绳子与竖直方向的夹角为θ，则这时m1的速度大小v1等于()A．v2sin θB．v 2/sin θC．v 2cos θD．v 2/cos θ4.如图所示，A、B以相同的速率v下降，C以速率v x上升，绳与竖直方向夹角α已知，则v x=______v。

高中物理专题绳拉船模型的分析

绳拉船模型
目标：1、进一步理解运动的合成和分解；
2、运动分解的原则：按效果分解；
3、绳拉船模型分析。

例1、如图所示，在河岸上利用定滑轮拉绳使小船靠岸，
拉绳速度为v,当船头绳长方向与水平方向夹
角为a 时，船的速度是多少？例2、如图所示，汽车沿水平路面以恒定速度
v 前进，则当拉绳与水平方向成角时，被吊起的物体M
的速度为M v 为多大？变式1、A 、B 两物体通过一根跨过定滑轮的轻绳相连放在水平面上，现物体A 以v 1的速度向右匀速运动，当绳被拉成与水平面夹角分别是α、β时，如图
所示．物体B 的运动速度v B 为(绳始终有拉力)(
) A ．v 1sin α/sin β B
．v 1cos α/sin βC ．v 1sin α/cos β D
．v 1cos α/cos β　例3、如图所示，杆
AB 的A 端靠在竖直墙上，B 端放在水平面上，此时杆与水平面的夹角为，且B 端的滑动速度为B v ，求A 端的滑动速度A v .。

绳子拉船问题

绳子拉船问题的理解与求解、绳子拉船问题的理解 1 •绳子拉船问题如图1所示，在水面上方h 高的岸上，某人利用绕过定滑轮0的轻绳匀速地拉动水面上的一只小船，如果人拉动绳子的速度大小为 V ，则当绳子0A 与水平面的夹角为B 时，小船运动的速度为多大。

2 •常见错误及原因分析对此问题，很多学生的常见错误是把拉动绳子的速率 V 沿竖直和水平两个方向分解，如图2所示，因此错误地认为船沿水面运动的速度，就是绳子沿水平方向的分速度，即 V 船=Vcos 0(1)造成上述错误的原因，就是没有分清楚合运动与分运动, 收缩方向是合运动，小船的运动为它的分运动。

实际上，绳子动与小船运动相同，也是水平向左，这才是合运动。

3 •常规解法如图1所示，当绳子拉着小船水平向左运动时，定滑轮右边的绳子运动有这样的效果：一方面，沿绳子方向收缩；另一方面，绳子绕定滑轮 0顺时针转动。

因此，可将绳 A 端(或小船)水平向左的实际运动(合运动)分解成上述两个方向的分运动，如图 3所示，而沿绳子收缩方向的分速度大小等于人通过定滑轮拉动绳子的速度大小V ，故小船运动的速度为^(2)1 •功能原理法设定滑轮的质量、滑轮与轴之间的摩擦均不计, 中，人拉轻绳所做的功等于绳子拉船所做的功，即间相同，则有：：，即P 人=P 船设人对绳子的拉力为 F ,则绳对船的拉力大小也为 F ,根据功率的计算公式 P=FVcos a,S3错误地认为与船相连的绳子沿 A 端与船相连，它的实际运则人在利用绕过定滑轮的绳子拉船过程 W 人=W 船，由于人拉绳与绳拉船的时 (3)(4)联立（3 ）、（4 ）、（5）式可得出COS©■题■绳联物体的速度分解问题【例题】如图所示，人用绳子通过定滑轮以不变的速度V o拉水平面上的物体A，当绳与水平方向成B角时，求物体A的速度。

★解析：解法一（分解法）：本题的关键是正确地确定物体A的两个分运动。

物体A的运动（即绳的末端的运动）可看作两个分运动的合成：一是沿绳的方向被牵引，绳长缩短。

专题一小船渡河问题绳拉物牵连速度问题

专题一小船渡河问题绳拉物牵连速度问题
目录
• 问题背景与基本概念 • 小船渡河问题分析 • 绳拉物牵连速度问题分析 • 典型例题解析与思路拓展 • 实验设计与验证环节 • 知识拓展与应用领域探讨
01 问题背景与基本概念
小船渡河问题及其实际应用
小船渡河问题
描述了一个小船在静水中和流水中的运动情况，涉及速度合成与分解的基本原理。
度之比。
解析
根据题目条件，两小球做匀速圆周运动，且绳子与竖直方向的夹角不同。结合牵连速度的概念和几何关系，可求解两小球的线速度之比。
解题思路拓展与技巧总结
小船渡河问题
理解合运动与分运动的关系，明确小船渡河的实际运动轨迹。
熟练掌握运动的合成与分解方法，能够根据题目条件选择合适的分解方式。
实际应用
该问题在现实生活中有广泛应用，如航空、航海、车辆行驶等领域中涉及速度合成与分解的问题。
绳拉物牵连速度问题描述
绳拉物问题
描述了一个通过绳子连接的物体在运动过程中，由于绳子的牵连作用而产生的速度变化问题。
牵连速度
指由于物体间的相互作用而产生的附加速度，与物体本身的运动速度不同。
相关物理概念及原理
第四季度
例题1
一端固定的绳子，另一端连接一个小球，小球在水平面上做匀速圆周运动，求小球的线速度和角速度。
解析
根据题目条件，小球做匀速圆周运动，线速度大小不变，方向时刻改变；角速度大小和方向均不变。结合线速度和角速度的定义及关系式
，可求解相关问题。
例题2
两根绳子分别连接两个小球，两小球在水平面上做匀速圆周运动，且绳子与竖直方向的夹角不同，求两小球的线速
02 小船渡河问题分析

绳子拉船问题

绳子拉船问题的理解和求解一、绳子拉船问题的理解1．绳子拉船问题如图1所示，在水面上方h高的岸上，某人利用绕过定滑轮O的轻绳匀速地拉动水面上的一只小船，如果人拉动绳子的速度大小为V，则当绳子OA和水平面的夹角为θ时，小船运动的速度为多大。

2．常见错误及原因分析对此问题，很多学生的常见错误是把拉动绳子的速率V沿竖直和水平两个方向分解，如图2所示，因此错误地认为船沿水面运动的速度，就是绳子沿水平方向的分速度，即V船=Vcosθ（1）造成上述错误的原因，就是没有分清楚合运动和分运动，错误地认为和船相连的绳子沿收缩方向是合运动，小船的运动为它的分运动。

实际上，绳子A端和船相连，它的实际运动和小船运动相同，也是水平向左，这才是合运动。

3．常规解法如图1所示，当绳子拉着小船水平向左运动时，定滑轮右边的绳子运动有这样的效果：一方面，沿绳子方向收缩；另一方面，绳子绕定滑轮O顺时针转动。

因此，可将绳A端（或小船）水平向左的实际运动（合运动）分解成上述两个方向的分运动，如图3所示，而沿绳子收缩方向的分速度大小等于人通过定滑轮拉动绳子的速度大小V，故小船运动的速度为（2）1．功能原理法设定滑轮的质量、滑轮和轴之间的摩擦均不计，则人在利用绕过定滑轮的绳子拉船过程中，人拉轻绳所做的功等于绳子拉船所做的功，即W人=W船，由于人拉绳和绳拉船的时间相同，则有，即P人= P船（3）设人对绳子的拉力为F，则绳对船的拉力大小也为F，根据功率的计算公式P=FVcosα，有P人= F·V （4）P 船 = F ·V 船cos θ （5）联立（3）、（4）、（5）式可得类型题：绳联物体的速度分解问题【例题】如图所示，人用绳子通过定滑轮以不变的速度0v 拉水平面上的物体A ，当绳和水平方向成θ角时，求物体A 的速度。

★分析：解法一（分解法）：本题的关键是正确地确定物体A 的两个分运动。

物体A 的运动（即绳的末端的运动）可看作两个分运动的合成：一是沿绳的方向被牵引，绳长缩短。

大学物理学(第三版)课后习题答案

1-4 在离水面高h 米的岸上，有人用绳子拉船靠岸，船在离岸S 处，如题1-4图所示．当人以0v (m ·1-s )的速率收绳时，试求船运动的速度和加速度的大小．图1-4解：设人到船之间绳的长度为l ，此时绳与水面成θ角，由图可知222s h l +=将上式对时间t 求导，得tss t l ld d 2d d 2= 题1-4图根据速度的定义，并注意到l ,s 是随t 减少的， ∴ tsv v t l v d d ,d d 0-==-=船绳即 θcos d d d d 00v v s l t l s l t s v ==-=-=船或 sv s h s lv v 02/1220)(+==船将船v 再对t 求导，即得船的加速度1-6 已知一质点作直线运动，其加速度为 a ＝4+3t 2s m -⋅，开始运动时，x ＝5 m ，v=0，求该质点在t ＝10s 时的速度和位置．解：∵ t tva 34d d +==分离变量，得 t t v d )34(d +=积分，得 12234c t t v ++= 由题知，0=t ,00=v ,∴01=c故 2234t t v += 又因为 2234d d t t t x v +==分离变量， t t t x d )234(d 2+= 积分得 232212c t t x ++= 由题知 0=t ,50=x ,∴52=c故 521232++=t t x 所以s 10=t 时m70551021102s m 190102310432101210=+⨯+⨯=⋅=⨯+⨯=-x v1-10 以初速度0v ＝201s m -⋅抛出一小球，抛出方向与水平面成幔 60°的夹角，求：(1)球轨道最高点的曲率半径1R ；(2)落地处的曲率半径2R ．(提示：利用曲率半径与法向加速度之间的关系)解：设小球所作抛物线轨道如题1-10图所示．题1-10图 (1)在最高点，o 0160cos v v v x == 21s m 10-⋅==g a n又∵ 1211ρv a n =∴ m1010)60cos 20(22111=︒⨯==n a v ρ(2)在落地点，2002==v v 1s m -⋅,而 o60cos 2⨯=g a n∴ m 8060cos 10)20(22222=︒⨯==n a v ρ1-13 一船以速率1v ＝30km ·h -1沿直线向东行驶，另一小艇在其前方以速率2v ＝40km ·h -1沿直线向北行驶，问在船上看小艇的速度为何?在艇上看船的速度又为何?解：(1)大船看小艇，则有1221v v v-=，依题意作速度矢量图如题1-13图(a)题1-13图由图可知 1222121h km 50-⋅=+=v v v方向北偏西 ︒===87.3643arctan arctan21v v θ (2)小船看大船，则有2112v v v-=，依题意作出速度矢量图如题1-13图(b)，同上法，得5012=v 1h km -⋅2-2 一个质量为P 的质点，在光滑的固定斜面（倾角为α）上以初速度0v 运动，0v 的方向与斜面底边的水平线AB 平行，如图所示，求这质点的运动轨道．解: 物体置于斜面上受到重力mg ，斜面支持力N .建立坐标：取0v方向为X 轴，平行斜面与X 轴垂直方向为Y 轴.如图2-2.题2-2图X 方向： 0=x F t v x 0= ①Y 方向： y y ma mg F ==αsin ②0=t 时 0=y 0=y v2sin 21t g y α=由①、②式消去t ，得220sin 21x g v y ⋅=α 2-4 质点在流体中作直线运动，受与速度成正比的阻力kv (k 为常数)作用，t =0时质点的速度为0v ，证明(1) t 时刻的速度为v ＝t mk ev )(0-；(2) 由0到t 的时间内经过的距离为x ＝(k mv 0)［1-t m ke )(-］；(3)停止运动前经过的距离为)(0kmv ；(4)证明当k m t =时速度减至0v 的e1，式中m 为质点的质量．答: (1)∵ tvm kv a d d =-=分离变量，得mtk v v d d -=即 ⎰⎰-=vv t mt k v v00d d m kte v v -=ln ln 0∴ tm k ev v -=0(2) ⎰⎰---===tttm k m ke kmv t ev t v x 000)1(d d (3)质点停止运动时速度为零，即t →∞，故有 ⎰∞-=='00d kmv t ev x tm k(4)当t=km时，其速度为 ev e v ev v km m k 0100===-⋅- 即速度减至0v 的e1. 2-10 一颗子弹由枪口射出时速率为10s m -⋅v ，当子弹在枪筒内被加速时，它所受的合力为F =(bt a -)N(b a ,为常数)，其中t 以秒为单位：(1)假设子弹运行到枪口处合力刚好为零，试计算子弹走完枪筒全长所需时间；(2)求子弹所受的冲量．(3)求子弹的质量．解: (1)由题意，子弹到枪口时，有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量⎰-=-=t bt at t bt a I 0221d )(将bat =代入，得 ba I 22=(3)由动量定理可求得子弹的质量202bv a v I m == 2-13 以铁锤将一铁钉击入木板，设木板对铁钉的阻力与铁钉进入木板内的深度成正比，在铁锤击第一次时，能将小钉击入木板内1 cm ，问击第二次时能击入多深，假定铁锤两次打击铁钉时的速度相同．解: 以木板上界面为坐标原点，向内为y 坐标正向，如题2-13图，则铁钉所受阻力为题2-13图ky f -=第一锤外力的功为1A⎰⎰⎰==-='=ssky ky y f y f A 112d d d ① 式中f '是铁锤作用于钉上的力，f 是木板作用于钉上的力，在0d →t 时，f 'f -=．设第二锤外力的功为2A ，则同理，有⎰-==21222221d y kky y ky A ② 由题意，有2)21(212kmv A A =∆== ③即222122k k ky =- 所以， 22=y于是钉子第二次能进入的深度为cm 414.01212=-=-=∆y y y2-15 一根劲度系数为1k 的轻弹簧A 的下端，挂一根劲度系数为2k 的轻弹簧B ，B 的下端一重物C ，C 的质量为M ，如题2-15图．求这一系统静止时两弹簧的伸长量之比和弹性势能之比．解: 弹簧B A 、及重物C 受力如题2-15图所示平衡时，有题2-15图Mg F F B A ==又 11x k F A ∆=22x k F B ∆=所以静止时两弹簧伸长量之比为1221k k x x =∆∆ 弹性势能之比为12222211121212k kx k x k E E p p =∆∆= 2-17 由水平桌面、光滑铅直杆、不可伸长的轻绳、轻弹簧、理想滑轮以及质量为1m 和2m 的滑块组成如题2-17图所示装置，弹簧的劲度系数为k ，自然长度等于水平距离BC ，2m 与桌面间的摩擦系数为μ，最初1m 静止于A 点，AB ＝BC ＝h ，绳已拉直，现令滑块落下1m ,求它下落到B 处时的速率．解: 取B 点为重力势能零点，弹簧原长为弹性势能零点，则由功能原理，有])(21[)(21212212l k gh m v m m gh m ∆+-+=-μ 式中l ∆为弹簧在A 点时比原长的伸长量，则h BC AC l )12(-=-=∆联立上述两式，得()()212221122m m khgh m m v +-+-=μ题2-17图2-19 质量为M 的大木块具有半径为R 的四分之一弧形槽，如题2-19图所示．质量为m 的小立方体从曲面的顶端滑下，大木块放在光滑水平面上，二者都作无摩擦的运动，而且都从静止开始，求小木块脱离大木块时的速度．解: m 从M 上下滑的过程中，机械能守恒，以m ，M ，地球为系统，以最低点为重力势能零点，则有222121MV mv mgR +=又下滑过程，动量守恒，以m ,M 为系统则在m 脱离M 瞬间，水平方向有0=-MV mv联立，以上两式，得()M m MgR v +=2习题八8-1 电量都是q 的三个点电荷，分别放在正三角形的三个顶点．试问：(1)在这三角形的中心放一个什么样的电荷，就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系?解: 如题8-1图示(1) 以A 处点电荷为研究对象，由力平衡知：q '为负电荷2220)33(π4130cos π412a q q a q '=︒εε解得 q q 33-=' (2)与三角形边长无关．题8-1图题8-2图8-2 两小球的质量都是m ，都用长为l 的细绳挂在同一点，它们带有相同电量，静止时两线夹角为2θ ,如题8-2图所示．设小球的半径和线的质量都可以忽略不计，求每个小球所带的电量．解: 如题8-2图示⎪⎩⎪⎨⎧===220)sin 2(π41sin cos θεθθl q F T mg T e解得 θπεθtan 4sin 20mg l q = 8-3 根据点电荷场强公式204r q E πε=，当被考察的场点距源点电荷很近(r →0)时，则场强→∞，这是没有物理意义的，对此应如何理解?解: 020π4r r q Eε=仅对点电荷成立，当0→r 时，带电体不能再视为点电荷，再用上式求场强是错误的，实际带电体有一定形状大小，考虑电荷在带电体上的分布求出的场强不会是无限大．8-4 在真空中有A ，B 两平行板，相对距离为d ，板面积为S ，其带电量分别为+q 和-q ．则这两板之间有相互作用力f ，有人说f =2024dq πε,又有人说，因为f =qE ,SqE 0ε=，所以f =Sq 02ε．试问这两种说法对吗?为什么? f 到底应等于多少?解: 题中的两种说法均不对．第一种说法中把两带电板视为点电荷是不对的，第二种说法把合场强Sq E 0ε=看成是一个带电板在另一带电板处的场强也是不对的．正确解答应为一个板的电场为Sq E 02ε=，另一板受它的作用力Sq S qq f 02022εε==，这是两板间相互作用的电场力． 8-5一电偶极子的电矩为l q p=，场点到偶极子中心O 点的距离为r ,矢量r与l 的夹角为θ,(见题8-5图)，且l r >>．试证P 点的场强E 在r 方向上的分量r E 和垂直于r 的分量θE 分别为r E =302cos r p πεθ, θE =304sin r p πεθ证: 如题8-5所示，将p 分解为与r平行的分量θsin p 和垂直于r 的分量θsin p ．∵ l r >> ∴ 场点P 在r 方向场强分量30π2cos r p E r εθ=垂直于r 方向，即θ方向场强分量300π4sin r p E εθ=题8-5图题8-6图8-6 长l =15.0cm的直导线AB 上均匀地分布着线密度λ=5.0x10-9C ·m-1的正电荷．试求：(1)在导线的延长线上与导线B 端相距1a =5.0cm 处P 点的场强；(2)在导线的垂直平分线上与导线中点相距2d =5.0cm 处Q 点的场强．解：如题8-6图所示(1)在带电直线上取线元x d ，其上电量q d 在P 点产生场强为20)(d π41d x a x E P -=λε222)(d π4d x a x E E l l P P -==⎰⎰-ελ]2121[π40l a l a +--=ελ)4(π220l a l-=ελ用15=l cm ，9100.5-⨯=λ1m C -⋅, 5.12=a cm 代入得21074.6⨯=P E 1C N -⋅方向水平向右(2)同理2220d d π41d +=x xE Qλε 方向如题8-6图所示由于对称性⎰=l QxE 0d ，即Q E只有y 分量，∵ 22222220dd d d π41d ++=x x x E Qyλε 22π4d d ελ⎰==l QyQy E E ⎰-+2223222)d (d l l x x2220d4π2+=l lελ以9100.5-⨯=λ1cm C -⋅, 15=l cm ,5d 2=cm 代入得21096.14⨯==Qy Q E E 1C N -⋅，方向沿y 轴正向8-7 一个半径为R 的均匀带电半圆环，电荷线密度为λ,求环心处O 点的场强．解: 如8-7图在圆上取ϕRd dl =题8-7图ϕλλd d d R l q ==，它在O 点产生场强大小为 20π4d d R R E εϕλ=方向沿半径向外则 ϕϕελϕd sin π4sin d d 0RE E x==ϕϕελϕπd cos π4)cos(d d 0RE E y-=-= 积分RR E x 000π2d sin π4ελϕϕελπ==⎰ 0d cos π400=-=⎰ϕϕελπRE y ∴ RE E x0π2ελ==，方向沿x 轴正向． 8-8 均匀带电的细线弯成正方形，边长为l ，总电量为q ．(1)求这正方形轴线上离中心为r 处的场强E ；(2)证明：在l r >>处，它相当于点电荷q 产生的场强E ．解: 如8-8图示，正方形一条边上电荷4q 在P 点产生物强PEd方向如图，大小为()4π4cos cos d 22021l r E P +-=εθθλ∵ 22cos 221l r l +=θ12cos cos θθ-=∴ 24π4d 22220l r l l r E P++=ελP Ed 在垂直于平面上的分量βcos d d P E E =⊥∴ 424π4d 2222220l r rl r l r lE +++=⊥ελ题8-8图由于对称性，P 点场强沿OP 方向，大小为2)4(π44d 422220l r l r lrE E P ++=⨯=⊥ελ∵ lq 4=λ∴ 2)4(π422220l r l r qrE P++=ε 方向沿OP8-9 (1)点电荷q 位于一边长为a 的立方体中心，试求在该点电荷电场中穿过立方体的一个面的电通量；(2)如果该场源点电荷移动到该立方体的一个顶点上，这时穿过立方体各面的电通量是多少?*(3)如题8-9(3)图所示，在点电荷q 的电场中取半径为R 的圆平面．q 在该平面轴线上的A 点处，求：通过圆平面的电通量．(xR arctan =α)解: (1)由高斯定理0d εqS E s⎰=⋅立方体六个面，当q 在立方体中心时，每个面上电通量相等 ∴ 各面电通量06εq e=Φ．(2)电荷在顶点时，将立方体延伸为边长a 2的立方体，使q 处于边长a 2的立方体中心，则边长a 2的正方形上电通量06εqe=Φ对于边长a 的正方形，如果它不包含q 所在的顶点，则24εq e =Φ，如果它包含q 所在顶点则0=Φe．如题8-9(a)图所示．题8-9(3)图题8-9(a)图题8-9(b)图题8-9(c)图(3)∵通过半径为R 的圆平面的电通量等于通过半径为22x R +的球冠面的电通量，球冠面积*]1)[(π22222xR x x R S +-+=∴ )(π42200x R Sq +=Φε02εq =[221xR x +-]*关于球冠面积的计算：见题8-9(c)图ααα⎰⋅=0d sin π2r r Sααα⎰⋅=02d sin π2r)cos 1(π22α-=r8-10 均匀带电球壳内半径6cm ，外半径10cm ，电荷体密度为2×510-C ·m -3求距球心5cm ，8cm ,12cm 各点的场强．解: 高斯定理0d ε∑⎰=⋅qS E s,02π4ε∑=qr E当5=r cm 时，0=∑q ,0=E8=r cm 时，∑q 3π4p=3(r )3内r - ∴ ()2023π43π4rr r E ερ内-=41048.3⨯≈1C N -⋅，方向沿半径向外． 12=r cm时,3π4∑=ρq -3(外r ）内3r ∴ ()420331010.4π43π4⨯≈-=r r r E ερ内外 1C N -⋅ 沿半径向外.8-11 半径为1R 和2R (2R ＞1R )的两无限长同轴圆柱面，单位长度上分别带有电量λ和-λ,试求:(1)r ＜1R ；(2) 1R ＜r ＜2R ；(3) r ＞2R 处各点的场强．解: 高斯定理0d ε∑⎰=⋅qS E s取同轴圆柱形高斯面，侧面积rl S π2=则 rl E S E Sπ2d =⋅⎰对(1) 1R r < 0,0==∑E q (2) 21R r R << λl q =∑ ∴ rE 0π2ελ=沿径向向外(3) 2R r > 0=∑q ∴ 0=E题8-12图8-12 两个无限大的平行平面都均匀带电，电荷的面密度分别为1σ和2σ，试求空间各处场强．解: 如题8-12图示，两带电平面均匀带电，电荷面密度分别为1σ与2σ，两面间， n E)(21210σσε-=1σ面外， n E)(21210σσε+-= 2σ面外， n E)(21210σσε+= n：垂直于两平面由1σ面指为2σ面．8-13 半径为R 的均匀带电球体内的电荷体密度为ρ,若在球内挖去一块半径为r ＜R 的小球体，如题8-13图所示．试求：两球心O 与O '点的场强，并证明小球空腔内的电场是均匀的．解: 将此带电体看作带正电ρ的均匀球与带电ρ-的均匀小球的组合，见题8-13图(a)． (1) ρ+球在O 点产生电场010=E，ρ-球在O 点产生电场'd π4π3430320OO r E ερ=∴ O 点电场'd 33030OO r E ερ= ；(2) ρ+在O '产生电场'dπ4d 3430301OO E ερπ='ρ-球在O '产生电场002='E∴ O ' 点电场 003ερ='E'OO题8-13图(a) 题8-13图(b)(3)设空腔任一点P 相对O '的位矢为r'，相对O 点位矢为r (如题8-13(b)图)则 03ερrE PO =，3ερr E O P '-=' ,∴ 0003'3)(3ερερερd OO r r E E E O P PO P=='-=+='∴腔内场强是均匀的．8-14 一电偶极子由q =1.0×10-6C 的两个异号点电荷组成，两电荷距离d=0.2cm ，把这电偶极子放在1.0×105N ·C -1的外电场中，求外电场作用于电偶极子上的最大力矩．解: ∵ 电偶极子p在外场E 中受力矩E p M⨯=∴ qlE pE M ==max 代入数字4536max 100.2100.1102100.1---⨯=⨯⨯⨯⨯⨯=M m N ⋅8-15 两点电荷1q =1.5×10-8C ，2q =3.0×10-8C ，相距1r =42cm ，要把它们之间的距离变为2r =25cm ，需作多少功?解: ⎰⎰==⋅=22210212021π4π4d d r r r rq q r r q q r F A εε )11(21r r - 61055.6-⨯-=J外力需作的功 61055.6-⨯-=-='A A J题8-16图8-16 如题8-16图所示，在A ，B 两点处放有电量分别为+q ,-q 的点电荷，AB 间距离为2R ，现将另一正试验点电荷0q 从O 点经过半圆弧移到C 点，求移动过程中电场力作的功．解: 如题8-16图示0π41ε=O U 0)(=-RqR q 0π41ε=O U )3(R qR q -Rq 0π6ε-= ∴ Rqq U U q A o C O 00π6)(ε=-= 8-17 如题8-17图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R ．试求环中心O 点处的场强和电势．解: (1)由于电荷均匀分布与对称性，AB 和CD 段电荷在O 点产生的场强互相抵消，取θd d R l =则θλd d R q =产生O 点Ed 如图，由于对称性，O 点场强沿y 轴负方向题8-17图θεθλππcos π4d d 2220⎰⎰-==R R E E yR 0π4ελ=［)2sin(π-2sin π-］ R0π2ελ-=(2) AB 电荷在O 点产生电势，以0=∞U⎰⎰===A B200012ln π4π4d π4d R R x x x x U ελελελ同理CD 产生 2ln π402ελ=U 半圆环产生 0034π4πελελ==R R U∴ 0032142ln π2ελελ+=++=U U U U O8-18 一电子绕一带均匀电荷的长直导线以2×104m ·s -1的匀速率作圆周运动．求带电直线上的线电荷密度．(电子质量0m =9.1×10-31kg ，电子电量e =1.60×10-19C)解: 设均匀带电直线电荷密度为λ，在电子轨道处场强rE 0π2ελ=电子受力大小 re eE F e0π2ελ== ∴ rv mr e 20π2=ελ得 1320105.12π2-⨯==emv ελ1m C -⋅ 8-19 空气可以承受的场强的最大值为E =30kV ·cm -1，超过这个数值时空气要发生火花放电．今有一高压平行板电容器，极板间距离为d =0.5cm ，求此电容器可承受的最高电压．解: 平行板电容器内部近似为均匀电场 ∴ 4105.1d ⨯==E U V8-20 根据场强E与电势U 的关系U E -∇=，求下列电场的场强：(1)点电荷q 的电场；(2)总电量为q ，半径为R 的均匀带电圆环轴上一点；*(3)偶极子ql p =的l r >>处(见题8-20图)．解: (1)点电荷 rqU 0π4ε=题 8-20 图∴ 0200π4r r q r r U E ε=∂∂-= 0r为r 方向单位矢量． (2)总电量q ，半径为R 的均匀带电圆环轴上一点电势220π4xR q U +=ε∴ ()i x R qxi x U E2/3220π4+=∂∂-=ε(3)偶极子l q p=在l r >>处的一点电势 200π4cos ])cos 21(1)cos 2(1[π4r ql llr qU εθθθε=+--=∴ 30π2cos r p r U E rεθ=∂∂-= 30π4sin 1r p U r E εθθθ=∂∂-=8-21 证明：对于两个无限大的平行平面带电导体板(题8-21图)来说，(1)相向的两面上，电荷的面密度总是大小相等而符号相反；(2)相背的两面上，电荷的面密度总是大小相等而符号相同．证: 如题8-21图所示，设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1σ，2σ，3σ，4σ题8-21图(1)则取与平面垂直且底面分别在A 、B 内部的闭合柱面为高斯面时，有0)(d 32=∆+=⋅⎰S S E sσσ∴ +2σ03=σ 说明相向两面上电荷面密度大小相等、符号相反； (2)在A 内部任取一点P ，则其场强为零，并且它是由四个均匀带电平面产生的场强叠加而成的，即0222204030201=---εσεσεσεσ 又∵ +2σ03=σ ∴ 1σ4σ=说明相背两面上电荷面密度总是大小相等，符号相同． 8-22 三个平行金属板A ，B 和C 的面积都是200cm 2，A 和B 相距4.0mm ，A 与C 相距2.0 mm ．B ，C 都接地，如题8-22图所示．如果使A 板带正电3.0×10-7C ，略去边缘效应，问B 板和C 板上的感应电荷各是多少?以地的电势为零，则A 板的电势是多少?解: 如题8-22图示，令A 板左侧面电荷面密度为1σ，右侧面电荷面密度为2σ题8-22图(1)∵ AB ACU U =，即 ∴ AB AB AC AC E E d d =∴2d d 21===ACABAB AC E E σσ 且 1σ+2σSq A =得 ,32Sq A =σ Sq A 321=σ而 7110232-⨯-=-=-=A Cq S q σCC10172-⨯-=-=S q B σ(2) 301103.2d d ⨯===AC ACAC A E U εσV 8-23 两个半径分别为1R 和2R （1R ＜2R )的同心薄金属球壳，现给内球壳带电+q ，试计算：(1)外球壳上的电荷分布及电势大小；(2)先把外球壳接地，然后断开接地线重新绝缘，此时外球壳的电荷分布及电势；*(3)再使内球壳接地，此时内球壳上的电荷以及外球壳上的电势的改变量．解: (1)内球带电q +；球壳内表面带电则为q -,外表面带电为q +，且均匀分布，其电势题8-23图⎰⎰∞∞==⋅=22020π4π4d d R R R qrr q r E U εε (2)外壳接地时，外表面电荷q +入地，外表面不带电，内表面电荷仍为q -．所以球壳电势由内球q +与内表面q -产生：0π4π42020=-=R q R q U εε(3)设此时内球壳带电量为q '；则外壳内表面带电量为q '-，外壳外表面带电量为+-q q ' (电荷守恒)，此时内球壳电势为零，且0π4'π4'π4'202010=+-+-=R q q R q R q U A εεε 得 q R R q 21=' 外球壳上电势()22021202020π4π4'π4'π4'R qR R R q q R q R q U B εεεε-=+-+-=8-24 半径为R 的金属球离地面很远，并用导线与地相联，在与球心相距为R d 3=处有一点电荷+q ，试求：金属球上的感应电荷的电量．解: 如题8-24图所示，设金属球感应电荷为q '，则球接地时电势0=O U8-24图由电势叠加原理有：=O U 03π4π4'00=+RqR q εε 得 -='q 3q8-25 有三个大小相同的金属小球，小球1，2带有等量同号电荷，相距甚远，其间的库仑力为0F ．试求：(1)用带绝缘柄的不带电小球3先后分别接触1，2后移去，小球1，2之间的库仑力；(2)小球3依次交替接触小球1，2很多次后移去，小球1，2之间的库仑力．解: 由题意知 2020π4r q F ε=(1)小球3接触小球1后，小球3和小球1均带电 2q q =',小球3再与小球2接触后，小球2与小球3均带电 q q 43=''∴ 此时小球1与小球2间相互作用力00220183π483π4"'2F rqr q q F =-=εε (2)小球3依次交替接触小球1、2很多次后，每个小球带电量均为 32q .∴ 小球1、2间的作用力 00294π432322F r q q F ==ε *8-26 如题8-26图所示，一平行板电容器两极板面积都是S ，相距为d ，分别维持电势A U =U ，B U =0不变．现把一块带有电量q 的导体薄片平行地放在两极板正中间，片的面积也是S ，片的厚度略去不计．求导体薄片的电势．解: 依次设A ,C ,B 从上到下的6个表面的面电荷密度分别为1σ，2σ，3σ，4σ,5σ,6σ如图所示．由静电平衡条件，电荷守恒定律及维持U U AB =可得以下6个方程题8-26图⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧++++==+=+-==+=+===+6543215432065430021001σσσσσσσσσσεσσσσεσσd US q S qdU U C S S q B A解得 Sq 261==σσSq d U2032-=-=εσσ Sq dU2054+=-=εσσ所以CB 间电场 S qd U E 00422εεσ+==)2d(212d 02Sq U E U U CB C ε+=== 注意：因为C 片带电，所以2U U C≠，若C 片不带电，显然2U U C =8-27 在半径为1R 的金属球之外包有一层外半径为2R 的均匀电介质球壳，介质相对介电常数为r ε，金属球带电Q ．试求： (1)电介质内、外的场强； (2)电介质层内、外的电势； (3)金属球的电势．解: 利用有介质时的高斯定理∑⎰=⋅q S D Sd(1)介质内)(21R r R <<场强 303π4,π4r rQ E r r Q D r εε ==内;介质外)(2R r <场强 303π4,π4r rQ E r Qr D ε ==外(2)介质外)(2R r >电势 rQE U 0r π4r d ε=⋅=⎰∞外介质内)(21R r R <<电势2020π4)11(π4R Q R r qr εεε+-=)11(π420R r Qr r -+=εεε (3)金属球的电势 r d r d 221⋅+⋅=⎰⎰∞R R RE E U 外内⎰⎰∞+=22220π44πdr R R Rr r Qdr r Q εεε)11(π4210R R Qr r-+=εεε 8-28 如题8-28图所示，在平行板电容器的一半容积内充入相对介电常数为r ε的电介质．试求：在有电介质部分和无电介质部分极板上自由电荷面密度的比值．解: 如题8-28图所示，充满电介质部分场强为2E，真空部分场强为1E，自由电荷面密度分别为2σ与1σ由∑⎰=⋅0d q S D得 11σ=D ，22σ=D 而 101E D ε=,202E D r εε=d21U E E ==∴r D D εσσ==1212 r d r d ⋅+⋅=⎰⎰∞∞rrE E U 外内题8-28图题8-29图8-29 两个同轴的圆柱面，长度均为l ，半径分别为1R 和2R (2R ＞1R )，且l >>2R -1R ，两柱面之间充有介电常数ε的均匀电介质.当两圆柱面分别带等量异号电荷Q 和-Q 时，求： (1)在半径r 处(1R ＜r ＜2R ＝，厚度为dr ，长为l 的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量； (2)电介质中的总电场能量； (3)圆柱形电容器的电容．解: 取半径为r 的同轴圆柱面)(S则 rlD S DS π2d )(=⋅⎰当)(21R r R <<时，Q q =∑ ∴ rlQ D π2=(1)电场能量密度 22222π82l r Q D w εε== 薄壳中 rlrQ rl r l r Q w W εευπ4d d π2π8d d 22222===(2)电介质中总电场能量 ⎰⎰===211222ln π4π4d d R RV R R l Q rl r Q W W εε(3)电容：∵ CQ W 22=∴ )/ln(π22122R R lW Q C ε== *8-30 金属球壳A 和B 的中心相距为r ，A 和B 原来都不带电．现在A 的中心放一点电荷1q ，在B 的中心放一点电荷2q ，如题8-30图所示．试求：(1) 1q 对2q 作用的库仑力，2q 有无加速度；(2)去掉金属壳B ，求1q 作用在2q 上的库仑力，此时2q 有无加速度．解: (1)1q 作用在2q 的库仑力仍满足库仑定律，即2210π41r q q F ε=但2q 处于金属球壳中心，它受合力．．为零，没有加速度． (2)去掉金属壳B ，1q 作用在2q 上的库仑力仍是2210π41r q q F ε=，但此时2q 受合力不为零，有加速度．题8-30图题8-31图8-31 如题8-31图所示，1C =0.25μF ，2C =0.15μF ，3C =0.20μF ．1C 上电压为50V ．求：AB U ．解: 电容1C 上电量111U C Q =电容2C 与3C 并联3223C C C += 其上电荷123Q Q =∴ 355025231123232⨯===C U C C Q U 86)35251(5021=+=+=U U U AB V 8-321C 和2C 两电容器分别标明“200 pF 、500 V ”和“300 pF 、900 V ”，把它们串联起来后等值电容是多少?如果两端加上1000 V的电压，是否会击穿?解: (1) 1C 与2C 串联后电容1203002003002002121=+⨯=+='C C C C C pF (2)串联后电压比231221==C C U U ，而100021=+U U∴ 6001=U V ,4002=U V即电容1C 电压超过耐压值会击穿，然后2C 也击穿． 8-33 将两个电容器1C 和2C 充电到相等的电压U 以后切断电源，再将每一电容器的正极板与另一电容器的负极板相联．试求：(1)每个电容器的最终电荷； (2)电场能量的损失．解: 如题8-33图所示，设联接后两电容器带电分别为1q ,2q题8-33图则⎪⎪⎩⎪⎪⎨⎧==-=-=+2122112121201021U U U C U C q q U C U C q q q q解得 (1) =1q UC C C C C q U C C C C C 21212221211)(,)(+-=+-(2)电场能量损失W W W -=∆0)22()2121(2221212221C q C q U C U C +-+= 221212U C C C C +=8-34 半径为1R =2.0cm 的导体球，外套有一同心的导体球壳，壳的内、外半径分别为2R =4.0cm 和3R =5.0cm ，当内球带电荷Q =3.0×10-8C 时，求：(1)整个电场储存的能量；(2)如果将导体壳接地，计算储存的能量； (3)此电容器的电容值．解: 如图，内球带电Q ，外球壳内表面带电Q -，外表面带电Q题8-34图(1)在1R r <和32R r R <<区域0=E在21R r R <<时 301π4r r Q E ε=3R r >时 302π4r r Q E ε=∴在21R r R <<区域⎰=21d π4)π4(21222001R R r r rQ W εε ⎰-==21)11(π8π8d 2102202R R R R Q r r Q εε 在3R r >区域⎰∞==32302220021π8d π4)π4(21R R Q r r rQ W εεε∴ 总能量 )111(π83210221R R R Q W W W +-=+=ε41082.1-⨯=J(2)导体壳接地时，只有21R r R <<时30π4r r Q E ε=,02=W∴ 4210211001.1)11(π8-⨯=-==R R Q W W ε J(3)电容器电容 )11/(π422102R R QW C -==ε 121049.4-⨯=F习题九9-1 在同一磁感应线上，各点B的数值是否都相等?为何不把作用于运动电荷的磁力方向定义为磁感应强度B的方向? 解: 在同一磁感应线上，各点B的数值一般不相等．因为磁场作用于运动电荷的磁力方向不仅与磁感应强度B的方向有关，而且与电荷速度方向有关，即磁力方向并不是唯一由磁场决定的，所以不把磁力方向定义为B的方向．9-2 (1)在没有电流的空间区域里，如果磁感应线是平行直线，磁感应强度B的大小在沿磁感应线和垂直它的方向上是否可能变化(即磁场是否一定是均匀的)?(2)若存在电流，上述结论是否还对?解: (1)不可能变化，即磁场一定是均匀的．如图作闭合回路abcd 可证明21B B=∑⎰==-=⋅0d 021I bc B da B l B abcdμ∴ 21B B=(2)若存在电流，上述结论不对．如无限大均匀带电平面两侧之磁力线是平行直线，但B方向相反，即21B B ≠.9-3 用安培环路定理能否求有限长一段载流直导线周围的磁场?答: 不能，因为有限长载流直导线周围磁场虽然有轴对称性，但不是稳恒电流，安培环路定理并不适用．9-4 在载流长螺线管的情况下，我们导出其内部nI B 0μ=，外面B =0，所以在载流螺线管外面环绕一周(见题9-4图)的环路积分⎰外B L·d l =0但从安培环路定理来看，环路L 中有电流I 穿过，环路积分应为⎰外B L·d l =I 0μ这是为什么?解: 我们导出nl B 0μ=内,0=外B 有一个假设的前提，即每匝电流均垂直于螺线管轴线．这时图中环路L 上就一定没有电流通过，即也是⎰∑==⋅LI l B 0d 0μ 外，与⎰⎰=⋅=⋅Ll l B 0d 0d外是不矛盾的．但这是导线横截面积为零，螺距为零的理想模型．实际上以上假设并不真实存在，所以使得穿过L 的电流为I ，因此实际螺线管若是无限长时，只是外B的轴向分量为零，而垂直于轴的圆周方向分量rIB πμ20=⊥,r 为管外一点到螺线管轴的距离．题 9 - 4 图9-5 如果一个电子在通过空间某一区域时不偏转，能否肯定这个区域中没有磁场?如果它发生偏转能否肯定那个区域中存在着磁场?解：如果一个电子在通过空间某一区域时不偏转，不能肯定这个区域中没有磁场，也可能存在互相垂直的电场和磁场，电子受的电场力与磁场力抵消所致．如果它发生偏转也不能肯定那个区域存在着磁场，因为仅有电场也可以使电子偏转．9-6 已知磁感应强度0.2=B Wb ·m-2的均匀磁场，方向沿x轴正方向，如题9-6图所示．试求：(1)通过图中abcd 面的磁通量；(2)通过图中befc 面的磁通量；(3)通过图中aefd 面的磁通量．解：如题9-6图所示题9-6图(1)通过abcd 面积1S 的磁通是24.04.03.00.211=⨯⨯=⋅=S BΦWb(2)通过befc 面积2S 的磁通量022=⋅=S BΦ(3)通过aefd 面积3S 的磁通量24.0545.03.02cos 5.03.0233=⨯⨯⨯=θ⨯⨯⨯=⋅=S B ΦWb(或曰24.0-Wb )题9-7图9-7 如题9-7图所示，AB 、CD 为长直导线，C B为圆心在O 点的一段圆弧形导线，其半径为R ．若通以电流I ，求O 点的磁感应强度．解：如题9-7图所示，O 点磁场由AB 、C B、CD 三部分电流产生．其中AB产生 01=B CD产生RIB 1202μ=，方向垂直向里CD段产生 )231(2)60sin 90(sin 24003-πμ=-πμ=︒︒R I R I B ，方向⊥向里 ∴)6231(203210ππμ+-=++=R I B B B B ，方向⊥向里． 9-8 在真空中，有两根互相平行的无限长直导线1L 和2L ，相距0.1m ，通有方向相反的电流，1I =20A,2I =10A ，如题9-8图所示．A ，B 两点与导线在同一平面内．这两点与导线2L 的距离均为5.0cm ．试求A ，B 两点处的磁感应强度，以及磁感应强度为零的点的位置．题9-8图解：如题9-8图所示,A B方向垂直纸面向里42010102.105.02)05.01.0(2-⨯=⨯+-=πμπμI I B A T(2)设0=B在2L 外侧距离2L 为r 处则02)1.0(220=-+rI r Iπμπμ 解得 1.0=r m题9-9图9-9 如题9-9图所示，两根导线沿半径方向引向铁环上的A ，B 两点，并在很远处与电源相连．已知圆环的粗细均匀，求环中心O 的磁感应强度．解：如题9-9图所示，圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生，但∞A 和∞B 在O 点产生的磁场为零。

绳子拉船的运动分解问题

绳子拉船问题的理解与求解芜湖博韬教育査显国绳子拉船问题是运动的合成与分解中的典型例子。

很多学生对此问题的理解都感到非常困难，怎样使学生正确地理解和掌握这个问题呢？下面谈一谈这个问题的理解及求解此问题的一些方法。

一、绳子拉船问题的理解1．绳子拉船问题如图1所示，在水面上方h高的岸上，某人利用绕过定滑轮O的轻绳匀速地拉动水面上的一只小船，如果人拉动绳子的速度大小为V，则当绳子OA与水平面的夹角为θ时，小船运动的速度为多大。

2．常见错误及原因分析对此问题，很多学生的常见错误是把拉动绳子的速率V沿竖直和水平两个方向分解，如图2所示，因此错误地认为船沿水面运动的速度，就是绳子沿水平方向的分速度，即V船=Vcosθ（1）造成上述错误的原因，就是没有分清楚合运动与分运动，错误地认为与船相连的绳子沿收缩方向是合运动，小船的运动为它的分运动。

实际上，绳子A端与船相连，它的实际运动与小船运动相同，也是水平向左，这才是合运动。

因此，可将绳A端（或小船）水平向左的实际运动（合运动）分解成上述两个方向的分运动，如图3所示，而沿绳子收缩方向的分速度大小等于人通过定滑轮拉动绳子的速度大小V，故小船运动的速度为（2）4．问题的理解上述的求解结果学生普遍都感到难以理解。

为了帮助学生更好地理解这个问题，我们就从小船运动的速度和拉动绳子的速度大小关系入手，由（2）式可知，小船运动的速度大于拉动绳子的速度，而（1）式则是小于拉动绳子的速度，因此只要证明小船运动的速度大于拉动绳子的速度，问题就比较容易理解了。

将绳子拉动船的过程中，绳子与水平方向的夹角设置两个特殊值来进行考虑，如图4所示，设在某时间t内，拉动船时绳子与水平面的夹角由300增大到450，则在这段时间内，小船前进的距离为绳子收缩的长度为由此可得S＞L，故小船运动的速度必大于人拉动绳子的速度。

用绳拉船靠岸的船速问题

在第二个例子中设人在由于绳的质量可以略去不计于是教师们为了回避向学生讲清这是人所作的功率为绳的张力对雪橇所作的功率为这两个功率应该相等于是有10我们也可以象第一个例子那样从功能原理来思考这个例子
16
工科物理 1999 V ol. 9 No. 1
用绳拉船靠岸的船速问题
钱树高 (云南工业大学物理教研室 ,昆明 650051)
人以速度 v 拉绳 ,随着时间的推移 ,人作的功将越来越多 ,同时 ,船也越来越靠近岸边 ,θ
越来越大 ,因而船速 V 也越来越大 ,人作的
功转化为船的动能的增加 ,这正是式 ( 6)的一
个物理含义 .
在第二个例子中 ,设人在 x 方向拉绳之
力为 F ,绳中张力为 T .由于绳的质量可以略
去不计 ,有
然而 ,要分清哪个是合速度、哪个是分速度 ,有时候是很不容易的 ;有些问题用速度合成与分解来求解 ,是比较困难的 ,或者容易出错的 .
2 作功法和几何法
这里 ,我们提供第三种解法—— 用作功
和能量的观点求解 .我们认为 ,多用几种方法
求解一个问题是很有好处的 ,借此可以互相
检验、比较、启发和补充 ,从而深化我们对问
有人提出 ,假如人以不变的加速度 a 拉着绳子向前奔跑 (如图 6所示 ) ,船的加速度是多少?
用类似于速度合成和分解那样的考虑 ,
工科物理 1999 V ol. 9 No. 1
图6
图7
船的加速度应是合加速度 ,而绳的加速度则是分加速度 . 因此 ,有
a′船 = a /co sθ 但是 ,有人认为 ,这个结果是错误的 ,船的加速度既不是 a co sθ,也不是 a /co sθ. 因为这个例子不属于速度合成与分解的问题 ,不能用速度、加速度合成与分解的概念去求解 , 哪怕它在速度问题上成功了 ,那只是一种“巧合” .这种看法究竟对不对呢?

也谈“用绳拉船靠岸的船速问题”

也谈“用绳拉船靠岸的船速问题”
程达三;刘兴来
【期刊名称】《工科物理》
【年(卷),期】2000(010)004
【摘要】指出解质这问题中运用的所谓“速度合成与分解方法”有两种含义，第一种是只在一个参考系中求解，运用速度的矢量性，将速度矢量按平行四边形法则合成和分解，最常用的是在直角坐标系或其它坐标系中合成和分解；第二种是借助两个有相对运动的参考系，运用相对运动中的速度定理求解；第二是借助两个相对运动的参考系，运用相对运动中的速度定理求解，同时澄清了有关文献中某些不当之处。

【总页数】5页(P29-32,34)
【作者】程达三;刘兴来
【作者单位】太原理工大学;华北工学院
【正文语种】中文
【中图分类】O311.1
【相关文献】
1.对绳拉船靠岸问题的再探讨 [J], 张浩波;
2.对绳拉船靠岸问题的分析 [J], 张浩波
3.用绳拉船靠岸的船速问题 [J], 钱树高;夏英齐
4.船的加速度和速度佯谬：再论用绳拉船靠岸的问题 [J], 钱树高;夏英齐
5.对绳拉船靠岸问题的再探讨 [J], 张浩波
因版权原因，仅展示原文概要，查看原文内容请购买。

绳子拉船问题讲解

绳子拉船问题的理解与求解一、绳子拉船问题的理解1．绳子拉船问题如图1所示，在水面上方h高的岸上，某人利用绕过定滑轮O的轻绳匀速地拉动水面上的一只小船，如果人拉动绳子的速度大小为V，则当绳子OA与水平面的夹角为θ时，小船运动的速度为多大。

实际上，绳子A端与船相连，它的实际运动与小船运动相同，也是水平向左，这才是合运动。

因此，可将绳A端（或小船）水平向左的实际运动（合运动）分解成上述两个方向的分运动，如图3所示，而沿绳子收缩方向的分速度大小等于人通过定滑轮拉动绳子的速度大小V，故小船运动的速度为（2）1．功能原理法设定滑轮的质量、滑轮与轴之间的摩擦均不计，则人在利用绕过定滑轮的绳子拉船过程中，人拉轻绳所做的功等于绳子拉船所做的功，即W人=W船，由于人拉绳与绳拉船的时间相同，则有，即P人= P船（3）设人对绳子的拉力为F，则绳对船的拉力大小也为F，根据功率的计算公式P=FVcosα，有P人= F·V （4）P 船 = F ·V 船cos θ （5）联立（3）、（4）、（5）式可得类型题：绳联物体的速度分解问题【例题】如图所示，人用绳子通过定滑轮以不变的速度0v 拉水平面上的物体A ，当绳与水平方向成θ角时，求物体A 的速度。

★解析：解法一（分解法）：本题的关键是正确地确定物体A 的两个分运动。

物体A 的运动（即绳的末端的运动）可看作两个分运动的合成：一是沿绳的方向被牵引，绳长缩短。