相交线计算题
知识点245 相交线(解答题)

245 相交线(解答题)1、平面上有10条直线,其中4条直线交于一点,另有4条直线互相平行,这10条直线最多有几个交点?它们最多能把平面分成多少个部分?2、(1)1条直线,最多可将平面分成1+1=2个部分;(2)2条直线,最多可将平面分成1+1+2=4个部分;(3)3条直线,最多可将平面分成_________个部分;(4)4条直线,最多可将平面分成_________个部分;(5)n条直线,最多可将平面分成_________个部分.3、如图,直线l1、l2、l3交于O点,图中出现了几对对顶角,若n条直线相交呢?4、我们知道,两条直线相交,有且只有一个交点,三条直线相交,最多只有三个交点,那么,四条直线相交,最多有多少个交点?一般地,n条直线最多有多少个交点?说明理由.5、附加题:(1)计算:3+(﹣1)=_________.(2)两直线相交有且只有_________个交点.6、将一个平面分成11部分,至少需几条直线?7、平面上有9条直线,任意两条都不平行,欲使它们出现29个交点,能否做到,如果能,怎么安排才能做到?如果不能,请说明理由.8、在同一平面内的三条直线有哪几种位置关系?请画图说明.9、在平面上有9条直线,无任何3条交于一点,则这9条直线的位置关系如何,才能使它们的交点恰好是26个,画出所有可能的情况(要求用直尺画正确).答案与评分标准1、平面上有10条直线,其中4条直线交于一点,另有4条直线互相平行,这10条直线最多有几个交点?它们最多能把平面分成多少个部分?考点:相交线。
专题:规律型。
分析:(1)画出图形,数出交点个数即可;(2)从规律看,4条平行线第一条直线和每条相交将会多出4+1个平面,第二条直线和每条相交将会多出5+1个平面依次类推.解答:解:如图,图中共有33个交点.4条平行线5部分,加一条线10部分,再加一条16部分,可以看出规律5→10→16,先加5再加6,所以答案是5+5+6+7+8+9+10=50.点评:此题考查了图形的变化规律,画出图形是解题的关键.先根据具体数值得出规律,即可计算出正确结果.2、(1)1条直线,最多可将平面分成1+1=2个部分;(2)2条直线,最多可将平面分成1+1+2=4个部分;(3)3条直线,最多可将平面分成7个部分;(4)4条直线,最多可将平面分成11个部分;(5)n条直线,最多可将平面分成个部分.考点:相交线。
人教版七年级下学期数学-5.1相交线(练习题)

人教版七年级下学期数学-5.1相交线练习题一、单选题1.如图,河道的同侧有、两地,现要铺设一条引水管道,从地把河水引向、两地.下列四种方案中,最节省材料的是()A.B.C.D.2.如图,直线AB、CD相交于O,且∠AOC=2∠BOC,则∠AOD的度数为()A.30°B.45°C.60°D.75°3.如图,直线AB,CD相交于点O,,OF平分,则的大小为()A.40°B.50°C.65°D.70°4.如图,在中,,,垂足为点D,那么点A到直线的距离是线段()的长.A.B.C.D.5.如图,直线AB,CD,EO相交于点O,已知OA平分∠EOC,若∠EOC:∠EOD=2:3,则∠BOD 的度数为()A.40°B.37°C.36°D.35°6.如图所示,与∠α构成同位角的角的个数为()A.1B.2C.3D.47.在下列语句中,正确的是().A.在平面上,一条直线只有一条垂线;B.过直线上一点的直线只有一条;C.过直线上一点且垂直于这条直线的直线有且只有一条;D.垂线段的长度就是点到直线的距离8.平面上三条直线两两相交最多能构成对顶角的对数是().A.7B.6C.5D.49.如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是()①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD =∠BOC.A.①②③B.①②④C.①③④D.②③④10.如图,下列6种说法:①∠1与∠4是内错角;②∠1与∠2是同位角;③∠2与∠4是内错角;④∠4与∠5是同旁内角;⑤∠2与∠4是同位角;⑥∠2与∠5是内错角.其中正确的有()A.1个B.2个C.3个D.4个二、填空题11.已知直线AB与直线CD相交于点O,∠AOC:∠BOC=2:1,射线OE⊥CD,则∠AOE的度数为.12.如图,直线AB、CD、EF相交于点O,若∠1+∠2=150°,则∠3=°.13.如图,直线AB、CD相交于点O,OE平分,OF平分.若,则的度数为°.14.若与是对顶角,与互余,且,则的度数为°.15.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOM=35°,则∠CON的度数为.三、计算题16.如图,O为直线AB上一点,OC⊥AB,并且∠AOD=130°.求∠COD的度数.17.如图所示,直线AB、CD、EF相交于点O,CD⊥AB,∠AOE:∠AOD=3:5,求∠BOF与∠DOF的度数.四、综合题18.如图,在所标注的角中.(1)对顶角有对,邻补角有对;(2)若,,求与的度数.19.如图,点在直线外,点在直线上,连接.选择适当的工具作图.(1)在直线上作点,使,连接;(2)在的延长线上任取一点,连接;(3)在,,中,最短的线段是,依据是.20.如图,直线、相交于点,且平分,平分.(1)求证:平分;(2)求的度数.答案解析部分1.【答案】D【解析】【解答】解:依据垂线段最短,以及两点之间,线段最短,可得最节省材料的是:故答案为:D.【分析】利用垂线段最短,以及两点之间线段最短求解即可。
相交线和平行线35道核心题——韩春成老师

韩春成个人题库资料
题不在多,而在于精!
韩老师告诉你个秘密:越付出越富有!
5.
【中】平面内两两相交的 6 条直线,其交点个数最少为几个?最多为几个?
6.
【中】 (北京市八一中学 2013 年初一数学第二学期期中试卷) 如图,直线 AB 、 CD 被直线 AC 所截,且 AB ∥CD ,按要求画图并填空: ⑴ 分别画 BAC 和 DCA 的平分线,且两线相交于点 E ; ⑵ AEC _____ ; ⑶ 过点 E 分别画 EF ⊥ AB , EG ⊥ AC ,垂足分别为 F , G . ⑷ 请借助刻度尺比较点 E 到直线 AB 的距离和点 E 到直线 AC 的距离的大小.
b, c, d ,且 a b , b c , c d ,则 a 与 d 的位 15. 【易】在同一平面内的四条直线 a , 置关系是( ) a d A. B. a ∥ d C.相交但不垂直 D.不能确定
16. 【易】⑴ 如图 1,在直角三角形 ABC 中, C 90°, CD AB 于 D ,比较线段 AC 、 AB 、 CD 的大小. ⑵ 如图 2, A 点处是一座小屋, BC 是一条公路,一人在 O 处, ①此人到小屋去,怎么走最近?理由是什么?②此人要到公路,怎么走最近?理由是 什么?
A D′ B C′ F C E D
26. 【中】 (北京五中分校 2013 年初一数学第二学期期中考试)如图, AB ∥ EF ∥CD , ABC 46 , CEF 154 ,则 BCE __________ .
A 46° E 154° C D B
F
27. 【中】 (2012 年青羊区初一下期末)已知:如图, BD ∥ AF ∥CE , ABD 72 , ACE 40 , AP 是 BAF 的平分线,求 PAC 的度数.
初一数学相交线与平行线28道典型题(含 答案和解析)

初一数学相交线与平行线28道典型题(含答案和解析及考点)1、若直线AB,CD相交于O,∠AOC与∠BOD的和为200°,则∠AOD的度数为.答案:80°.解析:∵∠AOC=∠BOD,∠AOC与∠BOD的和为200°.∴∠AOC=100°.∵∠AOD与∠AOC互补.∴∠AOD=80°.考点:几何初步——相交线与平行线——对顶角、邻补角.2、已知OA⊥OB,∠AOC∶∠AOB=2∶3,则∠BOC= .答案:30°或150°.解析:当OC在∠AOB内部时,∠BOC=30°;当OC在∠AOB外部时,∠BOC=150°.考点:几何初步——相交线与平行线——对顶角、邻补角——垂线.3、若直线a与直线b相交于点A,则直线b上到直线a距离等于2cm的点的个数是().A.0B.1C.2D.3答案:C.解析: 直线b的交点两侧各有一点到直线a的距离等于2cm.考点:几何初步——相交线与平行线——点到直线的距离.4、如图所示,在平面内,两条直线l1、l2相交于点O,对于平面内任意一点M,若p、q分别是点M到直线l1、l2的距离,则称(p,q)为点M的“距离坐标”.根据上述规定,“距离坐标”是(2,1)的点共有个.答案:4.解析:因为两条直线相交有四个角,因此每一个角内就有一个到直线l1、l2的距离分别是2、1,的点,即距离坐标是(2,1)的点,因而共有4个.考点:几何初步——相交线与平行线——点到直线的距离.5、若∠1和∠2是同旁内角,若∠1=50°,则∠2的度数为( ). A.45° B.135° C.45°或135° D. 不能确定 答案:D.解析:若∠1和∠2是同旁内角,若∠1=50°,则∠2的度数为不能确定. 考点:几何初步——相交线与平行线——三线八角.6、平面上n 条直线最少能将平面分为__________部分,最多能将平面分为__________部分. A. 最少能将平面分成n+1部分;最多分为n2+n+22.B. 最少能将平面分成n+2部分;最多分为n2+n−22.C. 最少能将平面分成n+1部分;最多分为n2+n−22. D. 最少能将平面分成n+2部分;最多分为n2−n+22.答案:A.解析:1条直线将平面分成2部分.2条直线最少将平面分成3部分,最多将平面分成4部分,其中4=1+1+2. 3条直线最少将平面分成4部分,最多将平面分成7部分,其中7=1+1+2+3. 4条直线最少将平面分成5部分,最多将平面分成11部分,其中11=1+1+2+3+4. ……n 条直线最少将平面分成n+1部分,最多将平面分成n2+n+22部分,其中n2+n+22=1+1+2+3+…+n .综上,n 条直线最少能将平面分成n+1部分,对多能将平面分成n2+n+22部分.考点:几何初步——相交线与平行线——相交线.7、如图,已知∠1=∠2,要使∠3=∠4,则需( ).A. ∠1=∠2B. ∠2=∠4C. ∠1=∠4D. AB ∥CD答案:D.解析:假设∠3=∠4,即∠BEF=∠CFE.由内错角相等,两直线平行,可得AB∥CD.故已知∠1=∠2,要使∠3=∠4,只要AB∥CD.考点:几何初步——相交线与平行线——平行线公理及推论.8、如图①是长方形纸带,将纸带沿EF折叠成图②,再沿BF折叠成图③.(1)若图①中的∠DEF=20°,则图②中的∠CFE度数是.(2)若图①中的∠DEF=α,则图③中的∠CFE度数是.(用含有α的式子表示)答案:(1)160°.(2)180°-3α.解析:(1)在图①中:∵AD∥BC.∴∠BFE=∠DEF=20°.∴∠CFE=160°.在图②中,根据折叠性质,∠CFE大小不变.∴∠CFE=160°.(2)在图①中,∠CFE=180°-∠BFE=180°-α.在图②中,∠CFB=∠CFE-∠BFE=180°-α.根据折叠性质,图③中∠CFB与图②中∠CFB相等.在图③中,∠CFE=∠CFB-∠BFE=180°-3α.∴图③中的∠CFE度数是180°-3α.考点:几何初步——角——角的计算与证明.相交线与平行线——平行线的性质.几何变换——图形的对称——翻折变换(折叠问题)——轴对称基础——轴对称的性质.9、已知:如图,∠D=110°,∠EFD=70°,∠1=∠2.求证:∠3=∠B.证明:∵∠D=110°,∠EFD=70°,(已知).∴∠D+∠EFD=180°.∴_____∥ _____.().又∵∠1=∠2,(已知).∴_____∥ _____.().∴_____∥ _____.().∴∠3=∠B.().答案:答案见解析.解析:∵∠D=110°,∠EFD=70°,(已知).∴∠D+∠EFD=180°.∴AD∥EF.(同旁内角互补,两直线平行).又∵∠1=∠2,(已知).∴AD∥BC.(内错角相等,两直线平行).∴EF∥BC.(平行于同一直线的两直线平行).∴∠3=∠B.(两直线平行,同位角相等).考点:几何初步——相交线与平行线——平行线的判定——平行线的性质.10、车库的电动门栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD的大小是().A.150°B.180°C.270°D.360°答案:C.解析:过B作CD的平行线BF,则CD∥BF∥AE.∴∠DCB+∠CBF=180°,∠ABF=90°.∴∠ABC+∠BCD=∠DCB+∠CBD+∠ABF=180°+90°=270°.考点:几何初步——角——角的计算与证明.相交线与平行线——平行线的性质.11、如图,一条公路修到湖边时,需拐弯绕湖而过;如果第一次拐角∠A是120°,第二次拐角∠B是150°,第三次拐角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是.答案:150°.解析:如图,作BE∥AD.∴∠1=∠A=120°.∴∠2=∠ABC=∠1=150°-120°=30°.∵AD∥CF.∴BE∥CF.∴∠C+∠2=180°.∴∠C=180°-30°=150°.考点:几何初步——相交线与平行线——平行线公理及推论——平行线的性质.12、如图所示,若AB∥CD,则角α,β,γ的关系为().A.α+β+γ=360°B.α-β+γ=180°C.α+β+γ=180°D.α+β-γ=180°答案:D.解析:过β角的顶点为E,作EF∥AB,α+β-γ=180°.考点:几何初步——相交线与平行线平行线的判定——平行线的性质——平行有关的几何模型.13、如图AB∥CD∥EF,CG平分∠ACE,∠A=140°,∠E=110°,则∠DCG=().A.13°B.14°C.15°D.16°答案:C.解析:∵EF∥CD,∴∠ECD=180°-∠E=70°.同理∠ACD=40°.∴∠ACE=110°.∵CG平分∠ACE.∴∠ECG=55°.∴∠DCG=∠ECD-∠ECG=70°-55°=15°.考点:几何初步——相交线与平行线——平行线——平行线的性质——平行有关的几何模型.14、如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,求∠GEF的度数.A.15°B.20°C.25°D.30°答案:D.解析:由AB∥EF∥CD,可知∠BED=∠B+∠D.已知∠B+∠BED+∠D=192°.∴2∠B+2∠D=192°,∠B+∠D=96°.又∠B-∠D=24°,于是可得关于∠B、∠D的方程组:{∠B+∠D=96°∠B−∠D=24°.解得∠B=60°.由AB∥EF知∠BEF=∠B=60°.因为EG平分∠BEF,所以∠GEF=12∠BEF=30°.考点:几何初步——相交线与平行线——平行线——平行有关的几何模型.15、把命题“在同一平面内,垂直于同一直线的两直线互相平行”改写成“如果……,那么……”的形式:.答案:“在同一平面内,如果两条直线都垂直于同一直线,那么这两直线互相平行”.解析:略.考点:命题与证明——命题与定理.16、下列命题中,假命题是().A. 如果两条直线都与第三条直线平行,那么这两条直线也互相平行.B. 两条直线被第三条直线所截,同旁内角互补.C. 两直线平行,内错角相等.D. 在同一平面内,过一点有且只有一条直线与已知直线垂直.答案:B.解析:两条直线被第三条直线所截,同旁内角不一定互补,只有两直线平行时,同旁内角互补.考点:命题与证明——命题与定理.17、已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.(1)求证:AB∥CD.(2)求∠C的度数.答案:(1)证明见解析.(2)∠C=25°.解析:(1)∵AE⊥BC,FG⊥BC.∴AE∥FG.∴∠2=∠A.∵∠1=∠2.∴∠1=∠A.∴AB∥CD.(2)∵AB∥CD.∴∠C=∠3.∵∠D=∠3+60°,∠CBD=70°,∠C+∠D+∠CBD=180°.∴∠C+∠C+60°+70°=180°.∴∠C=25°.考点:几何初步——相交线与平行线——平行线的判定——平行线的性质.18、已知:如图,在△ABC中,BD⊥AC于点D,E为BC上一点,过E点作EF⊥AC,垂足为F,过点D作DH∥BC交AB于点H.(1)请你补全图形.(2)求证:∠BDH=∠CEF.答案:(1)画图见解析.(2)证明见解析.解析:(1)补全图形.(2)∵BD⊥AC,EF⊥AC.∴BD∥EF.∴∠CEF=∠CBD.∵DH∥BC.∴∠BDH=∠CBD.∴∠BDH=∠CEF.考点:几何初步——相交线与平行线——平行线的判定——平行线的性质.尺规作图——过一点作已知直线的垂线——过一点作已知直线的平行线.19、已知,如图,AB∥CD,∠1=∠B,∠2=∠D.求证:BE⊥DE.答案:证明见解析.解析:过E点作EF∥AB,则∠B=∠3.又∵∠1=∠B.∴∠1=∠3.∵AB∥EF,AD∥CD.∴EF∥CD.∴∠A=∠D.又∵∠2=∠D.∴∠2=∠4.∵∠1+∠2+∠3+∠4=180°.∴∠3+∠4=90°,即∠BED=90°.∴BE⊥ED.考点:几何初步——角——角的计算与证明.相交线与平行线——平行线的判定——平行线的性质.20、如图,已知CD∥EF,∠1+∠2=∠ABC.求证:AB∥GF.答案:证明见解析.解析:延长CD、GF交于点H,∠1=∠H.故∠2+∠H=∠ABC.易得AB∥GF.考点:几何初步——相交线与平行线——平行线的判定——平行线的性质.21、如图,已知点A,E,B在同一条直线上,设∠CED=x,∠C+∠D=y.(1)若AB∥CD,试用含x的式子表示y,并写出x的取值范围.(2)若x=90°,且∠AEC与∠D互余,求证:AB∥CD.答案:(1)y=180°-x,其中x的取值范围是(0<x<180).(2)证明见解析.解析:(1)∵AB∥CD.∴∠AEC=∠C,∠BED=∠D.∵∠C+∠D=y.∴∠AEC+∠BED=y.∵∠CED=x,∠AEC+∠CED+∠BED=180°.∴x+y=180°.∴y=180°-x,其中x的取值范围是(0<x<180).(2)∵x=90°,即∠CED=90°.∴∠AEC+∠BED=90°.∵∠AEC与∠D互余.∴∠AEC+∠D=90°.∴∠BED=∠D.∴AB∥CD.考点:函数——函数基础知识——函数自变量的取值范围.几何初步——角——余角和补角——角的计算与证明.相交线与平行线——平行线的判定——平行线的性质.22、阅读材料:材料1:如图(a)所示,科学实验证明:平面镜反射光线的规律是:射到平面镜上的光线和反射出的光线与平面镜所夹的角相等.即∠1=∠2.材料2:如图(b)所示,已知△ABC,过点A作AD∥BC,则∠DAC=∠C,又∵AD∥BC,∴∠DAC+∠BAC+∠B=180°,∴∠BAC+∠B+∠C=180°.即三角形内角和为180°.根据上述结论,解决下列问题:(1)如图(c)所示,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射,若b反射出的光线n平行于m,且∠1=50°,则∠2= ,∠3= .(2)在(1)中,若∠1=40°,则∠3= ,若∠1=55°,则∠3= .(3)由(1)(2)请你猜想:当∠3= 时,任何射到平面镜a上的光线m经过平面镜a和b的两次反射后,入射光线m与反射光线n总是平行,请说明理由.答案:(1)1.100°.2.90°.(2)1.90°.2.90°.(3)90°.解析:(1)∵∠1=50°.∴∠4=∠1=50°.∴∠6=180°-50°-50°=80°.∵m∥n.∴∠2+∠6=180°.∴∠2=100°.∴∠5=∠7=40°.∴∠3=180°-50°-40°=90°.故答案为:100°,90°.(2)∵∠1=40°.∴∠4=∠1=40°.∴∠6=180°-40°-40°=100°.∵m∥n.∴∠2+∠6=180°.∴∠2=80°.∴∠5=∠7=50°.∴∠3=180°-50°-40°=90°.∵∠1=55°.∴∠4=∠1=55°.∴∠6=180°-55°-55°=70°.∵m∥n.∴∠2+∠6=180°.∴∠2=110°.∴∠5=∠7=35°.∴∠3=180°-55°-35°=90°.(3)当∠3=90°时,m∥n.理由是:∵∠3=90°.∴∠4+∠5=180°-90°=90°.∵∠4=∠1,∠7=∠5.∴∠1+∠7+∠4+∠5=2×90°=180°.∴∠2+∠6=180°-(∠1+∠4)+180°-(∠5+∠7)=180°.∴m∥n.故答案为:90°.考点:几何初步——相交线与平行线——平行线的判定——平行线的性质.23、如图,直线AC∥BD,连接AB,直线AC,BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°角)(1)如图1,当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD.,(2)如图2,当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?(请画出图形并直接回答成立或不成立)(3)如图3,当动点P落在第③部分时,探究∠PAC,∠APB,∠PBD之间的关系,请画出图形并直接写出相应的结论.答案:(1)证明见解析.(2)不成立.(3)证明见解析.解析:(1)过点P作直线AC的平行线,易知∠1=∠PAC,∠2=∠PBD.又∵∠APB=∠1+∠2,∴∠APB=∠PAC+∠PBD.(2)不成立.(3)①当动点P在射线BA的右侧时(如图4).结论是∠PBD =∠PAC+∠APB.②当动点P在射线BA上(如图5).结论是∠PBD =∠PAC+∠APB或∠PAC =∠PBD +∠APB或∠APB=0°,∠PAC=∠PBD.③当动点P在射线BA的左侧时(如图6).结论是∠PAC =∠PBD +∠APB.考点:几何初步——相交线与平行线——平行线的判定——平行线的性质——平行有关的几何模型.24、如图所示,在下列条件中:①∠1=∠2;②∠BAD=∠BCD;③∠3=∠4且∠ABC=∠ADC;④∠BAD+∠ABC=180°;⑤∠ABD=∠ACD;⑥∠ABC+∠BCD=180°.能判定AB∥CD的共有()个.A.2B.3C.4D.5答案:A.解析:由平行的判定知③⑥可以判定AB∥CD.考点:几何初步——相交线与平行线——平行线的判定.25、有下列四个命题:①如果两条直线都与第三条直线平行,那么这两条直线也互相平行.②两条直线被第三条直线所截,同旁内角互补.③在同一平面内,如果两条直线都与第三条直线垂直,那么这两条直线也互相垂直.④在同一平面内,过一点有且只有一条直线与已知直线垂直.其中所有正确的命题是().A. ①②B. ①④C. ②③D. ③④答案:B.解析:①④正确;②两条直线被第三条直线所截,同旁内角不一定互补,需要两条直线平行;③在同一平面内,如果两条直线都与第三条直线垂直,那么这两条直线互相平行. 考点:几何初步——相交线与平行线——平行线公理及推论——平行线的判定——平行线的性质.26、如图,DB ∥FG ∥EC ,∠ABD=60°,∠ACE=30°,AP 平分∠BAC ,求∠PAG 的度数.A.11°B.12°C.13°D.14°答案:B.解析:由DB ∥FG ∥EC.可得∠BAC=∠BAG+∠CAG=∠DBA+∠ACE=60°+36°=96°.由AP 平分∠BAC 得∠CAP=12∠BAC=12×96°=48°. 由FG ∥EC 得∠GAC=∠ACE=36°.∴∠PAG=48°-36°=12°.考点:几何初步——相交线与平行线——平行线——平行有关的几何模型.27、如图,AB ∥CD ,且∠BAP=60°-α,∠APC=45°+α,∠PCD=30°-α,则α=( ).A.10°B.15°C.20°D.30°答案:B.解析:得∠APC=∠BAP+∠DCP .∴45°+α=60°-α+30°-α.解得:α=15°.考点:几何初步——相交线与平行线——平行线的性质.28、已知,如图,AB∥CD,直线α交AB、CD分别于点E、F,点M在线段EF点上,P是直线CD 上的一个动点,(点P不与F重合).(1)当点P在射线FC上移动时,∠FMP、∠FPM和∠AEF之间的数量关系是:.(2)当点P在射线FD上移动时,∠FMP、∠FPM和∠AEF之间的数量关系是:. 答案:(1)∠FMP+∠FPM=∠AEF.(2)∠FMP+∠FPM+∠AEF=180°.解析:(1)当点P在射线FC上移动时.∵AB∥CD.∴∠AEF+∠CFE=180°.又∵∠FMP+∠FPM+∠CFE=180°.∴∠FMP+∠FPM=∠AEF.(2)当点P在射线FD上移动时.∵AB∥CD.∴∠AEF=∠MFD.又∵∠FMP+∠FPM+∠CFE=180°.∴∠FMP+∠FPM+∠AEF=180°.考点:几何初步——相交线与平行线——平行线的性质.。
相交线与平行线计算与证明题
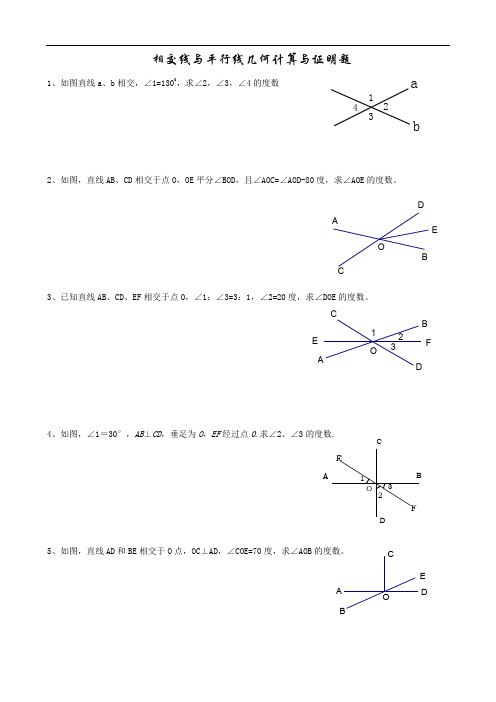
321OFE D C B AEODC B AE DO CBA 相交线与平行线几何计算与证明题1、如图直线a 、b 相交,∠1=1300,求∠2,∠3,∠4的度数2、如图,直线AB 、CD 相交于点O ,OE 平分∠BOD ,且∠AOC=∠AOD-80度,求∠AOE 的度数。
3、已知直线AB 、CD 、EF 相交于点O ,∠1:∠3=3:1,∠2=20度,求∠DOE 的度数。
4、如图,∠1=30°,AB ⊥CD ,垂足为O ,EF 经过点O .求∠2、∠3的度数.5、如图,直线AD 和BE 相交于O 点,OC ⊥AD ,∠COE=70度,求∠AOB 的度数。
13ab42ABCDO123EFFEDCB Ad ecb a 34126、如图,EO ⊥AB 于O ,直线CD 过O 点,∠EOD ∶∠EOB=1∶3,求∠AOC 、∠AOE 的度数.7、如图,直线EF 、BC 相交于点O ,∠AOC 是直角,∠AOE=1 15°,求∠COF 的度数。
8、已知:如图,AB ,CD ,EF 三直线相交于一点O ,OE⊥AB,∠COE=20°,OG 平分∠BOD,求∠BOG9、如图,AB ∥EF,∠ECD=∠E,求证:CD ∥AB.10、如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a 与c 平行吗?•为什么?OB CF EAGHKF EDC BA 11、如图:已知直线EF 与AB 、CD 分别相交于点G 、H ,∠1=∠3,那么AB ,CD 平行吗?为什么?12、如图,已知BD 平分∠ABC,∠1=∠2.求证:AB ∥CD.13、如图所示,已知直线EF 和AB,CD 分别相交于K,H,且EG ⊥AB,∠CHF=600,∠E=•30°,试说明AB ∥CD.14、如图,已知∠4=∠B,∠1=∠3.求证:AC 平分∠BAD. A BCD EFG H 1 315、如图,已知BE 是∠ABC 的平分线,交AC 于E ,其中∠l=∠2,那么DE ∥BC 吗?为什么?16、如图、已知∠BED=∠B +∠D.试说明AB 与CD 的位置关系。
相交线单元测试题

相交线单元测试题一、选择题(每题2分,共10分)1. 若两条直线相交,则它们的位置关系是:A. 垂直B. 平行C. 相交D. 重合2. 以下哪一项不是相交线的基本性质?A. 对顶角相等B. 邻补角互补C. 内错角相等D. 同位角相等3. 如果两条直线相交所形成的对顶角不相等,那么这两条直线:A. 垂直B. 平行C. 相交D. 无法确定4. 两条直线相交,其中一个角是直角,那么这两条直线:A. 垂直B. 平行C. 相交D. 重合5. 若两条直线相交,其中一个角是锐角,则其他三个角的度数之和为:A. 180°B. 270°C. 360°D. 450°二、填空题(每题2分,共10分)6. 当两条直线相交时,对顶角的度数______。
7. 两条直线相交,若一个角为45°,则其对顶角的度数为______。
8. 如果两条直线相交,其中一个角是钝角,则其他三个角的度数之和为______。
9. 两条直线相交,形成的邻补角的度数之和为______。
10. 当两条直线相交,如果其中一个角是30°,则其对顶角的度数为______。
三、简答题(每题10分,共20分)11. 解释什么是对顶角,并给出一个例子说明它们的性质。
12. 描述两条直线相交时,同位角、内错角和对顶角的概念,并说明它们的性质。
四、计算题(每题15分,共30分)13. 在一个平面直角坐标系中,直线L1的方程为 y = 2x + 3,直线L2的方程为 y = -x + 5。
求这两条直线的交点坐标。
14. 已知两条相交直线AB和CD,其中AB与CD相交于点E,且∠AED = 120°,∠BEC = 30°。
求∠AEC和∠DEC的度数。
五、证明题(每题15分,共15分)15. 已知两条直线AB和CD相交于点E,且∠AEB = ∠DEC。
证明:AB 和CD是平行的。
六、应用题(每题15分,共15分)16. 在一个平面几何问题中,你被要求证明两条直线相交的点E是两条直线的中点。
相交线练习题目

相交线练习题目在几何学中,相交线是指平面上的两条线段或射线相交的点。
相交线的研究在解决各种几何问题时起着重要的作用。
本篇文章将提供一些相交线的练习题目,帮助读者巩固对相交线的理解和运用。
1.求解相交线交点的坐标已知平面上两条直线的方程分别为:直线L1:y = 2x + 3直线L2:y = -x + 5求解直线L1和直线L2的交点坐标。
解答:将两条线段的方程联立起来,解得:2x + 3 = -x + 53x = 2x = 2/3将x的值代入其中一条线段方程,求得y的值:y = -x + 5y = -(2/3) + 5y = 13/3因此,直线L1和直线L2的交点坐标为(2/3, 13/3)。
2.判断直线是否相交已知平面上存在三条直线,方程分别为:直线L1:y = 2x + 1直线L2:y = -x + 3直线L3:y = 2x - 1判断直线L1、L2和L3是否相交。
解答:直线L1和直线L2的斜率分别为2和-1,斜率不相等,因此直线L1和直线L2相交。
直线L1和直线L3的斜率均为2,斜率相等,但截距不相等,因此直线L1和直线L3相交。
直线L2和直线L3的斜率均为-1,斜率相等,且截距也相等,因此直线L2和直线L3重合。
综上所述,直线L1、L2和L3相交的情况是:直线L1和L2相交,直线L1和直线L3相交,直线L2和L3重合。
3.求解相交线的夹角已知平面上两条直线的方程分别为:直线L1:y = 2x + 1直线L2:y = -x + 3求解直线L1和直线L2的夹角。
解答:直线L1的斜率为2,直线L2的斜率为-1。
两条直线的夹角公式为:tan(α) = (m2 - m1) / (1 + m1 * m2)其中,α表示直线L1和直线L2之间的夹角,m1和m2分别表示直线L1和直线L2的斜率。
将斜率代入公式,计算得到:tan(α) = (-1 - 2) / (1 + 2 * (-1))= -3 / (-1)= 3因此,直线L1和直线L2的夹角为tan^(-1)(3),约等于71.57度。
相交线和平行线测试题及答案

七年级相交线与平行线测试题一、选择题1。
下列正确说法的个数是()①同位角相等②对顶角相等③等角的补角相等④两直线平行,同旁内角相等A 。
1, B. 2, C。
3, D. 42. 下列说法正确的是()A。
两点之间,直线最短;B.过一点有一条直线平行于已知直线;C.和已知直线垂直的直线有且只有一条;D。
在平面内过一点有且只有一条直线垂直于已知直线.3. 下列图中∠1和∠2是同位角的是( )A. ⑴、⑵、⑶, B。
⑵、⑶、⑷, C。
⑶、⑷、⑸, D. ⑴、⑵、⑸4. 如果一个角的补角是150°,那么这个角的余角的度数是( )A。
30° B.60° C.90°D。
120°5. 下列语句中,是对顶角的语句为 ( )A。
有公共顶点并且相等的两个角B。
两条直线相交,有公共顶点的两个角C.顶点相对的两个角D.两条直线相交,有公共顶点没有公共边的两个角6。
下列命题正确的是( )A。
内错角相等B.相等的角是对顶角C。
三条直线相交,必产生同位角、内错角、同旁内角D。
同位角相等,两直线平行7. 两平行直线被第三条直线所截,同旁内角的平分线 ( )A。
互相重合B。
互相平行 C。
互相垂直 D。
无法确定8. 在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
下列图案中,不能由一个图形通过旋转而构成的是( )A B C D9。
三条直线相交于一点,构成的对顶角共有( )A、3对B、4对C、5对D、6对10。
如图,已知AB∥CD∥EF,BC∥AD,AC平分∠BAD,那么图中与∠AGE相等的角有( )A。
5个 B.4个 C.3个D。
2个11。
如图6,BO 平分∠ABC,CO 平分∠ACB ,且MN ∥BC,设AB =12,BC =24,AC =18,则△AMN 的周长为( )。
A 、30 B 、36 C 、42 D 、18 12. 如图,若AB ∥CD ,则∠A 、∠E 、∠D 之间的关系是 ( )A.∠A +∠E +∠D =180° B 。
小学数学相交线练习题

小学数学相交线练习题
小学数学练习题:相交线
一、选择题
1. 下图中,两条相交线的交点是()
A. 直角
B. 锐角
C. 退化角
D. 平角
2. 下图中,AB和CD为两条相交线,若AB为垂直于CD,那么角A和角B的关系是()
A. 互补角
B. 对顶角
C. 钝角
D. 垂角
3. 直线l与平行线m相交,形成的两组内错角分别为40°和()
A. 40°
B. 60°
C. 80°
D. 100°
4. 下图中,MN与PQ相交于点O,若角MON为130°,则角NOM
和角NOQ的关系是()
A. 互补角
B. 对顶角
C. 直角
D. 无关
二、填空题
1. 直线l与平行线m相交,形成的同旁内角分别为120°和()°。
2. 直线AB与CD相交于点O,若角AOC为60°,则角BOD为()°。
3. 直线l与平行线m相交,形成的同旁外角分别为80°和()°。
三、计算题
1. 下图中,直线l与m相交于点O,角BOC的度数为55°,求角AOD的度数。
(提示:角AOD与角BOC互补)
四、应用题
小明站在田地中央,看到一棵大树和一栋高楼的顶部在视线上重合。
他向前走了30米,再看到大树和高楼的顶部在视线上重合点后方6米。
已知大树的高度为12米,求高楼的高度。
(假设小明的眼睛高度为1.5米)
以上是关于小学数学相交线的练习题,希望对你有帮助!。
相交线与平行线测试题及答案

相交线与平行线测试题及答案1. 单选题:在平面上,两条互相垂直的直线称为()。
A. 平行线B. 垂直线C. 相交线D. 对称线答案:B. 垂直线2. 单选题:下面哪种说法是正确的?A. 平行线永远不会相交B. 相交线永远不会平行C. 平行线和相交线可以同时存在D. 平行线和相交线不能同时存在答案:C. 平行线和相交线可以同时存在3. 多选题:判断下列述句是否正确。
1) 平行线没有交点。
2) 相交线可以有无数个交点。
3) 两条垂直线的交点一定是直角。
A. 正确的有1)、2)、3)B. 正确的有1)、3)C. 正确的有2)、3)D. 正确的只有3)答案:B. 正确的有1)、3)4. 填空题:两条互相垂直的直线所成的角度为()度。
答案:90度5. 判断题:两条平行线的夹角为180度。
答案:错误6. 判断题:两条相交直线一定不平行。
答案:正确7. 计算题:已知直线L1与直线L2互相垂直,L1的斜率为2,过点(1,3)的直线L2的斜率为()。
答案:-1/28. 计算题:已知直线L1过点(1,2)且斜率为3/4,直线L2与L1平行且过点(3,5),求直线L2的斜率。
答案:3/49. 解答题:请解释什么是相交线和平行线,并举例说明。
答案:相交线是指两条直线或线段在平面上有唯一一点相交。
例如,在平面上有两条直线,一条通过点A和点B,另一条通过点C和点D,如果点A与点C不重合并且点B与点D不重合,则这两条直线相交于点E。
平行线是指在平面上没有任何交点的两条直线。
例如,在平面上有一条直线通过点A和点B,另一条直线通过点C和点D,如果两条直线没有任何一点相交,则这两条直线是平行线。
10. 解答题:如何通过直线的斜率来判断两条直线是否平行或垂直?答案:两条直线平行的充要条件是它们的斜率相等,即斜率相同的两条直线是平行线。
两条直线垂直的充要条件是它们的斜率的乘积为-1,即斜率之积为-1的两条直线是垂直线。
总结:在平面几何中,相交线是指两条直线或线段在平面上有唯一一点相交,平行线是指在平面上没有任何交点的两条直线。
《相交线与平行线》全章综合练习(含答案)

全章综合练习《相交线与平行线》全章综合练习相交线与平行线》学校:___________姓名:___________班级:___________考号:___________注释))单选题((注释一、单选题c b,直线b、c、d交于一点,若∠1=500,则∠2c a,⊥1、如图,直线a、b、c、d,已知⊥等于【】A.600B.500C.400D.3002、如图,⊥BC CD,∠EBC=∠BCF,那么,∠ABE与∠DCF的位置与大小关AB BC,⊥系是()A.是同位角且相等B.不是同位角但相等;C.是同位角但不等D.不是同位角也不等3、如果两个角的一边在同一直线上,另一边互相平行,那么这两个角只能()A.相等B.互补C.相等或互补D.相等且互补4、下列说法中,为平行线特征的是()①两条直线平行,同旁内角互补; ②同位角相等, 两条直线平行;③内错角相等, 两条直线平行; ④垂直于同一条直线的两条直线平行.A.①B.②③C.④D.②和④5、如图,∥∥AB CD EF,若∠ABC=50°,∠CEF=150°,则∠BCE=()A.60° B.50° C.30° D.20°AB CD,则角α、β、γ之间的关系为()6、如图,如果∥7、如图,由A到B 的方向是()A.南偏东30° B.南偏东60° C.北偏西30° D.北偏西60° AC ED,可知相等的角有()8、如图,由∥10、若∠1和∠2互余,∠1与∠3互补,∠3=120°,则∠1与∠2的度数分别为( )A .50°、40°B .60°、30°C .50°、130°D .60°、120°11、下列语句正确的是( )A .一个角小于它的补角B .相等的角是对顶角C .同位角互补,两直线平行D .同旁内角互补,两直线平行12、图中与∠1是内错角的角的个数是( )A .2个B .3个C .4个D .5个13、如图,直线AB 和CD 相交于点O ,∠AOD 和∠BOC 的和为202°,那么∠AOC 的度数为( )A .89°B .101°C .79°D .110°14、如图,∠1和∠2是对顶角的图形的个数有( )A .1个B .2个C .3个D .0个15、如图,直线a 、b 被直线c 所截,现给出下列四个条件:①∠∠1=5,②∠∠1=7,③∠∠2+3=180°,④∠∠4=7,其中能判定∥a b 的条件的序号是( )A .①②B .①③C .①④D .③④分卷II分卷II 注释评卷人得分注释))填空题((注释二、填空题DE BC交AC于E,若∠ACB=60°,∠B=74°,则∠EDC 16、如图,∠ACD=∠BCD,∥=___°,∠CDB=____°。
相交线例题

相交线例题一【例1】如图,直线AB和CD直交于点O,OE是射线,则:⑴∠1的对顶角是________,∠1的邻补角是______.⑵∠5的对顶角是________,∠3的邻补角是______.分析这道题是检查对顶角,邻补角的概念的,答题时应紧紧抓住这两个概念的本质特征来回答.解⑴∠1的对顶角是∠2,∠1的邻补角是∠5和∠AOD.⑵∠5的对顶角是∠AOD, ∠3的邻补角是∠BOE.评注两条直线相交时,一个角的邻补角有两个,它们是对顶角,如例1中的∠1的邻补角,不能漏掉其中任何一个.【例2】如图,三条直线AB,CD,EF交于一点O,且OF平分∠DOB,试问:OE是不是∠AOC 的平分线?为什么?分析判断OE是否为∠AOC的平分线,即考察∠3,∠4是否相等.由对顶角性质易知: ∠3=∠2, ∠4=∠1,而由条件可知∠1=∠2,所以可确定OE是∠AOC的平分线.解 OE是∠AOC的平分线.理由如下:因为 OF平分∠DOB,所以∠1=∠2(角平分线定义)因为∠3=∠2 ∠4=∠1(对顶角相等)所以∠3=∠4 (等量代换)所以∠OE是∠AOC的平分线. (角平分线的定义)评注几何中某个结论成立的理由常用“因为所以”的形式来表达.同学们应逐步熟悉和掌握.其中一步推理都要有根有据,在上面的解题过程中,我们把每一步的根据都写在后面的括号内,希望同学们开始也能这样做.【例3】如图,直线AB,CD,EF相交于点O,∠AOF=3∠FOB,∠AOC=900,求∠EOC的度数.分析由已知可知,∠EOC和∠AOE互余,所以求∠EOC的度数可先求∠AOE的度数,观察图形可知,∠AOE和∠BOF是对顶角,∠BOF和∠AOF是邻补角,利用它们的性质和已知条件,本题可解.解设∠BOF= x0,则∠AOF=3x0,x (邻补角定义)+x1803=解得x=450,即∠BOF=450所以∠AOE=∠BOF=450所以∠EOC=∠AOC-∠AOE=450评注几何计算题,常用到几何图形中的性质,因此解也要有根有据,另外几何计算题也常得用代数方法达到解题目的.。
相交线的练习题

相交线的练习题一、选择题1. 两条直线相交于一点,该点称为它们的:A. 交点B. 焦点C. 垂足D. 端点2. 在同一平面内,不相交的两条直线称为:A. 平行线B. 垂直线C. 相交线D. 异面直线3. 直线AB与直线CD相交于点O,若∠AOC=45°,则∠BOC的度数是:A. 45°B. 90°C. 135°D. 180°4. 在平面直角坐标系中,直线y=2x与直线y=-3x相交于:A. (0,0)B. (1,-3)C. (2,4)D. (-1,3)5. 若两条直线相交成直角,则这两条直线:A. 平行B. 垂直C. 异面D. 相交二、填空题6. 若直线l1: ax + by + c1 = 0与直线l2: dx + ey + f = 0相交,则它们的交点坐标为________。
7. 当两条直线相交,且其中一个角为直角时,这两条直线的位置关系是________。
8. 在平面直角坐标系中,若直线l1: y = x - 1与直线l2: y = -x + 2相交,则交点的横坐标为________。
9. 若两条直线相交于点P(x, y),则点P到两直线的________相等。
10. 在平面几何中,若两条直线相交,则它们相交的角的度数之和为________。
三、简答题11. 请简述如何判断两条直线是否相交,并给出相应的几何或代数方法。
12. 在平面直角坐标系中,若已知两条直线的方程,如何求它们的交点坐标?13. 解释什么是垂直线,并给出垂直线相交时的几何特征。
14. 若两条直线相交成30°角,求这两条直线与x轴正方向的夹角。
15. 在平面几何中,若两条直线相交,它们形成的角有哪些可能的组合?四、计算题16. 已知直线l1: 2x - 3y + 6 = 0与直线l2: x + y - 5 = 0,请求它们的交点坐标。
17. 若直线l: 3x + 4y - 12 = 0与x轴相交于点A,与y轴相交于点B,求点A和点B的坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相交线计算题 Revised by BETTY on December 25,2020
1.如图所示,在长方形的台球桌桌面上,选择适当的方法击打白球,可以使白球经过两次反弹后将黑球直接撞入中洞,此时∠1=∠2,∠3=∠4,且∠2+∠3=90°,∠4+∠5=90°.如果黑球与洞口连线和台球桌面边缘的夹角为∠5=40°,那么∠1应等于多少度才能保证黑球进入中洞?
2.取一张正方形纸片ABCD,如图
(1)折叠∠A,设顶点A落在点A′的位置,折痕为EF;如图(2)折叠∠B,使EB沿EA′的方向落下,折痕为EG.试判断∠FEG的度数是否是定值,并说明理由.
3.如图所示,直线AB,CD,EF相交于点O,∠AOF=3∠FOB,∠AOC=90°,求∠EOC的度数.
4.如图所示,O为直线AB上一点,
1
3
AOC BOC
∠=∠,OC是∠AOD的平分线.
(1)求∠COD的度数;
(2)判断OD与AB的位置关系,并说明理由.
5.如图所示,将长方形纸片折叠,使点A落在点A′处,BC为折痕,BD是∠A′BE的平分线,试求∠CBD的度数.
6.如图所示,点O在直线AB上,OE平分∠COD,且∠AOC︰∠COD︰∠DOB=1︰3︰2,求∠AOE的度数.
7.如图所示,直线AB、CD分别交EF于点G、H,若∠2=∠3,∠1=50°,求∠4的度数.
8.如图所示,直线AB,CD相交于点O,且∠AOC=80°,OE把∠BOD分成两部分,且∠BOE︰∠EOD=2︰3,则∠EOD=________.
9.如图所示,直线a,b,c两两相交,∠1=2∠3,∠2=65°,求∠4的度数.
10.如图所示,已知l
1,l
2
,l
3
相交于点O,∠1=∠2,∠3︰∠1=8︰1,求∠
4的度数.
11.如图所示,三条直线相交于一点,求∠1+∠2+∠3的度数.
12.如图,直线AB与CD相交于点E,∠1=∠2,EF平分∠AED,且∠1=50°,求∠AEC的度数.
13.如图所示,直线AB截直线CD和EF,构成8个角,指出图中的同位角、内错角、同旁内角.
14.如图所示,AO⊥BO于O,CO⊥DO于O,∠BOD=30°,求∠AOC的度数.15.如图所示,AB是一条河流,要铺设管道将河水引到C,D两个用水点,现有两种铺设管道的方案.方案一:分别过C,D作AB的垂线,垂足分别为E,
F ,沿CE ,DF 铺设管道;方案二:连接CD 交AB 于点P ,沿PC 、PD 铺设管道.问:这两种铺设管道的方案中哪一种更节省材料,为什么?
16.如图所示,直线AB ,CD 相交于点O ,OE ⊥CD ,OF ⊥AB ,∠DOF =65°,求∠BOE 和∠AOC .
17.如图所示,小明家在A 处,他要去在同一条路上的B ,C ,D ,E 四家商店中的某一家商店买东西,则他至少要走多少米才可以买到东西?
参考答案
1.40度
【解析】因为∠1=∠2,∠2+∠3=90°,所以∠1+∠3=90°.又因为∠3=∠4,所以∠1+∠4=90°,因为∠4+∠5=90°.∠5=40°,所以∠1=∠5=40°,所以∠1应等于40°才能保证黑球进入中洞.
2.为定值
【解析】由折叠可知,∠FEA′=∠FEA ,∠GEB =∠GEA′,所以
12FEA A EA ''∠=∠,12
GEA A EB ''∠=∠.因为∠A′EB+∠A′EA=180°,所以1111()180902222
GEA FEA A EB A EA A EB A EA ''''''∠+∠=∠+∠=∠+∠=⨯︒=︒,即∠FEG 的度数为定值.
3.设∠BOF =x°,则∠AOF =3x°.
因为x +3x =180(邻补角互补),所以x =45,即∠BOF =45°,
所以∠AOE =∠BOF =45°(对顶角相等),所以∠EOC =∠AOC -∠AOE =90°-45°=45°.
【解析】这是一道综合题,应综合运用“邻补角互补”、“对顶角相等”等知识转换已知条件,从而进行求解.
4.45° OD ⊥AB
【解析】(1)OC 平分∠AOD ,设∠COD =x°,则∠AOC =x°,∠BOD =2x°,∠AOC +∠COD +∠BOD =180°,即x°+x°+2x°=180°,解得x =45,所以∠COD =45°.
(2)由(1)知,∠BOD =2x°=90°,所以OD ⊥AB .
5.90°
【解析】因为点A 折叠后落到点A′处,所以∠ABC =∠A′BC.又因为BD 是∠A′BE 的平分线,所以∠A′BD=∠EBD ,所以
11()1809022
CBD CBA DBA ABA EBA ''''∠=∠+∠=∠+∠=⨯︒=︒,即∠CBD 的度数是90°.
6.75度
【解析】因为∠AOC ︰∠COD ︰∠DOB =1︰3︰2,
所以设∠AOC =x°,则∠COD =3x°,∠DOB =2x°.又因为AB 为直线,所以∠AOC +∠COD +∠DOB =180°,
即x+3x+2x=180,x=30.所以∠AOC=30°,∠COD=3x°=90°.
因为OE平分∠COD,所以
1
45
2
COE COD
∠=∠=︒,所以∠AOE=∠AOC+∠COE
=30°+45°=75°.
7.130度
【解析】因为∠2=∠3,∠2=∠1(对顶角相等),所以∠3=∠1=50°.所以∠4=180°-∠3=180°-50°=130°(邻补角性质).
8.48°
【解析】因为∠BOE︰∠EOD=2︰3.故可设∠BOE=2k°,∠EOD=3k°.根据对顶角相等可得出∠BOD=∠AOC=80°,所以2k°+3k°=80°,可得k=16°,所以∠EOD=3k°=3×16°=48°.
9.度
【解析】因为∠1=∠2(对顶角相等),且∠2=65°,所以∠1=65°.因为∠1=2∠3,所以∠3=°.因为∠4=∠3(对顶角相等),所以∠4=°.10.36度
【解析】因为∠1=∠2,∠3︰∠1=8︰1,所以
8
3180144
10
∠=︒⨯=︒.因为∠4
与∠3互为邻补角,所以∠4=36°.
11.180度
【解析】如图所示,由“对顶角相等”,可得∠2=∠4.由平角的定义,知∠1+∠4+∠3=180°,所以∠1+∠2+∠3=180°.
12.80度
【解析】因为∠1=∠2,∠1=50°,所以∠2=50°.
又因为EF平分∠AED,
所以∠AED=2∠2=100°.
又因为∠AED+∠AEC=180°(邻补角的性质),
所以∠AEC=80°.
13.解:同位角:∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8;内错角:∠1与∠7,∠4与∠6;同旁内角:∠1与∠6,∠4与∠7.
【解析】两条直线是CD、EF,截线是AB,根据同位角,内错角,同旁内角的概念即可得出答案.
14.解:因为AO⊥BO,CO⊥DO(已知),所以∠AOB=∠COD=90°(垂直的定义).
因为∠BOD=30°,所以∠BOC=∠COD-∠BOD=60°,∠AOD=∠AOB-∠BOD=60°.
所以∠AOC=∠AOD+∠BOD+∠BOC=150°.
【解析】本题是垂线定义的直接应用.由垂直的定义可知∠AOB、∠COD均为90°,又由∠BOD=30°可求得∠BOC、∠AOD,从而可求出∠AOC.
15.沿CE、DF铺设管道更节省材料.
【解析】按方案一铺设管道更节省材料.理由如下:因为CE⊥AB,DF⊥AB,而AB与CD不垂直,所以根据“垂线段最短”,可知DF<DP,CE<CP,
所以CE+DF<CP+DP,所以沿CE、DF铺设管道更节省材料.
16.65°25°
【解析】因为OF⊥AB,所以∠BOF=90°.又∠DOF=65°,所以∠BOD=90°-65°=25°.
因为∠AOC=∠BOD,所以∠AOC=25°.因为OE⊥CD,所以∠DOE=90°,所以∠BOE=90°-∠BOD=90°-25°=65°.
17.15米
【解析】由题图可知,小明到C商店买东西最近,所以至少要走15米才可以买到东西.。
