数学:第一章勾股定理复习课件(北师大版八年级上)
合集下载
北师大版八年级数学上册第一章勾股定理第1课探索勾股定理课件

2. 如图,正方形ABCD的面积为25 cm2,△ABP为直角三角形, ∠APB=90°,且PB=3 cm,那么AP的长为( C )
A. 5 cm
B. 3 cm
C. 4 cm
D. 不能确定
3. 在Rt△ABC中,斜边BC=4,则BC2+AB2+AC2= 32 . 4. 如图,所有的四边形都是正方形,所有的三角形都是直角三角 形,其中最大的正方形的边长为7 cm,则正方形A,B,C,D的面积之和 为 49 cm2.
第一章 勾股定理
1 探索勾股定理 第1课时
1. 直角三角形三边存在的关系:在直角三角形中,任意两条边确定了,另 外一条边也就随之 确定 ,三边之间存在着一种特定的 数量 关系.
2. 我国古代把直角三角形中较短的直角边称为 勾 ,较长的直角边称为 股 , 斜边称为 弦 .
3. 勾股定理:直角三角形两直角边的 平方和 等于斜边的 平方 .如果用a, b和c分别表示直角三角形的两直角边和斜边,那么 a2+b2=c2 .
4. 如图,在△ABC中,∠C=90°. (1)若已知a,b,则c2= a2+b2 ; (2)若已知a,c,则b2= c2-a2 ; (3)若已知b,c,则a2=长分别为3和4,下列说法中正确的是( C )
A. 斜边长为25
B. 三角形的周长为25
C. 斜边长为5
D. 三角形的面积为20
2. 三个正方形的面积如图所示,则S的值为( C )
A. 3
B. 4
C. 9
D. 12
3. 在Rt△ABC中,∠C=90°,AB=25,AC=7,则△ABC的面积为84 . 4. 如图,为了测得湖两岸点A和点B之间的距离,一个观测者在点C设桩, 使∠ABC=90°,并测得AC=20m,BC=16m,则点A和点B之间的距离是 12 m.
北师大版八年级数学上册1.1 第1课时 勾股定理的认识 课件(共23张PPT)

探究新知
1.在纸上画若干个直角三角形,分别测量它们的
三条边,看看三边长的平方之间有怎么样的关系?
c
a
b
直角三角形的两直角边的平方和等于斜边的平方,这就是
著名的“勾股定理”。
如果直角三角形的两条直角边为a、b,斜边为c,那么有
a2+b2=c2.
数学小知识
我国古代称直角三角形的较短的直角边为勾,较长的直角
求 的长.
解:因为 ⊥ ,
所以 ∠ = ∠ = 90∘ .
在 Rt △ 中, 2 = 2 − 2 = 102 − 82 = 36 ,
所以 = 6 .
设 = = ,则 = − 6 .
在 Rt △ 中, 2 = 2 + 2 ,
所以 △ =
1
2
1
2
⋅ = × 25 × 12 = 150 .
6. 如图,直线 上有三个正方形 , , .若 , 的面积分别
为 5 和 11 ,则 的面积为( C )
A. 4
B. 6
C. 16
D. 55
7. 如图,在 △ 中, = , = 10 , ⊥ ,垂足为 , = 8 .
(2) 已知 = 12 , = 16 ,求 .
【解】在 Rt △ 中, ∠ = 90∘ , = 12 , = 16 ,
所以 2 = 2 + 2 = 122 + 162 = 400 .
所以 = 20 .
例2 如图,在 △ 中, ⊥ 于点 ,且 + = 32 ,
因为 ∠ = 90∘ ,所以 2 + 2 = 2 .
北师大版八年级数学上册第一章勾股定理复习与小结课件

P
M
教学过程——典例精析
第一章 勾股定理
听一听
典例3 如图,长方形 ABCD 中,AB=3,AD=9,将此长方形折叠,使点 D与点B
重合,折痕为 EF,求△ABE 的面积。
A
B
E
D
F
C
教学过程——典例精析
第一章 勾股定理
听一听
A
解析:折叠问题中,要找到折叠前
后相等的线段或角,注意这些线段
与其他线段的关系,再利用勾股定
D. 若、、是的△ABC的三边,且 − = ,则∠A=90°
第一章 勾股定理
基础训练
第一章 勾股定理
2. 如图是商场的台阶的示意图,已知每级台阶的宽度都是20cm,每级台
阶的高度都是15cm,则连接AB的线段长为( B )
A. 100cm
B. 150cm
C. 200cm
D. 250cm
解:(1)供水站P的位置如图所示.
(2)过B作BM⊥,过A’作A’M⊥BM于M.
B
A
由已知可得A’M=8,BM=2+4=6.
在Rt△AMB中,
A’B2=AM2+BM2=82+62=100
解得A’B=10
5000×10+50000=100000.
故供水站修建完成后共计要花100000元.
∙∙
A’
∙
是直角三角形.
知识梳理
第一章 勾股定理
内容:直角三角形两
直角边的平方和等于
斜边的平方.
探索勾
股定理
表达式:用
和分别表示直角三
角形的两直角边和斜
边,那么
验证方法:面积法
北师大版八年级数学上第一章勾股定理复习课件
1m
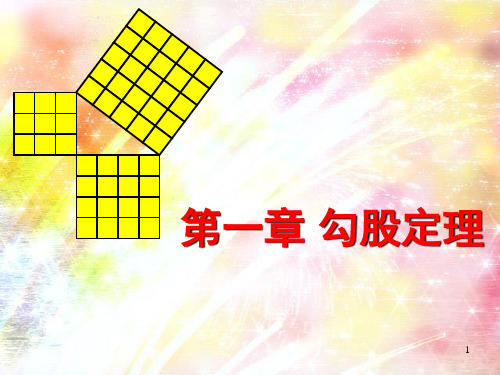
x (x+1)
3
22
在一棵树的10米高处B有两只猴子, 其中一只猴子爬下树走到离树20米的 池塘A,另一只猴子爬到树顶D后直接 跃向池塘的A处,如果两只猴子所经过 距离相等,试问这棵树有多高?
D
B.
C
A 23
专题三 折叠
折叠和轴对称密不可分,利用折叠前后 图形全等,找到对应边、对应角相等便可 顺利解决折叠问题
猜想
32=4+5 52=12+13 72=24+25
…… 132=b+c
请你结合该表格及相关知识,求出b、c的值. 即b= 84 ,c=___8_5____
15
例5、如图,四边形ABCD中,AB=3,
BC=4,CD=12,AD=13, ∠B=90°,求四 边形ABCD的面积
D
13
A
12 3┐
B4 C
2
∴ AB=25.
B
31
例4:.如图,长方体的长 为15 cm,宽为 10 cm, 高为20 cm,点B离点C 5 cm,一只蚂蚁如果要沿着 长方体的表面从点 A爬 到点B,需要爬行的最短 距离是多少?
5B
C
20
15
A 10
32
E
5B C
20
15
A 10 F
E C5 B
20
A 10
B5 C 10 E 20
35
A
x
1.5米
1.5米
2.2米
2.2米
1.5米
1.5米
Cx
B
X2=1.52+1.52=4.5
AB2=2.22+X2=9.34
AB≈3米
x (x+1)
3
22
在一棵树的10米高处B有两只猴子, 其中一只猴子爬下树走到离树20米的 池塘A,另一只猴子爬到树顶D后直接 跃向池塘的A处,如果两只猴子所经过 距离相等,试问这棵树有多高?
D
B.
C
A 23
专题三 折叠
折叠和轴对称密不可分,利用折叠前后 图形全等,找到对应边、对应角相等便可 顺利解决折叠问题
猜想
32=4+5 52=12+13 72=24+25
…… 132=b+c
请你结合该表格及相关知识,求出b、c的值. 即b= 84 ,c=___8_5____
15
例5、如图,四边形ABCD中,AB=3,
BC=4,CD=12,AD=13, ∠B=90°,求四 边形ABCD的面积
D
13
A
12 3┐
B4 C
2
∴ AB=25.
B
31
例4:.如图,长方体的长 为15 cm,宽为 10 cm, 高为20 cm,点B离点C 5 cm,一只蚂蚁如果要沿着 长方体的表面从点 A爬 到点B,需要爬行的最短 距离是多少?
5B
C
20
15
A 10
32
E
5B C
20
15
A 10 F
E C5 B
20
A 10
B5 C 10 E 20
35
A
x
1.5米
1.5米
2.2米
2.2米
1.5米
1.5米
Cx
B
X2=1.52+1.52=4.5
AB2=2.22+X2=9.34
AB≈3米
北师大版数学八年级上册第1章勾股定理单元复习课课件

6. 如图Z1-3所示是由三个直角三角形组成的梯形,根据图形, 写出一个正确的等式:___c_2=_a__2+_b_2___.
7. 已知a,b,c是一组勾股数,把这三个数分别扩大2倍,所得 的三个数还是勾股数吗?扩大k倍呢?验证你的结论. 解:因为2是正整数,a,b,c是一组勾股数, 所以2a,2b,2c都是正整数. 因为a2+b2=c2,所以(2a)2+(2b)2=(2c)2. 所以2a,2b,2c是一组勾股数. 因为a,b,c是一组勾股数,且k是正整数, 所以ak,bk,ck是三个正整数. 因为a2+b2=c2, 所以(ak)2+(bk)2=a2k2+b2k2=(a2+b2)k2=c2k2=(ck)2. 所以ak,bk,ck是一组勾股数.
D. 3
3. 如图Z1-2,由两个直角三角形和三个大正方形组成的图形,
其中阴影部分的面积是( B )
A. 16
B. 25
C. 144
D. 169
4. 在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是 (A )
5. 在△ABC中,∠C=90°,c2=2b2,则两直角边a,b的关系是( )C A. a<b B. a>b C. a=b D. 以上三种情况都有可能
专题2 勾股定理的应用
1. 放学以后,小红和小颖从学校分手,分别沿东南方向和西南方
向回家,若小红和小颖行走的速度都是40 米/分,小红用15分钟
到家,小颖用20分钟到家,则小红和小颖家的直线距离为( C )
A. 600米
B. 800米
C. 1 000米
D. 不能确定
2. 如图Z1-5,圆柱的底面半径是4,高是5,一只在A点的蚂蚁 想吃到B点的食物,需要爬行的最短路径是(π取3)( B ) A. 9 B. 13 C. 14 D. 25
北师大版初中数学八年级上册 第一章 勾股定理 复习 课件

八年级数学上册(北师大版)总复习(一)
勾股定理复习
导学1:
1.勾股定理的内容是什么?
a2+b2=c2
直角三角形两直1.Rt△ABC 的两直角边为3和4,则第三边的平
方__________
2.在Rt△ABC中,∠C=90°, ①若a=5,b=12,则c=___________;
AF2 AB2 BF2
EF2 CE 2 CF 2
(8 x)2 x2 42
8-x
x
4cm
行的最短路程是多少?( 取3)
A
2. 如图 1 分别以 Rt △ABC 三边为边向外作三个正方形, 其面积分别用 S1 、 S2 、 S3 表示,容易得出 S1 、 S2 、 S3
之间有的关系式 _S__2_+__S_3_=S1 ;猜想并证明当分别
以 Rt △ABC 三边为边向外作三个半圆时, S1 、 S2 、 S3 满足的关系式.
(4)三边满足(a+b)2-c2=2ab; 是 (5)∠A:∠B: ∠C=1:3:5 否
2.如图,求阴影部分面积. A
解:连接A,C
O
B 12
C
导学3:
你会用下面的图形验证勾股定理吗?(面积)
ab c
c b
a
中测三:勾股定理运用
1.如图,一油桶高8米,底面直径4米,
B
一只壁虎由A到B吃一害虫,需要爬
②若a=15,c=25,则b=___________; 3.已知直角三角形两直角边分别为5,12,则
第三边上的高为____.
导学2:勾股逆定理
A
b
c
B
aC
中测二:勾股逆定理运用
1.判断满足下列条件的三角形是不是直角三 角形?
勾股定理复习
导学1:
1.勾股定理的内容是什么?
a2+b2=c2
直角三角形两直1.Rt△ABC 的两直角边为3和4,则第三边的平
方__________
2.在Rt△ABC中,∠C=90°, ①若a=5,b=12,则c=___________;
AF2 AB2 BF2
EF2 CE 2 CF 2
(8 x)2 x2 42
8-x
x
4cm
行的最短路程是多少?( 取3)
A
2. 如图 1 分别以 Rt △ABC 三边为边向外作三个正方形, 其面积分别用 S1 、 S2 、 S3 表示,容易得出 S1 、 S2 、 S3
之间有的关系式 _S__2_+__S_3_=S1 ;猜想并证明当分别
以 Rt △ABC 三边为边向外作三个半圆时, S1 、 S2 、 S3 满足的关系式.
(4)三边满足(a+b)2-c2=2ab; 是 (5)∠A:∠B: ∠C=1:3:5 否
2.如图,求阴影部分面积. A
解:连接A,C
O
B 12
C
导学3:
你会用下面的图形验证勾股定理吗?(面积)
ab c
c b
a
中测三:勾股定理运用
1.如图,一油桶高8米,底面直径4米,
B
一只壁虎由A到B吃一害虫,需要爬
②若a=15,c=25,则b=___________; 3.已知直角三角形两直角边分别为5,12,则
第三边上的高为____.
导学2:勾股逆定理
A
b
c
B
aC
中测二:勾股逆定理运用
1.判断满足下列条件的三角形是不是直角三 角形?
北师大版八年级上册 数学第1讲:勾股定理课件 (共19张PPT)

• • 1. 勾股定理. • 【例1】已知△ABC中,AB=17,AC=10,BC边上的高AD=8,则 边BC的长为( ) • A.21 B.15 C.6 D.以上答案都不对. • 练1. 在△ABC中,AB=15,AC=13,BC上的高AD长为12,则 △ABC的面积为( ) • A.84 B.24 C.24或84 D.42或84 • 练2.如图所示,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE, 则AE= • 【例5】如图A,一圆柱体的底面周长为24cm,高 BD为4cm,BC是直径,一只蚂蚁从点D出发沿着圆 柱的表面爬行到点C的最短路程大约是( ) • • A.6cm B.12cm C.13cm D.16cm • • 练5.如图是一个长4m,宽3m,高2m的有盖仓库, 在其内壁的A处(长的四等分)有一只壁虎,B处 (宽的三等分)有一只蚊子,则壁虎爬到蚊子处最 短距离为( )m. • • A.4.8 B. C.5 D.17或
• 5.长方体的长、宽、高分别为8cm,4cm, 5cm.一只蚂蚁沿着长方体的表面从点A爬 到点B.则蚂蚁爬行的最短路径的长是 cm.
• 6.如图所示一棱长为3cm的正方体,把所 有的面均分成3×3个小正方形.其边长都 为1cm,假设一只蚂蚁每秒爬行2cm,则它 从下底面点A沿表面爬行至侧面的B点,最 少要用 秒钟. •
• 7.如图,一个长方体盒子,一只蚂蚁由A 出发,在盒子的表面上爬到点C1,已知 AB=5cm,BC=3cm,CC1=4cm,则这只蚂蚁 爬行的最短路程是 cm.
• 8.如图,今年的冰雪灾害中,一棵大树在 离地面3米处折断,树的顶端落在离树杆底 部4米处,那么这棵树折断之前的高度是 米.
• 9.如图所示的长方体是某种饮料的纸质包 装盒,规格为5×6×10(单位:cm),在 上盖中开有一孔便于插吸管,吸管长为 13cm,小孔到图中边AB距离为1cm,到上 盖中与AB相邻的两边距离相等,设插入吸 管后露在盒外面的管长为hcm,则h的最小 值大约为 cm.
北师大版数学八年级上册全册复习ppt课件

北师大版八年级上册 期末总复习典型题
CONTEN
目T录
第一章 勾股定理 第二章 实数
第三章 位置与坐标 第四章 一次函数
第五章 二元一次方程组
第六章 数据分析 第七章 平行线的证明
第一章 勾股定理
知识归纳
1.勾股定理
定义:如果直角三角形两直角边分别为 a、b,斜边为 c,那么a2+b2=c2
各种表达形式:在 RБайду номын сангаас△ABC 中,∠C=90°,∠A、∠B、∠C 的对边分
找出格点C,使△ABC是面积为1个平方单位的直角三角形,这样
的点有____6____个.
图1-8 图1-9
[解析] 如图1-9,当∠A为直角时,满足面积为1的点是A1、 A2;当∠B为直角时,满足面积为1的点是B1、B2;当∠C为直角 时,满足面积为1的点是C、C1,所以满足条件的点共有6个.
3.已知三角形的三边为 a=34,b=54,c=1,这个三角形是 直角三角形吗?
6.B、C 是河岸边两点,A 为对岸岸上一点,测得∠ABC=45°, ∠ACB=45°,BC=50 m,则河宽 AD 为( )
B
A.25 2 m B.25 m
50 C. 3 3 m
D.25 3 m
图 1-10
7.如图1-11,已知△ABC中,∠C=90°,BA=15,AC=12,
以直角边BC为直径作半圆,则这个半圆的面积是__8_81_π____.
图1-19
15.一个棱长为6的木箱(如图1-20),一只苍蝇位于左面的壁 上,且到该面上两侧棱距离相等的A处.一只蜘蛛位于右面壁上 ,且到该面与上、下底面两交线的距离相等的B处.已知A到下 底面的距离AA′=4,B到一个侧面的距离BB′=4,则蜘蛛沿这 个立方体木箱的内壁爬向苍蝇的最短路程为多少?
CONTEN
目T录
第一章 勾股定理 第二章 实数
第三章 位置与坐标 第四章 一次函数
第五章 二元一次方程组
第六章 数据分析 第七章 平行线的证明
第一章 勾股定理
知识归纳
1.勾股定理
定义:如果直角三角形两直角边分别为 a、b,斜边为 c,那么a2+b2=c2
各种表达形式:在 RБайду номын сангаас△ABC 中,∠C=90°,∠A、∠B、∠C 的对边分
找出格点C,使△ABC是面积为1个平方单位的直角三角形,这样
的点有____6____个.
图1-8 图1-9
[解析] 如图1-9,当∠A为直角时,满足面积为1的点是A1、 A2;当∠B为直角时,满足面积为1的点是B1、B2;当∠C为直角 时,满足面积为1的点是C、C1,所以满足条件的点共有6个.
3.已知三角形的三边为 a=34,b=54,c=1,这个三角形是 直角三角形吗?
6.B、C 是河岸边两点,A 为对岸岸上一点,测得∠ABC=45°, ∠ACB=45°,BC=50 m,则河宽 AD 为( )
B
A.25 2 m B.25 m
50 C. 3 3 m
D.25 3 m
图 1-10
7.如图1-11,已知△ABC中,∠C=90°,BA=15,AC=12,
以直角边BC为直径作半圆,则这个半圆的面积是__8_81_π____.
图1-19
15.一个棱长为6的木箱(如图1-20),一只苍蝇位于左面的壁 上,且到该面上两侧棱距离相等的A处.一只蜘蛛位于右面壁上 ,且到该面与上、下底面两交线的距离相等的B处.已知A到下 底面的距离AA′=4,B到一个侧面的距离BB′=4,则蜘蛛沿这 个立方体木箱的内壁爬向苍蝇的最短路程为多少?
北师大版八年级数学上册第一章全部课件

总结
勾股定理的验证主要是通过拼图法利用面积的 关系完成的,拼图又常以补拼法和叠合法两种方式拼 图,补拼是要无重叠,叠合是要无空隙;而用面积法 验证的关键是要找到一些特殊图形(如直角三角形、 正方形、梯形)的面积之和等于整个图形的面积,从 而达到验证的目的.
(来自《点拨》)
知1-练
1 用四个边长均为a,b,c的直角三角板,拼成如
(来自《典中点》)
知2-导
知识点 2 勾股定理的应用
例2 我方侦察员小王在距离东西向公路400m处侦察,发现一 辆敌方汽车在公路上疾驰.他赶紧拿出红外测距仪,测得 汽车与他相距400m,10s后,汽车与他相距500m,你能 帮小王计算敌方汽车的速度吗?
分析:根据题意,可以画出右图, 其中点A表示小王所在位置, 点C、点B表示两个时刻敌方 汽车的位置.
弦 勾
股 图1
北师大版八年级数学上册
C A
B C
图2-1
A
B
图2-2
(图中每个小方格代表一个单位面积)
知1-导
(1)观察图2-1 正方形A中含有 9 个 小方格,即A的面积 是 9 个单位面积. 正方形B的面积是 9 个单位面积.
正方形C的面积是 18 个单位面积.
北师大版八年级数学上册
C A
B C
(来自《点拨》)
知1-讲
总结
勾股定理的验证主要是通过拼图法利用面积的 关系完成的,拼图又常以补拼法和叠合法两种方式拼 图,补拼是要无重叠,叠合是要无空隙;而用面积法 验证的关键是要找到一些特殊图形(如直角三角形、 正方形、梯形)的面积之和等于整个图形的面积,从 而达到验证的目的.
(来自《点拨》)
知1-讲
1 课堂讲解 2 课时流程
勾股定理的验证主要是通过拼图法利用面积的 关系完成的,拼图又常以补拼法和叠合法两种方式拼 图,补拼是要无重叠,叠合是要无空隙;而用面积法 验证的关键是要找到一些特殊图形(如直角三角形、 正方形、梯形)的面积之和等于整个图形的面积,从 而达到验证的目的.
(来自《点拨》)
知1-练
1 用四个边长均为a,b,c的直角三角板,拼成如
(来自《典中点》)
知2-导
知识点 2 勾股定理的应用
例2 我方侦察员小王在距离东西向公路400m处侦察,发现一 辆敌方汽车在公路上疾驰.他赶紧拿出红外测距仪,测得 汽车与他相距400m,10s后,汽车与他相距500m,你能 帮小王计算敌方汽车的速度吗?
分析:根据题意,可以画出右图, 其中点A表示小王所在位置, 点C、点B表示两个时刻敌方 汽车的位置.
弦 勾
股 图1
北师大版八年级数学上册
C A
B C
图2-1
A
B
图2-2
(图中每个小方格代表一个单位面积)
知1-导
(1)观察图2-1 正方形A中含有 9 个 小方格,即A的面积 是 9 个单位面积. 正方形B的面积是 9 个单位面积.
正方形C的面积是 18 个单位面积.
北师大版八年级数学上册
C A
B C
(来自《点拨》)
知1-讲
总结
勾股定理的验证主要是通过拼图法利用面积的 关系完成的,拼图又常以补拼法和叠合法两种方式拼 图,补拼是要无重叠,叠合是要无空隙;而用面积法 验证的关键是要找到一些特殊图形(如直角三角形、 正方形、梯形)的面积之和等于整个图形的面积,从 而达到验证的目的.
(来自《点拨》)
知1-讲
1 课堂讲解 2 课时流程
北师大版初中八年级上册数学:第一章 勾股定理 复习课件

1m
x (x+1)
3
在一棵树的10米高处B有两只猴子, 其中一只猴子爬下树走到离树20米的池 塘A,另一只猴子爬到树顶D后直接跃向 池塘的A处,如果两只猴子所经过距离 相等,试问这棵树有多高?
D B.
C
A
专题三 折叠
折叠和轴对称密不可分,利用折叠前 后图形全等,找到对应边、对应角相等便 可顺利解决折叠问题。
第一章 勾股定理 复习课件
一、知识要点
一、勾股定理的发现
勾股定理:直角R三角形两A 直角边的平方 和等于斜边的平方。 Q
B
C
P
勾股定理
如果直角三角形两直角边分别为a,b,斜 边为c,那么:
a2+ b2=c2
即直角三角形两直角边的平方和等于斜边的平方。
二、勾股定理的证明
b
c
a
b
a
a
c
c
b
c
b
c
a
1.几何体的内部路径最值的问题,一般画出 几何体截面。 2.利用两点之间线段最短及勾股定理求解。
小明家住在18层的高楼,一天,他与妈妈去买竹竿。
买最长 的吧!
快点回家, 好用它凉衣
服。
糟糕,太 长了,放 不进去。
如果电梯的长、宽、高分别是1.5米、1.5米、2.2米, 那么,能放入电梯内的竹竿的最大长度大约是多少米?你能 估计出小明买的竹竿至少是多少米吗?
B
例4:如图,长方体的
长为15cm,宽为10 cm,高
为20cm,点B离点C5cm,
一只蚂蚁如果要沿着长方
体的表面从点A爬到点B,
需要爬行的最短距离是多
少?
A
5B
C
20
x (x+1)
3
在一棵树的10米高处B有两只猴子, 其中一只猴子爬下树走到离树20米的池 塘A,另一只猴子爬到树顶D后直接跃向 池塘的A处,如果两只猴子所经过距离 相等,试问这棵树有多高?
D B.
C
A
专题三 折叠
折叠和轴对称密不可分,利用折叠前 后图形全等,找到对应边、对应角相等便 可顺利解决折叠问题。
第一章 勾股定理 复习课件
一、知识要点
一、勾股定理的发现
勾股定理:直角R三角形两A 直角边的平方 和等于斜边的平方。 Q
B
C
P
勾股定理
如果直角三角形两直角边分别为a,b,斜 边为c,那么:
a2+ b2=c2
即直角三角形两直角边的平方和等于斜边的平方。
二、勾股定理的证明
b
c
a
b
a
a
c
c
b
c
b
c
a
1.几何体的内部路径最值的问题,一般画出 几何体截面。 2.利用两点之间线段最短及勾股定理求解。
小明家住在18层的高楼,一天,他与妈妈去买竹竿。
买最长 的吧!
快点回家, 好用它凉衣
服。
糟糕,太 长了,放 不进去。
如果电梯的长、宽、高分别是1.5米、1.5米、2.2米, 那么,能放入电梯内的竹竿的最大长度大约是多少米?你能 估计出小明买的竹竿至少是多少米吗?
B
例4:如图,长方体的
长为15cm,宽为10 cm,高
为20cm,点B离点C5cm,
一只蚂蚁如果要沿着长方
体的表面从点A爬到点B,
需要爬行的最短距离是多
少?
A
5B
C
20
北师大版八年级上册 第一章 勾股定理总复习课件 (共44张PPT)

6.一艘轮船以20海里/小时的速度离开港口O向东 北方向航行,另一艘轮船同时以15海里/小时的速 度离开港口向东南方向航行,2小时后两船相距多 远?
北
甲(A)
西
O
东
南
乙(B)
•9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。2021/9/62021/9/6Monday, September 06, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/9/62021/9/62021/9/69/6/2021 2:21:03 PM •11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/9/62021/9/62021/9/6Sep-216-Sep-21 •12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/9/62021/9/62021/9/6Monday, September 06, 2021
122 32 42 169
AB13
The end,thank you!
24
小试牛刀
练习1 练习2 练习3
4.如图,台阶A处的蚂蚁要
爬到B处搬运食物,求出它走的
最近距离。
20
B
3
2
A
AB 2152202625252
最近距 25离为
一、在数轴上表示无理数
数轴上的点有的表示有理数,有的表示
无理数,你能在数轴上画出表示 13 的
C. a:b:c2:2:3 D. a2b2 c2
9.已知 x12y13(z5)2 0,则以 x,y,z为边长的三_角 直_角_三形 _角_形是 __
北师大版八年级上册第一章勾股定理 复习 课件 (共20张PPT)

感恩你的陪伴, 相约下一段旅程!
立体图形
平面图形
做中感悟(一)
3.若直角三角形的三边长分别是6,8,x , 分类
则 x = 10或2 7 . 解析:两种可能 当第三边为斜边时, x= 62 82 =10 当第三边为直角边时, x= 8262= 28=2 7
智慧锦囊(一)
三个题目有什么共同特点?
已知直角三角形的两边 求第三边
做中感悟(二)
解:设BN=x 由折叠可得 DN=AN=9-x ∵D是BC的中点 ,BC=6 ∴BD=3 在Rt△DBN中, 由勾股定理得
DN2 =BD2+BN2 则(9-x)2=32+x2 解得 x=4 故线段BN的长为4.
方程思想智慧锦囊(二)方源自思想两个题目有什么共同特点?
已知直角三角形一边及另两 边的关系,求未知边长
边: 若三角形三边满足a2+b2=c2
是直角三角形
做中感悟(一)
S阴影部分 S S = 正方形ABCD - △ABE
1.如图,点E在正方形ABCD内, 满足∠AEB=90°, AE=5,BE=6,则阴影部分的面积是 46 .
解析:在Rt△ABE中,由勾股定理得 AB2=AE2+BE2=52+62 =61
的负半轴上,若将△DAB沿直线AD折叠,点B恰好落
在x轴正半轴上的点C处.
(1)A点的坐标是 ,B点的坐标 .
(2)求AB的长和点C的坐标.
(3)求直线CD的解析式.
A CB
3.乐凯中学有一块三角形劳动基地,量得两边长分别为40m,50m,第三 边上的高为30m,请你帮忙计算这块劳动基地的面积(结果保留根号)。
将未知量AB的高度设为xm ,则未知量AC=(x+1)m 又已知CB=5m 在Rt△ABC中,由勾股定理得 AC2=AB2+BC2 则有(x+1)2=x2+52 解得 x=12
北师大版八年级数学上册 (探索勾股定理)勾股定理教育教学课件

“弦高公式”,它常与勾股定理联合使用.
C
4
B
3.阴影部分是一个正方形,则此正方形的面积为
常用数据: 112=121 122=144 132=169 142=196 152=225 162=256 172=289 182=324 192=361
15 cm 17 cm
64.cm²
4.求出图中直角三角形第三边的长度.
a2 b2 c2
三、得出结论:勾股定理
直角三角形两直角边的平方和等于斜边的平方,如果用a,b,c 分别表示直角三角形的两直角边和斜边,那么
a2 b2 c2
B
几何语言:
c
a
∵在Rt △ABC,∠C=90°
C
b
A
∴a2+b2=c2
说明:勾股定理的应用条件是在直角三角形中;勾股定理是刻画 直角三角形三边平方的关系.
趣味小常识
直角三角形中 较短的直角边称为 勾 ,
较长的直角边称为 股 ,
在中国古代,
斜边称为 弦 .
人们把弯曲成直角
的手臂的上半部分 勾
弦
称为“勾”,下半
部分称为“股”.
(在西方称为毕达
股
勾2 + 股2 = 弦2
哥拉斯定理)
a2 b2 c2
四、探究活动
观察图片,分别求出正方形A,B,C的面积。
2. 思考:任意一个的直角三角形都满足你 所猜测的规律吗?用网格纸中画的直角三角 形尝试证明一下吧?
语言表述: 几何表示:
勾股定理 P3
A c
b
C
a
B
赵爽弦图
2002年国际数学家大会会标
1. 从这个会标中你能证明你的猜想吗?如何证明? 你的思路是什么? 2. 给四个完全一样的直角三角线,你能否把它们 拼成正方形?能同样推导出勾股定理吗?
北师版八年级上册第一章勾股定理的复习课件

B
பைடு நூலகம்
3
C
A
B
C
4
O
o
A
D
A
D
折叠问题
1、矩形纸片ABCD中,AD=4cm,AB=10cm,按 如图方式折叠,折痕是EF,求DE的长度?
E
A
B
D
(B)
FC
(C)
例1:折叠矩形ABCD的一边AD,点D落在
BC边上的点F处,已知AB=8CM,BC=10CM,
求 1.CF 2.EC. 10
D
A
8-X
8 10
26 A
B
10
24
C
五、勾股定理的综合运用
勾股定理与其逆定理综合的问题
1.如图,在四边形ABCD中,∠B= 90◦
AB=BC=4,CD=6,AD=2,求四边形ABCD的面积。
D
A
B
C
x z y 已知 x 6 y 8 z 102 0 ,则由
、
、
为三边的三角形是 三角形。
若△ABC的三边a、b、c满足 a2-6a+9+(b-4)2+(c-5)2=0,
E
8-X X
B
6
F4 C
一、情景导入
从行政
行政楼
楼A点走
教 学B 楼
A
到教学
楼B点怎
样走最
近?
你能说出
这样走的
理由吗?
在同一平面内,两点之间,线段最短
如图,学校有一块长方形花园,有极少数人
为了躲开拐角走“捷径”,在花园内走出了
一条“路”,仅仅少走了____4____步路, 却
踩伤了花草。 (假设1米为2步)
北师大版八年级数学上册课件1.1 探索勾股定理(第2课时) 勾股定理的验证及应用课件(26张PPT)

= 25 km .现要在铁路旁建一个农副产品收购站 ,使 站到 ,
两村的距离相等.你知道应该把 站建在距点 多远的地方吗?
【点拨】设 = km ,由垂直关系可以想到用勾股定理,根据 = 建立方程,
即可使问题得解.
【解】因为 = ,
所以 2 + 2 = 2 + 2 .
当它听到巢中幼鸟的叫声时,立即赶过去.如果它飞行的速度
为 5 m/s ,那么它至少需要多少时间才能赶回巢中?
解:如图,
由题意知 = 3 , = 14 − 1 = 13 , = 24 .
过点 作 ⊥ 于点 ,则 = 13 − 3 = 10 , = 24 .
答:教学楼走廊的宽度是 2.2 m .
作业布置
完成学生书对应课时练习
算,从理论上验证了勾股定理.
做一做
在纸上画一个直角三角形,分别以这个直角三角形的三边为边长向
外作正方形。
c
b
a
图1-4
为了方便计算图中大正方形的面积,
C
D
对其进行适当割补:
b
S正方形ABCD= c2+2ab=(a+b)2
c
A
B
a
c2=a2+b2
图1-5
D
b
c
a
图1-6
A
C
B
S正方形ABCD= c2-2ab=(b-a)2
第一章 勾股定理
1.1 探索勾股定理
第2课时 勾股定理的验证及应用
1.探索勾股定理
2.掌握勾股定理的内容,会用面积法验证勾股定理.
3.能运用勾股定理解决一些简单的实际问题.
探究新知
两村的距离相等.你知道应该把 站建在距点 多远的地方吗?
【点拨】设 = km ,由垂直关系可以想到用勾股定理,根据 = 建立方程,
即可使问题得解.
【解】因为 = ,
所以 2 + 2 = 2 + 2 .
当它听到巢中幼鸟的叫声时,立即赶过去.如果它飞行的速度
为 5 m/s ,那么它至少需要多少时间才能赶回巢中?
解:如图,
由题意知 = 3 , = 14 − 1 = 13 , = 24 .
过点 作 ⊥ 于点 ,则 = 13 − 3 = 10 , = 24 .
答:教学楼走廊的宽度是 2.2 m .
作业布置
完成学生书对应课时练习
算,从理论上验证了勾股定理.
做一做
在纸上画一个直角三角形,分别以这个直角三角形的三边为边长向
外作正方形。
c
b
a
图1-4
为了方便计算图中大正方形的面积,
C
D
对其进行适当割补:
b
S正方形ABCD= c2+2ab=(a+b)2
c
A
B
a
c2=a2+b2
图1-5
D
b
c
a
图1-6
A
C
B
S正方形ABCD= c2-2ab=(b-a)2
第一章 勾股定理
1.1 探索勾股定理
第2课时 勾股定理的验证及应用
1.探索勾股定理
2.掌握勾股定理的内容,会用面积法验证勾股定理.
3.能运用勾股定理解决一些简单的实际问题.
探究新知
北师大版八年级数学上册《勾股定理》复习课教学课件

北师大版八年级数学上册第一章《勾 股定理 》复习 课 课件 北师大版八年级数学上册第一章《勾 股定理 》复习 课 课件
北师大版八年级数学上册第一章《勾 股定理 》复习 课 课件
三、典例分析
例1、(1)已知直角三角形的两条直角边为 6cm和8cm,斜边是___1_0_c_m__, 则斜边上的高是 _4__.8_c_m__。 (2)若直角三角形的三边长分别为3、 6、x, 则x2=___4__5_或_2_7___。(分类思想)
新北师大版
八年级上册第一章 勾股定理复习
一、导课
商高,西周初数学家。商高在公元前 1000年发现勾股定理并完成证明。此发现 早于毕达哥拉斯定理五百到六百年。勾股定 理是中国数学家的独立发现,在中国早有记 载。勾股定理,我们把它称为世界第一定理。 勾股定理是我们数学史的奇迹,我们已经比 较完整地研究了这个先人给我们留下来的宝 贵的财富,这节课,我们将通过回顾与思考 中的几个问题更进一步了解勾股定理的应用。
六、当堂检测
1.在Rt△ABC中,∠C=90°,
2. ①若a=5,b=12,则c=___1_3_______; 3. ②若a=15,c=25,则b=__2_0________; 4. ③若c=61,b=60,则a=__1_1_______; 5.下列各组数中为勾股数的一组是( D )
A、7、12、13;B、1.5、2、2.5 C、3、4、7 D、8、15、17 3. 有一块田地的形状和尺寸如图所示,试求它的面积。
勾股定理的逆定理是判定一 个三角形是否是直角三角形 的一种重要方法,它通过 “数转化为形”来确定三角 形的可能形状,
北师大版八年级数学上册第一章《勾 股定理 》复习 课 课件
北师大版八年级数学上册第一章《勾 股定理 》复习 课 课件
北师大版数学八年级上册第一章《勾股定理》复习课件

BC=15 20
3 2 3 2 3 2
专题四 转化思想(将军饮马)
5.如图,A,B两个小镇在河岸l的同侧,到河岸的距离分别为AC= 10 ,BD=30 ,且CD=30 ,现在要在河边建一自来水厂,向A,B两 镇供水,铺设水管的费用为每千米3万元.请你在河岸l上选择自来水 厂的位置M,使铺设水管的费用最节省,并求出最少的费用是多少.
A.13 B.26 C.47 D.94
2、如图,直线l上由三个正方形a,b,c,若a,c的面积分别为5 和11,则b 的面积为 .
3、如图,在Rt△ABC中,AC=6,BC=8,分别以它的三边为直径作
B
A
例2:如图,正方体的棱长为5cm,一只蚂蚁欲从正方体底面上的
顶点A沿正方体的表面到顶点C′处吃食物,那么它需要爬行的最短
路程的长是多少?
C′
D′
C′
A′
B′
D
C
A
B
A
B
例3.有一个牛奶盒,把小蚂蚁放在点A处,并在点B处放了点儿火 腿肠粒,你能帮小蚂蚁找出吃到火腿肠粒的最短路线吗?
解:由题意知有三种展开方法,如 图.由勾股定理得
例3 如图,在 ABC中,D是BC边上一点,若AB=10,BD=6,AD=8,AC=17.求 ABC的周长和面积.
判定 ABD、 ACD
在Rt ACD中已知
已知三边求周长,
A
为直角三角形
两边求第三边
已知底和高求面
积。
B
D
C
练习:装修工人购买了一根装饰用的木条,乘电梯到小明家安装, 如果电梯的长、宽、高分别是1.5m, 1.5m, 2.2m,那么能放入电梯 内的木条的最大长度大约是多少米?你能估计出装修工人买的木条 至少是多少米吗?
3 2 3 2 3 2
专题四 转化思想(将军饮马)
5.如图,A,B两个小镇在河岸l的同侧,到河岸的距离分别为AC= 10 ,BD=30 ,且CD=30 ,现在要在河边建一自来水厂,向A,B两 镇供水,铺设水管的费用为每千米3万元.请你在河岸l上选择自来水 厂的位置M,使铺设水管的费用最节省,并求出最少的费用是多少.
A.13 B.26 C.47 D.94
2、如图,直线l上由三个正方形a,b,c,若a,c的面积分别为5 和11,则b 的面积为 .
3、如图,在Rt△ABC中,AC=6,BC=8,分别以它的三边为直径作
B
A
例2:如图,正方体的棱长为5cm,一只蚂蚁欲从正方体底面上的
顶点A沿正方体的表面到顶点C′处吃食物,那么它需要爬行的最短
路程的长是多少?
C′
D′
C′
A′
B′
D
C
A
B
A
B
例3.有一个牛奶盒,把小蚂蚁放在点A处,并在点B处放了点儿火 腿肠粒,你能帮小蚂蚁找出吃到火腿肠粒的最短路线吗?
解:由题意知有三种展开方法,如 图.由勾股定理得
例3 如图,在 ABC中,D是BC边上一点,若AB=10,BD=6,AD=8,AC=17.求 ABC的周长和面积.
判定 ABD、 ACD
在Rt ACD中已知
已知三边求周长,
A
为直角三角形
两边求第三边
已知底和高求面
积。
B
D
C
练习:装修工人购买了一根装饰用的木条,乘电梯到小明家安装, 如果电梯的长、宽、高分别是1.5m, 1.5m, 2.2m,那么能放入电梯 内的木条的最大长度大约是多少米?你能估计出装修工人买的木条 至少是多少米吗?
八年级数学北师大版上册课件:第1章 1.探索勾股定理(共16张PPT)
A.6 米 C.6.8 米
B.8.4 米 D.9.6 米
•9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。2021/9/102021/9/10Friday, September 10, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/9/102021/9/102021/9/109/10/2021 6:17:32 AM •11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/9/102021/9/102021/9/10Sep-2110-Sep-21 •12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/9/102021/9/102021/9/10Friday, September 10, 2021
13.如图,居民小区内有一块边长 AC=60 米的正方形草坪,在草坪 B 处有 健身器材,有的居民从 A 处去 B 处锻炼身体时,为了贪近,在草坪内踏出一 条路 AB,居委会王大妈想在 A 处立一个写有“少走 米,踏之何忍”的警 示牌,她在 处填上适当的数字应是 十 .
14.如图,直线 l 上有三个正方形 a、b、c,若 a、c 的面积为 5 和 11,则 b 的面积为 16 .
5.∴BD=10+x=15 m.
答:这棵树高 15 m.
13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成。2021/9/102021/9/102021/9/102021/9/109/10/2021 •14、谁要是自己还没有发展培养和教育好,他就不能发展培养和教育别人。2021年9月10日星期五2021/9/102021/9/102021/9/10 •15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年9月2021/9/102021/9/102021/9/109/10/2021 •16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021/9/102021/9/10September 10, 2021 •17、儿童是中心,教育的措施便围绕他们而组织起来。2021/9/102021/9/102021/9/102021/9/10
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
A
综合训练: 1.一个直角三角形周长为60, 一直角边与斜边之比为4:5, 则此三角形三边分别为 __________ 2.如图,求半圆面积 (结果保留 ).
6 6
3.如图,两个正方形面积 分别为64,49,则 AB=______
A B
一架云梯长25米,斜靠在 一面墙上,梯子底端离墙7 米,如果梯子顶端下滑4米, 则梯子底部在水平方向上 滑动几米?
问题导学: 1.勾股定理的内容是什么? 导学检测: 1〉直角三角形三边长为6,8,x,则 x=_______. 10或2 7
2.已知直角三角形两直角边分别为
8 2113 5,12,则三边上的高的和为____.
问题导学: 2.你会用下面的图形验证勾股定 理吗? a c a b b c
1.利用勾股定理验证三个 半圆面积之间的关系 SA+SB=SC
A C B
2.如图两阴 影部分都是 正方形,若它 们面积之比 为1:3,则它 们的面积分 9和7 别为___
问题导学: 3.如果一个三角形三边为a,b,c, 满足_________,则这个三角 形是 直角三角形. 4.四根长度分别为3,4,5,6的 木棒,取其中三根组成三角形, 4 有__种取法,能构成直角三 3,4,5 角形的是________
4.一直角三角 形纸片直角边 AC=6,BC=8, A 现将直角边 AC沿AD折叠, 使C与E重合, C 则CD=____.
E D B
5.折叠矩形的一边AD,使点 D落在点F处,已知 AB=8cm,BC=10cm,求EC.
A D E B F C
2.判断满足下列条件的三角形是不 是直角三角形? (1)△ABC中, A=15 , B=75 ; (2) ABC ,a=12,b=16,c=20; (2)△ABC中,a=12,b=16,c=20; (3)三边满足a -b =c ; (4)三边满足(a+b)2-c2=2ab; (5) A: B: C=1:5:6
2 2 2 o o
3.如图,求阴影部分面积.
12
问题导学四: 立体图形中线路最短问题, 通常把立体图形的表面 展开 平面 ____,得到____图形后, 运用勾股定理或逆定理解 决.
1.如图,一油桶高4米,底面 直径2米,一只壁虎由A到 B吃一害虫,需要爬行的最 短路程是多少?
B A
2.一长方体长宽高分别为 30cm,10cm,30cm,求A到 B的最短路程?
勾股定理复习
学习目标: 学习目标 1.掌握勾股定理 会用拼图法验证 掌握勾股定理,会用 掌握勾股定理 会用拼图法验证 勾股定理. 勾股定理 2.能应用勾股定理解决实际问题 能应用勾股定理解决实际问题. 能应用勾股定理解决实际问题 3.掌握判断一个三角形是 掌握判断一个三角形是 直角三角形的条件. 直角三角形的条件
A
综合训练: 1.一个直角三角形周长为60, 一直角边与斜边之比为4:5, 则此三角形三边分别为 __________ 2.如图,求半圆面积 (结果保留 ).
6 6
3.如图,两个正方形面积 分别为64,49,则 AB=______
A B
一架云梯长25米,斜靠在 一面墙上,梯子底端离墙7 米,如果梯子顶端下滑4米, 则梯子底部在水平方向上 滑动几米?
问题导学: 1.勾股定理的内容是什么? 导学检测: 1〉直角三角形三边长为6,8,x,则 x=_______. 10或2 7
2.已知直角三角形两直角边分别为
8 2113 5,12,则三边上的高的和为____.
问题导学: 2.你会用下面的图形验证勾股定 理吗? a c a b b c
1.利用勾股定理验证三个 半圆面积之间的关系 SA+SB=SC
A C B
2.如图两阴 影部分都是 正方形,若它 们面积之比 为1:3,则它 们的面积分 9和7 别为___
问题导学: 3.如果一个三角形三边为a,b,c, 满足_________,则这个三角 形是 直角三角形. 4.四根长度分别为3,4,5,6的 木棒,取其中三根组成三角形, 4 有__种取法,能构成直角三 3,4,5 角形的是________
4.一直角三角 形纸片直角边 AC=6,BC=8, A 现将直角边 AC沿AD折叠, 使C与E重合, C 则CD=____.
E D B
5.折叠矩形的一边AD,使点 D落在点F处,已知 AB=8cm,BC=10cm,求EC.
A D E B F C
2.判断满足下列条件的三角形是不 是直角三角形? (1)△ABC中, A=15 , B=75 ; (2) ABC ,a=12,b=16,c=20; (2)△ABC中,a=12,b=16,c=20; (3)三边满足a -b =c ; (4)三边满足(a+b)2-c2=2ab; (5) A: B: C=1:5:6
2 2 2 o o
3.如图,求阴影部分面积.
12
问题导学四: 立体图形中线路最短问题, 通常把立体图形的表面 展开 平面 ____,得到____图形后, 运用勾股定理或逆定理解 决.
1.如图,一油桶高4米,底面 直径2米,一只壁虎由A到 B吃一害虫,需要爬行的最 短路程是多少?
B A
2.一长方体长宽高分别为 30cm,10cm,30cm,求A到 B的最短路程?
勾股定理复习
学习目标: 学习目标 1.掌握勾股定理 会用拼图法验证 掌握勾股定理,会用 掌握勾股定理 会用拼图法验证 勾股定理. 勾股定理 2.能应用勾股定理解决实际问题 能应用勾股定理解决实际问题. 能应用勾股定理解决实际问题 3.掌握判断一个三角形是 掌握判断一个三角形是 直角三角形的条件. 直角三角形的条件
