北大数分讲义实数理论
《实数》 讲义

《实数》讲义一、实数的概念实数,这个在数学世界中极为基础且重要的概念,是我们理解数量关系和解决数学问题的关键。
简单来说,实数就是包括有理数和无理数的数集。
有理数,我们都很熟悉,像整数(正整数、零、负整数)和分数(正分数、负分数)都属于有理数。
而无理数呢,则是那些无限不循环小数,比如大家熟知的圆周率π,还有根号 2 等等。
实数可以直观地理解为在数轴上能找到对应点的数。
也就是说,数轴上的每一个点都代表着一个实数,反之,每一个实数也都能在数轴上找到对应的点。
二、有理数有理数是实数的重要组成部分。
整数,像-3、0、5 这样的数,它们没有小数部分,清晰明了。
分数呢,比如 1/2、3/4 ,可以表示为两个整数的比值。
有理数具有一些很重要的性质。
比如,两个有理数相加、相减、相乘或相除(除数不为 0),结果仍然是有理数。
而且,有理数是可以用有限小数或无限循环小数来表示的。
我们在日常生活中,很多常见的数量关系都可以用有理数来描述。
比如购物时的价格、物品的数量等等。
三、无理数无理数虽然不像有理数那样“规矩”,但在数学中同样不可或缺。
像根号 2 ,它的值约为 141421356……,这个小数无限且不循环。
圆周率π,约为31415926……,也是一个无限不循环小数。
无理数的发现,让人们对数学的认识更加深入和丰富。
虽然它们的数值看起来没有规律,但通过数学方法和计算,我们可以对它们进行近似和研究。
四、实数的运算实数的运算包括加法、减法、乘法、除法和乘方等。
加法和减法:实数的加法和减法遵循相同的规则,即将对应位上的数字相加或相减,并考虑进位和借位。
乘法:两个实数相乘,先将它们按照整数乘法的规则相乘,然后确定积的符号(同号得正,异号得负),最后根据小数位数确定积的小数点位置。
除法:将除数变为倒数,然后与被除数相乘。
乘方:一个实数的 n 次幂,就是将这个实数乘以自身 n 次。
在进行实数运算时,要特别注意运算顺序,先算乘方、开方,再算乘除,最后算加减。
北京大学版高等数学讲义1-1实数

1-1 实数 1. 有理数和无理数
集合 我们把具有某种特定性质的事物所组 成的总体称为一个集合。 成的总体称为一个集合。 组成这个集合的事物称为该集合的元素。 组成这个集合的事物称为该集合的元素。
A = {a1 , a 2 , L , a n }
M = { x x所具有的特征 } a ∈ M ,
证
2. 实数集合 的基本性质 实数集合R的基本性质 (1) R是一个数域 是一个数域 (2) 对乘法与加法满足交换律 结合律与分配律 对乘法与加法满足交换律,结合律与分配律 (3) 有序性 (4) 完备性 (连续性 连续性) 连续性 在实数域中,任意一个单调有界序列一定有极限 在实数域中 任意一个单调有界序列一定有极限
x − a < r ⇔ a − r < x < a + r.
1.设( a, b) 为任意的一个开区间,证明:( a, b)中必有有理数
2.设( a, b) 为任意的一个开区间,证明:( a, b)中必有无理数
序列 {an }有界 ⇔ 有 M > 0 使得 an ≤ M , n = 1, 2,L
an ≤ an +1 , {an }单调递增 a ≥ a , {a }单调递减 单调递增; n n+1 n
3. 数轴与区间
区间
数轴R ( −∞, +∞ )
介于某两个实数之间的全体实数构成 区间.这两个实数叫做区间的端点 这两个实数叫做区间的端点. 区间 这两个实数叫做区间的端点
若 a, b ∈ R, 且a < b.
开区间
{ x a < x < b}
o a
记作 (a , b )
闭区间
x b { x a ≤ x ≤ b} 记作 [a , b]
八年级数学 第三章 实数综合解说-北师大版

八年级数学第三章实数综合解说学习目标1 让同学们经历数系扩张、探求实数性质其运算规律的过程;从事借助计算器探索数学规律的活动,发展同学们的现象概括能力,并在活动中进一步发展同学们独立思考、合作交流的意识和能力。
2 结合具体情境,让同学们理解估算的意义,掌握估算的方法,发展同学们的数感和估算能力。
3 了解平方根、立方根、实数及其相关概念;会用根号表示并会求数的平方根、立方根;能进行有关实数的简单四则运算。
4能运用实数的运算解决简单的实际问题,提高同学们的应用意识,发展同学们解决问题的能力,从中体会数学的应用价值。
学法建议从有理数扩展到实数是第三段数系扩张的最后一个阶段,中学阶段的多数问题是在实数范围内进行的,同时实数也是后继内容学习(如一元二次方程、函数等)的基础。
人类对数的认识实在生活中不断加深和发展的,数系的每一次扩张都源于实际生活的需要。
同学们在六年级上学期已经经历了数系的第一次扩张在小学非负有理数知识的基础上引进负数,对数的了解扩充到有理数的范围,并学习了有理数的运算,本章在有理数和勾股定理等知识的基础上,进行熟悉的第二次扩张。
本章大致按照这样的线索展开内容;无理数的引用无理数的表示实数及其相关概念(包括实数运算),实数的应用贯穿于内容的始终。
具体地,本章首先通过拼图活动和计算器探索活动,给出无理数的概念,然后通过具体问题的解决,引入平方根和立方根的概念和开方运算,由于在实际生活中,对于无理数我们常常通过估算来求它的近似值,为此课本安排了一节内容:公园有多宽,介绍估算的方法,包括通过估算比较大小、检验计算数的相关概念、运算律和运算法则等。
在呈现具体内容时,课本继承了本套教材的一贯风格,关注现实性,力求从同学们的实际出发,以他们熟悉或感兴趣的问题情境引入学习主题,如大正方形的边长a是多少,公园有多宽等。
但考虑到本章的特点,以及随着同学们年龄的增长,他们的思维水平也在不断提高,因此本章在关注现实性的同时更加关注数学知识内部的挑战性,为此提供了许多有趣而富有数学含义的问题,如a可能是整数吗,a可能是分数吗,等等,让同学们进行数学思考与探索,进一步发展同学们的抽象思维水平。
实数初步(二)北师版初二数学上册讲义知识教案

实数初步(二)对应,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数。
实数有理数[正整数]I【例1】⑴在-0.3i,|,-V81,|,-V27,3.14,77,0.4829,1.020020002 •••,-洒,-扣房中无理数个。
⑵求下列各数的相反数及绝对值:①瑚②勿— 3.14③1-扳④V3-2整数<0.负整数•正分数.负分数[正无理数' 负无理数分数无理数,有限小数或无限循环小数无限不循环小数⑶已知x是4的平方根,y[y = -2,V15= z, 求x + 2y — z的值。
【例2】⑴如图所示,在点4和点8之间表示整数的点共有个。
A BI I I-V3 0 ^5【例3】⑴若ZW = A/40-4,则估计的范围是【易错门诊】平方等于本身的实数是; 平方根等于本身的实数是;立方等于本身的实数是; 立方根等于本身的实数是;【例4】若x、V分别是8-应整数部分与小数部分,求^xy-y1的值。
-Jn-lm + l +|16-m2|【例5]⑴已知 ----- ---------- =0,y/4-m则mn + n-2的倒数的算术平方根为⑵若m适合关系式。
』3x + 5y -2-m ++ 3y-m=Jx -199 + y • J199 - x - y,则o 【例6】已知M是满足不等式有整数口的和,N是满足不等式xW—-—的最大整数,求M+N的平方根。
I ⑵如图所示,数轴上表示1, Vi的对应点分别为,、B,I成C到点4的距离与点B到点4的距离相等,则C所表示的数是。
o C A BI _________ I I I )0 1 Vi 2⑵若实数VI的整数部分是3,则A的取值范围是【例7】⑴若龙为正整数,且Vi矿由是整数,试求性的值。
⑵若走为正整数,且面詩是整数,试求”的最小值。
实数北师大版八年级数学上册PPT精品课件2

A. ①②③ C. ②③⑤
B. ②③④ D. ②④⑤
三级拓展延伸练
14. 在一个半径为20 cm的圆形铁板上,截取一个面积 最大的长方形,且该长方形的长是宽的2倍,求长方形 的长和宽.
解:设长方形的宽为x cm,则长为2x cm.
若使长方形的面积最大,则长方形的对角线是圆
的直径.
所以x2+(2x)2=402,所以x=
●
7.文学本身就是将自己生命的感动凝 固成文 字,去 唤醒那 沉睡的 情感, 饥渴的 灵魂, 也许已 是跨越 千年, 但那人 间的真 情却亘 古不变 ,故事 仿佛就 在昨日 一般亲 切,光 芒没有 丝毫的 暗淡减 损。
●
8.只要我们用心去聆听,用情去触摸 ,你终 会感受 到生命 的鲜活 ,人性 的光辉 ,智慧 的温暖 。
7. 如图所示,已知OA=OB,则数轴上点A表示的数
是
.
8. 实数a,b,c是数轴上三点A,B,C所对应的数,
如图,化简:
.
三级检测练
一级基础巩固练
9. 计算与求值:
(1)计算:
;
(2)求x的值:4x2-25=0.
解:(1)原式=1+5-3-0.5=2.5.
(2)∵4x2-25=0,∴x2=
●
9.能准确 、有感 情的朗 读诗歌 ,领会 丰富的 内涵, 体会诗 作蕴涵 的思想 感情。
●
5.以景物 衬托情 思,以 幻境刻 画心理 ,尤其 动人。 凄清、 冷落的 景色, 衬托出 人物的 惆怅、 幽怨之 情,并 为全诗 定下了 哀怨不 已的感 情基调 。
●
6.石壕吏和老妇人是诗中的主要人物 ,要立 于善于 运用想 像来刻 画他们 各自的 动作、 语言和 神态; 还要补 充一些 事实上 已经发 生却被 诗人隐 去的故 事情节 。
北师大初中数学中考总复习:实数--知识讲解(提高).doc
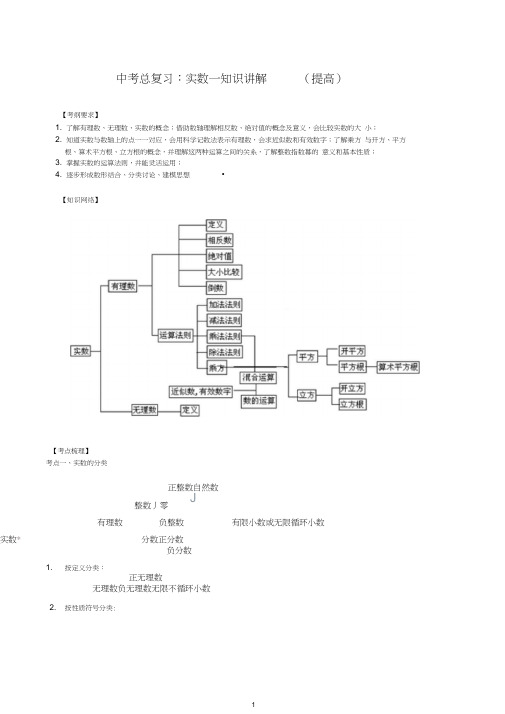
中考总复习:实数一知识讲解(提高)【考纲要求】1. 了解有理数、无理数、实数的概念;借助数轴理解相反数、绝对值的概念及意义,会比较实数的大 小;2. 知道实数与数轴上的点一一对应,会用科学记数法表示有理数,会求近似数和有效数字;了解乘方 与开方、平方根、算术平方根、立方根的概念,并理解这两种运算之间的关系,了解整数指数幕的 意义和基本性质;3. 掌握实数的运算法则,并能灵活运用;4. 逐步形成数形结合、分类讨论、建模思想•【知识网络】【考点梳理】 考点一、实数的分类1. 按定义分类:正无理数无理数负无理数无限不循环小数2. 按性质符号分类:整数丿零正整数自然数J有理数负整数 有限小数或无限循环小数实数*分数正分数负分数'正整数I 正有理数2 正实数 有 数 [正分数 正无理数实数零无理数:无限不循环小数叫无理数. 实数:有理数和无理数统称为实数. 要点诠释: 常见的无理数有以下几种形式:n Ji(1) 字母型:如n 是无理数,一、一等都是无理数,而不是分数;2 4(2) 构造型:如2.10100100010000…(每两个1之间依次多一个 0)就是一个无限不循环的小数;(3)根式型:辽、5、6…都是一些开方开不尽的数;(4) 三角函数型:sin 35 °、tan 27 °、cos29。
等. 考点二、实数的相关概念1. 相反数(1)代数意义:只有符号不同的两个数,我们说其中一个是另一个的相反数.0的相反数是0;(2) 几何意义:在数轴上原点的两侧,与原点距离相等的两个点表示的两个数互为相反数;3)互为相反数的两个数之和等于0.a 、b 互为相反数a+b=0.2. 绝对值(1)代数意义:正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0.a(a >0)可用式子表示为:a=0 (a=0)-a (a =0)(2)几何意义:一个数a 的绝对值就是数轴上表示数 a 的点与原点的距离. 距离是一个非负数, 以绝对值的几何意义本身就揭示了绝对值的本质,即绝对值是一个非负数.用式子表示:若 a 是实数,则|a| > 0.3. 倒数1(1) 实数a(a = 0)的倒数是一;0没有倒数;a(2)乘积是1的两个数互为倒数.a 、b 互为倒数二a b =1.4. 平方根(1)如果一个数的平方等于 a ,这个数就叫做a 的平方根.一个正数有两个平方根,它们互为相反 数;0有一个平方根,它是 0本身;负数没有平方根. a (a > 0 )的平方根记作一 .a . (2)一个正数a 的正的平方根,叫做 a 的算术平方根.a (a > 0)的算术平方根记作.a .5. 立方根如果x 3=a ,那么x 叫做a 的立方根.负实数 负有理数负分数负无理数有理数:整数和分数统称为有理数或者“形如m(m, n 是整数n ^O )”的数叫有理数. n一个正数有一个正的立方根;一个负数有一个负的立方根;0的立方根仍是0. 要点诠释:若a =a,则a王0; a =-a,则a兰0; a-b表示的几何意义就是在数轴上表示数a与数b的点之间的距离.考点三、实数与数轴规定了原点、正方向和单位长度的直线叫做数轴,数轴的三要素缺一不可.每一个实数都可以用数轴上的一个点来表示,反过来,数轴上的每一个点都表示一个实数. 要点诠释:(1)数轴的三要素:原点、正方向和单位长度(2)实数和数轴上的点是对应的.考点四、实数大小的比较1. 对于数轴上的任意两个点,靠右边的点所表示的数较大2. 正数都大于0,负数都小于0,正数大于一切负数;两个负数;绝对值大的反而小3. 对于实数a、b, 若a-b>0 a>b; a-b=0 = a=b; a-b<0 = a<b.4. 对于实数a, b, c,若a>b, b>c,贝U a>c.5. 无理数的比较大小:利用平方转化为有理数:如果a>b>0, a2>b2= a>bu .. a • .、b ;或利用倒数转化:如比较.、.17 -4与4-..15.要点诠释:实数大小的比较方法:(1)直接比较法:正数都大于0,负数都小于0,正数大于一切负数;两个负数,绝对值大的反而小•( 2)数轴法:在数轴上,右边的数总比左边的数大考点五、实数的运算1. 加法同号两数相加,取相同的符号,并把绝对值相加;绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;互为相反数的两个数相加得0个数同0相加,仍得这个数.满足运算律:加法的交换律a+b=b+a,加法的结合律(a+b)+c=a+(b+c).2. 减法减去一个数等于加上这个数的相反数.3. 乘法两数相乘,同号得正,异号得负,并把绝对值相乘几个非零实数相乘,积的符号由负因数的个数决定,当负因数有偶数个时,积为正;当负因数有奇数个时,积为负.几个数相乘,有一个因数为0,积就为0.乘法运算的运算律:(1)乘法交换律ab=ba; (2)乘法结合律(ab)c=a(bc) ; (3)乘法对加法的分酉己律a(b+c)=ab+ac .4. 除法(1)除以一个数,等于乘上这个数的倒数.(2)两个数相除,同号得正,异号得负,并把绝对值相除. 0除以任何一个不等于0的数都得0.5. 乘方与开方(1)求n个相同因数的积的运算叫做乘方,a n所表示的意义是n个a相乘.正数的任何次幕是正数,负数的偶次幕是正数,负数的奇次幕是负数.(2)正数和0可以开平方,负数不能开平方;正数、负数和0都可以开立方.(3)零指数与负指数要点诠释:-1(a^0), a(a^0).(1)加和减是一级运算,乘和除是二级运算,乘方和开方是三级运算•这三级运算的顺序是三、一•如果有括号,先算括号内的;如果没有括号,同一级运算中要从左至右依次运算.(2)实数的运算律加法交换律:a+b=b+a加法结合律:(a+b)+c=a+(b+c)乘法交换律:ab=ba乘法结合律:(ab)c=a(bc)乘法分配律:(a+b)c=ac+bc考点六、有效数字和科学记数法1. 近似数一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位•精确度的形式有两种:(1 )精确到哪一位;(2)保留几个有效数字.2. 有效数字一个近似数,从左边第一个不是0的数字起,到精确到的数位为止,所有的数字,都叫做这个近似数的有效数字.3. 科学记数法把一个数用土a x io n (其中u v 10, n为整数)的形式记数的方法叫科学记数法.要点诠释:(1)当要表示的数的绝对值大于1时,用科学记数法写成a x 10n,其中K a v 10, n为正整数,其值等于原数中整数部分的数位减去1;(2)当要表示的数的绝对值小于1时,用科学记数法写成a x 10n,其中K a v 10, n为负整数,其值等于原数中第一个非零数字前面所用零的个数的相反数(包括小数点前面的零)考点七、数形结合、分类讨论、建模思想1. 数形结合思想实数与数轴上的点一一对应,绝对值的几何意义等,数轴在很多时候可以帮助我们更直观地分析题目,从而找到解决问题的突破口;2. 分类讨论思想(算术)平方根,绝对值的化简都需要有分类讨论的思想,考虑问题要全面,做到既不重复又不遗漏;3. 从实际问题中抽象出数学模型以现实生活为背景的题目,我们要抓住问题的实质,明确该用哪一个考点来解决问题,然后有的放矢•【典型例题】类型一、实数的有关概念1 . (2015春?杭锦后旗校级期末)卫下列各数中,无理数有( :匚,,匸,-n二,0, 0.5757757775-(相邻两个x 6 2 V 9A. 2个B . 3个C . 4个D . 5个【答案】D; _ _【解析】无理数有::一,,-n , :, 0.5757757775-(相邻两个共有5个.故答案是:D.).5之间的7的个数逐次加1).5之间的7的个数逐次加1)n , 2 n等;开方开不尽【点评】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:的数;以及像0.1010010001-,等有这样规律的数.举一反三:【变式】(2015?安徽)与1+二最接近的整数是()A. 4 B . 3 C. 2 D. 1【答案】B. •/4V 5V 9,••• 2V 匸V 3.又5和4比较接近,•匸最接近的整数是2,•••与1+ :最接近的整数是3, 故选:B .类型二、实数有关的计算2.⑴有一列数_丄,2,_?,土,…,那么依此规律,第7个数是 _____________________________ ;2 510 17(2)已知_1 丄12 _1 丄1 3 _ 1 丄1 4 _1丄15…a1,a2,比 ,a4,,1 2 3 232 3 43 83 4 54 154 5 6524依据上述规律,则 a 99 =.-Z ;( 2)型.509999符号:单数为负,双数为正,所以第 7个为负.分子规律:第几个数就是几,即第 7个数分子就是7,分母规律:分子的平方加 1,第7个数分母就是50.所以第7个数是一工.50 1丄 1100a 99.99 100 101100 9999规律:(一1)n (n 为正整数);n 2+1规律: --------- 1--------- — n 1(n 为正整数)n(n +1)( n +2) n +1 n(n +2)【变式】a 是不为1的有理数,我们把-^―称为a 的差倒数.如:2的差倒数是=_1, -1的差1—a. ..1-2111 倒数是.已知a 1,a 2是a 1的差倒数,a 3是a ?的差倒数,是a 3的差倒数,…,1-(-1) 23【答案】(1)【解析】(1)(2) 【点评】(1)(2)举一反三:依此类推,则a2009二__________________ .1【答案】因为a1 - a23 a31-3=4, a411-4类型三、实数大小的比较3•若a 二2007, b=2008,试不用将分数化小数的方法比较a 、b 的大小.2008 2009•-2 2 2【答案与解析】a=2007 2009二(2008 ")(20081)=2008 -1, b 二20082008 汉 2009 2008 汉 20092008 汉 20092008 汉 200920082-12::: 20082,••• a<b .【点评】通过通分进行比较 . 举一反三:【变式】当b = 0时,比较1 + b 与1的大小. 【答案】(1):b M0时,• b > 0或b v 0.当 b >0 时,1 + b > 1, 当 b v 0 时,1 + b v 1.类型四、平方根的应用\ 2b 1 (c -2)2= 0,求 abc的值.a 53 ,a6 -41一3.=4,……..三个一循环,因此a 2oo9二a ?二【答案与解析】.2b 1 > 0, (c -2)2> 0,1 J _______汀宀十(一2)a+丄=0 3 • 2b 1 = 0 c —2=01a = 一一31解得彳b =--2c = 2 bc (于「3. 【点评】利用零,得一个三元一次方程组,解得2n>0 ( n 为自然数)等常见的三种非负数及其性质,分别令它们为a 、b 、c 的值,代入后本题得以解决。
北大数分讲义实数理论

我们用 x, y, z, L表示实数,即表示有理数的分划,用 a, b, c, L 表示有理数。用记号
R 表示实数的集合,记号 Q 表示有理数的集合。为了书写方便,用 Ax 表示实数 x 的下类,
Bx 表示实数 x 的上类, Bx0 表示 Bx 去掉最小数的集合。 定义 1 设有实数 x 、 y , 1) 若集合 Ax = Ay ,则称 x = y ; 2) 若集合 Ax ≠ Ay , Ax ⊂ Ay ,则称 x 小于 y ,或 y 大于 x ,记作 x < y 或 y > x 。
数集是稠密的,即对任意有理数 a 、b (a < b) ,总存在有理数 c ,使得 a < c < b 。由稠密
性虽得不出有理数连பைடு நூலகம்地分布在数轴上,但却是密密麻麻地分布在数轴上。另外,有理数满
足阿基米德原理,即对任意有理数 b > a > 0 ,必存在自然数 n ,使得 na > b 。
3.1 实数的运算
容易看出 A 、 B 构成有理数的一个分划,这时上类 B 有最小数1。
例2
A = { x | x ≤ 0 或 x > 0 且 x 2 < 2, x ∈ Q} ;
B = { x | x > 0 且 x2 > 2, x ∈ Q}。
显然 A 、 B 不空、不乱,因为没有有理数平方等于 2 ,所以不漏,下面证 A 无最大数。 设 a ≥ 0 , a 2 < 2 ,要证存在有理数 r > 0 ,使
事实上戴德金正是考虑怎么用严格的数学语言给出有理数是不连通的实数是连通的定义经反复研究发现用分划的办法是最恰当地描述连通性的数学语言对有理数作不空不漏不乱的分划时若下类无最大数则上类也可以无最小数所以按定义有理数是不连通的
最新北师大版初中数学九年级下册中考知识点梳理第1讲实数
(3)几何意义:数轴上表示互为相反数的两个点到原点的距离相等
a的相反数为-a,特别的0的绝对值是0.
例:3的相反数是-3,-1的相反数是1.
4.绝对值
(1)几何意义:数轴上表示的点到原点的距离
(2)运算性质:|a|= a (a≥0);|a-b|= a-b(a≥b)
(2)代数意义:ab=1a,b互为倒数
例:
-2的倒数是-1/2;倒数等于它本身的数有±1.
知识点三:科学记数法、近似数
6.科学记数法
(1)形式:a×10n,其中1≤|a|<10,n为整数
(2)确定n的方法:对于数位较多的大数,n等于原数的整数为减去1;对于小数,写成a×10-n,1≤|a|<10,n等于原数中左起至第一个非零数字前所有零的个数(含小数点前面的一个)
知识点四:实数的大小比较
8.实数的大小比较
(1)数轴比较法:数轴上的两个数,右边的数总比左边的数大.
(2)性质比较法:正数>0>负数;两个负数比较大小,绝对值大的反而小.
(3)作差比较法:a-b>0a>b;a-b=0a=b;a-b<0a<b.
(4)平方法:a>b≥0a2>b2.
例:
把1,-2,0,-2.3按从大到小的顺序排列结果为___1>0>-2>-2.3_.
使问题简单化
知识点五:实数的运算
9.
常见运算
乘方
几个相同因数的积;负数的偶(奇)次方为正(负)
例:
(1)计算:1-2-6=_-7__;(-2)2=___4__;
3-1=_1/3_;π0=__1__;
(2)64的平方根是_±8__,算术平方根是__8_,立方根是__4__.
初中数学《实数》教用课件北师大版1

6
若有理数的个数为x,无理数的个数为
x y,那么 y 等于 __1__6____.
总结: 2 是人们最早认识的无理数之一,这 节课我们从 2 谈起,谈到了哪些相关知识?
1.知识方面: (1)判断无理数的条件_是__无__限_不__循__环__小__数__; (2)_有__理_数__和__无__理__数_统称为实数; (3)实数与数轴上的点__一__一__对__应_____; (4)相反数、绝对值、数的大小比较法则同样
毕达哥拉斯(约公元前 560——480年)
但后来,这个学派的一位年轻成员 希伯索斯(Hippasus) 发现:边长为1的 正方形的对角线长不能用有理数来表示。
1 1
2 到底是怎样的一类数呢?
2 是不是有理数
2 是整数吗? 1 < 2 <2 2 是分数吗? 2 是有理数吗?
结论: 2 既不是_整__数__,也不是_分__数__。 所以, 2 不是_有__理__数_。
•
4.根据结构来梳理。按照情节的开端 、发展 、高潮 和结局 来划分 文章层 次,进而 梳理情 节。
•
5.根据场景来梳理。一般一个场景可 以梳理 为一个 情节。 小说中 的场景 就是不 同时间 人物活 动的场 所。
•
6.根据线索来梳理。抓住线索是把握 小说故 事发展 的关键 。线索 有单线 和双线 两种。 双线一 般分明 线和暗 线。高 考考查 的小说 往往较 简单,线 索也一 般是单 线式。
(1)在实数范围内,每一个数都可以用数轴上的 点表示出来;反过来,数轴上的每一个点都表示一 个实数,我们说实数和数轴上的点一一对应.
(2)在数轴上表示的两个实数,右边的数总比左 边的数大.
《实数》 讲义

《实数》讲义一、实数的定义实数,是数学中一个非常基础且重要的概念。
简单来说,实数包括了有理数和无理数。
有理数,就是可以表示为两个整数之比的数,例如整数、有限小数和无限循环小数。
像 2、-3、05(即 1/2)、0333(即 1/3)等都是有理数。
而无理数,则是无限不循环小数,不能写成两个整数之比的形式。
比如圆周率π(约为 314159)、根号 2(约为 1414)等。
实数可以直观地看作数轴上的点,每一个实数都对应数轴上的一个唯一的点,反过来,数轴上的每一个点也都对应着一个唯一的实数。
二、实数的分类实数的分类方式有多种,常见的分类方法如下:1、按符号分类(1)正实数:大于 0 的实数,如 2、35 等。
(2)负实数:小于 0 的实数,如-2、-35 等。
(3)零:既不是正数也不是负数的实数。
2、按性质分类(1)有理数:包括整数(正整数、0、负整数)和分数(有限小数、无限循环小数)。
(2)无理数:无限不循环小数。
三、实数的运算1、加法和减法实数的加法和减法运算遵循以下规则:(1)同号两数相加,取相同的符号,并把绝对值相加。
例如,3 + 5 = 8,-3 +(-5) =-8 。
(2)异号两数相加,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值。
例如,3 +(-5) =-2,-3 + 5 = 2 。
(3)减去一个数,等于加上这个数的相反数。
例如,5 3 = 5 +(-3) = 2 。
2、乘法和除法(1)乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘。
例如,3 × 5 = 15,-3 ×(-5) = 15,3 ×(-5) =-15 。
(2)除法法则:除以一个数等于乘以这个数的倒数。
例如,6 ÷ 3 = 6 × 1/3 = 2 。
3、乘方和开方(1)乘方:求 n 个相同因数乘积的运算,叫做乘方。
例如,2³= 2 × 2 × 2 = 8 。
新版北师大版八年级数学上册实数全章课件

新版北师大版八年级数学上册实数全章课件一、综述实数作为数学中的重要概念,具有广泛的应用和重要性。
在新版北师大版八年级数学上册中,实数全章作为核心内容之一,深入探讨了实数的定义、性质、分类及其运算规则。
本章课件的编写旨在帮助学生全面理解和掌握实数的相关知识,为后续的数学学习和实际应用打下坚实的基础。
实数全章的内容涵盖了有理数和无理数的概念,实数的分类及特性,包括绝对值的定义和性质,以及实数的基本运算规则。
通过这些内容的学习,学生可以深入理解实数的本质,掌握实数的运算技巧,提高数学运算能力。
本章内容也是培养学生数学思维和解决问题能力的重要途径。
为了帮助学生更好地理解和掌握实数全章的内容,本课件采用了直观、生动、形象的教学方式,结合丰富的实例和图形,使学生更加容易理解和接受实数的相关知识。
本课件还注重培养学生的探究能力和自主学习能力,通过引导学生思考和探索,激发学生的学习兴趣和动力,提高学生的数学素养和综合能力。
1. 介绍新版北师大版八年级数学上册的重要性及修订背景随着教育改革的不断深化和数学学科知识的持续更新,新版北师大版八年级数学上册在整个教育体系中占据了举足轻重的地位。
这本教材是义务教育阶段数学课程的重要组成部分,旨在培养学生的数学素养和解决问题的能力。
其修订背景反映了教育领域对课程内容和教学方法的不断优化和创新理念。
新版北师大版八年级数学上册的重要性体现在其对于学生数学基础和未来学习生涯的深远影响。
八年级是中学阶段的关键时期,数学作为一门基础学科,对学生逻辑思维、问题解决和创新能力有着重要作用。
该教材的修订,旨在更好地适应学生的认知发展,提供更为丰富、贴近实际的教学内容。
修订背景反映了教育改革的必然趋势。
随着教育理念的更新和教学方法的进步,原有的教材内容、结构、难度等方面可能已不能完全适应当前的教学需求。
对教材进行修订是适应教育改革、提高教育质量的重要举措。
修订过程中,教材编写团队充分考虑了当前教育发展的趋势,结合最新的教育理念和教学思想,对教材进行了全面优化和更新。
北师大版高中数学《实数》PPT课件分析1

▪
2.但是,情况终于改变了。一些急欲 挽救中 国的社 会改革 家发现 ,旧时 代的主 流意识 形态必 须改变 ,而那 些数千 年来深 入民间 社会的 精神活 力则应 该调动 起来。 因此, 大家又 重新惊 喜地发 现了墨 子。
▪
3.中国作家结识雨果已经近一百年。 当伟大 的雨果 以其壮 丽风采 开辟着 一个理 想的正 义世界 的时候 ,当他 以浪漫 主义的 狂飙之 势席卷 风云变 幻的欧 罗巴的 时候, 中国还 是一只 沉睡的 雄狮, 尚未向 世界打 开广泛 的视听 。
两个正实数绝对值大的数较大,两个负实数 绝对值大的数反而小。
练习:
比较下列各组是里两个数的大小:
(1) 2 , 1.4 (2) 5, 6
(3) -2, 3
试试看:你会比较 7 2 与 1 的大小吗?
3
3
5 2 6 的相反数
绝对值
课堂小结
▪ 这节课你有什么收获?
课堂作业
必做:课本第17页习题第2、3题 选做:求下列各数的相反数:
B
A
-2 2-1
0
122
每一个实数都可以用数轴上的一个点来表示;反 过来,数轴上的每一点都表示一个实数。即实数 和数轴上的点是一一对应的。
归纳
1、每一个有理数都可以用数轴上的点 表示; 2、每一个无理数都可以用数轴上的点 表示;
实数与数轴上的点是一一对应的
(1)a是一个实数,它的相反数为 a ,
▪
8.心理学上有一种认识——评估学说 ,即个 体对事 物有了 认识, 就会利 用头脑 中的旧 经验来 解释新 输入的 信息, 进行评 估,于 是产生 情绪体 验。而 个体对 事物究 竟体验 为积极 的情绪 还是消 极的情 绪,在 于怎样 认识事 物。
北师大版数学八年级上册6《实数》说课稿1

北师大版数学八年级上册6《实数》说课稿1一. 教材分析北师大版数学八年级上册6《实数》是学生在学习了有理数和无理数的基础上,进一步对实数进行系统的学习和掌握。
本节课的内容主要包括实数的定义、实数的分类、实数的性质等。
教材通过丰富的实例和生动的语言,引导学生理解和掌握实数的概念,培养学生的抽象思维能力。
二. 学情分析学生在学习本节课之前,已经掌握了有理数和无理数的相关知识,对数的运算和性质有一定的了解。
但实数作为一个新的概念,需要学生能够从更高的角度去理解和把握。
此外,实数与现实生活密切相关,学生需要能够将数学知识运用到实际问题中。
三. 说教学目标1.知识与技能目标:理解实数的定义,掌握实数的分类和性质,能够运用实数解决一些实际问题。
2.过程与方法目标:通过观察、分析和归纳,培养学生的抽象思维能力。
3.情感态度与价值观目标:激发学生对数学的兴趣,培养学生的团队合作精神。
四. 说教学重难点1.教学重点:实数的定义,实数的分类和性质。
2.教学难点:实数的性质的证明和运用。
五. 说教学方法与手段1.教学方法:采用问题驱动法、案例教学法和小组合作法。
2.教学手段:多媒体课件、黑板、粉笔。
六. 说教学过程1.导入新课:通过一个实际问题,引发学生对实数的思考,进而导入新课。
2.讲解实数的定义:通过实例和引导学生观察、分析,讲解实数的定义。
3.实数的分类:引导学生根据实数的定义,对实数进行分类。
4.实数的性质:通过实例和证明,引导学生理解和掌握实数的性质。
5.巩固练习:设计一些练习题,让学生巩固所学知识。
6.课堂小结:对本节课的内容进行总结,加深学生对实数概念的理解。
7.布置作业:设计一些作业题,让学生进一步巩固和提高。
七. 说板书设计板书设计要清晰、简洁,能够突出本节课的重点和难点。
主要包括实数的定义、实数的分类和性质等内容。
八. 说教学评价教学评价主要包括学生的学习效果评价和教师的教学评价。
学习效果评价可以通过课堂表现、作业完成情况和考试成绩等方面进行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§1 从空集到有理数
实数是在有理数基础上定义的,有理数又是在整数的基础上定义的,而整数又是在自 然数的基础上定义的,那么自然数如何定义呢?
有两个集合 A 和 B ,我们称它们为等价的,如果存在一个从 A 到 B 的映射 f ,它是1−1 的,又是满的。这时我们说 A 和 B 具有相同的势。我们首先承认空集 φ 是存在的,考虑一 个集合 {φ},它不是空集,凡与 {φ}等价的集合都有相同的势,我们把 {φ}简写为 1。再考 虑集合 {φ , {φ}},它与1 = {φ}是不等价的,我们把它简写为 2 。一般地如果有了 n 之后,
如果它是有理数,就应该有:
2 = m , (m, n) = 1 , n
n ≠0。
两边平方,得 2n2 = m 2 ,因为 m , n 都是整数,表明 m 2 中含 2 因子,即 m 中含 2 因子,
设 m = 2 p ,则 n 2 = 2 p 2 ,同样推理表明 n 中也含 2 因子,与 (m, n) = 1 矛盾,所以 2 不
比如假定单位线段由 q 个原子组成,被测量的线段由 p 个原子组成,则线段之长为: p , q
即有理数可以度量一切长度。但毕达哥拉斯学派弟子希伯斯发现正五角形的边长为 1时,对
角线长不能由有理数表示,希伯斯因此受到迫害。但后来发现有很多长度不能用有理数表示,
比如简单地取正方形边长为1,由勾股定理,它Байду номын сангаас对角线长度的平方应为2 ,我们记之为 2 ,
Z = {(m, n) : m, n ∈ N} ~ 。 在 Z 上 可 以 定 义 加 法 : (m, n) + (m′, n′) = (m + m′, n + n′) , 还 可 以 定 义 减 法 : (m, n) − (m′, n′) = (m + n′, m′ + n) 。可以验证它们在 Z 中封闭,而且互为逆运算。在 Z 中我们用 0 表示{ (n, n) : n ∈N},,即0 = 1 −1 = 2 − 2 = L ,用 k 表示{ (n + k, n) : n, k ∈ N} , 即 k = (k +1) −1 = (k + 2) − 2 = L , 用 − 1 表 示 { (n, n +1) : n ∈ N} , 即
容易看出 A 、 B 构成有理数的一个分划,这时上类 B 有最小数1。
例2
A = { x | x ≤ 0 或 x > 0 且 x 2 < 2, x ∈ Q} ;
B = { x | x > 0 且 x2 > 2, x ∈ Q}。
显然 A 、 B 不空、不乱,因为没有有理数平方等于 2 ,所以不漏,下面证 A 无最大数。 设 a ≥ 0 , a 2 < 2 ,要证存在有理数 r > 0 ,使
− 1= 1− 2 = 2 − 3 = L。
182
在集合{ ( p, q) : p, q ∈ Z, q ≠ 0 }中,考虑一个关系 ~ : ( p, q) ~ ( p′, q′) 当且仅当
pq′ = p′q ,它也是一个等价关系,有理数 Q 现在定义为: Q = {( p, q) : p, q ∈ Z, q ≠ 0} ~ 。
在 Q 中我们可以定义加法,减法,乘法,除法,还可证明加减法互为逆运算,乘除法互为
逆运算等性质,在 Q 中我们用 p ,且 ( p, q) = 1 表示其中一个有理数,比如用 1 表示
q
2
(n, 2n) 。
这样我们完成了从空集φ 出发到有理数集 Q 的定义。
在 2500 年前,毕达哥拉斯学派认为一切线段都由原子组成,而原子有一个固定长度,
个分划, A 称为分划的下类, B 称为分划的上类,记作 ( A | B) 。
定义中 4)不同于 1)—3),它是非实质性的,只是为了推理的方便。定义中 4)用到
有理数的稠密性(即两个有理数之间必有一有理数),如 A 有最大数,将此数放入 B ,则它 是 B 的最小数,这时 A 就无最大数;若 A 还有最大数,根据有理数的稠密性, A 的最大数 与 B 的最小数之间必有一有理数,这个有理数被漏掉了,这与分划的定义矛盾。
这样,有理数可以与有理分划建立一一对应,我们就用无理分划来填充直线上的“孔隙”。 于是有如下定义。
定义 2 有理数的任一无理分划称为无理数。
为了一致起见,称有理数的任一有理分划为有理数。有理数和无理数统称为实数 。
§3 实数的性质
为了研究实数的性质,我们回顾有理数的一些熟知性质,如有理数是全序域,所谓全 序域,简单地说就是可以比较大小,而且在有理数中可以作加、减、乘、除四则运算。有理
最小数。
可见,有理数的分划可以分为两类,第一类型是上类 B 有最小数,我们称这类分划为 有理分划;第二类型是上类 B 无最小数,我们称这类分划为无理分划。显然,任一有理分 划与其上类的最小有理数对应,反之任一有理数 b ,总可确定一有理分划:
A = { x | x < b, x ∈ Q} ;
B = { x | x ≥ b, x ∈Q}。
定义 1 将有理数全体组成的集合分成 A , B 两类,使满足以下性质: 1) A 与 B 都至少包含一个有理数(不空); 2) 任一有理数,或属于 A ,或属于 B (不漏);
183
3) A 中任一数 a 均小于 B 中任一数 b ,即 a ∈ A , b ∈ B ⇒ a < b (不乱); 4) A 中没有最大的数,即 a ∈ A , ∃ a′ ∈ A ,使 a < a′ 。则称 A , B 为有理数的一
是有理数的分划。
证明: A 、 B 满足分划不漏的条件是显然的,集合 A 无最大元素也是明显的。只要
证满足分划的不空和不乱条件即可。
先证 A 、 B 不空。 A 不空是显然的,证 B 不空。 因集合 Bx , By 不空, ∃b1 ∈ Bx ,
b2 ∈ By ,只要证 b1 + b2 ∈ B 。
这是一个最抽象的定义,比如说 2 ,它不指二个人,也不指二个物,而是指一个集合{φ , {φ}} , 这个集合有两个不同的元素{φ} 和φ 。凡是与它等价的集合,都与它有相同的势,于是二个 人,二个物… … ,都具有相同的势,按我们的理论,用{φ , {φ}} 作为它们的代表。
在 集 合{ (m, n) : m, n ∈ N } 中 , 考虑一个关系 ~ : (m, n) ~ (m′, n′) 当 且 仅 当 m + n′ = m′ + n ,容易证明 ~ 是一个等价关系。 整数 Z 现在定义为:
a2 ≥ b − a1 ,由分划 y 的不乱,得b − a1 ∈ Ay ,于是 b = a1 + (b − a1) ∈ A ,故矛盾。所以 a < b 。
因此 ( A | B) 是有理数的分划。
定义 2 在引理 1 条件下,称实数( A | B) 为实数 x 与 y 的和,记作 x + y 。 当 x 、 y 为有理分划时,和也为有理分划,且和的定义与把 x 、 y 看成有理数时和的
我们用 x, y, z, L表示实数,即表示有理数的分划,用 a, b, c, L 表示有理数。用记号
R 表示实数的集合,记号 Q 表示有理数的集合。为了书写方便,用 Ax 表示实数 x 的下类,
Bx 表示实数 x 的上类, Bx0 表示 Bx 去掉最小数的集合。 定义 1 设有实数 x 、 y , 1) 若集合 Ax = Ay ,则称 x = y ; 2) 若集合 Ax ≠ Ay , Ax ⊂ Ay ,则称 x 小于 y ,或 y 大于 x ,记作 x < y 或 y > x 。
存在有理数 q2 , q3 ,使
q1 < q2 < q3 , qi ∈ Ay , qi ∉ Ax (i = 2, 3) 。
有理数 q2 产生的有理分划记作 z ,容易看出 x < z < y ,即实数集是稠密的。
为了定义加法,我们需要下面引理。
引理 1 设 x 、y 为实数,令 A = {a1 + a2 | a1 ∈ Ax , a2 ∈ Ay} ,B = Q − A 。则 ( A | B)
数集是稠密的,即对任意有理数 a 、b (a < b) ,总存在有理数 c ,使得 a < c < b 。由稠密
性虽得不出有理数连续地分布在数轴上,但却是密密麻麻地分布在数轴上。另外,有理数满
足阿基米德原理,即对任意有理数 b > a > 0 ,必存在自然数 n ,使得 na > b 。
3.1 实数的运算
是有理数。这表明只有有理数是不够的,必须引入新的数,即无理数,它们合在一起称为实 数。
§2 实数的定义(戴德金分割)
定义实数有不同的方法,戴德金分割是一个比较标准的方法。直观地看,有理数 Q 在
实轴上没有填满,还有很多“孔隙”,戴德金分割就是在数轴上割一刀,把现有的有理数 Q
分成两部分,如果这一刀恰好砍在某个有理数上,这一分割对应的就是这个有理数,如果没 碰到任何有理数,这个分割就定义出一个无理数。
184
要使上式成立,只要 2br < b2 − 2 , r < b 2 − 2 。由于 b2 − 2 > 0 ,根据有理数的稠密性,
2b
2b
知存在有理数 r 使得 0 < r < b2 − 2 ,又由 b2 − 2 < b ,推知r < b ,对这样的r ,满足
2b
2b
b − r > 0 , (b − r) 2 > 2 ,这就证明了,在 B 中找到了比 b 更小的有理数 b − r ,所以 B 无
(a + r)2 < 2 。
即要证
a 2 + 2ar + r 2 < 2 ,或 2ar + r 2 < 2 − a 2 。
