东南大学几何与代数matlab实验报告
matlab实验报告

Matlab实验报告一、实验名称:matlab实验报告二、实验目的:熟悉并学会掌握matlab的基本操作。
三、实验内容:准确编写第二,三,四章课后习题的matlab程序。
四、实验数据处理第二章MATLAB 基本操作第一题:利用基本矩阵产生3X3和15X8的单位阵、全1阵、全0阵,随机分布矩阵([-1,1]之间)、正态分布随机阵(均值为1,方差为4)。
程序:>> A=eye(3)A = 1 0 00 1 00 0 1>> A=ones(3)A =1 1 11 1 11 1 1>> A=zeros(3)A =0 0 00 0 00 0 0>> A=1-2*rand(3)A =-0.9003 0.0280 0.08710.5377 -0.7826 0.9630-0.2137 -0.5242 -0.6428>> A=2*randn(3)+1A =0.1349 1.5754 3.3783-2.3312 -1.2929 0.92471.2507 3.3818 1.6546>> B=eye(2,3)B =1 0 00 1 0>> B=ones(2,3)B = 1 1 11 1 1>> B=zeros(2,3)B =0 0 00 0 0>> B=1-2*rand(2,3)B = 0.1106 -0.5839 -0.4764-0.2309 -0.8436 0.6475>> B=2*randn(2,3)+1B =1.3493 2.4516 5.36640.6266 -0.1766 0.7272第五题:利用rand函数产生(0,1)间均匀分布的5X5随机矩阵A,然后统计A中大于等于0.6的元素个数。
程序:A=rand(5)A =0.4057 0.0579 0.2028 0.0153 0.41860.9355 0.3529 0.1987 0.7468 0.84620.9169 0.8132 0.6038 0.4451 0.52520.4103 0.0099 0.2722 0.9318 0.20260.8936 0.1389 0.1988 0.4660 0.6721>> n=sum(sum(A>=0.6))n =9第六题:利用rand函数产生均值为0,方差为1的4X4正态分布随机矩阵A,然后统计A 中大于-0.5且小于0.5的元素个数。
4)MATLAB实验报告

4)MATLAB实验报告MATLAB实验报告一、引言MATLAB是一种强大的数学软件,广泛应用于科学研究、工程设计和数据分析等领域。
本实验报告旨在介绍使用MATLAB进行数据处理和可视化的基本方法,并通过实例展示其应用。
二、数据处理1. 数据导入与读取在MATLAB中,可以使用load函数或importdata函数导入外部数据文件。
load函数适用于导入MATLAB格式的数据文件,而importdata函数可以导入多种格式的数据文件,如文本文件、Excel文件等。
2. 数据清洗与转换数据清洗是指对原始数据进行去除异常值、缺失值填充等处理,以保证数据的准确性和完整性。
MATLAB提供了丰富的函数和工具箱,如统计工具箱、优化工具箱等,可以方便地进行数据清洗和转换操作。
3. 数据分析与建模MATLAB具有强大的数学和统计分析功能,可以进行数据的描述性统计、回归分析、时间序列分析等。
通过使用相关函数和工具箱,可以对数据进行深入分析,并建立相应的数学模型。
三、数据可视化1. 统计图表MATLAB提供了丰富的绘图函数和工具箱,可以绘制各种统计图表,如直方图、散点图、箱线图等。
这些图表可以直观地展示数据的分布、关系和趋势,有助于更好地理解和解释数据。
2. 三维可视化除了二维图表外,MATLAB还支持三维数据的可视化。
通过使用plot3函数、mesh函数等,可以将三维数据以曲线、曲面等形式展示出来,进一步提供对数据的深入理解。
3. 动态可视化MATLAB还支持动态可视化,即通过动画或交互式图形来展示数据的变化过程。
通过使用animate函数、interactiveplot函数等,可以将数据的变化以动态的方式展示出来,增加数据分析和呈现的趣味性。
四、实例应用以某电商平台销售数据为例,展示如何使用MATLAB进行数据处理和可视化。
首先,导入销售数据文件,清洗数据,去除异常值和缺失值。
然后,通过统计分析,计算销售额、销量、平均价格等指标,并绘制相应的统计图表。
(最新版)MATLAB实验报告

(最新版)MATLAB实验报告实验一典型环节的MATLAB仿真一、实验目的1.熟悉MATLAB桌面和命令窗口,初步了解SIMULINK功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、SIMULINK的使用MATLAB中SIMULINK是一个用来对动态系统进行建模、仿真和分析的软件包。
利用SIMULINK功能模块可以快速的建立控制系统的模型,进行仿真和调试。
1.运行MATLAB软件,在命令窗口栏“>>”提示符下键入simulink命令,按Enter 键或在工具栏单击按钮,即可进入如图1-1所示的SIMULINK仿真环境下。
2.选择File菜单下New下的Model命令,新建一个simulink 仿真环境常规模板。
3.在simulink仿真环境下,创建所需要的系统。
以图1-2所示的系统为例,说明基本设计步骤如下:1)进入线性系统模块库,构建传递函数。
点击simulink下的“Continuous”,再将右边窗口中“Transfer Fen”的图标用左键拖至新建的“untitled”窗口。
2)改变模块参数。
在simulink仿真环境“untitled”窗口中双击该图标,即可改变传递函数。
其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数,数字之间用空格隔开;设置完成后,选择OK,即完成该模块的设置。
3)建立其它传递函数模块。
按照上述方法,在不同的simulink 的模块库中,建立系统所需的传递函数模块。
例:比例环节用“Math”右边窗口“Gain”的图标。
4)选取阶跃信号输入函数。
用鼠标点击simulink下的“Source”,将右边窗口中“Step”图标用左键拖至新建的“untitled”窗口,形成一个阶跃函数输入模块。
5)选择输出方式。
用鼠标点击simulink下的“Sinks”,就进入输出方式模块库,通常选用“Scope”的示波器图标,将其用左键拖至新建的“untitled”窗口。
MATLAB实验报告(打印版)

MATLAB实验报告班别:09电气3班姓名:李嘉明学号:200924122301实验一/二 MATLAB的基础操作3.自定义一个变量,然后分别用8种不同的数字显示格式显示查看。
>> a=[1.1,1.2,1.3;1.4,1.5,1.6;1.7,1.8,1.9]a =1.1000 1.2000 1.30001.4000 1.5000 1.60001.7000 1.8000 1.9000>> format long>> aa =1.100000000000000 1.200000000000000 1.3000000000000001.400000000000000 1.500000000000000 1.6000000000000001.700000000000000 1.800000000000000 1.900000000000000>> format short e>> aa =1.1000e+000 1.2000e+000 1.3000e+0001.4000e+000 1.5000e+000 1.6000e+0001.7000e+000 1.8000e+000 1.9000e+000>> format long e>> aa =1.100000000000000e+000 1.200000000000000e+000 1.300000000000000e+0001.400000000000000e+000 1.500000000000000e+000 1.600000000000000e+0001.700000000000000e+000 1.800000000000000e+000 1.900000000000000e+000 >> format hex>> aa =3ff199999999999a 3ff3333333333333 3ff4cccccccccccd3ff6666666666666 3ff8000000000000 3ff999999999999a3ffb333333333333 3ffccccccccccccd 3ffe666666666666>> format +>> aa =+++++++++>> format rat>> aa =11/10 6/5 13/107/5 3/2 8/517/10 9/5 19/10>> format short>> aa =1.1000 1.2000 1.30001.4000 1.5000 1.60001.7000 1.8000 1.90005、己举例比较给矩阵的全行赋值,取出矩阵中某一个或几个元素,然后组成一个新的矩阵。
几何与代数Matlab报告

数学实验报告学号: , 姓名:, 得分: ______实验1. 求解线性方程组内容: 用MATLAB求解如下线性方程组Ax = b。
方法一:源程序如下:>> A=[ 5 6 0 0 0 0 0 0;1 5 6 0 0 0 0 0;0 1 5 6 0 0 0 0;0 0 1 5 6 0 0 0;0 0 0 1 5 6 0 0;0 0 0 0 1 5 6 0;0 0 0 0 0 1 5 6;0 0 0 0 0 0 1 5;];b=[0;4;0;1;0;2;1;0];B=[A b];R_A=rank(A);R_B=rank(B);n=8;if R_A==R_B&R_A==n,X=A\belseif R_A==R_B&R_A<n,C=rref(B)else X='Equation has no solves'end运行结果如下:X =-8.19996.8332-3.66111.9120-0.81650.36170.1680-0.0336方法二:过程如下:>> A=[ 5 6 0 0 0 0 0 0;1 5 6 0 0 0 0 0;0 1 5 6 0 0 0 0;0 0 1 5 6 0 0 0;0 0 0 1 5 6 0 0;0 0 0 0 1 5 6 0;0 0 0 0 0 1 5 6;0 0 0 0 0 0 1 5;];b=[0;4;0;1;0;2;1;0];B=[A b];C=rref(B)回车得:C=1.0000 0 0 0 0 0 0 0 -8.19990 1.0000 0 0 0 0 0 0 6.83320 0 1.0000 0 0 0 0 0 -3.66100 0 0 1.0000 0 0 0 0 1.91200 0 0 0 1.0000 0 0 0 -0.81650 0 0 0 0 1.0000 0 0 0.36170 0 0 0 0 0 1.0000 0 0.16790 0 0 0 0 0 0 1.0000 -0.0336继续输入:X=C(:,9)回车得:X =-8.19996.8332-3.66111.9120-0.81650.36170.1680-0.0336实验2. 研究三个平面的位置关系内容:π1: x + y + z = 1π2: -x + y = 2π3:2x+t^2z=t1、当t取何值时交于一点?2、当t取何值时交于一直线?3、当t取何值时没有公共的交点?过程如下:>> A=[1 1 1 1;-1 1 0 2];syms t;a=[2 0 t^2 t];Ar=rref(A); ar=rref(a);B=[Ar;ar]回车得:B= [ 1, 0, 1/2, -1/2][ 0, 1, 1/2, 3/2][ 1, 0, 1/2*t^2, 1/2*t]%要求三个平面只交于一个点,等价于B所代表的非其次线性方程组只有唯一解。
东南大学几何与代数matlab实验报告1

数学实验报告学号: 04211702 , 姓名: 武亚文, 得分:实验1 求解线性方程组实验内容: 用MATLAB求解如下线性方程组Ax = b, 其中A =5600000015600000015600000015600000015600000015600000015600000015⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦, b = [04211702] T.实验目的: 1. 了解MATLAB软件, 学会MATLAB软件的一些基本操作;2. 熟悉MATLAB软件的一些数值计算功能,如在矩阵方面的运算;3. 练习编写简单的MATLAB程序。
实验原理: 1. 对于齐次线性方程组Ax = b, 根据gramer法则, 其解为X i=D i/D;2. 当A可逆,即|A|≠0时, 方程组Ax = b的解为X=inv(A)*B;3. 当……时, 对增广矩阵[A, b]进行初等行变换, 把它化为最简形, 则原矩阵b对应的地方即为A-1*b,取最简形的最后一列赋给X即得线性方程组的解。
实验方案: 1. 在MATLAB命令窗口中输入如下命令:A=[5 6 0 0 0 0 0 0;1 5 6 0 0 0 0 0;0 1 5 6 0 0 0 0;0 0 1 5 6 0 0 0;0 0 0 1 5 6 0 0;0 0 0 0 1 5 6 0;0 0 0 0 0 1 5 6;0 0 0 0 0 0 1 5;];b=[0 4 2 1 1 7 0 2]';%输入矩阵A与bX=[]; %声明一个名为X的空矩阵D=det(A); %把A的行列式的值求出来赋给Dfor i=1:8 %开始循环语句A=[5 6 0 0 0 0 0 0;1 5 6 0 0 0 0 0;0 1 5 6 0 0 0 0;0 0 1 5 6 0 0 0;0 0 0 1 5 6 0 0;0 0 0 0 1 5 6 0;0 0 0 0 0 1 5 6;0 0 0 0 0 0 1 5;];b=[04211702]';A(:,i)=b; %把A的第i列替换成bX=[X,det(A)/D]; %把求出的每个值填入空矩阵X对应的列中i=i+1; %让i递增一控制循环的结束end %结束for循环X=X’%输出矩阵X的转置,即为线性方程组的解2. 在MATLAB命令窗口中输入如下命令:A=[5 6 0 0 0 0 0 0;1 5 6 0 0 0 0 0;0 1 5 6 0 0 0 0;0 0 1 5 6 0 0 0;0 0 0 1 5 6 0 0;0 0 0 0 1 5 6 0;0 0 0 0 0 1 5 6;0 0 0 0 0 0 1 5];b=[0 4 2 1 1 7 0 2]';%输入矩阵A和bX=inv(A)*b%把A逆与b相乘的结果赋给X,即为线性方程组的解3. 在MATLAB命令窗口中输入如下命令:A=[5 6 0 0 0 0 0 0;1 5 6 0 0 0 0 0;0 1 5 6 0 0 0 0;0 0 1 5 6 0 0 0;0 0 0 1 5 6 0 0;0 0 0 0 1 5 6 0;0 0 0 0 0 1 5 6;0 0 0 0 0 0 1 5];b=[0 4 2 1 1 7 0 2]'; %输入矩阵A和bC=rref([A,b]); %将A的增广矩阵[A,b]化为最简形并赋给CX=C(:,9) %取C的第九列并赋给X,即为线性方程组的解实验结果: 1. 2. 3.X =-15187/1877783/115-4515/1074238/175-2116/1637011/1009-401/163727/815 X =-15187/1877783/115-4515/1074238/175-2116/1637011/1009-401/163727/815X =.-15187/1877783/115-2152/51557/23-701/54674/97-123/5033/375对实验结果的分析:在上述3种方案中,前两种的结果完全相同,而与第三种方案的结果稍有不同,但差距极小,只要是由于不同的计算方法导致运算过程中近似程度不同,导致最终的精度不同。
matlab入门实验报告

matlab入门实验报告Matlab入门实验报告引言:Matlab是一种功能强大的数值计算和科学计算软件,广泛应用于工程、科学和金融等领域。
本实验报告旨在分享我在学习和使用Matlab过程中的一些经验和心得,希望对初学者有所帮助。
一、Matlab的基本操作Matlab的基本操作包括变量定义、运算符使用、矩阵操作等。
通过简单的例子,我们可以快速上手Matlab。
首先,我们可以定义一个变量并进行简单的运算。
例如,我们定义一个变量a,并赋值为5,然后进行加法运算。
a = 5;b = a + 3;disp(b);接下来,我们可以进行矩阵的操作。
例如,我们定义一个3x3的矩阵A,并对其进行转置操作。
A = [1 2 3; 4 5 6; 7 8 9];B = A';disp(B);二、Matlab的图形绘制功能Matlab具有强大的图形绘制功能,可以绘制各种类型的图形,如曲线图、散点图、柱状图等。
下面是一个简单的例子,展示了如何使用Matlab绘制曲线图。
首先,我们定义一个自变量x和一个因变量y,并生成一组数据。
x = linspace(0, 2*pi, 100);y = sin(x);然后,我们使用plot函数将数据绘制成曲线图。
plot(x, y);通过设置不同的参数,我们可以对图形进行进一步的美化和定制。
例如,我们可以设置x轴和y轴的标签,并添加图例。
xlabel('x');ylabel('y');legend('sin(x)');三、Matlab的数据分析功能Matlab提供了丰富的数据分析功能,可以进行数据的统计、拟合、回归等操作。
下面是一个简单的例子,展示了如何使用Matlab进行线性回归分析。
首先,我们生成一组随机数据,并假设其满足线性关系。
x = linspace(0, 10, 100);y = 2*x + 3 + randn(size(x));然后,我们使用polyfit函数进行线性回归分析,并得到拟合的系数。
(完整word版)Matlab数学实验报告

Matlab 数学实验报告一、实验目的通过以下四组实验,熟悉MATLAB的编程技巧,学会运用MATLAB的一些主要功能、命令,通过建立数学模型解决理论或实际问题。
了解诸如分岔、混沌等概念、学会建立Malthu模型和Logistic 模型、懂得最小二乘法、线性规划等基本思想。
二、实验内容2.1实验题目一2.1.1实验问题Feigenbaum曾对超越函数y=λsin(πx)(λ为非负实数)进行了分岔与混沌的研究,试进行迭代格式x k+1=λsin(πx k),做出相应的Feigenbaum图2.1.2程序设计clear;clf;axis([0,4,0,4]);hold onfor r=0:0.3:3.9x=[0.1];for i=2:150x(i)=r*sin(3.14*x(i-1));endpause(0.5)for i=101:150plot(r,x(i),'k.');endtext(r-0.1,max(x(101:150))+0.05,['\it{r}=',num2str(r)]) end加密迭代后clear;clf;axis([0,4,0,4]);hold onfor r=0:0.005:3.9x=[0.1];for i=2:150x(i)=r*sin(3.14*x(i-1));endpause(0.1)for i=101:150plot(r,x(i),'k.');endend运行后得到Feigenbaum图2.2实验题目二2.2.1实验问题某农夫有一个半径10米的圆形牛栏,长满了草。
他要将一头牛拴在牛栏边界的桩栏上,但只让牛吃到一半草,问拴牛鼻子的绳子应为多长?2.2.2问题分析如图所示,E为圆ABD的圆心,AB为拴牛的绳子,圆ABD为草场,区域ABCD为牛能到达的区域。
问题要求区域ABCD等于圆ABC的一半,可以设BC等于x,只要求出∠a和∠b就能求出所求面积。
几何与代数实验报告

几何与代数实验报告几何与代数实验报告实验人员:院(系) 学号 姓名_ __成绩___________实验05平面图形的几何变换(矩阵乘法与线性变换应用)一、 实验题目绘制由平面上六个点所围图形的MATLAB 程序如下,右边为所绘图形:clear all , clc,t=[1 3 5 11 13 15]*pi/8; x=sin(t); y=cos(t); fill(x,y,'r'); grid on ;axis([-2.4, 2.4, -2, 2])(1)请写出该图形每个顶点的齐次坐标;(2)编写MATLAB 程序,先将上面图形放大0.9倍;再逆时针旋转;最后进行横坐标加0.8、纵坐标减1的图形平移。
请分别绘制上述变换后的图形。
二、实验目的和意义利用MATLAB 进行矩阵乘法与线性变换三、计算公式该图形每个顶点的齐次坐标:⎪⎭⎫ ⎝⎛1,8cos ,8sin ππ,⎪⎭⎫ ⎝⎛1,83cos ,83sinππ,⎪⎭⎫ ⎝⎛1,85cos ,85sin ππ,⎪⎭⎫ ⎝⎛1,811cos ,811sin ππ,⎪⎭⎫ ⎝⎛1,813cos ,813sin ππ,⎪⎭⎫ ⎝⎛1,815cos ,815sin ππ 四、程序设计(1)作出原图>> t=[1 3 5 11 13 15]*pi/8 >> x=sin(t) >> y=cos(t) >> fill(x,y,'r') >> grid on>> axis([-2.4, 2.4, -2, 2])几何与代数实验报告(2) 将上面图形放大0.9倍>>A=[0.3827,0.9239,0.9239,-0.9239,-0.9239,-0.3827;0.9239,0.3827,-0.3827,-0.3827,0.3827,0.92 39;1,1,1,1,1,1]>> T1=[0.9,0,0;0,0.9,0;0,0,1]>> B=T1*A>> fill(B(1,:), B(2,:),'r')(3) 逆时针旋转>> T2=[cos(pi/3),-sin(pi/3),0;sin(pi/3),cos(pi/3),0;0,0,1]>> C=T2*B>> fill(C(1,:), C(2,:),'r')(4) 进行横坐标加0.8、纵坐标减1的图形平移>> T3=[1,0,0.8;0,1,-1;0,0,1]>> D=T3*C>> fill(D(1,:), D(2,:),'r')(5)将刚刚做的四幅图放在一张图上>> subplot(2, 2, 1),fill(x,y,'r'),subplot(2, 2, 2),fill(B(1,:), B(2,:),'r'),subplot(2, 2, 3),fill(C(1,:), C(2,:),'r'),subplot(2, 2, 4),fill(D(1,:), D(2,:),'r')五、程序运行结果(1)作出原图t =0.3927 1.1781 1.9635 4.3197 5.1051 5.8905x =0.3827 0.9239 0.9239 -0.9239 -0.9239 -0.3827y =0.9239 0.3827 -0.3827 -0.3827 0.3827 0.9239几何与代数实验报告(2) 将上面图形放大0.9倍A =0.3827 0.9239 0.9239 -0.9239 -0.9239 -0.38270.9239 0.3827 -0.3827 -0.3827 0.3827 0.92391.0000 1.0000 1.0000 1.0000 1.0000 1.0000 T1 =0.9000 0 00 0.9000 00 0 1.0000B =0.3444 0.8315 0.8315 -0.8315 -0.8315 -0.34440.8315 0.3444 -0.3444 -0.3444 0.3444 0.83151.0000 1.0000 1.0000 1.0000 1.0000 1.0000(3) 逆时针旋转T2 =0.5000 -0.8660 00.8660 0.5000 00 0 1.0000C =-0.5479 0.1175 0.7140 -0.1175 -0.7140 -0.89230.7140 0.8923 0.5479 -0.8923 -0.5479 0.11751.0000 1.0000 1.0000 1.0000 1.0000 1.0000几何与代数实验报告(4) 进行横坐标加0.8、纵坐标减1的图形平移T3 =1.0000 0 0.80000 1.0000 -1.00000 0 1.0000D =0.2521 0.9175 1.5140 0.6825 0.0860 -0.0923-0.2860 -0.1077 -0.4521 -1.8923 -1.5479 -0.88251.0000 1.0000 1.0000 1.0000 1.0000 1.0000(5)将刚刚做的四幅图放在一张图上几何与代数实验报告-1-0.500.51-1-0.500.51实验02平板的稳态温度分布问题(线性方程组应用)一、 实验题目已知平板内部有30个节点,每个节点的温度近似等于与它相邻的四个节点温度的平均值,例如4292530rd T T T T T +++=;设4条边界上的温度分别等于每位同学学号的后四位的5倍,例如学号为16308209的同学计算时,选择40=l T 、10=u T 、0=r T 、45=d T 。
matlab第一次实验报告

一、心得体会在此之前只接触过Matlab一段时间,通过本次上机实验初次体验,体会到Mathematica语法规则简单,操作使用方便,和其他语言交互,编程灵活方便,功能十分强大。
Mathematica和Matlab都可以实现某个方案,不同之处在于对不同的问题,处理的方法繁琐程度不一样。
软件掌握多少都不算多,类似的软件还有MathCAD、Maple等,关键在处理具体问题的时候那种软件更适合,或者那种软件处理问题普遍性强,而Mathematica和Matlab分别代表了符号计算和数据处理(或者数值计算)的两个方面普遍适用的软件。
个人感觉Mathematica符号计算强,便于公式推导和函数式制图。
Mathematica界面的窗口和菜单栏是分离式的,便于边计算边对照查看文档,其公式可以复制为公式格式,可直接粘贴于Word等文本中,也便于以公式的形式输入,但该功能在大量符号计算中可能作用不大,编写代码的执行效率肯定比手动输入公式要高的多。
输入和输出都是在同一个界面,便于查看每条代码的结果。
函数使用方式丰富,调用函数可以编写专门的文件,也可直接在输入界面中调用。
可把想到的代码都写成函数的形式,包括各种形式的代码,便于调用。
将所有的算法最终转化为表达式,以函数的形式体现。
例如绘图将表达式的变量范围指定即可,便于函数制图。
Matlab很强大,处理什么都比较得心应手,是款很好的数学式编程工具与计算工具,修改编辑很方便,但体积比较大。
Mathematica 个人感觉侧重于图像处理,尤其那些多边形,多维空间制图,曲面等很实用,而且软件体积比较少,运行速度快,是款和MATLAB 相辅相成的好工具。
通过以上,我自认为较好的解决方案是数据处理用Matlab ,然后将数据导入Mathematica 可视化处理。
符号计算就是Mathematica 了。
以后还需多进行实验,体会Mathematica 的功能。
二、指令运行关于Mathematica 绘图的基本功能以不同输出格式画曲面2||,2||,)(22≤≤=+-y x e z y x Plot3D[Exp[-(x^2+y^2)],{x,-2,2},{y,-2,2}]螺旋线:x=sint,y=cost,z=t/3的图形ParametricPlot3D[{Sin[t],Cos[t],t/8},{t,0,15},Axes →False]圆环面x=cost(3+cosu),y=sint(3+cosu),z=sinu,u≤t≤2π,0≤u≤2π的图形ParametricPlot3D[{Cos[t](3+Cos[u]),Sin[t](3+Cos[u]),Sin[u]},{t,0,2Pi},{u,0, 2Pi},Axes False]三、问题求解(Help)。
-MATLAB 数学实验报告

MATLAB 数学实验报告求下列解方程组:1.(1)⎪⎪⎩⎪⎪⎨⎧=+--=-+-=++-0202432143214321xxxx x xx x xx x x(2)⎪⎪⎩⎪⎪⎨⎧=+=+-=-+0302403231321321x x x x x x x x2. ⎪⎪⎩⎪⎪⎨⎧=++=+-=-+883111023224321321321x x x x x x x x x例1. 绘制函数表达式x²-y³的二维图形。
例2. 在极坐标下绘制函数表达式1+cost的二维图形。
例3. 根据表达式x=sint、y=cost、z=t,绘制三维曲线。
实验过程记录(含基本步骤,主要程序清单及异常情况记录等):1.解:(1) >> A=[1 -1 1 1;1 -1 1 -2;1 -1 -2 1];>> format rat>> n=4;>> RA=rank(A)RA =3>> if(RA==n)else B=null(A,'r')endB =11>> syms k>> x=k*Bx =kk(2) >> A=[2 3 -1;4 -2 1;1 0 3];>> format rat>> n=3;>> RA=rank(A)RA =3>> if(RA==n) x=[0 0 0]else B=null(A,'r')endx =0 0 0 2.解:>> A=[4 2 -1;3 -1 2;11 3 8];b=[2 10 8]';B=[A b];n=3;RA=rank(A)RA =3>> RB=rank(B)RB =3>> if(RA==RB&RA==n)X=A\belse if(RA==RB&RA<n)C=A\bD=null(A,'r')endX =97/40-169/40-3/4例1.解:>> syms x y>>ezplot(x^2-y^)3) 例2. 解: >> syms t>> ezpolar(1+cos(t)) 例3. 解: >> syms t>> ezplot3(sin(t),cos(t),t,[0,6*pi])实验结果报告及实验总结:1.(1)的解为x = kk 0 0(2)的解为x = 00 02的解为X =97/40 -169/40 -3/4 例1.图形结果:xyx 2-y 3 = 0例2.图形结果:902701800r = 1+cos(t)例3.图形结果:-1xx = sin(t), y = cos(t), z = tyz实验总结:对于以上题目的解析,这是我第一次用MATLAB 进行编程来求解实际问题,虽然过程有点艰辛,但每一步都亲力亲为,这让我收获很多,通过做次实验,让我对MATLAB有了进一步的了解,了解了它的强大的功能和他如何求解实际问题,激发了我学好MATLAB的决心。
MATLAB实验报告

MATLAB实验报告MATLAB 实验报告姓名:专业:学号:实验⼀ MATLAB环境的熟悉与基本运算⼀、实验⽬的:1.熟悉MATLAB开发环境2.掌握矩阵、变量、表达式的各种基本运算⼆、实验基本知识:1.熟悉MATLAB环境:MATLAB桌⾯和命令窗⼝、命令历史窗⼝、帮助信息浏览器、⼯作空间浏览器⽂件和搜索路径浏览器。
2.掌握MATLAB常⽤命令3.MATLAB变量与运算符变量命名规则如下:(1)变量名可以由英语字母、数字和下划线组成(2)变量名应以英⽂字母开头(3)长度不⼤于31个(4)区分⼤⼩写MATLAB中设置了⼀些特殊的变量与常量,列于下表。
MATLAB运算符,通过下⾯⼏个表来说明MATLAB的各种常⽤运算符表2 MATLAB算术运算符表3 MATLAB关系运算符表4 MATLAB逻辑运算符表5 MATLAB特殊运算4.MATLAB的⼀维、⼆维数组的寻访表6 ⼦数组访问与赋值常⽤的相关指令格式5.MATLAB的基本运算表7 两种运算指令形式和实质内涵的异同表6.MATLAB的常⽤函数表8 标准数组⽣成函数表9 数组操作函数三、实验内容1、学习安装MATLAB软件。
2、学习使⽤help命令,例如在命令窗⼝输⼊help eye,然后根据帮助说明,学习使⽤指令eye(其它不会⽤的指令,依照此⽅法类推)3、学习使⽤clc、clear,观察command window、command history和workspace 等窗⼝的变化结果。
4、初步程序的编写练习,新建M-file,保存(⾃⼰设定⽂件名,例如exerc1、exerc2、exerc3……),学习使⽤MATLAB的基本运算符、数组寻访指令、标准数组⽣成函数和数组操作函数。
注意:每⼀次M-file的修改后,都要存盘。
四、实验结果练习A:(1)help rand,然后随机⽣成⼀个2×6的数组,观察command window、command history和workspace等窗⼝的变化结果。
matlab实验报告

matlab实验报告实验报告:Matlab实验分析1. 实验目的本实验旨在通过Matlab软件完成一系列数值计算和数据分析的任务,包括绘制曲线、解方程、矩阵运算等,以加深对Matlab软件的理解和掌握。
2. 实验内容2.1 绘制函数曲线首先,我们通过在Matlab中输入函数的表达式来绘制函数曲线。
例如,我们可以输入y = sin(x)来绘制正弦函数的曲线。
另外,我们还可以设置曲线的颜色、线型和坐标轴范围等。
2.2 解方程接下来,我们使用Matlab来解方程。
对于一元方程,我们可以使用solve函数来求出方程的解。
例如,我们输入syms x; solve(x^2 - 2*x - 8)来解方程x^2 - 2x - 8 = 0。
而对于多元方程组,我们可以使用solve函数的向量输入形式来求解。
例如,我们输入syms x y; solve(x^2 + y^2 - 1, x - y - 1)来求解方程组x^2 + y^2 - 1 = 0和x - y - 1 = 0的解。
2.3 矩阵运算Matlab也可以进行矩阵运算。
我们可以使用矩阵相乘、相加和取逆等运算。
例如,我们可以输入A = [1 2; 3 4]和B = [5 6;7 8]来定义两个矩阵,然后使用A * B来计算它们的乘积。
3. 实验结果与分析在本实验中,我们成功完成了绘制函数曲线、解方程和矩阵运算等任务。
通过Matlab软件,我们可以快速、准确地进行数值计算和数据分析。
使用Matlab的高级函数和工具箱,我们可以更方便地处理复杂的数值计算和数据分析问题。
4. 实验总结通过本次实验,我们进一步加深了对Matlab软件的理解和掌握。
Matlab提供了丰富的函数库和工具箱,适用于各种不同的数值计算和数据分析任务。
在日常科研和工程实践中,Matlab是一个非常强大和方便的工具,可以帮助我们更高效地完成任务。
(完整word)Matlab实验报告
实验一:Matlab操作环境熟悉一、实验目的1.初步了解Matlab操作环境.2.学习使用图形函数计算器命令funtool及其环境。
二、实验内容熟悉Matlab操作环境,认识命令窗口、内存工作区窗口、历史命令窗口;学会使用format 命令调整命令窗口的数据显示格式;学会使用变量和矩阵的输入,并进行简单的计算;学会使用who和whos命令查看内存变量信息;学会使用图形函数计算器funtool,并进行下列计算:1.单函数运算操作。
求下列函数的符号导数(1)y=sin(x);(2) y=(1+x)^3*(2-x);求下列函数的符号积分(1)y=cos(x);(2)y=1/(1+x^2);(3)y=1/sqrt(1—x^2);(4)y=(x1)/(x+1)/(x+2)求反函数(1)y=(x-1)/(2*x+3); (2) y=exp(x);(3) y=log(x+sqrt(1+x^2));代数式的化简(1)(x+1)*(x-1)*(x-2)/(x-3)/(x—4);(2)sin(x)^2+cos(x)^2;(3)x+sin(x)+2*x—3*cos(x)+4*x*sin(x);2.函数与参数的运算操作。
从y=x^2通过参数的选择去观察下列函数的图形变化(1)y1=(x+1)^2(2)y2=(x+2)^2(3) y3=2*x^2 (4) y4=x^2+2 (5) y5=x^4 (6) y6=x^2/2 3.两个函数之间的操作求和(1)sin(x)+cos(x) (2) 1+x+x^2+x^3+x^4+x^5乘积(1)exp(—x)*sin(x) (2) sin(x)*x商(1)sin(x)/cos(x); (2) x/(1+x^2); (3) 1/(x—1)/(x—2); 求复合函数(1)y=exp(u) u=sin(x) (2) y=sqrt(u) u=1+exp(x^2)(3) y=sin(u) u=asin(x) (4) y=sinh(u) u=-x实验二:MATLAB基本操作与用法一、实验目的1.掌握用MATLAB命令窗口进行简单数学运算。
matlab实验报告

matlab实验报告《matlab 实验报告》一、实验目的通过本次实验,熟悉 MATLAB 软件的基本操作和功能,掌握使用MATLAB 进行数学计算、数据处理、图形绘制等方面的方法和技巧,提高运用 MATLAB 解决实际问题的能力。
二、实验环境1、计算机:_____2、操作系统:_____3、 MATLAB 版本:_____三、实验内容及步骤(一)矩阵运算1、创建矩阵在 MATLAB 中,可以通过直接输入元素的方式创建矩阵,例如:`A = 1 2 3; 4 5 6; 7 8 9`,创建了一个 3 行 3 列的矩阵 A。
还可以使用函数来创建特定类型的矩阵,如全零矩阵`zeros(m,n)`、全 1 矩阵`ones(m,n)`、单位矩阵`eye(n)`等。
2、矩阵的基本运算加法和减法:两个矩阵相加或相减,要求它们的维度相同,对应元素进行运算。
乘法:矩阵乘法需要满足前一个矩阵的列数等于后一个矩阵的行数。
转置:使用`A'`来获取矩阵 A 的转置。
(二)函数的使用1、自定义函数可以在 MATLAB 中自定义函数,例如定义一个计算两个数之和的函数:```matlabfunction s = add_numbers(a,b)s = a + b;end```2、调用函数在命令窗口中输入`add_numbers(3,5)`即可得到结果 8。
(三)数据的读取和写入1、读取数据使用`load`函数可以读取数据文件,例如`load('datatxt')`。
2、写入数据使用`save`函数可以将数据保存到文件中,例如`save('resulttxt',A)`,将矩阵 A 保存到`resulttxt`文件中。
(四)图形绘制1、二维图形绘制折线图:使用`plot(x,y)`函数,其中 x 和 y 分别是横坐标和纵坐标的数据。
绘制柱状图:使用`bar(x,y)`函数。
2、三维图形绘制三维曲线:使用`plot3(x,y,z)`函数。
东南大学几何与代数(B)数学实验报告
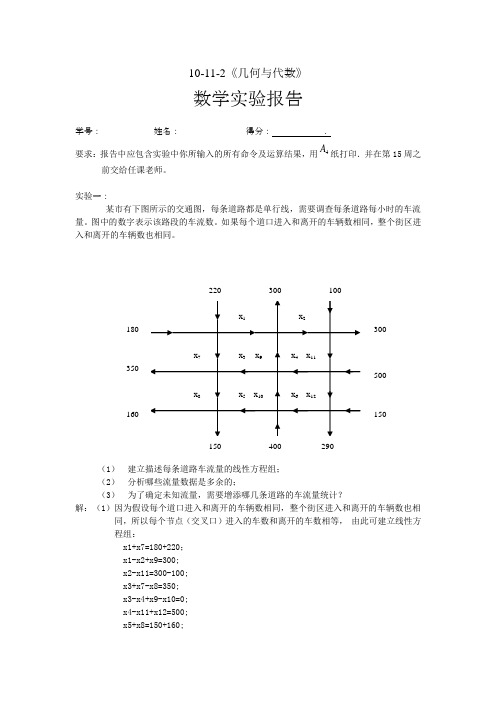
10-11-2《几何与代数》数学实验报告学号: 姓名: 得分: . 要求:报告中应包含实验中你所输入的所有命令及运算结果,用4A 纸打印.并在第15周之前交给任课老师。
实验一:某市有下图所示的交通图,每条道路都是单行线,需要调查每条道路每小时的车流量。
图中的数字表示该路段的车流数。
如果每个道口进入和离开的车辆数相同,整个街区进入和离开的车辆数也相同。
(1) 建立描述每条道路车流量的线性方程组; (2) 分析哪些流量数据是多余的;(3) 为了确定未知流量,需要增添哪几条道路的车流量统计?解:(1)因为假设每个道口进入和离开的车辆数相同,整个街区进入和离开的车辆数也相同,所以每个节点(交叉口)进入的车数和离开的车数相等, 由此可建立线性方程组:x1+x7=180+220; x1-x2+x9=300; x2-x11=300-100; x3+x7-x8=350; x3-x4+x9-x10=0; x4-x11+x12=500; x5+x8=150+160;x5-x6+x10=400;x6-x12=150-290;(2)把线性方程组的增广矩阵输入matlab软件:>>A=[1,0,0,0,0,0,1,0,0,0,0,0,400;1,-1,0,0,0,0,0,0,1,0,0,0,300;0,1,0,0,0,0,0,0,0,0,-1,0,200;0,0,1,0,0,0,1,-1,0,0,0,0,350;0,0,-1,1,0,0,0,0,-1,1,0,0,0;0,0,0,1,0,0,0,0,0,0,-1,1,500;0,0,0,0,1,0,0,1,0,0,0,0,310;0,0,0,0,1,-1,0,0,0,1,0,0,400;0,0,0,0,0,1,0,0,0,0,0,-1,-140]点击“回车”键,A =1 0 0 0 0 0 1 0 0 0 0 0 4001 -1 0 0 0 0 0 0 1 0 0 0 3000 1 0 0 0 0 0 0 0 0 -1 0 2000 0 1 0 0 0 1 -1 0 0 0 0 3500 0 -1 1 0 0 0 0 -1 1 0 0 00 0 0 1 0 0 0 0 0 0 -1 1 5000 0 0 0 1 0 0 1 0 0 0 0 3100 0 0 0 1 -1 0 0 0 1 0 0 4000 0 0 0 0 1 0 0 0 0 0 -1 -140把增广矩阵经初等变换成最简阶梯型矩阵>> rref(A)点击“回车”键,得到最简阶梯型矩阵ans =1 0 0 0 0 0 0 0 1 0 -1 0 5000 1 0 0 0 0 0 0 0 0 -1 0 2000 0 1 0 0 0 0 0 1 -1 -1 1 5000 0 0 1 0 0 0 0 0 0 -1 1 5000 0 0 0 1 0 0 0 0 1 0 -1 2600 0 0 0 0 1 0 0 0 0 0 -1 -1400 0 0 0 0 0 1 0 -1 0 1 0 -1000 0 0 0 0 0 0 1 0 -1 0 1 500 0 0 0 0 0 0 0 0 0 0 0 0由于最简阶梯型矩阵最后一行均为“0”,所以最后一个方程中的数据“150”和“290”是多余的。
实验报告二 Matlab图像代数运算和几何变换

实验二Matlab图像代数运算和几何变换一、实验目的1、掌握不同图像类型的转换2、掌握图像代数运算和几何变换的方法;3、掌握灰度级插值法的实验方法。
二、实验内容1、练习图像类型转换的相关命令(ind2rgb,mat2gray,grayslice,rgb2gray,rgb2ind,im2bw,ind2gray,dither)(p69-73);2、练习课本6.3.2(p139-p143)图像代数运算的内容;3、练习图像平移 (p148),图像比例变换(p153),图像旋转(p156),图像镜像变换(p158),图像切割(p160)Matlab实现例题;4、练习灰度级插值法(p171)。
三、实验步骤和结果1、练习图像类型转换的相关命令(ind2rgb,mat2gray,grayslice,rgb2gray,rgb2ind,im2bw,ind2gray,dither)(1)mat2gray()函数I=imread('rice.png');>> J=filter2(fspecial('sobel'),I);>> K=mat2gray(J);>> imshow(I);>> figure,imshow(K)(2)、grayslice()函数>> I=imread('snowflakes.png');>> X=grayslice(I,16);>> imview(I)imview(X,jet(16))(3)、rgb2ind()函数> RGB=imread('peppers.png');>> imshow(RGB);>> figure,imshow(RGB)>> [X,map]=rgb2ind(RGB,128);>> figure,imshow(X,map) (4)、im2bw()函数>> load trees>> BW=im2bw(X,map,0.4);>> figure,imshow(X,map)>> figure,imshow(BW)(5)、ind2gray()函数load trees>> I=ind2gray(X,map);>> figure,imshow(X,map)>> figure,imshow(I)(6)、dither()函数>> RGB=imread('peppers.png'); >> [X,map]=rgb2ind(RGB,256); >> I=dither(RGB,map);>> BW=dither(I);>> imshow(RGB,map);>> figure,imshow(RGB,map); >> figure,imshow(BW)Result:(1)转换后图像(2)索引色图像(3)索引色图像(4)索引色图像(4)二值化后的图像(5)转换后的灰度图像(6)索引色图像(6)抖动转换图像2、练习课本6.3.2(p139-p143)图像代数运算的内容(1)加法运算I=imread('rice.png');>> figure(1),imshow(I,[])>> I2=imread('cameraman.tif')>> figure(2),imshow(I2,[])>> K=imadd(I,I2,'uint16');>> figure(3),imshow(K,[])>> I=imread('lena.bmp');>> I2=imadd(I,50);>> figure(1),imshow(I)>> figure(2),imshow(I2)(2)、减法运算>> I=imread('rice.png'); >> I2=imread('cameraman.tif'); >> I3=imsubtract(I,I2);>> figure,imview(I3)(3)乘法&除法运算>> I=imread('lena.bmp');>> I2=immultiply(I,0.5);>> figure,imshow(I)>> figure,imshow(I2)>> I3=immultiply(I,1.5);>> figure,imshow(I3)>> I4=imdivide(I,0.5);>> figure,imshow(I4)>> I5=imdivide(I,1);>> figure,imshow(I5)Result:(1)加法运算后的图像(1)加入常数后的图像(2)减法运算(3)乘以0.5后的图像乘以1后的图像除以0.5后的图像除以1后的图像3、练习图像平移 (p148),图像比例变换(p153),图像旋转(p156),图像镜像变换(p158),图像切割(p160)Matlab实现例题;(a)图像平移>> I=imread('trees.tif');>> figure,imshow(I)>> I=double(I);>> I_movesult=zeros(size(I));>> H=size(I);>> Move_x=50;>> Move_y=50;>>I_movesult(Move_x+1:H(1),Move_y+1:H(2))=I(1:H(1)-Move_x,1:H(2)-Move_y);>> figure,imshow(uint8(I_movesult))(b)图像比例变换J=imread('trees.tif');>> figure,imshow(J);>> X1=imresize(J,2);>> X2=imresize(J,0.5);>> figure,imshow(X1)>> figure,imshow(X2)(C)图像旋转变换>> I=imread('peppers.png');>> figure,imshow(I)>> X1=imrotate(I,30,'nearest');>> figure,imshow(uint8(X1))>> X2=imrotate(I,45,'nearest');>> figure,imshow(uint8(X2))>> X3=imrotate(I,60,'nearest');>> figure,imshow(uint8(X3))>> X4=imrotate(I,90,'nearest');>> figure,imshow(uint8(X4))(d)图像镜像变换>> I=imread('forest.tif');>> I=double(I);>> figure,imshow(uint8(I));>> H=size(I);>> figure(2),>> I2(1:H(1),1:H(2))=I(H(1):-1:1,1:H(2));>> imshow(uint8(I2));>> figure,imshow(uint8(I2));>> I3(1:H(1),1:H(2))=I(1:H(1),H(2):-1:1);>> figure,imshow(uint8(I3));>> I4(1:H(1),1:H(2))=I(H(1):-1:1,H(2):-1:1);>> figure,imshow(uint8(I4));(e)图像切割>> I1=imread('peppers.png');>> I2=imcrop(I1,[75 68 220 100]);>> imview(I2)I3=imcrop(I1,[30 40 120 100]);>> imview(I3)(a)平移后的图像(b)放大后图像(b)缩小后的图像(c)旋转30°后的图像旋转45°后的图像旋转60°后的图像旋转90°后的图像(d)原始图像垂直镜像水平镜像对角镜像(e)原始图像一次切割后图像二次切割后图像4、练习灰度级插值法(p171)>> I=imread('lena.bmp');>> X1=imresize(I,1);>> X2=imresize(I,1,'bilinear');>> X3=imresize(I,1,'bicubic');>> figure,imshow(X1)>> figure,imshow(X2)>> figure,imshow(X3)最近邻差值法双线性插值法三次插值法四、实验体会在本次实验中掌握不同图像类型的转换,掌握了转换函数及其语法格式,如ind2rgb()函数将索引图像转换成真彩色。
Matlab数学实验报告

实验一 Matlab基本操作1.实验课程名称数学实验2.实验项目名称Matlab基本操作3.实验目的和要求了解Matlab的基本知识,熟悉其上机环境,掌握利用Matlab进行基本运算的方法。
4.实验内容和原理内容:三角形的面积的海伦公式为:area=)s-sa--)()(s(csb其中: s=(a+b+c)/2原理:将一般数学问题转化成对应的计算机模型并进行处理的能力。
了解Matlab的基本功能,会进行简单的操作。
5.主要仪器设备计算机与Windows 2000/XP系统;Matlab等软件。
6.操作方法与实验步骤步骤:(1)在M文件编辑窗口输入以下程序,并以文件名”area_helen.m”保存:a= input(‘a=‘) ; b= input(‘b=‘) ; c= input(‘c=‘) ;s= (a+b+c)/2;area=sqrt (s* (s-a) * (s-b) * (s-c))(2)在命令窗口输入文件名“area_helen”,按回车键,即可运行上面的程序,输入三边长,立即可得三角形面积(3)第二题在命令窗口输入b=6;a=3;c=a*b,d=c-2*b(4) 按回车键,即可运行上面的程序7.实验结果与分析<1> a=3; b=4; c=5;时,aera=6 当a为3,b为4,c为5时,s=6,aera=6<2> c= 18,d=6,a为3,b为6时,c=18,d=6实验二 Matlab的数值计算1.实验课程名称数学实验2.实验项目名称Matlab的数值计算3.实验目的和要求了解一些简单的矩阵、向量、数组和多项式的构造和运算方法实例,懂得编写简单的数值计算的Matlab程序。
熟悉一些Matlab的简单程序,会用Matlab的工具箱,懂得Matlab的安装和简单的使用。
4.实验内容和原理内容:从函数表:)1(),5.0(),2( ,0x 1x 021x 1x f(x) 32-⎪⎩⎪⎨⎧≤≤<>+=f f f x x求设)1(),2( ,1211)(2-⎩⎨⎧≤>+=f f x xx x x f 求设 原理:利用矩阵、向量、数组、和多项式的构造和运算方法,用常用的几种函数进行一般的数值问题求解。
matlab实验一实验报告

matlab实验一实验报告一、实验目的本次实验的主要目的是熟悉 MATLAB 软件的基本操作环境和编程语法,通过实际编写和运行简单的程序,初步掌握 MATLAB 在数值计算、图形绘制和数据处理方面的基本功能。
二、实验环境本次实验使用的是 MATLAB R2020a 版本,运行在 Windows 10 操作系统上。
计算机配置为:Intel Core i5 处理器,8GB 内存。
三、实验内容及步骤1、矩阵运算创建一个 3×3 的矩阵 A,元素分别为 1 到 9。
创建一个 3×3 的零矩阵 B。
计算 A+B 和 A×B 的结果。
在 MATLAB 中,我们可以使用以下代码实现:```matlabA = 1 2 3; 4 5 6; 7 8 9;B = zeros(3);C = A + B;D = A B;disp(C);disp(D);```2、数据类型转换定义一个整数变量 x 为 5。
将 x 转换为双精度浮点数。
将 x 转换为字符串类型。
代码如下:```matlabx = 5;y = double(x);z = num2str(x);disp(y);disp(z);```3、函数调用定义一个函数 fun,输入参数为 x,返回值为 x 的平方。
调用函数 fun,计算 3 的平方。
函数定义及调用代码:```matlabfunction y = fun(x)y = x^2;endresult = fun(3);disp(result);```4、图形绘制绘制函数 y = sin(x)在区间0, 2π上的图像。
使用以下代码实现:```matlabx = 0:001:2pi;y = sin(x);plot(x, y);```四、实验结果1、矩阵运算A+B 的结果为:```matlab1 2 34 5 67 8 9```A×B 的结果为:```matlab0 0 00 0 00 0 0```2、数据类型转换将整数 5 转换为双精度浮点数,结果为 50000。
东南大学-实验五--Matlab-Simulink仿真实验报告

东南大学自动控制实验室实验报告课程名称:自动控制原理实验实验名称:实验五Matlab/Simulink仿真实验院(系):自动化专业:自动化姓名:学号:实验室:417 实验组别:同组人员:实验时间:2016年12月09日评定成绩:审阅教师:目录一.实验目的 (3)二.预习要求 (3)三. 实验内容 (3)四、实验小结 (11)一、实验目的(1)学习系统数学模型的多种表达方法,并会用函数相互转换。
(2)学习模型串并联及反馈连接后的系统传递函数。
(3)掌握系统BODE图,根轨迹图及奈奎斯特曲线的绘制方法。
并利用其对系统进行分析。
(4)掌握系统时域仿真的方法,并利用其对系统进行分析。
二、预习要求参阅相关Matlab/Simulink参考书,熟悉能解决题目问题的相关Matlab函数。
三、实验内容1.已知,求H(s)的零极点表达式和状态空间表达式。
(1)运算代码>> num=[0.051];>> den=conv([0.2,1],[0.1,1]);>> sys=tf(num,den);>> zpk(sys)>> [a,b,c,d]=tf2ss(num,den)(2)结果零极点表达式:状态空间表达式:其中:2.已知,。
(1)求两模型串联后的系统传递函数。
运算代码:>> num1=[1,5];>> den1=conv([1,0],conv([1,1],[1,2]));>> sys1=tf(num1,den1);>> num2=[1];>> den2=[1 1];>> sys2=tf(num2,den2);>> sys3=series(sys1,sys2)结果:(2)求两模型并联后的系统传递函数。
运算代码:>> sys4=parallel(sys1,sys2)结果:(3)求两模型在负反馈连接下的系统传递函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学实验报告
学号: , 姓名: 吴雪松, 得分:
实验1 求解线性方程组
实验内容: 用MATLAB求解如下线性方程组Ax = b, 其中
A =
56000000
15600000
01560000
00156000
00015600
00001560
00000156
00000015
⎡⎤
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎣⎦
, b = [09009320] T.
实验目的: 1. 了解MATLAB软件, 学会MATLAB软件的一些基本操作;
2. 熟悉MATLAB软件的一些数值计算功能,如在矩阵方面的运算;
3. 练习编写简单的MATLAB程序。
实验原理: 1. 对于齐次线性方程组Ax = b, 根据gramer法则, 其解为X i=D i/D;
2. 当A可逆,即|A|≠0时, 方程组Ax = b的解为X=inv(A)*B;
3. 当……时, 对增广矩阵[A, b]进行初等行变换, 把它化为最简形, 则
原矩阵b对应的地方即为A-1*b,取最简形的最后一列赋给X即得线
性方程组的解。
实验方案: 1. 在MATLAB命令窗口中输入如下命令:
A=[5 6 0 0 0 0 0 0;
1 5 6 0 0 0 0 0;
0 1 5 6 0 0 0 0;
0 0 1 5 6 0 0 0;
0 0 0 1 5 6 0 0;
0 0 0 0 1 5 6 0;
0 0 0 0 0 1 5 6;
0 0 0 0 0 0 1 5;];
b=[0 9 0 0 9 3 2 0]';%输入矩阵A与b
X=[]; %声明一个名为X的空矩阵
D=det(A); %把A的行列式的值求出来赋给D
for i=1:8 %开始循环语句
A=[5 6 0 0 0 0 0 0;
1 5 6 0 0 0 0 0;
0 1 5 6 0 0 0 0;
0 0 1 5 6 0 0 0;
0 0 0 1 5 6 0 0;
0 0 0 0 1 5 6 0;
0 0 0 0 0 1 5 6;
0 0 0 0 0 0 1 5;];
b=[0 9 0 0 9 3 2 0]';
A(:,i)=b; %把A的第i列替换成b
X=[X,det(A)/D]; %把求出的每个值填入空矩阵X对应的列中
i=i+1; %让i递增一控制循环的结束
end %结束for循环
X=X’%输出矩阵X的转置,即为线性方程组的解
2. 在MATLAB命令窗口中输入如下命令:
A=[5 6 0 0 0 0 0 0;
1 5 6 0 0 0 0 0;
0 1 5 6 0 0 0 0;
0 0 1 5 6 0 0 0;
0 0 0 1 5 6 0 0;
0 0 0 0 1 5 6 0;
0 0 0 0 0 1 5 6;
0 0 0 0 0 0 1 5];
b=[0 9 0 0 9 3 2 0]';%输入矩阵A和b
X=inv(A)*b%把A逆与b相乘的结果赋给X,即为线性方程组的解3. 在MATLAB命令窗口中输入如下命令:
A=[5 6 0 0 0 0 0 0;
1 5 6 0 0 0 0 0;
0 1 5 6 0 0 0 0;
0 0 1 5 6 0 0 0;
0 0 0 1 5 6 0 0;
0 0 0 0 1 5 6 0;
0 0 0 0 0 1 5 6;
0 0 0 0 0 0 1 5];
b=[0 9 0 0 9 3 2 0]'; %输入矩阵A和b
C=rref([A,b]); %将A的增广矩阵[A,b]化为最简形并赋给C
X=C(:,9) %取C的第九列并赋给X,即为线性方程组的解
实验结果: 1. 2. 3.
X =
34.9644
-29.1370
19.9534
-11.7717
6.4842
-1.9415
1.0372
-0.2074 X =
34.9644
-29.1370
19.9534
-11.7717
6.4842
-1.9415
1.0372
-0.2074
X =
34.9643
-29.1370
19.9535
-11.7717
6.4842
-1.9415
1.0372
-0.2075
对实验结果的分析:
在上述3种方案中,前两种的结果完全相同,而与第三种方案的结果稍有不同,但差距极小,只要是由于不同的计算方法导致运算过程中近似程度不同,导致最终的精度不同。
实验2 研究三个平面的位置关系
实验内容: 用MATLAB研究下面的3个平面
π1: x + y + z = 1
π2: -x + y = 2
π3: 2x + t2z = t
当t取何值时交于一点? 当t取何值时交于一直线? 当t取何值时没
有公共的交点? 并在每一种情形下, 用MATLAB在同一个坐标系内
绘制出这3个平面的图形(其中, 没有公共的交点的情况, 只要给t取
一个适当的值即可).
实验目的: 1. 练习编写简单的MATLAB程序;
2. 掌握用MATLAB软件绘制简单图形的方法。
实验原理: 联立这3个平面的方程, 得方程组:
⎪⎩⎪
⎨⎧=+=+=++ t
z *t x *2 2
y x - 1 z y x 2
令A =[1,1,1;-1,1,0;2, 0,2t ], b = [1,2 t]’, B = [A , b ], 则原问题转化为线
性方程组Ax=b 的解问题,当t 取何值时有唯一解; 当t 取何值时有无穷多解; 当t 取何值时无解. 根据非齐次线性方程组的解的理论, 求出相应的t 的取值或取值范围,并用matlab 作出图形即可。
计算得:
当t ≠1且t ≠-1时,线性方程组只有一解,三平面交于一点; 当t=-1时,线性方程组有无穷多解,三平面交于一条直线; 当t=1时,线性方程组无解,三平面无公共点。
实验方案: 1. 在MATLAB 命令窗口中输入如下命令:
z=-2:0.1:2;y=z; %规定z 的取值范围和精确度 [Y ,Z]=meshgrid(y,z);
%用y 和z 产生“格点”矩阵 X1=-Y-Z+ ones(size(Z)); %平面p1 X2= Y+0*Z-2*ones(size(Z)); %平面p2 X3=-2*Z+1*ones(size(Z));%平面p3.取t=2
surf(X1,Y ,Z),hold on,mesh(X2,Y ,Z),mesh(X3,Y ,Z) %在同一个坐标系中作出三个平面的图形
2. 在MATLAB 命令窗口中输入如下命令:
z=-2:0.1:2;y=z; %规定z 的取值范围和精确度 [Y ,Z]=meshgrid(y,z);
%用y 和z 产生“格点”矩阵 X1=-Y-Z+ ones(size(Z)); %平面p1 X2= Y+0*Z-2*ones(size(Z)); %平面p2
X3=-(1/2)*Z-(1/2)*ones(size(Z)); % 平面p3. 取t=-1
surf(X1,Y ,Z),hold on,mesh(X2,Y ,Z),mesh(X3,Y ,Z)3. %在同一个坐标系中作出三个平面的图形
3. 在MATLAB 命令窗口中输入如下命令:
z=-2:0.1:2;y=z; %规定z 的取值范围和精确度 [Y ,Z]=meshgrid(y,z); %用y 和z 产生“格点”矩阵 X1=-Y-Z+ ones(size(Z)); %平面p1 X2= Y+0*Z-2*ones(size(Z)); %平面p2.
X3=-(1/2)*Z+(1/2)* ones (size(Z)); %平面p3. 取t=1.
surf(X1,Y ,Z),hold on, mesh(X2,Y ,Z),mesh(X3,Y ,Z) %在同一个坐标系中作出三个平面的图形
实验结果: 1.
2.
3.
对实验结果的分析:。
