力对点的矩与力对轴的矩(可修改).ppt
合集下载
(完整版)力与力矩

力矩的量纲是距离乘以力;依照国际单位制,力矩的单位是牛顿-米。
虽然牛顿与米的次序,在数学上,是可以变换的。
BIPM (国际重量测量局) 设定这次序应是牛顿-米,而不是米-牛顿。
事实上,力矩与能量的关系是能量和一个对数矢量2π[lnK]的乘积,即t=2πQ[lnK],[lnk]的方向垂直于作用平面。
因此用焦耳做单位也不是错误的。
做圆周运动时,K=e,因此使 1 牛顿-米的力矩,作用一全转,需要恰巧 2*Pi 焦耳的能量。
定义力对物体的作用效应,除移动效应外,还有转动效应。
当然,量纲相同并不尽是巧合;使 1 牛顿-米的力矩,作用一全转,需要恰巧 2*Pi 焦耳的能量。
静力观念当一个物体在静态平衡时,净作用力是零,对任何一点的净力矩也是零。
关于二维空间,平衡的要求是:x,y方向合力均为0,且合力矩为0.力矩电动机所谓的力矩电动机是一种扁平型多极永磁直流电动机。
其电枢有较多的槽数、换向片数和串联导体数,以降低转矩脉动和转速脉动。
力矩电动机有直流力矩电动机和交流力矩电动机两种。
其中,直流力矩电动机的自感电抗很小,所以响应性很好;其输出力矩与输入电流成正比,与转子的速度和位置无关;它可以在接近堵转状态下直接和负载连接低速运行而不用齿轮减速,所以在负载的轴上能产生很高的力矩对惯性比,并能消除由于使用减速齿轮而产生的系统误差。
交流力矩电动机又可以分为同步和异步两种,目前常用的是鼠笼型异步力矩电动机,它具有低转速和大力矩的特点。
一般地,在纺织工业中经常使用交流力矩电动机,其工作原理和结构和单相异步电动机的相同,但是由于鼠笼型转子的电阻较大,所以其机械特性较软。
动力观念力矩是角动量随时间的导数,就像力是动量随时间的导数。
刚体的角动量是转动惯量乘以角速度。
力对点之矩和轴之矩 ppt课件

矢量方向由右手定则确定; 矢量作用在Op点pt课,件垂直于r 和F所在的平面。 4
力对轴之矩的定义
定义:力使物体绕某一轴转动效应的度量,称 为力对该轴之矩.
力
对 轴
FFz
之
矩
实 例
Fx F
Fy
ppt课件
5
ppt课件
6
ppt课件
7
力对点的矩和力对轴的矩
ppt课件
8
ppt课件
9
力对轴之矩代数量的正负号
ppt课件
10
力对轴之矩的计算
方法一 : 将力向垂直于
该轴的平面投影 ,力的投 影与投影至轴的垂直距 离的乘积.
Mz (F) = Fxyd
= 2(OAB)
ppt课件
11
力对轴之矩的计算
方法二: 将力向三个坐 标轴方向分解,分别求三 个分力对轴之矩,然后 将三个分力对轴之矩 的代数值相加。
ppt课件
15
2
z
Mx 0
F
F z F sin 300
1
My
Fza
Fa 2
F y F cos300
M z F ya
y
3 Fa 2
300
or
x
M
y
zFx
Mx xFz
yF ZzFy 0 aF sin 300
1 2
Fa
M z xF ppt课y 件 yFx
• 1、试求图示中力F对O点的矩。
ppt课件
14
• (a)MO (F ) MO (Fx ) MO (Fy ) MO (Fy ) F sin l • (b)MO (F ) F sin l • (c)MO (F ) MO (Fx ) MO (Fy ) F cosFl2 sin (l1 l3) • (d) MO (F ) MO (Fx ) MO (Fy ) MO (Fy ) F sin l12 l22
力和力矩(课堂PPT)

21
N=mg=2.0×103×9.8 =1.96×104(N)
f=N=0.30×1.96×104
=5.88×103 (N) F=f=5.88×103 (N)
为了省力,可在车床底座下搁置 一些圆木或钢管,使车床在圆木 或钢管上滚动前进。
22
2.静摩擦力
(1)静摩擦实验
23
(2)静摩擦力
当一个物体相对于另一个物体有滑动趋势, 而没有相对滑动时,这个物体将受到另一个物 体的阻碍作用,这时产生的摩擦叫做静摩擦。
选择某一标度,如取10mm长的线段表示10N的力,作出 力的平行四边形,则表示F1的线段长30mm,表示F2的线段长 40mm。
用刻度尺量得表示合力F的对角线长为50mm,所以合力 的大小F=10×50/10=50N。
用角度尺量得合力F与力F1的夹角为53。 整个过程如下页动画所示。
35
36
3.多力合成
按力的性质分,有重力、弹力和摩擦力。 按力的作用效果分,有拉力、压力、支持 力、动力、阻力等。
6
二、重力
1.重力 由于地球吸引而使物体受到的力
叫做重力。
重力的方向是竖直向下的。 重力的大小G=mg。
7
例子:苹果成熟从树上落下。
8
2.重心
地球对物体的重 力作用在物体的各个 部分。从效果上看, 我们通常认为整个物 体受到的重力作用在 一个点上,这个点叫 做物体的重心。
平行四边形得
F1=G·sin F2=G·cos
47
§1.3 物体的受力分析
一、牛顿第三定律 二、物体的受力分析
48
一、牛顿第三定律
1.物体间的作用总是相互的
49
2.作用力与反作用力
我们把物体间相互作用的这一对力叫做作 用力与反作用力。如果把其中一个力叫做作用 力,那么另一个力就叫反作用力。
N=mg=2.0×103×9.8 =1.96×104(N)
f=N=0.30×1.96×104
=5.88×103 (N) F=f=5.88×103 (N)
为了省力,可在车床底座下搁置 一些圆木或钢管,使车床在圆木 或钢管上滚动前进。
22
2.静摩擦力
(1)静摩擦实验
23
(2)静摩擦力
当一个物体相对于另一个物体有滑动趋势, 而没有相对滑动时,这个物体将受到另一个物 体的阻碍作用,这时产生的摩擦叫做静摩擦。
选择某一标度,如取10mm长的线段表示10N的力,作出 力的平行四边形,则表示F1的线段长30mm,表示F2的线段长 40mm。
用刻度尺量得表示合力F的对角线长为50mm,所以合力 的大小F=10×50/10=50N。
用角度尺量得合力F与力F1的夹角为53。 整个过程如下页动画所示。
35
36
3.多力合成
按力的性质分,有重力、弹力和摩擦力。 按力的作用效果分,有拉力、压力、支持 力、动力、阻力等。
6
二、重力
1.重力 由于地球吸引而使物体受到的力
叫做重力。
重力的方向是竖直向下的。 重力的大小G=mg。
7
例子:苹果成熟从树上落下。
8
2.重心
地球对物体的重 力作用在物体的各个 部分。从效果上看, 我们通常认为整个物 体受到的重力作用在 一个点上,这个点叫 做物体的重心。
平行四边形得
F1=G·sin F2=G·cos
47
§1.3 物体的受力分析
一、牛顿第三定律 二、物体的受力分析
48
一、牛顿第三定律
1.物体间的作用总是相互的
49
2.作用力与反作用力
我们把物体间相互作用的这一对力叫做作 用力与反作用力。如果把其中一个力叫做作用 力,那么另一个力就叫反作用力。
力矩、力偶与力的平移

§2-2
力矩、力偶与力的平移
一、力对点之矩(力矩)
力对点之矩(力矩)是指力使物体绕某点转动效应 的量度。
矩心O
力臂d
力矩:力的大小(F)与力臂(d)的乘积再冠以适当的正负号(±)来 表示力F 使物体绕O点转动的效应,称为力F 对O 点的矩,简称力矩。
MO (F ) Fd
MO(F)——代数量(标量),单位:N· m。
§2-2 力矩、力偶与力的平移
2.力偶的性质 ①力偶在任意坐标轴上的投影等于零。力偶不能合成 为一个力,也不能用一个力来平衡,力偶只能由力偶 来平衡。
A
F
B
F F cos F cos 0
x
F
力和力偶是静力学的两个 基本要素。力偶对刚体只 有转动效应,而无移动效 x 应。
M
M
M
§2-2力矩、力偶与力的平移
三、力的平移定理
作用于刚体上的力,可平移至 该刚体内任一点,但须附加一力偶, 其力偶矩等于原力对平移点之矩。
M B M B (F ) Fd
F
A
(加)
F F A F' = -F" = F
B
B
d
F
B
MB
F
A
仅适应于同一刚体。
§2-2力矩、力偶与力的平移 力的平移定理的应用:
力矩、力偶与力的平移
例2-3已知Fn、、r,
求力 Fn 对于轮心O的力矩。 解:利用力矩定理计算
M O ( Fn ) M O ( Fr ) M O ( Fτ ) M O ( Fτ ) Fn r cos
Fτ
O
Fn
r
d
力矩、力偶与力的平移
一、力对点之矩(力矩)
力对点之矩(力矩)是指力使物体绕某点转动效应 的量度。
矩心O
力臂d
力矩:力的大小(F)与力臂(d)的乘积再冠以适当的正负号(±)来 表示力F 使物体绕O点转动的效应,称为力F 对O 点的矩,简称力矩。
MO (F ) Fd
MO(F)——代数量(标量),单位:N· m。
§2-2 力矩、力偶与力的平移
2.力偶的性质 ①力偶在任意坐标轴上的投影等于零。力偶不能合成 为一个力,也不能用一个力来平衡,力偶只能由力偶 来平衡。
A
F
B
F F cos F cos 0
x
F
力和力偶是静力学的两个 基本要素。力偶对刚体只 有转动效应,而无移动效 x 应。
M
M
M
§2-2力矩、力偶与力的平移
三、力的平移定理
作用于刚体上的力,可平移至 该刚体内任一点,但须附加一力偶, 其力偶矩等于原力对平移点之矩。
M B M B (F ) Fd
F
A
(加)
F F A F' = -F" = F
B
B
d
F
B
MB
F
A
仅适应于同一刚体。
§2-2力矩、力偶与力的平移 力的平移定理的应用:
力矩、力偶与力的平移
例2-3已知Fn、、r,
求力 Fn 对于轮心O的力矩。 解:利用力矩定理计算
M O ( Fn ) M O ( Fr ) M O ( Fτ ) M O ( Fτ ) Fn r cos
Fτ
O
Fn
r
d
力矩和力偶

公法线
G
A FN
公切线
节圆
20 FN
FN 20 压力角
车轮与钢轨
光滑点接触:
B
FNB
凸轮与顶杆
A
FNA FNA A
两轮齿啮合
O
G
B FNB
C FNC
FR
滑槽与销钉
滑道、导轨:约束力垂直于滑道、导轨,指向待定。
A O
B
FNB
3. 光滑铰链约束
(1) 光滑圆柱铰链 (中间铰链)约束
两个或两个以上物体上做出相同直径的孔并用一 个圆柱形销钉连接起来,即构成圆柱铰链(又称为中 间铰链)。
向,则投影为正
试分别求出图中各力在X轴和Y轴上投影。
已知 F1 100N F2 150N F3 F4 200N ,各力方向如图所示。
【解】可得出各力在x,y轴上的投影为
,
F1x F1 cos 45 100N 0.707 = 70.7N
,
F1y F1 sin 45 100N0.707 = 70.7N
R
F2
F1 a b cx 合力的投影
y
Rx
Ry R
x
试分别求出图中各力的合力在x轴和y轴上投影。
已知 F1 20N F2 40N F3 50N ,各力方向如图所示。
【解】 可得出各力的合力在x、y轴上的投影为
FRx
Fx F1 cos 90 F2 cos 0 F3
3 32 42
,
直于销钉轴线的平面内,通过铰链的中心,
方向未知,常用过铰链中心的两个正交分力
表示 。
A
FAx
FAy A
FAx
FAy
A
B
B
G
A FN
公切线
节圆
20 FN
FN 20 压力角
车轮与钢轨
光滑点接触:
B
FNB
凸轮与顶杆
A
FNA FNA A
两轮齿啮合
O
G
B FNB
C FNC
FR
滑槽与销钉
滑道、导轨:约束力垂直于滑道、导轨,指向待定。
A O
B
FNB
3. 光滑铰链约束
(1) 光滑圆柱铰链 (中间铰链)约束
两个或两个以上物体上做出相同直径的孔并用一 个圆柱形销钉连接起来,即构成圆柱铰链(又称为中 间铰链)。
向,则投影为正
试分别求出图中各力在X轴和Y轴上投影。
已知 F1 100N F2 150N F3 F4 200N ,各力方向如图所示。
【解】可得出各力在x,y轴上的投影为
,
F1x F1 cos 45 100N 0.707 = 70.7N
,
F1y F1 sin 45 100N0.707 = 70.7N
R
F2
F1 a b cx 合力的投影
y
Rx
Ry R
x
试分别求出图中各力的合力在x轴和y轴上投影。
已知 F1 20N F2 40N F3 50N ,各力方向如图所示。
【解】 可得出各力的合力在x、y轴上的投影为
FRx
Fx F1 cos 90 F2 cos 0 F3
3 32 42
,
直于销钉轴线的平面内,通过铰链的中心,
方向未知,常用过铰链中心的两个正交分力
表示 。
A
FAx
FAy A
FAx
FAy
A
B
B
力对点的矩与力对轴的矩
空间力系中,各力作用线与矩心所确定的力矩平面不再重合
F1
F2
F3
F4
F5
O
{ F1、F2、F3、F4 }
{ F1、F2、F4、F5 }
空间力系中,力对矩心的矩取决于三方面(要素)
①力矩的大小(F.d)
②力矩平面在空间中的方位(法线方位)
③力矩平面内,力使物体绕矩心的转向
——需用矢量表示空间力系中力对点的矩
Fv
= MO( Fv ) + MO( Fh )
§2.5 力对轴之矩
一、力对轴之矩的概念
F
xy
z
d
Fz
Fxy
过力 F 的始端做垂直力的平面 xy
将力 F 分解
Fz∥z 轴
Fxy⊥z 轴
定义: Fxy 对 O 点之矩为力 F 对 z 轴之矩:Mz ( F )
即 Mz ( F ) = MO ( Fxy ) =Fxy .d
同理力F 对 ox 轴的矩为
= -Fy.z + Fz .y
力F 对 oy 轴的矩为
= -Fz.x + Fx .z
2.5 力对轴之矩
二、力对点之矩与力对过该点的轴之矩的关系
Fx
Fy
Fz
Fxy
F
O
y
z
x
A
B
y
x
z
O′
A点坐标:x、y、z
F 投影:Fx、Fy、Fz
Mx (F )= yFz – zFy
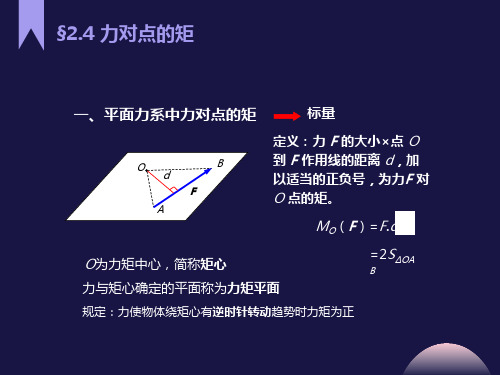
一、平面力系中力对点的矩
标量
O
F
d
A
B
1. 矩心不一定要选为物体可以绕之转动的固定点。
2. 力为0或力作用线过矩心时,力矩为0。
F1
F2
F3
F4
F5
O
{ F1、F2、F3、F4 }
{ F1、F2、F4、F5 }
空间力系中,力对矩心的矩取决于三方面(要素)
①力矩的大小(F.d)
②力矩平面在空间中的方位(法线方位)
③力矩平面内,力使物体绕矩心的转向
——需用矢量表示空间力系中力对点的矩
Fv
= MO( Fv ) + MO( Fh )
§2.5 力对轴之矩
一、力对轴之矩的概念
F
xy
z
d
Fz
Fxy
过力 F 的始端做垂直力的平面 xy
将力 F 分解
Fz∥z 轴
Fxy⊥z 轴
定义: Fxy 对 O 点之矩为力 F 对 z 轴之矩:Mz ( F )
即 Mz ( F ) = MO ( Fxy ) =Fxy .d
同理力F 对 ox 轴的矩为
= -Fy.z + Fz .y
力F 对 oy 轴的矩为
= -Fz.x + Fx .z
2.5 力对轴之矩
二、力对点之矩与力对过该点的轴之矩的关系
Fx
Fy
Fz
Fxy
F
O
y
z
x
A
B
y
x
z
O′
A点坐标:x、y、z
F 投影:Fx、Fy、Fz
Mx (F )= yFz – zFy
一、平面力系中力对点的矩
标量
O
F
d
A
B
1. 矩心不一定要选为物体可以绕之转动的固定点。
2. 力为0或力作用线过矩心时,力矩为0。
第三章 空间力系

M y (F) M y (Fx ) M y (Fy ) M y (Fz ) Fx z Fz x Mz (F) Fy x Fx y
MO (F)x yFz zFy M x (F ) MO (F ) y zFx xFz M y (F )
MO (F)z xFy yFx M z (F)
1)力 F 的大小为 F Fx2 Fy2 Fz2 5 2 kN
2)力 F 的方向余弦以及与坐标轴的夹角为
cos F ,i 3 0.424; F ,i θ 64.9 52
cos F , j 4 0.566 ; F , j β 55.55 52
cos F ,k 5 0.707 ; F ,k γ 180 45 135 52
Fx F cos , Fy F cos , Fz F cos (3 1)
5
第三章 空间力系
§3-1 空间汇交力系 2)二次投影法(间接投影法)
当力与轴Ox,Oy正向夹角不易确定 时,可先将 F 投影到坐标平面xy上,得 Fxy,再将Fxy投影到x,y轴上,于是投影 的大小为:
Fx Fxy cos F sing cos Fy Fxy sin F sing sin
x
解:由题知:
Fx 4.5kN ;Fy 6.3kN ;Fz 18kN
y Fy
β γ
\力F 的大小
Fz
F Fx2 Fy2 Fz2 19.6 kN
zF
力F 的方向余弦,及与坐标轴的夹角为
cos Fx 4.5 0.220, 76.7
F 19.6
cos Fy 6.3 0.322, 71.1
侧面 风力
b
(a)图为空间汇交力系;(b)图为空间任意力系 (b)图中去了风力为空间平行力系。
MO (F)x yFz zFy M x (F ) MO (F ) y zFx xFz M y (F )
MO (F)z xFy yFx M z (F)
1)力 F 的大小为 F Fx2 Fy2 Fz2 5 2 kN
2)力 F 的方向余弦以及与坐标轴的夹角为
cos F ,i 3 0.424; F ,i θ 64.9 52
cos F , j 4 0.566 ; F , j β 55.55 52
cos F ,k 5 0.707 ; F ,k γ 180 45 135 52
Fx F cos , Fy F cos , Fz F cos (3 1)
5
第三章 空间力系
§3-1 空间汇交力系 2)二次投影法(间接投影法)
当力与轴Ox,Oy正向夹角不易确定 时,可先将 F 投影到坐标平面xy上,得 Fxy,再将Fxy投影到x,y轴上,于是投影 的大小为:
Fx Fxy cos F sing cos Fy Fxy sin F sing sin
x
解:由题知:
Fx 4.5kN ;Fy 6.3kN ;Fz 18kN
y Fy
β γ
\力F 的大小
Fz
F Fx2 Fy2 Fz2 19.6 kN
zF
力F 的方向余弦,及与坐标轴的夹角为
cos Fx 4.5 0.220, 76.7
F 19.6
cos Fy 6.3 0.322, 71.1
侧面 风力
b
(a)图为空间汇交力系;(b)图为空间任意力系 (b)图中去了风力为空间平行力系。
理论力学ppt

三.力对点的矩
z
B
1.力对点的矩
mo(F)
mo(F) = r×F
mo(F)表示力F绕O点
A
r
O
y
转动的效应.O点称为矩
d
x
心.力矩矢是定位矢量.
力矩的三要素:力矩的大小;力矩平面的
方位;力矩在力矩平面内的转向.
力矩的几何意义: mo(F) =±2OAB面积=±Fd 力矩的单位: N·m 或 kN·m
a an2 at2 R 2 4
方向为
tan
at an
R 2R
2
结论: (1)在每一瞬时,转动刚体内所有各点的速度和加速 度的大小,分别与这些点到转轴的距离成正比。
(2)在每一瞬时,转动刚体内所有各点的全加速度 a 的方
向与半径间的夹角 都相同。
速度分布图
加速度分布图
四 刚体的转动惯量与飞轮的作用
1.转动惯量的概念
n
I mi i2 i 1
转动惯量反映物体转动时惯性的大小。物 体的转动惯量,一方面决定于物体的形状 ,另一方面又决定于转动轴的位置。
四 刚体的转动惯量与飞轮的作用
2.飞轮的作用 (1)使转速变化均匀 (2)改善扭转特性,减缓机械振动 (3)改善机器的启动和操纵性能
三.力对点的矩
2.合力距定理
定理:平面汇交力 系的合力对平面内任一 点之距,等于其所有分 力对于同一点力矩的代 数和
四.力偶及其性质
F
1力偶(F ,F)
B A
力偶作用面和力偶臂d.
F´
力偶无合力.因此力偶不能与一个力等效,也不 能用一个力来平衡.力偶只能与力偶等效或平衡.
四.力偶及其性质 2力偶的三要素
第3章(力偶系)

MO (F ) 与矩心的选择有关,为定位矢量
2. 力对点之矩矢的解析表达式
MO ( F ) r F
xi yj zk (Fx i Fy j Fz k ) ( ) i j k x y z Fx Fy Fz ( yFz zFy )i ( zFx xFz ) j ( xFy yFx )k [ MO (F )]x i [ MO (F )]y j [ MO (F )]z k
FA FA
OA O1 A sin 30o
解得: M 2 4 M1
作业 P46 3-1 c 3-2 3-5 3-8
二、力对坐标轴 之矩的解析表达式
M x (F ) Mx (Fy ) Mx (Fz ) zFy yFz M y (F ) M y ( Fz ) M y (Fx ) xFz zFx Mz (F ) Mz (Fx ) Mz (Fy ) yFx xFy
M Rz M z = M 2 M3 cos30 48.5 N.m
合力偶矩矢MR的大小和方向余弦分别为:
2 2 2 M R M Rx M Ry M Rz 7.22 202 48.52 52.95 N.m
cos( M R cos( M R cos( M R
M , i)
解:各杆受力图如图,由几何关系可得FA 、FC 垂直于AC 。建立平衡方程 M FA a 2 b 2 0 M 0: 解得:
FA M a 2 b2
FB FC FC FA M a 2 b2
例:图示机构,套筒A 穿过摆杆 O1B ,用销子连接在曲柄OA 上,已知长为 a ,其上作用有力偶 M1 。在图示位置β=30o ,机 械能维持平衡。不计各杆自重及摩擦,试求在摆杆 O1B 上所加力 偶的力偶矩 M2 。
力对点的矩与力对轴的矩

x
rOA投影(A点坐标):x、y、z rOA = x i +y j +z k
F 投影:Fx、Fy、Fz F =Fx i +Fy j +Fz k
i jk MO( F ) = rOA×F x y z
Fx Fy Fz
i jk MO( F ) = rOA×F x y z
Fx Fy Fz
yFz zFy i zFx xFz j xFy yFx k
力对某轴之矩,等于力在垂直于该轴的平 面上的分力对该轴与此平面交点的矩。
§2.5 力对轴之矩
一、力对轴之矩的概念
z
F
Fz
O
xy d
Fxy
Mz ( F ) =Fxy.d ★:注意
①力对轴之矩是代数量,正负由右手 螺旋法则确定;
②力作用线与轴平行或相交(即力 与轴共面)时,力对该轴矩为零;
③力沿其作用线移动时,它对轴之 矩不变。
对于平面汇交力系,各力对力系平面内任一点的矩矢量共 线,因此可看作代数量。
此时合力之矩等于各分力之矩的代数和。
MO( FR ) =Σ MO( Fi )
a O
b Fh
F
α
Fv
例:求力 F 对 O 的矩。
解:将力 F 沿水平垂直方向分解 则 MO( F ) =Σ MO( Fi ) = MO( Fv ) + MO( Fh )
{ F1、F2、F3、F4 }
O
F3
F5
F2
F4
F1
{ F1、F2、F4、F5 }
空间力系中,各力作用线与矩心所确定的力矩平面不再重合
空间力系中,力对矩心的矩取决于三方面(要素)
①力矩的大小(F.d) ②力矩平面在空间中的方位(法线方位) ③力矩平面内,力使物体绕矩心的转向
汽车机械基础课件 任务二 平面力系与力矩力偶

汇交力系平衡的必要与充分的 几何条件是:
力多边形自行封闭。
或:力系中各力的矢量和等于零。
FR
9
10
第三章 力矩与力偶分析 §3–1 力对点之矩 §3–2 力对轴之矩 §3–3 力偶的等效条件和性质
11
对图3-22所示的汽车方向盘操作进行分析,并掌握力矩与 力偶的平衡条件,力的平移定理以及应用,完成汽车方向 盘操作分析。
力偶矩矢
F'
力偶(F,F ' )对O点的转动效应可
O
y
用一矩矢 M 来度量。
F
B
M M O (F ) M O (F ) M OA F OB F
OA F OB F
OA OB F
M BA F
x
❖ 力偶矩矢 M 与O点位置 无关,是自由矢量。
❖ 力偶矩矢由其模、方位 和指向确定。
7 、正确判断二力构件。
§2-1 汇交力系合成与平衡的几何法
一、合成的几何法
1.两个共点力的合成
cos(180 ) cos
FR
FR
力的平行四边形法则
力的三角形法则
由余弦定理: FR F12 F22 2F1F2 cos
合力方向可应用正弦定理确定: F1 sin
FR sin(180o
)
7
2. 力矩的性质
(1)力F对点O的力矩,不仅取决于力的大小,同 时与力臂的大小有关。力臂不同,力矩随之改变。 (2)力F的作用点沿着其作用线移动,力F对任一 点的力矩不变,因为力和力臂的大小均未改变。 (3)力的大小为零,或力的作用线过矩心(即力
臂等于零),则力矩为零。
18
§3-2 力对轴之矩
一、力对轴之矩的概念与计算
第2章力、力矩、力偶

FNB
AP
B
24
例题2-3 解:
作圆柱O受力图。
C
AO B FW
FT
C
A
FNA
O FW
B
FNB
25
例题2-4
屋架受均布风力 q(N/m),屋架重为 P,画出 屋架的受力图。
26
解:取屋架
P
画出简图
P FAy
画出约束力
画出主动力
FAx
P
FN
B
27
例题2-5
水平均质梁 AB重为 P1 ,电动机重为 P 2 , 不计杆 CD自重,画杆 CD 和梁 AB的受力图。
MB = 4×2×1 = 8 kN ·m
45
例题:p22 2-7 已知:F=1kN,钢筋混凝土ρ1=2600kg/m3,
砖砌体ρ2=1900kg/m3,如图。问雨篷是否绕A 点倾覆?
46
二、 合力矩定理
平面内合力对任一点之矩,等于各分力对同一
点之矩的代数和。
F1
M 0(R)M 0(F1)M 0(F2) M 0(Fn)
作用线相同,但指向相反,并同时分别作用于这两 个物体上。
[例] 吊灯
二力作用在不同的物体上 在画物体受力图时要注意此公理的应用。
15
三、力的合成与分解 1、力的合成 几何方法:按力平行四边形法则对力进行合成。
1
A
2
F2
按比例作图——力三角形
F1 F1
R A 1
1800
2 F2 R
16
1、力的合成
力称为该力系的合力,而力系中的各个 力称为该合力的一个分力。
4
力的效应
外效应—改变物体运动状态的效应 内效应—引起物体变形的效应
力矩和转动点

力矩定义:力和力臂的乘积, 是描述力对物体转动效应的物 理量。
转动点选择:选择不同的转动 点,会影响力矩的转动效应。
力矩与转动点的关
03
系
力矩对转动点的影响
力矩是力和力臂的乘积,决定了转动点的角速度和方向 力矩的大小影响转动点的加速度和速度 转动点可以作为力矩的支点,改变力矩的方向和作用线
力矩和转动点的关系是机械运动中的重要概念,对于理解力学和机械原理具有重要意义
力矩的物理意义在于指导我们如何通过改变力臂或力的大小来改变物体的转动状态。
力矩的计算公式
力矩是力和力臂 的乘积
力矩的符号为M
力矩的单位是牛 顿米
力矩的计算公式 为M=FL
力矩的单位
国际单位制中的 单位是牛顿米 (N·m)
常用单位有公斤 力米(kgf·m)和 公吨力米(tf·m)
力矩的单位与力 的单位相同,都 是牛顿(N)
转动点是物体转动的支点,可以改变力矩的大小和方向。
力矩与转动点的相互作用是相互依存的,共同决定了物体的转动效果。 通过理解力矩与转动点的关系,可以更好地分析物体的运动状态和变化趋 势。
力矩和转动点的应
04
用
在日常生活中的应用
杠杆原理:利用 力矩平衡原理, 如用杆撬动重物、 用剪刀剪纸等。
自行车骑行:通 过调整档位改变 力矩,实现省力 或快速骑行。
车辆工程:在车辆设计中,力矩和转动点原理的应用可以提高车辆的操控性和稳定性,从而提高 行驶安全性。
在物理学中的重要性
力矩和转动点是物理学中描述物 体运动的重要概念,对于理解力 学原理和解决实际问题具有重要 意义。
力矩和转动点的理论和实践相结 合,有助于深入理解力学原理, 促进物理学理论的完善和发展。
力和力矩解析ppt课件

39
Fxy Fx i Fy j
M Z F xFy yFx
32
符号规定:按右手定则与z轴指向一致时为 正,反之为负。
33
例 1.3 槽形架在点O用螺栓固定,在点A处受倾斜角为
的力F 作用,尺寸如图示。求力F 对危险截面O处垂
直于力作用平面的Oz轴的力矩。 解:以O为原点作参考系(Oxyz),作矢径r =OA,
29
1.4 力对轴的矩
30
力对轴之矩的定义 M z (F ) M o (Fxy ) Fxy h
力F 对任一轴z之矩,等于该力在 垂直于z轴的平面内的分量Fxy对该 平面和z轴的交点o之矩。
力对轴的矩是标量
31
因此得到:
M z (F) (rxy Fxy ) k rxy x i y j
第一篇 静 力 学
静力学是研究物体在力系作用下平衡规律的科学。 静力学主要研究:
力系的简化和力系的平衡条件及其应用。
1
刚体 就是在力的作用下,大小和形状都不变的物体。 吊车梁简化为一刚性梁
2
平衡
是指物体相对于惯性参考系保持静止或作匀速直线运 动的状态。
3
力系:是指作用在物体上的一组力。
平衡力系:物体在力系作用下处于平衡, 我们称这个力系为平衡力系。
在已知力系上增加或减去任意一个平衡力系,并不改变作用线移到同一刚体内的任一 点,而不改变该力对刚体的效应。
11
力的平行四边形公理
在同一作用点上作用的两个力,其合力的大小与 方向由平行四边形的对角线来确定。
合力计算用余弦定理
F F F FF cos
My F FxzC Fz xC N m
Mz F Fy xC Fx yC N m
Fxy Fx i Fy j
M Z F xFy yFx
32
符号规定:按右手定则与z轴指向一致时为 正,反之为负。
33
例 1.3 槽形架在点O用螺栓固定,在点A处受倾斜角为
的力F 作用,尺寸如图示。求力F 对危险截面O处垂
直于力作用平面的Oz轴的力矩。 解:以O为原点作参考系(Oxyz),作矢径r =OA,
29
1.4 力对轴的矩
30
力对轴之矩的定义 M z (F ) M o (Fxy ) Fxy h
力F 对任一轴z之矩,等于该力在 垂直于z轴的平面内的分量Fxy对该 平面和z轴的交点o之矩。
力对轴的矩是标量
31
因此得到:
M z (F) (rxy Fxy ) k rxy x i y j
第一篇 静 力 学
静力学是研究物体在力系作用下平衡规律的科学。 静力学主要研究:
力系的简化和力系的平衡条件及其应用。
1
刚体 就是在力的作用下,大小和形状都不变的物体。 吊车梁简化为一刚性梁
2
平衡
是指物体相对于惯性参考系保持静止或作匀速直线运 动的状态。
3
力系:是指作用在物体上的一组力。
平衡力系:物体在力系作用下处于平衡, 我们称这个力系为平衡力系。
在已知力系上增加或减去任意一个平衡力系,并不改变作用线移到同一刚体内的任一 点,而不改变该力对刚体的效应。
11
力的平行四边形公理
在同一作用点上作用的两个力,其合力的大小与 方向由平行四边形的对角线来确定。
合力计算用余弦定理
F F F FF cos
My F FxzC Fz xC N m
Mz F Fy xC Fx yC N m
力和力矩.完美版PPT

静摩擦力大小
0≤f≤fmax
静摩擦应用
§1.2 力的合成与分解
一、力的合成 二、力的分解
一、力的合成
1.力的合成
(1)合力与分力 从效果上看,用一个力F可代替两个力F1和F2, 力F叫做力F1和F2的合力,力F1和F2叫做力F的分力。
点击 播放视频
(2)力的合成 求分力F1和F2的合力F叫做力的合成。
点击 播放视频
2.弹力
发生形变的物体,由于要恢复原状,对 跟它接触的物体要产生力的作用,这种力称 为弹力。
例题 一本书放在桌面上,试分析产生于书和桌面之间的 弹力。
压力的方向垂直于支承面指向被压物体,支持 力的方向垂直于支承面指向被支持的物体。
例题
电线下方悬挂电灯,分析产生于电线和电灯之间的弹力。
解 分析可知,车床共受到重力、拉力、地面的
弹力(支持力) 及摩擦力等四个力
N=mg=2.0×103×9.8 =1.96×104(N)
f=N=0.30×1.96×104
=5.88×103 (N) F=f=5.88×103 (N)
为了省力,可在车床底座下搁置 一些圆木或钢管,使车床在圆木 或钢管上滚动前进。
二、重力
1.重力 由于地球吸引而使物体受到的力
叫做重力。
重力的方向是竖直向下的。 重力的大小G=mg。
例子:苹果成熟从树上落下。
2.重心
地球对物体的重 力作用在物体的各个 部分。从效果上看, 我们通常认为整个物 体受到的重力作用在 一个点上,这个点叫 做物体的重心。
三、弹力
1.形变
在力的作用下,物体的形状或体积的 改变叫做形变。
法画出力的平行四边形。测量发现,钢丝绳上的拉 力大约是运动员体重的6倍。可见,钢丝绳上的拉 力比运动员体重大得多。为了运动员的安全,必须 使钢丝绳具有足够的强度。
0≤f≤fmax
静摩擦应用
§1.2 力的合成与分解
一、力的合成 二、力的分解
一、力的合成
1.力的合成
(1)合力与分力 从效果上看,用一个力F可代替两个力F1和F2, 力F叫做力F1和F2的合力,力F1和F2叫做力F的分力。
点击 播放视频
(2)力的合成 求分力F1和F2的合力F叫做力的合成。
点击 播放视频
2.弹力
发生形变的物体,由于要恢复原状,对 跟它接触的物体要产生力的作用,这种力称 为弹力。
例题 一本书放在桌面上,试分析产生于书和桌面之间的 弹力。
压力的方向垂直于支承面指向被压物体,支持 力的方向垂直于支承面指向被支持的物体。
例题
电线下方悬挂电灯,分析产生于电线和电灯之间的弹力。
解 分析可知,车床共受到重力、拉力、地面的
弹力(支持力) 及摩擦力等四个力
N=mg=2.0×103×9.8 =1.96×104(N)
f=N=0.30×1.96×104
=5.88×103 (N) F=f=5.88×103 (N)
为了省力,可在车床底座下搁置 一些圆木或钢管,使车床在圆木 或钢管上滚动前进。
二、重力
1.重力 由于地球吸引而使物体受到的力
叫做重力。
重力的方向是竖直向下的。 重力的大小G=mg。
例子:苹果成熟从树上落下。
2.重心
地球对物体的重 力作用在物体的各个 部分。从效果上看, 我们通常认为整个物 体受到的重力作用在 一个点上,这个点叫 做物体的重心。
三、弹力
1.形变
在力的作用下,物体的形状或体积的 改变叫做形变。
法画出力的平行四边形。测量发现,钢丝绳上的拉 力大约是运动员体重的6倍。可见,钢丝绳上的拉 力比运动员体重大得多。为了运动员的安全,必须 使钢丝绳具有足够的强度。
理论力学(哈尔滨工业大学)课件7.2 力对点的矩和力对轴的矩

解:把力F分解如图
M x (F ) = −Fz (l + a) = −F cosθ ⋅ (l + a) M y(F ) = −Fz ⋅ l = −F cosθ ⋅ l M z (F ) = −Fx (l + a) = −F sinθ ⋅ (l + a)
Fx θ Fz
F
由力对点的矩和力对轴的矩的关系,得到:
MMxy((FF))
= =
yzFFzx
− −
zxFFyz
r
[MO (F )]x = yFz − zFy = M x (F ) [MO (F )]y = zFx − xFz = M y (F ) [MO (F )]z = xFy − yFx = M z (F )
2、力对点的矩和力对轴的矩 空间汇交力系和空间力偶系
力对点的矩矢量在通过该点的某轴上投影,等于力 对该轴的矩。
2、力对点的矩和力对轴的矩
[MMz(OF(F) )]z
简单地说,力矩在某轴上的投影等于力对该轴的矩
空间汇交力系和空间力偶系
例2 摇手ABCD在Axy平面内,D点在垂直于y轴的平面内受力
F与竖直方向成θ角,摇手尺寸l,a已知。
求:F 对A点的力矩。
2、力对点的矩和力对轴的矩
空间汇交力系和空间力偶系
(1)空间力对点的矩(力矩矢)
力F 对O点的矩取决于三要素:
2、力对点的矩和力对轴的矩
a 大小:
力矩作用面内,力F与力臂的乘积.
Mo(F)
B
F
b 转向:
力矩作用面内,力F使物体绕O
点的转动方向. c 力矩作用面.
r A (x, y, z)
O h
三要素可由 r × F 表示
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
优选
13
Fxy
过力 F 的始端做垂直力的平面 xy 将力 F 分解
Fz∥z 轴 Fxy⊥z 轴
定义: Fxy 对 O 点之矩为力 F 对 z 轴之矩:Mz ( F )
即 Mz ( F ) = MO ( Fxy ) =Fxy .d
力对某轴之矩,等于力在垂直于该轴的平 面上的分力对该轴与此平面交点的矩。
优选
9
第二章 平面汇交力系与平面力偶系
F
α
Fv
例:求力 F 对 O 的矩。
解:将力 F 沿水平垂直方向分解
则 MO( F ) =Σ MO( Fi ) = MO( Fv ) + MO( Fh )
0 Fsin a2 b2
Fsin a2 b2
优选
8
第二章 平面汇交力系与平面力偶系
§2.5 力对轴之矩
一、力对轴之矩的概念
z
F
Fz
O
xy d
汇交力系的合力对任一点的力矩矢量,等于力系中各分 力对同一点的力矩矢量的矢量和。
——汇交力系合力之矩定理
对于平面汇交力系,各力对力系平面内任一点的矩矢量共 线,因此可看作代数量。
此时合力之矩等于各分力之矩的代数和。
MO( FR ) =优Σ选MO( Fi )
7
第二章 平面汇交力系与平面力偶系
a O
b Fh
优选
1
第二章 平面汇交力系与平面力偶系
§2.4 力对点的矩
一、平面力系中力对点的矩
标量
★注意
O
B
d
F
A
1. 矩心不一定要选为物体可以绕之转动的固定点。
2. 力为0或力作用线过矩心时,力矩为0。
3. 力沿其作用线滑动时,力矩值不变。
4. 必须指明矩心,力优选矩才有意义。
2
第二章 平面汇交力系与平面力偶系
§2.5 力对轴之矩
一、力对轴之矩的概念
z
F
Fz
O
xy d
Fxy
Mz ( F ) =Fxy.d ★:注意
①力对轴之矩是代数量,正负由右手 螺旋法则确定;
②力作用线与轴平行或相交(即力 与轴共面)时,力对该轴矩为零;
③力沿其作用线移动时,它对轴之 矩不变。
优选
10
第二章 平面汇交力系与平面力偶系
§2.5 力对轴之矩
MO(F)
O
①过矩心作垂直于力矩平面的矢量, 其长度表示力矩的大小
②矢量的方向表示力矩平面的法线方向
F
③矢量的指向按右手螺旋法则确定
空间力系中力对优选点的矩矢量 MO(F)
4
第二章 平面汇交力系与平面力偶系
z MO(F)
B
rOA
F A
O
y
d
|MO( F ) |= F.d =2S∆OAB
定义矢量 rOA
力F优选对 oy 轴的矩为 = -Fz.x + Fx .z 11
第二章 平面汇交力系与平面力偶系
§2.5 力对轴之矩
二、力对点之矩与力对过该点的轴之矩的关系
z Fz
A点坐标:x、y、z F 投影:Fx、Fy、Fz
B
O′
F
Mx (F )= yFz – zFy
A O Fx
zx
Fy
Fxy y
My (F )= zFx - xFz Mz (F )= xFy - yFx.
第二章 平面汇交力系与平面力偶系
§2.4 力对点的矩
一、平面力系中力对点的矩
标量小×点 O 到 F 作用线的距离 d,加 以适当的正负号,为力F 对 O 点的矩。
MO(F)=F.d
O为力矩中心,简称矩心
=2S∆OAB
力与矩心确定的平面称为力矩平面
规定:力使物体绕矩心有逆时针转动趋势时力矩为正
§2.4 力对点的矩
二、空间力系中力对点的矩
平面力系中,各力作用线与矩心所确定的力矩平面是重合的
{ F1、F2、F3、F4 }
O
F3
F5
F2
F4
F1
{ F1、F2、F4、F5 }
空间力系中,各力作用线与矩心所确定的力矩平面不再重合
优选
3
第二章 平面汇交力系与平面力偶系 空间力系中,力对矩心的矩取决于三方面(要素) ①力矩的大小(F.d) ②力矩平面在空间中的方位(法线方位) ③力矩平面内,力使物体绕矩心的转向 ——需用矢量表示空间力系中力对点的矩
y
力F 对 O 点之矩矢量的解析表达式
x
MO (F )=( yFz – zFy) i + ( zFx – xFz) j +( yFz – zFy) k
力对某点矩矢量在通过该点的优选任一轴上的投影等于力对该轴的1矩2
第二章 平面汇交力系与平面力偶系
[MO( F )]x = Mx ( F ) [MO( F )]y = My ( F ) [MO( F )]z = Mz ( F ) MO (F )=[Mx ( F )] i + [My ( F )] j + [Mz ( F )] k
二、力对点之矩与力对过该点的轴之矩的关系
z Fz
O′
A
O Fx
z y
B F
Fy
Fxy y
x
A点坐标:x、y、z F 投影:Fx、Fy、Fz 力F 对 oz 轴的矩为 Mz ( F ) = MO′ ( Fxy )
= MO′ ( Fx ) + MO′ ( Fy ) = -Fx.y + Fy .x
x
同理力F 对 ox 轴的矩为 = -Fy.z + Fz .y
[MO( F )]z = xFy - yFx
优选
6
第二章 平面汇交力系与平面力偶系
§2.4 力对点的矩
三、汇交力系合力之矩定理
n
对于由n个力组成的汇交力系 FR F1 F2 Fn Fi Fi i 1 MO( FR ) = rOA×FR = rOA×ΣFi =∑(rOA×Fi) =ΣMO( Fi )
MO( F ) = rOA×F
空间力系中,力对点的矩矢量 等于力始点相对于矩心的矢量 与力矢量的矢量积
x
rOA投影(A点坐标):x、y、z rOA = x i +y j +z k
F 投影:Fx、Fy、Fz F =Fx i +Fy j +Fz k
i jk
MO( F ) = rOA×F x y z
优选Fx Fy Fz
5
第二章 平面汇交力系与平面力偶系
i jk MO( F ) = rOA×F x y z
Fx Fy Fz
yFz zFy i zFx xFz j xFy yFx k
——力对点矩矢量的解析表达式
力对点的矩矢量在 x、y、z 轴上的投影
[MO( F )]x = yFz - zFy
[MO( F )]y = zFx - xFz
