第一章高分子的分子量和分子量分布.

合集下载

高分子化学--各章思考题

高分子化学思考题第一章绪论（思考题）1、解释下列名词或术语：高分子化合物：由许多简单的结构单元通过共价键连接起来的，分子量410~610的大分子所组成的化合物。

聚合物：即是高分子，其分子量高达410~610。

单体：能够形成高分子化合物中结构单元的低分子化合物。

结构单元：构成高分子链并决定高分子结构以一定方式连接起来的原子组合。

重复单元：聚合物中化学组成相同的最小单位的重复单元。

单体单元：聚合物中具有与单体相同化学组成而不同电子结构的单元。

链节：即是重复单元的俗称。

聚合度：即是重复单元数。

热塑性聚合物：线形或支链形大分子以物理力聚集成聚集成聚合物，加热时可熔融，并能溶于适当溶剂中。

热固性聚合物：有不少聚合物或预聚物，在树脂合成阶段，须控制原料配比和反应条件，使停留在线形或少量支链的低分子阶段（预聚阶段）。

在成型阶段，经加热再使其中潜在的活性官能团继续反应成交联结构而固化。

分子量分布指数：分子量和结构的多分散性连锁聚合反应逐步聚合反应2、高分子化合物和低分子化合物的根本区别是什么？与低分子化合物比较，高分子化合物有哪些主要特征？3、能否用蒸馏或重结晶的方法提纯聚合物？为什么？举例说明提纯聚合物的方法。

4、请写出聚合物的聚合度和分子量的关系式，试述聚合物平均分子量和分子量分布的表示方法，并简述产生分子量多分散性的原因。

5、高分子链结构的形状有哪几种？它们的物理机械性能各有哪些特点？6、化学组成和平均分子量都相同的聚合物，其物理机械性能是否相同？为什么？7、作为材料使用的聚合物，其分子量高些好还是低些好？分子量分布宽些好还是窄些好？说明理由。

8、衡量聚合物耐热性的重要指标是什么？聚合物的耐热性受哪些因素的影响？它们与高分子化学有何关系？9、试述聚合物的命名和分类方法。

10、试述常见的几种塑料、橡胶、纤维的名称（包括缩写符号）、结构式及其单体。

第二章自由基聚合反应（思考题）1、解释下列名词或术语：序列结构等活性理论凝胶效应动力学链长数均聚合度分子量调节剂引发剂引发效率引发剂半衰期诱导分解笼蔽效应诱导期阻聚剂缓聚剂聚合上限温度2、自由基聚合中，为什么聚合物链中单体单元大部分按头－尾方式连接，且所得聚合物多为无规立构？3、试述聚合反应时如何选择合适的引发剂，及怎样确定其用量？4、用悬浮法生产PVC时，为什么要采用高活性和中活性并用的引发体系？5、试推导引发剂引发时的聚合速率方程、动力学链长、数均聚合度的表达式。

凝胶色谱的讲义第一章(1)

凝胶色谱的讲义第一章(1)第一章前言一、高聚物及多糖平均分子量及其分布1、高聚物的平均分子量除天然聚合物外，合成聚合物都是以单体为原料经过聚合反应而制得的。

每个聚合物分子都是由数目很大的单体分子加成或缩合而成，所以合成聚合物的分子量比单体要大千百倍甚至成万倍。

另一方面，根据绝大多数的聚合反应机理预示，生成的聚合物的分子量是不均一的，也就是说每个聚合物分子可以由不同数目的单体分子聚合而成，所以各聚合物的分子量是不相等的，这种现象叫做聚合物的分子量的不均一性或多分散性。

高聚物分子量的多分散性使分子量的表征比小分子要复杂一些，拿一个高聚物试样来说，由于试样内包含有许许多多个高分子，这些高分子的分子量可以分布在相当大的范围内。

例如，试样中可以包含尚未聚合的单体、含二个、三个、四个、…单体的低聚物以及聚合度不同的高分子，对这样一个多分散的体系来说，我们要表征它的分子量就需要用统计的方法，求出试样分子量的平均值和分子量分布、由于应用统计方法的不同，即使对同一个试样，也可以有许多不同种类的平均分子量；例如，某一个高聚物试样中含有N1个分子量为M；的分子，N2个分子量为M2的分子，N3个分子量为M3的分子，……Ni-1个分子量为Mi-1的分子以及Ni个分子量为MI 的分子，我们就可以根据定义算出它的各种平均分子量。

下面是四种最常用的平均分子量定义：这里：YMx分子量名称Mn数均分子量1Mw重均分子量2MzZ均分子量3MZ+1Z+1均分子量Mw/Mn分子量分布Mp峰位分子量另外，粘均分子量：很显然，同一个试样应用不同的统计方法所算出来的不同种类的平均分子量的数值是不同的。

一般情况下，多分散样品的平均分子量有以下次序：Mz＞Mw ＞M η＞Mn 2．高聚物的分子量分布高聚物的分子量分布是指试样中各种大小不等的分子量组分在总量中所占的各自的分量，它可以用一条分布曲线或一个分布函数来表示。

例如，当我们知道高聚物试样中分于量为M1、M2、M3、…、Mi各组分在总重量中所占的重量分数分别为W1 、W2、W3 、…、Wi 时，我们就可以用对应的W和M作图，得到分子量分布曲线。

高分子物理重要知识点

高分子物理重要知识点(1人评价)|95人阅读|8次下载|举报文档高分子物理重要知识点(1人评价)|96人阅读|8次下载|举报文档1 高分子物理重要知识点第一章高分子链的结构 1.1高分子结构的特点和内容高分子与低分子的区别在于前者相对分子质量很高，通常将相对分子质量高于约1万的称为高分子，相对分子质量低于约1000的称为低分子。

相对分子质量介于高分子和低分子之间的称为低聚物（又名齐聚物）。

一般高聚物的相对分子质量为104~106，相对分子质量大于这个范围的又称为超高相对分子质量聚合物。

英文中“高分子”或“高分子化合物”主要有两个词，即polymers和Macromolecules。

前者又可译作聚合物或高聚物；后者又可译作大分子。

这两个词虽然常混用，但仍有一定区别，前者通常是指有一定重复单元的合成产物，一般不包括天然高分子，而后者指相对分子质量很大的一类化合物，它包括天然和合成高分子，也包括无一定重复单元的复杂大分子。

与低分子相比，高分子化合物的主要结构特点是：（1）相对分子质量大，由很大数目的结构单元组成，相对分子质量往往存在着分布；（2）主链有一定的内旋自由度使分子链弯曲而具有柔顺性；（3）高分子结构不均一，分子间相互作用力大；（4）晶态有序性较差，但非晶态却具有一定的有序性。

（5）要使高聚物加工成为有用的材料，需加入填料、各种助剂、色料等。

高分子的结构是非常复杂的，整个高分子结构是由不同层次所组成的，可分为以下三个主要结构层次（见表1－1）：表1-1高分子的结构层次及其研究内容名称内容备注链结构一级结构（近程结构）结构单元的化学组成键接方式构型（旋光异构，几何异构）几何形状（线形，支化，网状等）共聚物的结构指单个大分子与基本结构单元有关的结构二级结构（远程结构）构象（高分子链的形状）相对分子质量及其分布指由若干重复单元组成的链段的排列形状三级结构（聚集态结构、聚态结构、超分子结构）晶态非晶态取向态液晶态织态指在单个大分子二级结构的基础上，许多这样的大分子聚集在一起而成的聚合物材料的结构由于高分子结构的如上特点，使高分子具有如下基本性质：比重小，比强度高，弹性，可塑性，耐磨性，绝缘性，耐腐蚀性，抗射线。

高分子溶液与分子量及其分布

u (1 eGa kT )4 a2da 0
高分子链在稀溶液中以一个被溶剂化了的松散的链球散布在溶剂中，每个链球都占有一定的体积，他不能被其他分子的链段占有，称作“排斥体积”
以“1”表示溶剂分子，“2”表示高分子的链段，[1-2]表示溶剂分子与高分子链段的作用：
[1-2] > [2-2]：高分子被溶剂化，排斥体积u增大； [1-2] = [2-2]：高分子之间与溶剂一样可以互相贯穿，u=0，处于无扰状态； [1-2] <M[2at-e2ri]a：ls 高分子不能自发溶解。
高分子亚浓溶液和浓溶液
WHUT
WUHAN UNIVERSITY of TECHNOLOGY
• 稀溶液中，高分子线团互相分离，链段分布不均一，浓度增大，高分子线团互相穿插交叠趋于均一，称亚浓溶液。高分子线团靠近到开始线团密堆积的浓度称临界交叠浓度（c*）。
• 高分子浓溶液
–高聚物增塑体系 –纺丝液 –凝M胶at和eria冻ls 胶
i
ni Mi
ni
i
Ni M i
i
以重量为统计权重，重均分子量
ni
M
2 i
wi M i
M w i
i
niMi
wi
WiMi
i
i
i
以z值为统计权重，z均分子量 zi = wiMi
ziMi
wi
M
2 i
ni
M
3 i
M z i
zi
i
wi M i
i
ni
M
2 i
i
i
i
用稀溶液粘度法测得的分子量，粘均分子量
• 高分子与溶剂小分子尺寸悬殊，运动速度差别大，溶剂分子能较快地渗入聚合物而高分子向溶剂的扩散非常慢。

《合成高分子的基本方法》讲义

《合成高分子的基本方法》讲义一、引言高分子材料在我们的生活中无处不在，从塑料制品到合成纤维，从橡胶轮胎到涂料胶粘剂，它们的性能和用途千差万别。

而要了解这些高分子材料是如何被合成出来的，就需要掌握合成高分子的基本方法。

二、逐步聚合逐步聚合是指通过官能团之间的逐步反应来合成高分子的方法。

在逐步聚合反应中，单体通常含有两个或两个以上能够相互反应的官能团。

1、缩聚反应缩聚反应是逐步聚合中最常见的一种类型。

例如聚酯的合成，通过二元醇和二元酸的反应，脱去小分子水，逐步形成高分子链。

反应式可以表示为：n HOROH ＋n HOOCR'COOH → OROOCR'COn ＋（2n 1) H₂O在缩聚反应中，反应程度对于聚合物的分子量有着重要的影响。

反应程度越高，分子量越大。

同时，为了得到高分子量的聚合物，需要严格控制反应条件，如反应物的纯度、配比，以及反应温度和时间等。

2、逐步加成聚合逐步加成聚合也是逐步聚合的一种。

例如聚氨酯的合成，通过异氰酸酯与多元醇的反应，逐步形成高分子。

三、连锁聚合连锁聚合包括自由基聚合、离子聚合和配位聚合等。

1、自由基聚合自由基聚合是应用最为广泛的连锁聚合方法之一。

其反应过程通常包括链引发、链增长和链终止三个阶段。

在链引发阶段，通过引发剂产生自由基，引发单体聚合。

常见的引发剂有过氧化物和偶氮化合物等。

链增长阶段，自由基不断与单体加成，使链不断增长。

链终止方式主要有偶合终止和歧化终止。

2、离子聚合离子聚合包括阳离子聚合和阴离子聚合。

离子聚合对反应条件要求较为严格，例如需要在无水、无氧的条件下进行。

阳离子聚合常用的引发剂有质子酸、路易斯酸等。

阴离子聚合常用的引发剂有碱金属、有机金属化合物等。

3、配位聚合配位聚合能够制备具有规整结构的高分子，如高密度聚乙烯、等规聚丙烯等。

四、开环聚合开环聚合是指环状单体在一定条件下开环，然后形成线性高分子的过程。

例如，环氧乙烷开环聚合可以得到聚醚。

高分子物理4 高聚物的分子量和分子量分布

稀相分子量低的部分
浓相分子量高的部分
（1）高分子溶液的相分离
• 相分离的热力学条件：
溶剂在浓相和稀相中的化学位相等
1稀相 1/ 浓相
溶剂在稀相中的化学位变化溶剂在浓相中的化学位变化所以：相分离时应有
1 1 10
1/ 1/ 10
1
RT ln1
2
1
1 x
2
1
2 2
f 21x
（4）特性粘数与高分子链构象的关系
• Einstein粘度理论：
25
M ~
M ~
V Vh N
溶液中高分子线团的平均密度
VV~h一克个分高子分体子积线团的体M积平均分子量
N~ Avogadro常数
《4》特性粘数与高分子链构象的关系
• Einstein粘度理论 25 N~ Vh
M
设高分子线团半径为 Re
《1》分子量分布的表示
（1）图解表示法
《1》分子量分布的表示
（2）函数适应法
一般在函数中均包含二个可调参数 • Schulz-Elory函数:
WM
ln b
a b2 2
Mb1a M
• 董复和函数: • 对数正态分布函数:
参数式中a . b. y. z. β.Mp为可调
W M
1
1
1 e2
~ V1
化学位减小 1
当
~ V1
1时溶剂在两侧的化学位相等
——达到热力学的平衡条件
（3）渗透压与分子量的关系
• 对于小分子溶液 Van`t Hoff方程
• 对于高分子溶液
RT C 或 RT M CM
1
RT
ln 1

4聚合物的分子量和分子量分布详解

烷，它可通过氧化物或有机锡在室温进行交联（硫化）成网状分子，具有极重要的用途；
Characteristics of polymer molecular weights
高分子的分子量的特点
• 分子量非常大，范围从10,000到1,000,000 g/mol，甚至更大。
• 小分子的分子量是固定的，除了有限的几种蛋白质高分子外，聚合物分子量是不固定的，分子量的大小主要依赖于聚合方法。
高分子专业：
金属专业：
平均每个专业多少人？
210人
60人
无机非金属专业： 30人
210 60 30(总人数） 100 111 (专业个数）
Number average 数均
210 * 210 210 60 30
60 30 * 60 * 30 210 60 30 210 60 30 Weight average 重均
mi ni M i
数均分子量：按物质的量统计平均分子量重均分子量：按质量统计平均分子量
Mn
n M n
i i i i
i
Ni M i
i
Mw
mi M i
i
m
i

2 n M i i
i
n M
i i
i
i
Wi M i
i
Method of weighting 权重法
• 大部分高分子的分子量具有多分散性，可以看做包含很多组分的混合物。
• 分子量分布是聚合物最基本的结构参数之一，它对于高分子材料加工条件的控制均有重要意义： • ①高分子材料加工条件的控制
如：熔体强度与弹性与样品中高分子量部分有较大关系
• ②高分子材料使用性质

《高分子物理》思考题与习题合集

聚合物的电学性能及其它性能1. 名词解释：取向极化，介电损耗，电击穿，介电松弛谱，导电聚合物。

2. 高分子在电场中的极化有哪几种形式？各有什么特点？3. 比较聚合物介电损耗和力学损耗的异同点。

4. 讨论影响聚合物介电常数和介电损耗的因素。

5. 结构型导电聚合物的分子结构与导电性关系如何？举例说明。

6. 简述提高聚合物的耐热性和热稳定性的方法。

7. 讨论提高聚合物透明性的途径。

- 1 -高分子的分子量和分子量分布1. 解释下列名词：第二维利系数，相对粘度，增比粘度，比浓粘度，特性粘数，相对分子质量分布宽度指数，流体力学体积，GPC ，GPC 标定曲线（相对分子质量-淋出体积标定曲线）。

2. 已知聚苯乙烯试样中含有相对分子质量为104和l05两组分，试求下列两种情况下的n M 、w M ：（1）两组分分子数相同；（2）两组分重量相同。

3. 试计算100摩尔相对分子质量为105的聚乙烯分别与10摩尔相对分子质量为l04和106的聚乙烯混合时的n M 和w M ，并讨论计算的结果。

4. 测定聚合物数均和重均相对分子质量的方法有哪几种？每种方法适用的相对分子质量范围如何？5. 证明渗透压法测得的相对分子质量为数均相对分子质量，而光散射法测得的相对分子质量为重均相对分子质量。

6. 为什么说用粘度法测定相对分子质量是相对的方法，而不是绝对的方法？7. 粘度法测相对分子质量中，K 、α值是如何定出的？8. 试比较聚电解质与非聚电解质稀溶液粘度变化的特点。

9. 简述GPC 方法测定聚合物相对分子质量和相对分子质量分布的基本原理。

10. 现有一超高相对分子质量的聚乙烯试样，欲采用GPC 方法测定其相对分子质量和相对分子质量分布，试问：(1) 能否选择GPC 法的常用溶剂THF ？如果不行，应该选择何种溶剂？ (2) 常温下能进行测定吗？为什么？11. 什么叫相对分子质量微分分布曲线和积分分布曲线？两者如何相互转换？ 12. 相对分子质量分布的研究方法有哪几类？简述其原理及优缺点。

高分子化学知识点总结

第一章绪论单体：能通过聚合反应形成高分子化合物的低分子化合物，即合成聚合物的原料。

高分子：一个大分子由许多简单的结构单元通过共价键重复键接而成，并具有一定机械性能。

结构单元：在大分子链中出现的以单体结构基础的原子团称为结构单元。

重复单元：大分子链上化学组成和结构均可重复的最小单元，可能与结构单元相同，也可能由2个或多个结构单元组成。

单体单元：与单体中原子种类及个数相同的结构单元，仅电子结构有所变化。

重复单元或结构单元类似大分子链中的一个环节，故俗称链节由一种单体聚合而成的高分子称为均聚物; 由两种或两种以上的单体聚合而成的高分子则称为共聚物. 结构单元＝单体单元＝重复单元＝链节聚合度：聚合度是衡量高分子大小的一个指标。

合成尼龙-66具有另一特征：H 2N(CH 2)6NH 2+ HOOC(CH 2)4COOHH--NH(CH 2)6NH--CO(CH 2)4CO--OHn(2n-1) H 2O +结构单元结构单元重复结构单元有两种表示法：[1]以大分子链中的结构单元数目表示，记作:[2]:以大分子链中的重复单元数目表示，记作:由聚合度可计算出高分子的分子量： M 是高分子的分子量; M 0 是结构单元的分子量结构单元＝重复单元＝链节≠ 单体单元单体在形成高分子的过程中要失掉一些原子结构单元 ≠ 重复单元 ≠ 单体单元重复单元＝链节三大合成材料:橡胶，塑料，纤维玻璃化温度：聚合物从玻璃态到高弹态的热转变温度。

分子量及其分布数均分子量：按聚合物中含有的分子数目统计平均的分子量高分子样品中所有分子的总重量除以其分子(摩尔)总数∑∑∑∑∑∑====iii iiiii in Mx M WWNM N N WM )(式中，W i ，N i ，M i 分别为i -聚体的重量、分子数、分子量重均分子量：是按照聚合物的重量进行统计平均的分子量i -聚体的分子量乘以其重量分数的加和∑∑∑∑∑===iiiii i iii w Mw M NM N WM W M 2分布指数表示：重均分子量与数均分子量的比值，M w / M nM w / M n 分子量分布情况1 均一分布接近 1 (1.5 ~ 2）分布较窄远离 1 (20 ~ 50) 分布较宽聚合反应1．按单体-聚合物结构变化分类【1】缩聚【2】加聚【3】开环聚合 2．按聚合机理分类【1】逐步聚合【2】连锁聚合（活性种可以是自由基、阴离子、阳离子；过程由链引发、链增长、链终止等基元反应组成）n xDP n DP x n ==00M DP M x M n ⋅=⋅=第二章逐步聚合反应1逐步聚合的基本概念与连锁聚合不同，逐步聚合的基本特征是聚合度随时间逐步增长，而转化率在聚合初期即可达到很高，因此表现出与连锁聚合完全不同的规律。

分子量及其分布

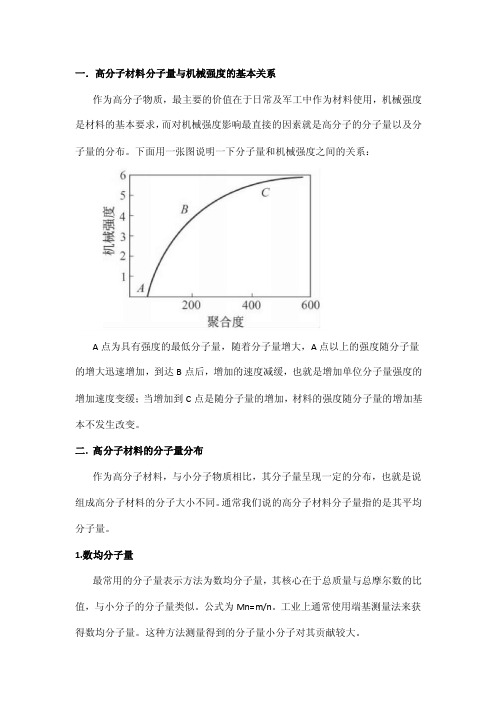
一．高分子材料分子量与机械强度的基本关系作为高分子物质，最主要的价值在于日常及军工中作为材料使用，机械强度是材料的基本要求，而对机械强度影响最直接的因素就是高分子的分子量以及分子量的分布。

下面用一张图说明一下分子量和机械强度之间的关系：A点为具有强度的最低分子量，随着分子量增大，A点以上的强度随分子量的增大迅速增加，到达B点后，增加的速度减缓，也就是增加单位分子量强度的增加速度变缓；当增加到C点是随分子量的增加，材料的强度随分子量的增加基本不发生改变。

二. 高分子材料的分子量分布作为高分子材料，与小分子物质相比，其分子量呈现一定的分布，也就是说组成高分子材料的分子大小不同。

通常我们说的高分子材料分子量指的是其平均分子量。

1.数均分子量最常用的分子量表示方法为数均分子量，其核心在于总质量与总摩尔数的比值，与小分子的分子量类似。

公式为Mn=m/n。

工业上通常使用端基测量法来获得数均分子量。

这种方法测量得到的分子量小分子对其贡献较大。

理解：假设有1千克材料，其中分子量100000左右的为900g，分子量为10000的为100g。

我们可以计算得到分子量100000左右材料的摩尔数为0.009mol；分子量10000左右材料的摩尔数为0.01mol；总的摩尔数为0.019，其平均分子量为1000/0.019=52631.6。

通过上面计算我们可以得出数均分子量的权重小分子部分占较大。

2.重均分子量Mw通常有光散射法，凝胶渗透色谱法来获得。

重均分子量其分子量较大的部分占有较高的权重。

3.粘均分子量Mv通常，分子量越大，其溶液体系的粘度也越大，由于其粘度测量的简便性，所以用粘度来表示分子量也是非常常见的。

通过一定固定参数的测定，可以将粘度转变为分子量。

通常三者有如下关系：Mw>Mv>Mn。

4.分子量分布分子量分布是表示聚合物分子量多分散性的指标。

通常用Mw/Mn来表示。

分子量分布对聚合物的性能影响较大，所以也是我们合成产品需要考虑的重要参数之一。

高分子物理第一章高分子链结构课件

型的高分子，每个结构单元都有一个不对称碳原子（手性中心（Chiral center)，按不对称碳原子上取代基的排列方式，可得到三种不同的旋光异构体：全同间同立构无规立构
（有规立构）
问题
(1) 高分子链是有规立构还是无规立构取决于什么？ (2) 有同学说：化学键C—C是可以内旋转的，那么可以通过C—C键的旋转来改变立构规整性，此提法对不对，为什么？
二、结构单元的键接方式
键接结构是指结构单元在聚合中是按什么方式键接成长链高分子的。
问题
对缩聚物有无此问题？对PE有无此问题？对单取代烯类单体，有无此问题？键接方式有那两种方式？
三、构型与构象：构型(Configuration)：
指分子中由化学键所固定的原子或基团在空间的几何排列。要改变构型必须通过化学键的断裂和重组。
1、空间：原子、分子、球晶、块体 2、时间：折叠链伸直链不稳定稳定几千年
由折叠链 → 伸直链
分子运动时间：几秒 → 几千年 3、浓度：极稀、亚浓、浓
二、高聚物结构的主要特点
• 大分子链由许多结构单元组成。 • 共价键组成的大分子分子间力很大（远大于共价键键能），高聚物无气态。 • 大分子链具有内旋自由度，因此高分子链具有刚柔性之分。 • 凝聚态结构包括：晶态、非晶态、取向态、织态、液晶态。
（3）实际高分子链既有键角限制、又有位垒限制柔性比前两种都差。
二、高分子链的构象统计：
(The Statistical Conformation of Polymer Chain) 长链分子主链单键的内旋转赋予高分子以柔性，致使高分子链可任意取不同的卷曲程度，高分子链的卷曲程度可以用高分子链的末端距来度量。

高分子化学导论第1章命名及结构分子量特征

n
1＋1
＝55000
M
＝1 104 2＋1 105 W 1104＋1105
2
＝91820
1
M
v＝1111004 41＋.8＋11100551.8
0.8
＝90530
设α=0.8
Mn W Ni
NiMi
Mw
WiMi
Wi
WiMi
1
Mv
N M 1 ii
NiMi
Polymer Chemistry
说明
低分子量部分对影响较大高分子量部分对影响较大一般用来表征聚合物更恰当，因为聚合物的性能如强度、熔体粘度更多地依赖于样品中较大的分子。
Polymer Chemistry
♣ 分子量多分散性的表示方法
单独一种平均分子量不足以表征聚合物的性能，还需
要了解分子量多分散性的程度
➢ 以分子量分布指数表示
常用凝胶渗透色谱仪（Gel Permeation Chromatography, GPC）测定。
Polymer Chemistry
说明
✓ 分子量分布是影响聚合物性能的因素之一。分子量过高部分使聚合物的强度增加，但加工成型时塑化困难；低分子量部分使聚合物强度降低，但易于加工。 ✓ 不同用途的聚合物应有其合适的分子量分布: 合成纤维：分子量分布宜窄塑料、橡胶：分子量分布可宽
Polymer Chemistry
♣ 高分子的强度与分子量密切相关
A
点是初具强度的最低聚合度，
强度
A点以上强度随分子量迅速增
B
C
加
A
B 点是临界点，强度增加逐渐
减慢
C 点以后强度不再明显增加
尼龙

高分子的分子量和分子量分布讲解

高分子物理
15
多分散系数 d
d M w 称为多分散系数，用来表征分散程度 Mn
d越大，说明分子量越分散 d＝１，说明分子量呈单分散（一样大） M n M w
（d ＝ 1.03～1.05 近似为单分散）
缩聚产物 d＝２左右自由基产物 d＝３～５有支化 d＝２５～３０（PE）
2019/6/4
1.2.3 高分子的分子量分布的测定方法
分子量分布的研究方法、分子量分布的表示方法、分子量分布的数据处理、凝胶渗透色谱(GPC)
2019/6/4
高分子物理
2
教学目的：
通过本节的学习，全面理解和掌握各种统计平均分子量和分子量分布的意义、表达式和分析测试方法及测试基本原理。
重点：
各种统计平均分子量和分子量分布的表达式、表示方法及测量手段；GPC测量分子量及分子量分布的方法和原理。
相对
超速离心沉降平衡法 1×104～1×106
动力学法
粘度法
1×104～1×107
Mw~ Mz M
色谱法
2019/6/4
凝胶渗透色谱法（GPC）
1×103～1×107 各种平均
高分子物理
相对相对相对
19
1.2.2.1 端基分析法
⑴适用对象：
① 分子量不大（3×104以下），因为分子量大，单位重量中所含的可分析的端基的数目就相对少，分析的相对误差大；
α为与溶液性质有光的常数 (0.5~1.0)
分子量高的组分在 Z 均中的贡献最大
2019/6/4
高分子物理
12
平均分子量的连续函数表示

Mn
n(M )MdM
0

高分子材料学

结晶温度： Tg< T < Tm
T>Tm 分子热运动自由能大于内能，难以形成有序结构。 T<Tg 链段运动被冻结，不能分子发生重排和形成结晶。
2 结晶与性能 ①结晶对力学性能的影响 ②密度 ③结晶度对阻隔性能的影响：
随着结晶度增加，透水性、透氧性变小。
④光学性质：物质的折光率与密度有关。
两相并存的聚合物--呈乳白色，不透明结晶度减少时--透明性增加完全非晶的聚合物--透明
PC PA POM ABS PET
特种工程塑料
导电、导磁、感光、压电等材料 ►共混型特种塑料合金 ①塑料共混 PE/PA-降低PA吸水性 PE/PC-改善PC耐应力开裂 ②橡塑共混 NR/PS-改善PS脆性 NBR/PVC-改善耐油、耐热及冲击性 ③塑料与其他材料共混：可制成导电、导磁、增强、耐热耐磨、减震等材料 ►共混制特种塑料合金的目的 ①提高塑料自身物理机械性能、电性能 ②改善耐老化性及环境应力开裂性能 ③改善某些塑料的成型工艺性能 ④废物回用，防污染，降低成本
含氯，极性，双键不易活动。耐老化、耐油，但耐低温性下降。
CI
2 端基端基的产生：引发剂的残基链终止方式链转移未反应的残留官能团端基对聚合物性能的影响： ①热性能-对熔点的影响 ②光热稳定性：PVC--不饱和端基引发脱HCI POM--降解从端基开始 ③利用端基对聚合物改性和功能化 PP-g-MAH与PA6的-NH2端基反应
4 热性能脆化温度Tc 使用温度热塑 50-90C° 玻璃化温度Tg 热固100-200C° 流动（粘流）温度Tf 晶性聚合物熔点温度Tm 分解温度Td 5 电性能一般比玻璃、陶瓷好 ► 介电常数及介质损耗小可减少电能消耗 ► 体积电阻及表面电阻大是理想绝缘材料 ► 某些塑料不受频率影响，用于雷达、电视等高频技术中 6 稳定性能 ► 耐化学腐蚀性：耐酸、碱、溶剂、油类 ► 耐光化性：光、热、射线等会使塑料老化变形，须加防老剂阻缓其老化 ► 收缩性：收缩率绝对值较大且易波动

高分子化学第一章(2)

5
--NH-(--CH2-)-CO-- + n H2O n 5
n
H2N(CH2)6NH2 + HOOC(CH2)4COOH
H--NH(CH2)6NH--CO(CH2)4CO--OH + (2n-1) H2O
n
8
单体单元、结构单元、重复单元、单体单元、结构单元、重复单元、高分子化学链节有何关系？链节有何关系？
3
聚氯乙烯PVC由什么组成？由什么组成？聚氯乙烯由什么组成
4
高分子化学
一、高分子化合物与单体
聚合物分子结构必须是由多个重复单元所组成，聚合物分子结构必须是由多个重复单元所组成，并且这些重复单元是由相应的小分子衍生而来。些重复单元是由相应的小分子衍生而来。
C 2-C C 2-C C 2-C H H H H H H C l C l C l
其重复单元由两种结构单元组成，组成，且结构单元与单体的组成不尽相同，组成不尽相同，所以，所以，不能称为单体单元。为单体单元。
H--NH(CH2)6NH--CO(CH2)4CO--OH+ (2n-1) H2O
n
结构单元结构单元重复结构单元
但单体在形成高分子的过程中要失掉一些原子
----( C 2--C = H H2 -)--(-C 2--C -)---H H C --C H Hy x
n
说明： y为任意值，故在分子链上结构单元的排列是任意的：说明： x, y为任意值，故在分子链上结构单元的排列是任意的：
∼ ∼M1M2M1M1M2M1M2M2M2 ∼ ∼ 在这种情况下，无法确定它的重复单元，仅在这种情况下，无法确定它的重复单元，
说明：n 表示重复单元数，也称为链节数,, 在此等于聚合度。表重复单元数，也称为链节数在此等于聚合度。

高分子科学基础总结(1)

高分子科学基础总结第一章绪论1.高分子：也称聚合物分子或大分子，分子量较高(一般为104～106)，其分子结构必须是由许多相同的、简单的基本单元通过共价键重复连接而成的。

2.聚合物：也称高分子化合物，是由许多单个聚合物分子（高分子）组成的物质。

3.单体：能够进行聚合反应，并形成高分子中基本结构组成单元的小分子化合物。

4.重复单元：高分子链上化学组成和结构均可重复的最小单元，也称链节。

5.结构单元：由一种单体分子通过聚合反应而进入聚合物重复单元的那一部分叫做结构单元。

6.单体单元：与单体的元素组成和排列相同，只是电子结构不同的结构单元。

7. 聚合物的多分散性：聚合物是由一系列不同分子量（或聚合度）的同系物高分子组成的混合物，这些同系物高分子之间的分子量差为重复单元分子量的倍数，这种同种聚合物分子小不一的特性称为聚合物的多分散性。

8.聚合反应分类：（1）根据单体与其生成的聚合物之间在分子组成与结构上的变化把聚合反应分为加聚反应和缩聚反应。

（2）根据反应机理和动力学性质的不同，分为逐步聚合反应和链式聚合反应9.聚合物的分类：a.按主链元素组成：碳链高分子：主链完全由C原子组成。

杂链高分子：构成主链的元素除C外，还含O,N,S,P等一些杂原子。

元素有机高分子:主链无碳原子，完全由 Si,B,Al,O,Ti, N,S,P等杂原子组成，但侧基却是含C,H,O 的有机基团。

b.按性质和用途：塑料，纤维，橡胶，涂料，胶黏剂，功能高分子。

第二章逐步聚合反应1. 逐步聚合反应：由低分子化合物经多次逐步进行的相似的化学反应形成大分子的过程。

2. 缩聚反应：缩合聚合反应的简称，是指带有两个或两个以上官能团的单体经过许多次的重复缩合反应而逐步形成聚合物的过程。

3. 单体官能度（f )：一个单体分子中能参与聚合反应的官能团数目称为单体官能度，以f 表示。

4. 平均官能度( f )：是指聚合反应体系中实际上能参与聚合反应的官能团数相对于体系中单体分子总数的平均值，用f 表示。