理论力学(机械工业出版社)第十一章动量矩定理习题解答
理论力学第十一章-2

dr 而 mv v mv 0 , r F M O ( F ) , dt d d [ M O (mv )] M O ( F ) 故: (r mv ) r F , dt dt 质点对任一固定点的动量矩对时间的导数,等于作用在质 点上的力对同一点之矩。这就是质点对固定点的动量矩定理。
[例4]:两小球质量皆为m,初始角速度 0 求:剪断绳后, 角时的 .
解: 取A、B小球为研究对象, 受力分析:作用于二小球 的外力对转轴的矩都为零。 运动分析: A、B二小球均 作圆周运动。
17
M z
(e)
0
A、B二小球对其转轴的动量矩守恒。
依动量矩守恒定理有:
0
时,
Lz1 2ma0 a 2ma20
1
, 2
,总体积流量V q
。
19
经△t 时间,水流动量矩改变为:
dLO Labcd LABCD LCDcd LABab
设叶片数为 n ,水密度为 ,有
1 LCDcd qV dt v2 r2 cos 2 n 1 LABab qV dt v1 r1 cos1 n 1 dLO qV dt (v2 r2 cos 2 v1r1 cos1 ) n dLO M O (F ) n qV (v2 r2 cos 2 v1r1 cos1 ) dt
7
2.定轴转动刚体
Lz M z (mi vi ) mi ri J z
2
定轴转动刚体对转轴的动量 矩等于刚体对该轴转动惯量 与角速度的乘积。 3.平面运动刚体 Lz M z (mvC ) J C 平面运动刚体对垂直于质量对称平面的固定轴的动 量矩,等于刚体随同质心作平动时质心的动量对该 轴的动量矩与绕质心轴作转动时的动量矩之和。
【精品】理论力学11动量矩定理分析解析幻灯片

0 Fox m2l amgFOy
FOymgm2lam 4g
§11-4 刚体对轴的转动惯量
一.定义: Jz miri2
z
i
对于质量连续分布的刚体,上式可写成积分
形式
Jz r2 dm
由定义可知,转动惯量不仅与 质量有关,而且与质量的分布有关;
ri
vi
mi
在国际单位制中,转动惯量的单位
是: kg·m2。同一刚体对不同轴的转
Jz mz2
回转半径的几何意义是:假想地将物体的质量集 中到一点处,并保持物体对轴的转动惯量不变,则该 点到轴的距离就等于回转半径的长度。
3、平行轴定理
定理:刚体对于任一轴的转动惯量,等于刚体 对于通过质心、并与该轴平行的轴的转动惯量,加 上刚体的质量与两轴间距离平方的乘积,
zC
z1
m
C
Jz1 JzC md2
dLO dt
MO(Fi(e))
若 Mz(F(e))0,则 Lz 常量。
dLz dt
Mz (Fi (e) )
例 高炉运送矿石的卷扬机如图。已知鼓轮的半径为R,质量 为m1,绕O轴转动。小车和矿石的总质量为m2。作用在鼓轮上
的力偶矩为M,鼓轮对转轴的转动惯量为J,轨道倾角为a。
设绳质量和各处摩擦不计,求小车的加速度a。
O u
A
mg
mg
解:以系统为研究对象,受力如图。
由于SMO(F (e))=0,且系统初始静止,所以LO=0。
设重物A上升的速度为v,则人的绝对速度va的大小为
va uv
v
LOmarvmv0 r
FOy
O
FOx
u
A mg mg
L Om (uv)rm v0r
理论力学课后习题答案

第11章 动量矩定理一、是非题(正确的在括号内打“√”、错误的打“×”)1. 质点系对某固定点(或固定轴)的动量矩,等于质点系的动量对该点(或轴)的矩。
(×)2. 质点系所受外力对某点(或轴)之矩恒为零,则质点系对该点(或轴)的动量矩不变。
(√)3. 质点系动量矩的变化与外力有关,与内力无关。
(√)4. 质点系对某点动量矩守恒,则对过该点的任意轴也守恒。
(√)5. 定轴转动刚体对转轴的动量矩,等于刚体对该轴的转动惯量与角加速度之积。
(×)6. 在对所有平行于质心轴的转动惯量中,以对质心轴的转动惯量为最大。
(×)7. 质点系对某点的动量矩定理e 1d ()d nOO i i t ==∑L M F 中的点“O ”是固定点或质点系的质心。
(√)8. 如图所示,固结在转盘上的均质杆AB ,对转轴的转动惯量为20A J J mr =+ 2213ml mr =+,式中m 为AB 杆的质量。
(×)9. 当选质点系速度瞬心P 为矩心时,动量矩定理一定有e 1d()d nP P i i t ==∑L M F 的形式,而不需附加任何条件。
(×)10. 平面运动刚体所受外力对质心的主矩等于零,则刚体只能做平动;若所受外力的主矢等于零,刚体只能作绕质心的转动。
(×)图二、填空题1. 绕定轴转动刚体对转轴的动量矩等于刚体对转轴的转动惯量与角速度的乘积。
2. 质量为m ,绕z 轴转动的回旋半径为ρ,则刚体对z 轴的转动惯量为2ρm J z =。
3. 质点系的质量与质心速度的乘积称为质点系的动量。
4. 质点系的动量对某点的矩随时间的变化规律只与系统所受的外力对该点的矩有关,而与系统的内力无关。
5. 质点系对某点动量矩守恒的条件是质点系所受的全部外力对该点之矩的矢量和等于零,质点系的动量对x 轴的动量矩守恒的条件是质点系所受的全部外力对x 轴之矩的代数和等于零。
理论力学:第11章 动量矩定理

对瞬心 C': LC IC
11.2 动量矩定理
一、 质点动量矩定理
由牛顿第二定律: ma F
易证:
dmO (mv )
dt
mO
(F)
微分形式动量矩定理
其中 O 为定点。
或
dmO (mv) mO (dS )
LH
P vr
b
1
Q r2
Q vC
r
b
sin
1
Q r2
g 2 2 g
g 2 2g
(P
2Q)r
P
b b
(1
sin
)
vC g
系统外力对 H 的力矩:
11-3
ΣmH
(F
(e)
)
m
P
r
b
Q
b
Q
sin
绳子剪断前为静力学问题,易求反力。
绳子剪断后为定轴转动动力学问题,用质心运动定理求: MaC
F (e)
但需要先求出 aC ,用刚体定轴转动微分方程可求: Iz mz (F (e) )
11-5
解:I. 绳子剪断前,受力如图(a)。 W
由对称性: N A0 2
II. 绳子剪断瞬时,受力、运动如图(b)。
11-2
欲用动量矩定理求 aC , aC 只跟三个运动物体有关,并且有一个“轴”O,如图。 但其中的 N 如何处理?
事实上,滚子沿斜面法向是静平衡的, N = Q cosα。 解:① 求加速度 aC 。
理论力学:第11章 动量矩定理

·1·第11章 动量矩定理11.1 主要内容11.1.1 质点系动量矩计算质点系对任意一点的动量矩为各质点的动量对同一点之矩的矢量和或质点系中各质点的动量对同一点的主矩,即∑∑==⨯==n i n i i i i i O O m m 11)(iv r v M L质点系对于某轴,例如对z 轴的动量矩为∑==n i i i z z m M L 1)(v刚体对转动轴z 轴的动量矩为z z I L =质点系相对于质心的动量矩为质点系中各点动量对质心的主矩,即i i ni i C m v r L ⨯'=∑=1i r '为第i 个质点对质心的矢径。
质点系对任意一点的动量矩等于质点系对质心的动量矩,与将质点系的动量集中于质心对于O 点动量矩的矢量和。
C v r L L m C C O ⨯+=当刚体作平面运动时,又可表示为d mv L L C ±=C O其中d 为点至v C 的垂直距离,当C L 与矩d mv C 的符号相同时取正值,反之取负值, 11.1.2 质点系的动量矩定理(1)对固定点的动量矩定理质点系对固定点O 的动量矩对于时间的一阶导数等于外力系对同一点的主矩,即)(e O O dt d M L =在直角坐标系上的投影式为·2·⎪⎪⎪⎭⎪⎪⎪⎬⎫∑=∑=∑=)()()()()()(e z z e y y e x x M dt dL M dt dL M dt dL F F F(2)质点系相对于质心的动量矩定理质点系相对于质心的动量矩对时间的一阶导数等于外力系对质心的主矩。
即(e)C C M L =dt d 或 (e)C Cr M L =dt d式中Cr L 为质点系相对于质心平移坐标系的运动对质心的动量矩。
(3) 动量矩守恒定律在特殊情况下外力系对O 点的主矩为零,则质点系对O 点的动量矩为一常矢量,即()0=e OM ,常矢量=O L 或外力系对某轴力矩的代数和为零,则质点系对该轴的动量矩为一常数,例如0)()(=∑e x M F ,L x =常数11.1.3 刚体绕定轴转动微分方程若刚体绕固定轴z 的转动惯量为I z ,则刚体绕固定轴z 的微分方程为z z M tI =22d d ϕ 或z z M I =ε在工程中,常将转动惯量表示为2z z m I ρ=z ρ称为回转半径。
理论力学第十一章,动量定理

的投影守恒。
y
α
px px0
vr m2g v
vm1
vr
A
FA m1g
x
vm1
α
B
FB
(b)
(a)
α
vm1
m2g x
p mi v i
p x mi vix
A
FA m1g
B
FB
例 题1
v
考虑到初始瞬时系统处于平衡,即有pox=0,于是有 px = m2vcos m1vm1 = 0 另一方面,对于炮弹应用速度合成定理,可得 v = ve + vr 考虑到 ve = vm1,并将上式投影到轴 x 和 y 上,就得到 vcos = vrcos vm1
质点系冲量定理投影形式
e e p2 y p1 y ( Fiy ) dt I iy t2 t1 e p2 z p1 z ( Fize ) dt I iz t2 t1
dp Fie dt
dpx e Fix dt
3,质点系动量守恒定律
Fi e 0 , 1)
y
α
vr vm1
m2g x
A
FA m1g
B
FB
(a)
例 题1
解: 取火炮和炮弹(包括炸药)这个系统作为研究对象。
设火炮的反座速度是 vm1,炮弹的发射速度是 v,对水平面的仰 角是 (图b)。 炸药(其质量略去不计)的爆炸力是内力,作用在系统上的外力 在水平轴 x 的投影都是零,即有Fx = 0;可见,系统的动量在轴 x 上
(m1 m2 ) C Fy m1 g m2 g y
质心 C 的坐标为
理论力学第十一章动量矩定理

JO
d 2
dt 2
mga
即:
d 2
dt 2
mga
JO
0
解: 令 2 mga
JO
——固有频率
得
2 0
通解为 O sin(
mgat )
JO
周期为 T 2 2 JO
mga
例11-3 用于测量圆盘转动惯量的三线摆中,
三根长度相等(l)的弹性线,等间距悬挂被测量的圆盘。
已知圆盘半径为 R、重量为W。
dt
dt dt
v dr dt
r d(mv) d(r mv)
dt
dt
dLO dt
MO F
矢量式
质点对固定点的动量矩对时间的导数等于作 用于质点上的力对该点的矩。
★ 质点系的动量矩定理
0
d
dt
i
ri mivi
i
MO (Fii )
i
MO (Fie )
MO (Fie )
i
F2
z
F1
LO rC mvC LC
dLO d
dt dt
rC mvC LC
ri Fie (rC + ri) Fie
rC Fie ri Fie
③
即
drC dt
mvC
rC
d dt
mvC
dLC dt
rC
Fie
dLC dt
由于
① ① drC dt
② vC ,
drC dt
mvC
★ 相对质心的动量矩
LC MC mivi ri mivi
vi vC vir
LC = rimivC rimivir
其中
ri mivC ( miri)vC 0 (rC
理论力学练习册及答案
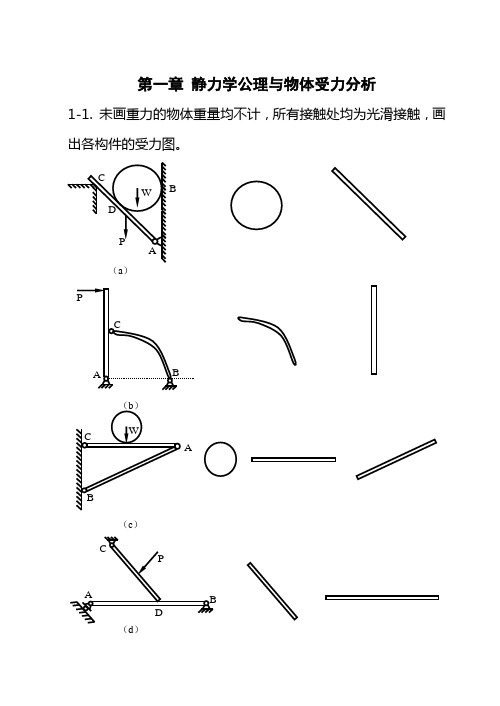
8-8.图示机构中,设当OA与水平线成450角的瞬时,曲柄OA有反时针方向的匀角速度ω=25 rad/s,连杆AB水平,扇形板BD铅垂。求扇形板绕定轴D转动的角加速度ε。
解:将力系向A点简化,并过A点建立如图所示坐标系。
由矢量式可得力系简化的最终结果为力螺旋,
作用点为:
3-2.已知A(1,0,1),B(0,1,2)(长度单位为米),F= kN。求力F对x、y、z轴的矩?
解:
3-3.如图所示,长方体边长为a、b、c,力F沿BD,试计算力F对AC轴之矩MAC(F)
解:力F对C点的矩为:
4-3.置于铅垂面内的均质正方形簿板重P= 100kN,与地面间的摩擦系数f= 0.5,欲使簿板静止不动,求作用在点A的力F的最大值?
4-4.折梯放在水平地面上,其两脚与地面的摩擦系数分别为fA= 0.2,fB= 0.6,折梯一边AC的中点D上有一重为P= 500N的重物,折梯重量不计,问折梯能否平衡?如果折梯平衡。试求出两脚与地面间的摩擦力。
第六章 刚体基本运动
6-1.在如图所示中,已知ω、。在图上标示出A、B两的速度、加速度。
6-2.在如图所示的平面机构中,半径为r的半圆盘在A和B处与杆铰接,已知 , ,曲柄O1A以匀角速度ω转动。求图示瞬时圆盘上M点的速度和加速度。
6-3.在如图所示的平面机构中,齿轮1紧固在杆AC上, ,齿轮1与半径为r2的齿轮2啮合,齿轮2可绕O2轴转动,。设 , ,试确定 时,轮2的角速度和角加速度。
解:动点取曲柄OA上A点,
理论力学第11章的课后习题答案

求:重物A下降的加速度以及轮C与地面接触点处的静摩擦力。
C B rO R
D A
C
B
r OR
m2 g Fs
FN
解:分别选轮子和重物A为研究对象,受力分析和运动分析 如图所示。轮子作平面运动,应用刚体平面运动微分方程,有
C B
FT
Fs
m2aO
D
rO
R
FT r Fs R m2 2
JO g W1R2
g
小车上升的加速度为
aห้องสมุดไป่ตู้
R
M W1R sinR
JO g W1R2
gR
a
FT
W1
FN
由小车的运动微分方程,有
FT
W1 sin
W1 g
a
解得绳子的拉力为
FT
W1 sin
W1 g
a
11-18 如图11.52所示结构中,重物A、B的质量分别为m1和m2 B物体与水平面间摩擦系数为f,鼓轮O的质量为M,
重物A的运动微分方程为 A
m1g FT' m1aA
C B r OR
m2 g Fs
FN
FT
F T'
a
A
m1g
其中: aO R
aA (R r)
FT' FT
联立求解,可得重物A下降的加速度为
aA
m1(R
m1(R r)2 r)2 m2 (R2
2)
g
轮C与地面接触点处的静摩擦力为
Fs
(2
m1(R r)2
FT'A
A
aA
Mg
A
m1g
重物A: m1g FTA m1a A
理论力学11—动量矩定理

11.2 动量矩定理
例3 高炉运送矿石的卷扬机如图。已知鼓轮的半径为R,质量 为 m1 ,绕O 轴转动。小车和矿石的总质量为 m2 。作用在鼓轮 上的力偶矩为 M,鼓轮对转轴的转动惯量为 J,轨道倾角为α。 设绳质量和各处摩擦不计,求小车的加速度a。 分析: 小车的速度对时间的一阶导数等 于加速度,利用动量矩定理可求 出小车速度的表达式。 解:以系统为研究对象,受力 如图。以顺时针为正,则
即:绕定轴转动刚体对其转轴的动量矩等 于刚体对转轴的转动惯量与转动角速度的 乘积。
11.1 质点和质点系的动量矩
注意:
对点的动量矩是矢量,对轴的动量矩是代数量。 计算质点系相对于质心的动量矩时,无论是用绝对运动的动 量,还是用相对于以质心为基点的平动坐标系的相对运动的 动量,其计算结果是相同的。
对质心之外的其它点,用上述两种方法计算的动量矩是不同 的,必须用绝对运动中的动量来计算动量矩。
11.1 质点和质点系的动量矩
例1 均质圆盘可绕轴O转动,其上缠有一绳, 绳下端吊一重物A。若圆盘对转轴O的转动惯 量为J ,半径为 r,角速度为 ,重物A的质量 为 m ,并设绳与圆盘间无相对滑动,求系统 对轴O的动量矩。
O
r
解:
A
mv
LO L盘 mvr J 块L LOL L mvr J 块 盘 2 2 2 J ( mr 2 mr ) mr J (mr J J )
刚体相对质心的转动的运动变化与外力系对质心的主矩的关系 将由本章的动量矩定理给出。
它揭示了物体机械运动规律的另一个侧面。
11.1 质点和质点系的动量矩
1 质点的动量矩
质点Q的动量对于点O的矩,定义为质点对于点O的动量矩 是矢量。
《理论力学》第十一章动量矩定理习题解详解

yx第十一章 动量矩定理 习题解[习题11-1] 刚体作平面运动。
已知运动方程为:23t x C =,24t y C =,321t =ϕ,其中长度以m 计,角度以rad 计,时间以s 计。
设刚体质量为kg 10,对于通过质心C 且垂直于图平面的惯性半径m 5.0=ρ,求s t 2=时刚体对坐标原点的动量矩。
解:)(1223|22m x t C =⨯== )(1624|22m y t C =⨯== t t dtddt dx v C Cx6)3(2=== )/(1226|2s m v t Cx =⨯== t t dtddt dy v C Cy8)4(2=== )/(1628|2s m v t Cy =⨯==2323)21(t t dt d dt d ===ϕω )/(6223|22s rad t =⨯==ω→→→+=k v m M J L C Z Cz O )]([ω→→-+=k y mv x mv m L C Cx C Cy O ][2ωρ→=→⨯-⨯+⨯⨯=k L t O ]1612121665.0[10|22→=→=k L t O 15|2 )/(2s m kg ⋅,→k 是z 轴正向的单位向量。
[习题11-2] 半径为R ,重为W 的均质圆盘固结在长l ,重为P 的均质水平直杆AB 的B 端,绕铅垂轴Oz 以角速度ω旋转,求系统对转轴的动量矩。
解:gPl l g P J ABz 33122,=⋅⋅=平动)(a O 转动绕定轴C )(b 转动绕定轴1 )(Oc O 在圆弧上作纯滚动)(d gl R W l g W g J l z 4)4(R W 412222,+=⋅+⋅⋅=圆盘ωω⋅+⋅=圆盘,,z AB z z J J Lω]4)4(3[222g l R W g Pl L z ++=ω)4443(222gWRg Wl g Pl L z ++= ω)4333(222gWR g Wl g Pl L z ++=ω)433(22R gW l g W P L z ++= [习题11-3] 已知均质圆盘质量为m ,半径为R ,当它作图示四种运动时,对固定点1O 的动量矩分别为多大?图中l C O =1。
《理论力学》第十一章 动量矩定理

§11-1 质点和质点系的动量矩
1.质点的动量矩
MO (mv)
mv
M z (mv)
r
[MO (mv)]z Mz (mv)
对点 O 的动量矩
MO (mv) r mv 对 z 轴的动量矩
M z (mv) MO (mv)xy
代数量,从 z 轴正向看, 逆时针为正,顺时针为负.
2.质点系的动量矩
对点的动量矩
n
LO MO (mivi ) i 1
对轴的动量矩
n
Lz M z (mivi ) i 1
即 LO Lxi Ly j Lzk
二者关系
[LO ]z Lz
(1) 刚体平移 LO MO (mvC ) Lz Mz (mvC )
(2) 刚体绕定轴转动 Lz J z
(JO m1r12 m2r22 )
MO (F (e) ) (m1r1 m2r2 )g
由
dLO dt
MO (F(e))
,得
d
dt
(m1r1 m2r2 )g JO m1r12 m2r22
FN
(2)由质心运动定理
FN (m m1 m2 )g (m m1 m2 )aCy
Jz JzC md 2 式中 zC 轴为过质心且与 z轴平行的轴,d 为 z
与 zC 轴之间的距离。
即:刚体对于任一轴的转动惯量,等于刚体对于通过
质心并与该轴平行的轴的转动惯量,加上刚体的质量
与两轴间距离平方的乘积.
证明:
JzC mi (x12 y12 )
Jz m i r2 m i (x2 y2) mi[x12 ( y1 d )2 ]
11 动量矩定理习题解答

R
O ve
r o B
vr
[解]
研究整体,由于∑Mz (F)= 0,且系统初始静止, 所以 Lz = 0,即 L z 盘+ L z 人 = 0 式中 Lz 盘= J z =
1P 2 R 2g
L z 人= 解得
ds Q (v -v )r, v = rω , vr at e r e dt g
解:重物 A 和 B 速度 v A vB r ,
LO m1v A r m2 vB r J O 1 m1r r m2 r r m3r 2 2
A
B (c)
vA
vB
m1 g
m2 g
1 2 m1 m2 m3 r 2
…….. ①
对 B 轮,有
…….. ②
P aB P FT1 g
…….. ③
FT1 FT1
…….. ④
再以轮与绳相切点 D 为基点,则轮心 B 的加速度
v B v D v BD ,式中 v D r A , v BD r B
∴ v B r A r B , 对上式求导得轮心 B 的加速度为
Fx maCx , FNA maCx , Fy maCy , FNB mg maCy , M C ( F ) J C , FNB l cos FNA l sin 1 ml 2 2 2 12
l 2 FNA 2 ( sin cos )m, l 2 FNB mg ( cos sin )m, 2 l l 1 2 FNB 2 cos FNA 2 sin 12 ml
A
理论力学:第11章 动量矩定理
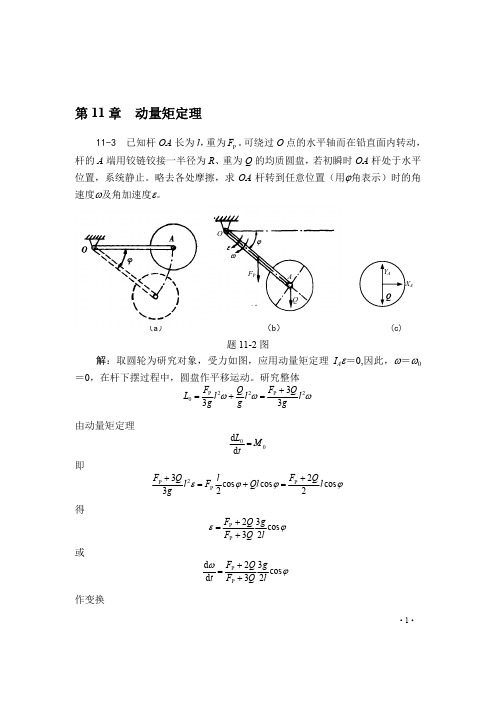
12 g g
12 9.8
9.8
由刚体绕定轴转动微分方程 IB kx BC FP BG (kx BC FP BG) / IB
(8750 76 103 0.6 200 0.1) /1.9 198.975rad/s2
由质心运动定理有
FN =1234N
Ff=370N FT 575N
11-28 题 11-28 图所示质量为 4kg 的矩形均质板,用两根等长的不变形的 软绳悬挂在图示位置(AB 水平)。该板处于静止状态时,B 端的绳子突然被剪断, 试求(1)此瞬时该板质心的加速度及 A 端绳子张力。(2)若将两绳换成弹簧, 在 B 端的弹簧突然被剪断时,质心加速度及 A 端弹簧张力将如何?
(2)轴承 O 的水平约束力。
·7·
FT
R
A
aA
mg
F
FN
(a)
B
M
R FOy
FT
O
FOx
m2g
(b)
题 11-33 图
(c)
解:(1)对系统进行整体受力分析,主动力元功之和为
dW Md m1g Rd sin (M m1gR sin )d
动能增量为
dT
FOx m1(m2gR sin cos 3M cos ) (3m1 m2 )R
·9·
d
m2
R
2
2 B
1
I
A
2 A
1
m1v
2 A
2
2
2
运动学补充条件,圆盘 A 纯滚动
vA A R
理论力学(11.10)--动量矩定理-思考题答案

第十一章 动量矩定理
答 案
11-1
11-2
质点系对任一点的动量矩为 ,当 时,对所有点的动量矩 都相等,即 。
11-3
11-4
不对。
11-5
圆盘作平移,因为圆盘所受的力对其质心的矩等于零,且初始角速度为零。
11-6
(a)质心不动,圆盘绕质心加速转动。
(b)质心有加速度 a=F/m ,向左;圆盘平移。
(c)质心有加速度 a=F/m ,向右;圆盘绕质心加速转动。
11-7
轮心加速度相同,地面摩擦力不同。
11-8
(1)站在地面看两猴速度相同,离地面的高度也相同;
(2)站在地面看两猴速度相同,离地面的高度也相同。
11-9
A,C正确。
11-10
均不相同。
由对定点的动量矩定理判定。
理论力学第11章动量矩定理

F1 b C
摆动的频率 ω0 和周期 T 分别是
mgb n ; JO
(a )
mg
21
第十一章结束
22
§11-3
23
2
ห้องสมุดไป่ตู้
§11-1
转动惯量
Z
一、刚体对轴的转动惯量
J Z mi ri 2
i 1
n
刚体对Z轴的转动惯量
ri
mi vi
刚体上所有各mi与ri2的乘积之和称为刚体对z
轴的转动惯量,用符号Jz表示。
一个刚体的各质点离轴越远,它对该轴的转动 惯量越大;反之越小。 转动惯量是刚体转动惯性的度量,总是正标量。 量纲: dim J ML2 2 常用单位:
即:定轴转动刚体对转轴的转动惯量与角加速度的乘积,等于作用于该刚体 上的所有外力对转轴的力矩的代数和。这就是刚体的定轴转动微分方程。16
d 2 或 J M z (F ) z 2 dt
刚体的转动惯量是刚体转动时的惯性的量度。
J z M z ( F )
解决两类问题:
—刚体定轴转动微分方程
例 题
解: 此系统所受的重力和轴承的约束
力对于转轴的矩都等于零,因此系统 对于转轴的动量矩守恒。 当θ=0时,动量矩
θ l B
a
z a
a
z a
l A l
θ
B
A l
Lz1 2 ma0 a 2ma20
当 θ≠ 0 时,动量矩
Lz 2 2m(a l sin )2
因为 Lz1=Lz2 ,得
dm A 2 rdr
2 2
4
于是: J z r 2 dm R A 2 r 3dr 1 AR 4 1 mR 2 m 0
理论力学第十一章动量定理.

[例1] 已知:为常量,均质杆OA=AB = l, 两杆质量皆为 m1,
滑块B质量 m2。 求: 质心运动方程、轨迹及系统动量。
解:设 ,t 质心运动方程为:
xC
m1
l 2
m1
3l 2
2m1 m2
2m2l
cos t
yA
2(m1 m2 ) l cos t
C B
2m1 m2
0,
则
px
恒量
4.例题分析
[例1] 电动机外壳固定在水平基础上,定子和外壳的质
量为 m1,转子质量为 m2。定子和机壳质心 O1 ,转子质
心 O2,O1O2 e,角速度 为常量。求基础的水平及
铅直约束力。
解: p m2e
px m2e cos t py m2 e sin t
qV — 流体在单位时间内流过截面的体积流量
dt内流过截面动量变化为:
管壁对流体 的约束力
设 F F F
F —静约束力;F —附加动约束力
F p Fa Fb 0
F qV (vb va )
p p0 pa1b1 pab
( pbb1 pa1b ) ( pa1b paa1 ) pbb1 paa1
[思考题 P255 11-3,习题 P256 11-10]
v mBvr kmBol
mA mb mA mb
11-3 质心运动定理
1.质心
rC
m iri m
,m m i
质心位置的确定:
xC
mixi m
,yC
miyi, m
《理论力学》第十一章 动量矩定理

LO lOi ri mi v i
将动量矩投影到以O为原点的直角坐标轴上
HOHAI UNIVERSITY ENGINEERING MECHANICS
Lx l x mv m yv z zv y
L y l y mv m zv x xv z Lz l z mv m xv y yv x
(二)质点系的动量矩L
设质点系由n个质点组成,其中第i个质点 的质量为mi,速度为vi。 质系对任意固定点O的动量矩:
HOHAI UNIVERSITY ENGINEERING MECHANICS
LO lOi ri mi v i
质系对任意固定点O的动量矩为各质点 的动量对O点矩的矢量和。
3、刚体动量矩的计算
1)刚体平动
HOHAI UNIVERSITY ENGINEERING MECHANICS
HOHAI UNIVERSITY ENGINEERING MECHANICS
例1:均质细长直杆长l,质量m1,与质量为m2,半径
为r,均质圆盘固结。已知角速度为,试求对转轴的 动量矩。 解:
HOHAI UNIVERSITY ENGINEERING MECHANICS
第十一章
HOHAI UNIVERSITY ENGINEERING MECHANICS
动量矩定理
§1 动量矩(表征物体转动的物理量)
一、动量矩的定义及计算
1. 对任意固定点O的动量矩(矢量):
质点对固定点的动量矩即质点的动量对固定点的矩: z lO r mv r p mv lo M r F
平轴z的转动惯量。轴z过O点垂直纸面
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习 题11-1 质量为m 的质点在平面Oxy 内运动,其运动方程为:t b y t a x ωω2sin ,cos ==。
其中a 、b 和w 均为常量。
试求质点对坐标原点O 的动量矩。
t a xv x ωωsin -== t b y v y ωω2cos 2== x mv y mv L y x O +-=)cos 2cos 22sin sin (t a t b t b t a m ωωωωωω⨯+⨯= )cos 2cos 22sin (sin t t t t mab ωωωωω⨯+⨯= )cos 2cos 2cos sin 2(sin t t t t t mab ωωωωωω⨯+⨯= )2cos (sin cos 22t t t mab ωωωω+= t mab ωω3cos 2=11-2 C 、D 两球质量均为m ,用长为2 l 的杆连接,并将其中点固定在轴AB 上,杆CD 与轴AB 的交角为θ,如图11-25所示。
如轴AB 以角速度w 转动,试求下列两种情况下,系统对AB 轴的动量矩。
(1)杆重忽略不计;(2)杆为均质杆,质量为2m 。
图11-25(1)θθ222sin 2)sin (2ml l m J z =⨯= θω22sin 2l m L z = (2)θθ2202sin 32d )sin (2ml x x lm J l z ==⎰杆 θ22sin 38ml J z = θω22sin 38l m L z =11-3 试求图11-26所示各均质物体对其转轴的动量矩。
各物体质量均为m 。
图11-26(a) ω231ml L O =(b) 22291)6(121ml l m ml J O =+= ω291ml L O -=(c) 2222452312121ml l m l m J O =⨯⨯+⨯⨯=ω2245ml L O = (d) 2222321mR mR mR J O =+= ω223mR L O =11-4 如图11-27所示,均质三角形薄板的质量为m ,高为h ,试求对底边的转动惯量J x 。
图11-27面密度为 bhm A 2=ρ在y 处 b hy b y = y y hm y b hy bhm y b bhm A m y A d 2d 2d 2d d 2=⨯⨯=⨯⨯==ρ 微小区域对于z 轴的转动惯量y y h y hmm y h J z d )(2d )(d 222-=-= ⎰⎰+-=+-=-=hh z mh y y hy y h h m y y h y h m J 002322222)413221(2d )2(2d )(2 261mh =11-5 三根相同的均质杆,用光滑铰链联接,如图11-28所示。
试求其对与ABC 所在平面垂直的质心轴的转动惯量。
图11-283)31(12122⨯⎥⎦⎤⎢⎣⎡+=h m ml J z l h 23= 2222213)121121(3)2331(121ml ml l m ml J z =⨯+=⨯⎥⎦⎤⎢⎣⎡⨯+=11-6 如图11-29所示,物体以角速度w 绕O 轴转动,试求物体对于O 轴的动量矩。
(1) 半径为R ,质量为m 的均质圆盘,在中央挖去一边长为R 的正方形,如图11-32a 所示。
(2) 边长为4a ,质量为m 的正方形钢板,在中央挖去一半径为a 的圆,如图11-32b 所示。
图11-29(1)2126121R m mR J C -= ππ221m m R R m ==222π61π3π6121mR R m mR J C -=⨯-=π)1(ππmm m m -=-=' 2222π67π9π)1(ππ61π3mR R m mR R m J J C O -=-+-='+=ωω2π6π97mR J L O O -=-=(2)21221)4(61a m a m J C -= m m a a m 16π16π221== 22296π325616π2138ma ma ma J C -=⨯-=m m m m 16π1616π-=-='222296π48896π3256816π1696π3256)22(mR a m ma a m J J C O -⨯+-=⨯-+-=⨯'+=296π511024mR -=ωω2961024π51mR J L O O -=-=11-7 如图11-30所示,质量为m 的偏心轮在水平面上作平面运动。
轮子轴心为A ,质心为C ,AC =e ;轮子半径为R ,对轴心A 的转动惯量为J A ;C 、A 、B 三点在同一直线上。
试求下列两种情况下轮子的动量和对地面上B 点的动量矩:(1)当轮子只滚不滑时,已知v A ;(2)当轮子又滚又滑时,已知v A 、w 。
图11-30ωω)()()(2me J e R mv J e R mv L A c C C B +-+-=-+-=(1)Rv A =ω ω)(e R v C+=Rv e R m me J R v me J R v e R m L A A A A A B ])([)()(2222++--=--+-=(2)ωe v v A C +=ωωC A B J e R e v m L -++-=))((ωω)()()(2me J e R me v e R m A A --+-+-= ])()([ωmeR J v e R m A A +++-=11-8 曲柄以匀角速度w 绕O 轴转动,通过连杆AB 带动滑块A 与B 分别在铅垂和水平滑道中运动,如图11-31所示。
已知OC =AC =BC =l ,曲柄质量为m ,连杆质量为2m ,试求系统在图示位置时对O 轴的动量矩。
图11-31ωω=AB (顺时针)AB OC O L L L +=ω231ml L OC =ωωωω222234322)()2)(2(1212ml ml ml l m l mv L AB C AB =-=-+=ω235ml L OC =11-9 如图11-32所示的小球A ,质量为m ,连接在长为l 的无重杆AB 上,放在盛有液体的容器中。
杆以初角速度w 0绕O 1O 2轴转动,小球受到与速度反向的液体阻力F =km w ,k 为比例常数。
问经过多少时间角速度w 成为初角速度的一半?图11-32ω2ml L z = ωkml M z -=z zM tL =d d 得 ωωlkt -=d d ⎰⎰-=tt l k0d d 0ωωωωt l k-=0ln ωωωω0ln k l t = 2ln k lt =11-10 水平圆盘可绕z 轴转动。
在圆盘上有一质量为m 的质点M 作圆周运动,已知其速度大小v 0=常量,圆的半径为r ,圆心到z 轴的距离为l ,M 点在圆盘上的位置由f 角确定,如图11-33所示。
如圆盘的转动惯量为J ,并且当点M 离z 轴最远(在点M 0)时,圆盘的角速度为零。
轴的摩擦和空气阻力略去不计,试求圆盘的角速度与f 角的关系。
图11-330=∑z M 常量=z L)(00r l mv L z += ϕωϕωcos )cos 2(0022l mv r mv lr r l m J L z z +++++= )(cos )cos 2(00022r l mv l mv r mv lr r l m J z +=+++++ϕωϕω )cos 2()cos 1(220ϕϕωlr r l m J v ml z +++-=11-11 两个质量分别为m 1、m 2的重物M 1、M 2分别系在绳子的两端,如图11-34所示。
两绳分别绕在半径为r 1、r 2并固结在一起的两鼓轮上,设两鼓轮对O 轴的转动惯量为J O ,试求鼓轮的角加速度。
图11-34222111r v m r v m J L O z ++=ω ω11r v = ω22r v =ω)(222211r m r m J L O z ++=2211gr m gr m M z -=∑z zM tL ∑=d d 2211222211)(gr m gr m r m r m J O -=++α2222112211r m r m J gr m gr m O ++-=α11-12 如图11-35所示,为求半径R =0.5m 的飞轮A 对于通过其重心轴的转动惯量,在飞轮上绕以细绳,绳的末端系一质量为m 1=8kg 的重锤,重锤自高度h =2m 处落下,测得落下时间t 1=16s 。
为消去轴承摩擦的影响,再用质量为m 2=4kg 的重锤作第二次试验,此重锤自同一高度落下的时间t 2=25s 。
假定摩擦力矩为一常数,且与重锤的重量无关,试求飞轮的转动惯量和轴承的摩擦力矩。
图11-35v RmR J mvR R v J mvR J L z )()()(2+-=+-=+-=ωmgR M M z -=∑fz zM tL ∑=d d f 2)(M mgR a RmR J -=+ R M mgR a mR J )()(f 2-=+R M mgR thmR J )(2)(f 22-=+hRt M mgR mR J 2)(2f 2-=+第一次试验22165.0)5.08(5.082f 2⨯⨯⨯-⨯⨯=⨯+M g J)4(322f M g J -=+ (1)第二次试验22255.0)5.04(5.042f 2⨯⨯⨯-⨯⨯=⨯+M g J)2(125.781f M g J -=+ (2)(1)-(2)f 125.4625.281Mg +-= m N 0238.6f ⋅=M 由(1)得2f m kg 6.10592)4(32⋅=--=M g J11-13 通风机风扇的叶轮的转动惯量为J ,以初角速度w 0绕其中心轴转动,见图11-36。
设空气阻力矩与角速度成正比,方向相反,即M =-k w ,k 为比例系数,试求在阻力作用下,经过多少时间角速度减少一半?在此时间间隔内叶轮转了多少转?图11-36刚体定轴转动微分方程ωωk M tJ -=∑=d dt J kd d -=ωω⎰⎰-=tt Jk 02d d 0ωωωωt J k -=21ln2ln kJt =11-14 两均质细杆OC 和AB 的质量分别为50kg 和100kg ,在C 点互相垂直焊接起来。
若在图11-37所示位置由静止释放,试求释放瞬时铰支座O 的约束力。
铰O 处的摩擦忽略不计。
图11-37 g g g g m g m M J e z O 125)10025(15.0)()(21-=+-=⨯-⨯-=∑=-F α15010031003501100210012115031222=++=⨯+⨯⨯+⨯⨯=O Jg g 65150125==α 质心运动定理αααα125)10025(5.0212211-=+-=⨯-⨯-=+=m m a m a m ma y C y C Cy0=Cx mae x Cx F ma ∑= e y Cy F ma ∑= Ox F =0 21125W W F Oy --=-α0=Ox F g m g m F g Oy 2165125--=⨯-N 449627565125150==⨯-=g g g F Oy11-15 质量为100kg 、半径为1m 的均质圆轮,以转速n =120r/min 绕O 轴转动,如图11-38所示。
