高考数学用补形法解立体几何题
2022高考数学立体几何外接球专题(含解析)
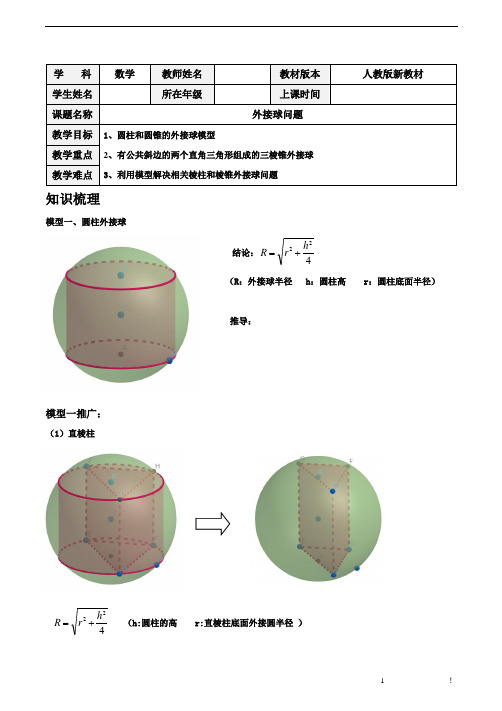
知识梳理模型一、圆柱外接球结论:422h r R +=(R:外接球半径 h:圆柱高 r:圆柱底面半径)推导:模型一推广:(1)直棱柱422h r R += (h:圆柱的高 r:直棱柱底面外接圆半径 )学 科 数学 教师姓名 教材版本 人教版新教材学生姓名所在年级上课时间课题名称外接球问题教学目标 1、圆柱和圆锥的外接球模型2、有公共斜边的两个直角三角形组成的三棱锥外接球3、利用模型解决相关棱柱和棱锥外接球问题教学重点 教学难点(2)侧面为三角形,底面为矩形,侧面和底面垂直的四棱锥(3)侧棱垂直于底面的棱锥【2017深二模】已知三棱锥S-ABC,△ABC是直角三角形,其斜边AB=8,SC⊥平面ABC,SC=6,则三棱锥的外接球的表面积为( )(A)64π(B)68π(C)72π(D)100π模型二、圆锥外接球结论:hh r R 222+=(R:外接球半径 h:圆锥高 r:圆锥底面半径)推导:模型二推广:(1)棱锥(上顶点在底面外心正上方)外接球hh r R 222+= (h:棱锥的高 r:棱锥底面外接圆半径 )【2018深一模】如图,网格纸上小正方形的边长为1,某几何体的三视图如图所示,则该几何体的外接球表面积为()A.B.C.16πD.25π【2017全国一卷文 16】已知三棱锥S−ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S−ABC的体积为9,则球O的表面积为______________.【2019 全国一卷理 12】已知三棱锥P−ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为A.B.C.D模型一、二总结题型:求几何体的外接球模型一: 422h r R += (圆柱模型) 模型二: h h r R 222+=(圆锥模型)适用于: 适用于:1、所有的圆柱、直棱柱 上顶点在底面外心正上方的棱锥2、侧棱垂直于底面的棱锥3、侧面为任意三角形,底面为矩形, 且侧面垂直于底面的四棱锥模型三、有公共斜边的两个直角三角形组成的三棱锥 ,球心在公共斜边的中点处如下图,∠ABC=∠ADC=90°,则O 为外接球球心1、在矩形ABCD 中,AB =4,BC =3,沿AC 将矩形ABCD 折成一个直二面角D AC B --,则四面体ABCD 的外接球的体积为A. π12125B.π9125C.π6125D.π31252.三棱锥S ABC -的所有顶点都在球O的球面上,且SA AC SB BC ====4SC =,则该球的体积为A 2563πB 323π C 16π D 64π专题练习类型一 构造法(补形法)【例1】已知是球上的点, , , ,则球的表面积等于________________.【例2】【辽宁省鞍山一中2019届高三三模】刘徽《九章算术•商功》中将底面为长方形,两个三角面与底面垂直的四棱锥体叫做阳马.如图,是一个阳马的三视图,则其外接球的体积为( )A .B .C .3πD .4π,,,S A B C O SA ABC ⊥平面AB BC ⊥1SA AB ==BC =O【举一反三】1、【山东省济宁市2019届高三一模】已知直三棱柱的底面为直角三角形,且两直角边长分别为1和,此三棱柱的高为,则该三棱柱的外接球的体积为A.B.C.D.2、【辽宁省师范大学附属中学2019届高三上学期期中】在三棱锥S−ABC中,,则三棱锥S−ABC外接球的表面积为()A.25ΠB.C.50ΠD.3、【河南省天一大联考2019届高三阶段性测试(五)】某多面体的三视图如图所示,其中正视图是一个直角边为2的等腰直角三角形,侧视图是两直角边分别为2和1的直角三角形,俯视图为一矩形,则该多面体的外接球的表面积为()A.7πB.8πC.9πD.10π类型二 正棱锥与球的外接【例3】正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为 ( ) A . B . C . D .【举一反三】1、球O 的球面上有四点S ,A ,B ,C ,其中O ,A ,B ,C 四点共面,△ABC 是边长为2的正三角形,平面SAB ⊥平面ABC ,则棱锥S-ABC 的体积的最大值为( )A .33 B . 3 C .2 3 D .42. 【四川省德阳市2018届高三二诊】正四面体ABCD 的体积为,则正四面体ABCD 的外接球的体积为______.814π16π9π274π3、【安徽省蚌埠市2019届高三下学期第二次检查】正三棱锥P −ABC 中,√2PA =AB =4√2,点E 在棱PA 上,且PE =3EA .正三棱锥P −ABC 的外接球为球O ,过E 点作球O 的截面α,α截球O 所得截面面积的最小值为__________.类型三 直棱柱的外接球【例4】直三棱柱的各顶点都在同一球面上,若,, 则此球的表面积等于 .【举一反三】1、【云南省2019年高三第二次统一检测】已知直三棱柱的顶点都在球O 的球面上,AB =AC =2,BC =2√2,若球O 的表面积为72Π,则这个直三棱柱的体积是( ) A .16 B .15C .D .2、已知三棱柱的6个顶点都在球的球面上,,,,则球的半径为()A B . C.D .3、 正四棱柱的各顶点都在半径为的球面上,则正四棱柱的侧面积有最111ABC A B C -12AB AC AA ===120BAC ∠=︒111ABC A B C -O 34AB AC ==,AB AC ⊥112AA =O 1321111ABCD A B C D -R值,为 .答案与解析类型一 构造法(补形法)【例1】已知是球上的点, , , ,则球的表面积等于________________. 【答案】 【解析】由已知S,A,B,C 是球O 表面上的点,所以 ,又,,所以四面体的外接球半径等于以长宽高分别以SA,AB,BC 三边长为长方体的外接球的半径,因为, ,所以,所以球的表面积.【指点迷津】当一三棱锥的三侧棱两两垂直时,可将三棱锥补成一个长方体,将问题转化为长方体(正方体)来解.长方体的外接球即为该三棱锥的外接球.【例2】【辽宁省鞍山一中2019届高三三模】刘徽《九章算术•商功》中将底面为长方形,两个三角面与底面垂直的四棱锥体叫做阳马.如图,是一个阳马的三视图,则其外接球的体积为( )A .B .C .3πD .4π,,,S A B C O SA ABC ⊥平面AB BC ⊥1SA AB ==BC =O 4πOA OB OC OS ===SA ABC ⊥平面AB BC ⊥S ABC -1SA AB ==BC =22,1R R ==O 244S R ππ==【答案】B【解析】由题意可知阳马为四棱锥,且四棱锥的底面为长方体的一个底面,四棱锥的高为长方体的一棱长,且阳马的外接球也是长方体的外接球,由三视图可知四棱锥的底面是边长为1的正方形,四棱锥的高为1,∴长方体的一个顶点处的三条棱长分别为1,1,1,∴长方体的对角线为,∴外接球的半径为,∴外接球的体积为.故选:B.【指点迷津】当一四面体或三棱锥的棱长相等时,可以构造正方体,在正方体中构造三棱锥或四面体,利用三棱锥或四面体与正方体的外接球相同来解即可.【举一反三】1、【山东省济宁市2019届高三一模】已知直三棱柱的底面为直角三角形,且两直角边长分别为1和,此三棱柱的高为,则该三棱柱的外接球的体积为A.B.C.D.【答案】C【解析】如图所示,将直三棱柱补充为长方体,则该长方体的体对角线为,设长方体的外接球的半径为R,则2R=4,R=2,所以该长方体的外接球的体积,故选C.2、【辽宁省师范大学附属中学2019届高三上学期期中】在三棱锥S−ABC中,,则三棱锥S−ABC外接球的表面积为()A.25蟺B.C.50蟺D.【答案】C【解析】解:如图,把三棱锥S−ABC补形为长方体,设长方体的长、宽、高分别为,则,∴三棱锥外接球的半径∴三棱锥S−ABC外接球的表面积为.故选:C.3、【河南省天一大联考2019届高三阶段性测试(五)】某多面体的三视图如图所示,其中正视图是一个直角边为2的等腰直角三角形,侧视图是两直角边分别为2和1的直角三角形,俯视图为一矩形,则该多面体的外接球的表面积为()A .7πB .8πC .9πD .10π 【答案】C 【解析】由三视图可得,该几何体为一个三棱锥,放在长、宽、高分别为2,1,2的长方体中,此三棱锥和长方体的外接球是同一个,长方体的外接球的球心在体对角线的中点处,易得其外接球的直径为,从而外接球的表面积为9π.故答案为:C.类型二 正棱锥与球的外接【例3】正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为 ( )A .B .C .D .【答案】A .814π16π9π274π【指点迷津】求正棱锥外接球的表面积或体积,应先求其半径,在棱锥的高上取一点作为外接球的球心,构造直角三角形,利用勾股定理求半径. 【举一反三】1、球O 的球面上有四点S ,A ,B ,C ,其中O ,A ,B ,C 四点共面,△ABC 是边长为2的正三角形,平面SAB ⊥平面ABC ,则棱锥S-ABC 的体积的最大值为( )A .33 B . 3 C .2 3 D .4 【答案】A【解析】 (1)由于平面SAB ⊥平面ABC ,所以点S 在平面ABC 上的射影H 落在AB 上,根据球的对称性可知,当S 在“最高点”,即H 为AB 的中点时,SH 最大,此时棱锥S -ABC 的体积最大.学科*网因为△ABC 是边长为2的正三角形,所以球的半径r =OC =23CH =23×32×2=233.在Rt △SHO 中,OH =12OC =33,所以SH =⎝ ⎛⎭⎪⎫2332-⎝ ⎛⎭⎪⎫332=1, 故所求体积的最大值为13×34×22×1=33.2. 【四川省德阳市2018届高三二诊】正四面体ABCD 的体积为,则正四面体ABCD 的外接球的体积为______. 【答案】【解析】 解:如图,设正四面体ABCD 的棱长为x ,过A 作AD ⊥BC , 设等边三角形ABC 的中心为O ,则AO =23AD =√33x ,,,即x=√2a.再设正四面体ABCD的外接球球心为G,连接GA,则,即.∴正四面体ABCD的外接球的体积为.故答案为:.3、【安徽省蚌埠市2019届高三下学期第二次检查】正三棱锥P−ABC中,√2PA=AB=4√2,点E在棱PA上,且PE=3EA.正三棱锥P−ABC的外接球为球O,过E点作球O的截面α,α截球O所得截面面积的最小值为__________.【答案】3π【解析】因为PA=PC=PB=4,AB=AC=BC=4√2,所以PA2+PC2=AC2,所以∠CPA=π2,同理∠CPB=∠BPA=π2,故可把正三棱锥补成正方体(如图所示),其外接球即为球O,直径为正方体的体对角线,故2R=4√3,设PA的中点为F,连接OF,则OF=2√2且OF⊥PA,所以OE=√8+1=3,当OE⊥平面α时,平面α截球O的截面面积最小,此时截面为圆面,其半径为√(2√3)2−32=√3,故截面的面积为3π.填3π.类型三 直棱柱的外接球 【例4】直三棱柱的各顶点都在同一球面上,若,, 则此球的表面积等于 . 【答案】【解析】在中,,可得,由正弦定理,可得外接圆半径r=2,设此圆圆心为,球心为,在中,易得球半径,故此球的表面积为.【指点迷津】直棱柱的外接球的球心在上、下底面的外接圆的圆心的连线上,确定球心,用球心、一底面的外接圆的圆心,一顶点构成一个直角三角形,用勾股定理得关于外接球半径的关系式,可球的半径. 【举一反三】1、【云南省2019年高三第二次统一检测】已知直三棱柱的顶点都在球O 的球面上,AB =AC =2,BC =2√2,若球O 的表面积为72蟺,则这个直三棱柱的体积是( ) A .16 B .15 C .D .【答案】A 【解析】 由题,,因为AB =AC =2,BC =2√2,易知三角形ABC 为等腰直角三角形, 故三棱柱的高故体积V =12脳2脳2脳8=16 故选A111ABC A B C -12AB AC AA ===120BAC ∠=︒ABC ∆2AB AC ==120BAC ∠=︒BC =ABC ∆O 'O RT OBO '∆R =2420R ππ=2、已知三棱柱的6个顶点都在球的球面上,若,,,则球的半径为 ( )A .B .C .D .【答案】C【解析】由球心作面ABC 的垂线,则垂足为BC 中点M.计算AM=,由垂径定理,OM=6,所以半径,选C.3、 正四棱柱的各顶点都在半径为的球面上,则正四棱柱的侧面积有最值,为 . 【答案】大111ABC A B C -O 34AB AC ==,AB AC ⊥112AA =O 213252132=1111ABCD A B C D -R。
7 例析利用割补法解题题型 高中常用数学方法的介绍 例析 体验 练习

【学生版】例析利用割补法解题题型所谓割补法:就是将复杂的或不熟悉的几何图形转化为简单的熟悉的几何图形(如:三角形、正方形、长方形、平行四边形或梯形等)或几何体(如:柱体、锥体和球体);也就是把一个复杂长度、面积或体积的计算分割成若干个简单图形的有关计算或将一个不易求出长度、面积或体积的几何图形补足为较易计算的几何图形;例如,把曲边形割补成规则图形、把斜棱柱割补成直棱柱、把三棱柱补成平行六面体、把三棱锥补成三棱柱或平行六面体、把多面体切割成锥体(特别是三棱锥)、把不规则的几何体割补成规则的几何体,从而把未知的转化为已知的、把陌生的转化为熟悉的、把复杂的转化为简单的、把不够直观的转化为直观易懂的。
一、“分割”非规则图形为规则图形几何图形或几何体的“分割”,即将已知的几何图形或几何体按照结论的要求,分割成若干个易求长度、面积或体积的几何图形或几何体。
例1、为测出所住小区的面积,某人进行了一些测量工作,所得数据如图所示,则小区的面积是( ) A .3+64 km 2B .3-64km 2C .6+34 km 2D .6-34km 2【提示】 【解析】 【评注】例2、如图是一个以A 1B 1C 1为底面的直三棱柱被一平面所截得到的几何体,截面为ABC ,已知A 1B 1=B 1C 1=2,∠A 1B 1C 1=90°,AA 1=4,BB 1=3,CC 1=2,求: (1)该几何体的体积; (2)截面ABC 的面积。
【提示】 【解析】二、将非规则图形“补形”规则图形几何图形或几何体的“补形”,即将已知的几何图形或几何体按照结论的要求,补全成若干个易求长度、面积或体积的几何图形或几何体。
例3、已知三棱锥A —BCD 的所有棱长都为2,则该三棱锥的外接球的表面积为________例4、如图,在直三棱柱A 1B 1C 1-ABC 中,∠BCA =90°,点E ,F 分别为AB ,AC 的中点, 若BC =CA =CC 1,则B 1E 与A 1F 所成的角的余弦值为________.三、几何体的“割补”几何体的割补,即将已知的几何体按照结论的要求,既要分割又要补全成若干个易求体积的几何体。
补形——求解三棱锥外接球半径的一条重要途径

教学争鸣新课程NEW CURRICULUM在立体几何的学习中,经常遇到求解三棱锥外接球体半径的问题,此类问题往往球心的位置难以找到。
我们知道,棱锥是柱体的一部分,因此,在求三棱锥外接球体的半径时,通过“补形”,将锥体还原成柱体,有时能起到柳暗花明的效果。
常见的“补形”方法有下列几种.例1.已知三棱锥P-ABC 中,PA ⊥PB ,PB ⊥PC ,PC ⊥PA ,且PA =3,PB =4,PC =5.则其外接球体的表面积为.思路:补成“长方体”解析:三棱锥P-ABC (图1)可以补成长方体,且它们拥有相同的外接球体(图2),再过长方体的一组对面上的对角线作轴截面得一圆的内接矩形(图3).其中矩形的一边为原长方体的棱,另一边为原长方体的面对角线,而该矩形的对角线则为球体的直径,易得外接球体的半径为522√图1图2图3例2.已知一正四面体的棱长为4,则其外接球体的体积为.思路:补成“正方体”解析:由于连接正方体的六条面对角线可以形成一个正四面体,因此,可将正四面体补成一个正方体,且它们拥有相同的外接球体(图4).再过该正方体的一组对面上的对角线作轴截面,易得外接球体的半径为6√,从而其体积为86√π.图4例3.已知三棱锥P-ABC 中,底面ABC 为正三角形,边长为2球为.图5图6图7思路一:补成“直三棱柱”解析:将三棱锥P-ABC (图5)补成直三棱柱(图6),同样,它们拥有相同的外接球体.再过PA 及球心作一截面如(图7),其中,球心O 为O 1O 2的中点,而O 1、O 2分别是两底面正三角形ABC 的中心,可得外接球体的半径OA =21√3.思路二:补成“圆柱”解析:将三棱锥P-ABC (图5)补成圆柱体(图8),且它们拥有相同的外接球体,再过PA 及圆柱体的轴作一截面得图9.其中,球心O 为O 1O 2的中点,而O 1是正三角形ABC 的中心,可得外接球体的半径OA =21√3.图8图9总之,“补形”是求解三棱锥外接球体半径的一条重要途径,且通常可补成上述几种模型。
高考数学的立体几何多选题含答案

高考数学的立体几何多选题含答案一、立体几何多选题1.已知球O 为正方体1111ABCD A B C D -的内切球,平面11A C B 截球O 的面积为24π,下列命题中正确的有( )A .异面直线AC 与1BC 所成的角为60°B .1BD ⊥平面11AC B C .球O 的表面积为36πD .三棱锥111B AC B -的体积为288 【答案】AD 【分析】连接11A C ,1A B ,通过平移将AC 与1BC 所成角转化为11A C 与1BC 所成角可判断A ;通过反证法证明B ;由已知平面11A C B 截球O 的面积为24π求出正方体棱长,进而求出内切球的表面积可判断C ;利用等体积法可求得三棱锥111B AC B -的体积可判断D. 【详解】对于A ,连接11A C ,1A B ,由正方体1111ABCD A B C D -,可知11//A C AC ,11AC B ∴∠为异面直线AC 与1BC 所成的角,设正方体边长为a,则1111AC A B BC ==,由等边三角形知1160A C B ∠=,即异面直线AC 与1BC 所成的角为60,故A 正确; 对于B ,假设1BD ⊥平面11A C B ,又1A B ⊂平面11A C B ,则11BD B A ⊥,设正方体边长为a ,则11A D a =,1A B =,1BD =,由勾股定理知111A D B A ⊥,与假设矛盾,假设不成立,故1BD 不垂直于平面11A C B ,故B 错误; 对于C ,设正方体边长为a,则11AC =,内切球半径为2a,设内切球的球心O 在面11A C B 上的投影为O ',由等边三角形性质可知O '为等边11A C B △的重心,则11123233O A AC a ='=⨯=,又12OA a =,∴球心O 到面11A C B 的距离6a ==,又球心与截面圆心的连线垂直于截面,∴=,又截面圆的面积2246S a ππ⎛⎫= ⎪ ⎪⎝⎭=,解得12a =,则内切球半径为6,内切球表面积214644S ππ==⨯,故C 错误;对于D ,由等体积法知111111111111212122812383B A C B B A C B A C B V V S a --==⨯⨯=⨯⨯=,故D 正确; 故选:AD【点睛】关键点点睛:本题考查了正方体和它的内切球的几何结构特征,关键是想象出截面图的形状,从而求出正方体的棱长,进而求出内切球的表面积及三棱锥的体积,考查了空间想象能力,数形结合的思想,属于较难题.2.如图,矩形ABCD 中,M 为BC 的中点,将ABM 沿直线AM 翻折成1AB M ,连结1B D ,N 为1B D 的中点,则在翻折过程中,下列说法中所有正确的是( )A .存在某个位置,使得1CN AB ⊥ B .翻折过程中,CN 的长是定值C .若AB BM =,则1AM BD ⊥D .若1AB BM ==,当三棱锥1B AMD -的体积最大时,三棱锥1B AMD -外接球的体积是43π 【答案】BD【分析】对于A ,取AD 中点E ,连接EC 交MD 与F ,可得到EN NF ⊥,又EN CN ⊥,且三线,,NE NF NC 共面共点,不可能;对于B ,可得由1NEC MAB ∠=∠(定值),112NE AB =(定值),AM EC =(定值),由余弦定理可得NC 是定值.对于C ,取AM 中点O ,连接1,B O DO ,假设1AM B D ⊥,易得AM ⊥面1ODB ,即可得OD AM ⊥,从而AD MD =,显然不一定成立.对于D ,当平面B 1AM ⊥平面AMD 时,三棱锥B 1﹣AMD 的体积最大,可得球半径为1,体积是43π. 【详解】对于A 选项:如图1,取AD 中点E ,连接EC 交MD 与F , 则11////NE AB NF MB ,,又11AB MB ⊥,所以EN NF ⊥, 如果1CN AB ⊥,可得EN CN ⊥,且三线,,NE NF NC 共面共点, 不可能,故A 选项不正确;对于B 选项:如图1,由A 选项可得1AMB EFN ≈△△,故1NEC MAB ∠=∠(定值),112NE AB =(定值),AM EC =(定值), 故在NEC 中,由余弦定理得222cos CN CE NE NE CE NEC =+-⋅⋅∠,整理得222212422AB AB AB CN AM AM BC AB AM =+-⋅⋅=+ 故CN 为定值,故B 选项正确.对于C 选项:如图,取AM 中点O ,连接1,B O DO , 由AB BM =,得1B O AM ⊥,假设1AM B D ⊥,111B D B O B =,所以AM ⊥面1ODB ,所以OD AM ⊥,从而AD MD =,显然不恒成立,所以假设不成立,可得C 选项不正确.对于D 选项:由题易知当平面1AB M 与平面AMD 垂直时,三棱锥1B AMD -的体积最大,此时1B O ⊥平面AMD ,则1B O OE ⊥,由1AB BM ==,易求得122BO =,2DM =22221122122B E OB OE ⎛⎫⎛⎫=+=+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 因此1EB EA ED EM ===,E 为三棱锥1B AMD -的外接球球心,此外接球半径为1,体积是43π.故D 选项正确. 故答案为:BD . 【点睛】本题主要考查了线面、面面平行与垂直的判定和性质定理,考查了空间想象能力和推理论证能力,属于难题.本题C 选项的解题的关键在于采用反证法证明,进而推出矛盾解题,D 选项求解的关键在于把握平面1AB M 与平面AMD 垂直时,三棱锥1B AMD -的体积最大.3.在长方体1111ABCD A B C D -中,4AB BC ==,18AA =,点P 在线段11A C 上,M 为AB 的中点,则( ) A .BD ⊥平面PACB .当P 为11AC 的中点时,四棱锥P ABCD -外接球半径为72C .三棱锥A PCD -体积为定值D .过点M 作长方体1111ABCD A B C D -的外接球截面,所得截面圆的面积的最小值为4π 【答案】ACD【分析】利用线面垂直的判定定理可判断A 选项的正误;判断出四棱锥P ABCD -为正四棱锥,求出该四棱锥的外接球半径,可判断B 选项的正误;利用等体积法可判断C 选项的正误;计算出截面圆半径的最小值,求出截面圆面积的最小值,可判断D 选项的正误. 【详解】对于A 选项,因为AB BC =,所以,矩形ABCD 为正方形,所以,BD AC ⊥, 在长方体1111ABCD A B C D -中,1AA ⊥底面ABCD ,BD ⊂平面ABCD ,1BD AA ∴⊥,1AC AA A ⋂=,AC 、1AA ⊂平面PAC ,所以,BD ⊥平面PAC ,A 选项正确;对于B 选项,当点P 为11A C 的中点时,PA ===同理可得PB PC PD ===因为四边形ABCD 为正方形,所以,四棱锥P ABCD -为正四棱锥, 取AC 的中点N ,则PN 平面ABCD ,且四棱锥P ABCD -的外接球球心在直线PN上,设该四棱锥的外接球半径为R ,由几何关系可得222PN R AN R -+=, 即2288R R -+=,解得92R =,B 选项错误; 对于C 选项,2114822ACDSAD CD =⋅=⨯=, 三棱锥P ACD -的高为18AA =,因此,116433A PCD P ACD ACD V V S AA --==⋅=△,C 选项正确;对于D 选项,设长方体1111ABCD A B C D -的外接球球心为E ,则E 为1BD 的中点, 连接EN 、MN ,则1142EN DD ==,122MN AD ==, E 、N 分别为1BD 、BD 的中点,则1//EN DD , 1DD ⊥平面ABCD ,EN ∴⊥平面ABCD ,MN ⊂平面ABCD ,EN MN ∴⊥,EM ∴==过点M 作长方体1111ABCD A B C D -的外接球截面为平面α,点E 到平面α的距离为d ,直线EM 与平面α所成的角为θ,则sin d EM θθ==≤ 当且仅当2πθ=时,等号成立,长方体1111ABCD A B C D -的外接球半径为R '==,所以,截面圆的半径()()222226252r R d '=-≥-=,因此,截面圆面积的最小值为4π,D 选项正确.故选:ACD. 【点睛】方法点睛:求空间多面体的外接球半径的常用方法:①补形法:侧面为直角三角形,或正四面体,或对棱二面角均相等的模型,可以还原到正方体或长方体中去求解;②利用球的性质:几何体中在不同面均对直角的棱必然是球大圆直径,也即球的直径; ③定义法:到各个顶点距离均相等的点为外接球的球心,借助有特殊性底面的外接圆圆心,找其垂线,则球心一定在垂线上,再根据带其他顶点距离也是半径,列关系求解即可.4.在三棱锥M ABC -中,下列命题正确的是( )A .若1233AD AB AC =+,则3BC BD = B .若G 为ABC 的重心,则111333MG MA MB MC =++C .若0MA BC ⋅=,0MC AB ⋅=,则0MB AC ⋅=D .若三棱锥M ABC -的棱长都为2,P ,Q 分别为MA ,BC 中点,则2PQ = 【答案】BC 【分析】作出三棱锥M ABC -直观图,在每个三角形中利用向量的线性运算可得. 【详解】对于A ,由已知12322233AD AB AC AD AC AB AD AC AB AD =+⇒=+⇒-=-,即2CD DB =,则32BD BD DC BC =+=,故A 错误; 对于B ,由G 为ABC 的重心,得0GA GB GC ++=,又MG MA AG =+,MG MB BG =+,MG MC CG =+,3MA MB MC MG ∴++=,即111333MG MA MB MC =++,故B 正确;对于C ,若0MA BC ⋅=,0MC AB ⋅=,则0MC MA BC AB ⋅+⋅=,即()00MA BC AC CB MA BC AC C MC C M B M C ⋅++=⇒⋅++⋅⋅=⋅()00MA BC A MC MC MC MC C BC MA BC AC ⋅⋅⋅⇒⋅+-=⇒-+=⋅()000MC M CA BC AC AC CB AC CB AC C MC ⇒+=⇒+=⇒+=⋅⋅⋅⋅⋅,即0MB AC ⋅=,故C 正确;对于D ,111()()222PQ MQ MP MB MC MA MB MC MA ∴=-=+-=+- ()21122PQ MB MC MA MB MC MA ∴=+-=+-,又()2222222MB MC MA MB MC MA MB MC MB MA MC MA+-=+++⋅-⋅-⋅2221112222222222228222=+++⨯⨯⨯-⨯⨯⨯-⨯⨯⨯=,1822PQ ∴==,故D 错误. 故选:BC 【点睛】关键点睛:本题考查向量的运算,用已知向量表示某一向量的三个关键点: (1)用已知向量来表示某一向量,一定要结合图形,以图形为指导是解题的关键.(2)要正确理解向量加法、减法与数乘运算的几何意义,如首尾相接的若干向量之和,等于由起始向量的始点指向末尾向量的终点的向量. (3)在立体几何中三角形法则、平行四边形法则仍然成立.5.已知正方体1111ABCD A B C D -的棱长为2,点O 为11A D 的中点,若以O 为球心,6为半径的球面与正方体1111ABCD A B C D -的棱有四个交点E ,F ,G ,H ,则下列结论正确的是( )A .11//A D 平面EFGHB .1AC ⊥平面EFGHC .11A B 与平面EFGH 所成的角的大小为45°D .平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7 【答案】ACD 【分析】如图,计算可得,,,E F G H 分别为所在棱的中点,利用空间中点线面的位置关系的判断方法可判断A 、B 的正确与否,计算出直线AB 与平面EFGH 所成的角为45︒后可得C 正确,而几何体BHE CGF -为三棱柱,利用公式可求其体积,从而可判断D 正确与否. 【详解】如图,连接OA ,则2115OA AA =+=,故棱1111,,,A A A D D D AD 与球面没有交点.同理,棱111111,,A B B C C D 与球面没有交点. 因为棱11A D 与棱BC 之间的距离为26>BC 与球面没有交点.因为正方体的棱长为2,而26<球面与正方体1111ABCD A B C D -的棱有四个交点E ,F ,G ,H , 所以棱11,,,AB CD C C B B 与球面各有一个交点, 如图各记为,,,E F G H .因为OAE △为直角三角形,故22651AE OE OA -=-=,故E 为棱AB 的中点. 同理,,F G H 分别为棱11,,CD C C B B 的中点.由正方形ABCD 、,E F 为所在棱的中点可得//EF BC ,同理//GH BC ,故//EF GH ,故,,,E F G H 共面. 由正方体1111ABCD A B C D -可得11//A D BC ,故11//A D EF因为11A D ⊄平面EFGH ,EF ⊂平面EFGH ,故11//A D 平面EFGH ,故A 正确.因为在直角三角1BA C 中,1A B =2BC = ,190A BC ∠=︒, 1A C 与BC 不垂直,故1A C 与GH 不垂直,故1A C ⊥平面EFGH 不成立,故B 错误.由正方体1111ABCD A B C D -可得BC ⊥平面11AA B B ,而1A B ⊂平面11AA B B , 所以1BC A B ⊥,所以1EF A B ⊥在正方形11AA B B 中,因为,E H 分别为1,AB BB 的中点,故1EH A B ⊥, 因为EFEH E =,故1A B ⊥平面EFGH ,所以BEH ∠为直线AB 与平面EFGH 所成的角,而45BEH ∠=︒, 故直线AB 与平面EFGH 所成的角为45︒,因为11//AB A B ,故11A B 与平面EFGH 所成的角的大小为45°.故C 正确. 因为,,,E F G H 分别为所在棱的中点,故几何体BHE CGF -为三棱柱, 其体积为111212⨯⨯⨯=,而正方体的体积为8, 故平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7,故D 正确. 故选:ACD. 【点睛】本题考查空间中线面位置的判断、空间角的计算和体积的计算,注意根据球的半径确定哪些棱与球面有交点,本题属于中档题.6.在边长为2的等边三角形ABC 中,点,D E 分别是边,AC AB 上的点,满足//DE BC 且AD ACλ=,(()01λ∈,),将ADE 沿直线DE 折到A DE '△的位置.在翻折过程中,下列结论不成立的是( )A .在边A E '上存在点F ,使得在翻折过程中,满足//BF 平面A CD 'B .存在102λ∈⎛⎫⎪⎝⎭,,使得在翻折过程中的某个位置,满足平面A BC '⊥平面BCDEC .若12λ=,当二面角A DE B '--为直二面角时,||A B '=D .在翻折过程中,四棱锥A BCDE '-体积的最大值记为()f λ,()f λ【答案】ABC 【分析】对于A.在边A E '上点F ,在A D '上取一点N ,使得//FN ED ,在ED 上取一点H ,使得//NH EF ,作//HG BE 交BC 于点G ,即可判断出结论.对于B ,102λ∈⎛⎫⎪⎝⎭,,在翻折过程中,点A '在底面BCDE 的射影不可能在交线BC 上,即可判断出结论. 对于C ,12λ=,当二面角A DE B '--为直二面角时,取ED 的中点M ,可得AM ⊥平面BCDE .可得22A B AM BM '=+,结合余弦定理即可得出.对于D.在翻折过程中,取平面AED ⊥平面BCDE ,四棱锥A BCDE '-体积()3133BCDE f S λλλλ=⋅⋅=-,()01λ∈,,利用导数研究函数的单调性即可得出.【详解】对于A.在边A E '上点F ,在A D '上取一点N ,使得//FN ED ,在ED 上取一点H ,使得//NH EF ,作//HG BE 交BC 于点G ,如图所示,则可得FN 平行且等于BG ,即四边形BGNF 为平行四边形, ∴//NG BE ,而GN 始终与平面ACD 相交,因此在边A E '上不存在点F ,使得在翻折过程中,满足//BF 平面A CD ',A 不正确.对于B ,102λ∈⎛⎫ ⎪⎝⎭,,在翻折过程中,点A '在底面BCDE 的射影不可能在交线BC 上,因此不满足平面A BC '⊥平面BCDE ,因此B 不正确. 对于C.12λ=,当二面角A DE B '--为直二面角时,取ED 的中点M ,如图所示:可得AM ⊥平面BCDE ,则22223111010()1()21cos120222A B AM BM '=+=++-⨯⨯⨯︒=≠,因此C 不正确;对于D.在翻折过程中,取平面AED ⊥平面BCDE ,四棱锥A BCDE '-体积()3133BCDE f S λλλλ=⋅⋅=-,()01λ∈,,()213f λλ'=-,可得3λ=时,函数()f λ取得最大值()312313f λ⎛⎫=-=⎪⎝⎭,因此D 正确. 综上所述,不成立的为ABC. 故选:ABC. 【点睛】本题考查了利用运动的观点理解空间线面面面位置关系、四棱锥的体积计算公式、余弦定理、利用导数研究函数的单调性极值与最值,考查了推理能力空间想象能力与计算能力,属于难题.7.M ,N 分别为菱形ABCD 的边BC ,CD 的中点,将菱形沿对角线AC 折起,使点D 不在平面ABC 内,则在翻折过程中,下列结论正确的有( )A .MN ∥平面ABDB .异面直线AC 与MN 所成的角为定值C .在二面角D AC B --逐渐变小的过程中,三棱锥D ABC -外接球的半径先变小后变大D .若存在某个位置,使得直线AD 与直线BC 垂直,则ABC ∠的取值范围是0,2π⎛⎫⎪⎝⎭【答案】ABD 【分析】利用线面平行的判定即可判断选项A ;利用线面垂直的判定求出异面直线AC 与MN 所成的角即可判断选项B ;借助极限状态,当平面DAC 与平面ABC 重合时,三棱锥D ABC -外接球即是以ABC ∆外接圆圆心为球心,外接圆的半径为球的半径,当二面角D AC B --逐渐变大时,利用空间想象能力进行分析即可判断选项C;过A 作AH BC ⊥,垂足为H ,分ABC ∠为锐角、直角、钝角三种情况分别进行分析判断即可判断选项D. 【详解】对于选项A:因为M ,N 分别为菱形ABCD 的边BC ,CD 的中点,所以MN 为BCD ∆的中位线,所以//MN BD ,因为MN ⊄平面ABD ,BD ⊂平面ABD ,所以MN ∥平面ABD ,故选项A 正确;对于选项B :取AC 的中点O ,连接,DO BO ,作图如下:则,AC DO AC BO ⊥⊥,BO DO O =,由线面垂直的判定知,AC ⊥平面BOD ,所以AC BD ⊥,因为//MN BD ,所以AC MN ⊥,即异面直线AC 与MN 所成的角为定值90,故选项B 正确;对于选项C:借助极限状态,当平面DAC 与平面ABC 重合时,三棱锥D ABC -外接球即是以ABC ∆外接圆圆心为球心,外接圆的半径为球的半径,当二面角D AC B --逐渐变大时,球心离开平面ABC ,但是球心在底面的投影仍然是ABC ∆外接圆圆心,故二面角D AC B --逐渐变小的过程中,三棱锥D ABC -外接球的半径不可能先变小后变大, 故选项C 错误;对于选项D:过A 作AH BC ⊥,垂足为H ,若ABC ∠为锐角,H 在线段BC 上;若ABC ∠为直角,H 与B 重合;若ABC ∠为钝角,H 在线段BC 的延长线上;若存在某个位置,使得直线AD 与直线BC 垂直,因为AH BC ⊥,所以CB ⊥平面AHD ,由线面垂直的性质知,CB HD ⊥,若ABC ∠为直角,H 与B 重合,所以CB BD ⊥,在CBD ∆中,因为CB CD =, 所以CB BD ⊥不可能成立,即ABC ∠为直角不可能成立;若ABC ∠为钝角,H 在线段BC 的延长线上,则在原平面图菱形ABCD 中,DCB ∠为锐角,由于立体图中DB DO OB <+,所以立体图中DCB ∠一定比原平面图中更小,,所以DCB ∠为锐角,CB HD ⊥,故点H 在线段BC 与H 在线段BC 的延长线上矛盾,因此ABC ∠不可能为钝角;综上可知,ABC ∠的取值范围是0,2π⎛⎫⎪⎝⎭.故选项D 正确; 故选:ABD 【点睛】本题考查异面垂直、线面平行与线面垂直的判定、多面体的外接球问题;考查空间想象能力和逻辑推理能力;借助极限状态和反证法思想的运用是求解本题的关键;属于综合型强、难度大型试题.8.在正方体1111ABCD A B C D -中,如图,,M N 分别是正方形ABCD ,11BCC B 的中心.则下列结论正确的是( )A .平面1D MN 与11BC 的交点是11B C 的中点 B .平面1D MN 与BC 的交点是BC 的三点分点 C .平面1D MN 与AD 的交点是AD 的三等分点 D .平面1D MN 将正方体分成两部分的体积比为1∶1 【答案】BC 【分析】取BC 的中点E ,延长DE ,1D N ,并交于点F ,连FM 并延长分别交,BC AD 于,P Q ,连1,D Q PN 并延长交11B C 与H ,平面四边形1D HPQ 为所求的截面,进而求出,,P Q H 在各边的位置,利用割补法求出多面体11QPHD C CD 的体积,即可求出结论.【详解】如图,取BC 的中点E ,延长DE ,1D N ,并交于点F , 连接FM 并延长,设FM BC P ⋂=,FM AD Q ⋂=, 连接PN 并延长交11B C 于点H .连接1D Q ,1D H ,则平面四边形1D HPQ 就是平面1D MN 与正方体的截面,如图所示.111111////,22NE CC DD NE CC DD ==,NE ∴为1DD F ∆的中位线,E ∴为DF 中点,连BF , ,,90DCE FBE BF DC AB FBE DCE ∴∆≅∆==∠=∠=︒, ,,A B F ∴三点共线,取AB 中点S ,连MS ,则12//,,23BP FB MS BP MS BC MS FS =∴==, 22111,33236BP MS BC BC PE BC ∴==⨯=∴=, E 为DF 中点,11//,233PE DQ DQ PE BC AD ∴===N 分别是正方形11BCC B 的中心,11113C H BP C B ∴==所以点P 是线段BC 靠近点B 的三等分点, 点Q 是线段AD 靠近点D 的三等分点, 点H 是线段11B C 靠近点1C 的三等分点. 做出线段BC 的另一个三等分点P ', 做出线段11A D 靠近1D 的三等分点G ,连接QP ',HP ',QG ,GH ,1H QPP Q GHD V V '--=, 所以111113QPHD C CD QPHQ DCC D V V V -==多面体长方体正方体 从而平面1D MN 将正方体分成两部分体积比为2∶1. 故选:BC.【点睛】本题考查直线与平面的交点及多面体的体积,确定出平面与正方体的交线是解题的关键,考查直观想象、逻辑推理能力,属于较难题.9.已知正四棱柱1111ABCD A B C D -的底面边长为2,侧棱11AA =,P 为上底面1111D C B A 上的动点,给出下列四个结论中正确结论为( )A .若3PD =,则满足条件的P 点有且只有一个B .若3PD =,则点P 的轨迹是一段圆弧C .若PD ∥平面1ACB ,则DP 长的最小值为2D .若PD ∥平面1ACB ,且3PD =,则平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形的面积为94π 【答案】ABD【分析】若3PD =,由于P 与1B 重合时3PD =,此时P 点唯一;()313PD =∈,,则12PD =,即点P 的轨迹是一段圆弧;当P 为11A C 中点时,DP 有最小值为3=,可判断C ;平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形为外接球的大圆,其半径为32=,可得D . 【详解】 如图:∵正四棱柱1111ABCD A B C D -的底面边长为2, ∴1122B D =11AA =, ∴()2212213DB =+=,则P 与1B 重合时3PD =,此时P 点唯一,故A 正确;∵()313PD =,,11DD =,则12PD P 的轨迹是一段圆弧,故B 正确; 连接1DA ,1DC ,可得平面11//A DC 平面1ACB ,则当P 为11A C 中点时,DP 有最小值为()22213+=C 错误;由C 知,平面BDP 即为平面11BDD B ,平面BDP 截正四棱柱1111ABCD A B C D -的外接2221322122++=,面积为94π,故D 正确. 故选:ABD . 【点睛】本题考查了立体几何综合,考查了学生空间想象,逻辑推理,转化划归,数学运算的能力,属于较难题.10.如图所示,在棱长为1的正方体1111ABCD A B C D -中,过对角线1BD 的一个平面交棱1AA 于点E ,交棱1CC 于点F ,得四边形1BFD E ,在以下结论中,正确的是( )A .四边形1BFD E 有可能是梯形B .四边形1BFD E 在底面ABCD 内的投影一定是正方形C .四边形1BFDE 有可能垂直于平面11BB D D D .四边形1BFD E 面积的最小值为62【答案】BCD 【分析】四边形1BFD E 有两组对边分别平行知是一个平行四边形四边形;1BFD E 在底面ABCD 内的投影是四边形ABCD ;当与两条棱上的交点是中点时,四边形1BFD E 垂直于面11BB D D ;当E ,F 分别是两条棱的中点时,四边形1BFD E 6【详解】过1BD 作平面与正方体1111ABCD A B C D -的截面为四边形1BFD E , 如图所示,因为平面11//ABB A 平面11DCC D ,且平面1BFD E 平面11ABB A BE =.平面1BFD E平面1111,//DCC D D F BE D F =,因此,同理1//D E BF ,故四边形1BFD E 为平行四边形,因此A 错误;对于选项B ,四边形1BFD E 在底面ABCD 内的投影一定是正方形ABCD ,因此B 正确; 对于选项C ,当点E F 、分别为11,AA CC 的中点时,EF ⊥平面11BB D D ,又EF ⊂平面1BFD E ,则平面1BFD E ⊥平面11BB D D ,因此C 正确;对于选项D ,当F 点到线段1BD 的距离最小时,此时平行四边形1BFD E 的面积最小,此时点E F 、分别为11,AA CC 的中点,此时最小值为162322=,因此D 正确. 故选:BCD【点睛】关键点睛:解题的关键是理解想象出要画的平面是怎么样的平面,有哪些特殊的性质,考虑全面即可正确解题.。
巧用补形法研究四面体问题
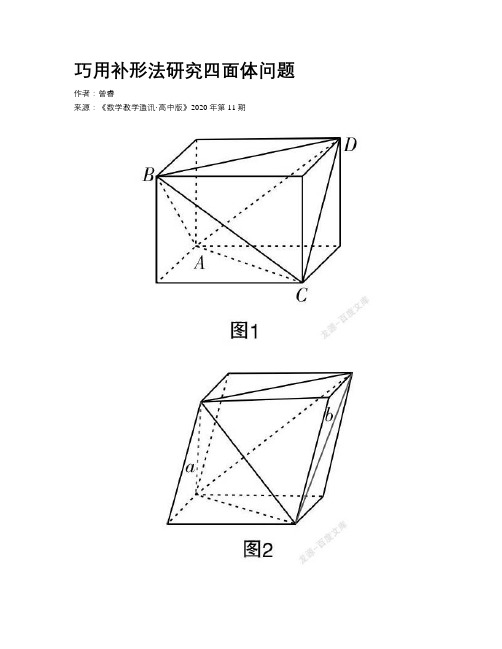
巧用补形法研究四面体问题作者:***来源:《数学教学通讯·高中版》2020年第11期[摘要] 立体几何问题中,有一类问题可以通过补形法,得到一个常见的几何体,使复杂的线面关系变得清晰明了. 文章从一道例题出发分析解决这类问题的方法,并在此基础上总结规律,归纳常见的一些四面体的补形方法.[关键词] 立体几何;四面体;补形教学中,遇到这样一个问题:已知在半径为2的球面上有A,B,C,D 四点,若AB=CD=2,则四面体ABCD的体积最大值为多少?这是某年数学全国卷的第12题,主要考查几何体的体积的计算、球的性质、异面直线间的距离,通过球这个载体考查学生的空间想象能力和推理计算能力.解答是这样的:过CD作平面PCD,使AB垂直于平面PCD,交AB于P. 设点P到CD的距离为h,则有V■=■×■×2×h×2=■h,当直径通过AB与CD中点时,h■=2■=2■,故V■=■.本小题这个解答当中,学生比较疑惑的有两点:(1)为什么可以过CD作平面PCD,使AB垂直于平面PCD,能这样作的前提是AB和CD要垂直,那为什么认定体积最大时AB和CD要垂直?(2)为什么直径通过AB与CD中点时,距离h最大?要解释清楚这两个疑点,首先需要补充说明一个公式.四面体体积公式:如果一个四面体的两条相对棱的长分别是a,b,它们的距离为d,所成的角为θ,那么它的体积为V■=■abdsinθ(证明见后).根据这个公式,我们首先得到结论:AB和CD必须垂直,即sinθ=90°时才能得到最大的体积.其次,由于AB=CD=R(球的半径),所以连结球心O和四个顶点,则容易知道△OAB 和△OCD都是正三角形.设AB的中点为E,CD的中点为F,则OE⊥AB,OF⊥CD.设AB与CD间的距离为d,有d≤EF≤OE+OF. (异面直线间公垂线段最短)因此,OEF共线时,四面体的体积可以达到最大值,因为OE=OF=■,故V■=■.?摇?摇这样解决一个选择题比较花费时间,而且在高中数学教学中,不涉及四面体的体积公式,异面直线的距离即公垂线段的长度在教学中也仅仅要求了解.下面我们用补形的思路来解决这个问题.因为题目当中两条线段长度一样,所以考虑把这个四面体补形成一个长方体:如图1:则四面体的外接球即是长方体的外接球,四面体的体积是长方体的体积减去四个全等的小三棱锥的体积.设长方体的边长为a,b,c,体对角线即为外接球的直径,得到:a2+b2+c2=42,b2+c2=22,所以a=2■,则V■=V■-4V■=abc-4×■×■abc=■abc=■.又b2+c2=22 ,所以V■=■≤■(b2+c2)=■,当且仅当b=c=■时,等号成立.从等号成立的条件可以比较容易地看出是在AB和CD垂直时,四面体的体积取到了最大值.我们会发现,使用补形,一下子把陌生的几何体变得熟悉了,原本错综复杂的线面关系也变得清晰起来. 利用这一方法解决某些几何问题,思路清晰明朗,较其他方法简洁明了.比如刚才提到的四面体的体积公式也可以用补形法得到.一个四面体的两条相对棱的长分别是a,b,它们的距离为d,所成的角为θ,将四面体补形成平行六面体(因为相对棱的长度不确定,相等的时候才能补成长方体).如图2:那么该平行六面体的底面积为S=■absinθ,平行六面体的体积为V■=■abdsinθ. 同样,该平行六面体由原四面体和四个全等的三棱锥构成. 三棱锥与平行六面体的高相等,底面积为平行六面体的一半,V■=■×■×■absinθ=■absinθ.所以V■=V■-4×V■=■absinθ.一起来看一下常见的几种四面体补形方式:一、把四面体的四个面各补上一个三棱锥,最后形成一个平行六面体. 其中正四面体是最特殊的形式,可以补成正方体. 而对棱相等的四面体则可以补形成一个长方体.例1:正四面体棱长为a,求外接球的半径R.正四面体补形为一个正方体,正四面体的外接球即为正方体的外接球.如图3:正方体的面对角线是正四面体的棱长,体对角线为外接球的直径.设正方体边长为b,则a=■b,2R=■b,所以R=■a.例2:在三棱锥A-BCD中,AB=CD=3,AD=BC=4,AC=BD=5,求三棱锥A-BCD外接球的半径.因为有三组对棱相等,把四面体补成一个长方形,如图4:长方体的三个面的面对角线是三棱锥的棱长,体对角线是外接球的直径.设长方体的棱长为a,b,c,外接球的半径为R,则a2+b2=32,b2+c2=42,a2+c2=52,(2R)2=a2+b2+c2,所以R=■.二、把四面体的一个角作为平行六面体的一个角补形成平行六面体.例3:四面体ABCD,侧棱AB,AC,AD两两垂直,AB=2,AC=3,AD=4,求四面体的外接球的半径R.因为四面体的侧棱两两垂直,所以可以把这个角看作长方体的一个角,把四面体补形成一个长方体,则四面体的外接球就是长方体的外接球四面体的三条侧棱就是长方体的长、宽、高,外接球的直径就是长方体的体对角线,则(2R)2=AB2+AC2+AD2=29,所以R=■.例4:若三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2■,AB=1,AC=2,∠BAC=60°,求球O的半径R.根据已知条件可以得到△ABC是直角三角形,把四面体补成一个长方体,则四面体的外接球就是长方体的外接球,外接球的直径就是长方体的体对角线.则(2R)2=SA2+AC2=16,所以R=2.例5:已知四面体PABC的侧面PAC与平面ABC垂直,∠ABC=90°,BC=2■,AB=2,且PA⊥PC,PA=PC,求异面直线PC与AB所成角的余弦值.解答:把四面体补成如图所示平行六面体,异面直线PC与AB所成角即為PC与CD所成角的补角的余弦值.取AC中点M,PA=PC,则PM⊥AC,又因为平面PAC与平面ABC垂直,所以PM⊥平面ABC.△ABC中,∠ABC=90°,AB=2,BC=2■,所以∠ACB=30°,AC=4.△PAC中,PA⊥PC,PA=PC,AC=4,所以PM=2,PC=2■.底面四边形ABDC中,DM2=DC2+CM2-2DC·CM·cos120°,得到DM=2■.Rt△PMD中,PD=4.△PCD中,cos∠PCD=■= -■.所以异面直线PC与AB所成角的余弦值为■.此题也可以用空间向量法解答,用补形能更好地体现线面关系.三、把四面体补形成三棱柱例6:已知某几何体底面ABC是棱长为1的等边三角形,PA⊥平面ABC,PA=3,求该几何体的外接球的半径.解答:将该四面体补形成一个三棱柱四面体的外接球就是三棱柱的外接球.先求三棱柱底面三角形外接圆半径r=■·■=■.又因为PA⊥平面ABC,PA=3,所以三棱柱的外接球半径为R=■=■.四面体的问题可以通过补形变成正方体、长方体乃至平行六面体的问题.尤其在正方体和长方体中,点线面的关系是我们所熟悉的. 一些几何题的证明和求解,由原几何图形分析探究会比较烦琐,通过补形填补成一个新的几何图形,能使原问题的本质得到充分的体现,解决起来比较容易. 本文着重讨论四面体的补形问题,希望窥一斑而知全豹,探究立体几何中补形法这一重要的转化策略.。
2022-2023学年高考数学二轮复习立体几何妙招 1外接球秒杀之补形法- Word版含解析

类型2:对棱相等
利用长方体相对面的对角线长度相等,把四面体放人其中
如图所示, ,三棱锥 可以放在长方体中,外接球直径 为长方体体对角线.
典型
【例1】已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是()
A. B. C. D.
【解析】用公式 ,则 ,
【答案】C.
A. B.8 C. D.
【解析】由题意可采用割补法,考虑到四面体 的四个面为全等的三角形,所以可在其每个面补上一个以 为三边的三角形作为底面,且以分别 长、两两垂直的侧棱的三棱锥,从而可得到一个长、宽、高分别为 的长方体,并且 ,则有 ( 为球的半径),得 ,所以球的表面积为 ,
【答案】 .
5.在三棱锥 中,底面 是等边三角形,顶点 在底面 的投影是底面的中心,侧面 侧面 ,则此三棱锥的体积与其外接球的体积之比为( )
【答案】D.
【例6】在四面体 中, 是边长为2的等边三角形, 是以 为斜边的等腰直角三的等腰直角三角形,平面 平面 ,则四面体 的外接球的表面积为( )
A. B. C. D.
【解析】在四面体 中, 是边长为2的等边三角形, 是以 为斜边的等腰直角三角形, ,平面 平面 ,如图,可知 平面 ,可得 ,所以 是等腰直角三角形,所以三棱锥 是正方体的一个角,如图:外接球的直径就是长方体的体对角线的长度,所以 ,四面体 的外接球的表面积为 .
【答案】 .
【例4】在三棱锥 中, ,则三棱锥 外接球的表面积为
【解析】将三棱锥补形为长方体,三个长度为三对面的对角线长,设长方体的长、宽、高分别为 ,则 .
【答案】 .
【例5】已知三棱锥 的四个顶点在球 的球面上, 是边长为2的正三角形, 分别是 的中点, ,则球 的体积为( )
空间几何体中几种常见的补形法

s△^船 ·AA =丁1×24×8=96 .
【小结 】比较 上述 两种 方 法 ,补 形
图3
法显 然 比分割法要简 洁得 多 ,计算 量也很 小 ,但 要抓 住 图形
的对 称性 ,巧妙的补成熟悉的几何 体 ,并找到 原几何 体 与补
形后 的几何体 的关 系 ,实现化繁为 简的奇效.
了一种构造思 想 ,同时也反 映了对 立统一的辩证思想 .
利用补形 法解决立体几何 问题 的基本 步骤是 :
第一步 :把不熟悉 的或 复杂 的几 何体 延 伸或 补加 成 熟
悉的或简单 的几何 体 ,把不完整 的图形 补成完整 的图形 ;
第二 步 :运用常见几何体 的知识 等计算结果 ;
第三 步 :得 出结论.
以外接球直径 2R= ,所 以 R= ,所 以外接 球 的表 面积
s球=挚.
方 法 二 联 系补 形 例 2 已知 三棱 锥 P—ABC,PA=BC=5,朋 :AC= 4,PC:AB= l,求三棱 锥的体积. 【思路 】如按常规求法 ,需求三棱锥 的底 面积和 高 ,而高 很 难求 出.由已知三组相对棱相 等这一 特点 ,联想长 方体对 面不平行 的对 角线恰 好组 成对 棱相 等 的三棱 锥 ,因此 可把 三棱锥 P—ABC补成长方体 ,再将长方体 分割成三棱锥 P— ABC和 四个相 同体积 的三棱锥.
在高考 中 ,补形法既可 以在选 择填空 题 中体 现 ,也 可以
在解答题 中体 现 ,常见的补形法 有对称 补形 、联系补 形 和还
原补形 ,还原补形主要涉及 台体 中“还台为锥 ”.下 面结合 实
例进行剖析 :
方法一 对称补形
立体几何中的补形与等效问题

立体几何中的补形与等效问题一.将正四面体放在正方体中主要结论:1.正四面体的每一个面是正三角形,反之亦然.2.正四面体是三组对棱都垂直的等面四面体.3.正四面体的对棱中点的连线都互相垂直且相等,等于棱长的22倍,反之亦真.4.正四面体的外接球与正方体外接球相同.例1.已知四面体ABCD 2,M ,N 分别为棱AD ,BC 的中点,F 为棱AB 上异于A ,B 的动点.有下列结论:①线段MN 的长度为1;②若点G 为线段MN 上的动点,则无论点F 与G 如何运动,直线FG 与直线CD 都是异面直线;③MFN ∠的余弦值的取值范围为55⎡⎢⎣⎭;④FMN ∆21.其中正确结论的个数为()A.1B.2C.3D.4解析:由于是一个正四面体,所以可以通过正方体来解决该问题.对于①,可根据,M N 分别为正方体前后两个面的中心可得出结论:正确对于②,F 取为AB 的中点,G 取为MN 的中点,此时FG 与CD 相交:错误对于③,计算可得35cos 35MBN ∠=>,由逼近思想可作出判断:正确对于④,空间问题平面化的技巧,将三角形ABC 与ABD 放在同一平面上,可计算出2≥+MF NF ,正确例2.如图,已知四面体ABCD 为正四面体,2,AB E F =,分别是,AD BC 中点.若用一个与直线EF 垂直,且与四面体的每一个面都相交的平面α去截该四面体,由此得到一个多边形截面,则该多边形截面面积最大值为.A.123D.2解析:补成正方体,如图.,EF α⊥Q ∴截面为平行四边形MNKL ,可得2NK KL +=,又//,//,MN AD KL BC 且,AD BC KN KL ⊥∴⊥可得L MNK S NK KL =⋅四边形2()1,2NK KL +≤=当且仅当NK KL =时取等号,选A.二.对棱相等的四面体四面体ABCD 中,==AB CD m ,==AC BD n ,==AD BC t ,这种四面体叫做对棱相等四面体,可以通过构造长方体来解决这类问题.如图,设长方体的长、宽、高分别为,,a b c ,则222222222⎧+=⎪+=⎨⎪+=⎩b c m a c n a b t ,三式相加可得:222++=a b c 222,2++m n t 而显然四面体和长方体有相同的外接球,设外接球半径为R ,则22224+=+a b c R ,所以2228++=m n t R.例3.在四面体ABCD 中,41,34,5,,AB CD AC BD AD BC E F =====分别是,AD BC 的中点.则下述结论:①四面体ABCD 的体积为20;②异面直线,AC BD 所成角的正弦值为2425;③四面体ABCD 外接球的表面积为50π;④若用一个与直线EF 垂直,且与四面体的每个面都相交的平面α去截该四面体,由此得到一个多边形截面,则该多边形截面面积最大值为6.其中正确的有_____.(填写所有正确结论的编号)解析:根据四面体特征,可以补图成长方体设其边长为,,a b c ,222222413425c b c a b a ⎧+=⎪+=⎨⎪+=⎩,解得3,4,5a b c ===,补成长,宽,高分别为3,4,5的长方体,在长方体中:①四面体ABCD 的体积为13454345203V ⨯⨯-⨯⨯⨯⨯==,故正确②异面直线,AC BD 所成角的正弦值等价于边长为5,3的矩形的对角线夹角正弦值,可得正弦值为1517,故错;③四面体ABCD外接球就是长方体的外接球,半径22R ==,其表面积为50π,故正确;④由于EF α⊥,故截面为平行四边形MNKL ,可得5KL KN +=,设异面直线BC 与AD 所成的角为θ,则sin sin HFB sin LKN θ∠∠==,算得2425sin θ=,224••6225MNKL KL KN S NK KL sin NKL +⎛⎫∴∠≤⨯= ⎪⎝⎭=.故正确.故答案为:①③④.三.墙角四面体墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模型,用构造法(构造长方体)解决.外接球的直径等于长方体的体对角线长(在长方体的同一顶点的三条棱长分别为a ,b ,c ,外接球的半径为R ,则2R =a 2+b 2+c 2.),有以下四种类型:例4.等腰△ABC 中,AB =AC =5,BC =6,将△ABC 沿BC 边上的高AD 折成直二面角B -AD -C ,则三棱锥B -ACD 的外接球的表面积为()A .5πB .203πC .10πD .34π解析:依题意,在三棱锥B -ACD 中,AD ,BD ,CD 两两垂直,且AD =4,BD =CD =3,因此可将三棱锥B ACD 补形成一个长方体,该长方体的长、宽、高分别为3,3,4,且其外接球的直径2R =32+32+42=34,故三棱锥B -ACD 的外接球的表面积为4πR 2=34π例5.已知球O 的球面上有四点A ,B ,C ,D ,DA ⊥平面ABC ,AB ⊥BC ,DA =AB =BC =2,则球O 的体积等于________.解析:如图,以DA ,AB ,BC 为棱长构造正方体,设正方体的外接球球O 的半径为R ,则正方体的体对角线长即为球O 的直径.∴CD =(2)2+(2)2+(2)2=2R ,因此R =62,故球O 的体积V =4πR 33=6π.四.圆锥等效于正棱锥,1.如图,P 的射影是A B C ∆的外心⇔三棱锥P A B C -的三条侧棱相等2.侧棱,底面半径,圆锥的高构成勾股定理.3.斜高,底面内切圆半径,圆锥的高构成勾股定理.例6:如图,D 为圆锥的顶点,O 是圆锥底面的圆心,AE 为底面直径,AE AD =.ABC是底面的内接正三角形,P 为DO 上一点,6PO DO =.(1)证明:PA ⊥平面PBC ;(2)求二面角B PC E --的余弦值.解析:(1)由题设,知DAE △为等边三角形,设1AE =,则2DO =,1122CO BO AE ===,所以6264PO DO ==,,,44PC PB ====又ABC 为等边三角形,则2sin 60BA OA = ,所以2BA =,22234PA PB AB +==,则90APB ∠= ,所以PA PB ⊥,同理PA PC ⊥,又PC PB P = ,所以PA ⊥平面PBC ;五.异面直线计算中的补形例7.如图,在四面体ABCD 中,AB ⊥BC ,CD ⊥BC ,BC =2,AB =CD =AB 与CD 所成的角为60 ,则四面体ABCD 的外接球的表面积为_________.解析:将四面体补形为直三棱柱如下图所示(设,O O '''为直三棱柱上下底面三角形的外接圆圆心):图(1)中60ABD '∠=︒,图(2)中120ABD '∠=︒,在图(1)(2)中可知:,,BC AB BC BD AB BD B ''⊥⊥= ,所以BC ⊥平面ABD ',图(1)(2)中取O O '''的中点O ,连接OB ,则O 为四面体ABCD 的外接球的球心,OB 为外接球的半径,图(1)中11122OO O O BC ''''===,且ABD '△为等边三角形,所以122cos30ABBO '==︒,所以R OB ===2420S R ππ==;图(2)中,11122OO O O BC ''''===,且O BD ''为等边三角形,所以BO AB '==所以R OB ==,所以外接球的表面积为2452S R ππ==;故答案为:20π或52π.。
立体几何建系方法
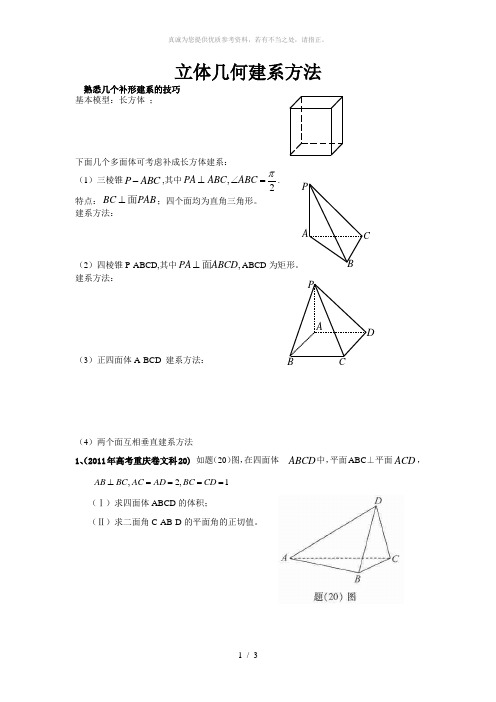
立体几何建系方法熟悉几个补形建系的技巧基本模型:长方体 ;下面几个多面体可考虑补成长方体建系: (1)三棱锥P ABC -,其中,2PA ABC ABC π⊥∠=.特点:BC PAB ⊥面;四个面均为直角三角形。
建系方法:(2)四棱锥P-ABCD,其中,PA ABCD ⊥面ABCD 为矩形。
建系方法:(3)正四面体A-BCD 建系方法:(4)两个面互相垂直建系方法1、(2011年高考重庆卷文科20) 如题(20)图,在四面体ABCD 中,平面ABC ⊥平面ACD ,,2,1AB BC AC AD BC CD ⊥====(Ⅰ)求四面体ABCD 的体积;(Ⅱ)求二面角C-AB-D 的平面角的正切值。
PA BCA B CDP2、(06山东),已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=2,PB⊥PD.(Ⅰ)求异面直线PD与BC所成角的余弦值;(Ⅱ)求二面角P-AB-C的大小;3、在直三棱柱ABC-A1B1C1中,AB=BC,D、E分别为BB1、AC1的中点.(Ⅰ)证明:ED为异面直线BB1与AC1的公垂线;(Ⅱ)设AA1=AC=2AB,求二面角A1-AD-C1的大小.A BCD EA1B1C14.如图,已知四棱锥P ABCD -,底面ABCD 为菱形,PA ⊥平面ABCD ,60ABC ∠=,E F ,分别是BC PC ,的中点. (Ⅰ)证明:AE PD ⊥; (Ⅱ)若H 为PD 上的动点,EH 与平面PAD 所成最大角的正切值 为2E AF C --的余弦值.5、(08安徽)如图,在四棱锥O ABCD -中,底面ABCD 四边长为1的 菱形,4ABC π∠=,OA ABCD ⊥底面, 2OA =,M 为OA 的中点.(1)求异面直线AB 与MD 所成角的大小; (2)求点B 到平面OCD 的距离.P BECD FA。
巧用补形法,妙解立体几何题

则G ()m =e m -ma ()m -1<e 2-e 2=0,而G ()m G ()2<0,所以存在零点x 0∈()1,2使G ()x =0,即F ()x 有唯一极值点且为极小值x 0∈()1,2,因为F ()x 0=ae x 0x 0-ln x0,G ()x 0=e x 0-x 0a ()x 0-1=0,e x=x 0a ()x 0-1,所以F ()x 0=1x 0-1-ln x 0,因为F '()x 0=-1()x 0-12-1x 0<0,所以F ()x 0=1x 0-1-ln x 0在()1,2上单调递减,故F ()x 0>F ()2=1-ln 2>0,所以F ()x >0,综上可知,当a >2e 2时,总有f ()x >0.该不等式中含有多项式,于是通过移项、作差,将不等式变形,以便构造出新函数F ()x =ae xx-ln x ,再利用导数法证明函数F ()x 的极小值大于0,从而达到证明不等式的目的.对于含有指数、对数式的不等式恒成立问题,在构造出新函数后,通常需借助导数法,对函数求导,研究导函数与函数单调性之间的关系,根据函数单调性求得函数的最值.由此可见,解答不等式恒成立问题,关键在于将不等式与函数关联起来,利用函数、导函数的性质来解题.这就需将不等式进行合适的变形,如分离参数、构造出函数,以将问题转化为函数最值问题来求解.(作者单位:江苏省南京市第一中学)有些立体几何问题较为复杂,或几何图形不规则,我们采用常规方法很难求得问题的答案.此时,可巧用补形法,根据已知条件和图形,添加合适的辅助线,将不规则的、陌生的、不易计算边角的几何图形割补为规则的、熟悉的、易计算边角的图形,取得化难为易的效果.而运用补形法求解立体几何问题,关键在于如何巧妙地割补图形,主要有以下几种思路.一、将棱锥补成棱柱棱锥是常见的几何体,如三棱锥、四棱锥、五棱锥等.有些棱锥的高很难找到或求得,此时我们可以将棱锥补成棱柱,如将正三棱锥补为正方体,将对棱的长相等的三棱锥补为长方体,再根据正方体、长方体的性质,便能快速求得三棱锥的边、角的大小,从而使问题顺利获解.例1.如图1所示,三棱锥S-ABCD 的所有棱长都为2,四个顶点在同一球面上,则球的表面积为().图1A.3πB.4πC.33πD.6π解:如图2,将正三棱锥补为正方体,并使正方体的棱长为1,图2解题宝典42则正方体的对角线长为1+1+1=3,故球的半径为r =,所以球的表面积为4π×èø2=3π,因此正确选项为A .我们仅根据三棱锥的特征,很难确定其外接球的球心,为了便于计算,需采用补形法,将正三棱锥补形为正方体,那么正方体的中心即为三棱锥外接球的球心,即正方体的对角线就是球的直径,据此建立关系式,即可快速求得球的半径和表面积.二、将斜三棱柱补成四棱柱对于正三棱锥,一般很容易确定其高,但对于斜三棱柱,我们却很难确定其高.此时可采用补形法,将斜三棱柱补形为四棱柱,这样根据四棱柱的特点,可快速确定其高,求得顶点与底面之间、点与点之间的距离.例2.已知斜三棱柱的侧面A 1ACC 1与平面ABC 垂直,∠ABC =90°,BC =2,AC =23,且AA 1⊥A 1C ,AA 1=A 1C ,求点C 到侧面A 1ABB 1的距离.图3解:如图3所示,将斜三棱柱ABC -A 1B 1C 1补为四棱柱,设点C 到侧面A 1ABB 1的距离为d ,由四棱柱的上下底面平行的性质可知,d 也是平面ABB 1A 1与平面CMM 1C 1的距离,作A 1D ⊥AC 于点D ,作A 1E ⊥AB 于点E ,∵AA 1=A 1C ,AC =23,AA 1⊥A 1C ,∴A 1D =3,∵∠ABC =90°,BC =2,∴AB =22,∵侧面A 1ACC 1与平面ABC 垂直,A 1D ⊥AC 于点D ,∴A 1D ⊥AB ,A 1E ⊥AB ,∴AB ⊥面A 1ED ,∴AB ⊥ED ,即∠ABC =90°,∴DE ∥BC ,D 为AC 中点,且DE =12BC =1,∴A 1E =A 1D 2+DE 2=2,而V 四棱柱=S ABMC ∙A 1D =S A 1ABB 1∙d ,∴d =S ABMC ∙A 1D S A 1ABB 1==3.为了便于计算,将斜三棱柱补为四棱柱,从而将线面距离转化为面面距离,再利用等体积变换法使问题得解.三、将棱台补为棱锥棱台较为特殊,它的上下底面平行,且成比例,但侧棱相交于一点.为了便于计算,我们可采用补形法,将棱台补形为棱锥,这样便可构造出几组相似的三角形、多边形,借助相似图形的性质建立关系式,便可顺利求得棱台的边、高的长度.例3.如图4所示,平面EB 1C 1F 将三棱柱ABC -A 1B 1C 1分成体积为V 1,V 2两部分,其中AB ,AC 的中点分别是E ,F ,则V 1:V 2为______.图4解:延长A 1A 到A 2,B 1B 到B 2,C 1C 到C 2,使得A 1A =AA 2,B 1B =BB 2,C 1C =CC 2,并延长B 1E ,C 1F ,可知V ABC -A 2B 2C 2=V ABC -A 1B 1C 1,∵A 2A :A 2A 1=1:2,∴V A 2-AEF=18V A 2-A 1B 1C 1,∵V A2-AEF=14V A2-ABC=14×13V ABC -A 2B 2C 2=112×V ABC -A 1B 1C 1,∴V AEF -A 1B 1C 1=7V A 2-AEF =712V ABC -A 1B 1C 1,∴V 1:V 2=7:5.将棱台补成棱锥,利用棱锥A 2-AEF 的性质以及相似三角形的性质求得各条棱的长和各个三棱锥的体积,再借助棱台ABC -A 1B 1C 1与棱柱ABC -A 2B 2C 2之间的位置关系进行转换,即可顺利解题.由上述分析可以看出,对于一些较为复杂的立体图形、立体几何问题,采用补形法求解,能使问题快速获解.因此,在解答立体几何问题时,同学们要学会联想,根据几何体的结构特征合理添加辅助线,将棱锥补成棱柱,将斜三棱柱补成四棱柱,将棱台补为棱锥,以便根据棱柱、四棱柱、棱锥的性质来解题.(作者单位:江苏省如皋市第二中学)解题宝典43。
立体几何习题课(分割法、补形法求体积等举例)

例4、三棱锥V-ABC中,VA底面ABC,ABC=90o, VA=a,VB=b,AC=c(cb),M是VC中点。
(1)求证:V,A,B,C四点在以M为球心的球面上; (2)求VC与AB所成的角的大小。
V
M
G
A
E
C
B
F
(arcco(bs2aa22)c(a22c2))
例6、三棱锥P-ABC中,AP=AC,PB=2,将此棱锥沿三
条侧棱剪开,其展开图是一个直角梯形P1P2P3A。 (1)求证:侧棱PB⊥ AC;
(2)求侧面PAC与底面ABC所成的角的余弦值。
P1
m
A
P
2
B
B
Ө
A
2
D
C (甲)
P2
m
m
D
C n E n P3 (乙)
解:(1)(略)
(2)甲图中,作PD⊥AC于D,连接BD,可得PDB
即为面PAC与面ABC所成二面角的平面角。
(KEY: 3 )
注意:分割法求体积。
例1、已知三棱锥的两个侧面都是边长为 6 的等边三角 形,另一个侧面是等腰直角三角形。求此三棱锥的体积。
(解法2)
S
A D B
法二:取AB中点D,连接SD,CD。易得△ABC
为等腰直角三角形,ACB=90o。则有SD⊥AB,
CD⊥AB。又SA=SB=SC,∴S在底面的射影为底
∴ cosPDB=4/5,为所求。
P
2
(甲)
B
Ө
A
D
C
P1
m
(乙)
A
2
B
m
m
2
D
P2
C n E n P3
(甘志国)补形法,正四面体的最佳解法

补形法,正四面体的最佳解法甘志国(该文已发表 数学金刊(高考),2011(3):39)在求解正四面体的问题时,若把它放在正方体中,常常便于求解.下面以普通高中课程标准实验教科书《数学·选修2-1·A 版》(人民教育出版社,2007年第2版) (下简称《选修2-1》)中的三道题来介绍这一技巧.例1 (《选修2-1》第111页练习第1题)如图1,空间四边形ABCD 的每条边和BD AC ,的长都等于a ,点N M ,分别是CD AB ,的中点,求证:CD MN AB MN ⊥⊥,.证明 易得正四面体ABCD ,把它放在正方体中(如图2),则欲证结论显然成立(因为MN 垂直于图2中正方体的上下表面).图1 图2例2 (《选修2-1》第112页习题第5(1)题)如图3,空间四边形OABC 的各边以及BO AC ,的长都是1,点E D ,分别是边BC OA ,的中点,连结DE .(1)计算DE 的长;(2)求点O 到平面ABC 的距离.图3 图4解 易得正四面体OABC ,把它放在正方体中(如图4).(1)DE 的长即图4中正方体的棱长22. (2)我们在图4中求正四面体OABC 的体积V :122222221314224423=⋅⎪⎪⎭⎫ ⎝⎛⋅⋅-⎪⎪⎭⎫ ⎝⎛=-=-=--OAGB OAB G V V V V V 正方体正方体设点O 到平面ABC 的距离为h ,得︒⋅⋅⋅⋅===∆60sin 11213131122h S V ABC 36=h例3 (《选修2-1》第107-108页例3)如图5,一块均匀的正三角形面的钢板的质量为500kg ,在它的顶点处分别受力F 1, F 2, F 3,每个力与同它相邻的三角形的两边之间的角都是︒60,且|F 1|=|F 2|=|F 3|=200 kg.这块钢板在这些力的作用下将会怎样运动?这三个力最小都为多少时,才能提起这块钢板?图5 图6 图 7《选修2-1》是按图6建立空间直角坐标系来求解的,确实运算量很大,思维量也不小,而下面的解法却很简洁.解 易知图5中的三个力F 1, F 2, F 3必交于一点(设为点F ),且有正四面体FABC ,可不妨设该正四面体的棱长为)0(2>a a .我们把正四面体FABC 放在图 7中的棱长为a 的正方体中,并按图7建立空间直角坐标系,得),0,0(),,,(),0,,0(),0,0,(a C a a a B a A a F),0,(),,,0(),0,,(a a a a a a -=--=-=a 2===及图5中的F 1, F 2, F 3满足|F 1|=|F 2|=|F 3|=200,得F 1),0(2200a a a -=,, F 2),0(2200a a a --=,, F 3),0(2200a a a -=, F 1+ F 2+F 3)1,1,1(2200)2a ,22(2200--=--=a a a ,|F 1+ F 2+F 3|6200= 因为5006200<,所以这块钢板在这些力的作用下将会静止不动.设|F 1|=|F 2|=|F 3|=x ,则可得F 1+ F 2+F 3)1,1,1(2)2,22(2--=--=x a a a a x,|F 1+ F 2+F 3|6x = 当且仅当5006>x 即63250>x 时,才能提起这块钢板.(请注意:原问题“这三个力最小都为多少时,才能提起这块钢板”是无法回答的,建议把此问改为“这三个大小相等的力满足怎样的条件才能提起这块钢板”.)例4 (2013年高考课标全国卷II 卷理科第7题也即文科第9题)一个四面体的顶点在空间直角坐标系xyz O -中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到的正视图可以为( )解 A.由图8可求解(先把这个正四面体放置在正方体中):图8本文介绍的技巧“把正四面体放在正方体中”实际上就是一种补形法,在立体几何中还有很多用补形法简洁解题的例子,比如把直角四面体(该四面体从一点出发的三条棱两两垂直)补成长方体,请读者留意.。
高考数学立体几何大题的八大解题技巧

高考数学立体几何大题的八大解题技巧1、平行、垂直位置关系的论证的策略(1)由已知想性质,由求证想判定,即分析法与综合法相结合寻找证题思路。
(2)利用题设条件的性质适当添加辅助线(或面)是解题的常用方法之一。
(3)三垂线定理及其逆定理在高考题中使用的频率最高,在证明线线垂直时应优先考虑。
2、空间角的计算方法与技巧主要步骤:一作、二证、三算;若用向量,那就是一证、二算。
(1)两条异面直线所成的角①平移法:②补形法:③向量法:(2)直线和平面所成的角①作出直线和平面所成的角,关键是作垂线,找射影转化到同一三角形中计算,或用向量计算。
②用公式计算。
(3)二面角①平面角的作法:(i)定义法;(ii)三垂线定理及其逆定理法;(iii)垂面法。
②平面角的计算法:(i)找到平面角,然后在三角形中计算(解三角形)或用向量计算;(ii)射影面积法;(iii)向量夹角公式。
3、空间距离的计算方法与技巧(1)求点到直线的距离:经常应用三垂线定理作出点到直线的垂线,然后在相关的三角形中求解,也可以借助于面积相等求出点到直线的距离。
(2)求两条异面直线间距离:一般先找出其公垂线,然后求其公垂线段的长。
在不能直接作出公垂线的情况下,可转化为线面距离求解(这种情况高考不做要求)。
(3)求点到平面的距离:一般找出(或作出)过此点与已知平面垂直的平面,利用面面垂直的性质过该点作出平面的垂线,进而计算;也可以利用“三棱锥体积法”直接求距离;有时直接利用已知点求距离比较困难时,我们可以把点到平面的距离转化为直线到平面的距离,从而“转移”到另一点上去求“点到平面的距离”。
求直线与平面的距离及平面与平面的距离一般均转化为点到平面的距离来求解。
4、熟记一些常用的小结论诸如:正四面体的体积公式是;面积射影公式;“立平斜关系式”;最小角定理。
弄清楚棱锥的顶点在底面的射影为底面的内心、外心、垂心的条件,这可能是快速解答某些问题的前提。
5、平面图形的翻折、立体图形的展开等一类问题要注意翻折前、展开前后有关几何元素的“不变性”与“不变量”。
2024全国高考真题数学汇编:立体几何初步章节综合

2024全国高考真题数学汇编立体几何初步章节综合一、单选题1.(2024天津高考真题)若,m n 为两条不同的直线, 为一个平面,则下列结论中正确的是()A .若//m ,//n ,则m nB .若//,//m n ,则//m nC .若//, m n ,则m nD .若//, m n ,则m 与n 相交2.(2024积为()A .B .C .D .3.(2024全国高考真题)已知正三棱台111ABC A B C -的体积为523,6AB ,112A B ,则1A A 与平面ABC 所成角的正切值为()A .12B .1C .2D .34.(2024全国高考真题)设 、为两个平面,m n 、为两条直线,且m .下述四个命题:①若//m n ,则//n 或//n②若m n ,则n 或n③若//n 且//n ,则//m n④若n 与 , 所成的角相等,则m n 其中所有真命题的编号是()A .①③B .②④C .①②③D .①③④5.(2024北京高考真题)如图,在四棱锥P ABCD 中,底面ABCD 是边长为4的正方形,4PA PB ,PC PD ).A .1B .2CD6.(2024天津高考真题)一个五面体ABC DEF .已知AD BE CF ∥∥,且两两之间距离为1.并已知123AD BE CF ,,.则该五面体的体积为()A B .142 C .2D .142二、填空题7.(2024全国高考真题)已知圆台甲、乙的上底面半径均为1r ,下底面半径均为2r ,圆台的母线长分别为 212r r , 213r r ,则圆台甲与乙的体积之比为.三、解答题8.(2024全国高考真题)如图,四棱锥P ABCD 中,PA 底面ABCD ,2PA AC ,1,BC AB .(1)若AD PB ,证明://AD 平面PBC ;(2)若AD DC ,且二面角A CP D ,求AD .9.(2024全国高考真题)如图,//,//AB CD CD EF ,2AB DE EF CF ,4,CD AD BC AE M 为CD 的中点.(1)证明://EM 平面BCF ;(2)求点M 到ADE 的距离.10.(2024上海高考真题)如图为正四棱锥,P ABCD O 为底面ABCD 的中心.(1)若5,AP AD ,求POA 绕PO 旋转一周形成的几何体的体积;(2)若,AP AD E 为PB 的中点,求直线BD 与平面AEC 所成角的大小.参考答案1.C【分析】根据线面平行的性质可判断AB 的正误,根据线面垂直的性质可判断CD 的正误.【详解】对于A ,若//m ,//n ,则,m n 平行或异面或相交,故A 错误.对于B ,若//,//m n ,则,m n 平行或异面或相交,故B 错误.对于C ,//, m n ,过m 作平面 ,使得s ,因为m ,故//m s ,而s ,故n s ,故m n ,故C 正确.对于D ,若//, m n ,则m 与n 相交或异面,故D 错误.故选:C.2.B【分析】设圆柱的底面半径为r ,根据圆锥和圆柱的侧面积相等可得半径r 的方程,求出解后可求圆锥的体积.【详解】设圆柱的底面半径为r而它们的侧面积相等,所以2ππr r 即故3r ,故圆锥的体积为1π93.故选:B.3.B【分析】解法一:根据台体的体积公式可得三棱台的高3h ,做辅助线,结合正三棱台的结构特征求得AM 进而根据线面夹角的定义分析求解;解法二:将正三棱台111ABC A B C -补成正三棱锥 P ABC ,1A A 与平面ABC 所成角即为PA 与平面ABC 所成角,根据比例关系可得18P ABC V ,进而可求正三棱锥 P ABC 的高,即可得结果.【详解】解法一:分别取11,BC B C 的中点1,D D ,则11AD A D ==可知1111166222ABC A B C S S 设正三棱台111ABC A B C -的为h ,则 11115233ABC A B C V h ,解得h 如图,分别过11,A D 作底面垂线,垂足为,M N ,设AM x ,则1AADN AD AM MN x =--=-,可得1DD 结合等腰梯形11BCC B 可得22211622BB DD,即 221616433x x,解得x 所以1A A 与平面ABC 所成角的正切值为11tan 1A M A AD AMÐ==;解法二:将正三棱台111ABC AB C -补成正三棱锥 P ABC ,则1A A 与平面ABC 所成角即为PA 与平面ABC 所成角,因为11113PA A B PA AB ,则111127P A B C P ABC V V ,可知1112652273ABC A B C P ABC V V,则18P ABC V ,设正三棱锥 P ABC 的高为d,则11661832P ABC V d,解得d ,取底面ABC 的中心为O ,则PO底面ABC ,且AO 所以PA 与平面ABC 所成角的正切值tan 1PO PAO AO.故选:B.4.A【分析】根据线面平行的判定定理即可判断①;举反例即可判断②④;根据线面平行的性质即可判断③.【详解】对①,当n ,因为//m n ,m ,则//n ,当n ,因为//m n ,m ,则//n ,当n 既不在 也不在 内,因为//m n ,,m m ,则//n 且//n ,故①正确;对②,若m n ,则n 与, 不一定垂直,故②错误;对③,过直线n 分别作两平面与, 分别相交于直线s 和直线t ,因为//n ,过直线n 的平面与平面 的交线为直线s ,则根据线面平行的性质定理知//n s ,同理可得//n t ,则//s t ,因为s 平面 ,t 平面 ,则//s 平面 ,因为s 平面 ,m ,则//s m ,又因为//n s ,则//m n ,故③正确;对④,若,m n 与 和 所成的角相等,如果//,// n n ,则//m n ,故④错误;综上只有①③正确,故选:A.5.D【分析】取点作辅助线,根据题意分析可知平面PEF 平面ABCD ,可知PO 平面ABCD ,利用等体积法求点到面的距离.【详解】如图,底面ABCD 为正方形,当相邻的棱长相等时,不妨设4,PA PB AB PC PD ,分别取,AB CD 的中点,E F ,连接,,PE PF EF ,则,PE AB EF AB ,且PE EF E ,,PE EF 平面PEF ,可知AB 平面PEF ,且AB 平面ABCD ,所以平面PEF 平面ABCD ,过P 作EF 的垂线,垂足为O ,即PO EF ,由平面PEF 平面ABCD EF ,PO 平面PEF ,所以PO 平面ABCD ,由题意可得:2,4PE PF EF ,则222PE PF EF ,即PE PF ,则1122PE PF PO EF ,可得PE PF PO EF,当相对的棱长相等时,不妨设4PA PC ,PB PD因为BD PB PD ,此时不能形成三角形PBD ,与题意不符,这样情况不存在.故选:D.6.C【分析】采用补形法,补成一个棱柱,求出其直截面,再利用体积公式即可.【详解】用一个完全相同的五面体HIJ LMN (顶点与五面体ABC DEF 一一对应)与该五面体相嵌,使得,D N ;,E M ;,F L 重合,因为AD BE CF ∥∥,且两两之间距离为1.1,2,3AD BE CF ,则形成的新组合体为一个三棱柱,该三棱柱的直截面(与侧棱垂直的截面)为边长为1的等边三角形,侧棱长为1322314,212111142ABC DEF ABC HIJ V 故选:C.7.4【分析】先根据已知条件和圆台结构特征分别求出两圆台的高,再根据圆台的体积公式直接代入计算即可得解.【详解】由题可得两个圆台的高分别为12h r r 甲,12h r r乙,所以21211313S S h V h V h S S h 甲甲甲乙乙乙.故答案为:4.8.(1)证明见解析【分析】(1)先证出AD 平面PAB ,即可得AD AB ,由勾股定理逆定理可得BC AB ,从而//AD BC ,再根据线面平行的判定定理即可证出;(2)过点D 作DE AC 于E ,再过点E 作EF CP 于F ,连接DF ,根据三垂线法可知,DFE 即为二面角A CP D 的平面角,即可求得tan DFE AD 的长度表示出,DE EF ,即可解方程求出AD .【详解】(1)(1)因为PA 平面ABCD ,而AD 平面ABCD ,所以PA AD ,又AD PB ,PB PA P ,,PB PA 平面PAB ,所以AD 平面PAB ,而AB 平面PAB ,所以AD AB .因为222BC AB AC ,所以BC AB ,根据平面知识可知//AD BC ,又AD 平面PBC ,BC 平面PBC ,所以//AD 平面PBC .(2)如图所示,过点D 作DE AC 于E ,再过点E 作EF CP 于F ,连接DF ,因为PA 平面ABCD ,所以平面PAC 平面ABCD ,而平面PAC 平面ABCD AC ,所以DE 平面PAC ,又EF CP ,所以 CP 平面DEF ,根据二面角的定义可知,DFE 即为二面角A CP D 的平面角,即sin DFEtan DFE 因为AD DC ,设AD x,则CDDE ,又242xCE,而EFC 为等腰直角三角形,所以2EF故22tan 4DFE xxAD9.(1)证明见详解;【分析】(1)结合已知易证四边形EFCM 为平行四边形,可证//EM FC ,进而得证;(2)先证明OA 平面EDM ,结合等体积法M ADE A EDM V V 即可求解.【详解】(1)由题意得,//EF MC ,且EF MC ,所以四边形EFCM 是平行四边形,所以//EM FC ,又CF 平面,BCF EM 平面BCF ,所以//EM 平面BCF ;(2)取DM 的中点O ,连接OA ,OE ,因为//AB MC ,且AB MC ,所以四边形AMCB 是平行四边形,所以AM BC又AD ,故ADM △是等腰三角形,同理EDM △是等腰三角形,可得,,3,OA DM OE DM OA OE又AE 222OA OE AE ,故OA OE .又,,,OA DM OE DM O OE DM 平面EDM ,所以OA 平面EDM ,易知122EDM S在ADE V 中,cos4DEA,所以1sin 22DEA DEA S 设点M 到平面ADE 的距离为d ,由M ADE A EDM V V ,得1133ADE EDM S d S OA ,得d故点M 到平面ADE10.(1)12π(2)π4【分析】(1)根据正四棱锥的数据,先算出直角三角形POA 的边长,然后求圆锥的体积;(2)连接,,EA EO EC ,可先证BE 平面ACE ,根据线面角的定义得出所求角为 BOE ,然后结合题目数量关系求解.【详解】(1)正四棱锥满足且PO 平面ABCD ,由AO 平面ABCD ,则PO AO ,又正四棱锥底面ABCD 是正方形,由 AD 3AO ,故4PO ,根据圆锥的定义,POA 绕PO 旋转一周形成的几何体是以PO 为轴,AO 为底面半径的圆锥,即圆锥的高为4PO ,底面半径为3AO ,根据圆锥的体积公式,所得圆锥的体积是21π3412π3(2)连接,,EA EO EC ,由题意结合正四棱锥的性质可知,每个侧面都是等边三角形,由E 是PB 中点,则,AE PB CE PB ,又,,AE CE E AE CE 平面ACE ,故PB 平面ACE ,即BE 平面ACE ,又BD 平面ACE O ,于是直线BD 与平面AEC 所成角的大小即为 BOE ,不妨设6AP AD ,则3BO BE ,sin2BOE,又线面角的范围是π0,2 ,故π4BOE .即为所求.。
三棱锥外接球半径常见解法含答案解析

三棱锥外接球半径常见解法含答案解析在立体几何中,求三棱锥外接球半径是一个常见且重要的问题。
掌握有效的解法不仅能够帮助我们解决具体的数学题目,还能加深对空间几何关系的理解。
下面将为大家介绍几种常见的求解三棱锥外接球半径的方法,并通过具体的例子进行答案解析。
一、补形法补形法是一种常用的技巧,通过将三棱锥补成一个特殊的几何体,如长方体、正方体等,然后利用这些特殊几何体的外接球半径与原三棱锥外接球半径的关系来求解。
例如,对于墙角三棱锥(三条侧棱两两垂直的三棱锥),我们可以将其补成长方体。
设三棱锥的三条侧棱长分别为\(a\)、\(b\)、\(c\),则长方体的体对角线就是三棱锥外接球的直径\(2R\),根据长方体体对角线公式可得:\\begin{align}2R&=\sqrt{a^2 + b^2 + c^2}\\R&=\frac{\sqrt{a^2 + b^2 + c^2}}{2}\end{align}\例 1:已知三棱锥\(P ABC\)中,\(PA\perp PB\),\(PB\perp PC\),\(PC\perp PA\),且\(PA = 3\),\(PB =4\),\(PC = 5\),求其外接球半径。
解:将三棱锥\(P ABC\)补成长方体,长方体的体对角线就是外接球的直径。
\\begin{align}2R&=\sqrt{3^2 + 4^2 + 5^2}\\&=\sqrt{9 + 16 + 25}\\&=\sqrt{50}\\&=5\sqrt{2}\end{align}\所以,外接球半径\(R =\frac{5\sqrt{2}}{2}\)二、确定球心位置法通过寻找三棱锥外接球的球心位置,利用球心到各顶点的距离等于外接球半径来求解。
对于正三棱锥,球心通常在高线上。
设正三棱锥底面边长为\(a\),高为\(h\),底面外接圆半径为\(r\)(可由正弦定理求得\(r =\frac{\sqrt{3}}{3}a\)),球心到底面距离为\(d\),则根据勾股定理有:\\begin{align}R^2&=d^2 + r^2\\d&=h R\end{align}\联立可得\(R\)的表达式。
补形法在立体几何中的妙用

补形法在立体几何中的妙用
张丽
【期刊名称】《天津教育》
【年(卷),期】1996(000)005
【摘要】补形法就是将一些不规则的图形补成我们熟悉的规则的图形.在立体几何题中,题目给出的图形往往是不规则的,其本质特征被掩盖,这就给解题带来一定的困难.如果我们能将图形进行适当的补形,使其转化为我们熟悉的具有某种特性的图形,如正三棱锥、长方体、正方体、直棱柱等,并利用其特有的性质,就可使问题化难为易.下面就常见的补形法举例说明.一、补成正三棱锥如果图形中含有等边三角形,则可考虑将其补成正三棱锥.例1.已知A、B、C是球面上三点,过这三点的截面与球心的距离等于球半径的一半,且AB=BC=CA=2,求球面面积.
【总页数】2页(P41-42)
【作者】张丽
【作者单位】天津耀华中学
【正文语种】中文
【中图分类】G633.6
【相关文献】
1.“补形法”——立体几何解题中的转化策略 [J], 简素宁
2.补形法在立体几何中的应用 [J], 陈念红
3.巧借补形法解立体几何问题 [J], 闫伟; 刘彦强
4.例谈补形法解立体几何题 [J], 刘立强;杜红全
5.例谈补形法解立体几何题 [J], 刘立强;杜红全
因版权原因,仅展示原文概要,查看原文内容请购买。
补形法在立体几何中的应用

三 将 不 规 则 的 几 何 体 补成 规 则 的 几 何体
如图 , ( 1 ) 四个截 面 是 正 三角 形 ( 如 AE F G、 AMN Q等 ) , 而 另 外 的 四
A
例 3 如图 , 三个 1 2×1 2 c m的正方 形 , 都被连 结 个 面 是 正 六 边 形 (如 正 六 边 形 F I P N M等) , 所以 留下 的多面体 不是 相邻两边 中点 的直线 分成 A、 曰两 片 [ 如 图( 1 ) ] , 把6 E 片粘在一个正六边形 的外 面 [ 如 图( 2 ) ] , 然后 折成 多 正 多 面 体 。
难的
一
题 如 果 采 用 割 补 法 解 此 题 就 相 当 简单 甚 至 补
, ,
,
解 题 可 考虑 采 用 补 形 法 即 补 形 的 技 巧 作 出辅
,
,
“
”
完后 由图 直 接 可 以 观 察 出结 果
二
。
几 何体 化 散 为 聚 化难 为易
, ,
“ ” “
。
它 反 映 了我 国传 统 数
,
补 长 方体
.
( 2 ) 正 四 面 体 的外 接 球 就 是 补 后 正 方 体 的 外 接
,
AP E Q/ /
,
PB QM / /
,
c QQ ∥尸
’
。
球 的 直径 为 正 方 体 的 对 角 线
,
。
所 以 正 四 面 体外接
\ l ‰ ≥ ? 扩 r 萄 一 >\
.
.
j
将它 补 成 长 方 体 QE
’
’
QE F M
用补形法解立体几何题的常用策略

用补形法解立体几何题的常用策略罗建中一、棱锥补成棱柱例1 一个四面体的所有棱长都为2,四个顶点在同一球面上,则球的表面积为 A. π3 B. π4 C. π33D. π6分析:正四面体可看作是正方体经过切割而得到,因而构造一个棱长为1的正方体ABCD 1111D C B A -,则四面体D BC A 11-就是棱长为2的正四面体,而正方体的外接球就是四面体的外接球,又正方体的对角线长就是球的直径,易知对角线长度为3,故球表面积2234S ⎪⎪⎭⎫ ⎝⎛π=π=3。
评注:对棱长全相等的正四面体通常把它补成正方体。
若是相对棱长相等的四面体,则可考虑把它补成长方体。
例2 如图1,在底面是直角梯形的四棱锥ABCD S -中,∠ABC=︒90,SA ⊥面ABCD ,SA=AB=BC=1,AD=21。
(1)求四棱锥ABCD S -的体积;(2)求面SCD 与面SBA 所成的二面角的正切值。
解:(1)解答略。
(2)以SA 为棱,构造正方体AECB-SFGH ,如图2,分别取棱SF 、HG 中点M 、N ,连结DM 、MN 、SN 、ND ,设ND 与SC 相交于O ,连接MO 。
则有面MDN ∥面SAB ,且SM ⊥面MDN ,所以所求的二面角等于二面角S-DN-M 。
在正方体AECB-SFGH 中,△NSD 与△NMD 都是等腰三角形,所以SO ⊥DN ,MO ⊥DN ,所以∠SOM 是二面角S-DN-M 的平面角。
又MO 21=SB=22,SM=21,所以22MO SM SOM tan ==∠,故所求二面角的正切值是22。
评注:从一顶点出发的三条棱互相垂直的锥体通常可考虑把它补成长方体或正方体。
二、三棱柱可补成四棱柱例3 已知斜三棱柱的侧面11ACC A 与平面ABC 垂直,∠ABC=︒90,BC=2,AC=32,且C A AA 11⊥,C A AA 11=,求点C 到侧面11ABB A 的距离。
解:把斜三棱柱ABC 111C B A -补成如图3所示的平行六面体,设所求的距离为d ,则d 也是平面11A ABB 与平面11C CMM 间距离,作AC D A 1⊥于点D ,作AB E A 1⊥于点F ,因为C A AA 11=,32AC =,C A AA 11⊥,所以3D A 1=,又∠ABC=︒90,BC=2,所以22AB =,因侧面11ACC A 与底面ABC 垂直,AC D A 1⊥于点D ,所以AB D A 1⊥,又AB E A 1⊥,知AB ⊥面ED A 1,因而AB ⊥ED ,又∠ABC=︒90,所以DE ∥BC ,D 为AC 中点,且1BC 21DE ==,故2DE D A E A 2211=+=,而d S D A S V 11ABB A 1ABMC ⋅=⋅=平行六面体。
2024高考数学专项立体几何系统班7、外接球与内切球

第7讲外接球与内切球知识与方法1.外接球与内切球是全国高考常考题型,模型杂、方法多,但归纳起来不外乎两大类处理方法.(1)补形:将几何体补全成长方体、正方体、直棱柱等常见几何体,计算外接球半径.(2)构建平面截球模型:寻找截面圆心以及球心到截面的距离,通过222R r d =+计算外接球半径.2.设球的半径为R ,有5个常用计算公式.(1)正方体外接球半径:R =,其中a 为正方体棱长,如图1.(2)长方体外接球半径:R =a ,b ,c 分别为长方体的长、宽、高,如图2.(3)正四面体外接球半径,4R a =,其中a 为正四面体棱长,如图3.(4)直三棱柱外接球半径:R =,其中r 为底面外接圆半径,h 为直三棱柱的高,如图4.(5)圆柱外接球半径:R =,其中r 为底面圆半径,h 为圆柱的母线长,如图5.提醒:①上面列出了一些简单模型的外接球半径计算公式,需结合图形将其记住,还有一些其他模型可以通过补形的方法转化为上述模型处理;②一些不能通过简单补形求解的模型,如球内接正棱锥,球内接圆锥等,可以通过分析几何关系,转化为平面截球模型计算外接球的半径.题组一1.(★★)已知一个正方体的所有顶点在一个球面上.若这个正方体的表面积为18,则这个球的体积为_______.【解析】设正方体的棱长为a ,则2618a =,故a =3322R a ==,其体积34932V R ππ==.【答案】92π2024高考数学专项立体几何系统班7、外接球与内切球【提炼】正方体棱长a 与其外接球半径R 之间的关系为32R =.2.(★★★)如图,在等腰梯形ABCD 中,22AB DC ==,60DAB ∠=︒,E 为AB 中点,将ADE 与BEC 分别沿ED ,EC 向上折起,使点A ,B 重合于点P ,则三棱锥P DCE -的外接球的体积为()【解析】由题意,可将平面图形等腰梯形ABCD 补全为正三角形FAB ,如图,那么在完成题干所描述的翻折后,还可将CDF △沿着CD 翻折,使得点F 也与点P 重合,显然此时得到的是一个棱长为1的正四面体,即三棱锥P DCE -是棱长为1的正四面体,其外接球半径R =343V R π==.【答案】C【提炼】正四面体的棱长为a ,则其外接球半径为64a ,内切球半径为612a ,证明方法可参考附赠的小册子《高考数学常用二级结论》.3.(★★)长方体的长,宽,高分别为3,2,1,其顶点都在球O 的球面上,则球O 的表面积为______.【解析】长方体的外接球半径R =,其中a ,b ,c 分别为长、宽、高,故R =O 的表面积2414S R ππ==.【答案】14π【提炼】设长方体的长、宽、高分别为a ,b ,c ,则其外接球半径2R =4.(★★)已知底面边长为1的正四棱柱的各顶点均在同一个球面上,则该球的体积为()A.323π B.4π C.2π D.43π【解析】首先得知道什么是正四棱柱,它指的是底面为正方形、侧棱与底面垂直的四棱柱,也是一种特殊的长方体,高考这种名词都是直接给,必须清楚其结构特征.外接球半径1R ==,故该球的体积34433V R ππ==.【答案】D5.(★★)已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是()A.16πB.20πC.24πD.32π【解析】设正四棱柱底面边长为a ,则2416a =,即2a =,其外接球的半径2242R ==,故所求球的表面积2424S R ππ==.【答案】C 6.(★★★)一个正四棱柱的各个顶点在一个直径为2的球面上,如果正四棱柱的底面边长为1cm ,那么该棱柱的表面积为______cm 2.【解析】设正四棱柱的高为h cm ,则1112=,故h =,即该棱柱的表面积(2S =+cm 2.【答案】2+题组二7.(★★★)已知三棱柱111ABC A B C -的6个顶点都在球O 的球面上,若3AB =,4AC =,AB AC ⊥,112AA =,则球O 的半径为()B. C.132D.【解析】这道题可能不少同学会有这么一个困惑,就是题干没给出三棱柱111ABC A B C -为直三棱柱,是不是题干有问题呢?当然不是,事实上,斜棱柱是没有外接球的,所以题干的说法本身就隐含了三棱柱111ABC A B C -为直三棱柱这一条件.本题的直三棱柱可通过补形为长方体来计算外接球半径,如图,三棱柱111ABC A B C -与长方体有相同的外接球,该球的半径为34121322R ==.【答案】C 8.(★★★)3______.【解析】本模型一般称为墙角三棱锥,可补形为正方体(或长方体)来处理.如图,将三棱锥B ACD -补全为正方体,并放到了球体之中,可以看到二者有相同的外接球,正方体棱332R =,故外接球表面积249S R ππ==.【答案】9π【提炼】三条侧棱两两垂直的三棱锥(墙角三棱锥)可补形为长方体或正方体来计算外接球半径.题组三9.(★★★)设三棱柱的侧棱垂直于底面,所有棱的长都为a ,顶点都在一个球面上,则该球的表面积为()A.2a π B.273a π C.2113a π D.25a π【解析】如图,设G 为ABC △的中心,ABC △外接圆半径233323r AG ==⨯=,1122a OG AA ==,球的半径22712R r OG a =+,故球的表面积22743S R a ππ==.【答案】B【提炼】①设直三棱柱底面外接圆半径为r ,高为h ,则其外接球半径222h R r ⎛⎫=+ ⎪⎝⎭;②关键是计算底面三角形外接圆半径,对于直角三角形,外接圆半径等于斜边长的一半,若是倍,等于高的23倍;若是普通的三角形,则可利用正弦定理计算外接圆半径.10.(★★★)直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA -==,120BAC ∠=︒,则此球的表面积等于______.【解析】如图,在ABC △中,由余弦定理得222122222122BC ⎛⎫=+-⨯⨯⨯-= ⎪⎝⎭,解得BC =.由正弦定理得42sin BC r BAC ==∠,解得2r =,故1112OG AA ==,所以球的半径R ==,故球的表面积2420S R ππ==.【答案】20π题组四11.(★★★)设A ,B ,C ,D 是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为,则三棱锥D ABC -体积的最大值为()A. B. C. D.【解析】如图,先计算ABC △外接圆的半径r ,设ABC △边长为a .则2122a ⋅⋅=,解得6a =,所以62sin 60r =︒,解得r =,所以2OG ==,当D 点位于GO 延长线上时,三棱锥D ABC -的高最大,底面积不变,此时体积最大,最大值为()1243V =⨯+=【答案】B【提炼】本题三棱锥D ABC -的体积最大时,D ABC -是正三棱锥,正三棱锥外接球的计算问题,解题的关键是构建AOG △,在这个三角形中,满足222OA AG OG =+,即222R r d =+,其实这就是前一小节的平面截球模型,只要是正棱锥,都可以采用这个办法处理.12.(★★★)正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为()A.814πB.16πC.9πD.274π【解析】如图,由题意,得14PO =,1AO =设外接球的半径为R ,则OA OP R ==,故14OO R =-.在1OO A △中,22211AO OO AO +=,即()2224R R +-=,解得94R =,故该球的表面积28144S R ππ==.【答案】A【提炼】正四棱锥外接球的有关计算,关键是构建1AOO ,在这个三角形中,利用22211OA AO OO =+建立等量关系,其实就是平面截球模型的处理方法.13.(★★★)正四棱锥S ABCD -点S ,A ,B ,C ,D 都在同一个球面上,则该球的体积为_____.【解析】解法1:如图1,设正方形ABCD 的中心为1O ,由题意,11AO =,11SO =.设正四棱锥外接球球心为O ,半径为R ,则OA R =,11OO R =-,在1AOO 中,22211OO AO AO +=,故()2211R R -+=,解得1R =,即外接球体积为34433V R ππ==.解法2:设正方形ABCD 的中心为1O ,由题意,11AO =,11SO ==,因为11SO AO =,所以1O 即为球心,球的半径为1,体积34433V R ππ==,本题实际的图形是图2.【答案】43π14.(2021·全国甲卷·理·11·★★★)已知A ,B ,C 是半径为1的球O 的球面上的三个点,且AC BC ⊥,1AC BC ==,则三棱锥O ABC -的体积为()A.212B.312C.24D.34【解析】如图,由题意,2AB =,设D 为ABC △的外心,则1222AD AB ==,2222OD OA AD =-=,所以1112211332212O ABC ABC V S OD -=⋅=⨯⨯⨯⨯ .【答案】A题组五15.(★★)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为()A.πB.34πC.2π D.4π【解析】如图,由题意得1OA =,112OO =,故132O A =,圆柱体积233124V ππ⎛⎫=⋅= ⎪ ⎪⎝⎭.【答案】B【提炼】圆柱外接球半径222h R r ⎛⎫=+ ⎪⎝⎭,其中r 为底面圆半径,h 为圆柱的高.16.(★★★★)如图,半径为R 的球O 中有一内接圆柱.当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是______.【解析】设圆柱的底面半径为r ,高为h ,则2224h r R rh +=≥,当且仅当2h r =时等号成立,故圆柱的侧面积2S rh π=的最大值为22R π,此时球的表面积与圆柱的侧面积之差为222422R R R πππ-=.【答案】22R π题组六17.(★★)正方体的内切球与其外接球的体积之比为()A. B.1:3C.1:D.1:9【解析】设正方体的棱长为a ,则其内切球、外接球的半径分别为12aR =,2R =,故正方体的内切球与其外接球的体积之比3113224343R V V R ππ==.【答案】C【提炼】设正方体的棱长为a ,则其内切球的半径2a R =.18.(★★)如图,圆柱12O O 内有一个球O ,该球与圆柱的上、下底面及母线均相切.记圆柱12O O 的体积为1V ,球O 的体积为2V ,则12V V 的值是______.【解析】如图,设球的半径为R ,则213223423V R R V R ππ⋅==.【答案】3219.(2020·新课标Ⅲ卷·理·15·★★★)已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_______.【解析】如图,该圆锥内半径最大的球即圆锥的内切球,设其半径为R ,则OB OG R ==,1AB AG ==.由题意得PG =OP R =-,2PB PA AB =-=.在POB 中,222OB PB OP =+,故()224R R +=,解得22R =,即球的体积3433V R π==.【答案】2320.(★★★★)在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球.若AB BC ⊥,6AB =,8BC =,13AA =,则V 的最大值是()A.4π B.92π C.6π D.323π【解析】要解决这道题,得先搞清楚一件事,那就是最大的球到底是和棱柱的侧面相切,还是与底面相切?如图,可求得底面直角三角形的斜边10AC =,将底面Rt ABC △单独拿出来分析其内切圆半径r ,图中BP NQ r ==,故8PC r =-,即8CM PC r ==-,PN BQ r ==,故6AQ r =-,即6AM AQ r ==-,所以8614210AC CM AM r r r =+=-+-=-=,解得2r =,由123r AA >=知最大球的半径为32,体积3439322V ππ⎛⎫=⨯=⎪⎝⎭.【答案】B题组七21.(★★★)已知A,B是球O的球面上两点,90AOB∠=︒,C为该球面上的动点.若三棱锥O ABC-体积的最大值为36,则球O的表面积为()A.36πB.64πC.144πD.256π【解析】设球O的半径为R,当点C位于如图所示位置(OC⊥平面AOB)时,三棱锥O ABC-的体积最大,最大值为321136326RR R⨯⨯==,即6R=,故球O的表面积24144S Rππ==.【答案】C22.(★★★)已知三棱锥S ABC-的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA AC=,SB BC=,三棱锥S ABC-的体积为9,则球O的表面积为________.【解析】如图,由题意知,SAC△,SBC△都是以SC为斜边的等腰直角三角形,设球O的半径为R,故31129323S ABCRV R R R-=⋅⋅⋅⋅==,即3R=,故球O的表面积2436S Rππ==.【答案】36π第8讲经典模型之对棱相等知识与方法四面体ABCD 中,AB CD m ==,AC BD n ==,AD BC t ==,这种四面体叫做对棱相等四面体,可以通过构造长方体来解决这类四面体的外接球问题.如图,设长方体的长宽高分别为a 、b 、c ,则222222222a b t b c n a c m ⎧+=⎪+=⎨⎪+=⎩,三式相加可得2222222m n t a b c ++++=,而显然四面体和长方体有相同的外接球,设外接球半径为R ,则22224a b c R ++=,所以R =.典型例题【例题】四面体ABCD中,AB CD ==AC BD ==,5AD BC ==,则该四面体外接球的体积为_______.【解析】由题意,四面体ABCD是对棱相等模型3464233R V R π⇒===.【答案】3变式1三棱锥A BCD -中,6AB CD ==,5AC BD AD BC ====,则该三棱锥外接球表面积为()C.432π D.43π【解析】由题意,四面体ABCD是对棱相等模型24432R S R ππ⇒====.【答案】D 变式2A 、B 、C 、D四点在半径为2的球面上,且5AC BD ==,AD BC ==,AB CD =,则四面体ABCD 的体积为______.【解析】由题意,四面体ABCD 是对棱相等模型,设AB CD x ==,则R x ==ABCD补全为如图所示的长方体,设长方体的长、宽、高分别为a 、b 、c ,则222222413425a b b c a c ⎧+=⎪+=⎨⎪+=⎩,解得:453a b c =⎧⎪=⎨⎪=⎩,所以四面体ABCD 的体积1134543452032V =⨯⨯-⨯⨯⨯⨯⨯=.【答案】20强化训练1.(★★★)四面体ABCD中,AB CD ==AC BD ==,AD BC ==,则四面体ABCD 外接球的表面积为()A.25πB.45πC.50πD.100π【解析】由题意,四面体ABCD是对棱相等模型,2524502R S R ππ====.【答案】C2.(★★★)半径为1的球面上有不共面的A 、B 、C 、D 四点,且AB CD x ==,BC AD y ==,AC BD z ==,则222x y z ++=()A.16B.8C.4D.2【解析】由题意,四面体ABCD是对棱相等模型,22218R x y z =⇒++=【答案】B3.(★★★)四面体ABCD 中,5AB CD ==,AC BD ==,AD BC ==接球的半径为()A.2B. C.132 D.13【解析】由题意,四面体ABCD是对棱相等模型,132R =【答案】C4.(★★★)在四面体ABCD 中,2AB CD ==,AC BD AD BC ====接球的表面积为_______.【解析】由题意,四面体ABCD是对棱相等模型,2144R S R ππ==⇒==【答案】4π5.(★★★★)在三棱锥P ABC -中,2PA BC ==,PB AC =,PC AB =,且4PB PC ⋅=,则三棱锥P ABC -的外接球的表面积的最小值为________.【解析】设PB AC x ==,PC AB y ==,则4xy =,所以三棱锥P ABC -的外接球半径62R =≥,当且仅当2x y ==时取等号,所以三棱锥P ABC -的外接球的表面积的最小值为246ππ⨯=⎝⎭.【答案】6π6.(★★★★)四面体ABCD 的顶点都在球O 的表面上,4AB BC CD DA ====,AC BD ==,E 为AC 中点,过点E 作球O 的截面,则截面面积的最大值与最小值之比为()A.5:42D.5:2【解析】四面体ABCD是对棱相等模型,所以R =,将四面体ABCD 放入长方体如图,截面面积的最大值为215S R ππ==,当截面面积最小时,截面与OE 垂直,其中O 为球心,设FA a =,FB b =,FC c =,则222222216182216a a b a c b OE b r c b c =⎧⎧+=⎪⎪+=⇒=⇒=⇒=⎨⎨⎪⎪=+=⎩⎩,即截面面积的最小值为222S r ππ==,故12:5:2S S =.【答案】D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学用补形法解立体几何题
1. 正四面体补为正方体
例1. 求棱长为1的正四面体的体积。
图1
分析:常规的思路是直接用三棱锥的体积公式去求,但要首先求出此三棱锥的高,求高比较繁琐。
如果将正四面体ABCD补形为正方
体(如图1),那么此正方体的棱长为,因此,求正四面体的体
积便有了新的求解思路:
例2. 如图2,正三棱锥S-ABC的侧棱与底面边长都相等,如果E、F、G分别是SC、AB、AC的中点,那么异面直线EF与BG所成角
的余弦值等于__________。
图2
分析:常规的思路是“平移法”,取GA的中点H,连结EH、FH,则∠EFH即为所求,但解△EFH的运算量较大。
联想到正四面体可补形为正方体(如图3),相当于求与BG所成角的余弦值。
在此正方体的左边补上一个大小相同的正方体,构成一个长方体(如图4),则相当于求长方体对角线BD与侧棱所成角的余弦值。
设正方体边长为1,则长方体对角线BD的长为。
在中,
2. 三条侧棱两两垂直的三棱锥或对棱相等的三棱锥或一条侧棱垂直于底面的三棱锥都可以考虑补形为长方体
例3. 如图5,是直二面角,
,,那么AB与面β所成的角等于()
图5
A. 90°
B. 60°
C. 45°
D. 30°
分析:由α⊥β,BD⊥CD,得BD⊥α同理得:AC⊥β因此,AC ⊥CD,BD⊥CD,AC⊥BD不妨把三棱锥A-BCD补形为长方体(如图5),易得∠ABC为所求的角。
在Rt△ABC中,,选D。
例4. 如图6,四面体P-ABC中,侧棱PA、PB、PC两两垂直,O为面ABC 上一点,且O到平面PAB、平面PAC、平面PBC的距离分别为2,3,4,求OP的长度。
分析:可补一个“小”长方体(如图6),由此可得“小”长方体的长、宽、高分别为2,3,4,求OP长可转化为求该“小”长方体的对角线长,得:
3. 一般三棱锥(三棱柱)可补形为三棱柱(平行六面体)
例5. 已知三棱锥P-ABC中,PA⊥BC,PA=BC=a,PA、BC的公垂线段DE=h,求证三棱锥的体积是。
分析:以ABC为底面,PA为侧棱补形为一个三棱柱ABC-,进一步补形为平行六面体ABCD-(如图7),那么
由异面直线PA、BC的距离为h知:两底面与平面的距离为h又PA⊥BC,PA=BC=a可求出底面的面积为,所以
例6. 已知正三棱柱ABC-,若,求与所成的角。
分析:在三棱柱ABC-的下方再补上一个大小形状一样的三棱柱-EFG,构成一个新的三棱柱ABC-EFG(如图8),连结,则∠FA1C即为所求。
易知由知:∠AB1G=90°故∠FA1C=90°
4. 其它不规则几何体可视情况补形为三棱柱或平行六面体
例7. 如图9,在多面体ABCDEF中,平面ABCD是正方形,且EF∥平
面ABCD。
若EF=3,且其余的棱长都是2,求该多面体的体积。
分析:先把该不规则多面体补形为三棱柱,进一步补形为平行六面体(如图9)。
可求得点F到平面
的距离为。
所以
从以上几例可知,补形后的运算很简捷,难点就在于如何突破“补形”这一关。
规律是原几何体经补形后常常置身于长方体、正方体、三棱柱或平行六面体等规则几何体中,由整体再回过头来看局部,则可化难为易。
