清华大学材料力学习题详解范钦珊6章
清华出版社工程力学答案-第6章 拉压杆件的应力变形分析与强度设计

∑ Fx = 0 , FNAC cos 45D + FNAD = 0
解得 AD 杆轴力大小为: FNAD = 15kN(拉)
2. 强度条件
拉杆:
AAD
=
FNAD [σ ]+
=
15 ×103 120 ×10−6
= 125mm2
压杆:
AAC
=
2. 钢杆的伸长量:
ΔlBC
=
FPlBC Es As
=
60×103 × 2.1 200×109 × π ×152 ×10−6
= 3.565mm
4
3. 钢杆 C 端向下移动的距离: uC = ΔlAB + ΔlBC = 0.935 + 3.565 = 4.50 mm
6-3 螺旋压紧装置如图所示。现已知工件所受的压紧力为 F=4 kN。装置中旋紧螺栓
10
习题 6-10 图
解:1.活塞杆 受到的轴力为:
FN
=
pA
=
p
⎡π ⎢ ⎣
(
D
2− 4
d2)⎤ ⎥ ⎦
=
⎡π 2.5⎢
⎣
(5602 − 4
1002
)
⎤ ⎥ ⎦
=
596.12kN
活塞杆的正应力: σ = FN = 596.12 ×103 = 75.9MPa A杆 π ×1002 / 4
工作安全系数: n = σ s = 300 = 3.95 σ 75.9
弹性模量E和泊松比ν 。
l0
b
解:1.计算弹性模量E
h 习题 6-11 图
11
εx
=
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第1章 静力学基础

eBook工程力学(静力学与材料力学)习题详细解答(教师用书)(第1章)范钦珊 唐静静2006-12-18(a) (b) 习题1-1图第1章 静力学基础1一1 图a 和b 所示分别为正交坐标系11y Ox 与斜交坐标系22y Ox 。
试将同一个力F 分别在两中坐标系中分解和投影,比较两种情形下所得的分力与投影。
解:图(a ):11 sin cos j i F ααF F +=分力:11 cos i F αF x = , 11 sin j F αF y = 投影:αcos 1F F x = , αsin 1F F y =讨论:ϕ= 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
图(b ): 分力:22)tan sin cos (i F ϕααF F x −= , 22sin sin j F ϕαF y =投影:αcos 2F F x = , )cos(2αϕ−=F F y讨论:ϕ≠90°时,投影与分量的模不等。
1一2 试画出图a 和b 两种情形下各构件的受力图,并加以比较。
比较:解a 图与解b 图,两种情形下受力不同,二者的F R D 值大小也不同。
DR习题1-2b 解图DR习题1-2a 解2图C习题1-2a 解1图(a) (b)习题1-2图1一3 试画出图示各构件的受力图。
习题1-3图B F 习题1-3a 解2图 B习题1-3a 解1图习题1-3b 解1图F Ay Ax 习题1-3c 解图 A习题1-3b 解2图习题1-3d 解1图习题1-3e 解1图习题1-3e 解2图1-4 图a 所示为三角架结构。
荷载F 1作用在B 铰上。
AB 杆不计自重,BD 杆自重为W ,作用在杆的中点。
试画出图b 、c 、d 所示的隔离体的受力图,并加以讨论。
习题1-4图1习题1-3f 解1图F习题1-3e 解3图'A习题1-3f 解2图1O 习题1-3f 解3图F F'F 1习题1-4d 解2图F y B 21习题1-4c 解1图 AA B 1B FDx y2B 习题1-4b 解2图 1习题1-4b 解3图 F y B 2习题1-4c 解2图 F A B1B FAxF'习题1-5b 解3图E D(a-3)E B F习题1-5b 解2图习题1-5b 解1图'AxFF B习题1-5c 解图1一5 试画出图示结构中各杆的受力图。
材料力学_范钦珊_习题参考解答
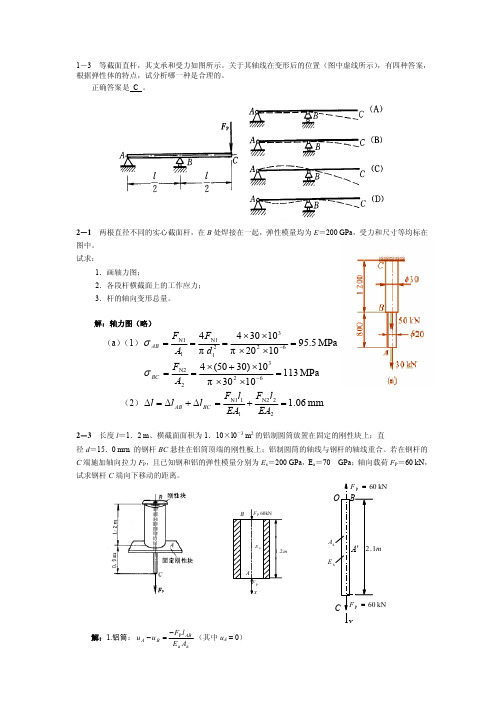
2-11 图示组合柱由钢和铸铁制成,组合柱横截面为边长为 2b 的正方形,钢和铸铁各占横截面的一 半(b×2b)。载荷 FP,通过刚性板沿铅垂方向加在组合柱上。已知钢和铸铁的弹性模量分别为 Es=196 GPa, Ei=98.0 GPa。今欲使刚性板保持水平位置,试求加力点的位置 x=?
解: ∑ M 0
( ) ( ) τmax
AB
= M xAB WPAB
= M xAB πd13
= π×
2936 70 ×10-3
3
= 43.6 MPa
16
16
BC 段:
M xBC = M e1 = 1171 N ⋅ m
( ) ( ) τmax
BC
=
M xBC WP 2
= M xBC
πd
3 2
= π×
1171 50 ×10−3
解:1. τ1max
=
Mx WP
=T WP
=T πd 3
= 3 ×103 ×16 = 70.7 MPa π× 0.063
16
∫ ∫ 2.
Mr =
ρ ⋅τdA =
A1
r
ρ
⋅
M
x
ρ ⋅ 2πρdρ
=
2πM x
⋅
r4
0 Ip
Ip
4
M r = 2πr 4 = 2πr 4 = 16r 4 = 16 × (15 )4 = 1 = 6.25%
Mx
4Ip
4 ⋅ πd 4
d4
60 16
32
3.
τ 2 max
=
Mx Wp
=
T
=75.4MPa
πd 3 ⎜⎛1 − ( 1 )4 ⎟⎞
高教范钦珊材料力学习题集_【有答案】

习题1-1图 习题1-2图习题1-3图习题1-4图习题1-5图习题1-6图 材料力学习题集第1章 引 论1-1 图示矩形截面直杆,右端固定,左端在杆的对称平面内作用有集中力偶,数值为M 。
关于固定端处横截面A -A 上的内力分布,有四种答案,根据弹性体的特点,试分析哪一种答案比较合理。
正确答案是 C 。
1-2 图示带缺口的直杆在两端承受拉力F P 作用。
关于A -A 截面上的内力分布,有四种答案,根据弹性体的特点,试判断哪一种答案是合理的。
正确答案是 D 。
1-3 图示直杆ACB 在两端A 、B 处固定。
关于其两端的约束力有四种答案。
试分析哪一种答案最合理。
正确答案是 D 。
1-4 等截面直杆在两端承受沿杆轴线的拉力F P 。
关于杆中点处截面A -A 在杆变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试判断哪一种答案是正确的。
正确答案是 D 。
1-5 图示等截面直杆在两端作用有力偶,数值为M ,力偶作用面与杆的对称面一致。
关于杆中点处截面A -A 在杆变形后的位置(对于左端,由A A '→;对于右端,由A A ''→),有四种答案,试判断哪一种答案是正确的。
正确答案是 C 。
1-6 等截面直杆,其支承和受力如图所示。
关于其轴线在变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试分析哪一种是合理的。
正确答案是 C 。
习题2-1图习题2-2图习题2-3图习题2-4图ABABC)(ql 2lM QF QF 454141第2章 杆件的内力分析2-1 平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
(A ))(d d Q x q x F =;Q d d F x M=; (B ))(d d Q x q x F -=,Q d d F x M-=; (C ))(d d Q x q x F -=,Q d d F x M=; (D ))(d d Q x q x F =,Q d d F xM-=。
(完整版)工程力学习题答案范钦珊蔡新着工程静力学与材料力学第二版

比较:图(a-1)与图(b-1)不同,因两者之1 - 3试画出图示各物体的受力图。
1 - 1图a 、b 所示,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一方 F 分别对两坐标系进行分解和投影,并比较分力与力的投影。
解:(a),图(c ):分力: 投影:=90 ° 时, (d ): F cos i 1 FX 1F y1 F sin F y1 F sinj l讨论:(b ),图F X 1 F cos投影与分力的模相等;分力是矢量, X 2投影是代数量。
F sinsin分力: j2BD(b)D(b-1)(a-3)投影: 工90°时, F X 2 F cos , 投影与分量的模不等。
讨论:1 -2试画出图a 、b 两情形下各物体的受力图,并进行比较。
F y2 F cos(F X 2 (F cos F sin tan )i 2 F y2(a)l F AyF A X1F RD 值大小也不同。
a5A■dFBFF CABB(a-1)(b-1)BC DBCBCWDAy或(b-2)(c-1)(d-1)DCABCDFt D或(d-2)(e-2)(e-1)CO iOyBFA(f-3)(e-3)IV2[fW(f-1)(c)习题1—3图F BF BF AxF AF DB FF cW(f-2)AOAF A力 F i 作用在,并加以讨论。
----------------- :B 铰上。
杆AB 不计自重,杆BD 杆自重为 W 。
试画出图1 —4图a 所示为三角架结构 b 、c 、d 所示的隔离体的受力图 A zz ” X Xzr 'i/A1rC[------------DF AxAB虾F 或(a_2)1 — 6图示刚性构件 ABC 由销钉A 和拉杆GH 支撑,在构件的点C 作用有一水平力F 。
试问如果将力 F 沿其作用线移至点 D 或点E (如图示),是否会改变销钉 A 的受力状况。
材料力学高教第二版范钦珊第6章习题答案要点

材料力学_高教第二版_范钦珊_第6章习题答案第6章杆件横截面的位移分析6-1 直径d = 36mm的钢杆ABC与铜杆CD在C处连接,杆受力如图所示。
若不考虑杆的自重,试: 1.求C、D二截面的铅垂位移;Fl2.令FP1 = 0,设AC段长度为l1,杆全长为l,杆的总伸长,写出E的表达式。
EA习题6-1图(a) (F)l(F)l解:(1)πdπdEsEs2332(FN)CDlCDπdEc4(2)EAEsAEcAEEsEclEcEs令FP6-2 承受自重和集中载荷作用的柱如图所示,其横截面积沿高度方向按材料的比重。
试作下列量的变化曲线: 1.轴力FNx(x); 2.应力; 3.位移u(x)。
解:(1),(FN变化,其中为FPFN(x)-FPx习题6-2图(a)FPFPA0FP(2)A(x)A0eFPFP— 89 —(3)A0,当。
∴,则EA0EA0EA06-3 图示连接件由两片宽20mm、厚6mm的铜片与一片同样宽厚的钢片在B处连接而成。
已知钢与铜的弹性模量分别为Es = 200GPa,Ec =105GPa,钢片与铜片之间的摩擦忽略不计。
试求E和B处的位移。
F习题6-3图解:6-4 长为1.2m、横截面面积为的铝制筒放置在固定刚块上,直径为15.0mm的钢杆BC悬挂在铝筒顶端的刚性板上,若二者轴线重合、载荷作用线与轴线一致,且已知钢和铝的弹性模量分别为kNEs = 200Gpa,Ea = 70GPa,FP = 60kN。
试求钢杆上C处位移。
Am EkN(a) 习题6-4图 (b)解:(其中uA = 0) EaAa ∴钢杆6-5 变截面圆锥杆下端B处固定,上端A处承受外力偶矩T作用,如图所示,试证明A端扭转角表达式为解:Mx = T习题6-5图6-6 试比较图示二梁的受力、内力(弯矩)、变形和位移,总结从中所得到的结论。
(a) 解:(b) wmaxFPl3 48EIFlEI— 90 —两者弯矩相同,挠曲线曲率相同,但(b)梁的最大挠度比(a)梁要大,即不相等。
理论力学课后答案范钦珊)

AyF FBCAAxF 'F CCDCF FAxF DR F FACBDAyFFDR F A CBD Ax F Ay F(a-1)第1篇 工程静力学基础第1章 受力分析概述1-1 图a 、b 所示,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一力F 分别对两坐标系进行分解和投影,并比较分力与力的投影。
习题1-1图解:(a )图(c ):11 sin cos j i F ααF F +=分力:11 cos i F αF x = , 11 sin j F αF y =投影:αcos 1F F x = , αsin 1F F y =讨论:ϕ= 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
(b )图(d ): 分力:22)cot sin cos (i F ϕααF F x -= ,22sin sin j F ϕαF y = 投影:αcos 2F F x = , )cos(2αϕ-=F F y讨论:ϕ≠90°时,投影与分量的模不等。
1-2 试画出图a 和b 两种情形下各物体的受力图,并进行比较。
习题1-2图1y F x1F 1yF α1x F yF (c ) 2x F 2y F 2y 2x 2x F 2y F F(d )比较:图(a-1)与图(b-1)不同,因两者之F R D 值大小也不同。
1-3 试画出图示各物体的受力图。
习题1-3图F AxF AyF D C B A B F或(a-2)FF AF DCA(a-1)BF AxF AAyF C(b-1)W F BD C AyF F(c-1)F F CB B F A或(b-2) αDAF ABCBFAx F AAyFDF DC αF1-4 图a 所示为三角架结构。
荷载F 1作用在铰B 上。
杆AB 不计自重,杆BC 自重为W 。
试画出b 、c 、d 所示的隔离体的受力图,并加以讨论。
习题1-4图C F CAAF (e-1) BF FCDBOOx F OyF W1O F A(f-1)FF DCABBF(e-3)'F AOOxF OyF AW(f-2)AF 1F A1O(f-3)F AF BF AAF xB 2F'yB 2F'1(c-1)F A B1B F(b-1)Dy F DDx F yB F C2(b-2)xB 2F'1F 1F'yB 2F'B(b-3)B WDxF DCyB F'(c-2)AF A D GF CH F H (a)1-5 图示刚性构件ABC 由销钉A 和拉杆D 支撑,在构件C 点作用有一水平力F 。
工程力学课后习题答案_范钦珊(合订版)

F Dx D
W
习题 1-4b 解 2 图
F'B1
B
F'B2x
F'B2 y F1
A B
F'B2x
习题 1-4c 解 1 图
F1 F'B2 y
FDx D FDy
F'B2x B
C
F'B2 y
W
F'B2 B
习题 1-4c 解 2 图
习题 1-4b 解 3 图
FA
A
B
F B1
习题 1-4d 解 1 图
F1
FDx D
图(b):
分力: Fx2 = (F cosα − F sin α tan ϕ )i2 ,
Fy2
=
F sinα sinϕ
j2
投影: Fx2 = F cosα ,
Fy2 = F cos(ϕ − α )
讨论: ϕ ≠90°时,投影与分量的模不等。
1 一 2 试画出图 a 和 b 两种情形下各构件的受力图,并加以比较。
M A = FR × AG = FR × 4.8
FR
=
20 4.8
=
25 kN 6
即
FR
= ( 5 , 10 )kN 23
作用线方程: y = 4 x + 4 3
讨论:本题由于已知数值的特殊性,实际 G 点与 E 点重合。
2-3三个小拖船拖着一条大船,如图所示。每根拖缆的拉力为5kN。试求:(1)作用于大 船上的合力的大小和方向。(2)当A船与大船轴线x的夹角θ为何值时,合力沿大船轴线方向。
(a)
(b)
习题 1-1 图
解:图(a): F = F cosα i1 + F sinα j1 分力: Fx1 = F cosα i1 , Fy1 = F sinα j1
工程力学(静力学+材料力学) 范钦珊
[ ] 等直杆: σ max
=
FN max A
≤
σ
三类强度计算问题:(1)强度校核;
(2)截面设计; (3)计算许可荷载
九、拉伸与压缩时材料的力学性能
1. 低碳钢拉伸时的力学性能 ( (12) )四 四个 个阶 强段 度指标σ
极限强度σb
局部变形阶段
屈服强度σs 弹性极限σe
2.力偶矩
M = ±F ⋅d
A
F Dd
B
C
F'
(1)代数量;
(2)正负号规定:表示力偶的转向;
+
(3)单位:力偶矩的单位与力矩相同。
-
3.力偶的性质
(1)力偶对任意点取矩都等于力偶矩,不因矩心的 改变而改变.
(2)力偶在任意坐标轴上的投影等于零.
(3)力偶没有合力,本身又不平衡,力偶只能由 力偶来平衡.
σ(MPa)
600
压缩 400 300
抗压强度>>抗拉强度
拉伸 0.05
0.10 ε
第6章 圆轴扭转
一、扭转的概念 Me
Me
主要发生扭转变形的杆
ϕ BA
轴
本章主要介绍
A
l
B
圆轴(实心或空心)扭转
二、外加扭转力偶矩与功率、转速之间的关系
Me
=
9549
P n
[N ⋅ m]
其中P为功率,单位为千瓦 (kW);n为轴的转速,单 位为转/分(r/min)。
Bh AF
F'
B M A
M = MB (F) = Fh
4
三、平面一般力系的简化结果
y F1
材料力学第6章拉压杆件的应力变形分析与强度设计

解:首先分析钢杆和铝筒的受力:钢杆BC承受拉伸,铝筒承受 压缩。C点的位移等于钢杆的伸长量与铝筒的压缩量之和:
Rigid plate
F´P B
FP AsB Ea
Aa Es
Fixed rigid plate
A
FP
l l
C F´P
第2类习题 变形计算
长为1.2m、横截面面积为1.10×10-3m2的铝制筒放置在固定刚块上,直径 为15.0mm的钢杆BC悬挂在铝筒顶端的刚性板上,若二者轴线重合、载荷作 用线与轴线一致,且已知钢和铝的弹性模量分别为Es = 200GPa,Ea = 70GPa, FP = 60kN。试求钢杆上C处位移。
50mm。求铝板与钢板横截面上的最大正应力。
steel aluminum
Rigid plate
FNs
Es As Es As Ea Aa
FP
FNa
Ea Aa Es As Ea Aa
FP
TSINGHUA UNIVERSITY
1.复合材料柱横截面上正应力与FP、b0、b1、h和Ea、Es之间的关系式
图示由铝板和钢板组成的复合材料柱,纵向截荷FP通过刚性平板沿着柱的中心线施加 在其上。试:
1.导出复合材料柱横截面上正应力与FP、b0、b1、h和Ea、Es之间的关系式; 2.已知FP = 385kN;Ea = 70GPa,Es = 200GPa;b0 = 30mm,b1 = 20mm,h =
50mm。求铝板与钢板横截面上的最大正应力。
铝板
a
FNa EaFP
Aa
b0hsE2b1haE
钢板
s A F s N sE sb 0 h E sE F P a2 b 1 hb 0 hs E E sF 2 P b 1 haE
《理论力学》(范钦珊)习题解答第2篇第4-6章

(b)υ(a)第2篇 工程运动学基础第4章 运动分析基础4-1 小环A 套在光滑的钢丝圈上运动,钢丝圈半径为R (如图所示)。
已知小环的初速度为v 0,并且在运动过程中小环的速度和加速度成定角θ,且 0 < θ <2π,试确定小环 A 的运动规律。
解:Rv a a 2nsin ==θ,θsin 2R v a =θθtan cos d d 2tR v a tv a ===,⎰⎰=t v v t R v v 02d tan 1d 0θ t v R R v t s v 00tan tan d d -==θθ⎰⎰-=t s t t v R R v s 0000d tan tan d θθtv R R R s 0tan tan ln tan -=θθθ4-2 质。
1.⎪⎩⎪⎨⎧-=-=225.1324tt y tt x , 2.⎩⎨⎧==t y t x 2cos 2sin 3解:1.由已知得 3x = 4y (1)⎩⎨⎧-=-=t y t x 3344 t v 55-=⎩⎨⎧-=-=34y x5-=a为匀减速直线运动,轨迹如图(a ),其v 、a 图像从略。
2.由已知,得 2arccos 213arcsin y x= 化简得轨迹方程:2942x y -= (2)轨迹如图(b ),其v 、a 图像从略。
4-3点作圆周运动,孤坐标的原点在O 点,顺钟向为孤坐标的正方向,运动方程为221Rt s π=,式中s 以厘米计,t 以秒计。
轨迹图形和直角坐标的关系如右图所示。
当点第一次到达y 坐标值最大的位置时,求点的加速度在x 和y 轴上的投影。
解:Rt s v π== ,R v a π== t ,222n Rt Rv a π==y 坐标值最大的位置时:R Rt s 2212ππ== ,12=∴tA习题4-1图习题4-2图习题4-3图e e -t(c)e e -t(b)R tR(a)习题4-6图R a a x π==t ,R a y 2π-=4-4 滑块A ,用绳索牵引沿水平导轨滑动,绳的另一端绕在半径为r 的鼓轮上,鼓轮以匀角速度ω转动,如图所示。
清华大学材料力学习题详解(范钦珊)第6章

6-3 几何图形尺寸如图所示(单位为 mm) 。试: 1、 确定形心主轴与水平方向的夹角; 2、 确定形心主惯性矩。
(a) 习题 6-3 图
(b)
解:1、确定形心位置 将组合图形分解为 1、2、3 三个矩形。根据反对称性,矩形 1 的形心 C1 即为组合图形 的形心。 2、建立初始坐标系,确定组合图形对于初始坐标系的惯性矩与惯性积 以 C1 为坐标原点,奖励 C1zy 坐标系,利用叠加的方法,求组合图形对于 z、y 轴的惯 性矩与惯性积
I y + Iz
−
= ( 9.422 − 8.223) ×106 = 1.199 × 106 mm 4 = 1.199 × 10−6 m 4 Iz0 = I y + Iz 2 I y + Iz + 1 2 −
(I
y
− I z ) + 4 ( I yz )
2
2
I y0 =
= ( 9.422 + 8.223) × 106 = 1.765 × 107 mm 4 = 1.765 × 10−5 m 4
—5—
(
)
I z = I z (1) + I z ( 2 ) + I z ( 3) ⎡ 20 × 703 ⎤ 10 × 1203 = + 2⎢ + 702 × 20 × 30 ⎥ 12 ⎣ 12 ⎦
(
)
= 1.44 ×106 + 2 4.667 × 104 + 6.86 × 106 = 15.17 × 106 mm 4
(
)
(
)
tanα 0 =
2 I yz I y − Iz
=
−2 × 5.88 ×106 = 1.023 ( 3.674 − 15.17 ) ×106
高教范钦珊材料力学习题集有答案完整版

高教范钦珊材料力学习题集有答案HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】习题1-2图习题1-4图材料力学习题集第1章 引 论1-1 图示矩形截面直杆,右端固定,左端在杆的对称平面内作用有集中力偶,数值为M 。
关于固定端处横截面A -A 上的内力分布,有四种答案,根据弹性体的特点,试分析哪一种答案比较合理。
图示带缺口的直杆在两端承受拉力F P 作用。
关于A -A 截面上的内力分布,有四种答案,根据弹性体的特点,试判断哪一种答案是合理的。
正确答案是 D 。
B 处固定。
关于其两端的约束力有四种答案。
试分析等截面直杆在两端承受沿杆轴线的拉力F P 。
关于杆中点处截面A -A 在杆变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试判断哪一种答案是正确的。
正确答案是 D 。
1-5 图示等截面直杆在两端作用有力偶,数值为M ,力偶作用面与杆的对称面一致。
关于杆中点处截面A -A 在杆变形后的位置(对于左端,由A A '→;对于右端,由A A ''→),有四种答案,试判断哪一种答案是正确的。
习题2-1图第2章 杆件的内力分析2-1 平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
(A ))(d d Q x q x F =;Q d d F xM=; (B ))(d d Q x q x F -=,Q d d F xM-=; (C ))(d d Q x q x F -=,Q d d F xM=; (D ))(d d Q x q xF =,Q d d F xM-=。
正确答案是 B 。
2-2 对于图示承受均布载荷q 的简支梁,其弯矩图凸凹性与哪些因素相关?试判断下列四种答案中哪几种是正确的。
习题2-3图习题2-4图 (a-1) (b-1)(a-2) (b-2)2-3 已知梁的剪力图以及a 、e 截面上的弯矩M a 和M e ,如图所示。
材料力学高教第二版范钦珊第6章习题答案要点

材料力学_高教第二版_范钦珊_第6章习题答案第6章杆件横截面的位移分析6-1 直径d = 36mm的钢杆ABC与铜杆CD在C处连接,杆受力如图所示。
若不考虑杆的自重,试: 1.求C、D二截面的铅垂位移;Fl2.令FP1 = 0,设AC段长度为l1,杆全长为l,杆的总伸长,写出E的表达式。
EA习题6-1图(a) (F)l(F)l解:(1)πdπdEsEs2332(FN)CDlCDπdEc4(2)EAEsAEcAEEsEclEcEs令FP6-2 承受自重和集中载荷作用的柱如图所示,其横截面积沿高度方向按材料的比重。
试作下列量的变化曲线: 1.轴力FNx(x); 2.应力; 3.位移u(x)。
解:(1),(FN变化,其中为FPFN(x)-FPx习题6-2图(a)FPFPA0FP(2)A(x)A0eFPFP— 89 —(3)A0,当。
∴,则EA0EA0EA06-3 图示连接件由两片宽20mm、厚6mm的铜片与一片同样宽厚的钢片在B处连接而成。
已知钢与铜的弹性模量分别为Es = 200GPa,Ec =105GPa,钢片与铜片之间的摩擦忽略不计。
试求E和B处的位移。
F习题6-3图解:6-4 长为1.2m、横截面面积为的铝制筒放置在固定刚块上,直径为15.0mm的钢杆BC悬挂在铝筒顶端的刚性板上,若二者轴线重合、载荷作用线与轴线一致,且已知钢和铝的弹性模量分别为kNEs = 200Gpa,Ea = 70GPa,FP = 60kN。
试求钢杆上C处位移。
Am EkN(a) 习题6-4图 (b)解:(其中uA = 0) EaAa ∴钢杆6-5 变截面圆锥杆下端B处固定,上端A处承受外力偶矩T作用,如图所示,试证明A端扭转角表达式为解:Mx = T习题6-5图6-6 试比较图示二梁的受力、内力(弯矩)、变形和位移,总结从中所得到的结论。
(a) 解:(b) wmaxFPl3 48EIFlEI— 90 —两者弯矩相同,挠曲线曲率相同,但(b)梁的最大挠度比(a)梁要大,即不相等。
工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第6章_圆轴扭转

该轴的扭转强度是安全的。
上一章
返回总目录
下一章
8
3
习题 6-5 图
解:1. τ 1 max =
Mx T T 3 × 10 3 × 16 = = = = 70.7 MPa WP WP π π× 0.06 3 d3 16
A1
2. M r =
∫
ρ ⋅ τdA =
∫
r
0
ρ⋅
2πM x r 4 Mx ρ ⋅ 2πρ d ρ = ⋅ 4 Ip Ip
Mr r4 r4 1 2π 2π 16r 4 15 = = = = 16 × ( ) 4 = = 6.25% 4 4 Mx 16 4I p 60 d d π 4⋅ 32 Mx T = 3. τ 2 max = =75.4MPa Wp 1 4⎞ π d3 ⎛ ⎜1 − ( ) ⎟ 16 ⎝ 2 ⎠
16 M x
3 π d1
=
16 M x
3 π D2 (1 − α 4 )
即
d1 = (1 − α 4 ) 3 D2
1
(a)
二者重量之比
W1 A1 d2 = = 2 1 2 W2 A2 D2 (1 − α )
(b)
式(a)代入式(b) ,得
W1 (1 − α 4 ) = W2 1−α2
2 3
所以,正确答案是
16 M x 3 16 × 10.53 × 10 6 = = 96.3 π [τ ] π × 60
(3)按刚度条件求轴的直径
θ=
Mx ≤ [θ ] GI P
[θ ] = 1D / 2m =
π
180 × 2 × 10 3
rad/mm
6
D≥4
32M x 32 × 10.53 × 10 6 =4 = 110.6mm Gπ [θ ] 82 × 10 3 π [θ ]
理论力学课后答案(范钦珊)

C(a-2)DR(a-3)(b-1)DR第1篇 工程静力学基础第1章 受力分析概述1-1 图a 、b 所示,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一力F 分别对两坐标系进行分解和投影,并比较分力与力的投影。
习题1-1图解:(a )图(c ):11 s i n c o s j i F ααF F +=分力:11 cos i F αF x = , 11 s i n j F αF y =投影:αcos 1F F x = , αs i n 1F F y =讨论:ϕ= 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
(b )图(d ): 分力:22)cot sin cos (i F ϕααF F x -= ,22sin sin j F ϕαF y = 投影:αcos 2F F x = , )cos(2αϕ-=F F y讨论:ϕ≠90°时,投影与分量的模不等。
1-2 试画出图a 和b习题1-2图比较:图(a-1)与图(b-1)不同,因两者之F R D 值大小也不同。
(c ) 22x(d )1-3 试画出图示各物体的受力图。
习题1-3图B或(a-2)B(a-1)(b-1)F(c-1) 或(b-2)(e-1)F(a)1-4 图a 所示为三角架结构。
荷载F 1作用在铰B 上。
杆AB 不计自重,杆BC 自重为W 。
试画出b 、c 、d 所示的隔离体的受力图,并加以讨论。
习题1-4图1-5 图示刚性构件ABC 由销钉A 和拉杆D 支撑,在构件C 点作用有一水平力F 。
试问如果将力F 沿其作用线移至D 或E (如图示),是否会改为销钉A 的受力状况。
解:由受力图1-5a ,1-5b 和1-5c 分析可知,F 从C 移至E ,A 端受力不变,这是因为力F 在自身刚体ABC 上滑移;而F 从C 移至D,则A 端受力改变,因为HG 与ABC 为不同的刚体。
1(f-1)'A(f-2)1O(f-3)F F'F 1(d-2)F yB 21(c-1)F A B1B FDx y(b-2)1(b-3)F yB 2 A A B1B F习题1-5图AxF(b-3)E D(a-3)B(b-2)(b-1)F 'CBC(c)AxF1-6 试画出图示连续梁中的AC 和CD 梁的受力图。
工程力学课后习题答案_范钦珊(合订版)

解:图(a):θ = arcsin 4 ,
5
∑ Fx = 0 ,
F sin(60° − θ ) − W sinθ = 0 , F = 1672 N
图(b):θ = 53.13° ,
∑ Fx = 0 , F cos(θ − 30°) − W sinθ = 0 , F = 217N
Fy
x
30D B
Wθ
y
5
习题 1-6 图
解:由受力图 1-6a,1-6b 和 1-6c 分析可知,F 从 C 移至 E,A 端受力不变,这是因 为力 F 在自身刚体 ABC 上滑移;而 F 从 C 移至 D,则 A 端受力改变,因为 HG 与 ABC 为 不同的刚体。
FA
A
G
FA A
FA
FG G
D
FH H
F
C
习题 1-6 解 1 图
M A = FR × AG = FR × 4.8
FR
=
20 4.8
=
25 kN 6
即
FR
= ( 5 , 10 )kN 23
作用线方程: y = 4 x + 4 3
讨论:本题由于已知数值的特殊性,实际 G 点与 E 点重合。
2-3三个小拖船拖着一条大船,如图所示。每根拖缆的拉力为5kN。试求:(1)作用于大 船上的合力的大小和方向。(2)当A船与大船轴线x的夹角θ为何值时,合力沿大船轴线方向。
= 114°35′
图(a):A 平衡: ∑ Fy = 0 , TA = 1⋅ sinϕ1
B 平衡: ∑ Fy = 0 , TB = 2 ⋅ sin ϕ 2
∵ TA = TB
10
(1)
(2) (3)
理论力学课后参考答案(范钦珊)

, ;
, ;
, (1)
取杆GE为研究对象,其受力如图(b)所示。
, ;
, ;
, ;
将FGy的值代入式(1),得:
3-18刚架的支承和载荷如图所示。已知均布载荷的集度q1=4kN/m,q2=1kN/m,求支座A、B、C三处的约束力。
解:取CE为研究对象,
解:取系统整体为研究对象,其受力如图(a)所示。
, ;
, ;
, (1)
取轮E和杆EF为研究对象,其受力如图(b)所示。
, (FT=P); (FT=P)
取杆CD为研究对象,其受力如图(c)所示。
, ;
将FAx的值代入式(1),得:
3-16滑轮支架系统如图所示。滑轮与支架ABC相连,AB和BC均为折杆,B为销钉。设滑轮上绳的拉力P=500N,不计各构件的自重。求各构件给销钉B的力。
解: ,
,
由图(a)计算结果,可推出图(b)中:FAB=10FDB=100F=80kN。
3-3起重机由固定塔AC与活动桁架BC组成,绞车D和E分别控制桁架BC和重物W的运动。桁架BC用铰链连接于点C,并由钢索AB维持其平衡。重物W=40kN悬挂在链索上,链索绕过点B的滑轮,并沿直线BC引向绞盘。长度AC=BC,不计桁架重量和滑轮摩擦。试用角 =∠ACB的函数来表示钢索AB的张力FAB以及桁架上沿直线BC的压力FBC。
解:可能是一个力,也可能平衡,但不可能是一个力偶。
因为(1),平面力系向一点简化的结果为一主矢和一主矩,而由已知是:向两点简化的主矩皆为零,即简化结果可能为( ),( )(主矢与简化中心无关),若 ,此时已是简化的最后结果:一合力 经过A点,又过B点。
工程力学(静力学与材料力学)范钦珊唐静静课后习题答案解析

= 114°35′
图(a):A 平衡: ∑ Fy = 0 , TA = 1⋅ sinϕ1
B 平衡: ∑ Fy = 0 , TB = 2 ⋅ sin ϕ 2
∵ TA = TB
10
(1)
(2) (3)
∴ sin ϕ1 = 2 sin ϕ 2 sin ϕ1 = 2 sin(114°35′ − ϕ1) ϕ1 = 84°44′
d =3
(2)
y
4 G
C
E
θ2
Dθ d −4.5 F O
FR
3
Ax
2
习题 2-2 解图
∴ F 点的坐标为(-3, 0) 合力方向如图所示,作用线过 B、F 点;
tan θ = 4 3
AG = 6 sinθ = 6 × 4 = 4.8 5
M A = FR × AG = FR × 4.8
FR
=
20 4.8
Fw
习题 1—9 图
FT1
F Fw
T2
FN
习题 1—9 解图
7
1 一 10 图示压路机的碾子可以在推力或拉力作用下滚过 100mm 高的台阶。假定力 F 都是沿着杆 AB 的方向,杆与水平面的夹角为 30°,碾子重量为 250 N。试比较这两种情形 下,碾子越过台阶所需力 F 的大小。
习题 1-10 图
(1) 油缸的受力图; (2) 活塞铆枪的受力图; (3) 铆钳的受力图。
6
习题 1-8 图
p
q FQ
p q'
FQ'
(b)
(c)
习题 1-8 解图
1—9 安置塔器的竖起过程如图所示,下端搁在基础上,C 处系以钢绳,并用绞盘拉住; 上端在 B 处系以钢缆,通过定滑轮 D 连接到卷扬机 E 上。设塔器的重量为 FW,试画出塔器 的受力图。
