光电检测论文-用干涉法测量细钢丝的微小伸长量

合集下载

细丝直径的测量

细丝直径的测量摘要：本次实验为细丝直径的测量，由于细丝利用普通的测量工具很难准确测量，误差很大，所以此次实验是利用等厚干涉原理，即由同一光源发出的平行单色光垂直入射分别经过空气劈尖所形成的空气薄膜上下表面反射后，在上表面相遇时产生的一组与棱边平行的，明暗相间，间隔相同的干涉条纹，由此来测量细丝的直径，使数据更加准确，本次试验就是利用干涉原理制作劈尖测量发丝的直径。

关键词：干涉原理空气劈尖直径光程差引言：本次实验是利用空气劈尖根据光的干涉原理测量发丝的直径，干涉和衍射是光的波动性的具体变现，利用光的等厚干涉由同一光源发出的平行光，分别经过劈尖间所形成的空气薄膜上下表面反射后产生干涉现象，形成明暗相间的条纹，使用显微镜观察明暗条纹间的距离，由此来计算发丝的直径实验原理：当两片很平的玻璃叠合在一起，并在其一端垫入细丝时，两片玻璃片之间就形成了一层空气薄膜，叫做空气劈尖。

在同一光源发出的单色平行光垂直照射下，经劈尖上下表面反射后将会产生干涉现象，在显微镜观察可发现明暗相间的干涉条纹，如图所示实验内容与步骤：实验仪器：读数显微镜 45度反射镜 2片光学玻璃钠光灯发丝1 将发丝夹在2片光学玻璃的一端，另一端直接接触，形成空气劈尖。

将劈尖放在读数显微镜的载物台上。

2 打开钠光灯，调节45度反射镜，使光线平行垂直射入充满视野，此时显微镜的视野由暗变亮。

3 调节显微镜物镜的焦距使视野内明暗相间的条纹清晰，调节显微镜目镜焦距以及叉丝的位置是否对齐和劈尖放置的位置，4 找出一段最清晰的条纹用读数显微镜读出两条明条纹或暗条纹之间的距离，同一方向转动测微鼓轮测量出5组明或暗条纹的间距。

5 使用游标卡尺测量出劈尖内细丝到较远一端的距离L6 根据公式和测量的数据计算出细丝的直径和不确定度数据处理与实验结果表达式：S=(0.212+0.220+0.216+0.218+0.220)÷5=0.2172mm L=45.2mm D=2λ•S L =2172.02.452103.5896-⨯•=0.061mmU l =0.01mmU s =t)1()(12--∑=n n S Snn i=2.78⨯0.00665=0.0185U r =22)()(SU L U S l +=00029.0=0.017U D =r U D ⨯=0.013⨯0.017=0.0221 最后结果为D=D ±U D =0.061±0.0221mm U r =DU D ⨯100%=1.61%结束语本次试验让我们学习到了光的等厚干涉原理，利用这一原理我们学会了如何测量细丝的直径，使我们受益匪浅，实验过程中我们应当多次测量，因为实验过程中存在较大误差，应该仔细认真以免读数发生错误。

利用光的干涉原理测量发丝直径

利用光的干涉原理测量发丝直径XXX（XXXX 大学 XXXX 学院 XXXX 班）摘要:利用等厚干涉可以测量微小角度、很微小长度、微小直径及检测一些光学元件的球面度、平整度、光洁度等。

本实验就是利用空气劈尖测量头发丝的直径。

关键词:等厚干涉;测量;头发丝;直径中图分类号：O436.10 引言干涉和衍射是光的波动性的具体表现。

利用等厚干涉，由同一光源发出的光，分别经过其装置所形成的空气薄膜上、下表面反射后，在上表面相遇产生的干涉。

等厚干涉是光的干涉中的重要物理实验。

本实验利用劈尖干涉法测定细丝直径是等厚干涉的具体应用。

光的干涉是两束光（频率相同、振动方向相同、相位差恒定）相互叠加时所产生的光强按空间周期性重新分布的一种光学现象。

光的等厚干涉是采用分振幅法产生的干涉，劈尖即是利用光的等厚干涉测量微小长度。

1 实验原理：将两块光学平板玻璃叠放在一起，在一端插入头发丝，则在两玻璃板间形成了空气劈尖，如图1所示：当一平行单色光垂直入射时，将会产生干涉现象，产生的干涉条纹是一系列的平行的、间隔相同的、明暗相间的条纹，如图2所示:设入射光波长为λ，两束光的光程差为 22λ+=∆e ,形成暗条纹的条件为图1 劈尖图2 干涉条纹⋅⋅⋅=+=+=∆,3,2,1,0,2)12(22k k e λλ 当k=0时，对应∆=0处为暗纹，第k 级暗纹处空气薄膜厚度为⋅⋅⋅==∆,3,2,1,0,2k k λ设从薄片左边至劈尖棱边的距离为L ，L 与左端之内的暗纹数为N ，可得薄片的厚度为2d λN =设每相邻两条暗纹间长度为l ∆，每△N 条暗纹测长度为L i ，△N ’=40 则N')/L (/d 4n 1i i 4i ∆-=∑==+L L )2 实验仪器：实验仪器名称仪器的量程仪器的精度其他参数读数显微镜50mm 0.01mm 钠光灯λ=589.3nm 劈尖头发丝刻度尺200mm 1.0mm3 实验步骤：1制作劈尖，将细丝夹在距劈尖一端的3-5mm 处，将此端夹紧，将细丝拉直与劈尖边缘平行，再将劈尖另一端适度夹紧。

基于改装的迈克尔逊干涉仪测量微小长度的三种方法

基于改装的迈克尔逊干涉仪测量微小长度的三种方法方法一：改装迈克尔逊干涉仪与扫描仪的结合这种方法结合了迈克尔逊干涉仪和扫描仪的特点，可以实现对微小长度的测量。

首先，在迈克尔逊干涉仪的其中一个反射镜上安装一个扫描仪，通过控制扫描仪的移动，可以扫描整个干涉仪的光程差。

同时，利用干涉仪的干涉图案的变化，可以测量微小长度的变化。

方法二：改装迈克尔逊干涉仪与光纤的结合这种方法利用了光纤对光信号的传输和探测功能。

首先，在迈克尔逊干涉仪的其中一个光路上连接一根光纤，通过控制光纤的长度变化，可以改变干涉仪的光程差。

同时，通过光纤连接到光电探测器，可以测量干涉仪的干涉图案的变化。

通过将光纤固定在待测物体上，可以实现对待测物体微小长度的测量。

方法三：改装迈克尔逊干涉仪与调制器的结合这种方法利用调制器对光信号进行调制，从而实现对微小长度的测量。

首先，在迈克尔逊干涉仪的一个光路上安装一个调制器，通过控制调制器的调制频率，可以改变干涉仪的光程差。

同时，通过光电探测器对干涉图案的变化进行测量。

通过将调制器固定在待测物体上，可以实现对待测物体微小长度的测量。

这三种方法都是通过改装迈克尔逊干涉仪来实现对微小长度的测量。

它们的不同之处在于采用不同的技术手段来实现对微小长度的测量，适用于不同的应用场景。

这些方法的优点是可以通过改装现有设备来实现微小长度的测量，具有成本低、实验操作方便等优点。

然而，不同方法也存在一些限制，比如测量范围有限、测量精度受限等。

因此，在选择合适的方法时需要考虑具体的应用需求和实验条件。

干涉法测微小量-实验报告

干涉法测微小量创建人：系统管理员总分：100实验目的学习掌握利用光的干涉原理检验光学元件表面集合特征的方法，用劈尖的等厚干涉测量细丝直径的方法，同时加深对光的波动性的认识。

实验仪器低频信号发生器、示波器、超声声速测定仪、频率计等实验原理1、用牛顿环测平凸透镜的曲率半径图1.牛顿环干涉条纹的形成当曲率很大的平凸透镜的凸面放在一平面玻璃上时，会产生一组以O为中心的明暗相接的同心圆环，称为牛顿环。

如图，1、2两束光的光成差22λδ+=∆，式中λ为入射光的波长，δ是空气层厚度，空气折射率1n ≈。

如果第m 个暗环处空气厚度为m δ，则有故得到：2m m λδ⋅=2、劈尖的等厚干涉测细丝直径图2.劈尖干涉条纹的形成两片叠在一起的玻璃片，在它们的一端口夹一直径待测的细丝，于是两片玻璃之间便形成一空气劈尖。

当用单色光垂直照射时，会产生干涉现象。

因为光程差相等的地方是平行两玻璃片交线的直线，所以等厚干涉条纹是一组明暗相间的、平行于交线的直线。

设入射光波长为λ，则得到第m 级暗纹处空气劈尖的的厚度2m λ⋅=d 。

由此可知，m=0时，d=0，即在两玻璃片交线处，为零级暗条纹。

如果在细丝处呈现m=N 级条纹，则待测细丝直径2λ⋅=N d 。

实验内容1、测平凸透镜的曲率半径（1）观察牛顿环1）将牛顿环仪按图3所示放置在读数显微镜镜筒和入射光调节木架的玻璃片的下方，木架上的透镜要正对着钠光灯窗口，调节玻璃片角度，使通过显微镜目镜观察时视场最亮。

图3.观测牛顿环实验装置图2）调节目镜，看清目镜视场内的十字叉丝后，使显微镜筒下降到接近玻璃片，然后缓慢上升，直到观察到干涉条纹，再微调玻璃片角度及显微镜，使条纹更清楚。

（2）测牛顿环直径1）使显微镜的十字叉丝交点与牛顿环中心重合，并使水平方向的叉丝与标尺平行（与显微镜筒移动方向平行）。

2）转动显微镜测微鼓轮，使显微镜沿一个方向移动，同时数出十字叉丝竖丝移过的暗环数，直到竖丝与第35环相切为止。

干涉法测微小量.

实验题目：干预法测细小量实验目的：学习、掌握利用光的干预原理查验光学元件表面会合特点的方法，用劈尖的等厚干预丈量细丝直径的方法，同时加深对光的颠簸性的认识。

实验原理： 1、用牛顿环测平凸面镜的曲率半径当曲率很大的平凸面镜的凸面放在一平面玻璃上时，会产生一组以O 为中心的明暗相间的齐心圆环，称为牛顿环。

如图， 1、2 两束光的光程差为2，式中λ为入射光2的波长，δ是空气层厚度，空气折射率n1。

假如第m个暗环处空气厚度为δm，则有2m(2m1),m0,1,2,3...22故获得：m m。

2利用几何关系有 R2r m2( R m ) 2，并依据m R ，得到m rm2，联系以上两式，有2 Rr m2mR换成直径，并考虑第m+n 个环和第m个环，有 D m2n4(m n )R ，D m24mR ，故D m2n D m2R4n那么丈量出 D m+n和 D m就能够依据这个表达式获得R。

2、劈尖的等厚干预测细丝直径两片叠在一同的玻璃片，在它们的一端夹向来径待测的细丝，于是两玻璃片之间形成一空气劈尖。

当用单色光垂直照耀时，会产生干预现象。

因为程差相等的地方是平行于两玻璃片交线的直线，因此等厚干预条纹是一组明暗相间、平行于交线的直线。

设入射光波为λ，则得第 m 级暗纹处空气劈尖的厚度d m。

2由此可知， m=0 时， d=0 ，即在两玻璃片交线处，为零级暗条纹。

假如在细丝处体现 m=N 级条纹，则待测细丝直径d N。

23、利用干预条纹查验光学表面面形实验内容：1．测平凸面镜的曲率半径（ 1）察牛1）将牛按 7.2.1-5 所示搁置在数微筒和入射光木架的玻璃片的下方，木架上的透要正着光灯窗口，玻璃片角度，使通微目察最亮。

2）目，看清目的十字叉后，使微筒降落到靠近玻璃片，而后慢上涨，直到察到干预条，再微玻璃片角度及微，使条更清楚。

（ 2）牛直径1）使微的十字叉交点与牛中心重合，并使水平方向的叉与尺平行（与微筒移方向平行）。

光电检测技术论文

光电检测技术的特点、应用现状及发展前景【摘要】光电检测技术是光电信息技术的主要技术之一，是利用光电传感器实现各类检测，即将被测量转换成光通量，再将光通量转换成电量。

随着现代科学技术以及复杂自动控制系统和信息处理技术的提高，它以测量精度高、速度快、非接触、频宽与信息容量极大、信息效率极高及自动化程度高等突出特点发展十分迅速，应用现状非常好，并且有着很好的发展前景。

【关键词】光电检测，光电传感器，特点，应用现状，发展前景引言：随着现代科学技术以及复杂自动控制系统和信息处理与技术的提高，光电检测技术作为一门研究光与物质相互作用发展起来的新兴学科，已成为现代信息科学的一个极为重要的组成部分。

光电检测技术具有测量精度高、速度快、非接触、频宽与信息容量极大、信息效率极高、以及自动化程度高等突出特点，令其发展十分迅速，并推动着信息科学技术的发展。

它将光学技术与现代电子技术相结合，广泛应用于工业、农业、家庭、医学、军事和空间科学技术等领域。

本文从光电检测技术本身特点出发，简述它在工业、资源、环境测温等领域的应用现状及其发展前景。

1，光电检测技术1.1光电检测技术的原理光电检测系统的工作原理图如下图所示：光电检测系统原理图1.2光电检测技术的特点光电检测技术将光学技术与电子技术相结合实现对各种量的检测，具有如下特点：①高精度。

光电检测的精度是各种检测技术中精度最高的一种，如用激光干涉法检测长度的精度可达0.05um/m;光栅莫尔条纹法测角可达0.04"；用激光测距法测量地球与月球之间距离的分辨率可达1m。

②高速度。

光电检测以光为媒介，而光是各种物质中传播速度最快的，无疑用光学的方法获取和传递信息是最快的。

③远距离、大量程。

光是最便于远距离传播的介质，尤其适用于遥控和遥测，如武器制导、光电跟踪、电视遥测等。

④非接触检测。

光照到被测物体上可以认为是没有测量力的，因此也无摩擦，可以实现动态测量，是各种检测方法中效率最高的一种。

干涉法测微小量实验报告

干涉法测微小量创建人:系统管理员总分:100实验目的学习掌握利用光的干涉原理检验光学元件表面集合特征的方法,用劈尖的等厚干涉测量细丝直径的方法,同时加深对光的波动性的认识。

实验仪器低频信号发生器、示波器、超声声速测定仪、频率计等实验原理1、用牛顿环测平凸透镜的曲率半径图1、牛顿环干涉条纹的形成当曲率很大的平凸透镜的凸面放在一平面玻璃上时,会产生一组以O为中心的明暗相接的同心圆环,称为牛顿环。

如图,1、2两束光的光成差22λδ+=∆,式中λ为入射光的波长,δ就是空气层厚度,空气折射率1n ≈。

如果第m 个暗环处空气厚度为m δ,则有故得到:2m m λδ⋅=2、劈尖的等厚干涉测细丝直径图2、劈尖干涉条纹的形成两片叠在一起的玻璃片,在它们的一端口夹一直径待测的细丝,于就是两片玻璃之间便形成一空气劈尖。

当用单色光垂直照射时,会产生干涉现象。

因为光程差相等的地方就是平行两玻璃片交线的直线,所以等厚干涉条纹就是一组明暗相间的、平行于交线的直线。

设入射光波长为λ,则得到第m 级暗纹处空气劈尖的的厚度2m λ⋅=d 。

由此可知,m=0时,d=0,即在两玻璃片交线处,为零级暗条纹。

如果在细丝处呈现m=N 级条纹,则待测细丝直径2λ⋅=N d 。

实验内容1、测平凸透镜的曲率半径(1)观察牛顿环1) 将牛顿环仪按图3所示放置在读数显微镜镜筒与入射光调节木架的玻璃片的下方,木架上的透镜要正对着钠光灯窗口,调节玻璃片角度,使通过显微镜目镜观察时视场最亮。

图3、观测牛顿环实验装置图2) 调节目镜,瞧清目镜视场内的十字叉丝后,使显微镜筒下降到接近玻璃片,然后缓慢上升,直到观察到干涉条纹,再微调玻璃片角度及显微镜,使条纹更清楚。

(2)测牛顿环直径1) 使显微镜的十字叉丝交点与牛顿环中心重合,并使水平方向的叉丝与标尺平行(与显微镜筒移动方向平行)。

2) 转动显微镜测微鼓轮,使显微镜沿一个方向移动,同时数出十字叉丝竖丝移过的暗环数,直到竖丝与第35环相切为止。

干涉法测微小量-实验报告

如图，1、2两束光的光成差22λδ+=∆，式中λ为入射光的波长，δ是空气层厚度，空气折射率1n ≈。

当用单色光垂直照射时，会产生干涉现象。

因为光程差相等的地方是平行两玻璃片交线的直线，所以等厚干涉条纹是一组明暗相间的、平行于交线的直线。

设入射光波长为λ，则得到第m 级暗纹处空气劈尖的的厚度2m λ⋅=d 。

由此可知，m=0时，d=0，即在两玻璃片交线处，为零级暗条纹。

如果在细丝处呈现m=N 级条纹，则待测细丝直径2λ⋅=N d 。

（2）测牛顿环直径1）使显微镜的十字叉丝交点与牛顿环中心重合，并使水平方向的叉丝与标尺平行（与显微镜筒移动方向平行）。

2）转动显微镜测微鼓轮，使显微镜沿一个方向移动，同时数出十字叉丝竖丝移过的暗环数，直到竖丝与第35环相切为止。

光电测量系统设计(测钢丝长度)

光电测量系统设计——设计题目：用干涉法测量钢丝钢丝热伸长度班级：光通2姓名：学号：指导教师：***用干涉法测量钢丝热伸长度设计目的1、了解干涉产生的原理、方法，了解个部分的作用，并能综合运用2、灵活运用所学光学知识，掌握光电测量系统中的光路部分的设计原理及方法3、根据所学知识，将干涉测量运用于设计一个光电测量系统中的光路部分一、迈克尔干涉仪测量原理迈克尔逊干涉仪的结构简图所示，G 2是一面镀上半透半反膜，M 1、M 2为平面反射镜，M 1是固定的，M 2和精密丝相连，使其可前后移动， M 1和M 2后各有几个小螺丝可调节其方位。

当M 2和M 1’严格平行时，M 2移动,表现为等倾干涉的圆环形条纹不断从中心“吐出”或向中心“消失”。

两平面镜之间的“空气间隙”距离增大时，中心就会“吐出”一个个条纹；反之则“吞进”一个个条纹。

M 2和M 1’不严格平行时，则表现为等厚干涉条纹，M 2移动时，条纹不断移过视场中某一标记位置，M 2平移距离 d 与条纹移动数 N 的关系满足2λN d =。

经M 2反射的光三次穿过分光板，而经M 1反射的光只通过分光板一次.补偿板就是为了消除这种不对称而设置的.在使用单色光源时，补偿板并非必要，可以利用空气光程来补偿；但在复色光源时，因玻璃和空气的色散不同，补偿板则是不可缺少的。

二、设计原理1、干涉测量原理干涉测量技术是一波长为单位的非接触精密测量方法，具有极其广泛的应用范围，其精度可达以上，且有很高的测量重复性，该方法可实现对长度、距离、位移、振动和运动速度等物理量的高精度非接触测量。

干涉测量基于光波叠加原理，在干涉场中产生明暗交替上网干涉条纹，通过分析条纹的运动状况来获取被测量的相关信息。

将相干光源出射的光束分为两束，一束投射至参考反射镜，并将其反射光作为参考光；另一束投射至被测反射镜，并用反射光作为检测光；再用一分光棱镜使参考光与检测光重合，产生干涉，所形成的干涉场的光强分布为：),(cos ),(),(2),(),(),(y x y x y x y x y x y x I I I I I t r t r Φ++=其中：),(y x I r ，),(y x I t 分别为参考光和检测光的强度；),(y x Φ为参考光和检测光之间的位相差。

干涉法测量微小量

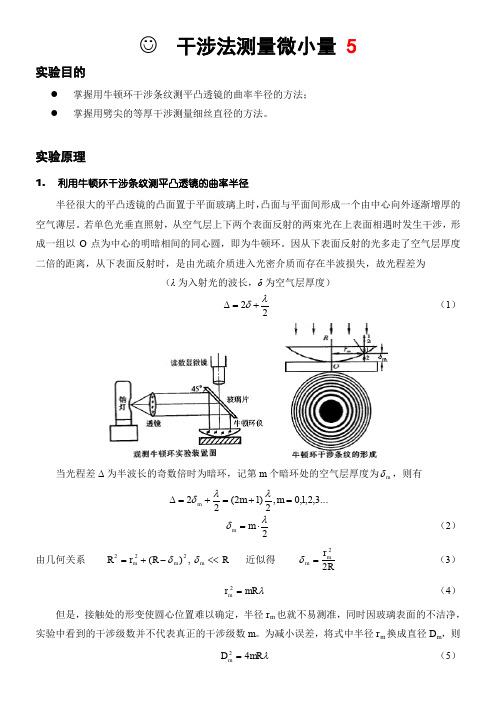
☺ 干涉法测量微小量 5实验目的● 掌握用牛顿环干涉条纹测平凸透镜的曲率半径的方法； ● 掌握用劈尖的等厚干涉测量细丝直径的方法。

实验原理1. 利用牛顿环干涉条纹测平凸透镜的曲率半径半径很大的平凸透镜的凸面置于平面玻璃上时，凸面与平面间形成一个由中心向外逐渐增厚的空气薄层。

若单色光垂直照射，从空气层上下两个表面反射的两束光在上表面相遇时发生干涉，形成一组以O 点为中心的明暗相间的同心圆，即为牛顿环。

因从下表面反射的光多走了空气层厚度二倍的距离，从下表面反射时，是由光疏介质进入光密介质而存在半波损失，故光程差为（λ为入射光的波长，δ为空气层厚度）22λδ+=∆ （1）当光程差Δ为半波长的奇数倍时为暗环，记第m 个暗环处的空气层厚度为m δ，则有...3,2,1,0,2)12(22=+=+=∆m m m λλδ2λδ⋅=m m （2）由几何关系222)(m mR r R δ-+=, R m <<δ近似得 Rr mm 22=δ（3）λmR r m =2 （4）但是，接触处的形变使圆心位置难以确定，半径r m 也就不易测准，同时因玻璃表面的不洁净，实验中看到的干涉级数并不代表真正的干涉级数m 。

为减小误差，将式中半径r m 换成直径D m ，则λmR D m 42= （5）对第m+n 个暗环有λR n m D n m )(42+=+ （6）故（7）所以，我们只需测D m 和D m+n ，就可利用上式计算曲率半径R 。

2. 劈尖的等厚干涉测细丝直径两玻璃片和细丝叠在一起如图所示，形成空气劈尖。

当用单色光垂直照射时，会产生一组明暗相间、平行于细丝的干涉条纹。

根据前面讨论知，在两玻璃片交线处，为零级暗条纹，第m 级暗纹处空气劈尖的厚度2λmd = （8）如果在细丝处呈现N 级条纹，则待测细丝直径实验室常用劈尖盒。

使用时切勿倒置木盒或将玻璃片倒出，以免细丝位置变动。

实验仪器单色光源，显微镜，牛顿环仪，待测细丝，平凸透镜。

光杠杆镜尺法测定钢丝的杨氏弹性模量微小长度变化的测量

2021/6/9
背景介绍
杨氏模量(Young‘s modulus)是表征在弹性限度内物质材料抗拉或抗压的物理量，它是沿纵向的弹性模量。1807年因英国医生兼物理学家托马斯杨(Thomas Young, 1773-1829) 所得到的结果而命名。
根据胡克定律，在物体的弹性限度内，应力与应变成正比，比值被称为材料的杨氏模量，它是表征材料性质的一个物理,杨氏模量的大小标志了材料的刚性。
最后结果
YYY
参考实验结果 Y=2.00×1011N/m2
2021/6/9
谢谢！
2021/6/9
2021/6/9
实验目的
●学习利用光杠杆测定长度量微小变化的方法。
●学习用逐差法处理实验数据。
2021/6/9
原理和方法
一根钢丝所受的应力 F 和应变 L成正
比，可以写成
S
L

F（1Y）L SL
比例系数E 称为钢丝的杨氏弹性模量，量纲是N•m-2(Pa)。
2021/6/9
在实验中，F 等于砝码所受的重力；
•加上初始负载（两块砝码），拉直钢丝， •逐次加上一定质量的砝码，再逐次减去砝
码，记录 xi、xi’
•多次测量钢丝直径d (6~10次)，单次测量
B、b、L。
•经过数据处理，最后得到 Y±σY。
2021/6/9
数据处理及误差分析
数据处理：逐差法
实验中单个砝码m=1Kg。如果采用多次测量，一次加1块，加7次，得到数据x0.x1.x2······x7，取平均后得到
砝码盘地面
2021/6/9
直尺
物镜调节旋纽准星
移动望远镜支架，在望远镜上侧能看到平面镜中直尺。

(整理)用光杠杆镜尺法测定钢丝的杨氏弹性模量

用光杠杆镜尺法测定钢丝的杨氏弹性模量贾肖婵实验内容测定钢丝的杨氏弹性模量教学要求1．掌握用光杠杆测量微小长度变化的方法，了解其应用。

2．学习用逐差法处理实验数据。

实验器材杨氏模量测定仪，望远镜标尺架，光杠杆，标准砝码（1kg ），钢卷尺，游标卡尺，螺旋测微计，重垂等。

力作用于物体所引起的效果之一是使受力物体发生形变，物体的形变可分为弹性形变和塑性形变。

固体材料的弹性形变又可分为纵向、切变、扭转、弯曲，对于纵向弹性形变可以引入杨氏模量来描述材料抵抗形变的能力。

杨氏模量是表征固体材料性质的一个重要的物理量，是工程设计上选用材料时常需涉及的重要参数之一，一般只与材料的性质和温度有关，与其几何形状无关。

实验测定杨氏模量的方法很多，如拉伸法、弯曲法和振动法（前两种方法可称为静态法，后一种可称为动态法）。

本实验是用静态拉伸法测定金属丝的杨氏模量。

在研究的纵向弹性形变时，根据杨氏弹性模量的特点，为了计算材料内部各点应力和应变的方便，可将材料做成柱状。

因此，本实验中的样品为一根粗细均匀的细钢丝。

为了测量细钢丝的微小长度变化，实验中使用了光杠杆放大法，利用光杠杆不仅可以测量微小长度变化，也可测量微小角度变化和形状变化。

由于光杠杆放大法具有稳定性好、简单便宜、受环境干扰小等特点，在许多生产和科研领域得到广泛应用。

本实验可以在实验方法，数据处理，长度测量等方面使学员得到基本的训练。

实验原理一、杨氏弹性模量设细钢丝的原长L ，横截面积为S ，沿长度方向施力F 后，其长度改变ΔL ，则细钢丝上各点的应力为F/S ，应变为ΔL/L 。

根据胡克定律，在弹性限度内有S F ＝LL E ∆∙ （3-１）则E ＝LL ∆S F （3-２）比例系数E 即为杨氏弹性模量。

在国际单位制中其单位为牛顿／米２，记为Ｎ·Ｍ－２。

通过分析知，作用力可由实验中钢丝下端所挂砝码的重量来确定，原长（起始状态）可由米尺测量，钢丝的横截面积S ，可先用螺旋测微计测出钢丝直径d 后算出S ＝42d π （3-３）现在的问题是如何测量ΔL ？用米尺准确度太低，用游标卡尺和螺旋测微计呢，测量范围又不够（在此实验中，当L ≈１ｍ时，F 每变化１ｋg 相应的ΔL 约为０．３ｍｍ）。

关于微小长度测量的研究

关于微小长度测量的研究诸霖（05A12301）（东南大学土木工程学院，南京市 211189）摘要：实验中，许多微小长度不易直接测量，所以在实际操作过程中，我们往往用一些特殊的装置将此类微小长度放大为可测的长度。

本文主要介绍了用光杠杆放大法测量微小长度变化量的方法。

关键词：微小长度；光杠杆；误差Researches on the changes of small lengthZhu Lin(05A12301)(Civil Engineering,Southeast University,Nanjing 211189)Abstract:In the experiment, many small length can not be measured directly, so in the actual operation process, we often use some special device such small length amplification as measurable length. This paper mainly introduces the method of amplification method for the measurement of tiny change in length with the optical lever.Key words:Small length;light bar;deviation0、引言实验中，往往会遇到微小长度的测量。

此类长度不易直接测量，需要通过特殊方法间接测量。

下面介绍用非接触式的长度放大测量方法——光杠杆测量法的测量原理及仪器设备，其次分析在这种测量方法下的实验操作注意事项以减小误差。

另外，不同的实验需要对不同的方法进行比较选择，从而得到最优方案。

作者简介：诸霖，女，1994-8-14，江苏无锡，东南大学土木工程学院邮箱：953666416@1、实验原理基本原理如下图：如图所示的架子上面悬挂有一带有重物的钢丝，一号是固定在钢丝上面的一个小块，2号是一个平面镜，平面镜下端支放在承物台上。

干涉法测微小量

干涉法测微小量
激光干涉法是一种用来测量微小量的精密仪器，它通过使用单边激光来实现定位和测量。

它基于物体反射激光束照射在一个固定的参考点，通过物体移动而改变激光束在参考点的位置，得出物体位移量的原理。

其原理是，一束激光从一个发射机发射出来，照射在物体的表面上，反射回另外一个探测机收集，由于物体位置的移动而导致反射激光束和发射激光之间的差异，从这个差异来检测物体位移量，所获得的信息通过传感器进行数据处理，从而实现。

激光干涉法测量优势很多，它不仅具有极高的精度，而且测量时间远快于传统的测量技术，可以准确测量微小量，范围可以达到纳米级，从而使激光干涉法变得非常灵活，可以满足各种精细的测量场合。

激光干涉法的应用也很盛行，它广泛应用于测量微小量，在电子封装、光机械行业以及航空航天等行业有着大量应用。

同时，它也广泛用于衡量望远镜、测量物体大小误差和扫描定位等测量工作中。

因此，激光干涉法在测量微小量上有着很大的作用。

激光干涉法的使用也很容易，几乎可以在任何空间中实现，仪器配件紧凑耐用，高精度，而且配置简单，可以满足客户的多种需求。

此外，本法还可以用于测量极低温和高强度环境，具有良好的适应性。

总之，激光干涉法是一种能实现微小量测量的精密仪器，它具有高精度，配置简单，环境适应性强等优势，在微小量测量中有着独特的优势和作用。

通过不断研发和改进，激光干涉法可以帮助我们更准确的测量微小量，发挥更大的价值。

干涉法测微小量

《干涉法测微小量》实验报告姓名学号学院专业班级一．实验目的学习掌握利用光的干涉原理检验光学元件表面集合特征的方法，用劈尖的等厚干涉测量细丝直径的方法，同时加深对光的波动性的认识二．实验仪器读数显微镜、钠光灯及电源、牛顿环仪、劈尖等三、实验原理1、用牛顿环测平凸透镜的曲率半径详见实验指导书2、劈尖的等厚干涉测细丝直径详见实验指导书四、实验步骤1. 观察牛顿环。

(1) 将牛顿环仪放置在读数显微镜镜筒和入射光调节架下方，调节玻璃片的角度，使通过显微镜目镜观察时视场最亮。

(2) 调节目镜，看清目镜视场的十字叉丝后，使显微镜镜筒下降到接近牛顿环仪然后缓慢上升，直到观察到干涉条纹，再微调玻璃片角度和显微镜，使条纹清晰。

2. 测牛顿环半径。

(1) 使显微镜十字叉丝交点和牛顿环中心重合，并使水平方向的叉丝和标尺平行（与显微镜移动方向平行）。

(2) 转动显微镜微调鼓轮，使显微镜沿一个方向移动，同时数出十字叉丝竖丝移过的暗环数，直到竖丝与第 45 环相切为止。

记录标尺读数。

(3) 反向转动鼓轮，当竖丝与第 40 环相切时，记录读数显微镜上的位置读数，然后继续转动鼓轮，使竖丝依次与第 35、30、25、20、15、10、5 环相切，顺次记下读数。

(4) 继续转动鼓轮,越过干涉圆环中心，记下竖丝依次与另一边的 5、10、15、20、25、30、35、40 环相切时的读数。

3．利用逐差法处理得到的数据，得到牛顿环半径 R。

4. 观察劈尖干涉条纹。

(1) 将劈尖放置在读数显微镜镜筒和入射光调节架下方，调节玻璃片的角度，使通过显微镜目镜观察时视场最亮。

(2) 调节目镜，看清目镜视场的十字叉丝后，使显微镜镜筒下降到接近劈尖然后缓慢上升，直到观察到干涉条纹，再微调玻璃片角度和显微镜，使条纹清晰。

5. 测量。

(1) 使显微镜的十字叉丝交点与劈尖中心重合，并使其与显微镜镜筒移动方向平行。

(2) 在劈尖玻璃面的三个不同部分，测出 20 条暗纹的总长度，测 3 个求平均值。

光电检测论文-用干涉法测量细钢丝的微小伸长量

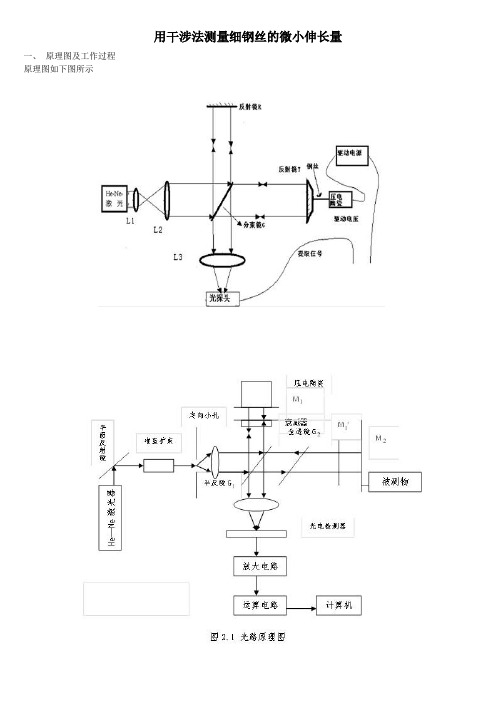
用干涉法测量细钢丝的微小伸长量一、原理图及工作过程原理图如下图所示工作过程简介：激光通过迈克尔逊干涉仪产生干涉条纹——明暗相间的同心圆环，细钢丝长度的改变引起光程差的变化，从而导致干涉条纹变化。

利用光电检测器将光信号转换为电信号，通过计数器测出干涉条纹的“吞吐”数目，再通过运算电路（或者计算机）便可以计算出钢丝长度的微小变化。

二、该光电检测系统设计思路1、光源要产生干涉现象，必须使用相干光。

激光具有单色性好，发散角小，亮度高，时间和空间相干性好等特点。

He-Ne 激光器是常用的激光器，并且满足设计要求，所以选用此激光器作为该光电检测系统的光源。

2、光学变换干涉测量技术是以波长为单位的非接触精密测量方法，具有极其广泛的应用范围，测量精度高，且有很高的测量重复性，该方法可实现对长度、距离、位移、振动和运动速度等物理量的高精度非接触测量。

迈克尔逊干涉仪是常用的利用干涉现象测量长度的实验仪器，通过该仪器实现将非光物理量转变为光学量，并且实现了光学量的量化。

3、光电探测器该设计采用雪崩光电探测器，雪崩光电探测器实现光学量到电信号的转换，使量化后的光信号转化成脉冲数字信号。

光伏探测器具有暗电流小、噪声低、响应速度快、光电特性的线性好、受温度的影响小等特点。

另外．雪崩光电二板管还有很大的内增益作用，不仅灵敏度高，还可以通过较大的电流。

4、信号处理干涉条纹向内收缩或向外发散一个条纹，对应的光程差为2λ。

由于钢丝的位移使条纹的变化，故2λN y =（式中y 为压电陶瓷位移，N 为干涉条纹数目，λ为选定激光波长）。

光源发出的光经迈克尔逊干涉仪量化后送给光电器件转换成脉冲数字信号，再送给数字电路处理或送给计算机进行处理或运算。

长度信息量L 经光学量化后形成n 个条纹信号，量化后的长度信息L 为 L = qn ，其中q=2λ。

三、雪崩二极管的工作原理及性能特点1、工作原理：雪崩光电二极管为具有内增益的一种光生伏特器件。

用伸长法和电热法测微小长度及光杠杆的扩展应用

用伸长法和电热法测微小长度及光杠杆的扩展应用作者：苏宝玺车沛强陈小君来源：《科技创新导报》2011年第10期摘要:随着科技的发展,微小长度的测量已经越来越先进,手段也越来越多。

本实验采用拉伸法和电热法测量微小长度的变化,从测量方法、仪器调整到数据处理在大学物理实验的公共物理实验都很具有代表性,是力、热学试验中很典型的实验。

关键词:伸长法电热法光杠杆系统平面反射原理扩展与应用中图分类号:O433 文献标识码:A 文章编号:1674-098X(2011)04(a)-0114-02杨氏模量和金属线胀系数是描述固体材料弹性形变能力的重要物理量,是选择机械零件材料的依据,是工程技术设计中常用的参数。

本实验中涉及的微小长度变化量的测量方法——光杠杆放大测量法,其原理广泛地应用在许多测量技术中,光杠杆还被许多高灵敏度的测量仪器(如灵敏电流计、冲击电流计等)所采用,并且在精密仪器加工、建筑、桥梁的设计中有着广泛的应用。

1 杨氏模量的测量原理在外力作用下,固体发生的形状变化叫形变,形变分弹性形变和范性形变。

本实验测量钢丝杨氏弹性模量是在钢丝的弹性范围内进行的,属弹性形变的问题,最简单的弹性形变是在弹性限度内棒状物受外力后的伸长和缩短。

设一根长度为L、横截面积为S的钢丝,沿长度方向施加外力F后,钢丝伸长ΔL。

根据胡克定律:胁变(ΔL/L)与胁强(F/S)成正比,胁变前比例系数是杨氏弹性模量即(1)Y就是该钢丝的杨氏弹性模量,单位是NM-2。

由式(1-1)可知,只要测量出等号右端的F、L、S、ΔL等量,即可测定杨氏弹性模量Y。

显然,F、L、S可用一般量具测出,而钢丝的微小伸长量ΔL,使用一般的量具进行精确的测量是困难的,这是因为ΔL很小,当L为1m,S为1mm2时,每牛顿力的伸长量ΔL约为5×10-3mm),不能用直尺测量,也不便于用大型卡尺和千分尺测量,所以,通常采用光杠杆法。

杠杆的放大原理是大家熟知的,若利用光的性质,采用适当的装置,使之起到同样放大作用,这种装置就称为光杠杆(图1)。

干涉法测量微小量

干预法测细小量（本文内容选自高等教育第一版社《大学物理实验》）光的干预现象表示了光的颠簸性质，干预现象在科学研究与计量技术中有着宽泛的应用。

在干预现象中，无论是何种干预，相邻干预条纹的光程差的改变都等于相关光的波长，可见光的波长固然很小，但干预条纹间的距离或干预条纹的数量倒是能够计量的。

所以，经过对干预条纹数量或条纹挪动数量的计量，可获得以光的波长为单位的光程差。

利用光的等厚干预现象能够丈量光的波长，查验表面的平面度、球面度、光洁度，精准的丈量长度、角度，丈量细小形变以及研究工作内应力的散布等。

经过本次实验，学习、掌握利用光的干预原理查验光学元件表面几何特点的方法，用劈尖的等厚干预丈量细丝直径的方法，同时加深对光的颠簸性的认识。

实验原理1．用牛顿环测平凸面镜的曲率半径当曲率半径很大的平凸面镜的凸面放在一平面玻璃上时，见图之间形成一个从中心 O 向周围渐渐增厚的空气层。

当单色光垂直照耀下来时，从空气层上下两个表面反射的光束 1 和光束 2 在上表面相遇时产生干预。

因为光程差相等的地方是以O 点为中心的齐心圆，所以等厚干预条纹也是一组以O 点为中心的明暗相间的齐心圆，称为牛顿环。

因为从下表面反射的光多走了二倍空气层厚度的距离，以及从下表面反射时，是从光疏介质到光密介质而存在半波损失，故1、 2 两束光的光程差为2（ 1）2，在透镜的凸面与平面式中λ为入射光的波长，δ是空气层厚度，空气折射率 n1。

当程差为半波长的奇数倍时为暗环，若第m 个暗环处的空气层厚度为m ，则有2 m( 2m1), m0,1,2,3...22mm（2）2由图 7.2.1-1 中的几何关系R2r m2(R m )2，以及一般空气层厚度远小于所使用的平凸面镜的曲率半径 R，即m R ，可得m r m2（ 3）2R式中 r m是第m 个暗环的半径。

由式（）和式（）可得23r m2mR（ 4）可见，我们若测得第 m 个暗环的半径 r m即可由已知λ求，或许由已知R 求λ了。