流体力学讲义——上海交通大学
上海交通大学流体力学

: (
我们取一个四面体流体微元(如图)建立它的运动方程(以 x 方向为例)
。
四面体微元体积
1
=
6
它在坐标平面上的三个三角形的面积构成斜切面矢量面积 = 在 x,y,z 方向上的投影
= = ( , , ) = ( , , ) = (
2
∬ 2 sin
=0 =0
+ 2 + 2 + 2
积分计算后可以得到
1
̅̅̅
= ( + + )
3
.
在一个相对平衡的流场中流体单元没有变形速度,根据流体的力学定义,它内部的任何切面
上切因力为零,应力张量矩阵为
同性的,它在一个空间点上的值与切面方向无关。实验测量证实了这个结论,这个法向应力
的大小就是热力学压强 p。由于它的作用方向与一个流体微元表面的的外法向方向相反,我
们有
= = = −
这个结论不仅对相对或绝对平衡的流体有效,因为在理想流体粘性切引力为零,它当然在运
动的理想流体中也是有效的。
张量为压强项,偏引力张量为粘性应力项。笛卡尔坐标系中:
(
− 0
)=( 0 −
0
0
0
0 )+(
−
)
或者用下标的形式
= − +
这个关系的张量表达式为: = − + , 为单位张量,笛卡尔坐标系中表达为对角线元素
为 1,其余为 0 的矩阵。下标表达式中 称为克罗内克符号,在 i=j 时为 1, ≠ 时为 0。
大学物理:第五章 流体力学 (Fluid Mechanics)

Aneurysm(动脉瘤)
若处动脉的半径增大N倍 血液流速就缩小N2倍 病灶处的压强大幅度上降 由于该处血管壁薄,使血 管容易破裂。
上海交通大学 物理系
Atherosclerosis(动脉粥样硬化)
动脉病变从内膜开始。一 般先有脂质和复合糖类积 聚、出血及血栓形成,纤 维组织增生及钙质沉着, 并有动脉中层的逐渐蜕变 和钙化,病变常累及弹性 及大中等肌性动脉,
?
? hB=0.5m
P0
?
0
1 2
v
2 c
ghc
Pc
1 2
v
2 A
ghA
PA
vc 2ghA 6 m / s
B,C点
1 2
v
2 c
ghc
Pc
1 2
v
2 B
ghB
PB
SBvB SCvC
PB P0 0.85g
PB P0 ghD
hD 0.85m
上海交通大学 物理系
一柱形容器,高1m、截面积为5x10-2 m2,储满水 ,在容器底部有一面积为2x10-4 m2 的水龙头,问 使容器中的水流尽需多少时间?
度变小,压强变大
压力
上海交通大学 物理系
马格纳斯效应
上海交通大学 物理系
机翼受到的举力
Q:用机翼上、下的流速变化,讨论其受到的升力,是否合理
上海交通大学 物理系
上海交通大学 物理系
压强的范围
太阳中心 地球中心 实验室能维持的最大压强 最深的海沟 尖鞋跟对地板 汽车轮胎 海平面的大气压 正常的血压 最好的实验室真空
四、液流连续原理(Principle of continuity of flow)
最新上海交通大学流体力学第三章只是分享精品课件

(2) 轴功率。 解: (1)由于b << d 可将轴承间隙内的周向流动简化为
无限大平行平板间的流动。
轴承固定, 而轴以线速度U=ωd /2运动, 带动润滑油作纯剪切流动, 即简单库埃特
u 1 dpy2
2dx
C1yC2
边界条件:
y = 0,u = 0,C2= 0
y
=
b,u
=
0,C1
1
2
dp dx
b
1.速度(sùdù)
分布
u 1 dp(y2 by)
2 dx
最大速度
(sùdù)
um
b2 8
dp dx
第三页,共49页。
C3.3.1 平板(píngbǎn)泊肃叶流动(4-4)
2. 切应力(yìnglì) 分布
流
2. 平均速度
V Q
R2
GR2
8
12umax
速度分布
u
2V
1
r2 R2
3. 沿程损失
hf pgGgl8glR 2V
第十四页,共49页。
C3.4.2 泊肃叶定律(dìnglǜ)(2-2)
4. 泊肃叶定律(dìnglǜ) 的意义
Q GR4 8
(1) 泊肃叶定律(dìnglǜ)解析式由哈根巴赫和纽曼(1859)分别用N-S 方程推出。哈根(1839)和泊肃叶(1840)分别用实验测得 Q 与 G、R4成正比关系;
T
0
udt
u=u+ u
基本方程
雷诺方程 包含雷诺应力
第十七页,共49页。
上海交大船舶流体力学课件5

Shanghai Jiao Tong UniversityShanghai Jiao Tong UniversityShanghai Jiao Tong University 加速度:当地加速度(局部加速度)变位加速度(迁移加速度)'(, y ,,)(,,,)lim t ()x x y z z t t x y z t t u v w t x y zt +∆+∆+∆+∆-=∆→∆∂∂∂∂=+⋅+⋅+⋅∂∂∂∂∂=+⋅∇∂V V a V V V V V V V2.1.3Euler Shanghai Jiao Tong University2.1.3Euler方法和Lagrange方法的区别Shanghai Jiao Tong University注意:Euler方法中的空间点(x, y, z)与Lagrange方法中质点位置x, y, z有区别,Euler方法中的空间点(x, y, z)是t 的独立变量即与t无关,而Lagrange方法中质点位置x, y, z是t 的函数。
2.1.3Euler Shanghai Jiao Tong University2.2迹线和流线Shanghai Jiao Tong University上一节主要从数学上描述流体运动。
在本节,将讲述流体运动的几何表示。
Shanghai Jiao Tong University 2.2.1迹线定义:流体质点在连续时间内描绘出来的曲线,就是迹线(pathline)。
由于迹线是流体质点运动过程的路径,在Lagrange 法中,就是流体质点的位置函数:(,,,)(,,,)(,,,)x x a b c t y y a b c t z z a b c t =⎧⎪=⎨⎪=⎩2.2.1迹线Shanghai Jiao Tong University2.2.1迹线Shanghai Jiao Tong University2.2.1迹线Shanghai Jiao Tong UniversityShanghai Jiao Tong University一般情况给出的是u v wShanghai Jiao Tong University定义为参变量,积分时作常数处理。
上海交通大学流体力学

∑
=
关于流体中的表面力我们会在下一节课中进一步讨论。
今天我们对流体中的长程力,也就是体积力或质量力进行进一步的探讨,
体积力与质量力;重力;体积力的势
长程力直接作用在每一个物体单元(无论是流体还是固体)以及它所占据的空间体积元上,
我们称之为质量力或体积力。我们定义单位质量上的作用力为 f,那么单位体积上的作用力
若质量力有势,许多计算可以简化。例如我们在质量力场中将一个质量为 m 的物体单元沿
一条路线 s 从 移至 ,那么质量力对这个物体所做的功为
2
2
2
∫ ∙ = ∫ ∙ = − ∫ ∙ = −[( ) − ( )]
1
1
1
即质量力做的功与路径无关,只与起点和终点的质量力势有关。
达式是 3x3 的矩阵,由理论力学知识可以得知,这个矩阵必须是对称的。
: (
)
一个微元面是两个物体分隔面的一部分,它的外法向方向从受力体垂直于微元面指向施力
体。一个面积大小为,外法向方向为 n 的微元面所受到的表面力为 为
= ∙ = ∙
= 被称为微元面的矢量面积。这个微元面上单位面积表面力 为
=
= ∙ → = ∑
=
这里下标指微元面的朝向, 并不一定与平行。单位面积表面力也称为应力。
我们观察一个占据空间体积τ的流体单元:其表面为 A。A 由无数微元面 = 构成。那
短程力的主要形式作用在物体与物体间的接触面上(也包括物体内部的切面)
,被称为表面
力,我们这里用 表示;单位面积上的表面力被称为应力。一般情况下,应力(物体内部切
上海交通大学流体力学第二章

v2 2
gz
p
常数
(全流场)
C2.2 一般概念(2-2)
3. 斯托克斯定理 (封闭曲线、涡束)
开尔文定理 (无粘、正压、有势力)
蜒l v dr A ndA
d
0 (沿封闭流体线) dt
[例C2.2.2] 有自由面的势涡:无旋流伯努利方程
已知: 涡量处处为零的涡旋运动称为势涡(参见C2.4.3),速度分布为 v=v0=C/r,C为常数,r为径向坐标。
2. 求解驻点位置(θcr)
2Usincr2 aຫໍສະໝຸດ 0crsin
1
4 aU
|Γ|<4πaU 有两个驻点
|Γ|=4πaU 有一个驻点
|Γ|>4πaU 无驻点(自由驻点)
3. 表面压强系数
Cp
1 4sin2
2 sin aU
4
2
2a2U 2
4. 压强合力
Fx=0,
Fy=ρUΓ 升力公式
C2.6 绕机翼的平面势流
C2.2 一般概念
C2.1 引言(工程背景) C2.2 一般概念
1. 欧拉运动方程 (无粘)
v t
v
v
f
p
兰姆—葛罗米柯方程 (无粘)
2. 欧拉积分(无粘、无旋 正压、重力 、定常)
v
t
v2 2
v v
f
p
v2 gz
2
dp 常数
(全流场)
伯努利积分(无粘、无旋 不可压、重力、定常)
x2
y
1 2C
2
1 4C 2
[例C2.4.4] 兰金半体绕流:均流+点源(2-1)
已知: 位于原点的强度为Q(Q>0)的点源与沿x方向速度为U的均流叠
上海交通大学流体力学第二章

物理背景 点源点汇无限接近(δ→0)形成的流场。 (偶极矩M = Qδ= 常数,源→汇)
当偶极子位于原点 M cos
vr 2 r2 M sin
v 2 r2
M
2
cos
r
M
2
x x2 y2
M
2
sin
r
M
2
y x2 y2
等势线Φ=C 流线 Ψ=C
x
1 2C
2
y2
1 4C 2
Ursin
Q 2
(a)
(2)速度分布式为
Urcos
Q 2
lnr
(b)
vr
r
Ucos
Q 2 r
(c)
v
1 r
Usin
(d)
(3)流线方程为
Ursin
Q 2
C
(e)
C 取不同值代表不同流线。其中通过駐点的流线的一部分为该流场绕流 物体的轮廓线,即物面流线。
[例C2.4.4] 兰金半体绕流:均流+点源(2-2)
C2.2 一般概念
C2.1 引言(工程背景) C2.2 一般概念
1. 欧拉运动方程 (无粘)
v t
v
v
f
p
兰姆—葛罗米柯方程 (无粘)
2. 欧拉积分(无粘、无旋 正压、重力 、定常)
v
t
v2 2
v v
f
p
v2 gz
2
dp 常数
(全流场)
伯努利积分(无粘、无旋 不可压、重力、定常)
(4)物面流线的左半支是负x轴的一部分(θ=π),驻点A(-b,0)由
下式决定
vr,
( Ucos
上海交通大学流体力学第三章
F
p x
dx
r2
2
rdx
0
dp 2
dx r
p仅与x 有关, τ与x 无关. 只有均为常数才相等. 令比压降为 G p dp 常数 l dx
1 dp r G r
2 dx 2 上式称为斯托克斯公式,说明切应力沿径向线性分布。
C3.4.1 用动量方程求解速度分布(2-2)
4. 平均速度
V
Q b
b2
12
dp dx
2 3
um
C3.3.2 平板库埃特流(2-1)
C3.3.2 平板库埃特流动
在平板泊肃叶流上再增加上板以U 运动条件,方程不变。
1. 速度分布
u
1
2
dp dx
y2
C1y
C2
y 0,u 0, C2 0
U b dp
yb,
u U
,
C1
b
2
dx
u U y 1 dp ( y2 by)
b 2 dx
平板剪切流
泊肃叶流
上式表示流场为平板剪切流与泊肃叶流叠加的结果。
无量纲形式为
u U
y b
B 1
y b
y b
,
B b2 dp
2U dx
C3.3.2 平板库埃特流(2-2)
平板库埃特流流场取决于U 和 dp(或B)的大小和方向。设U> 0 dx
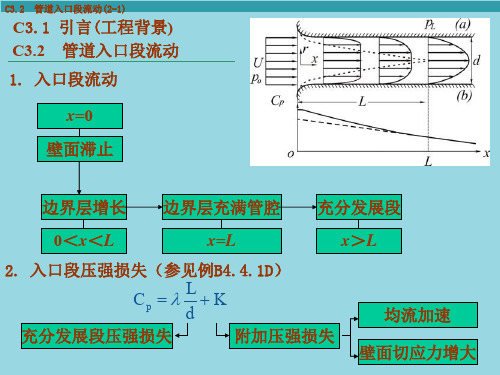
C3.2 管道入口段流动(2-1)
C3.1 引言(工程背景) C3.2 管道入口段流动 1. 入口段流动
x=0
上海交通大学流体力学第四章

C4.1 引言(工程背景) C4.2 边界层概念
例1:空气运动粘度 1.4105 m2 s
设汽车 h 1.5m , V 80 km/h 22 m/s
Re
Vh
22 1.5 1.4105
2.4 106
例2:水运动粘度 1106 m2 s
设船 l 10m ,V 10 km h 2.8 m s
x
5.0 Rex
(2) 对正弦曲线速度分布,边界层截面上的切应力分布为
无量纲切应力分布为
du dy
U 2
cos2y
w
y0
U 2
w
cos(2y)
(a)
对布拉修斯精确解, y Ux,f'(η)= u/U,切应力分布为
du dy
d dy
Uf
'()
Uf
''()
d
dy
Uf
"(
)
U
x
[例C4.5.1] 平板层流边界层近似计算(3-3)
(1) 按位移厚度的定义
* (1- u )dy (1- sin y )dy ( y 2 cos y ) 2 0.363
0U
0
2
2 0
(2) 按动量厚度的定义
u (1- u )dy sin y (1 sin y )dy 2 (sin y sin2 y)d( y)
(3)按湍流完全粗糙区(粗糙度ε=0.0008m)计算平板单面阻力
系数,并与层流区作比较。
解(1) :
平板绕流Rel
数为
Rel
Ul
(3m/s)(0.4m) 0.0110-4 m2 /s
1.2106
上海交通大学流体力学

13.1)定常绝热可压缩流体的基本方程和完全气体状态方程,等熵流动
在第五章时,我们已经给出过一般形式质量、动量和能量守恒方程:
质量:
+ ∙ () = 0
动量:
=
+ ∙ () = − + ∙
2
→ ∙ ( +
2
+ )=0
2
以及 ∙ = 0
这两个方程的物理含义是:对于理想流体绝热定常流动,在流动物理量可微的情况下(即物
理量无间断的情况下)1)沿速度方向(即沿流线)单位质量上的内能、动能和压力势能之
和为常数;2)沿流线单位质量上的熵不变,即沿流线是等熵流动。
方程和等熵关系。
声速和马赫数
声速 c 是小扰动物理量在连续介质中转播速度,c = √( ⁄) ,下标 s 指等熵状态下压强ຫໍສະໝຸດ 随速度的导数,对于完全气体:
= 常数 →
= −
→ = √( ) = √ = √
速度与当地声速之比为马赫数:
=
.
表达式。
驻点
临界点
极限点
0
0 } 流线最大值
0
∗ = 0.52830
∗ = 0.63390
∗ = 0.83330,
∞ = 0
∞ = 0
∞ = 0
0 = 0, 0 = 0
∗ = ∗, ∗ = 1
无量纲能量方程:我们一般用马赫数作为无量纲方程的参数,联等式中取
上海交通大学流体力学

关于流体的粘性我们归纳成以下两条:
1. 牛顿粘性流体中的切应力与流体运动的角变形速度成正比,正比系数称为流体的黏度;
2. 流体在与固壁的接触面上与固体同步运动,该固壁边界条件称为无滑移条件。
课后请大家计算二个问题:
1. 黏度为μ的液体通过半径为 R 的圆管在重力作用下(重力加速度 g)向下流动,管中压
这样的流体被称为牛顿粘性流体。小部分流体不满足正比关系,被称为非牛顿粘性流体。
各种流体的黏度各不相同,通常只与温度相关。气体的黏度随温度增加而升高,液体的黏度
随温度增加而降低。
空气和水在 20 摄氏度时的黏度分别为 10-3N s /m2 和 1.82 * 10-5N s /m2,它们的量级很小,
面积为 A,以恒定速度 V 向右拖动。
y 拖板:面积 A,速度 V,拖曳力 F
() =
底板:静止
H
Vδt
γ
x
经过测量表明,施加的拖拽力 F 与速度 V 成正比,与面积 A 成正比,与 H 成反比(不同材
质的平板对实验结果没用影响)
。也就是说
=
=
同时也可以观察到,流体在不同高度 y 的每一层都以各自的速度向右运动,运动速度 u 与高
点未动。那么这条线与原来的垂线位置就有了夹角 d γ,我们有角变形速度
̇ =
tan
/
= lim
= lim
= lim
=
→0
→0 →0
这样我们就得到了切应力与角变形速度的关系:
= ̇
实际上对于一个平行流动而言,角变形速度可以表达为【图示】
上海交通大学流体力学

= ,
= 0,
τ =
=0→
=0
如果是两种流体的界面,我们有
1 = 2 , 1 = 2 = 0,
1 = 2 ,
τ = 1
1
2
= 2
流场的边界若有流体流入或流出,对内流问题我们称为入口和出口边界条件,入口处一般可
=−
−
+ ( 2 + 2)
将
= 0, = 0
代入后得到
=−
1
2
1
( + ) + 2 , 0 = −
( + )
对第一个方程再作一次对 y 的偏导我们有
3
=0
3
我们注意到速度仅与自变量 y 相关, + 仅与自变量 x 相关。
∙=0 ∶
+
=0→
=0
根据动量方程
1
+ ∙ ∇ = − + ∆
对于定常问题我们有(为重力势)
1
2 2
+
=−
−
+ ( 2 + 2)
1
2 2
+
或者 = − sin ( − ℎ)
计算广义压力梯度
= −
( − − )
=
上海交通大学船舶流体力学课件

Shanghai Jiao Tong University课程名称:船舶流体力学(NA235) Introduction to Marine Hydrodynamics 主讲人:万德成dcwan@辅导老师:林志良linzhiliang@张驰zhangchi0309@课程安排Shanghai Jiao Tong University课程性质:专业基础课学时数:68 =58 (理论课) +4 (实验实践)+ 6 (三次课程设计)成绩:作业和课程设计30%,期末考试70%Shanghai Jiao Tong University《水动力学基础》,刘岳元、冯铁城、刘应中编,上海交通大学出版社,1990《流体力学》,许维德,国防工业出版社,1989《流体力学》(上、下册),吴望一,北京大学出版社,1982《流体力学》(上、中、下册),丁祖荣,高等教育出版社,2003《流体力学基础》(上、下册),潘文全等,机械工业出版社,1982《流体力学》,易家训著(章克本、张涤明等),高等教育出版社,1983Shanghai Jiao Tong UniversityHydrodynamics, H. Lamb, 6th edition, CambridgeUniversity Press, 1932Marine Hydrodynamics, J.N. Newman, MIT Press, 1977An Introduction to Fluid Dynamics, G.R. Batchelor,Cambridge University Press, 1967Introduction to Fluid Mechanics,James A. Fay,MITPress, 1994Fundamentals of Fluid Mechanics,B.R. Munson, D.F.Young & T.H. Okiishi, Wiley Asia Student Edition, 2005 Fluid Mechanics: Fundamentals and Applications, Y.A.Cengel& J.M. Cimbala, McGraw-Hill, 2006Fluid Mechanics,5th Ed., F.M.White, McGraw-Hill.Shanghai Jiao Tong University第0章序论第0章序论Shanghai Jiao Tong University•流体力学与现实生活•流体力学的发展过程•流体力学的研究方法•流体力学的研究内容流体力学与现实生活Shanghai Jiao Tong University船舶工程Shanghai Jiao Tong UniversityShanghai Jiao Tong University 船舶工程船舶工程Shanghai Jiao Tong UniversityShanghai Jiao Tong University 船舶工程Shanghai Jiao Tong University船舶工程Shanghai Jiao Tong University 船舶工程Shanghai Jiao Tong University船舶工程Shanghai Jiao Tong University 船舶工程Shanghai Jiao Tong University螺旋浆船舶工程船舶工程Shanghai Jiao Tong University船舶工程Shanghai Jiao Tong University海洋工程Shanghai Jiao Tong UniversityShanghai Jiao Tong University 海洋工程航空航天Shanghai Jiao Tong University航空航天Shanghai Jiao Tong University航空航天Shanghai Jiao Tong University航空航天Shanghai Jiao Tong UniversityShanghai Jiao Tong University航空航天水利工程Shanghai Jiao Tong University水利工程Shanghai Jiao Tong UniversityShanghai Jiao Tong University 汽车阻力来自前部还是后部?汽车发明于19世纪末,当时人们认为汽车的阻力主要来自前部对空气的撞击,因此早期的汽车后部是陡峭的,称为箱型车,阻力系数C D 很大,约为0.8。
上海交通大学精品课程流体力学课件 共325页

归纳两点:
1、平衡流体内不存在切向应力,表面力即为 法向应力(即静压强);
2、绝对平衡流体所受质量力只有重力,相对 平衡流体可能受各种质量力的作用。
三、 流体静压强的两个重要特性。 1、流体静压强的方向总是沿着作用面的内法线 方向。
2、平衡流体内任一点处的静压强的数值与其作 用面的方向无关,它只是该点空间坐标的函数。
温度内聚力 粘度 温度变化时对流体粘度的影响必须给于重视。
4、理想流体的概念 理想流体——假想的没有粘性的流体。
µ= 0 = 0
实际流体——事实上具有粘性的流体。
小
结
1、流体力学的任务是研究流体的平衡与宏观机械运动规律。
2、引入流体质点和流体的连续介质模型假设,把流体看成没有间隙 的连续介质,则流体的一切物理量都可看作时空的连续函数,可 采用连续函数理论作为分析工具。
质量 dxdydz
得:
fx
1
p x
0
同理:f y
1
p y
0
1 p
fz z 0
静止流体的平衡微分方程 (欧拉平衡微分方程)
方程的物理意义 : 在静止流体中,作用在单位质
量流体上的质量力与作用在该流体表面上的压力 相平衡。
四、综合表达式 将平衡微分方程的三个表达式分别乘以dx、dy、dz 然后相加
第一章 绪论 第二章 流体静力学 第三章 流体动力学 第四章 相似和量纲分析 第五章 管 中 流 动 第六章 孔口和缝隙流动 第七章 气体的一元流动
第一章 绪论
§1-1 流体力学研究的内容和方法 §1-2 流体的概念及其模型化 §1-3 流体的主要物理性质
第二章 流体静力学
流体力学基础——上海交通大学
2.6.1 圆管沿程阻力损失和莫迪图
圆管沿程阻力损失高度表达式,hf
l d
c
2 f
2g
适用于层流与紊流
层流:λ= 64/Re;
紊流:主要依靠实验。
圆管中的水流分成五个区域:
层流区
层流向紊流转变的临界区
紊流光滑区
0.4
或
4000 Re 80 d
紊流过渡区
0.4 6
或 80d Re1000d
紊流粗糙区
2020/5/19
6
或 Re 1000 d
29
工程中应用的管道与人工粗糙管道不同,实用管道的沿程 损失系数可由莫迪曲线图查取 。
2020/5/19
30
2.6.2 非圆形管道的沿程损失
非圆管道(如矩形、圆环形通道等)沿程损失计算,目前仍 采用圆形管道的计算公式,但要用当量直径de 代替式中的圆管 直径d
第二章 流体力学基础
2.1 基本概念 2.2 流体静力学的基本方程 2.3 流体运动的连续性方程和能量方程 2.4 流体的伯努利方程 2.5 层流和紊流 2.6 管内流动的沿程损失和局部损失 2.7 压水反应堆蒸汽发生器一次侧的压降
2020/5/19
1
2-1 基本概念
2.1.1流体的一般特性
流体
气体 液体
先按理想流体处理,然后再考虑粘性影响加以修正,以解决
工20程20/5实/19 际问题。
5
2-2 流体静力学的基本方程
流体静力学研究流体在静止状态下的力学规律。
2.2.1 静止流体中的应力特征
●流体不能承受拉力; ●静止时不存在切向应力,静止流体中的应力垂直于作用面,
这种法向应力称为压力(或压强) ●静止流体中的任意一给定点上,静压力 不论来自何方向,其值均相等。
上海交通大学精品课程流体力学课件 325页PPT文档

§1-2 流体的概念及其模型化
一、流体的物质属性
1、流体与固体 流体:可承受压力,几乎不可承受拉力,承受剪 切力的能力极弱。
易流性 —— 在极小剪切力的作用下,流体就将产 生无休止的(连续的)剪切变形(流动),直到 剪切力消失为止。
流体没有一定的形状。固体具有一定的形状。
固体:既可承受压力,又可承受拉力和剪切力,在 一定范围内变形将随外力的消失而消失。
温度内聚力 粘度 温度变化时对流体粘度的影响必须给于重视。
4、理想流体的概念 理想流体——假想的没有粘性的流体。
µ= 0 = 0
实际流体——事实上具有粘性的流体。
小
结
1、流体力学的任务是研究流体的平衡与宏观机械运动规律。
2、引入流体质点和流体的连续介质模型假设,把流体看成没有间隙 的连续介质,则流体的一切物理量都可看作时空的连续函数,可 采用连续函数理论作为分析工具。
dv dy
代表了粘性的大小
µ 的物理意义:产生单位速度梯度,相邻流 层在单位面积上所作用的内摩擦力(切应力)的 大小。
常用粘度表示方法有三种:
<1>动力粘度 µ 单位 : Pa s (帕 • 秒) 1 Pa s = 1 N/m2 s
<2>运动粘度:
单位:m2 / s
工程上常用:10 – 6 m2 / s (厘斯) mm2 / s 油液的牌号:摄氏 40ºC 时油液运动粘度的 平均厘斯( mm2 /s )值。
体积: dVdxdydz
分析微小正平行六面体微团受力:
一、质量力
dFmx = dxdydz fx dFmy = dxdydz fy dFmz = dxdydz fz
二、表面力
经典流体力学课件-上海交大

第七章 气体的一元流动
§8−1 声速和马赫数 §8–2 一元气流的基本方程和流动特性
§8–3 理想气体一元等熵流动的特征
§8–4 收缩喷管与拉伐尔喷管的计算
第八页,共324页。
第一章 绪 论
§1-1 流体力学研究的内容和方法
流体力学研究的主要内容:
1、建立描述流体平衡和运动规律的基本方程;
2、确定流体流经各种通道时速度、压强的分布 规律;
滑动(抵抗变形)的内摩擦力的性质称为流体的粘性。
第十六页,共324页。
内摩擦力: F A dv
dy
以切应力表示: F dv
A dy
牛顿内摩擦定律
式中:µ—— 与流体的种类及其温度有关的比例
常数;
dv —— 速度梯度(流体流速在其法线方
dy
向上的变化率)。
第十七页,共324页。
2、粘度及其表示方法
法向应力(即静压强);
2、绝对平衡流体所受质量力只有重力,相对 平衡流体可能受各种质量力的作用。
第二十七页,共324页。
三、 流体静压强的两个重要特性。
1、流体静压强的方向总是沿着作用面的内法线方 向。
2、平衡流体内任一点处的静压强的数值与其作用面的方向 无关,它只是该点空间坐标的函数。
证明:在平衡流体中取出一微小四面体ABOC,考察其 在外力作用下的平衡条件。
µ= 0 = 0
实际流体——事实上具有粘性的流体。
第二十二页,共324页。
小
结
1、流体力学的任务是研究流体的平衡与宏观机械运动规律。
2、引入流体质点和流体的连续介质模型假设,把流体看成没有间隙
的连续介质,则流体的一切物理量都可看作时空的连续函数,可 采用连续函数理论作为分析工具。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020/3/22
18
2.4.3 粘性流体总流的伯努利方程
理想流体总流的伯努利方程
z1p 121cgf21z2p222cgf22
理想流体运动:总机械能守恒; 粘性流体运动:流层间的摩擦阻力会消耗机械能,因此,
总机械能将沿流程减小。
z1p 12 1cgf21z2p 222c gf22hw
单位质量流体从断面 1-1到2-2消耗的机械
水力半径:液流断面面积A与湿周的比值 RA/U
de
4R
4A U
反映了液流断面形状、尺寸对过流能力 的影响,水力半径愈大,过流能力愈强
湿周 ,表示液流的有效断面与固体相接触的周界
2020/3/22
31
湿周
r
U2(hb)
de
2020/3/22
2hb hb
U(d1d2)
de d2 d1
U d
de
4S1S2
能—流体能量损失。
粘性流体的伯努利方程
2020/3/22
19
沿程损失—摩擦阻力引起的能 量损失与流程长度成正比 h f
局部损失—流体流经局部障碍 (如:管接头、弯头、闸阀、 管径突变)时,由于边界形状 急剧变化流体微团发生碰撞、
产生旋涡等引起能量损失 h j
沿程损失系数
hf
l d
c
2 f
2g
管长 管内流体的平均速度
11
2.3.2 迹线、流线
迹线—— 流体质点在空间运动的轨迹线。
流线——各点的速度矢量与之相切的有向曲线。 ●定常流动中,流线不随时间变化; ●除在速度为零或无穷大的那些点,流线不能相交。
2.3.3 流管、流束、总流
• 流管—某一瞬时,通过曲线C上 各点的所有流线构成一管状曲面。
• 流束—管内所有流线的总和。
g
hf
64 l Red
cf2 2g
l
d
cf2 2g
r0 d 2
Recfd
达西公式
64 Re
圆管层流的沿程损失系数与雷诺 数成反比,与管壁粗糙度无关。
2020/3/22
26
2.5.3 管内紊流
紧靠管壁处有一极薄的流体(厚度一般为十分之几毫米) 因受管壁限制,脉动现象很弱。粘性起主要作用,流速梯度 很大,这一极薄流体层称为粘性底层。在粘性底层之外,有 很薄的过渡层,过渡层之外是紊流核心区(紊流区),紊流 核心区脉动较为充分,速度分布趋于均匀化。圆管中紊流的 速度分布与流体性质及管壁情况有关。
比固体更易变形与压缩 流体只能承受压力,几乎不能承受拉力
2.1.2连续介质假设
1mm3水中有3.34×1020个分子,平均经过10-11s,分子就会 从一个平衡位置 转向另一平衡位置,而在一般工程问题中描 述流体运动的空间尺度精确到0.01mm就满足精度要求。
连续介质假设
流体力学研究流体的宏观特性,忽略流体的分子构成,把 它看作一种连续性的介质,认为其中没有任何间隙。
应用总流伯努利方程时应注意: (1) 流体是理想、不可压缩;流动是定常;质量力仅是重力; (2) 所取的两个有效断面一定要处于缓变流区域,但在这两个 有效断面之间可以有急变流; (3) 在所取的两个有效断面之间不能有能量输入或输出;
(4) 在缓变流的同一有效断面上 z p 是常数,因此可以在
断面上的任意点取值,一般取断面形心处的值较方便。
圆管内平均速度
cf, max
p
4l
r02
cf qA V 8plr0212cf,max 圆管层流的最大速度等
于平均速度的两倍。 ●阻力损失
水平等径圆管内仅有沿程损失,且沿程损失就等于压力损失。
h f p
2020/3/22
hf
8l r02
cf
25
hf
8l r02
cf
圆管层流沿程损失
与平均速度成正比
位置水头 压力水头 速度水头 三种水头之和称为总水头 (静压力) (动压力)
伯努利方程的几何意义
在流场中或沿流线, 任意点的位置水头、压 力水头与速度水头之和 是常数。
2020/3/22
16
2.4.2 总流的伯努利方程
工程实际(管道、渠道)中要解决的是总流流动的问题。由于 在总流的有效断面上,各运动参数一般是变化的,因此要将沿流 线的伯努利方程进行的修正。
把整个管子或渠道中的流体看作总的流束,这种由无限多微元 流束所组成的总的流束称为总流。
缓变流——流线几乎平行的直线的流动情况。
实验已证明缓变流沿有效断面 z p 常数
2020/3/22
17
z1p 112 cf2 g1 z2p 222 cf2 g 2 总流的伯努利方程
工业管道通常的工作状态下=1.051.12,一般可近似取1
气体
2020/3/22
h 1 1 2 c f 2 1 g z 1 h 2 1 2 c f 2 2 g z2 h 1 2 c f 2 g z
h11 2cf21h21 2cf22h1 2cf2
13
2-4 流体的伯努利方程
2.4.1 理想流体的伯努利方程
h u pv u p
h 1 1 2 c f 2 1 g z 1 h 2 1 2 c f 2 2 g z2 h 1 2 c f ห้องสมุดไป่ตู้ g z u 1 p 1 v 1 1 2 c f 2 1 g z 1 u 2 p 2 v 2 1 2 c f 2 2 g z 2 u p v 1 2 c f 2 g z
2.6.1 圆管沿程阻力损失和莫迪图
圆管沿程阻力损失高度表达式,hf
l d
c
2 f
2g
适用于层流与紊流
层流:λ= 64/Re;
紊流:主要依靠实验。
圆管中的水流分成五个区域:
层流区
层流向紊流转变的临界区
紊流光滑区
0.4
或
4000 Re 80 d
紊流过渡区
0.4 6
或 80d Re1000d
先按理想流体处理,然后再考虑粘性影响加以修正,以解决
工20程20/3实/22 际问题。
5
2-2 流体静力学的基本方程
流体静力学研究流体在静止状态下的力学规律。
2.2.1 静止流体中的应力特征
●流体不能承受拉力; ●静止时不存在切向应力,静止流体中的应力垂直于作用面,
这种法向应力称为压力(或压强) ●静止流体中的任意一给定点上,静压力 不论来自何方向,其值均相等。
2020/3/22
7
2.2.3 流体静力学基本方程
1. 流体静力学基本方程
假设:质量力仅为重力;
流体均质不可压缩( =常数)
dpgdz
dz dp 0
单位质量流体的位势能; 是相对于基准面的高度, 又称位置高度或位置水头
位势能与压力势能之和称为总势能; 位置水头与压力水头之和称为静水头
单位质量流体的 压力势能。
2020/3/22
23
判别准则 无量纲数Re数
定型尺寸
Re cfd cfd
动力粘度
运动粘度
圆管内流动 Re<2 320 层流
Re>2 320 紊流
104Re2320过度流 Re 104 旺盛紊流
2020/3/22
24
2.5.2 黏性流体圆管中的层流
●速度分布 半径为r0的水平直圆管,流体作定常流动, 层流的速度分布为 抛物线规律变化。
与一段液柱高度相当,
z p C
又称之为压力高度或 压力水头。
z1
p1
z2
p2
2020/3/22
流体静力学基本方程
9
2. 流体静力学基本方程物理意义:
z1p 1 z2p 2 zpC
当均质不可压缩流体在重力场中处于静止时,在流体中的 任意点上,单位重量流体的总势能是常数。也可叙述为:任 意点的静水头均相等。
3. 帕斯卡原理
流体静力学基本方程用于液面上一点
与液体内淹深为h的任意一点
z p zh p0
p p0 h
静止液体中,任意一点的压力等于液面
压力加上高度为h的液柱所产生的压力。
液面上的压力变化,液体内其余点的压力
也会随之变化同样的数值。
2020/3/22 --压力传递的帕斯卡原理。
10
2020/3/22
d
d
32
2.6.3 局部阻力损失
管路中流体在通过各种管件,如阀门、三通、弯管时,使 流体运动中产生旋涡和剧烈的碰撞摩擦形成的局部能量损失。
产生原因: ●旋涡流动的能量损失 ●流体质点的碰撞 ●速度重新分布带来的能量损失 ●流向改变造成的能量损失
由连续介质假设出发,流体运动中的压力、流动速度等都
可2视020为/3/22连续变量。
2
2.1.4 流体的粘性
●流体粘性的表现: ★流体与固体壁面相接触,
会粘附于固壁表面。
★相邻两层流体作相对运动时也会产生摩擦阻力。
●动力粘性系数和运动粘性系数 流体内摩擦力的大小与速度U成正比,与
接触面积A成正比,与两板间距离h成反比:
F AU h
动力粘性系数简称粘性系数或粘度,N·s/m2或Pa·s
2020/3/22
4
运动粘性系数 :—— 与流体密度 之比值
单位:m2/s。有时也用cm2/s,称为斯。
动力粘性系数 的大小与流体的种类、温度以及压
力有关。但压力的影响很小,一般只考虑温度的影响。
▲液体的粘性系数随温度升高而降低;
2cf2g1 z2p2
cf22 2g
单位质量流 体的位势能
单位质量流 单位质量流体的动能 体的压力势能
伯努利方程的物理意义
在流场中或沿流线,单位质量流体具有的位势能、压力 势能及动能之和是一个常数,或,总机械能是常数。
