初一数学竞赛专题 (7)
七年级数学竞赛试题精选(七)

七年级数学竞赛试题精选(七)一、拆分法及应用 例1、 计算:99163135115131++++。
(第三届华杯赛) 练习:(1)2081130170128141++++。
(2))2(1641531421311+⨯+⋅⋅⋅⋅⋅⋅+⨯+⨯+⨯+⨯n n 。
(60年上海) (3)2003减去它的21,再减去(第一次)余下的31,再减去(第二次)余下的41,、、、、、、,依次类推,一直到减去(第2001次)余下的20031,问最后余下的是多少?(第六届华杯赛)(4)计算20022002200320003200032002⨯-⨯。
(第四届迎春杯)二、错位相减法 例2、比较1234248162n n nS =++++⋅⋅⋅⋅⋅⋅+(n 为任意自然数)与2的大小。
练习:(1)12310011213110012222----+++⋅⋅⋅⋅⋅⋅+。
(2)21512412562561451212102411++⋅⋅⋅⋅⋅⋅+++。
三、观察归纳法 例 3 计算:⎪⎭⎫ ⎝⎛-⨯⋅⋅⋅⨯⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛+⨯⋅⋅⋅⨯⎪⎭⎫ ⎝⎛+⨯⎪⎭⎫ ⎝⎛+⨯⎪⎭⎫ ⎝⎛+9115113111011611411211 (第六届华杯赛)例4 计算:355133********1-----练习:901177211556113421113019201712156131++++++++。
(第四届华杯赛)五、放缩法 例5、已知19911198311982119811198011+⋅⋅⋅++++=S ,求 S 的整数部分。
例6、已知下式,求a 的整数部分:1006915681467136612651170156914681367126611⨯⨯+⨯+⨯+⨯+⨯⨯+⨯+⨯+⨯+⨯=a ,问a 的整数部分是多少? (第二届华杯赛)六、换元法 例7、计算:111121113114314119581958++++++++++练习:已知2000199920011998,2001199920001998,2001200019991998⨯⨯-=⨯⨯-=⨯⨯-=C B A 试比较C B A ,,的大小。
浙江初一初中数学竞赛测试带答案解析

浙江初一初中数学竞赛测试班级:___________ 姓名:___________ 分数:___________一、单选题1.计算:()A.3B.C.0.14D.2.下列各组数中互为倒数的是().A.与2B.与C.与D.与3.下列计算结果等于1的是()A.(-2)+(-3)B.(-3)-(-2)C.D.(-3)-(-2)4.对于,下列说法错误的是()A.>B.其结果一定是负数C.其结果与-3相同D.表示5个-3相乘5.下列说法正确的是()A.是六次多项式B.是单项式C.的系数是,次数是2次D.+1是多项式6.已知代数式的值是5,则代数式的值是()A.6B.-6C.11D.-97.有下列说法:①无限小数都是无理数;②数轴上的点和有理数一一对应;③在1和3之间的无理数有且只有,,,,,这6个;④;⑤近似数7.30所表示的准确数a的范围是:7.295≤a<7.305;其中正确的是()A.⑤B.④⑤C.③④⑤D.①④⑤8.有理数a,b在数轴上对应的位置如图所示,那么代数式-+-的值是()A.-1B.0C.1D.29.洪峰到来前,120名战士奉命加固堤坝,已知5人运沙袋3人堆垒沙袋,正好运来的沙袋能及时用上且不窝工,为了合理安排,如果设x人运送沙袋,其余人堆垒沙袋,那么以下所列方程正确的是()A.B.C.D.10.完成下列填空: ,解:化简,得:2.5-( )=0.6. 括号内填入的应该是( ) A .B .C .D .二、填空题1.在数轴上,与表示的点距离为5的数是____________ .2.用科学记数法表示-5259000=_______________;用科学记数法表示5259000≈ ____________(精确到万位)3.“x 的平方与 的算术平方根的和”用代数式可以表示为 ____________。
4.一件商品的进价是a 元,提高30%后标价,然后打9折销售,利润为 __________元.5.你的“24点游戏”玩的怎么样?(所给的四个数必须都使用一次且不能使用四个数之外的其他数)请你将“3,-3,8,-8”这四个数用加、减、乘、除或括号进行运算,使其结果为24,你写出的算式是________;如果可以用乘方、开方运算,那么3,4,8,8的“24点”算式是_______________(可以分步列式,每个数字只能用一次,例如:)6.先阅读再计算:取整符号[a ]表示不超过实数a 的最大整数,例如:[ 3.14 ]=3;[0.618]=0;如果在一列数X 1、X 2、X 3、……X n 中,已知X 1="2" ,且当k≥2 时, 满足,则求X 2016的值等于_____________三、解答题1.解下列方程 (1) (2)2.计算 (1) (2)(3)3.在一组实数,,,, 1+,(1)将它们分类,填在相应的括号内: 有理数{ … }; 无理数{ …};(2)请你选出2个有理数和2个无理数, 再用 “+,-,×,÷” 中的3种不同的运算符号将选出的4个数进行运算(可以用括号), 使得运算的结果是一个正整数. 4.(1)已知是有理数且满足:是-27的立方根,,求的值; (2)已知5.若,则单项式和是同类项吗?如果是,请把它们进行加法运算;如果不是同类项,请从下列代数式中找出同类项进行加法运算:,6.为了节约用水,某市居民生活用水按级收费,下面是东东家收到的自来水公司水费专用发票。
#初中数学竞赛分专题训练试题及解析(10套,76页)

初中数学竞赛专项训练(1)(实 数)一、选择题1、如果自然数a 是一个完全平方数,那么与a 之差最小且比a 大的一个完全平方数是( ) A. a +1B. a 2+1C. a 2+2a+1D. a+2a +12、在全体实数中引进一种新运算*,其规定如下:①对任意实数a 、b 有a *b=(a +b )(b -1)②对任意实数a 有a *2=a *a 。
当x =2时,[3*(x *2)]-2*x +1的值为 ( ) A. 34B. 16C. 12D. 63、已知n 是奇数,m 是偶数,方程⎩⎨⎧=+=+m y x n y 28112004有整数解x 0、y 0。
则( )A. x 0、y 0均为偶数B. x 0、y 0均为奇数C. x 0是偶数y 0是奇数D. x 0是奇数y 0是偶数4、设a 、b 、c 、d 都是非零实数,则四个数-ab 、ac 、bd 、cd ( ) A. 都是正数B. 都是负数C. 两正两负D. 一正三负或一负三正5、满足等式2003200320032003=+--+xy x y x y y x 的正整数对的个数是( ) A. 1B. 2C. 3D. 46、已知p 、q 均为质数,且满足5p 2+3q=59,由以p +3、1-p +q 、2p +q -4为边长的三角形是 A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形7、一个六位数,如果它的前三位数码与后三位数码完全相同,顺序也相同,由此六位数可以被( )整除。
A. 111B. 1000C. 1001D. 11118、在1、2、3……100个自然数中,能被2、3、4整除的数的个数共( )个 A. 4 B. 6C. 8D. 16二、填空题 1、若20011198********⋯⋯++=S ,则S 的整数部分是____________________2、M 是个位数字不为零的两位数,将M 的个位数字与十位数字互换后,得另一个两位数N ,若M -N 恰是某正整数的立方,则这样的数共___个。
初一数学竞赛教程含例题练习及答案⑺立体图形

初一数学竞赛讲座第7讲立体图形空间形体的想象能力是小学生的一种重要的数学能力,而立体图形的学习对培养这种能力十分有效。
我们虽然在课本上已经学习了一些简单的立体图形,如正方体、长方体、圆柱体、圆锥体,但有关立体图形的概念还需要深化,空间想象能力还需要提高。
将空间的位置关系转化成平面的位置关系来处理,是解决立体图形问题的一种常用思路。
一、立体图形的表面积和体积计算例1一个圆柱形的玻璃杯中盛有水,水面高 2.5cm,玻璃杯侧的底面积是72cm2,在这个杯中放进棱长6cm的正方体铁块后,水面没有淹没铁块,这时水面高多少厘米?解:水的体积为72×2.5=180(cm3),放入铁块后可以将水看做是底面积为72-6×6=32(cm2)的柱体,所以它的高为180÷32=5(cm)。
例2下图表示一个正方体,它的棱长为4cm,在它的上下、前后、左右的正中位置各挖去一个棱长为1cm的正方体,问:此图的表面积是多少?分析:正方体有6个面,而每个面中间有一个正方形的孔,在计算时要减去小正方形的面积。
各面又挖去一个小正方体,这时要考虑两头小正方体是否接通,这与表面积有关系。
由于大正方体的棱长为4cm,而小正方体的棱长为1cm,所以没有接通。
每个小正方体孔共有5个面,在计算表面积时都要考虑。
解:大正方体每个面的面积为4×4-1×1=15(cm2),6个面的面积和为15×6=90(cm2)。
小正方体的每个面的面积为1×1=1(cm2),5个面的面积和为1×5=5(cm2),6个小正方体孔的表面积之和为5×6=30(cm2),因此所求的表面积为90+30=120(cm2)。
想一想,当挖去的小正方体的棱长是2cm时,表面积是多少?请同学们把它计算出来。
例3正方体的每一条棱长是一个一位数,表面的每个正方形面积是一个两位数,整个表面积是一个三位数。
初一数学竞赛试题及答案

初一数学竞赛试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是最小的正整数?A. 0B. 1C. -1D. 2答案:B2. 一个数的相反数是它自己,这个数是:A. 0B. 1C. -1D. 2答案:A3. 如果一个角的补角是它的两倍,那么这个角的度数是:A. 30°B. 45°C. 60°D. 90°答案:C4. 以下哪个选项表示的是一次函数的图象?A. 一条直线B. 一个圆C. 一个椭圆D. 一个抛物线答案:A5. 一个数的平方是9,这个数是:A. 3B. -3C. 3或-3D. 以上都不对答案:C6. 一个数的立方是-27,这个数是:A. 3B. -3C. 3或-3D. 以上都不对答案:B7. 以下哪个选项是方程2x + 3 = 9的解?A. x = 3B. x = 6C. x = -3D. x = 0答案:A8. 一个数的绝对值是5,这个数可以是:A. 5B. -5C. 5或-5D. 以上都不对答案:C9. 下列哪个选项是不等式2x - 5 > 3的解集?A. x > 4B. x > 2C. x < 4D. x < 2答案:A10. 如果一个三角形的两边长分别是3和4,那么第三边的长度可以是:A. 1B. 2C. 3D. 4答案:C二、填空题(每题3分,共30分)1. 一个数加上它的相反数等于______。
答案:02. 一个数的绝对值是它本身,这个数是______。
答案:非负数3. 一个角的补角是它的三倍,那么这个角的度数是______。
答案:45°4. 一次函数y = 2x + 1的图象经过点(0,1),则这个点是该函数的______。
答案:截距5. 一个数的平方是16,这个数是______。
答案:±46. 一个数的立方是8,这个数是______。
答案:27. 方程3x - 7 = 2的解是______。
七年级数学竞赛试题及答案

七年级数学竞赛试题及答案一、选择题1. 已知a = 3,b = -4,则下列哪一个式子是正确的?A. a + b = 7B. a - b = -1C. a × b = -12D. a ÷ b = -3答案:B2. 如果a × b = 20,且b = 5,求a的值。
A. 4B. 5C. 10D. 25答案:C3. 打折前售价为120元的商品现以原价的95%出售,打折后的价格是多少?A. 108元B. 114元C. 119元D. 123元答案:B4. 若一边长为5的正方形的面积是矩形的面积的四分之一,则矩形的长为多少?A. 5B. 10C. 15D. 20答案:C5. 以下哪个数不是素数?A. 17B. 19C. 21D. 23答案:C二、解答题1. 一个数减去13等于19,求这个数是多少?解答:设这个数为x,根据题目可得方程x - 13 = 19,将方程两边同时加上13,则x = 32。
因此,这个数是32。
2. 计算1/4 + 2/3的值,结果用最简分数表示。
解答:首先计算通分,得到3/12 + 8/12 = 11/12。
因此,1/4 + 2/3 = 11/12。
3. 六边形ABCDEF的周长是42 cm,已知AB = CD = EF = 5 cm,BC = DE = 6 cm。
求六边形的面积。
解答:六边形由三个边长相等的正三角形组成,而正三角形的面积公式为S = (边长^2 * √3) / 4。
根据题目可得六边形的面积为3 * [(5^2 * √3) / 4] = (75√3) / 4。
因此,六边形的面积为(75√3) / 4。
4. 如图所示,一个长方体的表面积为94 cm²,其中长、宽和高的比为1:2:3。
求长方体的体积。
解答:设长、宽和高分别为x、2x和3x,则根据长方体的表面积公式2(x * 2x + 2x * 3x + x * 3x) = 94,化简为14x^2 = 94,解得x =√(94/14) = √(47/7)。
数学竞赛试题初一及答案

数学竞赛试题初一及答案一、选择题(每题3分,共15分)1. 下列哪个数是最小的正整数?A. 0B. 1C. 2D. 32. 如果一个数的平方等于该数本身,那么这个数可能是:A. 0B. 1C. -1D. 以上都是3. 一个圆的半径是5厘米,那么它的周长是多少厘米?A. 10πB. 15πC. 20πD. 25π4. 以下哪个表达式的结果等于0?A. 3 - 3B. 2 × 0C. 5 ÷ 5D. 4 + 05. 如果一个角的补角是它的3倍,那么这个角的度数是:A. 45°B. 60°C. 90°D. 120°二、填空题(每题2分,共10分)6. 一个数的相反数是它本身的数是______。
7. 一个数的绝对值是它本身的数是非负数,那么这个数是______或______。
8. 一个三角形的内角和等于______度。
9. 如果一个数的平方根是它本身,那么这个数是______或______。
10. 一个数的立方等于它本身,这个数是______、______或______。
三、计算题(每题5分,共20分)11. 计算下列表达式的值:(3 + 5) × (7 - 2)。
12. 计算下列表达式的值:(-2)³ - 3 × 2²。
13. 计算下列表达式的值:√(49) + √(16)。
14. 计算下列表达式的值:(-1)⁴ - 2²。
四、解答题(每题10分,共30分)15. 一个长方形的长是15厘米,宽是10厘米,求它的周长和面积。
16. 一个直角三角形的两条直角边分别是3厘米和4厘米,求它的斜边长度。
17. 一个数列的前三项是1,3,6,求这个数列的第四项。
五、证明题(每题25分,共25分)18. 证明:在一个直角三角形中,如果一个锐角是另一个锐角的两倍,那么较小的锐角的度数是30°。
答案:一、选择题1. B2. D3. C4. A5. D二、填空题6. 07. 正数,08. 1809. 0,110. 0,1,-1三、计算题11. 6412. -813. 714. 3四、解答题15. 周长:(15 + 10) × 2 = 50厘米;面积:15 × 10 = 150平方厘米。
2023初中数学培优竞赛例题+练习 专题36 全国初中数学竞赛分类汇编卷(七)三角形(提优)
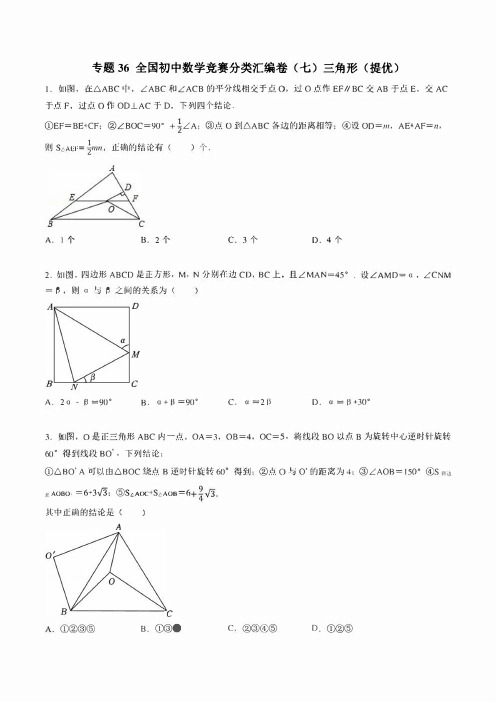
专题36全国初中数学竞赛分类汇编卷〈七〉三角形〈提优〉I.如|蜀,在.6.ABC中,LABC和ζACB的平分线相交子点。
,过0点作EF//BC交AB子点E,交AC 于点F,过点。
你OD_l_AC于D,下列四个结论.1①EF=BE+CF:②LBOC=90。
+2LA;@点O itl.6.ABC各边的距离相等;④设OD=m,AE+AF=n, 则S c,A EF=�mn,正确的结论有()个AB cA.l个B.2个 c.3个。
.4个2.如图,四边形ABCD是正方形,M,N分别在边CD,BC上,且LMAN=45。
.设LAMD=口,ζCNM =白,则。
与自之间的关系为(〉DcNA.2 a -白=90。
B.a+fJ=90。
C.a =2日。
.a=自+30。
3.如图,0是正三角形ABC内一点,OA=3,08=4, OC=S,将线段BO以点B为旋转中心逆时针旋转60。
得到线段BO’,下列结论:①.6.BO' A司以由.6.BOC绕点B逆时针旋转60。
得到;②点。
与O’的距离为4;③LAOB=l50。
④s P.!I地11;AOBO =削σ;⑤S叫+S c,A O时1士;中正E角的结论是〈)A℃B.①③④C②@④⑤ D.①@⑤4.AD与BE是6ABC的角平分线,D,E分别在BC,AC上,若AD=AB,BE=BC,贝�L'.C=()Bc AA.69。
ωTRU900c.(τ3)° D.不能确定5.在四边形ABCD中,AD=DC=2,ζDAB=ζDCB=90。
,BC,A D的延长线交于P,求AB•S i:.PAB的最小值pDBA6.着,1个等腰三角形的顶角a1、a2、…、an两两不等,它们的共同特点是:被一条直线分得的两个较小三角形也是等腰三角形,则a1+ a 2+…+an=·fα- 2b = m-7 7设。
、b分别是等腰三角形的两条边的长,m是这个三角形的周长,当。
、b、川满足方程t R Ja+b=号+2时,m的值是8.己知ID.ABC中,AB=AC,L'.BAC=90。
初一希望杯数学竞赛二试训练7

6.正整数 m和n有大于1的最大公约数,且满足m3+n=371,则mn=
.
7.关于x的方程ax+3=|x|有负根要但无正根,则a的取值范围是(
)
8.某市按以下规定收到每月煤气费:用煤气如果不超过60m3,每月按每立方米 0.8元收费,如果超过60m3,超过部分按每立方米1.2元收费,已知某户4月份的煤气 费平均每立方米0.88元,那么4月份该用户交煤气费为 元。
先判断出4月份所用煤气一定超过60m3,等量关系为:60×0.8+超过60米的立方数 ×1.2=0.88×所用的立方数,设4月份用了煤气x立方米,从而得出方程求解即可. 解:由4月份煤气费平均每立方米0.88元,可得4月份用煤气一定超过60m3, 设4月份用了煤气x立方米, 由题意得:60×0.8+(x-60)×1.2=0.88×x, 解得:x=75(立方米), 则所交电费=75×0.88=66元. 答:4月份这位用户应交煤气费66元.
9.一个凸n边形的内角中,恰有4个钝角,则n的最大值 是
。
10.一个半径为2005的圆中放入n个点,这n个点两两之间的距离都大于2005, 则n的最大值 为 。 解:作一圆的半径为2005. n个点两两之间的距离都大于2005.
A2
A3
O A4
A1
2Hale Waihona Puke 13 3 1611
8 10 5
6
9 7 12
当|z-x|=1时,z-x=1 或z-x=-1 而 x-y=0,把z-y=1 或z-y=-1 所以|z-x|+|x-y|+|y-z|=0+1+1=2
衢州数学竞赛初一试题及答案

衢州数学竞赛初一试题及答案一、选择题(每题3分,共30分)1. 一个数的平方等于它本身,这个数是()A. 1B. -1C. 0D. 1或-12. 如果一个三角形的三边长分别为a、b、c,且满足a^2 + b^2 = c^2,那么这个三角形是()A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定3. 下列哪个数是质数?()A. 4B. 9C. 13D. 164. 一个数的绝对值是它本身,这个数是()A. 正数B. 负数C. 零D. 正数或零5. 一个数的倒数是它本身,这个数是()A. 1B. -1C. 0D. 不存在6. 如果x^2 - 5x + 6 = 0,那么x的值是()A. 2B. 3C. 2或3D. 1或27. 一个圆的半径是5,那么它的周长是()A. 10πB. 20πC. 30πD. 50π8. 一个数的平方根是它本身,这个数是()A. 1B. -1C. 0D. 1或09. 如果一个数的立方等于它本身,那么这个数是()A. 0B. 1C. -1D. 0, 1或-110. 一个数的相反数是它本身,这个数是()A. 0B. 1C. -1D. 0或1二、填空题(每题3分,共15分)1. 若一个数的平方是16,那么这个数是______。
2. 直角三角形的斜边长度为13,两直角边长度分别为5和12,那么斜边上的高是______。
3. 一个数的绝对值是5,这个数可以是______。
4. 一个数的倒数是1/2,那么这个数是______。
5. 如果一个圆的直径是14,那么它的面积是______。
三、解答题(每题5分,共55分)1. 证明:如果a、b、c是三角形的三边长,且a^2 + b^2 = c^2,那么这个三角形是直角三角形。
2. 解方程:2x + 5 = 3x - 2。
3. 一个长方形的长是宽的两倍,如果它的周长是24厘米,求长方形的长和宽。
4. 一个数列的前三项是1, 1, 2,从第四项开始,每一项都是前三项的和。
数学竞赛试题及答案初一

数学竞赛试题及答案初一【试题一】题目:计算下列表达式的值:\[ 2^3 + 3 \times 4 - 5^2 \]【答案】首先计算指数部分:\[ 2^3 = 8 \]\[ 5^2 = 25 \]然后进行乘法运算:\[ 3 \times 4 = 12 \]接下来,按照运算顺序,先进行加法和减法:\[ 8 + 12 - 25 = 20 - 25 = -5 \]所以,表达式的值为 -5。
【试题二】题目:如果一个数的平方等于该数的两倍,求这个数。
【答案】设这个数为 \( x \),根据题意,我们有:\[ x^2 = 2x \]将等式两边同时除以 \( x \)(注意 \( x \neq 0 \)):\[ x = 2 \]所以,这个数是 2。
但我们还应该检查 \( x = 0 \) 的情况,因为 0 的平方也是 0 的两倍:\[ 0^2 = 2 \times 0 \]所以,这个数也可以是 0。
【试题三】题目:一个长方形的长是宽的两倍,如果长和宽都增加 2 米,那么面积增加了 24 平方米。
求原长方形的长和宽。
【答案】设原长方形的宽为 \( w \) 米,那么长为 \( 2w \) 米。
根据题意,长和宽都增加 2 米后,新的长为 \( 2w + 2 \) 米,新的宽为 \( w + 2 \) 米。
新的面积与原面积的差为 24 平方米:\[ (2w + 2)(w + 2) - 2w \times w = 24 \]展开并简化:\[ 2w^2 + 4w + 2w + 4 - 2w^2 = 24 \]\[ 6w + 4 = 24 \]\[ 6w = 20 \]\[ w = \frac{20}{6} = \frac{10}{3} \]所以原长方形的宽为 \( \frac{10}{3} \) 米,长为 \( 2 \times \frac{10}{3} = \frac{20}{3} \) 米。
【试题四】题目:一个班级有 40 名学生,其中 25% 的学生是男生。
初中数学竞赛讲座——数论部分7(同余)

第7讲同余的概念及基本性质数论有它自己的代数,称为同余理论.最先引进同余的概念与记号的是数学王子高斯.先看一个游戏:有n+1个空格排成一行,第一格中放入一枚棋子,甲乙两人交替移动棋子,每步可前移1,2或3格,以先到最后一格者为胜.问是先走者胜还是后走者胜?应该怎样走才能取胜?取胜之道是:你只要设法使余下的空格数是4的倍数,以后你的对手若走i格(i=1,2,3),你走4-i格,即每一次交替,共走了4格.最后只剩4个空格时,你的对手就必输无疑了.因此,若n除以4的余数是1,2或3时,那么先走者甲胜;若n除以4的余数是0的话,那么后走者乙胜.在这个游戏里,我们可以看出,有时我们不必去关心一个数是多少,而要关心这个数用m除后的余数是什么.又例如,1999年元旦是星期五,1999年有365天,365=7×52+1,所以2000年的元旦是星期六.这里我们关心的也是余数.这一讲中,我们将介绍同余的概念、性质及一些简单的应用.同余,顾名思义,就是余数相同.一、基础知识定义1 给定一个正整数m,如果用m去除a,b所得的余数相同,则称a与b对模m同余,记作a≡b(modm),并读作a同余b,模m.否则,就称a与b对于模m不同余,记作a≡b(mod m),根据定义,a与b是否同余,不仅与a、b有关,还与模m有关,同一对数a和b,对于模m同余,而对于模n也许就不同余,例如,5≡8(mod3),而5≡8(mod4),若a与b对模m同余,由定义1,有a=mq1+r,b=mq2+r.所以a-b=m(q1-q2),即m|a-b.反之,若m|a-b,设a=mq1+r1,b=mq2+r2,0≤r1,r2≤m-1,则有m|r1-r2.因|r1-r2|≤m-1,故r1-r2=0,即r1=r2.于是,我们得到同余的另一个等价定义:定义2若a与b是两个整数,并且它们的差a-b能被一正整数m整除,那么,就称a与b对模m同余.另外,根据同余的定义,显然有以下几种关系是成立的:⑴a≡a(mod n)⑵a≡b(modm)⇔b≡a(mod n)⑶a≡b(mod n)⇒a≡c(mod m)b≡c(modm)由此可见,同余是一种等价关系,以上这三条分别叫做同余的反射性,对称性和传递性,而等式也具有这几条性质.二、典型例题;例1.如果a≡b(mod m),以下命题正确的有哪些?请说明理由?⑴m| a-b⑵a=b+mt⑶a=k1m+ r1,b =k2m+r2(0≤r1,r2<m)⇔r1= r2解:⑴因a≡b(modm),所以可得a =k1m+r,b =k2m+ r,那么a-b=(k1-k2)m,由于k1-k2是整数,因此m|a-b是正确的.⑵根据⑴可得a-b= mt,即a=b+mt⑶根据⑴可得,m|r1-r2,又因为0≤| r1-r2 |<m,所以| r1-r2 |=0,故r1=r.2例2.判断正误,并说明理由.⑴如果a≡b(mod m)那么ka≡kb(mod m)⑵如果a≡b(modm),c是整数,那么a±c≡b±c(mod m)⑶如果a1≡b1(mod m),a2≡b2(mod m),那么a1±a2≡b1±b2 (modm),a1a2≡b1b2 (mod m).⑷如果3a≡3b(mod 6 ),那么a≡b (mod 6 )解:⑴∵a≡b(modm),∴m| a-b,∴m|k (a-b)即m|(ka-kb)∴ka≡kb(mod m) ⑴成正确⑵∵a≡b(mod m),∴m | a-b又因为c是整数,所以m| a-c-b+c,即m | (a-c)-(b-c)即a-c≡b-c(mod m)同理可得,a+c≡b+c(mod m)⑶仿照上面的两个小题的方汪,可以判定这个命题也是正确的⑷显然6≡12(mod6),而2≡4(mod 6),因此,这个命题不正确说明:⑶的结论可以得到同余的另一条性质,即a≡b(mod m)⇒a n≡b n(modm) 此题说明两个同余式能够象等式一样进行加、减、乘、乘方,但同余式两边却不能除以同一数,那么,同余式的两边在什么情况下可以同除以一个数呢?我们先看下面的例题.例3.由下面的哪些同余式可以得到同余式a≡b(mod5)①3a ≡3b (mo d 5) ②10a ≡10b (mod 5)③6a≡6b(mod 10) ④10a ≡10b (mod 20) 解:①因3a ≡3b (mod 5),所以5 | 3(a -b),而5 | 3 , 因此5 | a-b,故a ≡b(mod 5)②由10a≡10b (mo d 5)可以得到5 | 10(a -b ),而5 | 10,因此5不一定整除a -b ,故a ≡b (mod 5)就成立③由6a≡6b (mod 10)可得10 | 6(a -b ),而10=2×5,6=2×3,因此5 | a -b ,故a≡b(m od 5)成立④由10a ≡10b (mo d 20)可得到20 | 10(a-b ),而20= 4×5,4 | 10,因此5 | (a-b )故a≡b (mod 5)不成立综上所述,由3a ≡3b (m od 5)或6a ≡6b (mod 10)都可以得到a ≡b (mod 5)说明:在①中,因为(3,5)=1,因此由5 | 3(a -b )一定可以得到5 | a-b ,进而得到a ≡b (mod 5),一般地,如果(k ,m)=1,ka ≡kb (mo d m),那么a≡b (mod m )在③中,因(6,10)=2,因此由10| 6(a-b)一定可以得到5 | a -b ,进而得a ≡b(mo d 5),一般地,如果(k ,m )= d ,ka ≡kb (mod m ),那么a ≡b )(moddm .例4.如果a ≡b(mod 12)且a ≡b (mod 8),那么以下同余式一定成立的是哪些?①a ≡b(mod 4) ②a ≡b(mod 24) ③a ≡b(m od 20) ④a≡b (m od 48)解:正确的有①和②①由题中的条件可得12 | a -b,又因4 | 12,所以4 | a -b ,故a ≡b (mod 4).②因12 | a -b ,8| a -b ,所以a -b 是12和8的公倍数,又因为[8,12]=24,因此 a -b 必是24的倍数,即24 | a -b ,故a ≡b (mod 24).③显然,当a= 26,b = 2时满足条件a ≡b (mod 12)和a ≡b (mo d 8),但却不满足a≡b (mod 20).④同③,用a = 26,b = 2验证即可. 【说明】:⑴一般地,若a ≡b (mod m )且n | m ,那么a≡b (mo d n) ⑵若a ≡b (m od m ),a ≡b (mod n ),那么a ≡b (mod [m ,n ]),它的一个特殊情况就是: 如果a ≡b (mod m ),a ≡b (mo d n )且(m ,n )=1,那么a ≡b (mod m n )【一些结论】1.同余定义的等价形式①a ≡b(mod m ) m | a-b②a ≡b (mod m ) a = b+mt 2.同余式的同加、同乘性如果a 1≡b1(m od m ),a 2≡b 2(mod m )那么 ⑴a 1±a 2≡b 1±b 2(mod m) ⑵ka 1≡kb 1(mod m)(k ∈Z ) ⑶a 1a 2≡b 1b 2(m od m) ⑷a 1n ≡b 1n (m od m)(n是整数). 3.如果(k ,m )=d ,ka ≡kb (mod m ),那么a ≡b )(moddm. 这条性质的直接推论就是:如果(k ,m)=1,k a≡kb (mod m ),那么a ≡b (mo d m ) 4.如果a ≡b (mo d m )且n | m ,那么a ≡b(mod n )5.如果a≡b (m od m),a≡b (mo d n),那么a ≡b (mod [m,n ])这条性质的一个推论就是: 如果a ≡b(m od m ),a≡b (m od n )且(m ,n )=1,那么a ≡b (m od m n )例5.⑴求19992002除以9的余数;⑵求1010除以7的余数解:⑴∵9 | 1999-1000,∴1999≡1000≡1(mod 9)∴19992000≡12002≡1(mod 9),∴19992000除以9的余数是1⑵∵10≡3(mod 7),∴103≡33≡-1(mod 7)∴106≡(-1)2≡1(m od 7),∴1010≡104(mod 7) 又∵102≡9≡2(mod 7),∴102≡10 4≡22≡4(mod 7) 所以1010除以7的余数是4.说明:求较大数的余数时,可先设法找到与±1同余的数,然后利用同余式的性质,求出所求数的余数.例6.求14589+32002除以13的余数.解:∵145≡2(mod 13),∴1456≡26≡-1(mod 13)∴(1456)14≡(-1)14≡1(mod 13)即14584≡1(mod 13)又∵1455≡25≡6(mod 13)所以14589≡14584·1455≡6×1≡6(mod 13)又∵33≡1(mod 13),∴(33)667≡32001≡1(mo d 13),∴32002≡3(mod 13) 所以,14589+32002≡6+3≡9(mod 13)即14589+32002除以13的余数是9例7.求19982002的十位数字分析:此题可以通过19982002的末两位数来求解,与前面的方法类似解:∵199898≡-2(m od 100),∴19982002≡(-2)2002≡22002≡41001(mod 100)因为4≡4(m od 100),42≡16(m od 100),43≡64(m od 100),44≡56(mod100),45≡24(m od 100),46≡96(mod 100),47≡84(mod 100),48≡36(mod 100),49≡44(mo d 100),410≡76(m od 100),411≡4(mod 100)…所以4 n 除以100的余数是以4、16、64、56、24、96、84、36、44、76周期性出现的,因41001=410×100+1,所以41001≡4(m od 100),因此19982002≡4(m od 100),故19982002的十位数字是0.说明:正整数幂的末位数、末两位数、末三位数都具有周期性.例8(1998年匈牙利奥林匹克竞赛题)求使2n +1能被3整除的一切自然数n . 解∵∴则2n +1∴当n 为奇数时,2n+1能被3整除; 当n 为偶数时,2n +1不能被3整除.例9 求证31980+41981能被5整除. 证明 ∵∴∴∴例10.求20032002的末位数字.分析:此题就是求20032002除以10的余数解:∵2003≡3(mod 10),∴20034≡34≡1(mod 10),∴20032002≡(20034)500·20033≡1500·33≡27≡7(mod 10)∴20022002的末位数字是7.说明:对于十进制的整数011a a a a n n -有如下性质:)10(mod 0011a a a a a n n ≡- 例11.已知n 是正整数,证明48 | 72n ―2352n ―1 证明:∵48=3×16,(3,16)=1∴只需证明3| 72n ―2352n ―1且16 | 72n ―2352n ―1即可 ∵7≡1(mod 3),2352≡0(m od 3) ∴72n ―2352n ―1≡12n ―2352×0-1≡0(mod 3) ∴3 | 72n ―2352n ―1,又∵2352=16×147,∴2352≡0(m od 16) ∴72n ―2352n ―1≡49n -1≡1n -1≡0(m od 16)∴16 | 72n―2352n ―1,所以48| 72n ―2352n ―1.说明:当模很大时,可以用本题的方法把问题化为较小的模来求解,请同学位用这个方法重解例8.例12.已知n是任意的正整数,且m | 7n+12n―1,求正整数m的最大值.解:设an=7n+12n―1,那么,a1=7+12―1=18,a2=72+24―1=72∴(a1,a2)=(18,72)=18,∴m≤18,下面证明对任何正整数n,都有18 | 7n+12n―1又因为18=2×9,所以只须证明2| 7n+12n,9|7n+12n―1即可.∵7≡1(mod2),∴7n+12―1≡1n+0―1≡0(mod 2)即2 |7n+12n―1,对n进行分类讨论,⑴若n≡0(mod 3),则n=3k(k为正整数)7n+12n―1≡73k+36k+1≡(―2)3k+0―1≡(―8)k―1≡1k―1≡0(mod 9)⑵若n≡1(mod 3),则n=3k+1(k为非负整数)7n+12n―1≡73k+36k+127+12―1≡0(mod9)⑶若n≡2(mod 3),则n=3k+2(k为非负整数)7n+12n―1≡73k·72+36k+24―1≡72+24―1≡0(mod9)因此,对一切自然数n,都有9 | 7n+12n―1.综上所述,18 | 7n+12n―1,因此m的最大值为18.例13把1,2,3…,127,128这128个数任意排列为a1,a2,…,a128,计算出|a1-a2|,|a3-a4|,…,|a127-a128|,再将这64个数任意排列为b1,b2,…,b64,计算|b1-b2|,|b3-b4|,…,|b63-b64|.如此继续下去,最后得到一个数x,问x是奇数还是偶数?解因为对于一个整数a,有|a|≡a(mod2), a≡-a(mod2),所以b1+b2+…+b64=|a1-a2|+|a3-a4|+…+|a127-a128|≡a1-a2+a3-a4+…+a127-a128≡a1+a2+a3+a4+…+a127+a128(mod 2),因此,每经过一次“运算”,这些数的和的奇偶性是不改变的.最终得到的一个数x≡a1+a2+...+a128=1+2+ (12)=64×129≡0(mod2),故x是偶数.例14求证:一个十进制数被9除的余数等于它的各位数字之和被9除的余数.10≡1(mod9),故对任何整数k≥1,有10k≡1k=1(mod 9).因此即A被9除的余数等于它的各位数字之和被9除的余数.说明(1)特别地,一个数能被9整除的充要条件是它的各位数字之和能被9整除.(2)算术中的“弃九验算法”就是依据本题的结论.三、模拟训练1求证: (1)8|(551999+17);(2) 8(32n +7); (3)17|(191000-1).证 (1)因55≡-1(mod 8),所以551999≡-1(mo d 8),551999+17≡-1+17=16≡0(m od 8),于是8|(551999+17).(2)32=9≡1(m od 8),32n ≡1(mod 8),所以32n +7≡1+7≡0(mod 8),即8|(32n +7).(3)19≡2(mod 17),194≡24=16≡-1(m od 17),所以191000=(194)250≡(-1)250≡1(mod 17),于是17|(191000-1).2.求20032002的末位数字分析:此题就是求20032002除以10的余数解:∵2003≡3(m od 10),∴20034≡34≡1(mod 10),∴20032002≡(20034)500·20033≡1500·33≡27≡7(mod 10)∴20022002的末位数字是7说明:对于十进制的整数011a a a a n n -有如下性质:011a a a a n n -)10(mod 0a ≡.3求2999最后两位数码.解 考虑用100除2999所得的余数. ∵∴又∴∴∴2999的最后两位数字为88.4.求证:22000+1不能被7整数.分析:只需证明22000≡-1(mod 7)即可证明:∵26≡1(mod7),∴22000≡(26)333·22≡1·22≡4(mod 7),∴22000+1≡5(mod7)所以7 | 22000+15 对任意的自然数n,证明A=2903n-803n-464n+261n 能被1897整除.证1897=7×271,7与271互质.因为2903≡5(mod 7),803≡5(mod 7),464≡2(mod7),261≡2(mod7), 所以A=2903n-803n-464n+261n≡5n-5n-2n+2n=0(mod 7), 故7|A.又因为2903≡193(mod 271),803≡261(mod271),464≡193(mod 271),所以故271|A.因(7,271)=1,所以1897整除A.6任意平方数除以4余数为0和1(这是平方数的重要特征). 证因为奇数2=(2k+1)2=4k2+4k+1≡1(mod 4),偶数2=(2k)2=4k2≡0(mod 4),所以7任意平方数除以8余数为0,1,4(这是平方数的又一重要特征).证奇数可以表示为2k+1,从而奇数2=4k2+4k+1=4k(k+1)+1.因为两个连续整数k,k+1中必有偶数,所以4k(k+1)是8的倍数,从而奇数2=8t+1≡1(mod8),偶数2=(2k)2=4k2(k为整数).(1)若k=偶数=2t,则4k2=16t2=0(mod 8).(2)若k=奇数=2t+1,则4k2=4(2t+1)2=16(t2+t)+4≡4(mod 8),所以求余数是同余的基本问题.在这种问题中,先求出与±1同余的数是一种基本的解题技巧.8形如Fn=22n+1,n=0,1,2,…的数称为费马数.证明:当n≥2时,Fn的末位数字是7.证当n≥2时,2n是4的倍数,故令2n=4t.于是F n=22n+1=24t+1=16t+1≡6t+1≡7(mod 10),即F n的末位数字是7.说明费马数的头几个是F0=3,F1=5,F2=17,F3=257,F4=65537,它们都是素数.费马便猜测:对所有的自然数n,F n都是素数.然而,这一猜测是错误的.首先推翻这个猜测的是欧拉,他证明了下一个费马数F5是合数.。
数学竞赛试题初一及答案

数学竞赛试题初一及答案一、选择题(每题3分,共30分)1. 下列哪个数是最小的正整数?A. 0B. 1C. -1D. 2答案:B2. 计算下列哪个选项的结果等于10?A. 3 + 7B. 4 × 2C. 5 - 3D. 6 ÷ 2答案:A3. 如果一个数的平方等于9,那么这个数是:A. 3B. -3C. 3或-3D. 以上都不是答案:C4. 一个长方形的长是10厘米,宽是5厘米,那么它的面积是多少平方厘米?A. 20B. 30C. 50D. 60答案:C5. 一个数加上它的相反数等于:A. 0B. 1C. 2D. 无法确定答案:A6. 下列哪个分数是最简分数?A. 6/8B. 9/12C. 5/10D. 7/14答案:D7. 一个圆的直径是14厘米,那么它的半径是多少厘米?A. 7B. 14C. 28D. 无法确定答案:A8. 如果一个三角形的两个内角分别是40度和60度,那么第三个内角是多少度?A. 40B. 60C. 80D. 无法确定答案:C9. 一个数的立方等于8,那么这个数是:A. 2B. -2C. 2或-2D. 以上都不是答案:A10. 一个数的绝对值是5,那么这个数可能是:A. 5B. -5C. 5或-5D. 以上都不是答案:C二、填空题(每题4分,共20分)11. 一个数的平方根是4,那么这个数是______。
答案:1612. 如果一个数的一半是10,那么这个数是______。
答案:2013. 一个数的倒数是2,那么这个数是______。
答案:1/214. 一个数的立方等于27,那么这个数是______。
答案:315. 一个数的绝对值是3,那么这个数可能是______或______。
答案:3或-3三、解答题(每题10分,共50分)16. 计算下列表达式的值:(3x - 2) + (4x + 5),其中x = 2。
答案:首先将x的值代入表达式,得到(3×2 - 2) + (4×2 + 5) = 6 + 8 + 5 = 19。
初中数学竞赛辅导资料(初一用)

初中数学竞赛辅导资料第一讲 数的整除一、内容提要:如果整数A 除以整数B(B ≠0)所得的商A/B 是整数,那么叫做A 被B 整除。
0能被所有非零的整数整除.能被7整除的数的特征:①抹去个位数 ②减去原个位数的2倍 ③其差能被7整除.如 1001 100-2=98(能被7整除)又如7007 700-14=686, 68-12=56(能被7整除) 能被11整除的数的特征:①抹去个位数 ②减去原个位数 ③其差能被11整除 如 1001 100-1=99(能11整除)又如10285 1028-5=1023 102-3=99(能11整除) 二、例题例1已知两个三位数328和92x 的和仍是三位数75y 且能被9整除。
求x,y解:x ,y 都是0到9的整数,∵75y 能被9整除,∴y=6。
∵328+92x =567,∴x=3 例2已知五位数x 1234能被12整除,求x解:∵五位数能被12整除,必然同时能被3和4整除, 当1+2+3+4+x 能被3整除时,x=2,5,8 当末两位4x 能被4整除时,x =0,4,8∴x =8例3求能被11整除且各位字都不相同的最小五位数解:五位数字都不相同的最小五位数是10234,但(1+2+4)-(0+3)=4,不能被11整除,只调整末位数仍不行 调整末两位数为30,41,52,63,均可,∴五位数字都不相同的最小五位数是10263.练习一1、分解质因数:(写成质因数为底的幂的连乘积)①756②1859③1287④3276⑤10101⑥10296987能被3整除,那么a=_______________2、若四位数ax能被11整除,那么x=__________3、若五位数123435m能被25整除4、当m=_________时,59610能被7整除5、当n=__________时,n6、能被11整除的最小五位数是________,最大五位数是_________7、能被4整除的最大四位数是____________,能被8整除的最大四位数是_________。
平面基本图形浅说——初一数学竞赛系列讲座(7)

使原来的平面部分增加 3 仿此知 : 个. 第四条直线最多共使原来的平面 部分又增加 4 , 个 第五条直线最多共使原来的平面部分增加 5 个. 因此 , 同~ 平 面 内 , 在 5条直 线把 平 面 分 成 的部 分 最 多 , ( + 1 共 1 + 2 3 +5 1 + +4 一) 6部分 .
维普资讯
卢间的关 系 , 充 分 利 用平行 线 的 性质 . 应 因此 , 以延 长 AP 与 b 可
点 c, 或过点 P作直线 z a / . /
,
解
P一 口 +
如 图 5延 长 AP 交直 线 b于 点 C. ,
因为 口/ , /6所以 口 LA B. 一 C 因为 LA B 一 卢 P +LA B么 , 平面内这 5 条直线最多有几个交点呢? 5条直线 相 交 , 点尽可 能 多时 , 交 必须 满足 两个 条件 : 两条直 线都 每 有交点( 即无两条直线相互平行 )无三条直线共点. ; 因此, 每条直线与其 余 4条直线都有 1 个交点, 4 共 个点, 而每个点都在两条直线上, 5 故 条
多地画 出各直 线之 间 交点 个 数不 同 的 图形 , 试 并
说 明其 间的规律 .
分析
当 一6时 , 7条直 线 6个交 点 ,
仅 当其中 6条 直 线互 相 平 行 , 另一 条 直 线 与平 行 线相 交时 成立 ( 1 ; 图 )
由前知, 3 无 条直线共点的 7 直线的交点最
维普资讯
成 多 少部 分 ?这
这是平面基本图形的一个典型 问题 : 线、 点、 三角形是最基本 的平 面图形 , 值得认真研究. 基本 知 识 1 .过两点有且只有一条直线 ; 2 .平行线的判定与性质 ; 3 .三角形的内角和等于 10 8。 . 三角形的任意一个外角等于与它不相邻的两个 内角的和. 三角形的任意两边之和大于第三边 , 任意两边之差小于第三边. 在同一个三角形中, 等边所对的角相等, 等角所对的边相等 , 大角所 对 的边 较大 .
七年级(初一)数学竞赛试题及答案

1.若四边形ABCD中,∠A:∠B:∠C:∠D=1:3:5:6,则∠A,∠D的度数分别为()24°,144°2.已知a=255,b=344,c=533,d=622,那么a、b、c、d从小到大的顺序是解:∵a=255=(25)11,b=344=(34)11,c=533=(53)11,53>34>62>25,∴(53)11>(34)11>(62)11>(25)11,即a<d<b<c,3.7..对于有理数x,y,定义一种新的运算“*”:x*y=ax+by+c,其中a,b,c为常数,等式右边是通常的加法与乘法运算,已知3*5=15,4*7=28,求1*1的值.9.已知|a|=3,|b|=2,且|a-b|=b-a,则a+b= -1或-5解:∵|a-b|=b-a,∴知b>a,∵|a|=3,|b|=2,∴a=-3,b=2或-2,当a=-3,b=2时,a+b=-1,当a=-3,b=-2时,a+b=-5,∴a+b=-1或-5,故答案为-1或-5.10.设m2+m-1=0,则m3+2m2+2010=2011∵m2+m-1=0,①∴①×m得,m3+m2-m=0,②∴①+②得,m3+2m2-1=0,即m3+2m2=1,则m3+2m2+2010=1+2010=2011.15.把边长为40厘米的正方形ABCD沿对角线AC截成两个三角形,在两个三角形内如图,一个啤酒瓶的高度为30cm,瓶中装有高度12cm的水,将瓶盖盖好后倒置,解:设瓶的底面积为Scm,则左图V水=12Scm3,右图V空=10Scm3,∵V瓶=V水+V空=22Scm3,∴V水:V瓶=6:11.如图,长方形ABCD 被分成8块,图中的数字是其中5块的面积数,则图中阴影部分的面积为。
初一数学下竞赛试题及答案

初一数学下竞赛试题及答案一、选择题(每题3分,共30分)1. 若a和b互为相反数,且a+b=0,那么a的值是多少?A. 0B. 1C. -1D. 无法确定2. 下列哪个数是质数?A. 8B. 9C. 10D. 113. 一个数的平方根是4,这个数是多少?A. 16B. 8C. 4D. 24. 一个长方体的长、宽、高分别是a、b、c,它的体积是多少?A. abcB. a + b + cC. a - b - cD. a/b + c5. 一个圆的半径是5,它的周长是多少?A. 10πC. 25πD. 30π6. 一个数的绝对值是5,这个数可能是?A. 5B. -5C. 5或-5D. 都不是7. 如果x=2y,那么2x=?A. 2yB. 3yC. 4yD. 5y8. 一个直角三角形的两条直角边分别是3和4,斜边是多少?A. 5B. 6C. 7D. 89. 一个数的立方是-27,这个数是多少?A. 3B. -3C. 9D. -910. 一个数的倒数是1/4,这个数是多少?A. 4B. 1/4D. 1二、填空题(每题2分,共20分)11. 一个数的平方是25,这个数是________。
12. 一个数的立方是64,这个数是________。
13. 一个数的绝对值是10,这个数是________。
14. 如果一个数的相反数是-7,那么这个数是________。
15. 一个数的平方根是2或-2,这个数是________。
16. 一个数的倒数是3,这个数是________。
17. 如果x=3y,那么3x=________。
18. 一个直角三角形的两条直角边分别是5和12,斜边是________。
19. 一个圆的半径是10,它的周长是________。
20. 一个数的立方根是2,这个数是________。
三、解答题(每题10分,共50分)21. 证明勾股定理。
22. 解方程:x + 2 = 5。
23. 计算一个长方体的表面积,如果长方体的长、宽、高分别是2m、3m、4m。
初一数学竞赛测试题及答案

初一数学竞赛测试题及答案一、选择题(每题2分,共10分)1. 下列哪个数是最小的正整数?A. 0B. 1C. -1D. 2答案:B2. 如果一个数的平方等于这个数本身,那么这个数可能是:A. 0B. 1C. -1D. 2答案:A、B3. 一个数的绝对值是它本身,这个数是:A. 正数B. 负数C. 零D. 正数或零答案:D4. 下列哪个分数是最简分数?A. 4/8B. 5/10C. 3/4D. 6/9答案:C5. 如果一个三角形的三个内角分别为x°,y°和z°,那么x+y+z的值是:A. 180°B. 360°C. 90°D. 270°答案:A二、填空题(每题3分,共15分)6. 一个数的平方根是它本身,这个数可以是______。
答案:0或17. 如果a和b是两个连续的自然数,且a>b,那么a-b的值是______。
答案:18. 一个数的立方等于它本身,这个数可能是______。
答案:1或-1或09. 如果一个数的相反数是它本身,那么这个数是______。
答案:010. 一个数的绝对值等于它本身,这个数是非负数,即这个数是______。
答案:正数或零三、计算题(每题5分,共20分)11. 计算下列各题:(1) (-3) × (-4) = ______。
答案:12(2) 5 - (-3) = ______。
答案:8(3) (-2)² = ______。
答案:4(4) √16 = ______。
答案:4四、解答题(每题10分,共30分)12. 一个直角三角形的两条直角边分别为3厘米和4厘米,求斜边的长度。
答案:根据勾股定理,斜边长度为√(3² + 4²) = √(9 + 16) = √25 = 5厘米。
13. 一个数列的前三项为1, 1, 2,从第四项开始,每一项都是前三项的和。
求第10项的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初一数学竞赛第7讲 立体图形空间形体的想象能力是小学生的一种重要的数学能力,而立体图形的学习对培养这种能力十分有效。
我们虽然在课本上已经学习了一些简单的立体图形,如正方体、长方体、圆柱体、圆锥体,但有关立体图形的概念还需要深化,空间想象 能力还需要提高。
将空间的位置关系转化成平面的位置关系来处理,是解决立体图形问题的一种常用思路。
一、立体图形的表面积和体积计算例1 一个圆柱形的玻璃杯中盛有水,水面高 2.5cm ,玻璃杯内侧的底面积是72cm 2,在这个杯中放进棱长6cm 的正方体铁块后,水面没有淹没铁块,这时水面高多少厘米?解:水的体积为72×2.5=180(cm 3),放入铁块后可以将水看做是底面积为72-6×6=32(cm 2)的柱体,所以它的高为180÷32=5(cm )。
例2 下图表示一个正方体,它的棱长为4cm ,在它的上下、前后、左右的正中位置各挖去一个棱长为1cm 的正方体,问:此图的表面积是多少?分析:正方体有6个面,而每个面中间有一个正方形的孔,在计算时要减去小正方形的面积。
各面又挖去一个小正方体,这时要考虑两头小正方体是否接通,这与表面积有关系。
由于大正方体的棱长为4cm ,而小正方体的棱 长为1cm ,所以没有接通。
每个小正方体孔共有5个面,在计算表面积时都要考虑。
解:大正方体每个面的面积为4×4-1×1=15(cm 2),6个面的面积和为15×6=90(cm 2)。
小正方体的每个面的面积为1×1=1(cm 2),5个面的面积和为1×5=5(cm 2),6个小正方体孔的表面积之和为5×6=30(cm 2),因此所求的表面积为90+30=120(cm 2)。
想一想,当挖去的小正方体的棱长是2cm 时,表面积是多少?请同学们把它计算出来。
例3 正方体的每一条棱长是一个一位数,表面的每个正方形面积是一个两位数,整个表面积是一个三位数。
而且若将正方形面积的两位数中两个数码调过来则恰好是三位数的十位与个位上的数码。
求这个正方体的体积。
解:根据“正方体的每一条棱长是一个一位数,表面的每个正方形面积是一个两位数,整个表面积是一个三位数”的条件,可知正方体的棱长有5,6,7,8,9这五种可能性。
根据“将正方形面积的两位数中两个数码调过来恰好是三位数的十位上与个位上的数码”,可知这个正方体的棱长是7。
如右表: 因此这个正方体的体积是7×7×7=343。
例4一个长、宽和高分别为21cm,15cm和12cm的长方体,现从它的上面尽可能大地切下一个正方体,然后从剩余的部分再尽可能大地切下一个正方体,最后再从第二次剩余的部分尽可能大地切下一个正方体,剩下的体积是多少立方厘米?解:根据长方体的长、宽和高分别为21cm,15cm和12cm的条件,可知第一次切下尽可能大的正方体的棱长是12cm,其体积是12×12×12=1728(cm3)。
这时剩余立体图形的底面形状如图1,其高是12cm。
这样,第二次切下尽可能大的正方体的棱长是9cm,其体积是9×9×9=729(cm3)。
这时剩余立体图形可分割为两部分:一部分的底面形状如图2,高是12cm;另一部分的底面形状如图3,高是3cm。
这样,第三次切下尽可能大的正方体的棱长是6cm,其体积是6×6×6=216(cm3)。
因此,剩下的体积是21×15×12-(123+93+63)=3780-2673=1107(cm3)。
说明:如果手头有一个泥塑的长方体和小刀,那么做出这道题并不难。
但实际上,我们并没有依赖于具体的模型和工具,这就是想象力的作用。
我们正是在原有感性经验的基础上,想象出切割后立体的形状,并通过它们各个侧面的形状和大小表示出来。
因此,对一个立体图形,应该尽可能地想到它的原型。
例5右图是一个长27cm,宽8cm,高8cm的长方体。
现将它分为4部分,然后将这4部分重新组拼,能重组为一个棱长为12cm的正方体。
请问该怎么分?解:重组成的正方体的棱长是12cm,而已知长方体的宽是8cm,所以要把宽增加4cm,为此可按右图1中的粗线分开,分开重组成图2的形状;图2的高是8cm,也应增加4cm,为此可按图2中的虚线分开,分开后重组成图3的形状。
图3就是所组成的棱长为12cm的正方体。
说明:这里有一个朴素的思想,就是设法把不足12cm的宽和高补成12cm的棱长,同时按照某种对称的方式分割。
在解关于立体图形的问题时,需要有较丰富的想象力,要能把平面图形在头脑中“立”起来,另外还应有一定的作图本领和看图能力。
例6雨哗哗地不停地下着,如在雨地里放一个如右图那样的长方体的容器(单位:厘米),雨水将它下满要用1时。
有下列(1)~(5)不同的容器,雨水下满各需多长时间?解:根据题意知雨均匀地下,即单位面积内的降雨量相同。
所以雨水下满某容器所需的时间与该容器的容积和接水面(敞开部分)的面积之比有关。
因为在例图所示容器中:需1时接满,所以二、立体图形的侧面展开图例7 右图是一个立体图形的侧面展开图(单位:cm),求这个立体图形的表面积和体积。
解:这个立体图形是一个圆柱的四分之一(如右上图),圆柱的底面半径为10cm,高为8cm。
它的表面积为例8右图是一个正方体,四边形APQC表示用平面截正方体的截面。
请在右下方的展开图中画出四边形APQC的四条边。
解:把空间图形表面的线条画在平面展开图上,只要抓住四边形Array APQC四个顶点所在的位置这个关键,再进一步确定四边形的四条边所在的平面就可容易地画出。
(1)考虑到展开图上有六个顶点没有标出,可想象将展开图折成立体形,并在顶点上标出对应的符号,见右图。
(2)根据四边形所在立体图形上的位置,确定其顶点所在的点和棱,以及四条边所在的平面:顶点:A—A,C—C,P在EF边上,Q在GF边上。
边AC在ABCD面上,AP在ABFE 面上,QC在BCGF面上,PQ在EFGH面上。
(3)将上面确定的位置标在展开图上,并在对应平面上连线。
需要注意的是,立体图上的A,C点在展开图上有三个,B,D点在展开图上有二个,所以在标点连线时必须注意连线所在的平面。
连好线的图形如右上图。
例9如右图所示,剪一块硬纸片可以做成一个多面体的纸模型(沿虚线折,沿实线粘)。
这个多面体的面数、顶点数和棱数的总和是多少?解:从展开图可以看出,粘合后的多面体有12个正方形和8个三角形,共20个面。
这个多面体上部的中间是一个正三角形,这个正三角形的三边与三个正方形相连,这样上部共有9个顶点,下部也一样。
因此,多面体的顶点总数为 9×2=18(个)。
在20个面的边中,虚线有19条,实线有34条。
因为每条虚线表示一条棱,两条实线表示一条棱,所以多面体的总棱数为19+34÷2=36(条)。
综上所述,多面体的面数、顶点数和棱数之和为20+18+36=74。
说明:数学家欧拉曾给出一个公式:V+F-E=2。
公式中的V表示顶点数,E表示棱数,F表示面数。
根据欧拉公式,知道上例多面体的面数和顶点数之后,棱数便可求得:E=V+F-2=20+18-2=36(条)。
三、立体图形的截面与投影例10用一个平面去截一个正方体,可以得到几边形?解:如下图,可得到三角形、四边形、五边形和六边形。
例11一个棱长为6cm的正方体,把它切开成49个小正方体。
小正方体的大小不必都相同,而小正方体的棱长以厘米作单位必须是整数。
问:可切出几种不同尺寸的正方体?每种正方体的个数各是多少?解:13=1,23=8,33=27,43=64,53=125,63=216。
如果能切出1个棱长为5cm的正方体,那么其余的只能是棱长为1cm的正体体,共切出小正方体:1+(63-53)÷1=92(个)。
因为92>49,所以不可能切出棱长为5cm的正方体。
如果能切出1个棱长为4cm的正方体,那么其余的只能是棱长为1cm或2cm的正方体。
设切出棱长为1cm的正方体有a个,切出棱长为2cm的正方体有b个,则有设切出棱长为1cm的正方体有a个,棱长为2cm的正方体有b个,棱长为3cm 的正方体有c个,则解之得a=36,b=9,c=4。
所以可切出棱长分别为1cm,2cm和3cm的正方体,其个数依次为36,9和4。
例12现有一个棱长为1cm的正方体,一个长宽为1cm高为2cm的长方体,三个长宽为1cm高为3cm的长方体。
右侧图形是把这五个图形合并成某一立体图形时,从上面、前面、侧面所看到的图形。
试利用下面三个图形把合并成的立体图形(如上图)的样子画出来,并求出其表面积。
解:立体图形的形状如右图所示。
从上面和下面看到的形状面积都为9cm2,共18cm2;从两个侧面看到的形状面积都为7cm2,共14cm2;从前面和后面看到的形状面积都为6cm2,共12cm2;隐藏着的面积有2cm2。
一共有18+16+12+2=46(cm2)。
练习7深35cm,里面的水深10cm。
放进一个棱长20cm的正方体铁块后,水面高多少厘米?2.王师傅将木块刨成横截面如右图(单位:cm)那样的高40cm的一个棱柱。
虚线把横截面分成大小两部分,较大的那部分的面积占整个底面的60%。
这个棱柱的体积是多少立方厘米?3.在底面为边长60cm的正方形的一个长方体的容器里,直立着一根高1m,底面为边长15cm的正方形的四棱柱铁棍。
这时容器里的水半米深。
现在把铁棍轻轻地向正上方提起24cm,露出水面的四棱柱铁棍浸湿部分长多少厘米?4.下列各图形中,有的是正方体的展开图,写出这些图形的编号。
5.小玲有两种不同形状的纸板,一种是正方形,一种是长方形。
正方形纸板的总数与长方形纸板的总数之比是1∶2。
她用这些纸板做成一些竖式和横式的无盖纸盒(如右图),正好将纸板用完。
在小玲所做的纸盒中,竖式纸盒的总数与横式纸盒的总数之比是多少?6.请你在下面图(2)中画出3种和图(1)不一样的设计图,使它们折起来后都成为下图所示的长方形盒子(直线段与各棱交于棱的中点)。
7.在桌面上摆有一些大小一样的正方体木块,从正南方向看如下左图,从正东方向看如下右图,要摆出这样的图形至多用多少块正方体木块?至少需要多少块正方体木块?8.有一个正方体,它的6个面被分别涂上了不同的颜色,并且在每个面上至少贴有一张纸条。
用不同的方法来摆放这个正方体,并从不同的角度拍下照片。
(1)洗出照片后,把所拍摄的面的颜色种类不同的照片全部挑选出来,最多可以选出多少张照片?(2)观察(1)中选出的照片,发现各张照片里的纸条数各不相同。
问:整个正方体最少贴有多少张纸条?练习7答案1.15cm。
