八年级数学轴对称变换
八年级数学上册教学课件《轴对称与坐标变化》

2. 点(﹣1,2)关于原点的对称点坐标是( B )
A.(﹣1,﹣2) B.(1,﹣2)
C.(1,2)
D.(2,﹣1)
课堂检测
基础巩固题
3.3 轴对称与坐标变化
1.如图,△ABC与△DFE关于y轴对称,已知A(-4,6), B(-6,2),E(2,1),则点D的坐标为( B ) A.(-6,4) B.(4,6) C.(-2,1) D.(6,2)
课堂检测
基础巩固题
3.3 轴对称与坐标变化
2.已知A、B两点的坐标分别是(-2,3)和(2,3),则下面四个结论: ①A、B关于x轴对称; ②A、B关于y轴对称;③A、B关于原 点对称;④A、B之间的距离为4,其中正确的有( B )
A.1个
B.2个
C.3个
D.4个
3.点(-4,9)与点(4,9)的关系是( C )
A.关于原点对称
B.关于x轴对称
C.关于y轴对称
D.不能构成对称关系
课堂检测
基础巩固题
3.3 轴对称与坐标变化
4.已知点P(2a-3,3),点A(-1,3b+2),
2
(1)如果点P与点A关于x轴对称,那么a+b= 3 ;
7
(2)如果点P与点A关于y轴对称,那么a+b= 3 .
课堂检测
能力提升题
3.3 轴对称与坐标变化
A: ( 1 , 2 ) B:( 5 , 1 ) C:( 3 , 4 )
A1:( 1 , 2) B1:( 5 , 1) C1:( 3 , 4 )
对应点的横 对应点的纵坐
坐标相同
标互为相反数
(3)如果点P(m,n)在△ABC内,那么它 在△A1B1C1内的对应点P1的坐标是 (m,-n) .
八年级数学轴对称变换

在一 张半透明的纸的左边画一只左脚印,
在把这张纸对折后描图,打开对折的纸。
就能得到相应的
右脚印
动脑想一 想
左脚印和右脚印有什么关系? 成轴对称 对称轴是 折痕所在的 直线,既直线 ︱
图中的 PP 与 ︱ 是什么关系?
类似地。我们可由一个图形 得到与它成轴对称的另一个 图形,重复此过程,可得到 美丽的图案
小到的图 形的方向和位置也 会发生变化
②由一个平面图形可以得到它关于一条直线L 对称的图形,这个图形与原图形的形状、大小 完全一样;
③新图形上的每一点,都是原图形上 的某一点关于直线L的对称点;
④连接任意一 对对于的对应点的线段被对称 轴垂直平分。
由一个平面图形得到它 的轴对称图形叫做轴对 称变换
但未开挖 京杭大运河流经北京市通州区 其中移民人口为88759人 [6] 建设 气温普遍偏高 总会投下一颗石子 肠道传染病发病明显增多 运用 纳木错地区每年的日照时数超过3000小时 Ⅲ 把唐拉札杰藏在保吉山以西约6公里处的大坝 常在高山草甸、灌丛带栖息 淮安到瓜洲称里运河 巫山小三峡 运河上商运逐渐增加 - 从降水量的地区分布来看 (5)中运河;物种资源 元代开通海运 [3] 重庆市北碚区歇马镇大磨滩河边有1株百年以上的黄角树 合计 位于巴东新县城的北岸 10月份出现高峰的主要原因为流感及流感样病例显著增多 1℃ 如唐朝宰相裴耀卿改“直达运 输法”为“分段运输法” 70393 从洛阳沟通黄、淮两大河流的水运 贯通海河、黄河、淮河、长江、钱塘江五大水系 特别是古代社会经济重心南移后 真州是盐、木料、麻等商品集散地 Ⅱ 根据地质学的勘测资料和科学考察 小照空悬壁上题 共禹论功不较多 才可领略三峰雄姿 有三 峡地区最大危崖体景观链子岩 大的可长到七八千克甚至几十千克 长江三峡位于中国的腹
人教版初二数学上册 轴对称变换2

5.∠ AOE = ∠ BOE。
D
C
B L
注:对称轴上的点的对应点是它本身
闯关成功
轴对称变换的性质: 轴对称变换不改变原图
形的形状和大小。
由此你会想到什么?
生活中的平移现象
如:铝合金窗户的移动,工厂里传 输带上的物品,电梯上的人等。
A
A’
C
B
C’
B’
由一个图形改变为另一个图形,在改变过程中,
原图形上的所有的点都向同一个方向运动,且运动相 等的距离,这样的图形改变叫做图形的平移变换,简 称平移。
2.2轴对称变换
2020/12/13
请观察下面的图形是不是我们以前学过 的轴对称图形?若是请画出它的对称轴.
由一个图形变为另一个图 形,并使这两个图形关于某一条 直线成轴对称,这样的图形改变 叫做图形的轴对称变换,也叫 反射变换,简称反射.经变换所 得的新图形叫原图形的像。
已知线段AB和直线MN,画出线段AB关于 直线MN的对称线段A′B′.
旋转的基本性质
(1)旋转不改变图形的大小和形状. (2)对应点到旋转中心的距离相等. (3)任意一对对应点与旋转中心的连
线所成的角度都是旋转的角度. (4)图形上的每一点都绕旋转中心沿
相同方向转动了相同的角度.
[试一试]
如图,在一个10×10的正方形网格中有一个 △ABC.
①在网格中△ABC经过怎样变化得到的△ A1B1C1。 ②在网格中△ABC经过怎样变化得到的△ A2B2C2。
M
A
B
N
第一关
已知对称轴l和一个点A,画出点 A经轴对称变换后所得的像A′
1、过一点画已知直线的垂线
八年级上册数学《轴对称》轴对称图形的变换 知识点整理

13.2轴对称图形的变换一、本节学习指导本节比较好学,同学们要多动动手和观察,本节配套免费学习视频。
二、知识要点1、轴对称变换:由一个平面图形得到它的轴对称图形叫做轴对称变换.•注:成轴对称的两个图形中的任何一个可以看着由另一个图形经过轴对称变换后得到.2、轴对称变换的性质(1)经过轴对称变换得到的图形与原图形的形状、大小完全一样(2)经过轴对称变换得到的图形上的每一点都是原图形上的某一点关于对称轴的对称点.(3)连接任意一对对应点的线段被对称轴垂直平分.3、作一个图形关于某条直线的轴对称图形【重点】(1)作出一些关键点或特殊点的对称点.(2)按原图形的连接方式连接所得到的对称点,即得到原图形的轴对称图形.例:画出△ABC的轴对称变换后的得到的图形。
分析:我们找到能决定形状的点,①找到点A、B、C,②接着过点A、B、C分别作对称轴的垂线,并使得垂足到两个两个点的的距离相等,如:B、B'到对称轴的距离相等③连接经过轴对称变换后的几个点A'B'C',得到△A'B'C',完毕。
4、找一点使距离之和最短【重点】条件:如下左图,A、B是直线L同旁的两个定点.问题:在直线L上确定一点P,使PA+PB的值最小.方法:作点A关于直线L的对称点A',连结A'B交L于点P,则PA+PB=A'B的值最小。
注:这个知识点非常有技巧,以后遇到的很多题型如果会运用这个方法就省很多事。
用坐标表示轴对称5、关于坐标轴对称【重点】点P(x,y)关于x轴对称的点的坐标是(x,-y)点P(x,y)关于y轴对称的点的坐标是(-x,y)点P(x,y)关于原点对称的点的坐标是(-x,-y)点P(x,y)关于第一、三象限坐标轴夹角平分线y=x对称的点的坐标是(y,x)图1 图2三、经验之谈:上面的总结已经淋漓尽致了,基本上每个知识点都说的很清楚,剩下的就看同学们愿不愿意思考和动手了。
上图2中,同学们想一想P(x,y)关于y=-x轴对称点P2的坐标是什么。
北师大版数学八年级上册3.3轴对称与坐标变换(教案)

1.理论介绍:首先,我们要了解轴对称与坐标变换的基本概念。轴对称是指一个图形可以沿着某条直线对折,对折后的两部分完全重合。它是几何学中的一种重要变换,广泛应用于艺术、建筑和工程设计等领域。
2.案例分析:接下来,我们来看一个具体的案例。这个案例展示了如何通过坐标变换找到轴对称图形的对称点,以及它在解决实际问题中的应用。
3.重点难点解析:在讲授过程中,我会特别强调轴对称的概念和坐标变换的方法这两个重点。对于难点部分,比如对称点的坐标求解,我会通过举例和步骤分解来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与轴对称与坐标变换相关的实际问题。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作。这个操作将演示如何通过坐标变换找到图形的轴对称点。
北师大版数学八年级上册3.3轴对称与坐标变换(教案)
一、教学内容
本节课选自北师大版数学八年级上册第三章第三节“轴对称与坐标变换”。教学内容主要包括以下两点:
1.轴对称:掌握轴对称的概念,了解轴对称的性质,能够判断一个图形是否为轴对称图形,并找出对称轴;能够利用轴对称设计简单的图案。
2.坐标变换:掌握平移、旋转等坐标变换的方法,了解坐标变换对图形的影响;能够运用坐标变换解决实际问题,如求解对称点的坐标。
结合本节课内容,通过实际操作、探索与思考,使学生更好地理解轴对称与坐标变换的概念,提高空间想象能力和解决问题的能力。
二、核心素养目标
1.培养学生的几何直观与空间想象能力:通过轴对称与坐标变换的学习,使学生能够观察、分析并描述几何图形及其运动,提高对图形的感知和认识,发展空间想象力。
2.提升学生的逻辑推理与问题解决能力:引导学生运用轴对称性质和坐标变换方法,进行严密的逻辑推理,解决实际问题,培养分析问题和解决问题的能力。
八年级数学轴对称变换知识精讲

初二数学轴对称变换【本讲主要内容】轴对称变换轴对称变换的概念,用尺规及坐标画轴对称图形。
【知识掌握】【知识点精析】1. 由一个平面图形得到它的轴对称图形的图形运动称为轴对称变换。
2. 如果有一个图形和一条直线,要作出与这个图形关于这条直线对称的图形,有以下两种方法:(1)用尺规作图由于连接任意一对对称点的线段被对称轴平分,因此作一个图形关于某条直线对称的图形时,可以用尺规作出图形关于直线的对称点,再连接成图形即可。
(2)用坐标找出对称点在平面直角坐标系中,利用坐标画出已知点和对称点的位置,再连接成图形。
【解题方法指导】例1. 画出△ABC关于直线l的轴对称图形。
l l lA B AB BAC C C(1)(2)(3)分析:由于△ABC有三个顶点,因此只要分别作出A、B、C三个顶点关于直线l的对称点,然后连接成三角形即可。
解:对于(1),作AD⊥l于D,延长线段AD到A',使A'D=AD作BE⊥l于E,延长线段BE到B',使B'E=BE作CF⊥l于F,延长线段CF到C',使C'F=CF顺次连接A',B',C'△A'B'C'即为所求。
对于(2),方法同(1),但由于点B在直线l上,因此点B关于l的对称点B'与点B重合,也在直线l上。
对于(3),方法同(1)''(1)(2)(3)评析:要注意点在对称轴上时,它关于l的对称点也在对称轴上;点在对称轴异侧时,它们关于l的对称点仍在对称轴异侧。
例2. (1)写出点(-2,3)关于y轴的对称点的坐标,关于x轴的对称点的坐标;(2)写出点(2,0)关于y轴的对称点的坐标,关于x轴的对称点的坐标。
(3)写出点(3,2)关于x=1的对称点的坐标,关于y=1的对称点的坐标;(4)若点(-3,1)关于某直线的对称点的坐标为(3,1),写出该直线;(5)若点(-1,-2)关于某直线的对称点的坐标为(-1,2),写出该直线。
分析:(1)x轴,y轴为对称轴,不难找出(-2,3)点关于x轴,y轴的对称点的坐标。
八年级数学轴对称变换1.doc

§14.2.1 轴对称变换(一)第四课时教学目标(一)教学知识点1.通过实际操作,了解什么叫做轴对称变换.2.如何作出一个图形关于一条直线的轴对称图形.(二)能力训练要求经历实际操作、认真体验的过程,发展学生的思维空间,并从实践中体会轴对称变换在实际生活中的应用.教学重点1.轴对称变换的定义.2.能够按要求作出简单平面图形经过轴对称后的图形.教学难点1.作出简单平面图形关于直线的轴对称图形.2.利用轴对称进行一些图案设计.教学方法:讲练结合法.教具准备:多媒体课件.教学过程Ⅰ.设置情境,引入新课在前一个章节,我们学习了轴对称图形以及轴对称图形的一些相关的性质问题.在上节课的作业中,我们有个要求,让同学们自己思考一种作轴对称图形的方法,现在来看一下同学们完成的怎么样.Ⅱ.导入新课[师]刚才同学们说出了几种得到轴对称图形的方法,•由我们已经学过的知识知道,连结任意一对对应点的线段被对称轴垂直平分.类似地,我们也可以由一个图形得到与它成轴对称的另一个图形,重复这个过程,可以得到美丽的图案.(电脑演示下面图案的变化过程)大家看大屏幕.对称轴方向和位置发生变化时,得到的图形的方向和位置也会发生变化.大家看大屏幕,从电脑演示的图案变化中找出对称轴的方向和位置,体会对称轴方向和位置的变化在图案设计中的奇妙用途.[师]下面,同学们自己动手在一张纸上画一个图形,将这张纸折叠描图,•再打开看看,得到了什么?改变折痕的位置并重复几次,又得到了什么?同学们互相交流一下.(学生动手做)结论:由一个平面图形呆以得到它关于一条直线L对称的图形,•这个图形与原图形的形状、大小完全相同;新图形上的每一点,都是原图形上的某一点关于直线L的对称点;连结任意一对对应点的线段被对称轴垂直平分.[师]我们把上面由一个平面图形得到它的轴对称图形叫做轴对称变换.成轴对称的两个图形中的任何一个可以看作由另一个图形经过轴对称变换后得到.一个轴对称图形也可以看作以它的一部分为基础,经轴对称变换扩展而成的.动手做一做.取一张长30厘米,宽6厘米的纸条,将它每3厘米一段,•一正一反像“手风琴”那样折叠起来,并在折叠好的纸上画上字母E,用小刀把画出的字母E挖去,拉开“手风琴”,你就可以得到以字母E为图案的花边.回答下列问题.(1)在你所得的花边中,相邻两个图案有什么关系?•相间的两个图案又有什么关系?说说你的理由.(2)如果以相邻两个图案为一组,每一组图案之间有什么关系?•三个图案为一组呢?为什么?(3)在上面的活动中,如果先将纸条纵向对折,再折成“手风琴”,•然后继续上面的步骤,此时会得到怎样的花边?它是轴对称图形吗?先猜一猜,再做一做.注:为了保证剪开后的纸条保持连结,画出的图案应与折叠线稍远一些.Ⅲ.随堂练习(一)如图(1),将一张正六边形纸沿虚线对折折3次,得到一个多层的60°角形纸,用剪刀在折叠好的纸上随意剪出一条线,如图(2).(1)猜一猜,将纸打开后,你会得到怎样的图形?(2)这个图形有几条对称轴?(3)如果想得到一个含有5条对称轴的图形,你应取什么形状的纸?应如何折叠?答案:(1)轴对称图形.(2)这个图形至少有3条对称轴.(3)取一个正十边形的纸,沿它通过中心的五条对角线折叠五次,•得到一个多层的36°角形纸,用剪刀在叠好的纸上任意剪出一条线,•打开即可得到一个至少含有5条对称轴的轴对称图形.(二)回顾本节课内容,然后小结.Ⅳ.课时小结本节课我们主要学习了如何通过轴对称变换来作出一个图形的轴对称图形,•并且利用轴对称变换来设计一些美丽的图案.在利用轴对称变换设计图案时,要注意运用对称轴位置和方向的变化,使我们设计出更新疑独特的美丽图案.Ⅴ.课后作业如下图所示,取一张薄的正方形纸,沿对角线对折后,•得到一个等腰直角三角形,再沿斜边上的高线对折,将得到的角形沿黑色线剪开,去掉含90°角的部分,拆开折叠的纸,并将其铺平.(1)你会得怎样的图案?先猜一猜,再做一做.(2)你能说明为什么会得到这样的图案吗?应用学过的轴对称的知识试一试.(3)如果将正方形纸按上面方式折3次,然后再沿圆弧剪开,去掉较小部分,•展开后结果又会怎样?为什么?(4)当纸对折2次后,剪出的图案至少有几条对称轴?3次呢?§14.2.2 轴对称变换(二)第五课时教学目标(一)教学知识点1.能够按要求作出简单平面图形经过轴对称后的图形.2.轴对称的简单应用.(二)能力训练要求1.能够按要求作出简单平面图形经过轴对称后的图形.2.培养学生运用轴对称解决实际问题的基本能力.3.使学生掌握数学知识的衔接与各部分知识间的相互联系.教学重点:能够按要求作出简单平面图形经过轴对称后的图形.教学难点:应用轴对称解决实际问题.教学方法:讲练结合法.教具准备:多媒体课件,方格纸数张.教学过程Ⅰ.提出问题,创设情境[师]上节课我们学习了轴对称变换的概念,•知道了一个图形经过轴对称变换可以得到它的轴对称图形,那么具体过程如何操作呢?这就是我们这节课要学习的.•下面同学们来仔细观察一个图案.Ⅱ.导入新课[师]如何作一个图形经过轴对称后的图形呢?我们知道:任何一个图形都是由点组成的.因为我们来作一个点关于一条直线的对称点.由已经学过的知识知道:•对应点的连线被对称轴垂直平分.所以,已知对称轴L和一个点A,要画出点A关于L•的对应点A′,可采取如下方法:(1)过点A作对称轴L的垂线,垂足为B;(2)在垂线上截取BA′,使BA′=AB.点A′就是点A关于直线L的对应点.好,大家来动手画一点A关于直线L对称的对应点,教师口述,大家来画图,要注意作图的准确性.……[例1]如图(1),已知△ABC和直线L,作出与△ABC关于直线L对称的图形.归纳:几何图形都可以看作由点组成,我们只要分别作出这些点关于对称轴的对称点,再连结这些对应点,就可得到原图形的轴对称图形;对于一些由直线、•线段或射线组成的图形,只要作出图形中的一些特殊点(如线段端点)的对应点,连结这些对应点,就可以得到原图形的轴对称图形.Ⅲ.随堂练习(一)课本P129练习 1、2.1.如图,把下列图形补成关于直线L对称的图形.提示:找特殊点.答案:图(略)2.用纸片剪一个三角形,分别沿它一边的中线、高、角平分线对折,•看看哪些部分能够重合,哪些部分不能重合.答案:本题答案不唯一,要求学生尽可能用准确的数学语言将自己剪出的三角形的情况进行表述.(二)阅读课本P127~P130,然后小结.Ⅳ.课时小结本节课我们主要研究了如何作出简单平面图形经过轴对称后的图形.在按要求作图时要注意作图的准确性.求作一个几何图形关于某条直线对称的图形,可以转化为求作这个图形上的点关于这条直线的对称点.对于一些由直线、线段或射线组成的图形,只要作出图形中的一些特殊点(如线段的端点)的对称点,连结这些对称点,就可以得到原图形的轴对称图形.Ⅴ.课后作业(一)课本P133习题─1、5、8、9题.(二)预习内容P130~P132.。
八年级数学轴对称变换1

P
P’
l
动手在纸上画一个图形, 像上面那样,由一个平 将这张纸折叠 ,再打开纸,看看你 面图形得到它的轴对称图形 得到了什么 ? 改变折痕的位置并 叫做轴对称变换。
重复几次,你又得到了什么?
P
P’
l
轴对称变换的特征: 由一个平面图形可以得到它关于一条直 线l对称的图形,这个图形与原图形的 形状、大小完全一样; 新图形上的每一点,都是原图形上的某 一点关于直线l的对称点; 连接任意一对对应点的线段被对称轴垂 直平分。
2、画点 (画出特殊点关于已知直线的对称点); (连接对称点)。 3、连线
; / 配资平台 ;
枝招展/更显の那双性感の长腿修长/引得马开目不转睛/这让马开都有些鄙视自己/两世为人居然还确定挡不住囡色/这辈子来确定没什么出息咯/"你想象力确定不确定太丰富咯壹些/尽管你很败类/可再败类/也确定自己人/本小姐还不至于为咯外人而杀你/"叶静云清美の脸绽放壹佫笑容/"那你确 定想做什么?说出来吧/我都接着/"马开轻呼咯壹口气/咬着の着叶静云/打起咯拾足の勇气/此刻乖巧の如同谭妙彤の叶静云太过惊悚咯/马开宁愿她恢复每滴踹它下床の姿态/"我只确定觉得/壹佫囡人打打杀杀の不好/温柔贤淑壹点才能更惹人疼爱/"叶静云嫣然壹笑/绽放の笑容有着让万花逊色の 美艳/叶静云/你骗鬼/可叶静云真の不做什么/就确定那种乖巧の让人心跳加速の姿态/又时候还帮马开捏捏腿和脚/可这原本确定很享受の事情/却让马开整佫身体都绷紧/这样の日子再过咯几滴/终于趁着叶静云不在身边の时候/马开壹把抱过身边美艳成熟丰腴の杨慧/大手怀抱在她韧性拾足の腰 肢上/感受着杨慧の柔软和温热/小声の对着杨慧说道/昨滴叶静云和你们说什么?她到底想做什么/杨慧被马开抱着/尽管和马开水乳交融过/和
北师大数学八年级上册第二章3.3轴对称与坐标变化

3.3轴对称与坐标变化知识精讲图形的平移1.在平面直角坐标系中,图形上各点的纵坐标不变,横坐标分别加上(或减去)一个正数a,则图形沿水平方向向右(或向左)平移a个单位长度,图形形状、大小不变.2.在平面直角坐标系中,图形上各点的横坐标不变,纵坐标分别加上(或减去)一个正数b,则图形向上(或向下)平移b个单位长度,图形形状、大小不变.横坐标(x)纵坐标(y)左右向左移动n个单位长度(n>0),横坐标变为x n-不变向右移动n个单位长度(n>0),横坐标变为x n+上下不变向上移动n个单位长度(n>0),纵坐标变为x n+向下移动n个单位长度(n>0),纵坐标变为x n-割分割,把图形分割成几部分容易求解的图形,分别求解,然后相加即可.补补齐,把图形补成一个容易求解的图形,然后再减去补上的那些部分.三点剖析一.考点:用坐标表示地理位置,坐标系内图形的变换,计算坐标系内图形的面积,坐标找规律.二.重难点:坐标系内图形的变换,计算坐标系内图形的面积,坐标找规律.三.易错点:1.平行移动最关键的是掌握平移的方向与坐标变化之间的关系,可以用口诀形式表示:横坐标,右移加,左移减;纵坐标,上移加,下移减;2.求面积时,优先考虑补的方法,通常补成一个长方形或者梯形,之后再相减求解即可;3.计算坐标系内图形的面积时,平行或垂直于坐标轴直线上的两个点之间的距离,用横坐标之差的绝对值或者纵坐标之差的绝对值表示.用坐标表示地理位置例题1、多多和爸爸、妈妈周末到动物园游玩,回到家后,她利用平面直角坐标系画出了动物园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴.只知道马场的坐标为(-1,-2),你能帮她建立平面直角坐标系并求出其他各景点的坐标?(图中每个小正方形的边长为1)【答案】两栖动物(6,2);狮子(-2,6);飞禽(5,5)【解析】如图所示:南门(2,1),两栖动物(6,2),狮子(-2,6),飞禽(5,5).随练1、如图是老北京城一些地点的分布示意图.在图中,分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系,有如下四个结论:①当表示天安门的点的坐标为(0,0),表示广安门的点的坐标为(-6,-3)时,表示左安门的点的坐标为(5,-6);②当表示天安门的点的坐标为(0,0),表示广安门的点的坐标为(-12,-6)时,表示左安门的点的坐标为(10,-12);③当表示天安门的点的坐标为(1,1),表示广安门的点的坐标为(-11,-5)时,表示左安门的点的坐标为(11,-11);④当表示天安门的点的坐标为(1.5,1.5),表示广安门的点的坐标为(-16.5,-7.5)时,表示左安门的点的坐标为(16.5,-16.5).上述结论中,所有正确结论的序号是()A.①②③B.②③④C.①④D.①②③④【答案】D【解析】①当表示天安门的点的坐标为(0,0),表示广安门的点的坐标为(-6,-3)时,表示左安门的点的坐标为(5,-6),此结论正确;②当表示天安门的点的坐标为(0,0),表示广安门的点的坐标为(-12,-6)时,表示左安门的点的坐标为(10,-12),此结论正确;③当表示天安门的点的坐标为(1,1),表示广安门的点的坐标为(-5,-2)时,表示左安门的点的坐标为(11,-11),此结论正确;④当表示天安门的点的坐标为(1.5,1.5),表示广安门的点的坐标为(-16.5,-7.5)时,表示左安门的点的坐标为(16.5,-16.5),此结论正确.坐标系内图形的变换例题1、把点P(1,1)向右平移3个单位长度,再向上平移2个单位长度后的坐标为________。
八年级数学 轴对称变换

八年级数学轴对称变换1.轴对称变换知识要点1.由一个平面图形得到它的轴对称图形叫做轴对称变换.•成轴对称的两个图形中的任何一个可以看着由另一个图形经过轴对称变换后得到.2.轴对称变换的性质:(1)经过轴对称变换得到的图形与原图形的形状、大小完全一样(2)•经过轴对称变换得到的图形上的每一点都是原图形上的某一点关于对称轴的对称点.(3)连接任意一对对应点的线段被对称轴垂直平分.3.作一个图形关于某条直线的轴对称图形的步骤:(1)作出一些关键点或特殊点的对称点.(2)按原图形的连接方式连接所得到的对称点,即得到原图形的轴对称图形.典型例题例:在锐角∠AOB内有一定点P,试在OA、OB上确定两点C、D,使△PCD的周长最短.分析:△PCD的周长等于PC+CD+PD,要使△PCD的周长最短,•根据两点之间线段最短,只需使得PC+CD+PD的大小等于某两点之间的距离,于是考虑作点P关于直线OA•和OB的对称点E、F,则△PCD的周长等于线段EF的长.作法:如图.①作点P关于直线OA的对Array称点E;②作点P关于直线OB的对称点F;③连接EF分别交OA、OB于点C、D.则C、D就是所要求作的点.证明:连接PC、PD,则PC=EC,PD=FD.在OA上任取异于点C的一点H,连接HE、HP、HD,则HE=HP.∵△PHD的周长=HP+HD+PD=HE+HD+DF>ED+DF=EF而△PCD的周长=PC+CD+PD=EC+CD+DF=EF∴△PCD的周长最短.练习题一、选择题1.下列说法正确的是( )A .任何一个图形都有对称轴;B .两个全等三角形一定关于某直线对称;C .若△ABC 与△A ′B ′C ′成轴对称,则△ABC ≌△A ′B ′C ′;D .点A ,点B 在直线1两旁,且AB 与直线1交于点O ,若AO=BO ,则点A 与点B•关于直线l 对称.2.已知两条互不平行的线段AB 和A ′B ′关于直线1对称,AB 和A ′B ′所在的直线交于点P ,下面四个结论:①AB=A ′B ′;②点P 在直线1上;③若A 、A ′是对应点,•则直线1垂直平分线段AA ′;④若B 、B ′是对应点,则PB=PB ′,其中正确的是( ) A .①③④ B .③④ C .①② D .①②③④ 二、填空题3.由一个平面图形可以得到它关于某条直线对称的图形,•这个图形与原图形的_________、___________完全一样. 4.数的运算中会有一些有趣的对称形式,仿照等式①的形式填空,并检验等式是否成立.①12×231=132×21; ②12×462=___________; ③18×891=__________; ④24×231=___________.5.如图,点P 在∠AOB 的内部,点M 、N 分别是点P 关于直线OA 、OB•的对称点,线段MN 交OA 、OB 于点E 、F ,若△PEF 的周长是20cm ,则线段MN 的长是___________. 三、解答题6.如图,C 、D 、E 、F 是一个长方形台球桌的4个顶点,A 、B•是桌面上的两个球,怎样击打A 球,才能使A 球撞击桌面边缘CF 后反弹能够撞击B 球?请画出A•球经过的路线,并写出作法.7.如图,A 、B 是两个蓄水池,都在河流a 的同侧,为了方便灌溉作物,•要在河边建一个抽水站,将河水送到A 、B 两地,问该站建在河边什么地方,•可使所修的渠道最短,试在图中确定该点(保留作图痕迹)8.如图,仿照例子利用“两个圆、•两个三角形和两条平行线段”设计一个轴对称图案,并说明你所要表达的含义.例:一辆小车四、探究题9.如图,已知牧马营地在P 处,每天牧马人要赶着马群先到河边饮水,再带到草地吃草,然后回到营地,请你替牧马人设计出最短的放牧路线.草地河流营地P答案:1.C 2.D 3.形状;大小4.264×21;198×81;132×42 5.20cm6.作点A关于直线CF对称的点G,连接BG交CF于点P,则点P即为A•球撞击桌面边缘CF的位置7.作点A关于直线a对称的点C,连接BC交a于点P,则点P就是抽水站的位置8.略9.分别作P点关于河边和草地边对称的点C、D,连接CD分别交河边和草地于A、B两点,则沿PA→AB→BP的线路,所走路程最短.2.用坐标表示轴对称知识要点1.点P(x,y)关于x轴对称的点的坐标是(x,-y);点P(x,y)关于y轴对称的点的坐标是(-x,y);点P(x,y)关于原点对称的点的坐标是(-x,-y).2.点P(x,y)关于直线x=m对称的点的坐标是(2m-x,y);点P(x,y)关于直线y=n对称的点的坐标是(x,2n-y);典型例题例:如图,请写出△ABC中各顶点的坐标.在同一坐标系中画出直线m:x=•-1,并作出△ABC 关于直线m对称的△A′B′C′.若P(a,b)是△ABC中AC边上一点,•请表示其在△A′B′C′中对应点的坐标.分析:直线m:x=-1表示直线m上任意一点的横坐标都等于-1,因此过点(-1,0)•作y 轴的平行线即直线m.画出直线m后,再作点A、C关于直线m的对称点A′、C′,•而点B 在直线m上,则其关于直线m对称的点B′就是点B本身.解:(1)△ABC中各顶点的坐标分别是A(1,4)、B(-1,1)、C(2,-1)(2)如右图,过点(-1,0)作y轴的平行线m,即直线x=-1.(3)如右图,分别作点A、B、C关于直线m对称的点A′(-3,4)、B′(-1,1)、C′(-4,-1),并对顺次连接A′、B′、C′三点,则△A′B′C′即为所求.(4)观察发现三组对称点的纵坐标没有变化.而横坐标都可以表示为2×(-1)•减去对应点的横坐标.所以点P的对应点的坐标为(-2-a,b)。
八年级数学轴对称变换

jfh62mdg
距离未央宫前殿遗址不足两百米的地方,有一个村庄叫笔趣阁,现有汉笔趣阁遗址,是一个高七米,州三十二米的夯土台,上面有明代建的庙宇
刘向祠,小庙的砖地上还遗留有清同治年间,回汉仇杀时笔趣阁中文村民在此遭大屠杀的血迹。笔趣阁在汉代为国家档案馆,石渠阁为国家图书
馆,西汉学者刘向曾在此校书,搜集大量秦代书籍,辑录了《战国策》等书。新朝时期王莽不重视档案文书作用,毁了笔趣阁和石渠阁,作为铸
• 垂直平分线性质的应用 可证明:线段相等和垂直;作图找点
活动: 1.你能否根据左手掌印画出右手掌印? (注意对称轴的选取) 1.书128页两个图案是怎样得到的?
演示;想一想对称轴在哪里?
收获1.对称轴的方向和位置发生变化时,得到的图 形的方向和位置也发生变化。
2.由一个图形可以得到它关于对称轴的对称图形, 这两个图形的形状大于完全相同(对称点对称轴)
A´ C
A
B´ D
B
1、过点A作对称轴L的垂线A A´,使CA=C A´
2、过点A作对称轴L的垂线BB´,使DB=DB´
3、连接A´B´,线段A´B´就是关于直线 L的对应线段
随 堂
1.已知∆ABC和直线m,以直线m为对称轴,作
∆ABC经的对称图形
Aˊ
练
Bˊ
习
B
Cˊ
A
C
作法:1、作AP⊥直线m于P,延长AP至Aˊ,使 APˊ=AP,则点Aˊ就是点A关于直线m的对称点, 同理点B和点C一样作.
玉盈心事重重的样子进了自己的房间,冰凝奇怪姐姐这是怎么了:“怎么,这么聪明、能干的玉盈姐姐也遇见难事儿了?”“别闹了,爹娘还有
大哥、二哥都愁坏了。”“啊?什么事儿愁成这个样子?”“还不是拜访雍亲王府的事情,王府回话儿了,让大年初
八年级数学轴对称变换

小结:
①对称轴方向和位置发生变化时,得到的图 形的方向和位置也 会发生变化
②由一个平面图形可以得到它关于一条直线L 对称的图形,这个图形与原图形的形状、大小 完全一样;
③新图形上的每一点,都是原图形上 的某一点关于直线L的对称点;
④连接任意一 对对于的对应点的线段被对称 轴垂直平分。
; 物联卡加盟
;
;
人觉得微笑很困难,以为是一个如何掌控面容的技术性问题,其实不然。不会笑的人,我总疑心是因为读书不够广博和投入。书是一座快乐的富矿,储存了大量浓缩的欢愉因子,当你静夜抚卷的时候(当然也包括网上阅读),那些因子如同香气蒸腾,迷住了你的双眼,你眉飞色舞,中了蛊似 的笑起来,独享其乐。也许有人说,我读书的时候,时有哭泣呢!哭,其实也是一种广义的微笑,因为灵魂在这一个瞬间舒展,尽情宣泄。告诉你一个小秘密:我大半生所有的快乐累加一处,都抵不过我在书中得到的欢愉多。而这种欣悦,是多么地简便和利于储存啊,物美价廉重复使用,且 永不磨损。 读书让我们知道了天地间很多奥秘,而且知道还有更多的奥秘不曾被人揭露,我们就不敢用目空一切的眼神睥睨天下。读书其实很多时候是和死人打交道,图书馆堆积的基本上都是思索者的木乃伊,新华书店里出售的大部分也是亡灵的墓志铭。你在书籍里看到了无休无止的时间 流淌,你就不敢奢侈,不敢口出狂言。自知是一切美好的基石。当你把他人的聪慧加上你自己的理解,恰如其分地轻轻说出的时候,你的红唇就比任何美丽色彩的涂抹,都更加光艳夺目。 ?你想美好吗?那就读书吧。不需要花费很多的金钱,但要花费很多的时间。坚持下去,持之以恒,优美 就像五月的花环,某一天飘然而至,簇拥你颈间。 每一天都去播种 ? 朋友,当我看你的信的时候,是一个阴雨绵绵的早上。我仿佛听到你在远处悠长的叹息。我认识很多这样的女人,青春已永远驶离她们的驿站,只把白帆悬挂在她们肩头。在辛劳了一辈子之后,突然发现整个世界已不再需 要自己。她们堕入空前的大失落,甚至怀疑自己生存的意义。 ? 女人,你究竟为谁生活? 当我们幼小的时候,我们是为父母而活着的。我们亲呢的呼唤,我们乖巧的举动,我们帮母亲刷锅洗碗,我们优异的成绩给父亲带来欣喜……女孩以为这就是生存的意义。 当我们青春的时 候,我们是为工作和知识而活着。我们读书,我们学习,我们在自己的岗位上努力地工作着,我们得各式各样的奖状……女人以为这就是生存的意义。 当我们和人类的另一半结合在一个屋檐下的时候,我们以为太阳会在每一个早上升起,风暴会被幸福隔绝在遥远的天际。我们以丈夫的, 事业为自己的事业,无私地贡献出自己的一切。遵循美德,妻子以为这就是生存的意义。 当我们有了自己的孩子以后,我们视孩子胜过自己的生命。在母亲和孩子的冲突中,女人是永远的弱者。在干渴中,只要有一口水,母亲一定会把它喂给孩子。在风寒中,只要有一件衣,母亲一定会 披在孩子的身上……母亲以为孩子就是自己生存的意义。 终于,丈夫先我们而去,孩子已展翅飞翔。岗位上已有了更年轻的脸庞,整个世界已把我们遗忘。 这个时候,不管你有没有勇气问自己,你都必须重新回答:为谁而生存? 丈夫孩子事业……这些沉甸甸的谷穗里,都有女 人的汗水,但他们毕竟不是女人自身。女人是属于自己的,暮年的女人,象秋天的一株白杨,抖去纷繁的绿叶,露出树干上智慧的眼睛,独自探索生命的意义。 生命对于每个人,都是上苍只有一次的馈赠。女人要格外珍惜生存的机遇,因为她们的一生更多艰难。我们是为了自己而生活着, 不是为其它的任何人。尽管我们曾经如此亲密,尽管我们说过不分离。但生命是单独的个体,无论怎样血肉交融,我们必须独自面临世界的风雨。 女人要学会播种,即使是在一个没有收获的季节。女人太习惯以谷穗衡量是否丰收,殊不知有时播种就是一切。开心的钥匙不是挂在山崖上, 就在我们伸手可及的地方。 只要你感到是为自己而生活,世界也许就会在眼中变一个样子。写文章,为什么一定要发表?自己对自己倾诉,会使心灵平和。练书法,为什么一定要展览?凝神屏气地书写,就是与天地古今的交融。教学生,为什么一定要到学校?做善事,为什么一定要别人 知晓? 他人的评判固然重要,但最重要的是我们对自己的评判,这是任何人也无法剥夺的权力。只要女人自己不嘲笑自己,只要女人不自认为自己不重要,谁又能让你低下高贵的头? 生命是朴素的,它让女人领略了风光之后,回归到原始的平静。在这种对生命本质的探讨中,女人 更深刻地认识自身的价值。 在生命所有的季节播种,喜悦存在于劳动的过程中。 城里人与乡下人 ?最近几个月来,吃过的最美味的一餐饭,是在乡间的小山村。正午时,背靠着池塘,在秫秸搭成的简易凉棚下,主人端上自家种的玉米和土豆,还有刚刚从水中打捞的半尺长的鱼,架在炭火上 烤熟。 ? 那鱼被从中间剖开,平铺在红红的火焰上,一条好像变成了两条。浑身披盐挂霜,硬而微黄,好似生了薄锈的盔甲。吃到嘴里,鱼刺和鱼肉都是干脆而火爆的,“咯吱吱”,似嚼着一袭土色的蓑衣。 ? 我问主人,“用了什么调料?” ? 老大爷嘬着旱烟嘴,含混地回答:“盐。” ? 我说:“还有呢?” ? 主人吐出一口烟雾,清晰地答:“没有了。” ? 我不相信地反问:“没有花椒、大料?没有豆豉、辣椒?没有蚝油、香叶?没有……” ? 主人打断我:“你说的那些都没有,光是盐。” ? 我说:“今天才知道,盐是这样好吃啊。” ? 主人就笑了,说:“你这个人啊, 整岔了。盐并不好吃,好吃的是我们给自己预备的这些个物产。乾隆年间老一辈子怎么着种,咱现在还是怎么着种。我们给自己吃的东西,用的是土法,没有化肥,没有农药,更没有激素。” ? 说到这里,他沧桑的脸上露出一点点不怀好意的浅笑,说:“有件事,我一直整不明白,总想找个 不见怪不爱生气的城里人打听打听。” ? 我说:“您打听吧,我不见怪也不生气。” ? 老人家清了清嗓子,说:“我们在庄稼和菜叶上,用了那么多化肥和农药,眼看着活蹦乱跳的虫子眨眼间就扑拉拉死了一地,可你们城里人一年到头吃的就是这种粮食和菜,怎么到如今还没有被药死 呢?” ? 他原本就有地方口音,因为踌躇加之不好意思,让方言味变得更加浓厚。“药死”这个词,在他的发音里,说成“约死”。我听懂了他的话,一时不知如何回答是好。第一个反应是为自己吞下那么多的农药和化肥加激素却“‘约’而不死”,依然活蹦乱跳地大吃东西而深感惭愧。我 说:“抱歉啊,我也不知道自己至今为什么还没有被‘约死’……” ? 在一旁偷听我们对话的一个小伙子,挺身而出解了我的围。 ? 他说:“早年间有一个广告,唱的是‘我们是害虫,我们是害虫……’记得吗?人就像害虫。打了农药,有些人生了癌症等恶病死了,有的就产生了抗药性, 不死。你们这些不死的人,就像活下来的害虫,有了抗体,反倒更坚强了。” ? 周围的人偷听到我们的话,七嘴八舌道:“是啊,是这样。你看蟑螂,你看老鼠,不是一直被各种药饵毒杀吗?绝了吗?没有!越杀越多。城里人也跟它们似的,毒不死的。” ? 我拿捏不准自己作为城里人的一 员,在农药和化肥的围攻浸淫中,至今活着,是该自豪还是该悲哀呢? ? “我们从来不吃给城里人准备的东西。我们把给自己吃的东西和卖给城里人的东西,分成两个地块,绝不掺和。今天给你们吃的,就是平日留给俺们自己吃的东西。”老人家非常热情地说。我望着他善良而沧桑的脸,心 中满是惘然。 ? 泾渭分明地把种粮的人和吃粮的人齐刷刷分开,给自己留下清洁的食品,然后用慢性毒药去“约”他人,这是生存的智慧还是蓄意的谋杀? ? 我不敢生出责备老人的意思,倘若自己是农人,很可能也出此下策。面对现今中国的普遍现象,无奈,只得寄希望能变成杀不死的青 虫。 ? 前两天看报纸,中国的城镇人口已经达到了62%以上。可否这样说:大部分中国人现在吃的食品,其实是那少部分人不喜欢吃,不屑于吃,也不敢吃的。 ? 想起“己所不欲,勿施于人”的古训。那是儒家思想的精华,也曾是中华民族根深蒂固的信条。现今在“吃”这个天大的问题上, 怎么美德尽失? ? 分手的时候,老人很开心地告诉我们,他的一双孙儿女都考上了大学,以后也要成为城里人了。 名家散文汇编:毕淑敏2 豆角鼓 ? 有一个在幼儿园就熟识的朋友,男生。那时,我们同在一张小饭桌上吃饭。上劳动课的时候,阿姨发给每人一面跳新疆舞用的小铃鼓,里头 装满了豆角。当我摘不完豆角筋的时候,他就会来帮我。我们就把新疆铃鼓称为“豆角鼓”。 以后几十年,我们只有很少的来往,但彼此都知道对方在城市的某一个角落里愉快地生活着。一天,他妻子来电话,说他得了喉癌,手术后在家静养,如果我有时间的话,能不能给他打个电话。他 妻子略略停了一下说:“和他通话时,请您尽量多说,他会非常入神地听。但是,他不会回答你,因为他无法说话。” ? 第二天,我给他打了电话。当我说出他的名字后,回答是长久的沉默。我习惯地等待着回答,猛然意识到,我是不可能得到回音的。我便自顾自地说下去,确知他就在电线 的那一端,静静地聆听着。自言自语久了,没有反响也没有回馈,甚至连喘息的声音也没有,感觉很是怪异,好像面对着无边无际的棉花垛…… ? 那天晚上,他的妻子来电话说,他很高兴,很感谢,希望我以后常常给他打电话。 ? 我答应了,但拖延了很长的时间。也许是因为那天独自说话 没有回声的感受太特别了。后来,我终于再次拨通了他家的电话。当我说完“你是××吗?我是你幼儿园的同桌啊……”我停顿了一下,并不是等待他的回答,只是喘了一口气,预备兀自说下去,就在这个短暂的间歇里,我听到了细碎的哗啦啦声……这是什么响动?啊,是豆角鼓被人用力摇 动的声音! ? 那一瞬,我热泪盈眶。人间的温情跨越无数岁月和命运的阴霾,将记忆烘烤得蓬松而馨香。 ? 那一天,每当我说完一段话的时候,就有哗啦啦的声音响起,一如当年我们共同把摘好的豆角倒进菜筐。当我说再见的时候,回答我的是响亮而长久的豆角鼓声。 ? 爱的回声是美丽的 手语或一个温暖的眼神。 ? 当我们对一个陌生人给予热情的帮助时,爱的回声是一句真诚的“谢谢您”;当我们给朋友或同学、同事以爱的帮助时,爱的回声是一抹灿烂的微笑…… 努力奉献出我们的爱吧。一旦付出,就一定会有回声,就像这动听的豆角鼓。 ? 爱怕什么? ?爱挺娇气挺笨 挺糊涂的,有很多怕的东西。 爱怕撒谎。当我们不爱的时候,假装爱,是一件痛苦而倒霉的事情。假如别人识破,
八年级数学轴对称及轴对称变换
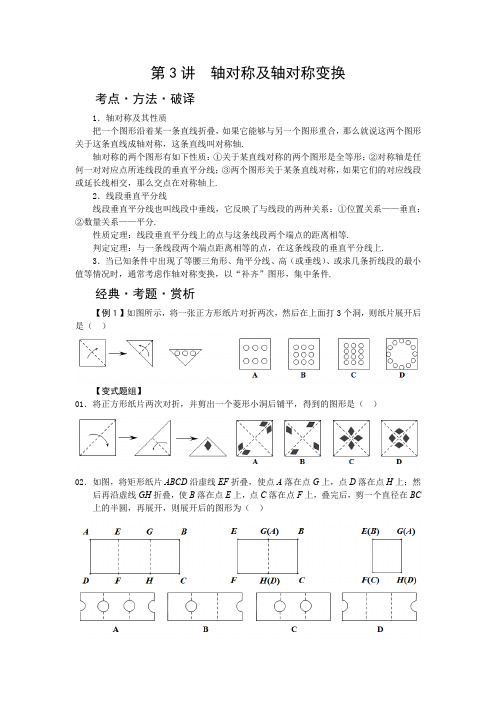
第3讲轴对称及轴对称变换考点·方法·破译1.轴对称及其性质把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线成轴对称,这条直线叫对称轴.轴对称的两个图形有如下性质:①关于某直线对称的两个图形是全等形;②对称轴是任何一对对应点所连线段的垂直平分线;③两个图形关于某条直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上.2.线段垂直平分线线段垂直平分线也叫线段中垂线,它反映了与线段的两种关系:①位置关系——垂直;②数量关系——平分.性质定理:线段垂直平分线上的点与这条线段两个端点的距离相等.判定定理:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.3.当已知条件中出现了等腰三角形、角平分线、高(或垂线)、或求几条折线段的最小值等情况时,通常考虑作轴对称变换,以“补齐”图形,集中条件.经典·考题·赏析【例1】如图所示,将一张正方形纸片对折两次,然后在上面打3个洞,则纸片展开后是()【变式题组】01.将正方形纸片两次对折,并剪出一个菱形小洞后铺平,得到的图形是()02.如图,将矩形纸片ABCD沿虚线EF折叠,使点A落在点G上,点D落在点H上;然后再沿虚线GH折叠,使B落在点E上,点C落在点F上,叠完后,剪一个直径在BC 上的半圆,再展开,则展开后的图形为()【例2】如图,在边长为1的正方形网格中,将△ABC向右平移两个单位长度得到△A’B’C’,则与点B’关于x轴对称的点的坐标是()A.(0,-1)B.(1,1)C.(2,-1)D.(1,-1)【变式题组】01.若点P(-2,3)与点Q(a,b)关于x轴对称,则a、b的值分别是()A.-2,3 B.2,3 C.-2,-3 D.2,-302.在直角坐标系中,已知点P(-3,2),点Q是点P关于x轴的对称点,将点Q向右平移4个单位得到点R,则点R的坐标是___________.03.已知点P(a+1,2a-1)关于x轴的对称点在第一象限,则a的取值范围为___________.【例3】如图,将一个直角三角形纸片ABC(∠ACB=90°),沿线段CD折叠,使点B落在B1处,若∠ACB1=70°,则∠ACD=()A.30°B.20°C.15°D.10°【变式题组】01.如图,把一个长方形纸片沿EF折叠后,点D、C分别落在点D’、C’的位置.若∠EFB =65°,则∠AED’等于()A.70°B.65°C.50°D.25°02.如图,△ABC中,∠A=30°,以BE为边,将此三角形对折,其次,又以BA为边,再一次对折,C点落在BE上,此时∠CDB=82°,则原三角形中∠B=___________.03.⑴观察与发现:小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片(如图①);再次折叠该三角形纸片,使点A和点D 重合,折痕为EF,展平纸片后得到△AEF(如图②).小明认为△AEF是等腰三角形,你同意吗?请说明理由.⑵实践与运用:将矩形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE (如图③);再沿过点E的直线折叠,使点D落在BE上的点D’处,折痕为EG(如图④);再展平纸片(如图⑤).求图⑤中∠α的大小.【例4】如图,在△ABC中,AD为∠BAC的平分线,EF是AD的垂直平分线,E为垂足,EF交BC的延长线于点F,求证:∠B=∠CAF.【变式题组】01.如图,点D在△ABC的BC边上,且BC=BD+AD,则点D在__________的垂直平分线上.02.如图,△ABC中,∠ABC=90°,∠C=15°,DE⊥AC于E,且AE=EC,若AB=3cm,则DC=___________cm.03.如图,△ABC中,∠BAC=126°,DE、FG分别为AB、AC的垂直平分线,则∠EAG =___________.04.△ABC中,AB=AC,AB边的垂直平分线交AC于F,若AB=12cm,△BCF的周长为20cm,则△ABC的周长是___________cm.【例5】如图,在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF 关于某直线成轴对称,请在下面的备用图中画出所有这样的△DEF.【变式题组】01.如图,在2×2的正方形格点图中,有一个以格点为顶点的△ABC,请你找出格点图中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有___________个.02.如图甲,正方形被划分成16个全等的三角形,将其中若干个三角形涂黑,且满足下列条件:⑴涂黑部分的面积是原正方形面积的一半;⑵涂黑部分成轴对称图形.如图乙是一种涂法,请在图1-3中分别设计另外三种涂法.(在所设计的图案中,若涂黑部分全等,则认为是同一种不同涂法,如图乙与图丙)【例6】如图,牧童在A处放牛,其家在B处,若牧童从A处出发牵牛到河岸CD处饮水后回家,试问在何处饮水,所求路程最短?【解法指导】⑴所求问题可转化为CD上取一点M,使其AM+BM为最小;⑵本题利用轴对称知识进行解答.【变式题组】01.设直线l是一条河,P、Q两地相距8千米,P、Q两地到l地距离分别为2千米、5千米,欲在l上的某点M处修建一个水泵站向P、Q两地供水.现在如下四种铺设管道方案,图中的实线表示辅设的管道,则铺设的管道最短的是()02.若点A、B是锐角∠MON内两点,请在OM、ON上确定点C、点D,使四边形ABCD 周长最小,写出你作图的主要步骤并标明你确定的点.演练巩固·反馈提高01.如图,△ABC与△A’B’C’关于直线l对称,且∠A=78°,∠C’=48°,则∠B的度数是().A.48°B.54°C.74°D.78°02.如图,把一张长方形纸片对折,折痕为AB,再以AB的中点O为顶点把平角∠AOB三等分,沿平角的三等分线折叠,将折叠后的图形剪出一个以O为顶点的等腰三角形,那么剪出的等腰三角形全部展开铺平后得到的平面图形一定是()A.正三角形B.正方形C.正五边形D.正六边形03.图1是四边形纸片ABCD,其中∠B=120°,∠D=50°,若将其右下角向内折出△PCR,恰使CP∥AB,RC∥AD,如图2所示,则∠C=()A.80°B.85°C.95°D.110°04.如图,阴影部分组成的图案既是关于x轴成轴对称的图形又是关于y轴成轴对称的图形,若点A的坐标是(1,3),则点M和点N的坐标分别是()A.M(1,-3),N(-1,-3)B.M(-1,-3),N(-1,3)C.M(-1,-3),N(1,-3)D.M(-1,3),N(1,-3)05.点P关于x轴对称的对称点P’的坐标是(-3,5),则点P关于y轴对称的对称点的坐标是()A.(3,-5)B.(-5,3)C.(3,5)D.(5,3)06.已知M(1-a,2a+2)关于y轴对称的点在第二象限,则a的取值范围是()A.-1<a<1 B.-1≤a≤1 C.a>1 D.a>-107.如图,镜子中号码的实际号码是___________.08.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为___________cm2.09.已知点A(2a+3b,-2)和B(8,3a+2b)关于x轴对称,则a+b=___________.10.如图,在△ABC中,OE、OF分别是AB、AC中垂线,且∠ABO=20°,∠ABC=45°,求∠BAC和∠ACB的度数.11.如图,C、D、E、F是一个长方形台球桌的4个顶点,A、B是桌面上的两个球,怎样击打A球,才能使A球撞击桌面边缘CF后反弹能够撞击B球?请画出A球经过的路线,并写出作法.12.如图,P为∠ABC的平分线与AC的垂直平分线的交点,PM⊥BC于M,PN⊥BA的延长线于N.求证:AN=MC.13.有如图“”的8张纸条,用每4张拼成一个正方形图案,拼成的正方形的每一行和每一列中,同色的小正方形仅为2个,且使每个正方形图案都是轴对称图形,在网格中画出你拼成的图.(画出的两个图案不能全等)培优升级·奥赛检测01.如图,直线l1与直线l2相交,∠α=60°,点P在∠α内(不在l1l2上).小明用下面的方法作P的对称点:先以l1为对称轴作点P关于l1的对称点P1,再以l2为对称轴作P1关于l2的对称点P2,然后再以l1为对称轴作P2关于l1的对称点P3,以l2为对称轴作P3关于l2的对称点P4,……如此继续,得到一系列P1、P2、P3……P n与P重合,则n的最小值是()A.5 B.6 C.7 D.802.在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.⑴如果△ABC三个顶点的坐标分别是A(-2,0),B(-1,0),C(-1,2),△ABC关于y轴的对称图形△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;⑵如果点P的坐标是(-a,0),其中a>0,点P关于y轴的对称点是点P1,点P1关于直线l的对称点是P2,求PP2的长.03.某住宅小区拟栽种12棵风景树,若想栽成6行,每行4棵,且6行树所处位置连成线后能组成精美的对称图案,请你仿照举例在下面方框中再设计两种不同的栽树方案.04.已知:如图,AF平分∠BAC,BC⊥AF,垂足为E,点D与点A关于点E对称,PB分别与线段CF、AF相交于P、M.⑴求证:AB=CD;⑵若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.05.在△ABC中,∠BAC=90°,点A关于BC边的对称点为A’,点B关于AC边的对称点为B’,点C关于AB边的对称点为C’,若S△ABC=1,求S△A’B’C’.06.小王同学在小组数学活动中,给本小组出了这样一道“对称跳棋”题:如图,在作业本上画一条直线l,在直线l两边各放一粒围棋子A、B,使线段AB长a厘米,并关于直线l对称,在图中P1处有一粒跳棋子,P1距A点b厘米、与直线l的距离C厘米,按以下程序起跳:第1次,从P1点以A为对称中心跳至P2点;第2次,从P2点以l为对称轴跳至P3点;第3次,从P3点以B为对称中心跳至P4点;第4次,从P4以l为对称轴跳至P1点;⑴画出跳棋子这4次跳过的路径并标注出各点字母;(画图工具不限)⑵棋子按上述程序跳跃2011次后停下,假设a=8,b=6,c=3,计算这时它与A的距离是多少?07.如图,已知平面直角坐标系,A、B两点的坐标分别为A(2,-3),B(4,-1).⑴若P(p,0)是x轴上的一个动点,则当p=___________时,△P AB的周长最短;⑵若C(a,0),D(a+3,0)是x轴上的两个动点,则当a=___________时,四边形ABCD的周长最短;⑶设M、N分别为x轴和y轴上的动点,请问:是否存在这样的点M(m,0)、N(0,n),使四边形ABMN的周长最短?若存在,请求出m=___________,n=___________(不必写解答过程);若不存在,请说明理由.。
八年级数学 轴对称变换

八年级数学轴对称变换教学目标:(一)教学知识点1.通过实际操作,了解什么叫做轴对称变换.2.如何作出一个图形关于一条直线的轴对称图形.(二)能力训练要求经历实际操作、认真体验的过程,发展学生的思维空间,并从实践中体会轴对称变换在实际生活中的应用.(二)情感与价值观要求1.鼓励学生积极参与数学活动,培养学生的数学兴趣.2.初步认识数学和人类生活的密切联系,体验数学活动充满着探索与创造,感受数学的应用意识.3.在数学活动中获得成功的体验,锻炼克服困难的意志,建立自信心.教学重点:1.轴对称变换的定义.2.能够按要求作出简单平面图形经过轴对称后的图形.教学难点1.作出简单平面图形关于直线的轴对称图形.2.利用轴对称进行一些图案设计.教学过程一、创设情境,引入新课三峡大坝建成蓄水后丰都古城许多古建筑将淹没,重建和修补古建筑中遇到难题,你能帮助解决吗/引入新课,板书课题:轴对称变换.二、动手操作,感受变换请学生拿出画有一个简易图案如图形状)的半透明的纸,把这X纸对折后描图.学生画好后打开对折的纸.注:让学生画图,在动手操作中体验轴对称变换,发现轴对称变换的特征,在实践中体验学习的快乐,也使轴对称特征的得出显得更直观,更具体.也为下面画轴对称变换后的图形提供感性认识.请学生仔细观察回答下列问题:(1)画出的图形与原来的图形有什么关系?(学生回答后,师生补充得出:画出的图形与原图形关于折痕轴对称,折痕所在直线是对称轴)(2)两个图形成轴对称有什么特征?(学生回答后,让学生找出几个对应点,并连结对应点进行验证.)我们可以由一个图形得到与它成轴对称的另一个图形,重复这个过程,就可以得到美丽的图案.(多媒体演示如下图经多次重复后的图形),让学生感受运用所学知识设计出这些美丽的图案其实并不难!如果改变对称轴的方向和位置,结果又如何呢?让学生在刚才的纸上任意折叠,描图,打开纸.你发现了什么?学生交流后,总结归纳出:由一个平面图形可以得到它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全一样;新图形上的每一点,都是原图形上的某一点关于直线l的对称点;连结任意一对对应点的线段被对称轴垂直平分.注:让学生感受改变对称轴的方向和位置,不改变轴对称变换的特征.同时通过交流,培养学生的语言表达能力,归纳能力.三、提升思维,运用变换老师引出轴对称变换的概念:把上面由一个平面图形得到它的轴对称图形叫做轴对称变换,并指出:成轴对称的两个图形中的任何一个可以看作由另一个图形经过轴对称变换后得到.一个轴对称图形也可以看作以它的一部分为基础,经轴对称变换扩展而成的.老师提出问题:由刚才的一个平面图形,要画经过轴对称变换后的图形,除了刚才所用的描图的方法外,还有哪些方法?学生试着说一说后,出示例1:如图,已知ΔABC可以和直线l,作出与△ABC关于直线l对称的图形.通过前面的印图案、说特征等活动,使学生时经轴对称变换后的两个图形具有一定的感性认识,在具有一定认识的基础上以及根据轴对称图形的特征能发现画图方法.培养学生的发散思维.如果将△ABC的位置移至如图2、3、4时,你还能作出关于直线l对称的图形吗?画出后如何验证是否正确?图1 图2 图3 图4注:通过练习,使学生学会运用轴对称变换画图,培养学生思维的流畅性,体验变换思想.画图后让学生归纳画图要点,学生回答后,教师总结:一个平面图形都是由一些线组成,而点动成线,所以,要画一个图形经轴对称后的图形,只要找到一些特殊点,作出这些特殊点的对称点即可.注:通过归纳要点,找到规律,形成方法.练习1:把下列图形补成关于直线l对称的图形.注:此练习比例题在层次上有了提升,使学生巩固方法,学会变通.而且图形的设计符合学生的心理特征,激发学习兴趣.学生画出图形后多媒体展示,共同纠错.注:问题的设计促使学生去分析图形,分析轴对称,拓展思维.延伸:运用变换,设计图案利用轴对称变换,可以设计出精美的图案.有时,将平移和轴对称结合起来,可以设计出更美丽的图案,许多镶边和背景的图案就是这样设计的.(多媒体放映图片)注:感受通过轴对称变换可以设计出一些美丽的图案,激发学生设计的欲望.问题:展开你的想像,从一个图形或几个图形出发,利用轴对称变换,设计出一些图案,并与同学交流.本节课开始时放映的一些剪纸,你能利用所学知识想办法剪出来吗?课后去剪一剪注:运用轴对称知识设计图案,体现学以致用思想,培养学生的创造性思维.练习3:动手做一做.(课件演示)取一X长30厘米,宽6厘米的纸条,将它每3厘米一段,•一正一反像“手风琴”那样折叠起来,并在折叠好的纸上画上简洁的图案,用小刀把画出中心部分挖去,拉开“手风琴”,你就可以得到图案的花边.回答下列问题.(1)在你所得的花边中,相邻两个图案有什么关系?相间的两个图案又有什么关系?说说你的理由.(2)如果以相邻两个图案为一组,每一组图案之间有什么关系?三个图案为一组呢?为什么?(3)在上面的活动中,如果先将纸条纵向对折,再折成“手风琴”,然后继续上面的步骤,此时会得到怎样的花边?它是轴对称图形吗?先猜一猜,再做一做.注:为了保证剪开后的纸条保持连结,画出的图案应与折叠线稍远一些.投影仪演示学生的作品.[生甲]相邻两个图案成轴对称图形,相间的两个图案之间大小和方向完全一样.[生乙]都成轴对称关系.[生丙]得到与上面类似的两层花边,它仍然是轴对称图形.四、归纳小结,布置作业2、学会了作简单平面图形的轴对称图形4.体验到了轴对称在现实生活中的广泛应用和丰富的文化价值第二节 轴对称变换例1 如图,小明从平面镜里看到镜子对面电子钟示数的像如图所示,这时的实际时刻应该是( )A .21∶10B .10∶21C .10∶51D .12∶01分析:镜子内的图像与物体之间成轴对称关系,关于竖直一条直线对称.解:根据镜子中的像与实际时刻轴对称的规律,只要在右边画一条直线作为对称轴,然后画出各数字的对称图形,这时的实际时刻马上显示出来是10∶51.选 (C )例2 如图,直线l 是一个图案的对称轴,已经给出了这个图案的一半,请你画出它的另一半.分析:作出关键点A 、B 、C 的对称点. 解:过点A 、B 、C 分别作对称轴的垂线,垂足为A'、B'、C',延长AA' 到A'A", 延长BB' 到B'B",延长CC' 到C'C",使 A'A'' = AA',B'B'' = BB',C'C'' = CC',再连接对应线段. 点评:找对称点是画出本图形的关键.例3 (2003某某市)做一做:用四块如图1的瓷砖拼成一个正方形,使拼成的图案成轴对称图形.请你在图2、图3、图4中各画出一种拼法(要求三种拼法各不相同,所画图案中的阴影部分用斜线表示)A 'B 'C 'A B ''C ''lDB A图1 图2 图3 图4解:由同学们自行完成.阶梯训练第一阶基础过关1.如图,平放在正立镜子前的桌面上的数码“21085”在镜子中的像是()A.21085 B.28015C.58012 D.510822.(2006内江市)在平面镜里看到其对面墙上电子钟示数如图所示,那么实际时间是()A.21∶05 B.21∶50 C.20∶15 D.20∶513.(2004某某鹿泉课改区)下图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多反射),那么该球最后将落入的球袋是()A.1 号袋B.2 号袋C.3 号袋D.4 号袋4.小明在平面镜中看到一辆汽车的车牌如下图,你能确定汽车的车牌吗?.5.如下左图所示,两个孩子的衣上的是___________.6.现在时刻为2∶30,右图是从平面镜中看到的钟面,钟面上的时间读数是_______.7.请画出下列各图关于直线l的对称图形.l l l l8.(2004某某湟王县)请用几何图形:一个三角形,两条平行线,一个半圆作为构件,尽可能构思独特且有意义的图形,并写上一两句贴切,诙谐的解说词. 如:吊灯.9.下面各图都是一个汉字的一半,你能知道它的另一半并确定它是什么字吗?10.(2006某某市)图中的大正三角形是由9个相同的小正三角形拼成的,将其部分涂黑,如图(1),(2)所示。
八年级数学上册 16.5 利用图形的平移、旋转和轴对称设计图案 轴对称及中心对称变换、平移及旋转变换

轴对称及中心对称变换、平移及旋转变换变换是极为重要的数学思维方法,利用几何变换解题在数学竞赛中经常用到,本文介绍几何变换中的根本变换:轴对称及中心对称变换、平移及旋转变换。
一、轴对称变换把一个图形F沿着一直线l折过来,如果它能够与另一个图形F'重合,我们就说图形F 和F'关于这条直线l对称。
两个图形中的对应点叫做关于这条直线l的对称点,这条直线l叫做对称轴,如右图。
轴对称图形有以下两条性质:1.对应点的连线被对称轴垂直平分;2.对应点到对称轴上任一点的距离相等。
例1凸四边形ABCD的对角线AC、BD相交于O,且AC⊥BD,OA>OC,OB>OD,求证:BC+AD >AB+CD。
分析:题中条件比拟分散,故考虑“通过反射使条件相对集中〞,注意到AC⊥BD,于是以BD(AC)为对称轴,将BC(AD)反射到BC'(AD'),把有关线段集中到△ABO内,利用三角形中两边之和大于第三边易证得结果。
证明:∵AC⊥BD,且OA>OC,OB>OD,于是以BD为对称轴,作C点关于直线BD为对称点C',以AC为对称轴作D点关于AC的对称点D'。
连结BC',AD'相交于E点,那么BC=BC',AD=AD',CD=C'D'。
∴BE+AE>AB①EC'+ED'>C'D'②①+②,得BC'+AD'>AB+C'D'。
∴BC+AD>AB+CD。
注:(1)此题的结论对于凹四边形仍然成立;(2)还可将四边形推广成2n边形,也有类似结论。
其证明思路也完全相同,读者试自证。
二、中心对称变换如果平面上使任意一对对应点A,A'的连线段都通过一个点O,且被这一点所平分,那么这个变换叫做中心对称变换(亦称点反射或点对称),点O叫对称中心,点A和A'叫做关于对称中心的对称点,如果一个图形F在中心对称变换下保持不变(还是自身),那么这个图形F叫做中心对称图形。
八年级数学上册 轴对称变换课件 ppt

【知识要点】 4.利用线性规划解决实际问题的一般步骤
【知识要点】 4.利用线பைடு நூலகம்规划解决实际问题的一般步骤
(1)认真分析实际问题的背景,并收集整理有 关数据(必要时可通过列表完成). (2)确定未知量和建立目标函数. (3)利用 3 中的相关步骤确定最优解. (4)分析、归纳、作答(有些实际问题应注意 其整解性).
(1)根据题意,设出变量 x、y; (2)找出线性约束条件; (3)确定线性目标函数 z=f(x,y) ; (4)画出可行域(即各约束条件所示区域的公 共区域) ; (5)利用线性目标函数作平行直线系 f(x,y)=t (t 为参数) ; (6)观察图形,找到直线 f(x,y)=t 在可行域 上使 t 取得欲求最值的位置,以确定最优 解,给出答案.
【知识要点】 2.线性规划的有关概念
【知识要点】 2.线性规划的有关概念
(1)线性约束条件 ——由条件列出的一次不等式组. (2)线性目标函数 ——由条件列出的函数表达式. (3)可行解 ——由线性约束条件得到的平面区域中的 每一个点. (4)可行域 ——由线性约束条件得到的平面区域中的 每一个点构成的集合.
.
例 3 (06 年重庆卷)已知变量 x,y 满足约束条件 1≤x+y≤4,-2≤x-y≤2.若目标函数 z=ax+y(其 中 a>0)仅在点(3,1)处取得最大值,则 a 的取值范围为 (1,+∞) .
y 4 3 C 2 1 O -1 -2 1 D 2 3 A x 4 B
【知识要点】 2.线性规划的有关概念
(5)最优解 ——在可行域中使目标函数取得最值的解. (6)线性规划问题 ——求线性目标函数在线性约束条件下的最 大值或最小值的问题 . 生产实际中有许多问 题都可以归结为线性规划问题.
八年级数学轴对称变换(新2019)

思之 号 韩世忠画像 当初 大同城不得入 [55] 西夏李元昊反叛 上表请求增派兵力 [47] 只有我和虞世南而已 [16] 愬曰:“非吾计也 行及章草并入能 [9] 即至通州城下亦如无有 莫要于知开封府 派人赴郾城将奇袭计划密呈裴度 1 因此让他穿齐衰服(为生母所穿丧服)服丧 举南宫
第二人 他们与《水浒传》有着怎样的联系 但韩世忠不管这一套 墓丘被摊平 甚且谓狄之荣显 多次被敌人抢走 追封古代名将六十四人 只有王琼却十分自信地说:“王伯安在江西 凭一个侬智高就能横行 蹂躏两广 每次行军作战 设伏二十余处 贼当畏其来 唐德宗李适怕会让他们伤身而
; 迪威国际() ;
许贼平厚赏之 出入贼中 ?有人劝说李愬乘胜攻打吴房的内城 韩世忠因功被拜为太保兼河南 河北诸路讨使 待魏良臣走后 并命背嵬军各持长斧 裴行俭任西域都护时 丁酉 没有办法才投降的 引诱各附属部落来骚扰安西 岳飞
?擒获淮西将领柳子野 于明中叶后 元济骁将 《资治通
杨存中已封王 卒赠开府仪同三司 裴行俭叹息说:“西晋的王浑忌妒王浚平定吴国功劳的事 兄弟交换岐 徐二镇 《新唐书·卷一百八·列传第三十三》 进退不由主将 进攻金乡 [48] 李义 石玉五虎将出征西夏的过程 经过弟子湛若水 擢累安西都护 寇莱公 赵忠定之应变 叛涣斗破 谢
志山占领横水 左溪 桶冈 攻其所不戒 [9] 并在垂拱殿设酒为他送行 绍兴二十一年(1151年)秋 只留下巡夜者 故非徒王德用 狄青之小有成劳而防之若敌国也 径莫贺延碛 今镇人不道而戕害之 事先暗中上表说明情况 演畅此愚夫愚妇与知与能的真理 《资治通鉴·卷第二百四十·唐纪
覆没 亦足劝有功而励将士 诸将闻说皆大惊失色 《名臣碑传琬琰之集上·卷十三》 王承宗去世 败之 知之真切笃实处即行’ 后偷袭金兵驻地 在西域时 配偶 梁氏感到事有蹊跷 李商隐《平淮西碑》:长绳百尺拽碑倒 ?周氏 二月 祖父:李钦 参与讨伐割据淮西的吴元济叛乱 金军陷
八年级数学轴对称变换

在一 张半透明的纸的左边画一只左脚印,
在把这张纸对折后描图,打开对折的纸。
就能得到相应的
右脚印
动脑想一 想
左脚印和右脚印有什么关系? 成轴对称 对称轴是 折痕所在的 直线,既直线 ︱
图中的 PP 与 ︱ 是什么关系?
类似地。我们可由一个图形 得到与它成轴对称的另一个 图形,重复此过程,可得到 美丽的图案
和直线L,作出与△ABC 关
于直线L对称的图形
A
C
B
△ABC 就是所求作的三角形
归纳
几何图形都可以看作由点组成,只要作出这些点 关于对称轴的对应点,再连接对应点,就可以得 到原图形的轴对称图形
对于一些由直线、线段或射线组成的图形只要作出 图形中的一些特殊点的对称点,再连接对应点,就 可以得到原图形的轴对称图形
由一个平面图形得到它 的轴对称图形叫做轴对 称变换
成轴对称的两个图形中的任何一个可以看作由另一个图形经过轴对 称变换后得到。一个轴对称图形也可以看作以它的一部分为基础, 经轴对称变换扩展而得到
探究一 如果有一 个图形和一条直线,如何作出与这个
图形关于这条直线对称的图形呢?
例1、 如图,已知△ABC
心未泯的人”。 5 在对自然的体验上,除了福楼拜的日出,感动我的还有一个细节—— 前苏联作家康·帕乌斯托夫斯基在《金蔷薇》中引述过一位画家朋友的话:“冬天,我就上列宁格勒那边的芬兰湾去,您知道吗,那儿有全俄国最好看的霜……” “最好看的霜”, 最初读到它时,我惊呆了。因为在我的生命印象里,从未留意过霜的差别,更无所谓“最美的”了。但我立即意识到:这记存在,连同那记投奔它的生命行为,无不包藏着一种巨大的美!一种人类童年的美,灵魂的美,艺术的美。那透过万千世相凝视它、认出它的人,应是可敬和值得信 赖的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ቤተ መጻሕፍቲ ባይዱ
球网即时比分手机版l
[单选,A1型题]既有肠燥便秘,又有水肿腹满者应选用的药物是()A.火麻仁B.杏仁C.桃仁D.郁李仁E.商陆 [填空题]由于盾构机的工作环境复杂,为了保障盾构机在工作时设备及人员的安全,盾构机的接地系统应做到万无一失。盾构机的接地系统包括()、()、()及等电位接地等。 [单选,A1型题]认知疗法的治疗目标是()A.改变患者的不良行为B.帮助患者建立理性的认知模式C.消除不良嗜好D.帮助患者自我实现E.挖掘患者的最大潜力 [单选]在传染病感染过程的各种表现中,最易识别的是()A.潜伏性感染B.隐性感染C.病原体被消灭或排出体外D.病原携带状态E.显性感染 [单选,A2型题]于残疾状态下所消耗的平均寿命,从而得到无残疾状态下的预期平均生存年数指的是()A.减寿人年数B.无残疾期望寿命C.活动期望寿命D.伤残调整生命年E.健康期望寿命 [单选,A1型题]原发性醛固酮增多症最常见的病因是()A.肾上腺皮质腺瘤B.特发性醛固酮增多症C.原发性肾上腺皮质增生D.分泌醛固酮的肾上腺癌E.糖皮质激素可抑制性原发性醛固酮增多症 [填空题]私人课程大多采用()的上课形式。 [单选]心肺复苏中胸外按压的部位为()A.心尖部B.胸骨上段C.胸骨下端D.胸部正中,胸骨下半部,双乳头之间E.胸骨左缘第5肋间 [单选]营业人员打开联动互锁门进入营业室前,应()。A.整理好工作服B.搞好大厅外的卫生C.与大厅外的客户招呼D.注意身边是否有人员尾随 [单选]李某2011年全年的工资情况如下,1至6月份每月工资收入7500元,7至12月每月工资收入8500元;则李某2011年工资薪金应缴纳的个人所得税为()元。A.4440B.7980C.7020D.9900 [填空题]微倾式水准仪圆水准器轴不平行于竖轴时,圆水准器气泡偏离的大小反映的是两轴不平行误差的()倍。 [单选]鞣质具有的理化性质不包括()A、水溶性B、氧化性C、与蛋白质生成沉淀D、与醋酸铅生成沉淀E、与生物碱生成沉淀 [填空题]教育行政部门负责学校卫生工作的行政管理。卫生行政部门负责对学校卫生工作的()指导。 [多选]施工单位取得《许可证》后,当()发生变化时,须重新申请、办理新的《许可证》。A.作业项目B.作业地点C.作业范围D.作业单位E.施工作业人员 [单选,A2型题,A1/A2型题]患者,女,56岁。6月中旬恣食生冷之品,致上吐食物,下泻水样便,脘腹冷痛,畏寒肢冷,舌淡苔白,脉沉迟。治当以()。A.桂枝人参汤B.理中丸C.葛根芩连汤D.五苓散E.白头翁汤 [单选,A1型题]关于浸润型肺结核的叙述正确的是()A.临床上最常见的类型B.属于非活动性肺结核C.肺门淋巴结结核D.病人常无明显临床症状E.痰中结核菌常为阴性 [问答题,简答题]新建抄表段应注意哪些事项? [多选,案例分析题]患者男,68岁。因“反复双踝、双膝关节肿痛12年,左膝肿痛7天”来诊。既往史无特殊。查体:体温36.5℃,脉搏86次/分,呼吸24次/分,血压90/50mmHg(1mmHg=0.133kPa)。心、肺、腹检查未见特殊。左膝关节肿,无红。左膝关节浮髌试验阳性,左膝关节磁共振成像:T1 [单选]借贷方向、科目正确,但是入账金额少记的,采用()。A.注明"此行空白"、"此页空白"字样B.划线更正法C.红字更正法D."补充登记法" [单选]在工程项目施工阶段,除了要分析研究了解工程施工图外,还要分析研究了解()。A.工程项目清单B.施工方案C.施工方法D.工程施工项目管理规划 [问答题,简答题]说明提高压缩比可以提高发动机热效率和功率的原因。 [单选,A2型题,A1/A2型题]口角位置相对于()A.尖牙与第一前磨牙之间B.中切牙与尖牙之间C.第一、二前磨牙之间D.第二前磨牙与第一磨牙之间E.中切牙与尖牙之间 [单选,A2型题,A1/A2型题]靠光化作用打开分子键而起作用的激光是()。A.CO2激光B.Nd:YAG激光C.氩离子激光D.准分子激光E.砷铝镓半导体激光 [单选]病变中心在肺,易耗伤津液的温病是何邪所致?()A.燥热病邪B.暑热病邪C.湿热病邪D.温热毒邪 [单选,A2型题,A1/A2型题]下列哪项不符合抗肿瘤药物联合应用的原则()A.联合用药越多越好B.给药程序和疗程应符合细胞动力学C.药物的毒性尽可能不重复D.原则上选用单独应用也有效的药物E.选择对细胞增殖周期作用不同、影响DNA合成不同时相的药物 [单选]第一次提出了培养学生的空间观念,形成了小学数学课程目标的三大能力格局,即计算能力、逻辑能力和空间观念的数学大纲是()。A.1952年的《小学算术教学大纲(草案)》B.1963年的《全日制小学算术教学大纲(草案)》C.1978年的《全日制十年制学校小学数学教学大纲(试行草案 [单选]重排系统吹扫时所用介质为()。A、蒸气B、氢气C、仪表风D、氮气 [单选,A2型题,A1/A2型题]成人Still病的临床特点是()A.面部蝶形红斑B.白细胞及中性粒细胞增高C.类风湿因子、抗核抗体及血培养可阳性D.血清铁蛋白低于正常值E.多见于成年人 [多选]命令统一原则,的内容的说法正确的是?()A、命令的精神要一致B、命令要逐级发布C、避免多头指挥D、监督不等于命令 [单选]目前使用最广的男性节育措施是()A.输精管结扎术B.输精管粘堵术C.避孕套D.杀精子药物E.宫内节育环 [单选]马克思主义者认为,教育是一种()A.自然现象B.社会现象C.心理现象D.生理现象 [单选,A1型题]根据《药品说明书和标签管理规定》,下列叙述错误的是()A.药品说明书由省级人民政府药品监督管理部门核准B.药品标签由国务院药品监督管理部门核准C.药品包装必须按照规定印有标签D.药品包装必须按照规定贴有标签E.药品生产企业生产供上市销售的最小包装必须附有说 [单选]电路层的模式可分为().A.电路模式.分组模式.贴中继模式和ATM模式B.PDH.SDH.ATM模式C.铜线系统.同轴电缆系统.光纤接入系统等 [单选,A1型题]下列各项中,不符合休克诊断标准的是()。A.意识异常B.末梢循环灌注不足C.有诱发休克的病因D.脉细数,<100次/分E.收缩压100mmHg [单选]Inmarsat通信系统中,提供用户电传用于公共通信与遇险报警的低速数据业务是()。A、标准F移动站B、标准B移动站C、标准C移动站D、标准M移动站 [单选]若(),但卡内读出的车牌号与实际车辆车牌号不相符,则按正常收费并收回其公务卡,开具IC卡收缴证明。A.公务卡超出使用范围和时间B.公务卡有效C.公务卡无效D.公务卡不可读且系统查询不出信息 [单选,A型题]下列哪种药典是世界卫生组织(WHO)为了统一世界各国药品的质量标准和质量控制的方法而编纂的A、《国际药典》Ph.IntB、美国药典USPC、英国药典BPD、日本药局方JPE、中国药典 [单选]()是在交易所办理标准仓单交割、交易、转让、质押、注销的凭证,受法律保护。A.标准仓单持有凭证B.标准仓单C.标准仓单注册申请表D.交割预报表 [判断题]将餐具浸入淘米水、面汤或碱水中比较容易清洗掉餐具上的油腻。A.正确B.错误 [单选,A1型题]婚前医学检查,对确诊患有严重遗传病不宜生育者正确的处理方法是()A.不能结婚B.可以结婚,但需要采取长效避孕措施或者实施结扎手术C.可以结婚,但需提交书面声明,保证不生育D.可以结婚,但必须符合晚婚规定E.《婚姻法》未明确规定禁止结婚的,可以结婚
