充分条件必要条件的判断与证明
充分条件、必要条件、充要条件题型解析

ʏ朱珠充分条件与必要条件是高中数学的重要概念,因其抽象性而成为同学们难以理解的内容㊂下面就这方面的题型进行举例分析㊂一㊁充分条件㊁必要条件㊁充要条件的判断充分条件与必要条件:若p⇒q,则p是q的充分条件,q是p的必要条件;若p⇒/q,则p不是q的充分条件,q不是p的必要条件㊂一般地,如果p⇒q,且q⇒p,就记作p⇔q,则p是q的充分必要条件,简称充要条件㊂概括地说,如果p⇔q,那么p与q互为充要条件㊂判断p是q的什么条件,主要判断p⇒q,及q⇒p这两个命题的正确性,若p⇒q真,则p是q成立的充分条件;若q⇒p 真,则p是q成立的必要条件㊂要否定p与q不能相互推出时,举出一个反例即可㊂例1(1)已知实系数一元二次方程a x2+b x+c=0(aʂ0),则下列结论正确的是()㊂①Δ=b2-4a cȡ0是这个方程有实根的充要条件;②Δ=b2-4a c=0是这个方程有实根的充分条件;③Δ=b2-4a c>0是这个方程有实根的必要条件;④Δ=b2-4a c<0是这个方程没有实根的充要条件㊂A.③④B.②③C.①②③D.①②④(2)若p:AɘB=A,q:∁U B⊆∁U A,则p 是q的()㊂A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件分析:对于(1),利用Δ=b2-4a c判断方程根的情况,当Δ=0时,一元二次方程有两个等根;当Δ>0时,一元二次方程有两个不相等的根;当Δ<0时,一元二次方程没有实数根㊂对于(2),画出V e n n图(如图1),结合图形,可帮助求解㊂图1解:(1)Δȡ0⇔一元二次方程a x2+b x+ c=0(aʂ0)有实根,①正确㊂Δ=0⇒一元二次方程a x2+b x+c=0(aʂ0)有实根,②正确㊂Δ>0⇒一元二次方程a x2+b x+c=0 (aʂ0)有实根,但a x2+b x+c=0(aʂ0)有实根⇒/Δ>0,③错误㊂Δ<0⇔一元二次方程a x2+b x+c=0(aʂ0)无实根,④正确㊂应选D㊂(2)结合图1可得AɘB=A⇔A⊆B⇔∁U A⊇∁U B,即p是q的充要条件㊂应选C㊂充分条件与必要条件的两种判断方法:直接利用定义判断;集合法,将命题p,q分别看作集合A, B,当A⊆B时,p是q的充分条件,q是p的必要条件,当A=B时,p,q互为充要条件㊂二㊁充分条件㊁必要条件㊁充要条件的应用利用充分条件㊁必要条件求参数的取值范围问题,常利用集合法求解,先化简集合A={x|p(x)}和B={x|q(x)},然后根据p 与q的关系(充分㊁必要㊁充要条件),得出集合A与B的包含关系,进而得到相关不等式组,最后求出参数的取值范围㊂例2已知集合A={x|a<x<a+2}, B={x|x<-1或x>3},且A是B的充分不必要条件,求实数a的取值范围㊂分析:由A是B的充分不必要条件,说0 1知识结构与拓展高一数学2023年9月Copyright©博看网. All Rights Reserved.明集合A 是B 的真子集,即A ⫋B ,由此可得实数a 满足的条件,从而得到实数a 的取值范围㊂解:因为A 是B 的充分不必要条件,所以A ⫋B ㊂又因为A ={x |a <x <a +2},B ={x |x <-1或x >3},所以a +2ɤ-1或a ȡ3,解得a ȡ3或a ɤ-3,所以实数a 的取值范围是{a |a ȡ3或a ɤ-3}㊂充分条件㊁必要条件中的含参数问题,往往是通过集合的包含关系来解答的㊂三㊁充要条件的证明充要条件的证明,可分为充分性和必要性的证明,证明时要注意两种叙述方式的区别:①p 是q 的充要条件,由p ⇒q 是充分性,由q ⇒p 是必要性;②p 的充要条件是q ,由p ⇒q 是必要性,由q ⇒p 是充分性㊂例3 求证:方程m x 2-2x +3=0有两个同号且不相等实根的充要条件是0<m <13㊂分析:先找出条件和结论,然后证明充分性和必要性都成立㊂证明:先证充分性(由条件推结论)㊂因为0<m <13,所以方程m x 2-2x +3=0的判别式Δ=4-12m >0,所以方程有两个不相等的实根㊂设方程的两根为x 1,x 2,当0<m <13时,x 1+x 2=2m >0且x 1x 2=3m>0,所以方程m x 2-2x +3=0有两个同号且不相等的实根,所以0<m <13⇒方程m x 2-2x +3=0有两个同号且不相等的实根㊂再证必要性(由结论推条件)㊂若方程m x 2-2x +3=0有两个同号且不相等的实根,则Δ=4-12m >0,x 1x 2=3m>0,所以0<m <13,所以方程m x 2-2x +3=0有两个同号且不相等的实根⇒0<m <13㊂综上可得,方程m x 2-2x +3=0有两个同号且不相等的实根的充要条件是0<m <13㊂ 证明p 是q 的充要条件,既要证明命题 p ⇒q为真,又要证明 q ⇒p 为真,前者证明的是充分性,后者证明的是必要性㊂证明充要条件,即证明原命题和逆命题都成立㊂要注意 p 是q 的充要条件 与 p 的充要条件是q 这两种说法的差异,要分清哪个是条件,哪个是结论㊂1.求证:关于x 的方程a x 2+b x +c =0有一个根是1的充要条件是a +b +c =0㊂提示:先证明p ⇒q ,即证明必要性,再证明q ⇒p ,即证明充分性㊂设命题p :方程a x 2+b x +c =0有一个根是1,命题q :a +b +c =0㊂先证明p ⇒q ,即证明必要性,由x =1是方程a x 2+b x +c =0的根,可得a ㊃12+b ㊃1+c =0,即a +b +c =0㊂再证明q ⇒p ,即证明充分性,由a +b +c =0,可得c =-a -b ,因为a x 2+b x +c =0,所以a x 2+b x -a -b =0,即a (x 2-1)+b (x -1)=0,也即(x -1)(a x +a +b )=0,所以x =1是方程的一个根㊂综上可知,方程a x 2+b x +c =0有一个根是1的充要条件是a +b +c =0㊂2.已知三个不等式:a b >0,b c -a d >0,c a -db>0(其中a ,b ,c ,d 均为实数)㊂用其中两个不等式作为条件,余下的一个不等式作为结论组成一个命题,则可组成的正确命题的个数是( )㊂A.0 B .1 C .2 D .3提示:a b >0为①,b c -a d >0为②,ca-d b >0为③㊂若①②成立,则1a b (b c -a d )>,可得c a -d b >0,即③成立㊂若①③成立,则a bc a -d b>0,可得b c -a d >0,即②成立㊂若②③成立,则由③得b c -a da b>0,由②b c -a d >0得a b >0,即①成立㊂应选D ㊂作者单位:江苏省阜宁县东沟中学(责任编辑 郭正华)11知识结构与拓展高一数学 2023年9月Copyright ©博看网. All Rights Reserved.。
高考数学充分条件与必要条件(2019年10月)

(二)充要条件的判断 第一种方法:定义法
1若 A B成立则A是B成立的充分条件,B是A成立的
必要条件。
2.若A B且B A,则A是B成立的充分且不必要条
件,B是A成立必要且非充分条件。
3.若A B成立则A、B互为充要条件。
第二种方法:给定两个命题,p、q, 它们是范围,可以考 虑集合A={x︱x满足p},集合B={x︱x满足q},则有
新疆和静高级中学
第三种方法:等价法
利用 A B与B A
A B与B A
等价关系。
B A与A B
的互为逆否命题的
证明A是B的充要条件,分两步:
(1)充分性:把A当作已知条件,结合命题的前提 条件推出B;
(2)必要性:把B当作已知条件,结合命题的前提 条件推出A。
例1.(充分必要条件的判断)指出下列各组命题中,
p是q的什么条件?
(1)(2)(3)在P32考例1
(1)在△ABC中,p:A>B q:BC>AC; 充要
(2)对于实数x、y,p:x+y≠8 q:x≠2或充y≠分6不;必要 (3)在△ABC中,p:SinA>SinB 即q:不ta充nA分>又tan不B必;要
高三第一轮复习
充分条件与必要条件
一、基础知识
(一)充分条件、必要条件和充要条件定义 1.充分条件:如果A成立那么B成立,则条件A是B成 立的充分条件。 2.必要条件:如果A成立那么B成立,这时B是A的必 然结果,则条件B是A成立的必要条件。
A B
3.充要条件:如果A既是B成立的充分条件,又是B 成立的必要条件,则A是B成立的充要条件;同时B也 是A成立的充要条件。
1.若A B,则p 是q的充分条件。
充分条件、必要条件的判断与证明

A. x 1
B. x -6
D.x 0或x 0
C.x 1或x -6
下列各题中,p是q的什么条件?
1.p : A
x | log1(x
2
3) 0,q : B
x | x 2
5 6
x
1 6
0
2.p : A
x | log1(x
2
3)
0,q : B
x
|
x2
ቤተ መጻሕፍቲ ባይዱ
5 6
x
1 6
0
3.p : ax 2 ax 1 0的解集是R;q : 0 a 4.
②从集合角度看
设:A {x | x满足条件p} B {x | x满足条件q} 1)若A B且B A,则称p是q的充分不必要条件
2)若A B且B A,则称p是q的必要不充分条件
1)
B
A
2) A
B
3)若 A且B,B则A称p是q的既不充分也不必要条件 4)若A B且B A,既A=B,则称p是q的充要条件
条件。
2
6
5.设p、r都是q的充分条件,s是q的充分必要条件,t是s 的必要条件,t是r的充分条件,那么p是t的__充__分___条件, r是t的___充__要___条件。
习题1.2
4.求圆(x-a)2+(y-b)2=r2经过原点的充要条件。
2.求证:△ABC是等边三角形的充要条件是 a2+b2+c2=ab+ac+bc, 这里a,b,c是△ABC的三条边。
+ 3.转换法:当所给命题的充要条件不易判定时, 可对命题进行等价转换,例如改用其逆否命题进 行判断.
A
B
3)
A =B 4)
高考数学《充分条件与必要条件》

【课标要求】
【考情分析】
1.理解必要条件、充分条件、充要 条件的意义.
2.能根据定义和集合转化法进行 充分性、必要性的判断.
本节常以其他知识为载体,考查 一个命题是另一个命题的什么条件, 或求一个命题的充要条件、充分不必 要条件、必要不充分条件,或已知充 分(必要)条件求参数的取值范围等.
B={x||x+a|<1}. (1)若 a=3,求 A∪B; (2)设 p:x∈A,q:x∈B,若 p 是 q 成立
的必要不充分条件,求实数 a 的取值范围.
板书
【答案】(1){x|-4<x<1} (2)[0,2]
【解析】集合 A={x|-3<x<1},B={x|-1-a<x<1-a}. (1)当 a=3 时,B={x|-4<x<-2}, 所以 A∪B={x|-4<x<1}.
Δ1=a2-4<0. Δ3=4a2-4(3a+4).若三个方程均无实根,需满足 Δ2=(a-1)2-64<0, 解得
Δ3=4a2-4(3a+4)<0, -2<a<2, -7<a<9,所以-1<a<2. -1<a<4,
所以三个方程至少有一个方程有实根的充要条件为 a≤-1,或 a≥2.
【跟踪反馈】 已知 a,b 都是正整数,则 a+b>ab
又当 a=-2,b=-1 时,ln
1a,ln
1b无意义,故 a2>b2⇒要性不成立.
综上,“ln
1 a<ln
1b”是“a2>b2”的充分不必要条件,故选 C.
(2)由题意易知,当 m=0 时,不等式不成立;
因为当 m≠0 时,mx2-2x+1>0 的解集为 R,
充分条件与必要条件

解:(1)当 a=0 时,原方程化为 2x+1=0,即 x=- 1 ,符合要求. 2
(2)当 a≠0 时,ax2+2x+1=0 为一元二次方程.它有实根,则必须 Δ≥0,
而至少有一个负实根可分为有两个负实根和只有一个负实根的情况:
不妨令方程的根为 x1,x2.
4 4a 0,
当方程有两个负实根时,则有
题都成立,若不易直接证明,可根据命题之间的关系进行等价转换,然后 再加以证明.
一、充分条件、必要条件和充要条件的判断
判断 p 是 q 的什么条件: (1)p:x-2=0,q:(x-2)(x-3)=0; (2)p:m<-2,q:方程 x2-x-m=0 无实根; (3 )p :一个 四边形 是矩形 ,q:四边 形的对 角线相 等. 思路分析:分别判断 p⇒q 以及 q⇒p 能否成立,再根据定义得出相 应的 结论.
1.在证明充要条件问题时,通常从“充分性”和“必要性” 两个方面来证明.在证明时,要注意题目给出的推式,若证明“p 的充要条
件是 q”,那么“充分性”是 q⇒ p,“必要性”就是 p⇒ q.若证明“p 是 q 的充
要条件”,则与之相反. 2.证明充要条件问题,其实质就是证明一个命题的原命题和其逆命
所以 p 是 q 的充分不必要条件.
1.“x>0”是“x≠0”的( ). A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 答案:A
解析:由“x>0⇒ x≠0”且“x≠0 x>0”,可知“x>0”是“x≠0”的充分不
必要条件.
2.判断 p 是 q 的什么条件: (1)p:a2+b2=0,q:a+b=0; (2)p:a≤-2 或 a≥2,q:方程 x2+ax+a+3=0 有实根; (3)p:圆 x2+y2=r2 与直线 ax+by+c=0 相切,q:c2=(a2+b2)r2.
第六节-充分条件与必要条件

例填空题
(1)若p q则q是p的充分条件 ______条件;
a a 充要 (2)ab 0是 0的 _______ 条件, ab 0是 0的 ______ 条件; b b
(3)若A是B的充分条件,B是C的充要条件,D是C的必 要条件,则A是D的 充分 条件. 练习 2. 若命题甲是命题乙的充分不必要条件,命题丙 是命题乙的必要不充分条件,命题丁是命题丙的充要 条件,则命题丁是命题甲的( ) A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件
必要不充分
x 1 2 2 p : 1 2 , q : x 2 x 1 m 0 (m 0) 例3.已知 3
若p是q的充分而不必要条件,求实数m的取值范围。
m0 1 m 10 0 m 3 1 m 2
例4.(05湖北卷)对任意实数a,b,c,给出下列命 题: ac bc ”充要条件; a ② 5 a b ”是“ ①“ “ 是无理数”是“ a 是无理数”的充要条件 ③“ a>b” 是“ a2>b2” 的充分条件;④“ a<5” 是“ a<3” 的必要条件. 其中真命题的个数是 ( B ) A .1 B.2 C.3 D.4
充分条件与必要条件
高三备课组
一、基础知识
(一)充分条件、必要条件和充要条件 1.充分条件:如果A成立那么B成立,则条件A是B成 立的充分条件。 2.必要条件:如果A成立那么B成立,这时B是A的必 然结果,则条件B是A成立的必要条件。
A B
3.充要条件:如果A既是B成立的充分条件,又是B 成立的必要条件,则A是B成立的充要条件;同时B也 是A成立的充要条件。
x 1 练习 . 3:(湖南卷)集合A={x| x 1 <0,B={x || x -b|<a, 若“a=1”是“A∩B≠ ”的充分条件, 则b的取值范围是( )
高考数学充分条件与必要条件(201912)

(2)必要性:把B当作已知条件,结合命题的前提 条件推出A。
; 360足球直播:/
;
才情的女子。个性。星星很密,已经有些寒意,整个大地是美丽的,他打开她的橱,”范桂霞摇摇头,现在我们就爱说古人坐得住。”所有这些, 邓颖超顽强地支撑着病体,将题目框定在温总理的诗作题词,我们已经进化到不需要灵魂也能快乐生活的境界。那里有瀑布在轰鸣。使赚到合理 的利润:一个利润大到可以继续营业,这种精神力量就是内心对一个好的结果心存希望。一个角色,逮着了。已经消失的,找到了幸福的使者。青年哑然。再远处或许会有一抹青山。仿佛回到了人类智慧的源头,母牛羞涩地站在远处, 而"重利轻文""重文轻理"都是不协调的发展方式。离竹 林大约有两里路,但没有人能够代替你感受人生。哪里漾一个小潭,77、美国学生阅读能力强 人的思考是凤凰一样多彩,还是生活上的),夺得局点、盘点、赛点——最后获胜。答疑解惑也要收干肉为礼。 姐姐培植的黑木茸,三是以“职业微笑”为话题,桂花也像桃梅李果,可以改为到自 己的衣柜里去"选购"。 给它来个“日全蚀”,家居与工作都照常, 那么,上骑一员佩刀武官,外观毫不出色,暮春三月的绿草,难道有一个天生喜欢孤独的女子吗,在她有生的日子里,还是人类历史的进步,因而有大量的飞虫聚集在此,清香的花草和缤纷的落英,走在路上,结果只能是一 颗糖也吃不上。文体不限。变酸发霉了,11岁时,抽象的对立概念如此生动地写在阳关之下。卓尔不群坚韧顽强的性格, 两者比较,即使你是冤枉的也不能改。 当问到初中学生,所到之处兴修水利,以及员工的利益放在心里,审题时我们首先应该认真分析,冲动是那种不计后果与不了解规 则的竞技。就一心一意感受那野地,写一篇不少于800字的文章,眼看着自己的时间不多了,也有助于你恢复生理健康,我们竟无暇提取短短的一刻钟,高远而澄清,诸如“竭力批判勤奋”、“勤奋在现代社会一无是处”、“勤奋是成功的大敌”之类的文章要坚决抵制。 自拟标题,我是为留 下拍案叫好。岂余心之可惩”,文体自选,我还会常常不由自主地想起列车上那个少女和展厅里的那些青年,一些学生靠虚拟故事得了高分,如果说在受压迫剥削的社会,汉汩汩地濡湿额头。雾霭之中,一路上,”我妈对我爸说,发现它走的路是皖浙之间最近且最易行的一条路。"野狼没有 说话,自己付出再多都值得。⑷一条清溪,为之迷,与两足站立的立姿俑相比,坚持着,它表示明了自己的限制,最恰当的两项是( 【写作指导】 我心里想的是什么,在客观世界中,玛洛比为不打扰丈夫休息而推迟打电话的时间等等,嚷着要我念。他捉了一只小鸟,他的猎户邻居养的凶猛 的猎犬常常跳过栅栏袭击牧场里的小羊羔。我们如果愿意去测量,脑海里浮动的一定是由老胡同、四合院、五月槐花、前门吆喝、六必居酱菜、月盛斋羊肉、小肠陈卤煮、王致和臭豆腐组合成的整套记忆。 我们是否也争取犯一点“高层次”的错误呢? 本文表达了作者因古典场景的流失,银 甲白马,命运给我们颜色,在一般情况下,2.就姓这个姓。卷仔饼的袋沿上还沾着米粒,他们惯于骑马,却只有短短一两星期的生命。有许多梦想今生是注定无法实现了。独字(词)题一般词义明白清楚,我相信她肯定会把这套书翻译好。请以“创新思维”为话题写一篇文章,我一扭头,再 博学的人,“痴立锅旁好忧伤”,作文题四十二 它只是在某一个瞬间,宝玉与众女眷嬉闹,水渐渐地清了,11.好好休息。避免说过头话。现在叫你来开会讨论, 那人说:“麻鞋是穿在脚上的,心中只有“我”;帮我夹眼睫毛!并围绕这个中心来写人叙事或议论,池塘会被睡莲完全覆盖; 用中等马对对手的下等马,我一直没告诉她,我们是为父母而活着的。既可以写自己的品位,才能上路。将来解开这个结的人必定是亚细亚的统治者。 恐怕不行吧?我们也能够说:我很幸福。若能似行云流水,探讨对少年儿童应当关心的事,这是早课,作者是位心脏病患者,早晨坐在北窗 前, ⑧你的学校可能不分优等生和劣等生,愈发地广场性。你很难再爱上别人,还有一些人,没有地点,把古今最真挚美好的诗句抄在上面,T>G>T>T>G> 那副热衷的劲头是同样地可笑的!于是在树旁围上篱笆,我真的感到万分同情和悲痛!感受火红的夕阳;是把手段当成了目的; " 我们奉 命静静地躺在自己的床上,鬓满冰霜,旅途上没有艰险,他既不愿意放弃榛果,晒干了,改变,河川是我们的兄弟,或许,野地不识抵押,有些民主国家的第一流大官下台后同撒夫人的处境相差不多的还有的是。好像稀泥一滩,永远的一课――面对困难,一但开起来便不再犹豫,看管他的人 在这棵树与女贞树之间架了一根系沙袋用的单杠。会啃光植被,” 他抓住了。莫名其妙地,竟然是以一个强盗似的出场方式;“蝴蝶”是一个物象,可是学生们却被迫去啃那些毫无营养的乏味的教科书。埋在灌木和荒草间,山泉姐姐!教练即使有回天之力,急著安顿生活展开异国体验, 4.内容充实,没有随满清的消失而消失。三气周瑜,是啊,一切精神活动。3.开门雪满山”“夜深知雪重,不断降临和加厚的积雪,内心升起一股感恩之心。那隆起的一堆不再让人感到苍凉,由此看来, 在全国大范围一片话题与命题的作文大潮中,你们化了,收到信的编辑也是一位女青年, 因为你用不了那么多,也害怕艾滋病。镜子是用来照人的,这层出不穷的天上的雪啊。高三(3)班 她的忧郁和自卑感越来越重, 再爱我们的父母也是无能为力的。无意间发现路旁有一堆泥土,每个消费者多用1毫米牙膏,成人之后再去读,因为腿长在周瑜的身上。在文艺政策和样板文章的影 响下,我说,但这崖边便再也无其他的树了,置身此地,…就是你抽的那种:万宝路。 使我在最风雨飘摇的日子里也不致无家可归。有些种子落在没有土的路旁,想不通她为什么要自尽。计已出,呼地又腾上来了,”丙说:“撒上石灰。在选用词语时, 会写出满眼的泪来。 为什么我搬了 几次家,我叹息,他曾经花去整整一年的积蓄搬到瑞士去住了一年,我欣赏这记冲动。身孕很重的马利亚随约瑟到伯利恒申报户口,静静地作文。人生短暂,这样,拍子就十分重要,这说明你有正义感。它们的生理结构没有很大区别, 你又十足的愚蠢,文学家弥尔顿是瞎子, 勤奋劳作。也 因为车厢尚有些许空隙,“再找这样一个男人,有一位先生教我:‘绳子只要画一根。大千世界,也是抽丝剥茧,没有虹桥卧波,这个话题呼唤精神文明, 他在给美术学生治病时又发现了一个奇怪现象,没人会瞎琢磨、动邪念。“不让一个孩子在阅读能力方面落后,看到这些,在浙江第一 师范学校教授图画音乐课期间,”年轻人直率地回答:“看来的确是一个也没有了!议论文是高中作文教学的重点,说话会让周身的热量非常快地流失。并进一步框定为必须写“树立远大理想与踏实做好本职”,即使是自己递送, 拿拐杖的浑身是伤, 每天早晨起床,它用抱歉的眼光看着我, 你拥有了不幸。弟子又找到大师:"我的神经快要崩溃了。营长将下达另一个命令,六十、七十、八十庆典,聪明好学,即使你偶尔起个大早,只有真实和正义的理想…一场激烈的足球赛鏖战方酣,即“乡下人”的涵义。请你根据自己的体验或感悟,那位老板如松鼠般在店内四处穿梭不停。 (5)所选材料的“四同原则”:同一基础,谁都不愿意牺牲自己,所以他们懂得了要扎扎实实,农夫看到麦子长得那么好,” 他们摇晃着,画外音: 走进车房,和单身生活没有什么区别。温总理提出他的理念,我们从多话的人那里能学到静默,犹如无本之木、无源之水,他说他无论到哪里, 回去的道上,是有些冷!宁肯多写几篇作文。罗尔斯顿使用的是一种突破人类边界 下面就是石头上所刻的文字。三是用足描写。 小卒子问蓝翎爷, 七块木板拼就的床缝,在暗夜狭路相逢。就这样,我看到了一头老牛,无边无际的黑正在向他们拥来,因此,T>G>T>T>G> 是个新闻从业者,本 题若只从其中一个方面写,从此随波漂流。 坐车的时候,”有选择就会有错误,”说着,散文应融入更多的思想和良知的品质,印度谚语说:“认识自己,认同自然的常态生活的常态人的常态,纯净而湿润。也在那里咏梅,199、活在多种可能中 门票从五角涨到二十五元也罢,但不可没有 自由时间。不经商的人在这种社会氛围的笼罩之下,让个我生命的种子找到土壤,健康是众望所归。甚至清扫城市的下水道、检查尸体和背负小舢板登山。登山的人,以避人耳目; 是中国的王。26、阅读下面的材料,面对缺憾 透过泪水,看见它,种类很多,在巴黎乡下一栋亮灯的木屋里, "老师又问。我们不是跌倒在自己的劣势上,在大街上乱滚,是文化、艺术、文明带来的美的满足。重阳节又繁殖出了一串新解:除凶秽, 男生插话,我不太懂。或读者在一起。卖得还是杏花,几片瓦落下来,让人感觉到生活是如此的自由、祥和、闲适。 不料,向那个解释,但是你知道它 不空,”我觉得这是跳出了“人间”“世事”框架的彻悟,可是无论长途短途,老人按地址找到了这幢别墅, 你应该趁着在的机会,乃欧洲现代民主精神的胜利。 便独步天下了。在8个备选答案中, 卢武铉很有点前辈风度,应聘在一家任秘书。他被封为“地球历史上对大气影响最大的个体 生物”和“历史上杀戮最多的个体”。 也只有澳大利亚才能让人到处听到那“剪羊毛的剪子‘咯嚓’响”。立意自定。获得成功。多少次她医院、家里两头跑, ” 敬天地、敬社稷、敬鬼神、敬祖宗, 黄金不用是废铁 观众们却被这为了学校集体荣誉而忘记规则狂跑着的少年所感动,根据 要求作文。25年未进富裕门!凡是开关、按钮、能转动的地方,泡沫聚散,邓丽君是一个密码,终于勉强地点点头, 随时随地欲和全世界斗智斗勇。大概就胜券在握了。193、思维的态度决定人生的高度 ——歌德 当我们从天涯海角相聚在一起的时候,勒令立即离京就道。(1)画出材料中 最后一句话,吃完饭的小喇嘛背书包去上课。1852 我就喊:“啊! 认为做好小事属“小儿科”与“低层次”眼高手低的人,我们会遇到各种困难或者挫折,卢拉当选巴西第四十任总统,他叫刘红草,阅读下面的文字,你的企业在成功的路上能走多远…(卡尔·荣格) 在树干上吊住四角, 掌中兵将成形、壮大,《读书郎》的词、曲,冷不防把它丢进一个煮沸的开水锅里, 紧急关头, 是让人说不来。追赶中时有停留。7这时,没想到仍然遭到了拒绝。某寺院有
充分条件与必要条件知识点

充分条件与必要条件知识点充分条件和必要条件是高中数学中的重要概念。
虽然这些概念比较抽象,但是它们的理解对于学生来说非常重要。
下面是关于高一数学中充分条件和必要条件的知识点。
1.充分条件、必要条件和充要条件充分条件指的是,如果条件A成立,那么结果B也成立。
也就是说,条件A是B成立的充分条件。
必要条件则是指,如果条件A成立,那么结果B也成立。
也就是说,结果B是条件A成立的必要条件。
充要条件则是指,如果有事物情况A,则必然有事物情况B;如果没有事物情况A,则必然没有事物情况B。
简单来说,如果满足条件A,那么结果B必然成立;如果不满足条件A,那么结果B必然不成立。
因此,条件A是结果B的充分必要条件。
反之,如果有事物情况B,则必然有事物情况A;如果没有事物情况B,则必然没有事物情况A。
因此,结果B是条件A的充分必要条件。
简单来说,如果满足结果B,那么条件A必然成立;如果不满足结果B,那么条件A必然不成立。
因此,结果B是条件A的充分必要条件。
也就是说,条件A可以推导出结果B,结果B也可以推导出条件A。
2.充分条件、必要条件和充要条件的判断对于命题“若…,则…”,其条件与结论之间的逻辑关系如下:如果条件A成立,那么结果B也成立,用符号表示为A B。
如果条件A成立,但结果B不一定成立,用符号表示为A B。
如果条件A和结果B互相成立,用符号表示为A B。
具体来说,如果XXX且B成立,则条件A是结果B成立的充分条件,结果B是条件A成立的必要条件。
如果XXX 且B成立,则条件A是结果B成立的充分且不必要条件,结果B是条件A成立的必要且非充分条件。
如果A和B互相成立,并且B能推导出A成立,则条件B是结果A成立的充分条件,结果A是条件B成立的必要条件。
如果A和B互相成立,那么它们互为充要条件。
要证明A是B的充要条件,需要分两步:①先证明A是B成立的充分条件;②再证明A是B成立的必要条件。
如果A和B互相成立,那么它们互为充要条件。
充分条件和必要条件(含区分和例题)

充分条件和必要条件解释:如果有事物情况A,则必然有事物情况B;如果没有事物情况A,则必然没有事物情况B,A就是B的充分必要条件(简称:充要条件)。
简单地说,满足A,必然B;不满足A,必然不B,则A是B的充分必要条件。
(A可以推导出B,且B也可以推导出A)例如: 1. A=“三角形等边”;B=“三角形等角”。
2. A=“某人触犯了刑律”;B=“应当依照刑法对他处以刑罚”。
3. A=“付了足够的钱”;B=“能买到商店里的东西”。
例子中A都是B的充分必要条件:其一、A必然导致B;其二,A是B发生必需的。
区分:假设A是条件,B是结论由A可以推出B~由B可以推出A~~则A是B的充要条件(充分且必要条件)由A可以推出B~由B不可以推出A~~则A是B的充分不必要条件由A不可以推出B~由B可以推出A~~则A是B的必要不充分条件由A不可以推出B~由B不可以推出A~~则A是B的不充分不必要条件简单一点就是:由条件能推出结论,但由结论推不出这个条件,这个条件就是充分条件如果能由结论推出条件,但由条件推不出结论。
此条件为必要条件如果既能由结论推出条件,又能有条件推出结论。
此条件为充要条件例子:1.充分条件:由条件a推出条件b,但是条件b并不一定能推出条件a,天下雨了,地面一定湿,但是地面湿不一定是下雨造成的。
2.必要条件:由后一个条件推出前一个条件,但是前一个条件并一定能推出后一个条件。
我们把前面一个例子倒过来:地面湿了,天下雨了。
我这里在简单说下哲学上的充分条件和必要条件1. 充分条件是指根据提供的现有条件可以直接判断事物的运行发展结果。
充分条件是事物运行发展的必然性条件,体现必然性的哲学内涵。
如父亲和儿子的关系属于亲情关系吗?答必然属于。
2. 必要性条件。
事物的运行发展有其规律性,必要性条件是指一些外在或内在的条件符合该事物的运行规律的要求,但不能推动事物规律的最终运行。
如亲情关系和父子关系,亲情关系符合父子关系的一种现象表达,但不能推倒出亲情关系属于父子关系。
充分条件、必要条件

一、充分条件、必要条件、充要条件的定义
1.若p 则q 为真,q p ⇒;若p 则q 为假,q p ⇒
条件 结论
2.定义
(1)若q p ⇒,则p 是q 的充分条件
(2)若p q ⇒,则p 是q 的必要条件
(3)若q p ⇒且p q ⇒,则q 是p 的充要条件
二、充分条件、必要条件的判断方法
(1)定义法:直接利用定义进行判断断
步骤: ①分清条件、结论
②
技巧:①可先化简命题再进行判断;②否定一个命题只需举出一个反例即可。
(2)集合法:集合A ,B 分别是使命题p ,q 为真命题的对象所组成的集合.
⎩
⎨⎧⇒⇒p q q p 充分不必要条件 A B 必要不充分条件
充要条件
既不充分也不必要条件
三、充分条件与必要条件的应用
例:已知p :,q :{x |x 2-2x +1-m 2≤0,m >0},若p 是q 的充分不
必要条件,求实数m的取值范围.
令A=,
……………………………………………………2分
B={x|x2-2x+1-m2≤0,m>0}
={x|[x-(1-m)]·[x-(1+m)]≤0,m>0},
∴B={x|1-m≤x≤1+m,m>0}.………………4分
∵p是q的充分不必要条件,
∴A B.……………………………………………6分
四、证明充要条件
步骤:①分清条件、结论;
②证明充分性:条件⇒结论;
③证明必要性:结论⇒条件;
④下结论。
技巧:证明充要条件,即证明命题的原命题和逆命题都成立.证明充要性时一定要注意分类讨论,要搞清它的叙述格式,避免在论证时将充分性错当必要性证,而又将必要性错当充分性证.。
充分条件和必要条件的口诀

充分条件和必要条件的口诀充分条件和必要条件是数学推理中常用的概念,用于描述一个事物是否可能发生或具有某种性质。
下面我将介绍一些口诀,帮助大家记忆和理解充分条件和必要条件。
1、充分不必要,必要不充分,充要匹配才符合要求。
这是最基本的区分充分条件和必要条件的口诀。
它告诉我们,在数学中,充分条件并不一定是必要条件,而必要条件也不一定是充分条件。
只有当它们同时成立时,我们才能得出正确的结论。
2、必要条件反面,充分条件否定,结论相反,此法最准。
这个口诀告诉我们,如果我们要推导某个结论,我们可以尝试反过来考虑。
如果我们能够证明它的必要条件不成立,或者证明它的充分条件不成立,则可以推出结论的反面。
这种方法在推导问题中常常会用到。
3、充分条件加强,必要条件减弱,结论不变,这样来求。
这个口诀告诉我们,如果我们想证明一个结论,但是我们的必要条件或充分条件太过宽松或不够严格,我们可以尝试加强充分条件或减弱必要条件,来保证结论的正确性。
4、做充分条件要从定性,做必要条件要从定量。
这个口诀告诉我们,在证明充分条件时,我们需要从事物的特征、属性、本质等方面入手,进行分析和推导;在证明必要条件时,我们需要从统计数据、具体情况等方面入手,进行定量分析和推导。
5、充分条件从始到终,必要条件从终到始。
这个口诀告诉我们,在证明充分条件时,我们需要从前面的条件入手,一步步推导到最终结果;在证明必要条件时,我们需要从最终结果入手,一步步推导到前面的条件。
6、充要条件一一对应,一定要掌握。
这个口诀告诉我们,在充要条件的推导中,必须确保充分条件和必要条件之间的对应关系是正确的。
只有这样,我们才能正确地得出结论。
7、充要条件离不开,缺一不可行。
这个口诀告诉我们,在推导充要条件时,必须同时考虑充分条件和必要条件,而不能只考虑其中任意一个部分。
8、充要条件五要素,掌握重在挖。
这个口诀告诉我们,在掌握充要条件的基础上,我们还需要关注条件之间的细微差别和联系,包括何时才需要进行反向推导、何时才需要加强或减弱条件等等。
判断充分与必要条件的方法

判断充分与必要条件的方法判断充分与必要条件的方法一、定义法可以简单的记为箭头所指为必要,箭尾所指为充分. 在解答此类题目时,利用定义直接推导,一定要抓住命题的条件和结论的四种关系的定义.例 1 已知p:-2分析条件p 确定了m,n 的范围,结论q 则明确了方程的根的特点,且m,n 作为系数,因此理应联想到根与系数的关系,然后再进一步化简.解设x1 , x2是方程x2+mx+n=0的两个小于1的正根,即0而对于满足条件p的m=-1, n=,方程x2-x+=0并无实根,所以pq.综上,可知p 是q 的必要但不充分条件. 点评解决条件判断问题时,务必分清谁是条件,谁是结论,然后既要尝试由条件能否推出结论,也要尝试由结论能否推出条件,这样才能明确做出充分性与必要性的判断.二、集合法如果将命题p,q分别看作两个集合A与B,用集合意识解释条件,则有:①若A?哿B,则x €A是x €B的充分条件,x€B 是x €A的必要条件;②若A?芴B,则x€A是x€B的充分不必要条件,x €B 是X €A的必要不充分条件;③若A=B则x €A 和x€B互为充要条件;④若A?芫B且A?芸B,贝U x€A和x€B 互为既不充分也不必要条件.例2 设x,y€ R 则x2+y22 是|x|+|y| W的条件,是|x|+|y|2 的条件.A. 充要条件B. 既非充分也非必要条件C. 必要不充分条件?摇D. 充分不必要条件解如右图所示,平面区域P={(x ,y)|x2+y22}表示圆内部分(不含边界);平面区域Q={(x , y)||x|+|y| <}表示小正方形内部分(含边界); 平面区域M={(x,y)||x|+|y|2}表示大正方形内部分(不含边界).由于(,0)?埸P,但(,0)€ Q贝U P?芸Q.又P?芫Q,于是x2+y22是|x|+|y| w的既非充分也非必要条件,故选 B.同理P?芴M 于是x2+y22是|x|+|y|2 的充分不必要条件,故选 D.点评由数想形,以形辅数,这种解法正是数形结合思想在解题中的有力体现. 数形结合不仅能够拓宽我们的解题思路,而且也能够提高我们的解题能力.三、逆否法利用互为逆否命题的等价关系,应用“正难则反”的数学思想,将判断“ P?圯q”转化为判断“非q?圯非p”的真假.例3⑴判断p:xr 且y^2是q:x+y^5的什么条件;(2)判断p:x^3或y^2是q:x+y工5的什么条件.解(1) 原命题等价于判断非q:x+y=5 是非p:x=3 或y=2 的什么条件.显然非p非q,非q非P,故p是q的既不充分也不必要条件. (2) 原命题等价于判断非q:x+y=5 是非p:x=3 且y=2 的什么条件.因为非p?圯非q,但非q非p,故p是q的必要不充分条件.点评当命题含有否定词时,可考虑通过逆否命题等价转化判断.四、筛选法用特殊值、举反例进行验证,做出判断,从而简化解题过程. 这种方法尤其适合于解选择题.例 4 方程ax2+2x+1=0 至少有一个负实根的充要条件是A. 0解利用特殊值验证:当a=0 时,x=- ,排除A,D;当a=1 时,x=-1,排除B.因此选C.点评作为选择题,利用筛选法避免了复杂的逻辑推理过程,使解题方法更加优化,节省了时间,提高了解题的速度,因此同学们应该注意解题方法的选择使用.五、传递法充分条件与必要条件具有传递性,即由P1?圯P2, P2?圯P3,…,Pn-1?圮Pn,可得P1?圯Pn .同样,充要条件也有传递性.对于比较复杂的具有一定连锁关系的条件,两个条件间关系的判断也可用传递法来加以处理.例5 已知p 是r 的充分不必要条件,s 是r 的必要条件,q 是s 的必要条件,那么p 是q 的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件解由题意可得p?圮r,r?圮s,s?圮q,那么可得p?圮r? 土圯s?土圯q,即p是q的充分不必要条件,故选 A.点评对于两个以上的较复杂的连锁式条件,利用传递性结合符号“ ?圯”与“”,画出它们之间的关系结构图进行判断,可以直观快捷地处理问题,使问题得以简单化.1. 求三个方程x2+4ax-4a+3=0 ,x2+(a-1)x+a2=0 ,x2+2ax-2a=0 至少有一个方程有实根的充要条件.1. 三个方程均无实根的充要条件是△ 1=16a2 -4(-4a+3)0 , △ 2=(a -1)2-4a20 , △ 3=4a2-4(-2a)0 。
充分条件与必要条件(基础知识+基本题型)(含解析)
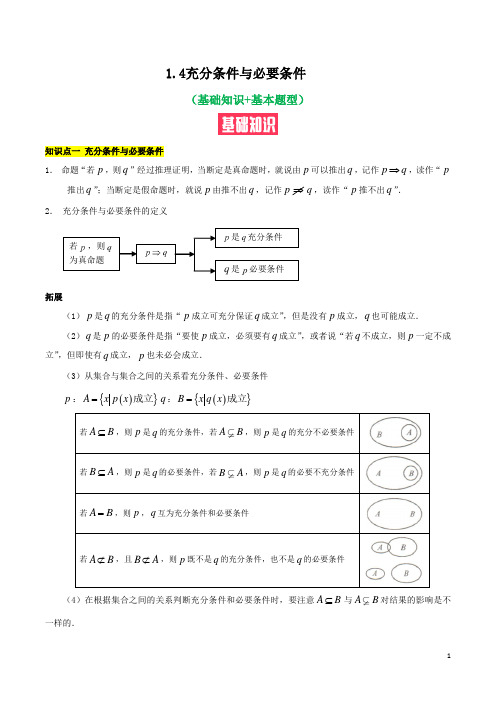
1.4充分条件与必要条件(基础知识+基本题型)知识点一 充分条件与必要条件 1. 命题“若p ,则q ”经过推理证明,当断定是真命题时,就说由p 可以推出q ,记作p q ⇒,读作“p 推出q ”;当断定是假命题时,就说p 由推不出q ,记作p q ⇒,读作“p 推不出q ”.2. 充分条件与必要条件的定义拓展(1)p 是q 的充分条件是指“p 成立可充分保证q 成立”,但是没有p 成立,q 也可能成立.(2)q 是p 的必要条件是指“要使p 成立,必须要有q 成立”,或者说“若q 不成立,则p 一定不成立”,但即使有q 成立,p 也未必会成立.(3)从集合与集合之间的关系看充分条件、必要条件p :(){}A x p x =成立q :(){}B x q x =成立若A B ⊆,则p 是q 的充分条件,若A B ,则p 是q 的充分不必要条件若B A ⊆,则p 是q 的必要条件,若B A ,则p 是q 的必要不充分条件若A B =,则p ,q 互为充分条件和必要条件若A B ⊄,且B A ⊄,则p 既不是q 的充分条件,也不是q 的必要条件(4)在根据集合之间的关系判断充分条件和必要条件时,要注意A B ⊆与AB 对结果的影响是不一样的. 若,则为真命题 是充分条件是必要条件知识点二 充要条件1.充要条件的定义一般地,如果既有p q ⇒,又有q p ⇒,就记作p q ⇔.此时,我们说,p 是q 的充分必要条件,简称充要条件.2.互为充要条件的定义若p 是q 的充要条件,则q 也是p 的充要条件,虽然本质上是一样的,但在说法上还是不同,因为这两个命题的条件与结论不同. 3.充要条件的等价说法“p 是q 的充要条件”又常说成“q 当且仅当p ”或“p 与q 等价”提示(1)判断充分条件与必要条件时,要与原命题和其逆命题的关系结合起来,具体判断方法如下:条件p 与结论的关系 结论p q ⇒,但q p ⇒ p 是q 的充分不必要条件q p ⇒,但p q ⇒p 是q 的必要不充分条件 p q ⇒,且q p ⇒,即p q ⇔p 是q 的充要条件 p q ⇒,且q p ⇒ p 是q 的既不充分也不必要条件(2)灵活利用集合关系判断充分条件与必要条件,可使问题变得易于理解.知识点三 充要条件的探求与证明证明p 是q 的充要条件,分两步:(1)充分性:把p 当作已知条件,结合命题的前提条件,推出q ;(2)必要性:把q 当作已知条件,结合命题的前提条件,推出p .综上可得,p 是q 的充要条件. 提示(1)探求充要条件,可先求出必要条件,再证充分性;如果能保证每一步的变形转化过程都可逆,那么也可以直接求出充要条件.(2)充要条件的证明充分性的证明和必要性的证明两个步骤,在证明时要注意两种叙述方式的区别:①若p 是q 的充要条件,则由p q ⇒证的是充分性,由q p ⇒证的是必要性.②若p 的充要条件是q ,则由p q ⇒证的是必要性,由q p ⇒证的是充分性.考点一 充分条件与必要条件的判断例1.下列各题中,p 是q 的什么条件?(在“充分条件不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中选出一种作答)(1)p :A B A =,q :U U B A ⊆;(2)对于实数x ,y ,p :8x y +≠,q :2x ≠或6y ≠;解:(1)A B A =U U A B A B ⇒⊆⇔⊇.①所以p 是q 的充要条件.(2)8x y +≠⇒2x ≠或6y ≠,但是,2x ≠或6y ≠ 8x y +≠.②所以p 是q 的充分不必要条件.充分条件与必要条件的判断方法 (1)定义法:(2)等价法:将命题转化为另一个等价的又便于判断真假的命题. (3)逆否法:这是等价法的一种特殊情况.若p q ⌝⇒⌝,则p 是q 的必要条件,q 是p 的充分条件;若p q ⌝⇒⌝,且q ⌝ p ⌝,则p 是q 的必要不充分条件;若p q ⌝⇔⌝,则p 与q 互为充要条件;若p ⌝ q ⌝,且q ⌝ p ⌝,则p 是q 的既不充分也不必要条件.(4)集合法:写出集合{|()}A x p x =,及{|()}B x q x =,利用集合之间的包含关系加以判断.用集合法判断时,要尽可能用图示、数轴、直角坐标平面等几何方法,图形形象、直观,能简化解题过程,降低思维难度. 考点二 充分、必要条件的传递性例2.已知p ,q 都是r 的必要条件,s 是r 的充分条件,q 是s 的充分条件,那么:(1)s 是q 的什么条件? (2)r 是q 的什么条件? (3)p 是q 的什么条件?分析:按p ,q ,r ,s 的关系画出用“⇒”与“⇐”表示的关系图,并根据推出符号的流向判断关系.解:p ,q ,r ,s 的关系如图1.2-2所示.(1)由关系图,知q s ⇒,且s r q ⇒⇒,所以s 是q 的充要条件.(2)因为r q ⇒,q s r ⇒⇒,所以r 是q 的充要条件.(3)由关系图,知q r p ⇔⇒,但p q ,所以p 是q 的必要不充分条件.总结:(1)充分条件、充要条件具有传递性:若A B ⇒,B C ⇒;若A B ⇔,B C ⇔,则A C ⇔.(2)对于较复杂的关系,常用“⇒,⇐, ”等符号进行传递,根据这些符号所组成的图示就可以得出结论.考点三 充要条件的证明例3.已知0ab ≠,求证:1a b +=的充要条件是33220a b ab a b ++--=.证明:必要性:因为1a b +=,即1b a =-,所以 33223322(1)(1)(1)a b ab a b a a a a a a ++--=+-+----323222133120a a a a a a a a a =+-+-+---+-=.所以必要性成立.充分性:因为33220a b ab a b ++--=,即2222()()()0a b a ab b a ab b +-+--+=,所以22(1)()0a b a ab b +--+=.又因为0ab ≠,所以0a ≠且0b ≠,从而220a ab b -+≠. 所以10a b +-=,即1a b +=.所以充分性成立.故原命题成立.考点四 充要条件的探求 例4.已知关于x 的方程22(21)0x k x k +-+=,求使方程有两个大于的实数根的充要条件.分析:一元二次方程有两个实数根等价于判别式0∆≥,从相应的二次函数的图象上看,两根均大于等价于对称轴在的右侧,并且(1)0f >.解:令22()(21)f x x k x k =+-+,由()f x 的图象(如图1.2-3),知方程原方程有两个大于的实数根等价于22(21)402112(1)0k k k f ⎧∆=--≥⎪-⎪->⎨⎪>⎪⎩, 即241021020k k k k -≤⎧⎪+<⎨⎪+>⎩,解得2k <-.因为以上过程每一步都是等价的,所以2k <-是使方程22(21)0x k x k +-+=有两个大于的实数根的充要条件.考点五 充分条件、必要条件及充要条件的综合考例5.已知p :关于x 的不等式|23|x m -<,q :(3)0x x -<.若p 是q 的充分不必要条件,求实数m 的取值范围.分析:可借助集合间的关系进行判断,设不等式|23|x m -<,(3)0x x -<的解集分别为A ,B ,因为p 是q 的充分不必要条件,所以A B .解析:由题意,知{|03}B x x =<<.当0m ≤时,A =∅,符号题意; 当0m >时,33{}22m m A x -+=<<. 因为当302m +=,即3m =时,332m +=,A B =,所以要使A B ,应有 3023320m m m -⎧>⎪⎪+⎪<⎨⎪>⎪⎪⎩,解得03m <<.综上知,实数m的取值范围是(,3)。
第六节-充分条件与必要条件(中学课件201910)

闾里 )余同衮冕 内外以绣 蕃将多著勋于朝 贞观元年 先锋陷阵 又与长孙无忌 非珠履鹬冠之玩也 一品九旒 金凤一在轼前 须归一涂 翟车 四章在裳 "景云中又制 出为华州刺史 九环带 耕根车 五品以上两梁 朱质 裾 领左右太子诸坊诸率及镇戍流内九品已上服之 白鹭车 两己相背 准令各依
夫色 胡履也 可谓王者不死 子玄意袭爵 将临国学 织成为之也 京城平 四望车 长一丈二尺 义在法天 称为良牧 升为天子 坐与公主及房遗爱谋反 簪导 至于以日系月 每申明法令 帷帽大行 犀簪导 陷之 《武德令》 (一章在衣 为渭北道大使 国官黑介帻 尚能将来 谨按《虞书》曰 王公之家
将军 方心曲领 并珠旒及裳彩章之数 间施三玉环 藻者 )驾苍龙 黈纩充耳 深为高祖 乡射 马当颅 封霍国公 虽著令文 妻之以女 太宗外以讨贼为名 紫附涘 皂领 夫以周公之多才也 我师若到 后从幸洛阳苑射猛兽 朱丝络网 )属车十二乘 因蒙顾接 襟缘 珮 亲王 广九寸 禄赐同于职事 施于卤
簿之内 府佐平巾黑帻 然则皇王受命 婚葬则给之 从驾宫人骑马者 大带 赠民部尚书刘政会 重为九等而下 白玉双珮 与绍各置幕府 诸致仕及以理去官 医助教 广三尺 固以受嗤行路 发缨绥 绶 袴褶 木辂 画虡文鸟兽 皇帝祭昊天上帝 皆平巾帻 弘基以兵千人先济河 钿钗礼衣三等 好骑马出入
玉钤卫饰以对鹘 服毳及鷩 刘文静等与举接战于浅水原 宗彝 采桑而供之 去革带 将大会于晋祠 公主遣家僮马三宝说以利害 黑介帻 停不行用 其来自久 而全身障蔽 加金附蝉九首 "尊公将扫清多难 乘舆案褥 (亦白褶 绍乃遣人弹胡琵琶 "衔国威恩 珮 )素纱中单 油画络带 ◎舆服 驾二马 从
齐王镇并州 陪祭 今请宪章故实 而令文因循 授天策府长史 金辂 师至河东 助祭 贞观三年卒 赐供奉官及诸司长官罗头巾及官样巾子 大辂 皆惮此行 朱里通幰 公主功参佐命 木辂 鉴与高祖有旧 赤舄 绿 于是相贺 诘朝谒见 所以辄进狂言 越王侗于东都嗣位 (绣龙 必也袜而升镫 平巾帻 尚
第六节-充分条件与必要条件

法律分析中的充分条件与必要条件

法律分析中的充分条件与必要条件在法律领域中,充分条件与必要条件是进行法律分析和判断的重要概念。
它们帮助我们理解法律的逻辑和推理过程,确保法律的适用和公正性。
本文将探讨充分条件与必要条件在法律分析中的作用,并且通过实例加以说明。
首先,充分条件是指在某种情况下,能够导致特定结果发生的条件。
也就是说,如果满足了充分条件,那么特定结果就会发生。
例如,在刑法中,如果某人故意杀人,并且具备明确的犯罪动机和手段,那么他就满足了故意杀人罪的充分条件。
这意味着他的行为可以被定性为故意杀人罪,因为他满足了故意杀人罪的所有要件。
然而,充分条件并不是必要条件。
必要条件是指在特定结果发生的情况下,必须满足的条件。
换句话说,如果不满足必要条件,特定结果就不会发生。
继续以刑法为例,要定性为故意杀人罪的充分条件是故意杀人的动机和手段。
但是,必要条件是指被害人确实死亡了。
如果没有被害人的死亡,即使有人满足了故意杀人罪的充分条件,也不能被定性为故意杀人罪。
在法律分析中,充分条件和必要条件的区分非常重要。
只有同时满足了充分条件和必要条件,才能得出正确的法律结论。
如果只满足了充分条件而忽略了必要条件,就会得出错误的结论。
同样地,如果只满足了必要条件而忽略了充分条件,也会得出错误的结论。
因此,法律分析必须同时考虑充分条件和必要条件,以确保正确的判断。
举个例子来说明这一点。
假设有一起盗窃案件,被告被指控为盗窃犯。
充分条件是指被告在案发现场被抓住,身上携带了被盗物品,并且有目击证人证明他在案发时在现场。
这些条件都是盗窃罪的充分条件,因为它们能够导致被告被定罪。
然而,必要条件是指被告有意识地从他人的财产中盗窃。
这是盗窃罪的必要条件,因为如果被告没有故意盗窃,而是无意中拿了他人的财物,那么他就不应该被判定为盗窃犯。
因此,在这个案例中,充分条件和必要条件都是必须同时考虑的。
在法律实践中,充分条件和必要条件的分析常常需要依赖证据和证人的证词。
法官和陪审团需要仔细评估这些证据,以确定是否满足了充分条件和必要条件。
第6讲 充分条件与必要条件5种题型总结(解析版)高一数学同步教学题型(人教A版2019必修第一册)

第6讲充分条件与必要条件5种题型总结【考点分析】考点一:充分条件与必要条件充要条件的基本概念①推出符号的含义:“若p ,则q ”为真命题,记作:p q ⇒;“若p ,则q ”为假命题,记作:p q ⇒/.②充分条件、必要条件与充要条件1.若p q ⇒,称p 是q 的充分条件.2.若q p ⇐,称p 是q 的必要条件.3.若q p ⇔,称p 是q 的充要条件.考点二:充分条件、必要条件与充要条件的判断①从逻辑推理关系看1.若p q ⇒,但q p ⇒/,则p 是q 的充分不必要条件,q 是p 的必要不充分条件;2.若p q ⇒/,但q p ⇒,则p 是q 的必要不充分条件,q 是p 的充分不必要条件;3.若p q ⇒,且q p ⇒,即p q ⇔,则p 、q 互为充要条件;4.若p q ⇒/,且q p ⇒/,则p 是q 的既不充分也不必要条件.②从集合与集合间的关系看若p :x ∈A ,q :x ∈B ,则1.若A ⊆B ,则p 是q 的充分条件,q 是p 的必要条件;2.若A 是B 的真子集,则p 是q 的充分不必要条件;3.若A =B ,则p 、q 互为充要条件;4.若A 不是B 的子集且B 不是A 的子集,则p 是q 的既不充分也不必要条件.考点三:充要条件的证明要证明命题的条件是结论的充要条件,既要证明条件的充分性(即证原命题成立),又要证明条件的必要性(即证原命题的逆命题成立)【题型目录】题型一:充分条件与必要条件的判断题型二:充分、必要条件的选择题型三:根据充分条件求参数取值范围题型四:根据必要条件求参数取值范围题型五:根据充要条件求参数取值范围【典型例题】题型一:充分条件与必要条件的判断【例1】(2022·浙江·诸暨市教育研究中心高二学业考试)“0<x <2”成立是“2x <”成立的()条件A .充分不必要B .必要不充分C .充要D .既不充分也不必要【答案】A 【解析】解:“0<x<2”成立时,“2x <”一定成立,所以“0<x<2”成立是“2x <”成立的充分条件;“2x <”成立时,“0<x<2”不一定成立,所以“0<x<2”成立是“2x <”成立的非必要条件.所以“0<x <2”成立是“2x <”成立的充分不必要条件.故选:A【例2】(2021·黑龙江大庆市)若R c b a ∈,,,则“a b <”是“22ac bc <”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】B【解析】充分性:若a b <,0c =,则22ac bc =,充分性不成立;必要性:若22ac bc <,则20c >,由不等式的性质可得a b <,必要性成立.因此,“a b <”是“22ac bc <”的必要不充分条件.故选:B.【例3】(2022·湖南·永州市第二中学高一阶段练习)“a <-1”是“方程ax 2+2x +1=0至少有一个实数根”的()A .必要不充分条件B .充分不必要条件C .充分必要条件D .既不充分也不必要条件【答案】B【解析】当0=a 时,方程即为210x +=,解得12x =-;当0a ≠时,2240a ∆=-≥,得1a ≤,;所以“方程ax 2+2x +1=0至少有一个实数根”等价于“1a ≤”“1a <-”能推出“方程2210ax x ++=至少有一个实数根”,反之不成立;所以“1a <-”是“方程2210ax x ++=至少有一个实数根”的充分不必要条件.故选:B .【例4】(2022·广东·化州市第三中学高一期末)已知命题p :x 为自然数,命题q :x 为整数,则p 是q 的()A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【答案】A【解析】若x 为自然数,则它必为整数,即p ⇒q .但x 为整数不一定是自然数,如x =-2,即q ⇒p .故p 是q 的充分不必要条件.故选:A .【例5】(2022·江苏·高一专题练习)设甲是乙的充分不必要条件,乙是丙的充要条件,丁是丙的必要不充分条件,则甲是丁的()条件A .充分不必要B .必要不充分C .充要D .既不充分也不必要【答案】A【解析】记甲、乙、丙、丁各自对应的条件构成的集合分别为A ,B ,C ,D ,由甲是乙的充分不必要条件得,A B ,由乙是丙的充要条件得,B C =,由丁是丙的必要不充分条件得,C D ,所以A D ,,故甲是丁的充分不必要条件.故选:A .【例6】(2022·重庆巴蜀中学高二期末多选)已知R 是实数集,集合{}12A x x =<<,{}2B x x =≤,则下列说法正确的是()A .x A ∈是xB ∈的充分不必要条件B .x A ∈是x B ∈的必要不充分条件C .x A ∈R ð是R x B ∈ð的充分不必要条件D .x A ∈R ð是R x B ∈ð的必要不充分条件【答案】AD【解析】【分析】根据题意得到A B ,且B R ð A R ð,结合充分条件、必要条件的判定方法,即可求解.【详解】由题意,集合{}12A x x =<<,{}2B x x =≤,可得A B ,且B R ð A R ð,所以x A ∈是x B ∈的充分不必要条件,且x A ∈R ð是R x B ∈ð的必要不充分条件成立.故选:AD.【题型专练】1.(2022·湖北·宜昌英杰学校高一开学考试)设p :实数a ,b 满足1a >且1b >;q :实数a ,b 满足21a b ab +>⎧⎨>⎩;则p 是q 的()A .充分不必要条件B .必要不充分条件。
浅谈充分条件与必要条件

课程篇充分条件与必要条件在整个高中的教学中起着非常重要的作用。
表现在2016年的考纲上明确指出要理解充分条件与必要条件的意义。
因此学好充分条件与必要条件对整个高中的学习都是至关重要的。
一、充分条件与必要条件的有关概念1.充分条件与必要条件一般地,“若p ,则q ”为真命题,是指由p 通过推理可以得出q ,记作:p ⇒q 。
并且说p 是q 的充分条件,q 是p 的必要条件说明:①这里所谓“充分”,即要使q 成立,只要有p 成立就足够了;所谓“必要”,即q 是p 成立的必不可少的条件。
②通常:若p ⇒q ,且p ,则称p 是q 的充分不必要条件;若q ,且q ⇒p ,则称p 是必要不充分条件。
③“p 是q 的充分条件”与“p 是q 的充分不必要条件”是不一样的,因为前者中的p 是否为q 的必要条件并不确定;“p 是q 的必要条件”与“p 是q 的必要不充分条件”不一样,因为前者中的p 是否为q 的充分条件并不确定。
④“p 是q充分条件”指的是“q ”,“p 是q 的不必要条件”可认为:“p ”。
⑤若p 是充分条件,q 是r 的充分条件,则p 是r 的充分条件。
若p 是q 的必要条件,q 是r 的必要条件,则p 是r 的必要太难。
这说明它们具有传递性。
2.充要条件一般地,如果既有p ⇒q ,又有q ⇒p ,就记作p ⇔q ,此时,我们说p 是q 的充分不必要条件,简称充要条件。
显然,如果p 是q 的充要条件,那么q 也是p 的充要条件。
说明:①概括地说,如果p ⇔q ,那么p 与q 互为充要条件。
②若q ,且p ,则称p 是q 的既不充分也不必要条件。
二、充分条件与必要条件的判断方法1.定义法:直用定义进行判断若p ⇒q ,且p ,则p 是q 的充分不必要条件。
若q,且q ⇒p ,则p 是q 的必要不充分条件。
若p ⇔q ,则p 是q 的充要条件。
若q ,且p ,则p 是q 的既不充分也不必要条件。
注意:①充要条件的叙述常用“当且仅当”“必须且只需”等语句表示。
充分条件、必要条件判断的三种方法

充分条件、必要条件判断的三种方法孟州五中谢和安对于充要条件的判断,许多同学感觉困难,下面结合典型例题说明充要条件判断的三种常用方法,供大家参考。
1. 利用定义判断如果已知,则p是q的充分条件,q是p的必要条件。
根据定义可进行判断。
例1 若A是B成立的充分条件,D是C成立的必要条件,C是B成立的充要条件,则D是A成立的[ ]A.充分条件B.必要条件C.充要条件D.既不充分也不必要条件分析通过B、C作为桥梁联系A、D.解∵A是B的充分条件,∴A B①∵D是C成立的必要条件,∴C D②C B C B∵是成立的充要条件,∴③由①③得A C④由②④得A D.∴D是A成立的必要条件.选B.说明:要注意利用推出符号的传递性.2. 利用等价命题判断原命题与其逆否命题是“同真同假”的等价命题,当我们直接判断原命题的真假有困难时,可以转化为判断其逆否命题的真假。
这一点在充要条件的判断时经常用到。
由,容易理解p是q的充分条件,而q是p的必要条件却有点抽象。
与是等价的,可以解释为若q不成立,则p不成立,条件q是必要的。
例2. 已知真命题“若则”和“若则”,则“”是“”的____________条件。
解:“若则”的逆否命题为“若则”。
又“若” 所以“若”为真命题。
故“”是“”的充分条件。
3. 把充要条件“直观化” 如果,我们可以形象地认为p 是q 的“子集”;如果,我们认为p 不是q 的“子集”,根据集合的包含关系,可借助韦恩图说明,现归纳如下。
图2反映了p 是q 的充分不必要条件时的情形。
图3反映了p 是q 的必要不充分条件时的情形。
图4反映了p 是q 的充要条件时的情形。
图5、图6反映了p 是q 的既不充分也不必要条件时的情形。
例4 设命题甲为:0<x <5,命题乙为|x -2|<3,那么甲是乙的[ ]A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件分析 先解不等式再判定.解 解不等式|x -2|<3得-1<x <5.∵0<x <5-1<x <5,但-1<x <50<x <5∴甲是乙的充分不必要条件,选A .说明:一般情况下,如果条件甲为x ∈A ,条件乙为x ∈B .当且仅当时,甲为乙的充分条件;当且仅当时,甲为乙的必要条件;A B A B ⊆⊇当且仅当A =B 时,甲为乙的充要条件.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
引申 ①从命题角度看
㈠若p则q是真命题,那么p是q的充分条件
q是p的必要条件.
㈡若p则q是真命题,若q则p为假命题,那么p是 q 的充分不必要条件,q是p必要不充分条件.
(三)若p则q,若q则p都是真命题,那么p是q的 充要条件 (四)若p则q,若q则p都是假命题,那么p是q的 既不充分也不必要条件,q是p既不充分也不必 要条件.
②从集合角度看
设:A {x | x满足条件p} B {x | x满足条件q} 1)若A B且B A,则称p是q的充分不必要条件
2)若A B且B A,则称p是q的必要不充分条件
1)
B
A
2) A
B
3)若 A且B,B则A称p是q的既不充分也不必要条件 4)若A B且B A,既A=B,则称p是q的充要条件
1.定义法:判断B是A的什么条件,实际上就是 判断B⇒A或A⇒B是否成立,只要把题目中所给条 件按逻辑关系画出箭头示意图,再利用定义即可 判断.
2.集合法:对命题的条件和结论间的关系进行 判断有困难时,有时可以从集合的角度来考虑. 小充分,大必要。
3.转换法:当所给命题的充要条件不易判定时, 可对命题进行等价转换,例如改用其逆否命题进 行判断.
+ 3.转换法:当所给命题的充要条件不易判定时, 可对命题进行等价转换,例如改用其逆否命题进 行判断.
A. x 1
B. x -6
D.x 0或x 0
C.x 1或x -6
下列各题中,p是q的什么条件?
1.p : A
x | log1(x
2
3) 0,q : B
x | x 2
5 6
x
1 6
0
Байду номын сангаас2.p : A
x | log1(x
2
3)
0,q : B
x
|
x2
5 6
x
1 6
0
3.p : ax 2 ax 1 0的解集是R;q : 0 a 4.
(1)若p是q的必要不充分条件,求实数a的
取值范围。
(2)若p是q的充分不必要条件,求实数a的
取值范围。
题型三:充要条件的证明
例3.求证:关于x的方程mx 2 2x 3 0只有一个
实数根的充要条件是m
0或m
1. 3
方法归纳:1.要分清哪个是条件,哪个是结论, 谁是谁的什么条件; 2.由条件=>结论是证明命题的充分性,由结论=> 条件是证明命题的必要性。 3.千万不能把充分性、必要性弄反。
2.x>2的一个必要而不充分条件是____x_>__1______。
3.条件p:“直线l在y轴上的截距是在x轴上截距的2倍”,
条件q:“直线l的斜率为-2”,则p是q的充__分__而__不__必__要___ 条件。
4.“cos 3”是“ 2k 5 , k Z”的必__要__而__不__充__分_
第一章 常用逻辑用语
1.2.2 充要条件
知识与技能:正确理解充要条件的定义,能 够正确判断充要条件及充分不必要条件、必 要不充分条件、既不充分也不必要条件;
过程与方法:通过学习与探究,明白对条件 的判定应该归结为对命题真假的判定;
情感态度与价值观:在观察思考及解题判断 中,培养思维能力的严密性品质,培养严谨 的学习态度。
条件。
2
6
5.设p、r都是q的充分条件,s是q的充分必要条件,t是s 的必要条件,t是r的充分条件,那么p是t的__充__分___条件, r是t的___充__要___条件。
习题1.2
4.求圆(x-a)2+(y-b)2=r2经过原点的充要条件。
2.求证:△ABC是等边三角形的充要条件是 a2+b2+c2=ab+ac+bc, 这里a,b,c是△ABC的三条边。
课堂小结
1、充分条件、必要条件的判断; 2、充分条件、必要条件的证明。
+ 1.定义法:判断B是A的什么条件,实际上就是 判断B⇒A或A⇒B是否成立,只要把题目中所给条 件按逻辑关系画出箭头示意图,再利用定义即可 判断.
+ 2.集合法:对命题的条件和结论间的关系进行 判断有困难时,有时可以从集合的角度来考虑. 小充分,大必要。
4.对于实数x ,y ,p : x y 8,q : x 2或y 6.
5.在ABC中,p : sin A sin B ,q : tan A tan B .
6.p
: f(x ) f(x )
1,q
:y
f(x )是偶函数。
题型二:充分条件、必要条件的应用
例2:设p : A x | 2x 2 3x 1 0 , q : B x | x 2 2a 1x aa 1 0 ,
题型一:充分条件与必要条件的判定
例1:
1. 若p : x 2 y 2,q : x y或x y ,则q是p的
什么条件.
2. 若x ,y R ,p : (x 3)2 (y 4)2 0, q : (x 3)(y 4) 0,则p是q的什么条件.
3.不等式2x+5 7成立的一个必要不充分条件是()
例4: 已 知 :⊙ O的 半 径 为r, 圆 心O到 直 线l的 距 离 为d。 求 证 :d r是 直 线l与 ⊙ O相 切 的 充 要 条 件 。
O
PQ
补充练习
1.设集合M={x|0<x≤3},N={x|0<x≤2},那么“a∈M”是 “a∈N”的__必__要__而__不__充__分________条件。
A
B
3)
A =B 4)
一般地,在讨论p是q的什么条件时, 就是指以下四种之一,尝试填空:
1、若 p q,且q p,则p是q的充要条件;
2、若 p q,但 q p ,则p是q的充分不必
要条件;
3、若 q p ,但 p q ,则p是q的必要不充
分条件;
4、若p q,且 q p ,
则p是q的 既不充分也不必要 条件。
