多元复合函数的求导法则

合集下载

§8.4 多元复合函数的求导法则与隐函数的求导公式

M
26
机动目目录录上上页页下下页页返返回回结结束束
定理2 若函数 F (x, y, z) 满足:
① 在点
的某邻域内具有连续偏导数 ,
② F (x0 , y0, z0) 0 ③ Fz (x0 , y0, z0) 0
则方程
在点
某一邻域内可唯一确
定一个单值连续函数 z = f (x , y) , 满足
机动目目录录上上页页下下页页返返回回结结束束
导数的另一求法 — 利用隐函数求导
sin y ex xy 1 0, y y(x) 两边对 x 求导
两边再对 x 求导
y x0
ex y cos y x (0,0)
sin y ( y)2 cos y y
令 x = 0 , 注意此时 y 0 , y 1
8
目录上页下页返回结束
例3 设 z uv sin t , u et , v cos t , 求全导数 dz .
dt
解 dz z du
z
dt u dt
t
z
vet
cos t
e t (cost sin t) cos t
uvt tt
注意：多元抽象复合函数求导在偏微分方程变形与验证解的问题中经常遇到, 下列两个例题有助于掌握这方面问题的求导技巧与常用导数符号.
x y
解 z
z v
x
v x
eu sin v eu cos v 1
z
z
z v
y
v y
eu sin v eu cos v 1
uv x yx y
7
目录上页下页返回结束
例2 u f (x, y, z) ex2 y2 z2 , z x2sin y, 求 u , u x y

多元复合函数的求导法则

分线相加
同理可得
z z u z v y u y v y
返回
一、多元复合函数求导法则 —链锁规则
设下列各公式中所出现的函数均满足所需条件，且有相应的导数或偏导数。 1、全导数情形1 链锁规则公式
u z x
全导数
v
dz z du z dv dx u dx v dx
dh h dV w dr dt V dt r dt 3 6V r 2 4 3 e r r
返回
dh 6 V r 2 (2 e ) dt r r
设t0时刻沙丘体积为60立方米、底面半径为6米，则
dh 6 60 6 2 (2 e ) dt t t0 6 6
3
dz ,求 . dt
〖解〗由多元复合函数求导法则得全导数为：
x z y
2
t
dz z dx z dy dt x dt y dt 2 cos t f x 3t f y
部分抽象函数
□
设f具有二阶连续偏导数，如何求二阶导数？
d z d dz 2 dt dt dt d 2 (cos t f x 3t f y ) dt
返回
视y为常数
视u,v为常数
【例8】设 u f ( x, y, z ), z g ( x, y), y h( x, t ), t ( x),
du 求 . dx
〖解〗方法1(链锁规则公式)
x u y z
x y
x
x
du f dx x
f h h d y x t dx
情形5
x z u v
x y
z f f u f v x x u x v x z f u y u y

多元函数的求导法则-精选

z z u z v y u y v y
x yx y
eusinvx eucovs1
e x y [x six n y ) (co x y s )( ]
山东农业大学
高等数学
主讲人：苏本堂
例2. u f(x ,y ,z ) e x 2 y 2 z 2 ,z x 2 sy i,求nu , u x y
山东农业大学
高等数学
主讲人：苏本堂
推广: 设下面所涉及的函数都可微 .
1) 中间变量多于两个的情形. 例如, zf(u,v,w ),
u ( t ) ,v ( t ) ,w ( t )
z
d z z du z dv z dw d t u d t v dt w dt
在点 t 可导, 且有链式法则 dzzduzdv dt u dt v dt
z
uv
证: 设 t 取增量△t , 则相应中间变量 t t
有增量△u ,△v ,
zzuzvo() (( u)2( v)2)
u vΒιβλιοθήκη 山东农业大学高等数学
主讲人：苏本堂
zzuzv o ( ) (( u)2( v)2)
山东农业大学
高等数学
主讲人：苏本堂
第四节多元复合函数的求导法则
一、多元复合函数求导的链式法则二、多元复合函数的全微分
山东农业大学
高等数学
主讲人：苏本堂
一、多元复合函数求导的链式法则
定理. 若函数 u (t),v (t)在 t可点 ,z导 f(u,v) 在点 (u,v)处偏导连续, 则复合函数 zf((t) ,(t))
e xy[x six ny ) (co x y s )]d(y 所以 zexy[ysixn y()co x sy)(]

多元复合函数的求导法则

多元复合函数的求导法则为了简化讲解，假设我们有一个复合函数f(g(x))，其中g(x)是一个一元函数，f(y)是一个多元函数。

我们希望计算该函数的导数。

下面是多元复合函数求导的三种基本法则。

法则一：链式法则链式法则是求导复合函数最常用的法则。

它可以帮助我们计算f(g(x))的导数。

根据链式法则，导数可以通过链式相乘的方式进行计算。

链式法则的公式为：(f(g(x)))'=f'(g(x))*g'(x)其中f'(y)是f(y)对变量y的导数，g'(x)是g(x)对变量x的导数。

通过链式法则，我们可以将f(g(x))的导数转化为f'(g(x))和g'(x)的乘积。

法则二：导数反函数法则导数反函数法则是求导复合函数的另一种常用法则。

它适用于求导符合函数的反函数的导数。

设y=g(x)是一个可逆函数，且g'(x)≠0，则它的反函数x=g⁻¹(y)的导数可以通过导数的反函数进行计算。

导数反函数法则的公式为：(g⁻¹(y))'=1/(g'(x))其中g'(x)是g(x)对变量x的导数。

通过导数反函数法则，我们可以计算得到反函数的导数。

法则三：隐函数法则隐函数法则适用于求导复合函数中的隐式函数。

隐式函数是一种表示函数关系的方程，它的导数可以通过隐函数法则进行计算。

假设我们有一个隐函数F(x,y)=0，其中y=g(x)是一个表示x与y的关系的函数。

我们可以使用隐函数法则计算y的导数。

隐函数法则的公式为：(dy/dx) = - (∂F/∂x) / (∂F/∂y)其中(∂F/∂x)和(∂F/∂y)分别表示F(x,y)对变量x和y的偏导数。

通过隐函数法则，我们可以计算得到复合函数的导数。

综上所述，链式法则、导数反函数法则和隐函数法则是求导复合函数的三种基本法则。

这些法则能够帮助我们解决复杂的多元函数求导问题，提高计算效率。

第四节多元复合函数的求导法则

第四节多元复合函数的求导法则多元函数是指含有多个自变量的函数，多元复合函数则是由多个函数相互组合而成的复合函数。

在求多元复合函数的导数时，我们需要运用多元复合函数的求导法则。

多元复合函数的求导法则有以下几种情况：1.复合函数的链式法则：设有两个变量x和y，其中y=f(u)是自变量u的函数，u=g(x)是自变量x的函数，则函数y=f(g(x))就是一个多元复合函数。

根据链式法则，该函数的导数可以表示为：dy/dx = dy/du * du/dx2.高阶多元复合函数的求导：对于高阶多元复合函数，我们需要运用多次链式法则来求导。

例如，考虑一个三元复合函数z=f(y),y=g(x),x=h(t)，其中t是自变量。

根据链式法则，可以得到如下公式：dz/dt = dz/dy * dy/dx * dx/dt这里 dz/dy 表示 z 关于 y 的导数，dy/dx 表示 y 关于 x 的导数，dx/dt 表示 x 关于 t 的导数。

3.多元复合函数中的偏导数：对于多元复合函数中的偏导数求导，我们需要运用偏导数的链式法则。

偏导数的链式法则可以表示为：∂z/∂x=(∂z/∂y)*(∂y/∂x)其中∂z/∂y表示z关于y的偏导数，∂y/∂x表示y关于x的偏导数。

同样地，对于高阶多元复合函数中的偏导数求导，我们需要运用多次链式法则来求解。

总结起来，多元复合函数的求导法则主要有链式法则和偏导数的链式法则。

通过这些法则，我们可以方便地求解多元复合函数的导数。

在实际应用中，求多元复合函数的导数常常用于最优化问题、概率统计、机器学习等领域。

这些领域中的问题往往涉及多个变量，而多元复合函数的导数可以帮助我们了解函数随变量的变化趋势，从而得出一些有用的结论。

9-4-多元复合函数求导法则

一、多元复合函数概念二、多元复合函数求导法则三、多元复合函数的高阶偏导数
元
x x(s,t)
复合
u f (x, y)
y
y(s, t )
u f (x(s,t), y(s,t)) F(s,t)
函
数
一、多元复合函数概念
类型一
➢复合关系图
类型二
➢复合关系图
类型三
➢复合关系图
s ux
t x uy t
xs u
yt
一、多元复合函数概念
类型
u f (x) x (s,t)
多
u f (x, y)
x x(t)
y
y(t)
u f (x(t), y(t)) F(t)
元复合
u f (x, y)
x x(s,t)
y
y(s, t )
u f (x(s,t), y(s,t)) F(s,t)
函数
x (t)
u f (x, y,t)
y
(t)
u f ((t), (t), t) F(t)
u f (x, y,(x, y)) F(x, y)
一、多元复合函数概念
类型一
➢复合关系图
类型二
➢复合关系图
类型三
➢复合关系图
类型四
➢复合关系图
类型五
➢复合关系图
s ux
t x uy t
xs u
yt
x
u
y t
t
xx
u
y z
y
二、多元复合函数求导法则
类型
u f (x) x (s,t)
u f ((s,t))
u f (x(t), y(t)) F(t)

9.4 多元复合函数求导法则(新)

x
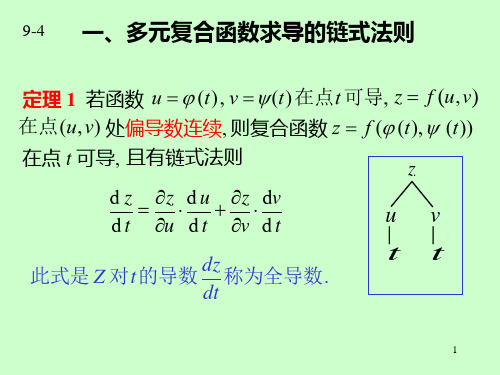
∂z 2 x = e cos y + ∂x x
∂z 1 x = −e sin y + ∂y y
18
z = f (u, v) =
u2v 2 2 , u +v ≠ 0 2 2 u +v
u =t , v =t
t 但，z = f (t, t ) = 2
dz 1 = dt 2
0,
u2 +v2 = 0
∂z du ∂z dv ≠ ∂u ⋅ dt + ∂v ⋅ dt = 0⋅1+ 0⋅1 = 0
2
常用导数符号
∂z = fv (u, v) = fv = f2′ ∂v ∂2 z ′′ = fvv (u, v) = fvv = f22 2 ∂v

称为混合偏导数
′′ ′′ ′′ ′′ 当 f12 和 f21 均连续时有 f12 = f21
3
推广: 推广设下面所涉及的函数都可微 . 1、中间变量多于两个的情形、中间变量多于两个的情形.
8
例 3.
u = f (x, y, z) = e
x2 + y2 +z2
, z = x sin y, 已知
2
∂u ∂u , . 可微，求 ∂x ∂ y
u
x y z
∂u ∂ f = 解: ∂x ∂x
x y
2 2 x2 + y2 +x4 sin 2 y
= 2 x (1+ 2 x sin y) e
∂u ∂ f ∂ f ∂z = + ⋅ ∂y ∂y ∂z ∂y
x
y x
y
5
z = eu sin v, u = xy , v = x + y , 求例2. 设

多元复合函数求导法则和隐函数求导公式

z
= e [ y ⋅ sin( x + y ) + cos( x + y )]
xy
u x yx
v y
∂ z ∂ z ∂u ∂ z ∂v = ⋅ + ⋅ ∂ y ∂u ∂ y ∂v ∂ y = e u sin v ⋅ x + e u cos v ⋅1 = e [ x ⋅ sin( x + y ) + cos( x + y )]
4
x 2 + y 2 + x 4 sin 2 y
dz . 例3. 设 z = u v + sin t , u = e , v = cos t , 求全导数 dt d z ∂ z du ∂ z dv ∂ z + = ⋅ + ⋅ 解: z d t ∂u d t ∂v dt ∂t
t
= v e t− u sin t + cos t = e t (cos t − sin t ) + cos t
u
x y z
= 2 x (1 + 2 x sin y ) e
2
x 2 + y 2 + x 4 sin 2 y
∂u ∂ f ∂ f ∂ z + ⋅ = ∂ y ∂ y ∂z ∂ y
x
cos y
y
= 2 ye
x2 + y2 + z 2
+2 z e
x2 + y2 + z 2⋅ x 2
= 2 ( y + x sin y cos y ) e
多元复合函数的求导法则
一元复合函数
y = f (u ), u = ϕ ( x)
dy dy d u 求导法则 = ⋅ dx du dx 微分法则 d y = f ′(u ) d u= f ′(u ) ϕ ′ ( x) d x

7(4)多元复合函数的求导法则

f u
u t
f v
v t
f w w t
kt k1
f
( x,
y, z)
tx
f u
t
y
f v
t
z
f w
tkt k1
f
(
x,
y,
z)
k tk f ( x, y, z) kf (u,v, w)
uxf ux
yv
f
vy
wz
f
wz
kf (xu,yv, wz )
(C ) x f y f z f kf ( x, y, z); x y z
求fxy (0, 0)和f yx (0, 0)
解当( x, y) (0,0)时, 有
f x ( x,
y)
3x2 y( x2 (x2
y2) x3 y y2 )2
2x
3x2 y x2 y2
2x4 y ( x2 y2 )2
,
fy(x, y)
x3 x2 y2
(
2 x2
x3
y2 y2
)2
.
19
设多元f 复( x合,函y)数的求x导2x法3则yy2 0
当( x, y) (0,0),
当(
x,
y
)
求f (0,0).
xy
(0,0)和f
xy
(0,0).
当( x, y) (0,0)时, 按定义得
f x (0,0)
lim x0
f
(0
x,0) x
f
(0,0)
lim 0 x0 x
0
f
y
4
多元复合函数的求导法则
分量原则
问: 函数对某自变量的偏导数之结构

多元复合函数求导法则

dz z du z dv z dw dt u dt v dt w dt
u
z
v
t
w
以上公式中的导数 dz 称为全导数.
dt
2.上定理还可推广到中间变量不是一元函数而是多元函数的情况：
如果 u (x, y) 及 v ( x, y) 都在点( x, y) 具有对 x和y 的偏导数，且函数 z f (u,v) 在对应点 (u,v) 具有连续偏导数，
zv x x
dz 试问 dx 与
f x
是否相同？为什么？
z f (u,v, x), u (x), v ( x)
u
dz f du f dv f
zv x
dx u dx v dx x
不相同.
x
等式左端的z是作为一个自变量x的函数，
而等式右端最后一项 f 是作为u, v, x的三元函数，
一、链式法则
一元复合函数
定理
求导法则
如果函数u (t) 及v (t)都在点 t 可导，
函数 z f (u,v)在对应点(u,v)具有连续偏导数，
则复合函数z f [(t), (t)] 在对应点 t 可导，
且其导数可用下列公式计算
dz z du z dv z
dt u dt v dt
u vt
证设 t 有增量 t，则 u (t t) (t), v (t t) (t); 由于函数z f (u,v) 在点
(u,v) 有连续偏导数，故可微，即
z z u z v o( ), ( (u)2 (v)2 )
复合结构如图示
u
x
z z u z v , z

8.6(2)多元复合函数的求导法则

解
由 u x 3 y 2 z ，可得
u 3 x 2 y 2 z x 3 y 2 z x x
再由所给方程，利用隐函数导数公式来求 z ． x
设 F ( x , y , z ) x 2 y 2 z 2 3 xyz ，则

Fx 2 x 3 yz ，
Fz 2 z 3 xy
v 1 (F ,G ) y J ( u, y )
u 1 (F ,G ) ， y J ( y, v )
例 16
u 3 xv y u v 设 3 ，求和． x y v yu x
解
此题采用推导公式（1）的方法求解
由所给方程可确定 u, v 是 x , y 的函数，
2
x2 y
2 x )dx
( x cos xy x e
x2 y
2 y )dy 0
x2 y
于是得
dy y cos xy 2 xye 2 x 2 x2 y dx x cos xy x e 2 y
例 14
设 u x 3 y 2 z ，其中 z f ( x , y ) 由方程 u 2 2 2 x y z 3 xyz 0 所确定，求 |(1,1,1) ． x
隐函数存在定理 3 设 F ( x , y , u , v ) 、 G ( x , y , u, v ) 在
点 P ( x0 , y0 , u0 , v0 )的某一邻域内有对各个变量的连
续偏导数，且 F ( x0 , y0 , u0 , v0 ) 0,G( x0 , y0 , u0 , v0 )
Fu Fx v 1 (F ,G ) Gu G x x J ( u, x )

高等数学多元复合函数的求导法则

x y
全微分形式不变性的实质：
无论 z是自变量u、v的函数或中间变量u、v
的函数，它的全微分形式是一样的.
dz z dx z dy x y
z u
u x
z v
v x
dx
z u z v dy u y v y
z u dx u dy z v dx v dy u x y v x y
e [ y sin( x y) cos(x y)]d x 且复合结构与原来的 f (u,v) 完全相xy同
利用全微分形式不变性，在逐步作微分运算的过程中，不论变量间的关系如何错综复杂，都可以不加辨认和区分，而一律作为自变量
来处理
exy[x sin(x y) cos(x y)]d y
z exy[x sin(x y) cos(x y)] y
z
uvw
f1 f2 f3
2) 中间变量是多元函数的情形.例如,
t tt
z f (u, v) , u (x, y), v (x, y)
z z u z v x u x v x
f11
f 2 1
z
uv
z z u z v y u y v y
f12 f2 2
x yx y
有增量△u ,△v ,
z z u z v o ( ) ( (u)2 (v)2 )
u v
z z u z v o( ) ( (u)2 (v)2 )
t u t v t t
令 t 0, 则有u 0, v 0,
z
u du , v dv t dt t dt
uv
o ( ) o( ) (u)2 ( v)2 0 t t
f21 1
f22 x y]
为简便起f11见

0804多元复合函数的求导法则

w x
f1 1
f2yz
f(x y z ,x y z ) y z f ( x y z ,x y z )
1
2
2w
xz
f1fxy
11
12
y
f 2
yz[f 1 21
f22xy]
为简便起f 见1 ,1 y 引( x 入记z ) 号f 1 f12 x y 2 z uff ,2 f12 y 2f 2 u2fv,
练习3 u f(x ,y ,z ) e x 2 y 2 z 2 ,z x 2 sy i,n 求 u , u x y
解: u f f z x x z x
2xex2y2z2 2zex2y2z22xsiny
u
2 x (1 2 x 2 s2 iy ) n e x 2 y 2 x 4 s2 iy n x y z
( 3 ) s f [ u ( x , y , z ) v ( x , y , z ) w ( x , , y , z )],
s f u f v f w , x u x v x w x
s y
f u f v u y v y
f w , w y
s f u f v f w . z u z v z w z
二、全微分形式不变性*: 若 zf(u,v)关于自 u,v具变有量连续 , 偏导则z的全微 dz分 f duf dv; u v 若又 u u (x 有 ,y)v , v(x ,y)关 x ,y 于偏导 , 数则 z 对 f[ u (x ,y )于 v ( ,x ,y )有 ]dzzdxzdy x y
t ut vt t
令t0, 则 u 有 0 , v 0 ,
udu, vdv t dt t dt
z

6.5 多元复合函数求导法则和隐函数求导公式

3uv , u e , v sin t , 求 . dt z du z dv dz 解 dt u dt v dt
2 4 t
(2uv 3v 4 ) e t ( u2 12uv 3 )cos t
(2e t sin t 3sin4 t )e t (e 2t 12e t sin3 t )cos t .
链导法则
特例1 若 z = f (u , v)，而 u ( x ), v ( x ) 都在点 x 处可导, 函数 z = f (u , v)在相应点(u , v)处可微，则复合函数 z f [ ( x ), ( x )] 在点 x 处可导， u 且 z x dz z du z dv 全导数 v
注意
情形(1) z f ( u, v , w ), u ( x , y ), v ( x , y ), w ( x , y ), 则 z u z v z w z x u
z
w
u
v
y
x y
z
z 是在 z f [ ( x , y ), x , y ] 中视 y 为常量，对 x 求偏导. x f 是在 z = f (u , x , y)中视 u , y 为常量，对 x 求偏导. x
类似一元函数具有微分形式不变性，二元函数具有全微分形式不变性. 设函数 z f ( u, v ), u ( x , y ), v ( x , y ) 均具有连续偏导数, 则复合函数 z f [ ( x , y ), ( x , y )] 的全微分为
z z dz dx dy x y z u z v z u z v dx dy u x v x u y v y z u u z v v dx dy dx dy u x y v x y

第九章-第4节多元复合函数求导法则

z z u z v o ( ) (
u v
z z u z v o ( )
t u t v t t
(u)2 (v)2 )
4
z z u z v t u t v t
o( )
t
(
(u)2 (v)2 )
z
令 t 0 ,则有 u 0, v 0,
u du , v dv
uv
t dt t dt
tt
o ( ) o( ) t
(
u)2 t
(
v t
)2
0
（ t 0时,根式前加“–”号)
dz z du z dv dt u dt v dt
( 全导数公式 )
5
说明: 若定理中
偏导数连续减弱为
偏导数存在, 则定理结论不一定成立.
例如: z f (u, v)
u2v u2 v
2
,
0,
u2 v2 0 u2 v2 0
ut, vt
易知:
但复合函数 z f ( t, t ) t 2
d z 1 z du z dv 0 1 0 1 0
d t 2 u dt v dt
6
推广:1）中间变量多于两个的情形。例如
z f (u,v, w) , u (t), v (t), w (t)
ex y[ y sin( x y) cos(x y)]
z y
z u u y
z v v y
eu sin v x eu cos v 1
ex y[x sin( x y) cos(x y)]
9
例2. u f ( x , y ,z ) e x2 y2 z2 , z x2 sin y ,
第九章多元函数微分法及其应用

9-4多元复合函数的求导法则

,
y z

f1dxyf2dzy
f1ydy2xxdyf2zdzy2ydz
fy1dxfz2xy21fdyyz22fd.z
□
返回
Ex 设z siu ncov、 suxy、 v y , 求 z 及 z x x y
46rV3 er
返回
dh 6 (2Ver)
dt r2 r
设t0时刻沙丘体积为60立方米、底面半径为6米，则
dh 6 (260e6)
dttt0
62
6
1 (15e6) [立方米/秒] □
3
返回
情形3
u
链锁规则公式
三元函数
全导数
zv x
w
情形4
ux
zv
wy
dzd(f xy,xy)f1dx yf2d(xy)
f121xyd(x)yf2(dxd)y
返回
f121xy(ydxd)yf2(d xd)y
2yx1fyf2dx2xx1全fy微f分2d形.y
式不变性
（2）
du
df
x y
解 dzcoucsovsd u siu s nivn dv
cu o cv o (s ydxsxd)ysiu s niv(n xy2
dx

1 x
dy
)
(ycoucsovsxy2sinusinv)dx
(xcoucsovs1sinusinv)dy x
z x
ycu o csv o xs y2 sinusinv
多元函数全微分也具有形式不变性。
返回
全微分形式不变性：设可微函数 zf(u,v)，则不
论u，v是否为自变量，微分形式
总是正确的。 d zfudufvdv 【证】当u,v为自变量时，d zfud ufvd;v