差异性检验(
均值比较及差异性检验2

❖ 两配对样本T检验的零假设H0为两总体均值 之间不存在显著差异。
❖ 首先求出每对观察值的差值,得到差值序 列;然后对差值求均值;最后检验差值序列 的均值,即平均差是否与零有显著差异。如 果平均差和零有显著差异,则认为两总体均 值间存在显著差异;否则,认为两总体均值 间不存在显著差异。
•均值比较及差异性检验
•均值比较及差异性检验
❖ 从两种情况下的T统计量计算公式可以看出, 如果待检验的两样本均值差异较小,t值较小, 则说明两个样本的均值不存在显著差异;相 反,t值越大,说明两样本的均值存在显著差 异。
•均值比较及差异性检验
❖ 在分析结果中,SPSS还自动给出了两样本均 值差值的估计标准误差(Std. Error Difference)。在方差相同的情况下,估计 标准误差的计算方法是
5.2 单样本T检验
❖ SPSS单样本T检验是检验某个变量的总体均 值和某指定值之间是否存在显著差异。统计 的前提是样本总体服从正态分布。也就是说 单样本本身无法比较,进行的是其均数与已 知总体均数间的比较。
•均值比较及差异性检验
❖ 单样本T检验的零假设为H0:总体均值和指 定检验值之间不存在显著差异。
•均值比较及差异性检验
5.1 Means过程
❖ Means过程是SPSS计算各种基本描述统计量 的过程。与计算某一样本总体均值相比, Means过程其实就是按照用户指定条件,对样 本进行分组计算均数和标准差,如按性别计 算各组的均数和标准差。
•均值比较及差异性检验
❖ 用户可以指定一个或多个变量作为分组变 量。如果分组变量为多个,还应指定这些分 组变量之间的层次关系。层次关系可以是同 层次的或多层次的。同层次意味着将按照各 分组变量的不同取值分别对个案进行分组; 多层次表示将首先按第一分组变量分组,然 后对各个分组下的个案按照第二组分组变量 进行分组。
均值差异性假设检验(二)方差分析.

●计算组间离差平方和(Between Group Sum 2 Squares): k
of
S A N xi μ
i 1
i=1,2...k 组间离差平方和SA,反映各水平均值差异。 ●计算组内离差平方和(Within Group Sum Squares) 2
of
Hale Waihona Puke SE xij xi
x
之间的差异,即进行不同系数的均值的二次方的差异 检验 按钮“Post Hoc”为不同水平多重对照分析选项,多 重对照分析是对不同水平下的均值进行如下比较: 当方差为齐性时,可以使用下面的14种多重检验方法
●LSD最小显著差异检验 ●Bonferroni修正的LSD检验(LSDMOD) ●Sidak多重配对比较检验 ●Scheffe同步进入的配对比较检验。 ●R-E-G-W F(Ryan-Einot-Gabriel-Welsch F)检验。 ●R-E-G-W Q(Ryan-Einot-Gabriel-Welsch range test) 检验。 ●S-N-K各组均值配对比较检验(Student NewmanKeuls)检验。 ●Tukey真实显著差异检验(Tukey's honestly significant difference)检验。 ●Tukey„ s-b 检验。
二、检验方法 假定某单因素影响下的试验数据如下:
水平数 样本数 1 2 … N 各水平均值 1 2 … k
X11 X12 X1n X1
X21 X22 X2n X2
Xk1 Xk2 Xkn Xk
表格中所有n×k个数据的总平均值为:μ N---同一水平下个案个数, K---因素水平数。 xi ---i水平均值。 μ ---总个案均值。
差异性、优效性、等效性和非劣效性检验的区别

差异性、优效性、等效性和非劣效性检验的区别在临床研究工作中,我想大部分临床研究者都听说过优效性、等效性和非劣效性检验等,有很多人也很明白,但也有人尚不太清楚它们之间的区别,本期我们将和大家一起来讨论这一问题。
1、什么是差异性检验?差异性检验,大家天天都在用,其实大家的论文里大部分用的都是差异性检验。
比如独立样本t检验,两个可选的假设分别是A=B和A≠B。
这就是差异性检验,或者叫不等的检验,意思就是A和B两组有差异、不相等。
什么意思呢?就是检验A-B=0这一公式成立与否。
比如同一批病人,我们随机分成A和B组,然后检验A组和B组患者血红蛋白水平的高低,这就是差异性检验。
即A组和B组之间有差异,什么叫有差异,就是两组间的差异不等于0。
跟上述内容相反的是,当我们将A组和B组之间的差异跟一个既定的值(Δ)比较时,就产生了一系列的检验,如优效性、等效性和非劣效性检验。
下面这个图可以先看一下:2、什么是优效性、等效性和非劣效性检验?上述三种检验在临床药物试验中应用最多,当我们研制一种新药物的时候我们总是盼着新药的疗效比较好,或者跟旧药差不多。
我想没有人会盼着研制的新药的疗效差于旧的药物,那么还研制它干嘛啊。
基于上述三种情况,就提出了三个用于新药临床试验的检验思路,分别是优效性、等效性和非劣效性检验。
下面分别说明,先假设一个例子,某研究者要研究A药与B药的关系,他能够接受的差值是Δ。
2.1 优效性检验研究目的:A药的效果好于B药。
研究假设:(1)无效假设:A-B≤Δ;(2)备择假设:A-B>Δ。
备注:用来证实新药A的效果好于旧药B,来判断新药A上市的情况。
它是一个单侧的检验。
2.2 等效性检验研究目的:A药的效果等于B药。
研究假设:(1)无效假设:A-B≤-Δ或A-B≥Δ;(2)备择假设:-Δ<A-B<Δ。
备注:常用于同一活性成分的药物之间的疗效比较,证实的是A药和B药的疗效相当。
它可以是单侧也可以是双侧的检验。
差异性检验

变差来源 组间变差 组内变差 总变差
变差 312 156 468
自由度 2 9 11
方差 156 17.3
F值 值 9
概率值 <0.01
北京印刷学院 出版传播与管理学院
第四节 常用非参数检验方法
卡方检验(拟合优度检验 拟合优度检验) 一、卡方检验 拟合优度检验)检验观察到的分布与期望分布之间的 拟合优度。 拟合优度。
北京印刷学院 出版传播与管理学院
第九章 显著性检验
第一次试用 更喜欢产品A 更喜欢产品 更喜欢产品B 更喜欢产品 合计 15 35 50 第二次试用 26 24 50
需要检验在两次试用中对产品的偏好模式是否存在显著差异 因为是配对样本,不能直接进行卡方检验。
北京印刷学院 出版传播与管理学院
第九章 显著性检验
产品A的评价分 与产品 的评价分Y之间的交叉表 产品 的评价分X与产品 的评价分 之间的交叉表 的评价分 与产品B的评价分
X=5 Y=5 Y=4 Y=3 Y=2 Y=1 合计 10 10 2 2 1 25
X=4 15 10 5 3 2 35
X=3 9 5 4 2 0 20
X=2 5 4 2 2 2 15
X=1 2 0 1 1 1 5
合计 41 29 14 10 6 100
北京印刷学院 出版传播与管理学院
第九章 显著性检验
检验原假设对产品的偏好没有显著差异 检验方法 b=“+”的个数 大于零的个数,评价 高于 的个数 的个数=D大于零的个数 高于B的个数 的个数 大于零的个数,评价A高于 c=“-”的个数 小于零的个数,评价 低于 的个数。 的个数=D小于零的个数 低于B的个数 的个数 小于零的个数,评价A低于 的个数。 卡方=( 服从自由度为1的卡方分布 卡方 (b-c)*(b-c)/(b+c)服从自由度为 的卡方分布。 服从自由度为 的卡方分布。
差异显著性检验t检验知识讲解

说,从而形成结论,或开始新一轮的试验以验证修改完善后的 假说,如此循环发展,使所获得的认识或理论逐步发展、深化
13
一、几个相关概念
9. 科学研究的基本过程
① 选题 ② 文献 ③ 假说 ④ 假说的检验 ⑤ 试验的规划与设计
质、仪器的不准等因素引起的真值与观测指间的差异; 通过努力可以克服 系统误差;
随机误差:随机误差又叫抽样误差(sampling error) ,这是由于许多无法控制的
内在和外在的偶然因素所造成的真值与观测指间的差异;在试验中,即使十 分小心也难以消除;随机误差影响试验的精确性;统计上的试验误差指随机 误差,这种误差愈小,试验的精确性愈高。
x 5 0 0 5 2 0 L 4 9 05 2 8 5= 5 2 8 .5
1 0
1 0
36
17.平均数
• 加权法 计算若干个来自同一总体的样本平均数的平均数 时,如果样本含量不等(或者其总要性程度不同), 也采用加权法计算
x fixi fx fi n
37
17.平均数
• 算术平均数的重要特性
17
一、几个相关概念
13. 单因素试验 指整个试验中只变更、比较一个试验因素的不同 水平,其他作为试验条件的因素均严格控制一致的试验。
18
一、几个相关概念
14 多因素试验 指在同一试验方案中包含2个或2个以上的试验因 素,各个因素都分为不同水平,其他试验条件均应严格控制一 致的试验。
19
一、几个相关概念
• 总体平均数
N
xi N i 1
39
17.平均数
第五部分--T检验和F检验

dfSig. (2-taD ileifdfe)rencLeower Upper
19
.000 3.05 1.58 4.52
8
标准差
标准差是用来反映变异程度,当两组观察值在
单位相同、均数相近的情况下,标准差越大,说
明观察值间的变异程度越大。在标准正态分布
曲线下,人们经常用均数加减标准差来计算样
本观察值数量的理论分布, 即: x ±1.96 s表
11
在实际工作中,由于抽取的样本较小,不呈标准正态分布,而 遵从t分布,所以常用t值代替1.96或2.58。可在t值表上查出 不同自由度下不同界值时的t值。可见到自由度越小, t值越 大,当自由度逐渐增大时, t值也逐渐接近1.96或2.58,当自 由度= ∞时, t值就完全被其代替了。所以,我们常用X±t 0.05Sx表示总体均数的95%可信区间,用x±t0.01Sx表示总体 均数的99%可信区间。综上所述,标准差与标准误尽管都是反 映变异程度的指标,但这是两个不同的统计学概念。标准差 描述的是样本中各观察值间的变异程度,而标准误表示每个 样本均数间的变异程度,描述样本均数的抽样误差,即样本均 数与总体均数的接近程度,也可以称为样本均数的标准差。 二者不可混淆。
12
练习题
7岁儿童的平均身高为102,现测得某班12名7岁儿童 身高分别为: 97、99、103、100、104、97、105、110、99、98、 103、99 请问该班儿童身高与平均水平是否存在差异?
13
Analyze / Compare Means/
one-samples T Test
14
One-Sample Statistics
Std. Error N Me Sa td n. DeviatM ioenan 儿 童 身 10 1高 1 2.1667 3.9041 1.512703
差异显著性检验课件

该方法通过比较两组数据的秩次(相 对大小)来检验差异显著性,特别适 用于处理小样本数据或数据不符合正 态分布的情况。它能够提供更准确的 差异显著性判断。
秩次检验
总结词
秩次检验是一种非参数统计方法,通过 比较数据的秩次来分析差异显著性。
VS
详细描述
秩次检验适用于处理不服从正态分布的数 据,尤其在处理小样本数据或数据分布不 明确时具有优势。它能够提供更全面的差 异显著性分析结果,包括差异的方向和显 著性水平。
,或者比较多个分类变量之间的
关联程度。
适用场景
实验研究
当需要比较实验组和对照组之 间的差异时,可以使用差异显
著性检验。
调查数据
在社会科学调查中,当需要比 较不同群体或地区的差异时, 可以使用差异显著性检验。
医学研究
在医学研究中,差异显著性检 验常用于比较不同治疗方案或 药物的效果。
质量控制
在生产过程中,差异显著性检 验可用于检测产品质量或过程 参数的波动是否在可接受范围
流行病学调查
分析不同人群的生理指标 差异,研究疾病的流行病 学特征。
心理学研究中的应用
人格特质研究
通过比较不同人格特质人群的心理指标, 探究人格特质与心理指标的关系。
认知能力评估
评估不同认知能力人群的心理指标差异, 了解认知能力的发展规律。
情绪状态分析
分析不同情绪状态下心理指标的变化,探 究情绪状态对心理指标的影响。
常用方法
t检验
用于比较两组均值的差异,包括 独立样本t检验和配对样本t检验。
01
方差分析
02 用于比较两组或多组数据的方差 是否存在显著差异,包括单因素 方差分析和多因素方差分析。
两斜率差异性检验
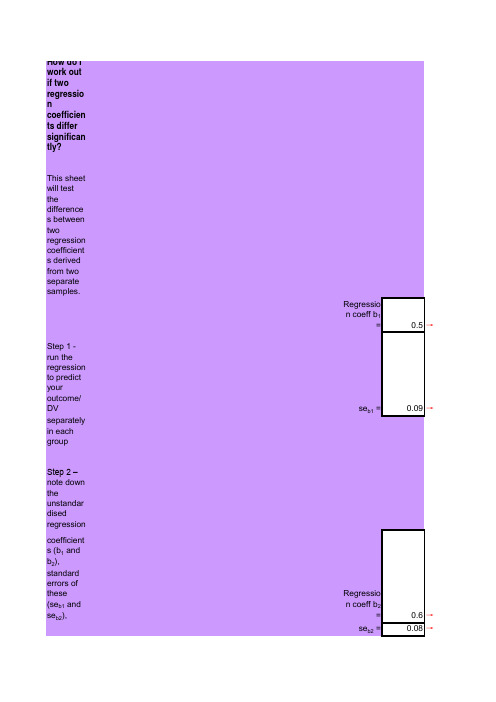
How do I work out if two regression coefficients differ significantly?This sheet will test the differences between two regressioncoefficients derived from two separate samples.Regression coeff b1 =0.5→Step 1 - run the regression to predict your outcome/DV se b1 =0.09→separately in each groupStep 2 – note down the unstandardised regressioncoefficients (b1 and b2), standard errors of these (se b1 and se b2),Regression coeff b2 =0.6→se b2 =0.08→Step 3 - look at the value of z and if it is greater than +/- 1.96 it issignificant ot the 0.05 level (check out tables of the standard normaldistribution for exact p values)Z =-0.83045→这是老做法,我们现在做调节效果分析可以直接参考笔者报告里面的内容类别1的非标准化系数(1)做Y对X和M的回归得R123.除了考虑交互项XM外高阶交互作用(如XM 2,表示非线扰效果)(2)做Y对X、M和XM回归得R 22,若R 22显著高于R 12,则M为干扰变量类别两个变量有交互作用的方差分析(2-way ANOVA),交互作用即干扰效果分割档案后做回归,得用费雪Z转换比较差异显著性,显有干扰连续X改成Dummy,做MC或标准化处理,做Y=aX+bM+cXM+e分层回归1.将M变成类别变量,2.分层回归分析同左如果要计算标准化系数,回Correlation(1)中的Fisher Z 转换根据建议,我们检验非标准化系数。
地区差异性检验步骤

地区差异性检验步骤
第一步:收集地区的相关资料:地理位置地形、气候、水文、植被等;人口、经济、文化、历史沿革等
第二步:资料的分析与整理:文字整理归类,数据分析,图表绘制等
第三步:地区差异分析、比较区域发展条件、区域经济分析、区域发展阶段评价
第四步:探索地区差异形成的原因
资料收集的方法
直接收集法: 通过对区域的实地考察和调查,得到第一手资料。
间接收集法: 通过会议、座谈上网或查阅报纸、杂质、书籍等收集资料。
地区差异分析的方法
定性的方法: 指对区域内的地理事象进行定性的描述和说明,包括文字叙述、图像展示和列表归纳等。
定量的方法: 指在已有资料的基础上,借助于数学手段对地理事象进行量化研究。
综合的方法: 指对研究对象所涉及的各种因素进行综合分析。
均值差异性假设检验(一)T检验假设检验是统计推断的一种重要手段,

均值差异性假设检验(一)T检验
三、检验结论
在输出报告中显示内容:
Paired Samples Test
Paired Differences
Mean Std. Deviation Std. Error Mean t df Sig. (2-tailed)
-2.1818 2.2279
.6717
-3.248 10 .009
95% Confidence
两独立样本均值差异性检验 一、检验条件 1.两组不相关样本,均呈正态分布。 2.一个或多个因变量,一个自变量(两水平) 个案数超过50,自动转换为Z检验 例如:在研究体重与性别的关系时,体重作为因变量, 则性别就是自变量。自变量的取值为两种水平:M和F 。T-检验是检验不同水平下的均值差异是否显著。 H0假设:两组样本均值的差异不显著。
样本统计量的值,在以期望值μ为中心的分布中出现的 概率。
判据 P〈= α拒绝H0 P 〉 α接受H0 上例题结果表明,用该学校的学生成绩情况不能正确反 映全区学生的总体情况。解决方法是重新抽样,或者是 增大原设样本的数量。
单样本的T检验 单样本的T检验(One-sample T Test)用于将某一个变量的均 值与特定的值进行比较,检验其差异的显著程度。 H0假设样本均值与设定的检验值差异不显著。 一、检验条件 变量的取值应当满足正态分布。 二、操作步骤 执行
假设检验是统计推断的一种重要手段,主要用于比较群体 间的某种属性的差异性。使用一定的统计检验,以确定差 异程度:是显著的差异还是不显著的差异。 均值差异性假设检验的概念 一、基本概念 ⒈对样本的总体分布或分布参数进行假设H0 例:样本为正态分布 总体样本与原设样本的方差差异不显著。 零假设:总体样本与原设样本的均值差异不显著。
《差异性检验》课件

多因素方差分析
要点一
总结词
用于比较两个或多个相关样本的平均值是否有显著差异, 同时考虑多个影响因素。
要点二
详细描述
多因素方差分析是差异性检验的一种,用于比较两个或多 个相关样本的平均值是否有显著差异,同时考虑多个影响 因素。它适用于样本来自正态分布且总体方差相等,同时 存在多个影响因素的情况。通过分析各因素之间的交互作 用,以及各因素对因变量的影响程度,判断各组之间的差 异是否具有统计学上的显著性。
考虑数据的分布情况
在选择检验方法时,需要考虑数据的分布情况, 如正态分布、非正态分布等。
3
考虑样本量和数据质量
在选择检验方法时,需要考虑样本量和数据质量 ,以确保检验结果的准确性和可靠性。
差异性检验的实施
数据输入与整理
将数据输入统计分析软件 中,并进行必要的整理和 转换。
执行差异性检验
根据选定的检验方法,执 行差异性检验,并记录检 验结果。
总结词
用于比较两个独立样本的平均值是否有验的一种,用于比较两个独立样本的平均值是否有显著差异。它适用于样本来自正态 分布且总体方差相等的两个独立样本。通过T统计量来评估两组数据的差异程度,并使用自由度来计算P值,判断 差异是否具有统计学上的显著性。
配对样本T检验
总结词
适用于非数值型数据或数据不符合正态分布 的情况。
详细描述
非参数检验方法包括卡方检验、秩和检验等 ,适用于非数值型数据或数据不符合正态分 布的情况。例如,卡方检验可以用于比较分 类数据的频数分布,秩和检验可以用于比较 等级数据的分布情况。这些方法在数据分析 中具有广泛的应用,尤其在处理不符合正态
当需要对两组或多组数据进行比较,以判断它们是否存在显著差异时,可以考虑使 用差异性检验。
差异性检验.

第九章 显著性检验
第一节 常用的抽样分布 一、样本均值的分布 有关概念:总体均值(期望)总体方差,总体标准差(皆为 总体的参数) 样本均值,样本方差,样本标准差皆为统计量。 样本均值的期望,样本均值的标准差---标准误差(SE) 非常简单随机样本(独立同分布样本)、样本均值的分布, 如果总体为正态分布,则为正态分布,如果为非正态分布, 则当n 较大时近似正态分布。 二、样本比例的分布(正态分布) 三、总体均值的置信区间(方差已知与未知) 四、总体比例置信区间
北京印刷学院 出版传播与管理学院
第九章 显著性检验
第二节、显著性检验基本概念 一、零假设和备选假设 二、显著性检验的分类 参数检验与非参数检验 三、显著性水平和两类错误
接受原假设
原假设为真 原假设不真 正确决策 第二类错误
拒绝原假设
第一类错误 正确决策
北京印刷学院 出版传播与管理学院
第九章 显著性检验
SE T
(P 1P 2) SE
t (n1 n2 2)
北京印刷学院 出版传播与管理学院
五、两个以上独立样本均值的假设检验 也叫单因子方差分析,方差分析在传统上主要用于分析 实验数据。但也可以用于分析调查的和观察的数据。 其零假设可以表示为: 有K个独立的样本,K个样本均值 样本容量分别为
A组(瓶装) 75 70
B组(罐装) 74 78
C组(袋装) 60 64
66
69
72
68
65
55
北京印刷学院 出版传播与管理学院
第九章 显著性检验
试检验三组是否有显著性差异。(显著性水平5%)
变差来源 变差 自由度 方差 F值 概率值
组间变差
第二节_两方差间的差异性检验

结论。由于第一个样本的方差既可能大于第二 个样本的方差,也可能小于第二个样本的方
差,故两样本方差比较的 F 检验是双侧检验。
2020年4月7日 9
例5-4 为研究国产四类新药阿卡波糖胶 囊的降血糖效果,某医院用40名II型糖尿病 病人进行同期随机对照试验。试验者将这些 病人随机等分到试验组(用阿卡波糖胶囊)和 对照组(用拜唐苹胶囊),分别测得试验开始 前和8周后的空腹血糖,算得空腹血糖下降 值见表5-4,用F 检验判断两总体空腹血糖 下降值的方差是否不等 ?
(3) 确定P值,作出推断结论
以 df1=19、df2=19 查附表 4 的 F 界值表。因
1.598<2.51= F0.05,20,19 ,故 P>0.05。按=0.05 水准,
不拒绝 H0,无统计学意义。还不能认为阿卡波糖 胶囊组与拜唐苹胶囊组空腹血糖下降值的总体方 差不等。
2020年4月7日 13
2020年4月7日 11
(1) 建立检验假设,确定检验水准
H0:
12=
2 2
,
HA:
2 1
2 2
,
=0.05
(2) 计算检验统计量
较大标准差:s1 3.0601mmol / L 较小标准差:s2 2.4205mmol / L
F 3.06012 1.598, 2.42052
df1 1 202011 1199, ,d2f2 20201 119 19 2020年4月7日 12
第二节 两方差间的差异性检验
2020年4月7日
➢ t 检验的应用条件是正态总体且方差齐性。 ➢ 进行两小样本t检验时,一般应对资料进行
方差齐性检验,尤其两样本方差悬殊时。 ➢ 若方差齐,采用一般的t 检验;若方差不齐,
差异显著性检验t检验课件

目录
• 差异显著性检验t检验概述 • t检验的数学模型 • t检验的实施步骤 • t检验的案例分析 • t检验的局限性及解决方法 • t检验的软件实现与结论
01
差异显著性检验t检验概述
定义与概念
差异显著性检验t检验是一种常用的统计分析方法,用 于比较两组数据的均值是否存在显著差异。它利用t分 布理论来评估数据的可靠性。
配对样本t检验案例
总结词
配对样本t检验用于比较两个相关样本的平均值之间是否存在显著差异。
详细描述
配对样本t检验(也称为两相关样本t检验)是一种常用的差异显著性检验方法,用于比较两个相关样 本的平均值之间是否存在显著差异。例如,假设我们有两个由同一组研究对象在不同时间点上收集的 样本,我们要检验这两个样本的平均血压值是否存在显著差异。
01 如果p值小于0.05,那么我们可以认为这两个样本
的均值存在显著差异。
02
如果p值大于0.05,那么我们不能认为这两个样本 的均值存在显著差异。
t检验的实际应用建议
t检验主要用于比较两个独立样 本的均值是否存在显著差异,或 者一个样本与一个已知值之间是
否存在显著差异。
在进行t检验之前,需要先对数 据进行正态性检验,因为t检验 的前提假设是数据符合正态分布
在科学、工程、医学等领域,差异显著性检验t检验被 广泛应用于验证实验结果、比较实验组与对照组之间的 差异等。
t检验的应用范围
确定两组数据的均值是否存在显著差异,如研究 01 对象的身高、体重、年龄等。
检验一个样本的均值与已知的参照值是否存在显 02 著差异,如检测产品的质量、评估治疗效果等。
比较两个或多个独立样本的均值是否存在显著差 03 异,如不同地区、不同时间的数据比较。
差异显著性检验

variable)。
如不同性别的游客对某景区提供的住宿条件的满意度存 在
显著差异,这里视性别为自变量,满意度为因变量,即 认
为这种因满变意量度的差别是因为性别自的变不量同(引类起别的变。量)
类别变量 连续变量
卡方检验
t检验、方差分析
5)确定设置和输出结果
所有设置确定无误后,点击“确定”按钮,输出分析 结果。
3. SPSS分析结果解读
独立双样本T检验的SPSS输出结果比较简单,仅包含描述 统计和T检验两个输出结果表。
描述性统计量性别 N 均值 标准差
住宿的环境卫 男性 204 3.4118 .74745
生
ห้องสมุดไป่ตู้
女性 198 3.2626 .77507
量的值。
(3) 对于给定的显著性水平α,决定临界值。
α的取值范围为α≤0.01,α≤0.05和α≤0.10,一般情况 下,常用α≤0.05。
当α≤0.05时,差异显著,当α≤0.01时,差异极显著。
(4) 对假设做出判断。
通过对计算获得的统计量与临界值的比较,作出接受
或
8
显著性水平值α定得越大,拒绝域就越大,就越不容易 接受原假设,反之,显著性水平值定得越小,拒绝域就越 小,就越容易接受原假设。因此,在统计检验的问题中, 要注意α值的确定问题。
10
二、独立样本T检验
(一)基本原理
当自变量为间断(类别)变量,因变量为连续变量时, 常使用T检验与方差检验进行有关分析。
SPSS软件提供的T检验有3种形式,分别是单样本T检验 (One-Sample T Test),独立样本T检验(Independent -Sample T Test)和成对样本T检验(Paired-Sample T
Z检验

什么是Z检验Z检验是一般用于大样本(即大于30)平均值差异性检验的方法。
它是用标准的理论来推断差异发生的概率,从而比较两个的差异是否显着。
当已知标准差时,验证一组数的均值是否与某一相等时,用Z检验。
另外,对于Z检验我国的统计学教材大多采用U检验的说法。
而国外英文统计学书籍,大多采用Z检验。
[]Z检验的步骤统计检验的基本原理统计检验是先对总体的分布规律作出某种假说,然后根据样本提供的数据,通过统计运算,根据运算结果,对假说作出肯定或否定的决策。
如果现要检验实验组和对照组的平均数(μ1和μ2)有没有差异,其步骤为:1.建立虚无假设,即先认为两者没有差异,用H0:μ1= μ2表示;2.通过统计运算,确定假设H0成立的概率P。
3. 根据P 的大小,判断假设H0是否成立。
如下表所示。
表P 与H0的关系P值H0成立概率大小差异显着程度H0成立概率极小差异非常显着H0成立概率较小差异显着H0成立概率较大差异不显着Z检验法适用于大样本(样本容量大于30)的两平均数之间差异显着性检验的方法。
它是通过计算两个平均数之间差的Z分数来与规定的理论Z值相比较,看是否大于规定的理论Z值,从而判定两平均数的差异是否显着的一种差异显着性检验方法。
其一般步骤:第一步:建立虚无假设H0:μ1= μ2,即先假定两个平均数之间没有显着差异,第二步:计算Z值,对于不同类型的问题选用不同的计算方法,1、如果检验一个样本平均数()与一个已知的总体平均数(μ0)的差异是否显着。
其Z值计算公式为:其中:•是检验样本的平均数;•μ0是已知的平均数;•S是样本的;•n是样本容量。
2、如果检验来自两个的两组样本平均数的差异性,从而判断它们各自代表的总体的差异是否显着。
其Z值计算公式为:其中:•是样本1,样本2的平均数;•S1,S2是样本1,样本2的标准差;•n1,n2是样本1,样本2的容量。
第三步:比较计算所得Z值与理论Z值,推断发生的概率,依据Z值与差异显着性关系表作出判断。
直线斜率差异显著性检验

直线斜率差异显著性检验(SPSS)熊荣川六盘水师范学院xiongrongchuan@变量与变量之间的关系可分为确定性关系和非确定性关系两类。
函数表达式确定关系。
研究变量间的非确定关系,构造变量间经验公式的数理统计方法称为回归分析。
线性回归是利用数理统计中的回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法之一,运用十分广泛。
分析按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。
如果在回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。
然后自变量的和因变量中的这种线性关系可能还会受到其他因子的影响,比如生物不同阶段的生长曲线等等。
当条件改变时,我们想检验不同条件下的回归关系是否有显著差异,这时候就需要对回归直线的回归系数进行检验,比如斜率和截距。
以下我们简单总结一下使用SPSS进行斜率差异性检验的详细步骤。
首先我们使用Excel模拟两组数据。
第一组为两条斜率相同的直线(如下图)可见,我们拟得到的结果是没有显著差异的。
先重新整理数据,将y2数据列加到y1下面,变成一个变量y;将x2数据列加到x1下面,变成一个变量x;然后再设定一个新的分组变量group,原来第1组值为1,第2组值为2.将数据拷贝到SPSS中,Analyze->General Linear Model->Univariate出现单变量方差分析对话框将y值设为应变量“Dependent Variable”, group设为固定因子“Fixed Factor”, x设为协变量“Covariate”点击“Model”按钮设置模型。
左边为备选变量,依次导入x,group,group*x到model框中注意,group*x为group和x的交叉项,使我们关注的焦点,它代表两组斜率的检验。
实战操作上,先点选group,按住Ctrl键点选x,然后导入model框中。
差异显著性检验

6
2
(2) 单侧检验
有一个临界值,一个拒绝域, 拒绝域的面积为α。
当所考察的数值越大越好时, 用单侧检验。
如考察灯泡的寿命
当所考察的数值越小越好时, 用单侧检验。
如考察产品的废品率
单侧检验按α查表求临界值。
h
7
4.假设检验的步骤
(1) 提出假设。
H0 :1 2
H1:12
(2) 选取检验统计量,并在原假设H0成立的条件下计算统计 量的值。
生等
h
24
假设 住 方差 宿 相等 的 舒 假设 适 方差 性 不相
等
方差方程的 Levene检验
F Sig.
.830 .363
均值方程的t检验
t
df
Sig. (双 侧)
均值 差值
标准 误差值
3.174 400 .002 .22772 .07174
3.174 399.030 .002 .22772 .07176
SPSS软件提供的T检验有3种形式,分别是单样本T检验 (One-Sample T Test),独立样本T检验(Independent -Sample T Test)和成对样本T检验(Paired-Sample T
Test)。
在旅游研究中,比较常用的是独立样本T检验,因而本
章仅讨论独立样本T检验。独立样本T检验在一些教科书中
序号与题项 09 交通的舒适性 10 交通的安全性 11 自然风光 12 卫生环境 13 旅游形象 14 门票价格 15 商品种类 16 商品特色
h
17 商品质量 18 娱乐项目种类 19 娱乐项目创新性 20 娱乐项目安全性 21 服务态度 22 服务效率 23 导向标志与解说
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学教师校类别的评价理念差异性检验(平均值±标准差) 从上表可知,利用t检验(全称为独立样本t检验)去研究学校类别对于评价理念共1项的差异性,从上表可以看出:学校类别样本对于评价理念全部均呈现出显著性(P<0.05),意味着不同学校类别样本对于评价理念均有着差异性。
分析可知:
您所在的学校在:对于评价理念呈现出0.05水平显著性(t=2.35,P=0.02),以及具体对比差异可知,不同您所在的学校在:样本对于评价理念全部均呈现出显著性差异。
县城的平均值(3.84),会明显高于村镇的平均值(3.47)。
(N=43) t p
* p<0.05 ** p<0.01
分析建议如果T检验显示呈现出显著性差异(P<0.05),可通过平均值对比具体差异,同时还可使用效应量(Effect size)研究差异幅度情况;
第一:T检验时使用Cohen's d 值表示效应量大小(差异幅度大小),该值越大说明差异越大;
第二:T检验使用Cohen's d 值表示效应量大小时,效应量小,中,大的区分临界点分别是:0.10,0.30和0.50。
不同性别教师评价理念差异性检验 (平均值±标准差)
t p
* p<0.05 ** p<0.01
去研究您的性别:对于评价理念共1项的差异性,从上表可以看出:不同您
的性别:样本对于评价理念全部均不会表现出显著性(P>0.05),意味着不同您的性别:样本对于评价理念全部均表现出一致性,并没有差异性。
总结可知:不同您的性别:样本对于评价理念全部均不会表现出显著性差异。
