最新梯形常见辅助线作法(教师版)
初二课件 怎样做梯形中的辅助线

怎样做梯形中的辅助线:如何做梯形的辅助线是四边形的难点也是重点,下面类聚了所有辅助线的类型,希望同学们理解并能熟练的运用解决梯形的有关问题,常常是通过添加恰当的辅助线,把梯形转化为三角形和平行四边形.下面列举数例,以说明梯形中常见辅助线的作法.一、平移一腰法例1如图1,梯形ABCD中,AB∥CD,以AC、AD为边作ACED.DC的延长线交BE于F.求证:EF=FB.二、平移对角线法例2如图2,等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD于O点.若中位线长为m,求梯形ABCD的面积S.三、延长双腰法例3如图3,梯形ABCD中,AD∥BC,E为AB上一点,EF∥AD交DC于F,若AD=2,BC=3,梯形AEFD的面积为5,梯形BCFE的面积为11,求EF的长.四、作高法例4如图4,梯形ABCD中.AD∥BC,AC=BD,AC⊥BD于D点.且高为10cm,求中位线MN的长度.五、作中位线法例5如图5,梯形ABCD中,AD∥BC,M、N分别是两腰AB、CD的中点,ME∥AN,交下底BC于E.求证:NE=AM.六、作对角线法例6如图6,梯形ABCD中,两底AD、BC的中点为M、N,则MN与AB、CD的关系是[ ](D)不能确定.七、三角形割补法即连结梯形一底端点与腰(或对角线)的中点,并延长与另一底相交构造全等三角形.这就相当于将梯形的一角割下,补在恰当位置构成三角形或平行四边形.例7 如图7,梯形ABCD中,AD∥BC,∠C=90°,E是AB中点,求证:DE=CE.例8如图8,梯形ABCD中.AD∥BC,E、F是对角线BD、AC的中点,理解反思梯形辅助线练习题1(行之中学月考题).如图9,梯形ABFD中,AD∥CE∥BF,AC∶CB=m∶n,AD=a,BF=b,求CE的长.2.(复旦兰生)如图10,等腰梯形ABCD中,AC、BD交于E点,∠AEB=60°,AC=BD=24cm,AB=3DC,求梯形的面积.3.(市三女中期末考试题)如图11.梯形ABCD中,AB∥CD(DC<AB),M为BC中点,若AD=18cm,点M到AD的距离为10cm,求梯形ABCD的面积.。
全等梯形问题中常见的8种辅助线的作法(有答案解析)

全等梯形问题中常见的8种辅助线的作法(有答案解析)梯形是一种四边形,其中两条边是平行而另外两条边不平行。
在解决全等梯形问题时,我们可以使用一些辅助线的方法来简化问题并找到解答。
以下是常见的8种辅助线的作法,每种方法都附有答案解析。
1. 垂直辅助线法:垂直辅助线法是最基本的辅助线作法之一,它通过引入垂直辅助线来将梯形划分为上下两个小三角形或小梯形,并利用全等三角形的性质来解题。
2. 高度辅助线法:高度辅助线法通过引入高度辅助线来找到梯形的高,并利用相似三角形的性质来解题。
3. 中位线辅助线法:中位线辅助线法通过引入中位线辅助线来将梯形划分为两个全等的平行四边形,并利用平行四边形的性质来解题。
4. 对角线辅助线法:对角线辅助线法通过引入对角线辅助线来将梯形划分为两个全等的三角形,并利用全等三角形的性质来解题。
5. 平行边辅助线法:平行边辅助线法通过引入平行边辅助线来将梯形划分为两个全等的梯形,并利用梯形的性质来解题。
6. 外接圆辅助线法:外接圆辅助线法通过引入外接圆辅助线来找到梯形的外接圆,并利用外接圆的性质来解题。
7. 中心对称辅助线法:中心对称辅助线法通过引入中心对称辅助线来将梯形划分为两个全等的三角形,并利用全等三角形的性质来解题。
8. 连接线辅助线法:连接线辅助线法通过引入连接线辅助线来划分梯形并利用形成的图形的性质来解题。
这些辅助线的作法可以帮助我们在解决全等梯形问题时更简单而有条理地进行推导和解答。
通过灵活运用这些方法,我们可以提高解决问题的效率和准确性。
请注意:本文档中的答案解析仅供参考,具体解答的正确性应根据实际情况进行确认。
例谈梯形中常见的辅助线的作法

数学篇梯形作为一种比较特殊的四边形,其特点就是只有一组对边是平行的.因此,解答梯形问题的基本思路是通过添加辅助线来“搭桥”,对梯形进行割补、拼接,将其转化为熟悉的基本图形来解答.合理、巧妙地添加辅助线,不仅可以极大地降低解题难度,而且可以提高同学们思维的灵活性和创造性.一、平移一(两)腰平移腰即从梯形的一个顶点作一腰的平行线,把梯形转化为一个三角形和一个平行四边形;或利用梯形中的某个特殊点,过此点作两腰的平行线,把两腰转化到同一个三角形中,进而为解题创造条件.例1如图1,在梯形ABCD 中,AD //BC ,∠B +∠C =90°,AD =10,BC =30,E 、F 分别是AD 、BC 的中点,连接EF ,求EF 的长.图1图2解:过E 作EG //AB 交BC 于G ,过E 作EH //CD 交BC 于点H ,如图2所示.∵AD //BC ,∴四边形ABGE 是平行四边形,∴AE =BG ,同理可得DE =CH ,∴BG +CH =AE +DE =AD =10,又∵BC =30,∴GH =BC -BG -CH =20,又∵E 、F 分别是AD 、BC 的中点,∴BF =CF ,且AE =DE ,又∵AE =BG ,DE =CH ,∴GF =FH ,即F 为GH 的中点,在Rt△EGH 中GH =20,F 是GH 的中点,由直角三角形中线与斜边关系可知,EF =12CH =10,即EF =10.评注:平移梯形的一腰或两腰,可把梯形转化成三角形和平行四边形,从而把相对分散的条件集中到一个图形中以方便解题.二、平移对角线平移对角线即过梯形上底的一个端点作梯形一条对角线的平行线,将梯形转化为一个平行四边形和几个三角形.当题目中有梯形的对角线相等或互相垂直时,可以平移对角线把两条对角线、上下底之和放在一个三角形中,就会出现等腰三角形、直角三角形等特殊三角形,然后利用特殊三角形的性质来解答此类问题.例2如图3,在等腰梯形ABCD 中,AD //BC ,AD =3,BC =7,BD =52,求证:AC ⊥BD.图3图4证明:过点C 作CE //BD 交AD 延长线于学思导引27数学篇学思导引E,如图4所示.∵AD//BC,∴四边形BCED为平行四边形,∴DE=BC且BD=CE,又∵AD=3,BC=7,∴AE=AD+DE=AD+BC=3+7=10,∵ABCD为等腰梯形,∴AC=BD,又∵BD=CE且BD=52,∴AC=CE=BD=52,在△ACE中,AC2+CE2=(52)2+(52)2=100,AE2=102=100,即AC2+CE2=AE2,所以,△ACE是以∠C为直角的直角三角形,即AC⊥BD.评注:过梯形的一个顶点平移对角线,把两条对角线转移到同一个三角形中,若对角线相等,则这个三角形是等腰三角形;若对角线垂直,则这个三角形是直角三角形;若对角线相等又垂直,则这个三角形是等腰直角三角形.这些结论可以为解题创造有利条件.三、延长两腰延长两腰即延长梯形的两腰使其交于一点,化梯形为两个(相似的)三角形.如果是等腰梯形,则得到两个分别以梯形两底为底的等腰三角形.延长两腰可以将梯形转化为多个三角形,从而借助三角形的性质定理等知识要点,为解题铺平道路.例3如图5所示,四边形ABCD中,AD不平行于BC,AC=BD,AD=BC.判断四边形ABCD的形状,并证明你的结论.图5图6解:四边形ABCD为等腰梯形,证明如下.延长AD、BC交于E,如图6所示.在△ABD和△BAC中,有ìíîïïBD=AC,AD=BC,AB=AB,∴△ABD≌△BAC,∴∠BAD=∠ABC,在△EAB中,∵∠BAD=∠ABC,∴△EAB为等腰三角形,即AE=BE,又∵AD=BC,∴DE=CE,∴DE AE=CE BE,即AB//CD,又∵AD=BC,∴四边形ABCD为等腰梯形.评注:预测四边形形状后根据需要寻找条件即可.此题要灵活运用三角形全等、对应线段成比例、平行线的判定等知识点.四、作对角线作对角线即连接对角线将梯形转化为三角形,再利用三角形的一些性质与规律去解答四边形的问题.尤其在特殊梯形中,将没有画出的对角线作出来,再利用特殊梯形对角线的性质(如等腰梯形对角线相等),将题目中的条件进行转化,可以实现有效解题.例4如图7,在直角梯形ABCD中,AD//BC,AB⊥AD,BC=CD,BE⊥CD于点E,求证:AD=DE.图7图8解:连接BD,如图8所示.∵AB⊥AD,∴∠BAD=90°,∵BE⊥CD,∴∠BED=90°,∵AD//BC,∴∠1=∠3,∵BC=CD,∴∠2=∠3,∴∠1=∠2,在△DBE和△DBA中,28数学篇学思导引有ìíîïï∠1=∠2,∠BAD =∠BED BD =BD ,,∴△DBE ≌△DBA ,∴AD =DE .评注:在直角梯形中连接对角线往往可以构造直角三角形,然后利用直角三角形与全等三角形的知识来证明.五、连接顶点和一腰中点并延长连接梯形上底一端点和一腰的中点,并延长与下底延长线相交,从而将梯形割补成几个三角形.这样作辅助线可以充分利用梯形中的平行和等量关系,将上下底之和统一到一段线段上来,再结合三角形全等和其他特殊三角形的性质使问题得到解答.例5如图9,在直角梯形ABCD 中,AD //BC ,E 是DC 的中点,连接AE 和BE ,求证:∠AEB =2∠CBE.1234图9图10证明:延长AE 、BC 交于F ,如图10所示,∵四边形ABCD 为直角梯形,且AD //BC ,∴AB ⊥BC ,∴△ABF 为以∠ABF 为直角的直角三角形.∵AD //BC ,∴∠1=∠2,又∵E 是DC 的中点,∴DE =CE ,在△ADE 和△FCE 中,有ìíîïï∠1=∠2,∠3=∠4,DE =CE ,∴△ADE ≌△FCE ,∴AE =EF ,即E 是AF 的中点,又∵△ABF 是直角三角形,∴BE =12AF =EF ,∴△BEF 是等腰三角形,∴∠F =∠CBE ,∴∠AEB =∠F +∠CBE =2∠CBE ,即∠AEB =2∠CBE .评注:在梯形中,只要有腰上的中点,可过中点构造全等三角形,从而把上下底之和与另一条腰集中在一个三角形中,而这个三角形又是一个特殊三角形,问题就简单了.在解答有关梯形的证明题和计算题时,辅助线的作法并不是单一的,有时可同时作两种或两种以上的辅助线,但目的是一致的,就是在梯形中构造三角形、平行四边形,再运用三角形、平行四边形的相关知识来解题.同学们要结合已知条件添加合适的辅助线,以探求简捷的解题方法.《〈圆〉拓展精练》参考答案1.D ;2.A ;3.C ;4.A ;5.23-π;6.6cm ;7.相离;8.30°或150°;9.100或700;10.(1)证明略;(2)S 阴影部分=S △OAC -S 扇形AOE =12×3×33-60π×32360=32π.11.(1)证明略;(2)解:由题意知方程x 2+(m -2)x +m +1=0有两个相等的实数根,∴Δ=(m -2)2-4(m +1)=0,∴m =0或8,当m =0时,方程为x 2-2x +1=0,解得x 1=x 2=1,∴CE =1.当m =8时,方程为x 2+6x +9=0,解得x 1=x 2=-3(不符合题意舍去).∴CE =1.综上所述,CE =1.29。
梯形中添加辅助线的六种常用技巧

梯形中添加辅助线的六种常用技巧Prepared on 22 November 2020梯形中添加辅助线的六种常用技巧浙江唐伟锋梯形是不同于平行四边形的一类特殊四边形,解决梯形问题的基本思路是通过添加辅助线,将梯形进行割补、拼接转化为三角形、平行四边形问题进行解决。
一般而言,梯形中添加辅助线的常用技巧主要有以下几种——一、平移一腰从梯形的一个顶点作一腰的平行线,将梯形转化为平行四边形和三角形,从而利用平行四边形的性质,将分散的条件集中到三角形中去,使问题顺利得解。
例1、如图①,梯形ABCD中AD∥BC,AD=2cm,BC=7cm,AB=4cm,求CD的取值范围。
解:过点D作DE∥AB交BC于E,∵AD∥BC,DE∥AB∴四边形ABED是平行四边形(两组对边分别平行的四边形是平行四边形)∴DE=AB=4cm,BE=AD=2cm∴EC=BC-BE=7-2=5cm在△DEC中,EC-DE<CD<EC+DE(三角形两边之和大于第三边,两边之差小于第三边)∴1cm<CD<9cm。
二、延长两腰将梯形的两腰延长,使之交于一点,把梯形转化为大、小两个三角形,从而利用特殊三角形的有关性质解决梯形问题。
例2、如图②,已知梯形ABCD中,AD∥BC,∠B=∠C,求证:梯形ABCD是等腰梯形。
证明:延长BA、CD,使它们交于E点,∵AD∥BC∴∠EAD=∠B,∠EDA=∠C(两直线平行,同位角相等)又∵B=∠C∴∠EAD=∠EDA∴EA=ED,EB=EC(等角对等边)∴AB=DC∴梯形ABCD是等腰梯形(两腰相等的梯形是等腰梯形)。
三、平移对角线从梯形上底的一个顶点向梯形外作一对角线的平行线,与下底延长线相交构成平行四边形和一特殊三角形(直角三角形、等腰三角形等)。
例3、如图③,已知梯形ABCD中,AD=1.5cm,B C=3.5cm,对角线AC⊥BD,且BD=3cm,AC=4cm,求梯形ABCD的面积。
解:过点D作DE∥AC交BC延长线于E∵AD∥BC,DE∥AC∴四边形ACED是平行四边形(两组对边分别平行的四边形是平行四边形)∴CE=AD=1.5cm,DE=AC=4cm∵AC ⊥BD∴DE ⊥BD∴S 梯形ABCD =111()()222AD BC h CE BC h BE h +⨯=+⨯=⨯(h 为梯形的高) 211346cm 22BD DE =⨯=⨯⨯= 。
梯形的几种辅助线做法

龙文学校个性化辅导讲义梯形问题常见辅助线的作法梯形是在学习了三角形和平行四边形后学习的又一种特殊的四边形,因此,利用化归的思想方法,我们可利用平移、旋转等作出辅助线,通过割补、拼接,把梯形的问题转化为我们已经熟悉和解决了的三角形和平行四边形问题,从而用三角形和平行四边形的有关知识解决梯形问题。
下面通过例题具体说明梯形问题常见的辅助线的做法及其应用。
一、平移梯形一腰 ,将梯形转化成平行四边形。
即过梯形上底或下底的一个端点作一腰的平行线,将梯形分割成三角形和平行四边形,并出现上下底的差,利用这些条件解决所给的问题。
例1、如图1,在梯形ABCD 中, AD ∥BC ,AB=DC ,BD ⊥DC ,且BD 平分∠ABC ,若梯形的周长为20cm ,求此梯形的中位线长。
二、平移梯形的一条对角线,将梯形转化成平行四边形的直角三角形。
即过梯形上底或下底的一个端点作一条对角线的平行线,将梯形割补成与之等积的三角形,并出现上下底的和,利用这些条件解决所给的问题。
例2、如图2,在梯形ABCD 中, AD ∥BC ,对角线AC ⊥BD ,且AC=5cm ,BD=12cm ,则该梯形中位线的长等于 cm 。
思考:分别过A 、B 、C 三点作对角线的平行线,是否可以解出此题呢?(提示:可以,解法同上。
)三、过上底的两个端点作梯形的高线,将梯形分成两个直角梯形和一个矩形。
例3、如图3,在梯形ABCD 中,已知AD ∥BC ,BC=BD ,AD=AB=4cm ,∠A=1200,求梯形ABCD 的面积。
图3ADBCEF图1A DBCE 图2ADBC E四、延长梯形两腰交于一点,构成两个相似三角形。
例4、如图4,梯形ABCD 中,AB ∥CD ,∠A+∠B=900,AB=a ,CD=b ,E 、F 分别是AB 、CD 中点,求EF 的长。
(说明:此题也可以通过过点E 平移两腰来求得,请同学们自己练习。
)五、连结上底的一端点与一腰的中点,延长交下底的延长线于一点,将梯形割补成与之等积的三角形。
梯形常见辅助线作法(教案)

梯形常见辅助线作法(教案)第一章:梯形的基本概念1.1 梯形的定义介绍梯形的定义:一个四边形,其中两边平行,两边不平行。
强调梯形的两个底和两个腰的概念。
1.2 梯形的性质介绍梯形的性质:对角相等,同底边上的角互补。
解释梯形的高的概念,并说明高的作法。
第二章:梯形的画法2.1 画一个梯形介绍画梯形的步骤:先画两个平行的底,再画两个腰。
强调画梯形时要注意的要点,如保持直角和角度的准确性。
2.2 用尺规作图画梯形介绍用尺规作图画梯形的步骤:先画一个圆,再画两个与圆相切的直线,连接两个切点与圆的端点。
强调用尺规作图时要注意的要点,如保持半径和角度的准确性。
第三章:梯形的对称性3.1 梯形的轴对称性介绍梯形的轴对称性:梯形关于底边的中垂线对称。
解释对称轴的概念,并说明如何找到梯形的对称轴。
3.2 梯形的中心对称性介绍梯形的中心对称性:梯形绕其中心点对称。
解释中心点的概念,并说明如何找到梯形的中心点。
第四章:梯形的面积计算4.1 梯形的面积公式介绍梯形的面积公式:梯形的面积等于上底加下底的和乘以高除以2。
强调面积公式的应用,并解释如何将梯形的形状分解为更简单的形状。
4.2 梯形的面积计算实例通过实例讲解如何计算梯形的面积:先画出梯形的辅助线,应用面积公式。
强调在计算面积时要准确地测量和计算底边和高的长度。
第五章:梯形的应用5.1 梯形在实际问题中的应用介绍梯形在实际问题中的应用:例如,计算梯形形状的农田的面积。
解释如何将实际问题转化为梯形的面积计算问题。
5.2 梯形的实际测量和作图介绍如何进行梯形的实际测量和作图:使用尺子和直尺测量底边和高的长度,并用画图工具画出梯形的形状。
强调在实际测量和作图时要准确地测量和绘制图形。
第六章:梯形的平行线性质6.1 梯形平行线的性质介绍梯形平行线的性质:如果一个梯形有两对平行边,这两对平行边之间的对应角相等。
强调平行线性质在解决梯形问题中的应用。
6.2 利用平行线性质解题通过实例讲解如何利用梯形平行线性质解决问题:如已知梯形的一对平行线和一对对应角,如何求另一对对应角。
梯形中常见辅助线的作法
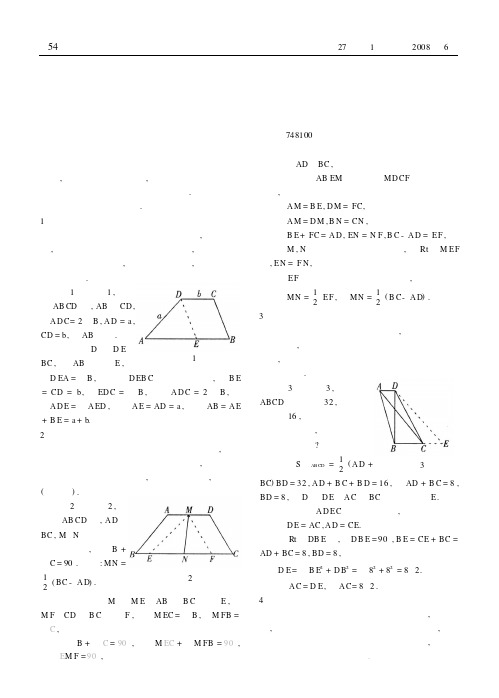
梯形中常见辅助线的作法岳雁翎甘肃省陇西县紫来学校 748100 在进行有关梯形的边、角、面积等计算和论证问题时,常常需要添加辅助线,将梯形问题转化为三角形、平行四边形、矩形等特殊图形问题.下面介绍六种常见辅助线的添加方法.1 平移一腰过梯形的一个顶点作一腰的平行线,通过平移腰,将梯形转化为三角形和平行四边形,利用三角形和平行四边形的性质,并结合题目条件,达到计算或证明的目的.图1例1 如图1,在梯形AB CD 中,AB ∥CD ,∠A D C=2∠B ,A D =a ,CD =b,求AB 的长.解 过D 作D E ∥BC ,交AB 与点E ,则∠D EA =∠B ,四边形D EB C 是平行四边形,故B E=CD =b,∠ED C =∠B ,由∠A D C =2∠B ,得∠A D E =∠A ED ,因而A E =AD =a ,所以AB =A E+B E =a +b .2 平移两腰过梯形的上底上的一点作两腰的平行线,将梯形转化为一个三角形和两个平行四边形,再利用三角形和平行四边形的性质,结合题目条件,来证明(或计算).图2例2 如图2,在梯形AB CD 中,A D ∥BC ,M 、N 分别为上、下底的中点,且∠B +∠C =90°.求证:MN =12(BC -A D).证明 过点M 作M E ∥AB 交B C 于点E ,作M F ∥CD 交B C 于点F ,则∠M EC =∠B ,∠M FB =∠,∵∠B +∠=°,∴∠M +∠M FB =°,即∠M F =°,又∵AD ∥BC ,∴四边形AB EM 和四边形MD CF 都是平行四边形,∴A M =B E ,D M =FC,∵A M =D M ,B N =CN ,∴B E +FC =A D ,EN =N F ,B C -A D =E F ,∵M ,N 分别是上、下底的中点,在Rt △M E F 中,E N =F N ,∴E F 是直角三角形斜边上的中线,∴MN =12E F ,即MN =12(B C-A D ).3 平移对角线过底的一端作对角线的平行线,通过作对角线的平行线,可以将梯形的上底加下底转化到一条线段上,也常通过作平行线将之转化为平行四边形的问题来解决.图3例3 如图3,已知梯形ABCD 的面积是32,两底与高的和为16,如果其中一条对角线与两底垂直,则另一条对角线的长为多少?解 S 梯形A B CD =12(A D +BC )BD =32,A D +BC +BD =16,得AD +B C =8,BD =8,过D 作DE ∥A C 交BC 的延长线于E.∴四边形A D E C 是平行四边形,∴D E =AC ,A D =CE.在Rt △DB E 中,∠D B E =90°,B E =CE +BC =AD +BC =8,BD =8,根据勾股定理得D E =B E 2+D B 2=82+82=8 2.因A C =D E ,故A C=8 2.4 作两条高过同一底的两个顶点作另一底的垂线,通过作高,将梯形分割成两个直角三角形和一个矩形,从而将梯形问题转化为直角三角形和矩形问题,用直角三角形和矩形的知识来解决45数学教学研究 第27卷第1期专辑 2008年6月C C 90EC 90E 90.图4例4 如图4,在等腰梯形AB CD 中,∠B =60°,AD =2,BC =4.计算梯形A BCD 的面积.解 过点A ,D 分别作A E ⊥B C,D F ⊥BC,垂足分别为E ,F ,则∠A EB =∠D F C =90°,A E ∥D F ,而A D ∥B C,∴四边形A E FD 是矩形,∴E F =A D =2,易证得△AB E ≌△DC F ,∴B E =F C =12(B C-A D )=12(4-2)=1.在Rt △AB E 中,A E =B Eta n ∠B =B Etan60°=1×3=3,∴S =12(2+4)×3=3 3.5 延长两腰构成三角形延长两腰交于一点,构造出两个相似三角形,利用相似三角形以及三角形的有关性质来解题.图5例5 如图5,等腰梯形的对角线分它的中位线为8c m ,20cm 的两部分,腰长为24c m.则梯形的下底角的度数为多少?解 延长A D ,BC 交于点G ,易证得E P ,F P 分别是△A D C,△CA B 的中位线,则D C =2E P =16c m ,AB=2P F =40cm ,由D C ∥AB ,得∠GD C =∠D AB ,∠GCD =∠GB A ,故△GD C ∽△GA B ,所以DC ∶AB =D G ∶AG ,即16∶40=D G ∶(D G +24),解得D G =16,则A G =40,同理可得B G =40,△GAB 为等边三角形,所以梯形的下底角的度数为60°.6 连结顶点与腰的中点,把梯形割补成三角形通过连结顶点与腰的中点并延长与另一底边相交,把梯形中的边、角转化到一个三角形中进行解决.图6例6 如图6,在梯形AB CD 中,A D ∥BC ,E ,F 分别为AB ,CD 边上的中点.求证E F 12(A D +B C ).证明 连结A F 并延长交BC 的延长线于点P.∵A D ∥BC(已知),∴∠AD F =∠P CF (两直线平行,内错角相等),在△AD F 和△P CF 中∠D FA =∠CF P (对顶角相等)D F =FC(已知)∠A D F =∠PCF (已证),△A D F ≌△P CF ,∴C P =AD ,A F =P F ,又∵A E =B E ,∴E F 是三角形AB C 的中位线,∴E F ∥B P ,E F 12B P ,即E F 12(A D +BC ).通过添加辅助线,将梯形分成一个或几个特殊图形是解决梯形问题的基本思路,它把分散的条件得以集中,隐含条件加以显现,把复杂的问题转化为容易解答的简单问题,体现了解数学问题的一个基本而重要的方法———化归法.只要细心观察、认真体会,就会找到解题的捷径.55第27卷第1期专辑 2008年6月 数学教学研究。
最新-八年级数学下册梯形辅助线的六种做法人教新课标版精品
B
C
AB=AD=2,∠ A=60°, BC=4,求 CD的长.
12、 已知:如图,在梯形 ABCD 中, ∠A+∠D=90°, M、 N 是 BC, AD 的中点。求证: MN=1 ( AD BC ) 。 2
B
N
三、从小底的两端向大底引垂线。
A
M
13、 如图,在梯形 ABCD 中,AD ∥ BC ,AB AC , B 45 ,AD 求 DC 的长.
如图,在梯形 ABCD中, AD∥BC, AB CD .若 AC⊥BD,
AD+B=C10 3 , 且 ABC 60 , 求 CD的长.
B
A
D
7、 已知在梯形 ABCD中, AD∥ BC,若两底 AD、BC的长分别为 2、8,两 B 条对角线 BD=6, AC=8, 求梯形的面积。
8、 已知:如图,在梯形 ABCD中, AD∥ BC,AC=D。B 求证: AB=D。C
梯形辅助线的做法
一、平移一条对角线。
1、 如图,在梯形 ABCD中, AD∥ BC, AB=CD, AC⊥ BD, AD= 6,
BC= 8, 则梯形的高为
。
A
D
2、 如图,在梯形 ABCD中, AD∥ BC, AC⊥BD, AC=8,
DB=6,则此梯形的高为
。
B
C
3、 如图,在梯形 ABCD中,AD∥ BC,AB= CD,对角线 AC⊥ BD,BD=6,则梯形的高为
2 ,BC 4 2 ,
A
C D
D
B
14、 如图,梯形 ABCD 中, AD ∥ BC ,∠ B 45 ,∠ D 120 ,CD 4 3cm ,求 AB A
的长.
B
梯形辅助线的常见作法

梯形辅助线的常见作法梯形辅助线的常见作法梯形是一种特殊的四边形。
它是平行四边形、三角形知识的综合,通过添加适当的辅助线将梯形问题化归为平行四边形问题或三角形问题来解决。
辅助线的添加成为问题解决的桥梁,梯形中常用到的辅助线有:(1)在梯形内部平移一腰。
例1(如图1)已知在梯形ABCD中,AD//BC,BA=DC。
求证:B=C证明:过点D作DM//AB交BC于点M。
因为 AD//BC DM//AB 所以AB=DM因为 BA=DC 所以 DM=DCDMC=CDMC=BB=C(2)梯形外平移一腰例2 (如图2)在梯形ABCD中,AB∥DC,作□ACED延长DC交BE于F求证:EF=FB证明:过点B作BG∥AD,交DC的延长线于G∴四边形ABGD是平行四边形∴AD=BG∵□ACED中,AD∥CE AD=CE∴CE∥BG且CE=BG ∴∠1=∠2又∵∠3=∠4 ∴⊿ECF≌⊿BGF ∴:EF=FB(3)梯形内平移两腰例3 (如图3)在梯形ABCD中,AD∥BC,AD﹤BC,E、F分别为AD、BC的中点,且EF⊥BC,试说明∠B=∠C解:过E作EM∥AB,EN∥CD,分别交BC于M,N得□ABME ,□NCDE ∴AE=BM DE=CN, ∵AE=DE ∴BM=CN又∵BF=CF ∴FM=FN ∵EF⊥BC ∴EM=EN ∴∠1=∠2∵EM∥AB,EN∥CD, ∴∠1=∠B , ∠2=∠C∴∠B=∠C(4)延长两腰例4(如图4)在梯形ABCD中, ∠B=∠C ,AD∥BC。
求证:梯形ABCD是等腰梯形。
证明:延长BA,CD交于点E∵∠B=∠C ∴BE=CE∵AD∥BC ∴∠EAD=∠B ∠EDA=∠C∵∠B=∠C ∴∠EAD=∠EDA∴AB=CD结论得证(5)过梯形上底的两端点向下底作高例5(如图5)在梯形ABCD中,DC∥AB,AD=BC,若AD=5,CD=2 ,AB=8,求梯形ABCD的面积。
解:过点D、C分别作DE⊥AB于E,CF⊥AB于F.根据等腰梯形的轴对称性可知,AE=BF.∵DC∥AB, DE⊥AB,CF⊥AB∴四边形CDEF是矩形∴DC=EF∴AE=(AB-EF)=(AB-CD)=3 ∴ DE===4 ∴=(2+8)x4=20(6)平移对角线例6求证:对角线相等的梯形是等腰梯形。
有关作梯形的辅助线常用方法

教学目标
1、进一步掌握掌握等腰梯形的性质,并会用梯形的有关性质进行计算和证明。
2、培养学生化归的思想和添加辅助线的能力。
教学重点
辅助线的添加方法
教学难点
辅助线的添加方法
教学过程
设计思路
在解决梯形问题时,往往因不能直接找到条件与结论之间的联系,这种情况下需要添加适当的辅助线,然后再运用三角形和四边形的知识来求解,下面举例介绍几种梯形中的常用辅助线。
所以∠E=50°,从而BC=EC=5
同理可得AD=ED=2
所以CD=EC-ED=5-2=3
三、作梯形的高
[例4]如图,在梯形ABCD中,∠C=600,AD//BC,AD=3,DC=6,求梯形的面积S.
解:过点A、D分别作AE⊥BC,DF⊥BC,垂足分别为E、F
在Rt△DFC中,因为∠C=600,所以∠1=300
A.30cm B.30cm C.60cm D.60cm
2、已知一个梯形的四条边的长分别为1,2,3,4。则此梯形的面积等于()
A. 4 B. 6 C. D.
3、在梯形ABCD中,AD∥BC,中位线EF分别与BD、AC交于点H、G。若AD=6,BC=10,则GH=。
4、四边形ABCD中,AB∥CD,∠D=2∠B,若AD=a,AB=b,求CD的长.
【点评】:从同一底边的两个端点作另一条底边的垂线,就可将梯形转化为两个直角三角形和一个矩形。
【点评】:旋转由梯形一底和一腰中点构成的三角形,可使梯形转化为三角形。
【点评】:已知梯形一腰中点,作梯形的中位线。既可轻松解决计算问题,也可以在证明中将梯形转化为三角形。
板书:
=49-15=34cm.
又∵AB=CD,∴DE=CD.
梯形中常见的辅助线(含答案)
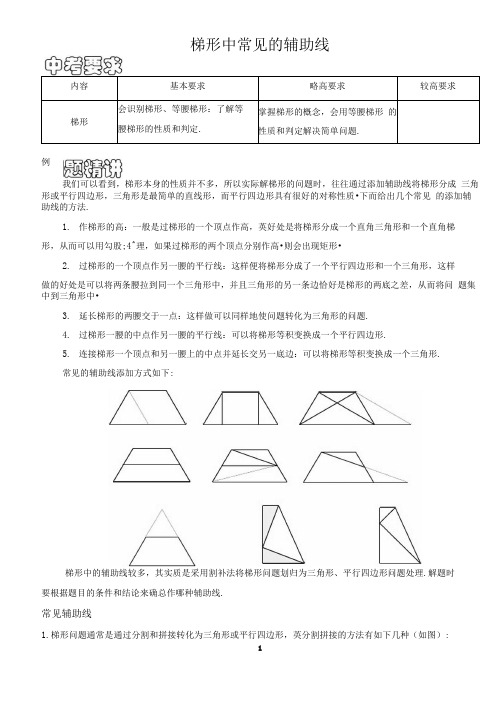
梯形中常见的辅助线内容基本要求略高要求较高要求梯形会识别梯形、等腰梯形:了解等腰梯形的性质和判定.掌握梯形的槪念,会用等腰梯形的性质和判定解决简单问题.例我们可以看到,梯形本身的性质并不多,所以实际解梯形的问题时,往往通过添加辅助线将梯形分成三角形或平行四边形,三角形是最简单的直线形,而平行四边形具有很好的对称性质•下而给出几个常见的添加辅助线的方法.1.作梯形的高:一般是过梯形的一个顶点作高,英好处是将梯形分成一个直角三角形和一个直角梯形,从而可以用勾股;4^理,如果过梯形的两个顶点分别作高•则会出现矩形•2.过梯形的一个顶点作另一腰的平行线:这样便将梯形分成了一个平行四边形和一个三角形,这样做的好处是可以将两条腰拉到同一个三角形中,并且三角形的另一条边恰好是梯形的两底之差,从而将问题集中到三角形中•3.延长梯形的两腰交于一点:这样做可以同样地使问题转化为三角形的问题.4.过梯形一腰的中点作另一腰的平行线:可以将梯形等积变换成一个平行四边形.5.连接梯形一个顶点和另一腰上的中点并延长交另一底边:可以将梯形等积变换成一个三角形.常见的辅助线添加方式如下:梯形中的辅助线较多,其实质是采用割补法将梯形问题划归为三角形、平行四边形问题处理.解题时要根据题目的条件和结论来确总作哪种辅助线.常见辅助线1.梯形问题通常是通过分割和拼接转化为三角形或平行四边形,英分割拼接的方法有如下几种(如图):1,把梯形分成一个平行四边形和一个三角形(图1所示):【答案】(1)作一腰的平行线; (2)作另一底边的垂线: (3)作对角线的平行线:(4)交于一点:(5)对称中心: (6)对称轴.【例1】 等腰梯形ABCD 中,AD//BC,若AD=3, AB=4・ BC=7,则ZB= 【答案】60° 如图,直角梯形ABCD 中,AB//CD. CB 丄AB, △ABD 是等边三角形,若AB=2,则BC=在梯形ABCD 中,AD//BC. AD=5, BC=7.若E 为DC 的中点,対线交BC 的延长线于F 点,则BF= •梯形ABCD 中.AD//BC,若对角线AC 丄BD ■且AC=5cm. BD=12cm,则梯形的而积等于((1)平移一腰,即从梯形的一个顶点(2)从同一底的两端. ,把梯形分成一个矩形和两个宜角三角形(图2所示);(3)平移对角线,即过底的一端图2,可以借助新得的平行四边形或三角形来研究梯形(图3所示):(4)延长梯形的两腰.图3,得到两个三角形,如果梯形是等腰梯形,则得到两个等腰三角形(图4所示):(5)以梯形一腰的中点为.图4,作某图形的中心对称图形(图5、图6所(6)以梯形一腰为.图5 图6,作梯形的轴对称图形(图7所【例2】【答案】 73【例3】【答案】 12 【例4】 A. 30cw- B. 60CW' C- 90cm~2D- } 69 cm-【例10】如图,等腰梯形ABCD 中,AB//CD.对角线AC 平分Z BAD, ZB=60。
梯形中添加辅助线的六种常用技巧

梯形中添加辅助线的六种常用技巧在几何学中,梯形是一种具有两条平行边的四边形。
为了解决梯形问题,往往需要在梯形中添加辅助线。
下面介绍六种常用的技巧。
1.连接两个对角线:首先,连接梯形的两个非平行边的中点,形成一条对角线。
然后,连接梯形的两个对角线中点,即可形成两个等腰三角形。
这样,可以通过等腰三角形性质来得到有关角度和边长的信息。
2.连接平行边的中点:将梯形的两条平行边的中点相连,可以形成一条平行于两条平行边的线段。
这条线段将梯形分成两个平行四边形,从而可以根据平行四边形的性质来解决问题。
3.连接一条平行边的中点和另一条边的中点:将梯形的一条平行边的中点和与之相对的边的中点连接,可以形成一条平行于梯形的底边的中线。
这样,可以通过中线分割线段的性质来得到有关线段和平行边的信息。
4.连接底边的中点和非平行边的中点:将梯形的底边的中点和非平行边的中点连接,可以形成一条平行于两条平行边的线段。
这样,可以根据平行四边形的性质来推导出梯形内部各部分的关系。
5.连接两个顶点和底边上的中点:将梯形的两个顶点和底边上的中点相连,可以得到两个等腰三角形。
利用等腰三角形的性质,可以推导出梯形的各个部分的角度和边长关系。
6.连接梯形的顶点和对角线交点:将梯形的两个顶点和另一条对角线的交点相连,可以形成一个三角形。
根据三角形的性质,可以得到角度和边长的关系,进而解决梯形问题。
这些添加辅助线的技巧可以帮助我们更好地理解和解决梯形问题。
通过巧妙地添加辅助线,可以将原来复杂的问题转化为简单的几何形状,从而更容易得到解答。
在解决梯形问题时,我们可以根据具体情况选择适合的添加辅助线的技巧,以便更加高效地解决问题。
梯形中常用的辅助线课件

梯形的性质
01
02
03
对角线性质
梯形的对角线互相平分, 且互相垂直。
平行线性质
梯形的两对边平行,且相 等。
面积计算
梯形的面积可以通过上底 、下底和高来计算。
02
梯形中常用的辅助线
延长两腰相交引出新线段
通过延长梯形的两腰,可以引出一条或两条新的线段,这些 线段可以用于构造新的三角形或平行四边形,从而简化问题 。
辅助线作法应有助于 明确题目的解题思路 ,使解题过程更加清 晰明了。
THANKS
在梯形中,延长两腰相交可以形成两个新的三角形。这些三 角形可以用于证明一些重要的几何定理,如塞瓦定理和梅纳 劳斯定理。此外,通过延长两腰,还可以构造出平行四边形 ,进一步简化梯形的问题。
作高
在梯形中作高是一种常见的辅助线方法,通过作高可以将梯形的问题转化为三角 形的问题,从而更容易解决。
作高是梯形问题中常用的辅助线方法之一。通过作高,可以将梯形的问题转化为 三角形的问题。在三角形中,可以利用三角形的性质和定理来解决问题。这种方 法在解决梯形面积、周长等问题时非常有效。
05
梯形中辅助线的注意事项
注意辅助线的作法是否符合题意
辅助线作法应符合题目的原始 条件和要求,不能随意添加或 改变题目的条件。
辅助线作法应与题目的图形和 已知条件相符合,不能出现矛 盾或错误的作法。
辅助线作法应与题目的解题目 标相符合,不能偏离解题的方 向。
注意辅助线的作法是否合理
辅助线作法应符合几何学的基本原理 和规律,不能出现不符合逻辑的作法 。
作中位线
在梯形中作中位线是一种重要的辅助线方法,通过作中位线可以将梯形的问题转化为平行四边形或矩 形的问题,从而更容易解决。
梯形中常见辅助线的作法
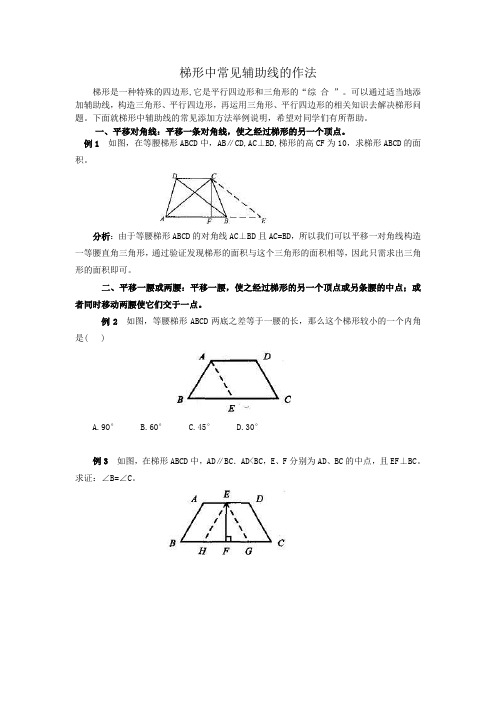
梯形中常见辅助线的作法梯形是一种特殊的四边形,它是平行四边形和三角形的“综合”。
可以通过适当地添加辅助线,构造三角形、平行四边形,再运用三角形、平行四边形的相关知识去解决梯形问题。
下面就梯形中辅助线的常见添加方法举例说明,希望对同学们有所帮助。
一、平移对角线:平移一条对角线,使之经过梯形的另一个顶点。
例1如图,在等腰梯形ABCD中,AB∥CD,AC⊥BD,梯形的高CF为10,求梯形ABCD的面积。
分析:由于等腰梯形ABCD的对角线AC⊥BD且AC=BD,所以我们可以平移一对角线构造一等腰直角三角形,通过验证发现梯形的面积与这个三角形的面积相等,因此只需求出三角形的面积即可。
二、平移一腰或两腰:平移一腰,使之经过梯形的另一个顶点或另条腰的中点;或者同时移动两腰使它们交于一点。
例2如图,等腰梯形ABCD两底之差等于一腰的长,那么这个梯形较小的一个内角是( )A.9O°B.6O°C.45°D.30°例3如图,在梯形ABCD中,AD∥BC.AD<BC,E、F分别为AD、BC的中点,且EF⊥BC。
求证:∠B=∠C。
三、延长两腰:将梯形两腰延长相交构造三角形。
例4在梯形ABCD中,AD∥BC,∠ABC=∠BCD=60°,AD+BC=30,BD平分∠ABC,求梯形的周长。
四、作梯形的高:过梯上底的两个端点分别作梯形的高。
例5已知等腰梯形的一个内角为60°,它的上底是3cm,腰长是4cm,则下底是。
梯形中添加辅助线的方法有很多,同学们在学习的过程中还须活学活用,也可以以口诀的形式记忆下来:“移动梯形对角线,两腰之和成一线;平行移动一条腰,两腰同在“△”现;延长两腰交一点,“△”中有平行线;作出梯形两高线,矩形显示在眼前;已知腰上一中线,莫忘作出中位线”。
梯形作辅助线做法及应用

F
G
B
E
C
H
2、当AC =BD时,∆BED又是什么三角形? 、 时 又是什么三角形
A 构造旋转变换
D O
( 五 ) 其 他 方
B
证明哪个定理是应用了这个方法
?? 梯形ABCD面积与哪个图形面积相等 面积与哪个图形面积相等? 梯形 面积与哪个图形面积相等
构造中位线
C
E
返
回
梯形辅助线做法应用
应 用
例题:
1、如图,梯形ABCD 中, AB∥CD, ∠D=70 ° , ∠ C=40 ° ∥
梯形中常用辅助线
作
法
一、梯形中常用辅助线
数学思想
梯形转化为三角形和平行四边形或 特殊平行四边形等
二 梯形中常用作辅助线
方 法
梯形中常用作辅助线
方法
(一) 平移腰 (二) 作 高 (三) 补为三角形 (四)平移对角线 (五)其他方法
梯形中常用作辅助线
平移腰
(一) 平移腰 一
A D A D
B
C
B
54º
36º
E
20
C
3、如图,梯形ABCD 中, AD∥BC, ∠B=60 °, ∠ C=45 ° ∥
AB= 2 3 , AD=2,则梯形周长=
A 2 D
2 3
B 60°
3
3 2
45 °
C
3
E` E
3
布置作业:
1、求证:对角线垂直的等腰梯形的高等于它的中位线 2、课本:196页17题、199页5题
例2:已知,梯形ABCD中,AD∥BC,E是腰AB的中点,
DE ⊥CE, 求证: AD+BC=CD。 A 证明:(一)延长DE交CB延长线于F D ∵在梯形ABCD中AD//B ,∠A= ∠ ABF E ∴ AE=BE,∠A= ∠ ABF,∠ AED= ∠ BEF ∴ ∆ADE≌∆BFE F B C ∴ DE=FE,AD=BF
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
梯形常见辅助线作法
1
1、平移法
2
(1)梯形内平移一腰(过一顶点做腰的平行线)
3
[例1]如图,在等腰梯形ABCD中,AD∥BC,AB=CD,∠C=60°,AD=15cm,
4
BC=49cm,求CD的长.
5
解:过D作DE∥AB交BC于E,则四边形ABED为平行四边形.
6
∴AD=BE=15cm,AB=DE.
7
∴EC=BC-BE=BC-AD=49-15=34cm.
8
又∵AB=CD,∴ DE=CD.
9
又∵∠C=60°,
10
∴△CDE是等边三角形,
11
即CD=EC=34cm.
12
(2)梯形外平移一腰(过一顶点做腰的平行线)
13
[例2]如图,在梯形ABCD中,AB∥CD,四边形ACED是平行四边形,延长DC交BE于F. 求14
证:EF=FB
15
证明:过点B作BG∥AD,交DC的延长线于G
16
∴四边形ABGD是平行四边形∴AD=BG
17
∵ACED中,AD∥CE AD=CE
18
∴CE∥BG且CE=BG ∴∠CEF=∠GBF 19
又∵∠CFE=∠GFB
20
∴△ECF≌△BGF( ASA)
21
∴EF=FB
22 A
D C
E
F
B
点评:过梯形上底或下底的一个端点作另一腰的平行线,可将梯形转化为一个平行四边形23
和三角形。
24
(3)梯形内平移两腰:利用梯形中的某个特殊点,过此点作两腰的平行线,把两腰转化到25
同一个三角形中。
26
[例3]如图,已知:梯形ABCD中,AD∥BC,
27
∠C+∠B=90°,M,N分别是AD,BC的中点.
28
求证:MN=1
() 2
BC AD
29
证明:过点E分别作AB、CD的平行线,交BC于点G、H ,
30
则四边形ABGE,EDCH为平行四边形∴AE=BG,ED=HC
31
∵AB∥EG ∴∠B=∠EGF
32
又∵DC∥EH ∴∠C=∠EHF
33
则∠EGH+∠EHG=∠B+∠C=90°,△EGH是直角三角形
34
∵E、F分别是AD、BC的中点∴AE=ED,BF=CF ∴GF=FH 35
则有EF=1
2
GH=
1
2
(BC-BG-HC)=
1
2
(BC-AD)
36
(4)平移对角线(过一顶点做对角线的平行线)37
[例4]求证:对角线相等的梯形是等腰梯形
38
已知:在梯形ABCD中,AD∥BC,对角线
39
求证:AB=DC
40
证明:过点D作DE∥AC交BC的延长线于点E 41
B B
则四边形ACED 是平行四边形 ∴AC=DE
42 ∵DE=AC=DB ∴∠DBC=∠E ∠ACB=∠E ∴∠DBC=∠ACB 43 又∵BD=CA BC=CB ∴△ABC ≌△DCB(SAS) 44 ∴AB=DC
45 点评:过梯形的一个顶点作对角线的平行线,将对角线的有关条件转化到一个三角形中。
46 2、作梯形的高
47 (1)作一条高,从底边的一个端点作另一条底边的垂线,把梯形转化为直角三角形或矩形 48 [例6]如图,在直角梯形ABCD 中,AB//DC ,∠ABC=90°,
49 AB=2DC ,对角线AC ⊥BD ,垂足为F ,过点F 作EF//AB , 50 交AD 于点E
51 求证:四边形ABFE 是等腰梯形
52 证明:过点D 作DG ⊥AB 于点G ,则易知四边形DGBC 是矩形,所以DC=BG 53 ∵AB=2DC ∴AG=GB 54 ∴DA=DB ∴∠DAB=∠DBA 55 又∵EF//AB
56 ∴四边形ABFE 是等腰梯形。
57 (2)作两条高:从同一底边的两个端点作另一条底边的垂线,把梯形转化为两个直角三角58 形和一个矩形
59 [例7]如图,在梯形ABCD 中,DC∥AB,AD=BC ,若AD=5,CD=2,AB=8,求梯形ABCD 的面积。
60
A
解:过点D 、C 分别作DE⊥AB 于E ,CF⊥AB 于F. 61 ∵DC∥AB, DE⊥AB,CF⊥AB
62 ∴四边形CDEF 是矩形 ∴DC=EF,DE=CF 63 易证△ADE ≌△DCF(HL) ∴AE=BF 64 ∴AE=
12(AB-EF)=1
2
(AB-CD)=3 65
2222534AD AB -=-=
66 3、延长两腰交于一点,可使梯形转化为三角形
67 [例5]如图,在梯形ABCD 中,AD//BC ,∠B=50°,∠C=80°,AD=2,BC=5, 68 求CD 的长。
69 解:延长BA 、CD 交于点E
70 ∵在△BCE 中,∠B=50°,∠C=80° 71 ∴∠E=50° ∴BC=EC=5
72 又∵AD//BC ∴∠EAD =∠B=50° ∴AD=ED=2 73 ∴CD=EC-ED=5-2=3 74 4、中位线法
75 (1)已知梯形一腰中点,作梯形的中位线
76 [例10]如图,在梯形ABCD 中,AB//DC ,O 是BC 的中点, 77 ∠AOD =90°,求证:AB +CD=AD
78 证明:取AD 的中点E ,连接OE ,则易知OE 是梯形ABCD 的中位线
79
D A
O
B
E
A
∴OE=2
1(AB +CD )
80 在△AOD 中,∠AOD=90°,AE=DE
81
∴AD 2
1
OE =
∴AB +CD=AD 82 点评:已知梯形一腰中点,作梯形的中位线,既可轻松解决计算问题,也可以在证明中将83 梯形转化为三角形。
84 (2)已知梯形两条对角线的中点,连接梯形一顶点与一条对角线中点,并延长与底边相交,85 使问题转化为三角形中位线
86 [例11]如图,在梯形ABCD 中,AD//BC ,E 、F 分别是BD 、AC 的中点, 87 求证:(1)EF//AD ;(2))AD BC (2
1EF -=
88 证明:连接DF ,并延长交BC 于点G ,易证△AFD≌△CFG (ASA )
89 则AD=CG ,DF=GF
90 ∵DE=BE ,∴EF 是△BDG 的中位线 91 ∴EF//BG 且BG 2
1EF = 92 又∵AD//BG ,BG=BC-CG=BC-AD 93 ∴EF//AD ,EF )AD BC (21
-= 94 5、构造全等三角形
95 (1)连接梯形一顶点及一腰的中点 96 [例8](梯形中位线的性质)
97 如图,已知在梯形ABCD 中,AD//BC ,M 、N 为腰AB 、DC 的中点,
98
B
求证:MN ∥AD ∥BC ,)(2
1
AD BC MN +=
99 证明:连结AN 并延长,交BC 的延长线于点E 100 ∵AD//BC , ∴∠D=∠DCE
101 易证△ADN ≌△ECN(ASA) ∴AN=EN ,AD=CE 102 又∵AM=MB 103 ∴EF ∥AD // BC
104
111
BC+CE =BC AD 222
MN BE =
=+()()
(三角形中位线性质) 105 (2)过一腰的中点作另一腰的平行线 106 [例9](梯形的中位线性质)
107 如图,已知在梯形ABCD 中,AD//BC ,M 、N 为腰AB 、DC 的中点,
108
求证:MN ∥AD ∥BC ,)(2
1
AD BC MN +=
109 证明:过F 作AB 的平行线,交AD 的延长线于点N ,交BC 于M 110 则四边形ANMB 为平行四边形
111 ∴AN=BM ,AB=MN ,AB//NM
112 ∵AD//BC , ∴∠N=∠CMF 113 易证△DNF ≌△CMF(ASA) 114 ∴DN=CM ,DF=CF
115
B
又∵AE=EB ∴AE=NF 且AE//NF ∴四边形AEFN 为平行四边形 116 ∴EF ∥AD // BC EF=AN=BM
117
∴111
EF AN BM AD+DN+BC-MC =BC AD 222
=+=+()()()
118
6、作对角线,使梯形转化为三角形
119 [例12]如图,在直角梯形ABCD 中,AD//BC , 120 AB ⊥AD ,BC=CD ,BE ⊥CD 于点E ,求证:AD=DE
121 证明:连结BD
122 ∵AD//BC ∴∠ADB=∠DBE
123 又∵BC=CD ∴∠DBC=∠BDC ∴∠ADB=∠BDE 124 又∵∠BAD=∠DEB=90°,BD=BD
125 ∴Rt △BAD ≌Rt △BED(AAS) ∴ AD=DE
126 以上的一些常用辅助线,实际上都体现了数学中的转化的数学思想,即将梯形的问题转化127 为三角形或平行四边形,在学习过程中希望同学们能细心体会并加以灵活运用。
128
C。
