乘法公式复习教案
乘法公式教案

乘法公式教案教案标题:乘法公式教案教案概述:本教案旨在帮助学生理解和掌握乘法公式并能够在实际问题中应用。
通过多种教学方法和活动,学生将能够发展其数学思维和解决问题的能力。
此外,本教案还将帮助学生掌握乘法的基本概念和技巧,以及培养他们的合作与沟通技巧。
教学目标:1. 理解和应用乘法公式。
2. 在实际问题中应用乘法公式解决问题。
3. 发展数学思维和解决问题的能力。
4. 掌握乘法的基本概念和技巧。
5. 培养合作与沟通技巧。
适用对象:适用于小学四年级学生。
教学准备:1. 教师:白板、彩色粉笔、投影仪。
2. 学生:教科书、练习册、铅笔、橡皮擦。
教学过程:引入:1.通过回顾学生已学的知识,帮助他们复习和理解加法和乘法的概念。
例如,教师可以向学生提问:“什么是加法?什么是乘法?他们有什么区别?”2.教师可给学生展示一些实际生活中使用乘法的例子(如购买物品的总价、计算矩形面积等),引发学生对乘法公式的兴趣。
教学主体:1.教师通过示意图和简单的实例向学生介绍乘法公式的定义和用法。
例如,“乘法公式是用来计算两个数的乘积的。
”2.教师向学生展示一些基本的乘法表格,并解释如何使用这些表格来帮助计算乘法问题。
3.教师引导学生一起进行乘法练习,从简单的算式开始,逐步增加难度,确保每个学生掌握基本的乘法技巧。
4.教师鼓励学生提问和互动,以帮助他们更好地理解乘法公式的概念并应用到实际问题中。
拓展活动:1.学生小组合作练习:教师组织学生分成小组,每组设计一个实际问题,要求其他小组员通过使用乘法公式来解决问题。
鼓励小组成员之间的讨论和合作。
2.互动游戏:教师设计一个乘法游戏,例如“乘法接龙”。
学生们在规定时间内以最快速度回答乘法问题,并在答题过程中不断提高难度,以增加挑战性。
总结:1. 教师和学生一起回顾和总结所学的乘法公式知识点,澄清学生对乘法公式的疑惑和困惑。
2. 鼓励学生主动思考和提问,帮助他们巩固所学的知识。
评估:教师可以通过课堂讨论、学生的练习册等形式对学生进行评估,以了解他们对乘法公式的理解和应用能力。
乘法公式初中教案

乘法公式初中教案教学目标:1. 理解乘法公式的概念和意义。
2. 学会运用乘法公式进行计算和解决问题。
3. 培养学生的逻辑思维能力和数学思维习惯。
教学重点:1. 乘法公式的概念和意义。
2. 乘法公式的运用和计算。
教学难点:1. 乘法公式的理解和记忆。
2. 乘法公式的灵活运用。
教学准备:1. 教学课件或黑板。
2. 练习题和答案。
教学过程:一、导入(5分钟)1. 引导学生回顾加法、减法、乘法、除法的定义和运算规则。
2. 提问:我们已经学过加法、减法、乘法、除法,那么有没有什么规律可以让我们更快地计算乘法呢?二、新课讲解(15分钟)1. 介绍乘法公式的概念:乘法公式是指在乘法运算中,两个数的乘积与它们的因数之间的关系。
2. 讲解乘法公式的意义:乘法公式可以帮助我们更快地计算乘法,避免繁琐的计算过程。
3. 举例讲解乘法公式:以2x3和3x2为例,解释它们的乘积都是6,强调乘法公式的交换律。
4. 讲解乘法公式的运用:通过例题展示如何运用乘法公式进行计算和解决问题。
三、课堂练习(15分钟)1. 布置练习题,让学生独立完成。
2. 选取部分学生的作业进行讲解和点评,纠正错误并巩固知识点。
四、拓展与应用(15分钟)1. 引导学生思考:乘法公式在日常生活中有哪些应用?2. 举例说明乘法公式在实际问题中的应用,如购物时计算总价、计算面积等。
3. 让学生尝试自己用乘法公式解决实际问题,培养学生的应用能力。
五、总结与反思(5分钟)1. 回顾本节课所学内容,让学生复述乘法公式的概念和意义。
2. 提问:通过本节课的学习,你们认为乘法公式在数学中的作用是什么?3. 鼓励学生积极思考,提出问题,培养学生的批判性思维。
教学评价:1. 课后作业:布置相关练习题,检验学生对乘法公式的掌握程度。
2. 课堂表现:观察学生在课堂上的参与程度、提问回答等情况,评估学生的学习效果。
3. 学生反馈:收集学生的学习心得和意见,不断改进教学方法,提高教学质量。
初中数学乘法公式教案

初中数学乘法公式教案教学目标:1. 理解乘法公式的含义和运用。
2. 掌握乘法公式的计算方法和步骤。
3. 能够灵活运用乘法公式解决实际问题。
教学重点:1. 乘法公式的含义和运用。
2. 乘法公式的计算方法和步骤。
教学准备:1. 教学课件或黑板。
2. 练习题。
教学过程:一、导入(5分钟)1. 引导学生回顾加法、减法、乘法、除法的定义和运算规律。
2. 提问:我们已经学习了加法、减法、乘法、除法,那么有没有一种方法可以快速计算两个数的乘积呢?二、新课讲解(15分钟)1. 介绍乘法公式的含义:乘法公式是一种用来计算两个数乘积的方法,它将乘法运算转化为加法运算。
2. 讲解乘法公式的计算方法和步骤:a. 将两个数写成加数的形式。
b. 将加数按照一定的顺序相加。
c. 得出结果。
3. 举例讲解乘法公式的运用:以2x3为例,将其写成加数的形式为2+2+2+2,然后按照顺序相加得到结果6。
三、课堂练习(15分钟)1. 让学生独立完成练习题,巩固乘法公式的计算方法和步骤。
2. 引导学生相互讨论,解决练习题中的问题。
四、总结与拓展(5分钟)1. 总结乘法公式的含义和运用,强调乘法公式的计算方法和步骤。
2. 提问:乘法公式可以用来计算两个数的乘积,那么能不能用来计算三个数或者更多数的乘积呢?五、课后作业(布置作业)1. 根据课堂练习的情况,布置适量的作业,让学生巩固乘法公式的计算方法和步骤。
教学反思:本节课通过讲解乘法公式的含义和运用,让学生掌握了乘法公式的计算方法和步骤,并能够灵活运用乘法公式解决实际问题。
在教学过程中,注意引导学生相互讨论,解决练习题中的问题,提高了学生的合作意识和解决问题的能力。
同时,通过提问和拓展,激发了学生的思考和探究欲望,为后续的学习打下了基础。
整式的乘法公式教案

整式的乘法公式教案一、教学目标:1. 知识与技能:(1)理解并掌握整式的乘法公式,包括平方差公式和完全平方公式;(2)能够运用整式的乘法公式进行简便计算。
2. 过程与方法:(1)通过实例演示和练习,引导学生发现整式乘法公式;(2)培养学生运用公式进行计算的能力。
3. 情感态度与价值观:(1)培养学生对数学的兴趣和自信心;(2)培养学生积极主动探究问题的习惯。
二、教学重点与难点:1. 教学重点:(1)掌握整式的乘法公式;(2)能够运用整式的乘法公式进行计算。
2. 教学难点:(1)整式乘法公式的推导过程;(2)灵活运用整式乘法公式解决实际问题。
三、教学准备:1. 教师准备:(1)教学课件或黑板;(2)练习题。
2. 学生准备:(1)预习整式乘法公式;(2)准备笔记本,记录重点知识。
四、教学过程:1. 导入:(1)复习相关知识,如整式的加减法;(2)提问:能否将整式的加减法推广到乘法?2. 知识讲解:(1)通过实例演示,引导学生发现整式乘法公式;(2)讲解平方差公式和完全平方公式的推导过程;(3)强调公式中的各项系数和指数的变化规律。
3. 练习与讲解:(1)让学生分组讨论,互相解答疑问;(2)选取典型题目进行讲解,分析解题思路;(3)引导学生运用整式乘法公式进行计算。
4. 课堂小结:(1)回顾本节课所学内容,总结整式乘法公式的特点;(2)强调学生在练习中需要注意的问题。
五、课后作业:1. 请学生完成课后练习题,巩固整式乘法公式的运用;2. 鼓励学生自主探究,发现整式乘法公式的拓展应用。
六、教学拓展:1. 平方差公式的拓展:(1)引导学生发现平方差公式的推广形式;(2)举例说明平方差公式在实际问题中的应用。
2. 完全平方公式的拓展:(1)引导学生发现完全平方公式的推广形式;(2)举例说明完全平方公式在实际问题中的应用。
七、课堂练习:1. 请学生独立完成练习题,检验对整式乘法公式的掌握程度;2. 教师选取部分学生的作业进行点评,指出优点和不足。
乘法整理和复习(教案 )- 2023-2024学年数学四年级上册 北师大版

教案标题:乘法整理和复习年级:四年级学科:数学教材版本:北师大版学年:2023-2024教学目标:1. 让学生掌握乘法的基本概念和性质。
2. 培养学生运用乘法解决实际问题的能力。
3. 巩固和提高学生对乘法口诀的记忆和应用。
教学内容:1. 乘法的基本概念和性质2. 乘法口诀的应用3. 乘法在实际问题中的应用教学步骤:一、导入(5分钟)1. 教师通过提问的方式引导学生回顾乘法的基本概念和性质。
2. 学生分享自己对乘法的理解和应用。
二、乘法口诀的复习(10分钟)1. 教师带领学生一起背诵乘法口诀表。
2. 学生进行乘法口诀的练习,巩固记忆。
三、乘法在实际问题中的应用(15分钟)1. 教师通过例题讲解乘法在实际问题中的应用。
2. 学生分组讨论,共同解决实际问题。
四、课堂小结(5分钟)1. 教师引导学生总结本节课的学习内容。
2. 学生分享自己的学习心得和收获。
五、课后作业(5分钟)1. 教师布置相关的乘法练习题,巩固课堂所学知识。
2. 学生认真完成作业,加强对乘法的理解和应用。
教学评价:1. 通过课堂提问和练习,了解学生对乘法基本概念和性质的理解程度。
2. 观察学生在解决实际问题时的运用能力,评价学生对乘法的掌握情况。
教学反思:本节课通过乘法整理和复习,学生对乘法的基本概念和性质有了更深入的理解,乘法口诀的记忆和应用也得到了巩固和提高。
在解决实际问题的过程中,学生能够灵活运用乘法,提高了数学思维能力。
但在教学过程中,仍需关注个别学生的掌握情况,及时给予指导和帮助,确保每个学生都能跟上教学进度。
需要重点关注的细节是:在解决实际问题的过程中,学生能够灵活运用乘法,提高了数学思维能力。
补充和说明:在解决实际问题的过程中,学生能够灵活运用乘法,是衡量学生对乘法知识掌握程度的重要标准。
因此,教师应注重培养学生的乘法应用能力,提高学生的数学思维能力。
以下是对这一重点细节的详细补充和说明:1. 实际问题的引入:教师应选择与学生生活密切相关的问题,引导学生运用乘法知识解决。
2024乘法公式人教版数学八年级上册教案

2024乘法公式人教版数学八年级上册教案一、教学目标1.让学生掌握多项式乘以多项式的法则。
2.能够灵活运用乘法公式解决实际问题。
3.培养学生的观察能力、逻辑思维能力和解决问题的能力。
二、教学重点与难点重点:多项式乘以多项式的法则。
难点:运用乘法公式解决实际问题。
三、教学过程1.导入新课(1)回顾已学的平方公式和立方公式。
(2)引导学生思考:如何将多项式相乘转化为平方和立方公式来解决?2.探究新知(1)引导学生观察多项式乘以多项式的特点,如(a+b)(c+d)。
(2)引导学生利用平方公式和立方公式,将(a+b)(c+d)转化为平方和立方公式的形式。
3.应用练习(1)让学生独立完成课本P30页的练习题1、2。
(2)教师选取部分学生板演,讲解解题过程。
(2)让学生举例说明如何运用乘法公式解决实际问题。
5.课堂小结(1)回顾本节课所学内容,让学生复述多项式乘以多项式的法则。
(2)强调乘法公式在解决实际问题中的应用。
6.课后作业(1)完成课本P31页的练习题3、4、5。
(2)预习下一节课的内容,思考如何运用乘法公式解决实际问题。
四、教学反思2.在探究环节,教师引导学生观察、思考,充分调动了学生的积极性,提高了课堂参与度。
3.在应用练习环节,教师选取部分学生板演,讲解解题过程,让学生在实践中巩固所学知识。
4.课堂小结环节,教师引导学生回顾所学内容,强化了知识点,提高了学生的学习效果。
五、教学策略1.采用启发式教学,引导学生主动探究、发现规律。
2.利用实例讲解,让学生在具体情境中感受乘法公式的应用。
3.注重课后作业的布置,巩固所学知识,提高学生的实际运用能力。
六、教学评价1.课堂参与度:观察学生在课堂上的发言、提问情况,了解学生的参与程度。
2.作业完成情况:检查学生的作业完成情况,了解学生对知识点的掌握程度。
3.测试成绩:通过测试,了解学生对乘法公式的掌握情况,评估教学效果。
重难点补充:1.教学重点:多项式乘以多项式的法则(1)难点解释:学生可能会混淆多项式乘法的步骤,比如在分配律的应用上出错。
乘法公式教案

乘法公式教案教案名称:乘法公式教案教案目标:1. 了解乘法公式及其应用;2. 能够熟练地运用乘法公式解决实际问题;3. 培养学生的数学思维和解决问题的能力。
教学重点:1. 掌握乘法公式的结构和应用方法;2. 能够正确运用乘法公式解决实际问题。
教学难点:1. 学生能够将实际问题抽象为乘法公式;2. 学生能够准确地运用乘法公式解决问题。
教学准备:1. 教师准备乘法公式的教学素材及练习题;2. 学生准备纸笔。
教学过程:一、导入(5分钟)1. 教师介绍乘法公式的概念和作用,并与学生进行互动交流。
二、讲解与示范(15分钟)1. 教师详细讲解乘法公式的结构和应用方法;2. 教师通过示范解决几个实际问题的方式,帮助学生理解乘法公式的使用。
三、练习与巩固(20分钟)1. 学生在纸上完成一些练习题,巩固乘法公式的应用;2. 学生自主解决一些实际问题,运用乘法公式解决;3. 学生与同桌交流和讨论解决问题的过程和方法。
四、拓展与运用(10分钟)1. 学生自行选择一个实际问题,运用乘法公式解决,并将解题过程写在纸上;2. 学生按照分享的顺序,将自己的解题过程展示给其他同学。
五、总结与反思(5分钟)1. 教师对本节课的内容进行总结,并指出学生在掌握乘法公式上存在的问题;2. 学生反思自己在解题过程中出现的困惑和需要改进的地方。
教学延伸:针对学生存在的问题,教师可以在下节课中进行针对性的讲解和练习,帮助学生更好地掌握乘法公式的运用。
教学评价:1. 学生在练习中的表现;2. 学生在实际问题中的解题能力和思考能力;3. 学生对乘法公式的掌握程度和应用能力。
乘法公式教案

乘法公式教案一、教学目标1. 知识目标:掌握乘法公式的概念、原理和应用。
2. 能力目标:能够灵活运用乘法公式解决实际问题。
3. 情感目标:培养学生对乘法公式的兴趣和探索精神,增强数学学科的学习动力。
二、教学重点与难点1. 教学重点:乘法公式的概念、原理和应用。
2. 教学难点:如何运用乘法公式解决实际问题。
三、教学准备1. 教具准备:黑板、彩色粉笔、乘法表。
2. 学具准备:学生练习册、习题集。
四、教学过程Step 1 引入新知1. 创设情境:小明要算一本书一共有多少页,他知道每页有24行,每行有32个字,他该如何计算?2. 导入问题:请同学们尝试解决这个问题,思考一下需要用到哪些数学方法?3. 引导讨论:请几位同学分享一下你们的解决思路。
Step 2 发现规律1. 呈现乘法表:在黑板上列出1-10的乘法表。
2. 观察与总结:请同学们观察乘法表,看看有没有什么规律或者特点?3. 引导思考:根据同学们的观察,我们能否总结出乘法公式的一般形式?Step 3 学习乘法公式1. 引入乘法公式:通过引导性的提问,教师介绍乘法公式的概念和原理。
2. 讲解乘法公式:详细讲解乘法公式的推导过程,并解释为什么可以使用乘法公式来解决实际问题。
3. 举例应用:提供具体实例,引导学生根据已学习的乘法公式解决实际问题。
Step 4 练习巩固1. 基础练习:在黑板上出示一些与乘法公式相关的习题,让学生上台做题并解释解题思路。
2. 拓展练习:提供一些较为复杂的应用题,要求学生分组讨论并给出解题思路和答案。
3. 自主练习:让学生在练习册上独立完成相关的练习题。
Step 5 归纳总结1. 归纳乘法公式:请同学们尝试总结乘法公式的基本形式和适用范围。
2. 教师点评:教师对同学们的总结给予点评和肯定。
五、课堂小结通过本节课的学习,我们掌握了乘法公式的概念、原理和应用,并且能够运用乘法公式解决实际问题。
六、作业布置1. 完成练习册上的相关练习题。
数学教案高中乘法公式汇总

数学教案高中乘法公式汇总主题:乘法公式汇总教学目标:1. 熟练掌握高中乘法公式的运用;2. 理解并掌握乘法公式的推导过程;3. 能够灵活运用乘法公式解决实际问题。
教学内容:1. 乘法的基本概念;2. 乘法公式的应用;3. 乘法公式的推导。
教学重点:1. 熟练掌握常见乘法公式;2. 灵活运用乘法公式解决问题。
教学难点:1. 掌握乘法公式的推导过程;2. 利用乘法公式解决实际问题的能力提升。
教学方法:1. 探究式教学;2. 合作学习。
教学过程:一、乘法的基本概念(5分钟)1. 引导学生回顾乘法的定义;2. 介绍乘法的基本性质。
二、乘法公式的应用(15分钟)1. 讲解常见乘法公式的应用;2. 练习乘法公式的运用。
三、乘法公式的推导(20分钟)1. 讲解乘法公式的推导过程;2. 举例说明乘法公式的推导。
四、练习与巩固(15分钟)1. 给学生一些练习题,巩固所学知识;2. 解答学生提出的问题。
五、拓展与应用(10分钟)1. 引导学生思考乘法公式在实际生活中的应用;2. 提出拓展问题,让学生独立思考。
六、总结与反思(5分钟)1. 对本节课所学内容进行总结;2. 学生进行自我反思,指出需要加强的地方。
教学反馈:1. 学生表现出对乘法公式的理解程度;2. 学生在练习中的表现;教学资料:1. 乘法公式的应用举例;2. 乘法公式推导过程的教学讲义;3. 练习题及答案。
教学评估:1. 学生在练习中的表现;2. 学生对乘法公式推导的理解程度。
(注:本教案仅供参考,教师可根据实际情况进行调整和修改。
)。
乘法公式教案

乘法公式教案乘法公式教案介绍:乘法公式是数学中非常重要的一部分,它能够帮助我们快速计算大量的乘法运算。
在小学阶段,学生们通常会学习到乘法公式的基本概念和应用方法。
本篇文章将为您介绍一份乘法公式的教案,帮助学生们更好地理解和掌握这一知识点。
一、教学目标通过本节课的学习,学生将能够:1. 理解乘法公式的概念和作用;2. 掌握乘法公式的基本应用方法;3. 运用乘法公式解决实际问题。
二、教学准备1. 教师准备:教案、黑板、彩色粉笔、习题册;2. 学生准备:课本、笔、作业本。
三、教学过程1. 导入教师可以通过提问的方式,引导学生回顾乘法的基本概念和运算方法。
例如:“请问,什么是乘法?我们怎样进行乘法运算?”2. 概念讲解教师通过讲解的方式,向学生介绍乘法公式的概念和作用。
可以使用图表或实例来帮助学生理解。
例如:“乘法公式是一种用于计算两个或多个数相乘的方法。
它可以帮助我们简化乘法运算,提高计算效率。
”3. 乘法公式的应用教师通过示范和练习的方式,向学生展示乘法公式的具体应用方法。
例如:“现在我们来看一个例子:计算5×7。
根据乘法公式,我们可以将5看作一个被乘数,将7看作一个乘数。
我们可以将5写成5×1,然后再将7分别乘以1,得到的结果相加。
这样我们就可以得到5×7的答案。
”4. 练习巩固教师布置一些练习题,让学生进行乘法公式的练习。
可以根据学生的不同水平,选择适当的难度。
例如:“请计算8×9,使用乘法公式进行计算。
”5. 拓展应用教师引导学生思考乘法公式在实际问题中的应用。
例如:“小明买了3个苹果,每个苹果的价格是2元。
请问,小明一共花了多少钱?你们可以使用乘法公式来解决这个问题。
”6. 总结教师对本节课的内容进行总结,并强调乘法公式的重要性和应用价值。
可以鼓励学生积极运用乘法公式,提高计算效率。
四、课后作业教师布置一些乘法公式的作业题,让学生巩固所学知识。
例如:“请计算6×4,使用乘法公式进行计算,并写出详细的解题过程。
乘法公式教案

乘法公式教案乘法公式教案一、教学目标:1. 理解乘法公式的概念和意义。
2. 能够正确运用乘法公式计算具体的乘法表达式。
3. 培养学生观察、分析和推理的能力。
二、教学重点:1. 乘法公式的概念和意义。
2. 乘法公式的运用。
三、教学难点:乘法公式的推导和运用。
四、教学过程:1. 引入乘法公式(10分钟)教师将一个简单的乘法算式写在黑板上,如3 × 4 = 12,并询问学生这个算式的结果是多少。
然后教师再列举一些简单的算式,让学生思考它们之间是否存在某种规律。
引导学生发现乘法的特点:乘法是将两个数相乘得到一个新的数。
2. 乘法公式的概念讲解(10分钟)教师解释乘法公式的概念和意义:乘法公式是一种用来表示乘法运算的数学语句。
它由被乘数、乘数和积三部分组成,被乘数和乘数相乘得到积。
3. 乘法公式的具体形式和推导(15分钟)教师将一个简单的推导过程写在黑板上,如4 × 3 = 12,然后通过分析推导过程让学生发现乘法公式的具体形式:a × b = b × a。
再通过多个例子的展示和讲解,让学生深入理解乘法公式的推导过程。
4. 乘法公式的运用(15分钟)教师给学生出示一些乘法算式,要求他们运用乘法公式计算出结果。
教师可以通过游戏的形式,让学生分组进行竞赛,提高学生的参与度和学习兴趣。
5. 乘法公式的应用(10分钟)教师通过实际问题的引入,让学生认识到乘法公式在日常生活中的应用。
例如,一个教室里有10排桌子,每排有12张桌子,学生们可以用乘法公式计算出这个教室里共有多少张桌子。
6. 总结和反思(10分钟)教师与学生一起总结乘法公式的概念、形式和运用,并提醒学生在学习中的注意事项。
然后让学生进行自我评价和反思,以确定下一步的学习目标。
五、课堂练习:1. 计算以下乘法算式的结果:5 × 3,8 × 4,9 × 2。
2. 计算以下乘法算式的结果,并写出乘法公式的推导过程:4× 6,7 × 2,3 × 8。
第一章整式的乘除复习(教案)

3.重点难点解析:在讲授过程中,我会特别强调整式的乘法法则和除法步骤这两个重点。对于难点部分,如合并同类项和运用平方差、完全平方公式,我会通过具体的例题和对比分析来帮助大家理解。
(三)实践活动
1.ห้องสมุดไป่ตู้组讨论:学生们将分成若干小组,每组讨论一个涉及整式乘除的实际问题。
2.实验操作:为了加深对整式乘除的理解,我们将进行一个简单的数学实验,通过实际操作来演示整式乘除的基本原理。
三、教学难点与重点
1.教学重点
-单项式乘以单项式的运算法则:重点掌握系数相乘、相同字母相乘、不同字母相乘的法则,并能够熟练运用。
-多项式乘以多项式的运算法则:强调先用一个多项式的每一项乘以另一个多项式的每一项,然后合并同类项。
-平方差公式和完全平方公式的应用:熟练掌握(a+b)(a-b)=a^2-b^2和(a+b)^2=a^2+2ab+b^2等公式,并能解决相关问题。
(二)新课讲授
1.理论介绍:首先,我们要复习整式的乘法和除法的基本概念。整式的乘法是指将两个或多个整式相乘,包括单项式乘单项式、单项式乘多项式、多项式乘多项式。整式的除法则是指将一个整式除以另一个整式,关键是找到商和余数。这些运算是解决许多数学问题的基础。
2.案例分析:接下来,我们通过一个具体的案例来分析整式的乘除在实际中的应用。例如,解决几何图形面积问题时,可能会涉及到整式的乘法和除法运算。
3.培养数学建模意识:将现实生活中的问题转化为整式的乘除运算,使学生体会数学建模的过程,提高解决实际问题的能力。
2024北师大版数学七年级下册1.6.3《乘法公式综合运用》教案3

2024北师大版数学七年级下册1.6.3《乘法公式综合运用》教案3一. 教材分析《乘法公式综合运用》是北师大版数学七年级下册1.6.3的教学内容。
这部分内容是在学生掌握了平方差公式、完全平方公式等乘法公式的基础上进行学习的。
通过这部分的学习,学生能够灵活运用乘法公式解决实际问题,提高他们的解决问题的能力。
二. 学情分析面对七年级的学生,他们在之前的学习中已经掌握了平方差公式、完全平方公式等乘法公式。
但是,他们在运用这些公式解决实际问题时,往往会存在理解不深、运用不灵活的情况。
因此,在教学这部分内容时,需要引导学生深入理解乘法公式的内涵,提高他们解决问题的能力。
三. 教学目标1.知识与技能:使学生掌握乘法公式的运用方法,能够灵活解决实际问题。
2.过程与方法:通过自主学习、合作交流,培养学生解决问题的能力。
3.情感态度与价值观:激发学生学习数学的兴趣,培养他们积极思考、勇于探索的精神。
四. 教学重难点1.重点:乘法公式的运用。
2.难点:灵活运用乘法公式解决实际问题。
五. 教学方法采用自主学习、合作交流、教师引导相结合的教学方法,让学生在探究中掌握知识,提高解决问题的能力。
六. 教学准备1.准备相关的乘法公式的资料,以便在教学中进行查阅。
2.准备一些实际问题,让学生进行练习。
七. 教学过程1.导入(5分钟)教师通过提问的方式,引导学生回顾之前学过的平方差公式、完全平方公式等乘法公式,为新课的学习做好铺垫。
2.呈现(10分钟)教师通过展示一些实际问题,让学生尝试运用乘法公式进行解决。
学生在解决问题的过程中,教师给予适当的引导和提示。
3.操练(10分钟)学生分组进行练习,教师给出一些运用乘法公式的问题,学生通过合作交流,共同解决问题。
4.巩固(5分钟)教师挑选一些学生解决的实际问题,让学生上台进行讲解,以此巩固乘法公式的运用。
5.拓展(5分钟)教师提出一些拓展问题,引导学生深入思考,提高他们解决问题的能力。
乘法公式教案

1.教学设计学科名称乘法公式(人教版八年级数学上册第15章)2.所在班级情况,学生特点分析学情分析:学生已有七年级上册所学习数的运算、字母表示数、合并同类项、去括号等内容,通过类比他们会产生“式是否也有相应的运算,如果有的话该怎样进行”等问题.为此本节课关注学生对公式的探索过程,有意识的培养学生的推理能力,让学生经历“特例→归纳→猜想→符号表示”的知识发生过程,并有条理地表达自己的思考过程,培养学生的数感和符号感,真正理解公式的来源、本质和应用。
3.教学内容分析本节课关注学生对公式的探索过程,有意识的培养学生的推理能力,鼓励学生经历根据特例进行归纳、建立猜想、用符号表示,有条理地表达自己的思考过程,培养学生的数感和符号感,真正理解公式的来源、本质和应用,为今后的学习打下坚实的基础.4.教学目标⑴.经历探索平方差公式的过程,进一步发展符号感和推理能力。
⑵.会推导平方差公式,并能运用公式进行简单计算。
⑶.认识平方差及其几何背景,使学生明白数形结合的思想。
⑷.在合作、交流和讨论中发掘知识,并体验学习的乐趣。
⑸.培养学生灵活运用知识、勇于探求科学规律的意识。
5.教学重、难点分析教学重点:体会公式的发现和推导过程,理解公式的本质,并会运用公式进行简单的计算。
教学难点:从广泛意义上理解公式中的字母含义,具体问题要具体分析,会运用公式进行计算。
6.教学课时:1课时7.教学过程一、创设问题情境,引导学生观察、设想。
教师发给每个学生一张正方形纸片(边长15cm),并用多媒体课件与正方形纸板显示正方形。
师:在一块45cm的正方形纸板上,因为工作的需要,中间挖去一块边长为15cm的正方形(如图),请问剩下部分的面积有多少平方厘米?师:计算剩下部分的面积可以有哪些方法?小组讨论:1.可以用大正方形面积减去小正方形面积得到。
2.可以把剩下的部分切割成几个矩形来计算。
师:从今天的问题来看,用哪一种方法比较好?你们小组能列出算式吗?或许有学生能迅速列出算式,得出答案是1800平方厘米。
高中数学乘法公式定律教案

高中数学乘法公式定律教案
教学目标:通过本节课的学习,学生应能够掌握常用的乘法公式及其运用,提高解决问题
的能力。
教学内容:
1. 乘法交换律:a * b = b * a
2. 乘法结合律:(a * b) * c = a * (b * c)
3. 乘法分配律:a * (b + c) = a * b + a * c
教学步骤:
1. 导入:通过一个简单的例子引入乘法公式定律的概念,让学生了解为什么需要掌握这些
定律。
2. 讲解:逐一介绍乘法交换律、乘法结合律和乘法分配律的概念,并给出示例进行解释。
3. 练习:让学生通过练习题巩固所学内容,帮助他们熟练掌握乘法公式定律的运用。
4. 拓展:引导学生思考更复杂的情况下如何应用乘法公式定律,帮助他们扩展解决问题的
能力。
5. 总结:对本节课学习的内容进行总结,让学生回顾所学的知识点。
教学资源:
1. 课件:包含乘法公式定律的概念解释及示例
2. 练习题:提供一些练习题,帮助学生巩固所学内容
3. 黑板和粉笔:用于讲解和演示
教学评估:
1. 课堂练习:观察学生在练习题上的解答情况,检验他们对乘法公式定律的理解程度。
2. 课堂表现:通过学生的问题讨论和回答,评估他们对乘法公式定律的理解和应用能力。
教学反思:
通过本节课的教学,我发现学生对乘法公式定律的理解需要进一步加强。
在以后的教学中,我将更多地注重实际问题的应用,帮助学生更好地掌握乘法公式定律并提高解决问题的能力。
高一乘法公式运用讲解教案

高一乘法公式运用讲解教案一、教学目标。
1. 知识目标。
(1)掌握乘法的基本概念和运算方法;(2)掌握乘法的运算规则和乘法公式;(3)能够灵活运用乘法公式解决实际问题。
2. 能力目标。
(1)培养学生的逻辑思维能力和数学计算能力;(2)培养学生的实际问题解决能力;(3)激发学生对数学学科的兴趣和热爱。
3. 情感目标。
(1)培养学生的合作意识和团队精神;(2)培养学生的自信心和自学能力;(3)培养学生的探究精神和创新意识。
二、教学重点与难点。
1. 教学重点。
(1)乘法的基本概念和运算方法;(2)乘法的运算规则和乘法公式;(3)乘法公式的灵活运用。
2. 教学难点。
(1)乘法公式的运用;(2)实际问题的解决。
三、教学过程。
1. 导入新课。
通过一个简单的例子引入乘法公式的概念,让学生了解乘法的基本概念和运算方法。
2. 概念讲解。
通过教师讲解和示范,让学生掌握乘法的运算规则和乘法公式,并进行相关练习。
3. 拓展练习。
让学生进行一些拓展练习,提高他们的运算能力和解决问题的能力。
4. 实际问题解决。
通过一些实际问题的解决,让学生灵活运用乘法公式,培养他们的实际问题解决能力。
5. 总结归纳。
让学生总结归纳乘法公式的运用方法,加深他们对乘法公式的理解和掌握。
四、教学方法。
1. 示范教学法。
通过教师的示范和讲解,让学生掌握乘法的基本概念和运算方法。
2. 合作学习法。
让学生进行合作学习,提高他们的合作意识和团队精神。
3. 情景教学法。
通过一些实际问题的解决,让学生在情景中灵活运用乘法公式,培养他们的实际问题解决能力。
五、教学工具。
1. 教学课件。
通过教学课件展示乘法公式的相关知识点和运用方法,提高教学效果。
2. 教学实物。
通过一些教学实物,让学生在实际中感受乘法的运算规则和乘法公式的运用。
3. 教学练习册。
通过一些教学练习册,让学生进行相关练习,提高他们的运算能力和解决问题的能力。
六、教学反思。
通过本节课的教学,学生对乘法公式的理解和掌握程度有了明显提高,学生的运算能力和解决问题的能力也得到了提高。
乘法公式的复习教案

乘法公式的复习(1)光明初级中学 杜颜教学目标1.通过学生自主练习以及教师点拨,进一步理解平方差公式和完全平方公式。
2.能够正确、熟练地运用公式。
3.在练习过程中体会数学的“整体”思想和“化归”思想。
教学重点能够正确、熟练地运用公式。
在练习过程中体会数学的“整体”思想和“化归”思想。
教学难点在练习过程中体会数学的“整体”思想和“化归”思想。
教学过程一、引入(上节课,我们已经复习了多项式乘以多项式的运算,那么现在我们来做一组练习。
)练习1计算: (32)(23)a b a b +- (32)(32)a b a b +-(2)(3)a b a b -- (2)(2)a b a b --公式,在适合的情况下使用乘法公式可以使计算得以简化。
(板书课题)二、复习公式结构练习2计算:① 11()()22a b a b +- ② 2(30.1)m n + ③ ()()x y x y ++ ④ 22(2)x y -(板书公式,分析结构。
)三、应用与巩固练习3计算:① 11()()22a b a b -+- ② (44)()a b a b +- 总结:如果遇到不能直接使用乘法公式的情况,可以尝试进行转化。
练习4计算:① 11()()22a b a b --- ② 21()2a b -+ ③ 11()()22a b b a -++ ④ 21()2a b -- 总结:善于使用“整体思想”考虑问题可以更快的实现“转化”目标。
四、巩固与提高练习5计算:(说说你的解题思路。
)① 2()a b c ++ ② 2)32(z y x +- ③ ()()b c a a b c ++--- ④ ))((z y x z y x -+++⑤ )14)(14(+--+y x y x ⑥ )32)(32(d b y x d b y x -+++-+总结:对于两项以上的多项式乘法再应该重视“整体思想”的应用,体会化归思想。
五、课堂小结(多项式乘法的一般步骤流程图)六、即时检测(课后练习)计算: ① ()()x a x b ++; (2)(3)x x +-; 11()()23ab ab --;② 1212()()m n m n a b a b -+-++-;③ 2323(0.50.2)(0.50.2)a b a b ---; 2323(0.50.2)(0.50.2)a b a b -+-;④ ()()x y z x y z +----; (321)(312)x y x y +-+-;()()b c a a b c +---;⑤ 2()a b c d +++; ()()a b c d a b c d -+-++--;⑥ 19961998199719972⨯-课堂操作单班级 学号 姓名 练习1计算: (32)(23)a b a b +- (32)(32)a b a b +-(2)(3)a b a b -- (2)(2)a b a b --练习2计算:① 11()()22a b a b +- ②2(30.1)m n + ③ ()()x y x y ++④ 22(2)x y -练习3计算:① 11()()22a b a b -+- ②(44)()a b a b +-练习4计算:① 11()()22a b a b ---② 21()2a b -+③ 11()()22a b b a -++ ④ 21()2a b --练习5计算:(说说你的解题思路。
苏科版七下《乘法公式》word教案4篇
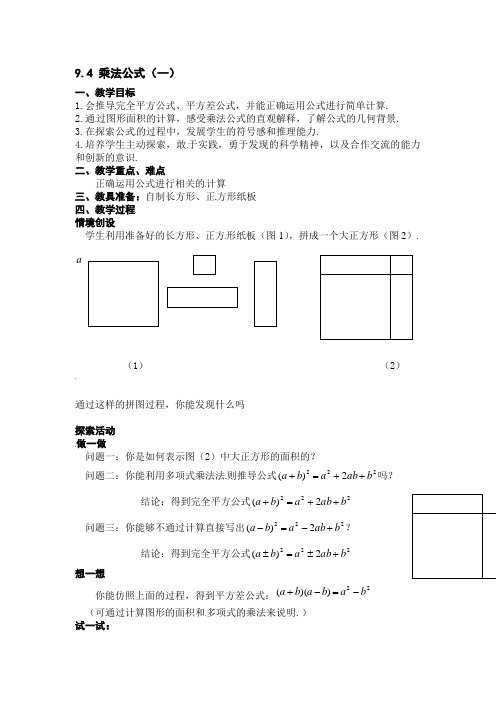
9.4 乘法公式(一)一、教学目标1.会推导完全平方公式、平方差公式,并能正确运用公式进行简单计算.2.通过图形面积的计算,感受乘法公式的直观解释,了解公式的几何背景.3.在探索公式的过程中,发展学生的符号感和推理能力.4.培养学生主动探索,敢于实践,勇于发现的科学精神,以及合作交流的能力和创新的意识.二、教学重点、难点正确运用公式进行相关的计算三、教具准备:自制长方形、正方形纸板 四、教学过程 情境创设学生利用准备好的长方形、正方形纸板(图1),拼成一个大正方形(图2). a(1) (2)通过这样的拼图过程,你能发现什么吗探索活动 做一做问题一:你是如何表示图(2)中大正方形的面积的?问题二:你能利用多项式乘法法则推导公式2222)(b ab a b a ++=+吗?结论:得到完全平方公式2222)(b ab a b a ++=+问题三:你能够不通过计算直接写出2222)(b ab a b a +-=-?结论:得到完全平方公式2222)(b ab a b a +±=±想一想你能仿照上面的过程,得到平方差公式:22))((b a b a b a -=-+(可通过计算图形的面积和多项式的乘法来说明.)试一试:1.计算(1)2)2(+x (2)2)2(-x (3))2)(2(-+x x (4)2)52(+a (5)2)52(--a 练一练(1)))()((22y x y x y x ++- (2)1)12)(12)(12)(12(842+++++ 3.计算(1)21.10 (2)2999练一练(1)98102⨯ (2)19952005⨯ 小结(1) 分别说出完全平方公式、平方差公式的特征(2) 在式子bd ad bc ac d c b a +++=++))((中当a 、b 、c 、d 满足什么关系时,由它可得到乘法公式?作业:P80练一练1、2、3、49.4 乘法公式课 题:9.4 乘法公式(第1课时) 课 型:新授型教学目标:(1) 探索并推导完全平方公式、平方差公式,并能运用公式进行简单的计算; (2) 引导学生感受转化的数学思想以及知识间的内在联系. 教学重点:完全平方公式;平方差公式教学难点:正确的应用完全平方公式、平方差公式进行计算 教学方法:探索、引导法b a教具准备:三角尺、投影仪 a 教学设想:−→−一. 情景创设 b如右图:你能通过不同的方法计算大正方形的面积吗? 从而你发现了什么? 二. 探索活动问题一:如何用字母表示上图中大正方形的面积? 生: 将上图看成一个大正方形,则面积为 2)(b a +.师:很好,还有没有其它的方法呢?生:可将上图看成是由两个小长方形和两个小正方形组成的图形,那么它的面积为2a2babab222b ab a ++.师:两种方法都求出了大正方形的面积,从而我们可以发现什么呢? 生:2)(b a +=222b ab a ++ 这个公式就叫做一个完全平方公式.问题二:你能用多项式的乘法法则推导公式2)(b a +=222b ab a ++吗? 生:2)(b a +=))((b a b a ++=22b ba ab a +++=222b ab a ++ 师:很好,你能用同样的方法计算2)(b a -吗?生:222222))(()(b ab a b ba ab a b a b a b a +-=---=--=- 即:2222)(b ab a b a +-=-,这是我们要学习的另一个完全平方公式. 完全平方公式:2)(b a +222b ab a ++=2222)(b ab a b a +-=-师:你能用文字语言叙述这两个公式吗?问题三:你能仿照上面的过程,完成对平方差公式的推导吗? 引导学生完成“试一试”中的平方差公式的推导. 平方差公式:22))((b a b a b a -=-+问题四:你知道乘法公式中的字母都可以代表什么吗?可分小组进行讨论,然后选一名代表回答.师再评议.三. 例题教学例 利用完全平方公式或平方差公式计算: ⑴2)2(+x ⑵)2)(2(-+x x ⑶2)(b a - ⑷2998⑸998102⨯ 解:略练一练:80p 1,2,3,4题四. 想一想⑴ 观察完全平方公式、平方差公式有什么特征?⑵在式子))((d c b a ++bd ad bc ac +++=中,当d c b a ,,,满足什么条件时,由它能得到完全平方公式,满足什么条件时能得到平方差公式?五. 小结这一节课你学到了什么?让学生试着小结,师再评议.六. 作业布置:1.8382-p 1,2,32.补充:.用乘法公式计算:(1)21001 (2) )3)(3(x x -+ (3)2)3(a - (4)10892⨯ 板书设计乘法公式(一)1.完全平方公式 : 3.例题教学2.平方差公式: 4.小结: 八.教后记:9.4乘法公式(2)课 题:9.4乘法公式(2)教学目标:通过图形面积的计算,感受乘法公式的直观解释. 教学重点:乘法公式的运用. 教学难点:灵活运用乘法公式 教学过程设想一.复习提问:叙述乘法公式的内容:2)(b a +=2a +2ab+2b2)(b a -=2a -2ab+2b(a+b )(a-b)=2a -2b学生回答,师板书. 二.情境创设让学生画一个正方形,再在其边上取3条线段c b a ,,,根据此图求是多少? 生:把)(b a +作为整体,得2)(c b a ++[]2)(c b a ++=把)(c a +作为整体,得2)(c b a ++[]2)(b c a ++=把)(c b +作为整体,得2)(c b a ++[]2)(c b a ++=三.学习例2.用乘法公式计算: ⑴2)35(p +⑵2)72(y x - ⑶2)52(--a ⑷)5)(5(b a b a -+直接用公式进行计算和上面公式进行对照和哪一个相似?a b cb第⑶题让学生先比较2)52(--a 与2)52(+a 的异同,并判断它们的值是否相等? 练一练 P.82.1. 学生板演,师小结. 四.学习例⒊计算:⑴)9)(3)(3(2++-x x x ⑵22)32()32(-+x x ⑶)4)(4(++-+y x y x思考:(1)如果先将第一、三项先乘进行比较,哪一种简便?(2)可否先运用完全平方公式再先乘,和例题进行比较哪一种简便?练一练 P.82.2 .3 .4 . 学生板演,师小结. 五.思维拓展回到开头,你能计算2)(c b a ++? 学生回答,师板书 六.巩固提高观察下式,你会发现什么规律? 3⨯5=15 而15=24-15⨯7=35 而35=26-1 …11⨯13=143 而143=212-1…请你将猜想到的规律用只含一个字母的式子表示出来.板书设计:2)(b a +=2a +2ab+2b 2)(c b a ++=2a +2b +2c +2ab+2bc+2ac 2)(b a -=2a -2ab+2b 例题2(a+b)(a-b)=2a -2b 例题39.4 乘法公式(二)一、教学目标:1.通过拼图探索计算2)(c b a ++的公式,并推导这个公式.2.进一步巩固完全平方公式和平方差公式,并会用乘法公式化简某些代数式. 二、教学重、难点: 如何灵活运用乘法公式 三、教学过程: 情境创设请同学们用准备好了的正方形和长方形纸板拼图,拼成如图所示的大正方形.问:通过这样的拼图过程,你能发现什么吗? 探索活动 做一做问题一:你是如何表示图中大正方形的面积的问题二:你能用2222)(b ab a b a ++=+推导2)(c b a ++吗? 结论:得到公式ca bc ab c b a c b a 222)(2222+++++=++小试牛刀计算(1)2)432(c b a ++ (2)2)23(z y x --例题教学 例1. 计算(1)2)35(p + (2)2)72(y x - (3))9)(3)(3(2++-x x x (4)22)32()32(+-x x (5))4)(4(++-+y x y x 练一练(1)22)10()10(+-x x (2)))((2222n mn m n mn m +-++(3)22)33()33(--+aa (4))3)(3()3(2y x y x y x +--+例2. 若,4,922-==+xy y x 求(1)2)(y x + (1)2)(y x -例3. 求代数式)(5)3()2(22n m m n m n m -+--+的值,其中51,101==n m . 小结(3) 说说完全平方公式、平方差公式的特征(4) 把b a +看成""x ,就可以用完全平方公式计算2)(c b a ++,运用这种转化的思想,你能计算3)(b a +、4)(b a +吗?作业P82习题9.4第1,4(2)、(4)、(6),6题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题:乘法公式(复习课)
教学目的:灵活运用乘法公式解题
重点难点:乘法公式的综合,灵活应用
教学过程:
一、知识点的回顾:
1、 平方差公式2
2))((b a b a b a -=-+
即:两个数的和与这两个数的差的乘积等于这两个数的平方数
2、 完全平方公式2222)(b ab a b a ++=+
2222)(b ab a b a +-=-
即:两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的两倍。
二、小试牛刀:
(一) 填空题:
1、=---))((y x y x
2、-+2)(b a 2)(b a -=
3、=+-
)3221)(2132(n n n n x y y x 4、如果162++mx x 是一个完全平方式,那么m=
(二)选择题:
1、下列各式中能用平方差公式计算的是 ( )
A 、(p+q )(-p-q )
B 、(p-q )(q -p )
C 、(5x+3y )(3y-5x )
D 、(2a+3b )(3a-2b )
2、))((2
2x y y x ++-再乘以一多项式得44y x -,则这个多项式是 ( ) A 、x-y B 、x+y C 、-x+y D 、-x-y
(三)计算:
1、22)2()2(b a b a +-
说明:n n b a b a •=•2)(的逆用
2、99810029992
⨯-(不用计算器)
分析:1002、998都与1000相差2,可以考虑用平方差公式
3、1)12)(12)(12)(12(842-++++
分析:1=2-1
(四)实际应用:
1、如图,一个长方形水池四周是分别以长方形ABCD 边长为边的四块正方形草地。
长方形
ABCD 的周长为16m ,四个正方形的面积和为68㎡,求长方形ABCD 的面积。
2、已知三角形ABC 的三边长a ,b ,c 满足条件2
222)()(3c b a c b a ++=++ , 试判断三角形ABC 是何种三角形,并说明理由。
三、小结:
1、平方差公式与完全平方公式不要混淆应用
2、注意公式的逆应用,如:n n n b a b a )(•=• ))((22b a b a b a -+=-
3、 关注知识的综合应用
三、布置作业:
(一) 填空
1、=++-))()((2
2b a b a b a
2、=-+--))((c b a b c a
3、=+++)15)(15)(15(42
(二)选择题
1、与)7(2y x -的积等于2449x y -的因式是 ( ) A 、)7(2y x - B 、)7(2
y x +
C 、)7(2y x --
D 、)7(2x y - 2、若7=+b a ,12=ab ,则22b ab a ++的值是 ( )
A 、61
B 、37
C 、13
D 、11
(三)已知a y x =+2)(、b y x =-2)(
求:22y x +、xy 的值
(四)三个连续整数之和等于它们的积,你能求出这三个整数吗?试试看。
