第三章 事故树计算题
事故树顶上事件发生概率公式含义及例题

上事件不发T生。
• 由最小径集定义可知,只要k个最小径集 中有一个不发生,顶事件就不会发生, 则:
k
T Dr
r 1
k
1 P(T ) P Dr r1
qi
qi L (1)k1
qi
r 1 xiEr
U 1rsk xiEr Es
r 1
U U U xiE1 E2 E3L Ek
• 式中:r、s、k—最小割集的序号,r<s<k;
i — 基本事件的序号,
1≤r<s≤k—k个最小割集中第r、s两个割集的组合 顺序;
xi Er—属于第r个最小割集的第i个基本事件;
X3
X4
2
P(T ) 1 (1 PEi ) 1 (1 PE1) (1 PE2 ) i 1
2
3
1 (1 qi ) (1 qi )
i 1
i 1
1 (1 q1q2 ) (1 q2q3q4 )
P(T ) 1 (1 0.50.2) (1 0.20.50.5) 0.145
r 1 xiPr
1rsk xiPr UPs
r 1 xiP1UP2 UP3L UPk
•公式中的第二项 “减去各最小径集P实现的概率的和”(将 各最小径集中的基本事件不发生的概率积 相加);但有重 复计算的情况,因此,
•在第二项中 “加上每两个最小径集同时实现的概率”(将 每两个最小径集并集中的各基本事件不发生的概率积 相 加);还有重复计算的情况,
U 1rsk xiEr Es
r 1
U U U xiE1 E2 E3L Ek
安全系统工程计算题总结
各基本事件概率分别为: 求各基本事件概率重要度系数。 解:用近似方法计算顶事件发生概率
各个基本事件的概率重要度系数近似为
四、基本事件的重要度分析
上面例子已得到的某事故树顶上事件概率为0.002,各基本事件的 概率重要度系数分别为:
则各基本事件的临界重要度系数为:
(3)求顶上事件的发生概率: g = qT = 1-(1-qA1)(1-q1) = 1-(1-0.04261)(1-0.01)= 0.05218
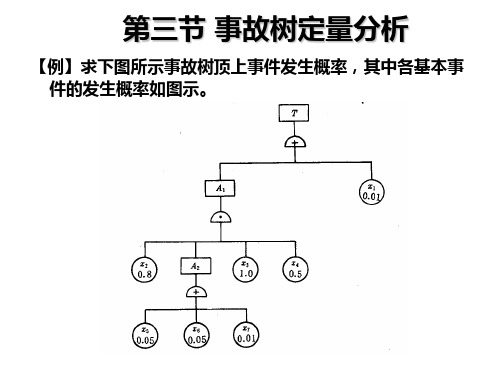
第三节 事故树定量分析
2)最小割集间有重复基本事件
若各个最小割集间有重复基本事件,则上述公式 不成立。 • 例如,某事故树有3个最小割集:E1={x1,x3}, E2={x2,x3},E3={x3,x4},则顶上事件的发生概 率等于各个最小割集的概率和,即
第三节 事故树定量分析
【例】求下图所示事故树顶上事件发生概率,其中各基本事
件的发生概率如图示。
第三节 事故树定量分析
(1)求A2的概率:
qA2 = 1-(1-q5)(1-q6)(1-q7) = 1-(1-0.05)(1-0.05)(1-0.01) = 0.106525
(2)求A1的概率:
qA1=q2 qA2q3ቤተ መጻሕፍቲ ባይዱ4 = 0.8×0.106525×1×0.5 = 0.04261
• 解:由直接分步计算公式,顶上事件的发生概率为 •
3
g qi r 1 xipr [(1 (1 q1)(1 q4 )][(1 (1 q2 )(1 q3)] [(1 (1 q5 )(1 q6 )] [1 (1 0.1)(1 0.4)][1 (1 0.2)(1 0.03)][1 (1 0.05)(1 0.16)]
第三节 事故树定量分析
事故树顶上事件发生概率公式含义及例题

q1=0.01; q2=0.02; q3=0.03; q4=0.04; q5=0.05
求顶上事件发生概率?
k
k
P(T)
qi
qi L (1)k1
qi
r 1 xiEr
•在第三项 “减去每三个最小径集同时实现的概率” (将每 三个最小径集并集的基本事件不发生的概率积 相加) ;
•以此类推,加减号交替,直到最后一项 “计算所有最小径 集同时实现的概率”
例如:某事故树共有4个最小径集,
P1={X1,X3 }, P2={X1,X5 }, P3={X3,X4}, P3={ X2, X4,X5} 已知各基本事件发生的概率为:
• 一般当各qi不等时,改变qi大的Xi较容易, 但概率重要度系数并未反映qi变化
• 考虑从本质上反映Xi在FT中的重要程度。
• 关键重要度分析,它表示第i个基本事件 发生概率的变化率引起顶事件概率的变 化率;
• 相比概率重要度关键重要度,更合理更 具有实际意义。
• 基本事件的关键重要度:
I
在第二项中 “减去每两个最小割集同时发生的概率”(将每两 个最小割集并集的基本事件的概率积 相加);还有重复计算 的情况,
在第三项 “加上每三个最小割集同时发生的概率” (将每三 个最小割集并集的基本事件的概率积 相加) ;
以此类推,加减号交替,直到最后一项 “计算所有最小割集同 时发生的概率”
例如:某事故树共有3个最小割集:试用 最小割集法计算顶事件的发生的概率。
U 1rsk xiEr Es
r 1
U U U xiE1 E2 E3L Ek
安全评价师事故树考试题

商业建筑发生特大火灾的原因是自动喷淋系统失效和火灾扑救不及时。
火灾扑救不及时是因为灭火器材失效或发现火灾不及时。
灭火器材失效的原因是消防器材失效和人员操作失败。
发现火灾不及时是因为报警系统失效和人员发现不及时。
人员发现不及时是因为值班人员失职,或值班人员未及时发现和火灾位置隐蔽。
要求1)确定顶上事件并画出事故树2)化简求最小割集和最小径集3)求顶上事件发生概率4)进行结构重要度、概率重要度、临界重要度分析5)最小径集和割集在预防控制事故方面的作用。
1、绘制事故树2、最小割集与最小径集的计算:T=B1*B2=(C1+C2)*B2=(X1*D+X5*X6)*B2=(X1*(X2+X3+X4)+X5*X6)*X7=X1*X2*X7+X1*X3*X7+X1*X4*X7+X5*X6*X7所以,该事故树最小割集为:K1={ X1, X2, X7} K2= {X1, X3, X7}K3= {X1, X4, X7} K4= {X5, X6, X7}最小径集:T ' = (X1' +X2‘ +X7) (X1' +X3‘ +X7) (X1' +X4‘ +X7)(X5‘ +X6 +X7‘)= X1' * X5‘+ X1' * X6‘+ X2‘* X3‘*X4' * X5‘ + X2' * X3‘*X4' * X6 ' + X7'用最小径集表示:T= (X1+X5 (X1+X6 (X2+X3+X4+X5 (X2+X3+X4+X6 X7所以最小径集为:{X1, X5} {X1, X6} {X2, X3, X4, X5} {X2, X3, X4, X6} {X7}3、顶上事故发生的概率为:P=1-(1-k1q)(1-k2q)(1-k3q)(1-k4q)=0.0004354、1)结构重要度计算:X i的结构重要度表达式: 1I (i)八2丄1 3 11 11 111 (1) = 23J X 3=4 I ⑵=23J =4 I (3) = 23」=4 " (4) = 23」匕1 1 1 1 11(5)=237=4 1 (6)=尹=7 1 (7)=尹X 4=1所以结构重要度的顺序为:I ⑺ > I (1) > I (2) = I (3) = I (4) = I -.(5) = I (6)2)概率重要度分析:基本事件的概率重要度:I g(i)=飞%3)临界重要度分析:临界重要度与概率重要系数的关系:。
安全评价师事故树考试题汇总

商业建筑发生特大火灾的原因是自动喷淋系统失效和火灾扑救不及时。
火灾扑救不及时是因为灭火器材失效或发现火灾不及时。
灭火器材失效的原因是消防器材失效和人员操作失败。
发现火灾不及时是因为报警系统失效和人员发现不及时。
人员发现不及时是因为值班人员失职,或值班人员未及时发现和火灾位置隐蔽。
要求1)确定顶上事件并画出事故树2)化简求最小割集和最小径集3)求顶上事件发生概率4)进行结构重要度、概率重要度、临界重要度分析。
5)最小径集和割集在预防控制事故方面的作用。
1、绘制事故树值班人员未发现商业建筑特大火灾事故自动喷淋系统失效火灾扑救不及时=发现火灾不及时灭火器材失效报警系统失效人员发现不及时无值班人员局部火灾屏蔽手提式干粉灭火器失效消防栓失效2、最小割集与最小径集的计算:T=B1*B2=(C1+C2)*B2=(X1*D+X5*X6)*B2=(X1*(X2+X3+X4)+X5*X6)*X7=X1*X2*X7+X1*X3*X7+X1*X4*X7+X5*X6*X7所以,该事故树最小割集为:K1={X1,X2,X7} K2={X1,X3,X7}K3={X1,X4,X7} K4={X5,X6,X7}最小径集:T ’=(X1’+X2’+X7’)(X1’+X3’+X7’)(X1’+X4’+X7’) (X5’+X6’+X7’)= X1’* X5’+ X1’* X6’+ X2’* X3’*X4’* X5’+ X2’* X3’*X4’* X6’+ X7’用最小径集表示:T=(X1+X5)(X1+X6)(X2+X3+X4+X5)(X2+X3+X4+X6)X7 所以最小径集为:{X1,X5}、{X1,X6}、{X2,X3,X4,X5}、{X2,X3,X4,X6}、{X7}3、顶上事故发生的概率为:P=1-(1-k1q)(1-k2q)(1-k3q)(1-k4q)=0.0004354、1)结构重要度计算:X i 的结构重要度表达式:∑-=121)(n i I φ)1(φI =1321-×3=43 )2(φI =1321-=41 )3(φI =1321-=41 )4(φI =1321-=41 )5(φI =1321-=41 )6(φI =1321-=41 )7(φI =1321-×4=1 所以结构重要度的顺序为:)7(φI >)1(φI >)2(φI =)3(φI =)4(φI =)5(φI =)6(φI2)概率重要度分析:基本事件的概率重要度:iq g g i I δδ=)( 3)临界重要度分析:临界重要度与概率重要系数的关系:)()(i I gq i CI g i g = 5、最小割集和最小径集在预防和控制顶项事故的作用能够引起顶项事故发生的最低限度的基本事件的集合,称为最小割集。
安全系统工程计算题总结

q1q2q3
率积中的重复事件。
并事件的概率公式来计算。
1
2
3
1
【例】某事故树有3个最小径集:P1={x1,x4}, P2={x2,x3},P3={x5,x6}。各基本事件的发生概率分 别为:q1=0.1,q2=0.2,q3=0.03,q4=0.4, q5=0.05,q6=0.16,求顶上事件的发生概率。
第三节 事故3 树
定量分析 g
qi
r 1 xipr
2
[(1 (1 q1)(1 q4 )解]:[(1由直(1接分q步2 )计(1算公q3式)], [顶(1上事(1件的q发5 )生(1概率q6为)]
[1 (1 0.1)(1 0.4)][1 (1 0.2)(1 0.03)] [1 (1 0.05)(1 0.16)]
3
g qkr
r 1
1 (1 qk1)(1 qk 2 )(1 qk 3 )
(q q q ) (q q q q q q ) q q q k1
k 2 式 中k 3, q k 1 , q k 2k是1最 小k 割2
集K1,K2交集的概率,
k所1
以
,k 3当
最
小
割k集2中
k
有
3重
k1 k 2 k3
0.02081408
第三节 事故 树定量分析
二.最小径集间有重复基本事件
若各个最小径集间有重复基本事件,则用直 接分步计算式不成立。此时,可以根据最小 径集与最小割集的对偶性,由下式计算顶上 事件的发生概率值。
布尔代数运算 定律
定理1: =A (对合律)
定理2:A+B=B+A,AB=BA (交换律)
如右图所示的事故树。已知各基本事件的发生概率
事故树计算题

1、列出顶上事件 发生的概率表达式
2、展开,消除每个概率积中 的重复的概率因子 qi ·qi=qi
3、将各基本事件的概率值带 入,计算顶上事件的发生概率
如果各个最小割集中彼此不存在重复的基本事 件,可省略第2步
最小径集法
• 根据最小径集与最小割集的对偶性,利 用最小径集同样可求出顶事件发生的概 率。
2.但当事故树含有重复出现的基本事件时, 或基本事件可能在几个最小割集中重复 出现时,最小割集之间是相交的,这时, 应按以下几种方法计算。
① 最小割集法
• 事故树可以用其最小割集的等效树来表示。这 时,顶上事件等于最小割集的并集。
•
设某事故树有K个最 Er、…、Ek,则有:
小
割E2
、
…
、
k
T Er
r 1
• 顶上事件发生概率为:
P(T )
P
k
Er
r1
• 化简,顶上事件的发生概率为:
k
k
P(T)
qi
qi L (1)k1
qi
r 1 xiEr
U 1rsk xiEr Es
r 1
U U U xiE1 E2 E3L Ek
• 式中:r、s、k—最小割集的序号,r<s<k;
• 式 2,中…:…qni—)—。第i个基本事件的发生概率(i=1,
例如:某事故树共有2个最小割集: E1={X1,X2}, E2={X2,X3,X4 }。 已知各基本事件发生的概率为:
q1=0.5; q2=0.2; q3=0.5; q4=0.5; 求顶上事件发生概率?
T
+
E1
E2
.
.
X1
X2
X2
安全评价师--事故树

• • • • • •
例:设某事故树有2个最小割集: K1={x1, x2} , K2={x2, x3, x4} 各基本事件发生概率分别为: q1, q2, q3, q4 求顶上事件发生概率。 PA=1-(1-q1q2)(1-q2q3q4)
利用最小径集计算
1、列出顶上事件发生概率的表达式; 2、展开,消除每个概率积中的重复的概率因 子(1-qi) · (1- qi)= (1- qi) 3、将各基本事件的概率值代入,计算顶上事 件的发生概基本原因事件 资料准备:有关生产工艺及设备性能资料,故障率数据 人力、时间:专业人员组成小组,一个小型单元需时一天 效果:可定性及定量,能发现事先未估计到的原因事件
• • • • • •
例:设某事故树有2个最小径集: K1={x1, x2} , K2={x2, x3} 各基本事件发生概率分别为: q1, q2, q3, 求顶上事件发生概率。 PA=(1-(1-q1) (1-q2)) (1- (1-q2) (1-q3))
小结
目的:找出事故发生的基本原因和基本原因组合
事故树定量分析
• 概率计算基本公式(独立事件) • 1、与门的概率 • PA=q1q2……qn
• 2、或门的概率 • P0=1-(1-q1)(1-q2)…… (1-qn)
利用最小割集计算
1、列出顶上事件发生概率的表达式; 2、展开,消除每个概率积中的重复的概率 因子qi · qi= qi 3、将各基本事件的概率值代入,计算顶上 事件的发生概率
事故树定量分析 利用最小割集计算 利用最小径集计算
例:设某事故树有2个最小径集: K1={x1, x2} , K2={x2, x3} 各基本事件发生概率分别为: q1, q2, q3, 求顶上事件发生概率。 PA=(1-(1-q1) (1-q2)) (1- (1-q2) (1-q3))
事故树计算题讲课文档

✓ 基本事件的临界重要度(关键重要度):
IgciIgi
qi P(T)
式中:I
c g
i
——第i个基本事件的临界重要度;
I g i ——第i个基本事件的概率重要度;
P(T) ——顶事件发生的概率;
qi ——第i个基本事件发生概率。
第二十八页,共29页。
例如:某事故树共有2个最小割集:E1={X1,X2}, E2={X2,X3}。已知各基本事件发生的概率为: q1=0.4; q2=0.2; q3=0.3;排列各基本事件的临界重要度,
T .
P1
P2
+
+
X1
X2
X2
X3
第二十一页,共29页。
二、基本事件的概率重要度
• 基本事件的重要度:一个基本事件对顶上事件发生 的影响大小。
• 基本事件的结构重要度分析只是按事故树的结构分析 各基本事件对顶事件的影响程度,所以,还应考虑各 基本事件发生概率对顶事件发生概率的影响,即对事 故树进行概率重要度分析。
k—最小径集数;
(1-qr)—第i个基本事件不发生的概率;
xi pr —属于第r个最小径集的第i个基本事件;
xi pr p—s 属于第r个或第s个最小径集的第i个基本
事件
第十五页,共29页。
k
k
P ( T ) 1 1 q i 1 q i 1 k 1 1 q i
r 1 x i P r
第二十二页,共29页。
✓ 事故树的概率重要度分析是依靠各基本事件的 概率重要度系数大小进行定量分析。所谓概率 重要度分析,它表示第i个基本事件发生的概率的
变化引起顶事件发生概率变化的程度。
✓ 由于顶上事件发生概率函数是n个基本事件发生概 率的多重线性函数, 对自变量qi求一次偏导,即可 得到该基本事件的概率重要度系数。
事故树的定性定量分析

事故树的定性定量分析一、计算题1、某事故树的最小割集为K1={X1,X2,X5};K2={X1,X3,X5};K3={X1,X4,X5},各基本事件的发生概率为q1=q3=q4=0.01,q2=0.1,q5=0.95,求顶上事件发生概率。
2、某事故树的最小割集为K1={X1,X2};K2={X3,X4};K3={X5,X6},各基本事件的发生概率为q1=q2 =0.01,q3=q4=0.02,q5=q6=0.05,求顶上事件发生概率3、某事故树有三个最小径集:P 1={ X1},P 2={ X2,X3},P 3={ X4, X5 ,X6}。
求基本事件的结构重要度。
二、选择题1、某事故树的最小径集为:Pl={Xl,X2,X4},P2={Xl,X2,X5},P3={Xl,X3,X6},P4={Xl,X3,X7},则结构重要程度为()A、I(1)>I(2)=I(3)>I(4)=I(5)B、I(1)>I(2)<I(3)>I(4)=I(5)C、I(1)>I(2)>I(3)<I(4)=I(5)D、I(3)>I(2)<I(1)>I(4)=I(5)三、填空题1、基本事件的概率重要度是指顶上事件发生概率对该基本事件发生概率的()。
2、临界重要度也称(),它是基本事件发生概率的变化率与顶上事件发生概率的变化率的比来确定基本事件的重要程度。
答案:一、1、,本题中最小割集有重复因子,因此需将公式展开后消去重复因子才能带入数据进行计算。
P(T)=q1q2q5+q1q3q5+q1q4q5-(q1q2q3q5+q1q2q4q5+q1q3q4q5)+ q1q2q3q4q5=1.12020 x10-32、本题中最小割集没有重复因子,因此公式不需要展开,直接带数据进行计算。
=1-(1-qK1)·(1-qK2)·(1-qK3)=1-(1-q1q2)(1-q3q4)(1-q5q6)=1.4996x10-3 3、I(1)>I(i) i=2,3 )> I(i)i= 4,5,6二、1、A三、1、变化率;2、危险重要度火力发电厂应当建在哪里我国某大型产煤矿区要建设坑口火力发电厂(p),已知有n 处产煤矿口,并且修建至电厂的运煤轨道的费用与产煤量及距离成正比(W*L ),运用MPA学科中定量分析的方式方法,为坑口火力发电厂选址,要求目标是费用最小。
第三章 事故树计算题

P(T ) qi
r 1 xi Er
k
1 r s k xi Er
qi
Es
(1)k 1
r 1 xi E1
E2 E3 Ek
k
qi
E1={X1,X2, X3 }, E2={X1,X4 } E3={X3,X5}
P(T ) q1q2 q3 q1q4 q3q5 q1q2 q3q4 q1q2 q3q5 q1q3q4 q5 q1q2 q3q4q5 0.001904872
• 由最小径集定义可知,只要k个最小径集 中有一个不发生,顶事件就不会发生, 则:
T Dr
r 1
k
1 P(T ) P Dr r 1
k
• 故顶上事件发生的概率:
P(T ) 1 1 qi
r 1 xi Pr k 1 r s k xi Pr Ps
T Er
r 1
k
• 顶上事件发生概率为:
P(T ) P Er r 1
k
• 化简,顶上事件的发生概率为:
P(T ) qi
r 1 xi Er k 1 r s k xi Er
qi
Es
(1)
k 1 r 1 xi E1
基本事件的临界重要度(关键重要度):
qi I i I g i P(T )
c g
c I 式中:g i ——第i个基本事件的临界重要度;
I g i ——第i个基本事件的概率重要度;
P(T) ——顶事件发生的概率; qi ——第i个基本事件发生概率。
例如:某事故树共有2个最小割集:E1={X1,X2}, E2={X2,X3}。已知各基本事件发生的概率为: q1=0.4; q2=0.2; q3=0.3;排列各基本事件的临界重要度,
起重钢丝绳断裂事故树

2005年6月26安全评价考试题----起重钢丝绳断裂事故树精选文档最小割集计算:T=A1+A2+A3=B1B2+X6X7+X8X9=(X1+X2+X3)(X4+X5)+X6X7+X8X9= X1X4+X1X5+X2X4+X2X5+X3X4+X3X5+X6X7+X8X9则最小割集有8个,即K1={X1,X4};K2={X1,X5};K3={X2,X4};K4={X2,X5};K5={X3,X4};K6={X3,X5};K7={X6,X7};K8={X8,X9}。
最小径集计算:T′=A1′·A2′·A3′=(B1′+B2′)(X6′+X7′)(X8′+X9′)=(X1′X2′X3′+X4′X5′)(X6′+X7′)(X8′+X9′)=(X1′X2′X3′X6′+X1′X2′X3′X7′+X4′X5′X6′+X4′X5′X7′)(X8′+X9′)= X1′X2′X3′X6′X8′+ X1′X2′X3′X6′X9′+ X1′X2′X3′X7′X8′+ X1′X2′X3′X7′X9′+ X4′X5′X6′X8′+ X4′X5′X6′X9′+ X4′X5′X7′X8′+ X4′X5′X7′X9′精选文档则故障树的最小径集为8个,即P1={X1,X2,X3,X6,X8};P2={X1,X2,X3,X6,X9};P3={X1,X2,X3,X7,X8};P4={X1,X2,X3,X7,X9};P5={X4,X5,X6,X8};P6={X4,X5,X6,X9};P7={X4,X5,X7,X8};P8={X4,X5,X7,X9};起重钢丝绳断裂事故发生概率计算:根据最小割集计算顶上事件的概率即g=1-(1-qk1)(1-qk2)(1-qk3)(1-qk4)(1-qk5)(1-qk6)(1-qk7)(1-qk8)=1-(1-q1q4)(1-q1q5)(1-q2q4)(1-q2q5)(1-q3q4)(1-q3q5)(1-q6q7)(1-q8q9)由于q1=q2=q3=q4=q5=q6=q7=q8=q9=0.1精选文档则g=1-(1-0.1×0.1)(1-0.1×0.1)(1-0.1×0.1)(1-0.1×0.1)(1-0.1×0.1)(1-0.1×0.1)(1-0.1×0.1)(1-0.1×0.1)=1-(1-0.1×0.1)8=1-0.998=0.07726一、论述题:(20分)试论述安全评价与安全管理的关系?二、案例分析题:(40分)轮式汽车起重吊车,在吊物时,吊装物坠落伤人是一种经常发生的起重伤人事故,起重钢丝绳断裂是造成吊装物坠落的主要原因,起重钢丝绳断裂与钢丝绳断脱、吊勾冲顶和吊装物超载有直接关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P(T ) 0.116; I g (1) 0.16; I g (2) 0.49; I g (3) 0.12 q1 0.4 I (1) I g (1) 0.16 0.552 P(T ) 0.116 q2 0.2 c I g (2) I g (2) 0.49 0.845 P(T ) 0.116 q3 0.3 c I g (3) I g (1) 0.12 0.310 P(T ) 0.116
• 由最小径集定义可知,只要k个最小径集 中有一个不发生,顶事件就不会发生, 则:
T Dr
r 1
k
1 P(T ) P Dr r 1
k
• 故顶上事件发生的概率:
P(T ) 1 1 qi
r 1 xi Pr k 1 r s k xi Pr Ps
以此类推,加减号交替,直到最后一项 “计算所有最小割集同 时发生的概率”
例如:某事故树共有3个最小割集:试用 最小割集法计算顶事件的发生的概率。 E1={X1,X2, X3 }, E2={X1,X4 } E3={X3,X5} 已知各基本事件发生的概率为: q1=0.01; q2=0.02; q3=0.03; q4=0.04; q5=0.05 求顶上事件发生概率?
I g (2) I g (1) I g (3)
T
+
P1
P2
.
X1 X2 X2
.
X3
四、基本事件的临界重要度(关键重要度) 一般当各 qi不等时,改变 qi大的 Xi较容易, 但概率重要度系数并未反映qi变化。 考虑从本质上反映 Xi 在事故树中的重要 程度。 临界重要度分析,它表示第i个基本事件 发生概率的变化率引起顶事件概率的变 化率; 相比概率重要度,临界重要度更合理更 具有实际意义。
1、列出顶上事件 发生的概率表达式 2、展开,消除每个概率积中 的重复的概率因子 qi ·qi=qi
3、将各基本事件的概率值带 入,计算顶上事件的发生概率 如果各个最小割集中彼此不存在重复的基本事 件,可省略第2步
②最小径集法
• 根据最小径集与最小割集的对偶性,利 用最小径集同样可求出顶事件发生的概 率。 • 设某事故树有 k个最小径集:P1、P2、…、 Pr、…、Pk。用Dr(r=1,2,…,k)表 示最小径集不发生的事件,用 T 表示顶 上事件不发生。
r 1 xi Pr
k
1 r s k xi Pr Ps
1 q
i
1
k 1
r 1 xi P 1 P 2 P 3
k
1 qi
Pk
P1={X1,X3 }, P2={X1,X5 }, P3={X3,X4}, P4={ X2, X4,X5}
P(T ) 1 [(1 q1 )(1 q3 ) (1 q1 )(1 q5 ) (1 q3 )(1 q4 ) (1 q2 )(1 q4 )(1 q5 )] [(1 q1 )(1 q3 )(1 q5 ) (1 q1 )(1 q3 )(1 q4 ) (1 q1 )(1 q2 )(1 q3 )(1 q4 )(1 q5 ) (1 q1 )(1 q5 )(1 q3 )(1 q4 ) (1 q1 )(1 q2 )(1 q4 )(1 q5 ) (1 q2 )(1 q3 )(1 q4 )(1 q5 )] [(1 q1 )(1 q3 )(1 q4 )(1 q5 ) (1 q1 )(1 q2 )(1 q3 )(1 q4 )(1 q5 ) (1 q1 )(1 q2 )(1 q3 )(1 q4 )(1 q5 ) (1 q1 )(1 q2 )(1 q3 )(1 q4 )(1 q5 )] (1 q1 )(1 q2 )(1 q3 )(1 q4 )(1 q5 )
i 1 n
• 式中:qi——第i个基本事件的发生概率(i=1, 2,……n)。
例如:某事故树共有2个最小割集: E1={X1,X2}, E2={X2,X3,X4 }。 已知各基本事件发生的概率为: q1=0.5; q2=0.2; q3=0.5; q4=0.5; 求顶上事件发生概率?
T
+
E1
E2
r 1 xi Er
k
1 r s k xi Er
qi
Es
(1)k 1
r 1 xi E1
E2 E3 Ek
k
qi
公式中的第一项 “求各最小割集E的发生概率的和”(将各最 小割集中的基本事件的概率积 相加);但有重复计算的情况, 因此, 在第二项中 “减去每两个最小割集同时发生的概率”(将每 两个最小割集并集的基本事件的概率积 相加);还有重复计 算的情况, 在第三项 “加上每三个最小割集同时发生的概率” (将每三 个最小割集并集的基本事件的概率积 相加) ;
的变化引起顶事件发生概率变化的程度。
由于顶上事件发生概率函数是n个基本事件发生
概率的多重线性函数, 对自变量qi求一次偏导,
即可得到该基本事件的概率重要度系数。
xi基本事件的概率重要度系数:
P(T ) I g i qi
式中:P(T)——顶事件发生的概率; qi ——第i个基本事件的发生概率。
1 q
i
1
k 1
r 1 xi P 1 P 2 P 3
k
1 qi
Pk
式中:Pr —最小径集(r=1,2,……k); r、s—最小径集的序数,r<s; k—最小径集数; (1-qr)—第i个基本事件不发生的概率; xi p r —属于第r个最小径集的第i个基本事件;
例如:某事故树共有4个最小径集, P1={X1,X3 }, P2={X1,X5 }, P3={X3,X4}, P4={ X2, X4,X5} 已知各基本事件发生的概率为: q1=0.01; q2=0.02; q3=0.03; q4=0.04; q5=0.05 试用最小径集法求顶上事件发生概率?
P(T ) 1 1 qi
☻利用上式求出各基本事件的概率重要度系数, 可确定降低哪个基本事件的概率能迅速有效地 降低顶上事件的发生概率。
例如:某事故树共有2个最小割集:E1={X1,X2}, E2={X2,X3}。已知各基本事件发生的概率为: q1=0.4; q2=0.2; q3=0.3;排列各基本事件的概率重要度,
P (T ) q1q2 q2 q3 q1q2 q3 0.116 P (T ) I g (1) q2 q2 q3 0.16 q1 P (T ) I g (2) q1 q3 q1q3 0.49 q2 P (T ) I g (3) q2 q1q2 0.12 q3
P(T ) qi
r 1 xi Er
k
1 r s k xi Er
qi
Es
(1)k 1
r 1 xi E1
E2 E3 Ek
k
qi
E1={X1,X2, X3 }, E2={X1,X4 } E3={X3,X5}
P(T ) q1q2 q3 q1q4 q3q5 q1q2 q3q4 q1q2 q3q5 q1q3q4 q5 q1q2 q3q4q5 0.001904872
Pk
① 第一项 “减去各最小径集P实现的概率的和”(将各最 小径集中的基本事件不发生的概率积 相加);但有重 复计算的情况,因此, ② 第二项 “加上每两个最小径集同时实现的概率”(将每 两个最小径集并集中的各基本事件不发生的概率积 相 加);还有重复计算的情况, ③ 第三项 “减去每三个最小径集同时实现的概率” (将 每三个最小径集并集的基本事件不发生的概率积 相 加) ; 以此类推,加减号交替,直到最后一项 “计算所有最小径 集同时实现的概率”
E2 E3 Ek
k
qi
• 式中:r、s、k—最小割集的序号,r<s<k;
i — 基本事件的序号, 1≤r<s≤k—k个最小割集中第r、s两个割集的组合 顺序;
xi Er—属于第r个最小割集的第i个基本事件;
xi Er Es
—属于第r个或第s个最小割集的第i个基
本事件。
P(T ) qi
xi pr ps —属于第r个或第s个最小径集的第i个 基本事件
P(T ) 1 1 qi
r 1 xi Pr
k
1 r s k xi Pr Ps
1 q
i
1
k 1
r 1 xi P 1 P 2 P 3
k
1 qi
2.但当事故树含有重复出现的基本事件时, 或基本事件可能在几个最小割集中重复 出现时,最小割集之间是相交的,这时, 应按以下几种方法计算。
① 最小割集法 • 事故树可以用其最小割集的等效树来表示。这 时,顶上事件等于最小割集的并集。 • 设某事故树有 K 个最小割集: E1 、 E2 、 … 、 Er、…、Ek,则有:
0.001904872
1、列出定上事件 发生的概率表达式 2、展开,消除每个概率积中的重 复的概率因子 (1-qi )·(1-qi)=1-qi
3、将各基本事件的概率值带 入,计算顶上事件的发生概率 如果各个最小径集中彼此不存在重复的基本事 件,可省略第2步
二、基本事件的概率重要度
• 基本事件的重要度:一个基本事件对顶上事件发
P(T ) 1 (1 0.5 0.2) (1 0.2 0.5 0.5) 0.145
P(T ) 1 (1 q1q2 q2 q3q4 q1q2 q2 q3q4 ) q1q2 q2 q3q4 q1q2 q3q4 0.5 0.2 0.2 0.5 0.5 0.2 0.5 0.5 0.5 0.125
