20秋启东作业九年级数学上(BS)作业55

合集下载

20秋启东作业九年级数学上(BS)作业44

第10题(1)
‹#›
返回目录
(2)填空：△AC′D′是等__腰__直__角__三角形．
第10题(2)
‹#›
返回目录
11．(2018·凉山州)如图，△ABC 在网格中．
第11题
图放大
‹#›
返回目录
第11题
图还原
‹#›
返回目录
(1)请在网格中建立平面直角坐标系，使 A(2， 3)，C(6，2)，并写出点 B 的坐标；
A．(2m，2n) B．(2m，2n)或(－2m，－2n)
C．12m，12n D．12m，12n或－12m，－12n
第7题
‹#›
返回目录
8．如图，每个小方格都是边长为 1 的小正方形，若△ABC 与△A1B1C1 是位似图形，且顶点都在小正方形顶点上，则它们的位似中心的坐标是__(9_，__0_)__．
图放大
‹#›
返回目录
第2题
图还原
‹#›
返回目录
3．(2018·锦州)如图，在平面直角坐标系中，每个小方格都是边长为 1 个单位长度的正方形，已知 △AOB 与△A1OB1 位似，位似中心为原点 O，且相似比为 3∶2，点 A，B 都在格点上，则点 B1 的坐标为___－__2_，__－__32_ _．
第3题
图放大
‹#›
返回目录
第3题
图还原
‹#›
返回目录
4．(2019·百色)如图，△ABC 与△A′B′C′是以坐标原点 O 为位似中心的位似图形，若点 A(2， 2)，B(3，4)，C(6，1)，B′(6，8)，则△A′B′C′ 的面积为__1_8_____．
第4题
图放大
‹#›
返回目录

20秋启东作业九年级数学上(BS)作业21

第11题(4)
‹#›
返回目录
12．(9 分)(2018·玉林)已知关于 x 的一元二次方程 x2－2x－k－2＝0 有两个不相等的实数根．
(1)求 k 的取值范围；解：∵方程 x2－2x－k－2＝0 有两个不相等的实数根，
∴Δ＝b2－4ac＝4－4(－k－2)＝12＋4k＞0，
解得 k＞－3.
‹#›
返回目录
综上所述，经过(5－ 2)s，5 s，(5＋ 2)s，△PBQ 的面积为 1 cm2.
第14题(3)
‹#›
返回目录
A．300(1＋x)＝507 B．300(1＋x)2＝507 C．300(1＋x)＋300(1＋x)2＝507 D．300＋300(1＋x)＋300(1＋x)2＝507
第5题
‹#›
返回目录
6．(2019·杭州期中)在一元二次方程 ax2＋bx＋1 ＝0 中，若系数 a，b 可以在 0，1，2，3 中取值，则其中有实数根的方程共有___3_____个，写出其中有两个相等实数根的一元二次方程_x_2＋__2_x_＋__1_＝__0_．
第14题
图放大
‹#›
返回目录
第14题
图还原
‹#›
返回目录
(1)点 P 从点 A 开始沿 AB 边向点 B 以 1 cm/s 的
速度移动，点 Q 从点 B 开始沿 BC 边向点 C 以 2 cm/s
的速度移动．如果点 P，Q 分别从点 A，B 同时出发，
经过几秒，△PBQ 的面积等于 8 cm2? 解：设运动时间为 x s，由题意得 AP＝x，BP＝
第10题
‹#›
返回目录
11．(8 分)用适当的方法解下列方程：
(1)2x2－3x－1＝0；

20秋启东作业九年级数学上(BS)作业50

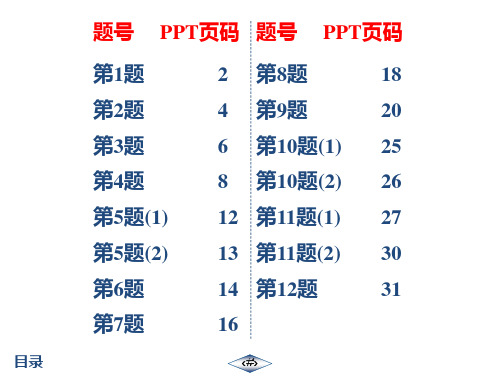
A．三棱锥 B．圆锥 C．三棱柱 D．圆柱
第1题
图放大
‹#›
返回目录
第1题
图还原
‹#›
返回目录
2．(2018·襄阳)一个几何体的三视图如图，则这个几何体是( C )
第2题
A
B
‹#›
C
D
图放大
返回目录
第2题
图还原
‹#›
返回目录
3．(2019·洛阳模拟)如图是一个长方体挖去一部分后得到的几何体，该几何体的左视图是( C )
题号 PPT页码题号 PPT页码
第1题第2题第3题第4题第5题(1) 第5题(2) 第6题第7题
2 第8题
18
4 第9题
20
6 第10题(1) 25
8 第10题(2) 26
12 第11题(1) 27
13 第11题(2) 30
14 第12题
31
16
目录
‹#›
1．如图是一个几何体的三视图，则这个几何体是( B )
‹#›
返回目录
8．如图是一个长方体的主视图和俯视图，由图示数据 ( 单位： cm) 可以得出该长方体的体积是 ___1_8____cm3.
第8题
图放大
‹#›
返回目录
第8题
图还原
‹#›
返回目录
9．如图是一个密封纸盒的三视图，请你根据图中数据计算这个密封纸盒的表面积．(结果保留根号)
第10题(2)
‹#›
返回目录
11．(2019·江宁区期末)如图①是由一些大小相同的小正方体组合成的简单几何体．
(1)请在图②的网格中分别画出它的主视图、左视图和俯视图；

20秋启东作业九年级数学上(BS)作业6

的面积是( C )
A．16
B．4 2
C．8
D．8 2
第1题
‹#›
返回目录
2．(2018·闵行区模拟)已知四边形 ABCD 是平行四边形，下列结论中不正确的是( D )
A．当 AB＝BC 时，四边形 ABCD 是菱形 B．当 AC⊥BD 时，四边形 ABCD 是菱形 C．当∠ABC＝90°时，四边形 ABCD 是矩形 D．当 AC＝BD 时，四边形 ABCD 是正方形
第4题
‹#›
返回目录
5．(2018·广安)如图，四边形 ABCD 是正方形， M 为 BC 上一点，连接 AM，延长 AD 至点 E，使得 AE＝AM，过点 E 作 EF⊥AM，垂足为 F.求证：AB ＝EF.
第5题
图放大
‹#›
返回目录
第5题
图还原
‹#›
返回目录
证明：∵四边形 ABCD 是正方形， ∴AD∥BC，∠B＝90°.∴∠AMB＝∠EAF. ∵EF⊥AM，∴∠AFE＝90°， ∴∠B＝∠AFE. 又 AM＝AE， ∴△AMB≌△EAF(AAS)， ∴AB＝EF.
第10题
‹#›
返回目录
11．在平面内，正方形 ABCD 与正方形 CEFH 如图放置，连接 DE，BH，两线段交于点 M.
第11题图放大‹#›返回目录第11题
图还原
‹#›
返回目录
求证：(1)BH＝DE；
证明：∵四边形 ABCD 与四边形 CEFH 是正方形， ∴∠BCD＝∠HCE＝90°， ∴∠BCD＋∠DCH＝∠HCE＋∠DCH，即∠BCH＝∠DCE.
BC＝DC，在△BCH 与△DCE 中，∠BCH＝∠DCE，
CH＝CE， ∴△BCH≌△DCE，∴BH＝DE.

20秋启东作业九年级数学上(BS)作业8

第10题
图放大
‹#›
返回目录
第10题
图还原
‹#›
返回目录
11．(8 分)(2019·岳阳)如图，在菱形 ABCD 中， E，F 分别为 AD，CD 边上的点，DE＝DF.求证：∠1 ＝∠2.
第11题
图放大
‹#›
返回目录
第11题
图还原
‹#›
返回目录
证明：∵四边形 ABCD 是菱形， ∴AD＝CD，
第13题(2)
‹#›
返回目录
14．(12 分)(2018·泰安)如图，在△ABC 中，D 是 AB 上一点，DE⊥AC 于点 E，F 是 AD 的中点， FG⊥BC 于点 G，与 DE 交于点 H，若 FG＝AF， AG 平分∠CAB，连接 GE，GD.
第14题
图放大
‹#›
返回目录
第14题
图还原
AD＝CD，
在△ADF 和△CDE 中，∠D＝∠D ， DF＝DE，
∴△ADF≌△CDE(SAS)， ∴∠1＝∠2.
第11题
‹#›
返回目录
12．(9 分)(2018·鼓交于点 O，BE∥AC，CE∥DB.
求证：四边形 OBEC 是正方形．
第12题
第13题
图放大
‹#›
返回目录
第13题
图还原
‹#›
返回目录
(1)求证：△BGF≌△FHC；证明：∵F，G，H 分别是 BC，BE，CE 的中点， ∴FH∥BE，FH＝12BE，FH＝BG， ∴∠CFH＝∠CBG. ∵BF＝CF，∴△BGF≌△FHC(SAS)．
第13题(1)
‹#›
返回目录
(2)设 AD＝a，当四边形 EGFH 是正方形时，求矩形 ABCD 的面积．

20秋启东作业九年级数学上(BS)作业60

图还原
‹#›
返回目录
(1)当购买这种月饼数量不超过 10 盒时，一盒月饼的价格为___2_4_0___元；
第15题(1)
‹#›
返回目录
(2)求出当 10＜x＜25 时，y 与 x 之间的函数关系式；
解：当 10＜x＜25 时，设 y＝kx＋b(其中 k，b 为常数且 k≠0)，
将 B(10，240)，C(25，150)代入 y＝kx＋b 中，得2150kk＋＋bb＝＝125400，，解得kb＝＝－3006，， ∴当 10＜x＜25 时，y＝－6x＋300.
第9题
‹#›
返回目录
10．(2019·晋江期中)已知 a－b＝4，(a－3)(b＋ 4)＜ab.
(1)b 的取值范围是__b_＜__－__4_； (2)若 a2＋a＋2ab－b＋b2＝40，则 a 的值是 ___－__1___．
第10题
‹#›
返回目录
11．(2019·丽水期中)现要在一个长为 40 m，宽为 26 m 的矩形花园中修建等宽的小道，剩余的地方种植花草．如图，要使种植花草的面积为 864 m2，那么小道的宽度应是___2_____m.
第11题
图放大
‹#›
返回目录
第11题
图还原
‹#›
返回目录
12．“校安工程”关乎生命、关乎未来．目前某省正在强力推进这一重大民生工程.2019 年，某市在省财政补助的基础上投入 600 万元的配套资金用于 “校安工程”，计划以后每年以相同的增长率投入配套资金，2021 年该市计划投入“校安工程”配套资金 1176 万元．从 2019 年到 2021 年，该市三年共投入“校安工程”配套资金__2_6_1_6___万元．

20秋启东作业九年级数学上(BS)作业16

第4题(4)
‹#›
返回目录
∴(x－6)2＝50， ∴x－6＝±5 2， ∴x1＝6＋5 2，x2＝6－5 2.
第4题(4)
‹#›
返回目录
4．用适当的方法解列一元二次方程：
(5)(x－ 3)＝ 2x(x－ 3);
解：原方程化为(x－ 3)－ 2x(x－ 3)＝0，
(x－
3)(1－
2x)＝0，∴x1＝
第1题(1)
‹#›
返回目录
1．用直接开平方法或配方法解下列一元二次方
程：
(2)2x2＋5x－1＝0. 解：二次项系数化为 1，得 x2＋52x－12＝0，
移项，得 x2＋52x＝12，
配方，得x＋542＝3136，
∴x1＝－5＋4
33，x2＝－5－4
33 .
第1题(2)
‹#›
返回目录
2．用公式法解下列一元二次方程： (1)x2－1＝2x；解：移项，得 x2－2x－1＝0， ∴b2－4ac＝(－2)2－4×1×(－1)＝8， ∴x＝2±2 8＝2±22 2， ∴x1＝1＋ 2，x2＝1－ 2.
3，x2＝
2 2.
第4题(5)
‹#›
返回目录
4．用适当的方法解下列一元二次方程： (6)(x＋3)2－(2x－3)2＝0；解：原方程化为－3x(x－6)＝0，∴x1＝0，x2＝ 6.
第4题(6)
‹#›
返回目录
4．用适当的方法解下列一元二次方程： (7)(2y＋1)2－8(2y＋1)＋15＝0; 解：原方程化为[(2y＋1)－3][(2y＋1)－5]＝0， (2y－2)(2y－4)＝0，4(y－1)(y－2)＝0， ∴y1＝1，y2＝2.
∴b2－4ac＝(－5)2－4×1×2＝17，

20秋启东作业九年级数学上(BS)作业11

第12题(1)
‹#›
返回目录
12．用配方法解下列方程： (2)x2－12x＝4；解：∵x2－12x＝4， ∴x2－12x＋36＝4＋36，即(x－6)2＝40，开方，得 x－6＝±2 10， ∴x1＝6＋2 10，x2＝6－2 10.
第12题(2)
‹#›
返回目录
12．用配方法解下列方程： (3)x2＋x＋1＝7x＋3; 解：x2＋x＋1＝7x＋3，移项，得 x2－6x＝2，配方，得(x－3)2＝11，开方，得 x－3＝± 11， ∴x1＝3＋ 11，x2＝3－ 11.
第11题(1)
‹#›
返回目录
11．用直接开平方法解下列方程： (2)(x－1)(x＋1)＝1；解：x2－1＝1，x2＝2，∴x1＝ 2，x2＝－ 2.
第11题(2)
‹#›
返回目录
11．用直接开平方法解下列方程：
(3)(2x－1)2＝( 2－1)2；
解：2x－1＝±(
2－1)，∴x1＝ 22，x2＝2－2
第14题
‹#›
返回目录
15．已知 x2＋y2－4x＋6y＋13＝0，求 x2－6xy ＋9y2 的值．
解：x2＋y2－4x＋6y＋13＝0， x2－4x＋4＋y2＋6y＋9＝0， (x－2)2＋(y＋3)2＝0，解得 x＝2，y＝－3， ∴ x2 － 6xy ＋ 9y2 ＝ (x － 3y)2 ＝ [2 － 3×( － 3)]2 ＝ 121.
第9题
‹#›
返回目录
10．(2018·顺义区模拟)把方程 x2－3＝2x 用配方法化为(x＋m)2＝n 的形式，则 m＝___－__1_____，n＝ ___4___．
第10题
‹#›
返回目录

20秋启东作业九年级数学上(BS)作业20

第9题(1)
‹#›
返回目录
解：由题意得， 5000m＋5000(m＋1)(m－1)＝55000，解得 m1＝3，m2＝－4(舍去)．当 m＝3 时，5000＋5000(m＋1)＝25000(斤)．答：小琴的父母 2020 年共收获 25000 斤梨．
第9题(1)
‹#›
返回目录
9．(2019·渠县月考)小琴的父母承包了一块荒山地种植一批梨树，2020 年收获一批梨，小琴的父母打算以 m 元/斤的零售价销售 5000 斤梨，剩余的 5000(m＋ 1)斤犁以比零售价低 1 元的批发价批给外地客商，预计总共可赚得 55000 元的毛利润．
返回目录
解：设该公司每个月生产成本的下降率为 x，根据题意得 400(1－x)2＝361，解得 x1＝210＝5%，x2＝3290＝1.95＞1(不合题意，舍去)．答：每个月生产成本的下降率为 5%.
第5题(1)
‹#›
返回目录
5．某公司 2020 年 1 月份的生产成本是 400 万元，由于改进生产技术，生产成本逐月下降，3 月份的生产成本是 361 万元．假设该公司 2，3，4 月每个月生产成本的下降率都相同．
题意，舍去．答：当每件商品降价 10 元时，该商店每天销售
利润为 1200 元．
第7题(2)
‹#›
返回目录
8．某校为响应全民阅读活动，利用节假日面向社会开放学校图书馆．据统计，第一个月进馆 128 人次，且进馆人次逐月增加，到第三个月末累计进馆 608 人次，若进馆人次的月平均增长率相同．
(1)求进馆人次的月平均增长率；
D．5001－1x02＝320
第2题
‹#›
返回目录
3．(2018·石家庄模拟)某商品的进价为每件 40

20秋启东作业九年级数学上(BS)作业68

＝4，4S3＝S1＋S2，且四边形 AEJH 和 CFKN 都是
正方形，则图中阴影部分 S3 的面积为( A )
A．2
B．5
C． 3
D．2 2
第5题
图放大
‹#›
返回目录
第5题
图还原
‹#›
返回目录
6．(2019·长丰县模拟)已知关于 x 的一元二次方程(a－1)x2－2x＋1＝0 有两个不相等的实数根，则 a 的取值范围是_a_＜__2_且__a_≠_1_______．
(1)求 k 的取值范围；解：当 k＝0 时，原方程为－3x＋1＝0，解得 x ＝13， ∴k＝0 符合题意；
第12题(1)
‹#›
返回目录
当 k≠0 时，原方程为一元二次方程， ∵该一元二次方程有实数根，
∴Δ＝(－3)2－4×k×1≥0，解得 k≤94.
综上所述，k 的取值范围为 k≤94.
第12题(1)
A．－2＜x＜0 或 0＜x＜4 B．x＜－2 或 0＜x＜4 C．x＜－2 或 x＞4 D．－2＜x＜0 或 x＞4
第4题
图放大
‹#›
返回目录
第4题
图还原
‹#›
返回目录
5．(2019·新吴区期末)如图，在矩形 ABCD 中，
矩形 EBFG 通过平移变换得到矩形 HMND，点 E，
F，N，H 都在矩形 ABCD 的边上．若 BE＝3，BF
第13题
图放大
‹#›
返回目录
第13题
图还原
‹#›
返回目录
(1)求 y 与 x 之间的函数关系式；解：设 y 与 x 之间的函数关系式为 y＝kx，根据题意，得 k＝xy＝60×5＝300，则 y 与 x 之间的函数关系式为 y＝30x0(x≥60)．

20秋启东作业九年级数学上(BS)作业10

第6题
‹#›
返回目录
7．根据下表，确定关于 x 的方程 x2＋4x＋c＝0
的解的取值范围是( B )
x
－7 －6 －5 … 1 2 3
x2＋4x＋c 12 3 －4 … －4 3 12
A．－7＜x＜－6 或 1＜x＜2
B．－6＜x＜－5 或 1＜x＜2
C．－7＜x＜－6 或 2＜x＜3
D．－6＜x＜－5 或 2＜x＜3
于 50 小于 51.
第10题
‹#›
返回目录
再列表取值如下：
x
… 50 50.7 50.8 50.9 51 …
x2＋14x－ … －100 －19.71 －8.16 3.41 15 …
3300
所以方程 x(x＋14)＝3300 的正根的取值范围为
50.8＜x＜50.9.
第10题
‹#›
返回目录
11．(2019·朝阳区期末)可以用如下方法估计方程 x2＋2x－10＝0 的解：
由上表可知，方程的解在 1～1.5 之间，
第12题
‹#›
返回目录
进一步列表取值如下：
x
1.1 1.2 1.3 1.4
x2－8x＋7.5 －0.09 －0.66 －1.21 －1.74
可知方程的解在 1.0～1.1 之间．
∵－0.09 距 0 近一些，∴方程的近似解是 1.1.
第12题
‹#›
返回目录
第13题
‹#›
返回目录
第11题(2)
‹#›
返回目录
解：∵方程 x2＋2x＋c＝0 有一个根在 0 和 1 之间，
∴c1＞＋02，＋c＜0或c1＜＋02，＋c＞0，解得－3＜c＜0.

20秋启东作业九年级数学上(BS)作业49

题号 PPT页码题号 PPT页码
第1题第2题第3题第4题第5题第6题第7题
2 第8题
16
3 第9题
18
5 第10题
20
7 第11题
22
9 第12题(1) 26
12 第12题(2) 27
14
目录
‹#›
1．(2019·湘潭)下列立体图形中，俯视图是三角形的是( C )
第1题
‹#›
返回目录
图还原
‹#›
返回目录
解：其主视图、俯视图和左视图如答图．
第5题
‹#›
返回目录
6．如图是一个正方体被截去一个直三棱柱得到的几何体，则该几何体的左视图是( A )
第6题
图放大
‹#›
返回目录
第6题
图还原
‹#›
返回目录
7．(2019·永州)某同学家买了一个外形非常接近球的西瓜，该同学将西瓜均匀切成了 8 块，并将其中一块(经抽象后)按如图所示的方式放在自己正前方的水果盘中，则这块西瓜的三视图是( B )
12．如图，一个工件是由大长方体上面中间部位挖去一个小长方体后形成，主视图是凹字形的轴对称图形．
第12题
图放大
‹#›
返回目录
第12题
图还原
‹#›
返回目录
(1)请在适当的位置补画该工件的俯视图；解：如答图．
第12题(1)
‹#›
返回目录
(2)已知制作这个工件的木料密度是 360 千克/立方米，则这个工件的质量是多少千克？如果工件整个需涂油漆，每千克油漆可以涂 4 平方米，根据图中尺寸，需要油漆多少千克？(单位：米)
第3题
图还原
‹#›

20秋启东作业九年级数学上(BS)作业15

第9题(1)
‹#›
返回目录
9．用因式分解法解下列方程： (2)(2018·梧州)2x2－4x－30＝0；解：x2－2x－15＝0， (x－5)(x＋3)＝0， ∴x1＝5，x2＝－3.
第9题(2)
‹#›
返回目录
9．用因式分解法解下列方程： (3)x(x－1)＝4x＋6; 解：x2－x＝4x＋6， x2－5x－6＝0， (x－6)(x＋1)＝0， ∴x1＝6，x2＝－1.
根据题意得，x(10－x)＝24，解得 x1＝4，x2＝6，当 x＝4 时，10－x＝6，当 x＝6 时，10－x＝4＜6，不合题意，舍去．答：边 AB 的长为 4 米．
第10题
‹#›
返回目录
11．阅读材料：解方程(x2－1)2－5(x2－1)＋4＝0 的过程如下：
设 x2－1＝y，则原方程可化为 y2－5y＋4＝0①，解得 y1＝1，y2＝4.
解：设 x＝a＋b，则原方程可化为 x2－7x＋10 ＝0，
解得 x1＝2，x2＝5，即 a＋b＝2 或 a＋b＝5，由斜边 c＝4，舍去 a ＋b＝2，
第11题(2)
‹#›
返回目录
∴Rt△ABC 的周长为 4＋5＝9. 由勾股定理得 a2＋b2＝42，则(a＋b)2－2ab＝16，解得 ab＝92，因此，Rt△ABC 的面积为12ab＝94.
A．(x＋5)(x－6) B．(x－5)(x＋6) C．(x＋5)(x＋6) D．(x－5)(x－6)
第2题
‹#›
返回目录
3．(2019·峄城区期末)方程 2(x－3)＝3x(x－3)的根是_x_1＝__3_，__x_2_＝__23_．
第3题
‹#›
返回目录

20秋启东作业九年级数学上(BS)作业64

第10题
图放大
‹#›
返回目录
第10题
图还原
‹#›
返回目录
11．(2019·吉林)已知 y 是 x 的反比例函数，并且当 x＝2 时，y＝6.
(1)求 y 关于 x 的函数解析式；解：设 y＝kx(k≠0)，当 x＝2 时，y＝6， ∴k＝xy＝12，∴y＝1x2.
第11题(1)
‹#›
返回目录
y＝－x6图象上的是( D )
A．(1，6)
B．(2，3)
C．(－2，－3)
D．(－3，2)
第2题
‹#›
返回目录
3．(2019·秦安县模拟)如图，A，B 是反比例函
数 y＝kx图象上的两点，过点 A，B 向坐标轴引垂线，
垂足分别为 C，D，E，F，若四边形 OCAD 的面积
为 8，则四边形 OEBF 的面积为( B )
返回目录
13．(2019·葫芦岛)如图，一次函数 y＝k1x＋b 的图象与 x 轴、y 轴分别交于 A，B 两点，与反比例函数 y＝kx2的图象分别交于 C，D 两点，点 C 的坐标是 (2，4)，B 是线段 AC 的中点．
第13题
图放大
‹#›
返回目录
第13题
图还原
‹#›
返回目录
(1)求一次函数 y＝k1x＋b 与反比例函数 y＝kx2的解析式；
第14题
图放大
‹#›
返回目录
第14题
图还原
‹#›
返回目录
(1)当 0≤x≤10 时，求水温 y(℃)与开机时间
x(min)的函数关系式；解：当 0≤x≤10 时，设水温 y(℃)与开机时间
x(min)的函数关系式为 y＝kx＋b，

20秋启东作业九年级数学上(BS)作业54

图放大
第8题
‹#›
返回目录
第8题
图还原
‹#›
返回目录
9．(2018·酒泉)如图，一次函数 y＝x＋4 的图象与反比例函数 y＝kx(k 为常数且 k≠0)的图象交于 A(－1，a)，B 两点，与 x 轴交于点 C.
第9题
图放大
‹#›
返回目录
第9题
图还原
‹#›
返回目录
(1)求此反比例函数的表达式；解：把点 A(－1，a)代入 y＝x＋4，得 a＝3， ∴点 A 的坐标为(－1，3)．把点 A(－1，3)代入反比例函数 y＝kx，得 k＝－ 3， ∴反比例函数的表达式为 y＝－3x.
第9题(1)
‹#›
返回目录
(2)若点 P 在 x 轴上，且 S△ACP＝32S△BOC，求点 P
的坐标． y＝x＋4，
解：联立两个函数表达式了，得 y＝－3x，解得xy＝＝3－，1，xy＝＝1－. 3， ∴点 B 的坐标为(－3，1)．
第9题(2)
‹#›
返回目录
当 y＝x＋4＝0 时，得 x＝－4， ∴点 C 的坐标为(－4，0)．设点 P 的坐标为(x，0)． ∵S△ACP＝32S△BOC， ∴12×3×|x－(－4)|＝32×12×4×1，即|x＋4|＝2，解得 x1＝－6，x2＝－2. ∴点 P 的坐标为(－6，0)或(－2，0)．
第9题(2)
‹#›
返回目录
10．反比例函数 y＝kx(k＞0)在第一象限内的图象如图所示，P 为该图象上的任意一点，PQ⊥x 轴，垂足为 Q，设△POQ 的面积为 S，那么 S 的值与 k 的值是否存在关系？若存在，请写出 S 与 k 之间的关系式；若不存在，请说明理由．

20秋启东作业九年级数学上(BS)作业56

阿基米德发现了杠杆平衡，后来人们把它归纳为
“杠杆原理”，即：阻力×阻力臂＝动力×动力
臂．小伟欲用撬棍撬动一块大石头，已知阻力和阻
力臂分别是 1200 N 和 0.5 m，则动力 F(单位：N)关
于动力臂 l(单位：m)的函数解析式正确的是( B )
A．F＝12l00
B．F＝60l 0
C．F＝50l 0
第9题(3)
‹#›
返回目录
(4)如果每小时排水量是 5 m3，那么排完水池中的水需要多少小时？
解：当 V＝5 时，t＝458＝9.6，即如果每小时排水量是 5 m3，那么排完水池中的水需要 9.6 h.
第9题(4)
‹#›
返回目录
10．(2019·鄂尔多斯)教室里的饮水机接通电源就进入自动程序，开机加热时每分钟上升 10 ℃，加热到 100 ℃停止加热，水温开始下降，此时水温 y(℃) 与开机后用时 x(min)成反比例关系，直至水温降至 30 ℃，饮水机关机，饮水机关机后即刻自动开机，重复上述自动程序．若在水温为 30 ℃时接通电源，水温 y(℃)与时间 x(min)的关系如图所示．
待334 min.
第10题(2)
‹#›
返回目录
第8题
‹#›
返回目录
9．如图是某一蓄水池的每小时排水量 V(m3)与排完水池中的水所用的时间 t(h)之间的函数关系图象．
第9题
图放大
‹#›
返回目录
第9题
图还原
‹#›
返回目录
(1)请你根据图象提供的信息求出此蓄水池的蓄水量；
解：由图象可知 4×12＝48，因此蓄水池的蓄水量 48 m3.
计算公式为 p＝FS，其中 p 是压强，F 是压力，S 是

20秋启东作业九年级数学上(BS)作业52

第15题(1)
‹#›
返回目录
15．(2019·西湖区期末)某游泳池有 900 立方米水，每次换水前后水的体积保持不变．设放水的平均速度为 v 立方米/小时，将池内的水放完需 t 小时．
(2)若要求在 2.5 小时至 3 小时内(包括 2.5 小时与 3 小时)把游泳池内的水放完，求 v 的取值范围．
B．y＝6000x
C．y＝30x00
D．y＝60x00
第8题
‹#›
返回目录
9．已知变量 y 与变量 x 之间的对应值如下表： x…123 4 5 6… y … 6 3 2 1.5 1.2 1 …
则变量 y 与 x 之间的函数关系式为___y＝__6x___．
第9题
‹#›
返回目录
10．一个圆柱的侧面展开图是一个面积为 10 的矩形，这个圆柱的高 l 与圆柱的底面半径 r 之间的函数表达式为__l＝__π_5r___，它是一个_反__比__例___函数．
第15题(2)
‹#›
返回目录
解：当 t＝2.5 时，v＝920.50＝360，当 t＝3 时，v＝9030＝300，所以 v 的取值范围为 300≤v≤360.
第15题(2)
‹#›
返回目录
解：由单价乘以油量等于总价，得 y＝4.75x，是正比例函数，不是反比例函数．
第5题(2)
‹#›
返回目录
5．列出下列问题中的函数关系式，并判断它们是否为反比例函数．
(3)小明完成 100 米赛跑时，时间 t(秒)与他跑步的平均速度 v(米/秒)之间的函数关系式．
解：由路程与时间的关系，得 t＝1v00，是反比例函数．
题号 PPT页码题号 PPT页码题号 PPT页码

20秋启东作业九年级数学上(BS)作业63

第11题
图放大
‹#›
返回目录
第11题
图还原
‹#›
返回目录
解：如答图，设墙上的影高 CD 落在地面上时的长度为 x m，树高为 h m，
∵某一时刻测得长为 1 m 的竹竿影长为 0.9 m，墙上的影高 CD 为 1.2 m，
第11题
‹#›
返回目录
∴01.9＝1x.2，解得 x＝1.08，经检验，x＝1.08 是原方程的解，
第7题
图放大
‹#›
返回目录
第7题
图还原
‹#›
返回目录
8．如图是由若干个大小相同的小正方体摆成的几何体，则三种视图中面积最小的是_左__视__图___．
第8题
图放大
‹#›
返回目录
第8题
图还原
‹#›
返回目录
9．(2018·滨州模拟)如图，正三棱柱的底面周长
为 15，截去一个底面周长为 6 的正三棱柱，所得几何体的俯视图的周长是___1_3____，面积是__2_1_4_3___．
A．21π m3 B．30π m3 C．45π m3 D．63π m3
第5题
图放大
‹#›
返回目录
第5题
图还原
‹#›
返回目录
6．(2019·齐齐哈尔)如图是由几个大小相同的小正方体搭建而成的几何体的主视图和俯视图，则搭
建这个几何体所需要的小正方体的个数至少为
( B) A．5 C．7
B．6 D．8
‹#›
返回目录
(1)说出这个几何体的名称__圆__柱____；
第12题(1)
‹#›
返回目录
(2)若如图所示的主视图的长、宽分别为 5，2，求该几何体的体积．(结果保留 π)

20秋启东作业九年级数学上(BS)作业9

4．(2018·苏州)若关于 x 的一元二次方程 x2＋mx ＋2n＝0 有一个根是 2，则 m＋n＝__－__2____．
第4题
‹#›
返回目录
5．把下列方程化为一元二次方程的一般形式，并指出它的二次项系数、一次项系数和常数项．
(1)2x2＝1－3x；解：2x2＝1－3x，一般形式为 2x2＋3x－1＝0，二次项系数为 2，一次项系数为 3，常数项为－1.
(2)如果一个直角三角形的两条直角边长之和为 14 cm，面积为 24 cm2，求它的两条直角边的长；
解：设其中一条直角边的长为 x cm，则另一条直角边的长为(14－x)cm，根据题意得12x(14－x)＝ 24，整理得 x2－14x＋48＝0.
第13题(2)
‹#›
返回目录
13．根据下列问题，列出关于 x 的方程，并将其化为一元二次方程的一般形式．
第13题(1)
‹#›
返回目录
解：设这个三位数的十位数字为 x，则个位数字为 x＋3，百位数字为 x＋2，
根据题意得[100(x＋2)＋10x＋(x＋3)]－9[(x＋ 3)2＋x2＋(x＋2)2]＝20，
整理得 9x2－7x－22＝0.
第13题(1)
‹#›
返回目录
13．根据下列问题，列出关于 x 的方程，并将其化为一元二次方程的一般形式．
A．1
B．2
C．－1
D．－2
第9题
‹#›
返回目录
10．一元二次方程(2＋x)(3x－4)＝5 的二次项系数是____3____，一次项系数是____2____，常数项是 __－__1_3___．
第10题
‹#›
返回目录
11．已知关于 x 的方程(m2－1)x2＋(m－1)x－2 ＝0，那么当 m__≠_±_1____时，方程为一元二次方程；当 m__＝__－__1__时，方程为一元一次方程．

20秋 启东作业九年级数学上(BS)作业55

20秋 启东作业九年级数学上(BS)作业44

20秋 启东作业九年级数学上(BS)作业21

20秋 启东作业九年级数学上(BS)作业50

20秋 启东作业九年级数学上(BS)作业6

20秋 启东作业九年级数学上(BS)作业8

20秋 启东作业九年级数学上(BS)作业60

20秋 启东作业九年级数学上(BS)作业16

20秋 启东作业九年级数学上(BS)作业11

20秋 启东作业九年级数学上(BS)作业20

20秋 启东作业九年级数学上(BS)作业68

20秋 启东作业九年级数学上(BS)作业10

20秋 启东作业九年级数学上(BS)作业49

20秋 启东作业九年级数学上(BS)作业15

20秋 启东作业九年级数学上(BS)作业64

20秋 启东作业九年级数学上(BS)作业54

20秋 启东作业九年级数学上(BS)作业56

20秋 启东作业九年级数学上(BS)作业52

20秋 启东作业九年级数学上(BS)作业63

20秋 启东作业九年级数学上(BS)作业9