《高等代数》(上)期末试卷(A)
高等数学a上期末考试试题和答案

高等数学a上期末考试试题和答案高等数学A上期末考试试题一、选择题(每题3分,共30分)1. 极限的定义是()。
A. 函数在某点的值B. 函数在某点的增量C. 函数在某点的导数D. 函数在某点的无穷小答案:D2. 函数f(x)=x^2在x=0处的导数是()。
A. 0B. 1C. 2D. 3答案:C3. 定积分∫₀¹x²dx的值是()。
A. 1/3B. 1/2C. 1D. 2答案:C4. 函数f(x)=sinx在x=π/2处的值是()。
A. 0B. 1C. -1D. π/2答案:B5. 函数f(x)=e^x的原函数是()。
A. e^xB. e^(-x)C. ln(x)D. x答案:A6. 函数f(x)=x^3-3x^2+2的极值点是()。
A. 0B. 1C. 2D. 3答案:B7. 函数f(x)=x^2+2x+1的最小值是()。
A. 0B. 1C. 2D. 3答案:B8. 函数f(x)=ln(x)的定义域是()。
A. (-∞, 0)B. (0, +∞)C. (-∞, +∞)D. [0, +∞)答案:B9. 函数f(x)=x^3-6x^2+11x-6的拐点是()。
A. 1B. 2C. 3D. 4答案:B10. 函数f(x)=x^4-4x^3+6x^2-4x+1的零点是()。
A. 0B. 1C. 2D. 3答案:B二、填空题(每题3分,共30分)11. 函数f(x)=x^3-3x^2+2的导数是______。
答案:3x^2-6x12. 函数f(x)=e^x的二阶导数是______。
答案:e^x13. 函数f(x)=ln(x)的不定积分是______。
答案:xln(x)-x+C14. 函数f(x)=x^2-4x+4的顶点坐标是______。
答案:(2, 0)15. 函数f(x)=sinx+cosx的周期是______。
答案:2π16. 函数f(x)=x^3-3x^2+2的单调增区间是______。
高等代数期末卷及答案

沈阳农业大学理学院第一学期期末考试《高等代数》试卷(1)1 •设 f (x) = x 4+x ? +4x - 9 ,贝H f (一3) = 69 .. 2•当 t = _2,-2 . 时,f(x)=x 3—3x+t 有重因式。
3.令f(x),g(x)是两个多项式,且f(x 3) xg(x 3)被x 2x 1整除,则 f(1)=_0_^ g(1)= 0 . 0 6 2=23 。
1 1 —-2 0 1x , 2x 2 2x 3 x 4 二 07. 2x 1 x 2 -2x 3 -2x 4 二 0 的一般解为x( ~'X 2 _'4x 3 ~3x 4 = 0题号-一--二二-三四五六七总分得分、填空(共35分,每题5 分)得分4.行列式1 -35.■’4 10"1 0 3-1、 -1 1 3'9 -2 -1 2 1 0 2」2 0 1< 9 9 11<1 3 4 丿6.z5 0 0 1 -1<0 2 1;0-2 3矩阵的积c 亠5 刘=2x3 X44x3, x4任意取值。
X2 二-2x^ --x4、(10分)令f(x),g(x)是两个多项式。
求证 当且仅当(f(x)g(x), f(x)g(x))=1。
证:必要性.设(f(x)g(x), f (x)g(x)) =1。
(1%令 p(x)为 f (x) g (x), f (x)g(x)的不可约公因式,(1% 则由 p(x) | f (x)g (x)知p(x)| f (x)或 p(x) |g(x) o (1%)不妨设 p(x) | f (x),再由 p(x)|(f(x) g (x))得 p(x) | g(x)。
故 p(x) |1 矛盾。
(2%)充分性.由(f (x)g(x), f (x)g(x)^1知存在多项式u(x), v(x)使u(x)(f(x) g(x)) v(x)f(x)g(x)=1,(2%)从而 u(x)f(x) g(x)(u(x) v(x) f(x)) =1,(2%)故(f (x), g(x)) =1 o (1%)ax 「bx 2 2x 3 =1 ax 1 (2 b -1)x 2 3x 3 =1 ax 1 bx 2 - (b 3)X 3 = 2b _1有唯一解、没有解、有无穷解?在有解情况下求其解。
高代期末考试试卷

高代期末考试试卷一、选择题(每题4分,共40分)1. 以下哪个矩阵是可逆的?A. [1 2; 3 4]B. [1 0; 0 0]C. [2 0; 0 2]D. [1 1; 1 1]2. 矩阵A的特征值是λ1和λ2,那么矩阵A^2的特征值是?A. λ1^2, λ2^2B. 2λ1, 2λ2C. λ1, λ2D. λ1+λ2, λ2+λ13. 线性方程组有非零解的条件是?A. 系数矩阵的行列式不等于0B. 系数矩阵的行列式等于0C. 增广矩阵的秩等于系数矩阵的秩D. 增广矩阵的秩不等于系数矩阵的秩4. 以下哪个向量组是线性无关的?A. [1, 0], [0, 1]B. [1, 1], [1, 2]C. [1, 2], [2, 4]D. [1, 2, 3], [4, 5, 6]5. 矩阵A的秩是3,那么矩阵A的零空间的维数是?A. 0B. 1C. 2D. 36. 以下哪个矩阵是对称矩阵?A. [1 2; 3 4]B. [1 3; 3 1]C. [2 1; 1 2]D. [1 0; 0 1]7. 以下哪个矩阵是正交矩阵?A. [1 0; 0 1]B. [1/√2 1/√2; -1/√2 1/√2]C. [1 1; 1 1]D. [1 2; 3 4]8. 以下哪个矩阵是幂等矩阵?A. [1 0; 0 1]B. [1 1; 1 1]C. [0 1; 1 0]D. [1 2; 3 4]9. 以下哪个矩阵是投影矩阵?A. [1 0; 0 0]B. [1 1; 1 1]C. [1 0; 0 1]D. [0 1; 1 0]10. 以下哪个矩阵是单位矩阵?A. [1 0; 0 1]B. [1 1; 1 1]C. [0 1; 1 0]D. [1 2; 3 4]二、填空题(每题4分,共20分)1. 矩阵的迹是其对角线元素的______。
2. 矩阵的转置是将矩阵的行和列进行______。
3. 矩阵的行列式可以通过______展开来计算。
《高等代数》期末考试卷

[ ϑ1 2 3 | | 22高等代数期末考试卷一、 单选题(32 分. 共 8 题, 每题 4 分)1)设 b 为 3 维行向量, V = {(x 1 , x 2 , x 3 ) | ( x 1 , x 2 , x 3 ) = b },则。
CA) 对任意的 b ,V 均是线性空间; B) 对任意的 b ,V 均不是线性空间; C) 只有当 b = 0 时,V 是线性空间;D) 只有当 b σ 0 时,V 是线性空间。
2)已知向量组 I :α1 ,α2 ,...,α s 可以由向量组 II : ⎭1 , ⎭2 ,..., ⎭t 线性表示,则下列叙述正确的是。
AA) 若向量组 I 线性无关,则 s t ; B) 若向量组 I 线性相关,则 s > t ; C) 若向量组 II 线性无关,则 s t ;D) 若向量组 II 线性相关,则 s > t 。
3)设非齐次线性方程组 AX = ⎭ 中未定元个数为 n ,方程个数为 m ,系数矩阵 A 的秩为 r ,则。
DA) 当 r < n 时,方程组 AX = ⎭ 有无穷多解; B) 当 r = n 时,方程组 AX = ⎭ 有唯一解;C) 当 r < m 时,方程组 AX = ⎭ 有解;D) 当 r = m 时,方程组 AX = ⎭ 有解。
4)设 A 是 m n 阶矩阵, B 是 n m 阶矩阵,且 AB = I ,则。
AA) r ( A ) = m , r (B ) = m ;B) r ( A ) = m , r (B ) = n ;C) r ( A ) = n , r (B ) = m ;D) r ( A ) = n , r (B ) = n 。
{1 1 1[5)设 K 上 3 维线性空间 V 上的线性变换ϕ 在基 ⋂ ,⋂ ,⋂ 下的表示矩阵是|1 0 1|,则 ϕ 在基|1 1 1|⋂1 , 2⋂2 ,⋂3 下的表示矩阵是。
2020-2021大学《高等代数》期末课程考试试卷A(含答案)

2020-2021《高等代数》期末课程考试试卷A适用专业: 考试日期:试卷类型:闭卷 考试时间:120分钟 试卷总分:100分一、填空(共40分,每小题4分)1.向量空间n P 的子空间12112{(,,,,0)0,}n k W x x x x x x P -=+=∈的维数为____________,它的一组基为__________________.2.已知111α⎛⎫ ⎪= ⎪ ⎪-⎝⎭是矩阵2125312A a b -⎛⎫⎪= ⎪ ⎪--⎝⎭的一个特征向量,则_______,_______a b ==特征向量α对应的特征值0___________λ=.3.k 满足___________时,二次型22212312132(1)22f x x k x kx x x x =--+---是负定的。
4.设矩阵20022311A x -⎛⎫ ⎪= ⎪ ⎪⎝⎭与10002000B y -⎛⎫⎪= ⎪ ⎪⎝⎭相似,则_________,________x y ==.5.在空间[]n P x 中,设变换σ为()(1)()f x f x f x →+-,则σ在基0(1)(1)1,(1,2,1)!i x x x i i n i εε--+===-下的矩阵为____________________.6.相似矩阵的特征值__________.7.向量)1,3,2,4(),4,3,2,1(==βα,则内积=),(βα___________. 8.若A 是实对称矩阵,则 A 的特征值为____________.9.n 元实二次型),,,(21n x x x f 是正定的充分必要条件是它的正惯性指数等于___________________.10.对于线性空间V 中向量)1(,,,21≥r r ααα ,若在数域P 中有r 个不全为零的数r k k k ,,,21 ,使02211=+++r r k k k ααα ,则向量r ααα,,,21 称为_________.二、(15分)设V 是实数域上由矩阵A 的全体实系数多项式组成的空间,其中2100100,200A ωωω⎛⎫- ⎪== ⎪ ⎪⎝⎭,求V 的维数和一组基.三、(15分)用非退化线性替换化二次型22212312132322448x x x x x x x x x ---++为标准形.四、(15分)在4P 中,求由基1234,,,εεεε到基1234,,,ηηηη的过渡矩阵,并求向量ξ在基1234,,,ηηηη下的坐标,设(1,0,1,0)ξ=1234(1,0,0,0)(0,1,0,0)(0,0,1,0)(0,0,0,1)εεεε=⎧⎪=⎪⎨=⎪⎪=⎩; 1234(2,1,1,1)(0,3,1,0)(5,3,2,1)(6,6,1,3)ηηηη=-⎧⎪=⎪⎨=⎪⎪=⎩.五、(15分)设1234,,,εεεε是四维线性空间V 的一组基,已知线性变换σ在这组基下的矩阵为1021121312552212⎛⎫⎪- ⎪⎪⎪--⎝⎭ 1)求σ在基11242234334442,3,,2ηεεεηεεεηεεηε=-+=--=+=下的矩阵; 2)求σ的核与值域.2020-2021《高等代数》期末课程考试试卷A 答案一、填空(共40分,每小题4分)1、向量空间n P 的子空间12112{(,,,,0)0,}n k W x x x x x x P -=+=∈的维数为__2n -__________,它的一组基为122(1,1,0,,0,0),(0,0,1,,0,0),,(0,0,0,,1,0)n εεε-=-==_。
高等代数上期末复习题

高等代数(1)复习题一、判断题1、四阶行列式中含因子2311a a 的项为42342311a a a a 和44322311a a a a 。
( )2、设D 为六阶行列式,则162534435261a a a a a a 是D 中带负号的项。
( )3、对任一排列施行偶数次对换后,排列的奇偶性不变。
( )4、排列()3211 -n n 的逆序数为n 。
( )5、排列()3211 -n n 为偶排列。
( )6、若行列式中所有元素都是整数,且有一行中元素全为偶数,则行列式的值一定是偶数。
( )7、若22B A =,则B A =或B A -=。
( )8、若AC AB =,0≠A ,则C B =。
( )9、若矩阵A 满足A A =2,则0=A 或E A =。
( ) 10、设A 是n 阶方阵,若0≠A ,则必有A 可逆。
( ) 11、若矩阵A 满足02=A ,则0=A 。
( )12、若矩阵B A ,满足0AB =,且0A ≠,则0B =。
( ) 13、对n 阶可逆方阵A ,B ,必有()111---=B A AB 。
( )14、对n 阶可逆方阵A ,B ,必有()111---+=+B A B A 。
( )15、设A ,B 为n 阶方阵,则必有B A B A +=+。
( ) 16、设A ,B 为n 阶方阵,则必有BA AB =。
( ) 17、若矩阵A 与B 等价,则B A =。
( )18、若A 与B 都是对称矩阵,则AB 也是对称矩阵。
( )19、若矩阵A 的所有1r +级的子式全为零,则A 的秩为r 。
( ) 20、设n m A ⨯,n m B ⨯为矩阵,则()()()B R A R B A R +≤+。
( ) 21、设A =0,则()0=A R 。
( )22、线性方程组0=⨯X A n n 只有零解,则0≠A 。
( ) 23、若b AX =有无穷多解,则0=AX 有非零解。
( )24、设n 级方阵C B A ,,满足ABC E =,E 为单位矩阵,则CAB E =。
高等代数2009-2010第一学期期末试卷答案

高等代数(北大版)第一学期考试卷答案一、选择题(每小题3分,共24分)1.D2.C3.B4.D5.A6.B7.C8.A二、填空题(每小题3分,共18分)1.322(1)5(1)7(1)1x x x -+-+-- 2.2x + 3.1()2n n +- 4.)1,,1,1( c x = 5.d6.⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=-3/13/1003/23/100005200211A三、计算题(本大题共3个小题,共22分.请写出必要的推演步骤和文字说明)1.(6分)设b ax x x x x f +++-=23463)(,1)(2-=x x g ,a 与b 是什么数时,)(x f 能被)(x g 整除?解:方法一、利用辗转相除法,得余式:7)3()(++-=b x a x r ,………………………………………..4分由已知, 7,3-==b a ……………………………………………..2分方法二、由于)(x f 能被)(x g 整除,而1)(2-=x x g 的零点为1和-1,所以1和-1也应是)(x f 的零点,即04)1(=++=b a f 和 010)1(=+-=-b a f …………5分 故7,3-==b a …………………………………………………...….1分2.(8分)已知B AX X +=,其中⎪⎪⎪⎭⎫ ⎝⎛---=101111010A ,⎪⎪⎪⎭⎫ ⎝⎛--=350211B ,求矩阵X 。
解:由 B AX X += 得 B X A E =-)(而 ⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛=-201101011101111010100010001A E 可逆…………….2分可以求得 ⎪⎪⎪⎭⎫ ⎝⎛--=--11012312031)(1A E ……………………………………….. .3分 所以 ⎪⎪⎪⎭⎫ ⎝⎛--=-=-11012312031)(1B A E X ⎪⎪⎪⎭⎫ ⎝⎛--350211=⎪⎪⎪⎭⎫ ⎝⎛--110213………………3分3.(8)b a ,取什么值时,线性方程组⎪⎪⎩⎪⎪⎨⎧=-+++=+++=-+++=++++bx x x x x x x x x a x x x x x x x x x x 5432154325432154321334536223231有解?在有解的情形求一般解。
厦门大学参考答案--08-09学年第一学期《高等代数》期末考试卷

厦门⼤学参考答案--08-09学年第⼀学期《⾼等代数》期末考试卷特别说明:答案写在答题纸上⼀、单选题(32分. 共8题, 每题4分)1.下列说法错误的是A) 若向量组123,,ααα线性⽆关,则其中任意两个向量线性⽆关; B) 若向量组123,,ααα中任意两个向量线性⽆关,则123,,ααα线性⽆关; C) 向量组122331,,αααααα---线性相关;D) 若向量组123,,ααα线性⽆关,则112123,,αααααα+++线性⽆关.2. 设n 维列向量12,,...,m ααα()m n <线性⽆关, 则n 维列向量12,,...,m βββ线性⽆关的充要条件是A) 向量组12,,...,m ααα可由向量组12,,...,m βββ线性表⽰; B) 向量组12,,...,m βββ可由向量组12,,...,m ααα线性表⽰; C) 向量组12,,...,m ααα与向量组12,,...,m βββ等价; D) 矩阵12(,,...,)m A ααα=与矩阵12(,,...,)m B βββ=相抵.3.设线性⽅程组0Ax =的解都是线性⽅程组0Bx =的解,则A) ()()r A r B <; B) ()()r A r B >; C) ()()r A r B ≥;D) ()()r A r B ≤.4.设n 阶⽅阵A 的伴随矩阵*0A ≠,⾮齐次线性⽅程组Ax b =有⽆穷多组解,则对应的齐次线性⽅程组0Ax =的基础解系 A) 不存在;B) 仅含⼀个⾮零解向量;C) 含有两个线性⽆关的解向量; D) 含有三个线性⽆关的解向量.5.下列⼦集能构成22R的⼦空间的是A) 221{|||0,}V A A A R ?==∈;B) 222{|()0,}V A tr A A R==∈;C) 2223{|,}V A A A A R ?==∈;D) 224{|,}V A A A A A R ?'==-∈或.6.设V 是数域K 上的线性空间, V 上的线性变换?在基12,,...,n ααα下的矩阵为A 且||2A =,若?在基11,,...,n n ααα-下的矩阵为B , 则||B =A) 2n; B) 2; C)12; D) 不能确定.7.设V 是n 维向量空间,?和ψ是V 上的线性变换,则dimIm dimIm ?ψ=的充分必要条件是A) ?和ψ都是可逆变换;B) Ker ?=Ker ψ;C) Im Im ?ψ=; D) ?和ψ在任⼀组基下的表⽰矩阵的秩相同. 8.设?是线性空间V 到U 的同构映射, 则下列命题中正确的有个. (Ⅰ) ?为可逆线性映射;(Ⅱ) 若W 是V 的s 维⼦空间, 则()?W 是U 的s 维⼦空间; (Ⅲ) ?在给定基下的表⽰矩阵为可逆阵;(Ⅳ) 若12V=V V ⊕, 则1212)))⊕=⊕(V V (V (V . A) 1B) 2C) 3D) 4⼆、填空题(32分. 共8题,每题4分)1. 若矩阵1234(,,,)A αααα=经过⾏初等变换化为1003002401050000-??-, 那么向量组1234,,,αααα的⼀个极⼤⽆关组是其余向量由此极⼤⽆关组线性表⽰的表⽰式为.2. 设3维向量空间的⼀组基为123(1,1,0),(1,0,1),(0,1,1)ααα===,则向量(2,0,0)β=在这组基.3. 设1V ,2V 均为线性空间V 的⼦空间,则12()L V V ?4. 数域K 上所有三阶反对称矩阵构成的线性空间的维数是的⼀组基. 5. 已知12K上的线性变换?定义如下:((,))(0,)ab a ?=-,则Ker ?=Im ?6. 设?是数域K 上n 维线性空间V 到m 维线性空间U 的线性映射, 则?为满射的充分必要条件是(请写出两个)7. 设12,,...,n ααα和12,,...,n βββ是线性空间V 的两组基,从12,,...,n ααα到12,,...,n βββ的过渡矩阵为P . 若?是V 上的线性变换且,()i i ?αβ=1,2,...,i n =,则?在基12,,...,n βββ下的表⽰矩阵是8. 设?是线性空间V 上的线性变换,?在基12,,...,n ααα下的表⽰矩阵为0A B C ??,其中A 为r r ?矩阵,则存在V 的⼀个⾮平凡?-,,)r α.三、(8分) 设线性空间V 的向量组12,,...,m ααα线性⽆关,V β∈,考虑向量组12,,,...,m βααα.求证:或者该向量组线性⽆关,或者β可由12,,...,m ααα线性表⽰. ,,m α线性相关,则存在不全为,,k m 使得+k m m α+=.事实上,若k +k m m α+=12,,...,ααα线性⽆关知1m k ==k =0.m ==k =0.,,k m 不全为0相⽭盾.mm k k α--从⽽,或者该向量组线性⽆关,或者β可由α四、(10分) 设1V ,2V 分别是数域K 上的齐次线性⽅程组12n x x x == =与120n x x x +++=的解空间. 证明112n KV V ?=⊕.1n V V a ?∈n n a a ==++=,则0n a ===1n n K a ??∈,11i V a n∈∑, 21n i i V a n =??∈?∑n a =1n i i a n =?∑+n a1n V V a ∈n n a a ==++=,则0n a ===(1)000011n n-?,1,1,,1)n ?,所以1.故1dim V (1)000011n n-? ?,1,1,,1)n ?,1dim 1,dim V =1n n K a ??∈,11i n V a n ?∈∑, 21n i i n V a n =??∈?∑n a =1n i i n a n =?∑+n n a五、(10分) 设m n A K ?∈. 证明:()r A r =的充分必要条件是存在m r B K ?∈,r n C K ?∈,使得()()r B r C r ==且A BC =.证明:充分性:由于m rB K∈,r nC K∈满⾜()()r B r C r ==且A BC =,所以()()()()()r r B r C r r A r BC r B r =+-≤=≤=故()r A r =.必要性:由于()r A r =,所以存在m 阶可逆矩阵P 及n 阶可逆矩阵Q 使得000rI A P Q ??=.令,(,0)0r r I B P C I Q ??==,则m r B K ?∈,r n C K ?∈满⾜()()r B r C r ==且A BC =.六、(8分) 设V , U, W 是有限维线性空间,:V U ?→,:W U ψ→是线性映射. 求证:存在线性映射:V W σ→使得?ψσ=的充分必要条件是Im Im ?ψ?.证明:充分性:法⼀:取V 的⼀组基12,,,n ααα,由于Im Im ?ψ?,所以()Im i ?αψ∈,1i n ?≤≤,即存在i W β∈使得()()i i ?αψβ=.定义线性映射:V W σ→满⾜(),1i i i n σαβ=?≤≤,则()()(),1i i i i n ψσαψβ?α==?≤≤.因此,ψσ?=.法⼆:取V 的⼀组基12,,,n ξξξ,U 的⼀组基12,,,m ηηη,W 的⼀组基12,,,s γγγ.设1212(,,,)(,,,)n m m n A ?ξξξηηη?= 1212(,,,)(,,,)s m m s B ψγγγηηη?=其中1212(,,,),(,,,)n s A B αααβββ==.由于I m I m ?ψ?,所以1212(,,,)(,,,)n s L L αααβββ?,即11,sj ij i i j n c αβ=?≤≤=∑.取()ij s n C c ?=,则A B C =.定义线性映射:V W σ→满⾜1212(,,,)(,,,)n s C σξξξγγγ=,则?ψσ=.必要性:对任意Im β?∈,存在V α∈使得()β?α=.由于?ψσ=,所以()β?α=(())Im ψ?αψ=∈从⽽,Im Im ?ψ?.附加题: (本部分不计⼊总分)设V , U, W 是有限维线性空间且dim dim V W =,:V U ?→,:W U ψ→是线性映射. 证明:存在可逆线性映射:V W σ→使得?ψσ=的充分必要条件是Im Im ?ψ=.证明:充分性:法⼀:由于d i m d i m V W =且Im Im ?ψ=,所以由维数公式知:d i m d i m Ke r K e r ?ψ=.取Ker ψ的⼀组基12,,,r ηηη;Ker ?的⼀组基12,,,r ξξξ,将其扩充为V的⼀组基121,,,,,r r n ξξξξξ+,则1(),()r n ?ξ?ξ+是Im ?的⼀组基.由于Im Im ?ψ=,所以1(),()r n ?ξ?ξ+是Im ψ的⼀组基.设()(),1i i r i n ?ξψη=?+≤≤,由于1(),,()r n ψηψη+线性⽆关,所以1,,r n ηη+线性⽆关.我们断⾔,121,,,,,,r r n ηηηηη+线性⽆关.事实上,若1122110r r r r n n k k k k k ηηηηη++++++++=,则将ψ作⽤于上式得11()()0r r n n k k ψηψη++++=.由于1(),,()r n ψηψη+线性⽆关,所以10r n k k +===.于是1122r r k k k ηηη+++=0.⼜12,,,r ηηη是Ker ψ的⼀组基,故10r k k ===从⽽,121,,,,,,r r n ηηηηη+线性⽆关.注意到dim W n =,故121,,,,,,r r n ηηηηη+是W 的⼀组基.定义线性映射:V W σ→满⾜(),1i i i n σξη=?≤≤.由于12,,,n ξξξ是V 的⼀组基,12,,,n ηηη是W的⼀组基,故σ可逆.⼜()()(),1i i i i n ψσξψη?ξ==?≤≤,从⽽?ψσ=.法⼆:取V 的⼀组基12,,,n ξξξ,U 的⼀组基12,,,s γγγ,W 的⼀组基12,,,n ηηη.设1212(,,,)(,,,)n s s n A ?ξξξγγγ?=1212(,,,)(,,,)n s s n B ψηηηγγγ?=且dimIm dimIm r ?ψ==,则()()r A r B r ==.于是,存在n 阶可逆矩阵,P Q 使得1(,0),AP A =1(,0)BQ B =,其中11,s r A B K ?∈列满秩.由于Im Im ?ψ=,所以同上题证明可知存在n 阶矩阵C 使得A BC =,则11(,0)()A AP BQ Q CP -==.设111212122X X Q CP X X -??=,其中11X 是r 阶⽅阵,则1112112122(,0)(,0)X X A B X X ??=.从⽽,1111A B X =.⼜1A 列满秩,所以存在2r sA K ?∈使得21r A A I =.于是,212111()r I A A AB X ==,即11X 是可逆矩阵.因此,存在可逆矩阵11100n r X X Q P I --??=使得()111111111111100(,0),0(,0)00n r n r X X BX BQ P B P B X P A P A I I ------=====定义线性映射:V W σ→满⾜1212(,,,)(,,,)n n X σξξξηηη=由于X 可逆且A BX =,故σ可逆且?ψσ=.必要性:由于?ψσ=,所以同上题证明可知Im Im ?ψ?.⼜由:V W σ→可逆可知1ψ?σ-=,所以Im Im ψ??.从⽽,Im Im ?ψ=.。
高等代数第一学期试卷及答案(A)

高等代数第一学期试卷及答案(A)1. 若 $b_1c_1=b_3m$,则 $a_2=$B. $-15m$2. $n$ 阶矩阵 $A$ 可逆的充分必要条件是 A. $\vertA\vert\neq0$3. 下列说法不正确的是 B. 如果 $f(x)\mid g(x)$,$g(x)\mid h(x)$,则 $f(x)\mid h(x)$4. 设向量组 $\alpha,\beta,\gamma$ 线性无关,$\alpha,\beta,\delta$ 线性相关,则() D. $\mathrm{\delta}$ 一定不能由 $\mathrm{\alpha,\beta,\gamma}$ 线性表示5. 对于 $n$ 元方程组,下列命题正确的是 B. 如果$Ax=0$ 只有零解,则 $Ax=b$ 也只有零解6. 若$A=\begin{pmatrix}1&2&3\\4&5&6\\5&6&7\end{pmatrix}$,则$\vert A\vert=$ $-3$7. $f(x)=x^4+x^3-1$,则 $f^\prime(x)=4x^3+3x^2$8. 已知 $\vert A\vert=-113$,则 $A_{12}-A_{22}+A_{32}-A_{42}=$ $-1145$9. 设$A=\begin{pmatrix}1&2&3\\2&4&6\\3&6&9\end{pmatrix}$,则$(A^{-1})^*=$ $\begin{pmatrix}0&0&1\\0&1&0\\1&0&0\end{pmatrix} $10. 若 $\alpha_1=(1,0,5,2)^T,\alpha_2=(3,-2,3,-4)^T,\alpha_3=(2,4,1,0)^T$,则 $\alpha_3$ 可以由$\alpha_1,\alpha_2$ 线性表示,且线性表示为 $\alpha_3=-\alpha_1+2\alpha_2$。
2021年高等代数-第一学期期末试卷答案

2009级数学与应用数学专业《高等代数》I (A 卷)第 1 页 共 6 页高等代数2011-2012第一学期期末试卷答案课程名称:《高等代数》参考答案及评分标准(A 卷)考试(考查):考试 时间:200 年 月 日本试卷共7页,满分100 分; 考试时间:120 分钟答题前请将密封线内的项目填写清楚一.选择题(本大题共8个小题,每小题3分,共24分.请在每小题的四个备选答案中选出一个正确的答案,并将其号码填入题后的括号内).1.在[]F x 里一定能整除任意多项式的多项式是 【 B 】A .零多项式B .零次多项式C .本原多项式D .不可约多项式2.设()1g x x =+是6242()44f x x k x kx x =−++−的一个因式,则=k 【 C 】A .4B .3C .2D .13.A ,B 是n 阶方阵,则下列结论成立的是 【 C 】A .AB O A O ≠⇔≠且B O ≠ B . 0A A O =⇔=C .0AB A O =⇔=或B O =D . 1||=⇔=A I A4.设n 阶矩阵A 满足220A A I −−=,则下列矩阵哪个不可逆 【 B 】A . 2A I +B . A I +C .A I −D .A5.设A 为3阶方阵,且1)(=A r ,则 【 A 】A .0)(*=A rB .1)(*=A rC .2)(*=A rD .3)(*=A r6.设*A 为n 阶方阵A 的伴随矩阵,则A A *= 【 D 】2009级数学与应用数学专业《高等代数》I (A 卷)第 2 页 共 6 页A . 2||n AB .||n AC .2||nnA − D . 21||nn A −+7.下列对于多项式的结论正确的是 【 D 】A .如果)()(,)()(x f x g x g x f ,那么)()(x g x f =B .如果多项式在有理数域上可约,则它一定存在有理根C .每一个多项式都有唯一确定的次数D .奇数次实系数多项式必有实根8. 方程组为b AX =,且()()r A r A r ==,则和原方程组同解的方程组为 【 A 】A .Pb PAX =(P 为可逆矩阵)B .b QAX =(Q 为初等矩阵)C . b X A T= D . 原方程组前r 个方程组成的方程组二.填空题(本大题共6个小题,每空3分,共24分.请将正确结果填在题中横线上).1.把5)(4−=x x f 表成1−x 的多项式是4)1(4)1(4)1(4)1(234−−+−+−+−x x x x ;2.设42()f x x x ax b =+++,2()2g x x x =+−,若((),())()f x g x g x =,则=a 6 ,=b 8 ;3.当k = 5 ,l = 4 时,5阶行列式D 的项53431212a a a a a l k 取“负”号;4. 设4122011121113101−−−−=A ,则=+++44342414A A A A -20 ;5.设n > 2,n a a a ,...,,21为互不相等的常数,则线性方程组⎪⎪⎩⎪⎪⎨⎧=++++=++++=++++−−−1......1...1...132211232222111321211nn n n n n n n n x a x a x a x x a x a x a x x a x a x a x 的解是 (1,0,…,0) ;2009级数学与应用数学专业《高等代数》I (A 卷)第 3 页 共 6 页6.01000020......... (00010)00n n−L LL L= !)1(1n n −−. 三.计算题(本大题共4个小题,共34分.请写出必要的推演步骤和文字说明).1111111111111111x xD y y+−=+−.:分分分解第一列第二列第三列第四列第二行第一行第四行第三行601401100001012001111001111:222)1()1()1()1(−−−−−=−−=−−−−−−−−−−−−−−−−+−−+==+−⨯+−⨯+−⨯+−⨯y x yy xyy x xyy y x x x2.(本小题8分)k 为何值时,齐次线性若方程组⎪⎩⎪⎨⎧=+−−=−+=++0300321321321x x x x kx x x x kx 有非零解,并求出它的一般解. 解: 组有非零解01131111=−−−⇔kk,得1−=k --------2分 对系数矩阵施行行初变换如下:1.(本小题6分)2009级数学与应用数学专业《高等代数》I (A 卷)第 4 页 共 6 页⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛−→⎪⎪⎪⎭⎫ ⎝⎛−−−−−00021102101113111111 --------6分 故一般解为323121,21x x x x −== (3x 为自由未知量) ---------8分3.(本小题8分)设A =⎪⎪⎪⎭⎫⎝⎛−321011330,B A AB 2+=,求B .解: 易知A I A B 1)2(−−= --------2分而⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛−−−=⎪⎪⎪⎭⎫⎝⎛−−−=−−−212121232121232321121011332)2(11I A --------6分 故⎪⎪⎪⎭⎫⎝⎛−=⎪⎪⎪⎭⎫⎝⎛−⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛−−−=011321330321011330212121232121232321B --------8分 4.(本小题12分)λ取何值时,线性方程组123123123(1)0(1)3(1)x x x x x x x x x λλλλ⎧+++=⎪⎪+++=⎨⎪⎪+++=⎩有唯一解?无解?有无穷多解?并在有解时写出解.2009级数学与应用数学专业《高等代数》I (A 卷)第 5 页 共 6 页解: 对增广阵施行行初变换如下:⎪⎪⎪⎭⎫⎝⎛+−+−−+→⎪⎪⎪⎭⎫ ⎝⎛+−+−−−−+→⎪⎪⎪⎭⎫⎝⎛+++→⎪⎪⎪⎭⎫ ⎝⎛+++=)3)(1()3(0030111)1()2(0301110111311111130111111111λλλλλλλλλλλλλλλλλλλλλλλλλλλA--------- 4分易知1) 当0)3(≠+λλ,即30−≠≠λλ且时,3)()(==A r A r ,组有唯一解λλλλ1,2,1321−==−=x x x ---------8分2) 当3−=λ时, <==2)()(A r A r 未知量个数,组有无穷多解,2,13231x x x x +−=+−=(3x 为自由未知量) ---------10分3) 当0=λ时, 2)()(1=≠=A r A r ,组无解 ---------12分2个小题,共18分.证明须写出必要的推演步骤和文字说明).1.(本小题10分) 证明:一个秩为r 的矩阵总可以表为r 个秩为1的矩阵的和.证: 设A 为m×n 矩阵且秩A=r ,则存在m 阶可逆矩阵p 及n 阶可逆矩阵Q ,使A I PAQ r =⎪⎪⎭⎫ ⎝⎛=00----------2分 又rr E E E A ΛΘ++=2211 ----------4分r rr B B B Q E p Q E P Q E P A +++=+++=∴−−−−−−ΛΛ211112211111----------8分由于秩B k =秩(P -1E rr Q -1)=秩E kk =1所以A 可表成r 个秩为1的矩阵之和. ----------10分2009级数学与应用数学专业《高等代数》I (A 卷)第 6 页 共 6 页2.(本小题8分)设)(x f 是一个整系数多项式,证明:若)0(f 与)1(f 都是奇数,则)(x f 不能有整数根.证明: 用反证法假设)(x f 有整数根α,则)()()(x g x x f α−=,其中)(x g 为整系数多项式,--------3分 于是)1()1()1(),0()0(g f g f αα−=−= --------5分即)1(|)1(),0(|f f αα−但)0(f 与)1(f 都是奇数,而αα−1,不同为奇数,因而矛盾. ----------7分 故)(x f 不能有整数根 ----------8分。
《高等代数》期末考试卷

1011学年第一学期厦门大学《高等代数》期末试卷厦门大学《高等代数》课程试卷数学科学学院 各 系 2010 年级 各 专业主考教师:杜妮、林鹭 试卷类型:(A 卷)2011.1.13一、 单选题(32 分. 共 8 题, 每题 4 分)1)设b 为 3 维行向量, 123123 V {(,,)|(,,)} x x x x x x b == ,则____。
CA) 对任意的b ,V 均是线性空间; B) 对任意的b ,V 均不是线性空间; C) 只有当 0 b = 时,V 是线性空间; D) 只有当 0 b ¹ 时,V 是线性空间。
2) 已知向量组 I : 12 ,,..., s a a a 可以由向量组 II : 12 ,,..., t b b b 线性表示,则下列叙述正确的是____。
AA) 若向量组 I 线性无关,则s t £ ; B) 若向量组 I 线性相关,则s t > ; C) 若向量组 II 线性无关,则s t £ ; D) 若向量组 II 线性相关,则s t > 。
3) 设非齐次线性方程组AX b = 中未定元个数为 n ,方程个数为m ,系数矩阵 A 的秩为 r ,则____。
DA) 当r n < 时,方程组AX b = 有无穷多解; B) 当r n = 时,方程组AX b = 有唯一解; C) 当r m < 时,方程组AX b = 有解; D) 当r m = 时,方程组AX b = 有解。
4)设 A 是m n ´ 阶矩阵,B 是n m ´ 阶矩阵,且AB I = ,则____。
AA) (),() r A m r B m == ; B) (),() r A m r B n == ; C) (),() r A n r B m == ;D) (),() r A n r B n == 。
5)设 K 上 3 维线性空间 V 上的线性变换j 在基 123 ,, x x x 下的表示矩阵是 111 101 111 æöç÷ç÷ ç÷ èø,则j 在基123 ,2, x x x 下的表示矩阵是____。
高代(一)期末试题

高等代数(一)期末试题一.填空题(每空2分,共20分):1.在由几个不同元素组成的一个排列中,所有逆序的总数,叫做这个排列的( )。
2.1020003400-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦( )。
3.设A 为三阶方阵,det 3A =-,则det (2)A A -=( )。
4.若矩阵A 的秩1r >,则A 的1r -阶子式的值( )。
5.设2是多项式43228x x ax bx -++-的二重根,则a =( ),b =( )。
6.设,A B 都是n 阶可逆矩阵,矩阵00A C B⎛⎫=⎪⎝⎭的逆矩阵为( )。
7.如行列式111213212223313233a a a a a a d a a a =,则111213212223313233333222a a a a a a a a a =---( )。
8.设,a b 是整数且( ),那么存在一对整数q 和r ,使得b aq r =+且( )。
满足以上条件的整数q 和r 是唯一确定的。
二.选择题(每小题2分,共10分):1.一个n 阶行列式,如果他的第1列上除了1111n a a ==外其余元素都为零,那么这行列式等于( )。
(A )1111(1)n n M M +-- (B )111n A A + (C )111n M M - (D )1111(1)n n A A ++-2.设3512A --⎛⎫=⎪⎝⎭,则A 的伴随矩阵*A =( )。
(A )3512--⎛⎫ ⎪⎝⎭ (B )2513⎛⎫⎪--⎝⎭(C)2153-⎛⎫ ⎪-⎝⎭(D) 1235⎛⎫⎪--⎝⎭3.初等方阵()(A )都是可逆阵 (B )所对应的行列式的值等于1(C )相乘仍为初等方阵 (D )相加仍为初等方阵 4.若集合{}|,F a bi a b R =+∈(这里R 是实数集)是数域,则,a b 应满足条件( )。
(A ),a b 是整数 (B ),a b 是有理数 (C )a 是有理数,b 是实数 (D ),a b 是任意数5.设A 是三阶方阵,*A 是其伴随矩阵。
《高等代数》期末闭卷考试题A
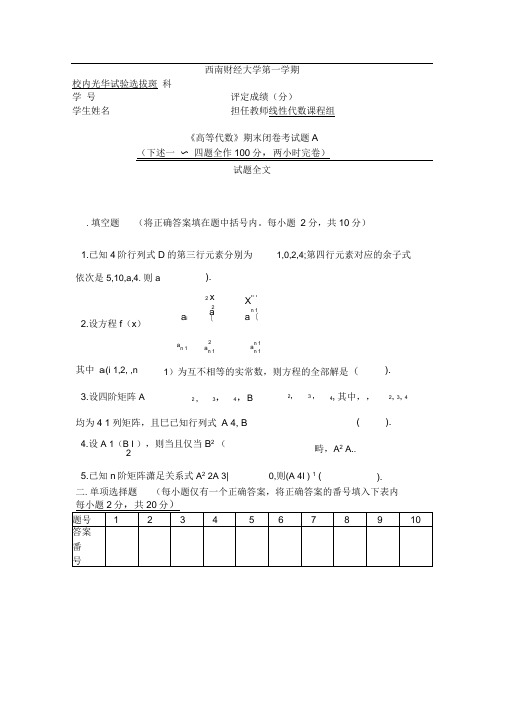
西南财经大学第一学期校内光华试验选拔斑 科 学 号 评定成绩(分)学生姓名担任教师线性代数课程组《高等代数》期末闭卷考试题A(下述一 〜 四题全作100分,两小时完卷)试题全文.填空题 (将正确答案填在题中括号内。
每小题 2分,共10分)1.已知4阶行列式D 的第三行元素分别为 1,0,2,4;第四行元素对应的余子式二.单项选择题 (每小题仅有一个正确答案,将正确答案的番号填入下表内依次是5,10,a,4.则a).2.设方程f (x )a i2x2a 〔n 1 Xn 1a 〔an 12an 1n 1 an 1其中 a i (i 1,2, ,n 1)为互不相等的实常数,则方程的全部解是().3.设四阶矩阵A2,3, 4,B2,3,4,其中,,2, 3,4均为4 1列矩阵,且巳已知行列式 A 4, B ().4.设A 1(B I ),则当且仅当B 2 (2畤,A 2 A..5.已知n 阶矩阵潇足关系式A 2 2A 3| 0,则(A 4I ) 1 ().1. 设A为方阵,则A 0的必要条件是()(A) 画行(歹0)元素对应成比例;(B) 任一列为其它列的线性组合;(C) 必有一列为其它列的线性组合;(D) A中至少有一歹0元素全为零.2. 设A为m阶方阵,B为n阶方阵,C,则 C ();3.4.5.6. (A) |AB;(C) ( 1)m n A|B;行列式103199301100200300204395600(B)(D)).(A) 1000;(C) 2000;(B)(D)AB;(1)mn AB.-10000;-2000.A是n阶矩阵,k是非零常数,则(kA)*((A) kA「(C) k n(n1)A n1;(B) k|A n).(D) k n 1设A,B为n阶对称矩阵,则下面四个结论不正确的是().(A)A B也是对称矩阵;(B)A B也是对称矩阵;(D) A m B m;(D)BA T AB T也是对称矩阵. 设A,B为n阶方阵,则下列结论成立的是(A) AB 0 A 0且B 0; (B) A A O;(C) AB 0 A 0或B 0;(D) A A 1.7. 设A为n阶可逆矩阵,则()(A)A 总可以只经过初等行变换变为I;(B) 对分块矩阵(A I )施行若干次初等变换,当子块变为I 时,相应地I变为A 1;(C) 由 AX BA 得 X A; (D) 以上三个结论都不正确.8. 设A 是m n 矩阵,其秩为r, C 是n 阶可逆阵,且AC B 的秩为r 1,则()正确. (A) r > r 1; (B) r v r 〔;9.(A)(B)(C) (D) (C) r r i ; (D) r 与%的关系依C 而定.设A,B 为同阶可逆方阵,则( AB BA; 存在可逆阵P,使P 1AP 存在可逆阵C,使C T AC存在可逆阵P,Q,使PAQ 10.设A,B 为n 阶非零矩阵,且AB(A )必有一个等丁零; (C ) 一个小丁 n, 一个等丁n;B;B;B.成立.O,则A 和B 的秩(). (B )都小丁 n; (D )都等丁 n.、计算题(每小题9分,共54分)1. 计算下列行列式:000100020019970000000019982. 计算下列n阶行列式的值:00000 000D n00000015. 已知矩阵A PQ,其中P 2 ,Q 2,1, 2 ,求矩阵A, A 2, A 100.13. 设矩阵Ak 1 1 11 k 1 1 1 1k 1 11,且R(A) 3,则k 为什么?1k1... ................................ • 0 6.设矩阵A 的伴随矩阵A1 00 0,且 ABA 1 BA 1 3I,其中 I 为 4 0 8阶单位矩阵,求矩阵B.四、证明题(每小题8分,共16分)1. 设A,B 是n 阶正交矩阵,且AB1,证明A B 0.0 0 10 1 032. 设A为n阶非奇异矩阵,为n元歹0, b为常数,记分块矩阵'A* A,Q计算并化简PQ;证明:矩阵Q可逆的充分必要条件是T A 1 b.1 矣4. 当A 危[1 2时,A6I,求A11.2 2。
(完整word版)高等代数期末考试题A答案

高等代数 课程 A 卷试题答案一、填空题(本题共10小题,每小题2分,满分20分. 把正确答案填在题中横线上)1. 8;2. 0;3. 0;4. 92111⎛⎫ ⎪⎝⎭;5. 1或52;6。
1()3A E E A -+=-;7. 2;8。
23a ≠; 9. 6;10。
112-⎛⎫⎪ ⎪⎝⎭。
二、选择题(本题共10小题,每小题2分,满分20分。
每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号(答题框)内)三、计算题(本题共2小题,每小题10分,满分20分.解答应写出文字说明、证明过程或演算步骤)1. 计算n阶行列式a b bb b a bb D b b ab b b ba=。
解:观察行列式,每一行只有一个a 而有1n -个b ,于是将第2列,第3列,……,第n 列分别乘以1加到第1列,得(1)...(1)...(1)..................(1)...a nb b b b a n b a b b D a n bb a b a n b b ba+-+-=+-+-[]1 (1)...(1)1 (1)...b b b a b ba nb b a b bba =+-[]1...00...0(1)00...0 000...b b b a b a n b a b a b-=+--- []1(1)()n a n b a b -=+--2. 设111111111A ⎛⎫ ⎪=- ⎪ ⎪-⎝⎭,123124051B ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭,求A AB 23-.解:1111231111111242111111051111323AB A -------⎛⎫⎛⎫⎛⎫⎪⎪ ⎪-= ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭05822221322305622221720.2902224292-⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=---=-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭四、解答题(本题共2小题,第1小题15分、第2小题10分,满分25分。
《高等代数》上A卷答案

仰恩大学2006—2007学年第二学期期末试卷《高等代数》上A 卷答案适用班级:06数学 时间:90分钟 形式:闭卷评分说明:1,评分方式为累计计分;2,不再计中间分.一,(每题6分,共30分)简答题:以下各题,应写出简单的解答过程及依据。
1,解: 将所有列加到第1列上, 2分则第1列与第4列成比例, 4分 故原式0=. 6分2,证明:由题设,T A A =-,T B B =, 1分()()()T T T T T T T AB BA AB BA B A A B +=+=+ 3分()()()B A A B AB BA =-+-=-+, 5分即AB BA +为反对称矩阵. 6分 3,解:由20A λ=->, 2分得到2λ>, 3分 即当2λ>时正定. 6分4,证明: 11A AA --=* , 1分11*()()A A A --∴=***, 3分∴*1()()A A A -=*** 4分1211()n n AA A AA ----==. 6分5,解:方程组的系数行列式1210121001a a -=--, 3分 当10a -≠即1a ≠时方程组有唯一解. 6分二,(12分)解:当n =2时,11212221212x x D x x x x ++==-++;1分当n >2时,将第一列乘以-1后加到其余各列, 则得到1211....111. (1).............. (1)1 (1)n n x n x n D x n +-+-=+- 3分其中有两列成比例,故0n D =. 5分 于是当n=2时,12n D x x =-;当n >2时,0n D =. 6分三,(13分)证明:由AB A B =+,得()()E A E B E --=; 2分()()E B E A E ⇒--=, 3分即得BA A B =+; 5分∴AB BA =. 6分四,(15分)解: 对A B ⎛⎫⎪⎝⎭进行初等列变换得到021213334123231A B ⎛⎫ ⎪-⎪⎛⎫ ⎪=-- ⎪⎪⎝⎭ ⎪ ⎪-⎝⎭ 2分120312433321132⎛⎫ ⎪- ⎪⎪→-- ⎪ ⎪ ⎪-⎝⎭ 6分 100010.001211474⎛⎫ ⎪ ⎪⎪→ ⎪-- ⎪ ⎪-⎝⎭11分 211474X --⎛⎫∴= ⎪-⎝⎭. 15分五,(15分)解:对增广矩阵进行初等行变换化为最简形矩阵,得到1111011131112312A ---⎛⎫ ⎪=-- ⎪ ⎪---⎝⎭1分12131111000241001212r r r r ----⎛⎫ ⎪→- ⎪ ⎪--⎝⎭4分 223210.511011200121200000r r r r r ⋅++--⎛⎫ ⎪→- ⎪ ⎪⎝⎭7分 可见()()R A R A -=,方程组有解,并有1243412212x x x x x =++⎧⎨=+⎩ 9分 取240x x ==,则1312x x ==,即得原方程组的一个特解0(12,0,12,0)γ=. 10分下面求导出组的基础解系:导出组与 124342x x x x x =+⎧⎨=⎩ 同解.取241,x x ==0,得1(1,1,0,0)η=;取240,x x ==1,得2(1,0,2,1)η=.此即为导出组的基础解系, 13分 于是原方程组的通解为 0112212,()k k kk R γγηη=++∈、. 15分 六,(15分)解 (1)二次型可化为222123121323(1)(1)(1)222x x x x x x x x x λλλ-+-+----, 1分它对应的矩阵是111111111λλλ---⎛⎫ ⎪--- ⎪ ⎪---⎝⎭; 2分 由二次型是正定的⇔它的矩阵的所有顺序主子式全大于零, 5分 可得到10λ->,(2)0λλ->,2(3)0λλ->, 9分 它等价于3λ>,即二次型是正定的3λ⇔>. 10分 (2)当3λ=时,二次型可化为222121323()()()0x x x x x x -+-+-≥, 13分 故二次型是半正定的. 15分。
西南科技大学高代期末考试A(上)

(2)求线性变换 A 关于基 ε1 = (1, 0, 0),ε2 = (0,1, 0),ε3 = (0,1,1) 的矩阵.
⎛0 1 2⎞
3.(10
分)设
A
=
⎜ ⎜
1
14⎟ ⎟,求 NhomakorabeaA−1
.
⎜⎝ 2 −1 0 ⎟⎠
4.(8 分)求向量组α1 = (1, −1,1),α2 = (1, 0, 2),α3 = (1,1,3),α4 = (1,1, −4) 的秩和一个 极大无关组.
.
−2 −7 3
4 . 设 A 为 m × n 矩 阵 , 齐 次 线 性 方 程 组 AX = 0 的 解 空 间 的 维 数 为 k , 则
rank( A) =
.
5.向量组α1 = (1, 2,1),α2 = (8, 7, −1),α3 = (8, −81, 21),α4 = (1,5,9) 是线性
0 0 " −1 0 0 0 " 0 −1
n
………4 分
………2 分
………2 分
2.(12 分)
解:(1)设α = (x1, x2 , x3 ), β = ( y1, y2 , y3 ) ∈V , k ∈ K ,由变换 A 的定义,有
A(α + β ) = (2(x1 + y1) − ( x2 + y2 ),( x1 + y1) − (x3 + y3 ), (x2 + y2 ))
h = JJ6JVG ABJCJDJG =
6× 41
= 82 .
BC × BD (3, 4, −1) × (6, 0, −3) 9
………5 分
7.(8 分)证明: 设α1,α2,",αr 是线性子空间 W 中任意 r 个线性无关的向量.
高数a上册期末试题及答案

高数a上册期末试题及答案一、选择题(每题5分,共20题)1. 设函数 $f(x) = \sqrt{3x-2}$,则其定义域为A. $(-\infty, \frac{2}{3}]$B. $\left[ \frac{2}{3}, \infty \right)$C. $[\frac{2}{3}, \infty)$D. $(-\infty, \frac{2}{3}) \cup [\frac{2}{3}, \infty)$答案:C2. 函数 $y = \sin^2 x + \cos^2 x$ 的值域为A. $(-\infty, 1]$B. $[0, 1]$C. $[1, \infty)$D. $[\frac{1}{2}, 1]$答案:B3. 设函数 $f(x) = e^x \ln x$,则 $f'(x) = $A. $e^x \ln x$B. $e^x \left( \frac{1}{x} + \ln x \right)$C. $e^x \left( \ln x - \frac{1}{x} \right)$D. $e^x \left( \frac{1}{x} - \ln x \right)$答案:B4. 若直线 $y = 3x + b$ 与抛物线 $y = ax^2 + bx + 1$ 相切,则 $a + b = $A. 2B. 3C. 4D. 5答案:D5. 函数 $f(x) = \frac{x-1}{\sqrt{x^2 + 1}}$ 的渐近线为A. $y = x - 1$B. $y = x + 1$C. $y = -x + 1$D. $y = -x - 1$答案:A6. 函数 $f(x) = \ln(1 + e^{2x})$ 的反函数为A. $f^{-1}(x) = \ln(x) - \ln(1 - x^2)$B. $f^{-1}(x) = \ln(x^2 - 1)$C. $f^{-1}(x) = \frac{e^x - 1}{2}$D. $f^{-1}(x) = \frac{1}{2} \ln(x) + \ln(1 - x)$答案:D7. 设函数 $f(x) = \arcsin (\sin x)$,则当 $x = \frac{5\pi}{6}$ 时,$f(x) =$A. $\frac{5\pi}{6}$B. $\frac{\pi}{6}$C. $\frac{\pi}{3}$D. $\frac{2\pi}{3}$答案:C8. 函数 $f(x) = \frac{\sin x}{\cos^2 x}$ 的最大值为A. 1B. $\sqrt{3}$C. 2D. $2\sqrt{3}$答案:D9. 函数 $f(x) = x^2 + 2x + 1$ 在区间 $[-1, 1]$ 上的最大值为A. 0B. 1C. 2答案:D10. 函数 $f(x) = \frac{x^2 - 1}{x^2 + 1}$ 的图像关于直线 $x = a$ 对称,则 $a = $A. 1B. 0C. -1D. 2答案:B11. 设 $\sin \alpha = \frac{1}{4}$,$\cos \beta = \frac{4}{5}$,且$\alpha$ 和 $\beta$ 都是第二象限角,则下列四个式子中成立的是A. $\sin (\alpha - \beta) = -\frac{3}{4}$B. $\sin (\alpha + \beta) = \frac{3}{8}$C. $\cos (\alpha - \beta) = \frac{1}{5}$D. $\cos (\alpha + \beta) = \frac{2}{5}$答案:C12. 如果点 $A(1, 2)$ 在抛物线 $y = -x^2 + 3x + k$ 上,那么 $k = $A. -3B. -5D. -9答案:B13. 设函数 $f(x) = x^3 - 3x^2 - 4x + 12$,则 $f'(x)$ 的零点有A. -2, 2B. -1, 3C. -4, 3D. -1, 4答案:A14. 设点 $P(x, y)$ 满足 $y^2 = px$,其中 $p > 0$ 是常数,则焦点所在的直线方程为A. $y = -\frac{p}{2}$B. $x = -\frac{p}{2}$C. $y = \frac{p}{2}$D. $x = \frac{p}{2}$答案:B15. 函数 $f(x) = x^3 - 3x + 1$ 在区间 $[0, 2\pi]$ 上的最小值为A. -1B. 0D. 2答案:A16. 设直线 $y = 2x + 1$ 与曲线 $y = x^2 + bx + c$ 相切,则 $b + c = $A. 0B. $\frac{1}{2}$C. 1D. 2答案:C17. 设函数 $f(x) = (1 - x^2) \cos x$,则 $f''(x)$ 的一个零点在A. $(0, \frac{\pi}{2})$B. $(0, \pi)$C. $(\pi, 2\pi)$D. $(\pi, 3\pi)$答案:B18. 设函数 $f(x) = \sin^2 x - \sqrt{3} \sin x \cos x + \cos^2 x$,则$f(x)$ 的最大值为A. 2B. $2\sqrt{2}$C. 3D. $2 + \sqrt{3}$答案:C19. 设函数 $f(x) = e^x$,$g(x) = x^2$,则 $f(x) \cdot g(x) = $A. $e^{x^2}$B. $x^2 e^x$C. $x^2 e^{x^2}$D. $x^2 + e^x$答案:B20. 设 $a > 0$,则 $\lim\limits_{x \to +\infty} \frac{x^a}{e^x}$ 的值为A. 0B. $\frac{1}{e}$C. 1D. $+\infty$答案:A二、计算题(每题10分,共4题)1. 求函数 $f(x) = \frac{2x^2 - 3x + 1}{x - 1}$ 的极限 $\lim\limits_{x\to 1} f(x)$.解:使用“分子分母可约”的性质,可将函数 $f(x)$ 化简为 $f(x) = 2x - 1$,则 $\lim\limits_{x \to 1} f(x) = \lim\limits_{x \to 1} (2x - 1) = 2(1) - 1 = 1$.答案:12. 求曲线 $y = e^x$ 与直线 $y = kx$ 相交的两个点的坐标,其中 $k > 0$ 是常数.解:将曲线 $y = e^x$ 和直线 $y = kx$ 代入方程中,得到 $e^x = kx$,然后可以使用迭代法或图像法求得相交点的坐标.答案:相交点的坐标为 $(x_1, e^{x_1})$ 和 $(x_2, e^{x_2})$,其中$x_1$ 和 $x_2$ 是满足方程 $e^x = kx$ 的两个解.3. 求曲线 $y = \sin x$ 与直线 $y = x$ 相交的点的个数,并说明理由.解:将曲线 $y = \sin x$ 和直线 $y = x$ 代入方程中,得到 $\sin x = x$,然后可以通过分析函数的周期性和图像来确定相交点的个数.答案:方程 $\sin x = x$ 的解存在无穷个,但相交点的个数取决于给定的区间. 在区间 $[0, \pi]$ 上,方程有一个解;在区间 $[2\pi, 3\pi]$ 上,方程又有一个解. 因此,相交点的个数是不确定的.4. 求函数 $y = x^2 + x$ 在区间 $[-2, 2]$ 上的最大值和最小值,并求出取得最大值和最小值的点.解:首先求导数 $y' = 2x + 1$,然后令 $y' = 0$,解得 $x = -\frac{1}{2}$,将 $x = -2, -\frac{1}{2}, 2$ 代入函数 $y = x^2 + x$,得到对应的 $y$ 值. 最大值为 $y = y_{\text{max}}$ 对应的点为 $(-\frac{1}{2},y_{\text{max}})$,最小值为 $y = y_{\text{min}}$ 对应的点为 $(-2,y_{\text{min}})$ 和 $(2, y_{\text{min}})$.答案:最大值为 $y_{\text{max}} = \frac{5}{4}$,取得最大值的点为 $(-\frac{1}{2}, \frac{5}{4})$;最小值为 $y_{\text{min}} = -2$,取得最小值的点为 $(-2, -2)$ 和 $(2, -2)$.三、证明题(每题20分,共2题)1. 证明函数 $f(x) = \frac{x^3}{3} - x^2 + 2x$ 的导数 $f'(x)$ 恒大于零.证明:求导数 $f'(x) = x^2 - 2x + 2$,我们可以通过判别式来判断 $f'(x)$ 的正负性.判别式为 $\Delta = (-2)^2 - 4(1)(2) = 4 - 8 = -4$,由于 $\Delta < 0$,所以判别式小于零,即 $f'(x)$ 的二次项系数小于零,说明二次项的系数是正的,从而导数 $f'(x)$ 恒大于零.证毕.2. 证明函数 $f(x) = x^3 - 3x^2 + 3$ 的图像关于直线 $x = 1$ 对称.证明:要证明函数的图像关于直线 $x = 1$ 对称,需证明对于任意$x$ 值,函数 $f(x)$ 和 $f(2 - x)$ 的函数值相等.将 $f(x) = x^3 - 3x^2 + 3$ 代入 $f(2 - x)$,得到 $f(2 - x) = (2 - x)^3 -3(2 - x)^2 + 3$,对其进行展开和化简得到 $f(2 - x) = (2 - x)^3 - 3(2 -x)^2 + 3 = x^3 - 3x^2 + 3 = f(x)$,即 $f(x) = f(2 - x)$,证明了函数的图像关于直线 $x = 1$ 对称.证毕.四、应用题(每题50分,共1题)1. 求函数 $f(x) = x^3 + x^2 - 3x$ 的驻点及其对应的极值.解:求导函数 $f'(x) = 3x^2 + 2x - 3$,令 $f'(x) = 0$,求得驻点的 $x$ 坐标,然后将其代入原函数求得对应的 $y$ 坐标.求导的一阶导数方程为 $f'(x) = 3x^2 + 2x - 3 = 0$,通过求根公式求得 $x = -1$ 和 $x = \frac{1}{3}$,将其代入原函数 $f(x)$ 得到对应的$y$ 坐标.将 $x = -1$ 代入 $f(x)$,得到 $f(-1) = (-1)^3 + (-1)^2 - 3(-1) = -1 + 1+ 3 = 3$,将 $x = \frac{1}{3}$ 代入 $f(x)$,得到 $f(\frac{1}{3}) =(\frac{1}{3})^3 + (\frac{1}{3})^2 - 3(\frac{1}{3}) = \frac{1}{27} +\frac{1}{9} - 1 = 0$.因此,函数 $f(x) = x^3 + x^2 - 3x$ 的驻点及其对应的极值为 $(-1, 3)$ 和 $(\frac{1}{3}, 0)$.答案:驻点为 $(-1, 3)$ 和 $(\frac{1}{3}, 0)$,分别对应极大值和极小值.。
高等代数期末复习试题

数学系《高等代数》期末考试试卷年级 专业 学号 姓名 注:考试时间120分钟,试卷满分100分 。
题号一二三四五总分签 名得分一得 分阅卷教师一.判断题(正确的在题后的括号内打“√”;错误的在题后的括号内打“×”.每小题2分,共18分)1.向量空间一定含有无穷多个向量. ( )2.若向量空间的维数,则没有真子空间. ( )3.维向量空间中由一个基到另一个基的过渡矩阵必为可逆矩阵. ( )4.线性变换把线性无关的向量组映成线性无关的向量组. ( )5.每一个线性变换都有本征值. ( )6.若向量是线性变换的属于本征值的本征向量,则由生成的子空间为的不变子空间. ( )7.保持向量间夹角不变的线性变换是正交变换. ( )8.两个复二次型等价的充分必要条件是它们有相同的秩. ( )9. 若两个阶实对称矩阵均正定,则它们的和也正定. ( )二得分阅卷教师二.单项选择题(在每小题的四个备选答案中,选出一个正确的答案,并将其号码填在题目的括号内.每小题2分,共10分) 1. 下列命题不正确的是 ( ).A. 若向量组线性无关,则它的任意一部分向量所成的向量组也线性无关;B. 若向量组线性相关,则其中每一个向量都是其余向量的线性组合;C.若向量组线性无关,且每一可由向量线性表示,则; D. 维向量空间的任意两个基彼此等价. 2. 下列关于同构的命题中,错误的是( ).A.向量空间的可逆线性变换是到的同构映射;B.数域上的维向量空间的全体线性变换所成向量空间与数域上的所有阶矩阵所成向量空间同构; C.若是数域上向量空间到的同构映射,则是到的同构映射;D.向量空间不能与它的某一个非平凡子空间同构.3.阶矩阵有个不同的特征根是与对角矩阵相似的 ( ).A.充分而非必要条件; B.必要而非充分条件; C.充分必要条件; D. 既非充分也非必要条件.装 订线4.二次型的矩阵是( ).A.; B.;C.; D.5.实二次型正定的充分且必要条件是 ( ).A.; B.秩为3; C.合同于三阶单位矩阵; D.对某一有.三.填空题(每小题分,共101. 复数域作为实数域上的向量空间,它的一个基是________.2. 设是数域上任意,定义,则是一个线性变换,且的核的维数等于______.3. 若是一个正交矩阵,则的行列式=________.4. 在欧氏空间中向量与的夹角=______.元二次型可分为_______类,属于同一类的二次型彼此等价,属于不同类的二次型互不等价.四得分阅卷教师四.计算题(每小题14分,共42分)1.求齐次线性方程组的解空间的一个基,再进一步实施正交化,求出规范正交基.2.设,求的特征根及对应的特征向量.问是否可以对角化?若可以,则求一可逆矩阵,使为对角形.3. 写出3元二次型的矩阵.试用非奇异的线性变换,将此二次型变为只含变量的平方项.得 分阅卷教师五五.证明题(每小题10分,共20分)1.设为阶矩阵的属于不同特征根,分别是的属于的特征向量,证明不是的特征向量.2.设是维欧氏空间的正交变换,且为单位变换,是关于的某一规范正交基的矩阵,证明为对称矩阵.数学系《高等代数》期末考试试卷(A 卷)年级 专业 学号 姓名 注:考试时间120分钟,试卷满分100分 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《高等代数》(上)期末试卷(A )
一、填空题(每空3分,共15分)
1.设方阵1112223
3
3b x c A b x c b x c ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,1
112
223
3
3b y c B b y c b y c ⎡⎤
⎢⎥=⎢
⎥⎢⎥⎣⎦
,且2,3A B =-=, 则行列式2A B += .
2.已知A 是一个34⨯矩阵,且秩()2A =,而102020103B ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦
,则秩()BA = . 3. 多项式2005
20042
322006()(54)31(8112)f x x x x x x ⎡⎤=--+-+⎣⎦
的所有系数之和
= ,常数项= .
4. ()f x 为多项式,用1x -除时余式为3,用3x -除时余式为5,则用(1)(3)x x --除时余式为 .
二、选择题(每题3分,共12分)
1.设n 维向量组12345,,,,ααααα的秩为3,且满足135230,ααα+-=
242,αα=则向量组的一个极大无关组为( )
A . 125,,ααα;
B . 124,,ααα; C. 245,,ααα; D. 135,,ααα. 2. A 是m n ⨯矩阵,B 是n m ⨯矩阵,则( )
A . 当m n >时,必有行列式0A
B ≠; B . 当m n >时,必有行列式0AB =;
C . 当n m >时,必有行列式0AB ≠;
D . 当n m >时,必有行列式0AB =.
3.设,A B 都是可逆矩阵,则矩阵0A C B ⎡⎤⎢⎥⎣⎦的逆矩阵为( )
A . 1
1
10A C
B ---⎡⎤
⎢⎥⎣⎦; B . 1110B C A ---⎡⎤⎢⎥⎣⎦
;
C . 1
11
10A A CB B ----⎡⎤
⎢⎥-⎣⎦; D .11110A B CA B ----⎡⎤
⎢⎥-⎣⎦
. 4.已知()p x 是数域P 上的不可约多项式,(),()[],f x g x P x ∈ 则下列命题中错误的是( )
A .若()|(),p x f x 则((),())1p x f x =;
B .若((),())1,p x f x =则()|()p x f x ;
C .若()()(),p x f x g x 且()|(),p x f x 则((),())1p x g x ≠;
D .若()()(),p x f x g x 则((),())1f x g x =.
三、计算题(共51分)
1. (12分)计算行列式111212122212
n n n n n n
a b a b a b a b a b a b D a b a b a b ------=
---.
2. (15分),a b 取什么值时,线性方程组1234512345
234512345132322635433x x x x x x x x x x a x x x x x x x x x b
++++=⎧⎪+++-=⎪⎨+++=⎪⎪+++-=⎩
有解?在有解的情形,求一般解.
3.(12分)已知AX B X =+,其中012114210A ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦, 112341B -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦
,求矩阵.X 4.(12)设 5
4
3
2
()2101616146f x x x x x x =-+-+-,
分别求()f x 在复数域、实数域和有理数域上的标准分解式. 四、证明题(共22分)
1. (12分)设*η 是非齐次线性方程组AX β=的一个解,12,,,n r ξξξ-是对应的齐
次线性方程组0AX =的一个基础解系,证明:
(1)12*,,,,n r ηξξξ-线性无关;
(2)12*,*,*,
,*n r ηηξηξηξ-+++线性无关.
(2、3题任意选作一题,10分)
2.设,A B 为n 阶矩阵,2
2
,,A A B B ==证明:2
()A B A B +=+当且仅当
0.AB BA ==
3.设(),()f x g x 是数域P 上的多项式,()f x 与()g x 的最小公倍式指的是[]P x 中满足以下条件的一个多项式():m x (a )()()f x m x 且()()g x m x ;
(b )如果[][]h x P x ∈且()()f x h x ,()()g x h x ,那么()()m x h x .
(1)证明:[]P x 中任意两个多项式都有最小公倍式,并且除了可能的零次因式的差别外,是唯一的;
(2)设(),()f x g x 都是最高次项系数是1的多项式,令[(),()]f x g x 表示()f x 与
()g x 最高次项系数是1的那个最小公倍式,证明:
()()()(),()[(),()].f x g x f x g x f x g x =。
