等积变形(附答案)
小学五年级奥数精讲等积变形求面积(含答案)

小学奥数精讲:等积变形求面积“三角形的面积等于底与高的积的一半”这个结论是大家熟知的,据此我们立刻就可以知道: 等底等高的两个三角形面积相等. 这就是说两个三角形的形状可以不同,但只要底与高分别相等,它们的面积就相等,当然这个问题不能反过来说成是“面积相等的两个三角形底与高一定分别相等”.另一类是两个三角形有一条公共的底边,而这条底边上的高相等,即这条底边的所对的顶点在一条与底边平行的直线上,如右图中的三角形A 1BC 与A 2BC 、A 3BC 的面积都相等。
图形割补是求图形面积的重要方法,利用割补可以把—些形状不规则的图形转换成与之面积相等但形状规则的图形,或把不易求面积的图形转换成易求面积的图形.利用添平行线或添垂线的办法,常常是进行面积割补的有效方法,利用等底等高的三角形面积相等这个性质则是面积割补的重要依据,抓住具体的图形的特点进行分析以确定正确的割补方法则是面积割补的关键.进行图形切拼时,应该有意识地进行计算,算好了再动手寻找切拼的方案.不要盲目地乱动手.本讲中.的几个例子都是经过仔细计算才切拼成功的。
例1、已知三角形ABC 的面积为1,BE = 2AB ,BC =CD ,求三角形BDE 的面积?例2、如下图,A 为△CDE 的DE 边上中点,BC=31 CD ,若△ABC(阴影部分)面积为5平方厘米,求△ABD 及△ACE 的面积.例3、 2002年在北京召开了国际数学家大会,大会会标如下图所示,它是由四个相同的直角基本概念例题分析三角形拼成(直角边长为2和3),问:大正方形面积是多少?例4、下图中,三角形ABC和DEF是两个完全相同的直角边长等于9厘米的等腰直角三角形,求阴影部分的面积.练习提高1、如图,已知平行四边形ABCD的面积是60平方分米,E、F分别是AB、AD边上的中点,图中阴影部分的面积是多少平方分米?2、右图中的长方形ABCD的长是20厘米,宽是12厘米,AF=BE,图中阴影部分的面积是多少平方厘米?3、如图,四边形ABCD 是平行四边形,DC =CE ,如果△BCE 的面积是15平方厘米,那么梯形ABED 的面积是多少平方厘米?4、正方形ABCD 的边长是12厘米,已知DE 是EC 长度的2倍,三角形DEF 的面积是多少平方厘米?CF 长多少厘米?5、如图,在平行四边形ABCD 中,AE =ED ,BF =FC ,CG =GD ,平行四边形ABCD 的面积是阴影三角形EFG 的多少倍?(4)6、一个长方形被两条直线分成四个长方形,其中三个面积分别是20平方米,25平方米和30平方米,阴影部分的面积是多少平方米?7、如右图,平行四边形ABCD 的面积是240平方厘米,如果平行四边形内任取一点0,连接AO 、BO 、CO 、DO ,三角形AOD 与三角形BOC 的面积和的21,加上三角形AOB 与三角形DOC 的面积和的31,结果是多少?8、图8-17中,三角形ABC的面积是30平方厘米,D是BC的中点,AE的长是ED的2倍,求三角形CDE的面积.9、如图,正方形的边长为10厘米,用一根铁丝弯成直角,把这根铁丝放到正方形上,使直角顶点与正方形的中心O重合,问正方形在直角内部的部分有多大面积?答案:【例题分析】例1. 4例2.三角形ABD=10平方厘米三角形ACE=15平方厘米例3. 13例4. 27【练习提高】1. 22.52. 1203. 454. 三角形DEF=24平方厘米 CF=6厘米5. 4倍6. 37.57. 1008. 59. 25。
小学四年级奥数题三角形的等积变形及答案【三篇】

小学四年级奥数题三角形的等积变形及答案【三篇】【第一篇】1. 三角形把一个等边三角形分别分成8块和9块形状、大小都一样的三角形.分析分成8块的方法是:先取各边的中点并把它们连接起来,得到4个大小、形状相同的三角形,然后再把每一个三角形分成一半,得到如下左图所示的图形.分成9块的方法是:先把每边三等分,然后再把分点彼此连接起来,得到加上右图所示的符合条件的图形.2.比较比较下面两个积的大小:A=987654321×123456789,B=987654322×123456788.分析经审题可知A的第一个因数的个位数字比B的第一个因数的个位数字小1,但A的第二个因数的个位数字比B的第二个因数的个位数字大1.所以不经计算,凭直接观察不容易知道A和B哪个大.但是无论是对A或是对B,直接把两个因数相乘求积又太繁,所以我们开动脑筋,将A和B先进行恒等变形,再作判断.解: A=987654321×123456789=987654321×(123456788+1)=987654321×123456788+987654321.B=987654322×123456788=(987654321+1)×123456788=987654321×123456788+123456788.因为 987654321>123456788,所以 A>B.【第二篇】如图,四边形ABCD和四边形DEFG都是正方形,已知三角形AFH的面积为6平方厘米,求三角形CDH的面积.三角形面积答案:通常求三角形的面积,都是先求它的底和高.题目中没有一条线段的长度是已知的,所以我们只能通过创造等积的方法来求.直接找三角形HDC 与三角形AFH 的关系还很难,而且也没有利用"四边形ABCD和四边形DEFG 是正方形"这一条件.我们不妨将它们都补上梯形DEFH 这一块.寻找新得到大三角形CEF 和大直角梯形DEFA 之间的关系.经过验算,可以知道它们的面积是相等的.从而得到三角形 HDC与三角形AFH面积相等,也是6平方厘米.【第三篇】如下图,BE=2AB,BC=CD。
小学数学《三角形的等积变形》练习题(含答案)

三角形ABC的面积=(12+4)×高÷2=8×高
三角形ADC的面积=4×高÷2=2×高
所以,三角形ABC的面积是三角形ABD面积的4/3倍;三角形ABD的面积是三角形ADC面积的3倍。
巩固理解结论:两个三角形等高时,面积的倍数=底的倍数
【例2】如右图,E在AD上,AD垂直BC,AD=12厘米,DE=3厘米。
而四边形CEFH是它们的公共部分,
所以三角形DHF的面积=三角形BCH的面积,
进而可得阴影面积=三角形BDF的面积=三角形BCD的面积= 10×10÷2=50(平方厘米)。
法2:连接CF,那么CF平行BD,
所以,阴影面积=三角形BDF的面积=三角形BCD的面积=50(平方厘米)。
附加题目
【附1】 如右图,四边形ABCD面积为1,且AB=AE,BC=BF,DC=CG,AD=DH.求四边形EFGH的面积.
巩固理解结论:两个三角形等底时,面积的倍数=高的倍数
【例3】用两种不同的方法,把任意一个三角形分成四个面积相等的三角形.
分析:法1:如图(1),将BC边四等分,连接各等分点,则△ABD、△ADE、△AEF、△AFC面积相等。
法2:如图(2),D是BC的二等分点,E、F是AC、AB的中点,从而得到四个等积三角形△ADF、△BDF、△DCE、△ADE.
【例7】图中△AOB的面积为15cm2,线段OB的长度为OD的3倍,求梯形ABCD的面积.
分析:
【例8】(北京市第一届“迎春杯”刊赛)如右图.将三角形ABC的BA边延长1倍到D,CB边延长2倍到E,AC边延长3倍到F.如果三角形ABC的面积等于l,那么三角形DEF的面积是?
分析:连结AE、BF、CD(如右下图).由于三角形AEB与三角ABC的高相等,而底边EB=2BC,所以三角形AEB的面积是2.同理,三角形CBF的面积是3,三角形ACD的面积是1.
【小升初专项训练】04 等积变形

第5讲等积变形第一关三角形的等积变形【例1】如图,在等腰直角三角形ABC中,已知AB的长是7厘米,那么这个直角三角形的面积为 平方厘米。
【答案】12.25【例2】如图,E、F分别是梯形ABCD两腰上的中点,已知阴影部分的面积是43c㎡,那么梯形ABCD 的面积是多少?【答案】172【例3】如图:三条直线互相平行,l1与l3之间的距离是7厘米,l2上AB=4厘米.求阴影部分三角形的面积是多少平方厘米? 【答案】14【例4】你能看出下面两个阴影部分A与B面积的大小关系吗?(两个长方形面积相等)【答案】A与B的面积相等【例5】如图,在斜边长为20cm的直角三角形ABC中去掉一个正方形EDFB,留下两个阴影部分直角三角形AED和DFC.若AD=8cm,CD=12cm,则阴影部分面积为多少?给出答案并说明你的计算依据.【答案】48【例6】如图,在直角三角形中有一个正方形,已知BD=10厘米,DC=7厘米,阴影部分的面积是多少?【答案】35平方厘米【例7】如图,梯形ABCD的面积是36,下底长是上底长的2倍,阴影三角形的面积是多少?【答案】16【例8】下图中阴影部分甲的面积与阴影部分乙的面积哪个大?【答案】图中甲乙的面积相等【例9】如图,在三角形ABC中,D是BC上靠近C的三等分点,E是AD中点,已知三角形ABC的面积为1,那么图中两个阴影三角形面积之和是多少?【答案】0.4【例10】已知△ABC面积为5,且BD=2DC,AE=ED,求阴影部分面积.要求写出关键的解题推理过程.【答案】2【例11】如图,将一个梯形分成四个三角形,其中两个三角形的面积分别为10与12.已知梯形的上底长度是下底的.请问:阴影部分的总面积是多少?【答案】23【例12】如图,已知梯形ABCD中,CD=10,梯形ABCD的高是4,那么阴影部分的面积是多少。
【答案】20【例13】(1)如图1,阴影部分的面积是多少?(2)如图2,一个长方形长4厘米,宽3厘米.A为长方形内的任意一点,阴影部分的面积是多少?【答案】(1)100;(2)6【例14】如图,在图中△ABE、ADF和四边形AECF面积相等.阴影部分的面积是多少?【答案】15【例15】如图,两个正方形(单位:厘米)中阴影部分的面积是多少平方厘米?【答案】8【例16】由面积为1,2,3,4的矩形拼成如图的长方形,图中阴影部分的面积为多少?【答案】【例17】如图所示,正方形ABCD的对角线BD长20厘米,BDFE是长方形.那么,五边形ABEFD的面积是多少平方厘米。
小学数学《三角形的等积变形》练习题(含答案)

内容概述
我们已经知道三角形面积的计算公式:三角形面积=底×高÷2
从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积.
如果三角形的底不变,高越大(小),三角形面积也就越大(小);
如果三角形的高不变,底越大(小),三角形面积也就越大(小);
这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的1/3,则三角形面积与原来的一样。这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.
于是:三角形ABD的面积=12×高÷2=6×高
三角形ABC的面积=(12+4)×高÷2=8×高
三角形ADC的面积=4×高÷2=2×高
所以,三角形ABC的面积是三角形ABD面积的4/3倍;三角形ABD的面积是三角形ADC面积的3倍。
巩固理解结论:两个三角形等高时,面积的倍数=底的倍数
【例2】如右图,E在AD上,AD垂直BC,AD=12厘米,DE=3厘米。
【例6】如右图所示,在平行四边形ABCD中,E为AB的中点,AF=2CF,三角形AFE(图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?
【例7】图中△AOB的面积为15cm2,线段OB的长度为OD的3倍,求梯形ABCD的面积.
【例8】(北京市第一届“迎春杯”刊赛)如右图.将三角形ABC的BA边延长1倍到D,CB边延长2倍到E,AC边延长3倍到F.如果三角形ABC的面积等于l,那么三角形DEF的面积是?
例题精讲
高斯小学奥数四年级上册含答案第21讲_等积变形
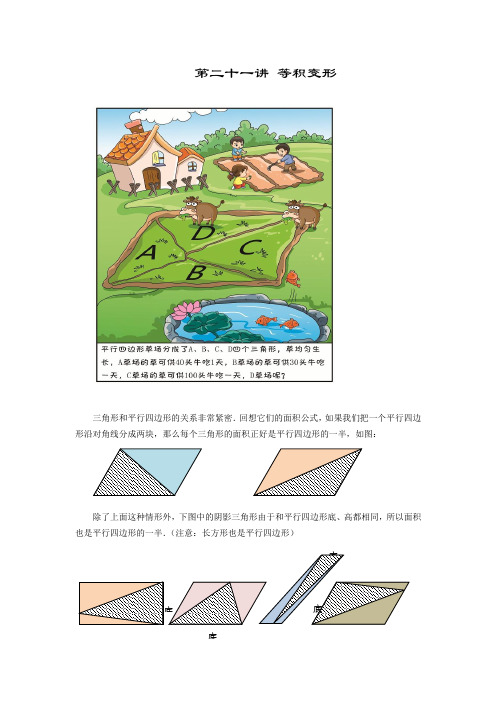
第二十一讲等积变形三角形和平行四边形的关系非常紧密.回想它们的面积公式,如果我们把一个平行四边形沿对角线分成两块,那么每个三角形的面积正好是平行四边形的一半,如图:除了上面这种情形外,下图中的阴影三角形由于和平行四边形底、高都相同,所以面积也是平行四边形的一半.(注意:长方形也是平行四边形)底底底底如图,已知平行四边形ABCD 的面积是100平方厘米,E 是其中的任意一点,那么图中阴影部分面积是多少平方厘米?「分析」辅助线把整个图形分成了左右两个平行四边形,两个阴影三角形与它们分别有什么关系呢?练习1如图,E 是平行四边形ABCD 中的任意一点,已知△AED 与△EBC 的面积和是40平方厘米,那么图中阴影部分的面积是多少?下图中,两条平行线间有四个三角形:三角形OAB 、三角形P AB 、三角形MAB 和三角形NAB ,它们的底相同,都是AB ;高相等,都是两条平行线间的距离,所以这四个三角形的面积是相等的.进一步,我们可以在直线ON 上任取若干个点,这些点分别与A 、B 两点形成若干个同底等高的三角形,这些三角形的面积是相等的.我们把这种“底相同,高相等”的情况简称为“同底等高”.“同底等高”是我们最早碰到的三角形等积变形的情形,而“等高”最常见的情况就是平行线间的距离相等.利用平行线间的距离相等,构造同底等高的三角形,是很常见的三角形等积变形.ADAD底AB如图,平行四边形ABCD 的底边AD 长20厘米,高CH 为9厘米;E 是底边BC 上任意的一点,那么两个阴影三角形的面积之和是多少平方厘米? 「分析」能否通过等积变形,把两个三角形变成一个三角形呢? 练习2如图,平行四边形ABCD 的面积是100平方厘米,那么阴影部分的面积是多少平方厘米?例题3如图所示,ABFE 和CDEF 都是长方形,AB 的长是4厘米,BC 的长是3厘米.那么图中阴影部分的面积是多少平方厘米?「分析」能否通过等积变形,把上层与下层的三角形分别变成一个三角形呢? 练习3如图,ABCD 和CDEF 都是平行四边形,四边形ABFE 面积为60平方厘米.请问:阴影部分面积是多少平方厘米?在利用同底等高三角形计算面积的题目中,最重要的一步就是去寻找其中的平行线,进 而寻找同底等高....、面积相等....的三角形. BEFDEABD例题4如图,梯形ABCD 中,E 是对角线AC 上的一点,已知DE 和AB 平行,那么与△ADC 面积相等的三角形一共有哪几个?「分析」要找同底等高面积相等的三角形,首先必须找到平行线哦!练习4如图,梯形ABCD 中,共有几个三角形?其中面积相等的三角形共有哪几对?画辅助线是解决几何问题最常用、最重要的方法之一,一条好的辅助线,往往能把无从下手的复杂题目变得非常简单.一般我们习惯把辅助线画成虚线.在上一讲中,我们已经接触过了一些需要画辅助线解决的题目,在利用同底等高三角形计算面积的题目中,我们往往需要自己画出平行线.....去构造、寻找同底等高的三角形进而进行面积转化. 例题5如图,大正方形的边长是10厘米,小正方形的边长是8厘米.求阴影部分的面积.「分析」图中的三角形底、高都是未知并且不可求的,能否通过等积变形,寻找与它们同底等高、面积相等的三角形呢?记得先找平行线哦!ABCDEADBO如右图,梯形ABCD 中,对角线相交于O 点,由于AD 与BC 平行,那么就有△ABC 与△DBC 同底等高、面积相等,△ABD 与△ACD 同底等高、面积相等.那么这个图中还有没有其他面积相等的三角形呢?我们观察一下,△ABC 与△BCD 都包含有△OBC ,而△ABC 与△BCD 面积相等,那么就有△ABO 与△CDO 面积相等.我们把梯形中出现的这第三对三角形面积相等称作“梯形的两翼相等”,因为△ABO 与△CDO 恰好如同两片翅膀一般,有的时候我们也称其为“蝴蝶模型”.“蝴蝶模型”在几何中应用非常广泛,尤其是在高年级学习比例之后,而且,应用蝴蝶模型,往往能够使得一些过去非常头疼的题目变得异常简单. 例题6如图所示,长方形ABCD 内的阴影部分的面积之和为70,AB =8,AD =15,四边形EFGO 的面积是多少?「分析」能否应用“蝴蝶模型”,使得三块分离的三角形合并呢?课堂内外蝴蝶定理蝴蝶定理(Butterfly theorem ),是古典欧式平面几何中最精彩的结果之一. 这个命题最早出现在1815年,而“蝴蝶定理”这个名称最早出现在《美国数学月刊》1944年2月号,1985年,在河南省《数学教师》创刊号上,杜锡录同志以《平面几何中的名题及妙解》为题,载文向国内介绍蝴蝶定理,从此蝴蝶定理在神州大地到处传开.这个定理最基本的叙述为:设M 为圆内弦PQ 的中点,过M 作弦AB 和CD ,设AD 和BC 分别相交PQ 于点X 和Y ,则M 是XY 的中点.从图中可以看出题目的图形像一只蝴蝶,该定理名字由此而得.实际上,在椭圆中,依然存在蝴蝶定理,把上图“压扁”即可.ABCDOA BC DOEGF这个定理的证法多的不胜枚举,至今仍然被数学热爱者研究,在高考等考试中时有出现各种变形,有人曾戏称“翩翩蝴蝶舞椭圆,飞落高考数学花”.混沌论中的“蝴蝶定理”:数学的一门分支是混沌论.混沌理论其实是人们对一系列残酷运动的名词描述:初始条件十分微小的变化经过不断放大,对其未来状态会造成极其巨大的差别.混沌理论最为人知的表述就是“蝴蝶效应”:一只南美洲亚马逊河流域热带雨林中的蝴蝶,偶尔扇动几下翅膀,可以在两周后引起美国德克萨斯州的一场龙卷风.西方流传的一首民谣形象的代表了“蝴蝶效应”:丢失一个钉子,坏了一只蹄铁; 坏了一只蹄铁,折了一匹战马; 折了一匹战马,伤了一位骑士; 伤了一位骑士,输了一场战斗; 输了一场战斗,亡了一个帝国.作业1. 如图所示,梯形ABCE 是由正方形ABCD 和等腰直角三角形CDE 构成的,已知等腰直角三角形的斜边是10厘米,那么△BCE 的面积是多少平方厘米?2. 如图,长方形ABCD 的面积为6,平行四边形BECF的面积为多少?ABCEDD3. 如图所示,一个长方形被分成4个不同的三角形,红色三角形的面积是9平方厘米,黄色三角形的面积是21平方厘米,绿色三角形的面积是10平方厘米,那么蓝色三角形的面积是多少平方厘米?4. 如图,长方形的长为16,宽为5.阴影三角形的面积和为多少?5. 如图,直角梯形ABCD 中,,,BD 和CD 垂直.那么三角形ABC 的面积是多少?40BD = 30CD =ABC第二十一讲等积变形1.例题1答案:50平方厘米详解:根据图中的辅助线,左边阴影面积为左边平行四边形的一半,右边阴影面积为右边平行四边形的一半,所以阴影总面积等于大平行四边形的一半,为50平方厘米.2.例题2答案:90平方厘米详解:平行四边形面积是180平方厘米.狗牙模型,通过同底等高可以将F拉到A点,把两个三角形合并成一个大三角形,即平行四边形的一半,面积为90平方厘米.3.例题3答案:6平方厘米详解:双层犬牙模型,可以把ABFE中的阴影面积转化成一个大的三角形,是ABFE面积的一半;CDEF中的阴影面积转化成一个大的三角形,是CDEF面积的一半.所以阴影部分的面积是长方形ABCD面积的一半,即6平方厘米.4.例题4答案:△ABD和△ABE详解:观察图中哪些线段平行,AD平行于BC,AB平行于DE.根据AD平行于BC,可以知道△ADC的面积等于△ABD;根据AB平行于DE,可以知道△ABD的面积等于△ABE.所以与△ADC 面积相等的三角形有△ABD和△ABE.5.例题5答案:50平方厘米;32平方厘米详解:(1)如图,连小正方形对角线,两个正方形对角线平行,所以阴影三角形与大正方形左半个等腰直角三角形同底(共同的底为大正方形对角线)等高、面积相等,等于大正方形面积的一半,为50平方厘米.(2)如图,连大正方形对角线,两个正方形对角线平行,所以阴影三角形与小正方形右半个等腰直角三角形同底(共同的底为小正方形对角线)等高、面积相等,等于小正方形面积的一半,为32平方厘米.6. 例题6 答案:10详解:梯形ADCF 中,阴影CDG 与AFG 面积相等,所以阴影总面积可以转换为△ABD 与四边形OEFG ,其中△ABD 面积为长方形一半60,所以四边形OEFG 面积为706010-=. 7. 练习1答案:40平方厘米详解:平行四边形中任意一点,与四个顶点连线,分成的四个小三角形面积关系:+=+上下左右. 8.练习2答案:50平方厘米详解:单层犬牙模型,通过同底等高可以将阴影部分的面积转化成一个大的三角形.这个三角形的面积是平行四边形面积的一半,所以阴影部分的面积是50平方厘米. 9.练习3答案:30平方厘米简答:双层犬牙模型,可以把ABCD 中的阴影面积转化成一个大的三角形,是ABCD 面积的一半;CDEF 中的阴影面积转化成一个大的三角形,是CDEF 面积的一半.所以阴影部分的面积是平行四边形ABFE 面积的一半,即30平方厘米. 10. 练习4答案:共8个三角形;△ABC 与△DBC 、△ABD 与△ACD 、△ABO 与△CDO简答:这是一个经典的梯形模型,共有三对三角形面积相等.根据AD 平行于BC ,可以知道△ABC 的面积等于△BCD 的面积;△ABD 的面积等于△ACD 的面积.△ABD 和△ACD 有一个共同的△AOD ,所以△ABO 和△OCD 的面积相等,我们称梯形的两翼面积相等. 11. 作业1答案:25平方厘米简答:根据等腰直角三角形的斜边,可以知道等腰直角三角形和正方形的面积分别是25平方厘米和50平方厘米.方法一:△BCE 的面积是正方形面积的一半,所以△BCE 的面积是25平方厘米;方法二:连接BD ,△BCE 和等腰直角三角形是同高等底的两个三角形,所以面积相等,则△BCE 的面积也是25平方厘米. 12. 作业2答案:6简答:三角形BCF的面积为长方形的一半,同时也是平行四边形的一半,所以平行四边形面积就等于长方形的面积,为6.13.作业3答案:22平方厘米简答:红蓝面积之和等于黄绿面积之和,都是长方形的一半.所以蓝色面积为:2110922+-=平方厘米.14.作业4答案:40简答:“狗牙”模型,阴影部分多个三角形根据同底等高三角形的转化可以转变为一个大三角形,面积为长方形的一半,面积为:165240⨯÷=.15.作业5答案:600简答:△ABC与△BCD同底等高,所以两个三角形面积相等,△BCD底CD长30、高BD长40,面积为30402600⨯÷=.。
小学五年级数学思维专题训练—等积变形(含答案解析)
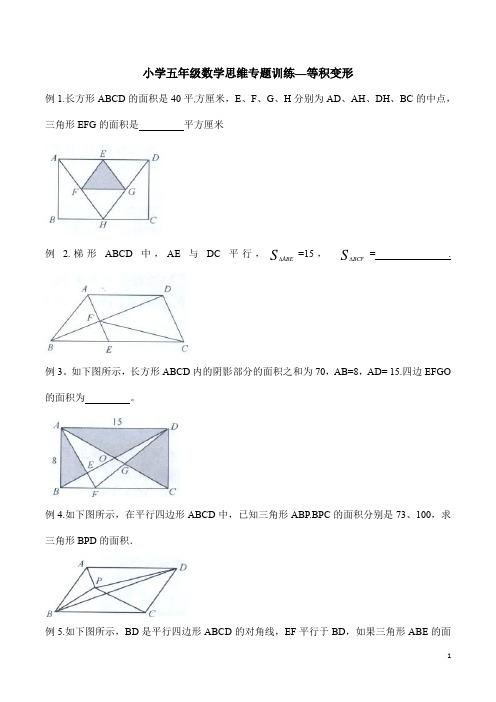
小学五年级数学思维专题训练—等积变形例1.长方形ABCD的面积是40平方厘米,E、F、G、H分别为AD、AH、DH、BC的中点,三角形EFG的面积是平方厘米例 2.梯形ABCD中,AE与DC平行,S ABE∆=15,S BCF∆= .例3。
如下图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD= 15.四边EFGO 的面积为。
例4.如下图所示,在平行四边形ABCD中,已知三角形ABP.BPC的面积分别是73、100,求三角形BPD的面积.例5.如下图所示,BD是平行四边形ABCD的对角线,EF平行于BD,如果三角形ABE的面积是12平方厘米,那么三角形AFD的面积是平方厘米。
例6.如下图所示,已知AE=EC,CD=DB,S ABC =60,求四边形FDCE的面积.例7.如右图所示,正方形ABC D和正方形ECGF并排放置,BF与CD相交于点H,已知AB=6厘米,则阴影部分的面积是平方厘米.例8.如下图所示,E、F、G、H分别是四边形ABCD各边的中点,EG与FH交于点O,S1、S2、S3及S4分别表示4个小四边形的面积.试比较S1+S3与S2+S4的大小.例9.将长15厘米、宽9厘米的长方形的长和宽都分成三等份,长方形内任意一点与分点及顶点连结,如右图所示,则阴影部分的面积是 平方厘米.例10.右图所示ABCD 是个直角梯形(∠DAB=∠ABC= 900),以 , AD 为一边向外作长方形ADEF ,其面积为6.36平方厘米,连接BE 交AD 于P ,再连接PC .则图中阴影部分的面积是 平方厘米。
A.6.36B.3.18C.2.12D.1.59例11.如下图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的 。
A .21B .32C .52D .125例12.如下图所示,矩形ABCD 的面积是24平方厘米,三角形ADM 与三角形BCN 的面积之和是7.8平方厘米,则四边形PMON 的面积是 平方厘米.例13.一个矩形分成4个不同的三角形(如下图),绿色三角形面积占矩形面积的15%,黄色三角形的面积是21平方厘米.问:矩形的面积是多少平方厘米?例14.如下图所示,正方形每条边上的三个点(端点除外)都是这条边的四等分点,则阴影部分的面积是正方形面积的。
等积变形(附解答)

三角形的等积变形我们已经掌握了三角形面积的计算公式:三角形面积=底×高÷2这个公式告诉我们:三角形面积的大小,取决于三角形底和高的乘积.如果三角形的底不变,高越大(小),三角形面积也就越大(小).同样若三角形的高不变,底越大(小),三角形面积也就越大(小).这说明;当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.本讲即研究面积相同的三角形的各种形状以及它们之间的关系.为便于实际问题的研究,我们还会常常用到以下结论:①等底等高的两个三角形面积相等.②底在同一条直线上并且相等,该底所对的角的顶点是同一个点或在与底平行的直线上,这两个三角形面积相等.③若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.它们所对的顶点同为A点,(也就是它们的高相等)那么这两个三角形的面积相等.同时也可以知道△ABC的面积是△ABD或△AEC面积的3倍.例如在图中,△ABC与△DBC的底相同(它们的底都是BC),它所对的两个顶点A、D在与底BC平行的直线上,(也就是它们的高相等),那么这两个三角形的面积相等.例如图中,△ABC与△DBC的底相同(它们的底都是BC),△ABC的高是△DBC 高的2倍(D是AB中点,AB=2BD,有AH=2DE),则△ABC的面积是△DBC面积的2倍.上述结论,是我们研究三角形等积变形的重要依据.例1、用三种不同的方法,把任意一个三角形分成四个面积相等的三角形.方法2:如右图,先将BC二等分,分点D、连结AD,得到两个等积三角形,即△ABD与△ADC等积.然后取AC、AB中点E、F,并连结DE、DF.以而得到四个等积三角形,即△ADF、△BDF、△DCE、△ADE等积.例2、用三种不同的方法将任意一个三角形分成三个小三角形,使它们的面积比为及1∶3∶4.方法 1:如下左图,将BC边八等分,取1∶3∶4的分点D、E,连结AD、AE,从而得到△ABD、△ADE、△AEC的面积比为1∶3∶4.DE,从而得到三个三角形:△ADE、△BDE、△ACD.其面积比为1∶3∶4.当然本题还有许多种其他分法,同学们可以自己寻找解决.例3、如图,在梯形ABCD中,AC与BD是对角线,其交点O,求证:△AOB与△COD面积相等.证明:∵△ABC与△DBC等底等高,∴S△ABC=S△DBC又∵ S△AOB=S△ABC—S△BOCS△DOC=S△DBC—S△BOC∴S△AOB=S△COD.例4、如图,把四边形ABCD改成一个等积的三角形.分析本题有两点要求,一是把四边形改成一个三角形,二是改成的三角形与原四边形面积相等.我们可以利用三角形等积变形的方法,如右图,把顶点A移到CB的延长线上的A′处,△A′BD与△ABD面积相等,从而△A′DC面积与原四边形ABCD面积也相等.这样就把四边形ABCD等积地改成了三角形△A′DC.问题是A′位置的选择是依据三角形等积变形原则.过A 作一条和DB平行的直线与CB的延长线交于A′点.解:①连结BD;②过A作BD的平行线,与CB的延长线交于A′.③连结A′D,则△A′CD与四边形ABCD等积.例5、如图,已知在△ABC中,BE=3AE,CD=2AD.若△ADE的面积为1平方厘米.求三角形ABC的面积.解法1:连结BD,在△ABD中∵ BE=3AE,∴ S△ABD=4S△ADE=4(平方厘米).在△ABC中,∵CD=2AD,∴ S△ABC=3S△ABD=3×4=12(平方厘米).解法2:连结CE,如右图所示,在△ACE中,∵ CD=2AD,∴ S△ACE=3S△ADE=3(平方厘米).在△ABC中,∵BE=3AE∴ S△ABC=4S△ACE=4×3=12(平方厘米).例6、如下图,在△ABC中,BD=2AD,AG=2CG,BE=EF=FC=解:连结BG,在△ABG中,∴ S△ADG+S△BDE+S△CFG例7、如右图,ABCD为平行四边形,EF平行AC,如果△ADE的面积为4平方厘米.求三角形CDF的面积.解:连结AF、CE,∴S△ADE=S△ACE;S△CDF=S△ACF;又∵AC与EF平行,∴S△ACE=S△ACF;∴ S△ADE=S△CDF=4(平方厘米).例8、如右图,四边形ABCD面积为1,且AB=AE,BC=BF,DC=CG,AD=DH.求四边形EFGH的面积.解:连结BD,将四边形ABCD分成两个部分S1与S2.连结FD,有S△FBD=S △DBC=S1所以S△CGF=S△DFC=2S1.同理 S△AEH=2S2,因此S△AEH+S△CGF=2S1+2S2=2(S1+S2)=2×1=2.同理,连结AC之后,可求出S△HGD+S△EBF=2所以四边形EFGH的面积为2+2+1=5(平方单位).例9、如右图,在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F,若S△ADE=1,求△BEF的面积.解:连结AC,∵AB//CD,∴S△ADE=S△ACE又∵AD//BC,∴S△ACF=S△ABF而 S△ACF=S△ACE+S△AEF∶S△ABF=S△BEF+S△AEF∴ S△ACE=S△BEF∴S△BEF=S△ADE=1.。
等积变形附答案

三角形的等积变形我们已经掌握了三角形面积的计算公式:三角形面积=底x高十2这个公式告诉我们:三角形面积的大小,取决于三角形底和高的乘积.如果三角形的底不变,高越大(小),三角形面积也就越大(小).同样若三角形的高不变,底越大(小),三角形面积也就越大(小).这说明;当三角形的面积变化时,它的底和高之中至少有一个要发生变化. 但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原耒的;.贝!I三角形面积与原来的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.本讲即研究面积相同的三角形的各种形状以及它们之间的关系.为便于实际问题的研究,我们还会常常用到以下结论:①等底等高的两个三角形面积相等.②底在同一条直线上并且相等,该底所对的角的顶点是同一个点或在与底平行的直线上,这两个三角形面积相等.③若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.例如在右圈中,若^ABD-^A AEC的底边相等(£D=DE=EC=|E.C)3它们所对的顶点同为A点,(也就是它们的高相等)那么这两个三角形的面积相等.同时也可以知道^ ABC勺面积是△ ABD或△ AEC面积的3倍.例如在图中,△ ABC与△ DBC的底相同(它们的底都是BC),它所对的两个顶点A D在与底BC平行的直线上,(也就是它们的高相等),那么这两个三角形的面积相等.例如图中,△ ABC与△ DBC的底相同(它们的底都是BC),AABC的高是△ DBC 高的2倍(D是AB中点,AB=2BD有AH=2DE)则^ ABC的面积是△ DBC面积的2倍.上述结论,是我们研究三角形等积变形的重要依据.例1、用三种不同的方法,把任意一个三角形分成四个面积相等的三角形.方法1=如右图,将RC边四等分(KD =DE=EF=FC=|B C),连结△ABE、△AEF、△AF对积*方法2:如右图,先将BC二等分,分点D连结AD得到两个等积三角形,即△ ABD与△ ADC等积.然后取AC AB中点E、F,并连结DE DF.以而得到四个等积三角形,即△ ADF △ BDF △ DCE △ ADE等积.C方法务如右图,先將BC四攀分,即:BD二一BC,连结直A再将AB三等分,aPAE-EF=FD--AD,连结CE、CF,从而得到四个尊积的三角形 ,即^AKD, △CDF, △CEE △ACE等积.例2、用三种不同的方法将任意一个三角形分成三个小三角形,使它们的面积比为及1 : 3 : 4.方法1 :如下左图,将BC边八等分,取1 : 3 : 4的分点D E,连结AD AE 从而得到^ ABD △ ADE △ AEC的面积比为1 : 3 : 4.方法厶如上右圈,先取EC中点D,再取yVB的才分点民连结AD、DE从而得到三个三角形:△ ADE △ BDE △ ACD其面积比为1 : 3 : 4.方法玉如右图,先恥止中点D,连结CD,再取CD上;分点兔连结4从而得到三个三角形;△ACE △ADE、△BCD,其面积比为1 ; 3 :4.C当然本题还有许多种其他分法,同学们可以自己寻找解决.例3、如图,在梯形ABCD中,AC与BD是对角线,其交点0,求证:△ A0B与△ CODS积相等.c证明:•••△ ABC与△ DBC等底等高, /. S^AB(=S A DBC又S △ AOB=S A ABC—S A BOC S △ DOC=S^ DBC—BOC/. S AAOB=S ACOD例4、如图,把四边形ABCDfe成一个等积的三角形.分析本题有两点要求,一是把四边形改成一个三角形,二是改成的三角形与原四边形面积相等.我们可以利用三角形等积变形的方法,如右图,把顶点A移到CB的延长线上的A'处,△ A BD与△ ABD面积相等,从而△ A DC面积与原四边形ABC®积也相等.这样就把四边形ABCD等积地改成了三角形^ A DC问题是A'位置的选择是依据三角形等积变形原则.过A 作一条和DB平行的直线与CB的延长线交于A'点.解:①连结BD②过A作BD的平行线,与CB的延长线交于A'.③连结A。
等积变形初一试题及答案

等积变形初一试题及答案一、选择题1. 一个长方体的长、宽、高分别为6cm、4cm、3cm,其体积是()。
A. 72cm³B. 48cm³C. 24cm³D. 36cm³2. 一个正方体的棱长为5cm,其体积是()。
A. 125cm³B. 100cm³C. 75cm³D. 50cm³3. 一个圆柱体的底面半径为4cm,高为5cm,其体积是()。
A. 200πcm³B. 100πcm³C. 80πcm³D. 40πcm³二、填空题1. 一个长方体的长、宽、高分别为8cm、6cm、5cm,其体积为_______cm³。
2. 一个正方体的体积为216cm³,其棱长为_______cm。
3. 一个圆柱体的底面半径为3cm,高为10cm,其体积为_______cm³。
三、解答题1. 一个长方体的长、宽、高分别为10cm、8cm、7cm,求其体积。
2. 一个正方体的棱长为4cm,求其体积。
3. 一个圆柱体的底面直径为6cm,高为9cm,求其体积。
答案:一、选择题1. A2. A3. B二、填空题1. 2402. 63. 942π三、解答题1. 长方体的体积为10cm × 8cm × 7cm = 560cm³。
2. 正方体的体积为4cm × 4cm × 4cm = 64cm³。
3. 圆柱体的体积为π × (3cm)² × 9cm = 81πcm³。
六年级奥数优胜教育第3讲:等积变形含答案

第三讲等积变形例1:如图,正方形ABCD的边长为6,AE=1.5,CF=2.长方形EFGH的面积为.例2:长方形ABCD的面积为36cm2,E、F、G为各边中点,H为AD边上任意一点,问阴影部分面积是多少?A H DE GB F C例3:如图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD=15,四边形EFGO的面积为.A DE OGB F C例4:已知ABC为等边三角形,面积为400,D、E、F分别为三边的中点,已知甲、乙、丙面积和为143,求阴影五边形的面积.(丙是三角形HBC)例5:如图,已知CD=5,DE=7,EF=15,FG=6,线段AB将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG的面积是.A AC D E F G C D E FGB B例6:如图在△ABC中,D,E分别是AB,AC上的点,且AD:AB=2:5,AE:AC=4:7,△S ADE=16平方厘米,求△ABC的面积.AAD DE EB C B C例7:如图在△ABC中,D在BA的延长线上,E在AC上,且AB:AD=5:2,AE:EC=3:2,△S ADE=12平方厘米,求△ABC的面积.DAEB CDAEB C例8:如图,平行四边形ABCD,BE=AB,C F=2CB,G D=3DC,HA=4A D,平行四边形ABCD的面积是2,求平行四边形ABCD与四边形EFGH的面积比.H HA B E A B EG D C G D CF例9:如图所示的四边形的面积等于多少?FC O131213D1312131212AB例10:如图所示,∆ABC中,∠ABC=90︒,AB=3,BC=5,以AC为一边向∆ABC外作正方形ACDE,中心为O,求∆OBC的面积.EEO DODA3B5CA3B5C F A1.如图所示,正方形ABCD的边长为8厘米,长方形EBGF的长BG为10厘米,那么长方形的宽为几厘米?_E_E_A_B_A_B_F_F_D_G_C_D_G_C2.在边长为6厘米的正方形ABCD内任取一点P,将正方形的一组对边二等分,另一组对边三等分,分别与P点连接,求阴影部分面积.A D A(P)D A DP PB C B C B CC C甲乙3.如图,长方形ABCD的面积是36,E是AD的三等分点,AE=2ED,则阴影部分的面积为.A E DA E DMNO OB B4.如图,三角形ABC中,AB是AD的5倍,AC是AE的3倍,如果三角形ADE的面积等于1,那么三角形ABC的面积是多少?A AD E DEB C B C5.如图,三角形ABC被分成了甲(阴影部分)、乙两部分,BD=DC=4,B E=3,AE=6,乙部分面积是甲部分面积的几倍?A AE B甲乙D C BED CB6.如图,以正方形的边AB为斜边在正方形内作直角三角形ABE,∠AEB=90︒,AC、B D 交于O.已知AE、BE的长分别为3cm、5cm,求三角形OBE的面积.C B C BO E OEFD A D A7.如下图,六边形ABCDEF中,AB=ED,AF=CD,BC=EF,且有AB平行于ED,AF 平行于CD,BC平行于EF,对角线FD垂直于BD,已知F D=24厘米,BD=18厘米,请问六边形ABCDEF的面积是多少平方厘米?B G BAC ACF D F DE E角形 BCD 的面积的 ,且 AO = 2 ,DO = 3 ,那么 CO 的长度是 DO 的长度的_________倍.EBE8.如图,三角形 ABC 的面积是 1 , E 是 AC 的中点,点 D 在 BC 上,且 BD : DC = 1: 2 , AD 与 BE 交于点 F .则四边形 DFEC 的面积等于 .AEBDFC9.如图,长方形 ABCD 的面积是 2 平方厘米, EC = 2DE , F 是 DG 的中点.阴影部分的面积是多少平方厘米?AD ADBGFECBxF x y Gy EC10.四边形 ABCD 的对角线 AC 与 BD 交于点 O (如图所示).如果三角形 ABD 的面积等于三13ADOBCC11.如图,平行四边形 ABCD 的对角线交于 O 点,△CEF 、△OEF 、△ODF 、△BOE 的面 积依次是 2、4、4 和 6.求:⑴求 △OCF 的面积;⑵求 △GCE 的面积.ADOF GBEC12.如图,长方形 ABCD 中, BE : EC = 2:3 , DF : FC = 1: 2 ,三角形 DFG 的面积为 2 平方 厘米,求长方形 ABCD 的面积.AGDFAGDFBCC13.如图,正方形ABCD面积为3平方厘米,M是AD边上的中点.求图中阴影部分的面积.B CGA M D14.在下图的正方形ABCD中,E是BC边的中点,AE与BD相交于F点,三角形BEF的面积为1平方厘米,那么正方形ABCD面积是平方厘米.A DFB E C15.已知ABCD是平行四边形,BC:CE3:2,三角形ODE的面积为6平方厘米.则阴影部分的面积是平方厘米.A DA DO OB C E B C E1.右图中ABCD是梯形,ABED是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是平方厘米.A D A D992121O44B E B E CCDA 的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数 ,那么,2.右图中 ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米), 阴影部分的面积是 平方厘米.AD AD881616O 2 2BEC BEC3.如图,长方形 ABCD 被 CE 、 DF 分成四块,已知其中 3 块的面积分别为 2、5、8 平方厘 米,那么余下的四边形 OFBC 的面积为___________平方厘米.A EFB A EFB225O ?5O ?88DC D C4.如图, ∆ABC 是等腰直角三角形, DEFG 是正方形,线段 AB 与 CD 相交于 K 点.已知正 方形 DEFG 的面积 48, AK : KB = 1:3 ,则 ∆BKD 的面积是多少?DA G DA GKKBEF C B E M F C5.下图中,四边形 ABCD 都是边长为 1 的正方形,E 、F 、G 、H 分别是 AB ,BC ,CD ,mn(m + n ) 的值等于.AH D A H DEG E GBFC BFC1.用三种不同的方法,把任意一个三角形分成四个面积相等的三角形.2.用三种不同的方法将任意一个三角形分成三个小三角形,使它们的面积比为及 1∶3∶4.3.如右图,在梯形 ABCD 中,AC 与 BD 是对角线,其交点 △O ,求证:AOB 与△COD 面积相等.4.如右图,把四边形 ABCD 改成一个等积的三角形.5.如右图,已知在△ABC 中,BE=3AE ,CD=2AD .若△ADE 的面积为 1 平方厘米.求三角形 ABC的面积.6.如下页图,在△ABC 中,BD=2AD ,AG=2CG ,BE=EF=FC=面积的几分之几?1 3BC ,求阴影部分面积占三角形 A BC7.如右图,ABCD 为平行四边形,EF 平行 △A C ,如果 ADE 的面积为 4 平方厘米.求三角形 CDF的面积.8.如右图,四边形ABCD面积为1,且AB=AE,BC=BF,DC=CG,AD=DH.求四边形EFGH的面积.9.如右图,在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F,若△S ADE=1,求△BEF的面积.△S ACD = △S BCD ,则可知直线 AB 平行于 CD .E第三讲 等积变形1.等积模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如图 S : S = a : b12③夹在一组平行线之间的等积变形,如图 △S ACD = △S BCD ;反之,如果④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于 它们的高之比. 2.鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在 △ABC 中,D , E 分别是 AB, AC 上的点如图 ⑴(或 D 在 BA 的延长线上, 在 AC 上),则S△ABC :S△ADE=(AB⨯AC):(AD⨯AE)3.蝶形定理任意四边形中的比例关系(“蝶形定理”):①S:S=S:S或者S⨯S=S⨯S②AO:OC=(S+S):(S+S)124313241243蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.DAS2S1OS4S3B C梯形中比例关系(“梯形蝶形定理”):①S:S=a2:b213②S:S:S:S=a2:b2:ab:ab;1324③S的对应份数为(a+b)2.4.相似模型(一)金字塔模型(二)沙漏模型A E F DAD F EB GC B G C①AD AE DE AF===AB AC BC AG;②:=AF2:AG2.△S ADE△S ABC所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具.在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.5.共边定理(燕尾模型和风筝模型)共边定理:若直线AO和BC相交于D(有四种情形),则有S∆ABO :S∆ACO=BD:DC在三角形ABC中,AD,BE,CF相交于同一点O,那么S:S=BD:DC.∆ABO∆ACO上述定理给出了一个新的转化面积比与线段比的手段,因为∆ABO和∆ACO的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径.AFEBOD C1.了解三角形的底、高与面积的关系,会通过分析以上关系解题。
小学五年级奥数精讲等积变形求面积(含答案)

小学五年级奥数精讲等积变形求面积(含答案)小学奥数精讲:等积变形求面积基本概念我们都知道“三角形的面积等于底与高的积的一半”,因此,我们可以得出等底等高的两个三角形面积相等的结论。
这意味着,即使两个三角形的形状不同,只要它们的底和高分别相等,它们的面积就相等。
但是,不能反过来说“面积相等的两个三角形的底和高一定分别相等”。
另一类三角形有一条公共底边,但这条底边上的高相等,即这条底边所对的顶点在一条与底边平行的直线上。
例如,右图中的三角形A1BC、A2BC和A3BC的面积都相等。
图形割补是求图形面积的重要方法。
通过割补,我们可以将一些形状不规则的图形转换成形状规则但面积相等的图形,或者将不易求面积的图形转换成易求面积的图形。
常用的割补方法包括添加平行线或垂线。
利用等底等高的三角形面积相等这个性质是面积割补的重要依据,而抓住具体的图形特点进行分析以确定正确的割补方法则是面积割补的关键。
在进行图形切拼时,应该有意识地进行计算,算好了再动手寻找切拼的方案。
不要盲目地乱动手。
本讲中的几个例子都是经过仔细计算才切拼成功的。
例题分析例1:已知三角形ABC的面积为1,BE=2AB,BC=CD,求三角形BDE的面积。
例2:如下图,A为△XXX的DE边上中点,BC=CD,若△ABC(阴影部分)面积为5平方厘米,求△ABD及△XXX的面积。
例3:2002年在北京召开了国际数学家大会,大会会标如下图所示,它是由四个相同的直角三角形拼成(直角边长为2和3)。
问:大正方形的面积是多少?例4:下图中,三角形ABC和DEF是两个完全相同的直角边长等于9厘米的等腰直角三角形,求阴影部分的面积。
练提高1、如图,已知平行四边形ABCD的面积是60平方分米,E、F分别是AB、AD边上的中点,图中阴影部分的面积是多少平方分米?2、右图中的长方形ABCD的长是20厘米,宽是12厘米,AF=BE,图中阴影部分的面积是多少平方厘米?3、如图,四边形ABCD是平行四边形,DC=CE,如果△BCE的面积是15平方厘米,那么梯形ABED的面积是多少平方厘米?4、正方形ABCD的边长是12厘米,已知DE是EC长度的2倍,三角形DEF的面积是多少平方厘米?CF长多少厘米?在平行四边形ABCD中,如果AE=ED,BF=FC,CG=GD,求平行四边形ABCD的面积是阴影三角形EFG的多少倍。
秋季小五班第1讲等积变形答案与补充

A.6问题补充:E ,F 在AB 上,从上到下依次为A,E,F,B 设梯形的高为H ,AE 所占的高为m. 则Sade + Sbcf = m ( AD + BC ) / 2 (1)Sadf + Sbce = ( H - m) * (AD + BC ) /2 ........(2) (1) + (2) = H * (AD + BC) / 2, 正好是梯形的面积(1) + (2)式的左边, Sade, Seof, Sbcf 被加了两次, 也就是说, Sade + Seof + Sbcf = Scod,所以 Seod + Scof = 34 - 11 * 2 = 12. B.1如图所示,在平行四边形ABCD 中,EF 与AC 平行。
如果三角形BFC 的面积是35平方厘米,那么三角形AEC 的面积能不能确定?如果能,它的面积是多少,应该怎么解?如果不能,请说出理由。
连接AF因为AB 平行于CD ,所以三角形BFC 的面积等于三角形AFC 的面积(同底等高) 又因为EF 平行于AC ,所以三角形AFC 的面积等于三角形AEC 的面积(同底等高) 所以三角形AEC 的面积能确定,它的面积是35平方厘米答案补充因为AD 平行于BC ,所以三角形AEB 的面积等于三角形AEC 的面积(同底等高) 所以还是35平方厘米B.6如图,有一个长6厘米,宽4厘米的长方形ABC D ,已知线段D G 、AH 、AE 、BF 的长度依次是1,2,3,4厘米,且四边形AEPH 的面积是5平方厘米,求四边形PFC G 的面积是多少平方厘米?PH GFE D C BAC.1三角形BDP 和三角形DCP 在BC边上的高是相同的,BD:DC=40:30三角形BDA 和三角形DCA 在BC边上的高是相同的,所以面积比等于BD:DC=40:30。
设三角形BFP面积为S1,三角形CEP面积为S2可得方程1(84+S1+40):(70+S2+30)=4:3又有三角形AFP与三角形BFP之比等于三角形AFC与三角形BFC之比,同等于点A到边CF的距离和点B到CF的距离之比。
【思维拓展】数学六年级思维拓展之等积变形(附答案)必考知识点

面积是三角形 AEF 面积的 2 倍,所以三角形 ABC 面积是三角形 AEF 面积的 3
倍;又因为平行四边形的面积是三角形 ABC 面积的 2 倍,所以平行四边形的面
积是三角形 AFE 面积的(3×2)=6 倍。因此,平行四边形的面积为 8 ×6=48(平
方厘米)。
6
10.【解答】连结 AE、BF、CD(如图)。由于三角形 AEB 与三角
PQRS。因此四块阴影的面积和就等于四边形 PQRS 的面积,即阴影部分与四边
形 PQRS 的面积之比为 1:1。
8. 【解答】连接 BD .设 SDCB S1, SDAB S2
∵ CB BF ,
∴ SCDF
CB BF CB
SCDB
2SCDB ,
又∵ DC CG ,
∴ SCFG SCDF 2S1 ,
4. 如图,在三角形 ABC 中,BC=8 厘米,AD=6 厘米,E、F 分别为 AB 和 AC
的中点,那么三角形 EBF 的面积是多少平方厘米?
A
E
F
B
C
1
5. 如图,已知三角形 ABC 面积为 1,延长 AB 至 D ,使 BD AB ;延长 BC 至 E , 使 CE 2BC ;延长 CA 至 F ,使 AF 3AC ,求三角形 DEF 的面积。
于是三角形 DEF 的面积等于三角形 ABC、AEB、CBF、ACD、AED、BEF、CFD
的面积之和,即 1+2+3+1+2+6+3=18。
11.【解答】连接辅 C 助线 E。
(三角形 BCE 的面积)︰(三角形 DCE 的面积)=BC﹕CD=1﹕1,
所以三角形 BCE 的面积等于三角形 DCE 的面积。
2024年 三角形中的重要模型等积模型(含答案)

专题07 三角形中的重要模型-等积模型三角形的面积问题在中考数学几何模块中占据着重要地位,等积变形是中学几何里面一个非常重要的思想,下面的五大模型也都是依托等积变形思想变化而成的,也是学生必须掌握的一块内容。
本专题就三角形中的等积模型(蝴蝶(风筝)模型,燕尾模型,鸟头模型,沙漏模型,金字塔模型)进行梳理及对应试题分析,方便掌握。
模型1. 等积变换基础模型1)等底等高的两个三角形面积相等;如图1,当AB //CD ,则ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB //CD 。
图1 图2 图32)两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比。
如图2,当点D 是BC 边上的动点时,则S △ABD ∶S △ADC =BD ∶DC 。
如图3,当点D 是BC 边上的动点,BE ⊥AD ,CF ⊥AD 时,则S △ABD ∶S △ADC =BE ∶CF 。
A .4B .3【答案】D 【分析】利用三角形面积公式,等高的三角形的面积比等于底边的比,由此利用已知条件可以分别求出BDC BED S S 、V V .A.9B.【答案】B【分析】利用中线等分三角形的面积进行求解即可.V【详解】解:∵BD是ABC【答案】12【分析】根据高相等的两个三角形的面积之比等于底之比可得答案.【详解】解::QCG GF=【答案】14.4【分析】连接BF , 12BDC ABC S S =V V ;根据示为2BDC S V 和3S V∵CD 为AB 边上中线,∵2BE CE =, S \V 2ABC BDC S S \==V V(1)如图2,延长ABC V 的边BC 到点D ,使CD BC =,连接DA (用含a 的代数式表示);(2)如图3,延长ABC V 的边BC 到点D ,延长边CA 到点E ,使面积为2S ,则2S = (用含a 的代数式表示);(3)在图3的基础上延长AB 到点F ,使BF AB =,连接FD ,积为3S ,则3S =(用含a 的代数式表示);Q 延长ABC V 的边BC 到点D ,延长边CA 到点E ,使CD BC =,AE \12ACD AED ECD S S S D D D ==,ACD ABC S D ,22ECD ABC S S a D D \==,即2S (3)由(2)得2ECD ABC S S D D ==同理:22EFA ABC S S a D D ==,2ECD BFD S a D D =,3ECD EFA S S S S D D \=++∵点E 是线段AD 的中点,12BCE ABC S =V .∥,连接,若过C作CE AB模型2.蝴蝶(风筝)模型蝴蝶模型(定理)提供了解决不规则四边形的面积问题的一个途径。
六年级下册数学试题-小升初专题培优:等积变形(含答案)全国通用

六年级下册数学试题-⼩升初专题培优:等积变形(含答案)全国通⽤我们已经知道三⾓形⾯积的计算公式:三⾓形⾯积=底×⾼÷2从这个公式我们可以发现:三⾓形⾯积的⼤⼩,取决于三⾓形底和⾼的乘积。
如果三⾓形的底不变,⾼越⼤(⼩),三⾓形⾯积也就越⼤(⼩);如果三⾓形的⾼不变,底越⼤(⼩),三⾓形⾯积也就越⼤(⼩);这说明当三⾓形的⾯积变化时,它的底和⾼之中⾄少有⼀个要发⽣变化。
但是,当三⾓形的底和⾼同时发⽣变化时,三⾓形的⾯积不⼀定变化。
⽐如当⾼变为原来的3倍,底变为原来的,则三⾓形⾯积与原来的⼀样。
这就是说:⼀个三⾓形的⾯积变化与否取决于它的⾼和底的乘积,⽽不仅仅取决于⾼或底的变化。
同时也告诉我们:⼀个三⾓形在⾯积不改变的情况下,可以有⽆数多个不同的形状。
在实际问题的研究中,我们还会常常⽤到以下结论:①等底等⾼的两个三⾓形⾯积相等;②两个三⾓形⾼相等,⾯积⽐等于它们的底之⽐;两个三⾓形底相等,⾯积⽐等于它们的⾼之⽐;如左图S1∶S2=a∶b③夹在⼀组平⾏线之间的等积变形,如右下图S△ACD=S△BCD;反之,如果S△ACD=S△BCD,则可知直线AB平⾏于CD。
④等底等⾼的两个平⾏四边形⾯积相等(长⽅形和正⽅形可以看作特殊的平⾏四边形);⑤三⾓形⾯积等于与它等底等⾼的平⾏四边形⾯积的⼀半;⑥两个平⾏四边形⾼相等,⾯积⽐等于它们的底之⽐;两个平⾏四边形底相等,⾯积⽐等于它们的⾼之⽐。
图中三⾓形ABC的⾯积是160平⽅厘⽶,D是BC的中点,AD的长是AE长的3倍,EF的长是BF长的3倍。
那么三⾓形AEF的⾯积是多少平⽅厘⽶?例1⼩升初——等积变形在边长为6厘⽶的正⽅形ABCD内任取⼀点P,将正⽅形的⼀组对边⼆等分,另⼀组对边三等分,分别与P点连接,求阴影部分⾯积。
如图,⼤长⽅形由⾯积是12平⽅厘⽶、24平⽅厘⽶、36平⽅厘⽶、48平⽅厘⽶的四个⼩长⽅形组合⽽成。
求阴影部分的⾯积。
(2009年第七届”希望杯”⼆试六年级)如图,在三⾓形ABC中,已知三⾓形ADE、三⾓形DCE、三⾓形BCD的⾯积分别是89,28,26。
人教版数学6年级下册 第3单元(圆柱和圆锥)专项训练《等积变形》(含答案)

人教版六年级数学下册第三单元专项训练《等积变形》(含答案)1.把一个圆柱底面平均分成若千个扇形,沿高切开拼成一个近似长方体。
这个长方体的宽是4厘米,高是20厘米,这个圆柱的体积是多少?2.把一个棱长是8分米的正方体铁块熔铸成一个底面直径是10分米的圆柱,这个圆柱的高大约是多少?(得数保留一位小数)3.一个圆柱形水池装满水,它的底面积是12.56平方米,深3米,将水池的水全部倒入一个长8米、宽3米、深2米的长方体水池,长方体的水面高是多少米?4.把一个棱长8分米的正方体木块加工成一个最大的圆柱,圆柱的体积是多少立方分米?5.一个圆柱体,如果把它的高截短2厘米,它的表面积就减少94.2平方厘米,这个圆柱体的体积减少多少立方厘米?6.将一个底面直径是20厘米,高为12厘米的金属圆锥体,全部浸没在直径是20厘米的圆柱形水槽中,水槽水面会升高多少厘米?7.一个圆锥形沙堆,底面积12.56平方米,高1.2米。
用这堆沙在10米宽的公路上铺2厘米厚的路面,能铺多少米?8.一个圆锥形沙堆,底面积是24平方米,高是1.8米。
用这堆沙子去填一个长7.5米、宽4米的长方体沙坑,沙坑里沙子的厚度是多少厘米?9.把一个长、宽、高分别是7厘米、3厘米、9厘米的长方体铁块和一个棱长是5厘米的正方体铁块,熔铸成一个底面直径是10厘米的圆柱,这个圆柱的高是多少?10.机灵狗有一块体积是753.6立方厘米的绿色橡皮泥,它用这块橡皮泥捏成了等底等高的一个圆柱体和一个圆锥体。
则这个圆柱体体积是多少立方分米?11.在底面半径为5厘米、高为18厘米的圆柱形玻璃缸中,放入一个底面半径3厘米、高为10厘米的圆锥形铅块,放水将铅块全部淹没。
当铅块取出后,玻璃缸中的水面下降了多少厘米?12.学校的跳远沙池长6.28米,宽2米,学校运来一堆沙子(堆放如图)。
如果把这些沙子均匀地铺在跳远沙池中,可以铺多厚?13.把一个棱长6分米的正方体木块削成一个最大的圆锥,需要削去多少立方分米的木头?14.把一个长是10厘米,宽和高都是5厘米的长方体铁块和一个棱长是4厘米的正方体铁块,一起熔铸成一个底面周长是314厘米的圆柱。
小学数学 几何问题之等积变形问题 完整版题型训练 PPT带答案带练习

练习6
6、右图ADEF为正方形,BD的长为9,FC的长为4,求右图沿阴影长方形的 四周作四个正方形,四个正方形的面积之和为68平方厘米,其阴影的长方形 的周长是16厘米,求阴影部分的面积。
设正方形ADEF边长为a 4×9=36=6×6 a=6 三角形ABC面积=(6+9)×(6+4)÷2=75
练习7 7、右图沿阴影长方形的四周作四个正方形,四个正方形的面积 之和为68平方厘米,其阴影的长方形的周长是16厘米,求阴影部 分的面积
设阴影长方形长与宽分别为a,b a×a+b×b=130÷2=65 a+b=22÷2=11 经尝试a,b分别为4,7 阴影长方形面积=4×7=28(平方厘米)
ห้องสมุดไป่ตู้
课后作业
练习1
1、如图,图形甲与乙的面积差又可以看做是长方形 ABCD与( 三角形 )的差
ABF
练习2
2、将右图通过平移的方法变成一个长方形
小学数学几何问题之 等积变形
例1 下图(单位:厘米)是两个相同的直角梯形重叠在一起: 求阴影部分的面积
20-5=15(厘米) (15+20)×8÷2=140(平方厘米)
例2
下图中,矩形ABCD的边AB为4厘米,BC为6厘米,三角 形ABF比三角形EDF的面积大9平方厘米,求ED的长。
4×6-9=15(平方厘米) EC=15×2÷6=5(厘米) ED=5-4=1(厘米)
设阴影长方形长与宽分别为a,b a×a+b×b=68÷2=34 A+b=16÷2=8 经尝试长与宽分别为5,3 阴影面积=3×5=15(平方厘米)
平行四边形ABCD面积--三角形BCE面积=10(平方 厘米) 三角形BCE面积=10×8÷2=40(平方厘米) 平行四边形ABCD面积=40+10=50(平方厘米)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
优质文档
人挪活树挪死三角形的等积变形
我们已经掌握了三角形面积的计算公式:
三角形面积=底×高÷2
这个公式告诉我们:三角形面积的大小,取决于三角形底和高的乘积.如果三角形的底不变,高越大(小),三角形面积也就越大(小).同样若三角形的高不变,底越大(小),三角形面积也就越大(小).这说明;当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来
角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.本讲即研究面积相同的三角形的各种形状以及它们之间的关系.为便于实际问题的研究,我们还会常常用到以下结论:
①等底等高的两个三角形面积相等.
②底在同一条直线上并且相等,该底所对的角的顶点是同一个点或在与底平行的直线上,这两个三角形面积相等.
③若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.
它们所对的顶点同为A点,(也就是它们的高相等)那么这两个三角形的面积相等.
同时也可以知道△ABC的面积是△ABD或△AEC面积的3倍.
例如在图中,△ABC与△DBC的底相同(它们的底都是BC),它所对的两个顶点A、D在与底BC平行的直线上,(也就是它们的高相等),那么这两个三角形的面积相等.。
