不合格品率控制图
全面质量管理的常用方法(二)
全面质量管理的常用方法（二）统计分析表方法统计分析表方法也叫质量调查表方法，它最早是由美国的菲根堡姆先生提出的，是在全面质量管理中利用统计图表来收集、统计数据，进行数据整理并对影响产品质量的原因作粗略的分析。
调查表中所利用的统计表格是一种为了便于收集和整理数据而自行设计的空白表。
统计分析表是最为基本的质量原因分析方法，也是最为常用的方法。
在实际工作中，经常把统计分析表和分层法结合起来使用，这样可以把可能影响质量的原因调查得更为清楚。
需要注意的是，统计分析表必须针对具体的产品，设计出专用的调查表进行调查和分析。
常见的统计分析表常用的统计分析表主要有以下几种：◆缺陷位置调查表若要对产品各个部位的缺陷情况进行调查，可将产品的草图或展开图画在调查表上，当某种缺陷发生时，可采用不同的符号或颜色在发生缺陷的部位上标出。
若在草图上划分缺陷分布情况区域，可进行分层研究。
分区域要尽可能等分。
缺陷位置调查表的一般格式可参照表8-1绘制。
所谓不合格品，是指不能满足质量标准要求的产品。
不合格品统计调查表用于调查产品质量发生了哪些不良情况及其各种不良情况的比率大小。
以内燃机车修理厂柴油机总装工段一次组装不合格的返修为例，如表8-2所示。
频数分布调查表是预先制好的一种频数分布空白表格。
该表应用于以产品质量特性值为计量值的工序中，其目的是为了掌握这些工序产品质量的分布情况，比直方图更为简单。
频数分布调查表的一般格式如表8-3所示。
直方图方法什么是直方图直方图也叫质量分布图、矩形图、柱形图、频数图。
它是一种用于工序质量控制的质量数据分布图形，是全面质量管理过程中进行质量控制的重要方法之一。
直方图适用于对大量计量数值进行整理加工，找出其统计规律，也就是分析数据分布的形态，以便对其整体的分布特征进行推断。
直方图是将测量所得到的一批数据按大小顺序整理，并将它划分为若干个区间，统计各区间内的数据频数，把这些数据频数的分布状态用直方形表示的图表。
均值极差控制图
R im{a1 X j} xm - {i1 X jn }
控制图
均值-极差控制图的作法
示例：
某手表厂为了提高手表的质量，应用排列图分析造成手表 不合格的各种原因，发现“停摆”占第一位。为了解决停 摆问题，再次应用排列图分析造成停摆的原因。结果发现 主要是由于螺栓松动引发的螺栓脱落造成的，为解决问题， 应用控制图对装配作业中的螺栓扭矩进行过程控制。
状态Ⅰ：统计控制状态与技术控制状态同时达到，是最理想的状态。 状态Ⅱ：统计控制状态未达到，技术控制状态达到。 状态Ⅲ：统计控制状态达到，技术控制状态未达到。 状态Ⅳ：统计控制状态与技术控制状态均未达到，是最不理想的状态。 一般改进的途径：状态Ⅳ→状态Ⅲ→状态Ⅰ
Page 4
控制图
控制图的目的 控制图和其它的统计图不同，因为它不但能够把数据用曲 线表示出来，观察其变化的趋势，而且能显示数据波动是 属于偶然波动还是异常波动，以指示某种现象是否正常， 从而采取适当的措施。
单值-移动极差控制图。多用于下列场合：(1)采用自动化检查
和测量对每一个产品都进行检验的场合；(2)取样费时、昂贵 的场合；(3)如化工等过程，样品均匀，多抽样也无太大意义 的场合。由于它不像前三种控制图那样能取得较多的信息，所 以它判断过程变化的灵敏度也要差一些。
Page 8
控制图
p控制图。用于控制对象为不合格品率或合格品率等计数 值质量指标的场合。
k X(X1X2X3.....X .K)/kX/ik(k为组 ) 数
i1
k R(R1R2R3.....R.k)/k R/ik
i1
X16.2356R1.2 480
Page 12
控制图
第四步，计算控制界限。 X 图中心线(CL)=X 控制上限(UCL)= X A2 R 控制下限(LCL)= X A2 R
第13章 统计过程控制与诊断(SPC与SPD)
统计过程控制与诊断（SPC与SPD）
均值-标准差控制图
均值控制图主要用于判断生产过程中的均值是否处于或保
持在所要求的统计控制状态
标准差控制图主要用于判断生产过程的标准差是否处于或
保持在所要求的统计控制状态
这两张图通常一起用，因此称为均值-标准差控制图，记为
x s
7 质量管理学
统计过程控制与诊断（SPC与SPD）
图（R图）代替，即得 x
R图
10
质量管理学
x
统计过程控制与诊断（SPC与SPD）
平均值-极差控制图设计过程
收集数据。根据选定的特性值，按一定的时间间隔， 抽取一个容量为n的样本，共取k个样本，一般要求 k≥25, n=4,5。 计算每一个样本的均值与级差。 计算k个样本的均值与级差的均值。 计算x 图与R图的上、下控制限。
22
当过程达到了我们所确定的状态后，才能将分析用控制图的控制线作 为控制用控制图。要用到判断稳态的准则（简称判稳准则），在稳定 之前还要用到判断异常的准则（简称判异准则）。
质量管理学
统计过程控制与诊断（SPC与SPD） 休图的设计思想
休图的设计思想是先定α，再看β。按照3σ方式确定UCL、 CL、LCL就等于确定了α＝0.27％。 80年代起出现经济质量控制（EQC）学派，从两种错误造 成的总损失最小这一点出发来设计控制图与抽样方案。其 学术带头人为德国乌尔茨堡（Wurzburg）大学经济质量控 制中心主任冯.考拉尼（Elart von Collani）教授。
13.6 控制图的判断准则
分析用控制图与控制用控制图
日本有句质量管理的名言：“始于控制图，终于控制图。”所谓“始 于控制图”是指对过程的分析从应用控制图对过程分析开始。 分析用控制图主要作分析以下两点： （1）所分析的过程是否处于统计控制状态，或称统计稳态？ （2）该过程的过程能力指数是否满足要求？ 所谓“终于控制图”是指对过程的分析结束，最终建立了控制用控制 图。
统计过程控制(SPC)重点在于什么
一、各阶段的质量管理重点二.数据的基本常识:⒈数据的分类⒉收集数据的目的⒊收集数据应按注意的事项①有效数字②数字的修约规则⒋数据的几个重要特征:①表示数据集中位置的特征数②表示数据离散程度的特征数:极差、方差、标准偏差(σ) ⒌标准差与平均值关系三、关于SPC理解SPC起源、背景最新版本 SPC的变化SPC的假设条件统计资料的类型(计数、计量)正态分布中值、极差、标准偏差的计算过程的变异四、控制图--SPC质量控制的基本元素是控制图。
⒈什么是控制图:(控制图原理:3σ原则)⒉控制图的主要用途:变异的本质:共同原因、特殊原因管制状态SPC两个阶段:分析阶段,监控阶段分析用的控制图主要目的:管理用的控制图主要作用:充分体现出SPC预防控制的作用。
⒊控制图的基本形式控制图的种类及主要用途 (表)⒋计量值控制图⑴平均值-极差控制图⑵中位数和极差控制图:案例:⑶单值─移动极差控制图(X-Rs)⑷平均值和标准偏差控制图案例:⑸控制线的修订分析⒌计数值控制图计数值控制图有不合格品率控制图(P图)、不合格品数控制图(Pn)图、单位缺陷控制图(u图)和缺陷控制图(C图)。
⑴不合格品率控制图(P控制图)主要用途P控制图几种画法:一是收集的样本大小n不等二是对上述控制界限的计算进行简化,不合格品率控制图(P控制图)画法:案例1:案例2:⑵不合格品数控制图(Pn控制图)案例:⑶单位缺陷数控制图(μ控制图)⑷缺陷数控制图(C图) (例子)⑸公差百分率控制图①什么是公差百分率控制图②中心线和控制界限的确定③公差百分率控制图的特点⒍控制图的观察分析控制图与工序变化的分析和判断⑴工序稳定状态的判断工序是否处于稳定状态,必须同时要满足两个原则⑵工序不稳定状态的判断①点子超出控制界限②点子处在警戒区内③点子在控制界限内,但点子排列有缺陷⒎控制图异常的处理⑴4种情况应重新计算控制界限并作控制图:⑵控制图两种错误的分析⑶3σ控制界限的意义⑷质量特性与控制图的选择要考虑的6个方面:⒏使用控制图的注意事项①分组问题、②分层问题、③控制界限的重新计算课堂练习五、工序能力分析⒈工序能力的含义:工序能力与生产能力、机械能力的区别⒉工序能力的数量表示:为什么用6σ来表示工序能力?⒊工序能力与公差图⒋工序能力指数Cp及其计算①正态分布②双向允差,工序分布中心与规格中心重合(即无偏移的情况)③双向允差,工序分布中心与规格中心有偏移有偏移时工序能力指数用符号CPK表示:例:④单向公差情况:只有公差上限TU时单向公差情况:只有公差下限TL时:例:⒌工序能力的判断及处置⑴工序能力判断标准⑵有偏离系数工序能力的判断标准⑶CP值对应的总体不合格品率表(%)⒍处置:CP>1.67时、1.33 < CP≤1.67时、1< CP≤1.33时、0.67 < CP≤1时、CP≤0.67时⒎改善及矫正措施⒏工序能力指数计算练习。
控制图计算公式
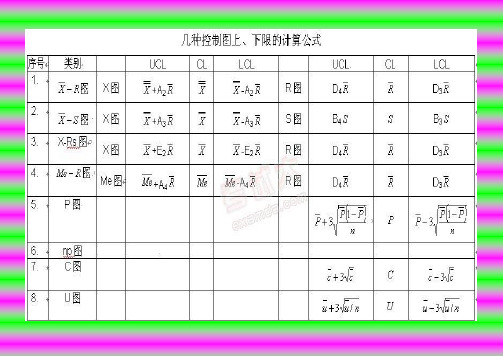
计量 值 控 制 图均值极差图图R X -X CL =R CL =中位数极差图 图R X -~X CL ~=R CL =单值移动极差控制图 图S R X - 计算简便效果差X CL =s R CL =S R UCL 267.3= LCL=不考虑平均值标准差图 图S X -X CL =S A X UCL 3+=S A X UCL 3-=S CL =S B UCL 4=S B UCL 3= 计 数 值 控 制 图不合格品数控制图Pn(Np) 样本数量相等n P CL =不合格品率控制图P样本数量可以不等计算量大，控制线凹凸不平（在特定条件下，控制线可为直线）P CL =缺陷数控制图C样本数量相等C CL = C C UCL 3+= C C UCL 3-=单位缺陷数控制图 U样本数量可以不等计算量大，控制线凹凸不平（在特定条件下，控制线可为直线） U CL = niU U UCL 3+= niU U UCL 3-= 标准差标准差(Standard Deviation) 也称均方差(mean square error)各数据偏离平均数的距离（离均差）的平均数，它是离差平方和平均后的方根。
用σ表()i P n p p P UCL -+=13RA X UCL X 2+=R A XLCL X 2-=RD R UCL 4=R D R LCL 3=R D R UCL 4=R D R LCL 3=RA X UCL m X 23~+=RA X UCL m X 23~-=S R X UCL 660.2+=S R X UCL 660.2-=()iP n pp Pn UCL -+=13()i P n pp Pn UCL --=13()iP n pp P UCL --=13=∑=--=ni i n X X S 121)(ˆσ在讨论控制图原理时，已经知道点子出界就判断异常，这是判断异常的最基本的一条准则。
为了增加控制图使用者的信心，即使对于在控制界限内的点子也要观察其排列是否随机。
控制图
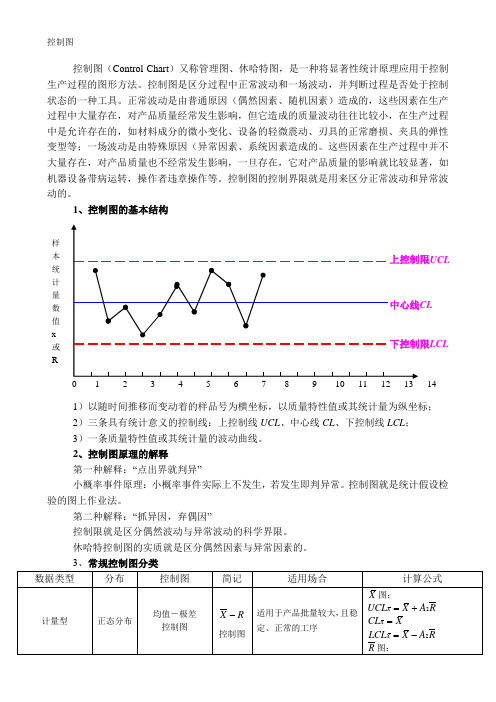
控制图控制图（Control Chart ）又称管理图、休哈特图，是一种将显著性统计原理应用于控制生产过程的图形方法。
控制图是区分过程中正常波动和一场波动，并判断过程是否处于控制状态的一种工具。
正常波动是由普通原因（偶然因素、随机因素）造成的，这些因素在生产过程中大量存在，对产品质量经常发生影响，但它造成的质量波动往往比较小，在生产过程中是允许存在的，如材料成分的微小变化、设备的轻微震动、刃具的正常磨损、夹具的弹性变型等；一场波动是由特殊原因（异常因素、系统因素造成的。
这些因素在生产过程中并不大量存在，对产品质量也不经常发生影响，一旦存在，它对产品质量的影响就比较显著，如机器设备带病运转，操作者违章操作等。
控制图的控制界限就是用来区分正常波动和异常波动的。
1、控制图的基本结构1）以随时间推移而变动着的样品号为横坐标，以质量特性值或其统计量为纵坐标； 2）三条具有统计意义的控制线：上控制线UCL 、中心线CL 、下控制线LCL ； 3）一条质量特性值或其统计量的波动曲线。
2、控制图原理的解释 第一种解释：“点出界就判异”小概率事件原理：小概率事件实际上不发生，若发生即判异常。
控制图就是统计假设检验的图上作业法。
第二种解释：“抓异因，弃偶因”控制限就是区分偶然波动与异常波动的科学界限。
休哈特控制图的实质就是区分偶然因素与异常因素的。
UCLLCL样本统计量数值x 或R14 15 16 17 18按用途分类1）分析用控制图——用于质量和过程分析，研究工序或设备状态；或者确定某一“未知的”工序是否处于控制状态；2）控制用控制图——用于实际的生产质量控制，可及时的发现生产异常情况；或者确定某一“已知的”工序是否处于控制状态。
4、R X -图的绘制1）确定控制对象（统计量）一般应选择技术上最重要的、能以数字表示的、容易测定并对过程易采取措施的、大家理解并同意的关键质量特性进行控制。
2）选择控制图对于计量数据而言，R X -控制图是最常用最基本的。
计数型控制图制作(工作指引)
工作指引
文件编号：XXX-XX-XX
修订本：A0
页数：1/6
标 题：
计数型控制图制作
一、 目的：明确计数型控制图制 作 方 法 ，并通过识别控制图来监视过程的变异情况。
二、 适用范围：用于控制对象用计数质量指标表示其质量状况的场合，如产品的不合 格品率、不合格品数等。
三、 控制图制作 结合公司产品实际特点特点，本文件将依次介绍以下三种计量型控制图制作方法： a) 不合格品率控制图（ p ）； b) 不合格品数控制图（ np ）； c) 单位不合格数控制图（u）; d) 不合格数控制图（c）。
b) 确定子组样本量“n”，一般要求较大的子组容量（例如10到200或更多）， 通常以一个检验批的数量作为子组样本量。注意u控制图子组的样本量不一 定是相同的。
XXXXX 有限公司
工作指引
文件编号：XXX-XX-XX
修订本：A0
页数：4/6
c) 数据收集整理。收集每个子组的检查数量（即子组样本量“n”）、子组不 合格数c，并按子组编号排列，作为编制单位不合格数控制图的数据源。
注：子组数和子组样本量的大小可根据实际情况选择，不一定要局限在上述要求内，但 收集数据越多，控制图越能真实反应实际生产情况。
2） 计算各子组的单位不合格数 ui 和平均单位不合格数 u
ui
ci ni
及
u c1 c2 ck n1 n2 nk
式中：ci 为第i组子组的单位不合格数； ni 为第i组子组的样本量； c1 、 c2 、… ck 为各子组的不合格数； n1 、 n2 、… nk 为各子组样本量。
4） 计算不合格品数控制图的控制限
中心线
计数型控制图分类及案例分析
计数型控制图分类及案例分析引言计数型控制图是一种常用的质量管理工具，用于监控和控制生产过程中的缺陷数量。
它可以帮助企业及时发现并解决生产过程中的质量问题，提高产品质量和生产效率。
本文将介绍计数型控制图的分类及其在实际生产中的应用案例分析。
一、计数型控制图分类根据被测量的质量特征的性质，计数型控制图可分为以下几类：1. P型控制图P型控制图是用于监控不合格品（缺陷品）的百分比的控制图。
它适用于对质量特征进行二元分类的场景，如产品是否合格、工作过程是否按照要求进行等。
在P型控制图中，我们记录每次生产中不合格品（缺陷品）的数量，然后计算不合格品的百分比。
2. C型控制图C型控制图是用于监控单位产品中缺陷次数的控制图。
它适用于对质量特征进行可计数的场景，如产品中缺陷的数量、设备故障次数等。
在C型控制图中，我们按照一定的时间间隔或生产批次来统计缺陷的数量。
3. U型控制图U型控制图是用于监控单位产品中缺陷的平均数的控制图。
U型控制图是对C型控制图的升级，它考虑了单位产品的不同大小或不同生产周期中的缺陷数量的波动。
通过综合考虑缺陷数目和单位产品的差异，U型控制图可以更加准确地监控和控制生产过程中的质量问题。
二、案例分析在实际生产中，计数型控制图被广泛应用于各个行业。
下面以汽车行业为例，进行案例分析。
1. P型控制图应用案例：汽车生产线上的不合格率监控汽车生产过程中存在着许多环节，如果某个环节的不合格品率过高，将严重影响整体生产效率和产品质量。
因此，汽车生产企业常常利用P 型控制图来监控生产线上的不合格品率。
在该案例中，汽车生产企业每天按照一定的时间间隔对生产线上的车辆进行抽检，记录不合格品的数量，并计算当天的不合格品率。
通过绘制P型控制图，汽车生产企业可以及时发现生产线上的不良情况，并采取相应的措施进行改进，从而提高产品质量和生产效率。
2. C型控制图应用案例：汽车发动机缺陷次数监控汽车发动机是汽车的核心部件之一，其质量直接影响到整车的可靠性和性能。
不合格品率控制图
3.5
UCL上控制界限
CL中心值
3.4
3.3
1
5
9
图1-1 单值控制图(X图)
横坐标：以时间先后排列的样本组号。
纵 坐 标 ： 质 量 特 性 或 样 本 统 计 量 ( 如 ： 样 本 平 均x值
上控制界限UCL：Upper Control Limit
下控制界限LCL：Lower Control Limit
3 x
LCL
2
图1-3 x 控制图 样本编号
3、控制图的分类
控制图的种类很多，若按统计量分类，一般可分为：
1)、计量值控制图
A、 控制图(单值控制图)。该图用于测量一个数据时有花费时间，费用高或样品
x 数 据 不 便 分 组 等 情 况 。
B、
控制图(平均值和极差控制图)。此图可以同时控制质量特性值的集中趋
• 控制界线并不能驾驭过程，他们仅仅反映当前 过程的状态。
上控制界线
瞬时失误
中心线
下控制界线 1 2 3 4 5 6 7 8 9 10 11 12
样本数
2、控制图的统计原理
1)、3 原理
x x 在生产过程中，仅有偶然性原因存在时，产品质量特性值 形成
某种确定的典型分布。当出现系统性x 原N因(时,，2 ) 就偏离原来的典型分
绝对值。此图用于数据不能分组时，如：对钢x 水R化学成分的控制等。
(面注的：示由例于中x仅举R了s
控制图在计量值控制图的实际运用中使用最为频繁，故在后 控制图的列子，其它控制图的使用可参考相关书
籍。)
xR
xR
2)、计数值控制图
Pn
A、 控制图(不合格品数控制图)，用于对不合格品数的管理。
第六章 控制图总结
例子
已知某产品的一个尺寸要求为12—o．1，试用随机抽样方 法确定x控制图的中心线及上下控制界限。
解：在一定生产条件下随机抽样n＝50，测出质量特性 值，计算其平均值和标准偏差为：
平均值与极差控制图(
x
-R及控制图)
控制图是计量值控制图，为 x 控制图与R控制图的并用 形式。计量值需作适当分组，求出每组的平均值 x 与 每组的极差R，分别在 x 和R控制图上打点。 控制图主要观察分析平均值的变化(组间变化） R控制图主要观察分析各组的离散波动变化（组内变 化：加工误差的变化）。 -R控制图常用于控制 尺寸、重量、时间、强度、成 分、阻值等计量值。
产品质量控制
对产品质量变异进行控制，采取了以时间序列方式的控制图。在控 制图中按照区分偶然因素和系统因素的数理统计的典型分布规律及 公差要求，定出两条平行的上下控制界限和中心线。 在生产过程进行之中，定期抽取试样，测得其样品的质量特性值。 将测得的数据用点子按时间序列一一描在具有坐标的控制图上，若 点子落在控制界限之中，表示生产处于稳定状态，生产过程正常， 不会出现废品；若点子越出控制界限，或者点子排列不正常，则判 断有异常原因存在，生产过程处于不正常状态。这时应采取措施加 以消除，直到生产过程能够保持稳定状态为止。有的控制图还可以 画出规格的上限和下限，越出规格界限，则说明生产过程已严重失 常，产生了废品。 由上可见，控制图是解决产品必然存在的质量变异而对工序进行质 量控制的主要手段。
a)R的正态分布与总体正态分布中的／j值无关； b）R的正态分布与总体正态分布中的 值有关，两者关 系式为：
（3）控制图的中心线和上下控制界限
（4）R控制图的中心线和上下控制界限
二、控制图的作法（实例）
食品质量管理的工具—控制图
控制图
控制图的应用
理论上讲，预备数据的组数应大于20组，在实际应用中最好取25组数据。 当个别组数据属于可查明原因的异常时，经剔除后所余数据依然大于20组时，
仍可利用这些数据作分析用控制图。若剔除异常数据后不足20组，则须在排除异 因后重新收集25组数据。
取样分组的原则是尽量使样本组内的变异小（由正常波动造成），样本组间的 变异大（由异常波动造成），这样控制图才能有效发挥作用。
因此，取样时组内样本必须连续抽取，而样本组间则间隔一定时间。
控制图
控制图的应用
应制定一个收集数据的计划，将其作为收集、记录及描图的依据。 在适当的时间内收集足够的数据，这样子组才能 反映潜在的变化，这些变化 原因可能是换班/操作人员更换/材料批次不同等原因引起。对正在生产的产品进 行监测的子组频率可以是每班2次，或一小时一次等。
控制图
控制图的应用 由表3中可知，当n=5时
UCL D4 R 2.114 27.44 58.01 CL R 27.44
LCL D3R 0 27.44 0
控制图
控制图的应用 以这些参数作R控制图，并将表1中的R数据在图上打点，结果如图1。
70
极 60 差
50
UCL=58.01
40
②取得预备数据；
控制图 制作步骤
③计算统计量； ④作控制图并打点；
⑤判断过程是否处于稳态；若稳，则进行步骤6； 若不稳，则除去可查明原因（异因）后转入步骤2；
⑥延长控制图的控制线，作控制用控制图，进行日常管理。
控制图的应用
控制图
控制图的应用
本任务以某厂生产的植物油为例，来说明控制图的在食品生产中的应用。
计算公式见表2。
UCL D4 R
第三章 统计过程控制(SPC)与控制图
级别 I II
过程能力评价参考
过程能力过高(应视具体情况而定) 过程能力过高(应视具体情况而定)
过程能力充分, 过程能力充分,表示技术管理能力已很 好,应继续维持 过程能力较差, III 过程能力较差,表示技术管理能力较勉 强,应设法提高为II级 应设法提高为II级 过程能力不足, IV 过程能力不足,表示技术管理能力已很 差,应采取措施立即改善
TL
TU
TL
TU
TL
TU
无偏移单侧规范情况
只有上限要求，无下限要求
CPU＝（TU－ µ）/3 σ ＝（T
只有下限要求，无上限要求
CPU＝（µ－ TL ）/3 σ ＝（µ
过程能力指数C 过程能力指数CP值的评价参考
Cp值范围 >1.67
[1.33,1.67) [1.0, 1.33) [0.67, 1.0)
控制图是如何贯彻预防原则的
对生产过程不断监控，有苗头就能够被察 觉
控制图是如何贯彻预防原则的
无预先征兆，突 然出现，采用20 然出现，采用20 字方针：
查出异因，采取 措施，保证消除， 不再出现，纳入 标准
统计控制状态
只有偶因 没有异因 控制的基准 是生产追求的目标
对产品的质量有99.73％的把握 对产品的质量有99.73％的把握 生产最经济 过程的变异最小
Tu +TL 18.025 +17.99 M= = =18.0075 = µ 2 2 T T −TL 18.025 −17.99 Cp = = U = = 0.897 6σ 6σ 2 p = 2Φ(−3Cp ) = 2Φ(−3×0.897) = 2Φ(−2.691) = 0.0072 q =1− 0.0072 = 0.9928
质量管理的统计方法--控制图
质量管理的统计方法--控制图控制图是用于确定生产或工作过程是否处于稳定状态的图形，通过它可以发现并及时消除生产和工作过程中的失控情况。
控制图是通过对过程中各特性值进行测定、记录、评估和监察过程是否处于控制状态的一种用统计方法设计的图。
在控制图中有两条平行的上下控制界限和中心线，并有按时间序列排列的样本统计量数值的描点序列。
如果控制图中描点落在控制界限之内，则表明过程正常；若控制图中描点落在控制界限之外或描点序列在界限之间有某一种或几种不正常的趋势，则表明过程异常。
（一）控制图的分类控制图可以分为两类，即计量值控制图和计数值控制图。
计量值控制图所依据的数据均属于由测量工具实际测量出来的数据，如长度、重量等控制特性，具有连续性，它包括：①单值控制图；②平均值与极差控制图；③平均值与标准差控制图；④中位值与极差控制图；⑤个别值与移动极差控制图。
计数值控制图所依据的数据均属于以单位个数或次数计算，如不合格品数、不合格品率等。
它包括：①不合格品数控制图；②不合格品率控制图；③缺陷数控制图；④单位缺陷数控制图。
（二）控制图的应用控制图可用于以下几方面：①预测，通过现有图形的分析和研究可大致预测下一步可能的位置。
②评价与诊断，可以评价过程的变化情况，评估过程的稳定性，并能与其他方法结合，可以找到产生状况的原因。
③控制，可对品质状况及时掌控，决定何时需要调整，何时需要保持原有状态。
④确认，比较后确认某一过程的改进。
[例题8] 控制图可用于（）A. 预测，通过现有图形的分析和研究可大致预测下一步可能的位置B. 评价与诊断，可以评价过程的变化情况，可以找到产生状况的原因C. 可以显示波动的状况D. 控制，可对品质状况及时掌控，决定何时需要调整，何时需要保持原有状态1E. 确认，比较后确认某一过程的改进答案：ABDE（三）控制图的作法（1）选择控制特性。
（2）选择合适的控制图。
（3）选取一定数量的数据，在生产过程中，定期抽取试样。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
固定的 样本大小
变化的 样本大小
样本大 小为1
固定的
可变的
样本大小 样本大小
C - 控制图 U - 控制图 Pn - 控制图 P - 控制图 X－控制图 X-控制图 R控制图
X-控制图 S控制图
page 12
Issued by: QCDE PC Team
4、控制图的作用
控制图主要是以预防为主，把影响产品质量的诸因素消灭在萌芽状态， 以保证质量、降低成本、提高生产效率、提高经济效益的目的。其具体作用 分述如下：
2)、控制图的控制界限
通常控制图根据 “ 3” 原则确定控制界限，如图-2所示，x图
的中心线和上、下控制界限为： x
中心线：CL (或 x)
上控制限：UCL 3 0(x)
3
下控制限：LCL 3
3
UCL 3
CL x
LCL 3
四、复习思考题----------------------------------------------------------------------------------59页
page 2
Issued by: QCDE PC Team
一、控制图概述
page 3
Issued by: QCDE PC Team
百分率
(样本大小变化)
不合格品 Pn - 控制图
P - 控制图
缺陷 C - 控制图 U - 控制图
page 11
Issued by: QCDE PC Team
控制图的类型
图表类型
计数值 (属性数据)
计件
分类 (是/否)
发生率 或 非一致性图表
缺陷数或 非一致性单位
计量值 (变量数据)
固定的 机率
可变的 机率
1、控制图的概念
早在1924年，美国的休哈特(W.A.Sheuhart)首先提出用控制图(也叫管 理图)进行工序控制，控制图是控制生产过程状态，保证工序加工产品质量 的重要工具。应用控制图可以对工序过程状态进行分析、预测、判断、监
x 控和改进。如图1-1所示，是以单值控x制图，即 图为例说明一般控制图的
据)中，平均约有3个数据超出分布范围。有997个落在 ( 3 , 3 ) 之
x 中，如果从处于统计控制状态的工序中任抽一个样品 ，我们可以认为
一定范围在分布范围 3 之中，而认为出现在分布范围之外是不可能
的，这就是3 原理。
page 7
Issued by: QCDE PC Team
X3
32 36 34 68 44 43 41 38 49 36 39 41 47 45 43 29 29 28 37 45 45 35 39 35 43
品的不合格品率变化来控制质量的。
C、 C 控制图(缺陷数控制图)，用于单件上缺陷数，如铸件上的气孔、砂
眼数、布匹上的疵点等的控制。
D、 控制图(单位缺陷数控制图)，用于单位面积、单位长度上缺陷数的
控制。
page 10
Issued by: QCDE PC Team
计数值控制图
数量
(样本大小不变)
x 在生产过程中，仅有偶然性原因存在时，产品质量特性值 形成某种 x 确定的典型分布。当出现系统性原因时， 就偏离原来的典型分布了。
设当工序不存在系统性原因时，x N (, 2 )，
则 P( 3 x 3 ) 0.9973 。
x 如图1-4如示， 落在两条虚线外的概率只有0.27%。即1000个样品(数
基本模式。3.6
3.5
UCL上控制界限
CL中心值
3.4
3.3
1
5
9
图1-1 单值控制图(X图)
横坐标：以时间先后排列的样本组号。
纵坐标：质量特性或样本统计量(如：样本平均值 x )。
上控制界限UCL：Upper Control Limit
下控制界限LCL：Lower Control Limit
中心线CL：Control Limit
二、控制图的设计------------------------------------------------------------------------------20页 1、计数值控制图的设计-------------------------------------------------------------------21页 1)、不合格品率控制图 (P控制图)-------------------------------------------------21页 2)、缺陷数控制图 (C控制图)-------------------------------------------------------30页 3)、不合格品数控制图 (Pn控制图)----------------------------------------------- 33页 4)、单位缺陷控制图 (U控制图)---------------------------------------------------- 37页
供较多的质量情报和较高的检出力。
C、 ~x R 控制图(中位值和极差控制图)。其用途与 x R 控制图相似， 其优点是可以减少计算，但检出力不如 x R控制图高。
D、 x Rs 控制图(单值与移动差控制图)。 为移动极差，即相邻数之差
的绝对值。此图用于数据不能分组时，如：对钢水化学成分的控制等。
日期
23-Dec 27-Dec 28-Dec 29-Dec 30-Dec
时间
8:50 11:30
1:45 3:45 4:20 8:35 9:00 9:40 1:30 2:50 8:30 1:35 2:25 2:35 3:55 8:25 9:25 11:00 2:35 3:15 9:35 10:20 11:35 2:00 4:25
3、控制图的分类
控制图的种类很多，若按统计量分类，一般可分为：
1)、计量值控制图
x A、 控制图(单值控制图)。该图用于测量一个数据时有花费时间，费用高或
样品数据不便分组等情况。
B、x R 控制图(平均值和极差控制图)。此图可以同时控制质量特性值的集中 趋势，即平均值 x的变化，以及其离中趋势，即极R差 的变化。该图可以提
5)、使工序的成本和质量成为可预测的。
6)、最终可以保证产品质量提高经济效益。
page 13
Issued by: QCDE PC Team
二、控制图的设计
page 14
Issued by: QCDE PC Team
1、计量值控制图的设计
在计量值控制图中，常用的典型控制图是“平均值----极差”控制图，x即 R
2、计量值控制图的设计-------------------------------------------------------------------38页
三、控制图的观察分析------------------------------------------------------------------------ 50页 1、受控状态--------------------------------------------------------------------------------- 51页 2、失控状态--------------------------------------------------------------------------------- -52页 3、应注意的几个问题---------------------------------------------------------------------- 58页
LCL下控制界限
13
page 4
Issued by: QCDE PC Team
控制图
概念：
• 控制图可用来监测那些处于临界状态的过程。 • 过程监测可鉴定和量化过程中的变化类型。 • 计量值
• 利用真实的测量值进行制表。
• 计数值
• 利用合格-不合格信息进行制表。
page 5
Issued by: QCDE PC Team
由表1-3查得，当n=4时，A2 0.729 , D3 0, D4 2.828 所以， 图的控制界限为： CL x 6.41
UCL x A2R 6.41 0.729 0.09 6.48
同理
，R图的
控制界限为：
LCL
x
A2
R
6.41
0.729
0.09
x 如图-3所示
控制图的控制界限为： 图1-2 3 控制图 样本编号
中心线：CL (或 x)
x
x
2
UCL
上控制限：UCL x 3
x (x)
下控制限：LCL x 3 x
3
x
CL
3 x
LCL
2
图1-3 x 控制图 样本编号
page 8
Issued by: QCDE PC Team
1)、能及时发现生产过程中的异常现象和缓慢变异，预防不合格品发生 ，从而降低生产费用和提高生产效率。
2)、能有效分析和判断生产过程工序质量的稳定性，从而降低检验、测 试费用。
3)、可查明设备和工艺手段的实际精度，以便作出正确的技术决定。
4)、 为真正地制定工序目标和规格界限，特别是对配合零部件的最优化 确立了可靠的基础，也为改变未能符合经济性的规格标准提供了依据。
测定值
X1
35 46 34 69 38 42 44 33 48 47 38 37 40 38 50 33 41 38 33 56 38 39 42 43 39