数值分析实验三分段线性插值
3 数值分析之分段插值与样条插值

注:I h ( x ) yi Li ( x )在x [xi ,xi 1]时
i 0
n
x xi 1 x xi I h ( x )=yi ( ) yi 1 ( ), xi xi 1 xi 1 xi
分段线性插值多项式
分段插值函数 I1 ( x ) n I 2 ( x) I h ( x ) yi Li ( x ) i 0 I ( x) n x [ x0 , x1 ) x [ x1, x2 ) ...... x [ xn1, xn ]
分段线性插值余项
Rh ( x ) f ( x ) I h ( x ) f ( ) =| ( x xi )( x xi 1 ) | (1 1)!
''
( xi 1 xi ) '' | f ( ) | 8 2 h '' | f ( ) | 8
2
分段线性插值
算法: 1.输入xi , yi (i 0,1,...,n) 2.按k 1,2,...,m做 (1)输入插值点u (2)对于j 1,2,...,n做 如果u x j 则
其中a j , b j , c j .d j为待定常数,插值条件 为: ( 1 )s ( x j ) f ( x j ) (j 0,1,...,n); (2) (n 1)内节点处连续及光滑性 条件: s ( x j 0) s ( x j 0) s( x j 0) s( x j 0) j 1,2,...,n 1 s( x j 0) s( x j 0)
二次样条插值
对于待定系数a j , b j , c j 称为边界条件。 j 1,2,...n,即3n个未知系数, 而插值条件为3n 1个,因此须给出一个补充条件,
数值分析分段插值

华长生制作
9
L(2k )( x)
yk 1
(x ( xk 1
xk )( x xk 1 ) xk )( xk 1 xk 1 )
yk
(x ( xk
xk 1 )( x xk 1 ) xk 1 )( xk xk 1 )
yk 1
(x ( xk 1
xk 1 )( x xk ) xk 1 )( xk 1 xk
3 fk t(t 1)(t 2) 3!
华长生制作
0 t 1 k 0,1, ,n 2
17
(7)
N2(xk th)
fk fk t
2 fk t(t 1) 2
Rn(x0 th)
f (3)( )
3!
h3t(t 1)(t 2)
3 fk t(t 1)(t 2) 3!
分段二次Newton
i0
1
2
3
4
5
xi 0.30 0.40 0.55 0.65 0.80 1.05 yi 0.30163 0.41075 0.57815 0.69675 0.87335 1.18885
求f (x)在x 0.36, 0.42, 0.75, 0.98,1.1处的近似值(用分段线性)
解: 分段线性Lagrange插值的公式为
f
(
6
)
(
x
xk
1
)(x
xk
)(
x
xk
1
)
, x [xk 1 , xk 1 ], 且与x有关
|R2 ( x)|
1 max | 6 axb
f
(x) | max xk1 xxk1
| (x
xk1)(x
xk )(x
计算方法 1.3 分段线性插值

x x x x i 1 i ˆ S ( x ) y y , x x x 1 i i 1 i i 1 x x x x i i 1 i 1 i 于是, S1 ( x ) 是在 [ a , b ] 上是连续函数。
x [xj , xj ] 1 x [xj, xj 1] 其他
2)在插值节点 x 0 上,插值基为:
2 ( x x ) l ( x ) x [ x ,x ] 0 0 0 1 B ( x ) 0 0 其他 3)在插值节点 x n 上,插值基为:
2 ( x x ) l ( x ) n n B ( x ) n 0
1
左,右连接起来!
x
j1
xj
x
j1
2 2 H ( x ) 1 2 l ( x ) l ( x ) y 1 2 l ( x ) l ( x ) y 3 j 1 j j j j 1 j 1 2 2 ( x x ) l ( x ) y ( x x ) l ( x ) y j j j j 1j 1 j 1
k axb
提示:类似于前面的误差估计。 几点说明:
1)只要节点间距充分小,插值法总能获得所要求的精度。 2)局部性。如果修改某个数据,则插值曲线仅在某个局部范围内受影响。
插值节点 x 上,取值为 0 .即 k,k j 1 lj (x k ) 0 k j k j
2 )在每个小区间 [x 上,插值基 lj (x )都是线性函数 . i, x i 1]
基于以上两方面,我们观察
1
右 左
x
j1
分段线性插值法

《数值分析》实验报告实验序号:实验五 实验名称: 分段线性插值法1、 实验目的:随着插值节点的增加,插值多项式的插值多项式的次数也增加,而对于高次的插值容易带来剧烈的震荡,带来数值的不稳定(Runge 现象)。
为了既要增加插值的节点,减小插值的区间,以便更好的逼近插值函数,又要不增加插值多项式的次数以减少误差,可采用分段线性插值。
2、 实验内容:求一个函数ϕ(x )用来近似函数f (x ),用分段线性插值的方法来求解近似函数ϕ(x )并画出近似函数图像及原函数图像。
设在区间[a,b]上,给定n+1个插值节点b x x x x a n =<<<<=...210与相应的函数值n y y y ,...,,10,求一个插值函数)(x ϕ,满足以下条件:(1)),...,2,1,0()(n j y x j j ==ϕ; (2) )(x ϕ在每一个小区间[1,+j j x x ]上就是线性函数。
对于给定函数11-,2511)(2≤≤+=x x x f 。
在区间[]11-,上画出f (x )与分段线性插值函数)(x ϕ的函数图像。
1. 分段线性插值的算法思想:分段线性插值需要在每个插值节点上构造分段线性插值基函数)(x l j ,然后再作它们的线性组合。
分段线性插值基函数的特点就是在对应的插值节点上函数值取 1,其它节点上函数值取0。
插值基函数如下:⎪⎩⎪⎨⎧≤≤--=其它 ,0,)(101010x x x x x x x x l ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≤<--≤≤--=+++---其它 ,0,,)(111111j j j j j j j j j j j x x x x x x x x x x x x x x x l⎪⎩⎪⎨⎧≤≤--=---其它 ,0,)(111n n n n n n x x x x x x x x l设在节点a≤x0<x1<…≤b=f(xi),(i=0,1,2,…,n)求折线函数L(x)满足:(1)L(x)∈C[a,b](2)L(x[i]=y[i])(3)L(x)在每个小区间(x[i],x[i+1])上就是线性插值函数¢(x)叫做区间[a,b]上对数据(x[j],y[j])(j=0,1,2,…,n)的分段区间函数。
插值数值实验报告(3篇)

第1篇一、实验目的1. 理解并掌握插值法的基本原理和常用方法。
2. 学习使用拉格朗日插值法、牛顿插值法等数值插值方法进行函数逼近。
3. 分析不同插值方法的优缺点,并比较其精度和效率。
4. 通过实验加深对数值分析理论的理解和应用。
二、实验原理插值法是一种通过已知数据点来构造近似函数的方法。
它广泛应用于科学计算、工程设计和数据分析等领域。
常用的插值方法包括拉格朗日插值法、牛顿插值法、样条插值法等。
1. 拉格朗日插值法拉格朗日插值法是一种基于多项式的插值方法。
其基本思想是:给定一组数据点,构造一个次数不超过n的多项式,使得该多项式在这些数据点上的函数值与已知数据点的函数值相等。
2. 牛顿插值法牛顿插值法是一种基于插值多项式的差商的插值方法。
其基本思想是:给定一组数据点,构造一个次数不超过n的多项式,使得该多项式在这些数据点上的函数值与已知数据点的函数值相等,并且满足一定的差商条件。
三、实验内容1. 拉格朗日插值法(1)给定一组数据点,如:$$\begin{align}x_0 &= 0, & y_0 &= 1, \\x_1 &= 1, & y_1 &= 4, \\x_2 &= 2, & y_2 &= 9, \\x_3 &= 3, & y_3 &= 16.\end{align}$$(2)根据拉格朗日插值公式,构造插值多项式:$$P(x) = \frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)}y_0 + \frac{(x-x_0)(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)}y_1 + \frac{(x-x_0)(x-x_1)(x-x_3)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)}y_2 + \frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1)(x_3-x_2)}y_3.$$(3)计算插值多项式在不同点的函数值,并与实际值进行比较。
数值分析实验报告(插值法)

武汉理工大学学生实验报告书实验课程名称数值分析开课学院计算机科学与技术学院指导老师姓名学生姓名学生专业班级2010—2010学年第一学期实验课程名称:数值分析第二部分:实验调试与结果分析(可加页)一、调试过程(包括调试方法描述、实验数据记录,实验现象记录,实验过程发现的问题等)(1)用拉格朗日插值法计算时,输入及运行结果如下:拉格朗日插值法牛顿插值法(2)利用二次插值计算时,输入及运行结果如下:拉格朗日插值法牛顿插值法(3)用艾尔米特插值法计算时,f(x)的插值多项式H5(x)=(1+4*x)*(x-0.5)*(x-0.5)*(x-2)*(x-2)+(3.90807-6.03838*x)*(x-2)*(x-2)*x*x+(2.34573-4.16674*x)*x*x*(x-0.5)*(x-0.5)(4)各插值算法的精度差异比较经过比较,拉格朗日插值法要比牛顿插值法算法的计算量多一些,拉格朗日插值法后一次计算时用到了前一次计算的结果,提高了运算的效率,但拉格朗日插值法在构造艾尔米特插值法时很方便,将坐标点和对应的导数结合起来的精度比线性插值的精度又要高一些。
但从实验数据来看,在坐标不是很多的情况下,已知的点越多精度也就相对较高。
对于实验要求的第二组数据用拉格朗日插值法(或者牛顿插值法)实验结果如下:一下分别是二阶、三阶、四阶、五阶插值得到的结果以上只是实验结果的一部分,改变插值的位置时,得到的实验结果精度也是有所不同的。
由以上结果分析可知,插值次数并不是越多越好,多了反而会让结果更加偏离真实结果,这充分说明了高次插值存在“病态性质”,在已知点很多的情况下应该采用分段低次插值,将拉格朗日插值法和牛顿插值法运用到分段低次插值法当中,这样得到的结果可能胡更加精确。
分段线性插值法

《数值分析》实验报告实验序号:实验五 实验名称: 分段线性插值法1、 实验目的:随着插值节点的增加,插值多项式的插值多项式的次数也增加,而对于高次的插值容易带来剧烈的震荡,带来数值的不稳定(Runge 现象)。
为了既要增加插值的节点,减小插值的区间,以便更好的逼近插值函数,又要不增加插值多项式的次数以减少误差,可采用分段线性插值。
2、 实验内容:求一个函数ϕ(x )用来近似函数f (x ),用分段线性插值的方法来求解近似函数ϕ(x )并画出近似函数图像及原函数图像。
设在区间[a,b]上,给定n+1个插值节点b x x x x a n =<<<<=...210和相应的函数值n y y y ,...,,10,求一个插值函数)(x ϕ,满足以下条件:(1)),...,2,1,0()(n j y x j j ==ϕ; (2) )(x ϕ在每一个小区间[1,+j j x x ]上是线性函数。
对于给定函数11-,2511)(2≤≤+=x x x f 。
在区间[]11-,上画出f (x )和分段线性插值函数)(x ϕ的函数图像。
1. 分段线性插值的算法思想:分段线性插值需要在每个插值节点上构造分段线性插值基函数)(x l j ,然后再作它们的线性组合。
分段线性插值基函数的特点是在对应的插值节点上函数值取 1,其它节点上函数值取0。
插值基函数如下:⎪⎩⎪⎨⎧≤≤--=其它 ,0,)(101010x x x x x x x x l ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≤<--≤≤--=+++---其它 ,0,,)(111111j j j j j j j j j j j x x x x x x x x x x x x x x x l⎪⎩⎪⎨⎧≤≤--=---其它 ,0,)(111n n n n n n x x x x x x x x l 设在节点a ≤x0<x1<…≤b=f(xi),(i=0,1,2,…,n)求折线函数L (x )满足:(1) L(x)∈C[a,b](2) L(x[i]=y[i])(3) L(x)在每个小区间(x[i],x[i+1])上是线性插值函数¢(x )叫做区间[a,b]上对数据(x[j],y[j])(j=0,1,2,…,n)的分段区间函数。
ch2-3分段线性插值

插值法
第三节 分段线性插值法
分段线性插值法的一般理论 分段线性插值多项式的构造 分段线性插值余项和误差估计
简单的分段高次插值多项式
分段线性插值法
一般来说,高次插值多项式是不妥当的,从 数值计算上可解释为高次插值多项式的计算会带 来舍入误差的增大,从而引起计算失真。因此, 实践上作插值时一般只用一次、二次最多用三次 插值多项式。 那么如何提高插值精度呢? 采用分段插值是一种办法。
h2 R( x ) f ( x ) ( x ) M, 8 其中h max ( xi 1 xi ), M max f ( x )
0 i n 1 a xb
分段线性插值多项式的构造
证明:由Lagrange 余项公式,当x∈[xi, xi+1]时
f ( )( x xi )( x xi 1 ) f ( x ) ( x ) R( x ) 2!
Newton向后插值公式为
t ( t 1) N 3 ( x 4 th) 0.64422 0.07958t 0.00563 2! t ( t 1)( t 2) 0.00083 3!
x x4 0.57891 0.7 t 1.2109 h 0.1
Newton向前插值公式为
等距节点插值公式
t ( t 1) N 3 ( x0 th) 0.38942 0.09001t 0.00480 2 t ( t 1)( t 2) 0.00083 6 x x0 t (0.57891 0.4) / 0.1 1.7891 h
sin 0.57891 N 3 (0.57891) 0.38942 0.09001 1.7891 1.7891 0.7891 0.00480 2 1.7891 0.7891 0.2109 0.00083 0.54711 6
计算方法分段线性_三次样条插值

计算方法分段线性_三次样条插值分段线性和三次样条插值是两种常用的插值方法,在数值分析和插值问题中广泛使用。
1.分段线性插值分段线性插值是一种简单直观的插值方法,将插值区间划分为若干个子区间,在每个子区间上用线性函数进行插值。
假设给定的插值节点有n+1 个,节点为 (x0, y0), (x1, y1), ..., (xn, yn),并且满足 x0 <x1 < ... < xn。
则对于任意 xx 使得 x 在 [xi, xi+1] 之间,可以通过线性插值得到其函数值 yy,即:yy = yi + (xx - xi) * (yi+1 - yi) / (xi+1 - xi)分段线性插值方法简单易懂,适用于一些较简单的插值问题。
但是由于插值函数在节点之间是线性的,可能不能准确地反映出数据的特征,因此不适用于一些需要高精度的插值问题。
三次样条插值是一种更复杂、更精确的插值方法,将插值区间划分为若干个子区间,在每个子区间上用三次多项式进行插值。
三次样条插值方法的基本思想是找到一组三次多项式,满足在每个子区间内插值点的函数值和一阶导数值相等,并且两个相邻多项式在节点处的二阶导数值也相等。
具体的求解步骤如下:(1) 假设有 n+1 个插值节点 (x0, y0), (x1, y1), ..., (xn, yn),构造 n 个三次多项式,即每个多项式在 [xi, xi+1] 之间插值。
(2) 对每个子区间内的多项式进行插值,设第 i 个子区间的多项式为 Si(x) = ai + bi(x-xi) + ci(x-xi)^2 + di(x-xi)^3、将插值节点的函数值和一阶导数值代入多项式中,可以得到 n 个线性方程,利用这 n 个线性方程可以求解出 n 个子区间的系数。
(3)由于n个子区间的多项式必须在节点处一阶导数值相等,因此再设立n-1个方程,利用这些方程可以求解出n-1个子区间的二阶导数值。
(4)将求解得到的系数和二阶导数值代入每个子区间的多项式中,得到完整的三次样条插值函数。
数值分析实验报告2——Runge现象
数值分析课程实验报告——插值逼近题目一.Runge 函数的插值1. Runge 函数Runge 函数的表达式为:21()125R x x =+ 其在[-1,1]区间上的函数图像如图1.1。
在课程学习中我们知道,对Runge 函数进行高次插值时有可能在两端出现不收敛的情况,即Runge 现象。
下面将分别用四种不同的插值方法在[-1,1]区间上对Runge 函数进行插值,并分析是否产生Runge 现象,比较插值效果。
图1.1.Runge 函数在[-1,1]区间的函数图像2.Newton 插值首先根据课本上的Newton 插值算法进行编程(代码略)。
核心思想就是用符号变量进行中间运算,以便将最终的插值函数用符号表达式表示出来,并进一步生成图像。
此处插值节点选择为等距插值节点,即:0.1(0,1,2,,)i x ih i =-+= (20)其中h=0.1。
插值曲线与原曲线的对比如图1.2(蓝色为原曲线,红色为插值曲线)。
从图中看出,在区间中部,二者吻合较好;但在区间两端二者则产生了明显偏差,甚至可以达到一个非常大的数值(e20量级)。
因此,在等距节点的20次Newton 插值下,产生了明显的Runge 现象。
图1.2.Newton 插值曲线与原曲线对比3. Lagrange 插值此处同样是根据Lagrange 插值的具体算法进行编程。
但插值节点不再是等距分布,而是如下形式:21cos()(0,1,2,,)42i i x i π+==…20 插值曲线与原曲线的对比如图1.3(蓝色为原曲线,红色为插值曲线)。
从图中看出,插值曲线与原曲线吻合的很好,没有产生明显的Runge 现象。
对比产生了明显Runge 现象的20次Newton 插值,Lagrange 插值的最高次数虽然也是20,但由于此处的插值节点不是等距分布的(事实上,此处采用的插值节点正是Chebyshev 多项式的零点),而是中间疏两边密,因此两侧较密的节点很好地抑制了Runge 现象。
数值分析实验报告Hermite插值法、Runge现象,比较Language插值、分段线性插值、分段三次Hermie插值

山东师范大学数学科学学院实验报告x 0.1 0.5 1 1.5 2 2.5 3y 0.95 0.84 0.86 1.06 1.5 0.72 1.9y' 1 1.5 2 2.5 3 3.5 4求质点在时刻1.8时的速度,并画出插值多项式的图像。
1)运用Hermite插值法画出图像,如图4-1,并求质点在时刻1.8时的速度。
>>clear>>clc>>X=[0.1 0.5 1 1.5 2 2.5 3;0.95 0.84 0.86 1.06 1.5 0.72 1.9;1 1.5 2 2.5 3 3.5 4];>> x=0.1:0.01:3;>> H=Hermite1(X,x);>> plot(x,H)>> hold on>> plot(X(1,:),X(2,:),'r*')>> H1_8=Hermite(X,1.8);>> plot(1.8,H1_8,'go')>> legend('插值图像','原始点','目标点');图4-1二、验证高次插值的Runge现象问题分析和算法设计(一)Language插值代码function [Ln] =Lagrange(X,x)%请输入2*n+1矩阵X,X中第一行每个元素都是插值节点,X中第二行每个元素都是插值节点对应的函数值;%第二章P24例一拉格朗日插值n=size(X,2);d=0;for m=1:1:nif x==X(1,m);d=m;breakendend运行结果和总结 运行结果 例:给定函数55,11)(2≤≤-+=x xx f ; (1) 验证表2-10的误差结果(高次插值的Runge 现象);(2) 以0.1为步长分别进行Language 插值、分段线性插值、分段三次Hermite插值,画出三种插值函数以及f(x)的图像,比较三种插值结果。
1-3分段线性插值解析

1 x 0.8
分段线性插值多项式的构造 所以f(-0.96) (-0.96)=0.04253 (2)插值节点为xi=-1+ ih (i=0,1,…,n),h=(b-a)/2=2/n
由分段线性插值的余项估计: |f(x)- (x) |=|R(x)| ≤Mh2/8
f ( x ) 50 x (1 25 x 2 ) 2
内容小结
内容小结
1. 分段线性插值法;
2. 分段线性插值多项式的构造.
命令格式
1. 插值多项式 命令InterpolatingPolynomial求一个多项式,使给定的数 据是准确的函数值,其调用格式如下: InterpolatingPolynomial[{f1,f2,…},x] 2,3,…时的函数值为f1,f2,…。 当自变量x为1,
75 x 2 1 | f ( x ) | 50 | | 1 2 3 (1 25 x ) M max f ( x ) R( x ) 0.125h2 10 4
段线性插值多项式的构造
分段二次插值即:选取跟节点 x最近的三个节点 xi-1,xi, xi+1 进行二次插值 , 即在区间 [xi-1, xi+1] , 取:
h2 R( x ) f ( x ) ( x ) M, 8 其中h max ( xi 1 xi ), M max f ( x )
0 i n 1 a xb
分段线性插值多项式的构造
证明:由Lagrange 余项公式,当x∈[xi, xi+1]时
f ( )( x xi )( x xi 1 ) f ( x ) ( x ) R( x ) 2!
x x , x i 1 x x i i 1 i x xi 1 li ( x ) , x i x x i 1 xi xi 1 0 其它
分段线性插值

1.4分段插值 一.分段线性插值即用折线代替曲线。
设f (x )连续 优点:计算简单,适用于光滑性要求不高的插值问题。
缺点:分段插值函数只能保证连续性,失去了原函数的光滑性。
二.分段三次(Hermite )插值不少实际插值问题不仅要求函数值相等,而且还要求导数值也相等。
这就导致下面的Hermite 插值。
并满足: 从而由此条件可得: 类似可得的表达式。
下面是matlab 函数pieceline (x ,y ,u )实现分段线性插值多项式的计算。
function v=pline(x,y,u) delta=diff(y)./diff(x); n=length(x); k=ones(size(u)); for j=2:n-1k(x(j)<=u)=j; ends=u-x(k);v=y(k)+s.*delta(k);在每个区间 上,用1阶多项式 (直线) 逼近 f (x):],[1+i i x x 11111)()(++++--+--=≈i ii ii i i i y x x x x y x x x x x P x f ],[for 1+∈i i x x x 记 易证:当 ||max 1i i x x h -=+0→h )()(1x f x P h →一致给定000,...,;,...,;,...,,n n n x x y y y y ''在 上利用两端点的 y 及 y' 构造3次Hermite 函数。
],[1+i i x x 31111()()()()()i i i i i i i i S x y x y x y x y x ααββ++++=+++''3311'331 1.(), (),(), ()i i i i i i i i S x y S x y S x y S x y ++++===='''1111111111111()1, ()0, ()0, ()0,()0, ()1, ()0, ()0,()0, ()0, ()1, ()0,()0, ()i i i i i i i i i i i i i i i i i i i i i i i i i i i i x x x x x x x x x x x x x x ααββααββααββαα+++++++++++++==============''''''1110, ()0, () 1.i i i i x x ββ+++==''1111122()12,2()().i i i i i i i i i i ii x x x x x x x x x x x x x x x x αβ+++++--⎛⎫⎛⎫=+ ⎪ ⎪--⎝⎭⎝⎭-⎛⎫=- ⎪-⎝⎭程序中,pline是分段线性插值函数;输入参数x——给定的数据点的横坐标所组成的向量Y——给定的数据点的纵坐标所组成的向量U——需要计算的点所组成的向量输出参数v——u所对应的分段线性插值多项式的值,即v(i)=s1(u(i)),其中s1是未来满足分段线性插值多项式Detla是计算差商的最后计算s、v。
分段线性插值法

(1) ; (x j ) y j ( j 0,1,2,..., n)
(2) (x) 在每一个小区间[ xj, xj1 ]上是线性函
2
数值分析实验报告
数。
对于给定函数 f (x) 1 ,-1 x 1。在区间-1,1上 1 25x2
画出 f(x)和分段线性插值函数(x) 的函数图像。 1. 分段线性插值的算法思想:
// Center icon in client rectangle
int
cxIcon
=
GetSystemMetrics(SM_CXICON);
int
cyIcon
=
GetSystemMetrics(SM_CYICON);
CRect rect;
GetClientRect(&rect);
int x = (rect.Width() - cxIcon + 1) / 2;
int y = (rect.Height() - cyIcon + 1) / 2;
14
数值分析实验报告
// Draw the icon dc.DrawIcon(x, y, m_hIcon); } else { CDialog::OnPaint(); } }
// The system calls this to obtain the cursor to display while the user drags
: CDialog(CLDlg::IDD, pParent)
{
//{{AFX_DATA_INIT(CLDlg)
// NOTE: the ClassWizard will add member initialization here
1-3分段线性插值

75 x 2 1 | f ( x ) | 50 | | 1 2 3 (1 25 x ) M max f ( x ) R( x ) 0.125h2 10 4
1 x 1
h 0.028
分段线性插值多项式的构造
分段二次插值即:选取跟节点 x最近的三个节点 xi-1,xi, xi+1 进行二次插值 , 即在区间 [xi-1, xi+1] , 取:
h2 R( x ) f ( x ) ( x ) M, 8 其中h max ( xi 1 xi ), M max f ( x )
0 i n 1 a xb
分段线性插值多项式的构造
证明:由Lagrange 余项公式,当x∈[xi, xi+1]时
f ( x ) ( x ) R( x )
内容小结
内容小结
1. 分段线性插值法;
2. 分段线性插值多项式的构造.
命令格式
1. 插值多项式 命令InterpolatingPolynomial求一个多项式,使给定的数 据是准确的函数值,其调用格式如下: InterpolatingPolynomial[{f1,f2,…},x] 2,3,…时的函数值为f1,f2,…。 当自变量x为1,
分段线性插值多项式的构造
对任意x [a , b], 都有 ( xi xi 1 ) 2 h2 R( x ) max { max f ( x ) } M 0 i n 1 x i x x i 1 8 8
证毕。
分段线性插值多项式的构造
1 例3.1 例 :设 f ( x ) -1 ≤x ≤1 2 1 25 x (1)将[-1,1] 10 等份,用分段线性插值近似计f(-0.96)。
数值分析常用的插值方法

数值分析常用的插值方法数值分析中常用的插值方法有线性插值、拉格朗日插值、分段线性插值、Newton插值、Hermite插值、样条插值等。
下面将对这些插值方法进行详细介绍。
一、线性插值(linear interpolation)线性插值是最简单的插值方法之一、假设已知函数在两个点上的函数值,通过这两个点之间的直线来估计中间点的函数值。
线性插值公式为:f(x)=f(x0)+(x-x0)*(f(x1)-f(x0))/(x1-x0)其中,f(x)表示要求的插值点的函数值,f(x0)和f(x1)是已知的两个点上的函数值,x0和x1是已知的两个点的横坐标。
二、拉格朗日插值(Lagrange interpolation)拉格朗日插值是一种基于多项式的插值方法。
它通过多个已知点的函数值构造一个多项式,并利用这个多项式来估计其他点的函数值。
拉格朗日插值多项式的一般形式为:f(x) = Σ[f(xi) * Li(x)] (i=0,1,2,...,n)其中,f(x)表示要求的插值点的函数值,f(xi)是已知的多个点的函数值,Li(x)是拉格朗日基函数。
拉格朗日基函数的表达式为:Li(x) = Π[(x-xj)/(xi-xj)] (i≠j,i,j=0,1,2,...,n)三、分段线性插值(piecewise linear interpolation)分段线性插值是一种逐段线性近似函数的方法。
通过将整个插值区间分成多个小段,在每个小段上使用线性插值来估计函数的值。
分段线性插值的过程分为两步:首先确定要插值的点所在的小段,在小段上进行线性插值来估计函数值。
四、Newton插值(Newton interpolation)Newton插值也是一种基于多项式的插值方法。
利用差商的概念来构造插值多项式。
Newton插值多项式的一般形式为:f(x)=f(x0)+(x-x0)*f[x0,x1]+(x-x0)*(x-x1)*f[x0,x1,x2]+...其中,f(x)表示要求的插值点的函数值,f(x0)是已知的一个点的函数值,f[xi,xi+1,...,xi+k]是k阶差商。
数值分析分段线性插值样条插值Runge函数Newton-Lagrange-Chebyshev插值多项式Runge现象matlab源程序代码
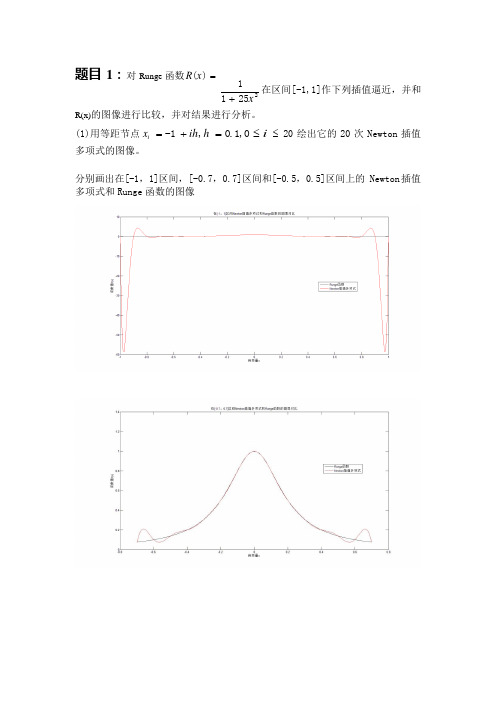
题目1:对Runge 函数R(x ) =1在区间[-1,1]作下列插值逼近,并和1 + 25x 2R(x)的图像进行比较,并对结果进行分析。
= -1 + ih,h= 0.1,0 ≤ i≤ 20 绘出它的20 次Newton 插值(1)用等距节点xi多项式的图像。
分别画出在[-1,1]区间,[-0.7,0.7]区间和[-0.5,0.5]区间上的 Newton 插值多项式和Runge 函数的图像从图中可以看出: 1)在[-0.5,0.5]区间 Newton 插值多项式和 Runge 函数的图像偏差较小,这说 明 Newton 插值多项式在此区间上可以较好的逼近 Runge 函数; 2)在边界(自变量 x=-1 和 x=1)附近,Newton 插值多项式和 Runge 函数的图像 偏差很大,Newton 插值多项式出现了剧烈的震荡。
(Runge 现象) (2)用节点 x = cos(2i + 1π)(, i = 0,1,2,⋅ ⋅ ⋅ ,20),绘出它的 20 次 Lagrangei 42 插值多项式的图像。
画出在[-1,1]区间上的 Lagrange 插值多项式和 Runge 函数的图像从图中可以看出:使用 Chebyshev 多项式零点构造的 Lagrange 插值多项式和 Runge 函数的图 像偏差较小,没有出现 Runge 现象。
(3)用等距节点 x i 的图像。
= -1 + ih ,h = 0.1,0 ≤ i ≤ 20 绘出它的分段线性插值函数画出在[-1,1]区间上分段线性插值函数和 Runge 函数的图像从图中可以看出:使用分段线性插值函数和 Runge 函数的图像偏差较小,也没有出现 Runge 现象,只在自变量 x=0 处有稍许偏差。
(4)用等距节点 x i 函数的图像。
= -1 + ih ,h = 0.1,0 ≤ i ≤ 20 绘出它的三次自然样条插值画出在[-1,1]区间上三次自然样条插值函数和 Runge 函数的图像从图中可以看出:使用三次自然样条插值函数和 Runge 函数的图像偏差较小,也没有出现 Runge 现象。
数值分析实验报告插值与拟合
结果分析:高次插值稳定性差,而低次插值对于较大区间逼近精度又不够,而且,随着节点的加密,采用高次插值,插值函数两端会发生激烈震荡。解决这一矛盾的有效方法就是采用分段低次代数插值。
(2)
通过采用分段线性插值得到以下结果:
结果分析:通过采用分段线性插值,发现随着插值节点增多,插值计算结果的误差越来越小,而且分段线性插值的优点是计算简单,曲线连续和一致收敛,但是不具有光滑性。
拟合是指通过观察或测量得到一组离散数据序列 ,i=1,2,…,m,构造插值函数 逼近客观存在的函数 ,使得向量 与 的误差或距离最小。
可知当基函数的选择不同时,拟合函数的误差也会不同,所以在对数据进行拟合时应选择适合的基函数。
三、练习思考
整体插值有何局限性?如何避免?
答:整体插值的过程中,若有无效数据则整体插值后插值曲线的平方误差会比较大,即在该数据附近插值曲线的震动幅度较大。在插值处理前,应对原始数据进行一定的筛选,剔除无效数据。
②相同点:通过已知一些离散点集M上的约束,求取一个定义在连续集合S(M包含于S)的未知连续函数,从而达到获取整体规律目的
四、本次实验的重点难点分析
答:加强了对插值和拟合的认识,了解了其算法思想,并使用matlab将其实现。学会了观察插值拟合后的图形,并分析其问题。
画图进行比较:
通过观察图像,经比较可知两结果是很接近的。
2.区间 作等距划分: ,以 ( )为节点对函数 进行插值逼近。(分别取 )
(1)用多项式插值对 进行逼近,并在同一坐标系下作出函数的图形,进行比较。写出插值函数对 的逼近程度与节点个数的关系,并分析原因。
(2)试用分段插值(任意选取)对 进行逼近,在同一坐标下画出图形,观察分段插值函数对 的逼近程度与节点个数的关系。
计算方法分段线性_三次样条插值

0x
1
设 | f(4)(x) | 1, x (0,1)
则3次插值多项式的误差
|
R(x)
||
f(4)(ξ) (x 4!
x0 )(x
x1)(x
x2 )(x
x3 )
|
41!| (x x0 )(x x1)(x x2 )(x x3 ) |
41!
1 3
1 3
2 3
1
S(x),S' (x),S' ' (x)
在a, b 上连续)
三次样条函数插值
则称S(x)为三次样条插值函数。
比线性插值要求严 苛得多!
y
y=f(x) (黑色)
y=S(x) (蓝色)
x0
xi
xi+1
xn
x
问题:这个S(x)是三次样条插值函数吗?
回答:不是。 原因: 1)在每个区间内都是3次多项式; 2)在小区区间端点xi处连续并且:f(xi)=S(xi) ; 3)S”(x)在xi 点不连续,即不光滑。
x0 )(x
x1)
(x
xn ),
ξ (a, b)
例:设函数f(x)定义在区间[0, 1]上 ,并且满足 |f(4) (x)|<1,xϵ[0, 1]。在4个插值节点 x0=0, x1=1/3, x2=2/3, x3=1, 对f(x)进行插值得多项式P3(x),估计误差。
下面讨论误差的情况:
x 0
1 f(0) 1
x 1
0 0
f(1)
1 x
x 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分段线性插值需要在每个插值节点上构造分段线性插值基函数,然后再作它们的线性组合。分段线性插值基函数的特点是在对应的插值节点上函数值取 1,其它节点上函数值取0。插值基函数如下:
设在节点a≤x0<x1<…≤b=f(xi),(i=0,1,2,…,n)求折线函数L(x)满足:
(1)L(x)∈C[a,b]
}
double yx[]={-1,-0.8,-0.6,-0.4,-0.2,0,0.2,0.4,0.6,0.8,1};
double yy[14];
for(i=0; i<=10; i++)
{
yy[i]=1.0/(1+25*yx[i]*yx[i]);
}
pDC->TextOut(-30,-10,"0");
pDC->TextOut(-30,430,"1");
求一个函数 (x)用来近似函数f(x),用分段线性插值的方法来求解近似函数 (x)并画出近似函数图像及原函数图像。
设在区间[a,b]上,给定n+1个插值节点 和相应的函数值 ,求一个插值函数 ,满足以下条件:
(1) ;
(2) 在每一个小区间[ ]上是线性函数。
对于给定函数 。在区间 上画出f(x)和分段线性插值函数 的函数图像。
L(x0)=0(x[1]≤x≤x[n])
分段线性方程的表达式:
¢(x)=∑(j=0,..,n)y[j]*L[j](x);
实验源代码
void CMy20141501069View::Onxxcz()
{
// TODO: Add your command handler code here
int x00=300,y00=350,i,j;
(2)L(x[i]=y[i])
(3)L(x)在每个小区间(x[i],x[i+1])上是线性
插值函数¢(x)叫做区间[a,b]上对数据(x[j],y[j])(j=0,1,2,…,n)的分段区间函数。
利用一介拉格朗日函数,直接得到线性插值函数为:
L(x0)=(x-x[1])/x[0]-x[1];(x[0]≤x≤x[1])
oldpen=pDC->SelectObject(&pen);
for(i=0; i<10; i++)
{
pDC->MoveTo(yx[i]*480,yy[i]*400);
pDC->LineTo(yx[i+1]*480,yy[i+1]*400);
}
}
实验结果
结果分析
分段线性插值的方法克服了Lagrange插值法当节点不断加密时,构造的插值多项式的次数不断升高,高次多项式虽然是连续的,但是不一定都收敛到相应的被插函数而产生Runge现象。分段线性插值因为在每一段小区间上都是线性插值而极大地降低了插值多项式的次数,从几何图形上可以看出,当节点取得较多时插值函数的逼近效果还是很好的,但是所求函数是一条以型值点为顶点的折线,这也表现出了它的缺点就是所求得的插值函数的光滑性较差,这就要求一种更好的方法来克服这一缺点了。
pDC->TextOut(490,-10,"1");
pDC->TextOut(-490,-10,"-1");
pDC->MoveTo(-10,680); //x箭头
pDC->LineTo(0,700);
pDC->MoveTo(0,700);
pDC->LineTo(10,680);
pDC->MoveTo(680,10); //y箭头
double x;
CDC *pDC=GetDC();
pDC->SetMapMode(MM_LOMETRIC);
pDC->SetViewportOrg(x00,y00);
//画坐标轴与原函数
for(i=-700; i<=700; i++)
{ห้องสมุดไป่ตู้
pDC->SetPixel(i,0,RGB(0,0,0));
pDC->SetPixel(0,i,RGB(0,0,0));
pDC->LineTo(700,0);
pDC->MoveTo(700,0);
pDC->LineTo(680,-10);
pDC->TextOut(-30,700,"y");
pDC->TextOut(700,-10,"x");
//线性分段差值的图像
CPen pen;
CPen*oldpen;
pen.CreatePen(PS_SOLID,5,RGB(0,0,0));
数值分析实验报告
专业:计算机科学与技术
班级:14汉(2)
学号:***********
姓名:***
指导教师:马季骕老师
实验项目
分段线性插值
算法介绍
随着插值节点的增加,插值多项式的次数也增加,而对于高次的插值容易带来剧烈的震荡,带来数值的不稳定(Runge现象)。为了既要增加插值的节点,减小插值的区间,以便更好的逼近插值函数,又要不增加插值多项式的次数以减少误差,可采用分段线性插值。
