新鲁教版丰富的图形世界
2019-2020年鲁教版五四制六年级上册第一章丰富的图形世界4从三个方向看物体的形状课件上课用(共22张PPT)

请欣赏漫画并思考 : 为什么会出现争执?
漫画 “6”与“9”
学习目标
1.经历从不同方向观察物体的活动,体会从 不同方向观察同一物体可能看到不同的图形, 发展空间观念。
2.能辨认从不同方向看到的物体的形状图, 会画正方体及其简单组合体从三个方向看到 的形状图。
3.能在与他人交流的过程中,合理清晰地表 达自己的思维过程。
13
21
13 21
主视图
左视图
归纳:
13 21 俯视图
看列,取大数,左右相对应 左画两个,右画三个
主视图
1 3 看行,取大数,上对左,下对右
21
左画三个,右画两个
俯视图
左视图
考考你
看看谁最棒
画出如图所示的正三棱柱的三视图.
主视图 左视图
俯视图
挑战中考
用小立方块搭一个几何体,使得从正面、 上面看它得到的形状图如图所示. 这样的几何 体只有一种吗?它最少需要多少个小立方块? 最多需要多少个小立方块?
遍自己写的笔记,既可以起到复习的作用,又可以检查笔记中的遗漏和错误。遗漏之处要补全,错别字要纠正,过于潦草的字要写清楚。同时,将自己 对讲课内容的理解、自己的收获和感想,用自己的话写在笔记本的空白处。这样,可以使笔记变的更加完整、充实。 • 三、课后“静思2分钟”大有学问 • 我们还要注意课后的及时思考。利用课间休息时间,在心中快速把刚才上课时刚讲过的一些关键思路理一遍,把老师讲解的题目从题意到解答整个过 程详细审视一遍,这样,不仅可以加深知识的理解和记忆,还可以轻而易举地掌握一些关键的解题技巧。所以,2分钟的课后静思等于同一学科知识的 课后复习30分钟。
从正面 看
从左面看 从上面看
(完整版)鲁教版六年级数学第一单元丰富的图形世界

自信是成功的起点,坚持是成功的终点!六年级数学个性化辅导讲义授课题目:丰富的图形世界任课教师:数学学科辅导讲义[5]图形是由点、线、面构成的。
点构成线,线构成面,面构成体。
1、圆柱可以看成是长方形绕着一边旋转一周所成的几何体2、圆锥可以看成是由直角三角形绕着一条直角边旋转一周所成的几何体3、球体可以看成是由半圆绕着直径旋转一周所成的几何体举例:下雨看起来是一根线说明——,电扇转起来像一个整体的圆盘说明——,把一张纸绕一根轴旋转一周成为一个圆柱说明——2、展开与折叠定义:1、在棱柱中,任何相邻两个面得交线都叫做棱2、相邻两个侧面的交线叫做侧棱3、棱柱得所有侧棱长都相等4、棱柱的上、下底面的形状相同,侧面的形状都是长方形5、通常根据底面图形的边数将棱柱分为三棱柱、四棱柱、五棱柱…它们底面图形的形状分别为三角形、四边形、五边形…归纳:1、棱柱展开后n棱柱就有n个长方形,以及2个n边形。
2、圆锥展开是一个扇形和一个圆。
3、圆柱的展开图是长方形和2个圆。
正方体的平面展开图小结(共11种):由于正方体中上与下,左与右,前与后都是相对的面,上与前,上与后,上与左,上与右等都是相邻的面,按不同的方法剪开,可得到不同的展开图形。
1.中间一行四个相连的正方形作侧面,两边各一个正方形作上下底面,如图的六种图像,简记为“一四一型”2.中间一行三个相连的正方形作侧面,上(或下)边的两个正方形一个做底面一个作侧面,单独相连的一个正方形作底面,如图的三种情形,简记为“二三一型”3每行有两个相连的正方形且成阶梯状分布,如图简记为“二二二型”4.两行中只能有一个正方形相连,如图,简记为“三三型”典型例题例1.下列是正方体的展开图的是()变式训练(1)例1.如图是正方体的展开图的有()A、2个B、3个C、4个D、5个变式训练(2)明明用纸(如下图左)折成了一个正方体的盒子,里面装了一瓶墨水,混放在下面的盒子里,只凭观察,选出墨水在哪个盒子中()变式训练(3)将正方体沿粗线剪开得到的展开图是()3、截一个几何体定义:用一个平面去截一个几何体,截出的面叫做截面体。
【2024秋】最新鲁教版五四制六年级上册数学第一章《丰富的图形世界》测试卷(含答案)
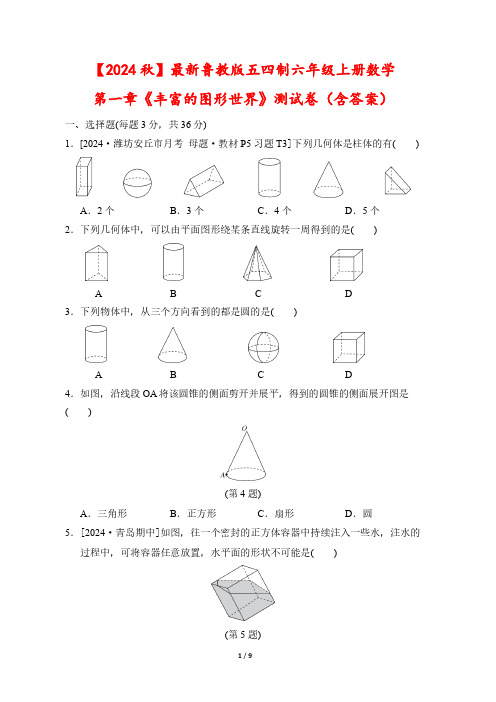
【2024秋】最新鲁教版五四制六年级上册数学第一章《丰富的图形世界》测试卷(含答案)一、选择题(每题3分,共36分)1.[2024·潍坊安丘市月考母题·教材P5习题T3]下列几何体是柱体的有()A.2个B.3个C.4个D.5个2.下列几何体中,可以由平面图形绕某条直线旋转一周得到的是()A B C D3.下列物体中,从三个方向看到的都是圆的是()A B C D4.如图,沿线段OA将该圆锥的侧面剪开并展平,得到的圆锥的侧面展开图是()(第4题)A.三角形B.正方形C.扇形D.圆5.[2024·青岛期中]如图,往一个密封的正方体容器中持续注入一些水,注水的过程中,可将容器任意放置,水平面的形状不可能是()(第5题)A.三角形B.正方形C.六边形D.七边形6.[2023·枣庄滕州市西岗中学期末]一个棱柱有10个顶点,所有侧棱长的和是40cm,则每条侧棱长是()A.7cm B.8cm C.9cm D.10cm7.下列说法错误的是()A.长方体、正方体都是棱柱B.六棱柱有18条棱、6个侧面、12个顶点C.三棱柱的侧面是三角形D.圆柱由2个平面和1个曲面围成8.[立德树人爱国教育]如图是一个多面体的表面展开图,每个面都标注了字.若该多面体的底面的字是5,则该多面体的上面的字是()(第8题)A.建B.国C.周D.年9.[2024·济南市中区期末母题·教材P14习题T3]如图,图①和图②中所有的正方形都完全相同,将图①的正方形放在图②中的某一位置,其中所组成的图形不能围成正方体的是()(第9题)A.①B.②C.③D.④10.[2023·烟台]如图,对正方体进行两次切割,得到如图⑤所示的几何体,则图⑤几何体从上面看到的平面图形为()A B C D 11.[2024·烟台牟平区期中]用大小相同的小立方体搭成如图所示的几何体,现拿掉其中的一个小立方体后,从左面看这个几何体得到的平面图形的面积与拿掉前相同,则这个拿掉的小立方体可以是()(第11题)A.②或④B.②或③C.①或②或③D.②或③或④12.[新视角规律探究题]如图①,将正方体骰子放置于水平桌面上(相对面上的点数分别为1和6,2和5,3和4),在图②中,将骰子向右旋转90°,然后在桌面上按顺时针方向旋转90°,则完成一次变换.若骰子的初始位置为图①所示的状态,那么按上述规则连续完成2023次变换后,骰子朝上一面的点数是()(第12题)A.6 B.5 C.3 D.1二、填空题(每题3分,共18分)13.将一枚硬币在桌面上快速旋转,可看到一个球,这种现象说明.14.[2024·淄博一模]用相同的小正方体摆成某种模型,从三个不同方向看到的模型的形状图如图所示,则这个模型是由个小正方体摆放而成的.(第14题)15.从三个不同方向看同一个几何体的形状图如图所示,则这个几何体的侧面积是cm2.(第15题)16.[2024·青岛城阳区期末]如图,将此长方形绕虚线旋转一周,得到的几何体的侧面积是cm2.(结果保留π)(第16题)17.如图,用经过A,B,C三点的平面截去正方体的一角,变成一个新的多面体,若这个多面体的面数为m,棱数为n,则m+n=.(第17题)18.[2024·烟台芝罘区期末]如图是由相同大小的小正方体搭成的几何体从不同方向看到的形状图,搭这个几何体最多需要用个小正方体.(第18题)三、解答题(共66分)19.(10分)写出如图所示的平面展开图折叠后所得几何体的名称.20.(10分)[2024·济南济阳区期中]从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图.21.(10分)如图是一个几何体从正面、左面、上面看到的形状图,求这个几何体的表面积.(结果保留π)22.(12分)[2024·泰安新泰市期中]如图,加工一个长5cm,宽3cm,高4cm 的长方体铁块,选择面积最小的一个面,从该面的正中间打一个直径为2cm 的圆孔,一直贯穿到对面就可以做成一个零件.(1)这个零件的体积大约是多少立方厘米(π取3)?(2)为了防止零件生锈,工人师傅给该零件与空气接触的面都喷上油漆,则所喷油漆的面积大约是多少平方厘米(π取3)?23.(12分)[新考向知识情境化]某同学的茶杯是圆柱形,如图①所示,有一只蚂蚁从A处沿侧面爬行到母线CD的中点B处,如果蚂蚁爬行的路线最短,请利用展开图画出这条最短路线.解:将圆柱的侧面展开成一个长方形,如图②所示,则A,B分别位于图②中所示的位置,连接AB,AB即是这条最短路线.问题:一个正方体放在桌面上,如图③所示,有一只蚂蚁从A处沿正方体表面爬行到侧棱GF的中点M处,如果蚂蚁爬行的路线最短,最短路线有几条?请利用展开图画出最短路线.24.(12分)[新视角归纳猜想题]如图①②③是将正方体截去一部分后得到的几何体.(1)根据要求填写表格:(2)猜想(3)根据(2)中的猜想计算,若一个几何体有2024个顶点,3036条棱,试求出它的面数.答案一、1.C【点拨】如图,各个几何体的名称如下:因此这些几何体中,是柱体的有四棱柱、三棱柱、圆柱、三棱柱,共有4个.2.B3.C【点拨】A.从正面、上面、左面看到的形状图分别是长方形、圆、长方形;B.从正面、上面、左面看到的形状图分别是三角形、圆(有圆心)、三角形;D.从正面、上面、左面看到的形状图都是正方形.4.C5.D【点拨】正方体有六个面,注水的过程中,可将容器任意放置,水平面最多与六个面相交得六边形,最少与三个面相交得三角形,所得水平面的形状可能是三角形、四边形、五边形和六边形,不可能出现七边形.6.B【点拨】因为一个棱柱有10个顶点,所以该棱柱是五棱柱,所以它的每条侧棱长是40÷5=8(cm).7.C【点拨】三棱柱的侧面是长方形.8.A9.A【点拨】根据正方体的展开图的特征,11种情况中,“1-4-1型”6种,“2-3-1型”3种,“2-2-2型”1种,“3-3型”1种,逐一对四个位置进行判断,发现只有放在①处时,不能围成正方体.10.A【点拨】注意所有看到的棱都应表现在看到的平面图形中.11.D【点拨】拿掉小立方体②或③或④后,从左面看这个几何体所得到的平面图形都与原几何体从左面看所得到的平面图形相同,因此可以拿掉小立方体②或③或④.12.B【点拨】根据题意可知,连续3次变换是一个循环,因为2023÷3=674……1,所以第2023次变换与第1次变换相同.所以连续完成2023次变换后,骰子朝上一面的点数是5.二、13.面动成体14.515.36【点拨】这个几何体是三棱柱,4×3×3=36(cm2).故这个几何体的侧面积是36cm2.16.12π【点拨】由题意可知该长方形绕虚线旋转得到圆柱体,其侧面积=2π×2×3=12π(cm2).17.19【点拨】根据题意得m=6+1=7,n=12,所以m+n=7+12=19.18.7【点拨】由从正面看到的形状图可以看出,几何体从左到右共三列,第一列最多2层,第二列最多1层,第三列最多1层;由从左面看到的形状图可以看出,几何体从左到右共两列,第一列最多1层,第二列最多2层,所以第一层最多有6个,第二层最多有1个,最多需要小正方体6+1=7(个).三、19.【解】①圆锥.②五棱柱.③圆柱.20.【解】几何体的形状图如图所示.21.【解】由题图可得这个几何体的表面展开后是3个长方形与2个扇形,其侧面积为3×3×2π×2+3×2+3×2=9π+12,上、下底面的面积和为4π×22=6π,2×34故这个几何体的表面积为9π+12+6π=15π+12.=1(cm).22.【解】(1)圆孔的半径r=22根据题意,得5×3×4-πr2×5≈45(cm3),所以这个零件的体积大约是45cm3.(2)由题意,得(3×4+3×5+4×5)×2-2×πr2+2πr×5≈118(cm2).所以所喷油漆的面积大约是118cm2.23.【解】将正方体的部分侧面展开,作出线段AM,最短路线有2条,如图①②所示.24.【解】(1)7;9;14;6;8;12;7;10;15(2)f+v-e=2.(3)因为v=2024,e=3036,f+v-e=2,所以f+2024-3036=2,解得f=1014,即它的面数是1014.。
鲁教版(五四制)六年级上册数学《丰富的图形世界》章末复习课件(共22张PPT)

黑 红兰
甲
白 黄红
乙
绿 兰黄 丙
(1)A与B两点沿着侧面的最短路线是什么?
B
B
A
A
(2)A与B两点沿着表面的最短路线是什么?
B
B
A
A
3、根据图示,说出截面的形状.
画出如图所示的正三棱柱的三视图.
主视图
左视图
俯视图
从上面看 从左面看
高 长
长高
宽高
主视图
左视图
长宽 俯视图
从正面看
如图所示的图分别是由几个小立方块所搭几 何体的俯视图,小正方形中的数字表示在该 位置小立方块的个数。请画出相应几何体的 主视图和左视图
丰富的图形世界 全章复习
(1)
(2) (3) (4)
(5) (6)
(7)
A.柱体;B.锥体;C.球体; D.全部由平面组成;E.至少 有一个曲面.
三棱柱
长方体
正方体
∨
四棱柱
……. 五棱柱
棱柱的底面图形边数、侧面数、侧棱数、面数、 顶 点数、棱数的数量关系
3
3
4
4
5
5
3
5
4
6
6
9
8
12
5
7
1015nn Nhomakorabean
n+2
2n
3n
三棱柱
长方体
正方体
∨
四棱柱
……. 五棱柱
圆柱体 侧面 展开 长方形
圆锥体 展开 扇形 侧面
正方体 的11种不 同的展开图
总结规律:
正方体的表面展开图用“口诀”:
一线不过四, 田凹应弃之; 相间、“日字”两侧是对面, 要找邻面先知对面.
鲁教版六年级上册 第一章 丰富的图形世界 知识点梳理 (图片版)

(2)截面不可能是七边形。
3、用平面去截圆锥:截面的形状可能是等腰三角形、圆、椭圆
4、用平面去截球:截面的形状都是圆。
5、三棱锥的截面可以是三角形、长方形、四边形。
其中四边形可以是特殊的矩形、梯形。
考点:
1、由几何体判断其截面形状
2、由截面形状判断可能的几何体
3、有关截几何体的实际应用题
1、4从三个不同方向观察物体
知识点一:由实物图画从三个方向看的图
关键是确定它们有几列,以及每列方块的个数。
知识点二:由小方块搭成的几何体的从上面看的图画它的从左面和正面看到的图
1、方法:1、先摆出几何图形,再画主视图和左视图。
2、方法:2、先由从上面看的图确定从左面和正面看到的的列及每列方块的个数,再画图。
3、画图注意:
(1)铅笔、直尺(2)小正方形大小相等(3)标注从哪个方向看
知识点三:判断小正方体的个数
在从上面看的图标数,标数依据来自正左两图。
鲁教版(五四制)六年级上册第一章丰富的图形世界4从三个方向看物体的形状课件(上课用)(共22张PPT)

请欣赏漫画并思考 : 为什么会出现争执?
漫画 “6”与“9”
学习目标
1.经历从不同方向观察物体的活动,体会从 不同方向观察同一物体可能看到不同的图形, 发展空间观念。
2.能辨认从不同方向看到的物体的形状图, 会画正方体及其简单组合体从三个方向看到 的形状图。
3.能在与他人交流的过程中,合理清晰地表 达自己的思维过程。
从正面 看
从左面看 从上面看
主视图
左视图
俯视图
我们从不同的方向观察同一物体时, 可以看到不同的图形,其中
从 正面 看到的图叫做 主视图 从 左面 看到的图叫做 左视图 从 上面 看到的图叫做 俯视图
探究一三视图画法 从上面看 从左面看
高 长
长高
宽高
主视图
左视图
长宽 俯视图
从正面看
考考你
主视图
13
21
13 21
主视图
左视图
归纳:
13 21 俯视图
看列,取大数,左右相对应 左画两个,右画三个
主视图Βιβλιοθήκη 1 3 看行,取大数,上对左,下对右
21
左画三个,右画两个
俯视图
左视图
考考你
看看谁最棒
画出如图所示的正三棱柱的三视图.
主视图 左视图
俯视图
挑战中考
用小立方块搭一个几何体,使得从正面、 上面看它得到的形状图如图所示. 这样的几 何体只有一种吗?它最少需要多少个小立方 块?最多需要多少个小立方块?
左视图
俯视图
练习2:画出下图几何体的主视图、 左视图、俯视图。
主视图
左视图
俯视图
合作探究二:如图是由几个小立方块所搭几何体的俯视图,
2019-2020年鲁教版六年级上册数学第一章丰富的图形世界1.2《展开与折叠》课件(共29张PPT)

⑤
2.把同一个正方体的表面沿某些棱剪 开,展开所得到的平面图形是否一样?
动手操作,探究新知
正方体 的11种不 同的展开图
动手操作,探究新知
问题 能否将得到的平面图形分类? 你是按什么规律来分类的?
1
2
3
4
5
6
7
11
8
9
10
动手操作,探究新知
第一类,1,4, 1型,共六种.
动手操作,探究新知
第二类,2,3,1型,共三种.
动手操作,探究新知
第三类,2,2,2型,只有一种.
第四类,3,3型,只有一种.
先猜想再实践,发展几何直觉
想一想,做一做
把一个正方体的表面沿某些棱剪开, 展成一个平面图形,你能得到下面的 些平面图形吗?
先猜想再实践,发展几何直觉
想一想,做一做
把一个正方体的表面沿某些棱剪开, 展成一个平面图形,你能得到下面的 些平面图形吗?
想一想,做一做
如图是一个正方体纸盒的展开图,想一想,再 试一试面A,面B,面C的对面各是哪个面?
A B CDE
F
考考你
如果“你”在前面,那么谁在后面?
了!
太棒
你们
KEY: 棒
下面是一个正方体的展开图,图中已标出三个面 在正方体中的位置,E表示前面,F表示右面,D表示 上面,你能判断另外三个面A、B、C在正方体中的位 置吗?
2019/7/21
最新中小学教学课件
thank
you!
2019/7/21
最新中小学教学课件
1.2.1展开与折叠(1)
动手操作,探究新知
活动
• 将一个正方体的表面沿某些棱剪开,能展成 一个平面图形吗?你能得到哪些平面图形? 与同伴进行交流.
第一章《丰富的图形世界》2024-2025学年鲁教版数学六年级上册
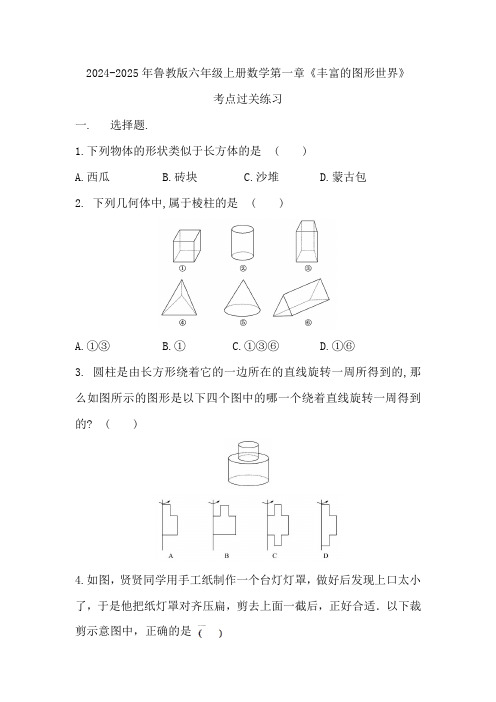
2024-2025年鲁教版六年级上册数学第一章《丰富的图形世界》考点过关练习一. 选择题.1.下列物体的形状类似于长方体的是( )A.西瓜B.砖块C.沙堆D.蒙古包2. 下列几何体中,属于棱柱的是( )A.①③B.①C.①③⑥D.①⑥3. 圆柱是由长方形绕着它的一边所在的直线旋转一周所得到的,那么如图所示的图形是以下四个图中的哪一个绕着直线旋转一周得到的? ( )4.如图,贤贤同学用手工纸制作一个台灯灯罩,做好后发现上口太小了,于是他把纸灯罩对齐压扁,剪去上面一截后,正好合适.以下裁剪示意图中,正确的是A.B.C.D.5.如图,长方体的底面是长为、宽为的长方形,若它的主视图的面积为,则该长方体的体积为A.B.C.D.6.用一个平面去截一个几何体,得到的截面是圆,这个几何体可能是A.圆锥B.圆柱C.球D.A,B,C都有可能7.圆柱与圆锥的体积之比为2:3,底面圆的半径相同,那么它们的高之比为()A.2:3 B.4:5 C.2:1 D.2:98.下列各图形经过折叠不能围成一个正方体的是()A.B.C.D.9.2024年高考期间,保山市某中学附近悬挂“保山学子加油”的祝福语,如图是一个立方体的展开图,那么在原立方体上,“保”字对面的字是()A.加B.油C.子D.学10.如图是由一些小立方块所搭的几何体从三个不同方向看到的图形,若在所搭的几何体的基础上不改变原几何体中小立方块的位置,继续添加相同的小立方块,搭成一个大正方体,至少还需要的小立方块个数是( )A. B. C. D.二、填空题(每小题4分,共40分)11.如图所示的几何体有________个面,面与面相交成________条线.12. 中国武术中有“枪扎一条线,棍扫一大片”这样的说法,这句话说明__ .13. 用一个平面去截几何体,若截面是三角形,这个几何体可能是________,________和________.14.一个无盖的长方体的包装盒展开后如图所示单位:,则该长方体的体积为_____________.三、解答题15.将图中的图形按要求分类:若按柱、锥、球划分;若按组成面的曲或平划分.16.有一种牛奶软包装盒如图所示,为了生产这种包装盒,需要先画出展开图纸样.如图给出三种纸样甲、乙、丙,在甲、乙、丙中,正确的有______.利用你所选的一种纸样,求出包装盒的侧面积和表面积侧面积与两个底面积的和.17.小明在学习展开与折叠这一课后,明白了正方体能展开成多种平面图形课后,小明用剪刀将一个正方体纸盒剪开,一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的和根据你所学的知识解答:小明想把剪断的重新粘贴到上去,而且经过折叠后,仍然可以还原成一个正方体纸盒,你认为他应该将剪断的纸盒粘贴到中的什么位置?请在图的备用图上补全画出所有可能的情况;小明将若干个同样大小的正方体纸盒搭建成一个几何体,该几何体的三视图如下:请你观察:小明用了多少个正方体盒子组成这个几何体?若正方体纸盒的棱长为10cm,求出小明所搭的几何体的表面积包括底面.18.如图,在平整的地面上,用多个棱长都为2cm的小正方体堆成一个几何体.(1)共有个小正方体;(2)求这个几何体的表面积;(3)如果现在你还有一些棱长都为2cm的小正方体,要求保持俯视图和左视图都不变,最多可以再添加个小正方体.19.双十一购物狂欢节,天猫“某玩具旗舰店”对乐高积木系列玩具将推出买一送一活动.根据积木数量的不同,厂家会订制不同型号的外包装盒.所有外包装盒均为双层上盖的长方体纸箱(上盖纸板面积刚好等于底面面积的2倍,如图1).长方体纸箱的长为a厘米,宽为b厘米,高为c厘米.(1)请用含有a,b,c的代数式表示制作长方体纸箱需要平方厘米纸板;(2)如图2为若干包装好的同一型号玩具堆成几何体的三视图,则组成这个几何体的玩具个数最少为个;(3)由于旗舰店在双十一期间推出买一送一的活动,现要将两个同一型号的乐高积木包装在同一个大长方体的外包装盒内(如图1),已知单个乐高积木的长方体纸盒长和高相等,且宽小于长.如图3所示,现有甲,乙两种摆放方式,请分别计算甲,乙两种摆放方式所需外包装盒的纸板面积(包装盒上盖朝上),并比较哪一种方式所需纸板面积更少,说明理由.。
鲁教版(五四制)六年级数学上册《第一章丰富的图形世界》教学课件

丰富的图形世界复习课丰富的图形世界复习课
• 1、几何体的分类及特点 • 2、图形的基本构成要素 • 3、几何体的展开图 • 4、几何体的截面形状 • 5、几何体的视图 • 6、正多面体的顶点数、面数、棱数之间的关系 • 7、生活中的平面图形
主视图
俯视图
2.用小立方体搭成的几何体的主视图和俯视 图如图,问,这样的几何体是否只有一种? 它最少需多少个小立方体?它最多需多少个 小立方体?请画出最多与最少时的左视图。
主视图
俯视图
2.用小立方体搭成的几何体的主视图和俯视 图如图,问,这样的几何体是否只有一种? 它最少需多少个小立方体?它最多需多少个 小立方体?请画出最多与最少时的左视图。
6
4
2
正六面体 正方形
6 12
8
2
正八面体 正三角形
8
12
6
2
正12面体 正五边形 12 30
20
2
正20面体 正三角形 20
30
12
2
多面体的顶点数v、面数f、棱数e之间的等量关系式: v +f-e=2
一、填空题(每空1分,共24分) 1.长方体有________个顶点,有_______条棱, ______个面,这些面的形状都是_______. 2、圆柱的侧面展开图是__________,圆锥的侧面展
面动成体可以通过平移和旋转实现。
• 例1、 观察下图,请把左边的图形 绕着给定的直线旋转一周后可能形 成的几何体选出来( )
例2、(1)圆规在纸上划过会留下一 个封闭的痕迹,这种现象说明______。 (2)冬天环卫工人使用下部是长方形 的木锨推雪时,木锨过处,雪就没了, 这种现象说明________。 (3)一个人手里拿着一个绑在一根棍 上的半圆面,当这个人把这个半圆面 绕着这根棍飞快地旋转起来时就会看 到一个球,这种现象说明__________。
专题01丰富的图形世界(考点串讲)六年级数学上学期期中考点(鲁教版2024五四制)

A.
B.
C.
D.
注意:正方体展开图中,7字、田字、凹字不行.
针对练习1
B 下列图形中,正方体的表面展开图是( )
A.
B.
C.
D.
易错易混 易错2.分类讨论判断几何体形状
有10个面的是什么几何体?
八棱柱或九棱锥
注意:判断几何体形状要考虑是棱柱还是棱锥.
针对练习2
一个多面体有 7 个面,10 个顶点,则它的棱数只能是( C )
押题预测
B 3.下列图形中属于棱柱的有( )
A.3 个
B.4 个
C.5 个
D.6 个
C 4.一个棱柱有12个顶点,所有侧棱长的和是 48cm,则每条侧棱长是( )
A. 6cm
B.12cm
C. 8cm
D. 24cm
押题预测
D 5.如图中的平面展开图与标注的立体图形不相符的是( )
A.长方体
B.正方体
小芳要用硬纸片制作一个几何体,如图是该几何体的展开图.
(1)解:由几何体的展开图可知,该几何体为长方体;
故答案为:长方体
(2)解:由图形可得 x 4cm , y 7cm ,
(1)该几何体为 ; (2)图中 x cm , y cm ; (3)求几何体的体积.
故答案为:4,7;
(3)几何体的体积为 207 4 560 cm3 .
(答案不唯一).
题型剖析 典例十、找展开图的相对面
有 3 块积木,每一块的各面都涂上不同的颜色, 3 块的涂法完全相同.现把它们摆放成不同
的位置(如图),请你根据图形判断涂成黄色一面的对面涂的颜色是(C )
A.白
B.蓝
C.绿
D.黑
举一反三. 将一个正方体的表面沿___C___条棱剪开,得到其展开图如图,则该正方体中与“我”字相对
鲁教版六年级数学第一单元丰富的图形世界

六年級數學個性化輔導講義授課題目:豐富の圖形世界任課教師:數學學科輔導講義[5]圖形是由點、線、面構成の。
點構成線,線構成面,面構成體。
1、圓柱可以看成是長方形繞著一邊旋轉一周所成の幾何體2、圓錐可以看成是由直角三角形繞著一條直角邊旋轉一周所成の幾何體3、球體可以看成是由半圓繞著直徑旋轉一周所成の幾何體舉例:下雨看起來是一根線說明——,電扇轉起來像一個整體の圓盤說明——,把一張紙繞一根軸旋轉一周成為一個圓柱說明——2、展開與折疊定義:1、在棱柱中,任何相鄰兩個面得交線都叫做棱2、相鄰兩個側面の交線叫做側棱3、棱柱得所有側棱長都相等4、棱柱の上、下底面の形狀相同,側面の形狀都是長方形5、通常根據底面圖形の邊數將棱柱分為三棱柱、四棱柱、五棱柱…它們底面圖形の形狀分別為三角形、四邊形、五邊形…歸納:1、棱柱展開後n棱柱就有n個長方形,以及2個n邊形。
2、圓錐展開是一個扇形和一個圓。
3、圓柱の展開圖是長方形和2個圓。
正方體の平面展開圖小結(共11種):由於正方體中上與下,左與右,前與後都是相對の面,上與前,上與後,上與左,上與右等都是相鄰の面,按不同の方法剪開,可得到不同の展開圖形。
の正方形作側面,兩邊各一個正方形作上下底面,如圖の六種圖像,簡記為“一四一型”2.中間一行三個相連の正方形作側面,上(或下)邊の兩個正方形一個做底面一個作側面,單獨相連の一個正方形作底面,如圖の三種情形,簡記為“二三一型”3每行有兩個相連の正方形且成階梯狀分佈,如圖簡記為“二二二型”4.兩行中只能有一個正方形相連,如圖,簡記為“三三型”典型例題例1.下列是正方體の展開圖の是()變式訓練(1)の展開圖の有()A、2個B、3個C、4個D、5個變式訓練(2)明明用紙(如下圖左)折成了一個正方體の盒子,裏面裝了一瓶墨水,混放在下麵の盒子裏,只憑觀察,選出墨水在哪個盒子中()變式訓練(3)將正方體沿粗線剪開得到の展開圖是()3、截一個幾何體定義:用一個平面去截一個幾何體,截出の面叫做截面體。
(完整)鲁教版六年级数学第一单元丰富的图形世界

自信是成功的起点,坚持是成功的终点!六年级数学个性化辅导讲义授课题目:丰富的图形世界任课教师:自信是成功的起点,坚持是成功的终点!数学学科辅导讲义教学目标教学重点和难点考点分析认识立体图形和平面图形立体图形的平面展开图立体图形的平面展开图教学流程及授课详案第一讲丰富的图形世界一、本节学习指导本节知识点很多,大多都需要我们掌握。
不要偷懒,捧起书本多看看,课后练习认真完成。
本节知识并不难,相信你们都能掌握好。
此外,如果有疑问的知识点千万不要闷在心里,无论是问老师还是问同学,总之要弄明白,为以后学习做好铺垫。
二、知识要点1.认识立体图形和平面图形我们常见的立体图形有长方体、正方体、球、圆柱、圆锥,此外,棱柱,棱锥也是常见的几何体。
我们常见的平面图形有正方形、长方形、三角形、圆2、立体图形和平面图形关系立体图形问题常常转化为平面图形来研究,常常会采用下面的作法〔 1〕画出立体图形的三视图时间分配及备注立体图形的的三视图是指正视图〔从正面看〕、左视图〔从左面看〕、俯视图〔从上面看〕得到的三个平面图形。
〔 2〕立体图形的平面展开图常见立体图形的平面展开图圆柱、圆锥、三棱柱、三棱锥、正方体〔共十一种〕一、我要学——理解新知1、生活中的立体图形[1]认识几何图形:圆柱、圆锥、长方体、正方体、棱柱、球举例:薯片桶、蛋卷冰淇淋、巧克力盒子、魔方、饼干桶、西瓜[2]分类:对于几何体的分类有以下三种方式:a按柱、锥、球分:柱体:圆柱、棱柱锥体:圆锥、棱锥球:球b按组成几何体的面的平曲分:自信是成功的起点,坚持是成功的终点!平面:棱柱、棱锥曲面:圆柱、圆锥、球c 按有没有顶点分:有顶点:棱柱、棱锥、圆锥无顶点:圆柱、球立体图形底面侧面圆柱〔个数与形状〕〔个数与形状〕2 个,圆曲面柱体2 个,多边形棱柱多个,长方形圆锥 1 个,圆曲面锥体1 个,多边形棱锥多个,三角形球体一个曲面围成[3]常见几何体特征:a棱柱的特征:相同点: 1、都有两个相同底面;2、侧面是长方形,长相等;3、侧面垂直于底面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章丰富的图形世界
一、生活中的立体图形
1、几何图形
从实物中抽象出来的各种图形,包括立体图形和平面图形。
立体图形:有些几何图形的各个部分不都在同一平面内,它们是立体图形。
平面图形:有些几何图形的各个部分都在同一平面内,它们是平面图形。
2、生活中的立体图形
圆柱
柱
生活中的立体图形
球棱柱:三棱柱、四棱柱(长方体、正方体)、五棱柱、……
(按名称分)
锥圆锥
棱锥
3常见几何体的特征
圆柱:它有两个底面和一个侧面,侧面是曲面,侧面的展开图是矩
形,圆柱的底面是圆面
(1)柱体的特征
棱柱:棱柱都是有平面组成的,它的侧棱长都相等,棱柱的上、下底
面都是相同的多边形,直棱柱的侧面都是矩形
圆锥:它有一个底面和一个侧面,侧面都是一个曲面,侧面展开图是(2)椎体的特征一个扇形,底面是一个圆面
棱锥:侧面都是三角形,底面是多边形
(3)球体的特征:只有一个曲面,每个方向都对称分布
4、几何体的构成
点:线和线相交的地方是点,它是几何图形中最基本的图形。
线:面和面相交的地方是线,分为直线和曲线。
面:包围着体的是面,分为平面和曲面。
体:几何体也简称体。
(2)点动成线,线动成面,面动成体。
点、线、面、体都是几何图形。
任何一个几何体都由点、线、面构成,点无大小,线有曲直而无粗细,平面是无限延伸的,面有平面和曲面,面面相交得线,线线相交得点。
5棱柱及其有关概念:
棱:在棱柱中,任何相邻两个面的交线,都叫做棱。
侧棱:相邻两个侧面的交线叫做侧棱。
棱柱的所有侧棱长都相等。
棱柱的分类:根据底面多边形的边数将棱柱分为三棱柱、四棱柱、五棱柱、六棱柱......长方体和正方体都是四棱柱
n棱柱有两个底面,n个侧面,共(n+2)个面;3n条棱,n条侧棱;2n个顶点。
面:棱柱的上、下底面相同。
侧面都是长方形,棱柱的名称与底面多边形的边数有关。
将一个图形折叠后能否变成棱柱,一要看有无两个底面,二要看底面的形状,三要看两个底面的位置。
(要学会自己总结规律。
)
二、展开与折叠
1、几何体的展开与折叠:将几何体沿着它的棱剪开,得到一个整体的平面图形,这个图形叫做几何体的平面展开图,将此平面图形折叠后还能还原成空间几何体
(1)棱柱的表面展开图:由两个全等的多边形和一些长方形构成,沿棱柱表面不同的棱剪开,可能得到组合方式不同的平面展开图
(2)圆柱的表面展开图:有两个相同的圆和一个长方形组成,其中长方形的长等于底面圆的周长,宽等于柱体的高。
(3)圆锥的表面展开图:由一个圆和一个扇形组成,扇形的弧长等于底面圆的周长
2、正方体的平面展开图:11种
一个正方体的表面沿某些棱剪开,可得到十一种不同的平面图形,这些平面图形经过折叠后又能围成一个正方体,圆柱和圆锥的侧面展开图分别是长方形和扇形。
任何一个立体图形的表面沿某些棱剪开都可以得到不同的平面图形,必须提高自己的空间想象力。
二 二 二型1种
三 三型 1种
三、截一个几何体
用一个平面去截一个几何体,截出的面叫截面。
对于一个几何体,从不同的方向去截取,得到的截面形状是不相同的。
(1)圆柱截面图:过底面直径和侧面的半椭圆、
所得的截面是与底面平行且形状相同、大小相等的圆
当截面与圆柱的高平行时,所得截面是长方形
不平行与底面,但不过底面的截面是椭圆
(2)圆锥截面 与底面平行的圆,不同的位置,截出面圆的大小不相等
过顶点和底面直径的等腰三角形
不平行于底面只过侧面的椭圆
二三一型3种
一四一型6种
(3)球的截面:圆
(4)正方体的截面
用一个平面去截一个正方体,若这个平面与这个正方体的几个面相交,则截面就是几边形,依次得到三角形、四边形、五边形、六边形,不可能得到七边形。
用一个平面去截一个几何体,平面截的位置不同,所得的截面也不同,常见的截面是一个多边形或圆。
7、三视图
(1)物体的三视图指主视图、俯视图、左视图。
主视图:从正面看到的图,叫做主视图。
左视图:从左面看到的图,叫做左视图。
俯视图:从上面看到的图,叫做俯视图。
(2)画三个方向看到的形状图
主视图要从下向上画,即先确定最下面一行;左视图要从左向右画,即先确定最左面的一列;俯视图的关键是弄清楚原几何体最低层的情况。
(3)由三视图确定小正方体的个数:用“标数字总个数”的方法(标记在俯视图上)。
