2016年欧几里得数学竞赛真题

合集下载

2016年各省高中数学联赛预选赛试题及详解答案(最值部分)

2016年各省高中数学联赛预选赛试及详解答案（最值部分）1、为正数y x ，，且y x a y x +≤+，则a 的最小值为（2）解：∵0y x >, ∴y x y x +，，均为正数，所以0a >y x xy 21y x yx a y x a y x 22++=⎪⎪⎭⎫⎝⎛++≥⇔+≤+，而1xy 2xy 2y x xy 2=≤+，所以211a 2=+≥ ∴2a ≥2、设1x 0<<，b a ，大于零的常数，x1b x a 22-+则的最小值为（()2b a +）解：∵1x 0<< ∴0x 1>-，又b a ,大于零的常数由柯西不等式可知：()()2222b a x1x b a x 1b x a +=-++≥-+，当且仅当b a a x +=时，等号成立。

3、已知正实数b a ，满足36b a 9=+，则b1a 1+最小值时，=ab （27）解：∵0b a >,，由柯西不等式可知：()943616b a 913b 1a 99b 1a 12==++≥+=+，即当且仅当b 1a 93=，代入36b a 9=+计算，得⎩⎨⎧==9b 3a 时，等号成立。

∴2793ab =⨯=4、若正数y x ，满足xy 5y 3x =+，则y 4x 3+的最小值为（5）解：∵0y x >, ∴xy 为正数∴5x39y 445x 3y 15xy y 3xy x xy 5y 3x =+⇔=+⇔=+⇔=+ 由柯西不等式可知：()5y 4x 3x3y 432x 39y 4452≥+⇔++≥+=当且仅当x 33y 42=，代入xy 5y 3x =+计算，得⎪⎩⎪⎨⎧==21y 1x 时，等号成立。

5、 z y x ，，为正数时，222z y x yz xz 4+++的最大值为（217）。

解：思路：如果分母的最小值可以化为类似常数项×()yz xz 4+的形式，那么最大值就为此常数项的倒数。

2016全国高中数学联赛试题及评分标准

2016全国高中数学联赛试题及评分标准9月将至，开学的同时，每年一年一度的全国高中数学联赛也即将来了，同学们可知道高中联赛的前世今生吗？从1956年起，在华罗庚、苏步青等老一辈数学家的倡导下，开始举办中学数学竞赛，在北京、上海、福建、天津、南京、武汉、成都等省市都开展了数学竞赛，并举办了由京、津、沪、粤、川、辽、皖合办的高中数学联赛。

1979年，我国大陆上的29个省、市、自治区都举办了中学数学竞赛。

1980年，在大连召开的第一届全国数学普及工作会议上，确定将数学竞赛作为中国数学会及各省、市、自治区数学会的一项经常性工作，每年9月第二个星期日举行“全国高中数学联合竞赛”。

竞赛分为一试和二试，在这项竞赛中取得优异成绩的全国约200名学生有资格参加由中国数学会奥林匹克委员会主办的“中国数学奥林匹克(CMO)暨全国中学生数学冬令营”(每年元月)。

各省的参赛名额由3人到8人不等，视该省当年的联赛考试成绩而定，且对于承办方省份有一定额外的优惠。

在CMO中成绩优异的60名左右的学生可以进入国家集训队。

经过集训队的选拔，将有6名表现最顶尖的选手进入中国国家代表队，参加国际数学奥林匹克(IMO)。

为了促进拔尖人才的尽快成长，教育部规定：在高中阶段获得全国数学联赛省、市、自治区赛区一等奖者便获得保送重点大学的资格，对于没有保送者在高考中加分，加分情况根据各省市政策而定，有些省、市、自治区保留了竞赛获奖者高考加5分到20分不等，而部分省级行政区已经取消了竞赛加分。

对二、三等奖获得者，各省、市、自治区又出台了不同的政策，其中包括自主招生资格等优惠录取政策。

为严格标准，中国数学会每年限定一等奖名额1000名左右，并划分到各省、市、自治区。

各省、市、自治区在上报一等奖候选人名单的同时，还要交上他们的试卷，最终由中国数学会对其试卷审核后确定获奖名单。

☆ 试题模式自2010年起，全国高中数学联赛试题新规则如下：联赛分为一试、加试（即俗称的“二试”）。

历届IMO试题(1-46届完整中文版)

1.求证(21n+4)/(14n+3) 对每个自然数 n都是最简分数。

2.设√(x+√(2x-1))+√(x-√(2x-1))=A，试在以下3种情况下分别求出x的实数解：(a) A=√2；(b)A=1；(c)A=2。

3.a、b、c都是实数，已知 cos x的二次方程a cos2x +b cos x +c = 0,试用a,b,c作出一个关于 cos 2x的二次方程，使它的根与原来的方程一样。

当a=4,b=2,c=-1时比较 cos x和cos 2x的方程式。

4.试作一直角三角形使其斜边为已知的 c，斜边上的中线是两直角边的几何平均值。

5.在线段AB上任意选取一点M，在AB的同一侧分别以AM、MB为底作正方形AMCD、MBEF，这两个正方形的外接圆的圆心分别是P、Q，设这两个外接圆又交于M、N，(a.) 求证 AF、BC相交于N点；（b.) 求证不论点M如何选取直线MN 都通过一定点 S；(c.) 当M在A与B之间变动时，求线断 PQ的中点的轨迹。

6.两个平面P、Q交于一线p，A为p上给定一点，C为Q上给定一点，并且这两点都不在直线p上。

试作一等腰梯形ABCD（AB平行于CD），使得它有一个内切圆，并且顶点B、D分别落在平面P和Q上。

1.找出所有具有下列性质的三位数 N：N能被11整除且 N/11等于N的各位数字的平方和。

2.寻找使下式成立的实数x：4x2/(1 - √(1 + 2x))2< 2x + 93.直角三角形ABC的斜边BC的长为a，将它分成 n 等份（n为奇数），令α为从A点向中间的那一小段线段所张的锐角，从A到BC边的高长为h，求证：tan α = 4nh/(an2 - a).4.已知从A、B引出的高线长度以及从A引出的中线长，求作三角形ABC。

5.正方体ABCDA'B'C'D'（上底面ABCD，下底面A'B'C'D'）。

Euclid欧几里得数学竞赛(Grade12)-数学Mathematics-2001-试题 exam

4.
appropriate box in the answer booklet. Marks may be given for work shown. Students are strongly encouraged to show their work. It is expected that all calculations and answers will be expressed as exact numbers such as 4 T , 2 7 , etc., except where otherwise indicated. What are the values of x such that 2 x – 3 2 ! 9 ? If f x ! x 2 – 3 x – 5 , what are the values of k such that f k ! k ? Determine all x, y such that x 2 y 2 ! 25 and x – y ! 1. The vertex of the parabola y ! x – b 2 b h has coordinates 2, 5 . What is the value of h? In the isosceles triangle ABC , AB ! AC and BAC ! 40r . Point P is on AC such that BP is the bisector of ABC . Similarly, Q is on AB such that CQ bisects ACB . What is the size of APB , in degrees?
Canadian Institute of Actuaries

(完整版)初中数学竞赛——勾股定理及其应用

(完整版)初中数学竞赛——勾股定理及其应用初中数学竞赛勾股定理与应用勾股定理直角三角形两直角边a，b的平方和等于斜边c的平方，即a2+b2=c2．勾股定理逆定理如果三角形三边长a，b，c有下面关系:a2+b2=c2那么这个三角形是直角三角形．早在3000年前,我国已有“勾广三,股修四,径阳五”的说法．关于勾股定理，有很多证法，在我国它们都是用拼图形面积方法来证明的．下面的证法1是欧几里得证法．证法1 如图2—16所示．在Rt△ABC的外侧，以各边为边长分别作正方形ABDE，BCHK,ACFG，它们的面积分别是c2,a2，b2．下面证明，大正方形的面积等于两个小正方形的面积之和．过C引CM∥BD，交AB于L，连接BG，CE．因为AB=AE，AC=AG，∠CAE=∠BAG,所以△ACE≌△AGB（SAS）．而所以 S AEML=b2．①同理可证 S BLMD=a2．②①+②得S ABDE=S AEML+S BLMD=b2+a2，即 c2=a2+b2．证法2 如图2—17所示．将Rt△ABC的两条直角边CA,CB 分别延长到D，F,使AD=a，BF=b．完成正方形CDEF（它的边长为a+b），又在DE上截取DG=b，在EF上截取EH=b，连接AG，GH，HB．由作图易知△ADG≌△GEH≌△HFB≌△ABC，所以AG=GH=HB=AB=c,∠BAG=∠AGH=∠GHB=∠HBA=90°,因此,AGHB为边长是c的正方形．显然，正方形CDEF 的面积等于正方形AGHB的面积与四个全等的直角三角形(△ABC，△ADG，△GEH，△HFB）的面积和，即化简得 a2+b2=c2．证法3 如图2—18．在直角三角形ABC的斜边AB上向外作正方形ABDE,延长CB，自E作EG⊥CB延长线于G，自D 作DK⊥CB延长线于K，又作AF， DH分别垂直EG于F，H．由作图不难证明，下述各直角三角形均与Rt△ABC全等：△AFE≌△EHD≌△BKD≌△ACB．设五边形ACKDE的面积为S,一方面S=S ABDE+2S△ABC，①另一方面S=S ACGF+S HGKD+2S△ABC．②由①，②所以 c2=a2+b2．关于勾股定理，在我国古代还有很多类似上述拼图求积的证明方法，我们将在习题中展示其中一小部分，它们都以中国古代数学家的名字命名．利用勾股定理，在一般三角形中，可以得到一个更一般的结论．定理在三角形中，锐角(或钝角)所对的边的平方等于另外两边的平方和，减去(或加上)这两边中的一边与另一边在这边（或其延长线）上的射影的乘积的2倍．(完整版)初中数学竞赛——勾股定理及其应用因此，我们常又称此定理为广勾股定理(意思是勾股定理在一般三角形中的推广）．由广勾股定理我们可以自然地推导出三角形三边关系对于角的影响．在△ABC中，（1）若c2=a2+b2,则∠C=90°；（2)若c2＜a2+b2,则∠C＜90°；(3)若c2＞a2+b2，则∠C＞90°．勾股定理及广勾股定理深刻地揭示了三角形内部的边角关系，因此在解决三角形（及多边形）的问题中有着广泛的应用．例1 如图2-21所示．已知：在正方形ABCD中，∠BAC 的平分线交BC于E，作EF⊥AC于F，作FG⊥AB于G．求证：AB2=2FG2．分析注意到正方形的特性∠CAB=45°,所以△AGF是等腰直角三角形，从而有AF2=2FG2，因而应有AF=AB,这启发我们去证明△ABE≌△AFE．说明事实上，在审题中，条件“AE平分∠BAC”及“EF ⊥AC于F”应使我们意识到两个直角三角形△AFE与△ABE全等，从而将AB“过渡"到AF,使AF(即AB）与FG处于同一个直角三角形中，可以利用勾股定理进行证明了．例2 如图2-22所示．AM是△ABC的BC边上的中线，求证：AB2+AC2=2(AM2+BM2）．推论△ABC的中线长公式：说明三角形的中线将三角形分为两个三角形,其中一个是锐角三角形,另一个是钝角三角形(除等腰三角形外)．利用广勾股定理恰好消去相反项,获得中线公式．①′，②′，③′中的m a，m b，m c分别表示a，b，c边上的中线长．例3 如图2-23所示．求证:任意四边形四条边的平方和等于对角线的平方和加对角线中点连线平方的4倍．分析如图2-23所示．对角线中点连线PQ，可看作△BDQ 的中线，利用例2的结论，不难证明本题．说明本题是例2的应用．善于将要解决的问题转化为已解决的问题，是人们解决问题的一种基本方法，即化未知为已知的方法．下面，我们再看两个例题，说明这种转化方法的应用．例4 如图2-24所示．已知△ABC中,∠C=90°，D，E分别是BC，AC上的任意一点．求证：AD2+BE2=AB2+DE2．分析求证中所述的4条线段分别是4个直角三角形的斜边，因此考虑从勾股定理入手．(完整版)初中数学竞赛——勾股定理及其应用例5 如图2-25所示．设直角三角形ABC中，∠C=90°，AM，BN分别是BC，AC边上的中线．求证:4(AM2+BN2）=5AB2．分析由于AM，BN,AB均可看作某个直角三角形的斜边，因此，仿例4的方法可从勾股定理入手，但如果我们能将本题看成例4的特殊情况——即M，N分别是所在边的中点,那么可直接利用例4的结论，使证明过程十分简洁．练习十一1．用下面各图验证勾股定理（虚线代表辅助线)：(1）赵君卿图(图2-27);（2)项名达图（2—28）；（3）杨作枚图(图2-29)．2．已知矩形ABCD，P为矩形所在平面内的任意一点,求证:PA2+PC2=PB2+PD2．（提示：应分三种情形加以讨论，P在矩形内、P在矩形上、P在矩形外,均有这个结论．）3．由△ABC内任意一点O向三边BC,CA，AB分别作垂线,垂足分别是D,E，F．求证:AF2+BD2+CE2=FB2+DC2+EA2．4．如图2-30所示．在四边形ADBC中，对角线AB⊥CD．求证：AC2+BD2=AD2+BC2．它的逆定理是否成立？证明你的结论．5．如图2—31所示．从锐角三角形ABC的顶点B,C分别向对边作垂线BE,CF．求证：BC2=AB·BF+AC·CE．。

2016年AMC12真题及答案

Solution
Problem 10
Five friends sat in a movie theater in a row containing seats, numbered to from left to right. (The directions "left" and "right" are from the point of view of the people as they sit in the seats.) During the movie Ada went to the lobby to get some popcorn. When she returned, she found that Bea had moved two seats to the right, Ceci had moved one seat to the left, and Dee and Edie had switched seats, leaving an end seat for Ada. In which seat had Ada been sitting before she got up?
Solution
Problem 6
A triangular array of coins has coin in the first row, coins in the second row, coins in the third row, and so on up to coins in the th row. What is the sum of the digits of ?
Solution
Problem 12
In , , , and . Point lies on , and bisects . Point lies on , and bisects . The bisectors intersect at . What is the ratio : ?

2016欧洲女子奥林匹克竞赛(EGMO)试题

2016欧洲女子奥林匹克竞赛EGMO·中英文对照版（无答案）试题提供来源：The Organizing Committee of EGMO 2016Bu șteni -RomaniaDay 1-SolutionsProblem 1.Let n be an odd positive integer,and let n x x x ,...,,21be non-negative real numbers.Show that()()1,...,1212,...,12max min +=+=≤+j j n j i i n i x x x x,where 11x x n =+.问题1.设n 是给定正奇数，记n x x x ,...,,21为n 个非整数的有理数.证明：()()1,...,1212,...,12max min +=+=≤+j j n j i i n i x x x x,其中11x x n =+.Problem 2.Let ABCD be a cyclic quadrilateral,and let diagonals AC and BD intersect at X.Let C 1,D 1and M be the midpoints of segments CX,DX and CD,respectively.Lines AD 1and BC 1intersect at Y ,and line MY intersects diagonals AC and BD at different points E and F,respectively.Prove that line XY is tangent to the circle through E,F and X.问题2.ABCD 为一圆内接四边形，记X 为对角线AC 和BD 交点.记C 1,D 1,M 分别为CX,DX,CD 中点.直线AD 1和BC 1交于Y ，并且直线MY 和对角线AC,BD 分别交于不同点E 和F.证明：直线XY 是过E,F,X 三点的圆的切线.Problem 3.Let m be a positive integer.Consider a m m 44⨯array of square unit cells.Two different cells are related to each other if they are in either the same rowor in the same column.No cell is related to itself.Some cells are coloured blue,such that every cell is related to at least two blue cells.Determine the minimum number of blue cells.问题3.设m 为已知正整数.考虑一个以m m 44⨯排列的正方形单元格表.如果两个单元格在同一列或同一行则认为这两个单元格是相关的，并且单元格与自己不是相关的.现将部分单元格涂成蓝色，使得每个单元格和至少两个蓝色单元格是相关的.求出格表中蓝色单元格的个数最小值.Day 2-SolutionsProblem 4.Two circles,1ωand 2ω,of equal radius intersect at different points X 1and X 2.Consider a circle ωexternally tangent to 1ωat a point T 1,and internally tangent to 2ωat a point T 2.Prove that lines X 1T 1and X 2T 2intersect at a point lying on ω.问题4.两个半径相等的圆1ω和2ω相交于不同点X 1和X 2.设圆ω和圆1ω外切于T 1，并且圆ω和圆2ω内切于T 2.证明直线X 1T 1和X 2T 2交点在圆ω上.Problem 5.Let k and n be integers such that 2≥k and 12-≤≤k n k .Place rectangular tiles,each of size k ⨯1or 1⨯k ,on an n n ⨯chessboard so that each tile covers exactly k cells,and no two tiles overlap.Do this until no further tile can be placed in this way.For each such k and n ,determine the minimum number of tiles that such an arrangement may contain.问题5.设k 和n 为已知整数且有2≥k 并且12-≤≤k n k .现在n n ⨯的棋盘上铺放k ⨯1或1⨯k 的长方形纸条使得每个纸条恰好覆盖k 个格子且任何两个长方形纸条均不相互重叠.一直持续上述操作直到无法再将纸条经上述操作放置在棋盘上.则对每一个满足条件的k 和n ，求存在摆放方案的最少的纸条个数.Problem 6.Let S be the set of all positive integers n such that 4n has a divisor in the range n n n n 2,...,2,1222+++.Prove that there are infinitely many elements of S of each of the forms 67,57,27,17,7++++m m m m m and no elements of S of the form 37+m or 47+m ,where m is an integer.问题6.设S 是满足在n n n n 2,...,2,1222+++中存在4n 的因数的所有正整数n 的集合.证明：集合S 中有无穷个可以写作67,57,27,17,7++++m m m m m 的形式的元素，但没有元素可以写成37+m 或47+m 的形式，其中m 是一个整数.。

高中数学竞赛-历届IMO试题（1-46届）

高中数学竞赛-历届IMO试题（1-46届）第1届IMO1.求证(21n+4)/(14n+3) 对每个自然数 n都是最简分数。

2.设√(x+√(2x-1))+√(x-√(2x-1))=A，试在以下3种情况下分别求出x的实数解：(a) A=√2；(b)A=1；(c)A=2。

3.a、b、c都是实数，已知 cos x的二次方程a cos2x +b cos x +c = 0,试用a,b,c作出一个关于cos 2x的二次方程，使它的根与原来的方程一样。

当a=4,b=2,c=-1时比较 cos x和cos 2x的方程式。

4.试作一直角三角形使其斜边为已知的c，斜边上的中线是两直角边的几何平均值。

6.两个平面P、Q交于一线p，A为p上给定一点，C为Q上给定一点，并且这两点都不在直线p上。

试作一等腰梯形ABCD（AB平行于CD），使得它有一个内切圆，并且顶点B、D分别落在平面P和Q 上。

第2届IMO1.找出所有具有下列性质的三位数 N：N能被11整除且 N/11等于N的各位数字的平方和。

2.寻找使下式成立的实数x：4x2/(1 - √(1 + 2x))2< 2x + 93.直角三角形ABC的斜边BC的长为a，将它分成 n 等份（n为奇数），令α为从A 点向中间的那一小段线段所张的锐角，从A到BC 边的高长为h，求证：tan α = 4nh/(an2 - a).4.已知从A、B引出的高线长度以及从A引出的中线长，求作三角形ABC。

5.正方体ABCDA'B'C'D'（上底面ABCD，下底面A'B'C'D'）。

数学奥林匹克中的欧几里得几何pdf

数学奥林匹克中的欧几里得几何pdf
欧几里得几何（Euclidean Geometry）是指基于古希腊数学家欧几里德（Euclid）的几何学原理的一种几何学理论。

其实质是一种空间平面几何，它以点、线、平面、直角三角形以及正方形等多维空间对象为基础，对对象的形态、大小、位置及彼此的关系进行定义、测量以及比较等。

欧几里得几何在数学奥林匹克竞赛中广泛地使用。

有许多题目涉及到欧几里得几何学，像是关于三角形面积和周长的问题，它们基于欧几里得几何中的定理。

另外，也有关于变换和图形识别的题目，它们需要使用欧几里得几何学中定义的变换函数和相关结构、性质。

此外，欧几里得几何还与矩阵计算有着密切的联系，可以帮助我们更便捷地解决复杂的问题。

2016年cmo试题解析

2016年cmo试题解析今天咱们来一起看看2016年cmo（中国数学奥林匹克）的试题解析呀。

虽然这些题有点难，但是咱们一起研究研究就会觉得很有趣的呢。

就拿其中一道题来说吧。

这道题就像是一个小迷宫一样，要找到出口可不容易。

它大概是关于数字和图形之间的关系的。

比如说，它给了我们一些奇怪的图形，每个图形上还有不同的数字标记。

这就好比是在一个神秘的城堡里，每个房间都有一个不同的数字密码。

我们要做的呢，就是像小侦探一样，找出这些数字和图形之间隐藏的规律。

我一开始看到这题的时候，真的是有点懵，就像走进了一个大雾弥漫的森林，根本不知道方向在哪里。

但是我没有放弃呀，我就从最简单的部分开始看。

我发现其中有几个图形，它们的形状特别相似，只是大小不太一样。

然后我再看看对应的数字，就好像发现了一点点小线索。

我就想啊，如果把图形的大小当成是一种变化的因素，那数字是不是也会按照某种规律跟着变化呢？我就拿笔在纸上画呀，把那些相似图形按照大小顺序排起来，再把对应的数字也写在旁边。

这时候就有点像在拼图了，一块一块地试着拼凑出正确的图案。

还有一道题是关于排列组合的。

这就像是在安排小伙伴们排队一样。

比如说有几个小朋友，他们要站成不同的队形，有的是一排，有的是几排。

题里给了一些条件，比如说某个小朋友必须站在另一个小朋友的左边之类的。

这就需要我们好好地思考怎么安排才能满足所有的条件。

我就想象自己是那个负责排队的小班长。

我先把那些有特殊要求的小朋友的位置确定好，就像先把队伍里的小队长安排好位置一样。

然后再根据剩下的条件，把其他小朋友一个一个地安排到合适的位置上。

这中间也会遇到一些小麻烦，比如说安排了几个小朋友之后，发现后面的小朋友没办法按照要求站了。

这时候我就重新调整前面小朋友的位置，就像重新规划队伍的排列一样。

通过做这些题，我学到了很多东西呢。

我知道了遇到难题不要害怕，就像走在黑暗的小路上，只要一步一步慢慢走，总会找到亮光的。

而且要善于从简单的地方开始找线索，就像搭积木一样，先把最下面的基础打好，然后再慢慢往上搭。

1959年至2016年历届IMO试题(不含答案)

第一届（1959年）罗马尼亚布拉索夫（Bra şov ，Romania ）1. 求证314421++n n 对每个自然数 n 都是最简分数。

（波兰）2. 设A x x x x =--+-+1212，试在以下3种情况下分别求出x 的实数解： a)2=A ；b)A =1；c)A =2。

（罗马尼亚）3. a 、b 、c 都是实数，已知关于 cos x 的二次方程0cos cos 2=++c x b x a试用 a,b,c 作出一个关于 cos 2x 的二次方程，使它的根与原来的方程一样。

当a =4,b =2,c =-1 时比较 cos x 和 cos 2x 的方程式。

（匈牙利）4. 试作一直角三角形使其斜边为已知的c ，斜边上的中线是两直角边的几何平均值。

（匈牙利）5. 在线段AB 上任意选取一点M ，在AB 的同一侧分别以 AM 、MB 为底作正方形AMCD 、 MBEF ，这两个正方形的外接圆的圆心分别是 P 、Q ，设这两个外接圆又交于 M 、N 。

a) 求证：AF 、BC 相交于N 点；b) 求证：不论点M 如何选取，直线MN 都通过定点S ；c) 当M 在A 与B 之间变动时，求线段PQ 的中点的轨迹。

（罗马尼亚）6. 两个平面P 、Q 的公共边为 p ，A 为P 上给定一点，C 为Q 上给定一点，并且这两点都不在直线p 上。

试作一等腰梯形ABCD （AB 平行于CD ），使得它有一个内切圆，并且顶点B 、D 分别落在平面P 和Q 上。

（捷克斯洛伐克）第二届（1960年）罗马尼亚锡纳亚（Sinaia ，Romania ）1. 找出所有具有下列性质的三位数N ：N 能被11整除且商等于N 的各位数字的平方和。

（保加利亚）2. 寻找使下式成立的实数x ：（匈牙利）()92211422+<+-x x x3. 直角三角形ABC 的斜边BC 的长为a ，将它分成n 等份（n 为奇数），令α为从A 点向中间的那一小段线段所张的锐角，从A 到BC 边的高长为h ，求证：（罗马尼亚）()a n nh 14tan 2-=α 4. 已知从A 、B 两点引出的高线长h a 、hb 以及从 A 引出的中线长m a ，求作三角形ABC 。

欧几里得国际数学竞赛题

欧几里得国际数学竞赛题
以下是一些欧几里得国际数学竞赛的试题:
1. 求解 2 + 3 =?
2. 将数组 [1, 4, 7, 10] 排序,求排序后的结果。

3. 一个整数 n 的阶乘等于 n! 的值为多少?
4. 求解方程 2x + 3 = 9 的解。

5. 在两个整数 a 和 b 中,如果 a 是 b 的倍数,则 a 乘以 b 的积一定是 a 的倍数。

求 a 和 b 的最小公倍数。

6. 求解方程 5x - 2 = 13 的解。

7. 将数组 [2, 3, 5, 7] 按从小到大的顺序排序,求排序后的结果。

8. 一个整数 n 的平方等于 n * n,求 n 的平方最小的正整数。

9. 求解方程 x + y = 15 的解。

10. 一个正整数 n,求 2n + 1 的值。

这些题目难度不同,但都考察了学生的数学思维和解决问题的能力。

2016年世界少年奥数赛八年级海选赛试题及答案解析

世界少年奥林匹克数学竞赛（中国区）选拔赛地方海选赛（2016年10月）选手须知：1、本卷共三部分，第一部分：填空题，共计50分；第二部分：计算题，共计12分；第三部分：解答题，共计58分。

2、答题前请将自己的姓名、学校、赛场、参赛证号码写在规定的位置。

3、比赛时不能使用计算工具。

4、比赛完毕时试卷和草稿纸将被收回。

八年级试题（Ａ卷）（本试卷满分120分，考试时间90分钟）一、填空题。

（每题5分，共计50分）1、36的平方根是。

2、若方程m x+n y=6的两个解是11y x 及12y x ，则m= ，n =。

3、已知1b a ，b a b a ,2522。

4、已知x=y+z=2，则xyz zy x 333223。

5、如果实数a ，b 满足条件,12|21|,12222a b a b a b a则a+b= 。

6、某班级春游时48人到杭州西湖划船。

已知每只小船坐3个人，租金16元；每只大船坐5个人，租金24元，则这个班级租金至少花元。

7、在△ABC 中，∠B=60°，∠C ＞∠A ，且222B A )C (）（）（,则△ABC 的形状是。

8、观察下列式子：181092；198100992；199810009992，……，按规律写出2999999。

（填写具体数字）9、如图，韩梅梅从A 点出发，沿直线前进10米后向左转30°，再沿直线前进10米，又向左转30°，照这样子走下去，他第一次回到起点A 时走了米。

10、如图直线L与∠A 的两边相交于点B、C，则图中以A、B、C为端点的射线有条。

二、计算题。

（每题6分，共计12分）11、 1+3+5+7+9+…+1997+199912、 1+5+52+53+…+5100三、解答题。

（第13题6分，第14题8分，第15题10分，第16题10分，第17题12分，第18题12分，共计58分）13、解方程510)5)(4(1)4)(3(1)3)(2(1)2)(1(1)1(1x x x x x x x x x x x 14、已知正实数a 、b 、c 满足方程组252182292222bc a c ab c b ac b a ，求a+b+c 的值。

2016滑铁卢竞赛试题答案

13, 2016
(outside of North America and South America)
Solutions
©2016 University of Waterloo

1. (a) The average is 5 + 15 + 25 + 35 + 45 + 55 (5 + 55) + (15 + 45) + (25 + 35) 60 + 60 + 60 = = = 30 6 6 6 (b) Since x2 = 2016, then (x + 2)(x − 2) = x2 − 4 = 2016 − 4 = 2012. (c) Since points P , Q and R lie on a straight line, then the slope of P Q equals the slope of P R. 30 − 5 25 2a − 5 and the slope of P R equals = = 5. The slope of P Q equals a−7 12 − 7 5 2a − 5 = 5 and so 2a − 5 = 5(a − 7). Therefore, a−7 This gives 2a − 5 = 5a − 35 or 3a = 30, and so a = 10. 2. (a) If n 25 = , then n2 = 25(9) = 225. Therefore, n = 15 or n = −15. 9 n (We can check by substitution that each of these values satisﬁes the original equation.)

通用版六年级数学竞赛试题（含答案）

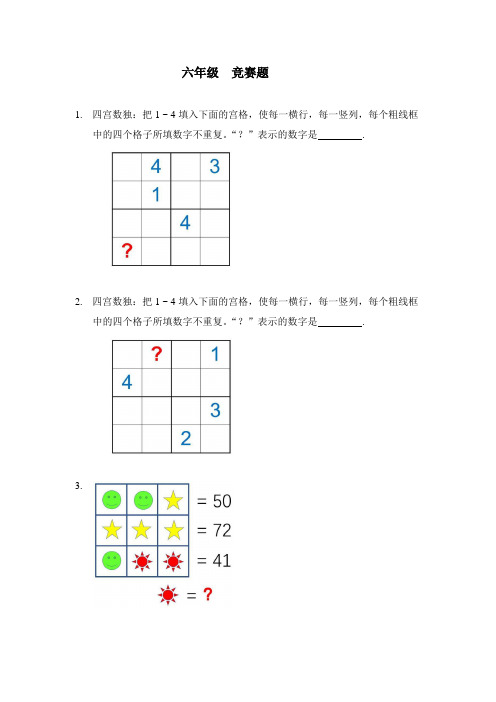
六年级竞赛题1.四宫数独：把1 ~ 4 填入下面的宫格，使每一横行，每一竖列，每个粗线框中的四个格子所填数字不重复。

“？”表示的数字是.2.四宫数独：把1 ~ 4 填入下面的宫格，使每一横行，每一竖列，每个粗线框中的四个格子所填数字不重复。

“？”表示的数字是.3.4.5.6.(A) (B) (C) (D)7.(A) (B) (C) (D)8.(A) (B) (C) (D)9.10.11.阿凡提来到了魔法城堡，魔法城堡的大门是一个智能密码锁，大门上有提示语：下面这个计算的结果就是打开大门的密码了．•••1000 - 3.4 28571⨯ 2.3 =请你输入打开魔法城堡大门的密码：．12.蓝精灵热爱学习，可是她被下面这道计算题给难住了，你能帮她吗？计算：5.4321×0.5679－0.4321×5.5679＋0.321＝．13.已知大白拥有的魔力磁铁数量的2比小宏的少10%，则用百分数表示，大白3拥有的魔力磁铁数量比小宏的多%．14.哈利波特用魔法杖改变了一个分数，变化后发现分子增加20%，分母减少19%，则新分数比原来分数增加了%.（四舍五入精确到1％）15.霍格沃兹的魔法世界里定义了一种新运算△，规定a△b=（a+b）÷b，那么：3 4△19= ．5 2016.迷糊老师在黑板上写了三个分数：2012，2013，2014，其中最大的分数是：2017 2018 2019.17.小猪佩奇的后花园是一个如图所示的梯形（单位：m ），梯形的面积是m2．18.猪八戒爱喝含糖的水，他有甲、乙两杯糖水，所含糖的重量之比为5:3，所含水的重量之比为3:5，糖水的总重量比为5:8，则甲杯的含糖量是．(结果用最简分数表示)19.皮卡丘爱做化学实验，她有一杯含盐7%的盐水重100 克，蒸发了一部分水后，盐水含盐10%，则蒸发的水是克．20.皮皮鲁在学习除法竖式，他发现一个三位数除以19，商是a，余数是b (a，b都是自然数)，则a＋b 的最大值是．21.鲁西西家里面有一个三层书架，其中第一，二层书的数量比为5:3，第二，三层书的数量比为7:13，若书架上的书总数不超过100 本，则第三层放有本书．22.数学王子高斯是一个数论高手，他的小学老师曾经考过他这么一个问题：从数字1，2，3，4，5，6，7，8，9 中任取3 个数组成三位数，所组成的数中，能被4 整除的三位数有个．23.欧几里得是一位伟大的古希腊时期的数学家，他写过一本书叫做《几何原本》.他曾经思考过这样一个问题：26. 小乔巴将 1 到 25 这 25 个数随意排成一行，然后将它们依次和 1，2，3，…，25 相减，并且都是大数减小数，把得到的 25 个差相加，结果最大是．27. 劳拉在最近的这次古墓任务中来到了古埃及，她在一个神秘金字塔里发现了1 , 3 , 5 , 7 , 9 , 11 , 13 ,1 123 5 8 13π取 3.14）24. 青青草原羊村里举行了一次智力大比拼．结果发现，前五名的平均成绩比前三名的平均成绩少 1 分，前七名的平均成绩比前五名的平均成绩少 3 分．若第四名到第七名的平均成绩为 84 分，则前三名的平均成绩是分．25. 神探夏洛克·福尔摩斯发现了一个密码宝箱，已知密码是一个三位数 A ．目前有一个线索，在 123，931，297，419 四个三位数中，每个数都恰好含有三位数 A 中的一个数字，且出现的位置和 A 中的位置不同，则三位数 A 是．一个有趣的数列，请你观察下面一列数的规律，这列数从左往右第 10 个数是．如图，OAB 是一个圆心角为 45°，半径为 12 m 的扇形，以 OA 为直径画一个半圆，交 OB 于点 C ，则图中阴影部分的面积是 m 2．（圆周率29. 阿里巴巴商城在举行促销活动，一套巴克球降价 5 元出售，和往日按原价销售相比，销量提高了 20%，获利提高了 10%，则降价后每套巴克球可获利元．30. 名侦探柯南在自己的笔记本上写了两个两位数，他发现其中一个数的 3等于其中的△ABF 和△AFD 的面积分别是 40 和 64. 则四边形 DFEC 的面积是．的 3 倍少 1 米，则短绳原来长米．1另一个数的 3，这两个数的差最大是．31. 龙猫家的大花园是一个平行四边形．如图，线段 AE 和 BD 将花园分成四块，32. 黄金梅丽号轮船从甲港经丙港到乙港，从甲港到丙港是逆水而行，从丙港到乙港是顺水而行，从甲港到丙港的路程是从丙港到乙港的 2．轮船逆水而行3的速度是顺水而行的速度的一半，轮船从甲港经丙港到乙港共行了 7 小时. 这艘轮船从乙港经丙港返回甲港需要小时．有两条绳子，长绳比短绳的 2 倍多 4 米，各截掉 6 米以后，长绳比短绳28. 所罗门是以色列最有智慧的君王，有一天，他给大臣们出了一道题：33.如图，正方形ABCD 与梯形CDEF 共边，AF 与BC 交于点G，若AD=DE=3，AG : GF＝1 : 2，则梯形CDEF 的面积为．34.精灵宝可梦从1~20 这20 个自然数中任取若干个（至少两个），使这些数的乘积的末位数字是3，则它共有种不同的取法．35. 步行的菲菲和骑自行车的猪猪侠，分别从相距40 千米的A、B 两地同时出发，相向而行．已知菲菲每小时行4 千米，但每行30 分钟就休息 5 分钟；猪猪侠每小时行12 千米，分钟后，两人在途中相遇．36. 数学家高斯在研究整数问题时，发明了取整记号[x ]，用[x ]表示不超过 x 的最大整数．问：自然数 n 的值依次取 1，2，3，…，2019 时，[ n ] + n + n的值共[ ] [ ]2 3 6有种可能．37. 甲、乙两个工程队合作一项大工程，计划按照甲、乙、甲、乙、……的顺序轮流施工，即每队施工一天后由另一队接替，这样甲和乙施工的天数刚好一样多；实际按照甲、乙、乙、甲、乙、乙、……的顺序施工，结果比原计划提前两天完工，且最后一天是甲施工．已知甲的工作效率是乙的 2，则完成3 这项工程实际用了天．38. 小聪明爱看故事书，他有一本故事书标记的页码是 1~m 页，所有页码的各位数字之和是 190，则 m ＝．39. 英国航海家库克船长在探险时发现了一个神秘的图形．如图，点 E ，F ，G ，H 分别是四边形 ABCD 各边上的点，若 2AF =FB ，2CH =HD ，BG =GC ，DE =EA ，四边形 ABCD 的面积是 12，则四边形 EFGH 的面积是．40. 史莱克和钢铁侠从同一地出发去环球影城，史莱克走得慢，比钢铁侠早出发5 分钟，钢铁侠出发后 15 分钟可追上史莱克．若史莱克每分钟多走 5 米，钢铁侠每分钟多走 10 米，其他条件不变，则钢铁侠出发后 13 分钟追上史莱克，则史莱克初始的速度是每分钟走米答案。

2016年AMC12真题及答案

2016年AMC12真题及答案2016 AMC12 AProblem 1What is the value of ?SolutionProblem 2For what value of does ?SolutionProblem 3The remainder can be defined for all realnumbers and with by where denotes the greatest integer less than or equal to . What is the value of ?SolutionProblem 4The mean, median, and mode of the data values are all equal to . What is the value of ?SolutionProblem 5Goldbach's conjecture states that every even integer greater than 2 can be written as the sum of two prime numbers (for example, ). So far, no one has been able to prove that the conjecture is true, and no one has found a counterexample to show that the conjecture is false. What would a counterexample consist of?SolutionProblem 6A triangular array of coins has coin in the first row, coins in the second row, coins in the third row, and so on up to coins in the th row. What is the sum of the digits of ?SolutionProblem 7Which of these describes the graph of ?SolutionProblem 8What is the area of the shaded region of the given rectangle?SolutionProblem 9The five small shaded squares inside this unit square are congruent and have disjoint interiors. The midpoint of each side of the middle square coincides with one of thevertices of the other four small squares as shown. The common side length is , where and are positive integers. What is ?SolutionProblem 10Five friends sat in a movie theater in a row containing seats, numbered to from left to right. (The directions "left" and "right" are from the point of view of the people as they sit in the seats.) During the movie Ada went to the lobby to get some popcorn. When she returned, she found that Bea had moved two seats to the right, Ceci had moved one seat to the left, and Dee and Edie had switched seats, leaving an end seat for Ada. In which seat had Ada been sitting before she got up?SolutionProblem 11Each of the students in a certain summer camp can either sing, dance, or act. Some students have more than one talent, but no student has all three talents. There are students who cannot sing, students who cannot dance, and students who cannot act. How many students have two of these talents?SolutionProblem 12In , , , and . Point lies on ,and bisects . Point lies on , and bisects . The bisectors intersect at . What is the ratio : ?SolutionProblem 13Let be a positive multiple of . One red ball and green balls are arranged in a line in random order. Let be the probability that at least of the green balls are on the same side of the red ball. Observe that andthat approaches as grows large. What is the sum of the digits of the least value of such that ?SolutionProblem 14Each vertex of a cube is to be labeled with an integer from through , with each integer being used once, in such a way that the sum of the four numbers on the vertices of a face is the same for each face. Arrangements that can be obtained from each other through rotations of the cube are considered to be the same. How many different arrangements are possible?SolutionProblem 15Circles with centers and , having radii and , respectively, lie on the same side of line and are tangent to at and , respectively,with between and . The circle with center is externally tangent to each of the other two circles. What is the area of triangle ?SolutionProblem 16The graphs of and are plotted on the same set of axes. How many points in the plane with positive -coordinates lie on two or more of the graphs?SolutionProblem 17Let be a square. Let and be the centers, respectively, of equilateral triangles with bases and each exterior to the square. What is the ratio of the area of square to the area of square ?SolutionProblem 18For some positive integer the number has positive integer divisors, including and the number How many positive integer divisors does the number have?SolutionProblem 19Jerry starts at on the real number line. He tosses a fair coin times. When he gets heads, he moves unit in the positive direction; when he gets tails, he moves unit in the negative direction. The probability that he reaches at some time during thisprocess is where and are relatively prime positive integers. What is (For example, he succeeds if his sequence of tosses is )SolutionProblem 20A binary operation has the properties that andthat for all nonzero real numbers and (Here the dot represents the usual multiplication operation.) The solution to theequation can be written as where and are relatively prime positive integers. What isSolutionProblem 21A quadrilateral is inscribed in a circle of radius Three of the sides of this quadrilateral have length What is the length of its fourth side?SolutionProblem 22How many ordered triples of positive integerssatisfy and ?SolutionProblem 23Three numbers in the interval are chosen independently and at random. What isthe probability that the chosen numbers are the side lengths of a triangle with positive area?SolutionProblem 24There is a smallest positive real number such that there exists a positive real number such that all the roots of the polynomial are real. In fact, for this value of the value of is unique. What is the value ofSolutionProblem 25Let be a positive integer. Bernardo and Silvia take turns writing and erasing numbers on a blackboard as follows: Bernardo starts by writing the smallest perfect square with digits. Every time Bernardo writes a number, Silvia erases the last digits of it. Bernardo then writes the next perfect square, Silvia erases the last digits of it, and this process continues until the last two numbers that remain on the board differ by atleast 2. Let be the smallest positive integer not written on the board. For example,if , then the numbers that Bernardo writes are , and the numbers showing on the board after Silvia erases are and , andthus . What is the sum of the digits of ?2016 AMC 12A Answer Key1 B2 C3 B4 D5 E6 D7 D8 D9 E10 B11 E12 C13 A14 C15 D16 D17 B18 D19 B20 A21 E22 A23 C24 B25 E。