三年级奥数40讲教案第5讲 巧数图形
小学三年级奥数精品讲义1-34讲全

小学三年级奥数精品讲义目录第一讲加减法的巧算(一)第二讲加减法的巧算(二)第三讲乘法的巧算第四讲配对求和第五讲找简单的数列规律第六讲图形的排列规律第七讲数图形第八讲分类枚举第九讲填符号组算式第十讲填数游戏第十一讲算式谜(一)第十二讲算式谜(二)第十三讲火柴棒游戏(一)第十四讲火柴棒游戏(二)第十五讲从数量的变化中找规律第十六讲数阵中的规律第十七讲时间与日期第十八讲推理第十九讲循环第二十讲最大和最小第二十一讲最短路线第二十二讲图形的分与合第二十三讲格点与面积第二十四讲一笔画第二十五讲移多补少与求平均数第二十六讲上楼梯与植树第二十七讲简单的倍数问题第二十八讲年龄问题第二十九讲鸡兔同笼问题第三十讲盈亏问题第三十一讲还原问题第三十二讲周长的计算第三十三讲等量代换第三十四讲一题多解第三十五讲总复习第一讲加减法的巧算森林王国的歌舞比赛进行得既紧张又激烈。
选手们为争夺冠军,都在舞台上发挥着自己的最好水平。
台下的工作人员小熊和小白兔正在统计着最后的得分。
由于他们对每个选手分数的及时通报,台下的观众频频为选手取得的好成绩而热烈鼓掌,同时,观众也带着更浓厚的兴趣边看边猜测谁能拿到冠军。
观众的情绪也影响着两位分数统计者。
只见分数一到小白兔手中,就像变魔术般地得出了答案。
等小熊满头大汗地算出来时,小白兔已欣赏了一阵比赛,结果每次小熊算得结果和小白兔是一样的。
小熊不禁问:“白兔弟弟,你这么快就算出了答案,有什么决窍吗?”小白兔说:“比如2号选手是93、95、98、96、88、89、87、91、93、91,去掉最高分98,去掉最低分87,剩下的都接近90为基准数,超过90的表示成90+‘零头数’,不足90的表示成90-‘零头数’。
于是(93+95+96+88+89+91+93+91)÷8=90+(3+5+6―2―1+1+3+1)÷8=90+2=92。
你可以试一试。
”小熊照着小白兔说的去做,果然既快又对。
巧数图形详解小学奥数ppt课件

A
三角形个数: 4+3+2+1=10
1 2 34
B C DE F
数三角形有时也可以用数线段的方法;有的图形要用 编号数图形的方法,还有的图形先要分成几部分分别 去数,再考虑几部分拼合起来看看有没有产生新三角 形。
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
拓展3、数出下面图形中分别有多少个三 角形?
蓝线退出后有8个三角形。 蓝线返回后增加7个三角形。
总共有:8+7= 15 个
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
搌4、数出下面图形中分别有多少个三角 形?
可看成由这个图形的3 个组合,单独一个有16 个三角形。
组合后增加8个三角形。
总共16×3+8=56
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
拓展9:下面图形中有多少个三角形?
拆走2条线后有3个三角形。 返回第1条线后增5个三角形。 返回第2条线后增8个三角形。
还原大长方形则增4
个
总共24+4总= 共282个8个
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
谢谢使用
1 234 5
(4+3+2+1)×2=20 个
三年级巧数图形PPT教案

三年级巧数图形
36
一星 训练
右图有( 60 )个长方形? 长所在线段:4+3+2+1=10(条) 宽所在线段:3+2+1=6(条)
10×6=60(个)
2020-12-06
三年级巧数图形
37
例7
在下图中,包含“*”号的长方形和正方形共有多少个?
分析:包含一小块的有1个;
包含2小块的有4个;包含3小块
点评: 可以看出数角的个数与数线段的条数方法是一样的,用数
线段的方法来数图形的个数还适用于数三角形,长方形等。
2020-12-06
三年级巧数图形
24
一星 训练 一共有( 15 )个角 ? 5+4+3+2+1=15(个)
2020-12-06
三年级巧数图形
25
例3 下列各图形中,三角形的个数各是多少?
为止。"梅姑若无其事地说。
"今天真热呀,来杯冰镇可乐怎么样?"
梅姑说着从冰箱里拿出冰块,每个杯子放了4块,再倒上
2020-12-06 可乐,递给矶川侦探一杯。三将年级藏巧数有图形钻石的冰块放到了自己的杯
42
Dr.Feng
2020-12-06
三年级巧数图形
44
Dr.Feng
2020-12-06
三年级巧数图形
的有4个;包含4小块的有7个;
*
包含5小块的有2个;
包含6小块的有6个;
包含8小块的有4个;
包含9小块的有3个;包含10小块的有
2个; 1包+4含+41+27小+2块+6的+4有+34+个2+;4+包2=含391(5小个块)的 答有:2个包。含“*”的长方形和正方形共有39个。
小学三年级奥数第五讲数图形,有答案

第5讲 图形个数一、知识要点同学们,你想学会数图形的方法吗?要想不重复也不遗漏地数出线段、角、三角形、长方形……那就必须要有次序、有条理地数,从中发现规律,以便得到正确的结果。
要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,然后再数出由基本图形组成的新的图形,并求出它们的和。
二、精讲精练【例题1】数出下图中有多少条线段?【思路导航】方法一:我们可以采用以线段左端点分类数的方法。
以A 点为左端点的线段有:AB 、AC 、AD 3条;以B 点为左端点的线段有:BC 、BD 2条;以C 点为左端点的线段有:CD 1条。
所以,图中共有线段3+2+1=6(条)。
方法二:把图中线段 AB 、BC 、CD 看做基本线段来数,那么,由1条基本线段构成的线段有:AB 、BC 、CD 3条;由2条基本线段构成的线段有:AC 、BD 2条;由3条基本线段构成的线段有:AD 1条。
所以,图中一共有3+2+1=6(条)线段。
练习1:(1)数出下图中有多少条线段? (2)数出下图中有几个长方形?【例题2】数出图中有几个角?【思路导航】数角的个数可以采用与数线段相同的方法来数。
方法一:以OA 为一边的角有:∠AOB 、∠AOC 、∠AOD 3个;以OB 为一边的角还有:∠BOC 、∠BOD 2个;以OC 为一边的角还有:∠COD 1个。
所以,图中共有角3+2+1=6(个)。
方法二:把图中∠AOB 、∠BOC 、∠COD 看做基本角来数,那么,由1个基本角构成的角有:∠AOB 、∠BOC 、∠COD 3个;由2个基本角构成的角有: ∠AOC 、∠BOD 2个;由3个基本角构成的角有:∠AOD 1个。
所以,图中一共有3+2+1=6DA B C E A B C D OD C B A DO CBA(个)角。
练习2:数出图中有几个角? (1) (2)【例题3】数出右图中共有多少个三角形?【思路导航】方法一:我们可以采用按边分类数的方法。
小学三年级奥数-数图形个数备课讲稿

A
B
O
C
• (2)
A
B
O
C
D
E
P
• 【例题3】数出右图中共有多少个三角形?
AB C D
【思路导航】方法一:我们可以采用按边分类数的方法。 以PA为边的三角形有:△PAB、△PAC、△PAD、3 个;以PB为边的三角形还有:△PBC、△PBD 2个; 以PC为边的三角形还有:△PCD 1个。所以,图中共 有三角形3+2+1=6(个)。
(3+2+1)×(2+1)=18(个)
答:图中共有18个
长方形。
练习4:
• (1)数出下图中有多少个长方形?
A
B
C
D
• (2)数出下图中有多少个正方形?
• 【例题5】有5个同学,每两个人握手一次,一共要握 手多少次?
• 【思路导航】这道题可以用数线段的方法来解答。根 据题意,画出线段图,每一个端点代表一个同学。
C
D
【思路导航】数图中有多少个长方形和数三角形的方法
一样,长方形是由长、宽两对线段围成,线段 CD上有
3+2+1=6(条)线段,其中每一条与AC中一条线段对应,
分别作为长方形的长和宽,这里共有6×1=6(个)长方
形,而AC上共有2+1=3(条)线段也就有6×3=18(个)
长方形。它的计算公式为:
长方形的总数=长边线段的总数×宽边线段的总数
• (2)有1,2,3,4,5,6,7,8等8个数字,能组 成多少个不同的两位数?
二、精讲精练
• 【例题1】数出下图中有多少条线段?
A
C
D
【思路导航】方法一:我们可以采用以线段左端点分类
三年级奥数--第五讲--巧数图形(二)
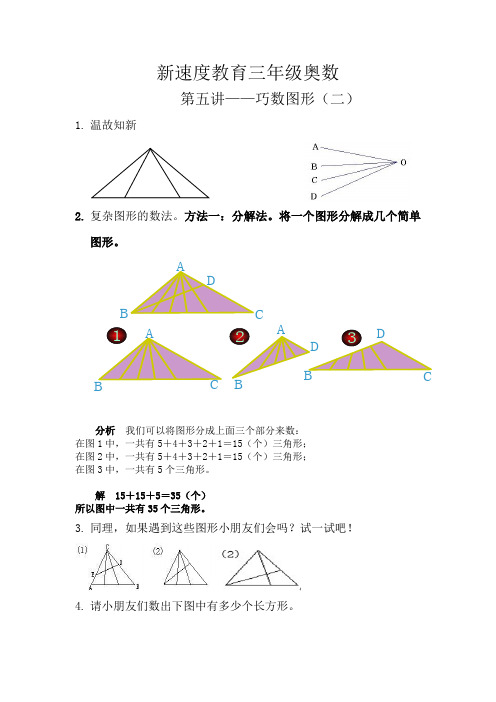
新速度教育三年级奥数
第五讲——巧数图形(二)
1. 温故知新
2. 复杂图形的数法。
方法一:分解法。
将一个图形分解成几个简单图形。
B C
分析 我们可以将图形分成上面三个部分来数:
在图1中,一共有5+4+3+2+1=15(个)三角形;
在图2中,一共有5+4+3+2+1=15(个)三角形;
在图3中,一共有5个三角形。
解 15+15+5=35(个)
所以图中一共有35个三角形。
3. 同理,如果遇到这些图形小朋友们会吗?试一试吧!
4. 请小朋友们数出下图中有多少个长方形。
分析:数图形中有多少个长方形和数三角形的方法一样,长方形是由长宽两对线段围成,线段CD 上有3+2+1=6条线段,其中每一条与AC 中一条线段对应,分别作为长方形的长和宽,这里共有6×1=6个长方形;而AC 上共2+1=3条线段也就有6×3=18个长方形。
它的计算公式为:
5. 方法二:长方形的总数=长边线段的总数×宽边线段的总数
6. 同理,如果遇到这些图形小朋友们会吗?试一试吧!
7. *请小朋友们数出下图中有多少个正方形。
分析:一个小正方形有9个,四个小正方形组成有4个,9个小正方形有1个,所以一共有1+4+9=15个
8.*方法三:公式法。
1*1+2*2+3*3+..+N*N=。
N 是一行正方形的个数。
9.练一练:
D B C
A。
小学奥数讲座标准教案-学案-三年级第5讲 图形个数

第5讲 图形个数计算: 308+203-399-97同学们,你想学会数图形的方法吗?要想不重复也不遗漏地数出线段、角、三角形、长方形……那就必须要有次序、有条理地数,从中发现规律,以便得到正确的结果。
要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,然后再数出由基本图形组成的新的图形,并求出它们的和。
【例题1】数出下图中有多少条线段?【思路导航】方法一:我们可以采用以线段左端点分类数的方法。
以A 点为左端点的线段有:AB 、AC 、AD 3条;以B 点为左端点的线段有:BC 、BD 2条;以C 点为左端点的线段有:CD 1条。
所以,图中共有线段3+2+1=6(条)。
方法二:把图中线段 AB 、BC 、CD 看做基本线段来数,那么,由1条基本线段构成的线段有:AB 、BC 、CD 3条;由2条基本线段构成的线段有:AC 、BD 2条;由3条基本线段构成的线段有:AD 1条。
所以,图中一共有3+2+1=6(条)线段。
(1)数出下图中有多少条线段? (2)数出下图中有几个长方形?【例题2】数出图中有几个角?EA B C D DABCODC BA【思路导航】数角的个数可以采用与数线段相同的方法来数。
方法一:以OA 为一边的角有:∠AOB 、∠AOC 、∠AOD 3个;以OB 为一边的角还有: ∠BOC 、∠BOD 2个;以OC 为一边的角还有:∠COD 1个。
所以,图中共有角3+2+1=6(个)。
方法二:把图中∠AOB 、∠BOC 、∠COD 看做基本角来数,那么,由1个基本角构成的角有:∠AOB 、∠BOC 、∠COD 3个;由2个基本角构成的角有: ∠AOC 、∠BOD 2个;由3个基本角构成的角有:∠AOD 1个。
所以,图中一共有3+2+1=6(个)角。
练习2:数出图中有几个角?(1) (2)【例题3】数出右图中共有多少个三角形?【思路导航】方法一:我们可以采用按边分类数的方法。
巧数图形教案

巧数图形教案教案标题:巧数图形教案教案目标:1. 理解巧数的概念,并能通过观察图形找出巧数。
2. 能够解释巧数图形的特征和规律。
3. 发展学生的逻辑思维和数学推理能力。
教学资源:1. 巧数图形的示例和问题。
2. 黑板/白板、彩色粉笔/白板笔。
3. 学生用纸和铅笔。
教学步骤:引入(10分钟):1. 谈论巧数的定义:巧数是指能够被3整除的数。
2. 引导学生列举一些巧数并讨论其规律:3、6、9、12、15等。
3. 提问学生:巧数有什么特征或规律?学生回答后进行解释和总结。
探究(20分钟):1. 展示一系列巧数图形的示例,例如由方块或圆圈组成的图形。
2. 让学生观察这些图形并尝试找出其中的巧数。
3. 学生思考并记录他们找到的巧数,并与同学交流发现。
整理(10分钟):1. 邀请学生分享他们找到的巧数,并将其记录在黑板/白板上。
2. 引导学生一起观察这些巧数图形的特征和规律,例如巧数图形中的方块或圆圈数量与巧数的关系。
3. 引导学生总结巧数图形的规律,并鼓励他们进行逻辑推理和解释。
拓展(15分钟):1. 给学生一些新的巧数图形示例,并鼓励他们找出其中的巧数。
2. 提问学生:是否可以用其他形状和不同的巧数找出新的巧数图形?3. 鼓励学生用纸和铅笔设计自己的巧数图形,并在班级中展示和分享。
巩固(5分钟):1. 总结巧数图形的概念和规律,并再次强调巧数是能够被3整除的数。
2. 提醒学生继续观察和思考数学中的规律,并勉励他们尝试解决更复杂的问题。
评估:观察学生在探究和拓展环节中的表现,包括他们参与讨论的贡献、解释和设计的巧数图形。
评估的重点在于学生对巧数概念和图形规律的理解和应用能力。
拓展活动或作业建议:1. 给学生布置巧数图形的作业,让他们设计和绘制一个符合巧数规律的图形,并解释其特征和规律。
2. 鼓励学生在日常生活中观察巧数,并记录下他们发现的巧数图形或情况。
在下堂课中,学生可以分享他们的发现。
3. 给学生提供更多的巧数和图形问题,让他们进行推理和解决。
三年级奥数(40讲):三年级奥数答案

第1讲寻找规律一、知识要点按照一定次序排列起来的一列数,叫做数列。
如自然数列:1,2,3,4,……双数列:2,4,6,8,……我们研究数列,目的就是为了发现数列中数排列的规律,并依据这个规律来填写空缺的数。
按照一定的顺序排列的一列数,只要从连续的几个数中找到规律,那么就可以知道其余所有的数。
寻找数列的排列规律,除了从相邻两数的和、差考虑,有时还要从积、商考虑。
善于发现数列的规律是填数的关键。
二、精讲精练【例题1】在括号内填上合适的数。
(1)3,6,9,12,( 15 ),( 18 )(2)1,2,4,7,11,( 16),( 22)(3)2,6,18,54,( 162 ),( 486 )练习1:在括号内填上合适的数。
(1)2,4,6,8,10,(),()(2)1,2,5,10,17,(),()(3)2,8,32,128,(),()(4)1,5,25,125,(),()(5)12,1,10,1,8,1,(),()【答案】(1)12,14(2)26,37(3)512,2048(4)625,3125(5)6,1【例题2】先找出规律,再在括号里填上合适的数。
(1)15,2,12,2,9,2,( 6 ),( 2 )(2)21,4,18,5,15,6,( 12 ),( 7 )练习2:按规律填数。
(1)2,1,4,1,6,1,(),()(2)3,2,9,2,27,2,(),()(3)18,3,15,4,12,5,(),()(4)1,15,3,13,5,11,(),()(5)1,2,5,14,(),()【答案】(1)8,1(2)81,2(3)9,6(4)7,9(5)41,122【例题3】先找出规律,再在括号里填上合适的数。
(1)2,5,14,41,( 128)41+3×3×3×3 (2)252,124,60,28,( 6 )减4除2 (3)1,2,5,13,34,(89)34×3-13 (4)1,4,9,16,25,36,(49) 7×7练习3:按规律填数。
小学三年级奥数之难点:巧数图形

小学三年级奥数之难点:巧数图形李正堂—2008—12—25 图形问题说来一直是三年级的一个难点,很多学生第一次接触这种题型的时候总是喜欢去数,可是如果只仅仅是靠数,我相信那不是你所想要的,大家一定要学会在掌握规律的同时学会分析。
下面我们一起来剖析一些题目,希望对大家有些帮助:【铺垫】:【分析】:具体推理过程不详述,大家一定要记住:总的长方形数目解答过程:宽的基本线段数3,长的基本线段数2(1+2+3)×(1+2)=18所以共有18个长方形【巩固】:【分析】:方法很清楚,也很明确,关键是它是一个不规则图形,可以先将该图分为两部分:通过图形可以帮助我们理解:第一个图形中有长方形(1+2+3+4)×(1+2+3+4)=100个第二个图形中有长方形(1+2)×(1+2+3+4+5+6)=63个而它们重复的图形中有长方形(1+2)×(1+2+3+4)=30个所以原图中共有:100+63-30=133个长方形【拓展】含有两个★在内的由小正方形组成的长方形(含正方形)共有_____个【分析】:采用间接的方法也许会比较困难,不妨采用直接法进行求解。
(1)两层的情况长为2个正方形边长:1长为3个正方形边长:22层的情况长为4个正方形边长:3 共12个长为5个正方形边长:3长为6个正方形边长:2长为7个正方形边长:1(2)三层的情况三层的情况有两种,所以只需要考虑一种情况就可以求解了:长为2个正方形边长:1长为3个正方形边长:23层的情况长为4个正方形边长:3 共12个(2个)长为5个正方形边长: 3长为6个正方形边长:2长为7个正方形边长:1三层的情况共有12×2=24个(3)4层的情况长为2个正方形边长:1长为3个正方形边长:24层的情况长为4个正方形边长:3 共12个(2个)长为5个正方形边长: 3长为6个正方形边长:2长为7个正方形边长:1四层的情况共有12×2=24个(4)5层的情况长为2个正方形边长:1长为3个正方形边长:25层的情况长为4个正方形边长:3 共12个长为5个正方形边长:3长为6个正方形边长:2长为7个正方形边长:1所以总共有12+24+24+12=72个【总结】我想大家通过这样的讲解也可以找到一些规律了,分了层之后其实边长分法都一样,所以只需要看宽的情况,宽的情况(层的情况)共有(1+2+2+1)=6种情况,故总共有6×12=72大家一定要学会采用适当的方法进行求解!。
三年级奥数第五讲 巧数图形

三年级奥数第五讲巧数图形
一、知识要点
数图形要根据图形的特点,按照一定的顺序有条理地来数,分类是数图形的一种重要方法,合理有序的分类可以大大地节省我们数的时间,也能使我们做到不重复、不遗漏。
二、例题精讲
例1 数出下图中有多少条线段。
分析图1中,基本线段2条,两条组成的有1条,因此,图中的线段共有2+1=3(条)图2中的线段共有3+2+1=6条。
图3中共有4+3+2+1=10条不同的线段。
例2 数一数下图中各有多少个三角形?
分析这个图形由5个基本三角形组成,由2个基本三角形组成的图形有4个,由3个基本三角形组成的图形有3个,由4个基本三角形组成的图形有2个,由5个基本三角形组成的图形有1个,合起来一共有5+4+3+2+1=15(个)
策略小结: 数图形的个数时,总是从最基本的图形开始数起,接着由两个基本图形组成的图形,依次类推。
三、巩固练习:
1.数出下列图形中有多少条线段。
有()条线段
2、
有()个三角形
四、拓展与提高
1、
有()个三角形
2分别数出图中各图里的长方形(包括正方形)的个数。
3、图中有多少个小于180°的角?
分析解答:
以A、B、C、D、E、F为顶点的角:各有3个,共6×3=18(个);
以O为顶点的角:单个的角6个,由两个角构成的角有6个,
共12个;
因此小于180°的角共有:18+12=30(个)
答:图中有30个小于180°的角.。
三年级 奥数 第5讲 图形个数

第5讲 图形个数一、知识要点同学们,你想学会数图形的方法吗?要想不重复也不遗漏地数出线段、角、三角形、长方形……那就必须要有次序、有条理地数,从中发现规律,以便得到正确的结果。
要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,然后再数出由基本图形组成的新的图形,并求出它们的和。
二、精讲精练【例题1】数出下图中有多少条线段?【思路导航】方法一:我们可以采用以线段左端点分类数的方法。
以A 点为左端点的线段有:AB 、AC 、AD 3条;以B 点为左端点的线段有:BC 、BD 2条;以C 点为左端点的线段有:CD 1条。
所以,图中共有线段3+2+1=6(条)。
方法二:把图中线段 AB 、BC 、CD 看做基本线段来数,那么,由1条基本线段构成的线段有:AB 、BC 、CD 3条;由2条基本线段构成的线段有:AC 、BD 2条;由3条基本线段构成的线段有:AD 1条。
所以,图中一共有3+2+1=6(条)线段。
练习1:(1)数出下图中有多少条线段? (2)数出下图中有几个长方形?【例题2】数出图中有几个角?【思路导航】数角的个数可以采用与数线段相同的方法来数。
方法一:以OA 为一边的角有:∠AOB 、∠AOC 、∠AOD 3个;以OB 为一边的角还有: ∠BOC 、∠BOD 2个;以OC 为一边的角还有:∠COD 1个。
所以,图中共有角3+2+1=6(个)。
方法二:把图中∠AOB 、∠BOC 、∠COD 看做基本角来数,那么,由1个基本角构成的角有:∠AOB 、∠BOC 、∠COD 3个;由2个基本角构成的角有: ∠AOC 、∠BOD 2个;由3个基本角构成的角有:∠AOD 1个。
所以,图中一共有3+2+1=6(个)角。
EA B C D DABCODC BA练习2:数出图中有几个角? (1) (2)【例题3】数出右图中共有多少个三角形?【思路导航】方法一:我们可以采用按边分类数的方法。
第5讲 分类数图形小学三年级奥数讲义

第5讲分类数图形一、知识要点我们在数数的时候,遵循不重复、不遗漏的原则,不能使数出的结果准确。
但是在数图形的个数的时候,往往就不容易了。
分类数图形的方法能够帮助我们找到图形的规律,从而有秩序、有条理并且正确地数出图形的个数。
二、精讲精练【例题1】下面图形中有多少个正方形?【思路导航】图中的正方形的个数可以分类数,如由一个小正方形组成的有6×3=18个,2×2的正方形有5×2=10个,3×3的正方形有4×1=4个。
因此图中共有18+10+4=32个正方形。
练习1:1.下图中共有多少个正方形?2.下图中共有多少个正方形?3.下图中共有多少个正方形,多少个三角形?【例题2】下图中共有多少个三角形?【思路导航】为了保证不漏数又不重复,我们可以分类来数三角形,然后再把数出的各类三角形的个数相加。
(1)图中共有6个小三角形;(2)由两个小三角形组合的三角形有3个;(3)由三个小三角形组合的三角形有4个;(4)由六个小三角形组合的三角形有1个。
所以共有6+3+4+1=14个三角形。
练习2:1.下面图中共有多少个三角形?2.数一数,图中共有多少个三角形。
3.数一数,图中共有多少个三角形?【例题3】数出下图中所有三角形的个数。
【思路导航】和三角形AFG一样形状的三角形有5个;和三角形ABF一样形状的三角形有10个;和三角形ABG一样形状的三角形有5个;和三角形ABE一样形的三角形有5个;和三角形AMD一样形状的三角形有5个,共35个三角形。
练习3:数出下面图形中分别有多少个三角形。
【例题4】如下图,平面上有12个点,可任意取其中四个点围成一个正方形,这样的正方形有多少个?【思路导航】把相邻的两点连接起来可以得到下面图形,从图中可以看出:(1)最小的正方形有6个;(2)由4个小正方形组合而成的正方形有2个;(3)中间还可围成2个正方形。
所以共有6+2+2=10个。
三年级巧数图形 备课

——巧数图形
王 晨 妍
知识GPS教育经
历
前铺知识: 飞速图形计数——二年级 几何计数问题进阶——二年级
后续知识: 图形计数进阶——四年级
知识点梳教 理
育 经 历
巧数线段
巧数图形
巧数长 (正)方形
巧数三角形
数线段: 点数×(点数-1)÷2 或者 基本线段数× (基本线段数+1)÷2
数正方形: ✓ m×n 型(m>n) ✓ n×n方阵型
数长方形: 一条长的线段数×一条宽 的线段数
数三角形: ✓ 公式法: 基本三角形数× (基本三角形数+1)÷2 ✓ 枚举法: 从小到大,不重不漏
数线段教育经
历
对应例题:例1(竞赛/强化)
点数×(点数-1)÷2 基本线段数×(基本线段数+1)÷2
端点数:6 基本线段数:5
6×(6-1)÷2=15(条) 5×(5+1)÷2=15(条)
1~3每步1分,4步3分,全错5分全扣
随堂测试3
竞赛——分类【提示:先数1×3长方形】
练习册8、14
【解析】直角边为3和1的三角形,一共有8种摆放方式,每种方式 在图形里有8个三角形,一共有8×8=64(个)三角形 【批改标准】填空题,答案对满分,错了酌情扣分,最多扣5分
强化——公式【教师版有误】
历
对应例题:例2 ~ 5(竞赛) 例2 ~ 4(强化)
数长方形:
一条长的线段数×一条宽的线段数
长上线段数:6×(6-1)÷2=15(条) 宽上线段数:2×(2+1)÷2=3(条) 长方形个数:15×3=45(个)
数三角教形育经
历
对应例题:例6、7(竞赛) 例5、6(强化)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5讲 图形个数
一、知识要点
同学们,你想学会数图形的方法吗?要想不重复也不遗漏地数出线段、角、三角形、长方形……那就必须要有次序、有条理地数,从中发现规律,以便得到正确的结果。
要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,然后再数出由基本图形组成的新的图形,并求出它们的和。
二、精讲精练
【例题1】数出下图中有多少条线段?
练习1:
(1)数出下图中有多少条线段? (2)数出下图中有几个长方形?
【例题2】数出图中有几个角?
E A B C D D
A B C O D
C B
A
练习2:数出图中有几个角?
(1) (2)
【例题3】数出下图中共有多少个三角形?
练习3:数出图中共有多少个三角形?
(1)
(2)
O C B A
E
D O C B A P D C B A F
E A K G I H G A。
